Progressive Rehabilitation Based on EMG Gesture Classification and an MPC-Driven Exoskeleton
Abstract
1. Introduction
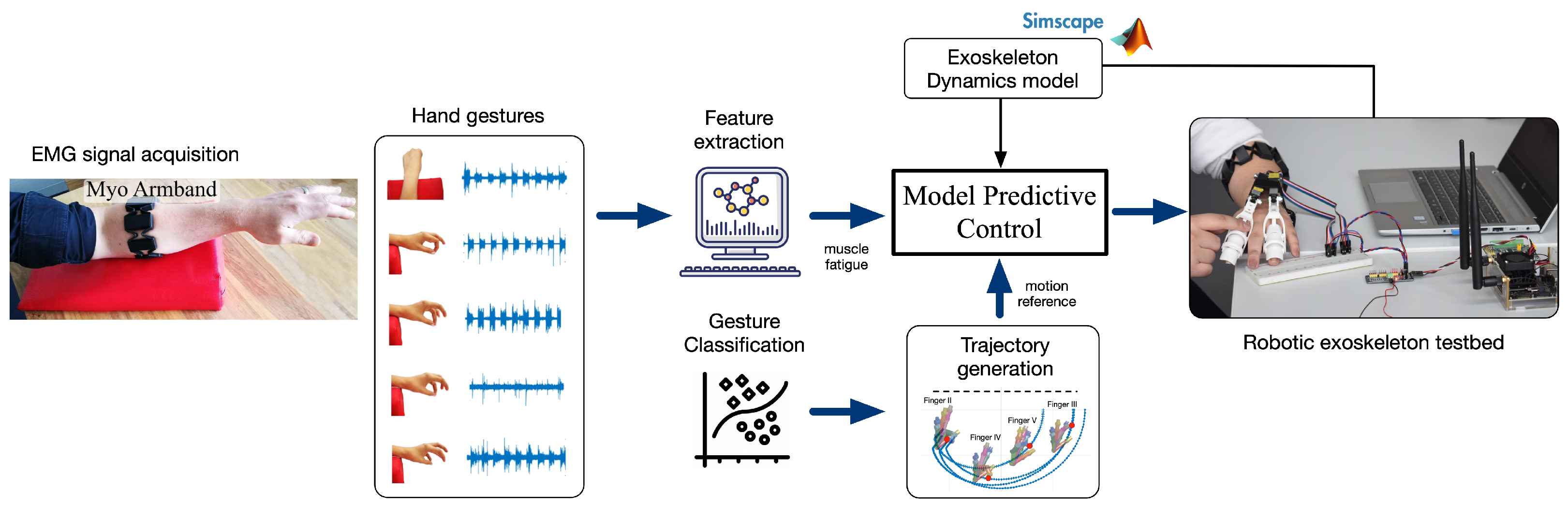
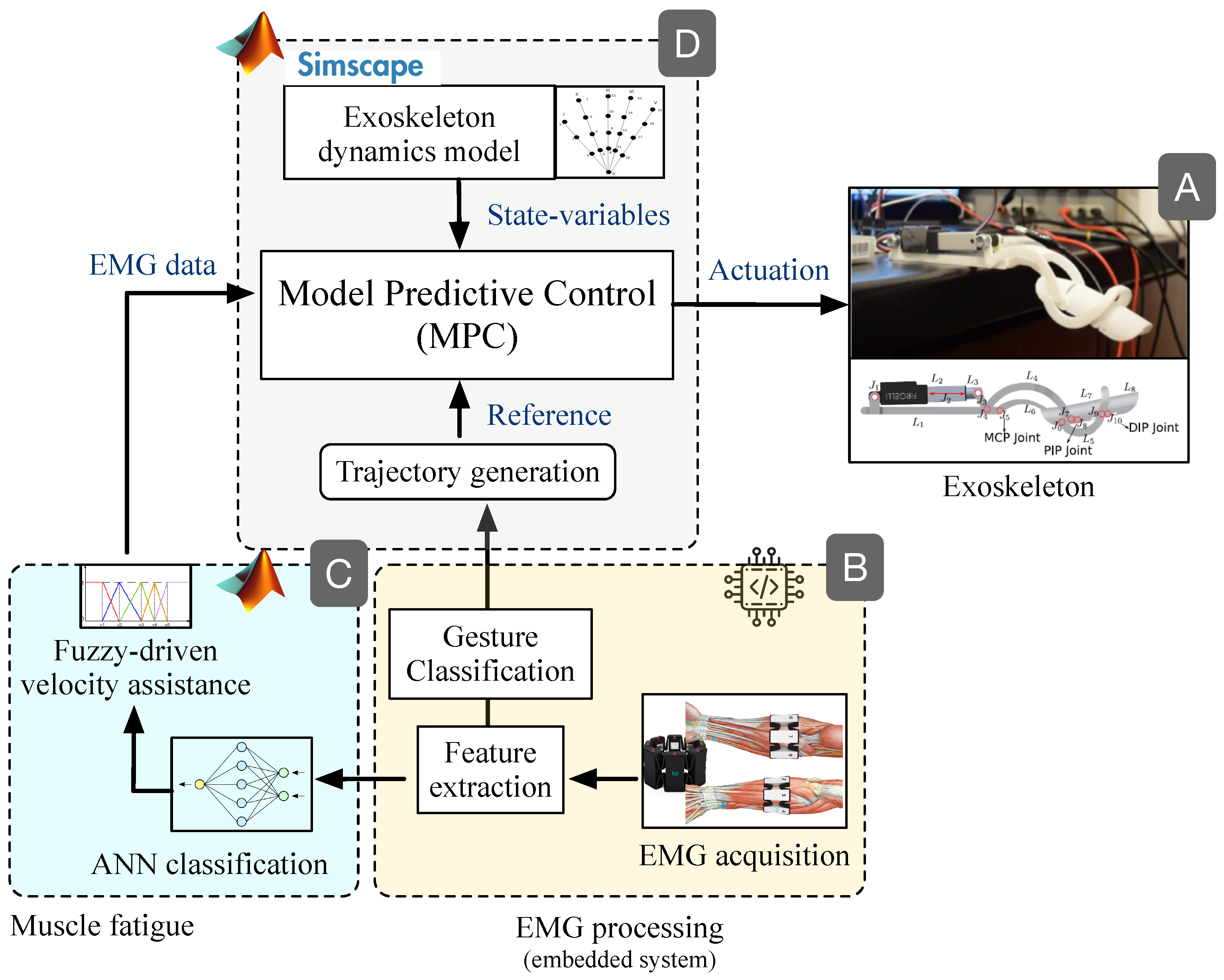
2. Materials and Methods
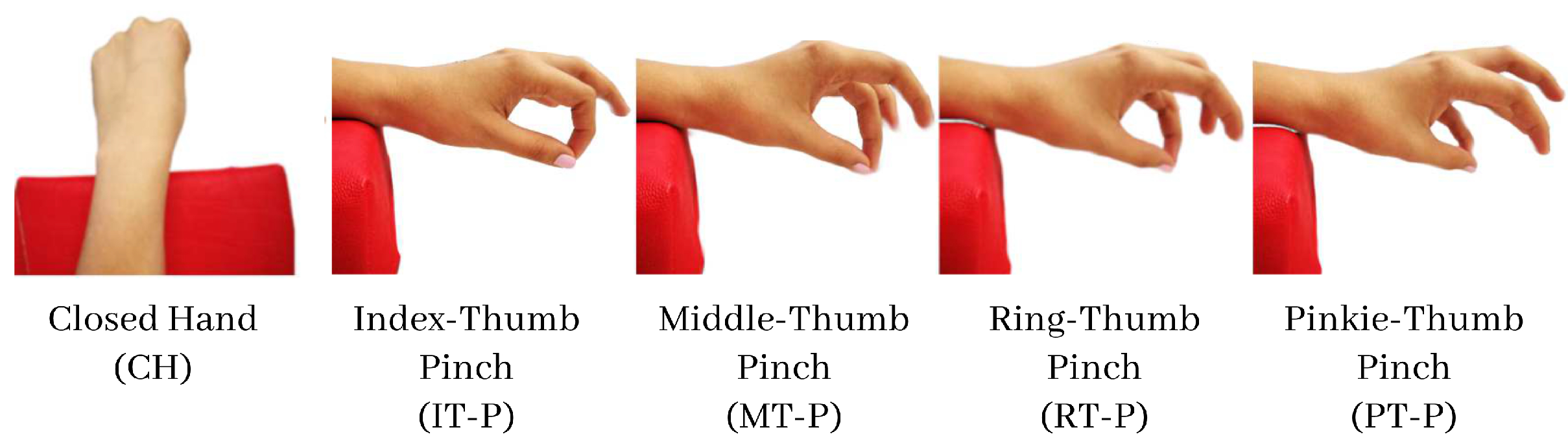
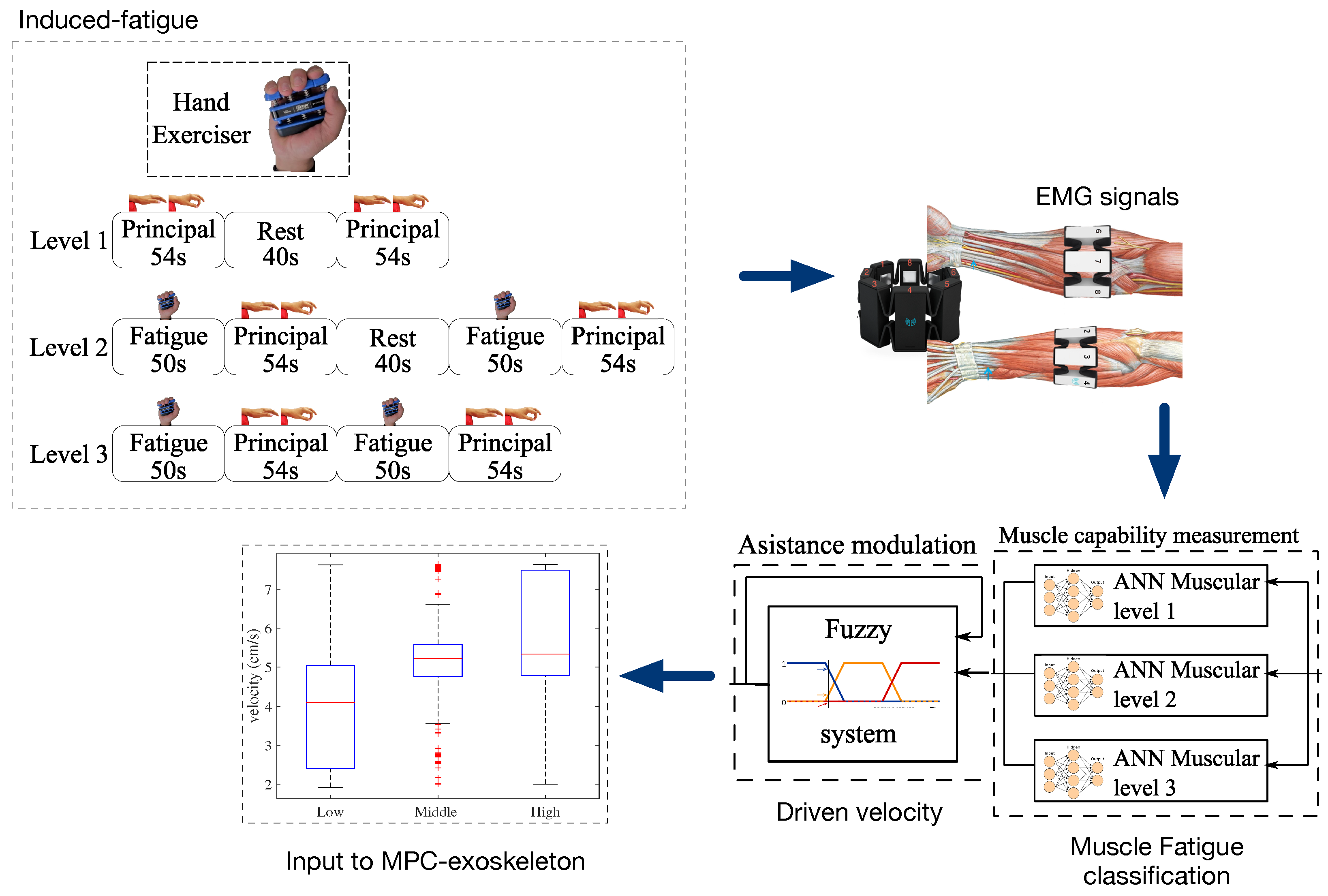
2.1. Data Acquisition
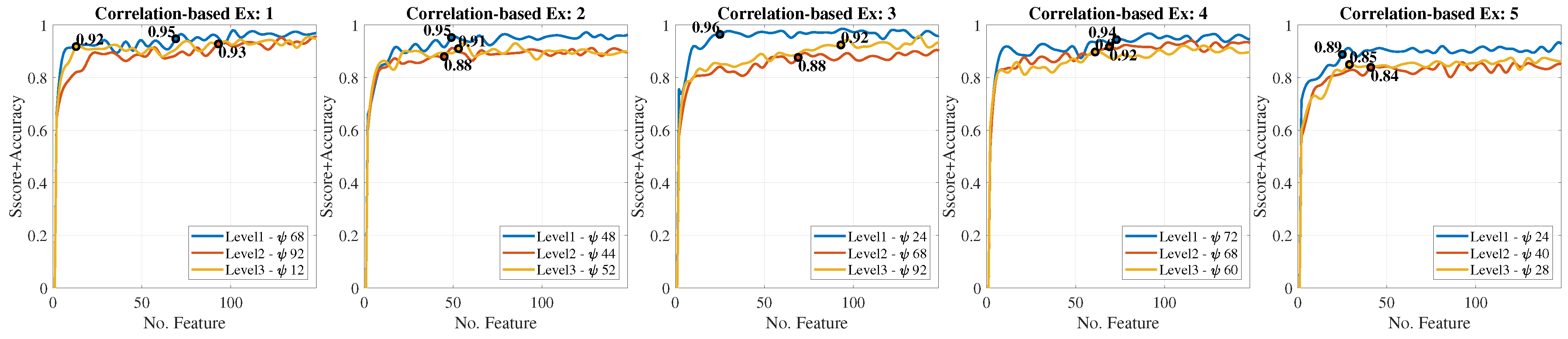
2.2. Feature Extraction
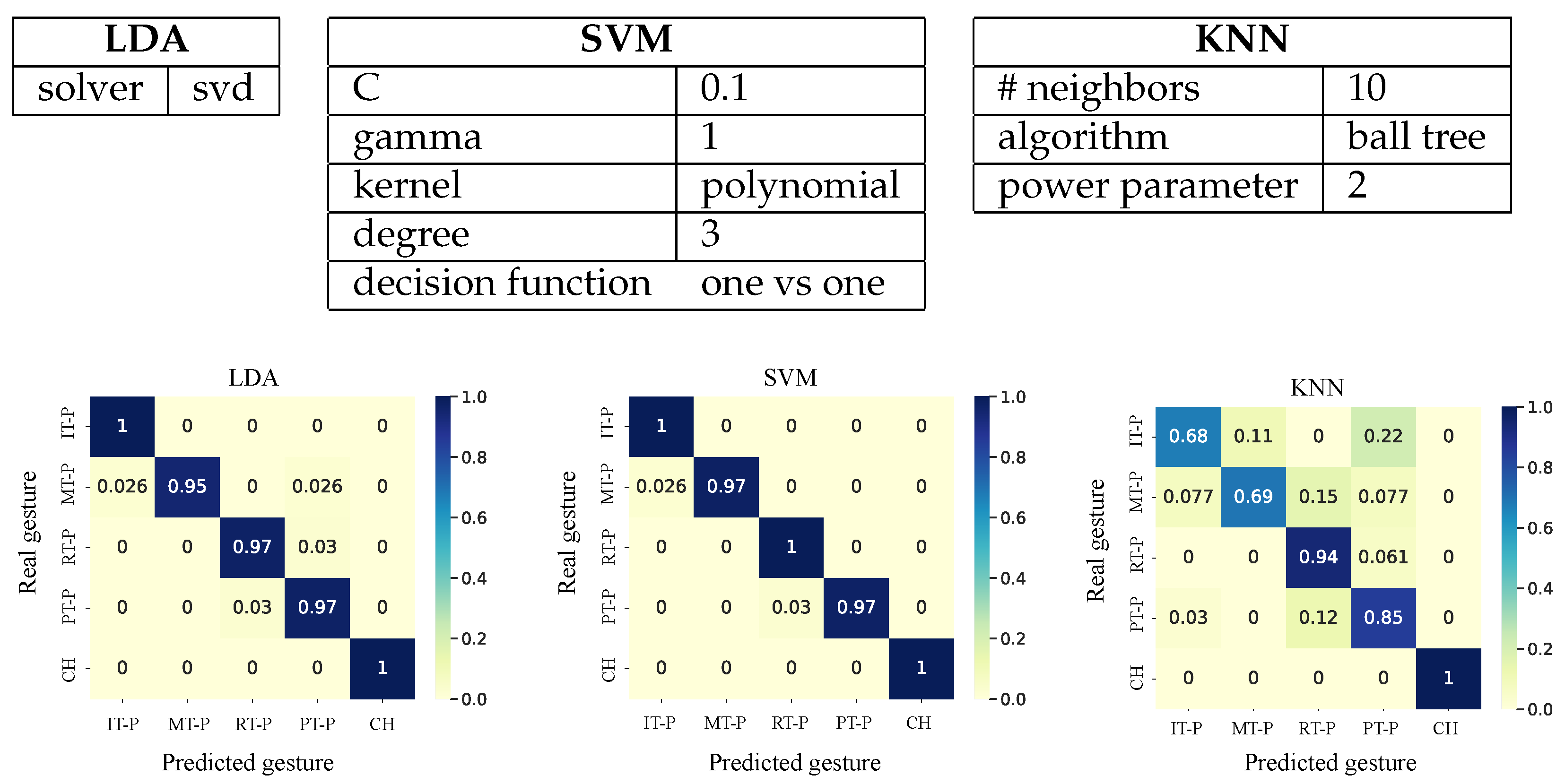
2.3. Gesture Classification
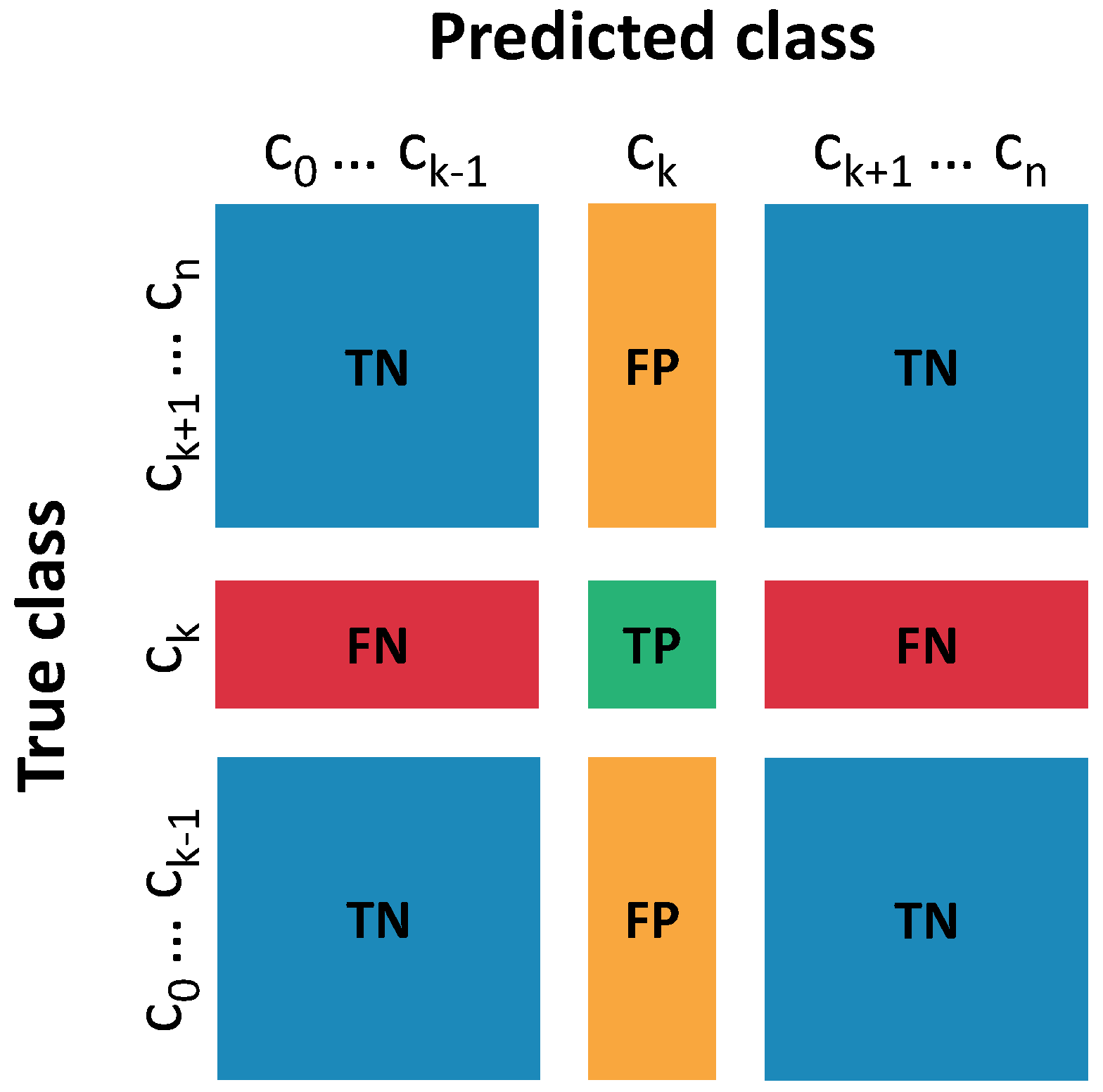
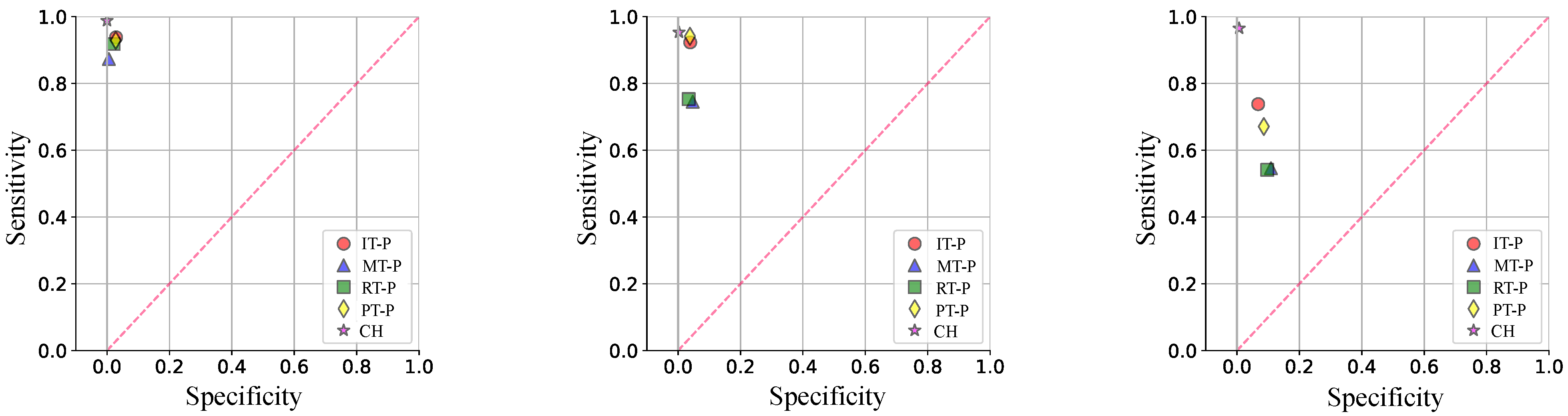
- Sensitivity:
- Specificity:
- Accuracy:
2.4. Exoskeleton
2.5. Muscle Fatigue
2.6. Model Predictive Control (MPC)
3. Results
3.1. Gesture Classification
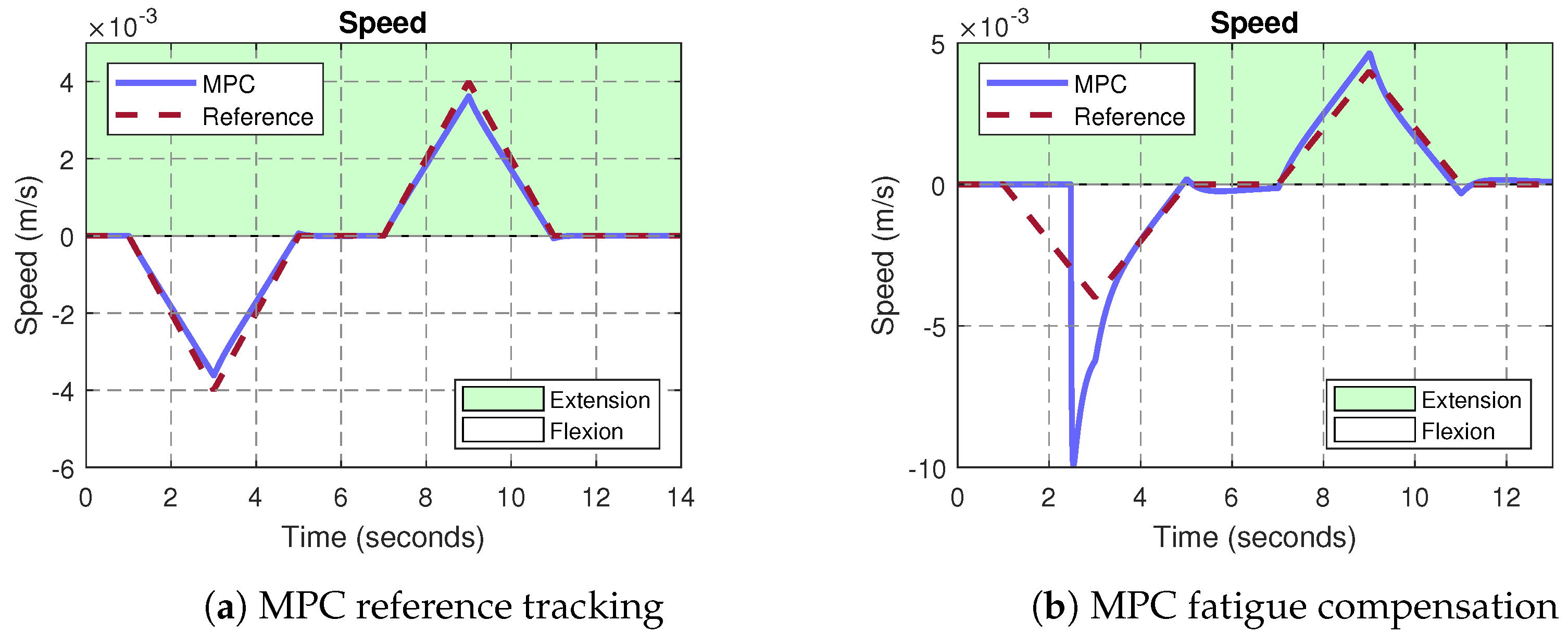
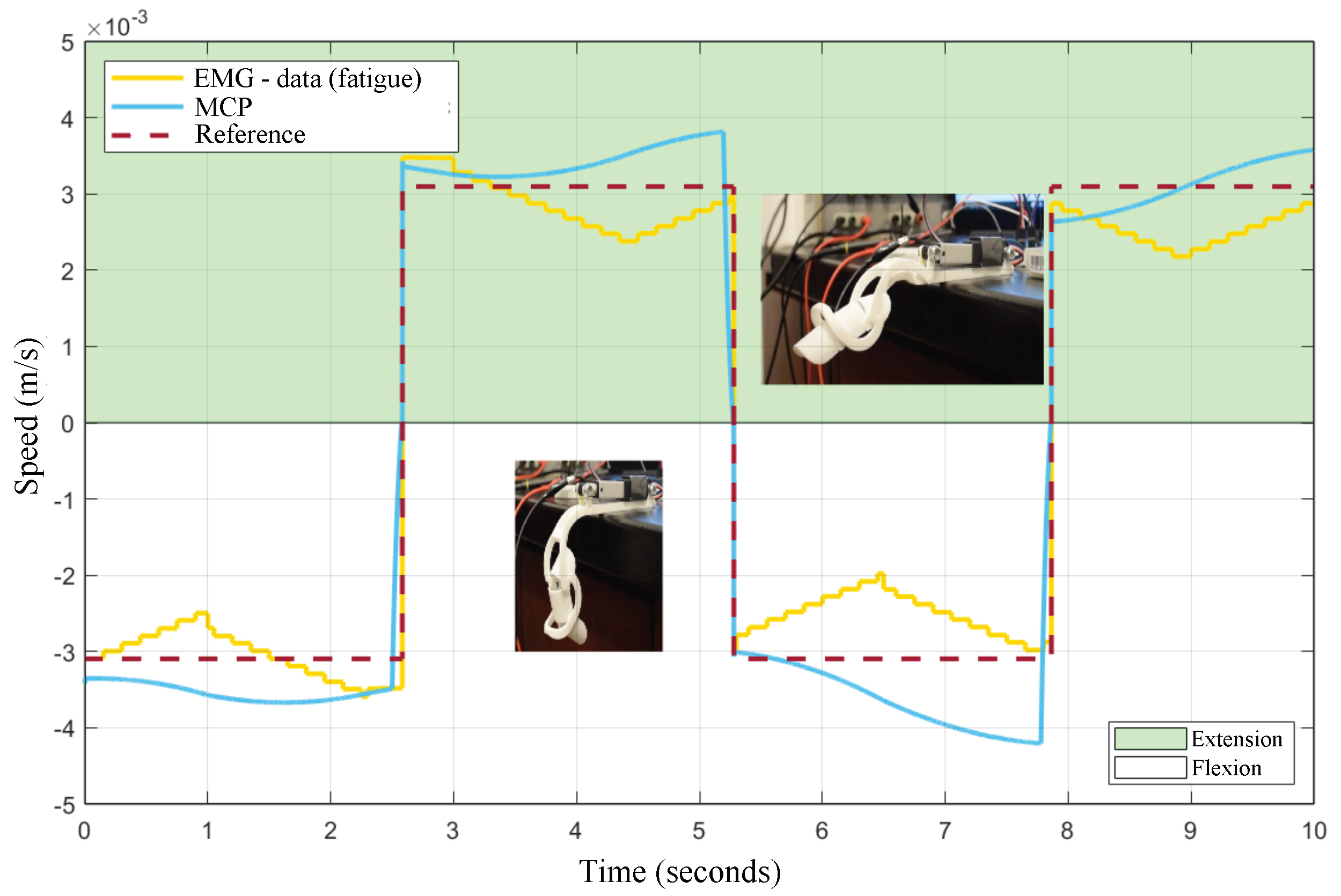
3.2. MPC Control of the Exoskeleton
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Morone, G.; Pichiorri, F. Post-Stroke Rehabilitation: Challenges and New Perspectives. J. Clin. Med. 2023, 12, 550. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. World Stroke Day 2022; Technical Report; World Health Organization: Geneva, Switzerland, 2022.
- Langhorne, P.; Coupar, F.; Pollock, A. Motor recovery after stroke: A systematic review. Lancet Neurol. 2009, 8, 741–754. [Google Scholar] [CrossRef] [PubMed]
- Hatem, S.M.; Saussez, G.; della Faille, M.; Prist, V.; Zhang, X.; Dispa, D.; Bleyenheuft, Y. Rehabilitation of motor function after stroke: A multiple systematic review focused on techniques to stimulate upper extremity recovery. Front. Hum. Neurosci. 2016, 10, 442. [Google Scholar] [CrossRef]
- Li, S. Spasticity, motor recovery, and neural plasticity after stroke. Front. Neurol. 2017, 8, 120. [Google Scholar] [CrossRef] [PubMed]
- Arteaga, M.V.; Castiblanco, J.C.; Mondragon, I.F.; Colorado, J.D.; Alvarado-Rojas, C. EMG-driven hand model based on the classification of individual finger movements. Biomed. Signal Process. Control 2020, 58, 101834. [Google Scholar] [CrossRef]
- Stinear, C.M. Prediction of motor recovery after stroke: Advances in biomarkers. Lancet Neurol. 2017, 16, 826–836. [Google Scholar] [CrossRef]
- Lee, K.B.; Lim, S.H.; Kim, K.H.; Kim, K.J.; Kim, Y.R.; Chang, W.N.; Yeom, J.W.; Kim, Y.D.; Hwang, B.Y. Six-month functional recovery of stroke patients: A multi-time-point study. Int. J. Rehabil. Res. 2015, 38, 173. [Google Scholar] [CrossRef]
- Sivan, M.; O’Connor, R.J.; Makower, S.; Levesley, M.; Bhakta, B. Systematic review of outcome measures used in the evaluation of robot-assisted upper limb exercise in stroke. J. Rehabil. Med. 2011, 43, 181–189. [Google Scholar] [CrossRef]
- Kim, W.S.; Cho, S.; Ku, J.; Kim, Y.; Lee, K.; Hwang, H.J.; Paik, N.J. Clinical application of virtual reality for upper limb motor rehabilitation in stroke: Review of technologies and clinical evidence. J. Clin. Med. 2020, 9, 3369. [Google Scholar] [CrossRef]
- Raghavan, P. The Nature of Hand Motor Impairment After Stroke and Its Treatment. Curr. Treat. Options Cardiovasc. Med. 2007, 9, 221–228. [Google Scholar] [CrossRef]
- Carey, L.M.; Matyas, T.A. Frequency of discriminative sensory loss in the hand after stroke in a rehabilitation setting. J. Rehabil. Med. 2011, 43, 257–263. [Google Scholar] [CrossRef]
- Asokan, A.; Vigneshwar, M. Design and Control of an EMG-based Low-cost Exoskeleton for Stroke Rehabilitation. In Proceedings of the 2019 Fifth Indian Control Conference (ICC), Delhi, India, 9–11 January 2019; pp. 478–483. [Google Scholar]
- Ullah, M.M.; Hafeez, U.; Shehzad, M.N.; Awais, M.N.; Elahi, H. A soft robotic glove for assistance and rehabilitation of stroke affected patients. In Proceedings of the 2019 International Conference on Frontiers of Information Technology (FIT), Islamabad, Pakistan, 16–18 December 2019; pp. 110–1105. [Google Scholar]
- Bouteraa, Y.; Abdallah, I.B.; Elmogy, A. Design and control of an exoskeleton robot with EMG-driven electrical stimulation for upper limb rehabilitation. Ind. Robot. Int. J. Robot. Res. Appl. 2020, 47, 489–501. [Google Scholar] [CrossRef]
- Micera, S.; Caleo, M.; Chisari, C.; Hummel, F.C.; Pedrocchi, A. Advanced Neurotechnologies for the Restoration of Motor Function. Neuron 2020, 105, 604–620. [Google Scholar] [CrossRef]
- Quinn, T.J.; Richard, E.; Teuschl, Y.; Gattringer, T.; Hafdi, M.; O’Brien, J.T.; Merriman, N.; Gillebert, C.; Huygelier, H.; Verdelho, A.; et al. European Stroke Organisation and European Academy of Neurology joint guidelines on post-stroke cognitive impairment. Eur. J. Neurol. 2021, 28, 3883–3920. [Google Scholar] [CrossRef]
- Landsmeer, J. Power grip and precision handling. Ann. Rheum. Dis. 1962, 21, 164. [Google Scholar] [CrossRef]
- Gustus, A.; Stillfried, G.; Visser, J.; Jörntell, H.; van der Smagt, P. Human hand modelling: Kinematics, dynamics, applications. Biol. Cybern. 2012, 106, 741–755. [Google Scholar] [CrossRef]
- Polygerinos, P.; Galloway, K.C.; Sanan, S.; Herman, M.; Walsh, C.J. EMG controlled soft robotic glove for assistance during activities of daily living. In Proceedings of the 2015 IEEE International Conference on Rehabilitation Robotics (ICORR), Singapore, 11–14 August 2015; pp. 55–60. [Google Scholar]
- Sultana, A.; Ahmed, F.; Alam, M.S. A systematic review on surface electromyography-based classification system for identifying hand and finger movements. Healthc. Anal. 2023, 3, 100126. [Google Scholar] [CrossRef]
- Naik, G.R.; Kumar, D.K. Identification of hand and finger movements using multi run ICA of surface electromyogram. J. Med. Syst. 2012, 36, 841–851. [Google Scholar] [CrossRef]
- Ariyanto, M.; Caesarendra, W.; Mustaqim, K.A.; Irfan, M.; Pakpahan, J.A.; Setiawan, J.D.; Winoto, A.R. Finger movement pattern recognition method using artificial neural network based on electromyography (EMG) sensor. In Proceedings of the 2015 International Conference on Automation, Cognitive Science, Optics, Micro Electro-Mechanical System, and Information Technology (ICACOMIT), Bandung, Indonesia, 29–30 October 2015; pp. 12–17. [Google Scholar]
- Zhang, Y.; Yang, F.; Fan, Q.; Yang, A.; Li, X. Research on sEMG-Based Gesture Recognition by Dual-View Deep Learning. IEEE Access 2022, 10, 32928–32937. [Google Scholar] [CrossRef]
- Tuncer, T.; Dogan, S.; Subasi, A. Novel finger movement classification method based on multi-centered binary pattern using surface electromyogram signals. Biomed. Signal Process. Control 2022, 71, 103153. [Google Scholar] [CrossRef]
- Baldacchino, T.; Jacobs, W.R.; Anderson, S.R.; Worden, K.; Rowson, J. Simultaneous force regression and movement classification of fingers via surface EMG within a unified Bayesian framework. Front. Bioeng. Biotechnol. 2018, 6, 13. [Google Scholar] [CrossRef] [PubMed]
- Sri-Iesaranusorn, P.; Chaiyaroj, A.; Buekban, C.; Dumnin, S.; Pongthornseri, R.; Thanawattano, C.; Surangsrirat, D. Classification of 41 hand and wrist movements via surface electromyogram using deep neural network. Front. Bioeng. Biotechnol. 2021, 9, 548357. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Yang, J.; Xie, H. Surface-electromyography-based gesture recognition using a multistream fusion strategy. IEEE Access 2021, 9, 50583–50592. [Google Scholar] [CrossRef]
- Lin, Y.; Palaniappan, R.; De Wilde, P.; Li, L. Reliability analysis for finger movement recognition with raw electromyographic signal by evidential convolutional networks. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 96–107. [Google Scholar] [CrossRef] [PubMed]
- Hudgins, B.; Parker, P.; Scott, R.N. A new strategy for multifunction myoelectric control. IEEE Trans. Biomed. Eng. 1993, 40, 82–94. [Google Scholar] [CrossRef] [PubMed]
- Oskoei, M.A.; Hu, H. Support vector machine-based classification scheme for myoelectric control applied to upper limb. IEEE Trans. Biomed. Eng. 2008, 55, 1956–1965. [Google Scholar] [CrossRef]
- Zhang, D.; Xiong, A.; Zhao, X.; Han, J. PCA and LDA for EMG-based control of bionic mechanical hand. In Proceedings of the 2012 IEEE International Conference on Information and Automation, Chengdu, China, 5–8 August 2012; pp. 960–965. [Google Scholar]
- Jiralerspong, T.; Nakanishi, E.; Liu, C.; Ishikawa, J. Experimental study of real-time classification of 17 voluntary movements for multi-degree myoelectric prosthetic hand. Appl. Sci. 2017, 7, 1163. [Google Scholar] [CrossRef]
- Azhiri, R.B.; Esmaeili, M.; Jafarzadeh, M.; Nourani, M. Emg signal classification using reflection coefficients and extreme value machine. In Proceedings of the 2021 IEEE Biomedical Circuits and Systems Conference (BioCAS), Virtual, 7–9 October 2021; pp. 1–6. [Google Scholar]
- Phinyomark, A.; Limsakul, C.; Phukpattaranont, P. Application of wavelet analysis in EMG feature extraction for pattern classification. Meas. Sci. Rev. 2011, 11, 45–52. [Google Scholar] [CrossRef]
- Shen, S.; Gu, K.; Chen, X.R.; Yang, M.; Wang, R.C. Movements classification of multi-channel sEMG based on CNN and stacking ensemble learning. IEEE Access 2019, 7, 137489–137500. [Google Scholar] [CrossRef]
- Ozdemir, M.A.; Kisa, D.H.; Guren, O.; Onan, A.; Akan, A. Emg based hand gesture recognition using deep learning. In Proceedings of the 2020 Medical Technologies Congress (TIPTEKNO), Antalya, Turkey, 19–20 November 2020; pp. 1–4. [Google Scholar]
- Ahmad, J.; Butt, A.M.; Hussain, M.; Akbar, M.A.; Rehman, W.U. The deep neural network based classification of fingers pattern using electromyography. In Proceedings of the 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 25–27 May 2018; pp. 455–461. [Google Scholar]
- Cipriani, C.; Antfolk, C.; Controzzi, M.; Lundborg, G.; Rosén, B.; Carrozza, M.C.; Sebelius, F. Online myoelectric control of a dexterous hand prosthesis by transradial amputees. IEEE Trans. Neural Syst. Rehabil. Eng. 2011, 19, 260–270. [Google Scholar] [CrossRef]
- Adewuyi, A.A.; Hargrove, L.J.; Kuiken, T.A. An analysis of intrinsic and extrinsic hand muscle EMG for improved pattern recognition control. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 24, 485–494. [Google Scholar] [CrossRef]
- Al-Timemy, A.H.; Bugmann, G.; Escudero, J.; Outram, N. Classification of finger movements for the dexterous hand prosthesis control with surface electromyography. IEEE J. Biomed. Health Inform. 2013, 17, 608–618. [Google Scholar] [CrossRef]
- Wahid, M.F.; Tafreshi, R.; Al-Sowaidi, M.; Langari, R. Subject-independent hand gesture recognition using normalization and machine learning algorithms. J. Comput. Sci. 2018, 27, 69–76. [Google Scholar] [CrossRef]
- Gautam, A.; Panwar, M.; Wankhede, A.; Arjunan, S.P.; Naik, G.R.; Acharyya, A.; Kumar, D.K. Locomo-net: A low-complex deep learning framework for sEMG-based hand movement recognition for prosthetic control. IEEE J. Transl. Eng. Health Med. 2020, 8, 1–12. [Google Scholar] [CrossRef]
- Castiblanco, J.C.; Mondragon, I.F.; Alvarado-Rojas, C.; Colorado, J.D. Assist-as-needed exoskeleton for hand joint rehabilitation based on muscle effort detection. Sensors 2021, 21, 4372. [Google Scholar] [CrossRef]
- Miao, Q.; Zhang, M.; Cao, J.; Xie, S.Q. Reviewing high-level control techniques on robot-assisted upper-limb rehabilitation. Adv. Robot. 2018, 32, 1253–1268. [Google Scholar] [CrossRef]
- Agarwal, P.; Deshpande, A.D. Subject-specific assist-as-needed controllers for a hand exoskeleton for rehabilitation. IEEE Robot. Autom. Lett. 2017, 3, 508–515. [Google Scholar] [CrossRef]
- Kaplanoglu, E.; Akgun, G. Data-Driven Predictive Control of Exoskeleton for Hand Rehabilitation with Subspace Identification. Sensors 2022, 22, 7645. [Google Scholar] [CrossRef]
- Schieber, M.H.; Lang, C.; Reilly, K.; McNulty, P.; Sirigu, A. Selective activation of human finger muscles after stroke or amputation. In Progress in Motor Control: A Multidisciplinary Perspective, Advances in Experimental Medicine and Biology; Springer: Boston, MA, USA, 2009; Volume 629, pp. 559–575. [Google Scholar]
- Borboni, A.; Mor, M.; Faglia, R. Gloreha—hand robotic rehabilitation: Design, mechanical model, and experiments. J. Dyn. Syst. Meas. Control 2016, 138, 111003. [Google Scholar] [CrossRef]
- Jiang, J.; Min, Z.; Ma, X.; Zhang, Y.; Song, S. Application of robot to hand function rehabilitation. Recent Pat. Mech. Eng. 2018, 11, 2–14. [Google Scholar] [CrossRef]
- Castiblanco, J.C.; Ortmann, S.; Mondragon, I.F.; Alvarado-Rojas, C.; Jöbges, M.; Colorado, J.D. Myoelectric pattern recognition of hand motions for stroke rehabilitation. Biomed. Signal Process. Control 2020, 57, 101737. [Google Scholar] [CrossRef]
- Cui, L.; Phan, A.; Allison, G. Design and fabrication of a three dimensional printable non-assembly articulated hand exoskeleton for rehabilitation. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 4627–4630. [Google Scholar] [CrossRef]
- Castiblanco, J.C.; Arteaga, M.V.; Mondragon, I.F.; Ortmann, S.; Alvarado-Rojas, C.; Colorado, J.D. Velocity modulation assistance for stroke rehabilitation based on EMG muscular condition. In Proceedings of the 2020 8th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), New York, NY, USA, 29 November–1 December 2020; pp. 509–514. [Google Scholar] [CrossRef]
- Tahamipour-Z, S.; Sani, S.H.; Akbarzadeh, A.; Kardan, I. An assistive strategy for compliantly actuated exoskeletons using non-linear model predictive control method. In Proceedings of the Iranian Conference on Electrical Engineering (ICEE), Mashhad, Iran, 8–10 May 2018; pp. 982–987. [Google Scholar]
- Clarke, D. Adaptive predictive control. Annu. Rev. Control 1996, 20, 83–94. [Google Scholar] [CrossRef]
- Arteaga, M.V.; Castiblanco, J.C.; Mondragon, I.F.; Colorado, J.D.; Alvarado-Rojas, C. EMG-based adaptive trajectory generation for an exoskeleton model during hand rehabilitation exercises. In Proceedings of the 2020 8th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), New York, NY, USA, 29 November–1 December 2020; pp. 416–421. [Google Scholar] [CrossRef]
- Al-Mulla, M.R.; Sepulveda, F.; Colley, M. A review of non-invasive techniques to detect and predict localised muscle fatigue. Sensors 2011, 11, 3545–3594. [Google Scholar] [CrossRef] [PubMed]
- Ertl, P.; Kruse, A.; Tilp, M. Detecting fatigue thresholds from electromyographic signals: A systematic review on approaches and methodologies. J. Electromyogr. Kinesiol. 2016, 30, 216–230. [Google Scholar] [CrossRef]
- Han, H.; Jo, S.; Kim, J. Comparative study of a muscle stiffness sensor and electromyography and mechanomyography under fatigue conditions. Med. Biol. Eng. Comput. 2015, 53, 577–588. [Google Scholar] [CrossRef]
- Kuthe, C.D.; Uddanwadiker, R.V.; Ramteke, A.A. Surface electromyography based method for computing muscle strength and fatigue of biceps brachii muscle and its clinical implementation. Inform. Med. Unlocked 2018, 12, 34–43. [Google Scholar] [CrossRef]
- Zeng, J.; Zhou, Y.; Yang, Y.; Yan, J.; Liu, H. Fatigue-Sensitivity Comparison of sEMG and A-Mode Ultrasound based Hand Gesture Recognition. IEEE J. Biomed. Health Inform. 2022, 26, 1718–1725. [Google Scholar] [CrossRef]
- Forman, G.N.; Sonne, M.W.; Kociolek, A.M.; Gabriel, D.A.; Holmes, M.W. Influence of muscle fatigue on motor task performance of the hand and wrist: A systematic review. Hum. Mov. Sci. 2022, 81, 102912. [Google Scholar] [CrossRef]
| Feature | Formulation |
|---|---|
| Mean Absolute Value (MAV) | |
| Willison amplitude (WAMP) | |
| Variance (VAR) | |
| Waveform length (WL) | |
| Zero-crossing (ZC) |
| Acronym | Name | Domain | # Feat. | Equation |
|---|---|---|---|---|
| Cumulative integration | time | 1 | ||
| Zero crossing | time | 1 | ||
| Multiple time window | time | 6 | ||
| Contraction force muscular | time | 1 | ||
| Muscle co-activation | time | 28 | ||
| Average of spectral density | frequency | 1 | ||
| Mean frequency | frequency | 1 | ||
| Median frequency | frequency | 1 | ||
| Power rate | frequency | 1 |
| Parameter | Value | Additional Considerations |
|---|---|---|
| Sample Time (ts) | 0.001 s | The plant works at that sample time. |
| Prediction Horizon (HP) | 20 | |
| Control Horizon (HC) | 2 | The higher its value, better response but greater the computational load. |
| Constraints (C-MV and C-MO) | C-MV = −inf,inf C-MO = −0.007, 0.007 ms | Soft constraints:
can leave the range minimally Hard constraints: cannot leave the range Recommended: not all constraints hard, optimal mathematical expression could not be found. |
| Weights (W-MV and W-MO) | W-MV = 0 and W-MO = 0.135 | Controls the deviation of the manipulated variable from the reference. |
| State-Estimator (SE) | Faster or slower | Faster: faster response and shorter settling time, but higher computational load. |
| Close-loop performance (CLP) | Robust or aggressive | Robust: less peak and allows for smoother towards the reference. Aggressive: Movement more abrupt. |
| Training | Test | |||||
|---|---|---|---|---|---|---|
| Sen. | Spe. | Acc. | Sen. | Spe. | Acc. | |
| Volunteer 1 | ||||||
| Volunteer 2 | ||||||
| Volunteer 3 | ||||||
| Volunteer 4 | ||||||
| Volunteer 5 | ||||||
| Average | ||||||
| Position | Speed | |
|---|---|---|
| 2 mm/s | 1.7161 × 10 | 3.5368 × 10 |
| 3 mm/s | 1.7062 × 10 | 4.1654 × 10 |
| 4 mm/s | 1.7617 × 10 | 4.5063 × 10 |
| 5 mm/s | 1.8025 × 10 | 4.7184 × 10 |
| 6 mm/s | 1.8367 × 10 | 4.8616 × 10 |
| 7 mm/s | 1.8631 × 10 | 4.9636 × 10 |
| Simulation Results | Experimental Results | |||
|---|---|---|---|---|
| Non-Muscle Fatigue | Muscle Fatigue | Non-Muscle Fatigue | Muscle Fatigue | |
| Correlation | Flexion = Extension = | Flexion = Extension = | Flexion = Extension = | Flexion = 0.91 Extension = 0.95 |
| MSE | 8.94 × 10 | 2.57 × 10 | 9.48 × 10 | 1.01 × 10 |
| RMSE | 9.45 × 10 | 1.60 × 10 | 9.74 × 10 | 1.00 × 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonilla, D.; Bravo, M.; Bonilla, S.P.; Iragorri, A.M.; Mendez, D.; Mondragon, I.F.; Alvarado-Rojas, C.; Colorado, J.D. Progressive Rehabilitation Based on EMG Gesture Classification and an MPC-Driven Exoskeleton. Bioengineering 2023, 10, 770. https://doi.org/10.3390/bioengineering10070770
Bonilla D, Bravo M, Bonilla SP, Iragorri AM, Mendez D, Mondragon IF, Alvarado-Rojas C, Colorado JD. Progressive Rehabilitation Based on EMG Gesture Classification and an MPC-Driven Exoskeleton. Bioengineering. 2023; 10(7):770. https://doi.org/10.3390/bioengineering10070770
Chicago/Turabian StyleBonilla, Daniel, Manuela Bravo, Stephany P. Bonilla, Angela M. Iragorri, Diego Mendez, Ivan F. Mondragon, Catalina Alvarado-Rojas, and Julian D. Colorado. 2023. "Progressive Rehabilitation Based on EMG Gesture Classification and an MPC-Driven Exoskeleton" Bioengineering 10, no. 7: 770. https://doi.org/10.3390/bioengineering10070770
APA StyleBonilla, D., Bravo, M., Bonilla, S. P., Iragorri, A. M., Mendez, D., Mondragon, I. F., Alvarado-Rojas, C., & Colorado, J. D. (2023). Progressive Rehabilitation Based on EMG Gesture Classification and an MPC-Driven Exoskeleton. Bioengineering, 10(7), 770. https://doi.org/10.3390/bioengineering10070770








