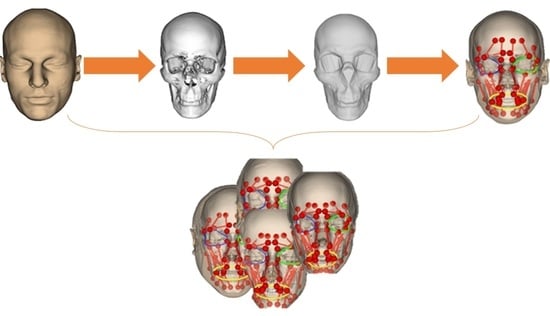
Novel Baseline Facial Muscle Database Using Statistical Shape Modeling and In Silico Trials toward Decision Support for Facial Rehabilitation
Abstract
1. Introduction
2. Materials and Methods
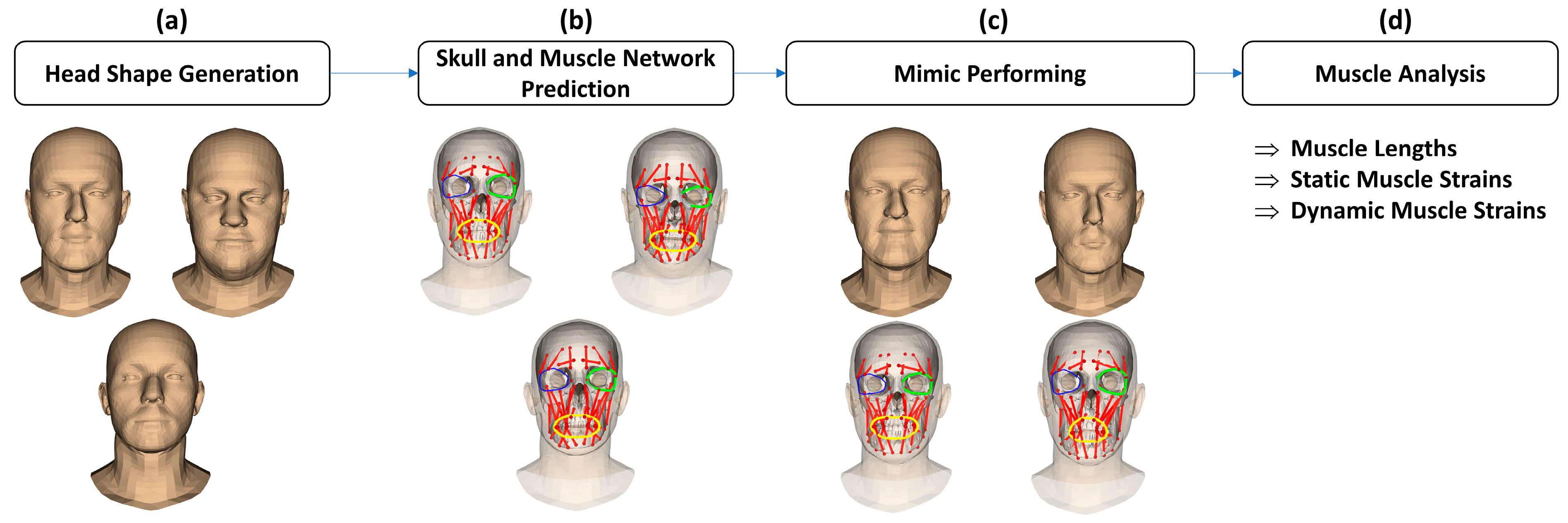
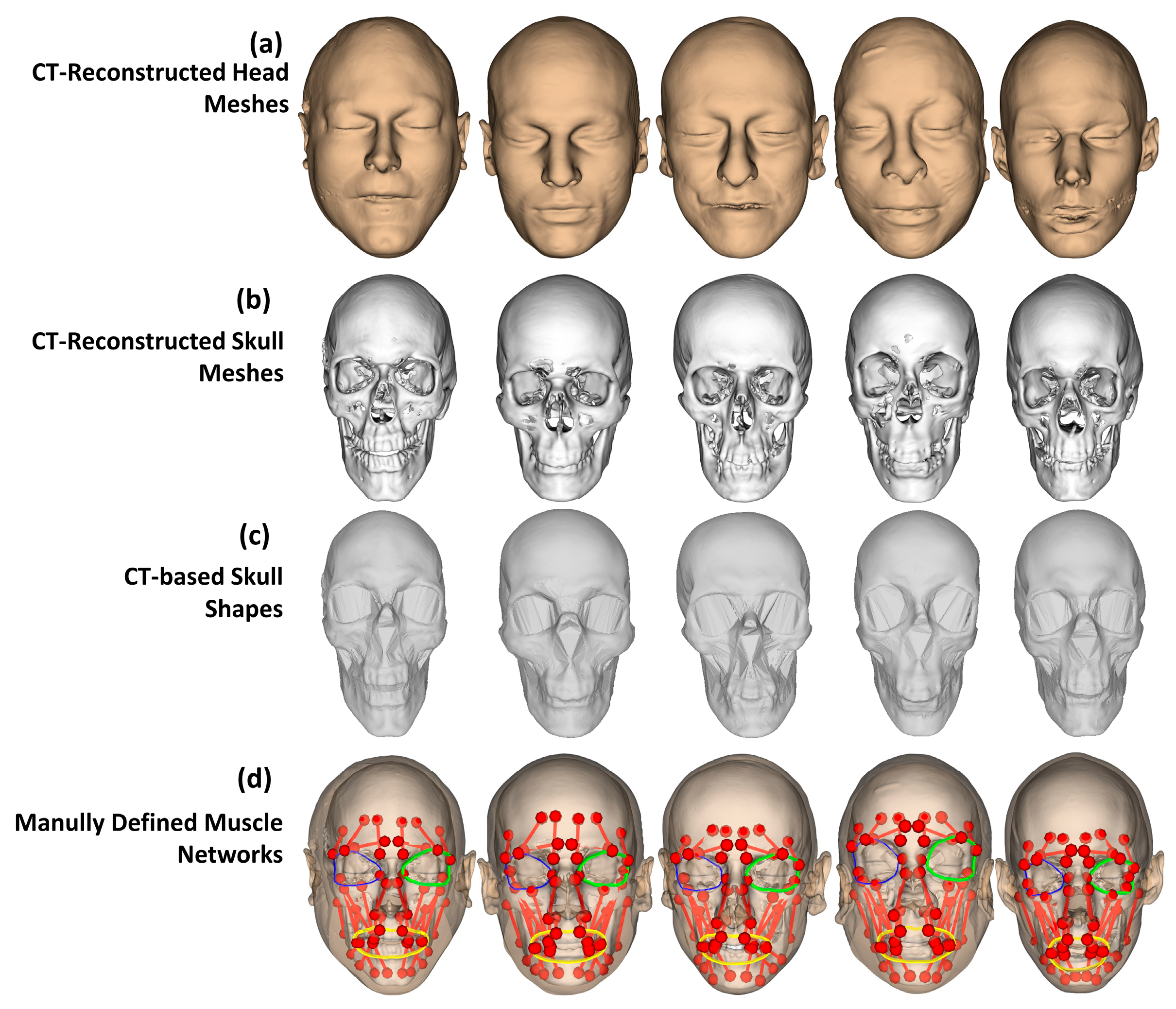
2.1. Overall Processing Workflow
- (a)
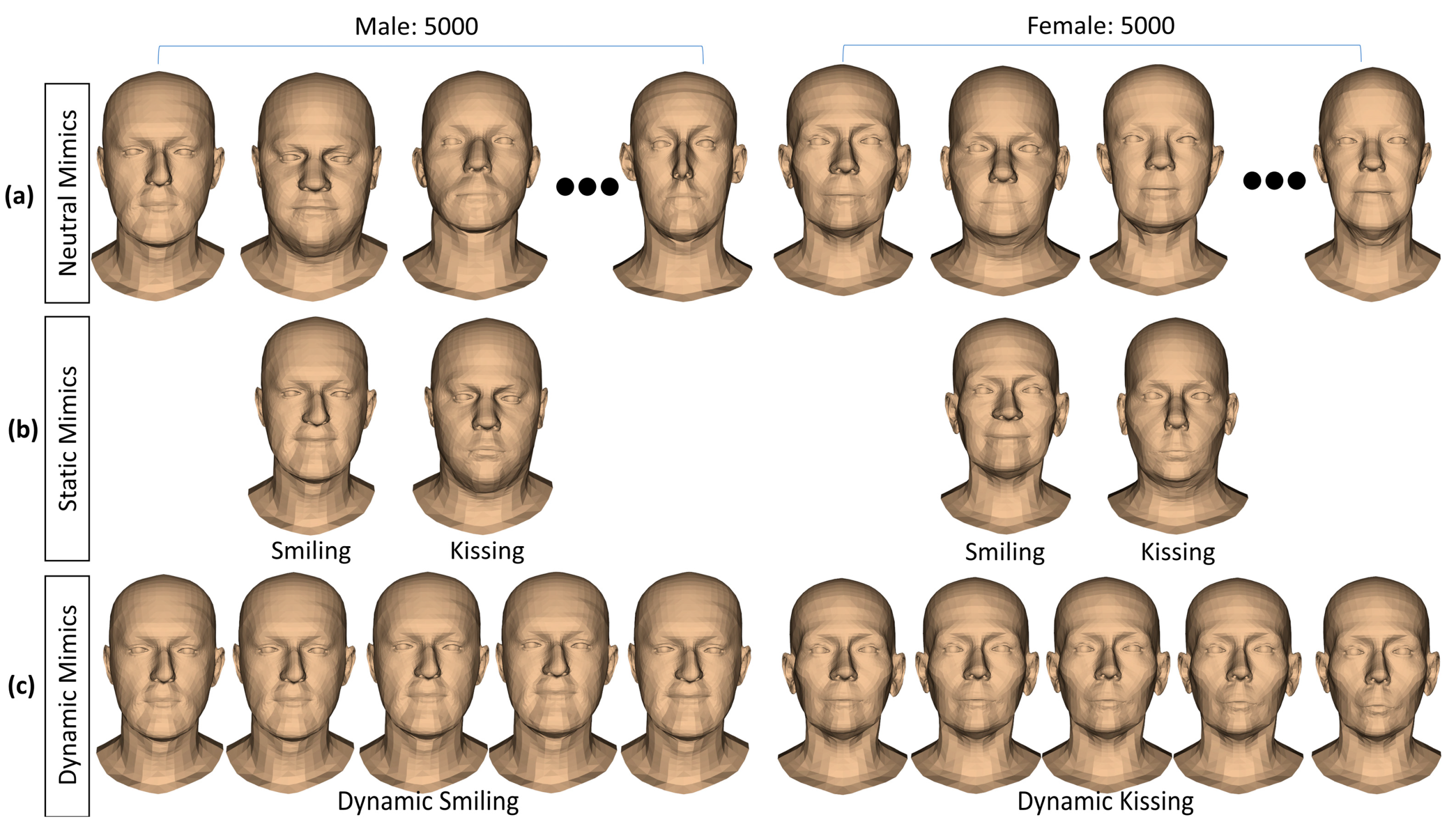
- Regarding head shape generation, we use the SSM head model, Faces Learned with an Articulated Model and Expressions (FLAME) [43], for generating variations in virtual subjects by controlling the FLAME shape parameters. The other parameter sets including translations, rotations, poses, and expressions were kept all to zeros to be on the neutral mimic positions. The details of this step are explained in Section 2.2.
- (b)
- Regarding the skull and muscle network prediction, based on the head shape of each virtual subject, a skull mesh was predicted thanks to our developed SSM-based head-to-skull prediction method [43]. Moreover, a muscle network including linear and circle muscles was defined as action lines connected from muscle attachment points on the skull mesh to the muscle insertion points on the head mesh. The insertion and attachment points were positioned based on their vertex indices on the head and skull meshes. This processing step is clearly explained in Section 2.3.
- (c)
- Regarding mimic performing, we controlled the expression and pose parameters of the FLAME model to perform smiling and kissing mimics on each virtual subject. In the static mimics, we set the max values on the smiling and kissing control parameters. In the dynamic mimics, we set these parameters from zero to their max values with the step size of 1/200 of these max values. The details are explained in Section 2.4.
- (d)
- Regarding muscle analysis, because the mesh structures of the head and skull meshes do not change during the non-rigid animations, muscle insertion, and attachment points were automatically updated according to the motions of head and skull vertices. Consequently, muscle lengths could also be computed according to the updated insertion and attachment points. Muscle strains were computed as relative differences between the muscle lengths in the current mimics and those in the neutral mimics. In this study, muscle strains of both static and dynamic mimics were computed and reported. The details are presented in Section 2.4.
2.2. Subject Identity and Mimic Generation
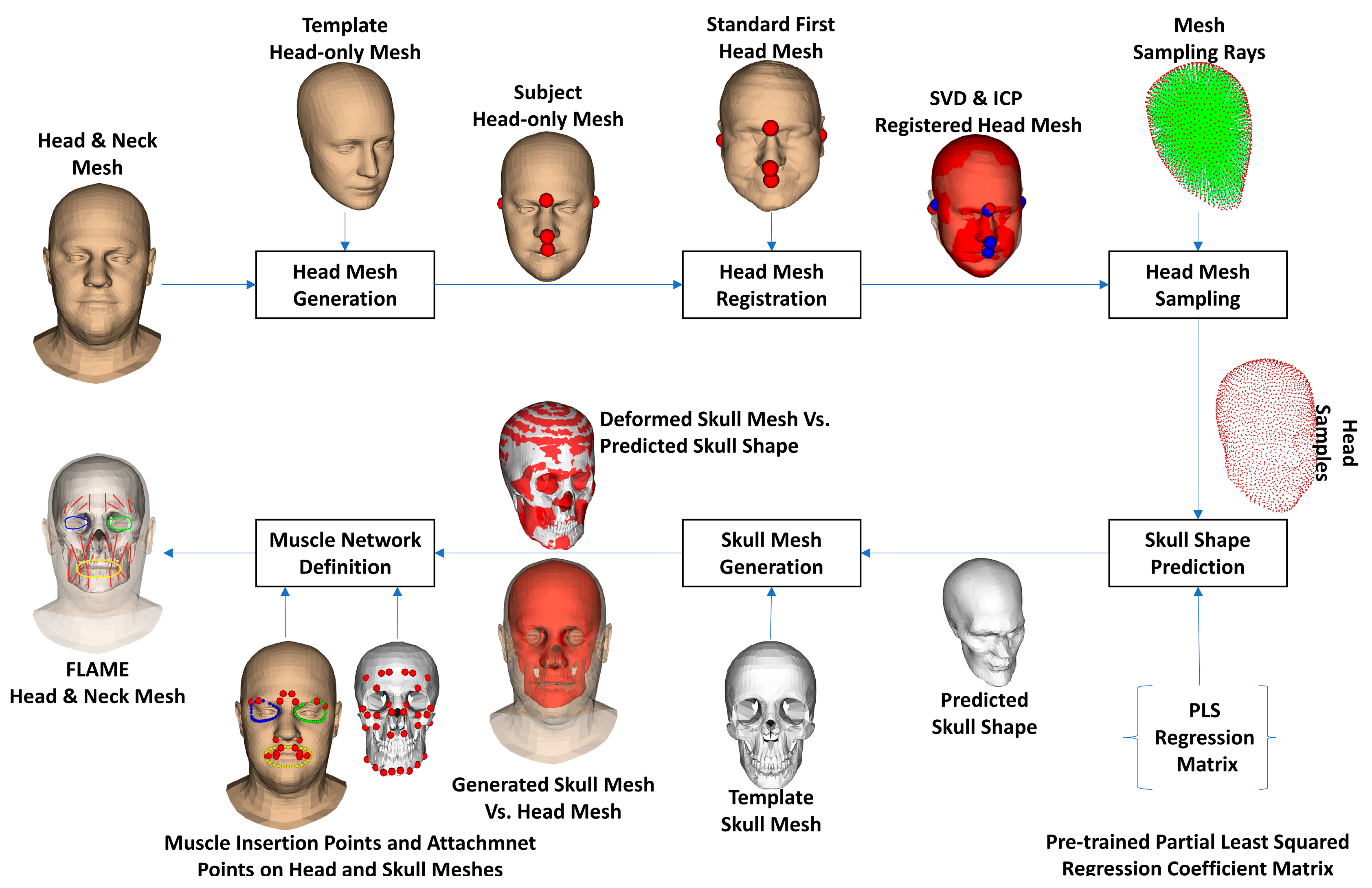
2.3. Skull and Muscle Network Generation
2.4. Muscle-Based Analyses
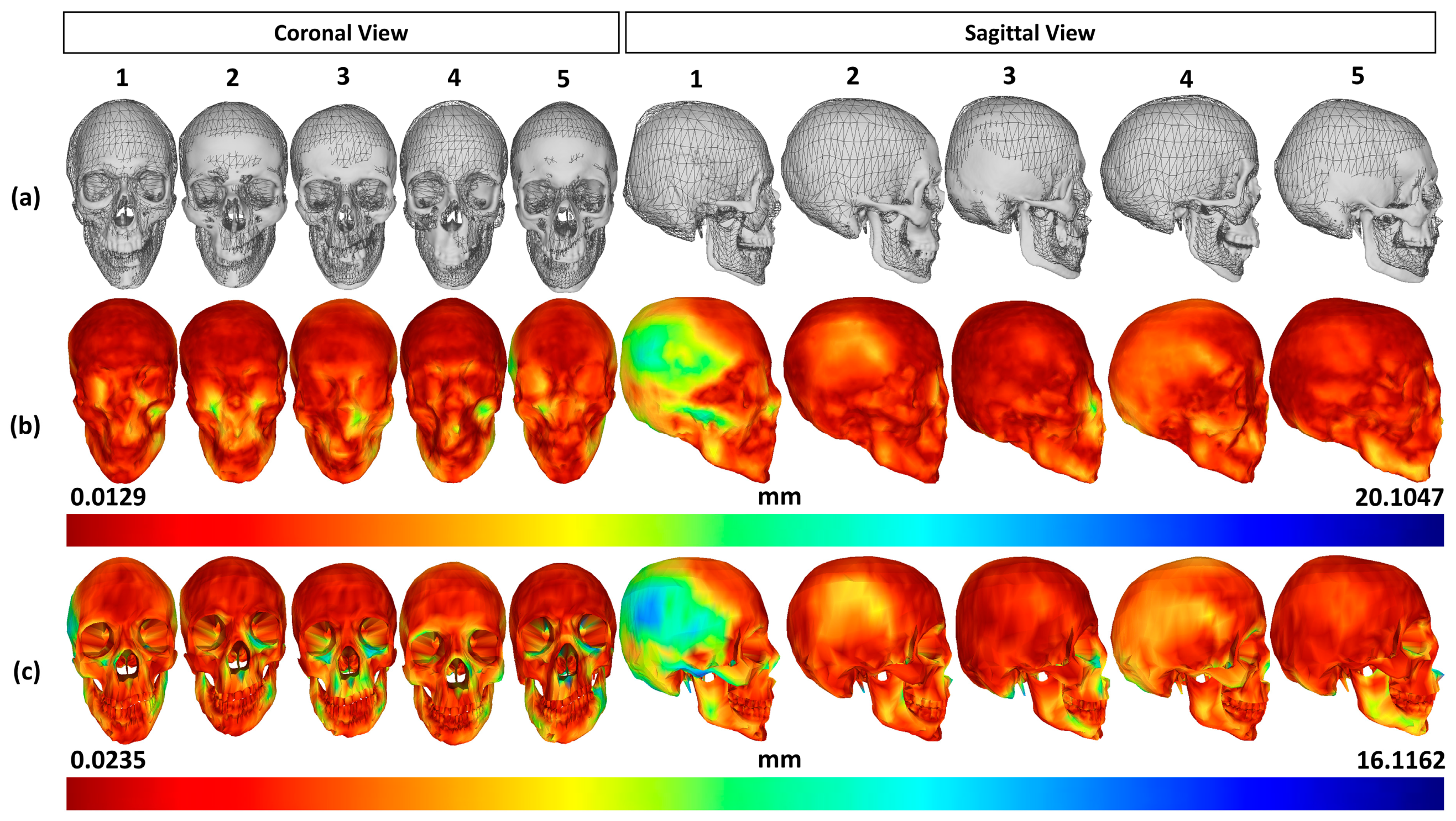
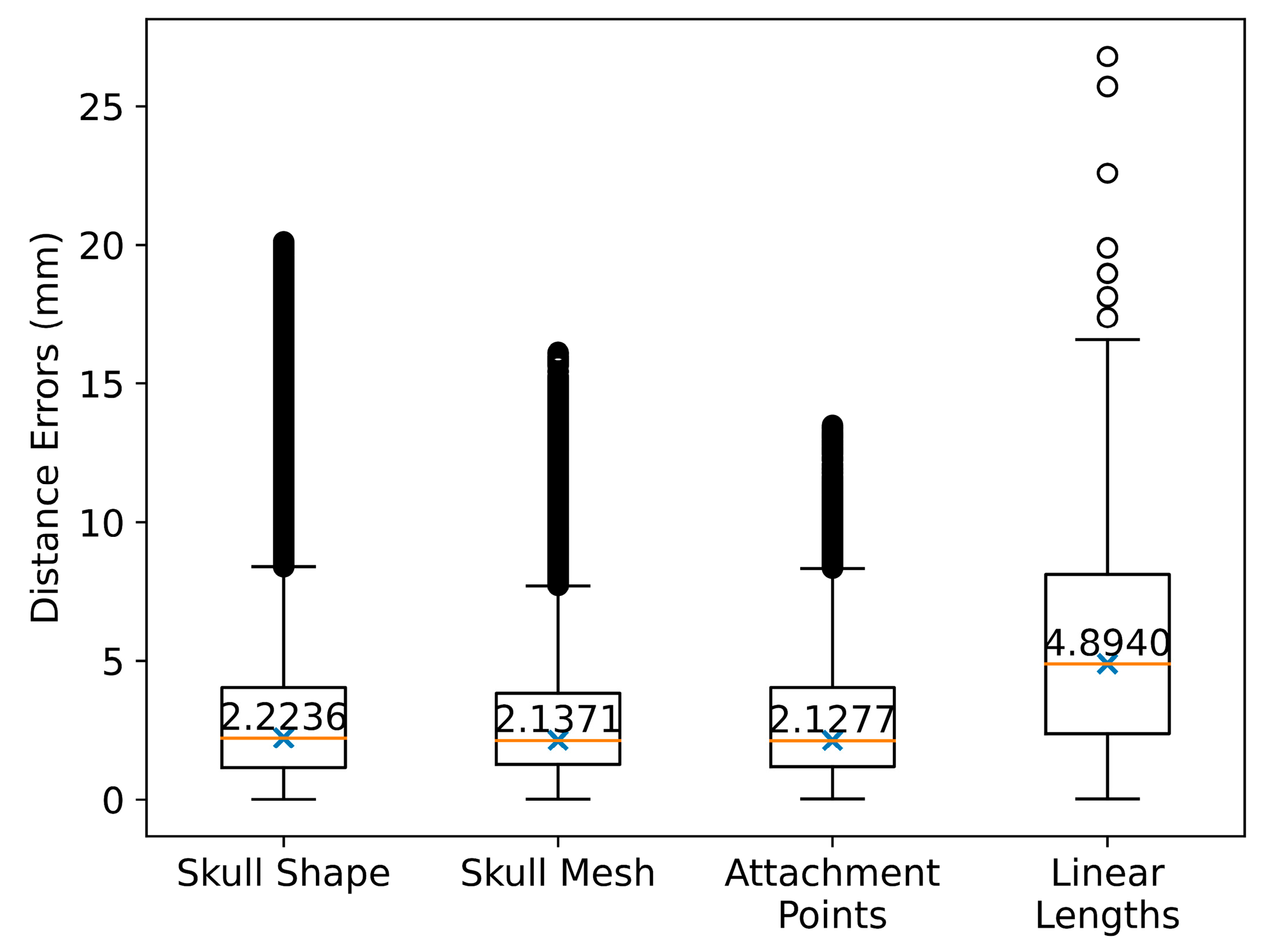
2.5. Validation
2.6. Used Technologies
3. Results
3.1. Validation Deviations in Comparison with CT-Reconstructed Data
3.2. Muscle Lengths in Neutral Mimics
3.3. Static Muscle Analysis
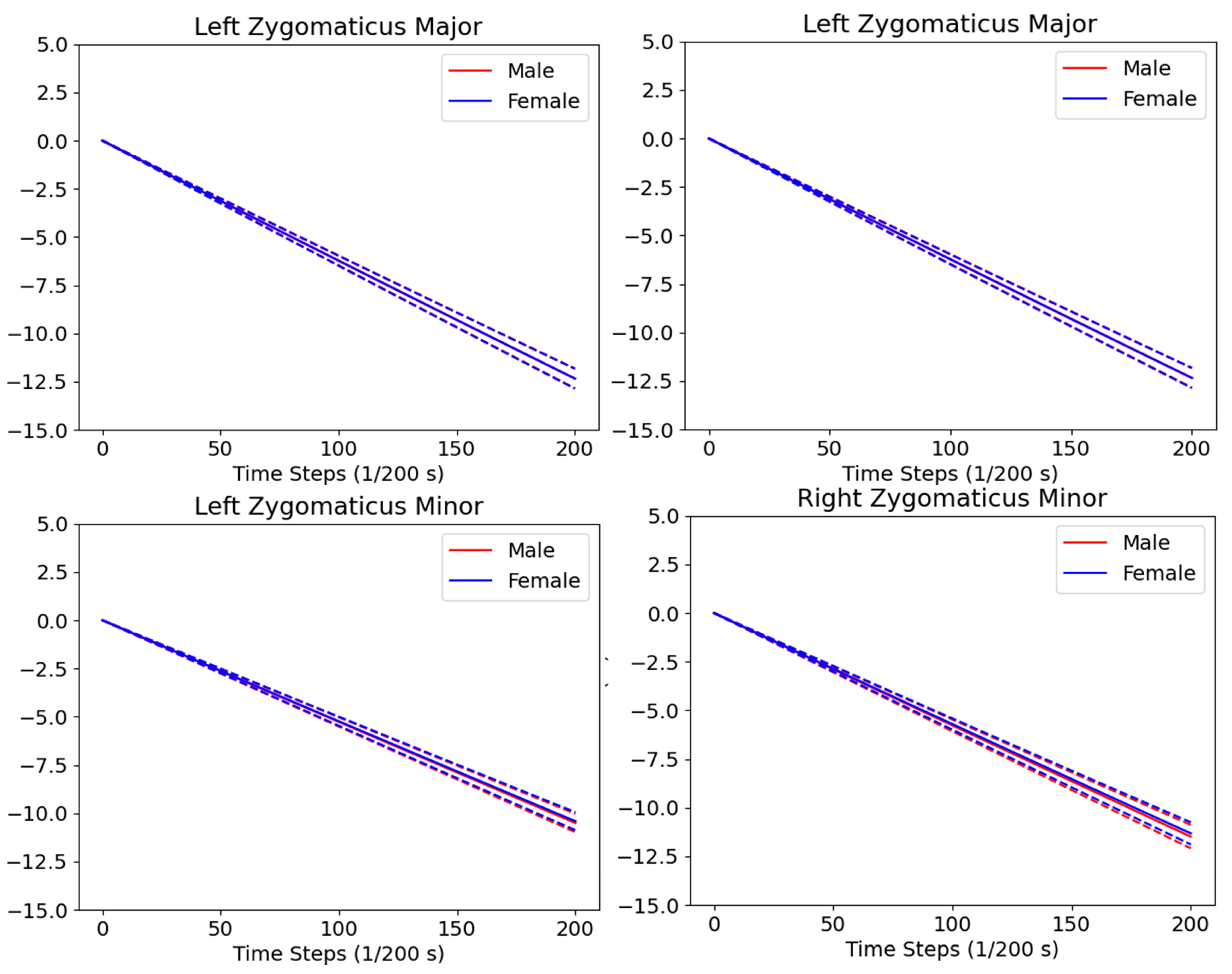
3.4. Dynamic Muscle Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Frith, C. Role of Facial Expressions in Social Interactions. Philos. Trans. R. Soc. B Biol. Sci. 2009, 364, 3453–3458. [Google Scholar] [CrossRef]
- Ishii, L.E.; Nellis, J.C.; Boahene, K.D.; Byrne, P.; Ishii, M. The Importance and Psychology of Facial Expression. Otolaryngol. Clin. N. Am. 2018, 51, 1011–1017. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Hung, A.P.L.; Hunter, P.; Mithraratne, K. Modelling Facial Expressions: A Framework for Simulating Nonlinear Soft Tissue Deformations Using Embedded 3D Muscles. Finite Elem. Anal. Des. 2013, 76, 63–70. [Google Scholar] [CrossRef]
- Fan, A.X.; Dakpé, S.; Dao, T.T.; Pouletaut, P.; Rachik, M.; Ho Ba Tho, M.C. MRI-Based Finite Element Modeling of Facial Mimics: A Case Study on the Paired Zygomaticus Major Muscles. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 919–928. [Google Scholar] [CrossRef] [PubMed]
- Dao, T.T.; Fan, A.X.; Dakpé, S.; Pouletaut, P.; Rachik, M.; Ho Ba Tho, M.C. Image-Based Skeletal Muscle Coordination: Case Study on a Subject Specific Facial Mimic Simulation. J. Mech. Med. Biol. 2018, 18, 1850020. [Google Scholar] [CrossRef]
- Rittey, C. The Facial Nerve. Pediatric ENT; Springer: Berlin/Heidelberg, Germany, 2007; Volume 83, pp. 479–484. [Google Scholar] [CrossRef]
- Jayatilake, D.; Isezaki, T.; Teramoto, Y.; Eguchi, K.; Suzuki, K. Robot Assisted Physiotherapy to Support Rehabilitation of Facial Paralysis. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 644–653. [Google Scholar] [CrossRef] [PubMed]
- Wernick Robinson, M.; Baiungo, J.; Hohman, M.; Hadlock, T. Facial Rehabilitation. Oper. Tech. Otolaryngol.—Head Neck Surg. 2012, 23, 288–296. [Google Scholar] [CrossRef]
- Constantinides, M.; Galli, S.K.D.; Miller, P.J. Complications of Static Facial Suspensions with Expanded Polytetrafluoroethylene (EPTFE). Laryngoscope 2001, 111, 2114–2121. [Google Scholar] [CrossRef]
- Dubernard, J.M.; Lengelé, B.; Morelon, E.; Testelin, S.; Badet, L.; Moure, C.; Beziat, J.L.; Dakpé, S.; Kanitakis, J.; D’Hauthuille, C.; et al. Outcomes 18 Months after the First Human Partial Face Transplantation. N. Engl. J. Med. 2007, 357, 2451–2460. [Google Scholar] [CrossRef]
- Anderl, H. Reconstruction of the Face through Cross-Face-Nerve Transplantation in Facial Paralysis. Chir. Plast. 1973, 2, 17–45. [Google Scholar] [CrossRef]
- Khalifian, S.; Brazio, P.S.; Mohan, R.; Shaffer, C.; Brandacher, G.; Barth, R.N.; Rodriguez, E.D. Facial Transplantation: The First 9 Years. Lancet 2014, 384, 2153–2163. [Google Scholar] [CrossRef] [PubMed]
- Lopez, J.; Rodriguez, E.D.; Dorafshar, A.H. Facial Transplantation; Elsevier Inc.: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Siemionow, M.Z.; Papay, F.; Djohan, R.; Bernard, S.; Gordon, C.R.; Alam, D.; Hendrickson, M.; Lohman, R.; Eghtesad, B.; Fung, J. First U.S. near-Total Human Face Transplantation: A Paradigm Shift for Massive Complex Injuries. Plast. Reconstr. Surg. 2010, 125, 111–122. [Google Scholar] [CrossRef] [PubMed]
- Lantieri, L. Man with 3 Faces: Frenchman Gets 2nd Face Transplant. AP NEWS, 17 April 2018. [Google Scholar]
- VanSwearingen, J. Facial Rehabilitation: A Neuromuscular Reeducation, Patient-Centered Approach. Facial Plast. Surg. 2008, 24, 250–259. [Google Scholar] [CrossRef]
- Samsudin, W.S.W.; Sundaraj, K. Clinical and Non-Clinical Initial Assessment of Facial Nerve Paralysis: A Qualitative Review. Biocybern. Biomed. Eng. 2014, 34, 71–78. [Google Scholar] [CrossRef]
- Owusu, J.A.; Stewart, C.M.; Boahene, K. Facial Nerve Paralysis. Med. Clin. N. Am. 2018, 102, 1135–1143. [Google Scholar] [CrossRef] [PubMed]
- Banks, C.A.; Bhama, P.K.; Park, J.; Hadlock, C.R.; Hadlock, T.A. Clinician-Graded Electronic Facial Paralysis Assessment: The EFACE. Plast. Reconstr. Surg. 2015, 136, 223e–230e. [Google Scholar] [CrossRef]
- Lou, J.; Yu, H.; Wang, F.Y. A Review on Automated Facial Nerve Function Assessment from Visual Face Capture. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 488–497. [Google Scholar] [CrossRef]
- Wang, S.; Li, H.; Qi, F.; Zhao, Y. Objective Facial Paralysis Grading Based OnPFace and Eigenflow. Med. Biol. Eng. Comput. 2004, 42, 598–603. [Google Scholar] [CrossRef]
- Desrosiers, P.A.; Bennis, Y.; Daoudi, M.; Amor, B.B.; Guerreschi, P. Analyzing of Facial Paralysis by Shape Analysis of 3D Face Sequences. Image Vis. Comput. 2017, 67, 67–88. [Google Scholar] [CrossRef]
- Gibelli, D.; De Angelis, D.; Poppa, P.; Sforza, C.; Cattaneo, C. An Assessment of How Facial Mimicry Can Change Facial Morphology: Implications for Identification. J. Forensic Sci. 2017, 62, 405–410. [Google Scholar] [CrossRef]
- Tanikawa, C.; Takada, K. Test-Retest Reliability of Smile Tasks Using Three-Dimensional Facial Topography. Angle Orthod. 2018, 88, 319–328. [Google Scholar] [CrossRef] [PubMed]
- Frey, M.; John Tzou, C.H.; Michaelidou, M.; Pona, I.; Hold, A.; Placheta, E.; Kitzinger, H.B. 3D Video Analysis of Facial Movements. Fac. Plast. Surg. Clin. N. Am. 2011, 19, 639–646. [Google Scholar] [CrossRef] [PubMed]
- Salgado, M.D.; Curtiss, S.; Tollefson, T.T. Evaluating Symmetry and Facial Motion Using 3D Videography. Fac. Plast. Surg. Clin. N. Am. 2010, 18, 351–356. [Google Scholar] [CrossRef] [PubMed]
- Trotman, C.-A.; Phillips, C.; Faraway, J.J.; Ritter, K. Association between Subjective and Objective Measures of Lip Form and Function: An Exploratory Analysis. Cleft Palate-Craniofac. J. 2003, 40, 241–248. [Google Scholar] [CrossRef]
- Hontanilla, B.; Aubá, C. Automatic Three-Dimensional Quantitative Analysis for Evaluation of Facial Movement. J. Plast. Reconstr. Aesthetic Surg. 2008, 61, 18–30. [Google Scholar] [CrossRef]
- Trotman, C.A.; Faraway, J.; Hadlock, T.; Banks, C.; Jowett, N.; Jung, H.J. Facial Soft-Tissue Mobility: Baseline Dynamics of Patients with Unilateral Facial Paralysis. Plast. Reconstr. Surg.—Glob. Open 2018, 6, 1955. [Google Scholar] [CrossRef]
- Al-Hiyali, A.; Ayoub, A.; Ju, X.; Almuzian, M.; Al-Anezi, T. The Impact of Orthognathic Surgery on Facial Expressions. J. Oral Maxillofac. Surg. 2015, 73, 2380–2390. [Google Scholar] [CrossRef]
- Popat, H.; Henley, E.; Richmond, S.; Benedikt, L.; Marshall, D.; Rosin, P.L. A Comparison of the Reproducibility of Verbal and Nonverbal Facial Gestures Using Three-Dimensional Motion Analysis. Otolaryngol.—Head Neck Surg. 2010, 142, 867–872. [Google Scholar] [CrossRef]
- Mishima, K.; Umeda, H.; Nakano, A.; Shiraishi, R.; Hori, S.; Ueyama, Y. Three-Dimensional Intra-Rater and Inter-Rater Reliability during a Posed Smile Using a Video-Based Motion Analyzing System. J. Cranio-Maxillofac. Surg. 2014, 42, 428–431. [Google Scholar] [CrossRef]
- Trotman, C.A.; Faraway, J.; Hadlock, T.A. Facial Mobility and Recovery in Patients with Unilateral Facial Paralysis. Orthod. Craniofac. Res. 2020, 23, 82–91. [Google Scholar] [CrossRef]
- Ekman, R. What the Face Reveals: Basic and Applied Studies of Spontaneous Expression Using the Facial Action Coding System (FACS); Oxford University Press: New York, NY, USA, 1997; ISBN 978-0195179644. [Google Scholar]
- Hamm, J.; Kohler, C.G.; Gur, R.C.; Verma, R. Automated Facial Action Coding System for Dynamic Analysis of Facial Expressions in Neuropsychiatric Disorders. J. Neurosci. Methods 2011, 200, 237–256. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.-N.; Dakpe, S.; Ho Ba Tho, M.-C.; Dao, T.-T. Kinect-Driven Patient-Specific Head, Skull, and Muscle Network Modelling for Facial Palsy Patients. Comput. Methods Programs Biomed. 2021, 200, 105846. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.-N.; Tran, V.-D.; Nguyen, H.-Q.; Dao, T.-T. A Statistical Shape Modeling Approach for Predicting Subject-Specific Human Skull from Head Surface. Med. Biol. Eng. Comput. 2020, 58, 2355–2373. [Google Scholar] [CrossRef]
- Freilinger, G.; Gruber, H.; Happak, W.; Pechmann, U. Surgical Anatomy of the Mimic Muscle System and the Facial Nerve: Importance for Reconstructive and Aesthetic Surgery. Plast. Reconstr. Surg. 1987, 80, 686–690. [Google Scholar] [CrossRef] [PubMed]
- Happak, W.; Liu, J.; Burggasser, G.; Flowers, A.; Gruber, H.; Freilinger, G. Human Facial Muscles: Dimensions, Motor Endplate Distribution, and Presence of Muscle Fibers with Multiple Motor Endplates. Anat. Rec. 1997, 249, 276–284. [Google Scholar] [CrossRef]
- Benington, P.C.M.; Gardener, J.E.; Hunt, N.P. Masseter Muscle Volume Measured Using Ultrasonography and Its Relationship with Facial Morphology. Eur. J. Orthod. 1999, 21, 659–670. [Google Scholar] [CrossRef]
- Pappalardo, F.; Russo, G.; Tshinanu, F.M.; Viceconti, M. In Silico Clinical Trials: Concepts and Early Adoptions. Brief. Bioinform. 2019, 20, 1699–1708. [Google Scholar] [CrossRef]
- Hodos, R.A.; Kidd, B.A.; Shameer, K.; Readhead, B.P.; Dudley, J.T. In Silico Methods for Drug Repurposing and Pharmacology. Wiley Interdiscip. Rev. Syst. Biol. Med. 2016, 8, 186–210. [Google Scholar] [CrossRef]
- Li, T.; Bolkart, T.; Black, M.J.; Li, H.; Romero, J. Learning a Model of Facial Shape and Expression from 4D Scans. ACM Trans. Graph. 2017, 36, 1–17. [Google Scholar] [CrossRef]
- Paysan, P.; Knothe, R.; Amberg, B.; Romdhani, S.; Vetter, T. A 3D Face Model for Pose and Illumination Invariant Face Recognition. In Proceedings of the 2009 Sixth IEEE International Conference on Advanced Video and Signal Based Surveillance, Genova, Italy, 2–4 September 2009; pp. 296–301. [Google Scholar]
- Sharma, S.; Kumar, V. 3D Face Reconstruction in Deep Learning Era: A Survey; Springer: Dordrecht, The Netherlands, 2022; Volume 29, ISBN 0123456789. [Google Scholar]
- Salam, H.; Séguier, R. A Survey on Face Modeling: Building a Bridge between Face Analysis and Synthesis. Vis. Comput. 2018, 34, 289–319. [Google Scholar] [CrossRef]
- Wang, H. A Review of 3D Face Reconstruction from a Single Image. arXiv 2021, arXiv:2110.09299. [Google Scholar]
- Berry, S.D.; Edgar, H.J.H. Announcement: The New Mexico Decedent Image Database. Forensic Imaging 2021, 24, 200436. [Google Scholar] [CrossRef]
- Loper, M.; Mahmood, N.; Romero, J.; Pons-Moll, G.; Black, M.J. SMPL: A Skinned Multi-Person Linear Model. ACM Trans. Graph. 2015, 34, 1–16. [Google Scholar] [CrossRef]
- Maćkiewicz, A.; Ratajczak, W. Principal Components Analysis (PCA). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]
- Robinette, K.M.; Daanen, H.A.M. Precision of the CAESAR Scan-Extracted Measurements. Appl. Ergon. 2006, 37, 259–265. [Google Scholar] [CrossRef]
- Cosker, D.; Krumhuber, E.; Hilton, A. A FACS Valid 3D Dynamic Action Unit Database with Applications to 3D Dynamic Morphable Facial Modeling. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2296–2303. [Google Scholar]
- Ekman, P.; Friesen, W.V. Facial Action Coding System. Environmental Psychology and Nonverbal Behavior; Kluwer Academic Publishers-Human Sciences Press: Dordrecht, The Netherlands, 1978. [Google Scholar]
- Henry, E.R.; Hofrichter, J. Singular Value Decomposition: Application to Analysis of Experimental Data; Academic Press: Cambridge, MA, USA, 1992; pp. 129–192. [Google Scholar]
- Jost, T.; Hügli, H. Fast ICP Algorithms for Shape Registration. In Proceedings of the 24th DAGM Symposium, Zurich, Switzerland, 16–18 September 2002; Springer: Berlin/Heidelberg, Germany, 2002; pp. 91–99. [Google Scholar]
- Geladi, P.; Kowalski, B.R. Partial Least-Squares Regression: A Tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Prendergast, P.M. Facial Anatomy. Adv. Surg. Facial Rejuvenation Art Clin. Pract. 2012, 9783642178, 3–14. [Google Scholar] [CrossRef]
- Fedorov, A.; Beichel, R.; Kalpathy-Cramer, J.; Finet, J.; Fillion-Robin, J.-C.; Pujol, S.; Bauer, C.; Jennings, D.; Fennessy, F.; Sonka, M.; et al. 3D Slicer as an Image Computing Platform for the Quantitative Imaging Network. Magn. Reson. Imaging 2012, 30, 1323–1341. [Google Scholar] [CrossRef]
- Jacobson, A.; Panozzo, D.; Schüller, C.; Diamanti, O.; Zhou, Q.; Pietroni, N. Libigl: A Simple C++ Geometry Processing Library 2018. Available online: http://hdl.handle.net/10453/167463 (accessed on 19 November 2022).
- Cignoni, P.; Ranzuglia, G.; Callieri, M.; Corsini, M.; Ganovelli, F.; Pietroni, N.; Tarini, M. MeshLab. 2011. Available online: https://air.unimi.it/handle/2434/625490 (accessed on 19 November 2022).
- Rusu, R.B.; Cousins, S. 3D Is Here: Point Cloud Library (PCL). In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Schroeder, W.J.; Avila, L.S.; Hoffman, W. Visualizing with VTK: A Tutorial. IEEE Comput. Graph. Appl. 2000, 20, 20–27. [Google Scholar] [CrossRef]
- Guennebaud, G.; Jacob, B. Eigen V3 2010. Available online: http://eigen.tuxfamily.org (accessed on 19 November 2022).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Dao, T.T.; Pouletaut, P.; Lazáry, Á.; Tho, M.C.H.B. Multimodal Medical Imaging Fusion for Patient-Specific Musculoskeletal Modeling of the Lumbar Spine System in Functional Posture. J. Med. Biol. Eng. 2017, 37, 739–749. [Google Scholar] [CrossRef]
- Robinson, M.W.; Baiungo, J. Facial Rehabilitation: Evaluation and Treatment Strategies for the Patient with Facial Palsy. Otolaryngol. Clin. N. Am. 2018, 51, 1151–1167. [Google Scholar] [CrossRef] [PubMed]
- Marcos, S.; Gómez-García-Bermejo, J.; Zalama, E. A Realistic, Virtual Head for Human-Computer Interaction. Interact. Comput. 2010, 22, 176–192. [Google Scholar] [CrossRef]
- Matsuoka, A.; Yoshioka, F.; Ozawa, S.; Takebe, J. Development of Three-Dimensional Facial Expression Models Using Morphing Methods for Fabricating Facial Prostheses. J. Prosthodont. Res. 2019, 63, 66–72. [Google Scholar] [CrossRef] [PubMed]
- Turban, L.; Girard, D.; Kose, N.; Dugelay, J.L. From Kinect Video to Realistic and Animatable MPEG-4 Face Model: A Complete Framework. In Proceedings of the 2015 IEEE International Conference on Multimedia & Expo Workshops (ICMEW), Turin, Italy, 30 July 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, H.; Rashid, T.; Habes, M. Cerebral Microbleed Detection Via Fourier Descriptor with Dual Domain Distribution Modeling. In Proceedings of the 2020 IEEE 17th International Symposium on Biomedical Imaging Workshops (ISBI Workshops), Iowa City, IA, USA, 4 April 2020; pp. 20–23. [Google Scholar] [CrossRef]
- Nguyen, T.-N. FLAME Based Head and Skull Predictions. Available online: https://drive.google.com/file/d/1ma6_PrRUucGhmg3a4-syKrIpAgTt1-zd/view?usp=share_link (accessed on 19 November 2022).
- Nguyen, T.-N. Clinical Decision Support System for Facial Mimic Rehabilitation. Ph.D. Thesis, University of Technology of Compiegne, Compiègne, France, 2020. [Google Scholar]
- Luthi, M.; Gerig, T.; Jud, C.; Vetter, T. Gaussian Process Morphable Models. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 1860–1873. [Google Scholar] [CrossRef] [PubMed]
- Abbas, A.; Rafiee, A.; Haase, M.; Malcolm, A. Geometrical Deep Learning for Performance Prediction of High-Speed Craft. Ocean Eng. 2022, 258, 111716. [Google Scholar] [CrossRef]
- Li, R.; Li, X.; Hui, K.-H.; Fu, C.-W. SP-GAN: Sphere-Guided 3D Shape Generation and Manipulation. ACM Trans. Graph. 2021, 40, 1–12. [Google Scholar] [CrossRef]


| Left/Rights | Muscle Types | Muscle IDs * | ||
|---|---|---|---|---|
| Males | Females | |||
| Left | Procerus | LP | 27.76 ± 2.41 | 27.56 ± 2.26 |
| Right | RP | 26.58 ± 2.33 | 26.63 ± 2.26 | |
| Left | Frontal Belly | LFB | 33.06 ± 1.84 | 32.07 ± 1.77 |
| Right | RFB | 32.60 ± 1.78 | 31.74 ± 1.79 | |
| Left | Temporoparietalis | LT | 30.69 ± 1.73 | 30.10 ± 1.70 |
| Right | RT | 22.89 ± 1.77 | 22.28 ± 1.79 | |
| Left | Corrugator Supperciliary | LCS | 29.83 ± 1.64 | 29.55 ± 1.67 |
| Right | RCS | 28.45 ± 1.69 | 28.26 ± 1.84 | |
| Left | Nasalis | LNa | 28.22 ± 1.94 | 27.56 ± 2.09 |
| Right | RNa | 29.05 ± 1.92 | 28.25 ± 2.12 | |
| Left | Depressor Septi Nasi | LDSN | 17.12 ± 2.66 | 16.39 ± 2.31 |
| Right | RDSN | 13.29 ± 2.38 | 13.11 ± 2.35 | |
| Left | Zygomaticus Minor | LZm | 59.21 ± 2.82 | 55.88 ± 2.74 |
| Right | RZm | 54.73 ± 2.89 | 52.25 ± 2.85 | |
| Left | Left Zygomaticus Major | LZM | 67.29 ± 2.71 | 63.70 ± 2.62 |
| Right | RZM | 62.93 ± 2.71 | 59.81 ± 2.68 | |
| Left | Risorius | LR | 36.84 ± 2.05 | 37.19 ± 1.98 |
| Right | RR | 36.04 ± 2.05 | 36.75 ± 1.88 | |
| Left | Depressor Anguli Oris | LDAO | 31.19 ± 3.17 | 30.19 ± 2.17 |
| Right | RDAO | 32.39 ± 3.64 | 31.47 ± 2.65 | |
| Left | Mentalis | LMe | 26.49 ± 3.23 | 26.76 ± 2.63 |
| Right | RMe | 29.07 ± 3.14 | 29.00 ± 2.60 | |
| Left | Levator Labii Superioris | LLLS | 50.28 ± 3.01 | 47.05 ± 2.87 |
| Right | RLLS | 46.54 ± 2.75 | 44.01 ± 2.82 | |
| Left | Levator Labii Superioris Alaeque Nasi | LLLSAN | 60.39 ± 2.83 | 57.16 ± 2.81 |
| Right | RLLSAN | 59.65 ± 2.74 | 56.63 ± 2.82 | |
| Left | Levator Anguli Oris | LLAO | 38.14 ± 2.87 | 34.96 ± 2.82 |
| Right | RLAO | 34.49 ± 2.80 | 31.76 ± 2.76 | |
| Left | Depressor Labii Inferioris | LDLI | 37.39 ± 2.20 | 37.33 ± 2.19 |
| Right | RDLI | 35.99 ± 2.65 | 35.52 ± 2.22 | |
| Left | Buccinator | LB | 55.65 ± 3.03 | 53.54 ± 3.05 |
| Right | RB | 52.32 ± 3.09 | 50.55 ± 2.94 | |
| Left | Masseter | LMa | 49.45 ± 2.38 | 47.02 ± 2.20 |
| Right | RMa | 52.14 ± 2.56 | 49.68 ± 2.23 | |
| Left | Orbicularis Oculi | LOO | 153.60 ± 5.01 | 150.45 ± 5.25 |
| Right | ROO | 148.66 ± 4.70 | 144.12 ± 4.81 | |
| Orbicularis Oris | OO | 176.43 ± 7.94 | 165.76 ± 6.36 | |
| Muscle IDs | Muscle Strains in Positions (Mean ± SD %) | |||
|---|---|---|---|---|
| Smiling | Kissing | |||
| Males | Females | Males | Females | |
| LP | 3.06 ± 0.34 | 3.00 ± 0.26 | −3.05 ± 0.34 | −3.00 ± 0.26 |
| RP | 3.39 ± 0.38 | 3.30 ± 0.30 | −3.38 ± 0.38 | −3.30 ± 0.30 |
| LFB | 2.88 ± 0.21 | 2.87 ± 0.21 | −2.84 ± 0.21 | −2.84 ± 0.21 |
| RFB | 2.52 ± 0.17 | 2.56 ± 0.16 | −2.49 ± 0.17 | −2.53 ± 0.16 |
| LT | 2.50 ± 0.20 | 2.46 ± 0.19 | −2.47 ± 0.20 | −2.44 ± 0.19 |
| RT | 3.05 ± 0.29 | 3.07 ± 0.27 | −3.02 ± 0.28 | −3.05 ± 0.26 |
| LCS | −0.26 ± 0.30 | −0.05 ± 0.26 | 0.35 ± 0.30 | 0.14 ± 0.26 |
| RCS | −0.50 ± 0.44 | −0.19 ± 0.38 | 0.63 ± 0.44 | 0.32 ± 0.38 |
| LNa | −9.69 ± 1.03 | −9.40 ± 0.95 | 10.44 ± 1.10 | 10.08 ± 1.01 |
| RNa | −6.72 ± 0.77 | −6.97 ± 0.72 | 7.74 ± 0.80 | 7.86 ± 0.78 |
| LDSN | −22.40 ± 4.18 | −22.76 ± 3.70 | 22.88 ± 4.49 | 23.12 ± 3.78 |
| RDSN | −21.63 ± 3.86 | −22.83 ± 3.85 | 25.41 ± 4.43 | 25.95 ± 4.37 |
| LZm | −10.50 ± 0.48 | −10.41 ± 0.47 | 10.64 ± 0.48 | 10.62 ± 0.48 |
| RZm | −11.49 ± 0.60 | −11.32 ± 0.57 | 11.69 ± 0.61 | 11.63 ± 0.59 |
| LZM | −12.34 ± 0.50 | −12.34 ± 0.52 | 12.66 ± 0.50 | 12.75 ± 0.52 |
| RZM | −12.78 ± 0.60 | −12.74 ± 0.60 | 13.23 ± 0.59 | 13.31 ± 0.60 |
| LR | −12.17 ± 1.72 | −12.92 ± 1.63 | 13.88 ± 1.64 | 14.55 ± 1.63 |
| RR | −10.57 ± 2.02 | −11.49 ± 1.72 | 12.76 ± 2.00 | 13.55 ± 1.76 |
| LDAO | 5.23 ± 2.53 | 4.33 ± 3.09 | 1.32 ± 2.78 | 3.47 ± 2.98 |
| RDAO | 9.91 ± 3.01 | 9.92 ± 3.34 | −5.18 ± 2.23 | −3.95 ± 2.61 |
| LMe | −0.14 ± 1.46 | −0.79 ± 1.87 | 2.82 ± 2.04 | 4.03 ± 2.29 |
| RMe | 1.31 ± 1.14 | 0.90 ± 1.59 | 0.88 ± 1.12 | 1.77 ± 1.46 |
| LLLS | −11.76 ± 0.77 | −11.57 ± 0.75 | 12.13 ± 0.77 | 12.08 ± 0.75 |
| RLLS | −12.24 ± 0.95 | −11.96 ± 0.90 | 12.87 ± 0.96 | 12.74 ± 0.91 |
| LLLSAN | −8.05 ± 0.45 | −7.77 ± 0.51 | 8.65 ± 0.46 | 8.48 ± 0.50 |
| RLLSAN | −7.44 ± 0.47 | −7.21 ± 0.51 | 8.17 ± 0.47 | 8.03 ± 0.49 |
| LLAO | −22.01 ± 1.86 | −22.67 ± 2.01 | 22.82 ± 1.86 | 23.66 ± 2.05 |
| RLAO | −19.84 ± 2.20 | −20.62 ± 2.19 | 22.23 ± 2.38 | 23.14 ± 2.34 |
| LDLI | −7.46 ± 1.30 | −8.20 ± 1.27 | 8.25 ± 1.30 | 8.98 ± 1.29 |
| RDLI | −6.55 ± 1.68 | −7.82 ± 1.57 | 7.76 ± 1.77 | 9.04 ± 1.67 |
| LB | −12.89 ± 0.79 | −13.46 ± 0.89 | 13.57 ± 0.82 | 14.10 ± 0.95 |
| RB | −12.21 ± 0.78 | −12.77 ± 0.83 | 13.14 ± 0.84 | 13.66 ± 0.91 |
| LMa | 0.22 ± 0.49 | −1.16 ± 0.58 | 0.02 ± 0.45 | 0.86 ± 0.54 |
| RMa | −0.65 ± 0.48 | −0.25 ± 0.57 | 0.74 ± 0.46 | 0.14 ± 0.57 |
| LOO | −2.14 ± 0.10 | −2.16 ± 0.11 | 2.27 ± 0.11 | 2.29 ± 0.11 |
| ROO | −2.31 ± 0.10 | −2.39 ± 0.11 | 2.46 ± 0.10 | 2.54 ± 0.12 |
| OO | 13.18 ± 0.68 | 14.46 ± 0.66 | −11.31 ± 0.64 | −12.44 ± 0.61 |
| Muscle IDs | Lengths of Facial Muscles in Neutral Mimics Reported in the Literature | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| This Study * | Nguyen et al., 2021 [36] | Freilinger et al., 1987 [38] | Happak et al., 1997 [39] | Bernington et al., 1999 [40] | Fan et al., 2017 [4] | Dao et al., 2018 [5] | ||||||||
| Subjects: 5000 M, 5000 F Ages: 29–49 Years Status: In Silico | Subjects: 2 M, 3 F Ages: 29–49 Status: 3 H, 2 P Weight: 52–71 Kg Height: 1.65–1.77 m BMI: 18–26 kg/m2 | Subjects: 20 Ages: 62–94 Status: Cadavers | Subject: 11 Ages: 53–73 Years Status: Cadavers | Subjects: 4 M, 6 F Ages: 15–31 Status: Patients | Subject: 1 F Ages: 24 Status: Healthy Height: 1.5 m Weight: 57 kg | |||||||||
| Males | Females | |||||||||||||
| Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | Mean | SD | Value | Value | |
| LZm | 59.21 | 2.82 | 55.88 | 2.74 | 51.05 | 3.82 | - | - | 51.8 | 7.4 | - | - | - | - |
| RZm | 54.73 | 2.89 | 52.25 | 2.85 | 53.90 | 2.05 | - | - | 51.8 | 7.4 | - | - | - | - |
| LZM | 67.29 | 2.71 | 63.70 | 2.62 | 58.45 | 3.85 | M: 0.67 F: 69.50 | 6.32 6.58 | 65.6 | 3.8 | - | - | 43.65 | 52 |
| RZM | 62.93 | 2.71 | 59.81 | 2.68 | 61.23 | 3.05 | M: 0.67 F: 69.50 | 6.32 6.58 | 65.6 | 3.8 | - | - | 43.65 | 52 |
| LDAO | 31.19 | 3.17 | 30.19 | 2.17 | 36.69 | 3.23 | M: 37.83 F: 38.33 | 4.38 8.02 | 48 | 5.1 | - | - | - | - |
| RDAO | 32.39 | 3.64 | 31.47 | 2.65 | 31.86 | 3.35 | M: 37.83 F: 38.33 | 4.38 8.02 | 48 | 5.1 | - | - | - | - |
| LLLS | 50.28 | 3.01 | 47.05 | 2.87 | 46.26 | 3.00 | M: 33.67 F: 35.50 | 4.13 6.69 | 47 | 7.5 | - | - | 29.3 | - |
| RLLS | 46.54 | 2.75 | 44.01 | 2.82 | 48.59 | 2.14 | M: 33.67 F: 35.50 | 4.13 6.69 | 47 | 7.5 | - | - | 29.3 | - |
| LLLSAN | 60.39 | 2.83 | 57.16 | 2.81 | 58.06 | 3.65 | - | - | 61.6 | 7.6 | - | - | - | - |
| RLLSAN | 59.65 | 2.74 | 56.63 | 2.82 | 59.46 | 2.81 | - | - | 61.6 | 7.6 | - | - | - | - |
| LLAO | 38.14 | 2.87 | 34.96 | 2.82 | 34.30 | 2.53 | - | - | 42 | 2.5 | - | - | 27.4 | - |
| RLAO | 34.49 | 2.80 | 31.76 | 2.76 | 35.51 | 2.30 | - | - | 42 | 2.5 | - | - | 27.4 | - |
| LDLI | 37.39 | 2.20 | 37.33 | 2.19 | 36.73 | 4.39 | - | - | 29 | 4.9 | - | - | - | - |
| RDLI | 35.99 | 2.65 | 35.52 | 2.22 | 37.01 | 4.16 | - | - | 29 | 4.9 | - | - | - | - |
| LB | 55.65 | 3.03 | 53.54 | 3.05 | 56.35 | 3.35 | - | - | 56 | 7.4 | - | - | - | - |
| RB | 52.32 | 3.09 | 50.55 | 2.94 | 55.18 | 2.01 | - | - | 56 | 7.4 | - | - | - | - |
| LMa | 49.45 | 2.38 | 47.02 | 2.20 | 44.93 | 2.35 | - | - | - | - | M: 45.9 F: 39.1 | 5.8 8.2 | - | - |
| RMa | 52.14 | 2.56 | 49.68 | 2.23 | 45.03 | 2.57 | - | - | - | - | M: 45.9 F: 39.1 | 5.8 8.2 | - | - |
| VLOO | 51.81 | 1.92 | 50.46 | 2.03 | 40.70 | 2.99 | - | - | 60 | 9.6 | - | - | - | |
| VROO | 46.72 | 1.63 | 45.29 | 1.93 | 41.62 | 2.13 | - | - | 60 | 9.6 | - | - | - | |
| HLOO | 36.47 | 1.73 | 35.68 | 1.67 | 56.53 | 3.23 | - | - | 65 | 5.6 | - | - | - | |
| HROO | 36.48 | 1.75 | 35.82 | 1.78 | 56.92 | 2.85 | - | - | 65 | 5.6 | - | - | - | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, V.-D.; Nguyen, T.-N.; Ballit, A.; Dao, T.-T. Novel Baseline Facial Muscle Database Using Statistical Shape Modeling and In Silico Trials toward Decision Support for Facial Rehabilitation. Bioengineering 2023, 10, 737. https://doi.org/10.3390/bioengineering10060737
Tran V-D, Nguyen T-N, Ballit A, Dao T-T. Novel Baseline Facial Muscle Database Using Statistical Shape Modeling and In Silico Trials toward Decision Support for Facial Rehabilitation. Bioengineering. 2023; 10(6):737. https://doi.org/10.3390/bioengineering10060737
Chicago/Turabian StyleTran, Vi-Do, Tan-Nhu Nguyen, Abbass Ballit, and Tien-Tuan Dao. 2023. "Novel Baseline Facial Muscle Database Using Statistical Shape Modeling and In Silico Trials toward Decision Support for Facial Rehabilitation" Bioengineering 10, no. 6: 737. https://doi.org/10.3390/bioengineering10060737
APA StyleTran, V.-D., Nguyen, T.-N., Ballit, A., & Dao, T.-T. (2023). Novel Baseline Facial Muscle Database Using Statistical Shape Modeling and In Silico Trials toward Decision Support for Facial Rehabilitation. Bioengineering, 10(6), 737. https://doi.org/10.3390/bioengineering10060737