OptEF-BCI: An Optimization-Based Hybrid EEG and fNIRS–Brain Computer Interface
Abstract
1. Introduction
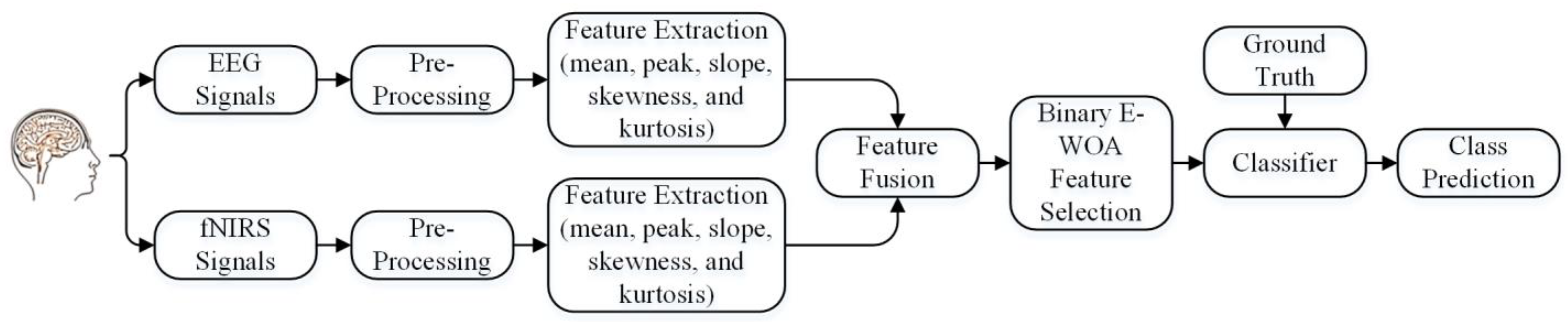
- First, the data acquired from both modalities were preprocessed to filter them and remove artifacts.
- Second, the statistical temporal features of both modalities were extracted with a 10 s interval.
- The features were fused, and the binary enhanced whale optimization algorithm (E-WOA) was used to select the optimal/efficient fused feature subset and to improve the efficiency of the multimodal characteristics by increasing their complementarity, redundancy, and significance in relation to classification labels.
- The support-vector-machine-based cost function was used to classify the data.
- An online MI dataset of 29 healthy individuals was used for validation.
- Finally, the performance results of the proposed approach were compared with those of conventional WOA, other optimization algorithms, and the published literature using the same dataset.
2. Proposed Framework
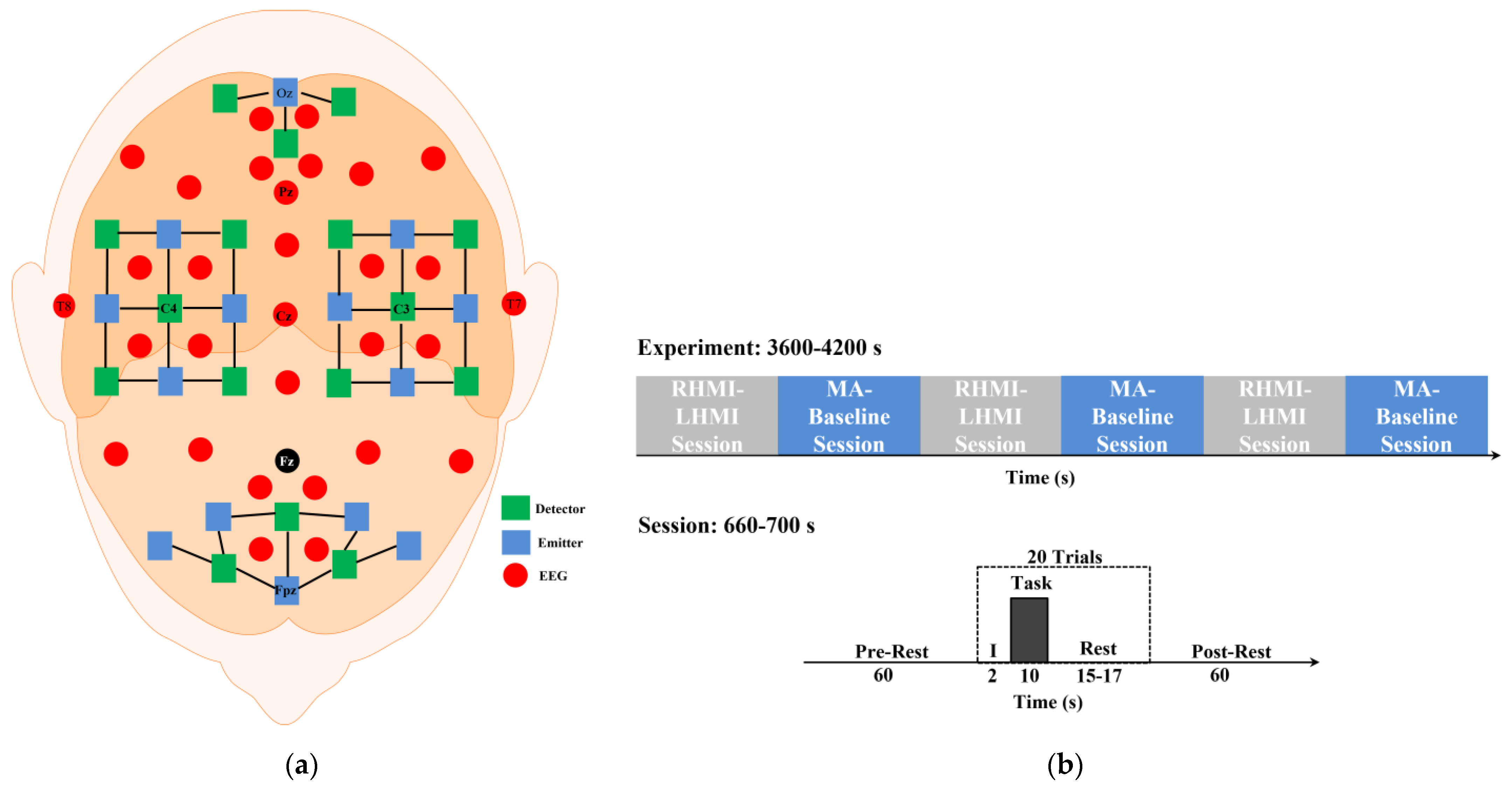
2.1. Data Acquisition
2.2. Preprocessing
2.3. Feature Extraction
2.4. Optimal Feature Selection Approach
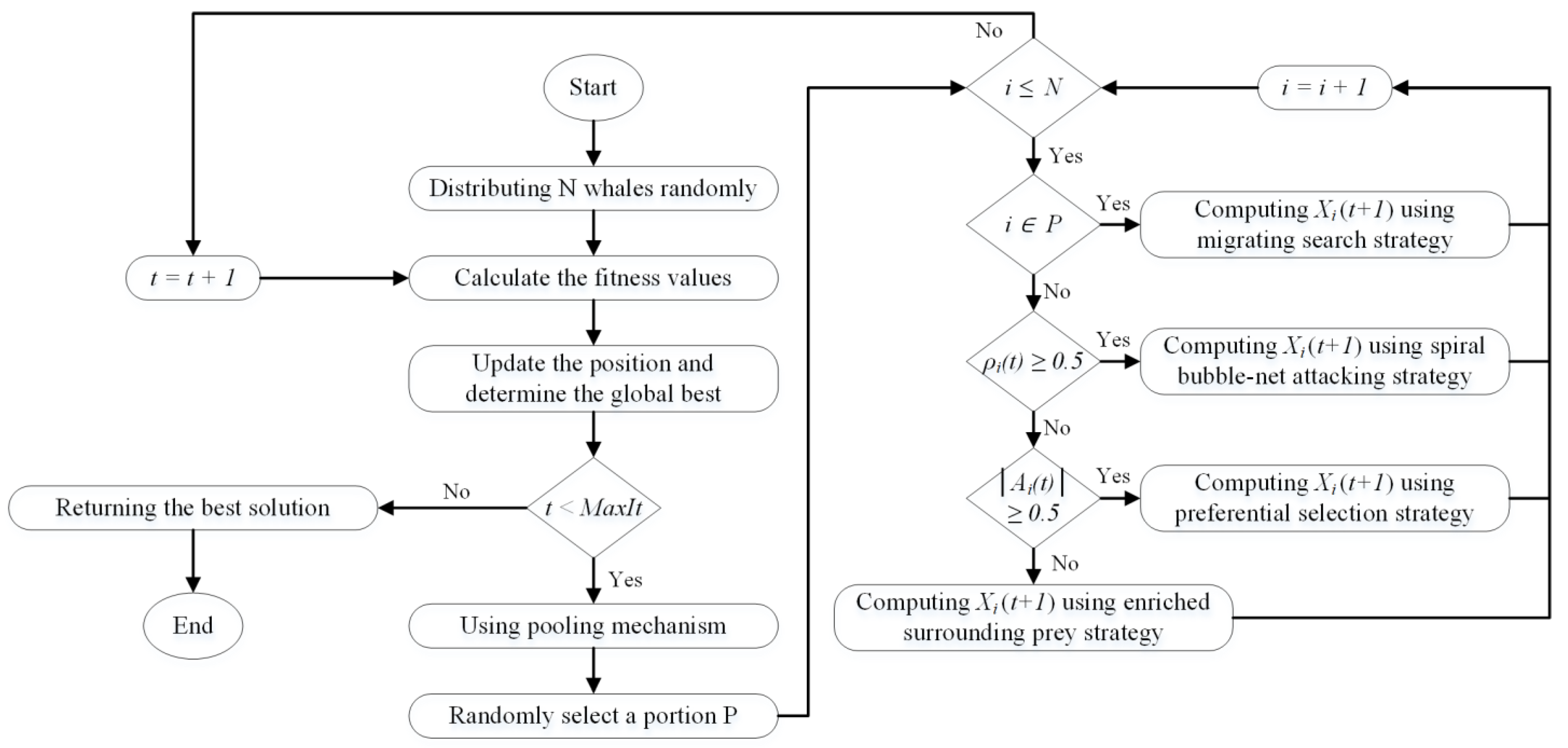
2.4.1. Whale Optimization Algorithm (WOA)
2.4.2. Enhanced WOA (E-WOA)
2.5. Support-Vector-Machine-Based Classification
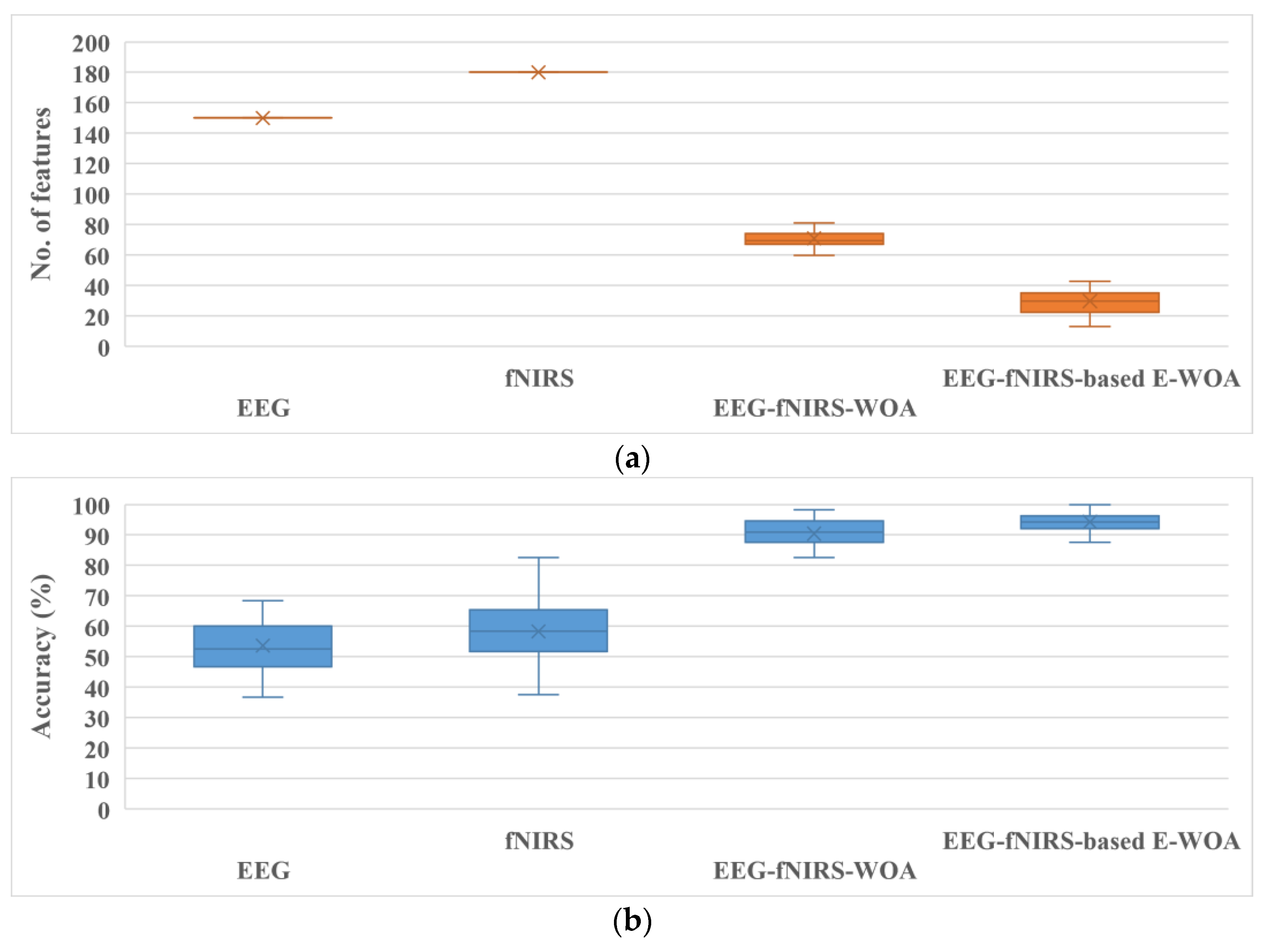
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nicolas-Alonso, L.F.; Gomez-Gil, J. Brain computer interfaces, a review. Sensors 2012, 12, 1211–1279. [Google Scholar] [CrossRef] [PubMed]
- Khosrowabadi, R.; Quek, C.; Ang, K.K.; Tung, S.W.; Heijnen, M. A Brain-Computer Interface for classifying EEG correlates of chronic mental stress. In Proceedings of the 2011 International Joint Conference on Neural Networks, San Jose, CA, USA, 31 July–5 August 2011; pp. 757–762. [Google Scholar]
- Hekmatmanesh, A.; Nardelli, P.H.; Handroos, H. Review of the state-of-the-art of brain-controlled vehicles. IEEE Access 2021, 9, 110173–110193. [Google Scholar] [CrossRef]
- Kaiser, V.; Kreilinger, A.; Müller-Putz, G.R.; Neuper, C. First steps toward a motor imagery based stroke BCI: New strategy to set up a classifier. Front. Neurosci. 2011, 5, 86. [Google Scholar] [CrossRef] [PubMed]
- Herath, H.M.K.K.M.B.; de Mel, W.R. Controlling an Anatomical Robot Hand Using the Brain-Computer Interface Based on Motor Imagery. Adv. Hum.-Comput. Interact. 2021, 2021, 5515759. [Google Scholar] [CrossRef]
- Kasemsumran, P.; Boonchieng, E. EEG-based motor imagery classification using novel adaptive threshold feature extraction and string grammar fuzzy K-nearest neighbor classification. J. Comput. 2019, 30, 27–40. [Google Scholar]
- Ang, K.K.; Guan, C.T.; Chua, K.S.G.; Ang, B.T.; Kuah, C.; Wang, C.C.; Phua, K.S.; Chin, Z.Y.; Zhang, H.H.; IEEE. Clinical study of neurorehabilitation in stroke using EEG-based motor imagery brain-computer interface with robotic feedback. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Buenos Aires, Argentina, 31 August–4 September 2010; pp. 5549–5552. [Google Scholar]
- Lule, D.; Diekmann, V.; Kassubek, J.; Kurt, A.; Birbaumer, N.; Ludolph, A.C.; Kraft, E. Cortical plasticity in amyotrophic lateral sclerosis: Motor imagery and function. Neurorehabilit. Neural Repair 2007, 21, 518–526. [Google Scholar] [CrossRef]
- Jeon, Y.; Nam, C.S.; Kim, Y.J.; Whang, M.C. Event-related (De)synchronization (ERD/ERS) during motor imagery tasks: Implications for brain-computer interfaces. Int. J. Ind. Ergon. 2011, 41, 428–436. [Google Scholar] [CrossRef]
- Hekmatmanesh, A.; Wu, H.; Motie-Nasrabadi, A.; Li, M.; Handroos, H. Combination of discrete wavelet packet transform with detrended fluctuation analysis using customized mother wavelet with the aim of an imagery-motor control interface for an exoskeleton. Multimed. Tools Appl. 2019, 78, 30503–30522. [Google Scholar] [CrossRef]
- Hekmatmanesh, A.; Asl, R.M.; Wu, H.; Handroos, H. EEG control of a bionic hand with imagination based on chaotic approximation of largest Lyapunov exponent: A single trial BCI application study. IEEE Access 2019, 7, 105041–105053. [Google Scholar] [CrossRef]
- Dagdevir, E.; Tokmakci, M. Optimization of preprocessing stage in EEG based BCI systems in terms of accuracy and timing cost. Biomed. Signal Process. Control. 2021, 67, 102548. [Google Scholar] [CrossRef]
- Sadiq, M.T.; Yu, X.J.; Yuan, Z.H.; Fan, Z.M.; Rehman, A.U.; Ullah, I.; Li, G.Q.; Xiao, G.X. Motor Imagery EEG Signals Decoding by Multivariate Empirical Wavelet Transform-Based Framework for Robust Brain-Computer Interfaces. IEEE Access 2019, 7, 171431–171451. [Google Scholar] [CrossRef]
- Hekmatmanesh, A.; Wu, H.; Jamaloo, F.; Li, M.; Handroos, H. A combination of CSP-based method with soft margin SVM classifier and generalized RBF kernel for imagery-based brain computer interface applications. Multimed. Tools Appl. 2020, 79, 17521–17549. [Google Scholar] [CrossRef]
- Hallez, H.; Vanrumste, B.; Grech, R.; Muscat, J.; De Clercq, W.; Vergult, A.; D’Asseler, Y.; Camilleri, K.P.; Fabri, S.G.; Van Huffel, S.; et al. Review on solving the forward problem in EEG source analysis. J. Neuroeng. Rehabil. 2007, 4, 46. [Google Scholar] [CrossRef]
- Quaresima, V.; Ferrari, M. A Mini-Review on Functional Near-Infrared Spectroscopy (fNIRS): Where Do We Stand, and Where Should We Go? Photonics 2019, 6, 87. [Google Scholar] [CrossRef]
- Fazli, S.; Mehnert, J.; Steinbrink, J.; Curio, G.; Villringer, A.; Muller, K.R.; Blankertz, B. Enhanced performance by a hybrid NIRS-EEG brain computer interface. Neuroimage 2012, 59, 519–529. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, M.; Quaresima, V. A brief review on the history of human functional near-infrared spectroscopy (fNIRS) development and fields of application. Neuroimage 2012, 63, 921–935. [Google Scholar] [CrossRef]
- Coyle, S.; Ward, T.; Markham, C.; McDarby, G. On the suitability of near-infrared (NIR) systems for next-generation brain–computer interfaces. Physiol. Meas. 2004, 25, 815. [Google Scholar] [CrossRef] [PubMed]
- Spüler, M.; Walter, A.; Rosenstiel, W.; Bogdan, M. Spatial filtering based on canonical correlation analysis for classification of evoked or event-related potentials in EEG data. IEEE Trans. Neural Syst. Rehabil. Eng. 2013, 22, 1097–1103. [Google Scholar] [CrossRef]
- Wu, D.; King, J.-T.; Chuang, C.-H.; Lin, C.-T.; Jung, T.-P. Spatial filtering for EEG-based regression problems in brain–computer interface (BCI). IEEE Trans. Fuzzy Syst. 2017, 26, 771–781. [Google Scholar] [CrossRef]
- Pfurtscheller, G.; Allison, B.Z.; Bauernfeind, G.; Brunner, C.; Solis Escalante, T.; Scherer, R.; Zander, T.O.; Mueller-Putz, G.; Neuper, C.; Birbaumer, N. The hybrid BCI. Front. Neurosci. 2010, 4, 3. [Google Scholar] [CrossRef] [PubMed]
- Dähne, S.; Biessmann, F.; Samek, W.; Haufe, S.; Goltz, D.; Gundlach, C.; Villringer, A.; Fazli, S.; Müller, K.-R. Multivariate machine learning methods for fusing multimodal functional neuroimaging data. Proc. IEEE 2015, 103, 1507–1530. [Google Scholar] [CrossRef]
- Deligani, R.J.; Borgheai, S.B.; McLinden, J.; Shahriari, Y. Multimodal fusion of EEG-fNIRS: A mutual information-based hybrid classification framework. Biomed. Opt. Express 2021, 12, 1635–1650. [Google Scholar] [CrossRef]
- Putze, F.; Hesslinger, S.; Tse, C.-Y.; Huang, Y.; Herff, C.; Guan, C.; Schultz, T. Hybrid fNIRS-EEG based classification of auditory and visual perception processes. Front. Neurosci. 2014, 8, 373. [Google Scholar] [CrossRef] [PubMed]
- Al-Shargie, F.; Tang, T.B.; Kiguchi, M. Stress Assessment Based on Decision Fusion of EEG and fNIRS Signals. IEEE Access 2017, 5, 19889–19896. [Google Scholar] [CrossRef]
- Shin, J.; von Lühmann, A.; Blankertz, B.; Kim, D.-W.; Jeong, J.; Hwang, H.-J.; Müller, K.-R. Open access dataset for EEG+ NIRS single-trial classification. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 25, 1735–1745. [Google Scholar] [CrossRef]
- Kwon, J.; Shin, J.; Im, C.-H. Toward a compact hybrid brain-computer interface (BCI): Performance evaluation of multi-class hybrid EEG-fNIRS BCIs with limited number of channels. PLoS ONE 2020, 15, e0230491. [Google Scholar] [CrossRef] [PubMed]
- Buccino, A.P.; Keles, H.O.; Omurtag, A. Hybrid EEG-fNIRS asynchronous brain-computer interface for multiple motor tasks. PLoS ONE 2016, 11, e0146610. [Google Scholar] [CrossRef]
- Sun, Z.; Huang, Z.; Duan, F.; Liu, Y. A Novel Multimodal Approach for Hybrid Brain–Computer Interface. IEEE Access 2020, 8, 89909–89918. [Google Scholar] [CrossRef]
- Zafar, A.; Ghafoor, U.; Yaqub, M.A.; Hong, K.-S. Initial-dip-based classification for fNIRS-BCI. In Proceedings of the Neural Imaging and Sensing 2019; SPIE: Bellingham, WA, USA, 2019; pp. 116–124. [Google Scholar]
- Asam, M.; Khan, S.H.; Akbar, A.; Bibi, S.; Jamal, T.; Khan, A.; Ghafoor, U.; Bhutta, M.R. IoT malware detection architecture using a novel channel boosted and squeezed CNN. Sci. Rep. 2022, 12, 15498. [Google Scholar] [CrossRef]
- Qi, Y.; Ding, F.; Xu, F.; Yang, J. Channel and Feature Selection for a Motor Imagery-Based BCI System Using Multilevel Particle Swarm Optimization. Comput. Intell. Neurosci. 2020, 2020, 8890477. [Google Scholar] [CrossRef]
- Naseer, N.; Hong, K.-S. fNIRS-based brain-computer interfaces: A review. Front. Hum. Neurosci. 2015, 9, 3. [Google Scholar] [CrossRef]
- Nazeer, H.; Naseer, N.; Khan, R.A.; Noori, F.M.; Qureshi, N.K.; Khan, U.S.; Khan, M.J. Enhancing classification accuracy of fNIRS-BCI using features acquired from vector-based phase analysis. J. Neural Eng. 2020, 17, 056025. [Google Scholar] [CrossRef]
- Zafar, A.; Dad Kallu, K.; Atif Yaqub, M.; Ali, M.U.; Hyuk Byun, J.; Yoon, M.; Su Kim, K. A Hybrid GCN and Filter-Based Framework for Channel and Feature Selection: An fNIRS-BCI Study. Int. J. Intell. Syst. 2023, 2023, 8812844. [Google Scholar] [CrossRef]
- Dien, J. Issues in the application of the average reference: Review, critiques, and recommendations. Behav. Res. Methods Instrum. Comput. 1998, 30, 34–43. [Google Scholar] [CrossRef]
- Mannan, M.M.N.; Jeong, M.Y.; Kamran, M.A. Hybrid ICA—Regression: Automatic identification and removal of ocular artifacts from electroencephalographic signals. Front. Hum. Neurosci. 2016, 10, 193. [Google Scholar] [CrossRef]
- Suk, H.I.; Lee, S.W. Subject and class specific frequency bands selection for multiclass motor imagery classification. Int. J. Imaging Syst. Technol. 2011, 21, 123–130. [Google Scholar] [CrossRef]
- Zafar, A.; Hong, K.-S. Neuronal activation detection using vector phase analysis with dual threshold circles: A functional near-infrared spectroscopy study. Int. J. Neural Syst. 2018, 28, 1850031. [Google Scholar] [CrossRef] [PubMed]
- Zafar, A.; Hong, K.-S. Reduction of onset delay in functional near-infrared spectroscopy: Prediction of HbO/HbR signals. Front. Neurorobot. 2020, 14, 10. [Google Scholar] [CrossRef]
- Hong, K.-S.; Khan, M.J.; Hong, M.J. Feature extraction and classification methods for hybrid fNIRS-EEG brain-computer interfaces. Front. Hum. Neurosci. 2018, 12, 246. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.A.H.; Khan, M.U.; Mishra, D. A Computationally Efficient Method for Hybrid EEG-fNIRS BCI Based on the Pearson Correlation. BioMed Res. Int. 2020, 2020, 1838140. [Google Scholar] [CrossRef]
- Zafar, A.; Hussain, S.J.; Ali, M.U.; Lee, S.W. Metaheuristic Optimization-Based Feature Selection for Imagery and Arithmetic Tasks: An fNIRS Study. Sensors 2023, 23, 3714. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Gholizadeh, H. A comprehensive survey: Whale Optimization Algorithm and its applications. Swarm Evol. Comput. 2019, 48, 1–24. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Zamani, H.; Mirjalili, S. Enhanced whale optimization algorithm for medical feature selection: A COVID-19 case study. Comput. Biol. Med. 2022, 148, 105858. [Google Scholar] [CrossRef]
- Aydin, E.A. Subject-Specific feature selection for near infrared spectroscopy based brain-computer interfaces. Comput. Methods Programs Biomed. 2020, 195, 105535. [Google Scholar] [CrossRef]
- Hong, K.-S.; Zafar, A. Existence of initial dip for BCI: An illusion or reality. Front. Neurorobot. 2018, 12, 69. [Google Scholar] [CrossRef]
- Bairathi, D.; Gopalani, D. A novel swarm intelligence based optimization method: Harris’ hawk optimization. In Proceedings of the Intelligent Systems Design and Applications: 18th International Conference on Intelligent Systems Design and Applications (ISDA 2018), Vellore, India, 6–8 December 2018; Volume 2, pp. 832–842. [Google Scholar]
- Kamel, S.; Hamour, H.; Ahmed, M.H.; Nasrat, L. Atom Search optimization Algorithm for Optimal Radial Distribution System Reconfiguration. In Proceedings of the 2019 International Conference on Computer, Control, Electrical, and Electronics Engineering (ICCCEEE), Khartoum, Sudan, 21–23 September 2019; pp. 1–5. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Fister, I.; Fister Jr, I.; Yang, X.-S.; Brest, J. A comprehensive review of firefly algorithms. Swarm Evol. Comput. 2013, 13, 34–46. [Google Scholar] [CrossRef]
- Yang, X.-S. (Ed.) Chapter 11—Bat Algorithms. In Nature-Inspired Optimization Algorithms, 2nd ed.; Academic Press: Cambridge, MA, USA, 2021; pp. 157–173. [Google Scholar]
- Ali, M.U.; Hussain, S.J.; Zafar, A.; Bhutta, M.R.; Lee, S.W. WBM-DLNets: Wrapper-Based Metaheuristic Deep Learning Networks Feature Optimization for Enhancing Brain Tumor Detection. Bioengineering 2023, 10, 475. [Google Scholar] [CrossRef]
- Jiang, X.; Gu, X.; Xu, K.; Ren, H.; Chen, W. Independent decision path fusion for bimodal asynchronous brain–computer interface to discriminate multiclass mental states. IEEE Access 2019, 7, 165303–165317. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Z.; Ji, H.; Li, J.; Liu, L.; Zhuang, J. Cross-Modal Transfer Learning from EEG to Functional Near-Infrared Spectroscopy for Classification Task in Brain-Computer Interface System. Front. Psychol. 2022, 13, 833007. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Feng, L.; Jiang, G.; Xie, P. Multimodal Multitask Neural Network for Motor Imagery Classification With EEG and fNIRS Signals. IEEE Sens. J. 2022, 22, 20695–20706. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Ming, D. Early-stage fusion of EEG and fNIRS improves classification of motor imagery. Front. Neurosci. 2023, 16, 1062889. [Google Scholar] [CrossRef] [PubMed]


| Subject | EEG | fNIRS | ||
|---|---|---|---|---|
| No. of Features | Accuracy (%) | No. of Features | Accuracy (%) | |
| 1 | 150 | 45.83 ± 11.95 | 180 | 50 ± 12.42 |
| 2 | 51.67 ± 12.91 | 66.67 ± 14.16 | ||
| 3 | 52.5 ± 11.82 | 71.67 ± 18.92 | ||
| 4 | 63.33 ± 12.55 | 62.5 ± 9 | ||
| 5 | 57.5 ± 10.72 | 46.67 ± 9.78 | ||
| 6 | 52.5 ± 6.86 | 60 ± 12.91 | ||
| 7 | 50.83 ± 14.41 | 51.67 ± 10.97 | ||
| 8 | 45 ± 11.92 | 58.33 ± 18.43 | ||
| 9 | 61.67 ± 10.54 | 53.33 ± 17.66 | ||
| 10 | 42.5 ± 12.08 | 65.83 ± 10.72 | ||
| 11 | 55.83 ± 12.45 | 55 ± 11.92 | ||
| 12 | 47.5 ± 11.82 | 58.33 ± 11.11 | ||
| 13 | 51.67 ± 12.91 | 65 ± 15.61 | ||
| 14 | 55 ± 18.51 | 53.33 ± 14.27 | ||
| 15 | 45.83 ± 7.08 | 51.67 ± 16.57 | ||
| 16 | 58.33 ± 15.71 | 54.17 ± 9 | ||
| 17 | 42.5 ± 12.08 | 44.17 ± 11.15 | ||
| 18 | 51.67 ± 14.59 | 64.17 ± 10.43 | ||
| 19 | 57.5 ± 10.72 | 37.5 ± 10.58 | ||
| 20 | 61.67 ± 13.72 | 65 ± 15.61 | ||
| 21 | 51.67 ± 12.3 | 65.83 ± 12.7 | ||
| 22 | 36.67 ± 5.83 | 38.33 ± 9.78 | ||
| 23 | 64.17 ± 14.72 | 51.67 ± 10.24 | ||
| 24 | 50.83 ± 13.29 | 55.83 ± 4.03 | ||
| 25 | 66.67 ± 14.16 | 60.83 ± 11.15 | ||
| 26 | 68.33 ± 6.57 | 66.67 ± 14.7 | ||
| 27 | 63.33 ± 5.83 | 74.17 ± 17.32 | ||
| 28 | 55.83 ± 9.66 | 82.5 ± 7.3 | ||
| 29 | 45.83 ± 15.34 | 60.83 ± 13.64 | ||
| Average | 53.59 ± 7.88 | 58.33 ± 10.13 | ||
| Subject | Conventional WOA | Binary E-WOA | ||
|---|---|---|---|---|
| No. of Features | Accuracy (%) | No. of Features | Accuracy (%) | |
| 1 | 96.8 ± 28.11 | 82.5 ± 13.86 | 54.4 ± 23.89 | 91.67 ± 5.56 |
| 2 | 69.3 ± 10.33 | 95 ± 4.3 | 22.5 ± 26.44 | 97.5 ± 7.91 |
| 3 | 81 ± 31.06 | 90.83 ± 10.72 | 37.5 ± 19.45 | 96.67 ± 4.3 |
| 4 | 77.9 ± 12.12 | 87.5 ± 9.82 | 35.6 ± 34.7 | 90 ± 6.57 |
| 5 | 74.2 ± 12.55 | 82.5 ± 9.17 | 33.6 ± 21.11 | 94.17 ± 5.62 |
| 6 | 63.3 ± 9.65 | 85.83 ± 11.82 | 12.9 ± 9.24 | 92.5 ± 4.73 |
| 7 | 67.1 ± 10.24 | 88.33 ± 5.83 | 23.1 ± 23.48 | 93.33 ± 3.51 |
| 8 | 77.5 ± 14.97 | 93.33 ± 8.61 | 31.7 ± 15.38 | 96.67 ± 4.3 |
| 9 | 74 ± 12.44 | 94.17 ± 5.62 | 58.2 ± 38.31 | 95.83 ± 4.39 |
| 10 | 73 ± 8.62 | 90 ± 7.66 | 42.6 ± 22.78 | 92.5 ± 8.29 |
| 11 | 73.3 ± 9.07 | 89.17 ± 7.91 | 18.8 ± 21.09 | 92.5 ± 4.73 |
| 12 | 61.4 ± 10.5 | 82.5 ± 7.3 | 13.2 ± 9.53 | 90 ± 7.66 |
| 13 | 74.7 ± 10.86 | 95.83 ± 5.89 | 29.8 ± 23.38 | 95 ± 5.83 |
| 14 | 59.7 ± 8.26 | 92.5 ± 6.15 | 22.1 ± 17.49 | 95.83 ± 5.89 |
| 15 | 68 ± 6.41 | 87.5 ± 8.1 | 21.9 ± 14.9 | 90.83 ± 7.3 |
| 16 | 72.3 ± 10.79 | 89.17 ± 7.91 | 30.7 ± 24.91 | 91.67 ± 6.8 |
| 17 | 75.5 ± 10.62 | 95 ± 5.83 | 29 ± 21.29 | 94.17 ± 5.62 |
| 18 | 65.1 ± 6.3 | 92.5 ± 4.73 | 36.2 ± 15.5 | 95.83 ± 5.89 |
| 19 | 69.1 ± 10.29 | 93.33 ± 6.57 | 30.4 ± 26.88 | 96.67 ± 4.3 |
| 20 | 69.3 ± 10.88 | 94.17 ± 5.62 | 35.8 ± 15.45 | 95 ± 5.83 |
| 21 | 66.9 ± 8.54 | 90.83 ± 6.15 | 28.9 ± 17.07 | 94.17 ± 6.86 |
| 22 | 66.1 ± 12.72 | 76.67 ± 13.49 | 22.2 ± 25.66 | 87.5 ± 8.1 |
| 23 | 68.7 ± 11.21 | 95 ± 8.05 | 34.2 ± 36.01 | 95 ± 5.83 |
| 24 | 73.4 ± 10.38 | 88.33 ± 8.96 | 32.2 ± 17.86 | 89.17 ± 6.86 |
| 25 | 68.2 ± 14.31 | 92.5 ± 9.98 | 30.9 ± 27.94 | 95.83 ± 5.89 |
| 26 | 69.5 ± 8.51 | 96.67 ± 5.83 | 27.3 ± 17.55 | 100 ± 0 |
| 27 | 59.9 ± 8.81 | 97.5 ± 4.03 | 22.5 ± 9.57 | 100 ± 0 |
| 28 | 70.5 ± 10.32 | 98.33 ± 3.51 | 26.6 ± 13.06 | 99.17 ± 2.64 |
| 29 | 68 ± 8.6 | 83.33 ± 8.78 | 14.3 ± 12.79 | 93.33 ± 5.27 |
| Average | 90.37 ± 7.66 | 94.22 ± 5.39 | ||
| Reference | Year | Approach | Accuracy (%) |
|---|---|---|---|
| Shin et al. [27] | 2016 | Common spatial pattern, mean, slope, shrinkage LDA | 67.5 |
| Sun et al. [30] | 2020 | p-th-Order polynomial fusion | 77.53 |
| Jiang et al. [56] | 2019 | Independent decision path fusion | 78.56 |
| Wang et al. [57] | 2022 | R-CSP-E transfer and ensemble learning | 66.83 |
| He et al. [58] | 2022 | End-to-end multimodal multitask neural network | 82.11 |
| Present Study | 2023 | Temporal features and binary E-WOA | 94.22 ± 5.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, M.U.; Kim, K.S.; Kallu, K.D.; Zafar, A.; Lee, S.W. OptEF-BCI: An Optimization-Based Hybrid EEG and fNIRS–Brain Computer Interface. Bioengineering 2023, 10, 608. https://doi.org/10.3390/bioengineering10050608
Ali MU, Kim KS, Kallu KD, Zafar A, Lee SW. OptEF-BCI: An Optimization-Based Hybrid EEG and fNIRS–Brain Computer Interface. Bioengineering. 2023; 10(5):608. https://doi.org/10.3390/bioengineering10050608
Chicago/Turabian StyleAli, Muhammad Umair, Kwang Su Kim, Karam Dad Kallu, Amad Zafar, and Seung Won Lee. 2023. "OptEF-BCI: An Optimization-Based Hybrid EEG and fNIRS–Brain Computer Interface" Bioengineering 10, no. 5: 608. https://doi.org/10.3390/bioengineering10050608
APA StyleAli, M. U., Kim, K. S., Kallu, K. D., Zafar, A., & Lee, S. W. (2023). OptEF-BCI: An Optimization-Based Hybrid EEG and fNIRS–Brain Computer Interface. Bioengineering, 10(5), 608. https://doi.org/10.3390/bioengineering10050608








