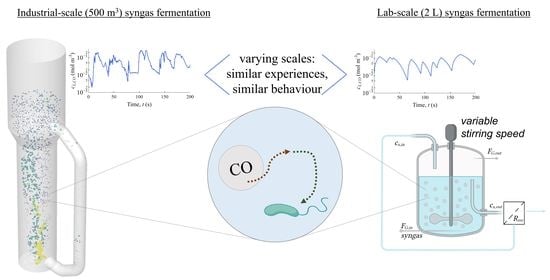
Downscaling Industrial-Scale Syngas Fermentation to Simulate Frequent and Irregular Dissolved Gas Concentration Shocks
Abstract
1. Introduction
2. Methods
2.1. Eulerian Concentration Field
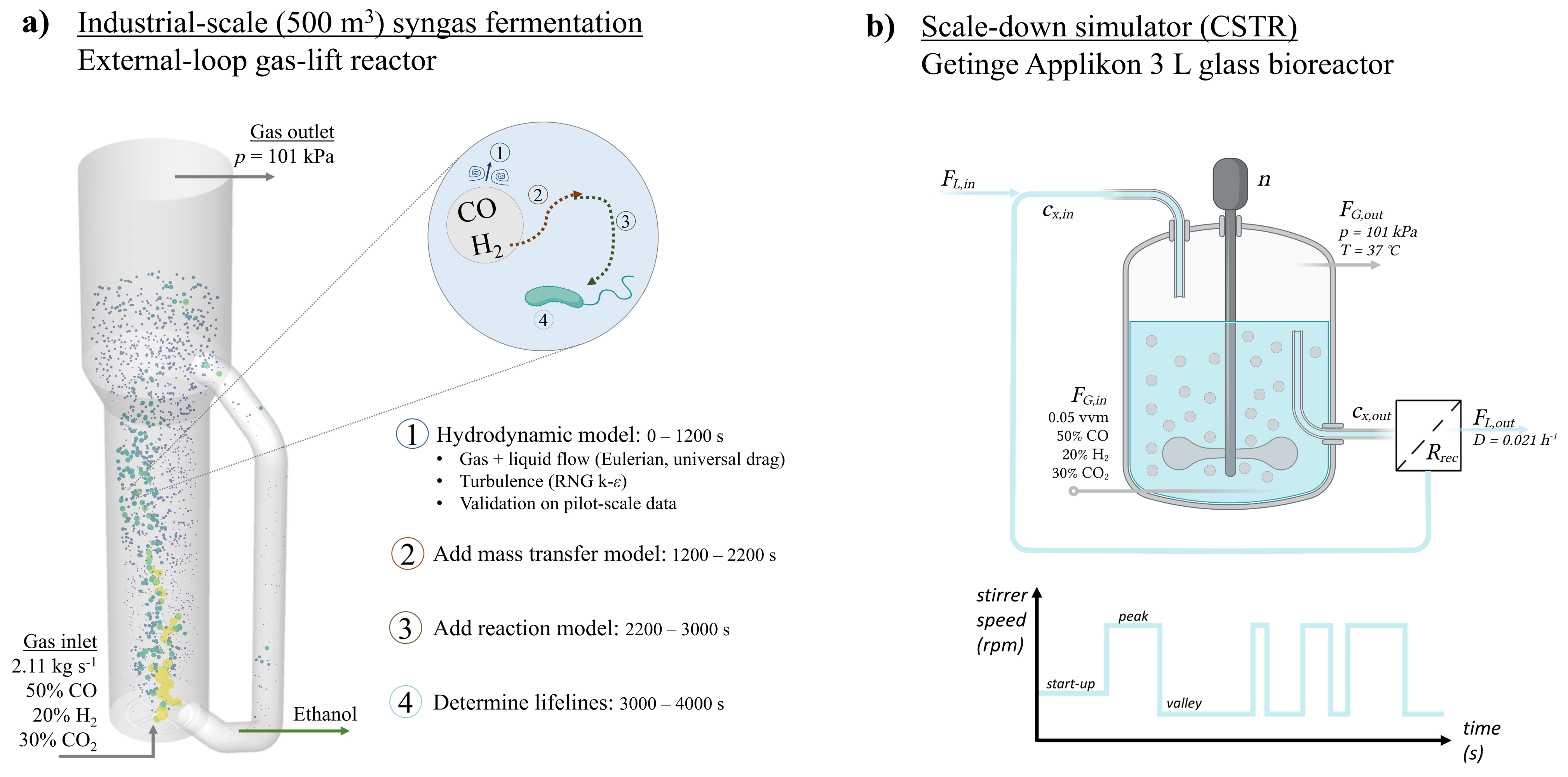
2.1.1. Geometry and Flow Field
2.1.2. Mass Transfer Model
2.1.3. Biological Reaction Modelling
2.2. Lifeline Analysis
2.3. Design of a Scale-Down Simulator
3. Results
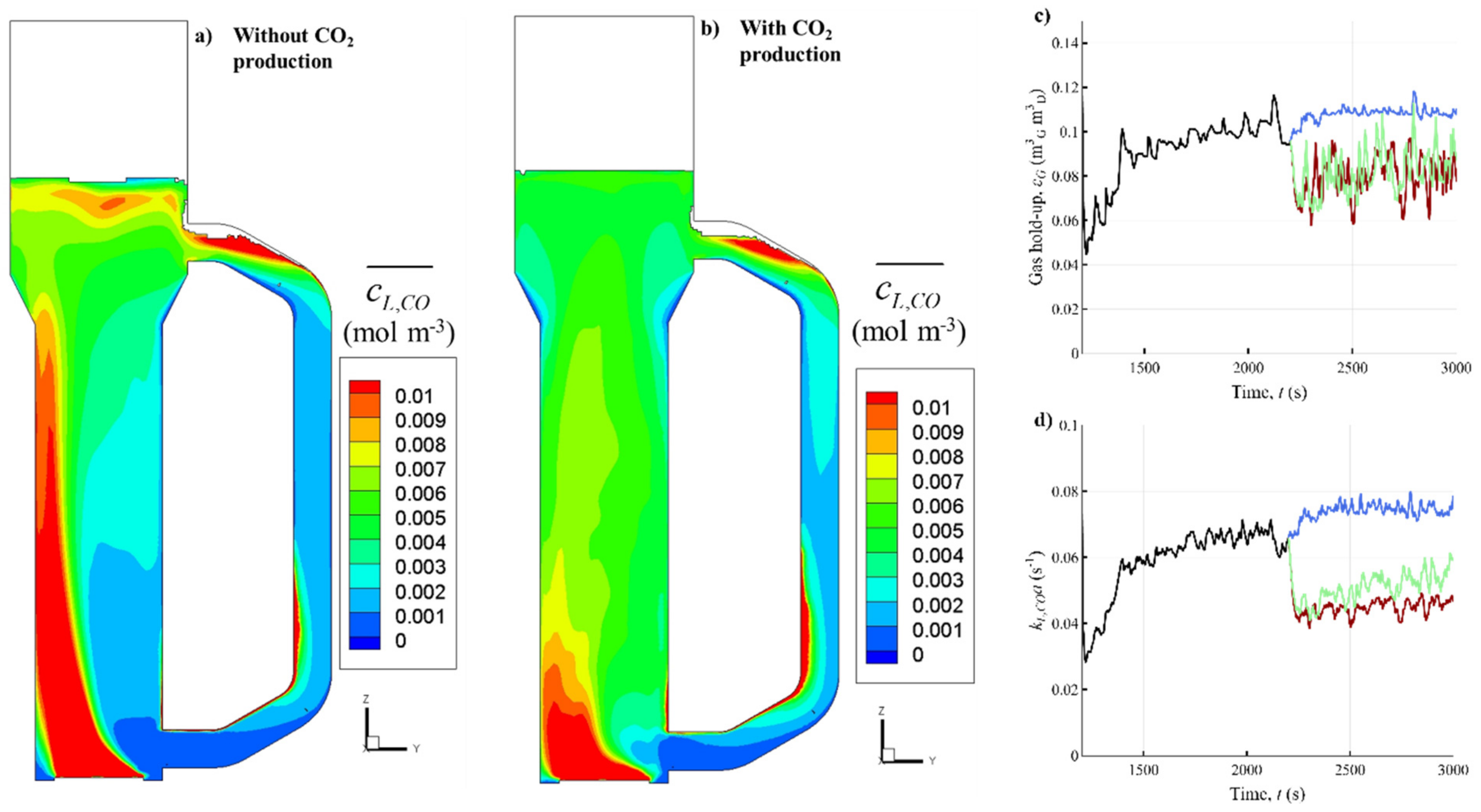
3.1. Eulerian Concentration Gradients in the Industrial Reactor
3.1.1. Influence of Gas Production
3.1.2. Influence of Biomass Concentration
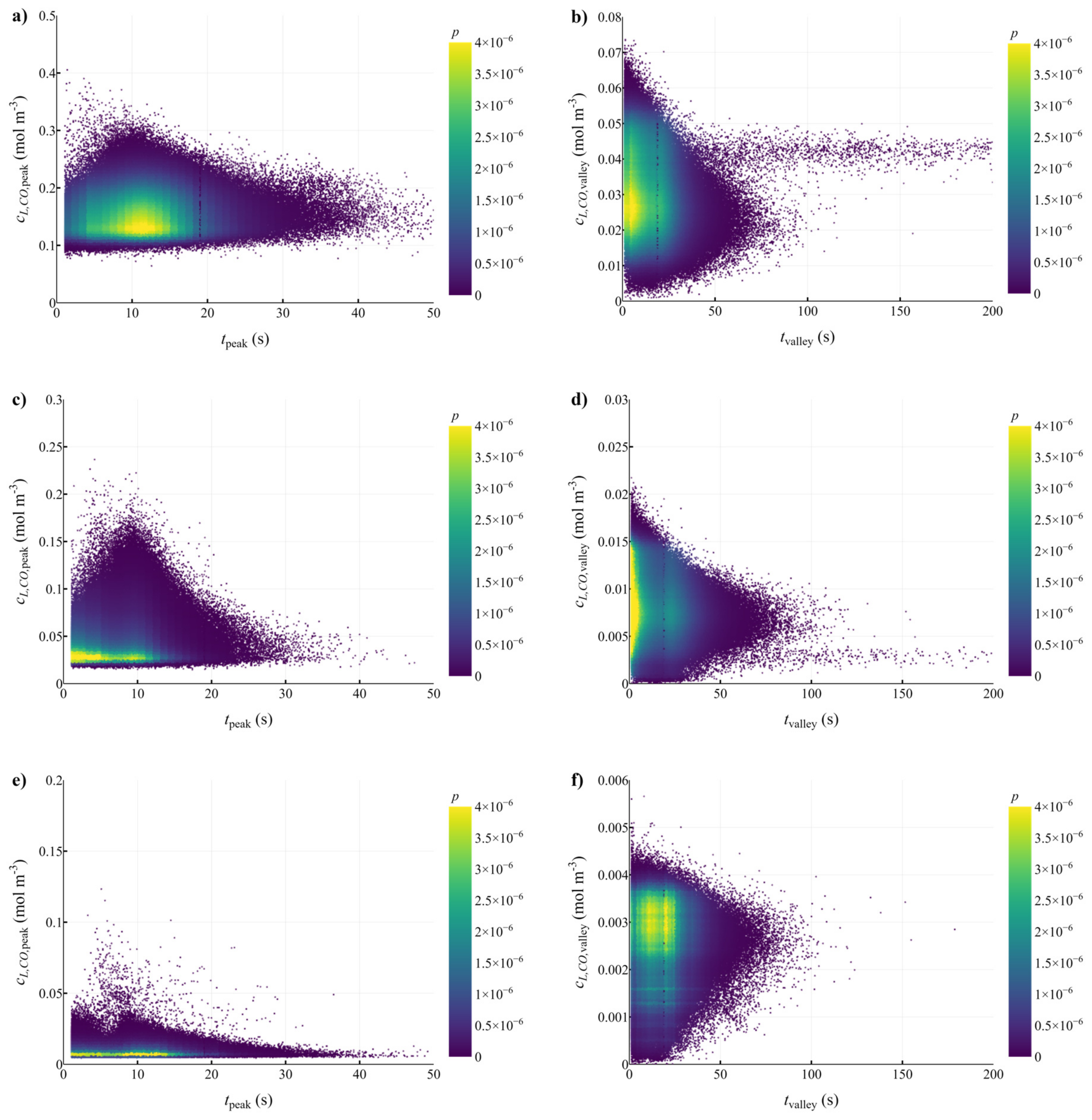
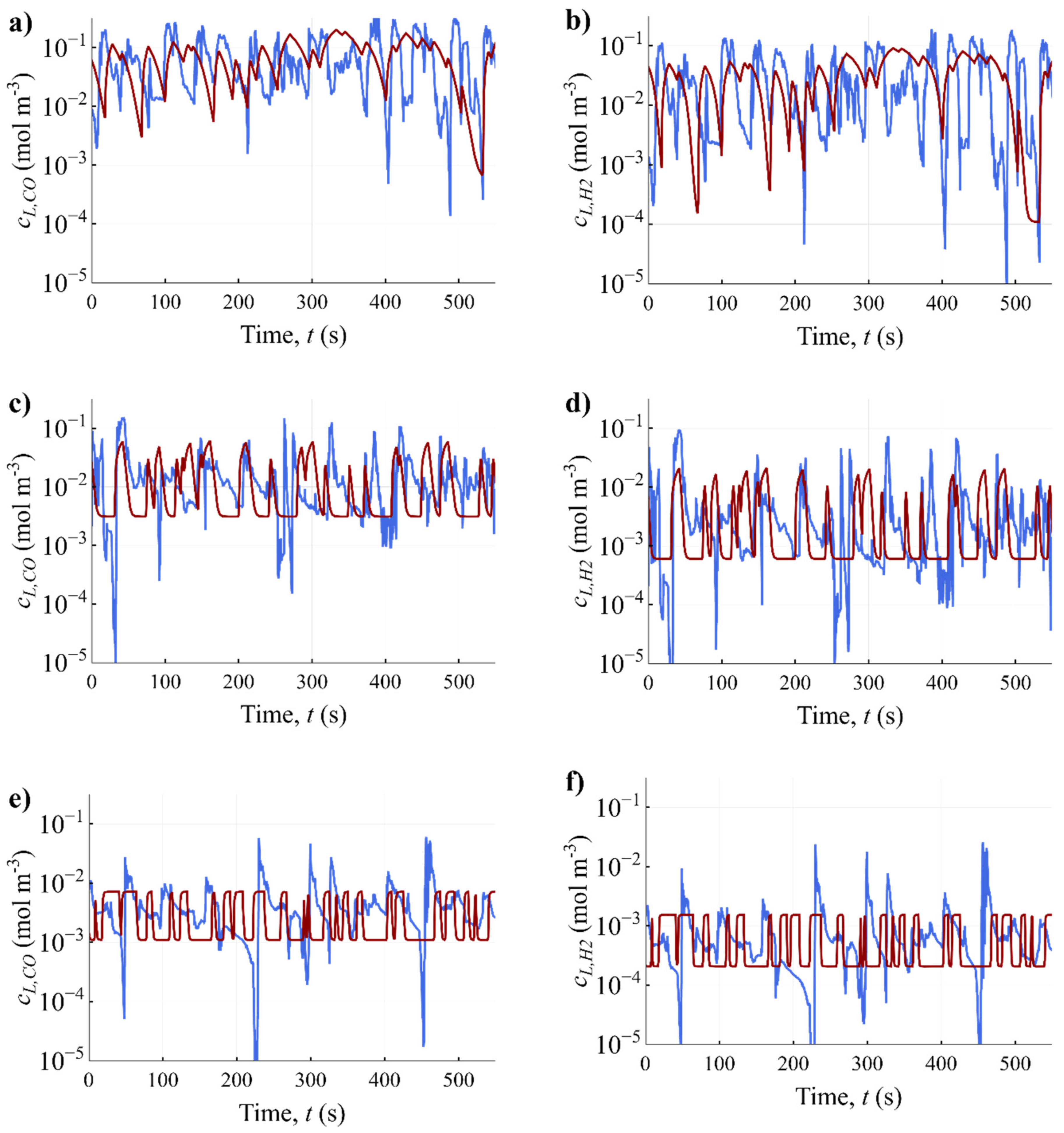
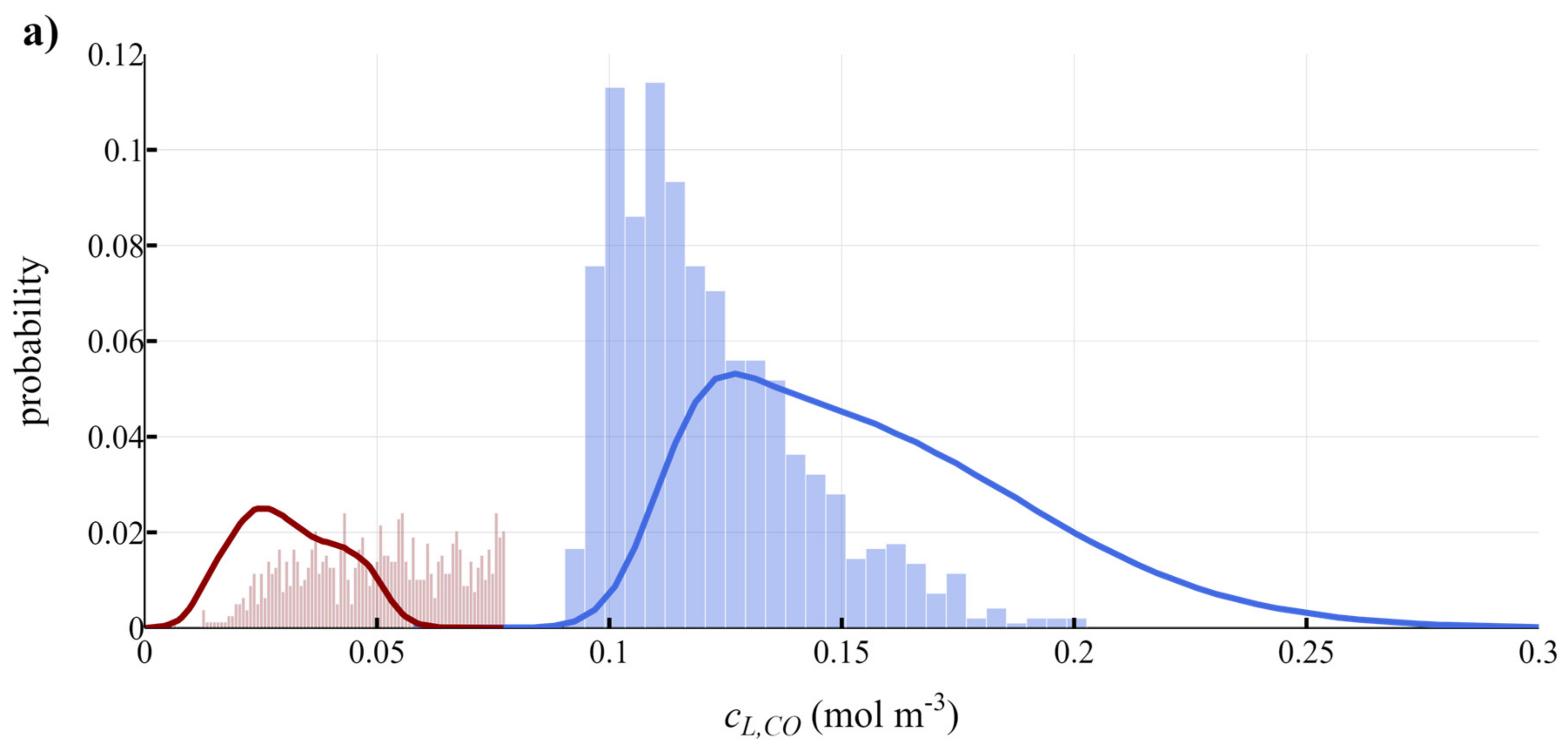
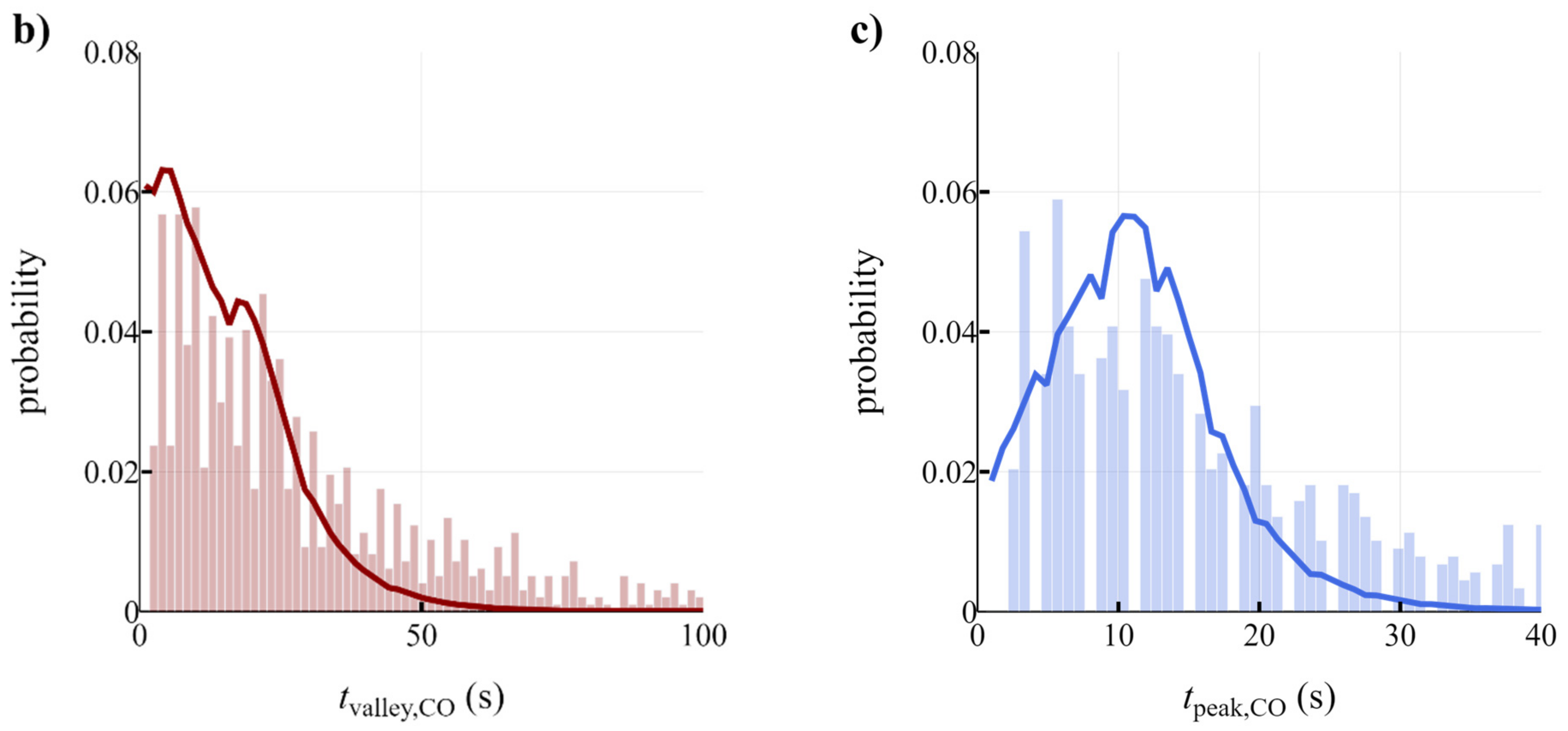
3.2. Lifeline Analysis
3.3. Development of Scale-Down Simulator
3.4. Outlook
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Latin | ||
| c | Concentration | mol m−3 or g L−1 |
| D | Dilution rate | h−1 |
| DL | Diffusion coefficient in liquid phase | m2 s−1 |
| db | Bubble diameter | m |
| di | Impeller diameter | m |
| f | Correction factor | - |
| F | Flow rate | m3 s−1 |
| H | Henry coefficient | kg m−3 Pa−1 |
| k | Turbulent kinetic energy | m2 s−2 |
| kL | Liquid-side mass transfer coefficient | m s−1 |
| kLa | Volumetric mass transfer coefficient | s−1 |
| KI | Inhibition constant | mol m−3 or mol2 m−6 |
| KS | Half-saturation constant | mol m−3 |
| MTR | Mass transfer rate | g L−1 h−1 |
| n | Stirrer speed | rot s−1 |
| Np | Number of particles | - |
| NPo | Power number | - |
| Npeaks | Number of peaks | - |
| Ntc | Number of circulation times | - |
| p | Pressure | Pa |
| P | Power | W |
| q | Biomass-specific uptake rate | mol molx−1 h−1 |
| R | Universal gas constant | J mol−1 K−1 |
| r | Reaction rate | g L−1 h−1 |
| Rrec | Recycling ratio | - |
| t | Time | s |
| tm | 95% mixing time | s |
| T | Temperature | K |
| V | Volume | m3 |
| vslip | Slip velocity | m s−1 |
| us | Superficial velocity | m s−1 |
| X | Conversion | - |
| y | Mole fraction | mol molG−1 |
| Yi/j | Yield | moli molj−1 |
| Greek | ||
| ε | Energy dissipation rate | m2 s−3 |
| εG | Gas hold-up | mG3 mD−3 |
| μ | Biomass-specific growth rate | h−1 |
| ν | Kinematic viscosity | m2 s−1 |
| τ | Characteristic time | s |
| Sub- and superscripts | ||
| 0 | Initial | |
| ∞ | Final | |
| c | Circulation | |
| D | Dispersion | |
| G | Gas | |
| H | Headspace | |
| in | Inlet | |
| L | Liquid | |
| MT | Mass transfer | |
| SD | Scale-down | |
| out | Outlet | |
| rxn | Reaction | |
| X | Biomass | |
References
- Köpke, M.; Simpson, S.D. Pollution to products: Recycling of ‘above ground’ carbon by gas fermentation. Curr. Opin. Biotechnol. 2020, 65, 180–189. [Google Scholar] [CrossRef]
- Fackler, N.; Heijstra, B.D.; Rasor, B.J.; Brown, H.; Martin, J.; Ni, Z.; Shebek, K.M.; Rosin, R.R.; Simpson, S.D.; Tyo, K.E.; et al. Stepping on the Gas to a Circular Economy: Accelerating Development of Carbon-Negative Chemical Production from Gas Fermentation. Annu. Rev. Chem. Biomol. Eng. 2021, 12, 439–470. [Google Scholar] [CrossRef]
- Liew, F.E.; Nogle, R.; Abdalla, T.; Rasor, B.J.; Canter, C.; Jensen, R.O.; Wang, L.; Strutz, J.; Chirania, P.; De Tissera, S.; et al. Carbon-negative production of acetone and isopropanol by gas fermentation at industrial pilot scale. Nat. Biotechnol. 2022, 40, 335–344. [Google Scholar] [CrossRef] [PubMed]
- Puiman, L.; Abrahamson, B.; van der Lans, R.G.J.M.; Haringa, C.; Noorman, H.J.; Picioreanu, C. Alleviating mass transfer limitations in industrial external-loop syngas-to-ethanol fermentation. Chem. Eng. Sci. 2022, 259, 117770. [Google Scholar] [CrossRef]
- Abubackar, H.N.; Veiga, M.C.; Kennes, C. Biological conversion of carbon monoxide: Rich syngas or waste gases to bioethanol. Biofuels Bioprod. Biorefining 2011, 5, 93–114. [Google Scholar] [CrossRef]
- Phillips, J.R.; Huhnke, R.L.; Atiyeh, H.K. Syngas Fermentation: A Microbial Conversion Process of Gaseous Substrates to Various Products. Fermentation 2017, 3, 28. [Google Scholar] [CrossRef]
- Liew, F.M.; Martin, M.E.; Tappel, R.C.; Heijstra, B.D.; Mihalcea, C.; Köpke, M. Gas Fermentation-A flexible platform for commercial scale production of low-carbon-fuels and chemicals from waste and renewable feedstocks. Front. Microbiol. 2016, 7, 694. [Google Scholar] [CrossRef]
- Xu, H.; Liang, C.; Chen, X.; Xu, J.; Yu, Q.; Zhang, Y.; Yuan, Z. Impact of exogenous acetate on ethanol formation and gene transcription for key enzymes in Clostridium autoethanogenum grown on CO. Biochem. Eng. J. 2020, 155, 107470. [Google Scholar] [CrossRef]
- Valgepea, K.; de Souza Pinto Lemgruber, R.; Abdalla, T.; Binos, S.; Takemori, N.; Takemori, A.; Tanaka, Y.; Tappel, R.; Köpke, M.; Simpson, S.D.; et al. H2 drives metabolic rearrangements in gas-fermenting Clostridium autoethanogenum. Biotechnol. Biofuels 2018, 11, 55. [Google Scholar] [CrossRef]
- Lara, A.R.; Galindo, E.; Ramírez, O.T.; Palomares, L.A. Living with heterogeneities in bioreactors. Mol. Biotechnol. 2006, 34, 355–381. [Google Scholar] [CrossRef]
- Nadal-Rey, G.; McClure, D.D.; Kavanagh, J.M.; Cornelissen, S.; Fletcher, D.F.; Gernaey, K.V. Understanding gradients in industrial bioreactors. Biotechnol. Adv. 2021, 46, 107660. [Google Scholar] [CrossRef] [PubMed]
- Benalcázar, A.E. Modeling the anaerobic fermentation of CO, H2 and CO2 mixtures at large and micro-scales. Doctoral dissertation, Delft University of Technology, Delft, The Netherlands, 2023. [Google Scholar]
- Delvigne, F.; Takors, R.; Mudde, R.; van Gulik, W.; Noorman, H. Bioprocess scale-up/down as integrative enabling technology: From fluid mechanics to systems biology and beyond. Microb. Biotechnol. 2017, 10, 1267–1274. [Google Scholar] [CrossRef] [PubMed]
- Noorman, H.J.; Heijnen, J.J. Biochemical engineering’s grand adventure. Chem. Eng. Sci. 2017, 170, 677–693. [Google Scholar] [CrossRef]
- Hartmann, F.S.F.; Udugama, I.A.; Seibold, G.M.; Sugiyama, H.; Gernaey, K.V. Digital models in biotechnology: Towards multi-scale integration and implementation. Biotechnol. Adv. 2022, 60, 108015. [Google Scholar] [CrossRef]
- Haringa, C.; Tang, W.; Deshmukh, A.T.; Xia, J.; Reuss, M.; Heijnen, J.J.; Mudde, R.F.; Noorman, H.J. Euler-Lagrange computational fluid dynamics for (bio)reactor scale down: An analysis of organism lifelines. Eng. Life Sci. 2016, 16, 652–663. [Google Scholar] [CrossRef]
- Siebler, F.; Lapin, A.; Hermann, M.; Takors, R. The impact of CO gradients on C. ljungdahlii in a 125 m3 bubble column: Mass transfer, circulation time and lifeline analysis. Chem. Eng. Sci. 2019, 207, 410–423. [Google Scholar] [CrossRef]
- McClure, D.D.; Kavanagh, J.M.; Fletcher, D.F.; Barton, G.W. Characterizing bubble column bioreactor performance using computational fluid dynamics. Chem. Eng. Sci. 2016, 144, 58–74. [Google Scholar] [CrossRef]
- Haringa, C.; Deshmukh, A.T.; Mudde, R.F.; Noorman, H.J. Euler-Lagrange analysis towards representative down-scaling of a 22 m3 aerobic S. cerevisiae fermentation. Chem. Eng. Sci. 2017, 170, 653–669. [Google Scholar] [CrossRef]
- Kuschel, M.; Takors, R. Simulated oxygen and glucose gradients as a prerequisite for predicting industrial scale performance a priori. Biotechnol. Bioeng. 2020, 117, 2760–2770. [Google Scholar] [CrossRef]
- Kuschel, M.; Siebler, F.; Takors, R. Lagrangian Trajectories to Predict the Formation of Population Heterogeneity in Large-Scale Bioreactors. Bioeng. 2017, 4, 27. [Google Scholar] [CrossRef]
- Lapin, A.; Müller, D.; Reuss, M. Dynamic behavior of microbial populations in stirred bioreactors simulated with Euler-Lagrange methods: Traveling along the lifelines of single cells. Ind. Eng. Chem. Res. 2004, 43, 4647–4656. [Google Scholar] [CrossRef]
- Haringa, C.; Tang, W.; Wang, G.; Deshmukh, A.T.; van Winden, W.A.; Chu, J.; van Gulik, W.M.; Heijnen, J.J.; Mudde, R.F.; Noorman, H.J. Computational fluid dynamics simulation of an industrial P. chrysogenum fermentation with a coupled 9-pool metabolic model: Towards rational scale-down and design optimization. Chem. Eng. Sci. 2018, 175, 12–24. [Google Scholar] [CrossRef]
- Norman, R.O.J.; Millat, T.; Schatschneider, S.; Henstra, A.M.; Breitkopf, R.; Pander, B.; Annan, F.J.; Piatek, P.; Hartman, H.B.; Poolman, M.G.; et al. Genome-scale model of C. autoethanogenum reveals optimal bioprocessconditions for high-value chemical production from carbon monoxide. Eng. Biol. 2019, 3, 32–40. [Google Scholar] [CrossRef]
- Greene, J.; Daniell, J.; Köpke, M.; Broadbelt, L.; Tyo, K.E.J. Kinetic ensemble model of gas fermenting Clostridium autoethanogenum for improved ethanol production. Biochem. Eng. J. 2019, 148, 46–56. [Google Scholar] [CrossRef]
- Wang, G.; Haringa, C.; Tang, W.; Noorman, H.; Chu, J.; Zhuang, Y.; Zhang, S. Coupled metabolic-hydrodynamic modeling enabling rational scale-up of industrial bioprocesses. Biotechnol. Bioeng. 2020, 117, 844–867. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Haringa, C.; Noorman, H.; Chu, J.; Zhuang, Y. Developing a Computational Framework To Advance Bioprocess Scale-Up. Trends Biotechnol. 2020, 38, 846–856. [Google Scholar] [CrossRef]
- Tang, W.; Deshmukh, A.T.; Haringa, C.; Wang, G.; van Gulik, W.; van Winden, W.; Reuss, M.; Heijnen, J.J.; Xia, J.; Chu, J.; et al. A 9-pool metabolic structured kinetic model describing days to seconds dynamics of growth and product formation by Penicillium chrysogenum. Biotechnol. Bioeng. 2017, 114, 1733–1743. [Google Scholar] [CrossRef]
- Mahamkali, V.; Valgepea, K.; de Souza Pinto Lemgruber, R.; Plan, M.; Tappel, R.; Köpke, M.; Simpson, S.D.; Nielsen, L.K.; Marcellin, E. Redox controls metabolic robustness in the gas-fermenting acetogen Clostridium autoethanogenum. Proc. Natl. Acad. Sci. USA 2020, 117, 13168–13175. [Google Scholar] [CrossRef]
- Neubauer, P.; Junne, S. Scale-down simulators for metabolic analysis of large-scale bioprocesses. Curr. Opin. Biotechnol. 2010, 21, 114–121. [Google Scholar] [CrossRef]
- Puiman, L.; Elisiário, M.P.; Crasborn, L.M.L.; Wagenaar, L.E.C.H.; Straathof, A.J.J.; Haringa, C. Gas mass transfer in syngas fermentation broths is enhanced by ethanol. Biochem. Eng. J. 2022, 185, 108505. [Google Scholar] [CrossRef]
- Zanghi, A.; Lin, D.; Balsara, T.; Young, L.; Wolf, B.; Huang, P. Increased Efficiency and Product Quality with the UniVessel ® Single Use Bioreactor for CHO Fed-Batch Cultures. 2017. Available online: http://www.sartorius.com (accessed on 30 August 2022).
- Higbie, R. The Rate of Absorption of a Pure Gas into a Still Liquid during Short Periods of Exposure. Trans. AIChE. 1935, 31, 365–389. [Google Scholar]
- Lamont, J.C.; Scott, D.S. An eddy cell model of mass transfer into the surface of a turbulent liquid. AIChE J. 1970, 16, 513–519. [Google Scholar] [CrossRef]
- Roels, J.A.; Heijnen, J.J. Power dissipation and heat production in bubble columns: Approach based on nonequilibrium thermodynamics. Biotechnol. Bioeng. 1980, 22, 2399–2404. [Google Scholar] [CrossRef]
- Gimbun, J.; Rielly, C.D.; Nagy, Z.K. Modelling of mass transfer in gas-liquid stirred tanks agitated by Rushton turbine and CD-6 impeller: A scale-up study. Chem. Eng. Res. Des. 2009, 87, 437–451. [Google Scholar] [CrossRef]
- Heijnen, J.J.; Van’t Riet, K. Mass transfer, mixing and heat transfer phenomena in low viscosity bubble column reactors. Chem. Eng. J. 1984, 28, B21–B42. [Google Scholar] [CrossRef]
- Jamialahmadi, M.; Müller-Steinhagen, H. Effect of alcohol, organic acid and potassium chloride concentration on bubble size, bubble rise velocity and gas hold-up in bubble columns. Chem. Eng. J. 1992, 50, 47–56. [Google Scholar] [CrossRef]
- Prins, A.; Riet, K.V. Proteins and surface effects in fermentation: Foam, antifoam and mass transfer. Trends Biotechnol. 1987, 5, 296–301. [Google Scholar] [CrossRef]
- ANSYS Inc. Ansys Fluent Theory Guide, Release 2021.2; ANSYS Inc.: Pittsburgh, PA, USA, 2021. [Google Scholar]
- Mohammadi, M.; Mohamed, A.R.; Najafpour, G.D.; Younesi, H.; Uzir, M.H. Kinetic studies on fermentative production of biofuel from synthesis gas using clostridium ljungdahlii. Sci. World J. 2014, 2014, 910590. [Google Scholar] [CrossRef] [PubMed]
- de Medeiros, E.M.; Posada, J.A.; Noorman, H.; Filho, R.M. Modeling and Multi-Objective Optimization of Syngas Fermentation in a Bubble Column Reactor. Comput. Aided Chem. Eng. 2019, 46, 1531–1536. [Google Scholar] [CrossRef]
- Sander, R. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmos. Chem. Phys. 2015, 15, 4399–4981. [Google Scholar] [CrossRef]
- Cussler, E.L. Diffusion: Mass Transfer in Fluid Systems, 3rd ed.; Cambridge University Press: Cambridge, MA, USA; New York, NY, USA, 2011. [Google Scholar]
- Garcia-Ochoa, F.; Gomez, E. Bioreactor scale-up and oxygen transfer rate in microbial processes: An overview. Biotechnol. Adv. 2009, 27, 153–176. [Google Scholar] [CrossRef]
- Riet, K.V. Review of Measuring Methods and Results in Nonviscous Gas-Liquid Mass Transfer in Stirred Vessels. Ind. Eng. Chem. Process Des. Dev. 1979, 18, 357–364. [Google Scholar] [CrossRef]
- Benalcázar, A.E.; Noorman, H.; Filho, R.M.; Posada, J.A. Modeling ethanol production through gas fermentation: A biothermodynamics and mass transfer-based hybrid model for microbial growth in a large-scale bubble column bioreactor. Biotechnol. Biofuels. 2020, 13, 59. [Google Scholar] [CrossRef]
- Richter, H.; Martin, M.E.; Angenent, L.T. A two-stage continuous fermentation system for conversion of syngas into ethanol. Energies 2013, 6, 3987–4000. [Google Scholar] [CrossRef]
- Valgepea, K.; de Souza Pinto Lemgruber, R.; Meaghan, K.; Palfreyman, R.W.; Abdalla, T.; Heijstra, B.D.; Behrendorff, J.B.; Tappel, R.; Köpke, M.; Simpson, S.D.; et al. Maintenance of ATP Homeostasis Triggers Metabolic Shifts in Gas-Fermenting Acetogens. Cell Syst. 2017, 4, 505–515.e5. [Google Scholar] [CrossRef]
- Galaction, A.I.; Cascaval, D.; Oniscu, C.; Turnea, M. Prediction of oxygen mass transfer coefficients in stirred bioreactors for bacteria, yeasts and fungus broths. Biochem. Eng. J. 2004, 20, 85–94. [Google Scholar] [CrossRef]
- Merchuk, J.C.; Siegel, M.H. Air-lift reactors in chemical and biological technology. J. Chem. Technol. Biotechnol. 1988, 41, 105–120. [Google Scholar] [CrossRef]
- Gaugler, L.; Mast, Y.; Fitschen, J.; Hofmann, S.; Schlüter, M.; Takors, R. Scaling-down biopharmaceutical production processes via a single multi-compartment bioreactor (SMCB). Eng. Life Sci. 2022, 23, e2100161. [Google Scholar] [CrossRef]
- Oosterhuis, N.M.G. Scale-Up of Bioreactors: A Scale-Down Approach. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1984. [Google Scholar]
- Wang, G.; Tang, W.; Xia, J.; Chu, J.; Noorman, H.; van Gulik, W.M. Integration of microbial kinetics and fluid dynamics toward model-driven scale-up of industrial bioprocesses. Eng. Life Sci. 2015, 15, 20–29. [Google Scholar] [CrossRef]
- Riet, K.V.; van der Lans, R.G.J.M. Mixing in Bioreactor Vessels. Compr. Biotechnol. 2011, 2, 63–80. [Google Scholar] [CrossRef]
- Esperança, M.N.; Buffo, M.M.; Mendes, C.E.; Rodriguez, G.Y.; Béttega, R.; Badino, A.C.; Cerri, M.O. Linking maximal shear rate and energy dissipation/circulation function in airlift bioreactors, Biochem. Eng. J. 2022, 178, 108308. [Google Scholar] [CrossRef]
- Smith, J.J.; Lilly, M.D.; Fox, R.I. The effect of agitation on the morphology and penicillin production of Penicillium chrysogenum. Biotechnol. Bioeng. 1990, 35, 1011–1023. [Google Scholar] [CrossRef]
- Abrini, J.; Naveau, H.; Nyns, E.J. Clostridium autoethanogenum; sp. nov., an anaerobic bacterium that produces ethanol from carbon monoxide. Arch. Microbiol. 1994, 161, 345–351. [Google Scholar] [CrossRef]
- Nienow, A.W. The Impact of Fluid Dynamic Stress in Stirred Bioreactors—The Scale of the Biological Entity: A Personal View. Chem. Ing. Tech. 2021, 93, 17–30. [Google Scholar] [CrossRef]
- de Lima, L.A.; Ingelman, H.; Brahmbhatt, K.; Reinmets, K.; Barry, C.; Harris, A.; Marcellin, E.; Köpke, M.; Valgepea, K. Faster Growth Enhances Low Carbon Fuel and Chemical Production Through Gas Fermentation. Front. Bioeng. Biotechnol. 2022, 10, 879578. [Google Scholar] [CrossRef] [PubMed]
- Mann, M.; Miebach, K.; Büchs, J. Online measurement of dissolved carbon monoxide concentrations reveals critical operating conditions in gas fermentation experiments. Biotechnol. Bioeng. 2021, 118, 253–264. [Google Scholar] [CrossRef]
- Dang, J.; Wang, N.; Atiyeh, H.K. Review of Dissolved CO and H2 Measurement Methods for Syngas Fermentation. Sensors 2021, 21, 2165. [Google Scholar] [CrossRef]
- Benalcázar, E.A.; Noorman, H.; Filho, R.M.; Posada, J. A Systematic Approach for the Processing of Experimental Data from Anaerobic Syngas Fermentations. Comput. Aided Chem. Eng. 2022, 51, 1303–1308. [Google Scholar] [CrossRef]
- de Jonge, L.P.; Buijs, N.A.A.; Pierick, A.T.; Deshmukh, A.; Zhao, Z.; Kiel, J.A.K.W.; Heijnen, J.J.; van Gulik, W.M. Scale-down of penicillin production in Penicillium chrysogenum. Biotechnol. J. 2011, 6, 944–958. [Google Scholar] [CrossRef]
- Marcellin, E.; Angenent, L.T.; Nielsen, L.K.; Molitor, B. Recycling carbon for sustainable protein production using gas fermentation. Curr. Opin. Biotechnol. 2022, 76, 102723. [Google Scholar] [CrossRef]
- Diender, M.; Stams, A.J.M.; Sousa, D.Z. Production of medium-chain fatty acids and higher alcohols by a synthetic co-culture grown on carbon monoxide or syngas. Biotechnol. Biofuels. 2016, 9, 1–11. [Google Scholar] [CrossRef]
- Lagoa-Costa, B.; Abubackar, H.N.; Fernández-Romasanta, M.; Kennes, C.; Veiga, M.C. Integrated bioconversion of syngas into bioethanol and biopolymers. Bioresour. Technol. 2017, 239, 244–249. [Google Scholar] [CrossRef] [PubMed]
- Köpke, M.; Mihalcea, C.; Bromley, J.C.; Simpson, S.D. Fermentative production of ethanol from carbon monoxide. Curr. Opin. Biotechnol. 2011, 22, 320–325. [Google Scholar] [CrossRef]
- Ishaq, H.; Dincer, I.; Crawford, C. A review on hydrogen production and utilization: Challenges and opportunities. Int. J. Hydrogen Energy. 2022, 47, 26238–26264. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Selected Papers of Hirotugu Akaike; Springer: New York, NY, USA, 1998; pp. 199–213. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning. Available online: https://www.microsoft.com/en-us/research/uploads/prod/2006/01/Bishop-Pattern-Recognition-and-Machine-Learning-2006.pdf (accessed on 1 March 2023).
- Haringa, C.; Noorman, H.J.; Mudde, R.F. Lagrangian modeling of hydrodynamic–kinetic interactions in (bio)chemical reactors: Practical implementation and setup guidelines. Chem. Eng. Sci. 2017, 157, 159–168. [Google Scholar] [CrossRef]
- Van’t Riet, K.; Van der Lans, R. Mixing in bioreactor vessels. In Comprehensive Biotechnology, 2nd ed.; Moo-Young, M., Ed.; Elsevier: Amsterdam, The Netherlands, 2011; Volume 2, pp. 63–80. [Google Scholar]


| Name | Symbol | CO | H2 | CO2 | Unit | Source |
|---|---|---|---|---|---|---|
| Inlet gas fraction | yi,in | 0.5 | 0.2 | 0.3 | moli molG−1 | [29] |
| Henry coefficient | 2.30 × 10−7 | 1.47 × 10−8 | 1.06 × 10−5 | kg m−3 Pa−1 | [43] | |
| Diffusion coefficient | 2.71 × 10−9 | 6.01 × 10−9 | 2.56 × 10−9 | m2 s−1 | [44] | |
| Maximum uptake rate | 1.459 | 2.565 | - | mol molX−1 h−1 | [12] | |
| Half-saturation coefficient | 0.042 | 0.025 | - | mol m−3 | [12] | |
| Inhibition coefficients | 0.246 | 0.025 | - | mol2 m−6, mol m−3 | [12] |
| Name | Symbol | CO | H2 | CO2 | Biomass | Unit | Source |
|---|---|---|---|---|---|---|---|
| Inlet gas fraction | 0.5 | 0.2 | 0.3 | - | moli molG−1 | - | |
| Inlet liquid concentration | 0 | 0 | 0 | mol mL−3 | - | ||
| Biomass yield | 0.041 | 0.0070 | - | - | molX moli−1 | [47] | |
| Initial liquid concentration | 0.1 | 0.03 | 7.4 | 2.03 | mol mL−3 | - |
| Peak | Valley | Recycle | ||||||
|---|---|---|---|---|---|---|---|---|
| (g L−1) | n (rpm) | (h−1) | P/V (W m−3) | n (rpm) | (h−1) | P/V (W m−3) | Rrec (-) | (g L−1) |
| 5 | 910 | 153 | 23,000 | 20 | 1.3 | 0.11 | 0.5 | 0.54 |
| 10 | 900 | 150 | 22,000 | 150 | 15 | 70 | 0.91 | 1.44 |
| 25 | 500 | 71 | 3400 | 70 | 5.6 | 6.1 | 0.96 | 3.27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puiman, L.; Almeida Benalcázar, E.; Picioreanu, C.; Noorman, H.J.; Haringa, C. Downscaling Industrial-Scale Syngas Fermentation to Simulate Frequent and Irregular Dissolved Gas Concentration Shocks. Bioengineering 2023, 10, 518. https://doi.org/10.3390/bioengineering10050518
Puiman L, Almeida Benalcázar E, Picioreanu C, Noorman HJ, Haringa C. Downscaling Industrial-Scale Syngas Fermentation to Simulate Frequent and Irregular Dissolved Gas Concentration Shocks. Bioengineering. 2023; 10(5):518. https://doi.org/10.3390/bioengineering10050518
Chicago/Turabian StylePuiman, Lars, Eduardo Almeida Benalcázar, Cristian Picioreanu, Henk J. Noorman, and Cees Haringa. 2023. "Downscaling Industrial-Scale Syngas Fermentation to Simulate Frequent and Irregular Dissolved Gas Concentration Shocks" Bioengineering 10, no. 5: 518. https://doi.org/10.3390/bioengineering10050518
APA StylePuiman, L., Almeida Benalcázar, E., Picioreanu, C., Noorman, H. J., & Haringa, C. (2023). Downscaling Industrial-Scale Syngas Fermentation to Simulate Frequent and Irregular Dissolved Gas Concentration Shocks. Bioengineering, 10(5), 518. https://doi.org/10.3390/bioengineering10050518