Accelerated Diffusion-Weighted MRI of Rectal Cancer Using a Residual Convolutional Network
Abstract
1. Introduction
2. Materials and Methods
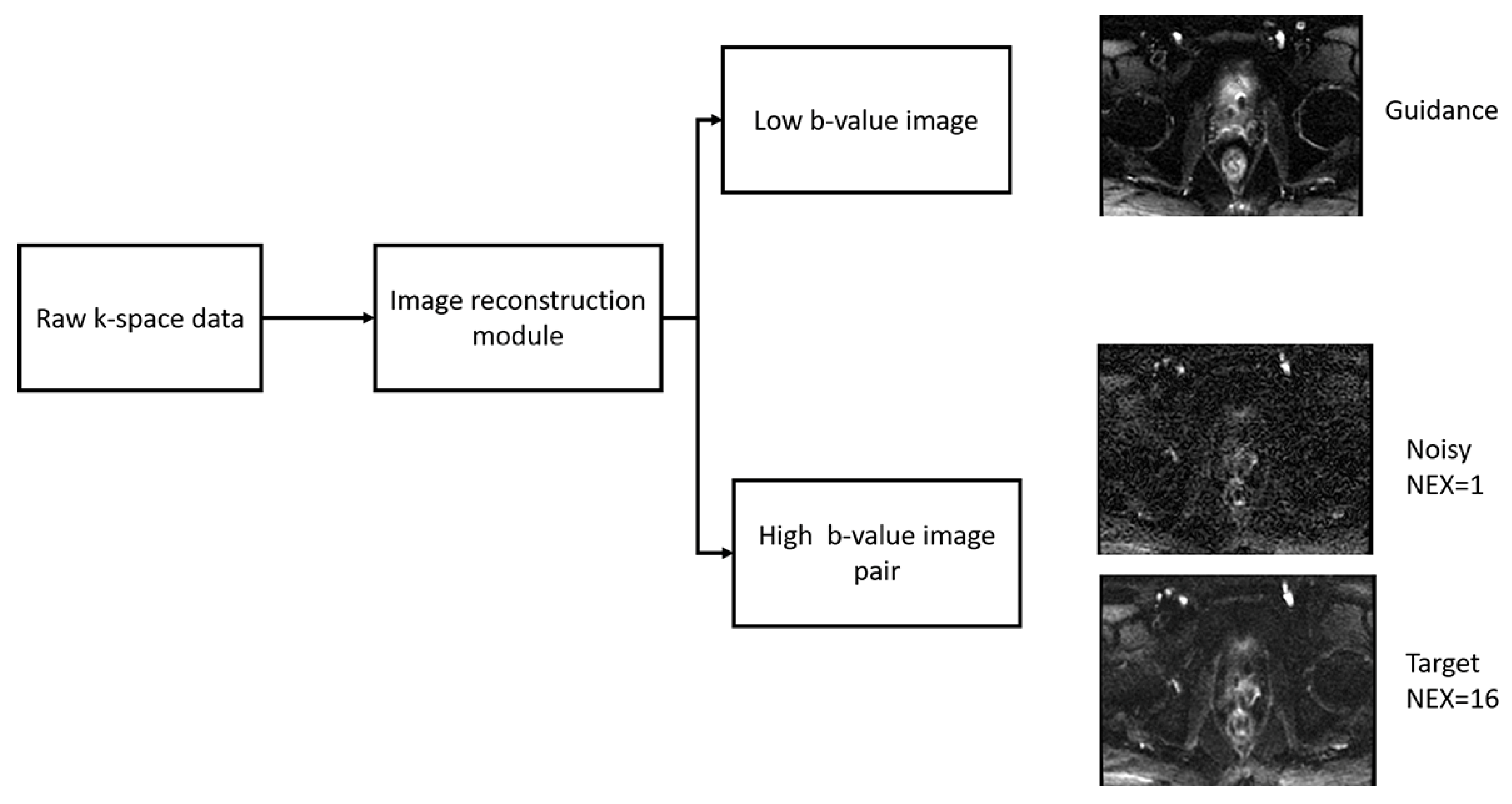
2.1. Data Acquisition
2.2. Image Reconstruction
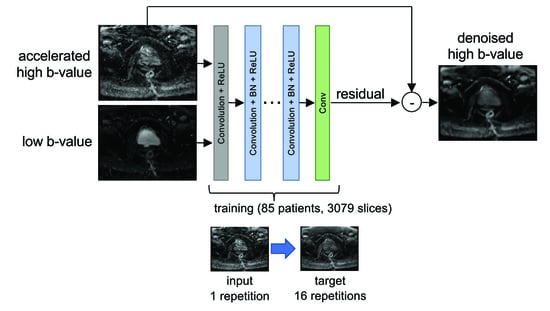
2.3. Denoising Convolutional Neural Network (DCNN)
2.4. Quantitative Evaluation
2.5. Qualitative Evaluation by Expert Body Radiologist
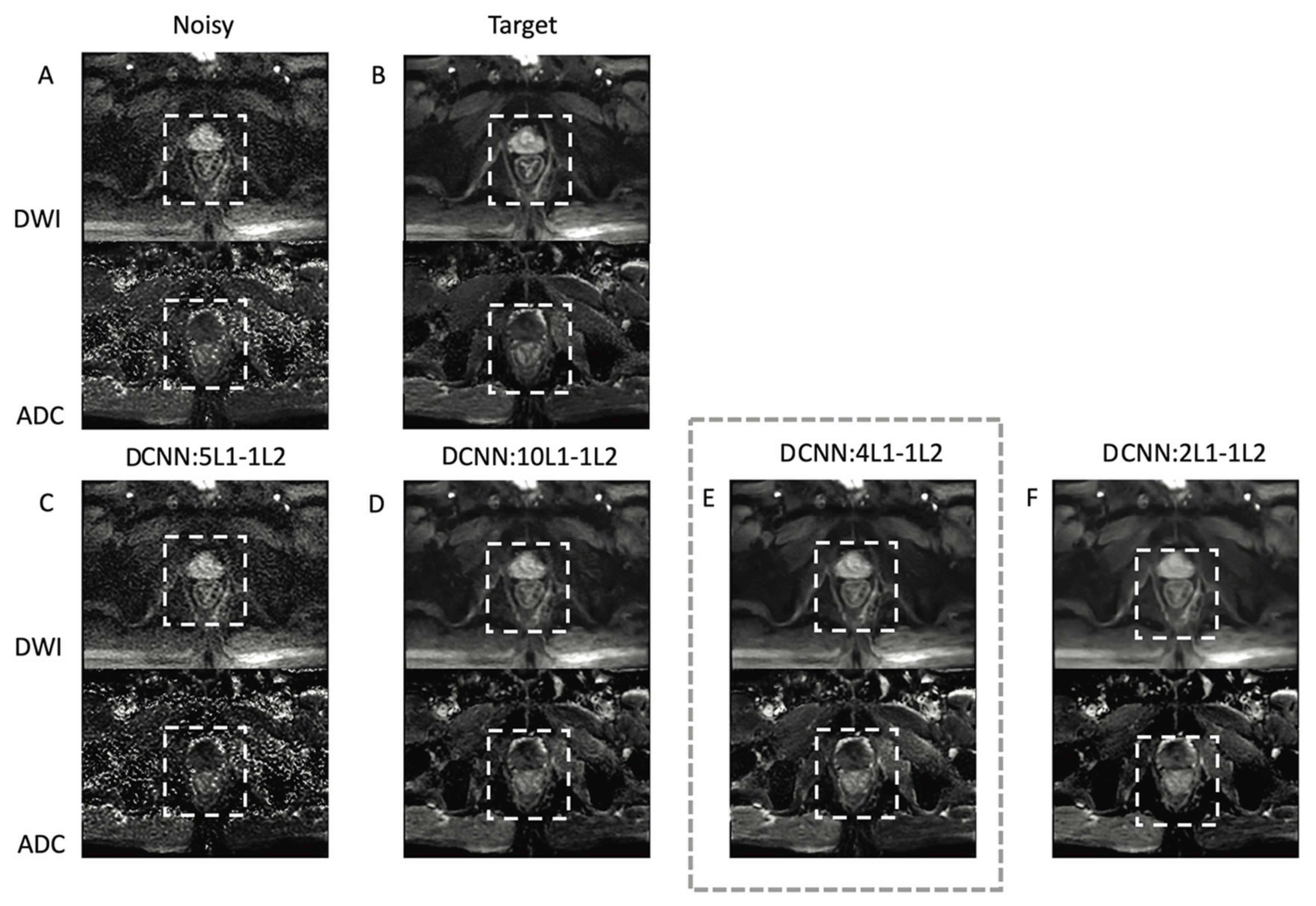
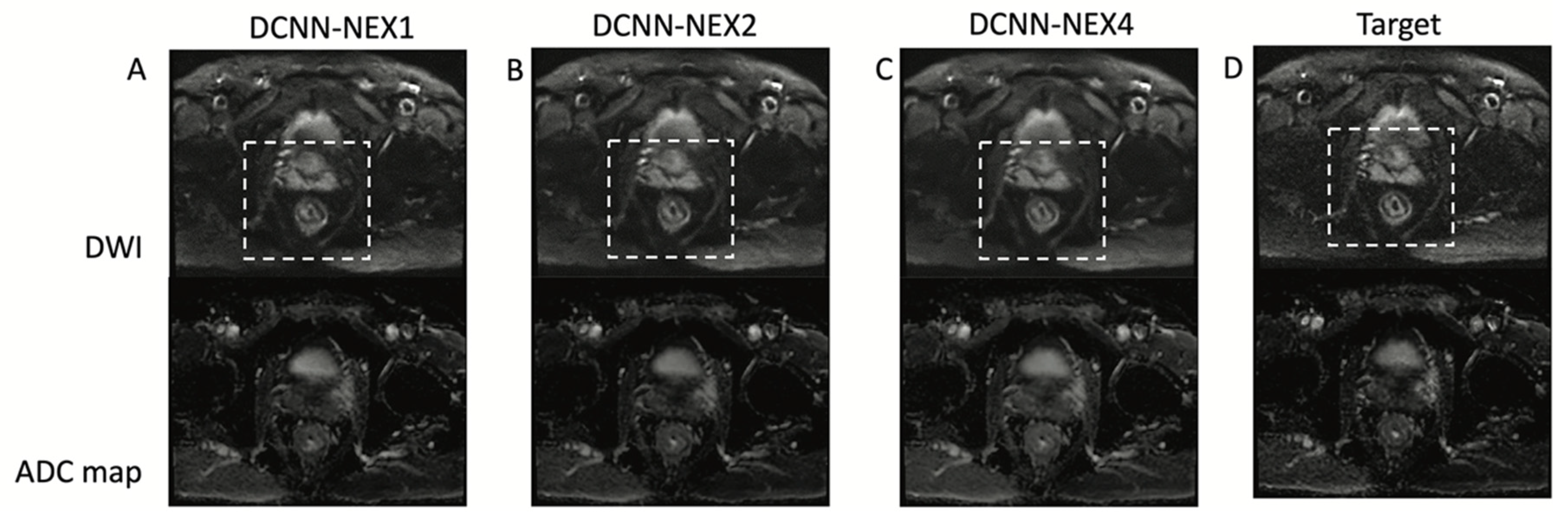
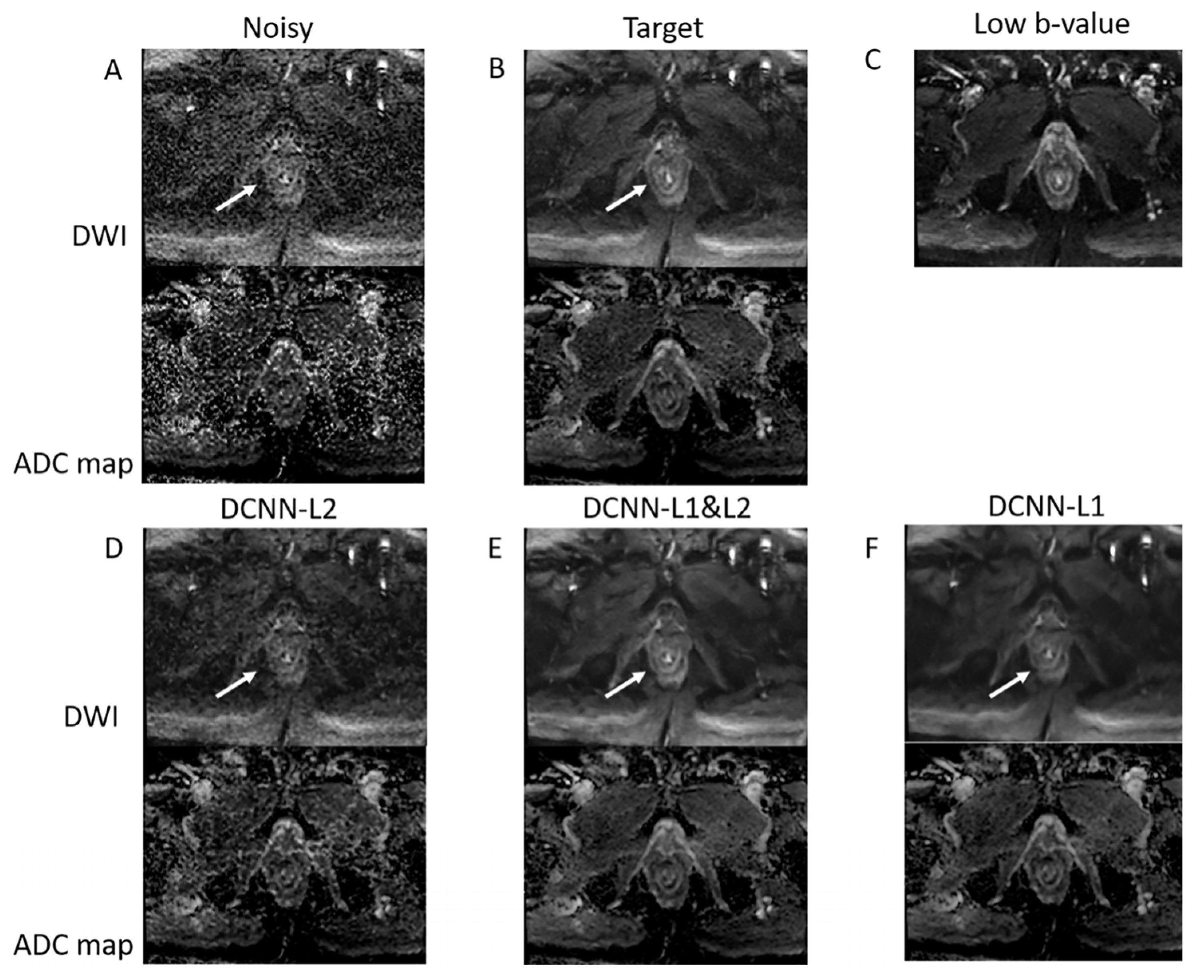
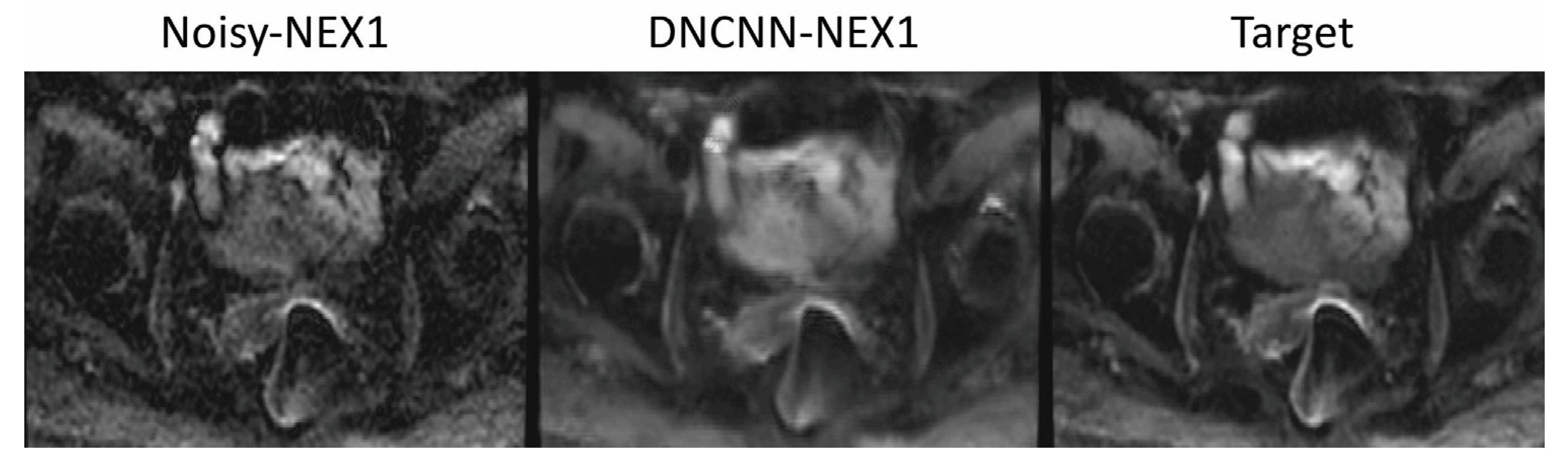
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Siegel, R.L.; Miller, K.D.; Fuchs, H.E.; Jemal, A. Cancer Statistics, 2021. CA A Cancer J. Clin. 2021, 71, 7–33. [Google Scholar] [CrossRef] [PubMed]
- Kasi, A.; Abbasi, S.; Handa, S.; Al-Rajabi, R.; Saeed, A.; Baranda, J.; Sun, W. Total Neoadjuvant Therapy vs Standard Therapy in Locally Advanced Rectal Cancer: A Systematic Review and Meta-analysis. JAMA Netw. Open. 2020, 3, e2030097. [Google Scholar] [CrossRef] [PubMed]
- Maas, M.; Lambregts, D.M.J.; Nelemans, P.J.; Heijnen, L.A.; Martens, M.H.; Leijtens, J.W.A.; Sosef, M.; Hulsewé, K.W.E.; Hoff, C.; Breukink, S.O.; et al. Assessment of Clinical Complete Response After Chemoradiation for Rectal Cancer with Digital Rectal Examination, Endoscopy, and MRI: Selection for Organ-Saving Treatment. Ann. Surg. Oncol. 2015, 22, 3873–3880. [Google Scholar] [CrossRef] [PubMed]
- Patel, U.B.; Brown, G.; Rutten, H.; West, N.; Sebag-Montefiore, D.; Glynne-Jones, R.; Rullier, E.; Peeters, M.; Van Cutsem, E.; Ricci, S.; et al. Comparison of magnetic resonance imaging and histopathological response to chemoradiotherapy in locally advanced rectal cancer. Ann. Surg. Oncol. 2012, 19, 2842–2852. [Google Scholar] [CrossRef]
- Sclafani, F.; Brown, G.; Cunningham, D.; Wotherspoon, A.; Mendes, L.S.T.; Balyasnikova, S.; Evans, J.; Peckitt, C.; Begum, R.; Tait, D.; et al. Comparison between MRI and pathology in the assessment of tumour regression grade in rectal cancer. Br. J. Cancer 2017, 117, 1478–1485. [Google Scholar] [CrossRef] [PubMed]
- Siddiqui, M.R.; Gormly, K.L.; Bhoday, J.; Balyansikova, S.; Battersby, N.J.; Chand, M.; Rao, S.; Tekkis, P.; Abulafi, A.M.; Brown, G. Interobserver agreement of radiologists assessing the response of rectal cancers to preoperative chemoradiation using the MRI tumour regression grading (mrTRG). Clin. Radiol. 2016, 71, 854–862. [Google Scholar] [CrossRef]
- Rao, S.-X.; Zeng, M.-S.; Chen, C.-Z.; Li, R.-C.; Zhang, S.-J.; Xu, J.-M.; Hou, Y.-Y. The value of diffusion-weighted imaging in combination with T2-weighted imaging for rectal cancer detection. Eur. J. Radiol. 2008, 65, 299–303. [Google Scholar] [CrossRef]
- Schurink, N.W.; Lambregts, D.M.; Beets-Tan, R.G. Diffusion-weighted imaging in rectal cancer: Current applications and future perspectives. Br. J. Radiol. 2019, 92, 20180655. [Google Scholar] [CrossRef]
- Horvat, N.; Veeraraghavan, H.; Khan, M.; Blazic, I.; Zheng, J.; Capanu, M.; Sala, E.; Garcia-Aguilar, J.; Gollub, M.J.; Petkovska, I. MR Imaging of Rectal Cancer: Radiomics Analysis to Assess Treatment Response after Neoadjuvant Therapy. Radiology 2018, 287, 833–843. [Google Scholar] [CrossRef]
- Charles-Edwards, E.M.; deSouza, N.M. Diffusion-weighted magnetic resonance imaging and its application to cancer. Cancer Imaging 2006, 6, 135–143. [Google Scholar] [CrossRef]
- Ichikawa, T.; Haradome, H.; Hachiya, J.; Nitatori, T.; Araki, T. Diffusion-weighted MR imaging with single-shot echo-planar imaging in the upper abdomen: Preliminary clinical experience in 61 patients. Abdom. Imaging 1999, 24, 456–461. [Google Scholar] [CrossRef] [PubMed]
- Ichikawa, T.; Erturk, S.M.; Motosugi, U.; Sou, H.; Iino, H.; Araki, T.; Fujii, H. High-b Value Diffusion-Weighted MRI for Detecting Pancreatic Adenocarcinoma: Preliminary Results. Am. J. Roentgenol. 2007, 188, 409–414. [Google Scholar] [CrossRef] [PubMed]
- Farzaneh, F.; Riederer, S.J.; Pelc, N.J. Analysis of T2 limitations and off-resonance effects on spatial resolution and artifacts in echo-planar imaging. Magn. Reson. Med. 1990, 14, 123–139. [Google Scholar] [CrossRef] [PubMed]
- Hagmann, P.; Jonasson, L.; Maeder, P.; Thiran, J.-P.; Wedeen, V.J.; Meuli, R. Understanding Diffusion MR Imaging Techniques: From Scalar Diffusion-weighted Imaging to Diffusion Tensor Imaging and Beyond. Radiographics 2006, 26 (Suppl. 1), S205–S223. [Google Scholar] [CrossRef]
- Hashemi, R.H.; Bradley, W.G.; Lisanti, C.J. MRI: The Basics; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2010. [Google Scholar]
- Pruessmann, K.P.; Weiger, M.; Scheidegger, M.B.; Boesiger, P. SENSE: Sensitivity encoding for fast MRI. Magn. Reson. Med. 1999, 42, 952–962. [Google Scholar] [CrossRef]
- Griswold, M.A.; Jakob, P.M.; Heidemann, R.M.; Nittka, M.; Jellus, V.; Wang, J.; Kiefer, B.; Haase, A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn. Reson. Med. 2002, 47, 1202–1210. [Google Scholar] [CrossRef]
- Soyer, P.; Lagadec, M.; Sirol, M.; Dray, X.; Duchat, F.; Vignaud, A.; Fargeaudou, Y.; Placé, V.; Gault, V.; Hamzi, L.; et al. Free-breathing diffusion-weighted single-shot echo-planar MR imaging using parallel imaging (GRAPPA 2) and high b value for the detection of primary rectal adenocarcinoma. Cancer Imaging 2010, 10, 32–39. [Google Scholar] [CrossRef]
- Bammer, R.; Auer, M.; Keeling, S.L.; Augustin, M.; Stables, L.A.; Prokesch, R.W.; Stollberger, R.; Moseley, M.E.; Fazekas, F. Diffusion tensor imaging using single-shot SENSE-EPI. Magn. Reson. Med. 2002, 48, 128–136. [Google Scholar] [CrossRef]
- Bammer, R.; Keeling, S.L.; Augustin, M.; Pruessmann, K.P.; Wolf, R.; Stollberger, R.; Hartung, H.P.; Fazekas, F. Improved diffusion-weighted single-shot echo-planar imaging (EPI) in stroke using sensitivity encoding (SENSE). Magn. Reson. Med. 2001, 46, 548–554. [Google Scholar] [CrossRef]
- Cercignani, M.; Horsfield, M.A.; Agosta, F.; Filippi, M. Sensitivity-encoded diffusion tensor MR imaging of the cervical cord. AJNR Am. J. Neuroradiol. 2003, 24, 1254–1256. [Google Scholar]
- Jaermann, T.; Crelier, G.; Pruessmann, K.P.; Golay, X.; Netsch, T.; van Muiswinkel, A.M.; Mori, S.; van Zijl, P.C.; Valavanis, A.; Kollias, S.; et al. SENSE-DTI at 3 T. Magn. Reson. Med. 2004, 51, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Jaermann, T.; Pruessmann, K.P.; Valavanis, A.; Kollias, S.; Boesiger, P. Influence of SENSE on image properties in high-resolution single-shot echo-planar DTI. Magn. Reson. Med. 2006, 55, 335–342. [Google Scholar] [CrossRef] [PubMed]
- Taviani, V.; Alley, M.T.; Banerjee, S.; Nishimura, D.G.; Daniel, B.L.; Vasanawala, S.S.; Hargreaves, B.A. High-resolution diffusion-weighted imaging of the breast with multiband 2D radiofrequency pulses and a generalized parallel imaging reconstruction. Magn. Reson. Med. 2017, 77, 209–220. [Google Scholar] [CrossRef]
- Zhang, C.; Arefin, T.M.; Nakarmi, U.; Lee, C.H.; Li, H.; Liang, D.; Zhang, J.; Ying, L. Acceleration of three-dimensional diffusion magnetic resonance imaging using a kernel low-rank compressed sensing method. Neuroimage 2020, 210, 116584. [Google Scholar] [CrossRef]
- Cheng, J.; Shen, D.; Basser, P.J.; Yap, P.-T. Joint 6D k-q Space Compressed Sensing for Accelerated High Angular Resolution Diffusion MRI. Inf. Process. Med. Imaging 2015, 24, 782–793. [Google Scholar] [PubMed]
- Haldar, J.P.; Wedeen, V.J.; Nezamzadeh, M.; Dai, G.; Weiner, M.W.; Schuff, N.; Liang, Z.-P. Improved diffusion imaging through SNR-enhancing joint reconstruction. Magn. Reson. Med. 2013, 69, 277–289. [Google Scholar] [CrossRef]
- Manjón, J.V.; Coupé, P.; Concha, L.; Buades, A.; Collins, D.L.; Robles, M. Diffusion weighted image denoising using overcomplete local PCA. PLoS ONE 2013, 8, e73021. [Google Scholar] [CrossRef]
- Lam, F.; Babacan, S.D.; Haldar, J.P.; Weiner, M.W.; Schuff, N.; Liang, Z.-P. Denoising diffusion-weighted magnitude MR images using rank and edge constraints. Magn. Reson. Med. 2014, 71, 1272–1284. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, G.; Yap, P.-T.; Shen, D. Multifold Acceleration of Diffusion MRI via Deep Learning Reconstruction from Slice-Undersampled Data. Inf. Process. Med. Imaging 2019, 11492, 530–541. [Google Scholar]
- Kawamura, M.; Tamada, D.; Funayama, S.; Kromrey, M.-L.; Ichikawa, S.; Onishi, H.; Motosugi, U. Accelerated Acquisition of High-resolution Diffusion-weighted Imaging of the Brain with a Multi-shot Echo-planar Sequence: Deep-learning-based Denoising. Magn. Reson. Med. Sci. 2021, 20, 99–105. [Google Scholar] [CrossRef]
- Kaye, E.A.; Aherne, E.A.; Duzgol, C.; Häggström, I.; Kobler, E.; Mazaheri, Y.; Fung, M.M.; Zhang, Z.; Otazo, R.; Vargas, H.A.; et al. Accelerating Prostate Diffusion-weighted MRI Using a Guided Denoising Convolutional Neural Network: Retrospective Feasibility Study. Radiol. Artif. Intell. 2020, 2, e200007. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zheng, R.; Dai, F.; Wang, Q.; Wang, C. High-field mr diffusion-weighted image denoising using a joint denoising convolutional neural network. J. Magn. Reson. Imaging 2019, 50, 1937–1947. [Google Scholar] [CrossRef] [PubMed]
- Yaman, B.; Hosseini, S.A.H.; Moeller, S.; Ellermann, J.; Uğurbil, K.; Akçakaya, M. Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data. Magn. Reson. Med. 2020, 84, 3172–3191. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Horé, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar]
- Sosna, J.; Pedrosa, I.; Dewolf, W.C.; Mahallati, H.; Lenkinski, R.E.; Rofsky, N.M. MR imaging of the prostate at 3 tesla: Comparison of an external phased-array coil to imaging with an endorectal coil at 1.5 tesla. Acad. Radiol. 2004, 11, 857–862. [Google Scholar] [CrossRef] [PubMed]
- Shah, Z.; Elias, S.N.; Abaza, R.; Zynger, D.L.; DeRenne, L.A.; Knopp, M.V.; Guo, B.; Schurr, R.; Heymsfield, S.B.; Jia, G. Performance Comparison of 1.5-T Endorectal Coil MRI with 3.0-T Nonendorectal Coil MRI in Patients with Prostate Cancer. Acad. Radiol. 2015, 22, 467–474. [Google Scholar] [CrossRef]
- O’Donohoe, R.L.; Dunne, R.M.; Kimbrell, V.; Tempany, C.M. Prostate MRI using an external phased array wearable pelvic coil at 3T: Comparison with an endorectal coil. Abdom. Radiol. 2019, 44, 1062–1069. [Google Scholar] [CrossRef]
- Horvat, N.; Veeraraghavan, H.; Pelossof, R.A.; Fernandes, M.C.; Arora, A.; Khan, M.; Marco, M.; Cheng, C.-T.; Gonen, M.; Pernicka, J.S.G.; et al. Radiogenomics of rectal adenocarcinoma in the era of precision medicine: A pilot study of associations between qualitative and quantitative MRI imaging features and genetic mutations. Eur. J. Radiol. 2019, 113, 174–181. [Google Scholar] [CrossRef]
- Fan, L.; Zhang, F.; Fan, H.; Zhang, C. Brief review of image denoising techniques. Vis. Comput. Ind. Biomed. Art 2019, 2, 7. [Google Scholar] [CrossRef]
- Antun, V.; Renna, F.; Poon, C.; Adcock, B.; Hansen, A.C. On instabilities of deep learning in image reconstruction and the potential costs of AI. Proc. Natl. Acad. Sci. USA 2020, 117, 30088–30095. [Google Scholar] [CrossRef]
- Chen, N.-K.; Guidon, A.; Chang, H.-C.; Song, A.W. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). NeuroImage 2013, 72, 41–47. [Google Scholar] [CrossRef] [PubMed]


| Score | Overall Image Quality | Rectum Margin and Rectal Wall Layers Demarcation | Noise Suppression | Image Sharpness |
|---|---|---|---|---|
| 1 | Nondiagnostic/poor | No visualization or inability to trace structures clearly | Significant noise that hampers diagnostic capability of readers | Nondiagnostic, blurred, hampering diagnostic capability |
| 2 | Fair | Fair demarcation | Substantial noise with significant image quality degradation | Substantially blurred, not hampering diagnostic capability but low image quality |
| 3 | Good | Nearly complete and clear demarcation | Moderate noise | Mild blur with mild image quality degradation |
| 4 | Excellent | Complete and clear demarcation | Minimal noise without image quality degradation | Minimal or no blur |
| Loss Function | PSNR Denoised | PSNR Noisy | SSIM Denoised | SSIM Noisy |
|---|---|---|---|---|
| L1 | 84.13 ± 4.6 | 80.29 ± 5.1 | 0.89 ± 0.03 | 0.85 ± 0.1 |
| L2 | 82.63 ± 5.2 | 0.90 ± 0.07 | ||
| Joint L1–L2 | 84.33 ± 5.1 | 0.94 ± 0.03 |
| Image Quality | Rectum Margin and Rectal Wall Layers Demarcation | Noise Suppression | Image Sharpness | |
|---|---|---|---|---|
| Reader 1 | ||||
| Noisy, NEX = 1 | 2 ± 1 | 2 ± 1 | 2 ± 1 | 2.5 ± 0.5 |
| Noisy, NEX = 2 | 2 ± 0.5 | 2 ± 0.5 | 2 ± 1 | 3 ± 0.5 |
| Noisy, NEX = 4 | 2 ± 0.5 | 2 ± 0.5 | 2 ± 0.5 | 2 ± 0.5 |
| Denoised NEX = 1 | 2.5 ± 0.6 | 2 ± 0.6 | 3 ± 1 | 2.5 ± 0.5 |
| Denoised NEX = 2 | 2.5 ± 0.6 | 2 ± 0.1 | 3.5 ± 1 | 3 ± 0.5 |
| Denoised NEX = 4 | 3 ± 0.6 | 3 ± 0.5 | 4 ± 0.5 | 3 ± 1 |
| Target | 3 ± 1 | 3 ± 1 | 3 ± 0.8 | 3 ± 1 |
| Reader 2 | ||||
| Noisy, NEX = 1 | 2 ± 0.6 | 2 ± 0.7 | 2 ± 1 | 2 ± 0.5 |
| Noisy, NEX = 2 | 2 ± 0.5 | 2 ± 0.5 | 2.5 ± 0.5 | 2 ± 0.5 |
| Noisy, NEX = 4 | 2 ± 0.5 | 2 ± 0.5 | 2.5 ± 0.5 | 2 ± 0.5 |
| Denoised NEX = 1 | 2 ± 0.5 | 2 ± 0.5 | 3 ± 1 | 3 ± 0.5 |
| Denoised NEX = 2 | 3 ± 0.5 | 3 ± 0.5 | 4 ± 0.5 | 3 ± 0 |
| Denoised NEX = 4 | 3 ± 0.5 | 3 ± 0.5 | 4 ± 0.5 | 3 ± 0.5 |
| Target | 2 ± 0.5 | 2 ± 0.5 | 3 ± 0.5 | 2.5 ± 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammadi, M.; Kaye, E.A.; Alus, O.; Kee, Y.; Golia Pernicka, J.S.; El Homsi, M.; Petkovska, I.; Otazo, R. Accelerated Diffusion-Weighted MRI of Rectal Cancer Using a Residual Convolutional Network. Bioengineering 2023, 10, 359. https://doi.org/10.3390/bioengineering10030359
Mohammadi M, Kaye EA, Alus O, Kee Y, Golia Pernicka JS, El Homsi M, Petkovska I, Otazo R. Accelerated Diffusion-Weighted MRI of Rectal Cancer Using a Residual Convolutional Network. Bioengineering. 2023; 10(3):359. https://doi.org/10.3390/bioengineering10030359
Chicago/Turabian StyleMohammadi, Mohaddese, Elena A. Kaye, Or Alus, Youngwook Kee, Jennifer S. Golia Pernicka, Maria El Homsi, Iva Petkovska, and Ricardo Otazo. 2023. "Accelerated Diffusion-Weighted MRI of Rectal Cancer Using a Residual Convolutional Network" Bioengineering 10, no. 3: 359. https://doi.org/10.3390/bioengineering10030359
APA StyleMohammadi, M., Kaye, E. A., Alus, O., Kee, Y., Golia Pernicka, J. S., El Homsi, M., Petkovska, I., & Otazo, R. (2023). Accelerated Diffusion-Weighted MRI of Rectal Cancer Using a Residual Convolutional Network. Bioengineering, 10(3), 359. https://doi.org/10.3390/bioengineering10030359