An Investigation of Acoustic Back-Coupling in Human Phonation on a Synthetic Larynx Model
Abstract
1. Introduction
2. Materials and Methods
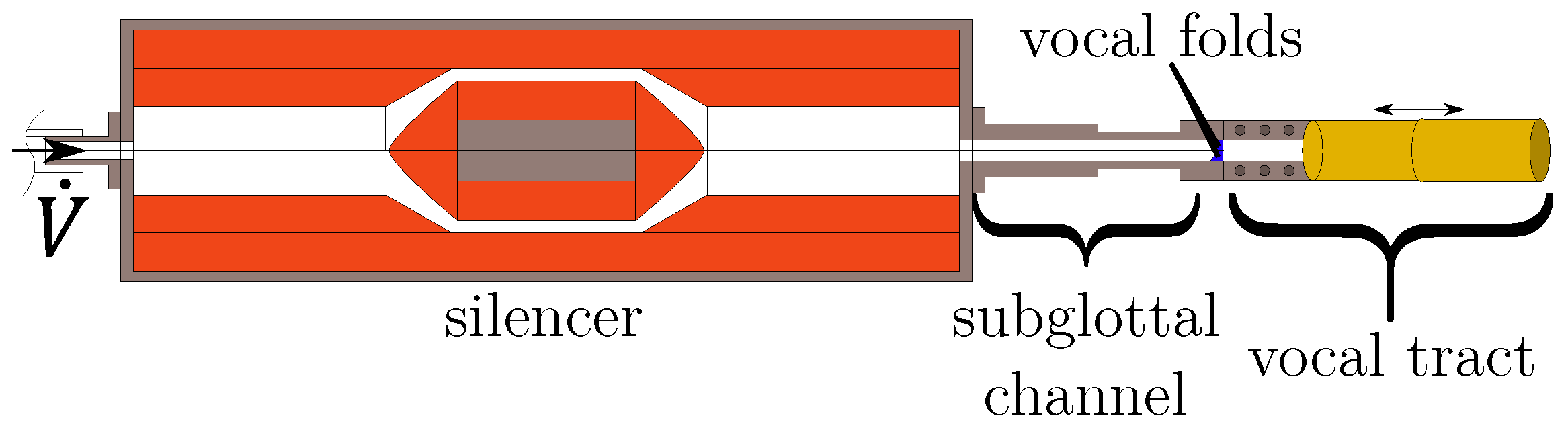
2.1. Basic Experimental Setup
2.2. Measurement Setup
2.3. Aeroacoustic Source Computation
2.4. Acoustic Characterization of the Vocal Tract
3. Results and Discussion
3.1. General Results
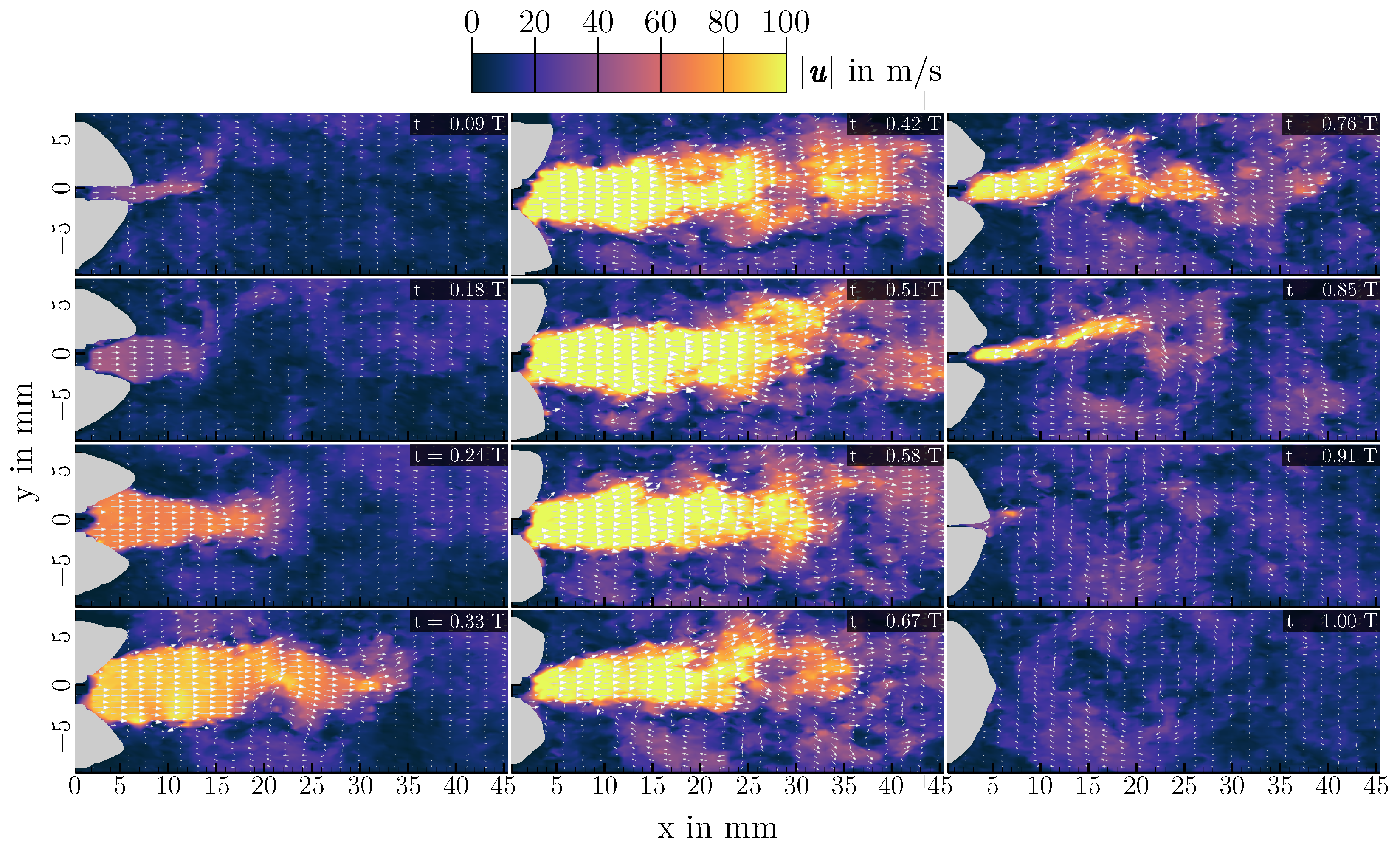
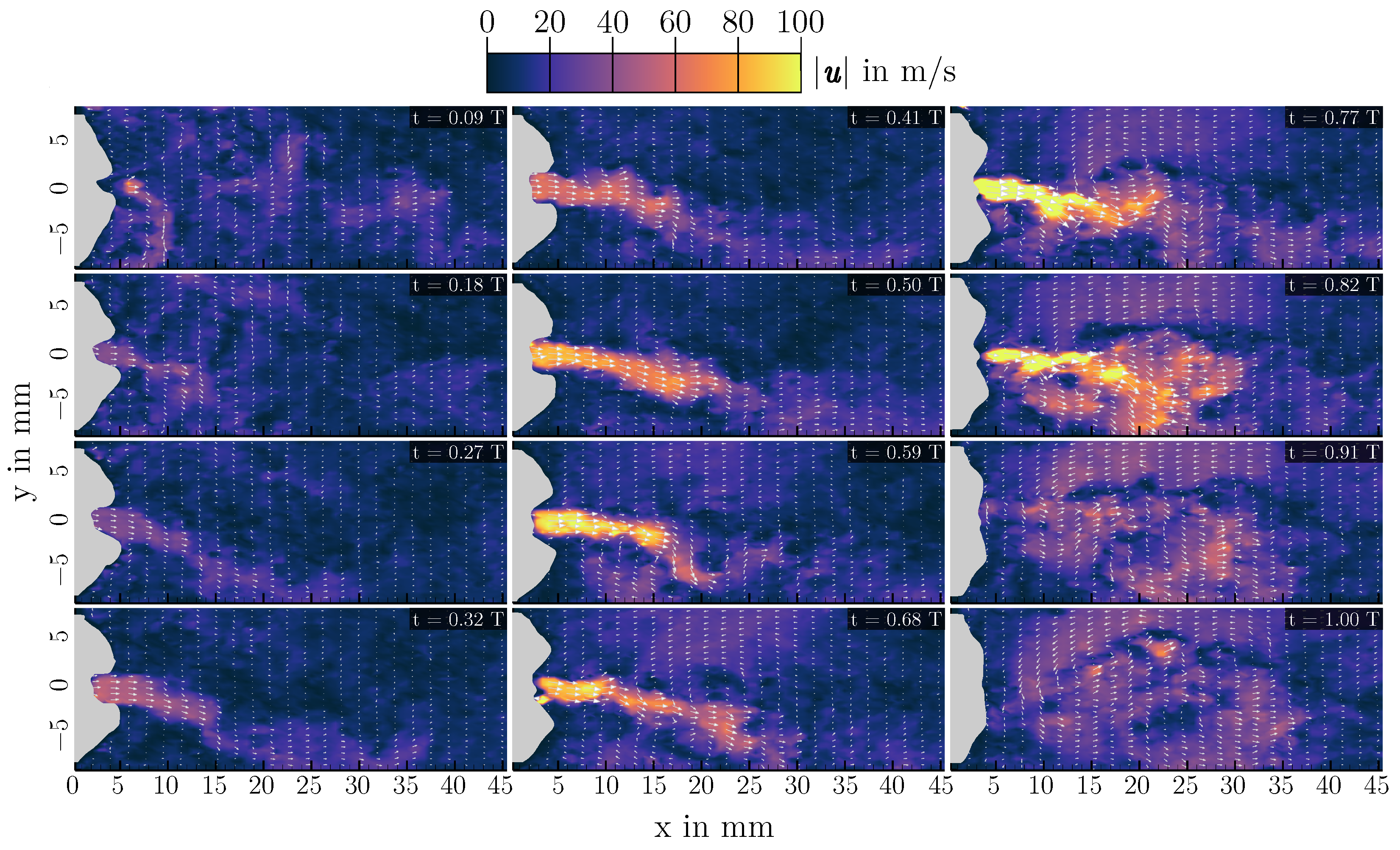
3.2. Supraglottal Aerodynamics
3.3. Aeroacoustic Sources
3.4. Acoustic Radiation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CPP | Cepstral Peak Prominence |
| FSAI | Fluid–Structure–Acoustic Interaction |
| GAT | Glottis Analysis Tools |
| HNR | Harmonics-to-Noise Ratio |
| PIV | Particle Image Velocimetry |
| POD | Proper Orthogonal Decomposition |
| PSD | Power Spectral Density |
| RMS | Root Mean Square |
| ROI | Region Of Interest |
| SNR | Signal-to-Noise Ratio |
| SPL | Sound Pressure Level |
| VE | Vocal Efficiency |
References
- Mittal, R.; Erath, B.D.; Plesniak, M.W. Fluid Dynamics of Human Phonation and Speech. Annu. Rev. Fluid Mech. 2013, 45, 437–467. [Google Scholar] [CrossRef]
- Bodaghi, D.; Xue, Q.; Zheng, X.; Thomson, S. Effect of Subglottic Stenosis on Vocal Fold Vibration and Voice Production Using Fluid–Structure–Acoustics Interaction Simulation. Appl. Sci. 2021, 11, 1221. [Google Scholar] [CrossRef]
- Döllinger, M.; Zhang, Z.; Schoder, S.; Šidlof, P.; Tur, B.; Kniesburges, S. Overview on state-of-the-art numerical modeling of the phonation process. Acta Acust. 2023, 7, 25. [Google Scholar] [CrossRef]
- Schoder, S.; Maurerlehner, P.; Wurzinger, A.; Hauser, A.; Falk, S.; Kniesburges, S.; Döllinger, M.; Kaltenbacher, M. Aeroacoustic Sound Source Characterization of the Human Voice Production-Perturbed Convective Wave Equation. Appl. Sci. 2021, 11, 2614. [Google Scholar] [CrossRef]
- Lodermeyer, A.; Bagheri, E.; Kniesburges, S.; Näger, C.; Probst, J.; Döllinger, M.; Becker, S. The mechanisms of harmonic sound generation during phonation: A multi-modal measurement-based approach. J. Acoust. Soc. Am. 2021, 150, 3485–3499. [Google Scholar] [CrossRef]
- Titze, I.R.; Story, B.H. Acoustic interactions of the voice source with the lower vocal tract. J. Acoust. Soc. Am. 1997, 101, 2234–2243. [Google Scholar] [CrossRef]
- Fant, G. Acoustic Theory of Speech Production; De Gruyter Mouton: The Hague, Netherlands, 1971. [Google Scholar] [CrossRef]
- Titze, I.R. Nonlinear source–filter coupling in phonation: Theory. J. Acoust. Soc. Am. 2008, 123, 2733–2749. [Google Scholar] [CrossRef]
- Howe, M.S.; McGowan, R.S. Sound generated by aerodynamic sources near a deformable body, with application to voiced speech. J. Fluid Mech. 2007, 592, 367–392. [Google Scholar] [CrossRef]
- McGowan, R.S.; Howe, M.S. Source-tract interaction with prescribed vocal fold motion. J. Acoust. Soc. Am. 2012, 131, 2999–3016. [Google Scholar] [CrossRef]
- Zañartu, M.; Mongeau, L.; Wodicka, G.R. Influence of acoustic loading on an effective single mass model of the vocal folds. J. Acoust. Soc. Am. 2007, 121, 1119–1129. [Google Scholar] [CrossRef]
- Lucero, J.C.; Lourenço, K.G.; Hermant, N.; Hirtum, A.V.; Pelorson, X. Effect of source–tract acoustical coupling on the oscillation onset of the vocal folds. J. Acoust. Soc. Am. 2012, 132, 403–411. [Google Scholar] [CrossRef]
- Erath, B.D.; Peterson, S.D.; Weiland, K.S.; Plesniak, M.W.; Zañartu, M. An acoustic source model for asymmetric intraglottal flow with application to reduced-order models of the vocal folds. PLoS ONE 2019, 14, e0219914. [Google Scholar] [CrossRef]
- Wade, L.; Hanna, N.; Smith, J.; Wolfe, J. The role of vocal tract and subglottal resonances in producing vocal instabilities. J. Acoust. Soc. Am. 2017, 141, 1546–1559. [Google Scholar] [CrossRef]
- Echternach, M.; Herbst, C.T.; Köberlein, M.; Story, B.; Döllinger, M.; Gellrich, D. Are source-filter interactions detectable in classical singing during vowel glides? J. Acoust. Soc. Am. 2021, 149, 4565–4578. [Google Scholar] [CrossRef]
- Zhang, Z.; Neubauer, J.; Berry, D.A. Influence of vocal fold stiffness and acoustic loading on flow-induced vibration of a single-layer vocal fold model. J. Sound Vib. 2009, 322, 299–313. [Google Scholar] [CrossRef]
- Smith, B.L.; Nemcek, S.P.; Swinarski, K.A.; Jiang, J.J. Nonlinear Source-Filter Coupling Due to the Addition of a Simplified Vocal Tract Model for Excised Larynx Experiments. J. Voice 2013, 27, 261–266. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Migimatsu, K.; Tokuda, I.T. Experimental study on nonlinear source–filter interaction using synthetic vocal fold models. J. Acoust. Soc. Am. 2019, 146, 983–997. [Google Scholar] [CrossRef] [PubMed]
- Oren, L.; Khosla, S.; Gutmark, E. Intraglottal geometry and velocity measurements in canine larynges. J. Acoust. Soc. Am. 2014, 135, 380–388. [Google Scholar] [CrossRef] [PubMed]
- Oren, L.; Khosla, S.; Gutmark, E. Intraglottal pressure distribution computed from empirical velocity data in canine larynx. J. Biomech. 2014, 47, 1287–1293. [Google Scholar] [CrossRef] [PubMed]
- Lodermeyer, A.; Becker, S.; Döllinger, M.; Kniesburges, S. Phase-locked flow field analysis in a synthetic human larynx model. Exp. Fluids 2015, 56, 77. [Google Scholar] [CrossRef]
- Kniesburges, S.; Lodermeyer, A.; Becker, S.; Traxdorf, M.; Döllinger, M. The mechanisms of subharmonic tone generation in a synthetic larynx model. J. Acoust. Soc. Am. 2016, 139, 3182–3192. [Google Scholar] [CrossRef] [PubMed]
- Lodermeyer, A.; Tautz, M.; Becker, S.; Döllinger, M.; Birk, V.; Kniesburges, S. Aeroacoustic analysis of the human phonation process based on a hybrid acoustic PIV approach. Exp. Fluids 2018, 59, 13. [Google Scholar] [CrossRef]
- Lighthill, M. On sound generated aerodynamically I. General theory. Proc. Roy. Soc. Lond. 1952, 211, 564–587. [Google Scholar] [CrossRef]
- Kaltenbacher, M.; Hüppe, A.; Reppenhagen, A.; Zenger, F.; Becker, S. Computational Aeroacoustics for Rotating Systems with Application to an Axial Fan. AIAA J. 2017, 55, 3831–3838. [Google Scholar] [CrossRef]
- de Luzan, C.F.; Oren, L.; Maddox, A.; Gutmark, E.; Khosla, S.M. Volume velocity in a canine larynx model using time-resolved tomographic particle image velocimetry. Exp. Fluids 2020, 61, 63. [Google Scholar] [CrossRef]
- Scherer, R.C.; Shinwari, D.; Witt, K.J.D.; Zhang, C.; Kucinschi, B.R.; Afjeh, A.A. Intraglottal pressure profiles for a symmetric and oblique glottis with a divergence angle of 10 degrees. J. Acoust. Soc. Am. 2001, 109, 1616–1630. [Google Scholar] [CrossRef]
- Thomson, S.L.; Mongeau, L.; Frankel, S.H. Aerodynamic transfer of energy to the vocal folds. J. Acoust. Soc. Am. 2005, 118, 1689–1700. [Google Scholar] [CrossRef]
- Zhang, Z.; Neubauer, J.; Berry, D.A. The influence of subglottal acoustics on laboratory models of phonation. J. Acoust. Soc. Am. 2006, 120, 1558–1569. [Google Scholar] [CrossRef]
- Durst, F.; Heim, U.; Ünsal, B.; Kullik, G. Mass flow rate control system for time-dependent laminar and turbulent flow investigations. Meas. Sci. Technol. 2003, 14, 893–902. [Google Scholar] [CrossRef]
- Kist, A.M.; Gómez, P.; Dubrovskiy, D.; Schlegel, P.; Kunduk, M.; Echternach, M.; Patel, R.; Semmler, M.; Bohr, C.; Dürr, S.; et al. A Deep Learning Enhanced Novel Software Tool for Laryngeal Dynamics Analysis. J. Speech Lang. Hear. Res. 2021, 64, 1889–1903. [Google Scholar] [CrossRef]
- Maryn, Y.; Verguts, M.; Demarsin, H.; van Dinther, J.; Gomez, P.; Schlegel, P.; Döllinger, M. Intersegmenter Variability in High-Speed Laryngoscopy-Based Glottal Area Waveform Measures. Laryngoscope 2020, 130, E654–E661. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.E.; Scarano, F.; Kähler, C.J.; Wereley, S.T.; Kompenhans, J. Particle Image Velocimetry; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Samimy, M.; Lele, S.K. Motion of particles with inertia in a compressible free shear layer. Phys. Fluids A Fluid Dyn. 1991, 3, 1915–1923. [Google Scholar] [CrossRef]
- Mendez, M.; Raiola, M.; Masullo, A.; Discetti, S.; Ianiro, A.; Theunissen, R.; Buchlin, J.M. POD-based background removal for particle image velocimetry. Exp. Therm. Fluid Sci. 2017, 80, 181–192. [Google Scholar] [CrossRef]
- Adatrao, S.; Sciacchitano, A. Elimination of unsteady background reflections in PIV images by anisotropic diffusion. Meas. Sci. Technol. 2019, 30, 035204. [Google Scholar] [CrossRef]
- Westerweel, J.; Scarano, F. Universal outlier detection for PIV data. Exp. Fluids 2005, 39, 1096–1100. [Google Scholar] [CrossRef]
- Sondhi, M.; Schroeter, J. A hybrid time-frequency domain articulatory speech synthesizer. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 955–967. [Google Scholar] [CrossRef]
- Story, B.H.; Laukkanen, A.M.; Titze, I.R. Acoustic impedance of an artificially lengthened and constricted vocal tract. J. Voice 2000, 14, 455–469. [Google Scholar] [CrossRef]
- Flanagan, J.L. Speech Analysis, Synthesis and Perception; Springer: Berlin/Heidelberg, Germany, 1972; p. 444. [Google Scholar]
- Fulcher, L.; Lodermeyer, A.; Kähler, G.; Becker, S.; Kniesburges, S. Geometry of the Vocal Tract and Properties of Phonation near Threshold: Calculations and Measurements. Appl. Sci. 2019, 9, 2755. [Google Scholar] [CrossRef]
- Titze, I. Principles of Voice Production; Prentice Hall: Hoboken, NJ, USA, 1994. [Google Scholar]
- Neubauer, J.; Zhang, Z.; Miraghaie, R.; Berry, D.A. Coherent structures of the near field flow in a self-oscillating physical model of the vocal folds. J. Acoust. Soc. Am. 2007, 121, 1102–1118. [Google Scholar] [CrossRef] [PubMed]
- Erath, B.D.; Plesniak, M.W. The occurrence of the Coanda effect in pulsatile flow through static models of the human vocal folds. J. Acoust. Soc. Am. 2006, 120, 1000–1011. [Google Scholar] [CrossRef]
- Erath, B.D.; Plesniak, M.W. An investigation of asymmetric flow features in a scaled-up driven model of the human vocal folds. Exp. Fluids 2010, 49, 131–146. [Google Scholar] [CrossRef]
- Erath, B.D.; Plesniak, M.W. Impact of wall rotation on supraglottal jet stability in voiced speech. J. Acoust. Soc. Am. 2011, 129, EL64–EL70. [Google Scholar] [CrossRef] [PubMed]
- Lighthill, M.J. On sound generated aerodynamically II. Turbulence as a source of sound. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1954, 222, 1–32. [Google Scholar] [CrossRef]
- Howe, M.S. Acoustics of Fluid-Structure Interactions; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar] [CrossRef]
- Howe, M.; McGowan, R. Aerodynamic sound of a body in arbitrary, deformable motion, with application to phonation. J. Sound Vib. 2013, 332, 3909–3923. [Google Scholar] [CrossRef] [PubMed]
- Titze, I.R.; Maxfield, L.; Palaparthi, A. An Oral Pressure Conversion Ratio as a Predictor of Vocal Efficiency. J. Voice 2016, 30, 398–406. [Google Scholar] [CrossRef] [PubMed]
- Qi, Y.; Hillman, R.E.; Milstein, C. The estimation of signal-to-noise ratio in continuous speech for disordered voices. J. Acoust. Soc. Am. 1999, 105, 2532–2535. [Google Scholar] [CrossRef] [PubMed]
- Yumoto, E.; Sasaki, Y.; Okamura, H. Harmonics-to-Noise Ratio and Psychophysical Measurement of the Degree of Hoarseness. J. Speech Lang. Hear. Res. 1984, 27, 2–6. [Google Scholar] [CrossRef]
- Hillenbrand, J.; Cleveland, R.A.; Erickson, R.L. Acoustic Correlates of Breathy Vocal Quality. J. Speech Lang. Hear. Res. 1994, 37, 769–778. [Google Scholar] [CrossRef]
- Hillenbrand, J.; Houde, R.A. Acoustic Correlates of Breathy Vocal Quality: Dysphonic Voices and Continuous Speech. J. Speech Lang. Hear. Res. 1996, 39, 311–321. [Google Scholar] [CrossRef]
- Semmler, M.; Berry, D.A.; Schützenberger, A.; Döllinger, M. Fluid-structure-acoustic interactions in an ex vivo porcine phonation model. J. Acoust. Soc. Am. 2021, 149, 1657–1673. [Google Scholar] [CrossRef]
- Peters, G.; Jakubaß, B.; Weidenfeller, K.; Kniesburges, S.; Böhringer, D.; Wendler, O.; Mueller, S.K.; Gostian, A.O.; Berry, D.A.; Döllinger, M.; et al. Synthetic mucus for an ex vivo phonation setup: Creation, application, and effect on excised porcine larynges. J. Acoust. Soc. Am. 2022, 152, 3245–3259. [Google Scholar] [CrossRef] [PubMed]
- Gorris, C.; Maccarini, A.R.; Vanoni, F.; Poggioli, M.; Vaschetto, R.; Garzaro, M.; Valletti, P.A. Acoustic Analysis of Normal Voice Patterns in Italian Adults by Using Praat. J. Voice 2020, 34, 961.e9–961.e18. [Google Scholar] [CrossRef] [PubMed]
- Gojayev, E.K.; Büyükatalay, Z.Ç.; Akyüz, T.; Rehan, M.; Dursun, G. The Effect of Masks and Respirators on Acoustic Voice Analysis during the COVID-19 Pandemic. J. Voice 2021. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, D.D.; Madill, C. Auditory-perceptual Parameters as Predictors of Voice Acoustic Measures. J. Voice 2023. [Google Scholar] [CrossRef]
- Story, B.H.; Titze, I.R.; Hoffman, E.A. Vocal tract area functions from magnetic resonance imaging. J. Acoust. Soc. Am. 1996, 100, 537–554. [Google Scholar] [CrossRef]



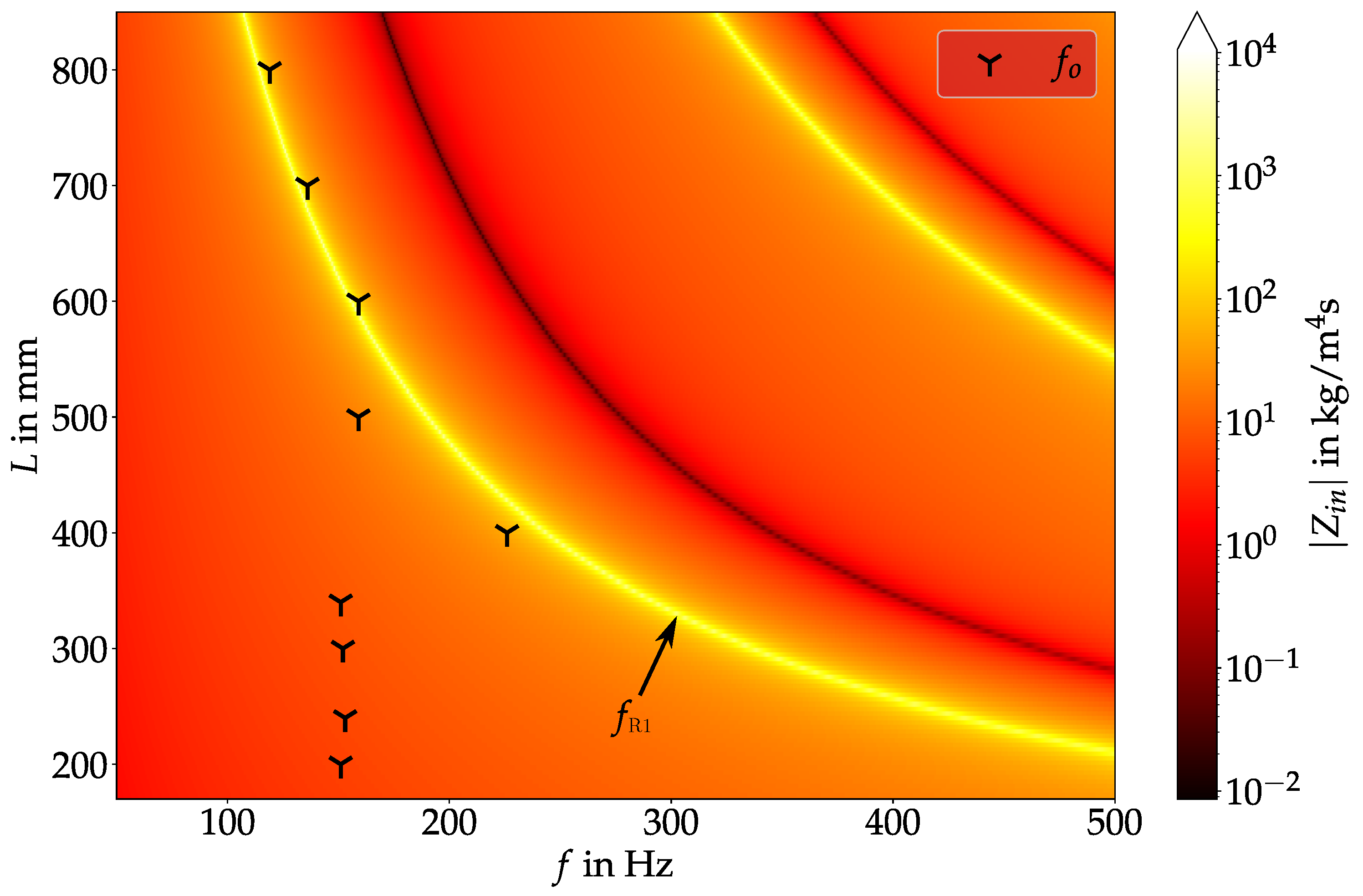

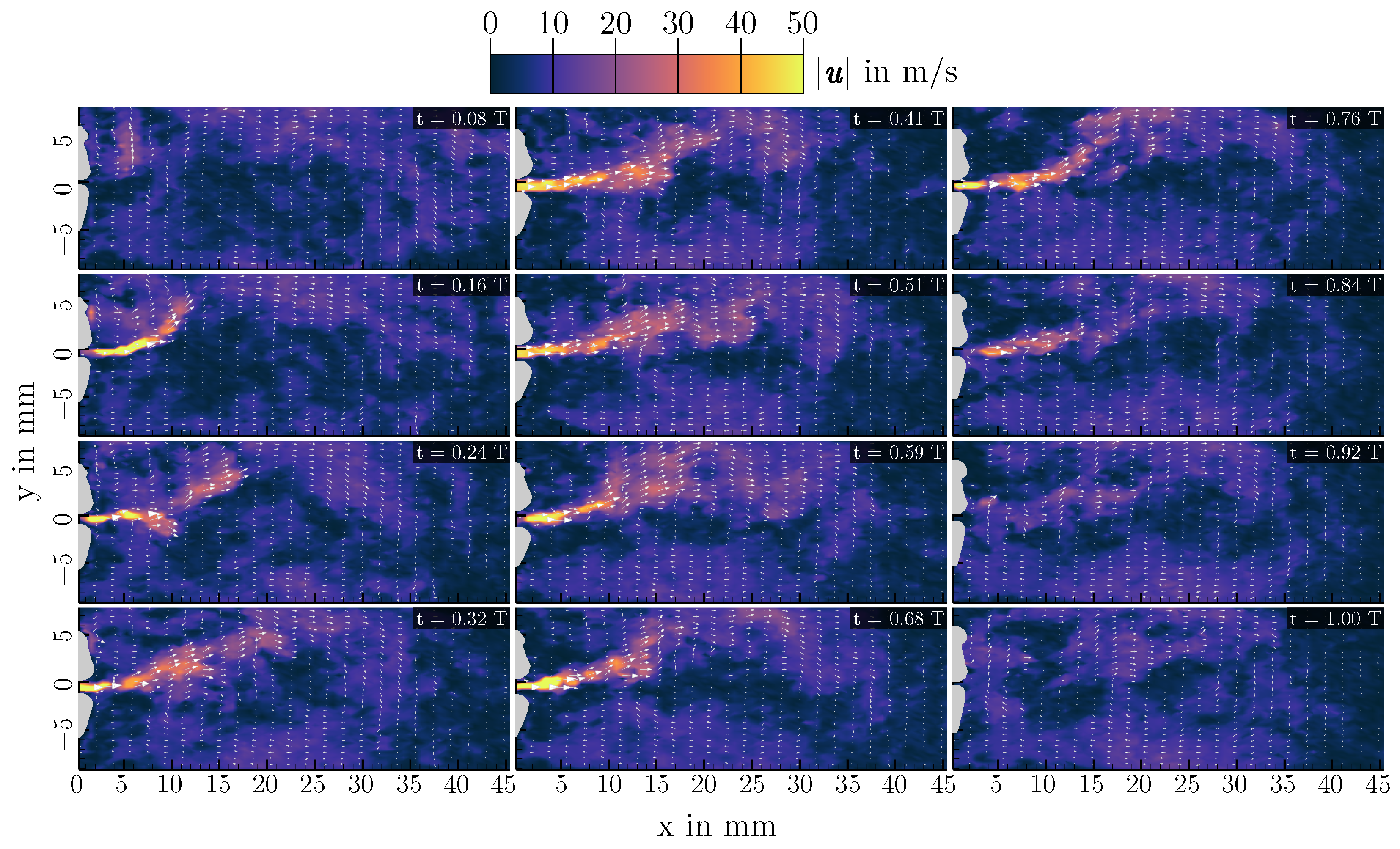

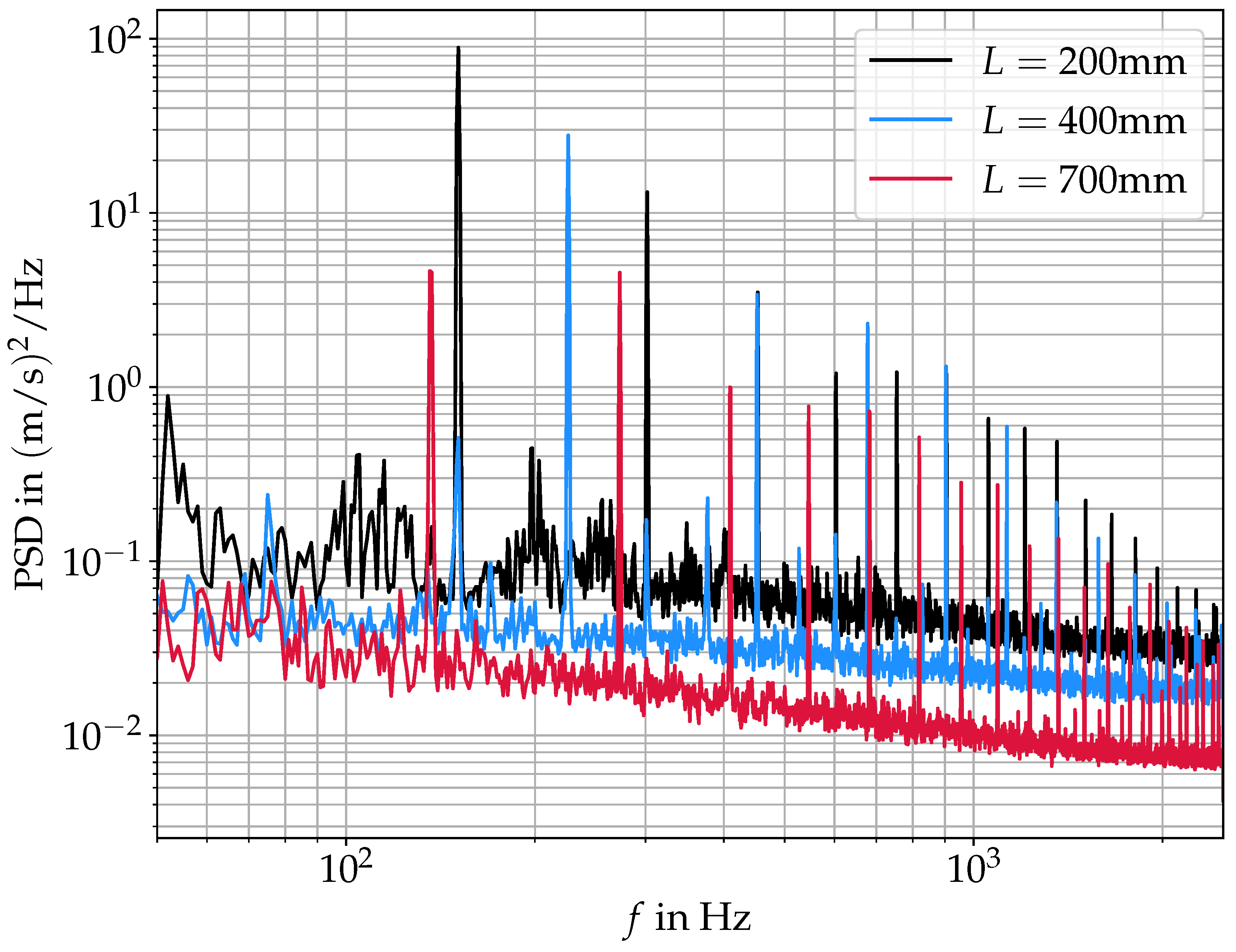
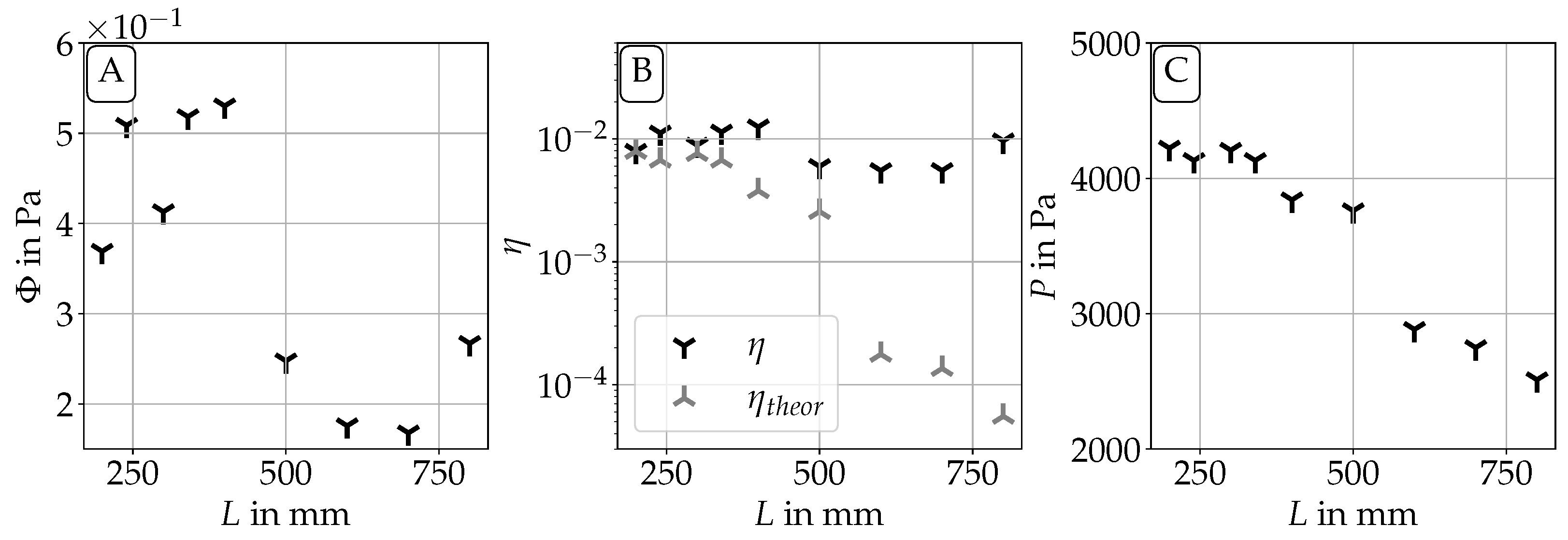

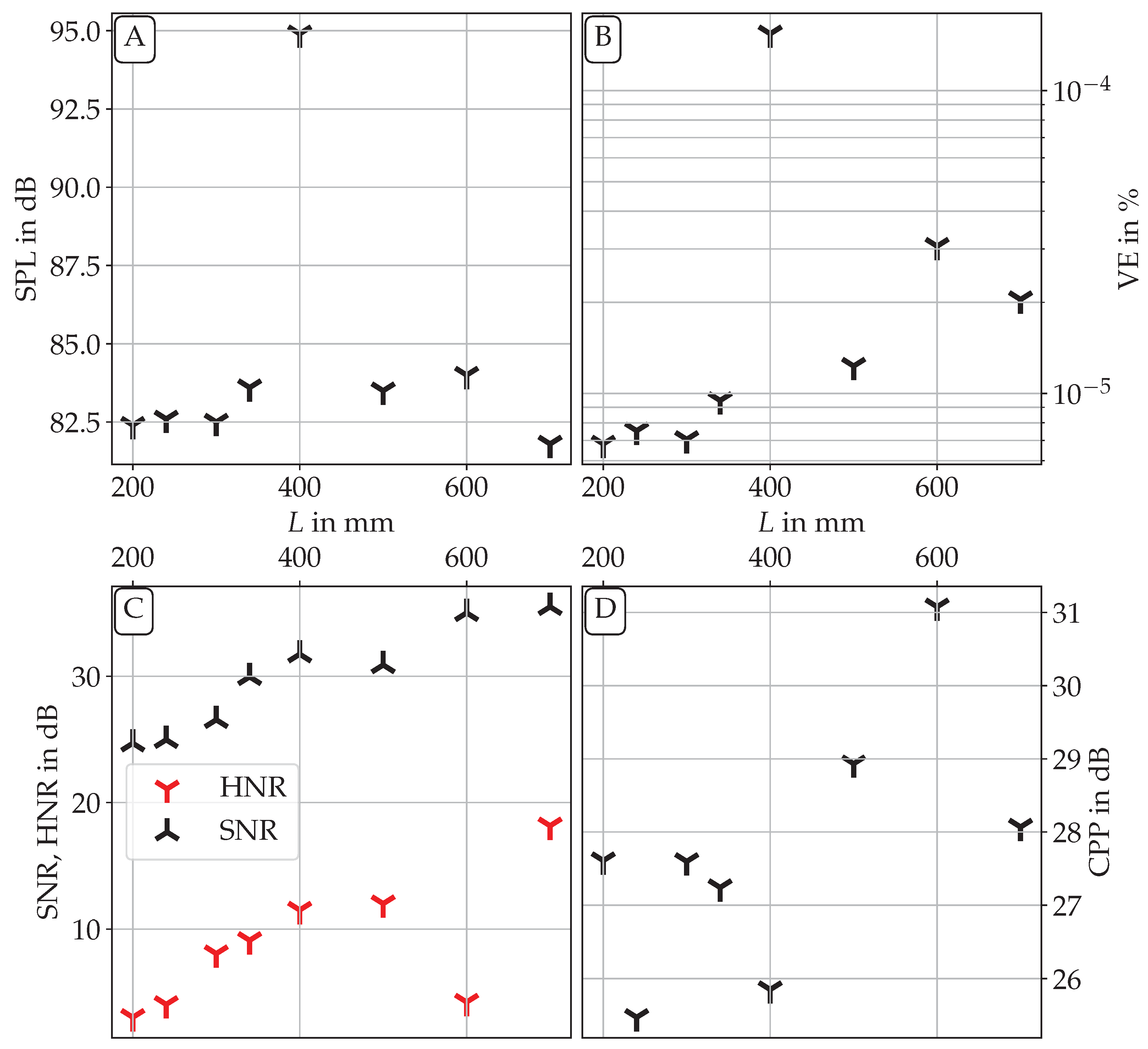
| L in mm | in l/min | in Pa | in Hz | in Hz |
|---|---|---|---|---|
| 200 | 124 | 4208 | 151.3 | 527 |
| 240 | 120 | 4100 | 152.9 | 433 |
| 300 | 123 | 4188 | 151.3 | 337 |
| 340 | 120 | 4122 | 150.5 | 293 |
| 400 | 107 | 3791 | 225.7 | 244 |
| 500 | 99 | 3617 | 158.6 | 190 |
| 600 | 58 | 2659 | 158.6 | 156 |
| 700 | 55 | 2527 | 136.8 | 132 |
| 800 | 46 | 2266 | 119.0 | 114 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Näger, C.; Kniesburges, S.; Tur, B.; Schoder, S.; Becker, S. An Investigation of Acoustic Back-Coupling in Human Phonation on a Synthetic Larynx Model. Bioengineering 2023, 10, 1343. https://doi.org/10.3390/bioengineering10121343
Näger C, Kniesburges S, Tur B, Schoder S, Becker S. An Investigation of Acoustic Back-Coupling in Human Phonation on a Synthetic Larynx Model. Bioengineering. 2023; 10(12):1343. https://doi.org/10.3390/bioengineering10121343
Chicago/Turabian StyleNäger, Christoph, Stefan Kniesburges, Bogac Tur, Stefan Schoder, and Stefan Becker. 2023. "An Investigation of Acoustic Back-Coupling in Human Phonation on a Synthetic Larynx Model" Bioengineering 10, no. 12: 1343. https://doi.org/10.3390/bioengineering10121343
APA StyleNäger, C., Kniesburges, S., Tur, B., Schoder, S., & Becker, S. (2023). An Investigation of Acoustic Back-Coupling in Human Phonation on a Synthetic Larynx Model. Bioengineering, 10(12), 1343. https://doi.org/10.3390/bioengineering10121343






