A Novel Registration Method for a Mixed Reality Navigation System Based on a Laser Crosshair Simulator: A Technical Note
Abstract
:1. Introduction
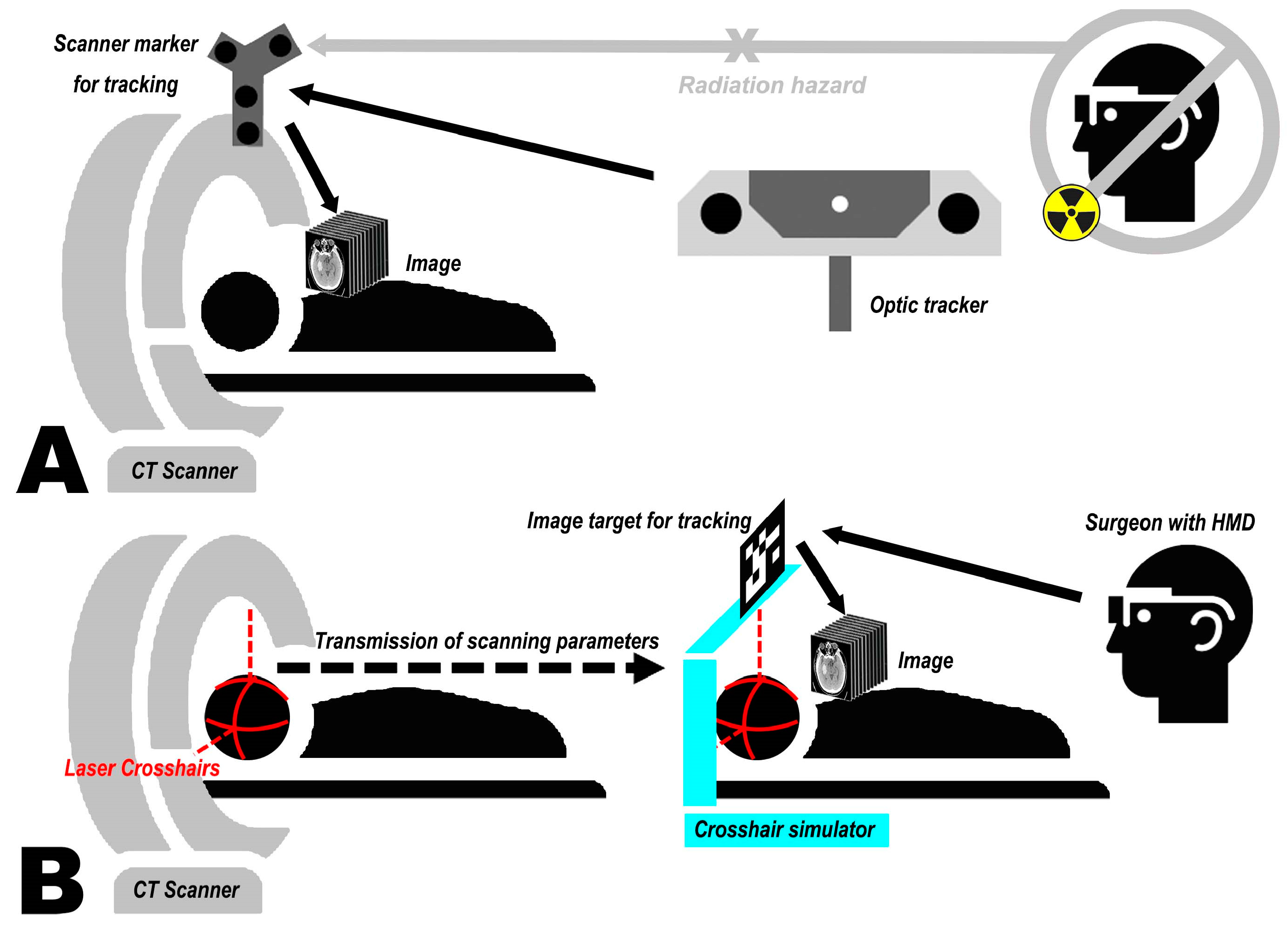
2. Materials and Methods
2.1. The Crosshair Simulator
2.1.1. Concept and Design of the Crosshair Simulator
- The rack is an “L” shaped basic frame for mounting other components such as the laser emitters. Users can flexibly adjust its position and orientation in space using a handle and then securely lock it in place with a mechanical arm (see Figure 2A).
- Two laser emitters (wavelength: 650 nm, power: 12 mW) are horizontally and vertically fixed on the arms of the rack. They project two sets of laser crosshairs inside the simulator, with the centerlines of the crosshairs located coplanar and perpendicular to each other. This configuration creates three orthogonal planes in space, forming the simulator coordinate system (SCS). When an object is exposed to the laser, it will receive a crosshair projection on its top and side surfaces, analogous to the positioning crosshairs observed in CT or MRI scanners (see Figure 2B).
- The MR interface consists of a stainless-steel panel (size: 6 cm × 6 cm) printed with a visually recognizable target image. It is firmly fixed on the rack. The MR interface establishes the relationship between the tracking and virtual spaces. Once the target images are detected and recognized by the HMD, the virtual space is initialized with the geometric center of the target image as the origin. This process is implemented using the Vuforia Software Development Kit (SDK) (Version 10.14, PTC, Inc., Boston, MA, USA).
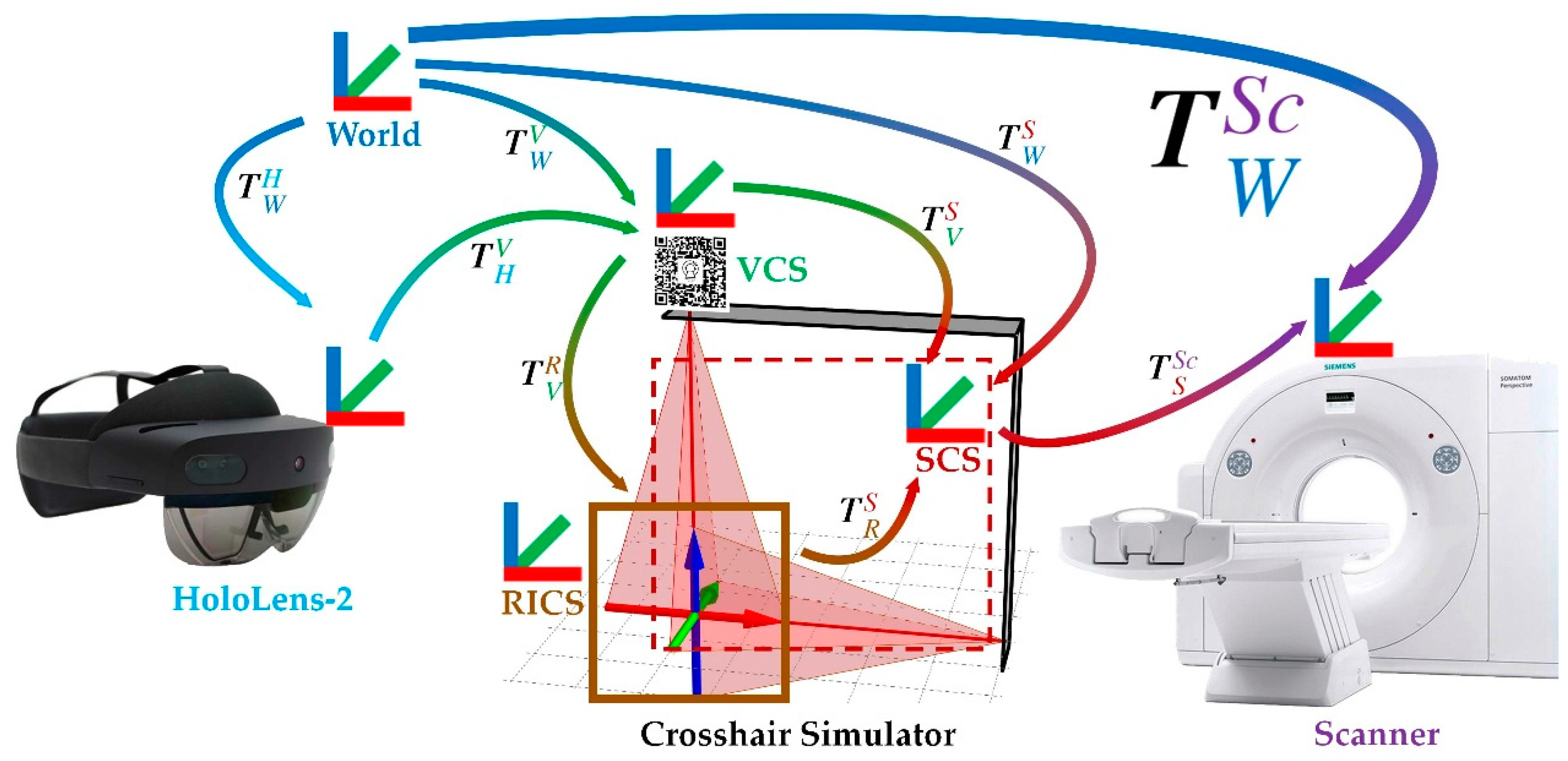
2.1.2. Coordinate Systems
- The simulator coordinate system (SCS) is defined from the laser crosshairs’ geometric-optic relationships.
- The reference image coordinate system (RICS), defined by the scanner during reference image acquisition, either in MRI or CT procedures. This coordinate system is established at the position where the gantry laser positioning lines are projected. In the case of MRI, the first “localizer scan” at the beginning of the scanning session establishes this coordinate system, while in CT procedures, a similar “scout scan” is used for the same purpose.
- The virtual coordinate system (VCS) is defined by recognition of the MR interface.
2.1.3. Calibration
2.1.4. Mathematical Model for Crosshair Simulator-Based Registration
2.2. The Components of the MR Platform
2.2.1. MR HMD
2.2.2. MR Platform Development
2.3. Practical Workflow of MRN System
2.3.1. Image Acquisition and Laser Projection Marking
2.3.2. Image Segmentation and Holograms Generation
2.3.3. Crosshair Simulator Deployment
2.3.4. Holograms Registration and Update
2.4. Experimental Design for Proof-of-Concept
2.4.1. Image Data Source
2.4.2. Head Phantom Creation
2.4.3. Creation of Holograms for Validation
2.4.4. MRN Registration and Holograms Deployment
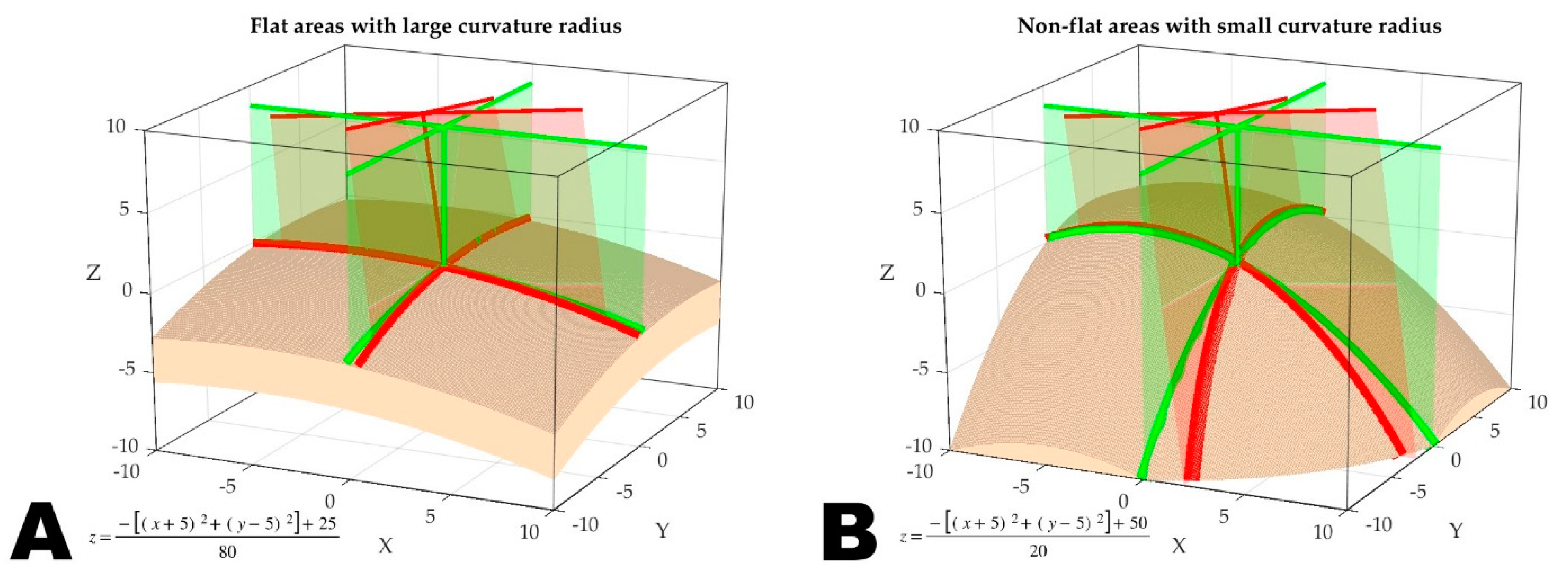
2.4.5. Accuracy Evaluation
2.4.6. Statistical Analysis
3. Results
3.1. Workflow Analysis
3.2. Accuracy Analysis
4. Discussion
- From a technical perspective, the crosshair simulator provides surgeons with an intuitive reference for physical positioning, while the MR Platform furnishes a visual reference for anatomical structures. This combination ensures reliable physical positioning and aids in a deeper comprehension of the surgical area.
- Regarding visual tracking, the crosshair simulator furnishes a stable CV tracking reference in physical space, whereas the MR Platform ensures visual stability through spatial anchors as the user moves. The spatial anchors signify holographic visualization optimization when surgeons need to relocate or change angles during surgery.
- In the context of practical workflow, the crosshair simulator can be rapidly deployed during surgical preparation, followed by the activation of the MR Platform to provide clear visual references and planning for surgeons. In the event of technical failures in either system, the Crosshair simulator can act as a backup physical reference location, while the MR Platform can concurrently optimize CV tracks. Hence, this fusion enhances efficiency, reliability, and robustness.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | Two-Dimensional |
| 3D | Three-Dimensional |
| AR | Augmented Reality |
| CBCT | Cone Beam Computed Tomography |
| CT | Computed Tomography |
| CV | Computer vision |
| DICOM | Digital Imaging and Communications in Medicine |
| DOF | Degrees of Freedom |
| EVD | Extra-Ventricular Drainage |
| FLE | Fiducial Localization Errors |
| FoV | Field of View |
| GCA | Great Circle Arc |
| HMD | Head-Mounted Display |
| HL-2 | HoloLens-2 |
| IMU | Inertial Measurement Unit |
| IPD | Interpupillary Distance |
| MR | Mixed Reality |
| MRI | Magnetic Resonance Imaging |
| MRN | Mixed Reality Navigation |
| MRTK | Mixed Reality Toolkit |
| OR | Operating Room |
| PV | Photos-Videos |
| PCP | Primary Calibration Position |
| RICS | Reference Image Coordinate System |
| RMSE | Root Mean Square Error |
| SCA | Small Circle Arc |
| SCS | Simulator Coordinate System |
| SCP | Secondary Calibration Position |
| SDK | Software Development Kit |
| SLAM | Synchronous Localization and Mapping |
| TRE | Target Registration Error |
| VCS | Virtual Coordinate System |
| VLC | Visible Light Cameras |
| VR | Virtual Reality |
| UWP | Universal Windows Platform |
References
- Carl, B.; Bopp, M.; Saß, B.; Pojskic, M.; Gjorgjevski, M.; Voellger, B.; Nimsky, C. Reliable navigation registration in cranial and spine surgery based on intraoperative computed tomography. Neurosurg. Focus 2019, 47, E11. [Google Scholar] [CrossRef]
- Watanabe, Y.; Fujii, M.; Hayashi, Y.; Kimura, M.; Murai, Y.; Hata, M.; Sugiura, A.; Tsuzaka, M.; Wakabayashi, T. Evaluation of errors influencing accuracy in image-guided neurosurgery. Radiol. Phys. Technol. 2009, 2, 120–125. [Google Scholar] [CrossRef] [PubMed]
- Bopp, M.H.A.; Corr, F.; Saß, B.; Pojskic, M.; Kemmling, A.; Nimsky, C. Augmented Reality to Compensate for Navigation Inaccuracies. Sensors 2022, 22, 9591. [Google Scholar] [CrossRef] [PubMed]
- Kantelhardt, S.R.; Gutenberg, A.; Neulen, A.; Keric, N.; Renovanz, M.; Giese, A. Video-assisted navigation for adjustment of image-guidance accuracy to slight brain shift. Oper. Neurosurg. 2015, 11, 504–511. [Google Scholar] [CrossRef] [PubMed]
- Stieglitz, L.H.; Fichtner, J.; Andres, R.; Schucht, P.; Krähenbühl, A.-K.; Raabe, A.; Beck, J. The silent loss of neuronavigation accuracy: A systematic retrospective analysis of factors influencing the mismatch of frameless stereotactic systems in cranial neurosurgery. Neurosurgery 2013, 72, 796–807. [Google Scholar] [CrossRef] [PubMed]
- Incekara, F.; Smits, M.; Dirven, C.; Vincent, A. Clinical Feasibility of a Wearable Mixed-Reality Device in Neurosurgery. World Neurosurg. 2018, 118, e422–e427. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Wang, N.; Zhang, W.; Li, D.; Zhang, L.; Qu, X.; Cheng, W.; Xu, Y.; Chen, W.; et al. A wearable mixed-reality holographic computer for guiding external ventricular drain insertion at the bedside. J. Neurosurg. 2018, 131, 1599–1606. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, W.; Wang, N. Wearable mixed-reality holographic guidance for catheter-based basal ganglia hemorrhage treatment. Interdiscip. Neurosurg. 2023, 34, 101821. [Google Scholar] [CrossRef]
- Qi, Z.; Li, Y.; Xu, X.; Zhang, J.; Li, F.; Gan, Z.; Xiong, R.; Wang, Q.; Zhang, S.; Chen, X. Holographic mixed-reality neuronavigation with a head-mounted device: Technical feasibility and clinical application. Neurosurg. Focus 2021, 51, E22. [Google Scholar] [CrossRef]
- van Doormaal, T.P.C.; van Doormaal, J.A.M.; Mensink, T. Clinical Accuracy of Holographic Navigation Using Point-Based Registration on Augmented-Reality Glasses. Oper. Neurosurg. 2019, 17, 588–593. [Google Scholar] [CrossRef]
- Meola, A.; Cutolo, F.; Carbone, M.; Cagnazzo, F.; Ferrari, M.; Ferrari, V. Augmented reality in neurosurgery: A systematic review. Neurosurg. Rev. 2017, 40, 537–548. [Google Scholar] [CrossRef] [PubMed]
- Kiya, N.; Dureza, C.; Fukushima, T.; Maroon, J.C. Computer Navigational Microscope for Minimally Invasive Neurosurgery. Minim. Invasive Neurosurg. 1997, 40, 110–115. [Google Scholar] [CrossRef] [PubMed]
- Léger, É.; Drouin, S.; Collins, D.L.; Popa, T.; Kersten-Oertel, M. Quantifying attention shifts in augmented reality image-guided neurosurgery. Healthc. Technol. Lett. 2017, 4, 188–192. [Google Scholar] [CrossRef] [PubMed]
- Drouin, S.; Kochanowska, A.; Kersten-Oertel, M.; Gerard, I.J.; Zelmann, R.; De Nigris, D.; Bériault, S.; Arbel, T.; Sirhan, D.; Sadikot, A.F.; et al. IBIS: An OR ready open-source platform for image-guided neurosurgery. Int. J. Comput. Assist. Radiol. Surg. 2017, 12, 363–378. [Google Scholar] [CrossRef] [PubMed]
- De Mauro, A.; Raczkowsky, J.; Halatsch, M.E.; Wörn, H. Mixed Reality Neurosurgical Microscope for Training and Intra-operative Purposes. In Virtual and Mixed Reality; Springer: Berlin/Heidelberg, Germany, 2009; pp. 542–549. [Google Scholar]
- Pojskić, M.; Bopp, M.H.A.; Saß, B.; Carl, B.; Nimsky, C. Microscope-Based Augmented Reality with Intraoperative Computed Tomography-Based Navigation for Resection of Skull Base Meningiomas in Consecutive Series of 39 Patients. Cancers 2022, 14, 2302. [Google Scholar] [CrossRef]
- Bopp, M.H.A.; Saß, B.; Pojskić, M.; Corr, F.; Grimm, D.; Kemmling, A.; Nimsky, C. Use of Neuronavigation and Augmented Reality in Transsphenoidal Pituitary Adenoma Surgery. J. Clin. Med. 2022, 11, 5590. [Google Scholar] [CrossRef]
- Mahvash, M.; Besharati Tabrizi, L. A novel augmented reality system of image projection for image-guided neurosurgery. Acta Neurochir. 2013, 155, 943–947. [Google Scholar] [CrossRef]
- Besharati Tabrizi, L.; Mahvash, M. Augmented reality–guided neurosurgery: Accuracy and intraoperative application of an image projection technique. J. Neurosurg. JNS 2015, 123, 206–211. [Google Scholar] [CrossRef]
- Yavas, G.; Caliskan, K.E.; Cagli, M.S. Three-dimensional–printed marker–based augmented reality neuronavigation: A new neuronavigation technique. Neurosurg. Focus 2021, 51, E20. [Google Scholar] [CrossRef]
- Shu, X.-j.; Wang, Y.; Xin, H.; Zhang, Z.-z.; Xue, Z.; Wang, F.-y.; Xu, B.-n. Real-time augmented reality application in presurgical planning and lesion scalp localization by a smartphone. Acta Neurochir. 2022, 164, 1069–1078. [Google Scholar] [CrossRef]
- Alves, M.O.; Dantas, D.O. Mobile Augmented Reality for Craniotomy Planning. In Proceedings of the 2021 IEEE Symposium on Computers and Communications (ISCC), Athens, Greece, 5–8 September 2021; pp. 1–6. [Google Scholar]
- de Almeida, A.G.C.; Fernandes de Oliveira Santos, B.; Oliveira, J.L.M. A Neuronavigation System Using a Mobile Augmented Reality Solution. World Neurosurg. 2022, 167, e1261–e1267. [Google Scholar] [CrossRef] [PubMed]
- Cenzato, M.; Fratianni, A.; Stefini, R. Using a Smartphone as an Exoscope Where an Operating Microscope is not Available. World Neurosurg. 2019, 132, 114–117. [Google Scholar] [CrossRef]
- Deng, W.; Li, F.; Wang, M.; Song, Z. Easy-to-Use Augmented Reality Neuronavigation Using a Wireless Tablet PC. Stereotact. Funct. Neurosurg. 2013, 92, 17–24. [Google Scholar] [CrossRef] [PubMed]
- Satoh, M.; Nakajima, T.; Yamaguchi, T.; Watanabe, E.; Kawai, K. Application of Augmented Reality to Stereotactic Biopsy. Neurol. Med.-Chir. 2019, 59, 444–447. [Google Scholar] [CrossRef] [PubMed]
- Chiou, S.-Y.; Zhang, Z.-Y.; Liu, H.-L.; Yan, J.-L.; Wei, K.-C.; Chen, P.-Y. Augmented Reality Surgical Navigation System for External Ventricular Drain. Healthcare 2022, 10, 1815. [Google Scholar] [CrossRef] [PubMed]
- Abe, Y.; Sato, S.; Kato, K.; Hyakumachi, T.; Yanagibashi, Y.; Ito, M.; Abumi, K. A novel 3D guidance system using augmented reality for percutaneous vertebroplasty: Technical note. J. Neurosurg. Spine SPI 2013, 19, 492–501. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, V.; Cutolo, F. Letter to the Editor: Augmented reality–guided neurosurgery. J. Neurosurg. JNS 2016, 125, 235–237. [Google Scholar] [CrossRef] [PubMed]
- Gsaxner, C.; Li, J.; Pepe, A.; Jin, Y.; Kleesiek, J.; Schmalstieg, D.; Egger, J. The HoloLens in medicine: A systematic review and taxonomy. Med. Image Anal. 2023, 85, 102757. [Google Scholar] [CrossRef]
- Hayasaka, T.; Kawano, K.; Onodera, Y.; Suzuki, H.; Nakane, M.; Kanoto, M.; Kawamae, K. Comparison of accuracy between augmented reality/mixed reality techniques and conventional techniques for epidural anesthesia using a practice phantom model kit. BMC Anesthesiol. 2023, 23, 171. [Google Scholar] [CrossRef]
- McJunkin, J.L.; Jiramongkolchai, P.; Chung, W.; Southworth, M.; Durakovic, N.; Buchman, C.A.; Silva, J.R. Development of a Mixed Reality Platform for Lateral Skull Base Anatomy. Otol. Neurotol. Off. Publ. Am. Otol. Soc. Am. Neurotol. Soc. Eur. Acad. Otol. Neurotol. 2018, 39, e1137–e1142. [Google Scholar] [CrossRef]
- Pepe, A.; Trotta, G.F.; Mohr-Ziak, P.; Gsaxner, C.; Wallner, J.; Bevilacqua, V.; Egger, J. A Marker-Less Registration Approach for Mixed Reality-Aided Maxillofacial Surgery: A Pilot Evaluation. J. Digit. Imaging 2019, 32, 1008–1018. [Google Scholar] [CrossRef] [PubMed]
- Peters, T.M.; Linte, C.A.; Yaniv, Z.; Williams, J. Mixed and Augmented Reality in Medicine; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Zhou, Z.; Yang, Z.; Jiang, S.; Zhuo, J.; Li, Y.; Zhu, T.; Ma, S.; Zhang, J. Validation of a surgical navigation system for hypertensive intracerebral hemorrhage based on mixed reality using an automatic registration method. Virtual Real. 2023, 27, 2059–2071. [Google Scholar] [CrossRef]
- Zhou, Z.; Yang, Z.; Jiang, S.; Zhuo, J.; Zhu, T.; Ma, S. Surgical Navigation System for Hypertensive Intracerebral Hemorrhage Based on Mixed Reality. J. Digit. Imaging 2022, 35, 1530–1543. [Google Scholar] [CrossRef] [PubMed]
- Gharios, M.; El-Hajj, V.G.; Frisk, H.; Ohlsson, M.; Omar, A.; Edström, E.; Elmi-Terander, A. The use of hybrid operating rooms in neurosurgery, advantages, disadvantages, and future perspectives: A systematic review. Acta Neurochir. 2023, 165, 2343–2358. [Google Scholar] [CrossRef] [PubMed]
- Fick, T.; van Doormaal, J.A.M.; Hoving, E.W.; Willems, P.W.A.; van Doormaal, T.P.C. Current Accuracy of Augmented Reality Neuronavigation Systems: Systematic Review and Meta-Analysis. World Neurosurg. 2021, 146, 179–188. [Google Scholar] [CrossRef] [PubMed]
- Fick, T.; Meulstee, J.W.; Köllen, M.H.; Van Doormaal, J.A.M.; Van Doormaal, T.P.C.; Hoving, E.W. Comparing the influence of mixed reality, a 3D viewer, and MRI on the spatial understanding of brain tumours. Front. Virtual Real. 2023, 4, 1214520. [Google Scholar] [CrossRef]
- Colombo, E.; Bektas, D.; Regli, L.; van Doormaal, T. Case report: Impact of mixed reality on anatomical understanding and surgical planning in a complex fourth ventricular tumor extending to the lamina quadrigemina. Front. Surg. 2023, 10, 1227473. [Google Scholar] [CrossRef]
- Colombo, E.; Esposito, G.; Regli, L.; Fierstra, J.; Seboek, M.; Germans, M.; van Doormaal, T. Mixed Reality applied to surgical planning and customization of Carotid Endarterectomies. Brain Spine 2023, 3, 102030. [Google Scholar] [CrossRef]
- Colombo, E.; Regli, L.; Esposito, G.; Germans, M.; Fierstra, J.; Serra, C.; van Doormaal, T. Impact of mixed reality on surgical planning: A single center usability study with 119 subsequent cases. Brain Spine 2023, 3, 102325. [Google Scholar] [CrossRef]
- Jean, W.C.; Piper, K.; Felbaum, D.R.; Saez-Alegre, M. The Inaugural “Century” of Mixed Reality in Cranial Surgery: Virtual Reality Rehearsal/Augmented Reality Guidance and Its Learning Curve in the First 100-Case, Single-Surgeon Series. Oper. Neurosurg. 2023. [Google Scholar] [CrossRef]
- Gibby, W.; Cvetko, S.; Gibby, A.; Gibby, C.; Sorensen, K.; Andrews, E.G.; Maroon, J.; Parr, R. The application of augmented reality-based navigation for accurate target acquisition of deep brain sites: Advances in neurosurgical guidance. J. Neurosurg. 2021, 137, 489–495. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Lu, Z.; He, M.; Sui, J.; Lin, T.; Xie, K.; Sun, J.; Ni, X. Augmented reality-guided positioning system for radiotherapy patients. J. Appl. Clin. Med. Phys. 2022, 23, e13516. [Google Scholar] [CrossRef]
- Qi, Z.; Zhang, S.; Xu, X.; Chen, X. Augmented reality–assisted navigation for deep target acquisition: Is it reliable? J. Neurosurg. 2022, 138, 1169–1170. [Google Scholar] [PubMed]
- Fick, T.; van Doormaal, J.A.M.; Hoving, E.W.; Regli, L.; van Doormaal, T.P.C. Holographic patient tracking after bed movement for augmented reality neuronavigation using a head-mounted display. Acta Neurochir. 2021, 163, 879–884. [Google Scholar] [CrossRef]
- Gibby, J.T.; Swenson, S.A.; Cvetko, S.; Rao, R.; Javan, R. Head-mounted display augmented reality to guide pedicle screw placement utilizing computed tomography. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 525–535. [Google Scholar] [CrossRef] [PubMed]
- Akulauskas, M.; Butkus, K.; Rutkūnas, V.; Blažauskas, T.; Jegelevičius, D. Implementation of Augmented Reality in Dental Surgery Using HoloLens 2: An In Vitro Study and Accuracy Assessment. Appl. Sci. 2023, 13, 8315. [Google Scholar] [CrossRef]
- Eom, S.; Sykes, D.; Rahimpour, S.; Gorlatova, M. NeuroLens: Augmented Reality-based Contextual Guidance through Surgical Tool Tracking in Neurosurgery. In Proceedings of the 2022 IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Singapore, 17–21 October 2022; pp. 355–364. [Google Scholar] [CrossRef]
- Gsaxner, C.; Li, J.; Pepe, A.; Schmalstieg, D.; Egger, J. Inside-Out Instrument Tracking for Surgical Navigation in Augmented Reality. In Proceedings of the 27th ACM Symposium on Virtual Reality Software and Technology, Osaka, Japan, 8–10 December 2021; p. 4. [Google Scholar]
- Martin-Gomez, A.; Li, H.; Song, T.; Yang, S.; Wang, G.; Ding, H.; Navab, N.; Zhao, Z.; Armand, M. STTAR: Surgical Tool Tracking using Off-the-Shelf Augmented Reality Head-Mounted Displays. IEEE Trans. Vis. Comput. Graph. Trans. Vis. Comput. Graph. 2023, arXiv:2208.08880. [Google Scholar] [CrossRef] [PubMed]
- Schneider, M.; Kunz, C.; Pal’a, A.; Wirtz, C.R.; Mathis-Ullrich, F.; Hlaváč, M. Augmented reality–assisted ventriculostomy. Neurosurg. Focus FOC 2021, 50, E16. [Google Scholar] [CrossRef]
- Chien, J.-C.; Tsai, Y.-R.; Wu, C.-T.; Lee, J.-D. HoloLens-Based AR System with a Robust Point Set Registration Algorithm. Sensors 2019, 19, 3555. [Google Scholar] [CrossRef]
- Dewitz, B.; Bibo, R.; Moazemi, S.; Kalkhoff, S.; Recker, S.; Liebrecht, A.; Lichtenberg, A.; Geiger, C.; Steinicke, F.; Aubin, H. Real-time 3D scans of cardiac surgery using a single optical-see-through head-mounted display in a mobile setup. Front. Virtual Real. 2022, 3, 949360. [Google Scholar] [CrossRef]
- Haxthausen, F.v.; Chen, Y.; Ernst, F. Superimposing holograms on real world objects using HoloLens 2 and its depth camera. Curr. Dir. Biomed. Eng. 2021, 7, 111–115. [Google Scholar] [CrossRef]
- Li, W.; Fan, J.; Li, S.; Tian, Z.; Zheng, Z.; Ai, D.; Song, H.; Yang, J. Calibrating 3D Scanner in the Coordinate System of Optical Tracker for Image-To-Patient Registration. Front. Neurorobot. 2021, 15, 636772. [Google Scholar] [CrossRef] [PubMed]
- Liebmann, F.; Roner, S.; von Atzigen, M.; Scaramuzza, D.; Sutter, R.; Snedeker, J.; Farshad, M.; Fürnstahl, P. Pedicle screw navigation using surface digitization on the Microsoft HoloLens. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 1157–1165. [Google Scholar] [CrossRef] [PubMed]
- Meulstee, J.W.; Nijsink, J.; Schreurs, R.; Verhamme, L.M.; Xi, T.; Delye, H.H.; Borstlap, W.A.; Maal, T.J. Toward holographic-guided surgery. Surg. Innov. 2019, 26, 86–94. [Google Scholar] [CrossRef]
- Carl, B.; Bopp, M.; Saß, B.; Nimsky, C. Intraoperative computed tomography as reliable navigation registration device in 200 cranial procedures. Acta Neurochir. 2018, 160, 1681–1689. [Google Scholar] [CrossRef]
- Saß, B.; Pojskic, M.; Bopp, M.; Nimsky, C.; Carl, B. Comparing fiducial-based and intraoperative computed tomography-based registration for frameless stereotactic brain biopsy. Stereotact. Funct. Neurosurg. 2021, 99, 79–89. [Google Scholar] [CrossRef]
- Burström, G.; Persson, O.; Edström, E.; Elmi-Terander, A. Augmented reality navigation in spine surgery: A systematic review. Acta Neurochir. 2021, 163, 843–852. [Google Scholar] [CrossRef]
- Elmi-Terander, A.; Nachabe, R.; Skulason, H.; Pedersen, K.; Söderman, M.; Racadio, J.; Babic, D.; Gerdhem, P.; Edström, E. Feasibility and Accuracy of Thoracolumbar Minimally Invasive Pedicle Screw Placement with Augmented Reality Navigation Technology. Spine 2018, 43, 1018–1023. [Google Scholar] [CrossRef]
- Skyrman, S.; Lai, M.; Edström, E.; Burström, G.; Förander, P.; Homan, R.; Kor, F.; Holthuizen, R.; Hendriks, B.H.W.; Persson, O.; et al. Augmented reality navigation for cranial biopsy and external ventricular drain insertion. Neurosurg. Focus 2021, 51, E7. [Google Scholar] [CrossRef]
- Wald, L.L.; McDaniel, P.C.; Witzel, T.; Stockmann, J.P.; Cooley, C.Z. Low-cost and portable MRI. J. Magn. Reson. Imaging 2020, 52, 686–696. [Google Scholar] [CrossRef]
- Cooley, C.Z.; McDaniel, P.C.; Stockmann, J.P.; Srinivas, S.A.; Cauley, S.F.; Śliwiak, M.; Sappo, C.R.; Vaughn, C.F.; Guerin, B.; Rosen, M.S. A portable scanner for magnetic resonance imaging of the brain. Nat. Biomed. Eng. 2021, 5, 229–239. [Google Scholar] [CrossRef] [PubMed]
- Basser, P. Detection of stroke by portable, low-field MRI: A milestone in medical imaging. Sci. Adv. 2022, 8, eabp9307. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.J.; Ouyang, P.R.; Sun, Z.H. A novel hybridization design principle for intelligent mechatronics systems. Abstr. Int. Conf. Adv. Mechatron. Evol. Fusion IT Mechatron. ICAM 2010, 5, 67–74. [Google Scholar] [CrossRef]
- Schlaier, J.; Warnat, J.; Brawanski, A. Registration accuracy and practicability of laser-directed surface matching. Comput. Aided Surg. 2002, 7, 284–290. [Google Scholar] [CrossRef] [PubMed]
- Paraskevopoulos, D.; Unterberg, A.; Metzner, R.; Dreyhaupt, J.; Eggers, G.; Wirtz, C.R. Comparative study of application accuracy of two frameless neuronavigation systems: Experimental error assessment quantifying registration methods and clinically influencing factors. Neurosurg. Rev. 2011, 34, 217–228. [Google Scholar] [CrossRef]
- Krombach, G.; Schmitz-Rode, T.; Wein, B.; Meyer, J.; Wildberger, J.; Brabant, K.; Günther, R. Potential of a new laser target system for percutaneous CT-guided nerve blocks. Neuroradiology 2000, 42, 838–841. [Google Scholar] [CrossRef]
- Moser, C.; Becker, J.; Deli, M.; Busch, M.; Boehme, M.; Groenemeyer, D.H. A novel Laser Navigation System reduces radiation exposure and improves accuracy and workflow of CT-guided spinal interventions: A prospective, randomized, controlled, clinical trial in comparison to conventional freehand puncture. Eur. J. Radiol. 2013, 82, 627–632. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, X.; Wang, L.; Zhu, J.; Yu, J. Development and feasibility evaluation of an AR-assisted radiotherapy positioning system. Front. Oncol. 2022, 12, 921607. [Google Scholar] [CrossRef]
- Poggi, S.; Pallotta, S.; Russo, S.; Gallina, P.; Torresin, A.; Bucciolini, M. Neuronavigation accuracy dependence on CT and MR imaging parameters: A phantom-based study. Phys. Med. Biol. 2003, 48, 2199. [Google Scholar] [CrossRef]
- Frantz, T.; Jansen, B.; Duerinck, J.; Vandemeulebroucke, J. Augmenting Microsoft’s HoloLens with vuforia tracking for neuronavigation. Healthc. Technol. Lett. 2018, 5, 221–225. [Google Scholar] [CrossRef]
- Furuse, M.; Ikeda, N.; Kawabata, S.; Park, Y.; Takeuchi, K.; Fukumura, M.; Tsuji, Y.; Kimura, S.; Kanemitsu, T.; Yagi, R. Influence of surgical position and registration methods on clinical accuracy of navigation systems in brain tumor surgery. Sci. Rep. 2023, 13, 2644. [Google Scholar] [CrossRef] [PubMed]
- Dho, Y.-S.; Kim, Y.J.; Kim, K.G.; Hwang, S.H.; Kim, K.H.; Kim, J.W.; Kim, Y.H.; Choi, S.H.; Park, C.-K. Positional effect of preoperative neuronavigational magnetic resonance image on accuracy of posterior fossa lesion localization. J. Neurosurg. 2019, 133, 546–555. [Google Scholar] [CrossRef]
- Bi, Z.M.; Lin, Y.; Zhang, W.J. The general architecture of adaptive robotic systems for manufacturing applications. Robot. Comput.-Integr. Manuf. 2010, 26, 461–470. [Google Scholar] [CrossRef]
- Ouyang, P.R.; Zhang, W.J.; Gupta, M.M. An adaptive switching learning control method for trajectory tracking of robot manipulators. Mechatronics 2006, 16, 51–61. [Google Scholar] [CrossRef]
- Wu, J.Q.; Yuan, C.W.; Yin, R.X.; Sun, W.; Zhang, W.J. A Novel Self-Docking and Undocking Approach for Self-Changeable Robots. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 12–14 June 2020; pp. 689–693. [Google Scholar]





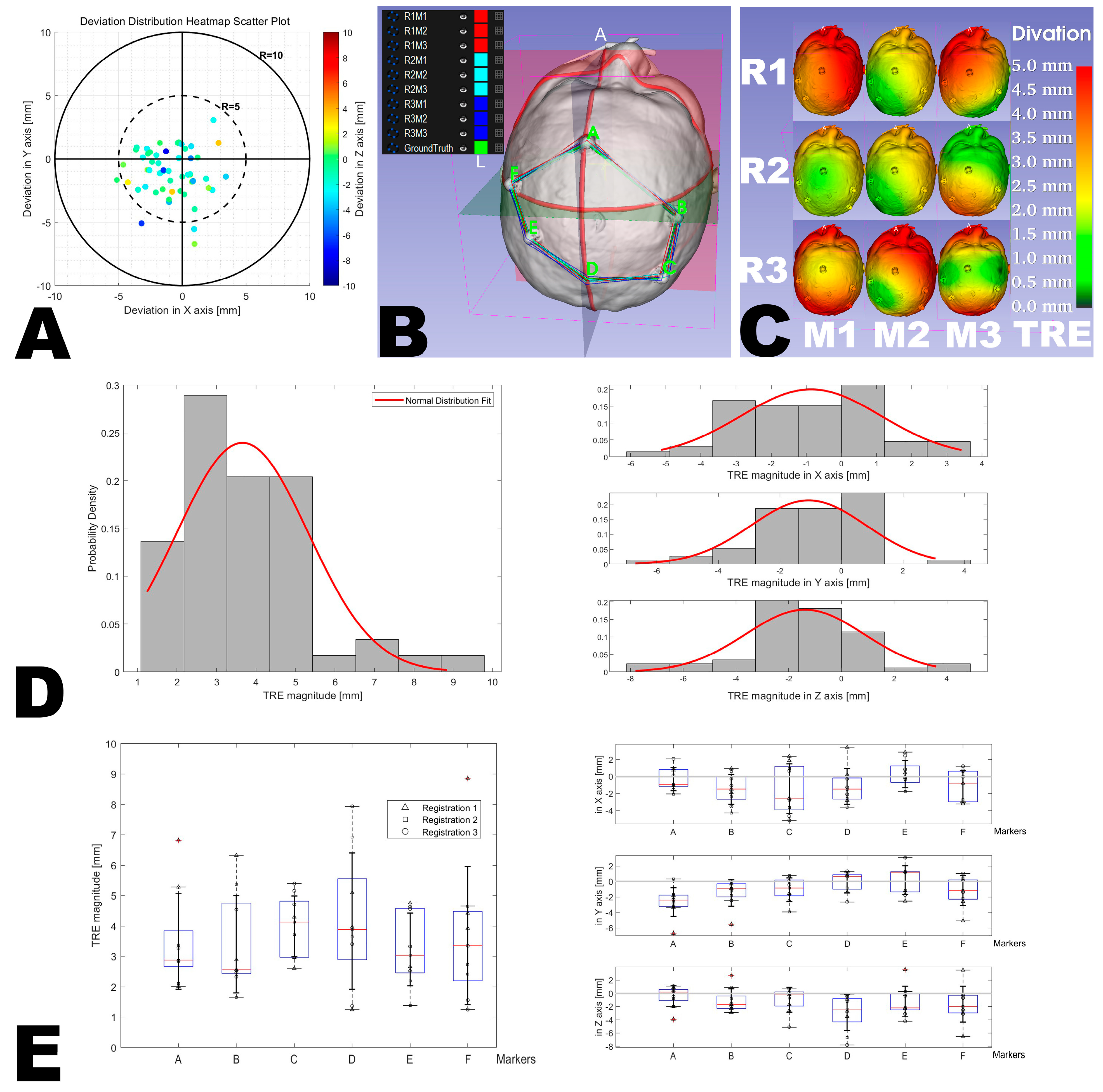
| Group | TRE * [mm] | Min [mm] | Max [mm] |
|---|---|---|---|
| Registration 1 | 4.1 ± 1.9 | 1.2 | 8.9 |
| Registration 2 | 3.3 ± 1.4 | 1.4 | 6.9 |
| Registration 3 | 3.6 ± 1.7 | 1.2 | 7.9 |
| Marker A | 3.5 ± 1.6 | 2.0 | 6.8 |
| Marker B | 3.4 ± 1.6 | 1.6 | 6.3 |
| Marker C | 4.0 ± 1.0 | 2.6 | 5.4 |
| Marker D | 4.2 ± 2.2 | 1.2 | 7.9 |
| Marker E | 3.2 ± 1.2 | 1.4 | 4.8 |
| Marker F | 3.7 ± 2.3 | 1.2 | 8.9 |
| Total | 3.7 ± 1.7 | 1.2 | 8.9 |
| Aspect | The Crosshair Simulator | The MR Platform | Complementarity | Compatibility |
|---|---|---|---|---|
| Technical principle | Provides physical positioning | Offers 3D visualization and virtual interaction | Combines benefits of physical and 3D visualization | Calibration process ensures synchronization and consistency between the crosshair simulator and MR |
| Visual tracking | Fixed visual tracking reference | Spatial anchors stabilize the MR view | Physical location back up and optimized CV vision tracking | Seamless transition between the two tracking modes |
| Practical workflow | Rapid physical positioning with low user dependency | Provides 3D visual references once activated | Quick re-registration; Remedial static guidance | Efficient and intuitive registration, simplifying interaction |
| Reference | Registration Method | Object | Measurement Method * | Accuracy # [mm] |
|---|---|---|---|---|
| Li et al., 2018 [7] | Manual | Patient | Indirect | 4.34 ± 1.63 |
| Li et al., 2023 [8] | Manual | Patient | Indirect | 5.46 ± 2.22 |
| Gibby et al., 2019 [48] | Manual | Phantom | Indirect | 2.50 ± 0.44 |
| McJunkin et al., 2019 [32] | Manual | Phantom | Direct | 5.76 ± 0.54 |
| Zhou et al., 2022 [36] | Fiducial | Phantom and Patient | Direct | Phantom: 1.65 Patient: 1.94 |
| Gibby et al., 2021 [44] | Fiducial | Phantom | Indirect | 3.62 ± 1.71 |
| Gsaxner et al., 2021 [51] | Fiducial | Phantom | Direct | 1.70 ± 0.81 |
| Martin-Gomez et al., 2023 [52] | Fiducial | Phantom | Direct | 3.64 ± 1.47 |
| Zhou et al., 2023 [35] | Fiducial | Phantom | Direct | 1.74 ± 0.38 |
| Eom et al., 2022 [50] | Fiducial | Phantom | Direct | 3.12 ± 2.53 |
| Akulauskas et al., 2023 [49] | Fiducial | Phantom | Direct | Stationary: 3.32 ± 0.02 Dynamic: 4.77 ± 0.97 |
| Von Haxthausen et al., 2021 [56] | Surface | Phantom | Direct | 14.0 |
| Pepe et al., 2019 [33] | Surface | Phantom | Direct | X: 3.3 ± 2.3 Y: −4.5 ± 2.9 Z: −9.3 ± 6.1 |
| Liebmann et al., 2019 [58] | Surface | Phantom | Indirect | 2.77 ± 1.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Z.; Bopp, M.H.A.; Nimsky, C.; Chen, X.; Xu, X.; Wang, Q.; Gan, Z.; Zhang, S.; Wang, J.; Jin, H.; et al. A Novel Registration Method for a Mixed Reality Navigation System Based on a Laser Crosshair Simulator: A Technical Note. Bioengineering 2023, 10, 1290. https://doi.org/10.3390/bioengineering10111290
Qi Z, Bopp MHA, Nimsky C, Chen X, Xu X, Wang Q, Gan Z, Zhang S, Wang J, Jin H, et al. A Novel Registration Method for a Mixed Reality Navigation System Based on a Laser Crosshair Simulator: A Technical Note. Bioengineering. 2023; 10(11):1290. https://doi.org/10.3390/bioengineering10111290
Chicago/Turabian StyleQi, Ziyu, Miriam H. A. Bopp, Christopher Nimsky, Xiaolei Chen, Xinghua Xu, Qun Wang, Zhichao Gan, Shiyu Zhang, Jingyue Wang, Haitao Jin, and et al. 2023. "A Novel Registration Method for a Mixed Reality Navigation System Based on a Laser Crosshair Simulator: A Technical Note" Bioengineering 10, no. 11: 1290. https://doi.org/10.3390/bioengineering10111290
APA StyleQi, Z., Bopp, M. H. A., Nimsky, C., Chen, X., Xu, X., Wang, Q., Gan, Z., Zhang, S., Wang, J., Jin, H., & Zhang, J. (2023). A Novel Registration Method for a Mixed Reality Navigation System Based on a Laser Crosshair Simulator: A Technical Note. Bioengineering, 10(11), 1290. https://doi.org/10.3390/bioengineering10111290











