Abstract
In early corneal examinations, the relationships between the morphological and biomechanical features of the cornea were unclear. Although consistent links have been demonstrated between the two in certain cases, these are not valid in many diseased states. An accurate assessment of the corneal biomechanical properties is essential for understanding the condition of the cornea. Studies on corneal biomechanics in vivo suggest that clinical problems such as refractive surgery and ectatic corneal disease are closely related to changes in biomechanical parameters. Current techniques are available to assess the mechanical characteristics of the cornea in vivo. Accordingly, various attempts have been expended to obtain the relevant mechanical parameters from different perspectives, using the air-puff method, ultrasound, optical techniques, and finite element analyses. However, a measurement technique that can comprehensively reflect the full mechanical characteristics of the cornea (gold standard) has not yet been developed. We review herein the in vivo measurement techniques used to assess corneal biomechanics, and discuss their advantages and limitations to provide a comprehensive introduction to the current state of technical development to support more accurate clinical decisions.
1. Introduction
Mechanical characteristics are important features of the cornea. These are dependent on the distribution of collagen fibers in the stroma, the thickest layer of the cornea. The alignment of these internal collagen fibers is directly related to the biomechanical properties and (eventually) to the morphology of the cornea, which further influence its optical properties. Parameters determining corneal biomechanical characteristics can be used to reflect the states of corneal diseases.
A broader and deeper knowledge of corneal biomechanics could promote the evaluation of corneal ectasia patients [1] and facilitate research on treatments such as corneal cross-linking (CXL) [2,3], laser refractive surgery [4,5,6], and corneal transplantation [7]. It could also improve the understanding of the mechanisms of ophthalmic diseases such as refractive abnormalities [8], the effects of various corneal incisions on the corneal structure and function [9], and intraocular pressure determination.
Various parameters are currently used to quantify the corneal biomechanical properties. The longitudinal, shear, and Young’s moduli are the three main classical mechanical parameters that are used. Though different machines gave various terms for the description of corneal biomechanics, they can almost all be related to these three biomechanical features. This review explains the differences between them and their clinical implications. The shear modulus is often used to describe the rigidity of a material and is also referred to as the rigidity modulus. The Young’s modulus, on the other hand, reflects the stiffness of the material [10]. In dynamic loading conditions, the cornea demonstrates viscoelastic behavior; this material property is usually described by the dynamic modulus [11]. The difference between the biomechanical behavior of the cornea during energy storage and energy dissipation is known as “hysteresis” [12]. This property makes accurate measurement of the Young’s modulus of the cornea difficult: the hysteresis during loading and unloading of the intraocular pressure (IOP) causes the Young’s modulus to vary in real time with the IOP [12]. Accurate measurement of the corneal biomechanical properties in vivo is of immense importance in clinical practice. At present, various instruments based on different inherent principles are employed to evaluate the cornea based on different biomechanical parameters.
In vivo biomechanical measurements of the cornea are still in the nascent stage. The tonometer, which measures corneal rigidity using contact technology, has been available since the early 1900s [13]. Earlier noncontact methods for evaluating corneal mechanical properties were based on the use of air turbulence to cause corneal deformation, enabling noninvasive measurement of the biomechanical properties [14]. Less destructive corneal deformation technologies, such as air puff [15] and ultrasound [16,17], were developed later. Currently, commercial devices are used in clinical settings for measuring the corneal biomechanical properties, but these types of equipment are destructive. Current techniques usually reflect only a few mechanical properties of the cornea, such as longitudinal modulus, shear modulus, or Young’s modulus. There is no device that can comprehensively and accurately measure the various corneal biomechanical parameters. These techniques also make it difficult to reflect the biomechanical properties of different areas of the cornea at the three-dimensional level, often measuring only at the axial level, or showing the average properties of a large area. Moreover, IOP, central corneal thickness (CCT), eye movements, and other factors can cause measurement errors. The development of optical techniques in recent years has made it possible to evaluate corneal mechanical properties in nonperturbative ways [18], and the extensive use of finite element methods in corneal simulations has accelerated these developments [19,20] (Figure 1). These new techniques could provide the spatial distribution of corneal biomechanical features, which is valuable information for clinical use. However, these techniques are still in the early stages of research. There is currently still a lack of a gold-standard technique that can comprehensively quantify the various mechanical parameters of the cornea and describe the corneal biomechanical properties.
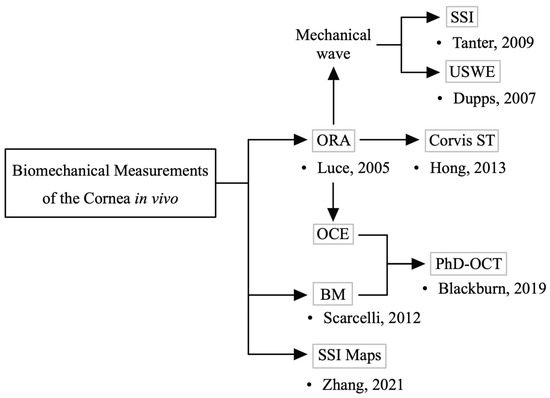
Figure 1.
Development of in vivo corneal biomechanical measurements. Initial techniques for assessing the corneal mechanical characteristics utilized air puffs (e.g., ocular response analyzer (ORA)) [14]. Later, less destructive corneal deformation techniques, such as ultrasound (mechanical waves) [16,17], were developed. In recent years, new technologies such as brillouin microscopy (BM) [18] have emerged. Some commercial devices (ORA, corneal visualization Scheimpflug technology (Corvis ST)) are now used in clinical settings.
This review focuses on various techniques for collecting biomechanical measurements of the cornea in vivo and describes their principles of operation, milestones during their development, and application prospects, thus providing an introduction to these existing assessment techniques and their recent developments. We expect this review to inspire new ideas that can promote the development of corneal biomechanical measurement in the future, which will be conducive to the improvement and development of new and more reliable measurements, especially the realization of in vivo tracking of corneal stress distribution.
2. Perturbation-Based Measurements
Corneal deformation induced by external pressure is a prerequisite for the assessment of corneal mechanical characteristics using perturbation techniques, although the mechanical parameters of interest and modes of analysis may differ within this broad category of techniques. The current direction of development in measurement techniques based on perturbation is from invasive to minimally invasive and noninvasive, with the hope that a noninvasive, noncontact technique will be developed to evaluate corneal biomechanical characteristics.
2.1. Ocular Response Analyzer
Early studies conducted to measure the corneal mechanical characteristics usually relied on pneumatic loads to deform the cornea from the inner side. Thus, these studies could only assess the local corneal mechanical properties in vitro [21,22,23]. In vivo tests implemented by injecting saline into the eyeballs were performed subsequently to determine the pressure–volume relationship and the stiffness of the living cornea [24]. Following this, devices were also developed to measure IOP and corneal rigidity using an in vivo contact plunger to flatten the cornea inwards [13]. The ocular response analyzer (ORA) is the first noncontact commercial device to employ this principle to assess corneal stiffness. It estimates the overall biomechanical behavior of the cornea by capturing the corneal deformation as the cornea is subjected to air pressure. The external machine provides an air pressure that varies in magnitude over time to deform the cornea in the inward direction. During this process, two critical points are captured and recorded as P1 and P2 when the central region of the cornea is in a flat shape. The deformation of the cornea is monitored using collimated infrared laser light by detecting the intensity of the reflected infrared signal [14].
Upon data processing, the ORA is able to reveal two parameters: corneal hysteresis (CH) and corneal resistance factor (CRF). The former of these quantifies the corneal viscoelastic properties and the latter is an indicator of the overall corneal resistance, reflecting the corneal elastic characteristics [12,14]. These parameters help to differentiate keratoconus from healthy corneas [25]. Furthermore, the ORA is considered a new IOP measurement technology because biomechanical indicators can be used to obtain the IOP data more accurately, thus providing Goldman-related IOP (IOPg) and corneal-compensated IOP (IOPcc) [14].
Although CH and CRF can reflect the corneal biomechanical properties, it is difficult to distinguish between the biomechanical properties of different areas of the cornea according to their principle and function [26]. The mathematical relationship between CH, CRF, and elastic modulus remains unclear, thus limiting the clinical use of this technique [26]. Additionally, CCT and IOP can influence CRF and CH data. Therefore, the weighted value of the CRF is often used in clinical applications of the ORA [27,28].
To overcome these limitations, several new studies have defined additional parameters [29,30]. These include the hysteretic loop area, which can improve the sensitivity of the ORA by extending the detection range and analyzing the relationship between pressure and displacement throughout the deformation process [30]. The ORA (Reichert Inc., Depew, NY, USA) is now commercially available for clinical use.
2.2. Corneal Visualization Scheimpflug Technology
Corneal visualization Scheimpflug technology (Corvis ST) was developed as an improvement of the ORA via the addition of an ultrafast Scheimpflug camera that allows direct monitoring of corneal deformation [31,32,33]. Both the ORA and Corvis ST require similar air perturbations, but the difference is that Corvis ST can maintain a consistent air pressure across different measurements. As a result, Corvis ST can record the process of corneal shape change more accurately, thus enabling more precise assessments [34,35].
Corvis ST reports two parameters, namely, the corneal biomechanical index (CBI) and the total biomechanical index (TBI). Both are new parameters based on a linear regression analysis combining corneal morphology and stiffness parameters, which can improve the detection rate of conical corneas [36]. Other parameters based on Corvis ST that are able to characterize the corneal biomechanical features in vivo have recently been proposed [37]. Figure 2 shows an example of keratoconus identified using Corvis ST (Oculus Inc., Wetzlar, Germany), and multiple parameters are quantified.
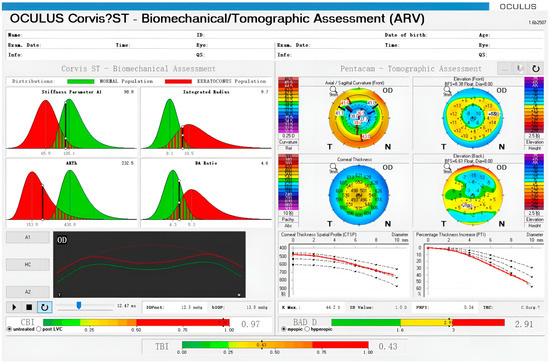
Figure 2.
Example of an ectatic eye observed using Corvis ST and Pentacam. Corneal parameters are displayed in the upper left and corneal deformation morphology is displayed in the lower left. Corneal morphological data are shown on the right. The Belin−Ambrósio display (BAD) D is a parameter based on corneal morphology to assess the risk of corneal ectasia. The corneal biomechanical index (CBI) and the total biomechanical index (TBI) are shown at the bottom.
However, Corvis ST cannot be used to analyze the corneal mechanical behavior in a specific direction. Furthermore, its results are also affected by factors such as the IOP [26]. Repeated experiments using Corvis ST have demonstrated that single measurements do not yield accurate results, and some form of averaging is generally required [38,39]. However, these limitations have not hindered the application of Corvis ST in clinical studies. Corvis ST has been shown to improve the screening accuracy in refractive surgery screening [40]. Corvis ST (Oculus Inc., Wetzlar, Germany) is currently commercially produced and is in clinical use.
2.3. Optical Coherence Elastography
Optical coherence tomography (OCT) is a technique used to examine the microscopic structures in biological tissues. The study that first reported it did not target ocular components [41]. Optical coherence elastography (OCE) is an imaging method that combines OCT with external loading to measure the corneal elasticity in vivo. It uses tomography for nondestructive estimation of the material properties of the cornea [42]. The evaluation can be performed without a significant increase in the IOP generated by using a pressure source to flatten the cornea. It utilizes the short coherence length of a broadband light source to achieve precise axial and lateral segmentation on a high-scattering medium with high resolution. According to the concept of OCE, the observed tissue deformation can be mathematically modeled and analyzed to approximate the Young’s modulus [43] in order to achieve noninvasiveness. Extensive research has been performed in this area. In addition to the pressure source, a miniature air-puff perturbation method has been proposed which can use a short, high-intensity air puff to cause a local displacement in the cornea; the pulse is propagated in the form of elastic waves, and can thus avoid the measurement errors originating from IOP changes [15,44,45]. The corneal viscoelasticity can also be quantitatively assessed [46].
Some studies have quantified the corneal biomechanical properties after CXL treatment in rabbit eyes using OCE [47], and have assessed the ability of OCE to perform in vivo measurements in humans [48]. A number of techniques have been developed based on OCE. Other studies further established a novel noncontact OCE imaging technique that uses interference from external pressure to assess the material properties of the cornea [49]. Air-puff-based corneal deformation is the basis of air-puff OCE [50]. Similarly to ORA, measurements can only be taken on a single axis, so only one-dimensional data can be obtained [50]. Additionally, the mechanical properties of the cornea show heterogeneous variations across the cornea, which makes the specificity of the measurement limited. For the same reason, measurement accuracy can be affected by IOP and CCT [50]. Shear-wave OCE can reflect corneal stiffness by measuring the speed of surface wave propagation through the corneal tissue with an ultrasound device. This makes it possible to take measurements in two or even three dimensions [51]. The results of the measurements still correlate with IOP, CCT, and eye movements [52]. Pulsed laser excitation OCE [53] and acoustic radiation force OCE [54] utilize laser-induced surface acoustic waves and ARF systems as excitation, respectively, which are then monitored in conjunction with OCT techniques. Both allow the Young’s modulus of the cornea to be measured in real time. It is well known that the mechanical properties of the cornea vary with factors such as IOP, and real-time testing can avoid the lagging problems associated with changes in IOP [53]. The techniques are still in the in vitro testing phase and in vivo measurements have not yet been achieved.
2.4. Mechanical Waves
Mechanical waves can be used in perturbation techniques to induce slight tissue displacement. These techniques can reflect the biomechanical properties of the cornea based on propagation analyses of mechanical waves induced in the corneal tissue, thus serving as a new noninvasive technique type used to assess corneal biomechanical properties.
2.4.1. Supersonic Shear-Wave Imaging
Supersonic shear-wave imaging (SSWI) is a novel ultrasound technique that can provide real-time and quantitative mapping of the corneal viscoelasticity in noninvasive conditions to objectively assess soft-tissue stiffness [16,55]. A conventional ultrasonic probe causes corneal displacements, and the ultrasound wave in the tissue evolves into shear waves that propagate and reflect the local elasticity of the cornea based on the speed of their propagation [16]. This technique reflects the viscoelastic index and Young’s modulus of the cornea and is directly applicable to in vivo studies.
SSWI can be used to quantify the corneal elastic anisotropy in vivo [56], quantitatively estimate the local corneal stiffness, and generate a two-dimensional elastogram of the cornea [16]. SSWI has also shown good evaluation capabilities in CXL treatments [57,58]. This technique has been applied to assess the stiffness of many biological tissues in addition to in vivo measurements of corneal biomechanics [59,60,61].
2.4.2. Ultrasound Surface Wave Elastometry
Ultrasound surface wave elastometry (USWE) uses an ultrasound probe to measure the time of wave propagation between two transducers set at a fixed distance; the propagation time can be used to determine the corneal elasticity. This technique reflects the local mechanical properties of the cornea and compares the stiffness values in the central, radial, and other directions [17]. This technique was used for donor tissues in the past [17], but has been successfully applied to in vivo examinations of corneas recently [62].
USWE has been applied to the determination of corneal biomechanics in CXL studies [63]. However, this technique has not been adequately studied; as a result, relevant commercial instruments are unavailable.
3. Non-Perturbation-Based Measurements
Unlike perturbation-based measurements, non-perturbation-based measurements do not rely on corneal deformation. These techniques usually involve direct corneal biomechanical assessments based on the inherent structural properties of the corneal tissue. The acquisition of the intrinsic corneal tissue parameters can be currently achieved using techniques such as optical or computational simulations.
3.1. Brillouin Microscopy
Brillouin microscopy (BM) uses the Brillouin shift between Stokes and anti-Stokes scattering to measure the longitudinal or bulk modulus in order to describe the mechanical compressibility of tissue. BM imaging techniques can be used to obtain volumetric images of the elastic characteristics of the cornea [18]. A low-power, near-infrared laser beam is used to analyze the spectral data of the echo signal and generate a three-dimensional map of the longitudinal modulus of the corneal surface and the corneal thickness.
BM observations can describe the local biomechanical characteristics of the cornea and reflect its three-dimensional spatial heterogeneity. The downsides are the narrow measurement range and the long acquisition time, which limits the large-scale use of BM approaches [64,65]. As for biomechanical properties, BM can be used to assess the longitudinal modulus of the cornea. However, the technology is not currently available for the assessment of Young’s modulus and stress–strain behavior.
Many clinical studies have utilized BM for in vivo corneal measurements [65], detection of keratoconus [66], and other applications. Clinical trials are being conducted using BM to demonstrate that corneal CXL treatments can increase corneal stiffness [67]. This technique is expected to become a standard and valid clinical examination technique for the assessment of the biomechanical characteristics of the cornea [68].
3.2. Phase-Decorrelation OCT
Phase-decorrelation OCT (PhD-OCT) is a new technique used to characterize corneal biomechanics by combining OCT and BM. Unlike BM, which uses Brillouin scattering, PhD-OCT uses dynamic light scattering of particles in a fluid to obtain the relevant parameters. After scanning, the attenuation constant of the particles, which is related to the viscoelasticity of the material, is calculated using the Fourier transform [69].
PhD-OCT can reflect the corneal spatial heterogeneity in three dimensions [70]. Moreover, PhD-OCT can circumvent most of the disadvantages of corneal biomechanical measurements, such as IOP dependence and extended assessment time, thus making it a promising technique.
3.3. Finite Element Method
The finite element method is an in silico technique that can mimic real-world physical or mathematical problems by discretizing the complex geometry into a finite number of small volumes with regular shapes, the so-called elements. Regarding the corneal assessment applications, the cornea and its surrounding structures can be represented as a large number of brick or pyramid elements, which are connected through nodes and defined with specific material properties that are ideally derived from patient-specific measurements. The responses to changes in the simulated structure are then obtained by calculating the stiffness matrix. For large deformation analyses, calculation iterations are needed until a converged solution of the entire structure is obtained [71].
The finite element method has been used extensively in several studies of the cornea, and many techniques based on these models have been developed for evaluating corneal biomechanical properties [70,72].
Stress–Strain Index Mapping
Stress–strain index mapping is an emerging approach used to assess the biomechanics of corneal materials. This method is based on material model simulations using the finite element method [20] and can be used to analyze the distribution of collagen fibers in the cornea [73,74]. It uses inverse analysis to obtain two-dimensional maps of the corneal stiffness, calculate the material tangential modulus at different IOP levels, and estimate the stress–strain behavior [75]. This approach relies on the proven link between the corneal tissue microstructure and stiffness distribution, and on the concept of the stress–strain index (SSI) proposed in a previous study on Corvis ST [76]. SSI can be used to quantify the corneal Young’s modulus, which is an independent material property that is not influenced by IOP and CCT [75,77]. It has been demonstrated that the SSI parameter gradually decreases as keratoconus progresses [78]. This indicates that the concept of SSI can reflect the biomechanical properties of the cornea and is almost completely independent of corneal morphology and IOP.
The SSI map is a comprehensive analysis of the local SSI values obtained via Corvis ST, using the geometric information and collagen distribution principles to derive the final stress–strain index map. In view of the nonlinear nature of the stress–strain behavior of the cornea, SSI maps can provide more accurate measurements of biomechanical parameters. Before exporting the SSI maps, it is necessary to diagnose the presence and type of corneal ectasia to select the appropriate model for computational analysis. In the case of a healthy cornea, the derived SSI maps show only slight fluctuations in the SSI values across the corneal surface, whereas keratoconus shows great disparities in the SSI value over some areas [75]. Two-dimensional images provide a new tool for the assessment of local changes of corneal stiffness. SSI maps visually quantify the biomechanical characteristics of the corneal surface and provide direct insight into the mechanism of progression of the patient’s keratoconus. However, it should also be noted that the current technique is based on a single model of corneal fiber distribution and does not take into account differences between individual eyes. Moreover, the study only included a fairly small number of keratoconus cases, which makes the final results unrepresentative, and more data need to be included in subsequent research.
The SSI mapping technique has evolved very rapidly and is now in clinical trials. Recent studies have evaluated the progression of keratoconus using SSI maps [79] and demonstrated the technique’s potential for commercial clinical applications.
4. Corneal Biomechanics in Clinical Settings
The concern about corneal biomechanics stems directly from clinical problems. The corneal stroma is essentially a thin tissue made up of multiple layers of interwoven fibers, so any disruption of the corneal structure will alter the biomechanical properties of the cornea [80]. One of the most relevant diseases is keratoconus. The most important changes in keratoconus are the reduction in stromal layer thickness and the rupture of the Bowman layer. The collagen fiber content in the cornea is also decreased significantly [81]. This results in a change in the corneal biomechanical properties, which eventually manifests in the morphology of the cornea, with a reduction in the central corneal thickness and a conical shape of the cornea. A study using the OCE technique to assess changes in corneal biomechanical properties in vitro in keratoconus and to map the two-dimensional distribution of Young’s modulus showed that the Young’s modulus in the central conical region was much lower than that in healthy corneas [82]. Such comparisons are expected to enable early detection of the changes in biomechanical properties associated with keratoconus and to aid clinical diagnosis. Some systemic connective tissue diseases that manifest in the eye as keratoconus, as well as keratoconus as a complication of refractive surgery, may also be associated with this pathogenesis [83]. To reduce the probability of keratoconus as a complication refractive surgery, most current refractive procedures restrict postoperative corneal stromal bed thickness to a minimum of 250 μm [84]. CXL treatment, which is an effective means of increasing corneal resistance by forming new molecular bonds between the corneal laminae and collagen fibers, is primarily used to treat keratoconus [85]. It has been shown to be effective in enhancing the biomechanical resistance of the cornea, increasing the Young’s modulus in the central conical region, and stiffening the cornea [57].
Outside the field of refraction, glaucoma is also associated with the corneal biomechanical properties. The measurement of IOP is inextricably linked to corneal viscoelasticity [86]. Furthermore, corneal hysteresis (CH) can be an important indicator for the diagnosis of glaucoma and as a prognostic factor for the associated risk: lower CH values may be associated with damage such as lower visual field indices and higher degrees of optic disc defects [86]. It is now thought that CH may be more relevant to changes in glaucoma structure and function than parameters such as CCT. The accurate measurement of CH using ORA has also accelerated the progress and application of related research.
5. Conclusions
In recent years, the field of corneal biomechanics has been an area of focus owing to the continuous development of refractive surgery techniques. Table 1 provides an overview of some of the currently available measurement techniques. Several techniques are available for the in vivo evaluation of biomechanical characteristics of the cornea, among which ORA (Reichert Inc., Depew, NY, USA) and Corvis ST (Oculus Inc., Wetzlar, Germany) are already in commercial production. Both commercially available devices enable noninvasive, more accurate measurements of biomechanical properties by analyzing the process of corneal large-amplitude deformation. However, the large-amplitude deformation of the cornea shows a nonlinear character, and IOP and CCT can affect the accuracy of the measurement. The analysis method is also based on ultrafast photographic equipment that precludes the possibility of spatially resolved measurements. In response to these problems, measurement techniques such as SSI, USWE, and OCE have been developed. These low-perturbation, low-amplitude techniques enable two-dimensional and even three-dimensional spatial measurements, reflecting variability in the biomechanical properties of different regions of the cornea and improving the safety of detection. It should be noted that these devices still measure based on the perturbation principle, which makes it difficult to avoid sources of interference such as IOP, CCT, eye movements, etc. In view of the unavoidable measurement inaccuracies associated with perturbations, techniques such as BM and SSI mapping have subsequently emerged to assess the biomechanical properties of the cornea, based on optical principles or finite element modeling of the internal structures of the eye. These techniques allow for high-accuracy measurements of the cornea and provide a more comprehensive picture of various corneal biomechanical properties. However, these techniques are still in the early stages of research: BM allows detection in three dimensions, but it has considerable limitation of range and takes a long time to evaluate; while SSI maps are currently only available in two dimensions and need to be modeled separately for multiple diseases and different types of corneas, which is costly. These features limit the use of these devices in clinical applications, such as the early diagnosis of corneal ectasia and incision selection for refractive surgery.

Table 1.
Overview of methods used for in vivo corneal biomechanical measurements.
These assessment techniques are being developed and have the potential to enable noncontact, noninvasive clinical examinations, and to provide real-time, three-dimensional, high-resolution maps of the distribution of corneal biomechanical parameters. These measurements will provide more accurate clinical tools for issues such as early screening of keratoconus or risk assessment for refractive surgery, and improve the understanding of corneal diseases.
Author Contributions
Conceptualization, F.L. and Z.L.; methodology, F.L., K.W. and Z.L.; investigation, F.L., K.W. and Z.L.; writing—original draft preparation, F.L.; writing—review and editing, K.W. and Z.L.; visualization, F.L.; supervision, K.W. and Z.L.; funding acquisition, K.W. and Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China, grant numbers 81900826 and 82000878.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Written informed consent has been obtained from the patient to publish this paper.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Salomão, M.Q.; Hofling-Lima, A.L.; Gomes Esporcatte, L.P.; Lopes, B.; Vinciguerra, R.; Vinciguerra, P.; Bühren, J.; Sena, N.; Luz Hilgert, G.S.; Ambrósio, R. The role of corneal biomechanics for the evaluation of ectasia patients. Int. J. Environ. Res. Public Health 2020, 17, 2113. [Google Scholar] [CrossRef] [PubMed]
- Beshtawi, I.M.; Akhtar, R.; Hillarby, M.C.; O’Donnell, C.; Zhao, X.; Brahma, A.; Carley, F.; Derby, B.; Radhakrishnan, H. Biomechanical changes after repeated collagen cross-linking on human corneas assessed in vitro using scanning acoustic microscopy. Investig. Ophthalmol. Vis. Sci. 2014, 55, 1549–1554. [Google Scholar] [CrossRef] [PubMed]
- Shajari, M.; Kolb, C.M.; Agha, B.; Steinwender, G.; Müller, M.; Herrmann, E.; Schmack, I.; Mayer, W.J.; Kohnen, T. Comparison of standard and accelerated corneal cross-linking for the treatment of keratoconus: A meta-analysis. Acta Ophthalmol. 2019, 97, e22–e35. [Google Scholar] [CrossRef]
- Pepose, J.S.; Feigenbaum, S.K.; Qazi, M.A.; Sanderson, J.P.; Roberts, C.J. Changes in corneal biomechanics and intraocular pressure following LASIK using static, dynamic, and noncontact tonometry. Am. J. Ophthalmol. 2007, 143, 39–47. [Google Scholar] [CrossRef] [PubMed]
- Seitz, B.; Torres, F.; Langenbucher, A.; Behrens, A.; Suárez, E. Posterior corneal curvature changes after myopic laser in situ keratomileusis. Ophthalmology 2001, 108, 666–672, discussion 73. [Google Scholar] [CrossRef]
- Slade, S.G.; Durrie, D.S.; Binder, P.S. A prospective, contralateral eye study comparing thin-flap LASIK (sub-Bowman keratomileusis) with photorefractive keratectomy. Ophthalmology 2009, 116, 1075–1082. [Google Scholar] [CrossRef]
- Baradaran-Rafii, A.; Eslani, M.; Sadoughi, M.M.; Esfandiari, H.; Karimian, F. Anwar versus Melles deep anterior lamellar keratoplasty for keratoconus: A prospective randomized clinical trial. Ophthalmology 2013, 120, 252–259. [Google Scholar] [CrossRef]
- Wu, W.; Dou, R.; Wang, Y. Comparison of corneal biomechanics between low and high myopic eyes-A meta-analysis. Am. J. Ophthalmol. 2019, 207, 419–425. [Google Scholar] [CrossRef]
- Wallace, H.B.; Misra, S.L.; Li, S.S.; McKelvie, J. Biomechanical changes in the cornea following cataract surgery: A prospective assessment with the Corneal Visualisation Scheimpflug Technology. Clin. Exp. Ophthalmol. 2019, 47, 461–468. [Google Scholar] [CrossRef]
- Liu, J.; Roberts, C.J. Influence of corneal biomechanical properties on intraocular pressure measurement: Quantitative analysis. J. Cataract Refract. Surg. 2005, 31, 146–155. [Google Scholar] [CrossRef]
- Hatami-Marbini, H. Viscoelastic shear properties of the corneal stroma. J. Biomech. 2014, 47, 723–728. [Google Scholar] [CrossRef]
- Dupps, W.J., Jr. Hysteresis: New mechanospeak for the ophthalmologist. J. Cataract Refract. Surg. 2007, 33, 1499–1501. [Google Scholar] [CrossRef]
- Friedenwald, J.S. Contribution to the Theory and Practice of Tonometry. Am. J. Ophthalmol. 1937, 20, 985–1024. [Google Scholar] [CrossRef]
- Luce, D.A. Determining in vivo biomechanical properties of the cornea with an ocular response analyzer. J. Cataract Refract. Surg. 2005, 31, 156–162. [Google Scholar] [CrossRef]
- Wang, S.; Larin, K.V.; Li, J.; Vantipalli, S.; Manapuram, R.K.; Aglyamov, S.; Emelianov, S.; Twa, M.D. A focused air-pulse system for optical-coherence-tomography-based measurements of tissue elasticity. Laser Phys. Lett. 2013, 10, 075605. [Google Scholar] [CrossRef]
- Tanter, M.; Touboul, D.; Gennisson, J.L.; Bercoff, J.; Fink, M. High-resolution quantitative imaging of cornea elasticity using supersonic shear imaging. IEEE Trans. Med. Imaging 2009, 28, 1881–1893. [Google Scholar] [CrossRef] [PubMed]
- Dupps, W.J., Jr.; Netto, M.V.; Herekar, S.; Krueger, R.R. Surface wave elastometry of the cornea in porcine and human donor eyes. J. Refract. Surg. 2007, 23, 66–75. [Google Scholar] [CrossRef]
- Scarcelli, G.; Pineda, R.; Yun, S.H. Brillouin optical microscopy for corneal biomechanics. Investig. Ophthalmol. Vis. Sci. 2012, 53, 185–190. [Google Scholar] [CrossRef]
- Pandolfi, A.; Holzapfel, G.A. Three-dimensional modeling and computational analysis of the human cornea considering distributed collagen fibril orientations. J. Biomech. Eng. 2008, 130, 061006. [Google Scholar] [CrossRef] [PubMed]
- Studer, H.; Larrea, X.; Riedwyl, H.; Büchler, P. Biomechanical model of human cornea based on stromal microstructure. J. Biomech. 2010, 43, 836–842. [Google Scholar] [CrossRef] [PubMed]
- Hjortdal, J.O. Regional elastic performance of the human cornea. J. Biomech. 1996, 29, 931–942. [Google Scholar] [CrossRef]
- Boyce, B.L.; Grazier, J.M.; Jones, R.E.; Nguyen, T.D. Full-field deformation of bovine cornea under constrained inflation conditions. Biomaterials 2008, 29, 3896–3904. [Google Scholar] [CrossRef]
- Elsheikh, A.; Anderson, K. Comparative study of corneal strip extensometry and inflation tests. J. R. Soc. Interface 2005, 2, 177–185. [Google Scholar] [CrossRef]
- Pallikaris, I.G.; Kymionis, G.D.; Ginis, H.S.; Kounis, G.A.; Tsilimbaris, M.K. Ocular rigidity in living human eyes. Investig. Ophthalmol. Vis. Sci. 2005, 46, 409–414. [Google Scholar] [CrossRef] [PubMed]
- Mohammadpour, M.; Etesami, I.; Yavari, Z.; Naderan, M.; Abdollahinia, F.; Jabbarvand, M. Ocular response analyzer parameters in healthy, keratoconus suspect and manifest keratoconus eyes. Oman J. Ophthalmol. 2015, 8, 102–106. [Google Scholar] [CrossRef]
- Kling, S.; Marcos, S. Contributing factors to corneal deformation in air puff measurements. Investig. Ophthalmol. Vis. Sci. 2013, 54, 5078–5085. [Google Scholar] [CrossRef]
- Touboul, D.; Roberts, C.; Kérautret, J.; Garra, C.; Maurice-Tison, S.; Saubusse, E.; Colin, J. Correlations between corneal hysteresis, intraocular pressure, and corneal central pachymetry. J. Cataract Refract. Surg. 2008, 34, 616–622. [Google Scholar] [CrossRef] [PubMed]
- Shah, S.; Laiquzzaman, M.; Cunliffe, I.; Mantry, S. The use of the Reichert ocular response analyser to establish the relationship between ocular hysteresis, corneal resistance factor and central corneal thickness in normal eyes. Cont. Lens Anterior Eye 2006, 29, 257–262. [Google Scholar] [CrossRef] [PubMed]
- Luz, A.; Lopes, B.; Hallahan, K.M.; Valbon, B.; Fontes, B.; Schor, P.; Dupps, W.J.; Ambrósio, R. Discriminant value of custom ocular response analyzer waveform derivatives in forme fruste keratoconus. Am. J. Ophthalmol. 2016, 164, 14–21. [Google Scholar] [CrossRef]
- Hallahan, K.M.; Sinha Roy, A.; Ambrosio, R.; Salomao, M.; Dupps, W.J. Discriminant value of custom ocular response analyzer waveform derivatives in keratoconus. Ophthalmology 2014, 121, 459–468. [Google Scholar] [CrossRef]
- Correia, F.F.; Ramos, I.; Roberts, C.J.; Steinmueller, A.; Krug, M.; Ambrósio, R. Impact of chamber pressure and material properties on the deformation response of corneal models measured by dynamic ultra-high-speed Scheimpflug imaging. Arq. Bras. Oftalmol. 2013, 76, 278–281. [Google Scholar] [CrossRef]
- Koprowski, R.; Ambrósio, R., Jr.; Reisdorf, S. Scheimpflug camera in the quantitative assessment of reproducibility of high-speed corneal deformation during intraocular pressure measurement. J. Biophotonics 2015, 8, 968–978. [Google Scholar] [CrossRef] [PubMed]
- Lee, R.; Chang, R.T.; Wong, I.Y.; Lai, J.S.; Lee, J.W.; Singh, K. Novel parameter of corneal biomechanics that differentiate normals from glaucoma. J. Glaucoma 2016, 25, e603–e609. [Google Scholar] [CrossRef] [PubMed]
- Salvetat, M.L.; Zeppieri, M.; Tosoni, C.; Felletti, M.; Grasso, L.; Brusini, P. Corneal deformation parameters provided by the Corvis-ST pachy-tonometer in healthy subjects and glaucoma patients. J. Glaucoma 2015, 24, 568–574. [Google Scholar] [CrossRef] [PubMed]
- Hashemi, H.; Asgari, S.; Mortazavi, M.; Ghaffari, R. Evaluation of corneal biomechanics after excimer laser corneal refractive surgery in high myopic patients using dynamic Scheimpflug technology. Eye Contact Lens 2017, 43, 371–377. [Google Scholar] [CrossRef]
- Vinciguerra, R.; Ambrósio, R., Jr.; Elsheikh, A.; Hafezi, F.; Yong Kang, D.S.; Kermani, O.; Koh, S.; Lu, N.; Padmanabhan, P.; Roberts, C.J.; et al. Detection of postlaser vision correction ectasia with a new combined biomechanical index. J. Cataract Refract. Surg. 2021, 47, 1314–1318. [Google Scholar] [CrossRef] [PubMed]
- Roberts, C.J.; Mahmoud, A.M.; Bons, J.P.; Hossain, A.; Elsheikh, A.; Vinciguerra, R.; Vinciguerra, P.; Ambrósio, R. Introduction of two novel stiffness parameters and interpretation of air puff-induced biomechanical deformation parameters with a dynamic Scheimpflug analyzer. J. Refract. Surg. 2017, 33, 266–273. [Google Scholar] [CrossRef]
- Nemeth, G.; Hassan, Z.; Csutak, A.; Szalai, E.; Berta, A.; Modis, L. Repeatability of ocular biomechanical data measurements with a Scheimpflug-based noncontact device on normal corneas. J. Refract. Surg. 2013, 29, 558–563. [Google Scholar] [CrossRef]
- Bak-Nielsen, S.; Pedersen, I.B.; Ivarsen, A.; Hjortdal, J. Repeatability, reproducibility, and age dependency of dynamic Scheimpflug-based pneumotonometer and its correlation with a dynamic bidirectional pneumotonometry device. Cornea 2015, 34, 71–77. [Google Scholar] [CrossRef]
- Vinciguerra, R.; Elsheikh, A.; Roberts, C.J.; Ambrósio, R.; Kang, D.S.; Lopes, B.T.; Morenghi, E.; Azzolini, C.; Vinciguerra, P. Influence of pachymetry and intraocular pressure on dynamic corneal response parameters in healthy patients. J. Refract. Surg. 2016, 32, 550–561. [Google Scholar] [CrossRef]
- Schmitt, J. OCT elastography: Imaging microscopic deformation and strain of tissue. Opt. Express 1998, 3, 199–211. [Google Scholar] [CrossRef]
- Ford, M.R.; Dupps, W.J., Jr.; Rollins, A.M.; Sinha, R.A.; Hu, Z. Method for optical coherence elastography of the cornea. J. Biomed. Opt. 2011, 16, 016005. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.; Li, J.; Singh, M.; Wu, C.; Liu, C.H.; Raghunathan, R.; Aglyamov, S.R.; Vantipalli, S.; Twa, M.D.; Larin, K.V. Optical coherence elastography assessment of corneal viscoelasticity with a modified Rayleigh-Lamb wave model. J. Mech. Behav. Biomed. Mater. 2017, 66, 87–94. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Larin, K.V. Shear wave imaging optical coherence tomography (SWI-OCT) for ocular tissue biomechanics. Opt. Lett. 2014, 39, 41–44. [Google Scholar] [CrossRef]
- Singh, M.; Li, J.; Han, Z.; Wu, C.; Aglyamov, S.R.; Twa, M.D.; Larin, K.V. Investigating elastic anisotropy of the porcine cornea as a function of intraocular pressure with optical coherence elastography. J. Refract. Surg. 2016, 32, 562–567. [Google Scholar] [CrossRef]
- Han, Z.; Aglyamov, S.R.; Li, J.; Singh, M.; Wang, S.; Vantipalli, S.; Wu, C.; Liu, C.H.; Twa, M.D.; Larin, K.V. Quantitative assessment of corneal viscoelasticity using optical coherence elastography and a modified Rayleigh-Lamb equation. J. Biomed. Opt. 2015, 20, 20501. [Google Scholar] [CrossRef]
- Twa, M.D.; Li, J.; Vantipalli, S.; Singh, M.; Aglyamov, S.; Emelianov, S.; Larin, K.V. Spatial characterization of corneal biomechanical properties with optical coherence elastography after UV cross-linking. Biomed. Opt. Express 2014, 5, 1419–1427. [Google Scholar] [CrossRef] [PubMed]
- De Stefano, V.S.; Ford, M.R.; Seven, I.; Dupps, W.J. Live human assessment of depth-dependent corneal displacements with swept-source optical coherence elastography. PLoS ONE 2018, 13, e0209480. [Google Scholar] [CrossRef]
- Kling, S. Optical coherence elastography by ambient pressure modulation for high-resolution strain mapping applied to patterned cross-linking. J. R. Soc. Interface 2020, 17, 20190786. [Google Scholar] [CrossRef] [PubMed]
- Alonso-Caneiro, D.; Karnowski, K.; Kaluzny, B.J.; Kowalczyk, A.; Wojtkowski, M. Assessment of corneal dynamics with high-speed swept source optical coherence tomography combined with an air puff system. Opt. Express 2011, 19, 14188–14199. [Google Scholar] [CrossRef]
- Wang, S.; Larin, K.V. Noncontact depth-resolved micro-scale optical coherence elastography of the cornea. Biomed. Opt. Express 2014, 5, 3807–3821. [Google Scholar] [CrossRef] [PubMed]
- Lan, G.; Aglyamov, S.R.; Larin, K.V.; Twa, M.D. In Vivo Human Corneal Shear-wave Optical Coherence Elastography. Optom. Vis. Sci. 2021, 98, 58–63. [Google Scholar] [CrossRef]
- Li, C.; Guan, G.; Huang, Z.; Johnstone, M.; Wang, R.K. Noncontact all-optical measurement of corneal elasticity. Opt. Lett. 2012, 37, 1625–1627. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.; Qian, X.; Chen, R.; Wodnicki, R.; Sun, Y.; Li, R.; Li, Y.; Shung, K.K.; Chen, Z.; Zhou, Q. 2-D Ultrasonic Array-Based Optical Coherence Elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2021, 68, 1096–1104. [Google Scholar] [CrossRef]
- Bercoff, J.; Tanter, M.; Fink, M. Supersonic shear imaging: A new technique for soft tissue elasticity mapping. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2004, 51, 396–409. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.M.; Aubry, J.F.; Fink, M.; Bercoff, J.; Tanter, M. In Vivo evidence of porcine cornea anisotropy using supersonic shear wave imaging. Investig. Ophthalmol. Vis. Sci. 2014, 55, 7545–7552. [Google Scholar] [CrossRef] [PubMed]
- Touboul, D.; Gennisson, J.L.; Nguyen, T.M.; Robinet, A.; Roberts, C.J.; Tanter, M.; Grenier, N. Supersonic shear wave elastography for the in vivo evaluation of transepithelial corneal collagen cross-linking. Investig. Ophthalmol. Vis. Sci. 2014, 55, 1976–1984. [Google Scholar] [CrossRef]
- Nguyen, T.M.; Aubry, J.F.; Touboul, D.; Fink, M.; Gennisson, J.L.; Bercoff, J.; Tanter, M. Monitoring of cornea elastic properties changes during UV-A/riboflavin-induced corneal collagen cross-linking using supersonic shear wave imaging: A pilot study. Investig. Ophthalmol. Vis. Sci. 2012, 53, 5948–5954. [Google Scholar] [CrossRef]
- Ferraioli, G.; Parekh, P.; Levitov, A.B.; Filice, C. Shear wave elastography for evaluation of liver fibrosis. J. Ultrasound Med. 2014, 33, 197–203. [Google Scholar] [CrossRef]
- Chen, X.M.; Cui, L.G.; He, P.; Shen, W.W.; Qian, Y.J.; Wang, J.R. Shear wave elastographic characterization of normal and torn achilles tendons: A pilot study. J. Ultrasound Med. 2013, 32, 449–455. [Google Scholar] [CrossRef]
- Detorakis, E.T.; Drakonaki, E.E.; Ginis, H.; Karyotakis, N.; Pallikaris, I.G. Evaluation of iridociliary and lenticular elasticity using shear-wave elastography in rabbit eyes. Acta Med. 2014, 57, 9–14. [Google Scholar] [CrossRef] [PubMed]
- Sit, A.J.; Lin, S.C.; Kazemi, A.; McLaren, J.W.; Pruet, C.M.; Zhang, X. In Vivo noninvasive measurement of Young’s modulus of elasticity in human eyes: A feasibility study. J. Glaucoma 2017, 26, 967–973. [Google Scholar] [CrossRef] [PubMed]
- Rocha, K.M.; Ramos-Esteban, J.C.; Qian, Y.; Herekar, S.; Krueger, R.R. Comparative study of riboflavin-UVA cross-linking and “flash-linking” using surface wave elastometry. J. Refract. Surg. 2008, 24, S748–S751. [Google Scholar] [CrossRef] [PubMed]
- Scarcelli, G.; Yun, S.H. Confocal Brillouin microscopy for three-dimensional mechanical imaging. Nat. Photon. 2008, 2, 39–43. [Google Scholar] [CrossRef] [PubMed]
- Scarcelli, G.; Yun, S.H. In vivo Brillouin optical microscopy of the human eye. Opt. Express 2012, 20, 9197–9202. [Google Scholar] [CrossRef]
- Scarcelli, G.; Besner, S.; Pineda, R.; Yun, S.H. Biomechanical characterization of keratoconus corneas ex vivo with Brillouin microscopy. Investig. Ophthalmol. Vis. Sci. 2014, 55, 4490–4495. [Google Scholar] [CrossRef]
- Scarcelli, G.; Kling, S.; Quijano, E.; Pineda, R.; Marcos, S.; Yun, S.H. Brillouin microscopy of collagen crosslinking: Noncontact depth-dependent analysis of corneal elastic modulus. Investig. Ophthalmol. Vis. Sci. 2013, 54, 1418–1425. [Google Scholar] [CrossRef]
- Zhang, J.; Scarcelli, G. Mapping mechanical properties of biological materials via an add-on Brillouin module to confocal microscopes. Nat. Protoc. 2021, 16, 1251–1275. [Google Scholar] [CrossRef]
- Blackburn, B.J.; Gu, S.; Ford, M.R.; de Stefano, V.; Jenkins, M.W.; Dupps, W.J.; Rollins, A.M. Noninvasive assessment of corneal crosslinking with phase-decorrelation optical coherence tomography. Investig. Ophthalmol. Vis. Sci. 2019, 60, 41–51. [Google Scholar] [CrossRef]
- Pandolfi, A.; Manganiello, F. A model for the human cornea: Constitutive formulation and numerical analysis. Biomech. Model. Mechanobiol. 2006, 5, 237–246. [Google Scholar] [CrossRef]
- Woo, S.L.; Kobayashi, A.S.; Schlegel, W.A.; Lawrence, C. Nonlinear material properties of intact cornea and sclera. Exp. Eye Res. 1972, 14, 29–39. [Google Scholar] [CrossRef]
- Simonini, I.; Pandolfi, A. Customized finite element modelling of the human cornea. PLoS ONE 2015, 10, e0130426. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D.; Abass, A.; Lopes, B.; Eliasy, A.; Hayes, S.; Boote, C.; Meek, K.M.; Movchan, A.; Movchan, N.; Elsheikh, A. Fibril density reduction in keratoconic corneas. J. R. Soc. Interface 2021, 18, 20200900. [Google Scholar] [CrossRef] [PubMed]
- Bell, J.S.; Hayes, S.; Whitford, C.; Sanchez-Weatherby, J.; Shebanova, O.; Vergari, C.; Winlove, C.P.; Terrill, N.; Sorensen, T.; Elsheikh, A.; et al. The hierarchical response of human corneal collagen to load. Acta Biomater. 2018, 65, 216–225. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Eliasy, A.; Lopes, B.; Abass, A.; Vinciguerra, R.; Vinciguerra, P.; Ambrósio, R.; Roberts, C.J.; Elsheikh, A. Stress–strain index map: A new way to represent corneal material stiffness. Front. Bioeng. Biotechnol. 2021, 9, 640434. [Google Scholar] [CrossRef]
- Magnon, C.; Hall, S.J.; Lin, J.; Xue, X.; Gerber, L.; Freedland, S.J.; Frenette, P.S. Autonomic nerve development contributes to prostate cancer progression. Science 2013, 341, 1236361. [Google Scholar] [CrossRef] [PubMed]
- Eliasy, A.; Chen, K.J.; Vinciguerra, R.; Lopes, B.T.; Abass, A.; Vinciguerra, P.; Ambrósio, R.; Roberts, C.J.; Elsheikh, A. Determination of Corneal Biomechanical Behavior in-vivo for Healthy Eyes Using CorVis ST Tonometry: Stress–strain Index. Front. Bioeng. Biotechnol. 2019, 7, 105. [Google Scholar] [CrossRef]
- Padmanabhan, P.; Lopes, B.T.; Eliasy, A.; Abass, A.; Elsheikh, A. In Vivo biomechanical changes associated with keratoconus progression. Curr. Eye Res. 2022, 47, 982–986. [Google Scholar] [CrossRef]
- Lopes, B.T.; Elsheikh, A. In Vivo corneal stiffness mapping by the stress–strain index maps and Brillouin microscopy. Curr. Eye Res. 2022, 1–7. [Google Scholar] [CrossRef]
- Winkler, M.; Shoa, G.; Xie, Y.; Petsche, S.J.; Pinsky, P.M.; Juhasz, T.; Brown, D.J.; Jester, J.V. Three-dimensional distribution of transverse collagen fibers in the anterior human corneal stroma. Investig. Ophthalmol. Vis. Sci. 2013, 54, 7293–7301. [Google Scholar] [CrossRef]
- Rabinowitz, Y.S. Keratoconus. Surv. Ophthalmol. 1998, 42, 297–319. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, H.; Li, Y.; Wang, Y.; Han, X.; Zhu, Y.; Zhang, Y.; Huang, G. Quantitative Assessment of Biomechanical Properties of the Human Keratoconus Cornea Using Acoustic Radiation Force Optical Coherence Elastography. Transl. Vis. Sci. Technol. 2022, 11, 4. [Google Scholar] [CrossRef]
- Bowen, J.M.; Sobey, G.J.; Burrows, N.P.; Colombi, M.; Lavallee, M.E.; Malfait, F.; Francomano, C.A. Ehlers-Danlos syndrome, classical type. Am. J. Med. Genet. C Semin. Med. Genet. 2017, 175, 27–39. [Google Scholar] [CrossRef] [PubMed]
- Ou, R.J.; Shaw, E.L.; Glasgow, B.J. Keratectasia after laser in situ keratomileusis (LASIK): Evaluation of the calculated residual stromal bed thickness. Am. J. Ophthalmol. 2002, 134, 771–773. [Google Scholar] [CrossRef] [PubMed]
- Wollensak, G.; Spoerl, E.; Seiler, T. Riboflavin/ultraviolet-a-induced collagen crosslinking for the treatment of keratoconus. Am. J. Ophthalmol. 2003, 135, 620–627. [Google Scholar] [CrossRef] [PubMed]
- Liang, L.; Zhang, R.; He, L.Y. Corneal hysteresis and glaucoma. Int. Ophthalmol. 2019, 39, 1909–1916. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).