ECG Measurement Uncertainty Based on Monte Carlo Approach: An Effective Analysis for a Successful Cardiac Health Monitoring System
Abstract
1. Introduction
- Contribute to filling a small gap in the state of the art of evaluating the uncertainty of measurements performed with an ECG;
- Present a methodology capable of identifying opportunities for improvement in measurement system projects, using measurement uncertainty as a parameter.
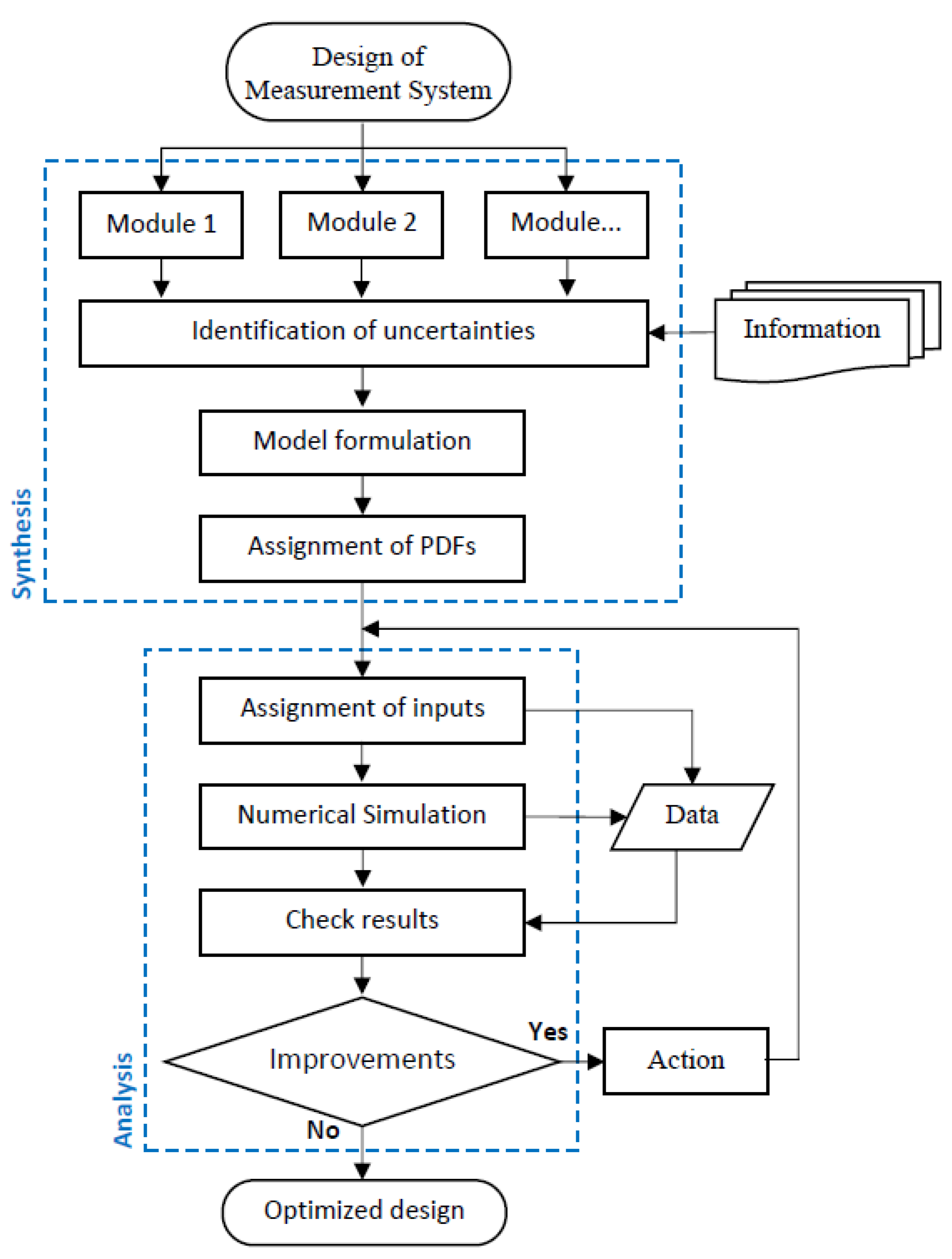
2. Materials and Methods
2.1. Datasets
2.2. Methods
| Algorithm 1 MCM implementation. |
//Initialize M (number of iterations) // The array A is declared //Assigns random number with proper PDF ⋮ //The array Y is declared //Function g defines the mathematical model //The array B is declared with n lines constants to n |
3. Results
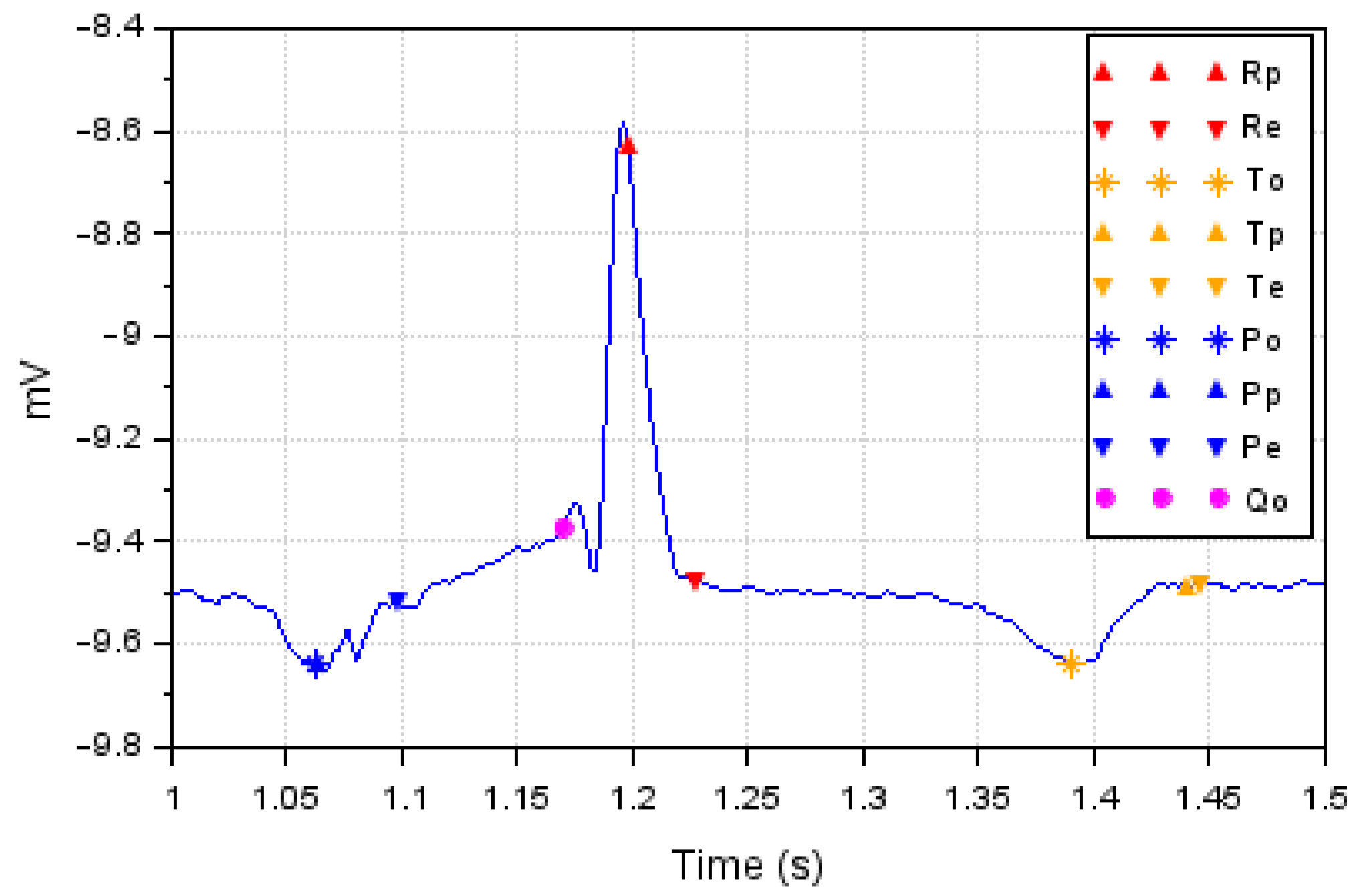
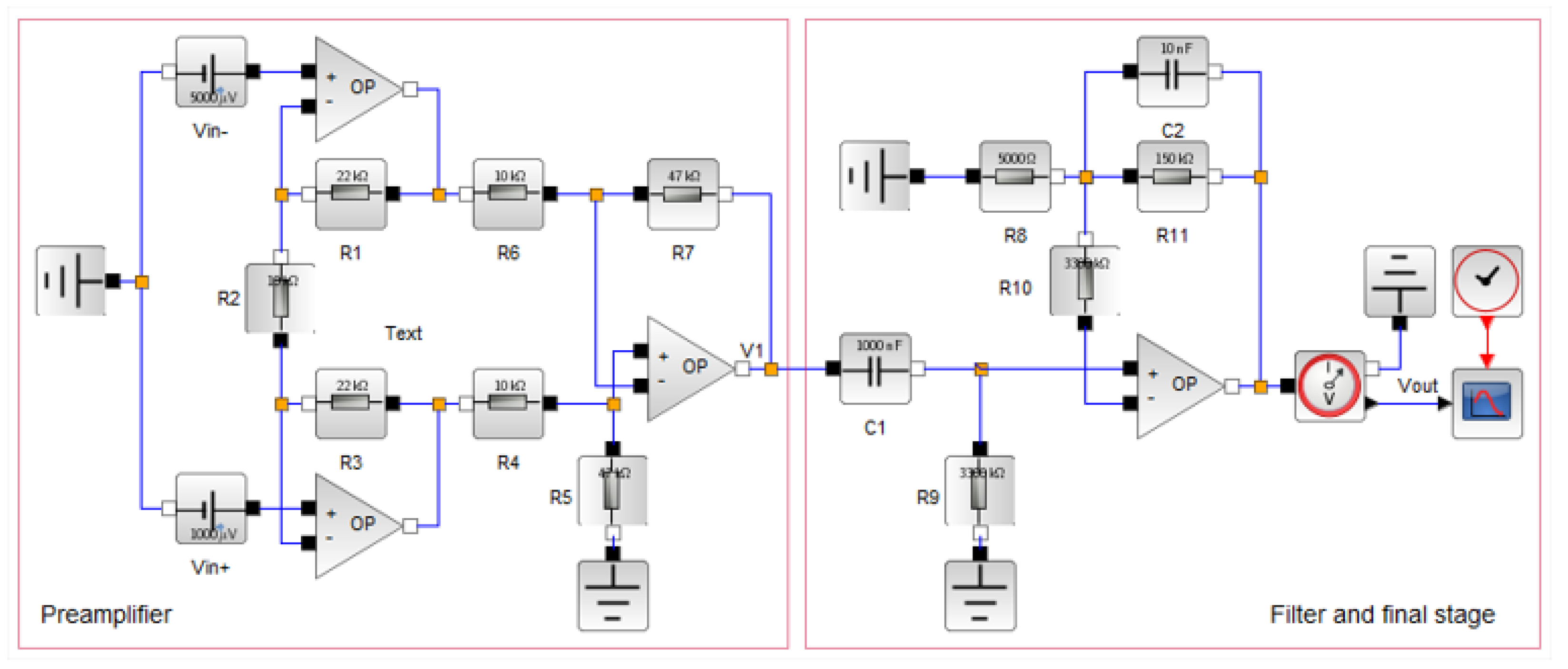
3.1. Formulation of the Model
3.2. PDF Assignment
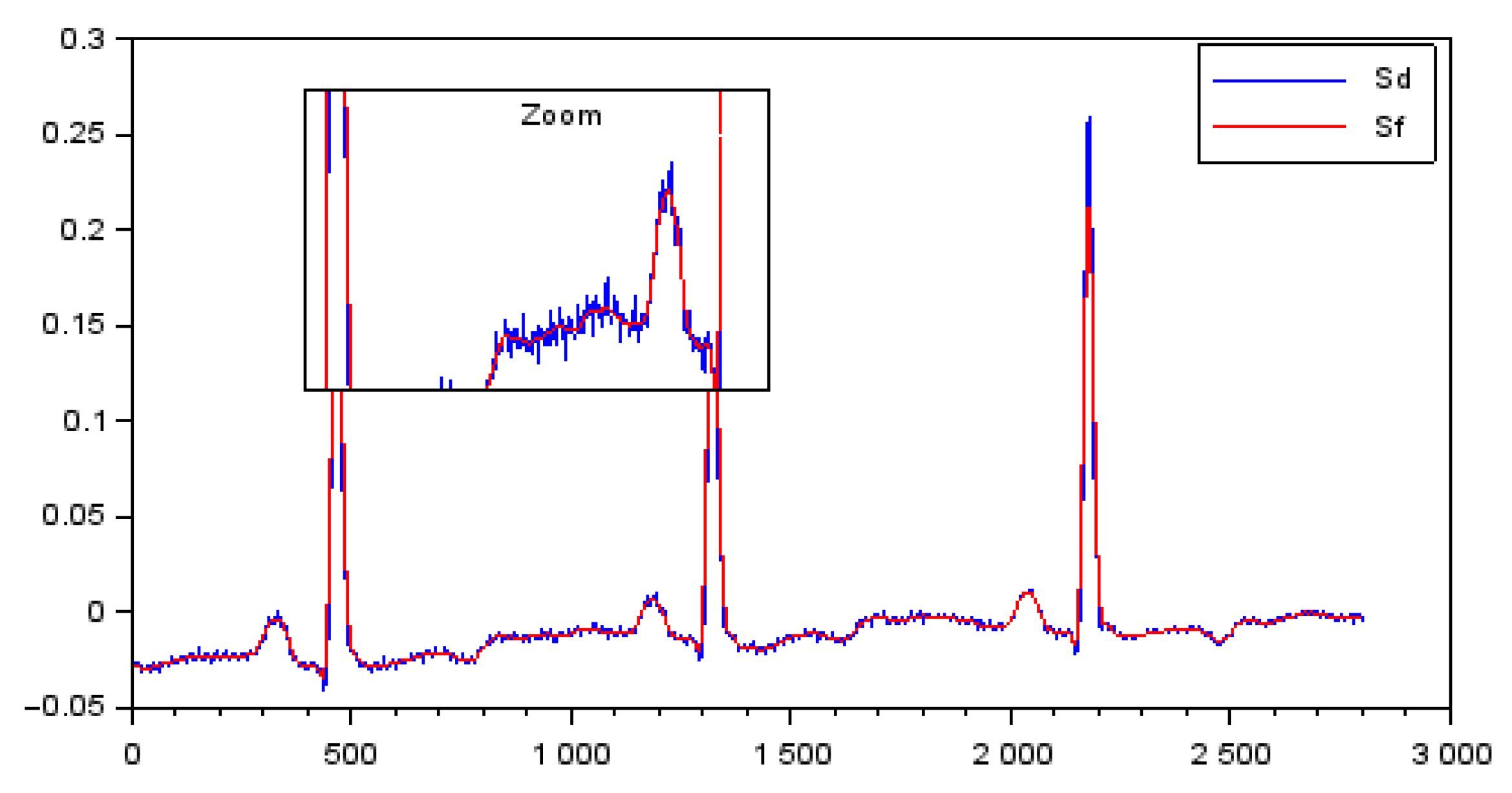
3.3. Validation and Comparisons with the Literature
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, D.; Tang, Y. An improved failure mode and effects analysis method based on uncertainty measure in the evidence theory. Qual. Reliab. Eng. Int. 2020, 36, 1786–1807. [Google Scholar] [CrossRef]
- Bennett, K.J.; Pizzolato, C.; Martelli, S.; Bahl, J.S.; Sivakumar, A.; Atkins, G.J.; Solomon, L.B.; Thewlis, D. EMG-informed neuromusculoskeletal models accurately predict knee loading measured using instrumented implants. IEEE Trans. Biomed. Eng. 2022, 69, 2268–2275. [Google Scholar] [CrossRef] [PubMed]
- Cox, M.; Harris, P.; Siebert, B.L. Evaluation of measurement uncertainty based on the propagation of distributions using Monte Carlo simulation. Meas. Tech. 2003, 46, 824–833. [Google Scholar] [CrossRef]
- Von Clarmann, T.; Compernolle, S.; Hase, F. Truth and Uncertainty. A critical discussion of the error concept versus the uncertainty concept. Atmos. Meas. Tech. 2022, 15, 1145–1157. [Google Scholar] [CrossRef]
- Gitelson, A.; Viña, A.; Inoue, Y.; Arkebauer, T.; Schlemmer, M.; Schepers, J. Uncertainty in the evaluation of photosynthetic canopy traits using the green leaf area index. Agric. For. Meteorol. 2022, 320, 108955. [Google Scholar] [CrossRef]
- Separovic, L.; Lourenço, F.R. Measurement uncertainty evaluation of an analytical procedure for determination of terbinafine hydrochloride in creams by HPLC and optimization strategies using Analytical Quality by Design. Microchem. J. 2022, 178, 107386. [Google Scholar] [CrossRef]
- da Silva, R.J.B.; Saame, J.; Anes, B.; Heering, A.; Leito, I.; Näykki, T.; Stoica, D.; Deleebeeck, L.; Bastkowski, F.; Snedden, A.; et al. Evaluation and validation of detailed and simplified models of the uncertainty of unified pHabsH2O measurements in aqueous solutions. Anal. Chim. Acta 2021, 1182, 338923. [Google Scholar] [CrossRef]
- Petri, D.; Carbone, P.; Mari, L. Quality of measurement information in decision-making. IEEE Trans. Instrum. Meas. 2020, 70, 1003816. [Google Scholar] [CrossRef]
- Yang, H.; Cai, Y.; Zhu, B.; Xuan, G.; Li, X.; Sun, L.; Cheng, L. A Universal Measurement Method for Nanoparticle Number Concentration Based On Atomic Force Microscope. IEEE Trans. Nanotechnol. 2021, 20, 852–859. [Google Scholar] [CrossRef]
- Galli, A.; Giorgi, G.; Narduzzi, C. Standardized Gaussian Dictionary for ECG Analysis a Metrological Approach. IEEE Open J. Instrum. Meas. 2022, 1, 4000209. [Google Scholar] [CrossRef]
- Li, N.; Wang, L.; Jia, J.; Yang, Y. A novel method for the image quality improvement of ultrasonic tomography. IEEE Trans. Instrum. Meas. 2020, 70, 5000810. [Google Scholar] [CrossRef]
- Uguz, D.U.; Canbaz, Z.T.; Antink, C.H.; Lüken, M.; Leonhardt, S. A Novel Sensor Design for Amplitude Modulated Measurement of Capacitive ECG. IEEE Trans. Instrum. Meas. 2022, 71, 4000710. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, L.; Yang, T.; Liao, Z.; Xue, X.; Wu, B.; Zhang, W.; Zang, J.; Cui, D.; Zhang, Z.; et al. A mathematical model of a piezoelectric micro-machined hydrophone with simulation and experimental validation. IEEE Sens. J. 2021, 21, 13364–13372. [Google Scholar] [CrossRef]
- Lim, A.; Schonewille, A.; Forbrigger, C.; Looi, T.; Drake, J.; Diller, E. Design and Comparison of Magnetically-Actuated Dexterous Forceps Instruments for Neuroendoscopy. IEEE Trans. Biomed. Eng. 2020, 68, 846–856. [Google Scholar] [CrossRef] [PubMed]
- Lux, R.L. Uncertainty of the electrocardiogram: Old and new ideas for assessment and interpretation. J. Electrocardiol. 2000, 33, 203–208. [Google Scholar] [CrossRef]
- Randazzo, V.; Puleo, E.; Paviglianiti, A.; Vallan, A.; Pasero, E. Development and Validation of an Algorithm for the Digitization of ECG Paper Images. Sensors 2022, 22, 7138. [Google Scholar] [CrossRef]
- Aseeri, A.O. Uncertainty-Aware Deep Learning-Based Cardiac Arrhythmias Classification Model of Electrocardiogram Signals. Computers 2021, 10, 82. [Google Scholar] [CrossRef]
- Jahmunah, V.; Ng, E.; Tan, R.S.; Oh, S.L.; Acharya, U.R. Uncertainty quantification in DenseNet model using myocardial infarction ECG signals. Comput. Methods Programs Biomed. 2023, 229, 107308. [Google Scholar] [CrossRef]
- Sadda, P.; Ghebermicael, D.; Emerenini, U. Uncertainty modeling can identify erroneous computer ECG reads. Heart Rhythm 2021, 18, 1. [Google Scholar] [CrossRef]
- Honarvar, H.; Agarwal, C.; Somani, S.; Vaid, A.; Lampert, J.; Wanyan, T.; Reddy, V.Y.; Nadkarni, G.N.; Miotto, R.; Zitnik, M.; et al. Enhancing convolutional neural network predictions of electrocardiograms with left ventricular dysfunction using a novel sub-waveform representation. Cardiovasc. Digit. Health J. 2022, 3, 220–231. [Google Scholar] [CrossRef]
- Al-Obaidi, K.; Valyrakis, M. A sensory instrumented particle for environmental monitoring applications: Development and calibration. IEEE Sens. J. 2021, 21, 10153–10166. [Google Scholar] [CrossRef]
- Luo, X.; Shi, C.; Zeng, H.Q.; Ewurum, H.C.; Wan, Y.; Guo, Y.; Pagnha, S.; Zhang, X.B.; Du, Y.P.; He, X. Evolutionarily Optimized Electromagnetic Sensor Measurements for Robust Surgical Navigation. IEEE Sens. J. 2019, 19, 10859–10868. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Ghaderpour, S. Least-squares spectral and wavelet analyses of V455 Andromedae time series: The life after the super-outburst. Publ. Astron. Soc. Pac. 2020, 132, 114504. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Pagiatakis, S.D. Least-squares wavelet analysis of unequally spaced and non-stationary time series and its applications. Math. Geosci. 2017, 49, 819–844. [Google Scholar] [CrossRef]
- Tolić, I.; Miličević, K.; Tokić, A. Measurement uncertainty of transmission line resistance calculation using ‘Guide to the Expression of Uncertainty in Measurement’and adaptive Monte–Carlo method. IET Sci. Meas. Technol. 2017, 11, 339–345. [Google Scholar] [CrossRef]
- Dao, D.V.; Adeli, H.; Ly, H.B.; Le, L.M.; Le, V.M.; Le, T.T.; Pham, B.T. A sensitivity and robustness analysis of GPR and ANN for high-performance concrete compressive strength prediction using a Monte Carlo simulation. Sustainability 2020, 12, 830. [Google Scholar] [CrossRef]
- Pokropek, A.; Davidov, E.; Schmidt, P. A Monte Carlo simulation study to assess the appropriateness of traditional and newer approaches to test for measurement invariance. Struct. Equ. Model. Multidiscip. J. 2019, 26, 724–744. [Google Scholar] [CrossRef]
- Lozanovski, B.; Downing, D.; Tran, P.; Shidid, D.; Qian, M.; Choong, P.; Brandt, M.; Leary, M. A Monte Carlo simulation-based approach to realistic modelling of additively manufactured lattice structures. Addit. Manuf. 2020, 32, 101092. [Google Scholar] [CrossRef]
- Cui, J.; Wang, L.; He, X.; De Albuquerque, V.H.C.; AlQahtani, S.A.; Hassan, M.M. Deep learning-based multidimensional feature fusion for classification of ECG arrhythmia. Neural Comput. Appl. 2021, 1–15. [Google Scholar] [CrossRef]
- de Albuquerque, V.H.C.; Nunes, T.M.; Pereira, D.R.; Luz, E.J.d.S.; Menotti, D.; Papa, J.P.; Tavares, J.M.R. Robust automated cardiac arrhythmia detection in ECG beat signals. Neural Comput. Appl. 2018, 29, 679–693. [Google Scholar] [CrossRef]
- Luz, E.J.d.S.; Nunes, T.M.; De Albuquerque, V.H.C.; Papa, J.P.; Menotti, D. ECG arrhythmia classification based on optimum-path forest. Expert Syst. Appl. 2013, 40, 3561–3573. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, M.; Wu, W.; de Albuquerque, V.H.C. Hybrid feature fusion for classification optimization of short ECG segment in IoT based intelligent healthcare system. Neural Comput. Appl. 2021, 1–15. [Google Scholar] [CrossRef]
- Betts, J.G.; Young, K.A.; Wise, J.A.; Johnson, E.; Poe, B.; Kruse, D.H.; Korol, O.; Johnson, J.E.; Womble, M.; DeSaix, P. Anatomy and Physiology; Jordan University of Science and Technology: Ar-Ramtha, Jordan, 2013. [Google Scholar]
- Berkaya, S.K.; Uysal, A.K.; Gunal, E.S.; Ergin, S.; Gunal, S.; Gulmezoglu, M.B. A survey on ECG analysis. Biomed. Signal Process. Control 2018, 43, 216–235. [Google Scholar] [CrossRef]
- Wesselius, F.J.; van Schie, M.S.; De Groot, N.M.; Hendriks, R.C. An accurate and efficient method to train classifiers for atrial fibrillation detection in ECGs: Learning by asking better questions. Comput. Biol. Med. 2022, 143, 105331. [Google Scholar] [CrossRef] [PubMed]
- Webster, J.G. Medical Instrumentation: Application and Design; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Bond, R.R.; Novotny, T.; Andrsova, I.; Koc, L.; Sisakova, M.; Finlay, D.; Guldenring, D.; McLaughlin, J.; Peace, A.; McGilligan, V.; et al. Automation bias in medicine: The influence of automated diagnoses on interpreter accuracy and uncertainty when reading electrocardiograms. J. Electrocardiol. 2018, 51, S6–S11. [Google Scholar] [CrossRef] [PubMed]
- Perez, Y.; Tobert, K.E.; Saunders, M.J.; Sorensen, K.B.; Bos, J.M.; Ackerman, M.J. Diagnostic accuracy of the 12-lead electrocardiogram in the first 48 hours of life for newborns of a parent with congenital long QT syndrome. Heart Rhythm 2022, 19, 969–974. [Google Scholar] [CrossRef] [PubMed]
- Monedero, I. A novel ECG diagnostic system for the detection of 13 different diseases. Eng. Appl. Artif. Intell. 2022, 107, 104536. [Google Scholar] [CrossRef]
- Merdjanovska, E.; Rashkovska, A. Comprehensive survey of computational ECG analysis: Databases, methods and applications. Expert Syst. Appl. 2022, 203, 117206. [Google Scholar] [CrossRef]
- Wong, K.C.; Klimis, H.; Lowres, N.; von Huben, A.; Marschner, S.; Chow, C.K. Diagnostic accuracy of handheld electrocardiogram devices in detecting atrial fibrillation in adults in community versus hospital settings: A systematic review and meta-analysis. Heart 2020, 106, 1211–1217. [Google Scholar] [CrossRef]

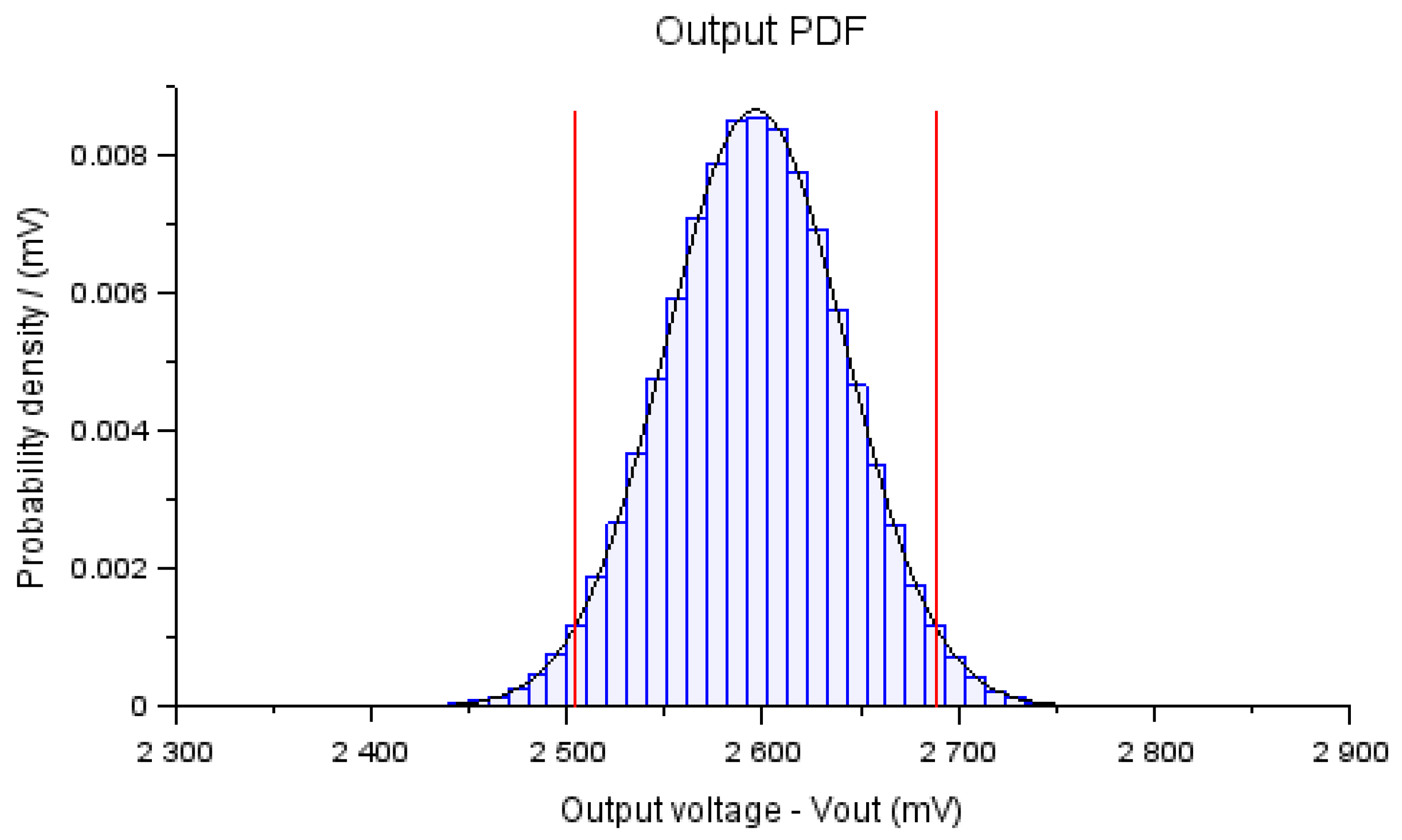

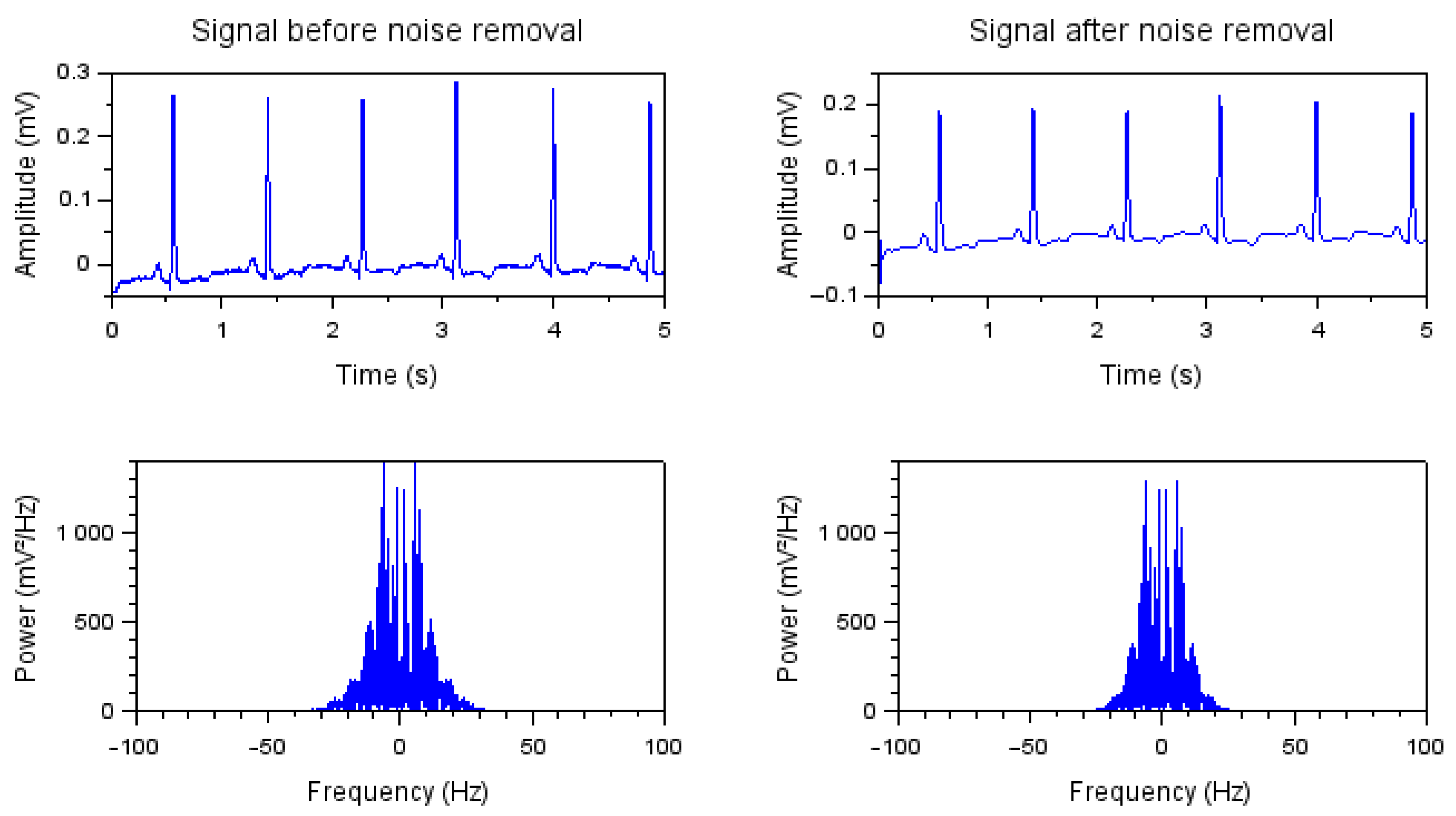
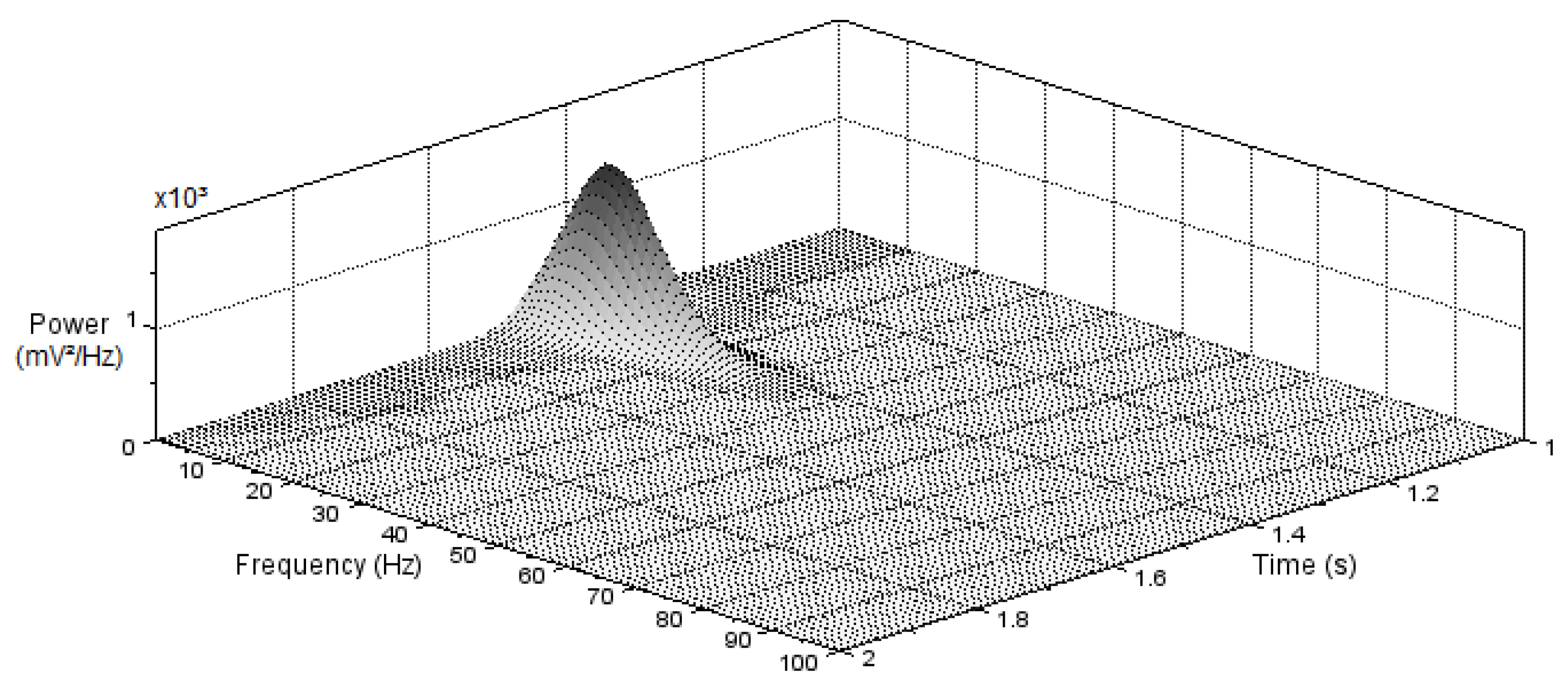
| Requirement Description | Min/Max | Units | Value |
|---|---|---|---|
| Operating conditions: | |||
| Line voltage | Range | V RMS | 104 to 1127 |
| Frequency | Range | Hz | |
| Temperature | Range | C | |
| Relative humidity | Range | % | |
| Atmospheric pressure | Range | kPa | 70 to 106 |
| Input Dynamic Range: | |||
| Range of linear operations of input signal | Min | mV | |
| Allowed variation of amplitude with dc offset | Max | % | |
| Gain control, accuracy, and stability: | |||
| Gain error | Max | % | 5 |
| Gain change rate/min | Max | %/min | |
| Total gain change/h | Max | % | |
| Time base selection and accuracy: | |||
| Time base error | Max | % | |
| Output display: | |||
| Error of rulings | Max | % | |
| Time marker error | Max | % | |
| Accuracy of input signal reproduction: | |||
| Overall error for signals | Max | % | |
| Error in lead weighting factors | Max | % | 5 |
| Hysteresis after 15 mm deflection from baseline | Max | mm | |
| Standardizing voltage: | |||
| Amplitude error | Max | % | |
| System noise: | |||
| Multichannel crosstalk | Max | % | 2 |
| Baseline stability: | |||
| Baseline drift rate RTI | Max | V/s | 10 |
| Total baseline drift RTI (2 min period) | Max | V | 500 |
| Quantity | Parameters | |||||
|---|---|---|---|---|---|---|
| a | b | Unit | ||||
| Measurand: | ||||||
| mV | ||||||
| mV | ||||||
| Baseline | mV | |||||
| Measuring system: | ||||||
| k | ||||||
| k | ||||||
| k | ||||||
| k | ||||||
| k | ||||||
| M | ||||||
| k | ||||||
| F | ||||||
| nF | ||||||
| Environment: | ||||||
| Noise | mV | |||||
| Source of Uncertainty | Vout (mV) | |||
|---|---|---|---|---|
| Measurand: | ||||
| 2596 | 44 | 87 | ||
| Baseline | 2596 | 8 | 15 | |
| Measuring system: | ||||
| Preamplifier | 2596 | 27 | 54 | |
| Final stage | 2596 | 20 | 39 | |
| Environment: | ||||
| Noise | 2596 | 8 | 15 | |
| Source of Uncertainty | Vout (mV) | |||
|---|---|---|---|---|
| Measurand: | ||||
| 2596 | 45 | 87 | ||
| Baseline | 2596 | 8 | 15 | |
| Measuring system: | ||||
| Preamplifier | 2596 | 3 | 5 | |
| Final stage | 2596 | 2 | 4 | |
| Environment: | ||||
| Noise | 2596 | 8 | 15 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, J.H.B.d.; Cortez, P.C.; Jagatheesaperumal, S.K.; de Albuquerque, V.H.C. ECG Measurement Uncertainty Based on Monte Carlo Approach: An Effective Analysis for a Successful Cardiac Health Monitoring System. Bioengineering 2023, 10, 115. https://doi.org/10.3390/bioengineering10010115
Silva JHBd, Cortez PC, Jagatheesaperumal SK, de Albuquerque VHC. ECG Measurement Uncertainty Based on Monte Carlo Approach: An Effective Analysis for a Successful Cardiac Health Monitoring System. Bioengineering. 2023; 10(1):115. https://doi.org/10.3390/bioengineering10010115
Chicago/Turabian StyleSilva, Jackson Henrique Braga da, Paulo Cesar Cortez, Senthil K. Jagatheesaperumal, and Victor Hugo C. de Albuquerque. 2023. "ECG Measurement Uncertainty Based on Monte Carlo Approach: An Effective Analysis for a Successful Cardiac Health Monitoring System" Bioengineering 10, no. 1: 115. https://doi.org/10.3390/bioengineering10010115
APA StyleSilva, J. H. B. d., Cortez, P. C., Jagatheesaperumal, S. K., & de Albuquerque, V. H. C. (2023). ECG Measurement Uncertainty Based on Monte Carlo Approach: An Effective Analysis for a Successful Cardiac Health Monitoring System. Bioengineering, 10(1), 115. https://doi.org/10.3390/bioengineering10010115










