Supercritical Flow over a Submerged Vertical Negative Step
Abstract
:1. Introduction
2. Theory
3. Experiments
3.1. Setup and Procedure
3.2. Results
4. Numerical Modeling
4.1. Governing Equations
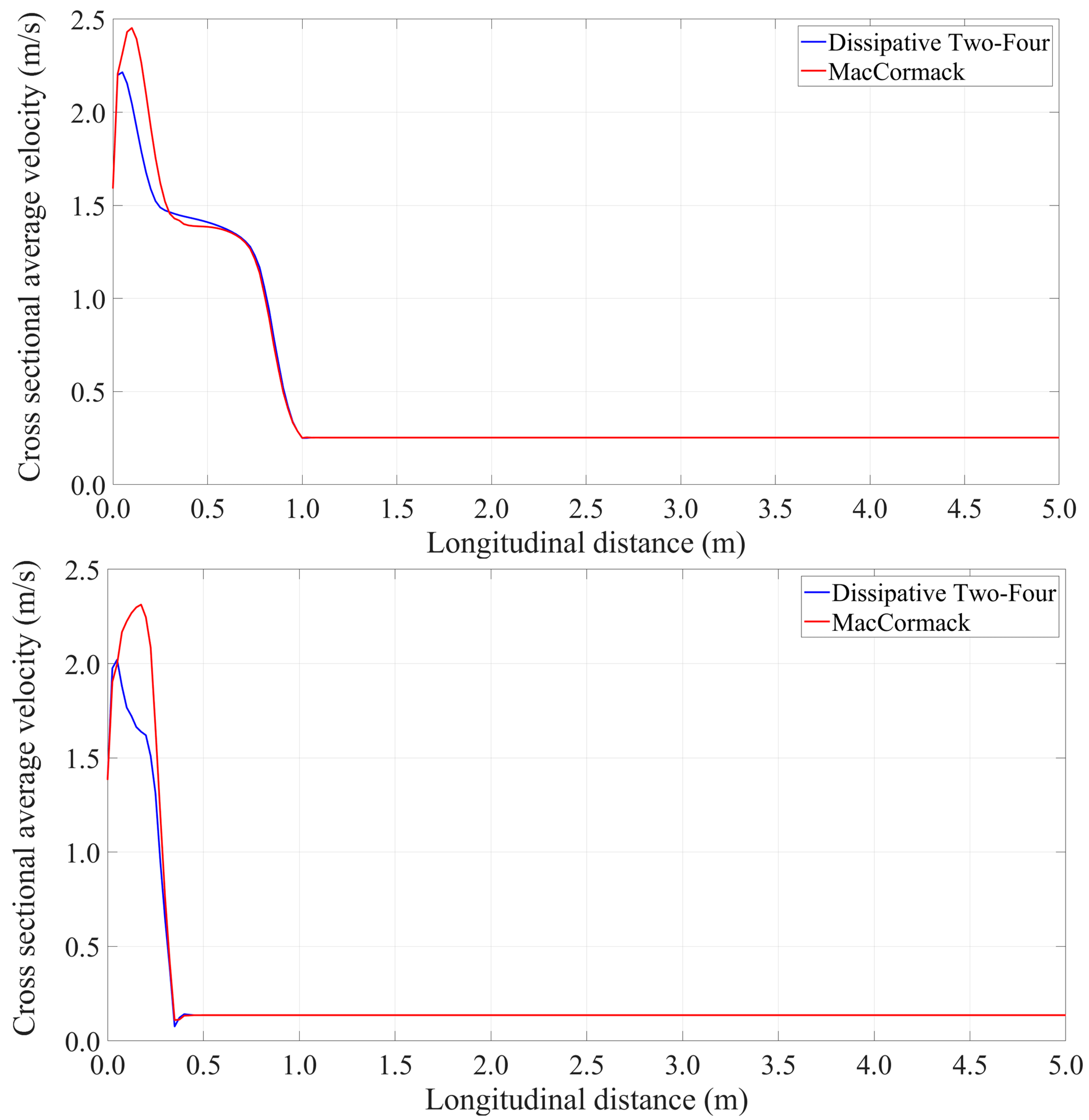
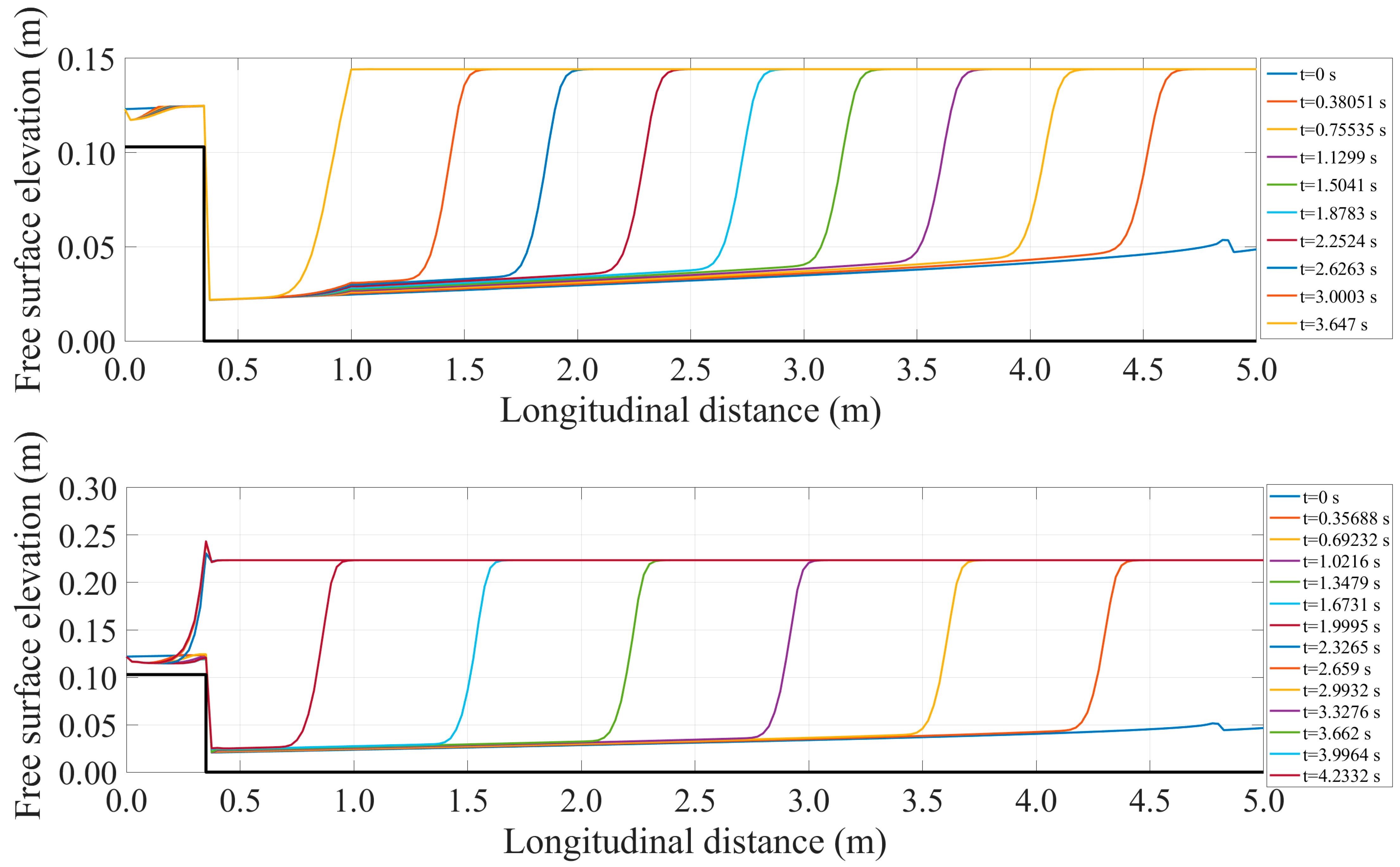
4.2. Results
5. Discussion
6. Conclusions
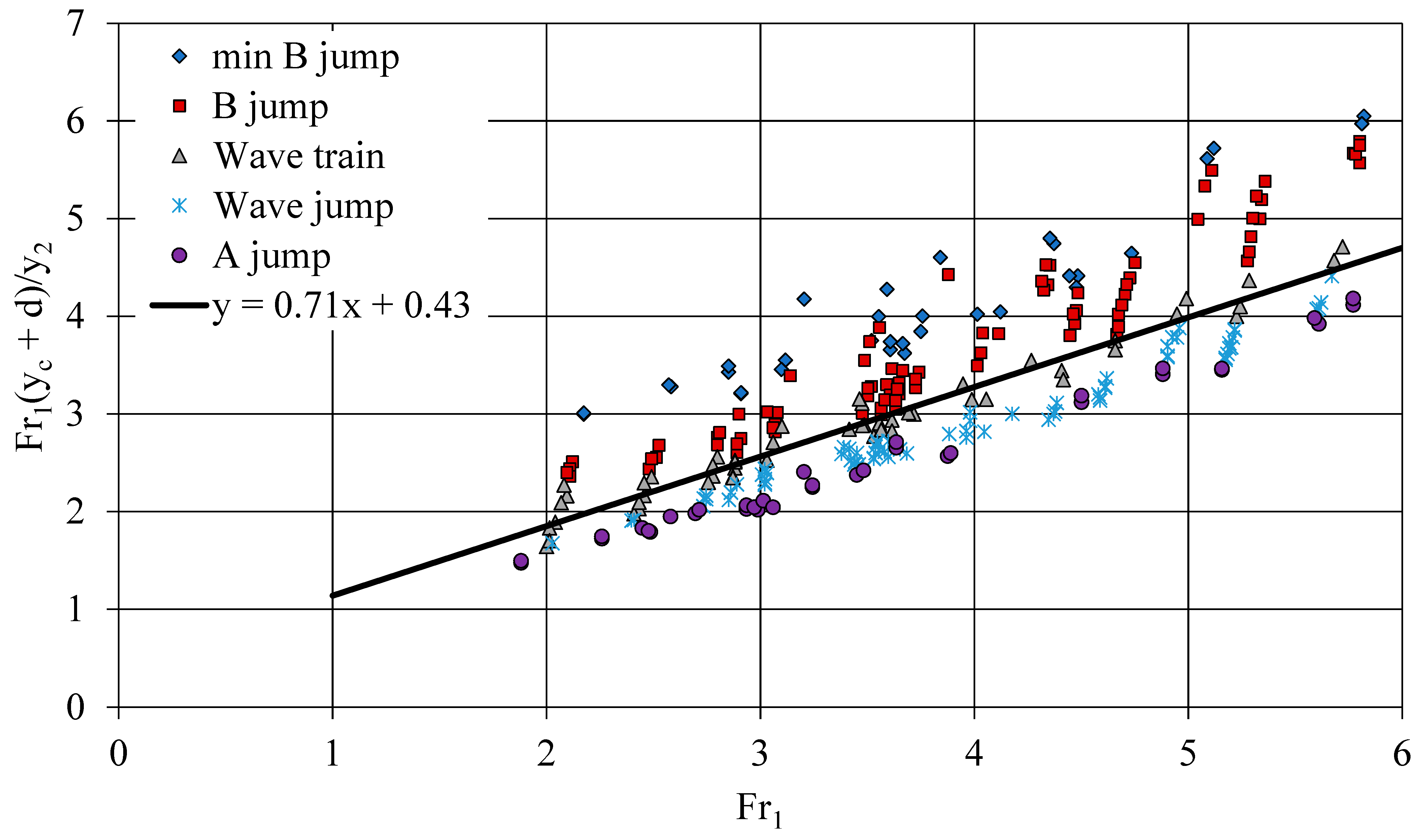
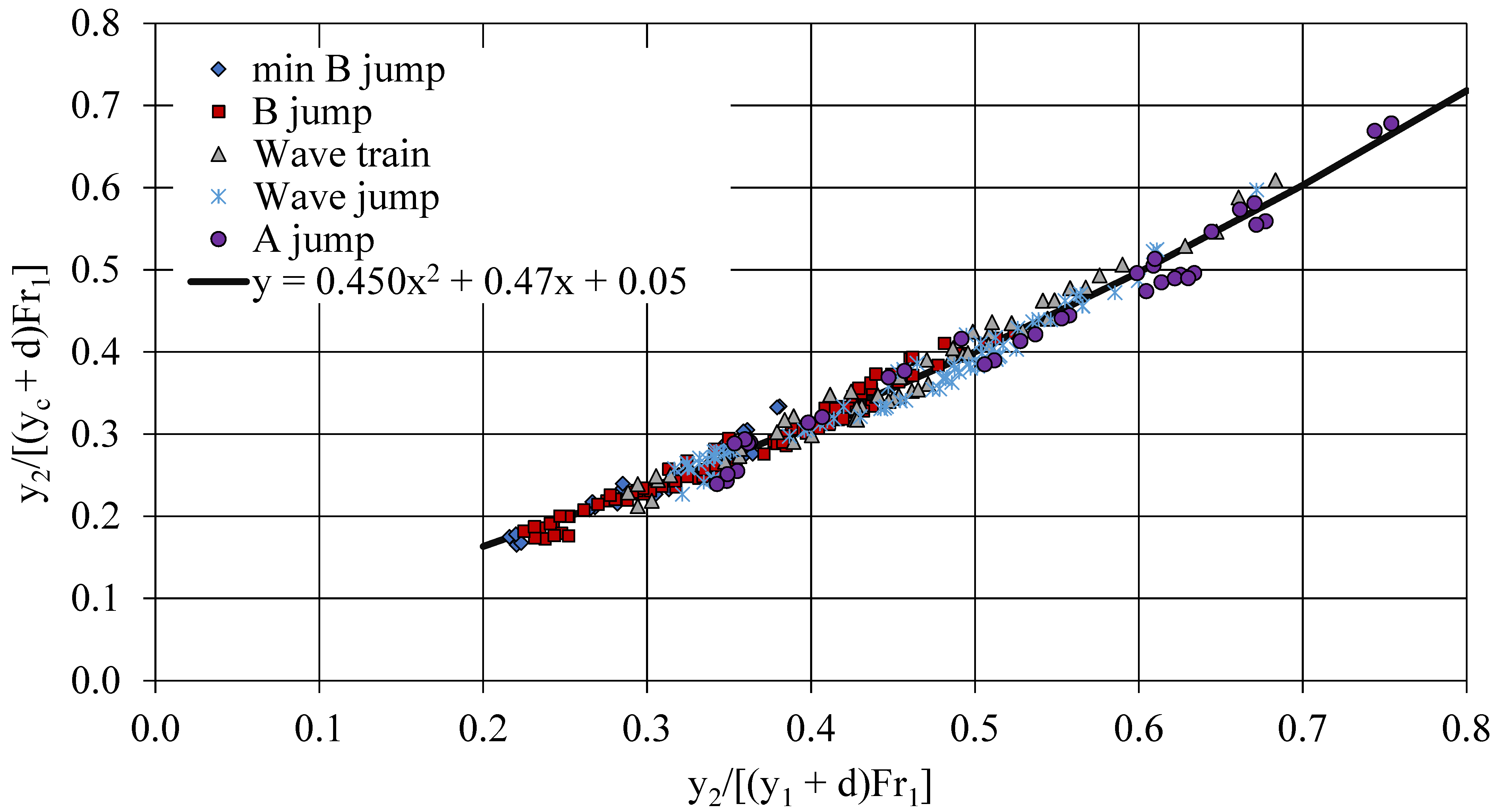
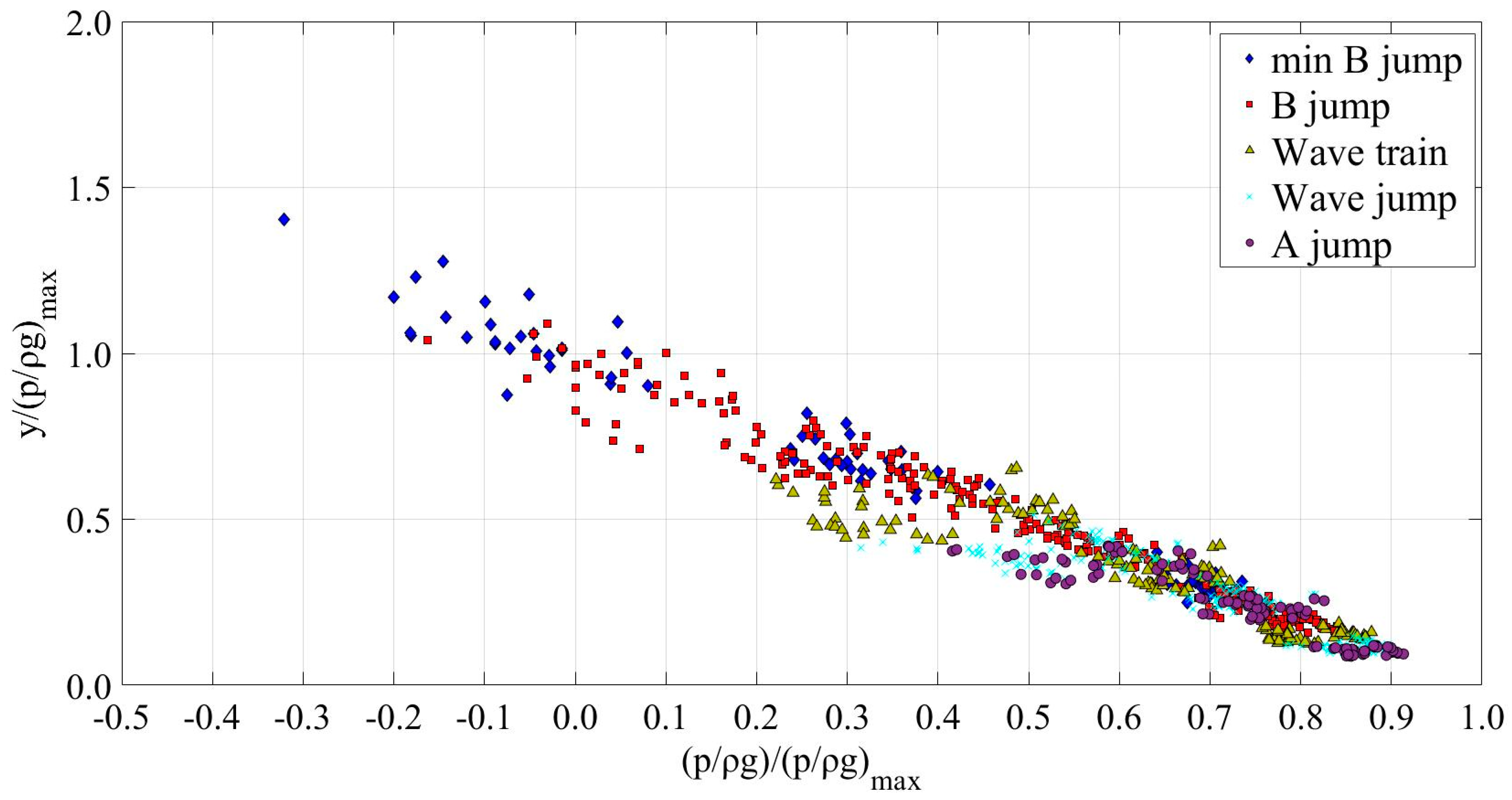
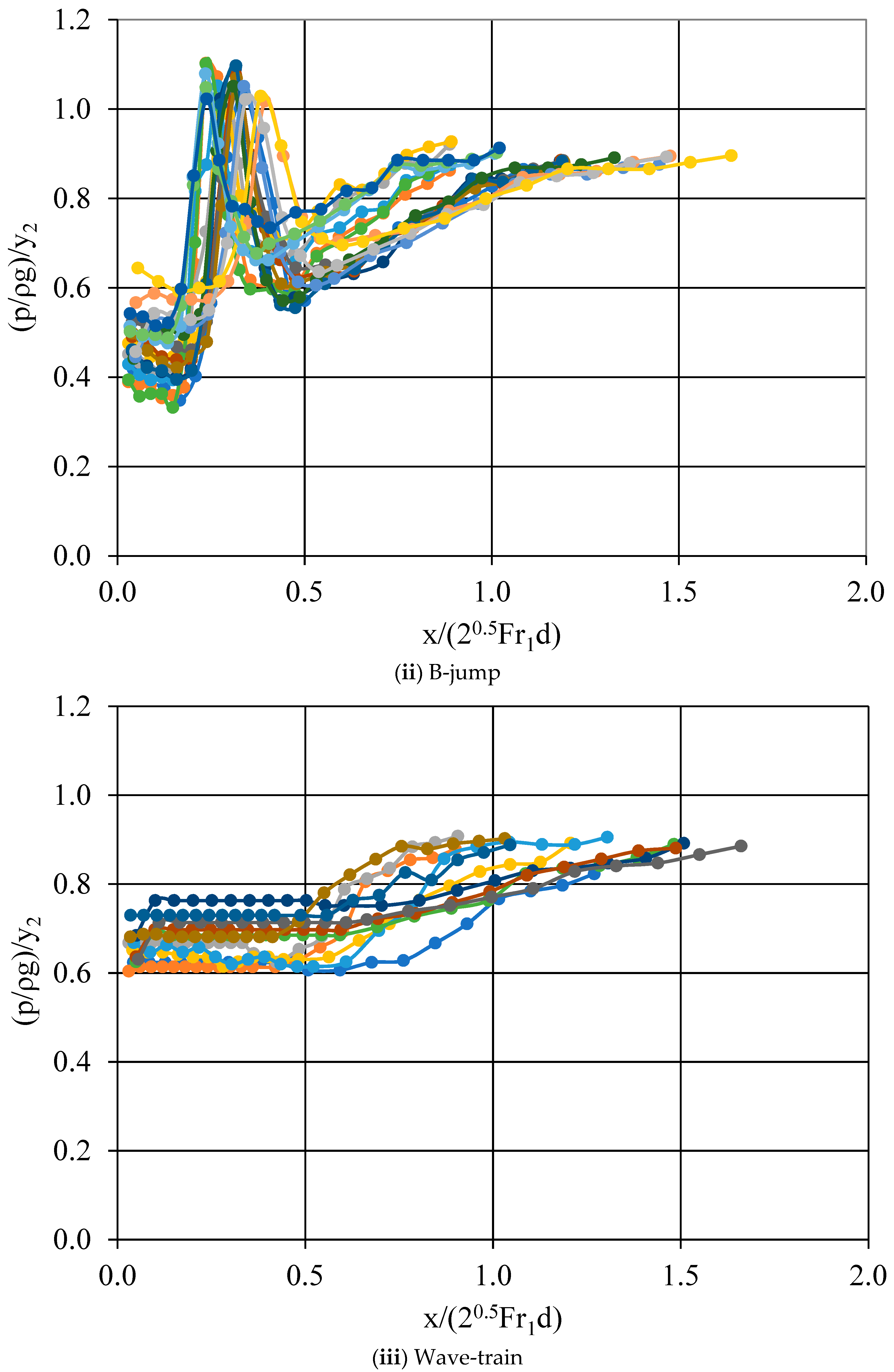
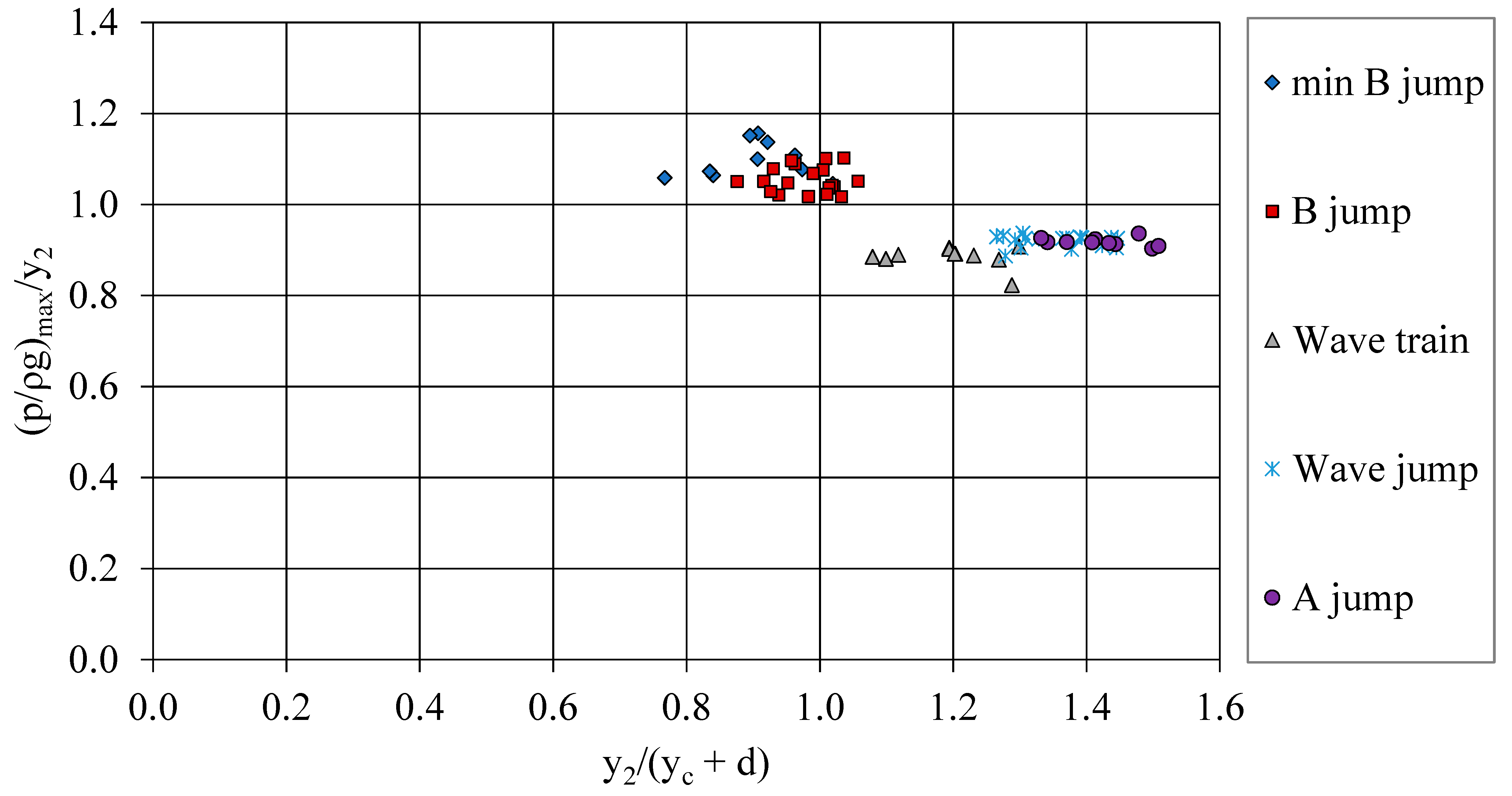
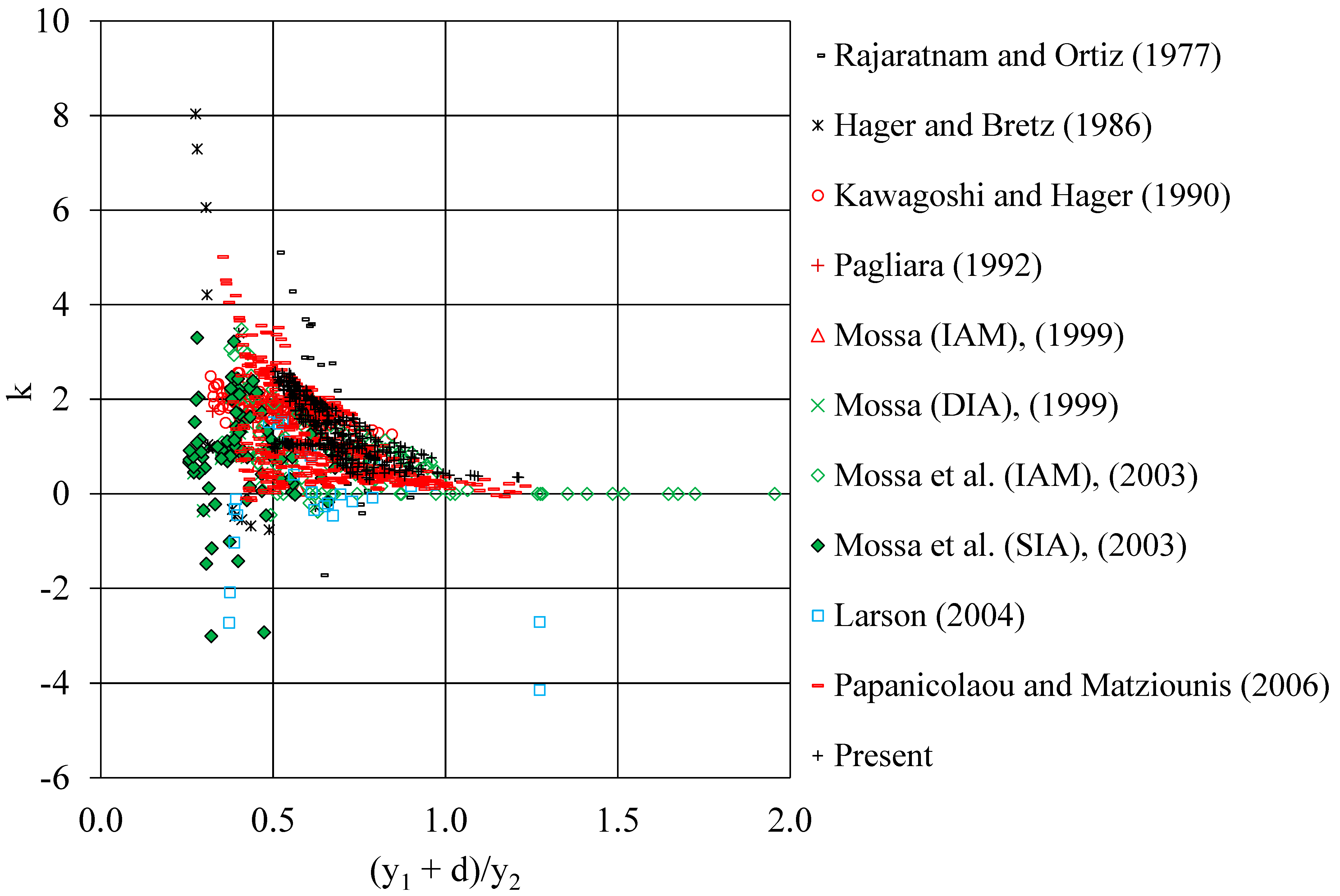
- Five different types of subcritical flow are observed downstream of a submerged vertical step in an orthogonal channel, minimum B-jump and B-jump where the supercritical jet impinges at the bottom if dimensionless depth y2/(yc + d) < 1.07, and wave-train, wave jump and A-jump when the water jet moves at the surface if y2/(yc + d) > 1.07. These can be distinguished if the normalized depth Fr1(yc + d)/y2 is plotted against Fr1.
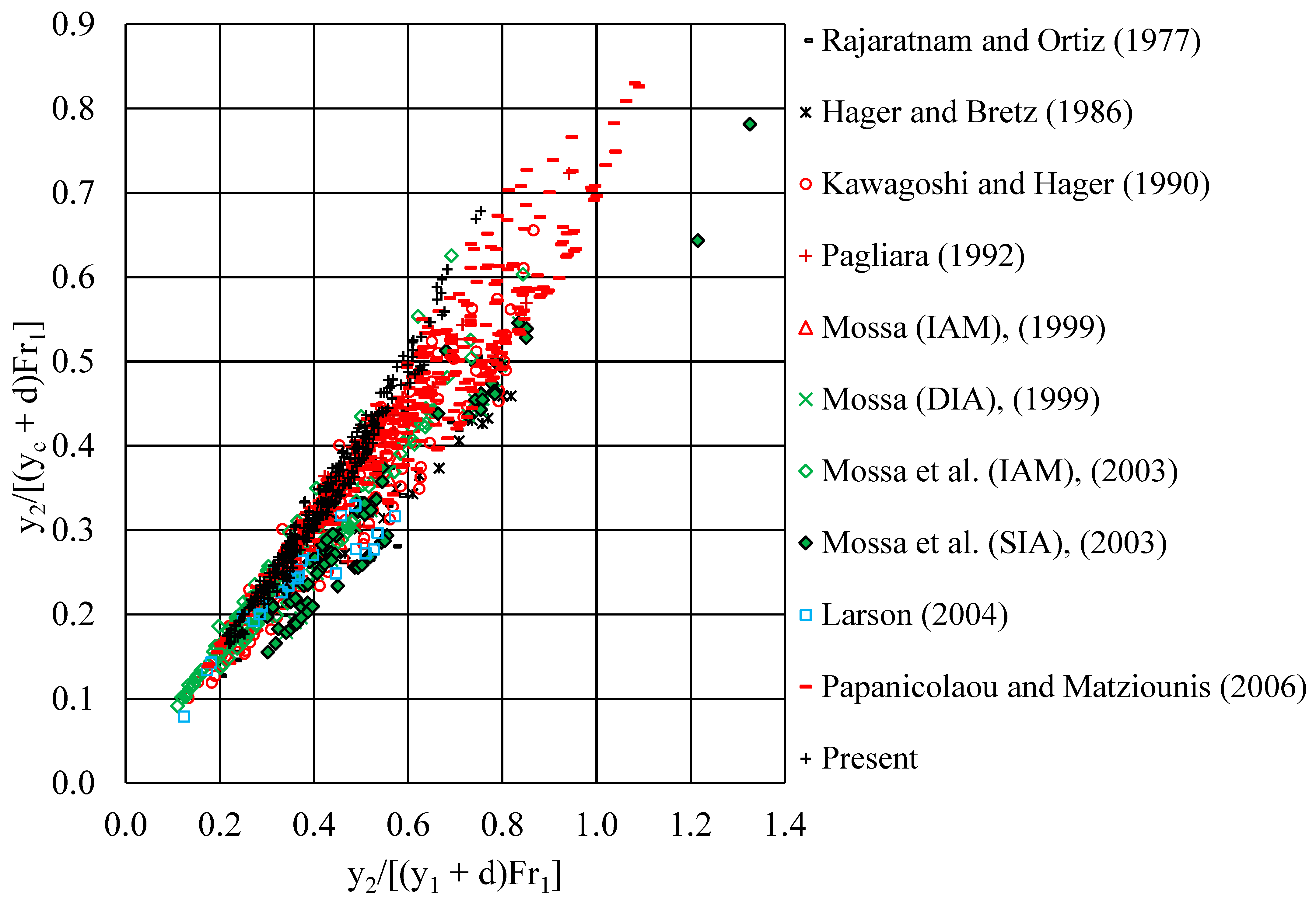
- For all five different types of flow, there is an equation relating the upstream and downstream depths y1 and y2, the critical depth and Froude number (Figure 5), from which one may compute the step height that fulfills these data.
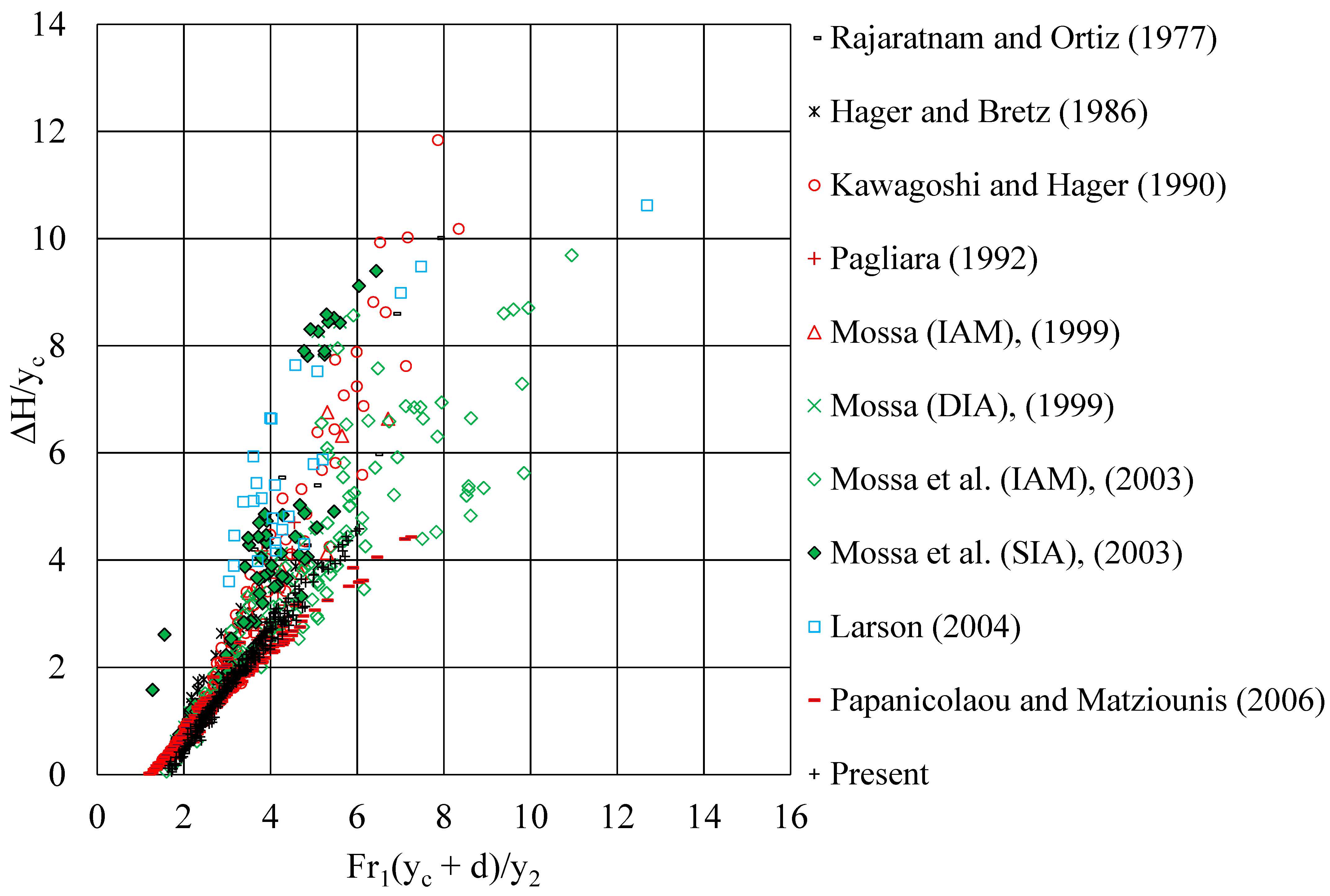
- The energy loss in dimensionless form ΔH/yc for each type of flow can be estimated using Figure 6, where it is plotted versus the normalized length Fr1(yc + d)/y2.
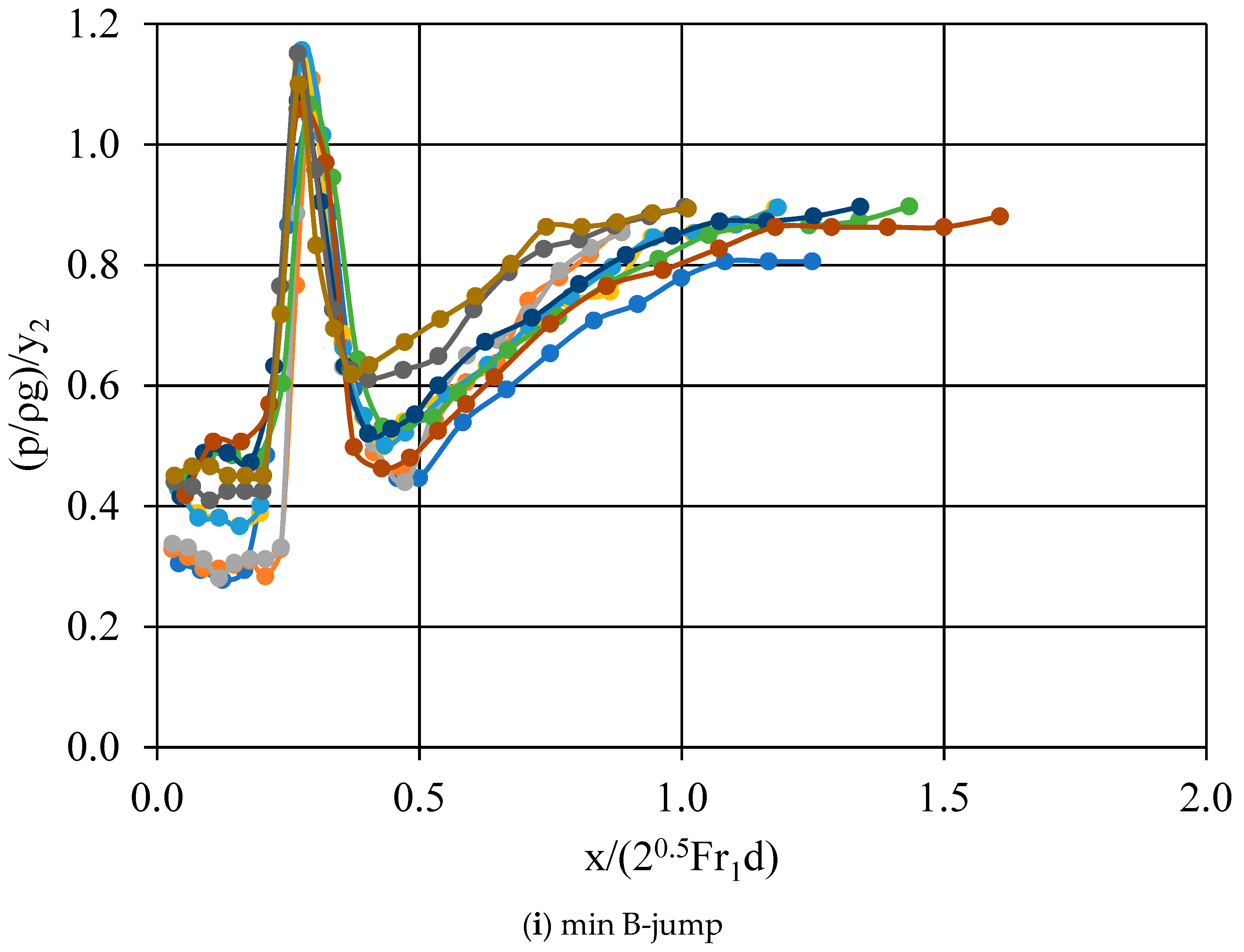
- Regarding the closure of momentum equation, for the limiting case of minimum B-jump the pressure correction coefficient k = 1/2 is equivalent to pressure force upstream from a linear pressure distribution extended to depth y1 + d but reduced by gd(y1 + d/2)/2 for closure; for the limiting case of A-jump the pressure correction coefficient k = 1 is equivalent to pressure force downstream from hydrostatic pressure distribution to depth (y2 − d) from free the surface for closure.
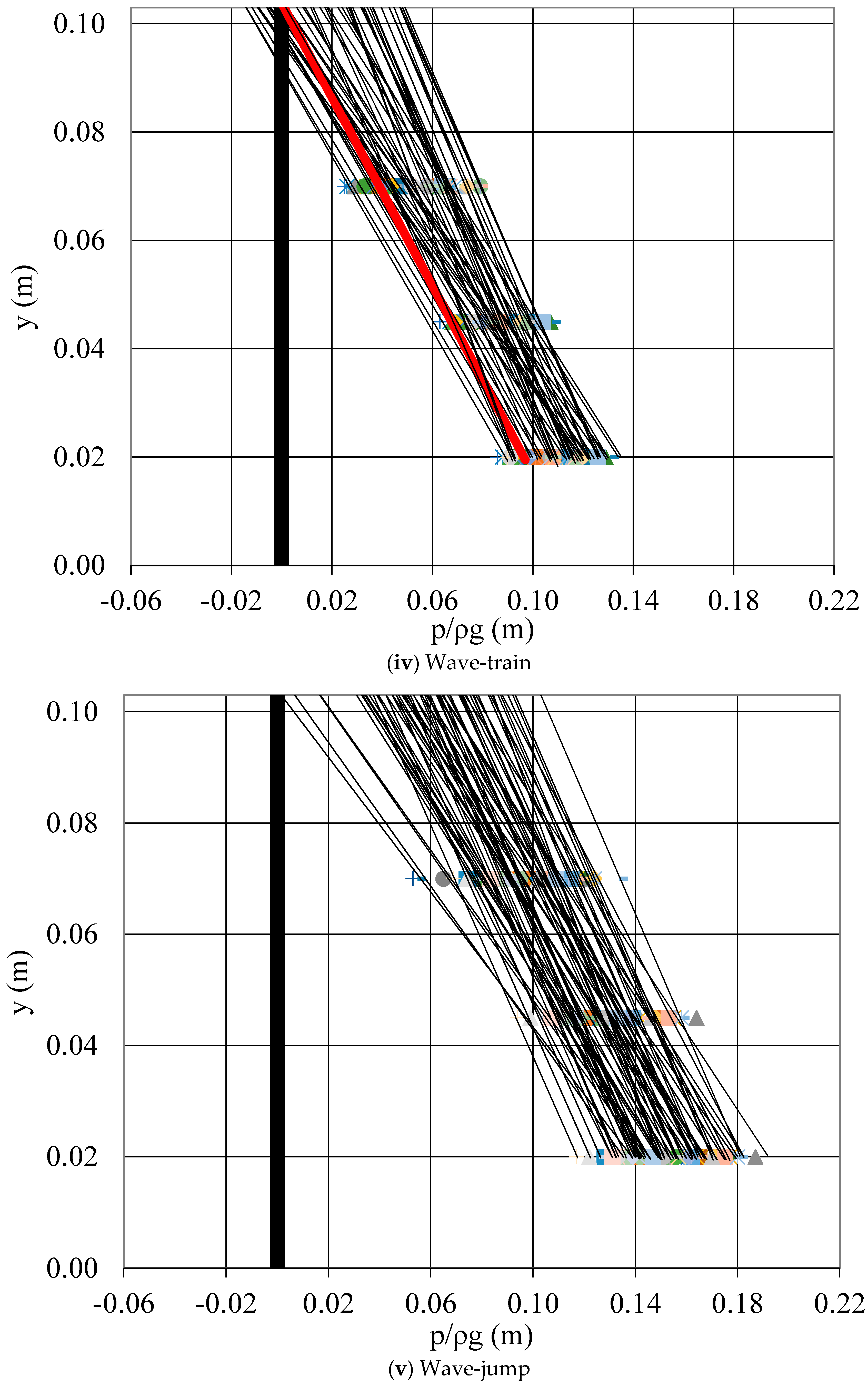
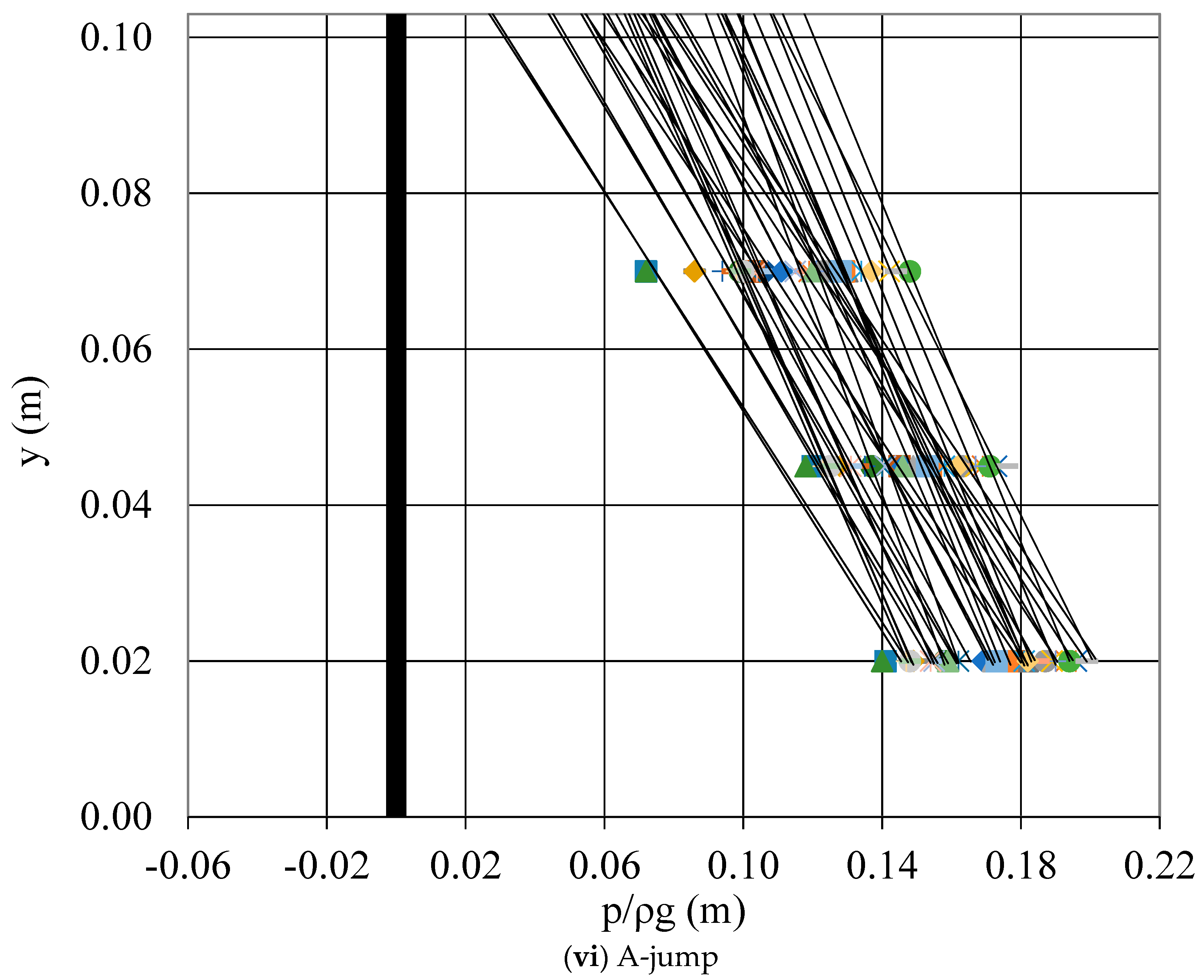
- The pressure distribution measured at the face of the step was linear. If extended to the top of the step, there was a regime of negative pressure for the minimum B-jump and B-jump types of flow. The pressure head at the bottom downstream of the step showed a maximum that exceeded the tailwater depth for the minimum B-jump and B-jump types of flow, while around the toe was less than y2 for all other types of flow.
- The present experiment can be useful to the hydraulic engineer in the design of stilling basins with abrupt negative steps and other structures relevant to the dissipation of kinetic energy of water.
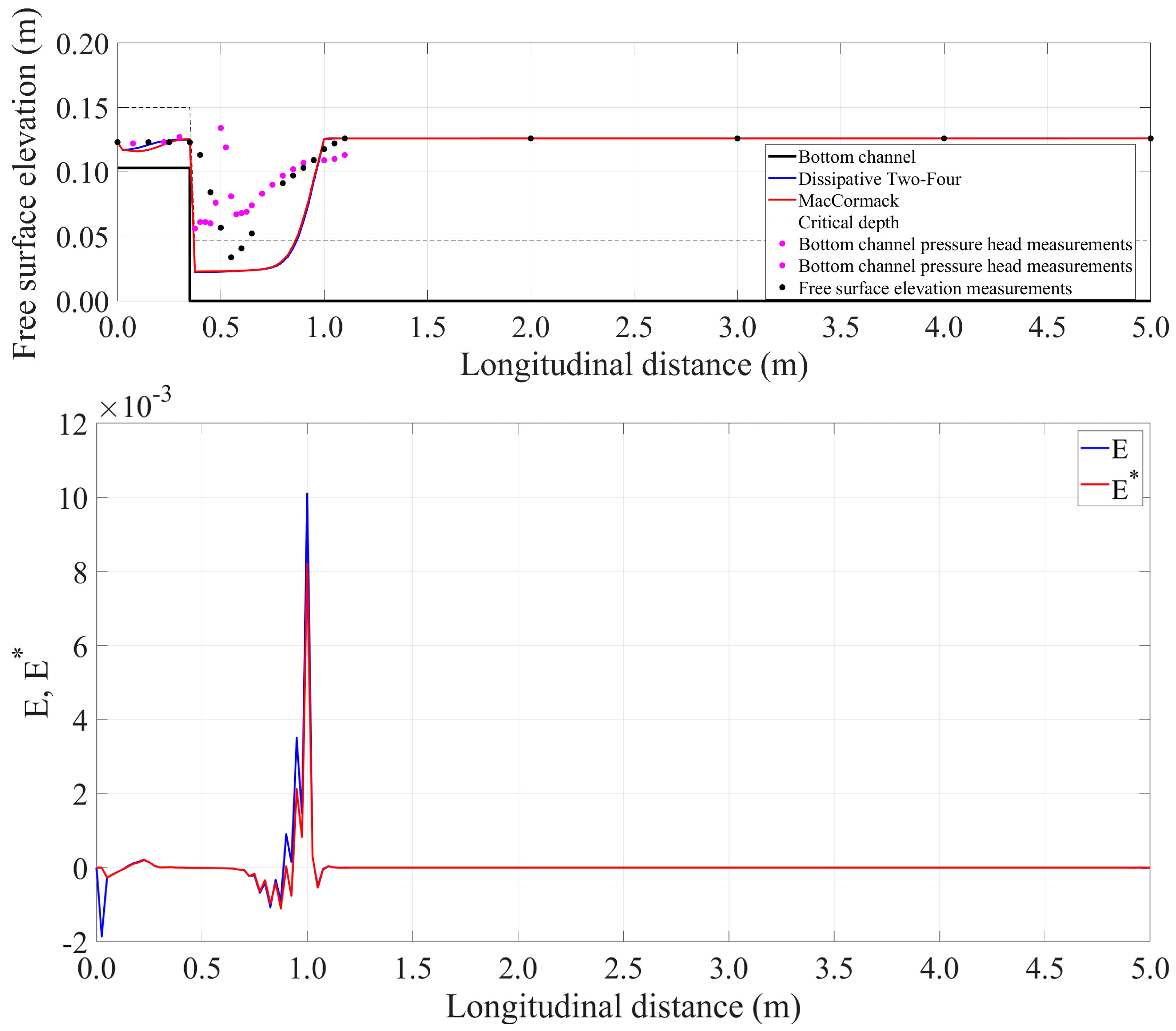
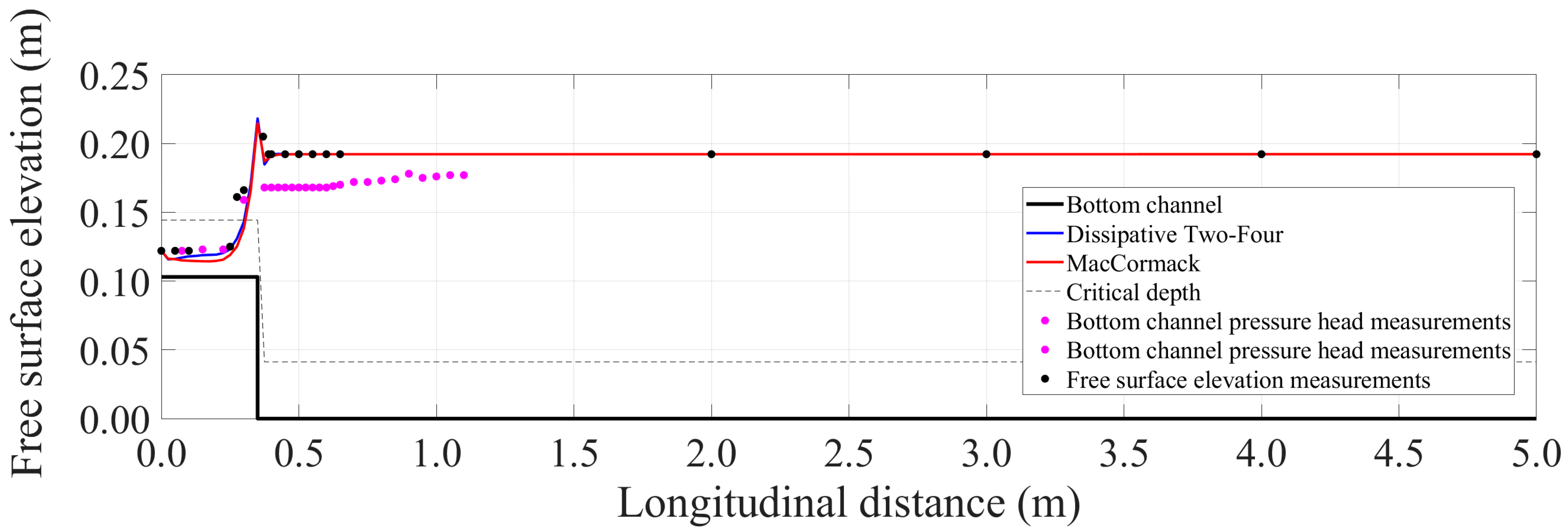
- The numerical results showed that Boussinesq equations can simulate the basic flow characteristics of the minimum B-jump and the A-jump with acceptable accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
On the Numerical Solution of Boussinesq Equations

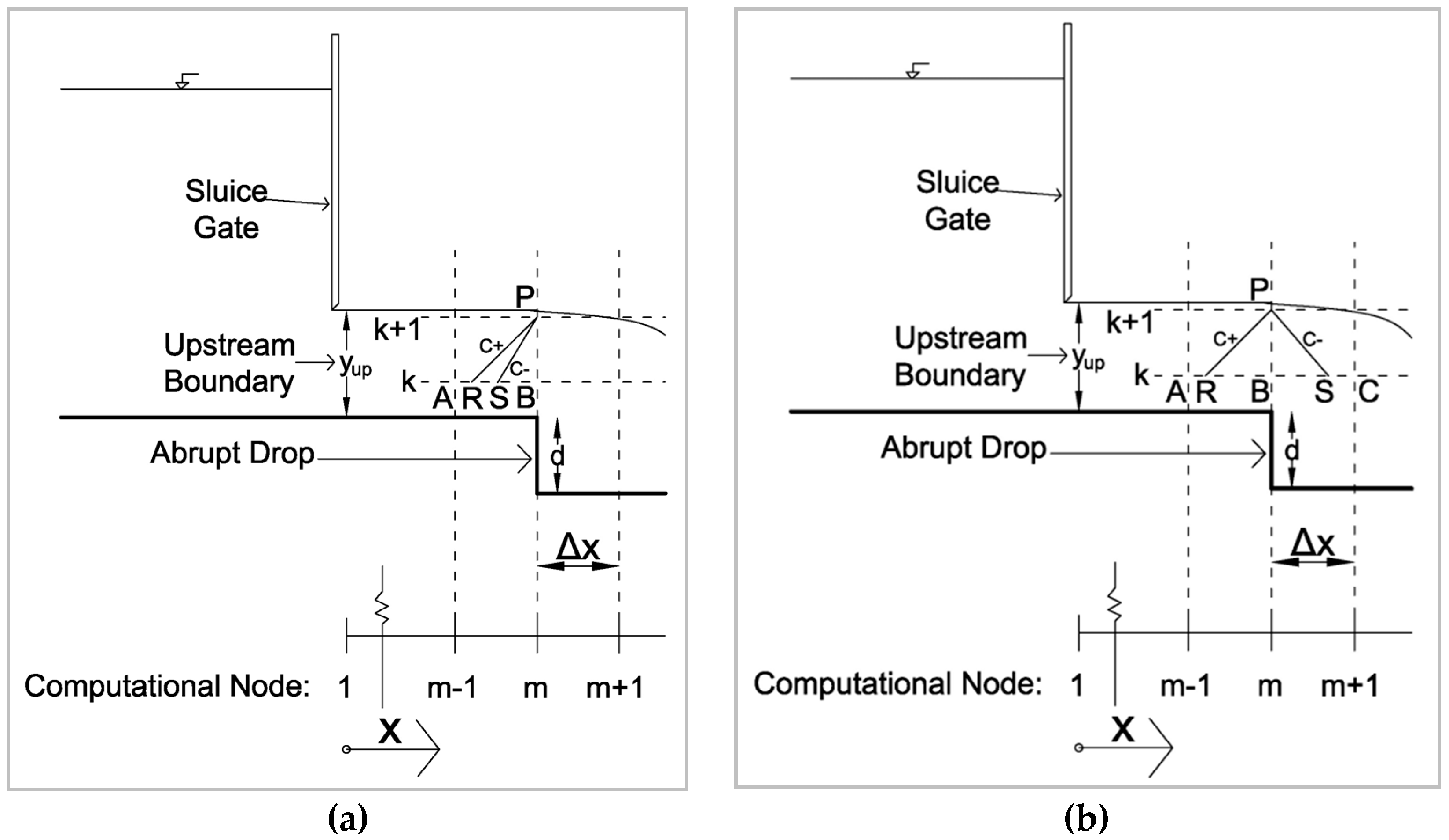
- Compute the flow depth and velocity at all computational spatial nodes at initial time (t = 0) according to the initial condition of the problem.At first iteration:
- Set up the depths yup and ydo at the upstream and downstream boundary nodes respectively, known from the experimental measurements.
- Compute the vector in the predictor step, the vector in the corrector step and the vector Gi for all internal computational spatial nodes except for the node where the drop is placed.
- Compute the vector Gi at the location of the drop and the velocity at the downstream boundary node with the specified intervals method.
- Compute ξi and ξi±(1/2) and modify the flow depth and velocity according to Equation (A30).
- Repeat steps 2–5, with the computed depth and velocity of the present iteration to be the starting values for the next iteration. The algorithm iterates until the change of the depth between two successive iterations in all computational spatial nodes is less than a fixed convergence value. Then the minimum B-jump or the A-jump form as part of the steady state solution.
References
- Gualtieri, C.; Chanson, H. Physical and Numerical Modelling of Air-Water Flows: An Introductory Review. Environ. Model. Softw. 2021, 143, 105109. [Google Scholar] [CrossRef]
- Moore, W.L.; Morgan, C.W. The Hydraulic Jump at an Abrupt Drop. J. Hydraul. Div. Proc. Am. Soc. Civ. Eng. 1957, 83, 1–21. [Google Scholar] [CrossRef]
- Ohtsu, I.; Yasuda, Y. Transition from Supercritical to Subcritical Flow at an Abrupt Drop. J. Hydraul. Res. 1991, 29, 309–328. [Google Scholar] [CrossRef]
- Mossa, M.; Petrillo, A.; Chanson, H. Tailwater Level Effects on Flow Conditions at an Abrupt Drop. J. Hydraul. Res. 2003, 41, 39–51. [Google Scholar] [CrossRef] [Green Version]
- Hager, W.H. B-Jumps at Abrupt Channel Drops. J. Hydraul. Eng. 1985, 11, 861–866. [Google Scholar] [CrossRef]
- Hager, W.H.; Bretz, N.V. Hydraulic Jumps at Positive and Negative Steps. J. Hydraul. Res. 1986, 24, 237–253. [Google Scholar] [CrossRef]
- Pagliara, S. Wave Type Flow at Abrupt Drop: Flow Geometry and Energy Loss, Entropy and Energy Dissipation in Water Resources. In Water Science and Technology Library; Kluwer Academic Publishers: Drive Norwell, MA, USA, 1992; Volume 9, pp. 469–479. [Google Scholar]
- Ohtsu, I.; Yasuda, Y. Discussion of Hydraulic Jumps at Positive and Negative Steps by Hager and Bretz. J. Hydraul. Res. 1987, 25, 407–413. [Google Scholar] [CrossRef]
- Pagliara, S. Discussion of Transition from Supercritical to Subcritical Flow at an Abrupt Drop by Ohtsu and Yasuda. J. Hydraul. Res. 1992, 30, 428–432. [Google Scholar] [CrossRef]
- Negm, M.A. Analysis of Pressure Distribution Coefficient on Steps Under Hydraulic Jump Conditions in Sloping Stilling Basins. Trans. Ecol. Environ. 1998, 19, 1–10. [Google Scholar]
- Giudice, D.G.; Gisonni, C.; Rasulo, G. Vortex Drop Shaft for Supercritical Flow. In Proceedings of the 16th IAHR-APD Congress and 3rd Symposium of IAHR-ISHS, Nanjing, China, 20–23 October 2008. [Google Scholar]
- Rajaratnam, N.; Ortiz, N. Hydraulic Jumps and Waves at Abrupt Drops. J. Hydraul. Div. Proc. Am. Soc. Civ. Eng. 1977, 103, 381–394. [Google Scholar] [CrossRef]
- Mossa, M. On the Oscillating Characteristics of Hydraulic Jumps. J. Hydraul. Res. 1999, 37, 541–558. [Google Scholar] [CrossRef]
- Sunik, S.M. Tailwater Level Effect on Flow Conditions at an Abrupt Drop. In Proceedings of the Nasional Aplikasi Teknologi Prasarana, Wilayah, India, 2 January 2009. [Google Scholar]
- Armenio, V.; Toscano, P.; Fiorotto, V. On the Effects of a Negative Step in Pressure Fluctuations at the Bottom of a Hydraulic Jump. J. Hydraul. Res. 2000, 38, 359–368. [Google Scholar] [CrossRef]
- Matziounis, P.; Papanicolaou, P. Subcritical and Supercritical Flow Conditions at a Submerged Forward Facing Step. In Proceedings of the 1st International Conference on Experiments/Process/System Modelling/Simulation/Optimization, Athens, Greece, 6–9 July 2005. [Google Scholar]
- Esfahani, M.; Bajestan, M. Dynamic Force Measurement of Roughened Bed B-jump at an Abrupt Drop. Arch. Sci. 2012, 65, 47–54. [Google Scholar]
- Riazi, R.; Bejestan, M. Analysis Location of Pressure Fluctuation in Hydraulic Jump Over Roughened Bed with Negative Step. Bull. Environ. Pharmacol. Life Sci. 2014, 3, 103–110. [Google Scholar]
- Kawagoshi, N.; Hager, W.H. Wave Type Flow at Abrupt Drops. J. Hydraul. Res. 1990, 28, 235–252. [Google Scholar] [CrossRef]
- Quraishi, A.; Al-Brahim, A.M. Hydraulic Jump in Sloping Channel with Positive or Negative Step. J. Hydraul. Res. 1992, 30, 769–782. [Google Scholar] [CrossRef]
- Ohtsu, I.; Yasuda, Y. Discussion of Hydraulic Jump in Sloping Channel with Positive or Negative Step by Quraishi and Al-Brahim. J. Hydraul. Res. 1993, 31, 712–716. [Google Scholar] [CrossRef]
- Larson, E. Energy Dissipation in Culverts by Forcing a Hydraulic Jump at the Outlet. Master’s Thesis, Department of Civil and Environmental Engineering, Washington State University, Pullman, WA, USA, 2004. [Google Scholar]
- Papanicolaou, P.; Matziounis, P. Supercritical Flow Conditions Around a Submerged Forward Facing Step. In Proceedings of the 10th National Congress in Management of Water Resources and Protection of Environment, Hellenic Hydrotechnical Association, Xanthi, Greece, 13–16 December 2006. [Google Scholar]
- Bakhti, S.; Hazzab, A. Comparative Analysis of the Positive and Negative Steps in a Forced Hydraulic Jump. Jordan J. Civ. Eng. 2010, 4, 197–204. [Google Scholar]
- Simsek, O.; Soydan, N.; Gumus, V.; Akoz, M.; Kirkgoz, M. Numerical Modeling of B-Type Hydraulic Jump at an Abrupt Drop. Tek. Dergi 2015, 24, 7215–7240. [Google Scholar]
- Padova, D.; Mossa, M.; Sibilla, S. SPH Modelling of Hydraulic Jump Oscillations at an Abrupt Drop. Water 2017, 9, 790. [Google Scholar] [CrossRef] [Green Version]
- Chaudhry, H.M. Open-Channel Flow, 2nd ed.; Springer: New York, NY, USA, 2008; pp. 1–528. [Google Scholar]
- Gottlieb, D.; Turkel, E. Dissipative Two-Four Methods for Time-Dependent Problems. Math. Comput. 1976, 30, 703–723. [Google Scholar] [CrossRef]
- MacCormack, R.W. The Effect of Viscosity in Hypervelocity Impact Cratering. In Proceedings of the AIAA Hypervelocity Impact Conference, Cincinnati, OH, USA, 30 April–2 May 1969. [Google Scholar] [CrossRef]
- Valero, D.; Viti, N.; Gualtieri, C. Numerical Simulation of Hydraulic Jumps. Part 1: Experimental Data for Modelling Performance Assessment. Water 2019, 11, 36. [Google Scholar] [CrossRef] [Green Version]
- Viti, N.; Valero, D.; Gualtieri, C. Numerical Simulation of Hydraulic Jumps. Part 2: Recent Results and Future Outlook. Water 2019, 11, 28. [Google Scholar] [CrossRef] [Green Version]
- Chanson, H. Environmental Hydraulics of Open Channel Flows, 1st ed.; Elsevier: Oxford, UK, 2004; pp. 1–485. [Google Scholar] [CrossRef] [Green Version]


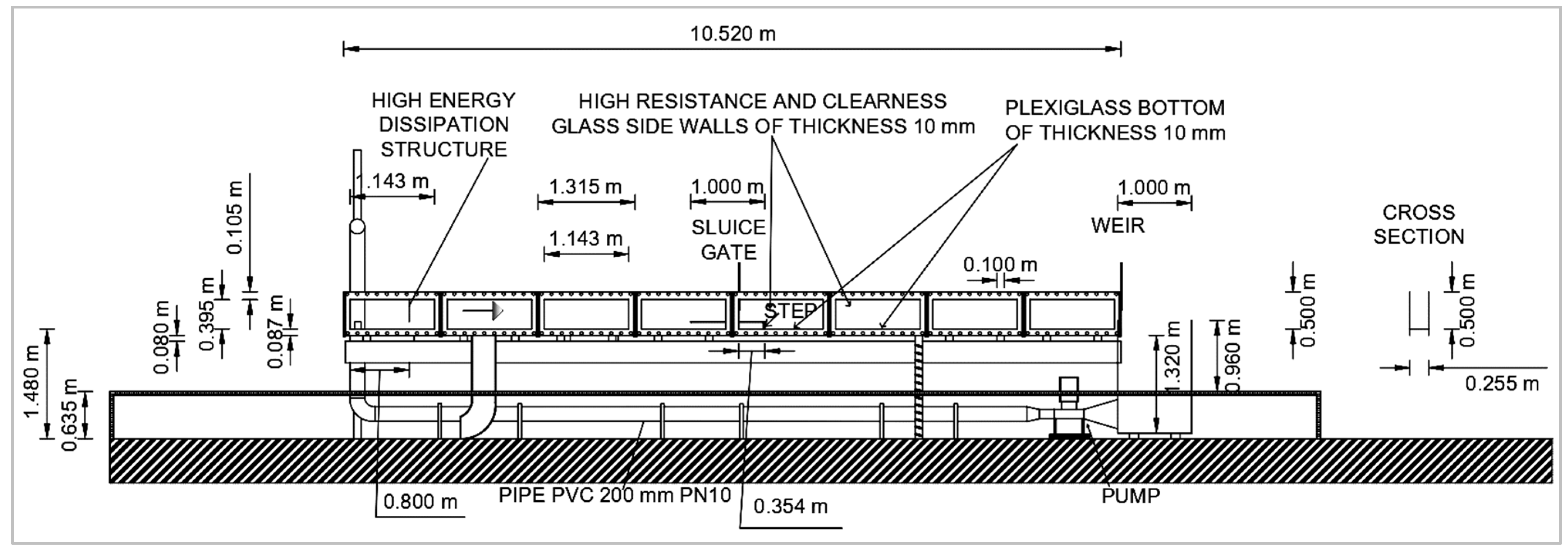







| Q (L/s) | q (L/s/m) | y1 (cm) | y2 (cm) | Inflow Fr1 | Inflow Re |
|---|---|---|---|---|---|
| 6.46–17.50 | 25.32–68-67 | 1.4–3.6 | 25.8–26.8 | 1.88–5.82 | 23,000–63,000 |
| Test Case/Experiment | Q (L/s) | Fr | yup (m) | ydo (m) | Type of Jump |
|---|---|---|---|---|---|
| 1 | 8.11 | 3.59 | 0.0200 | 0.1259 | minimum B |
| 2 | 9.88 | 4.37 | 0.0200 | 0.1442 | minimum B |
| 3 | 6.70 | 3.20 | 0.0190 | 0.1922 | A jump |
| 4 | 9.41 | 4.50 | 0.0190 | 0.2234 | A jump |
| Test Case/Experiment | Numerical Scheme | Maximum Mass Conservation Error (%) | Iterations |
|---|---|---|---|
| 1 | Dissipative Two-Four MacCormack | 4.01 3.59 | 6117 5779 |
| 2 | Dissipative Two-Four MacCormack | 4.07 3.64 | 4866 5067 |
| 3 | Dissipative Two-Four MacCormack | 2.45 2.13 | 5474 4934 |
| 4 | Dissipative Two-Four MacCormack | 3.92 4.09 | 5965 6355 |
| Researchers | b (m) | d (cm) | q (l/s/m) | Fr1 | d/yc | Flow Dimensionality |
|---|---|---|---|---|---|---|
| Rajaratnam & Ortiz 1977 [12] | 0.410 | 3.60–7.60 | 35.79–145.24 | 2.97–10.55 | 0.40–1.43 | 3D |
| Hager & Bretz 1986 [6] | 0.500 | 7.60 | 60.00–400.00 | 3.93–5.71 | 0.36–1.06 | 3D |
| Kawagoshi & Hager 1990 [19] | 0.500 | 5.00–7.70 | 5.98–179.56 | 1.99–13.68 | 0.37–5.00 | 3D |
| Pagliara 1992 [7,9] | 0.500 | 3.72–8.45 | 9.80–138.00 | 1.85–6.90 | 0.45–2.78 | 3D |
| Mossa 1999 [13] | 0.300 0.400 | 5.30–10.00 3.20–6.52 | 23.33–62.00 33.93–80.30 | 3.19–8.87 2.77–9.92 | 0.72–1.68 0.41–1.06 | 3D |
| Mossa et al., 2003 [4] | 0.300 0.400 | 5.30–16.00 3.20–6.52 | 21.47–65.11 33.68–80.37 | 1.56–10.24 1.78–10.33 | 0.72–3.58 0.39–1.07 | 3D |
| Larson 2004 [22] | 0.610 | 9.72–30.48 | 95.63–386.22 | 4.10–6.41 | 0.39–2.22 | 3D |
| Papanicolaou & Matziounis 2006 [23] | 0.100 | 2.50–10.00 | 29.90–71.50 | 1.73–4.91 | 0.31–2.17 | 3D |
| Present | 0.255 | 10.30 | 25.32–67.08 | 1.88–5.82 | 1.34–2.56 | 3D |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Retsinis, E.; Papanicolaou, P. Supercritical Flow over a Submerged Vertical Negative Step. Hydrology 2022, 9, 74. https://doi.org/10.3390/hydrology9050074
Retsinis E, Papanicolaou P. Supercritical Flow over a Submerged Vertical Negative Step. Hydrology. 2022; 9(5):74. https://doi.org/10.3390/hydrology9050074
Chicago/Turabian StyleRetsinis, Eugene, and Panos Papanicolaou. 2022. "Supercritical Flow over a Submerged Vertical Negative Step" Hydrology 9, no. 5: 74. https://doi.org/10.3390/hydrology9050074
APA StyleRetsinis, E., & Papanicolaou, P. (2022). Supercritical Flow over a Submerged Vertical Negative Step. Hydrology, 9(5), 74. https://doi.org/10.3390/hydrology9050074






