The Seasonal Water Balance of Western-Juniper-Dominated and Big-Sagebrush-Dominated Watersheds
Abstract
1. Introduction
2. Materials and Methods
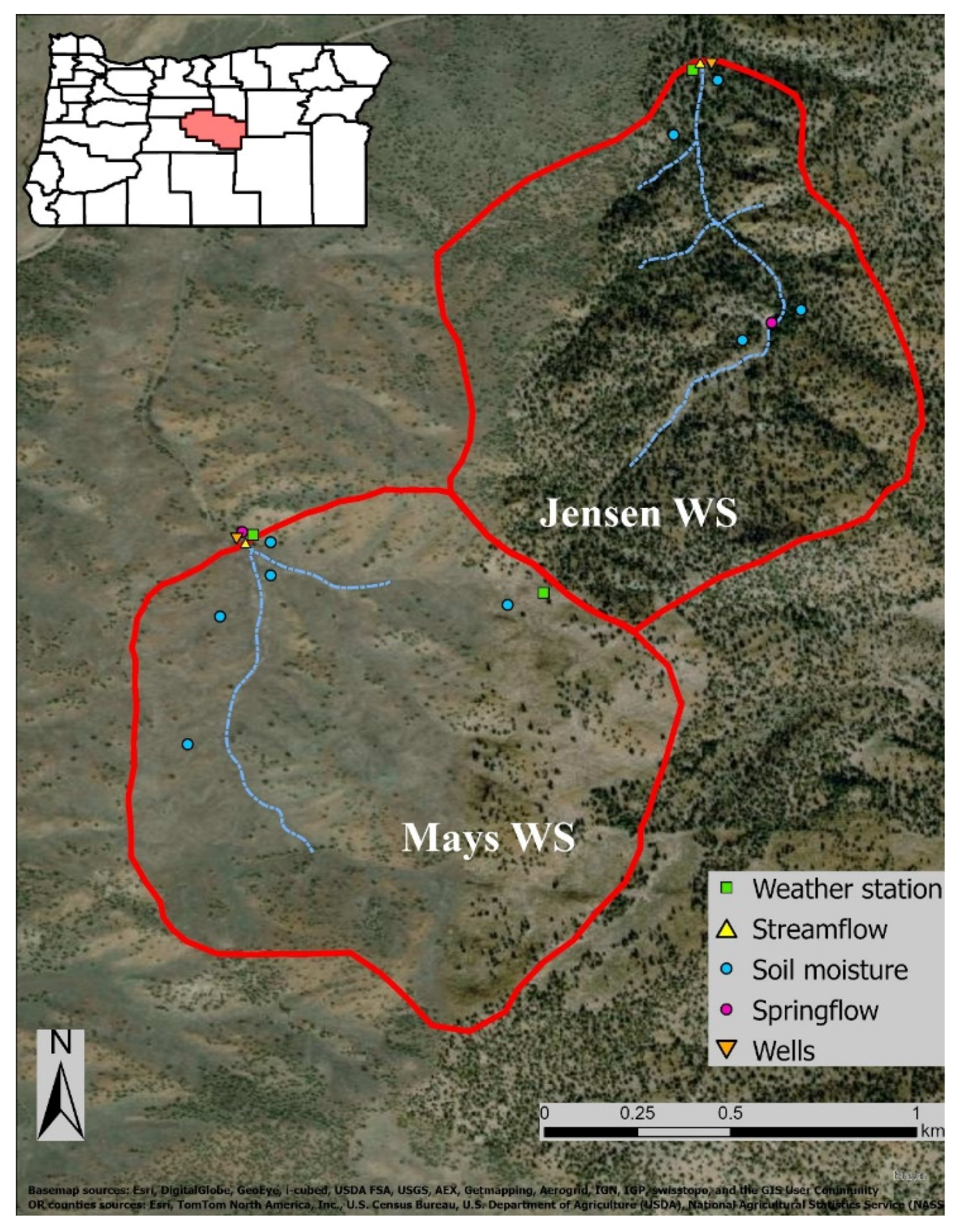
2.1. Site Description
2.2. Water Balance
2.3. Subsurface Flow and Shallow Aquifer Response to Seasonal Precipitation
3. Results
3.1. Water Balance
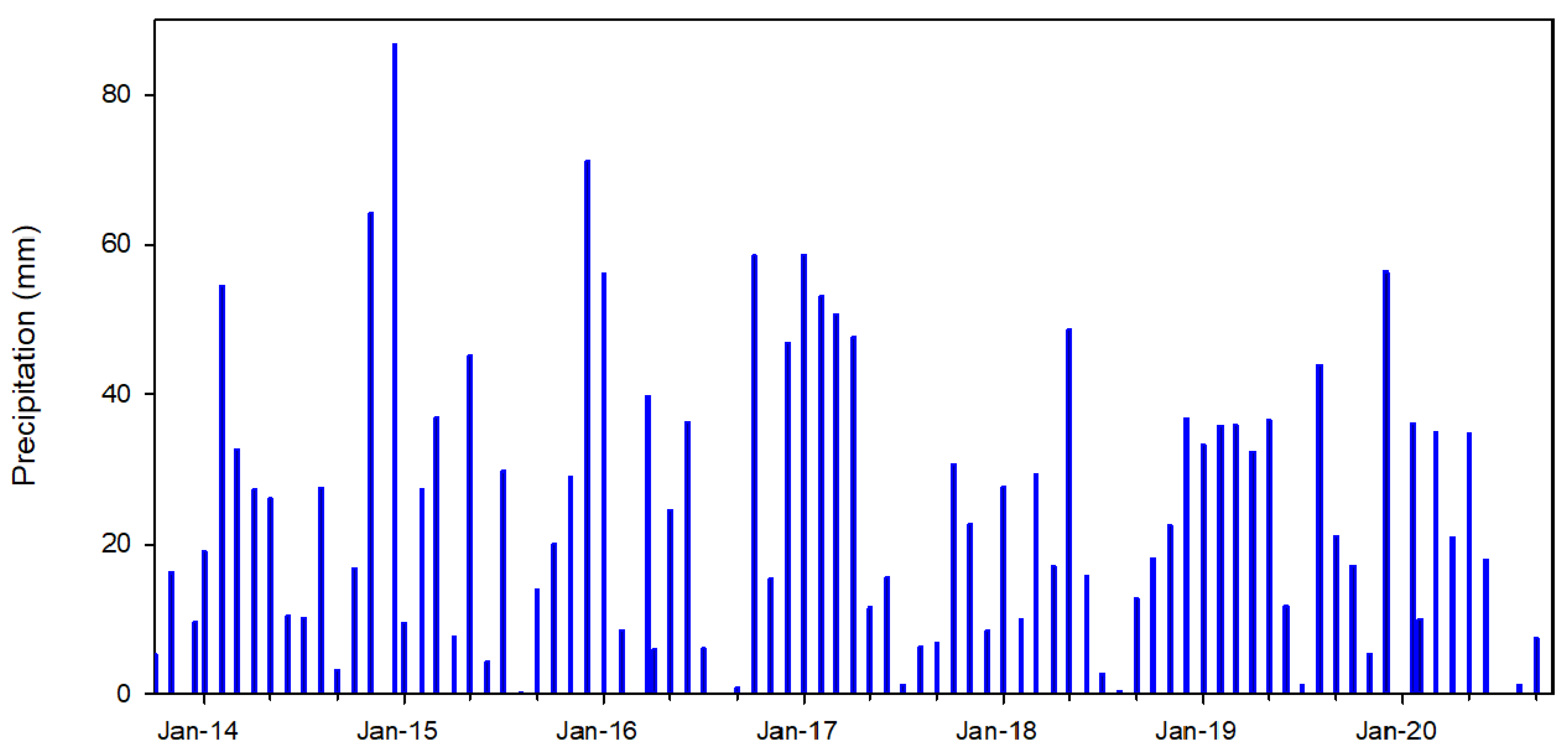
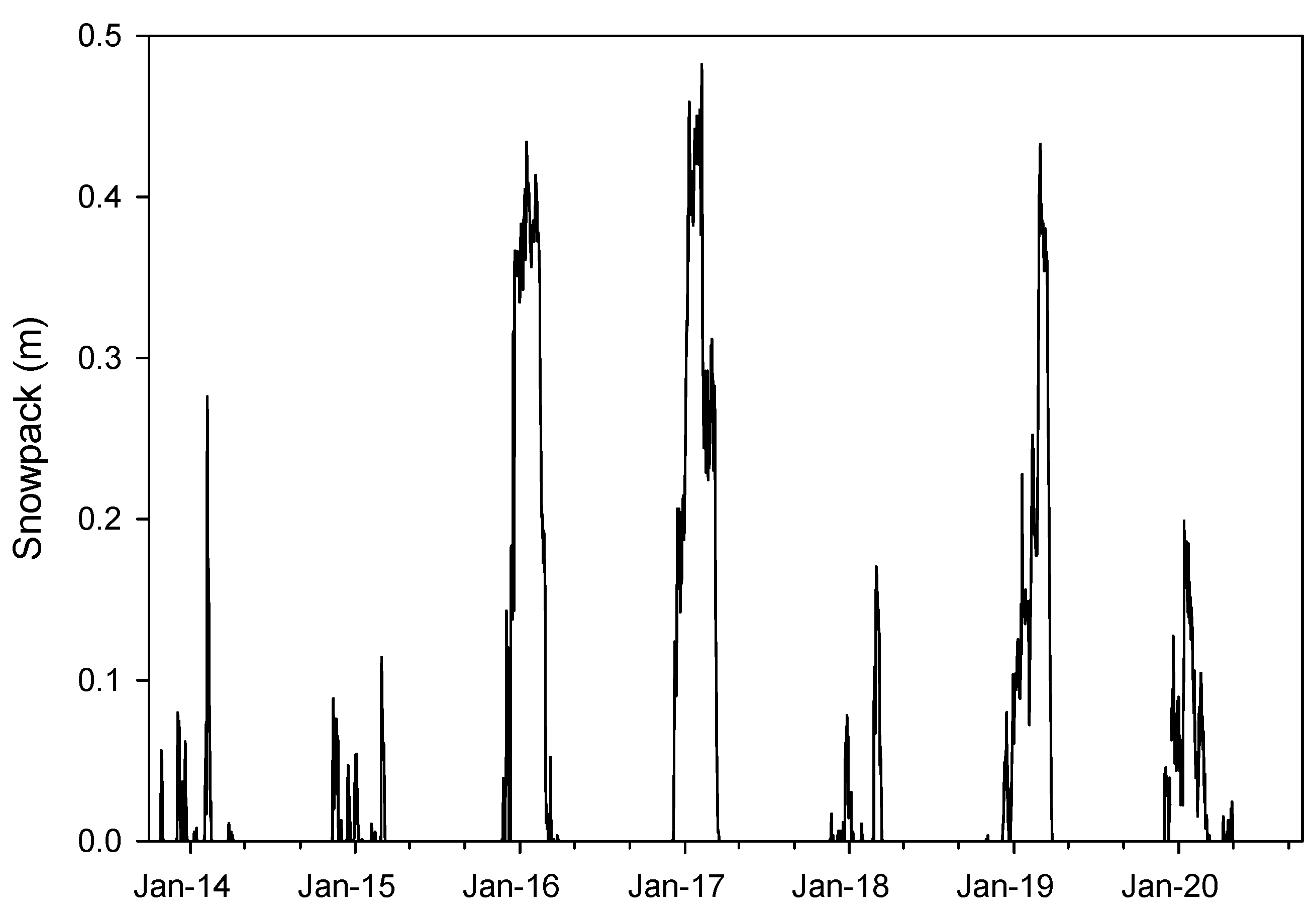
3.1.1. Snowpack and Precipitation Patterns
3.1.2. Streamflow
3.1.3. Soil-Water-Content Change
3.1.4. Seasonal PET
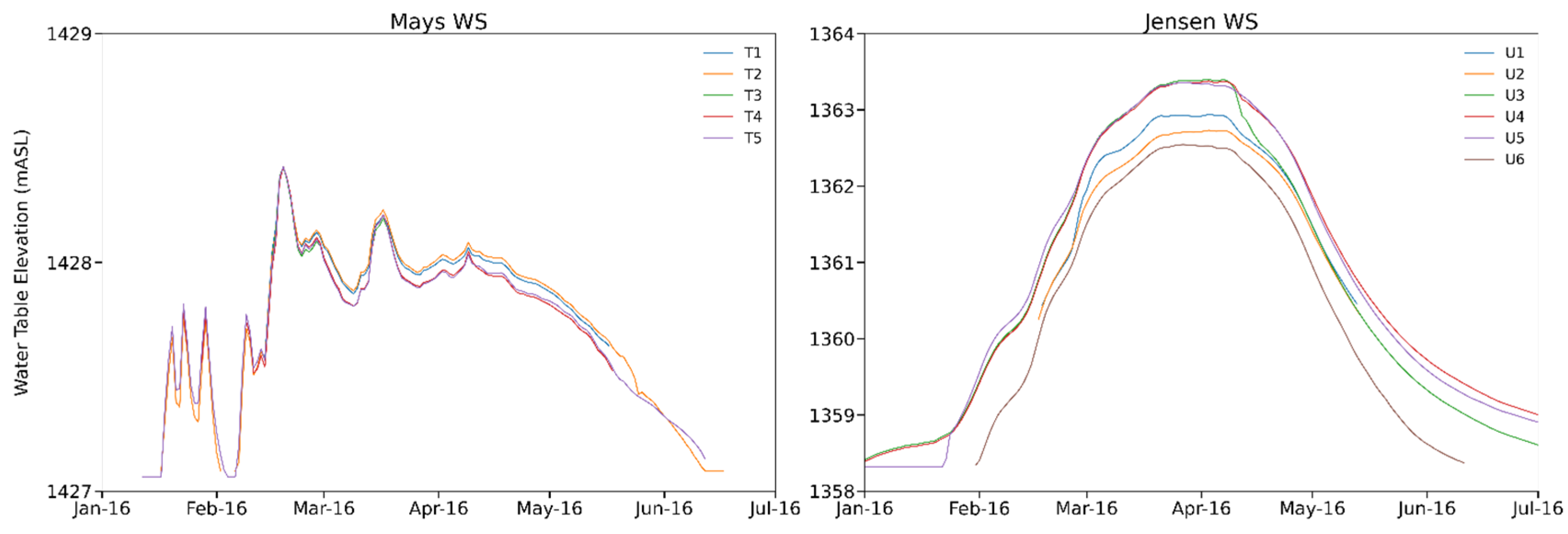
3.2. Subsurface Flow and Shallow Aquifer Response to Seasonal Precipitation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bradford, J.B.; Schlaepfer, D.R.; Lauenroth, W.K. Ecohydrology of Adjacent Sagebrush and Lodgepole Pine Ecosystems: The Consequences of Climate Change and Disturbance. Ecosystems 2014, 17, 590–605. [Google Scholar] [CrossRef]
- Palmquist, K.A.; Schlaepfer, D.R.; Bradford, J.B.; Lauenroth, W.K. Mid-Latitude Shrub Steppe Plant Communities: Climate Change Consequences for Soil Water Resources. Ecology 2016, 97, 2342–2354. [Google Scholar] [CrossRef] [PubMed]
- Abdulla, F.; Eshtawi, T.; Assaf, H. Assessment of the Impact of Potential Climate Change on the Water Balance of a Semi-Arid Watershed. Water Resour. Manag. 2009, 23, 2051–2068. [Google Scholar] [CrossRef]
- Eckhardt, K.; Ulbrich, U. Potential Impacts of Climate Change on Groundwater Recharge and Streamflow in a Central European Low Mountain Range. J. Hydrol. 2003, 284, 244–252. [Google Scholar] [CrossRef]
- Meixner, T.; Manning, A.H.; Stonestrom, D.A.; Allen, D.M.; Ajami, H.; Blasch, K.W.; Brookfield, A.E.; Castro, C.L.; Clark, J.F.; Gochis, D.J.; et al. Implications of Projected Climate Change for Groundwater Recharge in the Western United States. J. Hydrol. 2016, 534, 124–138. [Google Scholar] [CrossRef]
- Schlaepfer, D.R.; Lauenroth, W.K.; Bradford, J.B. Consequences of Declining Snow Accumulation for Water Balance of Mid-Latitude Dry Regions. Glob. Chang. Biol. 2012, 18, 1988–1997. [Google Scholar] [CrossRef]
- Konapala, G.; Mishra, A.K.; Wada, Y.; Mann, M.E. Climate Change Will Affect Global Water Availability through Compounding Changes in Seasonal Precipitation and Evaporation. Nat. Commun. 2020, 11, 3044. [Google Scholar] [CrossRef]
- Bradford, J.B.; Schlaepfer, D.R.; Lauenroth, W.K.; Burke, I.C. Shifts in Plant Functional Types Have Time-Dependent and Regionally Variable Impacts on Dryland Ecosystem Water Balance. J. Ecol. 2014, 102, 1408–1418. [Google Scholar] [CrossRef]
- Pierson, F.B.; Jason Williams, C.; Hardegree, S.P.; Clark, P.E.; Kormos, P.R.; Al-Hamdan, O.Z. Hydrologic and Erosion Responses of Sagebrush Steppe Following Juniper Encroachment, Wildfire, and Tree Cutting. Rangel. Ecol. Manag. 2013, 66, 274–289. [Google Scholar] [CrossRef]
- Kormos, P.R.; Marks, D.; Pierson, F.B.; Williams, C.J.; Hardegree, S.P.; Havens, S.; Hedrick, A.; Bates, J.D.; Svejcar, T.J. Ecosystem Water Availability in Juniper versus Sagebrush Snow-Dominated Rangelands. Rangel. Ecol. Manag. 2017, 70, 116–128. [Google Scholar] [CrossRef]
- Petersen, S.L.; Stringham, T.K. Infiltration, Runoff, and Sediment Yield in Response to Western Juniper Encroachment in Southeast Oregon. Rangel. Ecol. Manag. 2008, 61, 74–81. [Google Scholar] [CrossRef]
- Bradley, B.A. Assessing Ecosystem Threats from Global and Regional Change: Hierarchical Modeling of Risk to Sagebrush Ecosystems from Climate Change, Land Use and Invasive Species in Nevada, USA. Ecography 2010, 33, 198–208. [Google Scholar] [CrossRef]
- Creutzburg, M.K.; Halofsky, J.E.; Halofsky, J.S.; Christopher, T.A. Climate Change and Land Management in the Rangelands of Central Oregon. Environ. Manag. 2015, 55, 43–55. [Google Scholar] [CrossRef] [PubMed]
- Valayamkunnath, P.; Sridhar, V.; Zhao, W.; Allen, R.G. A Comprehensive Analysis of Interseasonal and Interannual Energy and Water Balance Dynamics in Semiarid Shrubland and Forest Ecosystems. Sci. Total Environ. 2019, 651, 381–398. [Google Scholar] [CrossRef] [PubMed]
- Scott, R.L.; Biederman, J.A. Critical Zone Water Balance Over 13 Years in a Semiarid Savanna. Water Resour. Res. 2019, 55, 574–588. [Google Scholar] [CrossRef]
- Lewis, D.; Singer, M.J.; Dahlgren, R.A.; Tate, K.W. Hydrology in a California Oak Woodland Watershed: A 17-Year Study. J. Hydrol. 2000, 240, 106–117. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, D.L.; Anwar, M.R.; O’Leary, G.; Macadam, I.; Yang, Y. Water Use Efficiency and Crop Water Balance of Rainfed Wheat in a Semi-Arid Environment: Sensitivity of Future Changes to Projected Climate Changes and Soil Type. Theor. Appl. Climatol. 2016, 123, 565–580. [Google Scholar] [CrossRef]
- Kundu, S.; Khare, D.; Mondal, A. Past, Present and Future Land Use Changes and Their Impact on Water Balance. J. Environ. Manag. 2017, 197, 582–596. [Google Scholar] [CrossRef]
- Chauvin, G.M.; Flerchinger, G.N.; Link, T.E.; Marks, D.; Winstral, A.H.; Seyfried, M.S. Long-Term Water Balance and Conceptual Model of a Semi-Arid Mountainous Catchment. J. Hydrol. 2011, 400, 133–143. [Google Scholar] [CrossRef]
- Marc, V.; Robinson, M. The Long-Term Water Balance (1972–2004) of Upland Forestry and Grassland at Plynlimon, Mid-Wales. Hydrol. Earth Syst. Sci. 2007, 11, 44–60. [Google Scholar] [CrossRef]
- Ward, A.S.; Gooseff, M.N.; Voltz, T.J.; Fitzgerald, M.; Singha, K.; Zarnetske, J.P. How Does Rapidly Changing Discharge during Storm Events Affect Transient Storage and Channel Water Balance in a Headwater Mountain Stream? Water Resour. Res. 2013, 49, 5473–5486. [Google Scholar] [CrossRef]
- Wang, D.; Alimohammadi, N. Responses of Annual Runoff, Evaporation, and Storage Change to Climate Variability at the Watershed Scale. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- do Nascimento, M.G.; Herdies, D.L.; de Souza, D.O. The South American Water Balance: The Influence of Low-Level Jets. J. Clim. 2016, 29, 1429–1449. [Google Scholar] [CrossRef]
- Weltz, M.A.; Blackburn, W.H. Water Budget for South Texas Rangelands. J. Range Manag. 1995, 48, 45–52. [Google Scholar] [CrossRef]
- Wilcox, B.P.; Dowhower, S.L.; Teague, W.R.; Thurow, T.L. Long-Term Water Balance in a Semiarid Shrubland. Rangel. Ecol. Manag. 2006, 59, 600–606. [Google Scholar] [CrossRef]
- Bugan, R.; Jovanovic, N.; De Clercq, W. The Water Balance of a Seasonal Stream in the Semi-Arid Western Cape (South Africa). WSA 2012, 38, 201–212. [Google Scholar] [CrossRef]
- Cantón, Y.; Villagarcía, L.; Moro, M.J.; Serrano-Ortíz, P.; Were, A.; Alcalá, F.J.; Kowalski, A.S.; Solé-Benet, A.; Lázaro, R.; Domingo, F. Temporal Dynamics of Soil Water Balance Components in a Karst Range in Southeastern Spain: Estimation of Potential Recharge. Hydrol. Sci. J. 2010, 55, 737–753. [Google Scholar] [CrossRef][Green Version]
- Deus, D.; Gloaguen, R.; Krause, P. Water Balance Modeling in a Semi-Arid Environment with Limited in Situ Data Using Remote Sensing in Lake Manyara, East African Rift, Tanzania. Remote Sens. 2013, 5, 1651–1680. [Google Scholar] [CrossRef]
- Eilers, V.H.M.; Carter, R.C.; Rushton, K.R. A Single Layer Soil Water Balance Model for Estimating Deep Drainage (Potential Recharge): An Application to Cropped Land in Semi-Arid North-East Nigeria. Geoderma 2007, 140, 119–131. [Google Scholar] [CrossRef]
- Ochoa, C.; Caruso, P.; Ray, G.; Deboodt, T.; Jarvis, W.; Guldan, S. Ecohydrologic Connections in Semiarid Watershed Systems of Central Oregon USA. Water 2018, 10, 181. [Google Scholar] [CrossRef]
- Ray, G.; Ochoa, C.G.; Deboodt, T.; Mata-Gonzalez, R. Overstory–Understory Vegetation Cover and Soil Water Content Observations in Western Juniper Woodlands: A Paired Watershed Study in Central Oregon, USA. Forests 2019, 10, 151. [Google Scholar] [CrossRef]
- Mollnau, C.; Newton, M.; Stringham, T. Soil Water Dynamics and Water Use in a Western Juniper (Juniperus Occidentalis) Woodland. J. Arid Environ. 2014, 102, 117–126. [Google Scholar] [CrossRef]
- Abdallah, M.A.B.; Durfee, N.; Mata-Gonzalez, R.; Ochoa, C.G.; Noller, J.S. Water Use and Soil Moisture Relationships on Western Juniper Trees at Different Growth Stages. Water 2020, 26, 1596. [Google Scholar] [CrossRef]
- Angell, R.F.; Miller, R.F. Simulation of Leaf Conductance and Transpiration in Juniperus Occidentalis. For. Sci. 1994, 40, 5–17. [Google Scholar]
- Scott, R.L. Using Watershed Water Balance to Evaluate the Accuracy of Eddy Covariance Evaporation Measurements for Three Semiarid Ecosystems. Agric. For. Meteorol. 2010, 150, 219–225. [Google Scholar] [CrossRef]
- Todd, R.W.; Evett, S.R.; Howell, T.A. The Bowen Ratio-Energy Balance Method for Estimating Latent Heat Flux of Irrigated Alfalfa Evaluated in a Semi-Arid, Advective Environment. Agric. For. Meteorol. 2000, 103, 335–348. [Google Scholar] [CrossRef]
- Valayamkunnath, P.; Sridhar, V.; Zhao, W.; Allen, R.G. Intercomparison of Surface Energy Fluxes, Soil Moisture, and Evapotranspiration from Eddy Covariance, Large-Aperture Scintillometer, and Modeling across Three Ecosystems in a Semiarid Climate. Agric. For. Meteorol. 2018, 248, 22–47. [Google Scholar] [CrossRef]
- Yeşilırmak, E. Temporal Changes of Warm-Season Pan Evaporation in a Semi-Arid Basin in Western Turkey. Stoch. Environ. Res. Risk Assess. 2013, 27, 311–321. [Google Scholar] [CrossRef]
- López-Urrea, R.; Martín de Santa Olalla, F.; Fabeiro, C.; Moratalla, A. Testing Evapotranspiration Equations Using Lysimeter Observations in a Semiarid Climate. Agric. Water Manag. 2006, 85, 15–26. [Google Scholar] [CrossRef]
- Kume, T.; Otsuki, K.; Du, S.; Yamanaka, N.; Wang, Y.-L.; Liu, G.-B. Spatial Variation in Sap Flow Velocity in Semiarid Region Trees: Its Impact on Stand-Scale Transpiration Estimates. Hydrol. Process. 2012, 26, 1161–1168. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Todorovic, M.; Karic, B.; Pereira, L.S. Reference Evapotranspiration Estimate with Limited Weather Data across a Range of Mediterranean Climates. J. Hydrol. 2013, 481, 166–176. [Google Scholar] [CrossRef]
- Raziei, T.; Pereira, L.S. Estimation of ETo with Hargreaves–Samani and FAO-PM Temperature Methods for a Wide Range of Climates in Iran. Agric. Water Manag. 2013, 121, 1–18. [Google Scholar] [CrossRef]
- Thornthwaite, C.; Mather, J. The Water Balance, Climatology, VIII(1); Drexel Institute of Technology, Laboratory of Climatology: Centerton, NJ, USA, 1955. [Google Scholar]
- Thornthwaite, C.W.; Mather, J.R. Instructions and Tables for Computing Potential Evapotranspiration and the Water Balance; Laboratory of Climatology: Centerton, NJ, USA, 1957; Volume 10, 132p. [Google Scholar]
- Gudulas, K.; Voudouris, K.; Soulios, G.; Dimopoulos, G. Comparison of Different Methods to Estimate Actual Evapo-transpiration and Hydrologic Balance. Desalination and Water Treatment 2013, 51, 2945–2954. [Google Scholar] [CrossRef]
- Alley, W.M. On the Treatment of Evapotranspiration, Soil Moisture Accounting, and Aquifer Recharge in Monthly Water Balance Models. Water Resour. Res. 1984, 20, 1137–1149. [Google Scholar] [CrossRef]
- Barlow, P.; Leake, S. Streamflow Depletion by Wells: Understanding and Managing Effects of Groundwater Pumping on Streamflow; Circular 1376; US Geological Survey: Reston, VA, USA, 2012.
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; Van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M.; et al. Ground Water and Climate Change. Nat. Clim. Chang. 2013, 3, 322–329. [Google Scholar] [CrossRef]
- Sophocleous, M. Interactions between Groundwater and Surface Water: The State of the Science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Ochoa, C.G.; Fernald, A.G.; Guldan, S.J.; Tidwell, V.C.; Shukla, M.K. Shallow Aquifer Recharge from Irrigation in a Semiarid Agricultural Valley in New Mexico. J. Hydrol. Eng. 2013, 18, 1219–1230. [Google Scholar] [CrossRef]
- Caruso, P.; Ochoa, C.G.; Jarvis, W.T.; Deboodt, T. A Hydrogeologic Framework for Understanding Local Groundwater Flow Dynamics in the Southeast Deschutes Basin, Oregon, USA. Geosciences 2019, 9, 57. [Google Scholar] [CrossRef]
- Seyfried, M.S.; Schwinning, S.; Walvoord, M.A.; Pockman, W.T.; Newman, B.D.; Jackson, R.B.; Phillips, F.M. Ecohydrological Control of Deep Drainage in Arid and Semiarid Regions. Ecology 2005, 86, 277–287. [Google Scholar] [CrossRef]
- Ryel, R.J.; Caldwell, M.M.; Leffler, A.J.; Yoder, C.K. Rapid Soil Moisture Recharge to Depth by Roots in a Stand of Artemisia Tridentata. Ecology 2003, 84, 757–764. [Google Scholar] [CrossRef]
- Flerchinger, G.N.; Cooley, K.R. A Ten-Year Water Balance of a Mountainous Semi-Arid Watershed. J. Hydrol. 2000, 237, 86–99. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Healy, R.W.; Cook, P.G. Choosing Appropriate Techniques for Quantifying Groundwater Recharge. Hydrogeol. J. 2002, 10, 347. [Google Scholar] [CrossRef]
- Kendy, E.; Gérard-Marchant, P.; Walter, M.T.; Zhang, Y.; Liu, C.; Steenhuis, T.S. A Soil-Water-Balance Approach to Quantify Groundwater Recharge from Irrigated Cropland in the North China Plain. Hydrol. Process. 2003, 17, 2011–2031. [Google Scholar] [CrossRef]
- Okumura, A.; Hosono, T.; Boateng, D.; Shimada, J. Evaluations of the Downward Velocity of Soil Water Movement in the Unsaturated Zone in a Groundwater Recharge Area Using Δ18 O Tracer: The Kumamoto Region, Southern Japan. Geol. Croat. 2018, 71, 65–82. [Google Scholar] [CrossRef]
- Sammis, T.W.; Evans, D.D.; Warrick, A.W. Comparison of Methods to Estimate Deep Percolation Rates1. JAWRA J. Am. Water Resour. Assoc. 1982, 18, 465–470. [Google Scholar] [CrossRef]
- Healy, R.W.; Cook, P.G. Using Groundwater Levels to Estimate Recharge. Hydrogeol. J. 2002, 10, 91–109. [Google Scholar] [CrossRef]
- Jassas, H.; Merkel, B. Estimating Groundwater Recharge in the Semiarid Al-Khazir Gomal Basin, North Iraq. Water 2014, 6, 2467–2481. [Google Scholar] [CrossRef]
- Risser, D.W.; Gburek, W.J.; Folmar, G.J. Comparison of Recharge Estimates at a Small Watershed in East-Central Pennsylvania, USA. Hydrogeol. J. 2009, 17, 287–298. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, G.; Xu, Y.J. Spatiotemporal Groundwater Recharge Estimation for the Largest Rice Production Region in Sanjiang Plain, Northeast China. J. Water Supply Res. Technol.—AQUA 2014, 63, 630–641. [Google Scholar] [CrossRef]
- Acharya, B.S.; Kharel, G.; Zou, C.B.; Wilcox, B.P.; Halihan, T. Woody Plant Encroachment Impacts on Groundwater Recharge: A Review. Water 2018, 10, 1466. [Google Scholar] [CrossRef]
- Moore, G.W.; Barre, D.A.; Owens, M.K. Does Shrub Removal Increase Groundwater Recharge in Southwestern Texas Semiarid Rangelands? Rangel. Ecol. Manag. 2012, 65, 1–10. [Google Scholar] [CrossRef]
- Anderson, E.W.; Borman, M.M.; Krueger, W.C. The Ecological Provinces of Oregon: A Treatise on the Basic Ecological Geography of the State; SR 990; Oregon Agricultural Experiment Station, Oregon State University: Corvallis, OR, USA, 1998. [Google Scholar]
- Durfee, N.; Ochoa, C.G.; Mata-Gonzalez, R. The Use of Low-Altitude UAV Imagery to Assess Western Juniper Density and Canopy Cover in Treated and Untreated Stands. Forests 2019, 10, 296. [Google Scholar] [CrossRef]
- Ray, G.L. Long-term Ecohydrologic Response to Western Juniper (Juniperus occidentalis) Control in Semiarid Watersheds of Central Oregon: A Paired Watershed Study. Master’s Thesis, Oregon State University, Corvallis, OR, USA, 2015. [Google Scholar]
- Bates, J.D.; Svejcar, T.; Miller, R.; Davies, K.W. Plant Community Dynamics 25 Years after Juniper Control. Rangel. Ecol. Manag. 2017, 70, 356–362. [Google Scholar] [CrossRef]
- Cooperative Climatological Data Summaries, Western Regional Climate Center. Available online: http://www.wrcc.dri.edu/cgi-bin/cliMAIN.pl?or0501 (accessed on 10 December 2020).
- Fisher, M. Analysis of Hydrology and Erosion in Small, Paired Watersheds in a Juniper-Sagebrush Area of Central Oregon. Ph.D. Thesis, Oregon State University, Corvallis, OR, USA, 2004. [Google Scholar]
- Soil Survey Staff Natural Resources Conservation Service Official Soil Series Descriptions (OSDs) | NRCS Soils. Available online: https://www.nrcs.usda.gov/wps/portal/nrcs/detail/soils/home/?cid=nrcs142p2_053587 (accessed on 13 May 2018).
- USDA Natural Resources Conservation Service. SNOwpack TELemetry Network (SNOTEL). NRCS. 2021. Available online: https://data.nal.usda.gov/dataset/snowpack-telemetry-network-snotel (accessed on 18 September 2021).
- Kilpatrick, F.A.; Schneider, V.R. Use of Flumes in Measuring Discharge; Techniques of Water-Resources Investigations; US Government Printing Office: Washington, DC, USA, 1983.
- Samani, Z. Discussion of “History and Evaluation of Hargreaves Evapotranspiration Equation”by George H. Hargreaves and Richard G. Allen. J. Irrig. Drain Eng. 2004, 130, 447–448. [Google Scholar] [CrossRef]
- Dingman, S.L. Physical Hydrology, 3rd ed.; Waveland Press, Inc.: Long Grove, IL, USA, 2015. [Google Scholar]
- Deboodt, T.L. Watershed Response to Western Juniper Control. Ph.D. Thesis, Oregon State University, Corvallis, OR, USA, 2008. [Google Scholar]
- Brooks, K.N.; Ffolliott, P.F.; Gregersen, H.M.; Debano, L.F. Groundwater. In Hydrology and the Management of Watersheds; Iowa State Press: Ames, IA, USA, 2003; pp. 107–121. [Google Scholar]
- Dilts, T.E.; Weisberg, P.J.; Dencker, C.M.; Chambers, J.C. Functionally Relevant Climate Variables for Arid Lands: A Climatic Water Deficit Approach for Modelling Desert Shrub Distributions. J. Biogeogr. 2015, 42, 1986–1997. [Google Scholar] [CrossRef]
- Lesica, P.; Kittelson, P.M. Precipitation and Temperature Are Associated with Advanced Flowering Phenology in a Semi-Arid Grassland. J. Arid Environ. 2010, 74, 1013–1017. [Google Scholar] [CrossRef]
- Niemeyer, R.J.; Link, T.E.; Seyfried, M.S.; Flerchinger, G.N. Surface Water Input from Snowmelt and Rain Throughfall in Western Juniper: Potential Impacts of Climate Change and Shifts in Semi-Arid Vegetation. Hydrol. Process. 2016, 30, 3046–3060. [Google Scholar] [CrossRef]
- Yaseef, N.R.; Yakir, D.; Rotenberg, E.; Schiller, G.; Cohen, S. Ecohydrology of a semi-arid forest: Partitioning among water balance components and its implications for predicted precipitation changes. Ecohydrology 2010, 3, 143–154. [Google Scholar] [CrossRef]
- Kwon, H.; Pendall, E.; Ewers, B.E.; Cleary, M.; Naithani, K. Spring Drought Regulates Summer Net Ecosystem CO2 Exchange in a Sagebrush-Steppe Ecosystem. Agric. For. Meteorol. 2008, 148, 381–391. [Google Scholar] [CrossRef]
- Young, J.A.; Evans, R.A.; Easi, D.A. Stem Flow on Western Juniper (Juniperus Occidentalis) Trees. Weed Sci. 1984, 32, 320–327. [Google Scholar] [CrossRef]
- Sturges, D.L.; Trlica, M.J. Root Weights and Carbohydrate Reserves of Big Sagebrush. Ecology 1978, 59, 1282–1285. [Google Scholar] [CrossRef]
- Blarasin, M.; Quinodóz, F.B.; Cabrera, A.; Matteoda, E.; Alincastro, N.; Albo, G. Weekly and Monthly Groundwater Recharge Estimation in A Rural Piedmont Environment Using the Water Table Fluctuation Method. Int. J. Environ. Agric. Res. 2016, 2, 10. [Google Scholar]
- Rutledge, A.T. Computer Programs for Describing the Recession of Ground-Water Discharge and for Estimating Mean Ground-Water Recharge and Discharge from Streamflow Records-Update; Water-Resources Investigations Report; Supercedes WRI 93-4121; US Geological Survey: Reston, VA, USA, 1998.
- Delin, G.N.; Healy, R.W.; Lorenz, D.L.; Nimmo, J.R. Comparison of Local- to Regional-Scale Estimates of Ground-Water Recharge in Minnesota, USA. J. Hydrol. 2007, 334, 231–249. [Google Scholar] [CrossRef]



| Mays WS | Jensen WS | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Water Year | PET | P | Q | Δθ | ETA | DP | P | Q | Δθ | ETA | DP |
| 2014 Q1 | 47.9 | 35.8 | 0.0 | −29.3 | 47.9 | 17.2 | 26.1 | 0.0 | −18.3 | 44.4 | 0.0 |
| 2014 Q2 | 46.2 | 111.5 | 0.4 | 63.1 | 46.2 | 1.8 | 100.8 | 0.0 | 56.6 | 44.2 | 0.0 |
| 2014 Q3 | 233.8 | 67.3 | 0.0 | −27.8 | 95.1 | 0.0 | 60.2 | 0.0 | −25.6 | 85.8 | 0.0 |
| 2014 Q4 | 287.3 | 51.3 | 0.4 | −14.5 | 65.4 | 0.0 | 30.5 | 0.0 | −10.3 | 40.8 | 0.0 |
| 2014 Total | 615.2 | 265.9 | 0.8 | −8.5 | 254.6 | 19.0 | 217.6 | 0.0 | 2.4 | 215.2 | 0.0 |
| 2015 Q1 | 46.6 | 169.9 | 0.0 | 36.8 | 46.6 | 86.5 | 165.6 | 0.0 | 53.2 | 46.6 | 65.8 |
| 2015 Q2 | 56.8 | 69.3 | 24.1 | 20.9 | 24.3 | 0.0 | 78.2 | 0.0 | 15.5 | 56.8 | 5.9 |
| 2015 Q3 | 224.9 | 59.4 | 0.0 | −31.3 | 90.7 | 0.0 | 54.6 | 0.0 | −40.0 | 94.6 | 0.0 |
| 2015 Q4 | 286.6 | 42.9 | 0.0 | −27.0 | 69.9 | 0.0 | 44.7 | 0.0 | −27.5 | 72.2 | 0.0 |
| 2015 Total | 614.9 | 341.6 | 24.1 | −0.6 | 231.6 | 86.5 | 343.2 | 0.0 | 1.2 | 270.2 | 71.7 |
| 2016 Q1 | 44.2 | 129.3 | 0.0 | 25.7 | 44.2 | 78.2 | 111.5 | 0.0 | 42.1 | 44.2 | 25.2 |
| 2016 Q2 | 41.8 | 97.8 | 19.9 | 35.2 | 41.8 | 0.9 | 111.3 | 0.0 | 32.8 | 41.8 | 36.6 |
| 2016 Q3 | 232.4 | 69.3 | 4.1 | −11.4 | 121.9 | 0.0 | 64.5 | 0.0 | −29.4 | 93.9 | 0.0 |
| 2016 Q4 | 305.8 | 1.8 | 0.0 | −42.5 | 44.3 | 0.0 | 12.2 | 0.0 | −43.1 | 55.3 | 0.0 |
| 2016 Total | 624.3 | 298.2 | 24.0 | 7.0 | 252.1 | 79.1 | 299.5 | 0.0 | 2.4 | 235.2 | 61.8 |
| 2017 Q1 | 44.0 | 116.6 | 0.0 | −2.1 | 44.0 | 74.7 | 125.5 | 0.0 | 5.8 | 44.0 | 75.7 |
| 2017 Q2 | 37.6 | 169.1 | 26.1 | 86.1 | 37.6 | 45.8 | 156.0 | 1.5 | 88.6 | 37.6 | 28.3 |
| 2017 Q3 | 220.2 | 75.4 | 35.3 | −43.7 | 83.8 | 0.0 | 73.9 | 2.1 | −48.4 | 120.2 | 0.0 |
| 2017 Q4 | 332.4 | 15.0 | 0.8 | −30.5 | 44.7 | 0.0 | 14.0 | 0.1 | −32.8 | 46.7 | 0.0 |
| 2017 Total | 634.1 | 376.1 | 62.2 | 9.8 | 210.1 | 120.5 | 369.3 | 3.7 | 13.2 | 248.5 | 103.9 |
| 2018 Q1 | 52.4 | 55.0 | 0.0 | −10.0 | 52.4 | 12.6 | 68.4 | 0.0 | −9.4 | 52.4 | 25.4 |
| 2018 Q2 | 43.6 | 61.0 | 0.0 | 51.4 | 9.6 | 0.0 | 72.9 | 0.0 | 49.7 | 23.2 | 0.0 |
| 2018 Q3 | 223.1 | 82.8 | 0.0 | −26.4 | 109.2 | 0.0 | 80.1 | 0.5 | −20.1 | 99.7 | 0.0 |
| 2018 Q4 | 364.0 | 27.5 | 0.0 | −31.6 | 59.1 | 0.0 | 4.1 | 0.1 | −21.5 | 25.5 | 0.0 |
| 2018 Total | 683.0 | 226.3 | 0.0 | −16.6 | 230.3 | 12.6 | 225.5 | 0.6 | −1.3 | 200.7 | 25.4 |
| 2019 Q1 | 54.2 | 74.7 | 0.0 | 15.4 | 54.2 | 5.1 | 80.3 | 0.0 | −1.1 | 54.2 | 27.2 |
| 2019 Q2 | 50.0 | 108.0 | 1.0 | 94.1 | 12.9 | 0.0 | 101.7 | 2.4 | 70.3 | 29.0 | 0.0 |
| 2019 Q3 | 207.9 | 83.2 | 26.7 | −45.0 | 101.5 | 0.0 | 77.8 | 1.1 | −29.2 | 105.9 | 0.0 |
| 2019 Q4 | 288.3 | 60.3 | 0.0 | −30.9 | 91.2 | 0.0 | 71.6 | 0.0 | −28.0 | 99.6 | 0.0 |
| 2019 Total | 600.4 | 326.1 | 27.7 | 33.6 | 259.8 | 5.1 | 331.4 | 3.5 | 12.0 | 288.8 | 27.2 |
| 2020 Q1 | 45.6 | 87.6 | 0.0 | 17.4 | 45.6 | 24.7 | 70.1 | 0.0 | 11.5 | 45.6 | 12.9 |
| 2020 Q2 | 46.0 | 88.3 | 0.0 | 61.9 | 26.4 | 0.0 | 73.5 | 0.0 | 31.6 | 41.9 | 0.0 |
| 2020 Q3 | 187.9 | 81.0 | 0.0 | −68.7 | 149.7 | 0.0 | 66.0 | 0.0 | −38.7 | 104.7 | 0.0 |
| 2020 Q4 | 306.8 | 9.0 | 0.0 | −25.7 | 34.7 | 0.0 | 8.3 | 0.0 | −16.2 | 24.5 | 0.0 |
| 2020 Total | 586.3 | 265.9 | 0.0 | −15.2 | 256.4 | 24.7 | 217.8 | 0.0 | −11.8 | 216.7 | 12.9 |
| Mays WS | Jensen WS | |||
|---|---|---|---|---|
| Water Year | ReGW | P | ReGW | P |
| 2014 | 276 | 266 | 219 | 218 |
| 2015 | 862 | 342 | 659 | 343 |
| 2016 | 862 | 298 | 1311 | 300 |
| 2017 | 1263 | 376 | 1441 | 369 |
| 2018 | 0 | 226 | 35 | 226 |
| 2019 | 1371 | 326 | 1360 | 331 |
| 2020 | 318 | 266 | 632 | 218 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Durfee, N.; Ochoa, C.G. The Seasonal Water Balance of Western-Juniper-Dominated and Big-Sagebrush-Dominated Watersheds. Hydrology 2021, 8, 156. https://doi.org/10.3390/hydrology8040156
Durfee N, Ochoa CG. The Seasonal Water Balance of Western-Juniper-Dominated and Big-Sagebrush-Dominated Watersheds. Hydrology. 2021; 8(4):156. https://doi.org/10.3390/hydrology8040156
Chicago/Turabian StyleDurfee, Nicole, and Carlos G. Ochoa. 2021. "The Seasonal Water Balance of Western-Juniper-Dominated and Big-Sagebrush-Dominated Watersheds" Hydrology 8, no. 4: 156. https://doi.org/10.3390/hydrology8040156
APA StyleDurfee, N., & Ochoa, C. G. (2021). The Seasonal Water Balance of Western-Juniper-Dominated and Big-Sagebrush-Dominated Watersheds. Hydrology, 8(4), 156. https://doi.org/10.3390/hydrology8040156







