Estimation of Peak Discharges under Different Rainfall Depth–Duration–Frequency Formulations
Abstract
1. Introduction
2. Study Area and Dataset
3. Methodology
3.1. Formulations of DDF/IDF Curves
3.2. Error Measures
3.3. SCS-CN Method
Application of SCS-CN Method
4. Results and Discussion
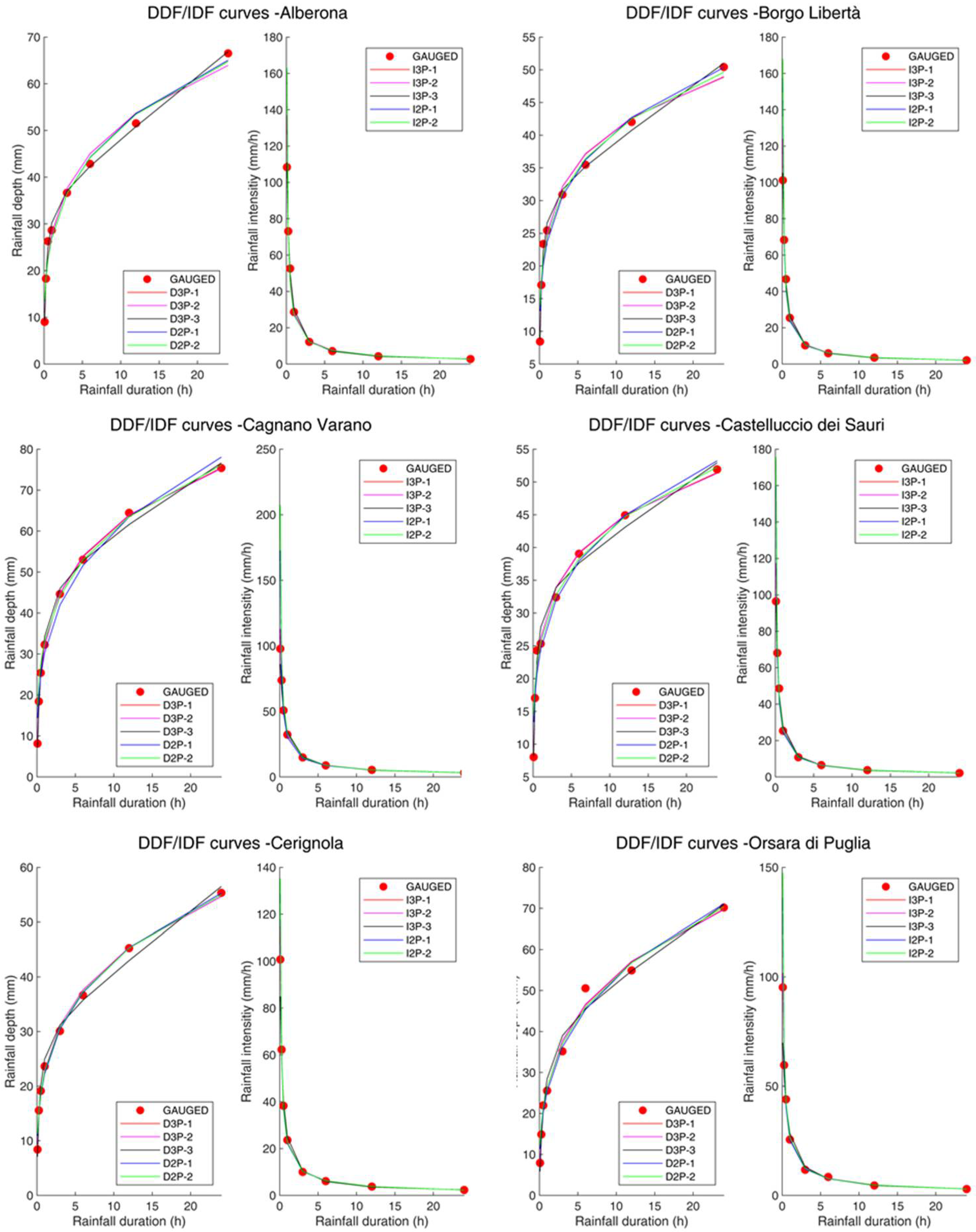
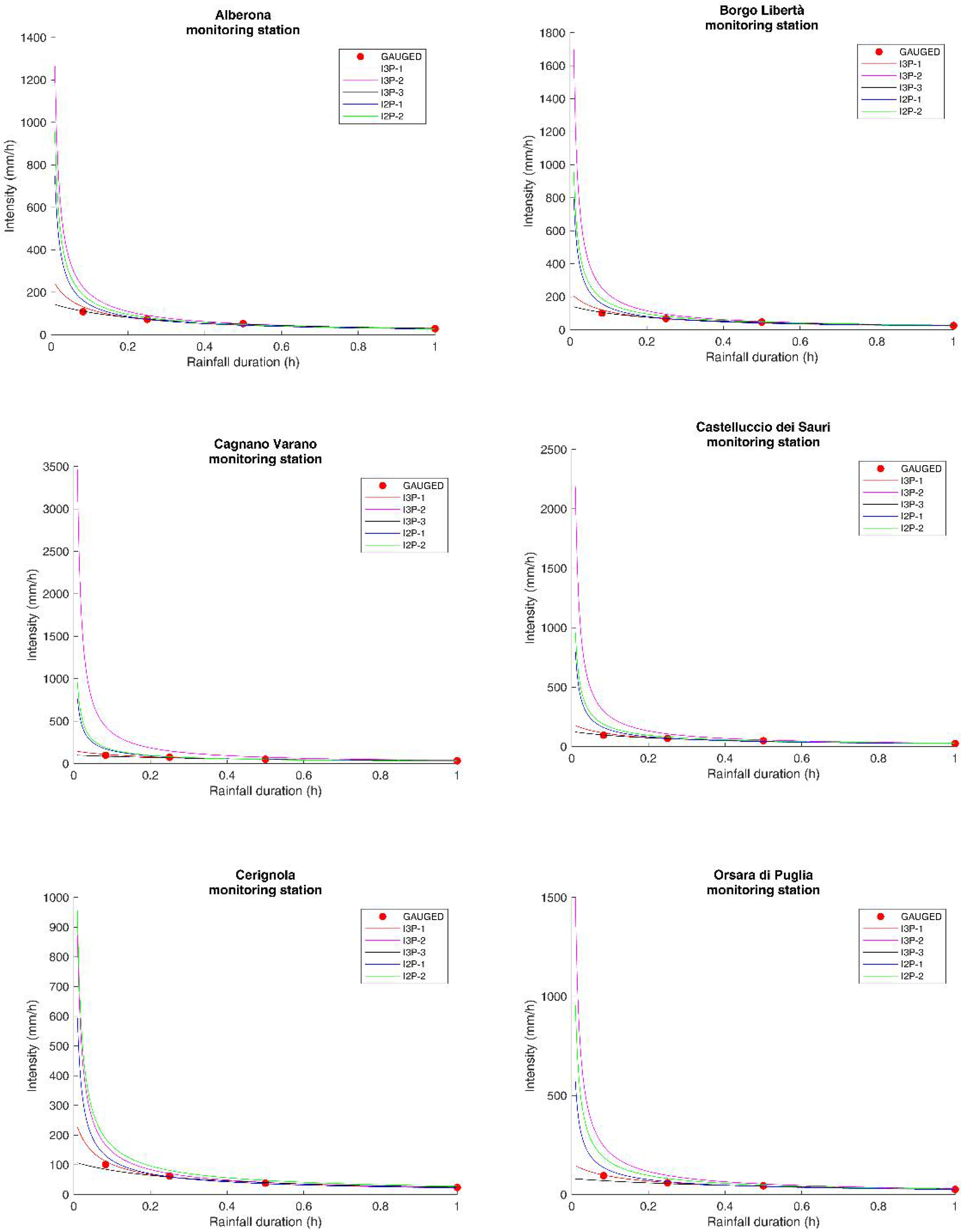
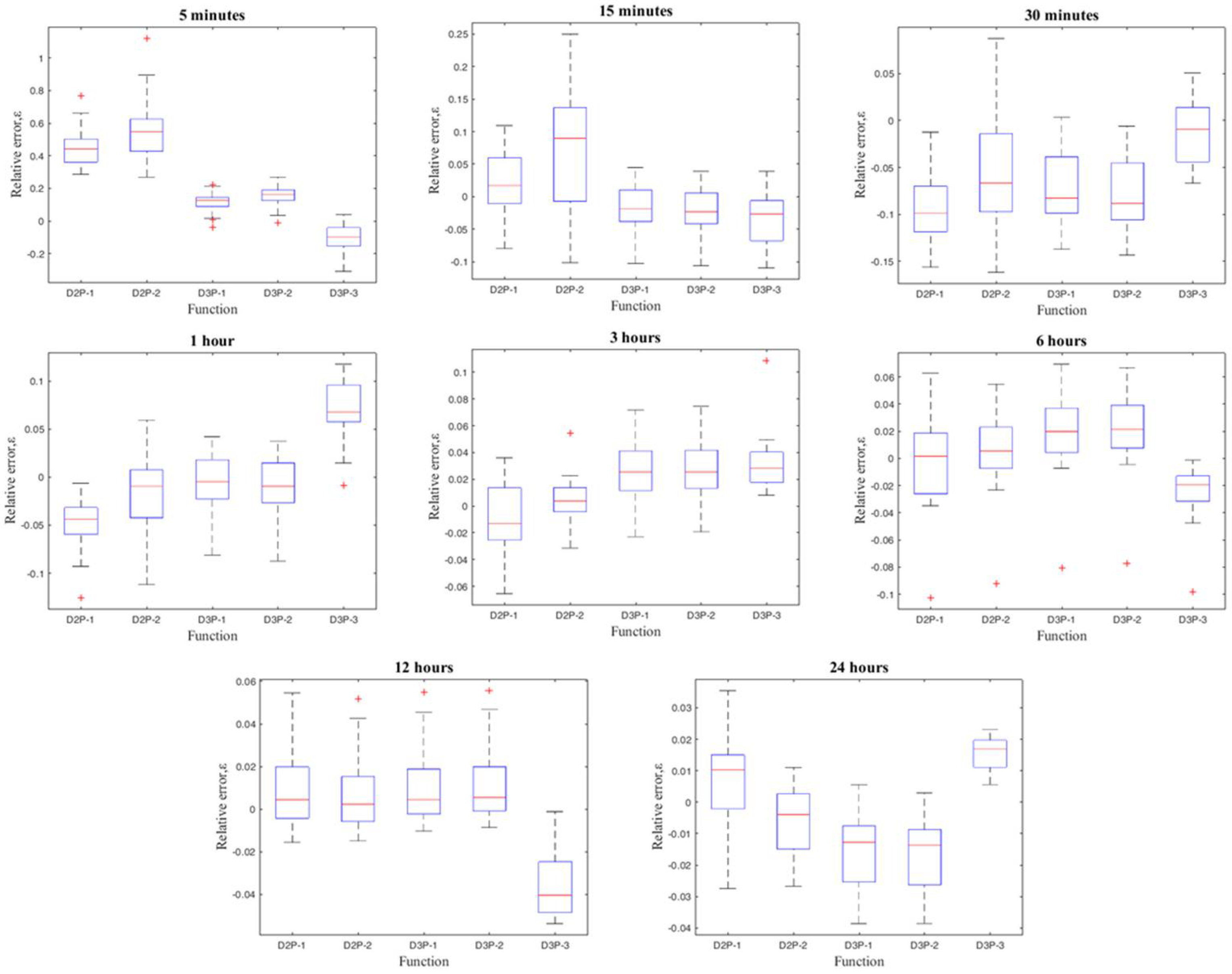
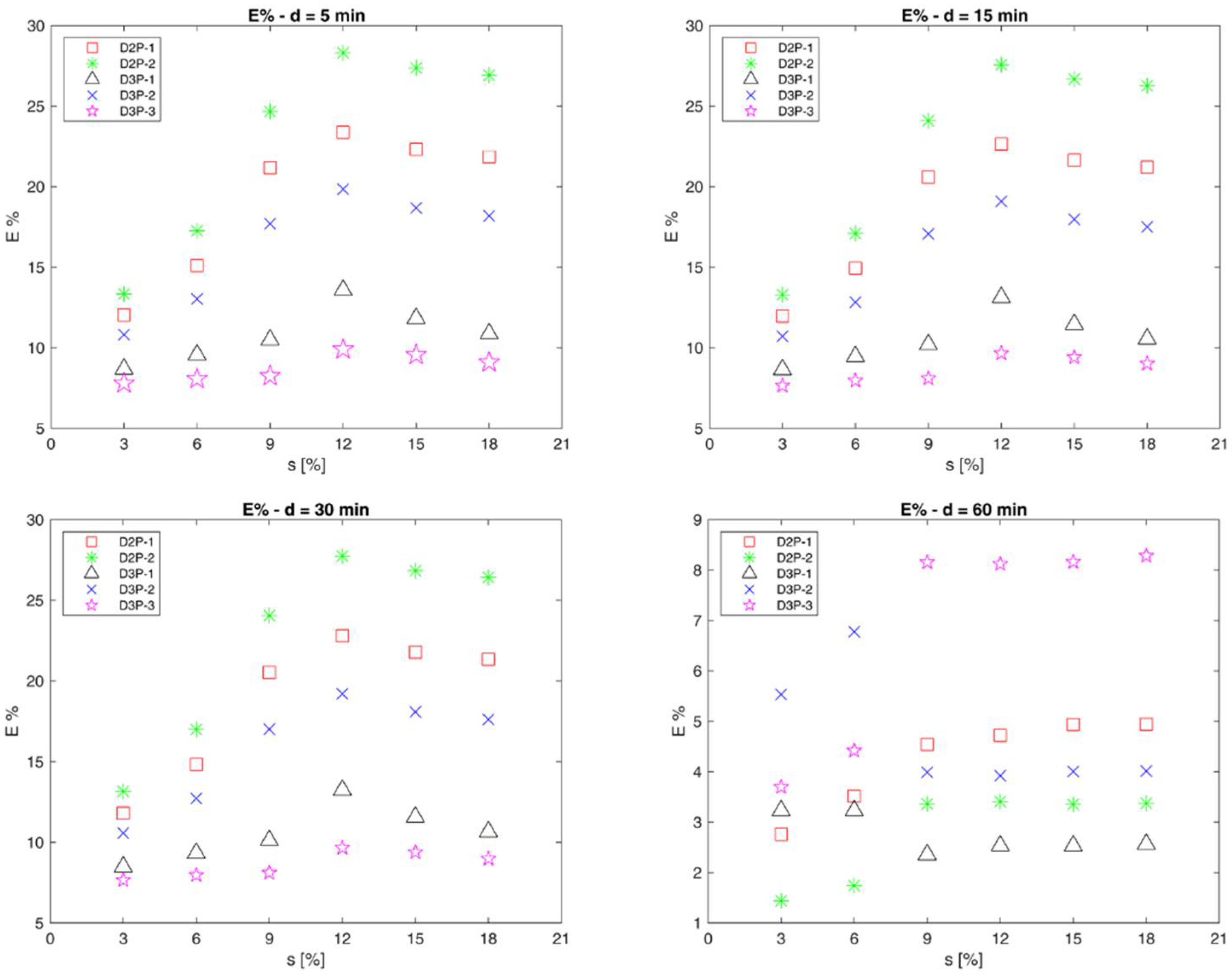
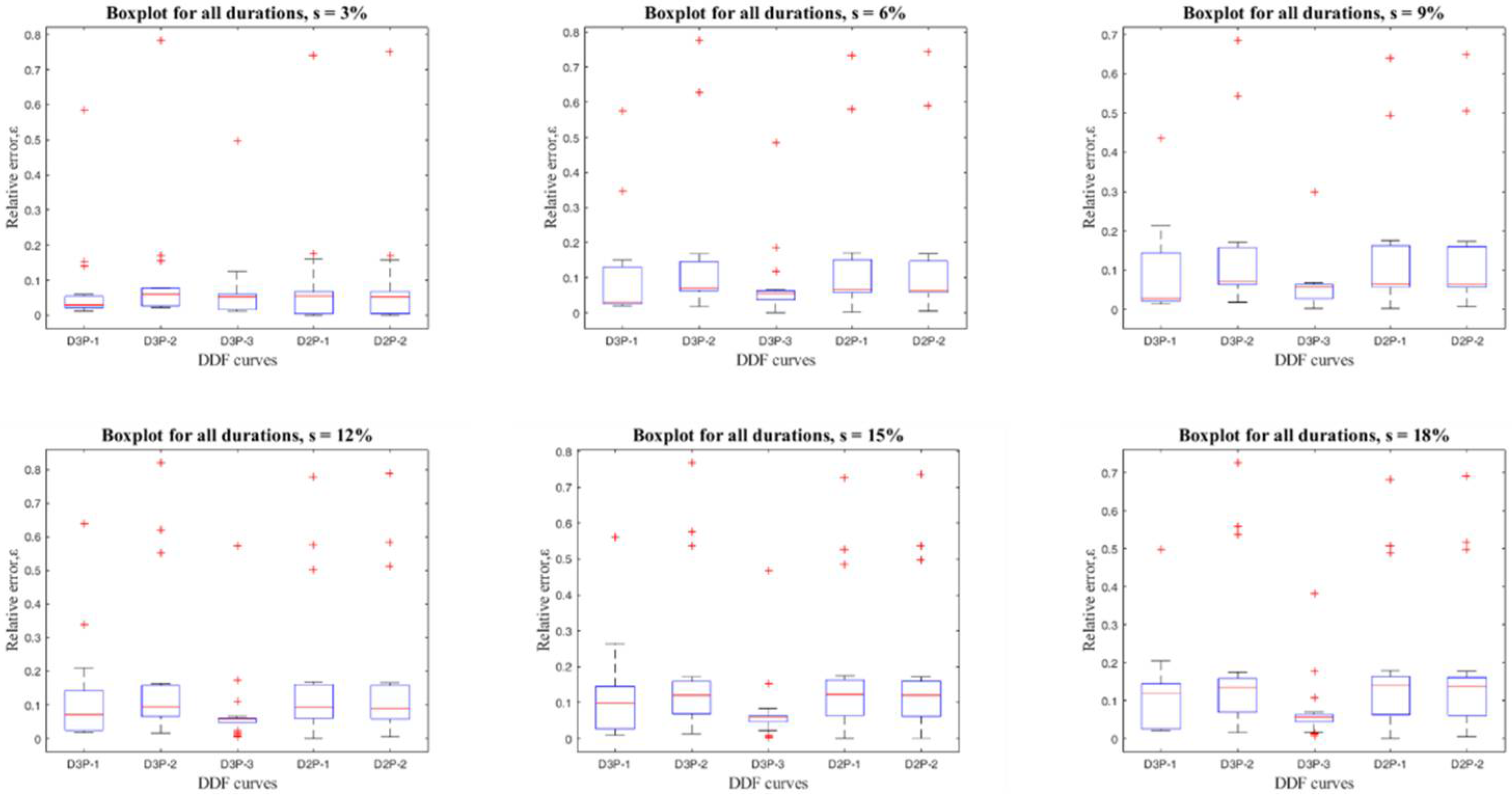
4.1. Results of DDFs Error Measures
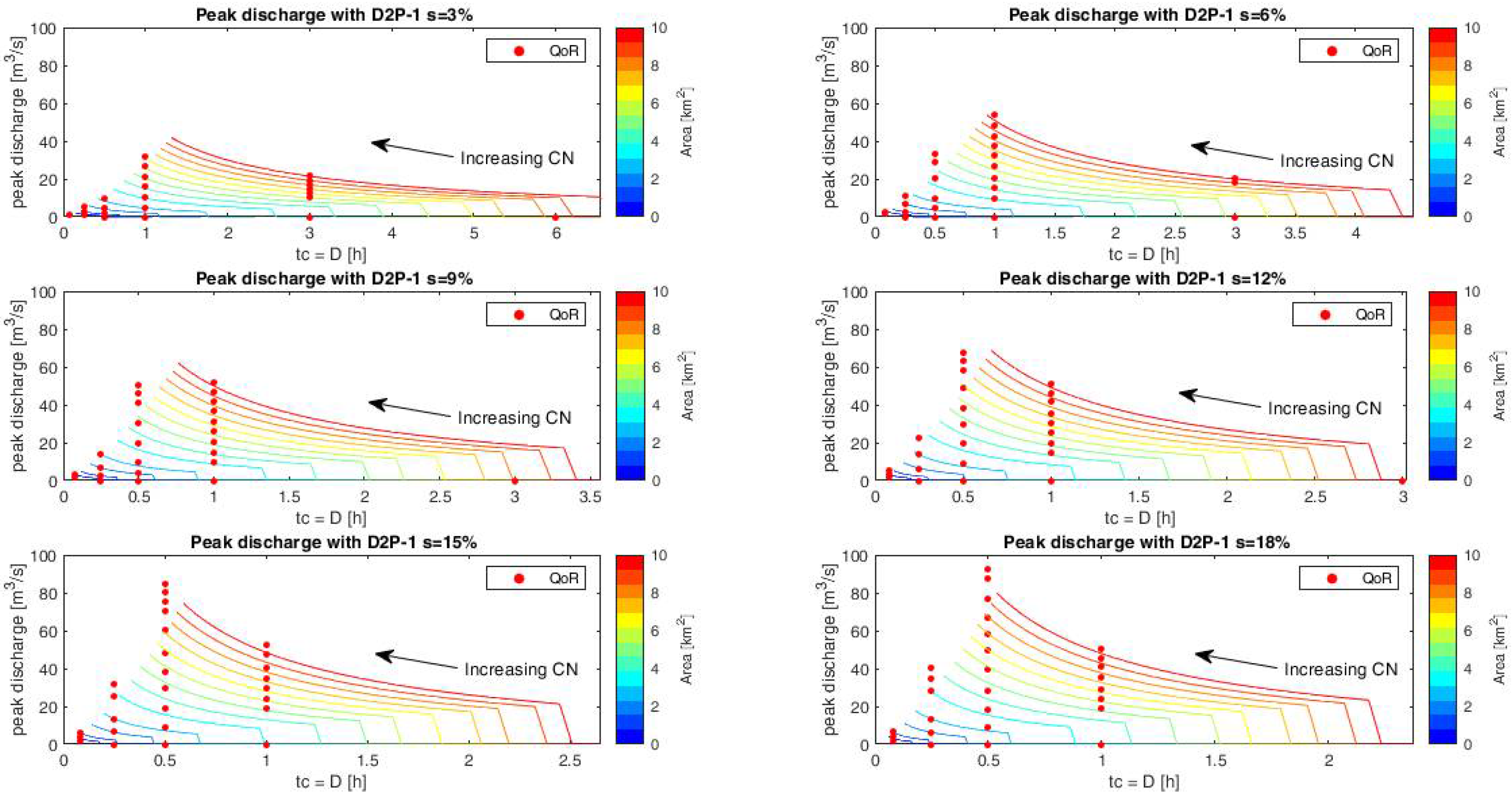
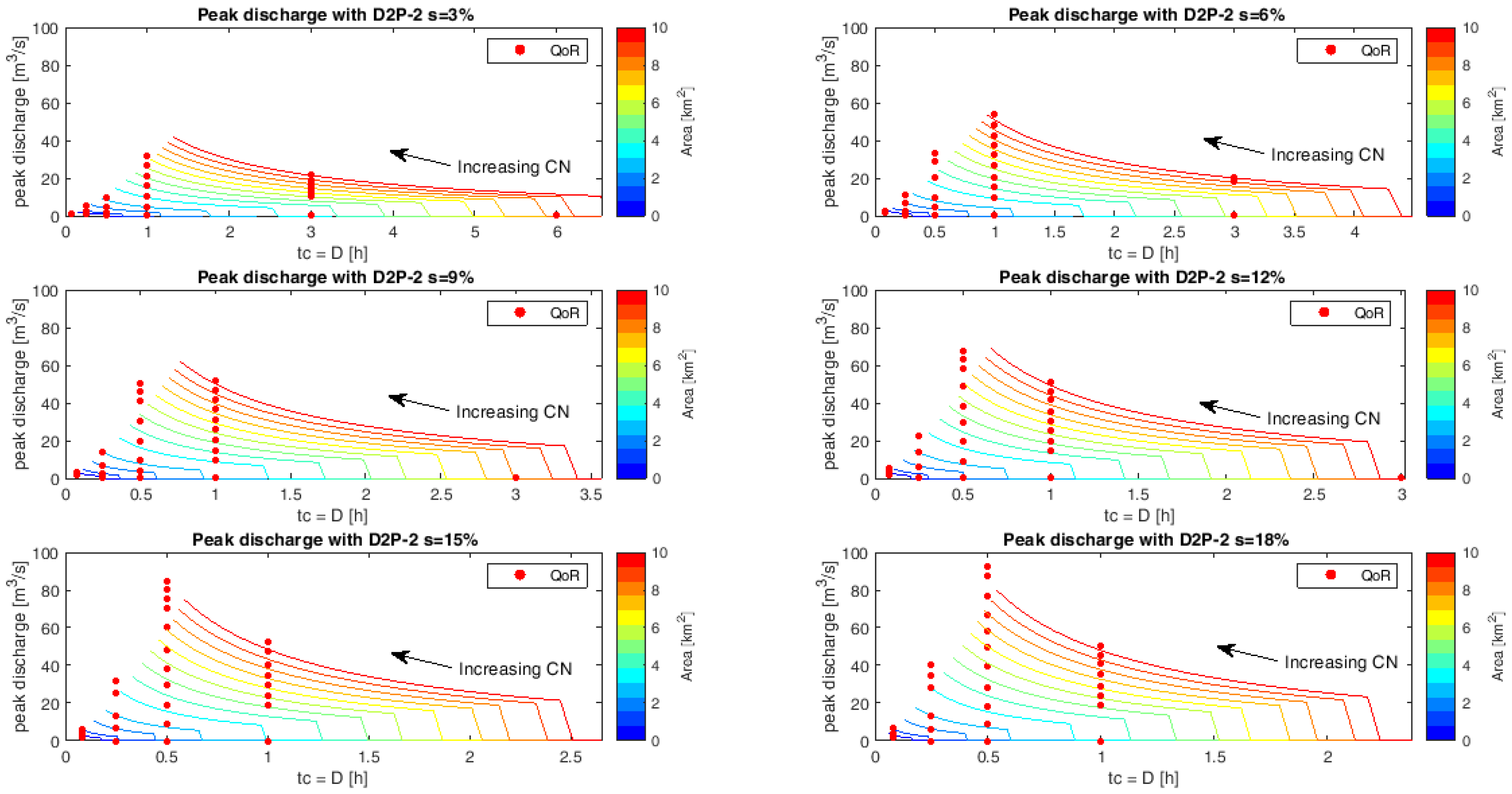
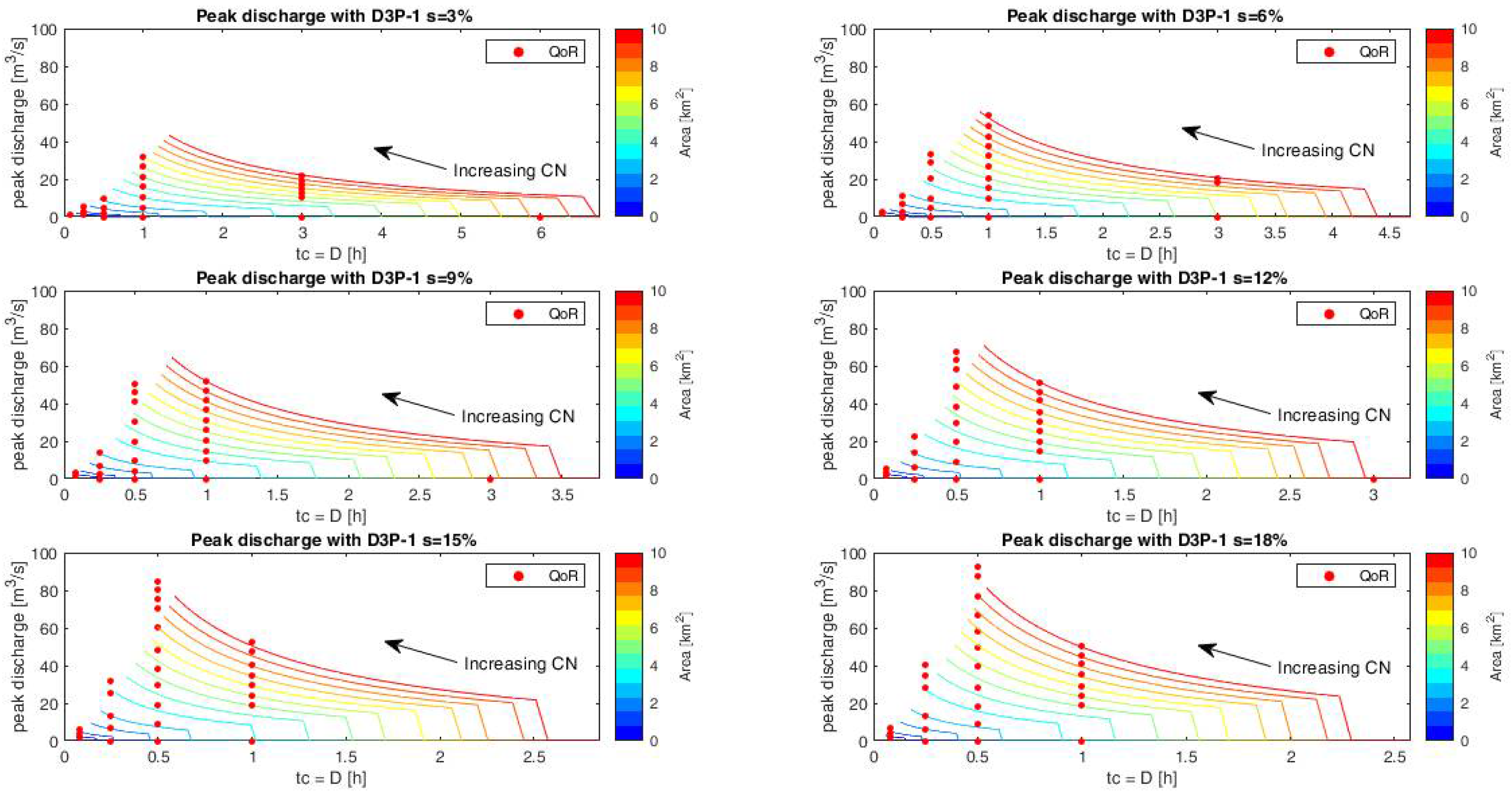
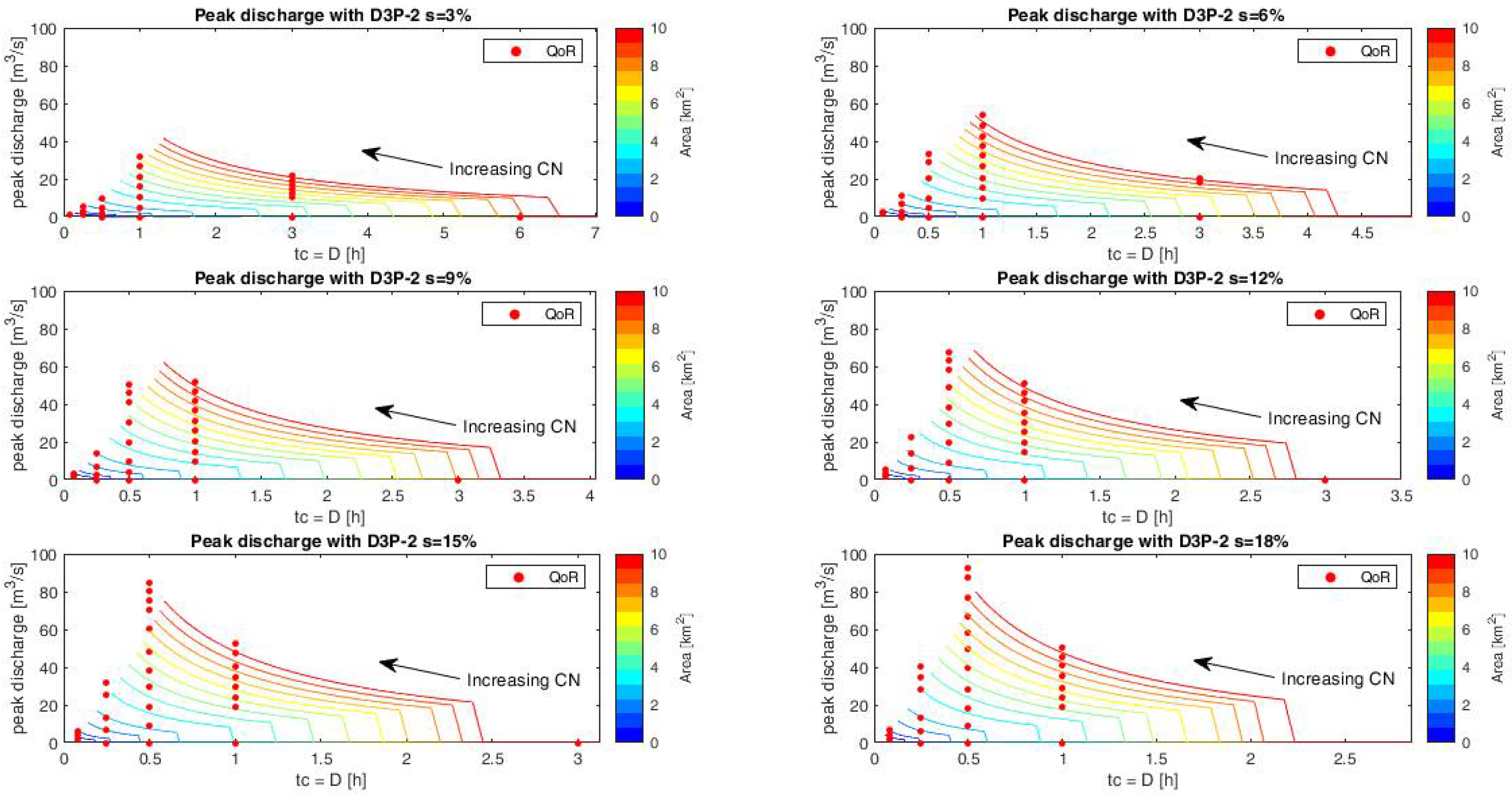
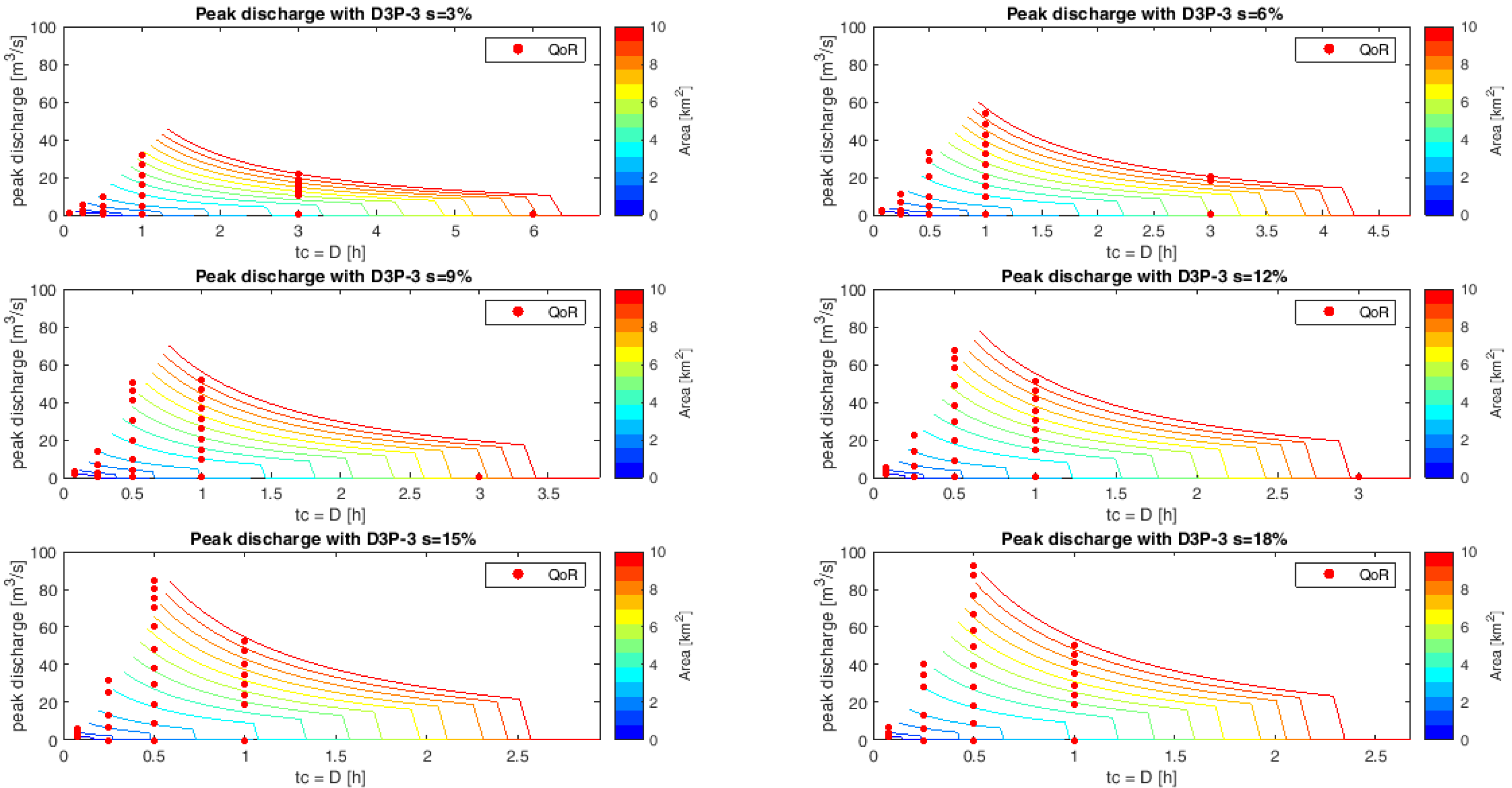
4.2. Results of Applications of SCS-CN Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, Y.; Wendi, D.; Kim, D.E.; Liong, S.Y. Deriving intensity–duration–frequency (IDF) curves using downscaled in situ rainfall assimilated with remote sensing data. Geosci. Lett. 2019, 6, 17. [Google Scholar] [CrossRef]
- Di Baldassarre, G.; Brath, A.; Montanari, A. Reliability of different depth-duration-frequency equations for estimating short-duration design storms. Water Resour. Res. 2006, 42, 1–6. [Google Scholar] [CrossRef]
- García-Bartual, R.; Schneider, M. Estimating maximum expected short-duration rainfall intensities from extreme convective storms. Phys. Chem. Earth Part B Hydrol. Ocean. Atmos. 2001, 26, 675–681. [Google Scholar] [CrossRef]
- Burlando, P.; Rosso, R. Scaling and multiscaling models of depth-duration-frequency curves for storm precipitation. J. Hydrol. 1996, 187, 45–64. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A mathematical framework for studying rainfall intensity-duration-frequency relationships. J. Hydrol. 1998, 206, 118–135. [Google Scholar] [CrossRef]
- Veneziano, D.; Furcolo, P. Multifractality of rainfall and scaling of intensity-duration-frequency curves. Water Resour. Res. 2002, 38, 42-1–42-12. [Google Scholar] [CrossRef]
- Agilan, V.; Umamahesh, N.V. Is the covariate based non-stationary rainfall IDF curve capable of encompassing future rainfall changes? J. Hydrol. 2016, 541, 1441–1455. [Google Scholar] [CrossRef]
- Silva, D.F.; Simonovic, S.P.; Schardong, A.; Goldenfum, J.A. Assessment of non-stationary IDF curves under a changing climate: Case study of different climatic zones in Canada. J. Hydrol. Reg. Stud. 2021, 36, 100870. [Google Scholar] [CrossRef]
- Vu, T.M.; Mishra, A.K. Nonstationary frequency analysis of the recent extreme precipitation events in the United States. J. Hydrol. 2019, 575, 999–1010. [Google Scholar] [CrossRef]
- Ganguli, P.; Coulibaly, P. Does Nonstationarity in Rainfall Requires Nonstationary Intensity-Duration-Frequency Curves? Hydrol. Earth Syst. Sci. Discuss 2017, 21, 6461–6483. [Google Scholar] [CrossRef]
- Salas, J.D.; Obeysekera, J. Revisiting the Concepts of Return Period and Risk for Nonstationary Hydrologic Extreme Events. J. Hydrol. Eng. 2014, 19, 554–568. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
- Cooley, D. Return Periods and Return Levels under Climate Change. In Extremes in a Changing Climate; AghaKouchak, A., Easterling, D., Hsu, K., Schubert, S., Sorooshian, S., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 97–113. [Google Scholar] [CrossRef]
- Gioia, A.; Bruno, M.F.; Totaro, V.; Iacobellis, V. Parametric assessment of trend test power in a changing environment. Sustainability 2020, 12, 3889. [Google Scholar] [CrossRef]
- Totaro, V.; Gioia, A.; Iacobellis, V. Numerical investigation on the power of parametric and nonparametric tests for trend detection in annual maximum series. Hydrol. Earth Syst. Sci. 2020, 24, 473–488. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann-Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Wang, F.; Shao, W.; Yu, H.; Kan, G.; He, X.; Zhang, D.; Ren, M.; Wang, G. Re-evaluation of the Power of the Mann-Kendall Test for Detecting Monotonic Trends in Hydrometeorological Time Series. Front. Earth Sci. 2020, 8, 14. [Google Scholar] [CrossRef]
- Vogel, R.M.; Rosner, A.; Kirshen, P.H. Brief Communication: Likelihood of societal preparedness for global change: Trend detection. Nat. Hazards Earth Syst. Sci. 2013, 13, 1773–1778. [Google Scholar] [CrossRef]
- Yarnell, D.L. Rainfall Intesity-Frequency Data; U.S. Department of Agricolture: Washington, DC, USA, 1935; p. 35. [Google Scholar]
- Rossi, F.; Villani, P. Valutazione Delle Piene in Campania; CNR-GNDCI: Salerno, Italy, 1995. [Google Scholar]
- Grimaldi, S.; Nardi, F.; Piscopia, R.; Petroselli, A.; Apollonio, C. Continuous hydrologic modelling for design simulation in small and ungauged basins: A step forward and some tests for its practical use. J. Hydrol. 2021, 595, 125664. [Google Scholar] [CrossRef]
- Rallison, R.E. Origin and evolution of the SCS runoff equation. In Symposium on Watershed Management 1980; American Society of Civil Engineers: New York, NY, USA, 1980; Volume II, pp. 912–924. [Google Scholar]
- SCS. Section 4: Hydrology. In National Engineering Handbook; Soil Conservation Service, USDA: Washington, DC, USA, 1956. [Google Scholar]
- De Luca, C.; Furcolo, P.; Rossi, F.; Villani PVitolo, C. Extreme rainfall in the Mediterranean. In Proceedings of the International Workshop Advances in Statistical Hydrology, Taormina, Italy, 23–25 May 2010. [Google Scholar]
- Alpert, P.; Neeman, B.U.; Shay-El, Y. Climatological analysis of Mediterranean cyclones using ECMWF data. Tellus A Dyn. Meteorol. Oceanogr. 1990, 42, 65–77. [Google Scholar] [CrossRef]
- Bruno, M.F.; Saponieri, A.; Molfetta, M.G.; Damiani, L. The DPSIR Approach for Coastal Risk Assessment under Climate Change at Regional Scale: The Case of Apulian Coast (Italy). J. Mar. Sci. Eng. 2020, 8, 531. [Google Scholar] [CrossRef]
- Protezione Civile Puglia—Centro Funzionale Decentrato. Available online: https://protezionecivile.puglia.it/centro-funzionale-decentrato/ (accessed on 1 July 2021).
- Soulis, K.X. Soil Conservation Service Curve Number (SCS-CN) Method: Current Applications, Remaining Challenges, and Future Perspectives. Water 2021, 13, 192. [Google Scholar] [CrossRef]
- Baltas, E.A.; Dervos, N.A.; Mimikou, M.A. Technical note: Determination of the SCS initial abstraction ratio in an experimental watershed in Greece, Hydrol. Earth Syst. Sci. 2007, 11, 1825–1829. [Google Scholar] [CrossRef]
- Mishra, S.K.; Singh, V.P. Another look at SCS-CN method. J. Hydrol. Eng. ASCE 1999, 4, 257–264. [Google Scholar] [CrossRef]
- Holman, P.; Hollis, J.M.; Bramley, M.E.; Thompson, T.R.E. The contribution of soil structural degradation to catchmentflooding: A preliminary investigation of the 2000 floodsin England and Wales. Hydrol. Earth Syst. Sci. 2003, 7, 755–766. [Google Scholar] [CrossRef][Green Version]
- Hua, J. Application of SCS model in Lanhe watershed. J. Taiyuan Univ. Technol. 2003, 34, 735–762. (In Chinese) [Google Scholar]
- Romero, P.; Castro, G.; Gómez, J.A.; Fereres, E. Curve number values for olive orchards under different soil management. Soil Sci. Soc. Am. J. 2007, 71, 1758–1769. [Google Scholar] [CrossRef]
- Lewis, M.J.; Singer, M.J.; Tate, K.W. Applicability of SCS curve number method for a California Oak Woodlands Watershed. J. Soil Water Conserv. 2000, 55, 226–230. [Google Scholar]
- Soulis, K.X.; Valiantzas, J.D. SCS-CN parameter determination using rainfall-runoff data in heterogeneous watersheds—The two-CN system approach. Hydrol. Earth Syst. Sci. 2012, 16, 1001–1015. [Google Scholar] [CrossRef]
- Xianzhao, L.; Jiazhu, L. Application of SCS Model in Estimation of Runoff from Small Watershed in Loess Plateau of China. Chin. Geogr. Sci. 2008, 18, 235–241. [Google Scholar] [CrossRef]
- Hoesein, A.A.; Pilgrim, D.H.; Titmarsh, G.W.; Cordery, I. Assessment of the US Conservation Service method for estimating design floods. In New Directions for Surface Water Modeling (Proceedings of the Baltimore Symposium, May 1989); International Association of Hydrological Sciences: Wallingford, CT, USA; Oxfordshire, UK, 1989. [Google Scholar]
- Pilgrim, D.H.; Cordery, I. Flood Runoff. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1992. [Google Scholar]
- Mockus, V. Use of Storm and Watershed Characteristics in Synthetic unit Hydrograph Analysis And Application; USSCS: Washington, DC, USA, 1957. [Google Scholar]
- Folmar, N.D.; Miller, A.C.; Woodward, D.E. History and Development of the NRCS Lag Time Equation. J. Am. Water Resour. Assoc. 2007, 43, 829–838. [Google Scholar] [CrossRef]
- Ward, A.D.; Elliot, W.J. Environmental Hydrology; CRC Press: New York, NY, USA, 1995. [Google Scholar]
- Hack, J.T. Studies of Longitudinal Stream Profiles in Virginia and Maryland; United States Geological Survey Professional: Washington, DC, USA, 1957; pp. 259-B, 45–97. [Google Scholar]
- Maritan, A.; Rinaldo, A.; Rigon, R.; Giacometti, A.; Rodriguez-Iturbe, I. Scaling Laws for River Networks. Phys. Rev. E 1996, 53, 1510. [Google Scholar] [CrossRef]
- Rinaldo, A.; Banavar, J.R.; Maritan, A. Trees, Networks, and Hydrology. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Marra, F.; Morin, E. Use of radar QPE for the derivation of Intensity–Duration–Frequency curves in a range of climatic regime. J. Hydrol. 2015, 531, 427–440. [Google Scholar] [CrossRef]
- Pöschmann, J.M.; Kim, D.; Kronenberg, R.; Bernhofer, C. An analysis of temporal scaling behaviour of extreme rainfall in Germany based on radar precipitation QPE data. Nat. Hazards Earth Syst. Sci. 2021, 21, 1195–1207. [Google Scholar] [CrossRef]
- Breña-naranjo, J.A.; Pedrozo-acuña, A.; Rico-ramirez, M.A. World’s greatest rainfall intensities observed by satellites. Atmos. Sci. Lett. 2015, 16, 420–424. [Google Scholar] [CrossRef]
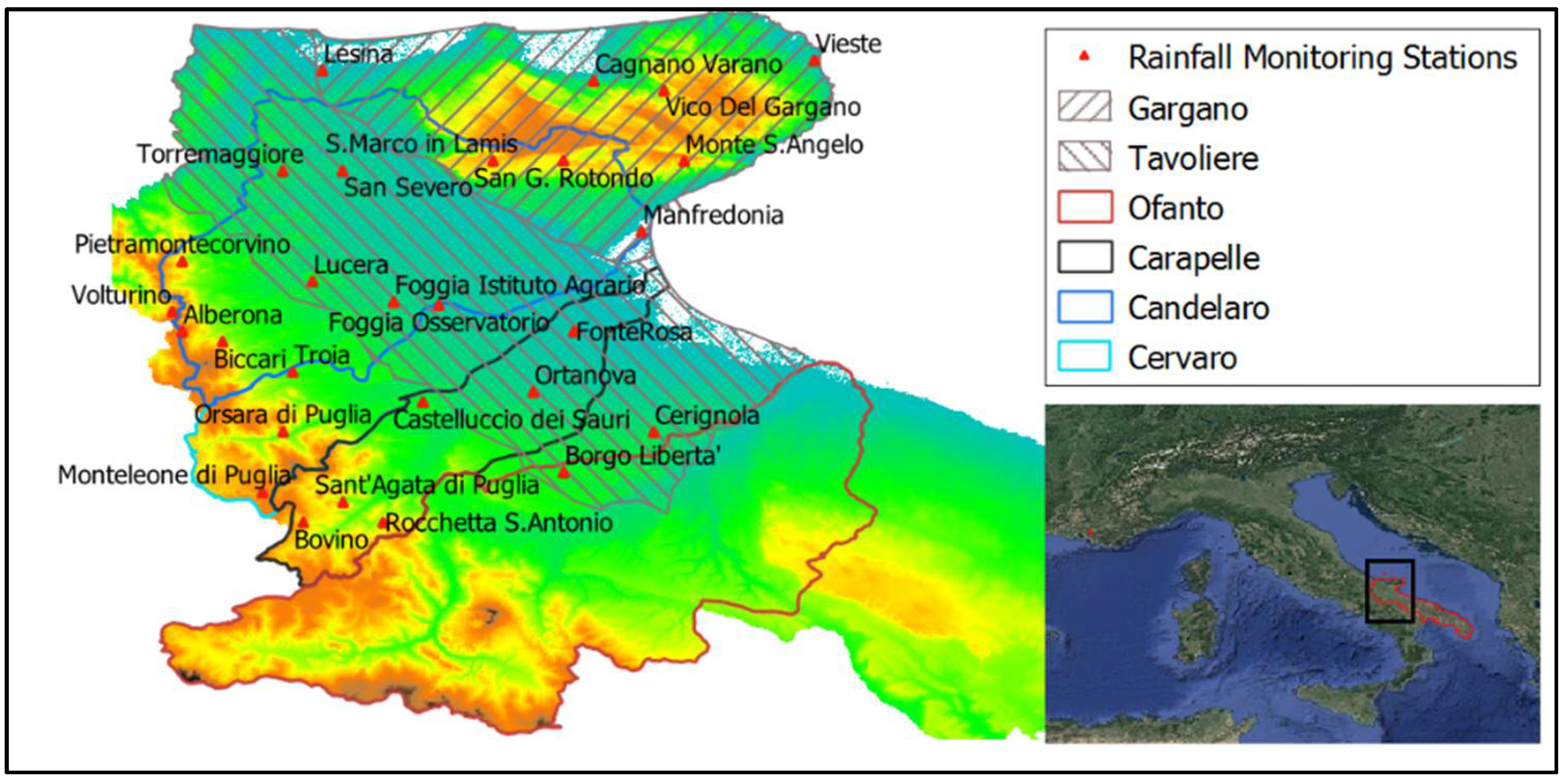

| Rainfall Monitoring Stations | Altitude (m a.s.l.) | River Basin/Area | Installation Year |
|---|---|---|---|
| Alberona | 663 | Candelaro | 1917 |
| Biccari | 484 | Candelaro | 1922 |
| Borgo Liberta’ | 235 | Ofanto | 1924 |
| Bovino | 623 | Carapelle | 1917 |
| Cagnano Varano | 165 | Gargano | 1921 |
| Castelluccio dei Sauri | 190 | Carapelle | 1922 |
| Cerignola | 118 | Tavoliere | 1921 |
| Foggia Osservatorio | 99 | Candelaro | 1873 |
| Foggia Istituto Agrario | 85 | Candelaro | 1949 |
| Fonte Rosa | 25 | Tavoliere | 1925 |
| Lesina | 6 | Gargano | 1928 |
| Lucera | 246 | Candelaro | 1917 |
| Manfredonia | 68 | Tavoliere | 1900 |
| Monte Sant’Angelo | 799 | Gargano | 1920 |
| Monteleone di Puglia | 828 | Cervaro | 1920 |
| Orsara di Puglia | 689 | Cervaro | 1921 |
| Ortanova | 53 | Carapelle-Tavoliere | 1921 |
| Pietramontecorvino | 441 | Candelaro | 1928 |
| Rocchetta Sant’Antonio | 724 | Carapelle | 1922 |
| Sant’Agata di Puglia | 703 | Carapelle | 1917 |
| San Giovanni Rotondo | 619 | Candelaro-Gargano | 1923 |
| San Marco in Lamis | 566 | Candelaro-Gargano | 1917 |
| San Severo | 114 | Candelaro-Tavoliere | 1928 |
| Torremaggiore | 195 | Candelaro-Tavoliere | 1917 |
| Troia | 469 | Candelaro | 1907 |
| Vico Del Gargano | 459 | Gargano | 1921 |
| Vieste | 96 | Gargano | 1921 |
| Volturino | 615 | Candelaro | 1964 |
| D2P-1 | D2P-2 | D3P-1 | D3P-2 | D3P-3 | |
|---|---|---|---|---|---|
| E (d5)% | 44.58 | 55.26 | 11.82 | 15.36 | 11.63 |
| E (d15)% | 4.40 | 9.54 | 3.11 | 3.21 | 3.99 |
| E (d30)% | 9.26 | 7.47 | 7.34 | 8.00 | 2.82 |
| E (d60)% | 4.76 | 3.03 | 2.26 | 2.43 | 7.17 |
| E (d180)% | 2.40 | 1.19 | 2.73 | 2.80 | 3.12 |
| E (d360)% | 2.15 | 1.87 | 2.57 | 2.67 | 2.38 |
| E (d720)% | 1.54 | 1.45 | 1.48 | 1.48 | 3.48 |
| E (d1440)% | 1.41 | 0.96 | 1.55 | 1.64 | 1.54 |
| D2P-1 | D2P-2 | D3P-1 | D3P-2 | D3P-3 | |
|---|---|---|---|---|---|
| RMSE | 1.64 | 1.68 | 1.14 | 1.21 | 1.33 |
| D2P-1 | D2P-2 | D3P-1 | D3P-2 | D3P-3 | |
|---|---|---|---|---|---|
| E (s = 3%)% | 8.90 | 8.93 | 7.53 | 10.24 | 6.75 |
| E (s = 6%)% | 12.91 | 12.94 | 9.36 | 13.95 | 7.48 |
| E (s = 9%)% | 13.31 | 13.31 | 8.90 | 14.11 | 5.99 |
| E (s = 12%)% | 16.46 | 16.49 | 11.45 | 17.37 | 7.89 |
| E (s = 15%)% | 15.94 | 15.94 | 11.07 | 16.76 | 7.07 |
| E (s = 18%)% | 15.47 | 15.52 | 10.71 | 16.35 | 6.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gioia, A.; Lioi, B.; Totaro, V.; Molfetta, M.G.; Apollonio, C.; Bisantino, T.; Iacobellis, V. Estimation of Peak Discharges under Different Rainfall Depth–Duration–Frequency Formulations. Hydrology 2021, 8, 150. https://doi.org/10.3390/hydrology8040150
Gioia A, Lioi B, Totaro V, Molfetta MG, Apollonio C, Bisantino T, Iacobellis V. Estimation of Peak Discharges under Different Rainfall Depth–Duration–Frequency Formulations. Hydrology. 2021; 8(4):150. https://doi.org/10.3390/hydrology8040150
Chicago/Turabian StyleGioia, Andrea, Beatrice Lioi, Vincenzo Totaro, Matteo Gianluca Molfetta, Ciro Apollonio, Tiziana Bisantino, and Vito Iacobellis. 2021. "Estimation of Peak Discharges under Different Rainfall Depth–Duration–Frequency Formulations" Hydrology 8, no. 4: 150. https://doi.org/10.3390/hydrology8040150
APA StyleGioia, A., Lioi, B., Totaro, V., Molfetta, M. G., Apollonio, C., Bisantino, T., & Iacobellis, V. (2021). Estimation of Peak Discharges under Different Rainfall Depth–Duration–Frequency Formulations. Hydrology, 8(4), 150. https://doi.org/10.3390/hydrology8040150








