Reinvestigating the Parabolic-Shaped Eddy Viscosity Profile for Free Surface Flows
Abstract
:1. Introduction
2. Literature for Eddy Viscosity Models for Open-Channel Flows
2.1. Parabolic Eddy Viscosity
2.2. Log-Wake-Modified Eddy Viscosity Profile
2.3. Mixing Length and Mixing Velocity
3. Proposed Eddy Viscosity Models for Free Surface Flows
3.1. Mixing Velocity from TKE Profile
3.2. Damping Function for Free Surface
3.3. First Formulation: Exponential-Type Profile of Eddy Viscosity
3.4. Second Formulation: Eddy Viscosity Formulation Based on Miwing Length Equation from Similarity Hypothesis
4. Results
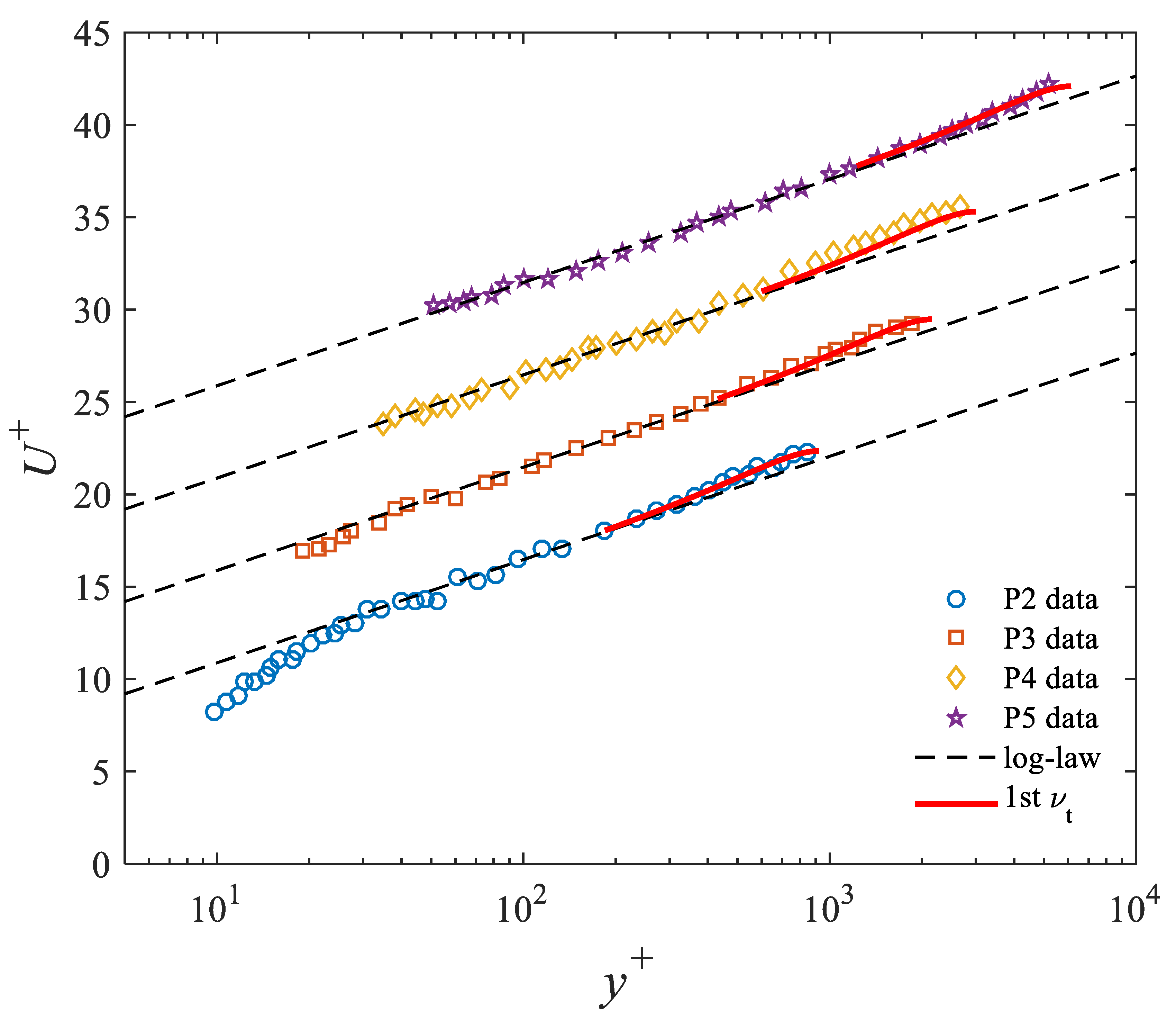
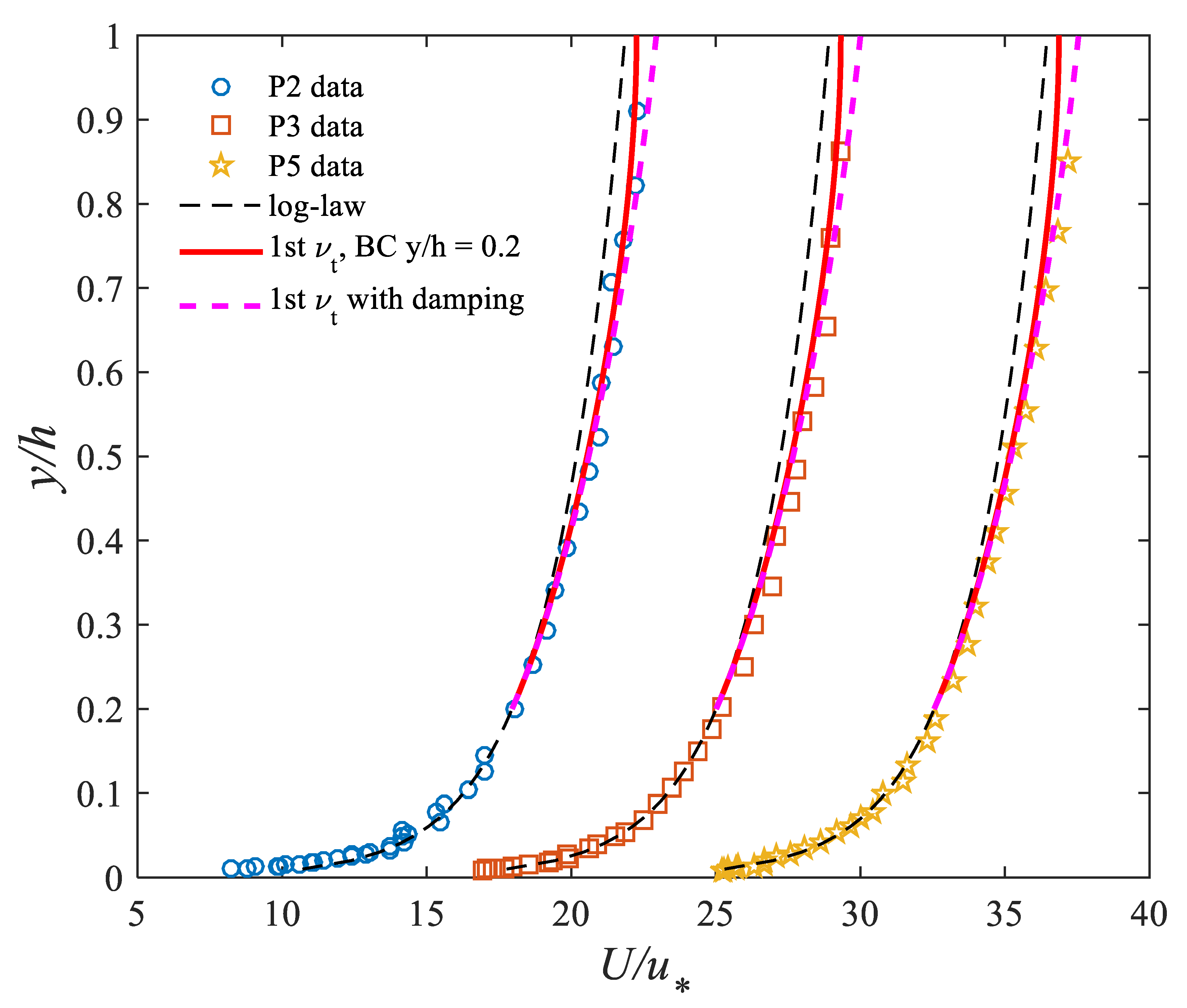
4.1. Velocity Profiles from the First Eddy Viscosity Formulation: Exponential-Type Profile
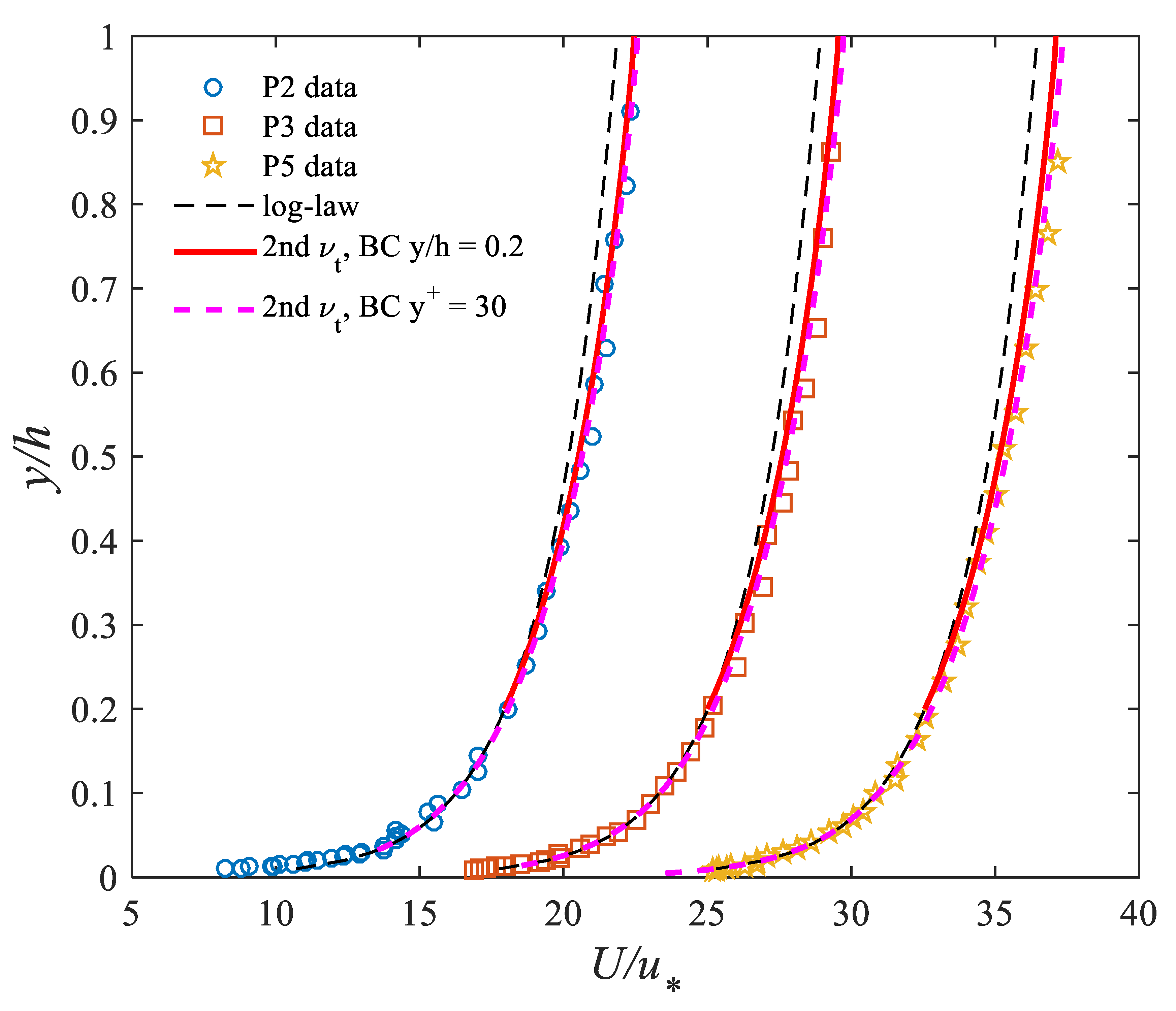
4.2. Velocity Profiles from the Second Eddy Viscosity Formulation Based on Von Karman’s Similarity Hypothesis
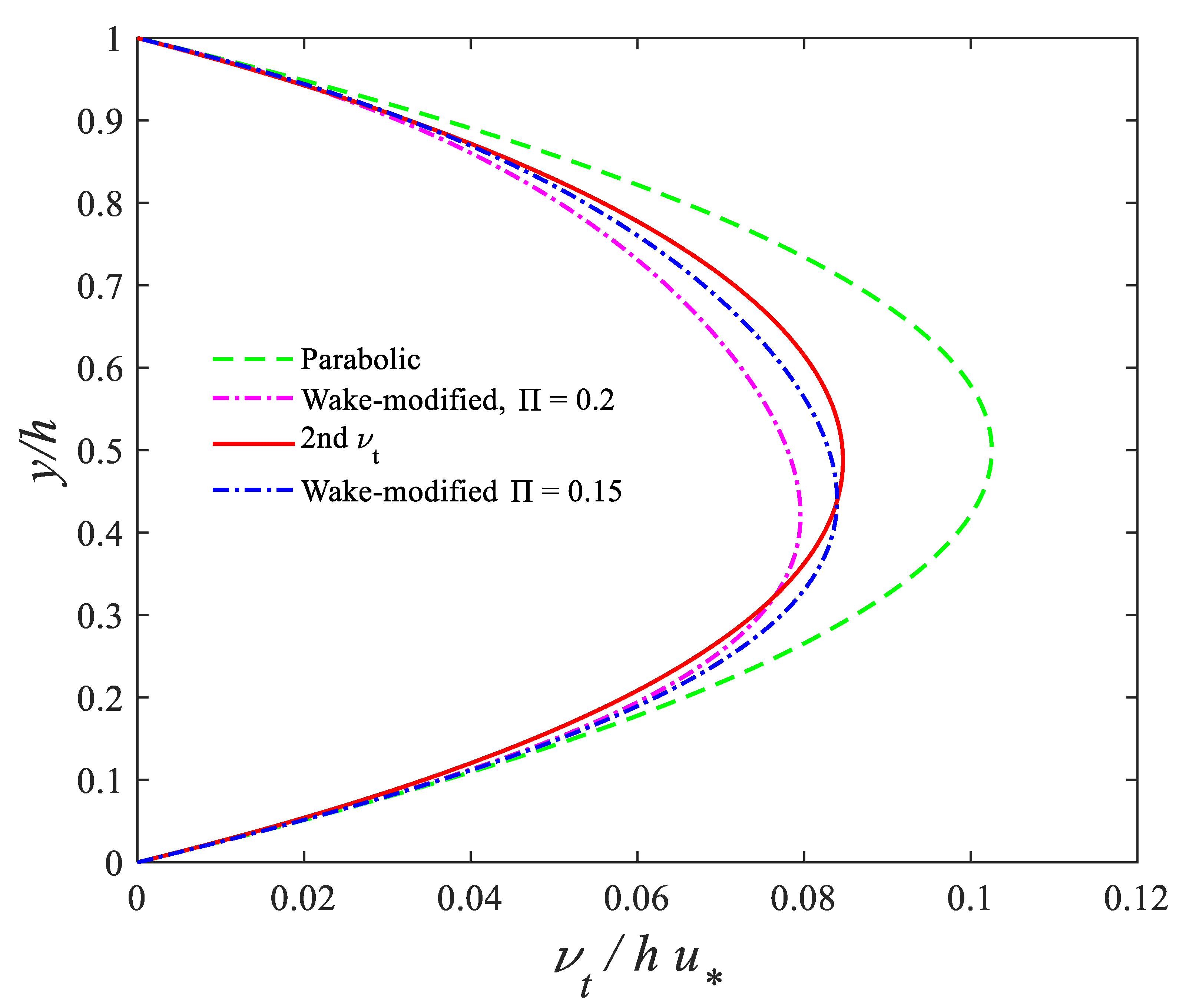
4.3. Eddy Viscosity Profiles
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Figuérez, J.; Galán, Á.; González, J. An Enhanced Treatment of Boundary Conditions for 2D RANS Streamwise Velocity Models in Open Channel Flow. Water 2021, 13, 1001. [Google Scholar] [CrossRef]
- Nazari-Sharabian, M.; Karakouzian, M.; Hayes, D. Flow Topology in the Confluence of an Open Channel with Lateral Drainage Pipe. Hydrology 2020, 7, 57. [Google Scholar] [CrossRef]
- Zhu, Z.; Yu, J.; Dou, J.; Peng, D. An Expression for Velocity Lag in Sediment-Laden Open-Channel Flows Based on Tsallis Entropy Together with the Principle of Maximum Entropy. Entropy 2019, 21, 522. [Google Scholar] [CrossRef] [Green Version]
- MacVicar, B.J.; Roy, A.G. Hydrodynamics of a forced riffle pool in a gravel bed river: 1. Mean velocity and turbulence intensity. Water Resour. Res. 2007, 43, W12401. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Nayamatullah, M. Semianalytical Solutions for One-Dimensional Unsteady Nonequilibrium Suspended Sediment Transport in Channels with Arbitrary Eddy Viscosity Distributions and Realistic Boundary Conditions. J. Hydraul. Eng. 2014, 140, 04014011. [Google Scholar] [CrossRef]
- Johnson, E.D.; Cowen, E.A. Estimating bed shear stress from remotely measured surface turbulent dissipation fields in open channel flows. Water Resour. Res. 2017, 53, 1982–1996. [Google Scholar] [CrossRef]
- Macvicar, B.J.; Sukhodolov, A.N. Sampling strategies to improve scaling parameter estimates in rivers. J. Hydraul. Res. 2019, 57, 1–10. [Google Scholar] [CrossRef]
- Sukhodolov, A.N.; Krick, J.; Sukhodolova, T.A.; Cheng, Z.; Rhoads, B.L.; Constantinescu, G.S. Turbulent flow structure at a discordant river confluence: Asymmetric jet dynamics with implications for channel morphology. J. Geophys. Res. Earth Surf. 2017, 122, 1278–1293. [Google Scholar] [CrossRef]
- Sukhodolov, A.N. Field-based research in fluvial hydraulics: Potential, paradigms and challenges. J. Hydraul. Res. 2014, 53, 1–19. [Google Scholar] [CrossRef]
- Gualtieri, C.; Shao, D.; Angeloudis, A. Advances in Environmental Hydraulics. Water 2021, 13, 1192. [Google Scholar] [CrossRef]
- Nezu, I.; Nakagawa, H. Turbulence in Open Channel Flows; Balkema, A.A., Ed.; Balkema: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Yokosi, S. The structure of river turbulence. Bull. Disaster Prev. Res. Inst. Kyoto Univ. 1967, 17, 1–29. [Google Scholar]
- McQuivey, R.S. Summary of turbulence data from rivers, conveyance channels and laboratory flumes. US Geol. Surv. Prof. 1973, N802B, B1–B66. [Google Scholar]
- Grinvald, D.I. Turbulence of Natural Flows (in Russian); Hydrometeoizdat: Leningrad, Russia, 1974. [Google Scholar]
- Iwasa, Y.; Asano, T. Characteristics of turbulence in rivers and conveyance channels. In Proceedings of the Third International Symposium on Stochastic Hydraulics, Delft, The Netherlands, 5–8 August 1980; pp. 565–576. [Google Scholar]
- Nikora, V.I.; Smart, G.M. Turbulence characteristics of New Zealand gravel-bed rivers. J. Hydraul. Eng. 1997, 123, 764–773. [Google Scholar] [CrossRef]
- Grass, A.J. Structural features of turbulent flow over smooth and rough boundaries. J. Fluid Mech. 1971, 50, 233–255. [Google Scholar] [CrossRef]
- Nezu, I.; Rodi, W. Open channel measurements with a laser Doppler anemometer. J. Hyd. Eng. ASCE 1986, 112, 335–355. [Google Scholar] [CrossRef]
- Absi, R. A simple eddy viscosity formulation for turbulent boundary layers near smooth walls. C. R. Mec. 2009, 337, 158–165. [Google Scholar] [CrossRef] [Green Version]
- Guo, J. Modified log-wake-law for smooth rectangular open channel flow. J. Hydraul. Res. 2014, 52, 121–128. [Google Scholar] [CrossRef]
- Sukhodolov, A.; Thiele, M.; Bungartz, H. Turbulence Structure in a River Reach with Sand Bed. Water Resour. Res. 1998, 34, 1317–1334. [Google Scholar] [CrossRef]
- Franca, M.J.; Lemmin, U. A field study of extremely rough, three-dimensional river flow. In Proceedings of the 4th IAHR International Symposium on Environmental Hydraulics, Hong Kong, China, 15–18 December 2004. [Google Scholar]
- Afzal, N.; Seena, A.; Bushra, A. Power Law Velocity Profile in Fully Developed Turbulent Pipe and Channel Flows. J. Hydraul. Eng. ASCE 2007, 133, 1080–1086. [Google Scholar] [CrossRef]
- Cheng, N.S. Power-law index for velocity profiles in open channel flows. Adv. Water Res. 2007, 30, 1775–1784. [Google Scholar] [CrossRef]
- Coles, D.E. The law of the wake in the turbulent boundary layer. J. Fluid Mech. 1956, 1, 191–226. [Google Scholar] [CrossRef] [Green Version]
- Hinze, J.O. Turbulence; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Krug, D.; Philip, J.; Marusic, I. Revisiting the law of the wake in wall turbulence. J. Fluid Mech. 2017, 811, 421–435. [Google Scholar] [CrossRef] [Green Version]
- Cebeci, T.; Smith, M.O. Analysis of Turbulent Boundary Layers; Academic: San Diego, CA, USA, 1974. [Google Scholar]
- Cardoso, A.H.; Graf, W.H.; Gust, G. Uniform flow in a smooth open channel. J. Hydraul. Res. 1989, 27, 603–616. [Google Scholar] [CrossRef]
- Kirkgoz, M.S. The turbulent velocity profiles for smooth and rough channel flow. J. Hydraul. Eng. 1989, 115, 1543–1561. [Google Scholar] [CrossRef]
- Li, X.; Dong, Z.; Chen, C. Turbulent flows in smooth-wall open channels with different slope. J. Hydraul. Res. 1995, 33, 333–347. [Google Scholar]
- Absi, R. An ordinary differential equation for velocity distribution and dip-phenomenon in open channel flows. J. Hydraul. Res. 2011, 49, 82–89. [Google Scholar] [CrossRef]
- Absi, R. Rebuttal on A mathematical model on depth-averaged β-factor in open-channel turbulent flow. Environ. Earth Sci. 2020, 79, 113. [Google Scholar] [CrossRef]
- Gualtieri, C.; Angeloudis, A.; Bombardelli, F.; Jha, S.; Stoesser, T. On the Values for the Turbulent Schmidt Number in Environmental Flows. Fluids 2017, 2, 17. [Google Scholar] [CrossRef] [Green Version]
- Absi, R. Eddy viscosity and velocity profiles in fully-developed turbulent channel flows. Fluid Dyn. 2019, 54, 137–147. [Google Scholar] [CrossRef]
- Absi, R. Analytical eddy viscosity model for velocity profiles in the outer part of closed- and open-channel flows. Fluid Dyn. 2021, 56, 577–586. [Google Scholar] [CrossRef]
- Absi, R. Wave boundary layer instability near flow reversal. In Coastal Engineering 2002, Proceedings of the 28th International Conference Coastal Engineering, ASCE, Wales, UK, 19 November 2002; Smith, J.M., Ed.; World Scientific Publishing: Singapore, 2002; Volume 1, pp. 532–544. [Google Scholar]
- Absi, R. Comment on Turbulent diffusion of momentum and suspended particles: A finite-mixing-length theory. Phys. Fluids 2005, 17, 079101. [Google Scholar] [CrossRef] [Green Version]
- Absi, R. A roughness and time dependent mixing length equation. JSCE Doboku Gakkai Ronbunshuu B Jpn. Soc. Civ. Eng. 2006, 62, 437–446. [Google Scholar] [CrossRef] [Green Version]
- Yalin, M.S. Mechanics of Sediment Transport; Pergamon Press: Oxford, UK, 1977. [Google Scholar]
- Absi, R. Comments on Turbulent velocity profile in fully-developed open channel flows. Environ. Fluid Mech. 2008, 8, 389–394. [Google Scholar] [CrossRef]
- Absi, R. Comments on Modeling stratified suspension concentration distribution in turbulent flow using fractional advection–diffusion equation. Environ. Fluid Mech. 2021. Submitted. [Google Scholar]
- Absi, R. Analytical solutions for the modeled k-equation. ASME J. Appl. Mech. 2008, 75, 044501. [Google Scholar] [CrossRef]
- Nakagawa, H.; Nezu, I.; Ueda, H. Turbulence of open channel flow over smooth and rough beds. Jpn. Soc. Civ. Eng. 1975, 241, 155–168. [Google Scholar] [CrossRef]
- Langhi, M.; Hosoda, T.; Dey, S. Analytical Solution of k-ϵ Model for Nonuniform Flows. J. Hydraul. Eng. ASCE 2018, 144, 04018033. [Google Scholar] [CrossRef]
- Welderufael, M.; Absi, R.; Mélinge, Y. Assessment of velocity profile models for turbulent smooth wall open channel flows. ISH J. Hyd. Eng. 2021, in press. [Google Scholar]
- Hosoda, T. Turbulent Diffusion Mechanism in Open Channel Flows. Ph.D. Thesis, Kyoto University, Kyoto, Japan, 1990. [Google Scholar]
- Businger, J.A.; Arya, S.P.S. Heights of the mixed layer in the stable stratified planetary boundary layer. Adv. Geophys. 1974, 18A, 73–92. [Google Scholar]
- Hsu, T.W.; Jan, C.D. Calibration of Businger-Arya type of eddy viscosity model’s parameters. J. Waterw. Port Coastal. Ocean. Eng. ASCE 1998, 124, 281–284. [Google Scholar] [CrossRef]
- Absi, R. Discussion of Calibration of Businger-Arya type of eddy viscosity model’s parameters. J. Waterw. Port Coastal. Ocean. Eng. ASCE 2000, 126, 108–109. [Google Scholar] [CrossRef]
- Absi, R. Time-Dependent Eddy Viscosity Models for Wave Boundary Layers. In Coastal Engineering 2000, Proceedings of the 27th International Conference Coastal Engineering, Sydney, Australia, 16–21 July 2000; Edge, B.L., Ed.; ASCE: Reston, VA, USA; pp. 1268–1281.
- Absi, R. Concentration profiles for fine and coarse sediments suspended by waves over ripples: An analytical study with the 1-DV gradient diffusion model. Adv. Water Res. 2010, 33, 411–418. [Google Scholar] [CrossRef] [Green Version]
- Absi, R.; Tanaka, H.; Kerlidou, L.; André, A. Eddy viscosity profiles for wave boundary layers: Validation and calibration by a k-ω model. In Proceedings of the 33th International Conference Coastal Engineering, Santander, Spain, 1–6 July 2012. [Google Scholar]
- Absi, R. Stress length and momentum cascade in turbulent channel flows. Phys. Rev. Fluids 2021. Submitted. [Google Scholar]
- Yang, S.Q.; Tan, S.K.; Lim, S.Y. Velocity distribution and dip-phenomenon in smooth uniform open channel flows. J. Hydraul. Eng. 2004, 130, 1179–1186. [Google Scholar] [CrossRef]
- Nezu, I. Open-Channel Flow Turbulence and Its Research Prospect in the 21st Century. J. Hydraul. Eng. ASCE 2005, 131, 229–246. [Google Scholar] [CrossRef]
- Ueda, H.; Moller, R.; Komori, S.; Mizushina, T. Eddy diffusivity near the free surface of open channel flow. Int. J. Heat Mass Transf. 1977, 20, 1127–1136. [Google Scholar] [CrossRef]
- von Kármán, T. Mechanische ahnlichkeit und turbulenz. Math. -Phys. Kl. 1930, 5, 58–76. [Google Scholar]

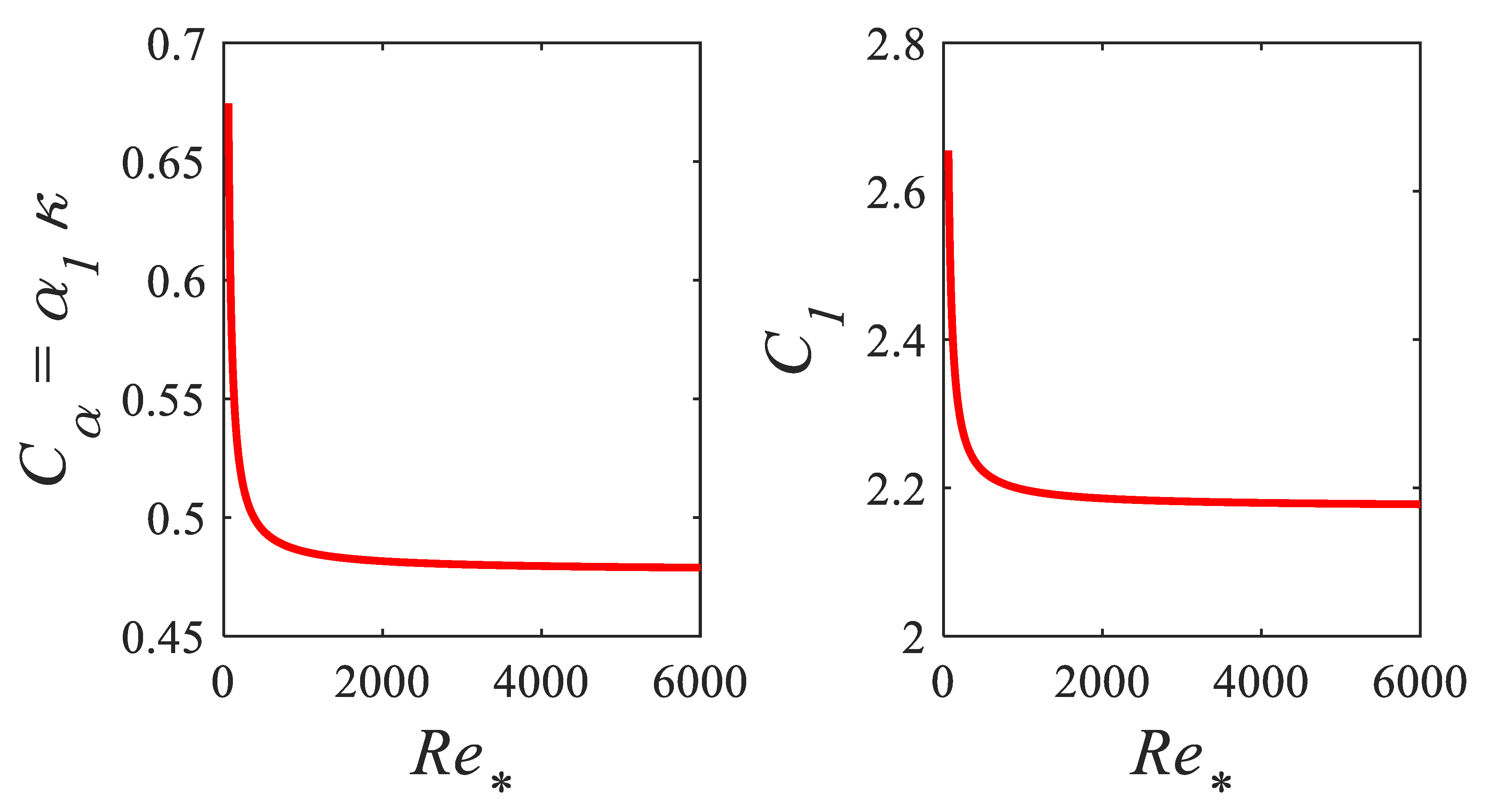
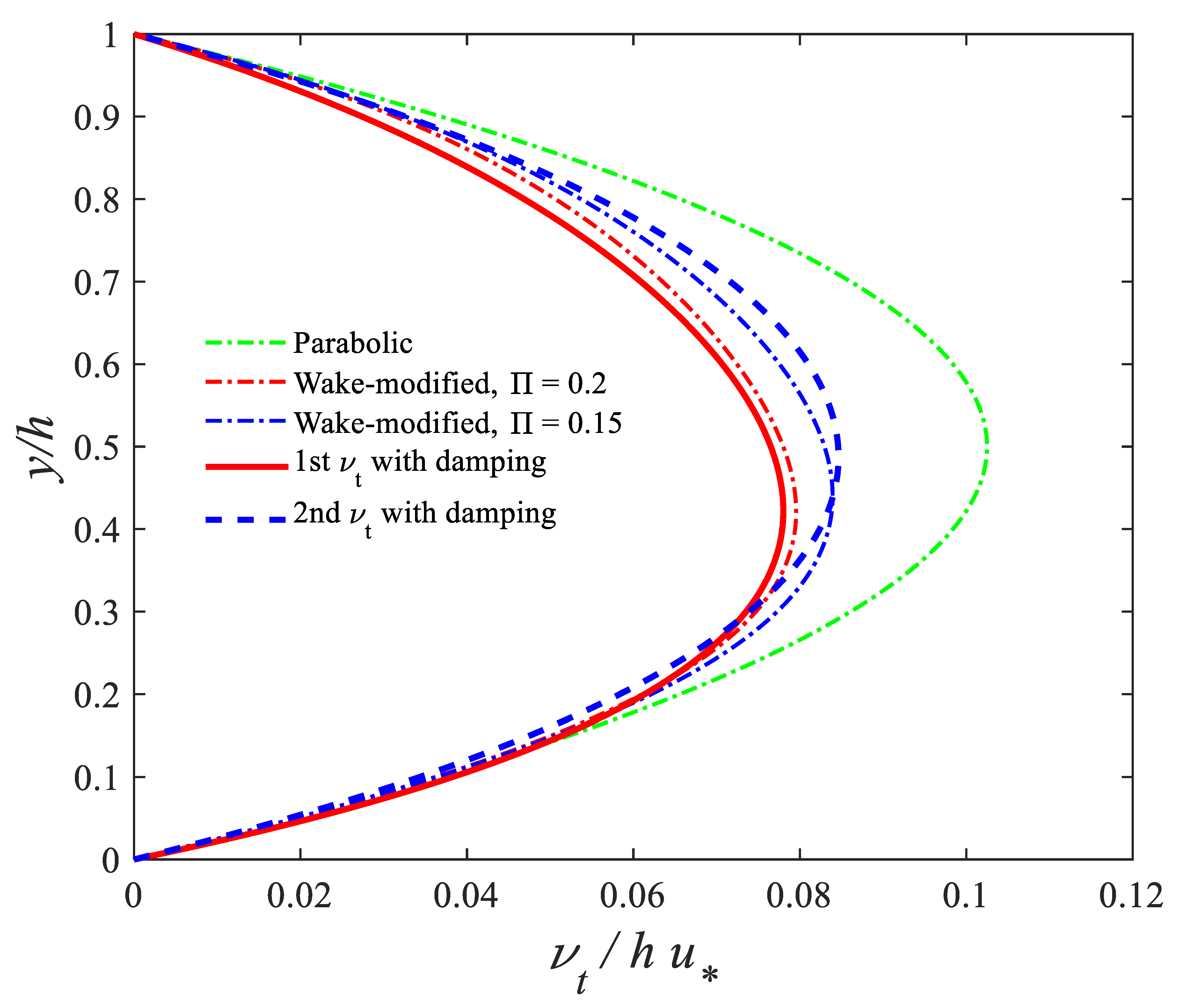
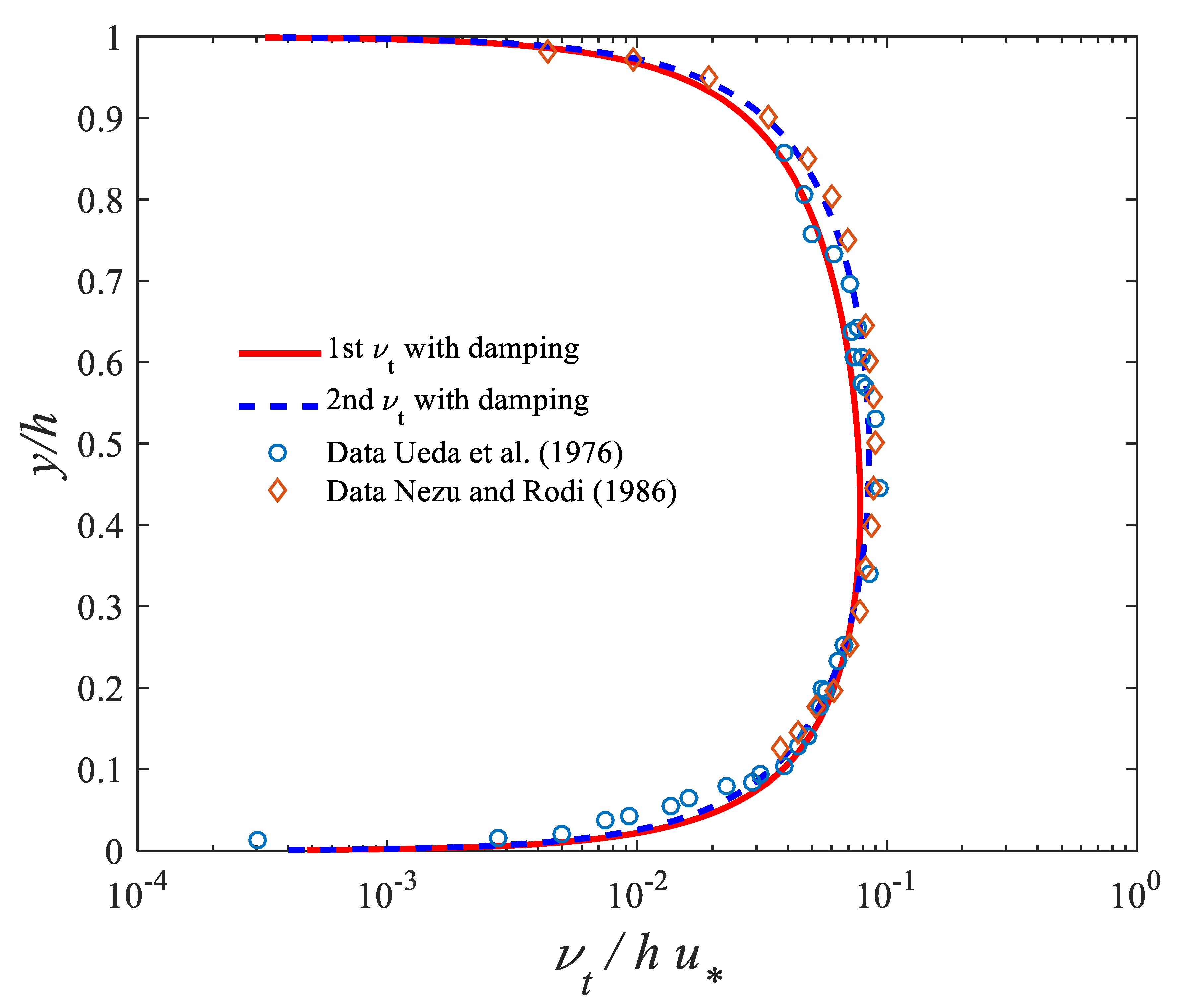
| Case | Depth of Flow, h (cm) | Width to Depth Ratio | |||
|---|---|---|---|---|---|
| P2 | 10.3 | 5.9 | 5.5 × 104 | 0.189 | 923 |
| P3 | 10.0 | 6.0 | 14.3 × 104 | 0.488 | 2156 |
| P4 | 10.0 | 6.0 | 21.0 × 104 | 0.704 | 3001 |
| P5 | 10.5 | 5.7 | 44.0 × 104 | 1.170 | 6139 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Absi, R. Reinvestigating the Parabolic-Shaped Eddy Viscosity Profile for Free Surface Flows. Hydrology 2021, 8, 126. https://doi.org/10.3390/hydrology8030126
Absi R. Reinvestigating the Parabolic-Shaped Eddy Viscosity Profile for Free Surface Flows. Hydrology. 2021; 8(3):126. https://doi.org/10.3390/hydrology8030126
Chicago/Turabian StyleAbsi, Rafik. 2021. "Reinvestigating the Parabolic-Shaped Eddy Viscosity Profile for Free Surface Flows" Hydrology 8, no. 3: 126. https://doi.org/10.3390/hydrology8030126
APA StyleAbsi, R. (2021). Reinvestigating the Parabolic-Shaped Eddy Viscosity Profile for Free Surface Flows. Hydrology, 8(3), 126. https://doi.org/10.3390/hydrology8030126






