A Global-Scale Investigation of Stochastic Similarities in Marginal Distribution and Dependence Structure of Key Hydrological-Cycle Processes
Abstract
1. Introduction
2. Methodology
2.1. Dependence Structure Metrics
2.2. Marginal Structure Metrics
2.3. Global-Scale Data Extraction and Processing
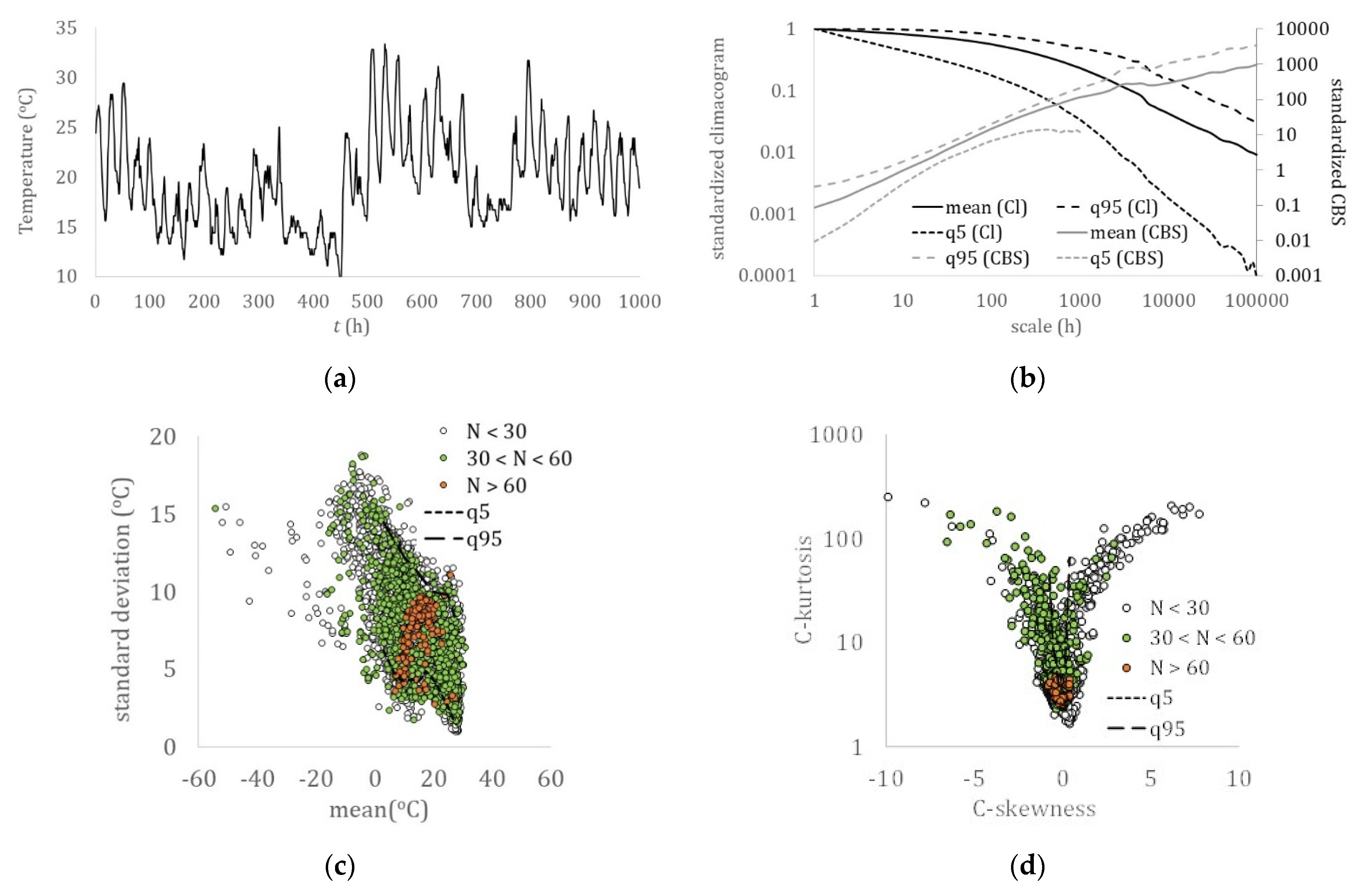
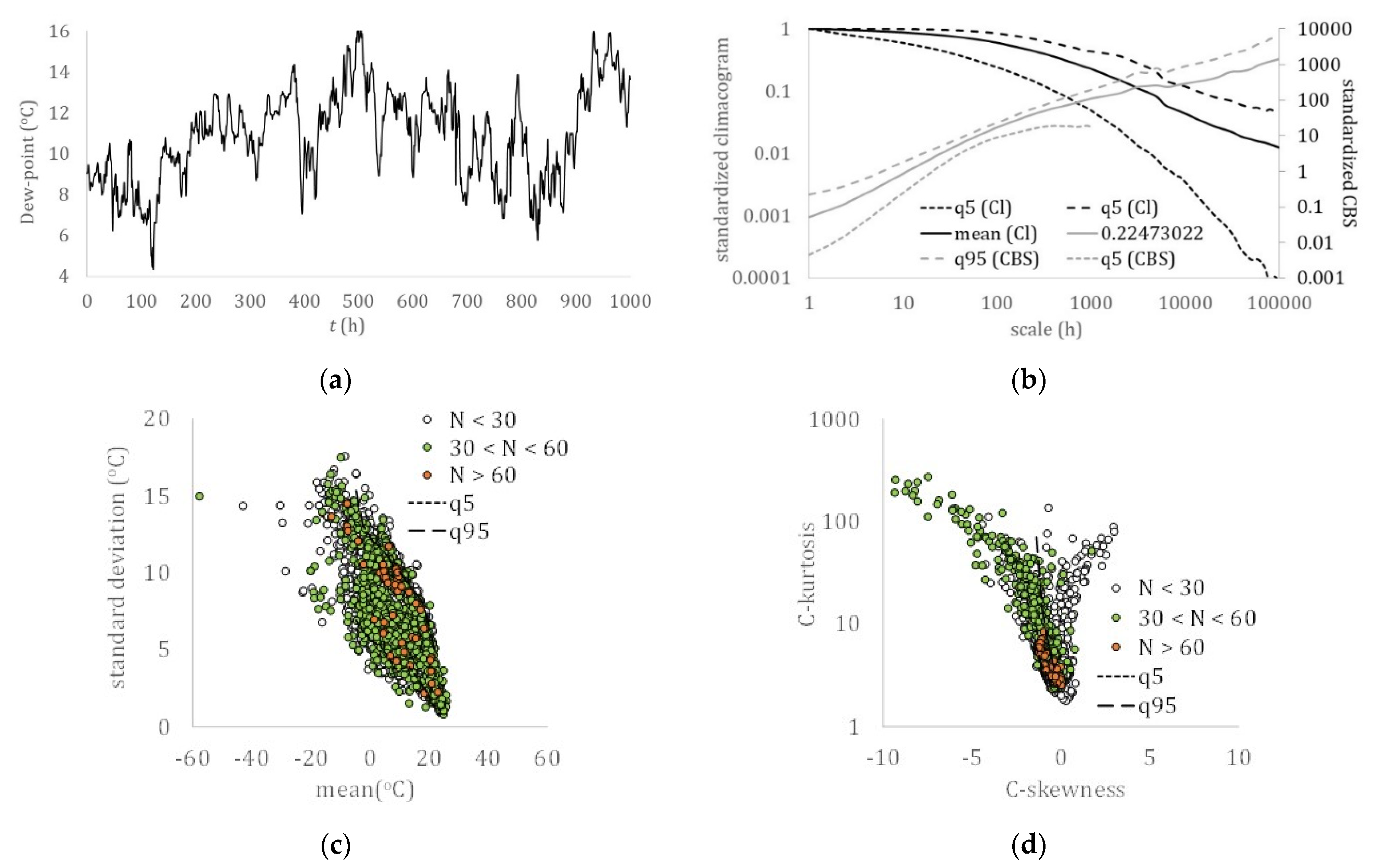
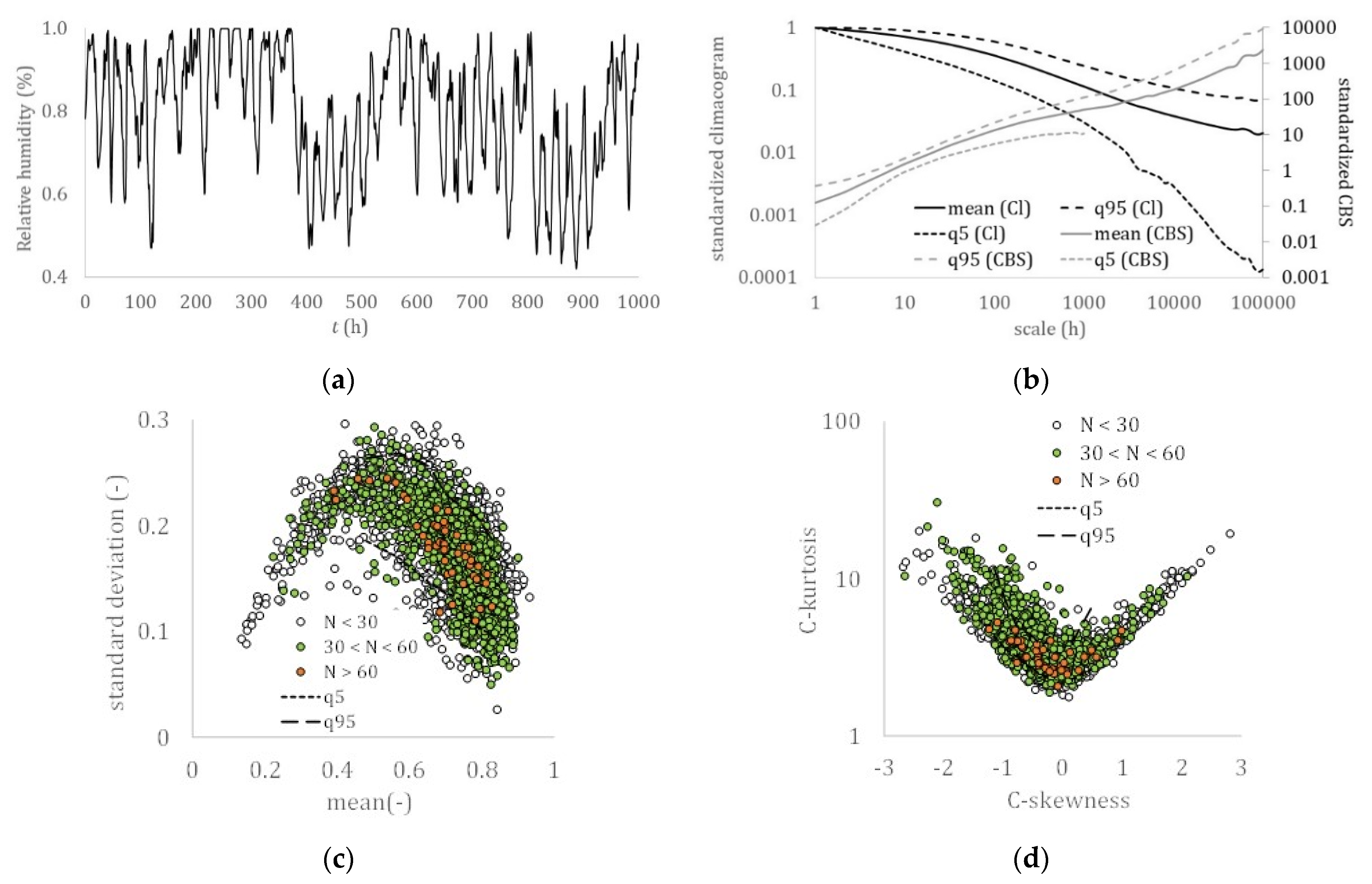
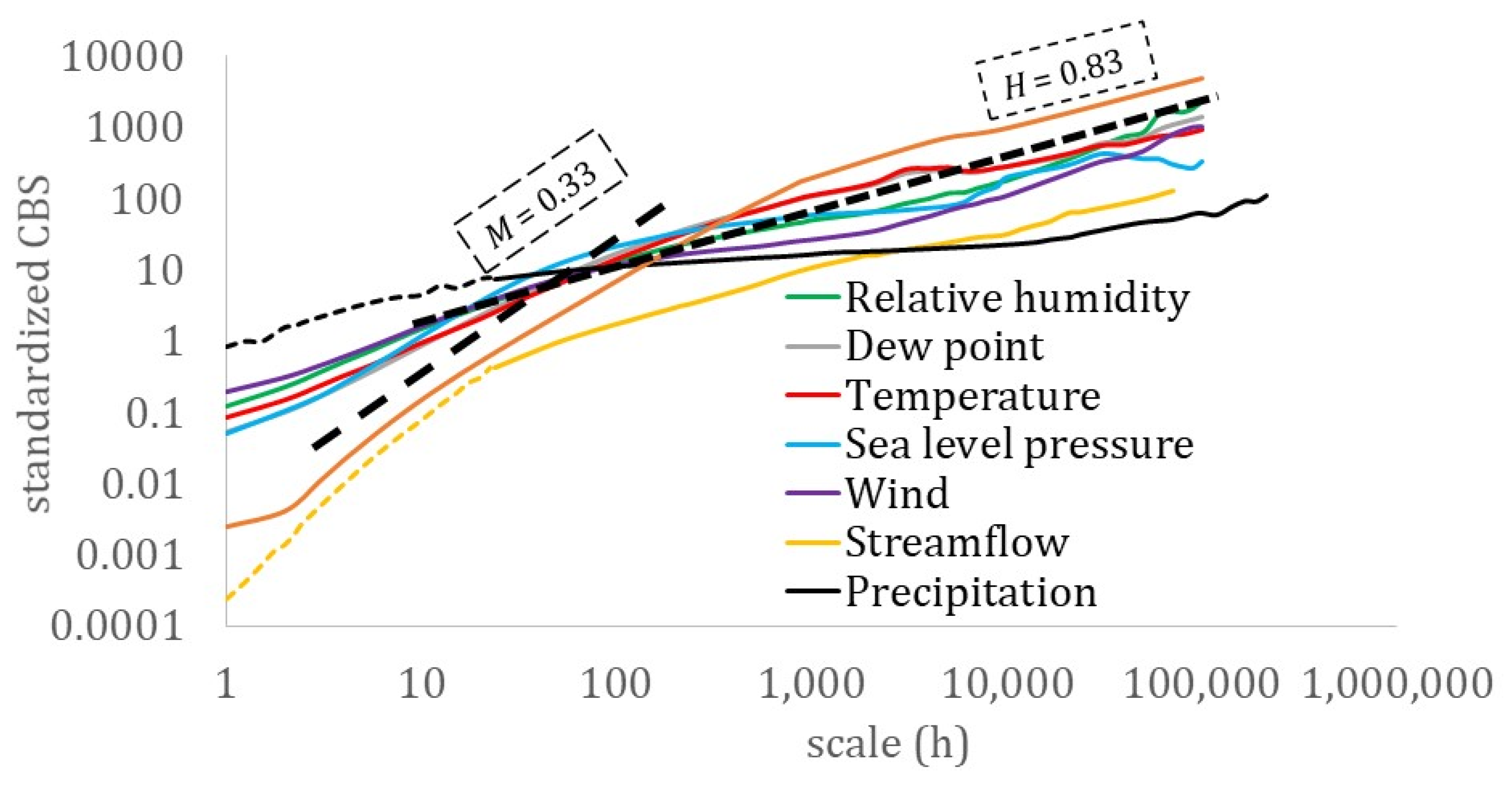
3. Results
4. Discussion
5. Conclusions
- (1)
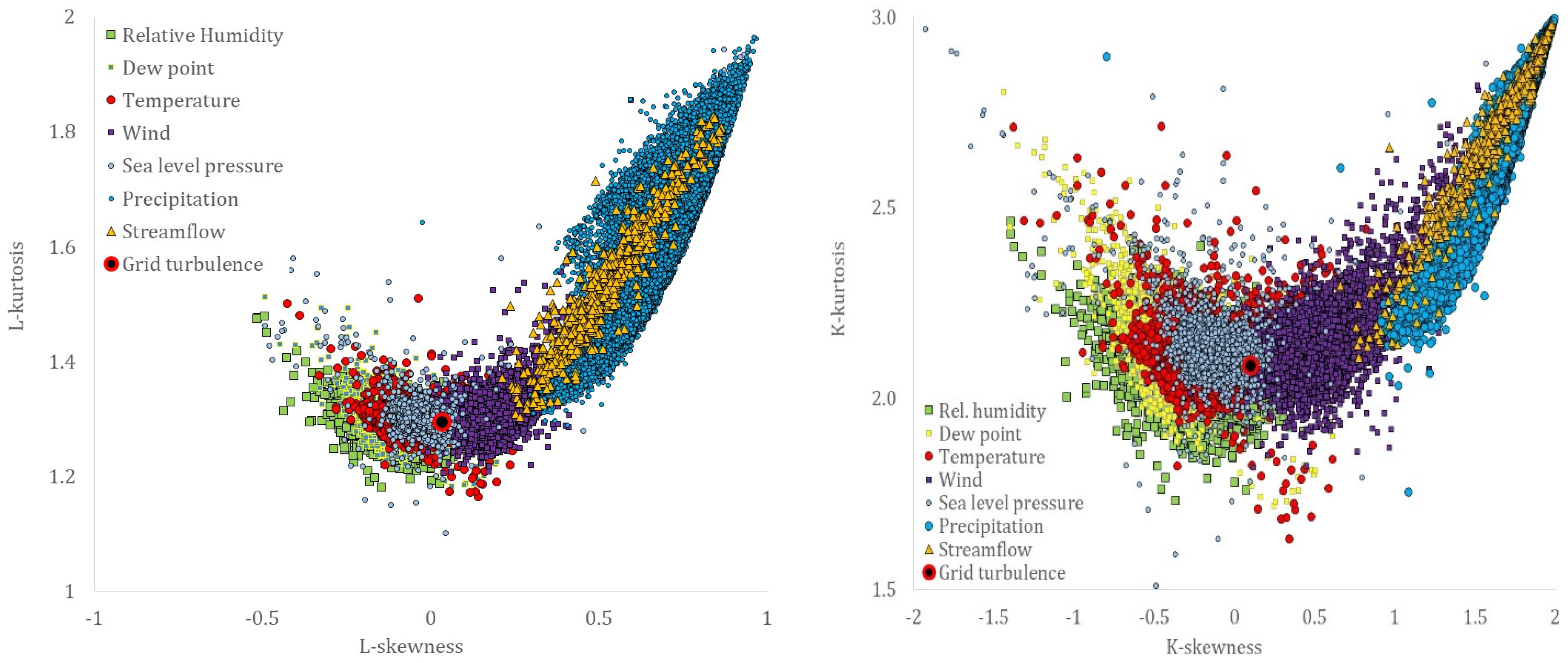
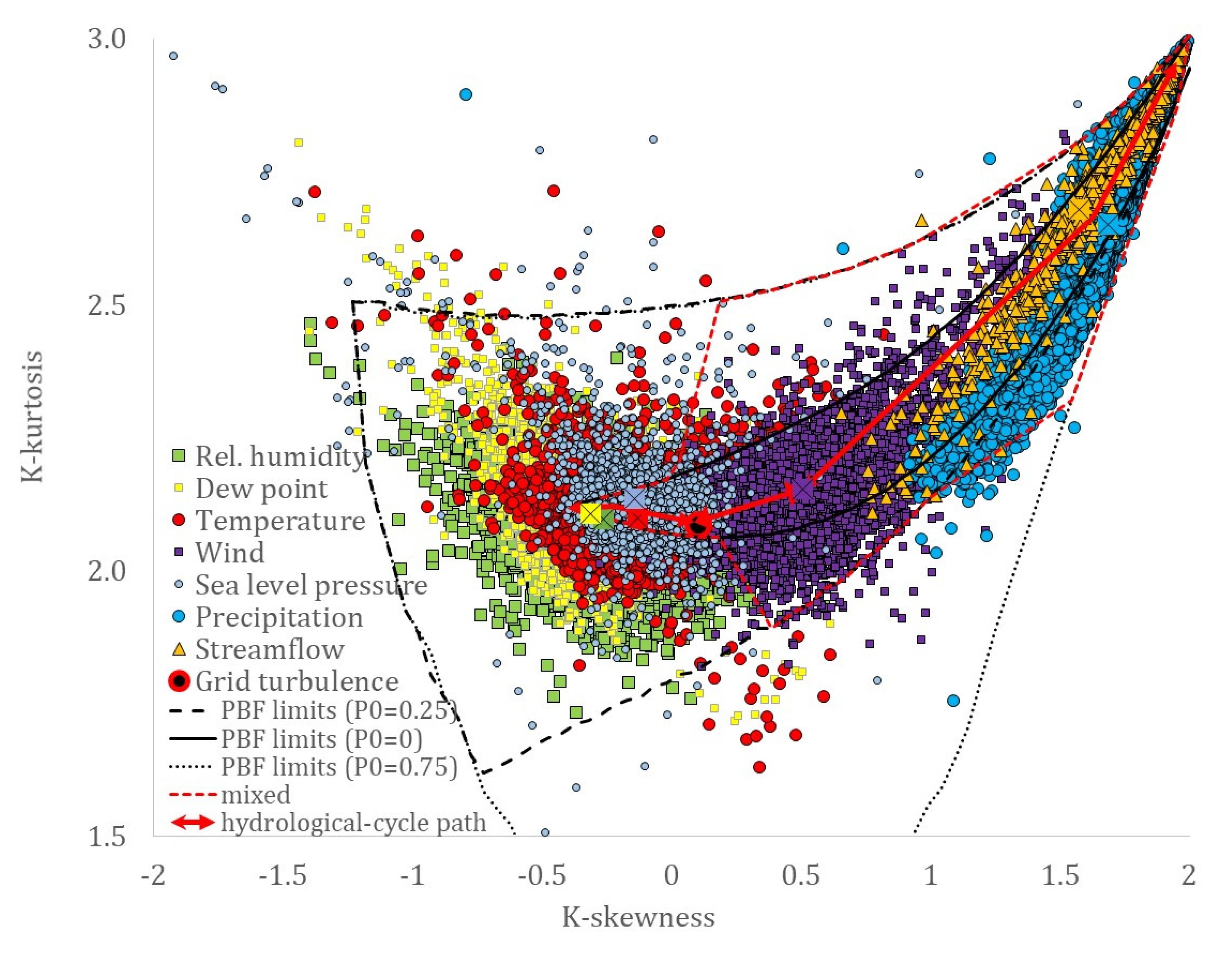
- A hierarchy related to the hydrological cycle was identified with the dew point, temperature, relative humidity, solar radiation, and sea level pressure all exhibiting a lower skewness over kurtosis absolute ratio than the turbulent processes, wind speed, and ocean waves, and with a stronger long-term persistence (LTP) behavior in the dependence structure (H > 0.75), followed by streamflow and precipitation, both of which exhibit a smaller skewness–kurtosis absolute ratio and a weaker LTP behavior (H ≤ 0.75).
- (2)
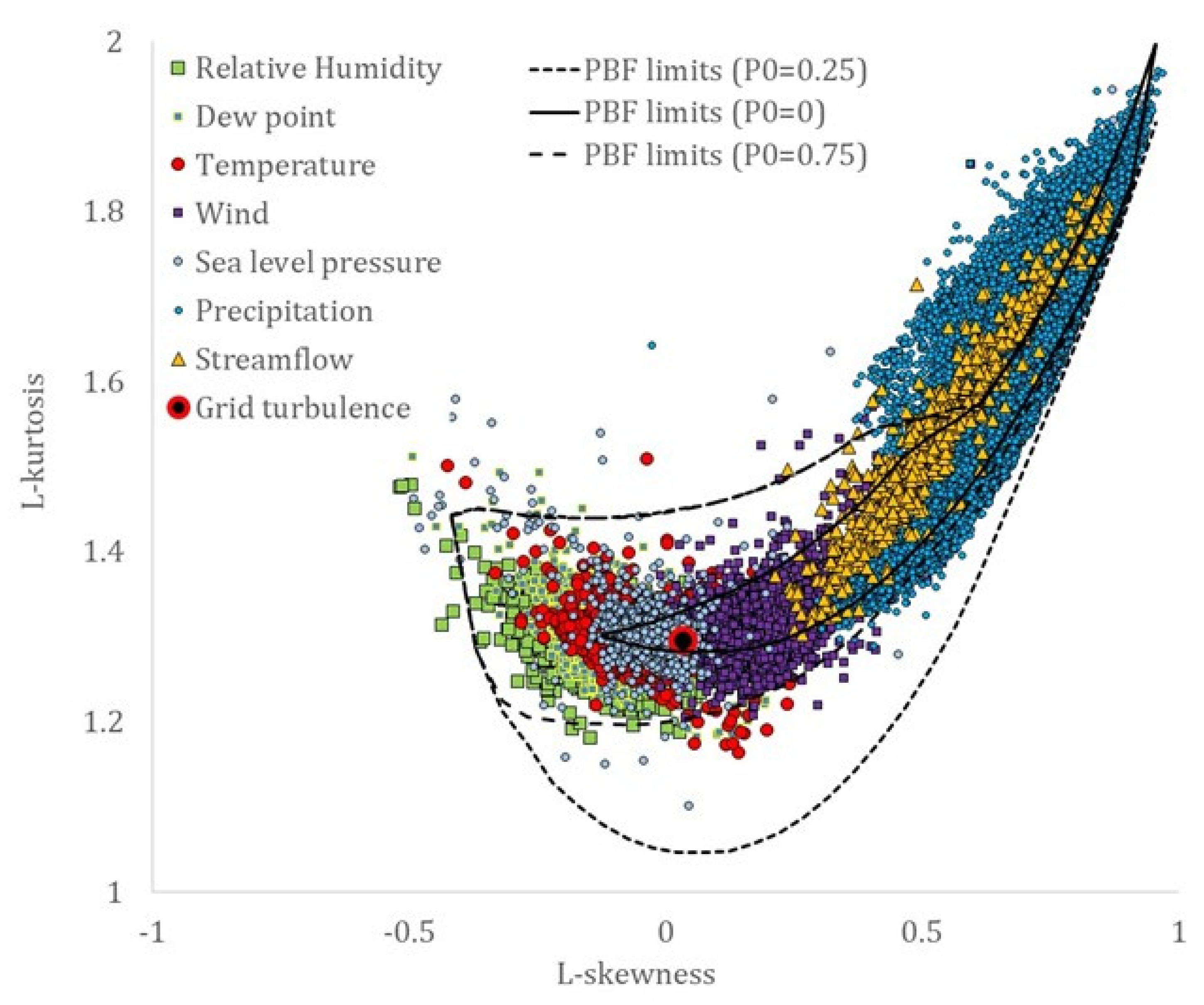
- All the examined processes can be adequately simulated by the truncated mixed-PBF distribution, adjusting for probability dry and lower (or upper) truncation, in terms of the first four moments, and ranging from (truncated) nearly Gaussian to Pareto-type tails.
- (3)
- As the sample size increases, different records of the same process from several locations converge to a smaller area of the nondimensionalized statistics (skewness–kurtosis), indicating a common marginal behavior.
- (4)
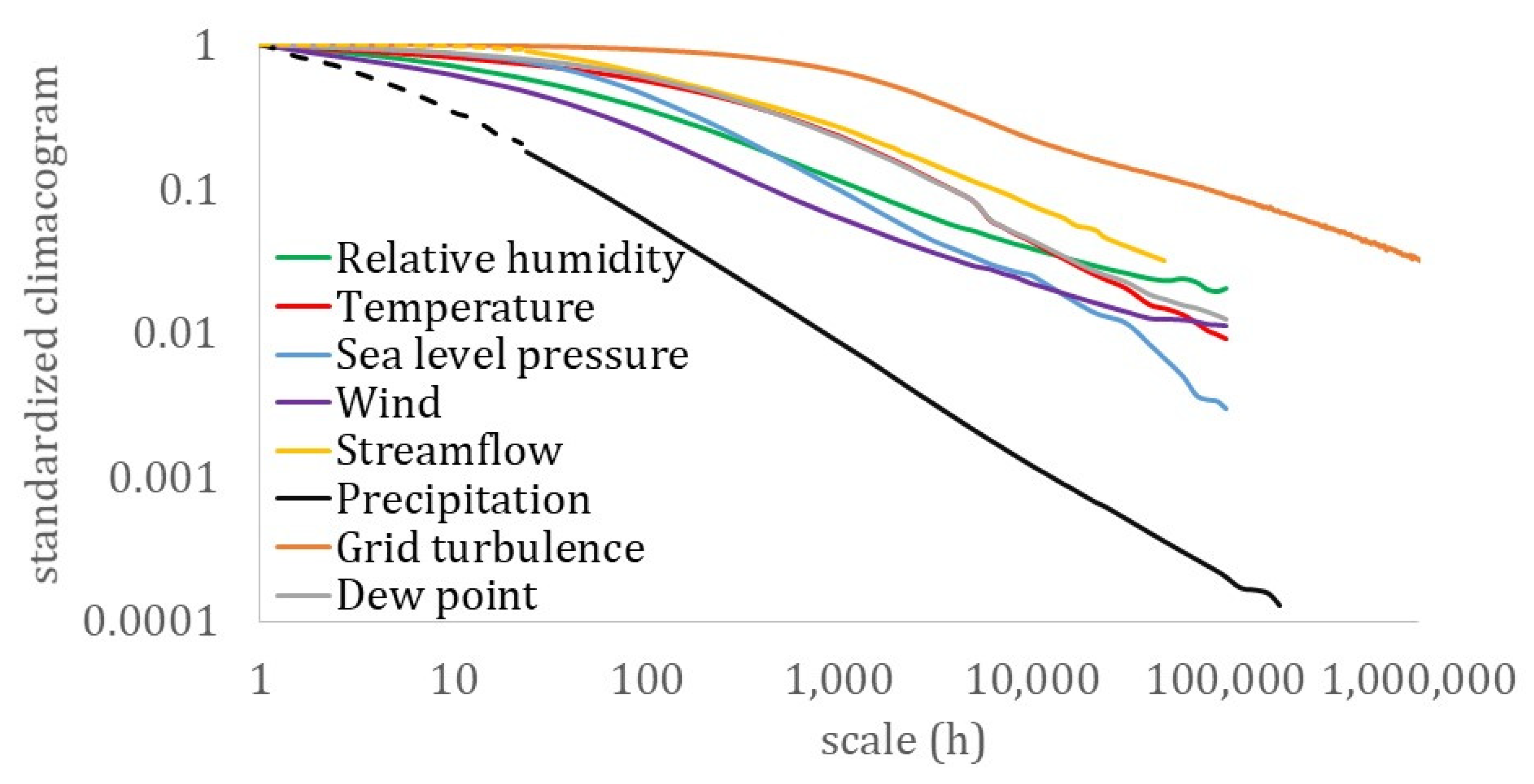
- All the examined hydrological-cycle processes exhibit a similar dependence structure that extends from the fractal behavior with roughness (M < 0.5) located at the small-intermittent scales to the LTP behavior at large scales (H > 0.5), while both indicate large uncertainty and high climatic variability.
- (5)
- Finally, since the above empirical findings are consistent with previous studies and can be justified by the principle of maximum entropy, they allow for a uniting stochastic view of the hydrological-cycle processes under the Hurst–Kolmogorov (HK) dynamics in terms of both the marginal and dependence structures.
Author Contributions
Funding

Acknowledgments
Conflicts of Interest
References
- Poincaré, H. Sur le probleme des trois corps et les équations de la dynamique. Acta Math. 1890, 13, A3–A270. [Google Scholar]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmospheric Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Stochastics of Hydroclimatic Extremes—A Cool Look at Risk; Edition 0; National Technical University of Athens: Athens, Greece, 2021; 330p. [Google Scholar]
- Dimitriadis, P.; Koutsoyiannis, D. Climacogram versus autocovariance and power spectrum in stochastic modelling for Markovian and Hurst–Kolmogorov processes. Stoch. Environ. Res. Risk Assess. 2015, 29, 1649–1669. [Google Scholar] [CrossRef]
- Falkovich, G.; Fouxon, A.; Stepanov, M.G. Acceleration of rain initiation by cloud turbulence. Nat. Cell Biol. 2002, 419, 151–154. [Google Scholar] [CrossRef]
- Langousis, A.; Veneziano, D. Long-term rainfall risk from tropical cyclones in coastal areas. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Wilson, J.D.; Sawford, B.L. Review of Lagrangian stochastic models for trajectories in the turbulent atmosphere. Bound. Layer Meteorol. 1996, 78, 191–210. [Google Scholar] [CrossRef]
- Ghannam, K.; Katul, G.G.; Bou-Zeid, E.; Gerken, T.; Chamecki, M. Scaling and Similarity of the Anisotropic Coherent Eddies in Near-Surface Atmospheric Turbulence. J. Atmospheric Sci. 2018, 75, 943–964. [Google Scholar] [CrossRef]
- Ayet, A.; Katul, G.G.; Bragg, A.D.; Redelsperger, J.L. Scalewise Return to Isotropy in Stratified Boundary Layer Flows. J. Geophys. Res. Atmos. 2020, 125. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Wiener Spirals and Some Other Interesting Curves in a Hilbert Space; Selected Works of Mathematics and Mechanics; Kolmogorov, A.N., Tikhomirov, V.M., Eds.; Kluwer: Dordrecht, The Netherlands, 1991; pp. 303–307. [Google Scholar]
- Mandelbrot, B.B. A Fast Fractional Gaussian Noise Generator. Water Resour. Res. 1971, 7, 543–553. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. HESS opinions, A random walk on water. Hydrol. Earth Syst. Sci. 2010, 14, 585–601. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Hurst–Kolmogorov dynamics as a result of extremal entropy production. Phys. A: Stat. Mech. its Appl. 2011, 390, 1424–1432. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Hurst-Kolmogorov dynamics and uncertainty. J. Am. Water Resourc. Assoc. 2011, 47, 481–495. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Entropy: From Thermodynamics to Hydrology. Entropy 2014, 16, 1287–1314. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Entropy Production in Stochastics. Entropy 2017, 19, 581. [Google Scholar] [CrossRef]
- Dimitriadis, P. Hurst-Kolmogorov Dynamics in Hydrometeorological Processes and in the Microscale of Turbulence. Ph.D. Thesis, National Technical University of Athens, Athens, Greece, 2017; 167p. [Google Scholar]
- Koutsoyiannis, D. The Hurst phenomenon and fractional Gaussian noise made easy. Hydrol. Sci. J. 2002, 47, 573–595. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Generic and parsimonious stochastic modelling for hydrology and beyond. Hydrol. Sci. J. 2016, 61, 225–244. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. A generalized mathematical framework for stochastic simulation and forecast of hydrologic time series. Water Resour. Res. 2000, 36, 1519–1533. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Time’s arrow in stochastic characterization and simulation of atmospheric and hydrological processes. Hydrol. Sci. J. 2019, 64, 1013–1037. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Simple stochastic simulation of time irreversible and reversible processes. Hydrol. Sci. J. 2020, 65, 536–551. [Google Scholar] [CrossRef]
- Lombardo, F.; Volpi, E.; Koutsoyiannis, D. Rainfall downscaling in time: Theoretical and empirical comparison between multifractal and Hurst-Kolmogorov discrete random cascades. Hydrol. Sci. J. 2012, 57, 1052–1066. [Google Scholar] [CrossRef][Green Version]
- Efstratiadis, A.Y.; Dialynas, S.; Kozanis; Koutsoyiannis, D. A multivariate stochastic model for the generation of synthet-ic time series at multiple time scales reproducing long-term persistence. Environ. Model. Softw. 2014, 62, 139–152. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Koutsoyiannis, D. Stochastic synthesis approximating any process dependence and distribution. Stoch. Environ. Res. Risk Assess. 2018, 32, 1493–1515. [Google Scholar] [CrossRef]
- Kossieris, P.; Makropoulos, C.; Onof, C.; Koutsoyiannis, D. A rainfall disaggregation scheme for sub-hourly time scales: Coupling a Bartlett-Lewis based model with adjusting procedures. J. Hydrol. 2018, 556, 980–992. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Markonis, Y.; Lombardo, F.; AghaKouchak, A.; Foufoula-Georgiou, E. Precise Temporal Disaggregation Preserving Marginals and Correlations (DiPMaC) for Stationary and Nonstationary Processes. Water Resour. Res. 2018, 54, 7435–7458. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Serinaldi, F. Random Fields Simplified: Preserving Marginal Distributions, Correlations, and Intermittency, With Applications from Rainfall to Humidity. Water Resour. Res. 2020, 56. [Google Scholar] [CrossRef]
- Tsoukalas, I.; Makropoulos, C.; Koutsoyiannis, D. Simulation of Stochastic Processes Exhibiting Any-Range Dependence and Arbitrary Marginal Distributions. Water Resour. Res. 2018, 54, 9484–9513. [Google Scholar] [CrossRef]
- Tsoukalas, I.; Kossieris, P.; Makropoulos, C. Simulation of Non-Gaussian Correlated Random Variables, Stochastic Processes and Random Fields: Introducing the anySim R-Package for Environmental Applications and beyond. Water 2020, 12, 1645. [Google Scholar] [CrossRef]
- Papoulis, A.; Pillai, S.U. Stochastic Processes; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Lombardo, F.C.; Volpi, E.; Koutsoyiannis, D.; Papalexiou, S.M. Just two moments! A cautionary note against use of high-order moments in multifractal models in hydrology. Hydrol. Earth Syst. Sci. 2014, 18, 243–255. [Google Scholar] [CrossRef]
- Geweke, J.; Porter-Hudak, S. The estimation and application of long memory time series models. J. Time Ser. Anal. 1983, 4, 221–238. [Google Scholar] [CrossRef]
- Beran, J. Statistical Methods for Data with Long-Range Dependence. Stat. Sci. 1992, 7, 404–416. [Google Scholar]
- Beran, J. Estimation, Testing and Prediction for Self-Similar and Related Processes. Ph.D. Thesis, ETH, Zurich, Switzerland, 1986. [Google Scholar]
- Mandelbrot, B.B.; Wallis, J.R. Noah, Joseph and operational hydrology. Water Resour. Res. 1968, 4, 909–918. [Google Scholar] [CrossRef]
- Granger, C.W.J.; Joyeux, R. An Introduction to Long-memory Time Series, Models and Fractional Differencing. J. Time Ser. Anal. 1980, 1, 15–29. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Climate change impacts on hydrological science: A comment on the relationship of the climacogram with Allan variance and variogram. ResearchGate 2018. [Google Scholar] [CrossRef]
- Smith, F.H. An empirical law describing heterogeneity in the yields of agricultural crops. Agric. Sci. 1938, 28, 1–23. [Google Scholar] [CrossRef]
- Cox, D.R. Long-Range Dependence: A review, Statistics: An Appraisal. In Proceedings of the 50th Anniversary Conference; David, H.A., David, H.T., Eds.; Iowa State University Press: Iowa City, IA, USA, 1984; pp. 55–74. [Google Scholar]
- Beran, J. A Test of Location for Data with Slowly Decaying Serial Correlations. Biometrika 1989, 76, 261. [Google Scholar] [CrossRef]
- Beran, J. Statistical Aspects of Stationary Processes with Long-Range Dependence; Mimeo Series 1743; Department Statistics University: Chapel Hill, NC, USA, 1988. [Google Scholar]
- Montanari, A.; Rosso, R.; Taqqu, M.S. Fractionally differenced ARIMA models applied to hydrologic time series: Identification, estimation, and simulation. Water Resour. Res. 1997, 33, 1035–1044. [Google Scholar] [CrossRef]
- Montanari, A.; Taqqu, M.S.; Teverovsky, V. Estimating long-range dependence in the presence of periodicity: An empiri-cal study. Math. Comput. Modeling 1999, 29, 217–228. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Hydrologic Persistence and the Hurst Phenomenon, Water Encyclopedia; Surface and Agricultural Water; Lehr, J.H., Keeley, J., Eds.; Wiley: New York, NY, USA, 2005; Volume 4, pp. 210–221. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Climate change, the Hurst phenomenon, and hydrological statistics. Hydrol. Sci. J. 2003, 48, 3–24. [Google Scholar] [CrossRef]
- Tyralis, H.; Koutsoyiannis, D. Simultaneous estimation of the parameters of the Hurst–Kolmogorov stochastic process. Stoch. Environ. Res. Risk Assess. 2010, 25, 21–33. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Encolpion of Stochastics: Fundamentals of Stochastic Processes; Department of Water Resources and Environmental Engineering—National Technical University of Athens: Athens, Greece, 2013. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Paschalis, A.; Theodoratos, N. Two-dimensional Hurst–Kolmogorov process and its application to rainfall fields. J. Hydrol. 2011, 398, 91–100. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Koutsoyiannis, D.; Onof, C. N-Dimensional generalized Hurst-Kolmogorov process and its application to wind fields. In Proceedings of the Facets of Uncertainty: 5th EGU Leonardo Conference—Hydrofractals 2013—STAHY 2013, Kos Island, Greece, 17–19 October 2013; European Geosciences Union, International Association of Hydrological Sciences. International Union of Geodesy and Geophysics: Prague, Czech Republic, 2013. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Hydrology and Change. Hydrol. Sci. J. 2013, 58, 1177–1197. [Google Scholar] [CrossRef]
- Markonis, Y.; Koutsoyiannis, D. Climatic Variability over Time Scales Spanning Nine Orders of Magnitude: Connecting Milankovitch Cycles with Hurst–Kolmogorov Dynamics. Surv. Geophys. 2012, 34, 181–207. [Google Scholar] [CrossRef]
- Markonis, Y.; Koutsoyiannis, D. Scale-dependence of persistence in precipitation records. Nat. Clim. Chang. 2015, 6, 399–401. [Google Scholar] [CrossRef]
- Tyralis, H.; Koutsoyiannis, D. A Bayesian statistical model for deriving the predictive distribution of hydroclimatic varia-bles. Clim. Dyn. 2014, 42, 2867–2883. [Google Scholar] [CrossRef]
- Iliopoulou, T.S.M.; Papalexiou, Y.; Markonis; Koutsoyiannis, D. Revisiting long-range dependence in annual precipita-tion. J. Hydrol. 2018, 556, 891–900. [Google Scholar] [CrossRef]
- Kossieris, P.; Tsoukalas, I.; Makropoulos, C.; Savic, D. Simulating Marginal and Dependence Behaviour of Water Demand Processes at Any Fine Time Scale. Water 2019, 11, 885. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. Understanding Persistence to Avoid Underestimation of Collective Flood Risk. Water 2016, 8, 152. [Google Scholar] [CrossRef]
- Serinaldi, F. Can we tell more than we can know? The limits of bivariate drought analyses in the United States. Stoch. Environ. Res. Risk Assess. 2015, 30, 1691–1704. [Google Scholar] [CrossRef]
- Tsekouras, G.; Koutsoyiannis, D. Stochastic analysis and simulation of hydrometeorological processes associated with wind and solar energy. Renew. Energy 2014, 63, 624–633. [Google Scholar] [CrossRef]
- Mamassis, N.; Efstratiadis, A.; Dimitriadis, P.; Iliopoulou, T.; Ioannidis, R.; Koutsoyiannis, D. Water and Energy, Handbook of Water Resources Management: Discourses, Concepts and Examples; Bogardi, J.J., Tingsanchali, T., Nandalal, K.D.W., Gupta, J., Salamé, L., van Nooijen, R.R.P., Kolechkina, A.G., Kumar, N., Bhaduri, A., Eds.; Springer Nature: Cham, Switzerland, 2021; Chapter 20; pp. 617–655. [Google Scholar] [CrossRef]
- Koudouris, G.P.; Dimitriadis, T.; Iliopoulou, N.; Mamassis; Koutsoyiannis, D. A stochastic model for the hourly solar ra-diation process for application in renewable resources management. Adv. Geosci. 2018, 45, 139–145. [Google Scholar] [CrossRef]
- Moschos, E.; Manou, G.; Dimitriadis, P.; Afendoulis, V.; Koutsoyiannis, D.; Tsoukala, V. Harnessing wind and wave resources for a Hybrid Renewable Energy System in remote islands: a combined stochastic and deterministic approach. Energy Proc. 2017, 125, 415–424. [Google Scholar] [CrossRef]
- Aguilar, C.; Montanari, A.; Polo, M.-J. Real-time updating of the flood frequency distribution through data assimilation. Hydrol. Earth Syst. Sci. 2017, 21, 3687–3700. [Google Scholar] [CrossRef]
- Giglioni, M.; Lombardo, F.; Mineo, C. Investigating the Hurst-Kolmogorov Behavior of Sicily’s Climatological Time Series. In Proceedings of the International Conference of Numerical Analysis and Applied Mathematics (ICNAAM 2016), Rhodes, Greece, 19–25 September 2016; AIP Publishing: College Park, MD, USA, 2017; Volume 470004. [Google Scholar]
- Markonis, Y.Y.; Moustakis, C.; Nasika, P.; Sychova, P.; Dimitriadis, M.; Hanel, P.; Máca; Papalexiou, S.M. Global estima-tion of long-term persistence in annual river runoff. Adv. Water Resour. 2018, 113, 1–12. [Google Scholar] [CrossRef]
- Pappas, C.M.D.; Mahecha, D.C.; Frank, F.; Babst; Koutsoyiannis, D. Ecosystem functioning is enveloped by hydromete-orological variability. Nature Ecol. Evol. 2017, 1, 1263–1270. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Tzouka, K.; Koutsoyiannis, D.; Tyralis, H.; Kalamioti, A.; Lerias, E.; Voudouris, P. Stochastic investigation of long-term persistence in two-dimensional images of rocks. Spat. Stat. 2019, 29, 177–191. [Google Scholar] [CrossRef]
- Jovanovic, D.; Jovanovic, T.; Mejía, A.; Hathaway, J.; Daly, E. Technical note: Long-term persistence loss of urban streams as a metric for catchment classification. Hydrol. Earth Syst. Sci. 2018, 22, 3551–3559. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Dimitriadis, P.; Lombardo, F.; Stevens, S.; Tsonis, A.A. From Fractals to Stochastics: Seeking Theoretical Consistency in Analysis of Geophysical Data. In Advances in Nonlinear Geosciences; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 237–278. [Google Scholar]
- Tsoukalas, I.; Efstratiadis, A.; Makropoulos, C. Building a puzzle to solve a riddle: A multi-scale disaggregation approach for multivariate stochastic processes with any marginal distribution and correlation structure. J. Hydrol. 2019, 575, 354–380. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Coupling stochastic models of different time scales. Water Resour. Res. 2001, 37, 379–391. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Langousis, A. Precipitation, Treatise on Water Science; Wilderer, P., Uhlenbrook, S., Eds.; Academic Press: Oxford, UK, 2011; Volume 2, pp. 27–78. [Google Scholar]
- Papalexiou, S.-M.; Koutsoyiannis, D.; Montanari, A. Can a simple stochastic model generate rich patterns of rainfall events? J. Hydrol. 2011, 411, 279–289. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Koutsoyiannis, D.; Tzouka, K. Predictability in dice motion: How does it differ from hydrometeorological processes? Hydrol. Sci. J. 2016, 61, 1611–1622. [Google Scholar] [CrossRef]
- Dimitriadis, P.D.; Koutsoyiannis; Papanicolaou, P. Stochastic similarities between the microscale of turbulence and hydrometeorological processes. Hydrol. Sci. J. 2016, 61, 1623–1640. [Google Scholar] [CrossRef]
- Park, J.; Onof, C.; Kim, D. A hybrid stochastic rainfall model that reproduces some important rainfall characteristics at hourly to yearly timescales. Hydrol. Earth Syst. Sci. 2019, 23, 989–1014. [Google Scholar] [CrossRef]
- Kim, D.; Onof, C. A stochastic rainfall model that can reproduce important rainfall properties across the timescales from several minutes to a decade. J. Hydrol. 2020, 589, 125150. [Google Scholar] [CrossRef]
- Sargentis, G.-F.; Dimitriadis, P.; Ioannidis, R.; Iliopoulou, T.; Koutsoyiannis, D. Stochastic Evaluation of Landscapes Trans-formed by Renewable Energy Installations and Civil Works. Energies 2019, 12, 2817. [Google Scholar] [CrossRef]
- Sargentis, G.-F.; Ioannidis, R.; Iliopoulou, T.; Dimitriadis, P.; Koutsoyiannis, D. Landscape Planning of Infrastructure through Focus Points’ Clustering Analysis. Case Study: Plastiras Artificial Lake (Greece). Infrastructures 2021, 6, 12. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Koutsoyiannis, D. The mode of the climacogram estimator for a Gaussian Hurst-Kolmogorov process. J. Hydroinformatics 2019, 22, 160–169. [Google Scholar] [CrossRef]
- Pizarro, A.P.; Dimitriadis, C.; Samela, D.; Koutsoyiannis, O.; Link; Manfreda, S. Discharge Uncertainty on Bridge Scour Process, European Geosciences Union General Assembly 2018; Geophysical Research Abstracts; EGU2018-8045; European Geosciences Union: Vienna, Austria, 2018; Volume 20. [Google Scholar]
- Sargentis, G.F.P.; Dimitriadis, T.; Iliopoulou, R.; Ioannidis; Koutsoyiannis, D. Stochastic investigation of the Hurst-Kolmogorov behaviour in arts, European Geosciences Union General Assembly 2018; Geophysical Research Abstracts; EGU2018-17740-1; European Geosciences Union: Vienna, Austria, 2018; Volume 20. [Google Scholar]
- Sargentis, G.-F.; Dimitriadis, P.; Koutsoyiannis, D. Aesthetical Issues of Leonardo Da Vinci’s and Pablo Picasso’s Paintings with Stochastic Evaluation. Heritage 2020, 3, 17. [Google Scholar] [CrossRef]
- Sargentis, G.-F.; Dimitriadis, P.; Iliopoulou, T.; Koutsoyiannis, D. A Stochastic View of Varying Styles in Art Paintings. Heritage 2021, 4, 21. [Google Scholar] [CrossRef]
- Sargentis, G.-F.T.; Iliopoulou, S.; Sigourou, P.; Dimitriadis; Koutsoyiannis, D. Evolution of clustering quantified by a stochastic method—Case studies on natural and human social structures. Sustainability 2020, 12, 7972. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Knowable moments for high-order stochastic characterization and modelling of hydrological processes. Hydrol. Sci. J. 2019, 64, 19–33. [Google Scholar] [CrossRef]
- Markonis, Y.; Pappas, C.; Hanel, M.; Papalexiou, S.M. A cross-scale framework for integrating multi-source data in Earth system sciences. Environ. Model. Softw. 2021, 139, 104997. [Google Scholar] [CrossRef]
- Glynis, K.T.; Iliopoulou, P.; Dimitriadis, D. Koutsoyiannis, Stochastic investigation of daily air temperature extremes from a global ground station network. Stoch. Environ. Res. Risk Assess. 2021. [Google Scholar]
- Katikas, L.; Dimitriadis, P.; Koutsoyiannis, D.; Kontos, T.; Kyriakidis, P. A stochastic simulation scheme for the long-term persistence, heavy-tailed and double periodic behavior of observational and reanalysis wind time-series. Appl. Energy 2021. [Google Scholar]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. J. Soc. Ind. Appl. Math. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH freeman: New York, NY, USA, 1983; Volume 173, p. 51. [Google Scholar]
- Gneiting, T. Power-law correlations, related models for long-range dependence and their simulation. J. Appl. Probab. 2000, 37, 1104–1109. [Google Scholar] [CrossRef]
- Gneiting, T.; Schlather, M. Stochastic Models That Separate Fractal Dimension and the Hurst Effect. SIAM Rev. 2004, 46, 269–282. [Google Scholar] [CrossRef]
- Gneiting, T.; Ševčíková, H.; Percival, D.B. Estimators of Fractal Dimension: Assessing the Roughness of Time Series and Spatial Data. Stat. Sci. 2012, 27, 247–277. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. R. Stat. Soc. Ser. B Stat. Methodol. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Singh, S.K.; Maddala, G.S. A Function for Size Distribution of Incomes: Reply. Economic 1978, 46, 461. [Google Scholar] [CrossRef]
- Newman, M.E.J. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef]
- Burr, I.W. Cumulative Frequency Functions. Ann. Math. Stat. 1942, 13, 215–232. [Google Scholar] [CrossRef]
- Feller, W. Law of large numbers for identically distributed variables. Introd. Probab. Theory Appl. 1971, 2, 231–234. [Google Scholar]
- Arnold, B.C.; Press, S. Bayesian inference for pareto populations. J. Econ. 1983, 21, 287–306. [Google Scholar] [CrossRef]
- Lott, J.N.; Baldwin, R. The FCC Integrated Surface Hourly Database, a New Resource of Global Climate Data. In Proceedings of the 13th Symposium on Global Change and Climate Variations, Orlando, FL, USA, 13–17 January 2002; Paper 27792. American Meteorological Society: Boston, MA, USA, 2002. Available online: https://ams.confex.com/ams/annual2002/webprogram/Paper27792.html (accessed on 15 December 2020).
- Lott, J.N. The Quality Control of the Integrated Surface Hourly Database. In Proceedings of the 14th Conference on Applied Climatology, Seattle, WA, USA, 11–15 January 2004; Paper 71929. American Meteorological Society: Boston, MA, USA, 2004. [Google Scholar]
- Lott, J.N.; Baldwin, R.; Anders, D.D. Recent Advances in in-Situ Data Access, Summarization, and Visualization at NOAA’s National Climatic Data Center. In Proceedings of the 22nd International Conference on Interactive Information Processing Systems for Meteorology, Oceanography, and Hydrology (IIPS), Atlanta, GA, USA, 18–22 September 2006; Paper 100684. American Meteorological Society: Boston, MA, USA, 2006. [Google Scholar]
- Del Greco, S.A.; Lott, J.N.; Hawkins, S.K.; Baldwin, R.; Anders, D.D.; Ray, R.; Dellinger, D.; Jones, P.; Smith, F. Surface data integration at NOAA’s National Climatic Data Center: Data format, processing, QC, and product generation. In Proceedings of the 22nd Interna-tional Conference on Interactive Information Processing Systems for Meteorology, Oceanography, and Hydrology (IIPS), Atlanta, GA, USA, 18–22 September 2006; Paper 100500. American Meteorological Society: Boston, MA, USA, 2006. [Google Scholar]
- Del Greco, S.A.; Lott, J.N.; Ray, R.; Dellinger, D.; Smith, F.; Jones, P. Surface data processing and integration at NOAA’s National Climatic Data Center. In Proceedings of the 23rd Conference on Interactive Information Processing Systems for Meteorology, Oceanog-raphy, and Hydrology (IIPS), San Antonio, TX, USA, 15–18 January 2007; Paper 116367. American Meteorological Society: Boston, MA, USA, 2007. [Google Scholar]
- Baldwin, R.; Ansari, S.; Lott, N.; Reid, G. Accessing Geographic Information Services and Visualization Products at NOAA’s National Climatic Data Center. In Proceedings of the 22nd International Conference on Interactive Information Processing Systems for Meteorology, Oceanography, and Hydrology (IIPS), San Antonio, TX, USA, 28 January–2 February 2006; Paper 116734. American Meteorological Society: Boston, MA, USA, 2007. [Google Scholar]
- Lott, J.N.; Vose, R.S.; del Greco, S.A.; Ross, T.R.; Worley, S.; Comeaux, J.L. The Integrated Surface Database: Partner-Ships and Progress. In Proceedings of the 24th Conference on Interactive Information Processing Systems for Meteorology, Oceanography, and Hydrology (IIPS), New Orleans, LA, USA, 20–24 January 2008; Paper 131387. American Meteorological Society: Boston, MA, USA, 2008. [Google Scholar]
- Smith, A.; Lott, N.; Vose, R.S. The Integrated Surface Database: Recent Developments and Partnerships. Bull. Am. Meteorol. Soc. 2011, 92, 704–708. [Google Scholar] [CrossRef]
- Dunn, R.J.H.; Willett, K.M.; Thorne, P.W.; Woolley, E.V.; Durre, I.; Dai, A.; Parker, D.E.; Vose, R.E. HadISD: A quality-controlled global synoptic report database for selected variables at long-term stations from 1973–2011. Clim. Past 2012, 8, 1649–1679. [Google Scholar] [CrossRef]
- Rennie, J.J.; Lawrimore, J.; Gleason, H.; Thorne, B.E.; Morice, P.W.; Menne, C.P.; Williams, M.J.; de Almeida, N.C.; Christy, W.G.; Flannery, J.M.; et al. The international surface temperature initia-tive global land surface databank: Monthly temperature data release description and methods. Geosci. Data J. 2014, 1, 75–102. [Google Scholar] [CrossRef]
- Newman, A.; Sampson, K.; Clark, M.P.; Bock, A.; Viger, R.J.; Blodgett, D. A Large-Sample Watershed-Scale Hydrometeorological Dataset for the Contiguous USA; UCAR/NCAR: Boulder, CO, USA, 2014. [Google Scholar] [CrossRef]
- Newman, A.J.; Clark, M.P.; Sampson, K.; Wood, A.; Hay, L.E.; Bock, A.; Viger, R.J.; Blodgett, D.; Brekke, L.; Arnold, J.R.; et al. Development of a large-sample watershed-scale hydrometeorological dataset for the contiguous USA: dataset characteristics and assessment of regional variability in hydrologic model performance. Hydrol. Earth Syst. Sci. 2015, 19, 209–223. [Google Scholar] [CrossRef]
- Addor, N.; Newman, A.; Mizukami, M.; Clark, M.P. Catchment Attributes for Large-Sample Studies; UCAR/NCAR: Boulder, CO, USA, 2017. [Google Scholar] [CrossRef]
- Addor, N.; Newman, A.J.; Mizukami, N.; Clark, M.P. The CAMELS data set: Catchment attributes and meteorology for large-sample studies. Hydrol. Earth Syst. Sci. 2017, 21, 5293–5313. [Google Scholar] [CrossRef]
- Ryberg, K.R.; Kolars, K.A.; Kiang, J.E.; Carr, M.L. Flood-Frequency Estimation for Very Low Annual Exceedance Probabilities Using Historical, Paleoflood, and Regional Information with Consideration of Nonstationarity; Scientific Investigations Report, 2020–5065; U.S. Nuclear Regulatory Commission: Rockville, MD, USA, 2020. [CrossRef]
- Vose, R.S.; Schmoyer, R.L.; Steurer, P.M.; Peterson, T.C.; Heim, R.; Karl, T.R.; Eischeid, J.K. The Global Historical Climatology Network: Long-Term Monthly Temperature, Precipitation, Sea Level Pressure, and Station Pressure Data; NOAA: Washington, DC, USA, 1992. [CrossRef]
- Lawrimore, J.H.; Menne, M.J.; Gleason, B.E.; Williams, C.N.; Wuertz, D.B.; Vose, R.S.; Rennie, J. An overview of the Global Historical Climatology Network monthly mean temperature dataset, version 3. J. Geophys. Res. 2011, 116, D19121. [Google Scholar] [CrossRef]
- Menne, M.J.I.; Durre, B.G.; Gleason, T.G.; Houston; Vose, R.S. An overview of the Global Historical Climatology Net-work-Daily database. J. Atmos. Ocean. Technol. 2012, 29, 897–910. [Google Scholar] [CrossRef]
- Durre, I.; Menne, M.J.; Vose, R.S. Strategies for Evaluating Quality Assurance Procedures. J. Appl. Meteorol. Clim. 2008, 47, 1785–1791. [Google Scholar] [CrossRef]
- Durre, I.; Menne, M.J.; Gleason, B.E.; Houston, T.G.; Vose, R.S. Comprehensive Automated Quality Assurance of Daily Surface Observations. J. Appl. Meteorol. Clim. 2010, 49, 1615–1633. [Google Scholar] [CrossRef]
- Montanari, A. Hydrology of the Po River: Looking for changing patterns in river discharge. Hydrol. Earth Syst. Sci. 2012, 16, 3739–3747. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Yao, H.; Georgakakos, A. Medium-range flow prediction for the Nile: A comparison of stochastic and deterministic methods / Prévision du débit du Nil à moyen terme: Une comparaison de méthodes stochastiques et déterministes. Hydrol. Sci. J. 2008, 53, 142–164. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Clausius-Clapeyron equation and saturation vapour pressure: Simple theory reconciled with practice. Eur. J. Phys. 2012, 33, 295–305. [Google Scholar] [CrossRef]
- Gaffen, D.J.; Ross, R.J. Climatology and Trends of U.S. Surface Humidity and Temperature. J. Clim. 1999, 12, 811–828. [Google Scholar] [CrossRef]
- Dettinger, M.D.; Diaz, H.F. Global Characteristics of Stream Flow Seasonality and Variability. J. Hydrometeorol. 2000, 1, 289–310. [Google Scholar] [CrossRef]
- Yang, G.Y.; Slingo, J. The diurnal cycle in the tropics. Mon. Weather Rev. 2001, 129, 784–801. [Google Scholar] [CrossRef]
- Nesbitt, S.W.; Zipser, E.J. The diurnal cycle of rainfall and convective intensity according to three years of TRMM meas-urements. J. Clim. 2003, 16, 1456–1475. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Koutsoyiannis, D. Application of stochastic methods to double cyclostationary processes for hourly wind speed simulation. Energy Procedia 2015, 76, 406–411. [Google Scholar] [CrossRef][Green Version]
- Deligiannis, I.; Dimitriadis, P.; Daskalou, O.; Dimakos, Y.; Koutsoyiannis, D. Global Investigation of Double Periodicity οf Hourly Wind Speed for Stochastic Simulation; Application in Greece. Energy Procedia 2016, 97, 278–285. [Google Scholar] [CrossRef]
- Villarini, G. On the seasonality of flooding across the continental United States. Adv. Water Resour. 2016, 87, 80–91. [Google Scholar] [CrossRef]
- Iliopoulou, T.; Koutsoyiannis, D.; Montanari, A. Characterizing and Modeling Seasonality in Extreme Rainfall. Water Resour. Res. 2018, 54, 6242–6258. [Google Scholar] [CrossRef]
- Tegos, A.H.; Tyralis, D.; Koutsoyiannis; Hamed, K.H. An R function for the estimation of trend signifcance under the scaling hypothesis- application in PET parametric annual time series. Open Water J. 2017, 4, 66–71. [Google Scholar]
- Tegos, A.; Malamos, N.; Efstratiadis, A.; Tsoukalas, I.; Karanasios, A.; Koutsoyiannis, D. Parametric Modelling of Potential Evapotranspiration: A Global Survey. Water 2017, 9, 795. [Google Scholar] [CrossRef]
- Kardakaris, K.M.; Kalli, T.; Agoris, P.; Dimitriadis, N.; Mamassis; Koutsoyiannis, D. Investigation of the Stochastic Structure of Wind Waves for Energy Production. In Proceedings of the European Geosciences Union General Assembly 2019, Geophysical Research Abstracts, Vienna, Austria, 7–12 April 2019; EGU2019-13188. European Geosciences Union: Munich, Germany, 2019; Volume 21. [Google Scholar]
- Kang, H.S.; Chester, S.; Meneveau, C. Decaying turbulence in an active-grid-generated flow and comparisons with large-eddy simulation. J. Fluid Mech. 2003, 480, 129–160. [Google Scholar] [CrossRef]
- Castro, J.J.; Carsteanu, A.A.; Fuentes, J.D. On the phenomenology underlying Taylor’s hypothesis in atmospheric tur-bulence. Rev. Mex. Física 2011, 57, 60–64. [Google Scholar]
- Papanicolaou, P.N.; List, E. Statistical and spectral properties of tracer concentration in round buoyant jets. Int. J. Heat Mass Transf. 1987, 30, 2059–2071. [Google Scholar] [CrossRef]
- Papanicolaou, P.N.; List, E.J. Investigations of round vertical turbulent buoyant jets. J. Fluid Mech. 1988, 195, 341. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Papanicolaou, P. Hurst-Kolmogorov dynamics applied to temperature field of horizontal turbulent buoyant jets. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 2–7 May 2010; p. 10644. [Google Scholar]
- Dimitriadis, P.; Papanicolaou, P.; Koutsoyiannis, D. Hurst-Kolmogorov Dynamics Applied to Temperature fields for Small Turbulence Scales. In Proceedings of the European Geosciences Union General Assembly; Geophysical Research Abstracts; EGU2011-772; European Geosciences Union: Vienna, Austria, 2011; Volume 13. [Google Scholar] [CrossRef]
- Montanari, A.; Young, G.; Savenije, H.H.G.; Hughes, D.; Wagener, T.; Ren, L.L.; Koutsoyiannis, D.; Cudennec, C.; Toth, E.; Grimaldi, S.; et al. Panta Rhei—everything flows”: Change in hydrology and society—The IAHS Scientific Decade 2013–2022. Hydrol. Sci. J. 2013, 58, 1256–1275. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Revisiting the global hydrological cycle: Is it intensifying? Hydrol. Earth Syst. Sci. 2020, 24, 3899–3932. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Rethinking climate, climate change, and their relationship with water. Water 2021, 13, 849. [Google Scholar] [CrossRef]
- Beran, J.; Feng, Y.; Ghosh, S.; Kulik, R. Long-Memory Processes. Long-Mem. Process. 2013. [Google Scholar] [CrossRef]
- O’Connell, P.; Koutsoyiannis, D.; Lins, H.F.; Markonis, Y.; Montanari, A.; Cohn, T. The scientific legacy of Harold Edwin Hurst (1880–1978). Hydrol. Sci. J. 2016, 61, 1571–1590. [Google Scholar] [CrossRef]
- Graves, T.; Gramacy, R.; Watkins, N.; Franzke, C. A Brief History of Long Memory: Hurst, Mandelbrot and the Road to ARFIMA, 1951–1980. Entropy 2017, 19, 437. [Google Scholar] [CrossRef]
- Cohn, T.A.; Lins, H.F. Nature’s style—Naturally trendy. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Iliopoulou, T.; Koutsoyiannis, D. Revealing hidden persistence in maximum rainfall records. Hydrol. Sci. J. 2019, 64, 1673–1689. [Google Scholar] [CrossRef]
- Iliopoulou, T.; Koutsoyiannis, D. Projecting the future of rainfall extremes: Better classic than trendy. J. Hydrol. 2020, 588, 125005. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Montanari, A. Statistical analysis of hydroclimatic time series: Uncertainty and insights. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Tyralis, H.P.; Dimitriadis, D.; Koutsoyiannis, P.E.; O’Connell, K.; Tzouka; Iliopoulou, T. On the long-range dependence properties of annual precipitation using a global network of instrumental measurements. Adv. Water Resour. 2018, 111, 301–318. [Google Scholar] [CrossRef]
- Sahoo, B.B.; Jha, R.; Singh, A.; Kumar, D. Long short-term memory (LSTM) recurrent neural network for low-flow hydrological time series forecasting. Acta Geophys. 2019, 67, 1471–1481. [Google Scholar] [CrossRef]
- Xian, M.; Liu, X.; Song, K.; Gao, T. Reconstruction and Nowcasting of Rainfall Field by Oblique Earth-Space Links Network: Preliminary Results from Numerical Simulation. J. Remote Sens. 2020, 12, 3598. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Papalexiou, S.M.; Langousis, A.; Khatami, S.; Volpi, E.; Grimaldi, S. Global-scale massive feature extraction from monthly hydroclimatic time series: Statistical characterizations, spatial patterns and hydrological similarity. arXiv 2020, arXiv:2010.12833. [Google Scholar]
- Vogel, R.M.; Tsai, Y.; Limbrunner, J.F. The regional persistence and variability of annual streamflow in the United States. Water Resour. Res. 1998, 34, 3445–3459. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. Irreversibility and complex network behavior of stream flow fluctuations. Phys. A Stat. Mech. Appl. 2016, 450, 585–600. [Google Scholar] [CrossRef]
- Charakopoulos, A.Κ.; Karakasidis, T.E.; Papanicolaou, P.N.; Liakopoulos, A. The application of complex network time series analysis in turbulent heated jets. Chaos: Interdiscip. J. Nonlinear Sci. 2014, 24, 024408. [Google Scholar] [CrossRef] [PubMed]
- Charakopoulos, A.K.; Karakasidis, T.E.; Papanicolaou, P.N.; Liakopoulos, A. Nonlinear time series analysis and clustering for jet axis identification in vertical turbulent heated jets. Phys. Rev. E 2014, 89, 032913. [Google Scholar] [CrossRef]
- Nordin, C.F.; McQuivey, R.S.; Mejia, J.M. Hurst phenomenon in turbulence. Water Resour. Res. 1972, 8, 1480–1486. [Google Scholar] [CrossRef]
- Helland, K.N.; Van Atta, C.W. The ‘Hurst phenomenon’in grid turbulence. J. Fluid Mech. 1978, 85, 573–589. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The local Structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 1941, 30, 299–303. (In Russian) [Google Scholar]
- Kolmogorov, A.N. Dissipation of energy in the locally isotropic turbulence. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1991, 434, 15–17. [Google Scholar] [CrossRef]
- Tessier, Y.; Lovejoy, S.; Hubert, P.; Schertzer, D.; Pecknold, S. Multifractal analysis and modeling of rainfall and river flows and scaling, causal transfer functions. J. Geophys. Res. Space Phys. 1996, 101, 26427–26440. [Google Scholar] [CrossRef]
- Schmitt, F.; Schertzer, D.; Lovejoy, S.; Brunet, Y. Empirical study of multifractal phase transitions in atmospheric turbu-lence, Nonlin. Processes Geophys. 1994, 1, 95–104. [Google Scholar] [CrossRef]
- Lovejoy, S.; Schertzer, D. Scale, scaling and multifractals in geophysics: twenty years on. In Nonlinear Dynamics in Geosciences; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Schertzer, D.; Lovejoy, S. Multifractals, generalized scale invariance and complexity in geophysics. Int. J. Bifurc. Chaos 2011, 21, 3417–3456. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Rybski, D.; Zschiegner, S.A.; Braun, P.; Koscielny-Bunde, E.; Livina, V.; Havlin, S.; Bunde, A. Multifractality of river runoff and precipitation: Comparison of fluctuation analysis and wavelet methods. Phys. A Stat. Mech. Its Appl. 2003, 330, 240–245. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.E.; Koscielny-Bunde, D.; Rybski, P.; Braun, A.; Bunde; Havlin, S. Long-term persistence and multifractality of precipitation and river runoff records. J. Geophys. Res. 2006, 111, D01106. [Google Scholar] [CrossRef]
- Monahan, A.H. The probability distribution of sea surface wind speeds, Part I. Theory and sea winds observations. J. Clim. 2006, 19, 497–520. [Google Scholar] [CrossRef]
- Kiss, P.; Jánosi, I.M. Comprehensive empirical analysis of ERA-40 surface wind speed distribution over Europe. Energy Convers. Manag. 2008, 49, 2142–2151. [Google Scholar] [CrossRef]
- Morgan, E.C.; Lackner, M.; Vogel, R.M.; Baise, L.G. Probability distributions for offshore wind speeds. Energy Convers. Manag. 2011, 52, 15–26. [Google Scholar] [CrossRef]
- Mishra, V.J.M.; Wallace; Lettenmaier, D.P. Relationship between hourly extreme precipitation and local air tempera-ture in the United States, Geophys. Res. Lett. 2012, 39, L16403. [Google Scholar] [CrossRef]
- McMahon, T.A.; Vogel, R.M.; Peel, M.C.; Pegram, G.G.S. Global streamflows—Part 1: Characteristics of annual stream-flows. J. Hydrol. 2007, 347, 243–259. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Statistics of extremes and estimation of extreme rainfall, 1, Theoretical investigation. Hydrol. Sci. J. 2004, 49, 575–590. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Statistics of extremes and estimation of extreme rainfall, 2, Empirical investigation of long rainfall records. Hydrol. Sci. J. 2004, 49, 591–610. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Uncertainty, entropy, scaling and hydrological stochastics, 1, Marginal distributional properties of hydro-logical processes and state scaling. Hydrol. Sci. J. 2005, 50, 381–404. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Uncertainty, entropy, scaling and hydrological stochastics. 2. Time dependence of hydrological processes and time scaling / Incertitude, entropie, effet d’échelle et propriétés stochastiques hydrologiques. 2. Dépendance temporelle des processus hydrologiques et échelle temporelle. Hydrol. Sci. J. 2005, 50, 405–426. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. Entropy based derivation of probability distributions: A case study to daily rainfall. Adv. Water Resour. 2012, 45, 51–57. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. Battle of extreme value distributions: A global survey on extreme daily rainfall. Water Resour. Res. 2013, 49, 187–201. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Papalexiou, S.M. Extreme Rainfall: Global Perspective, Handbook of Applied Hydrology, 2nd ed.; Singh, V.P., Ed.; McGraw-Hill: New York, NY, USA, 2017; pp. 74.1–74.16. [Google Scholar]
- Ye, L.; Hanson, L.S.; Ding, P.; Wang, D.; Vogel, R.M. The probability distribution of daily precipitation at the point and catchment scales in the United States. Hydrol. Earth Syst. Sci. 2018, 22, 6519–6531. [Google Scholar] [CrossRef]
- Uliana, E.M.; Da Silva, D.D.; Fraga, M.D.S.; Lisboa, L. Estimate of reference evapotranspiration through continuous probability modelling. Eng. Agrícola 2017, 37, 257–267. [Google Scholar] [CrossRef][Green Version]
- Khanmohammadi, N.; Rezaie, H.; Montaseri, M.; Behmanesh, J. Regional probability distribution of the annual reference evapotranspiration and its effective parameters in Iran. Theor. Appl. Climatol. 2018, 134, 411–422. [Google Scholar] [CrossRef]
- Castaing, B.; Gagne, Y.; Hopfinger, E. Velocity probability density functions of high Reynolds number turbulence. Phys. D Nonlinear Phenom. 1990, 46, 177–200. [Google Scholar] [CrossRef]
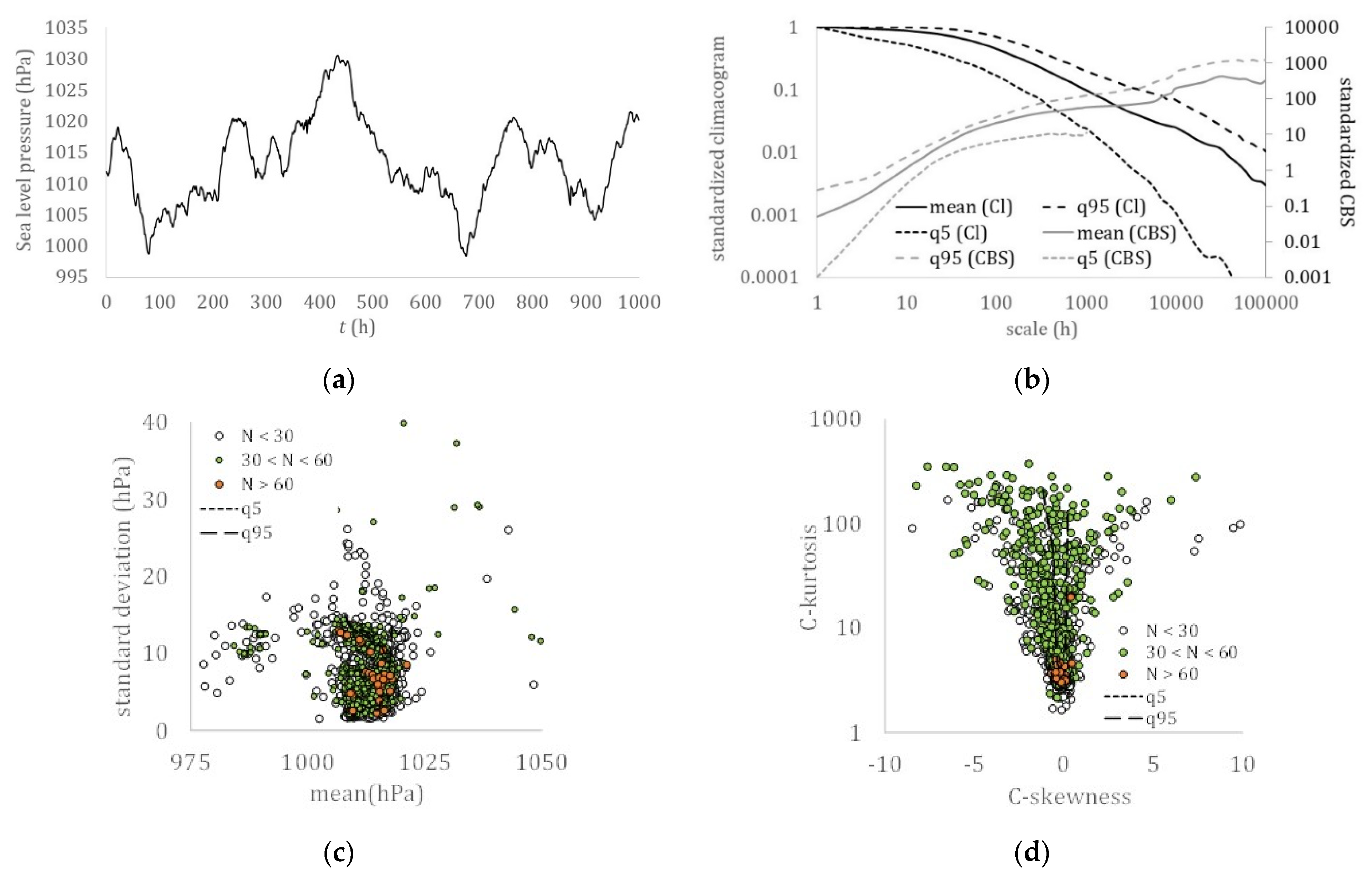
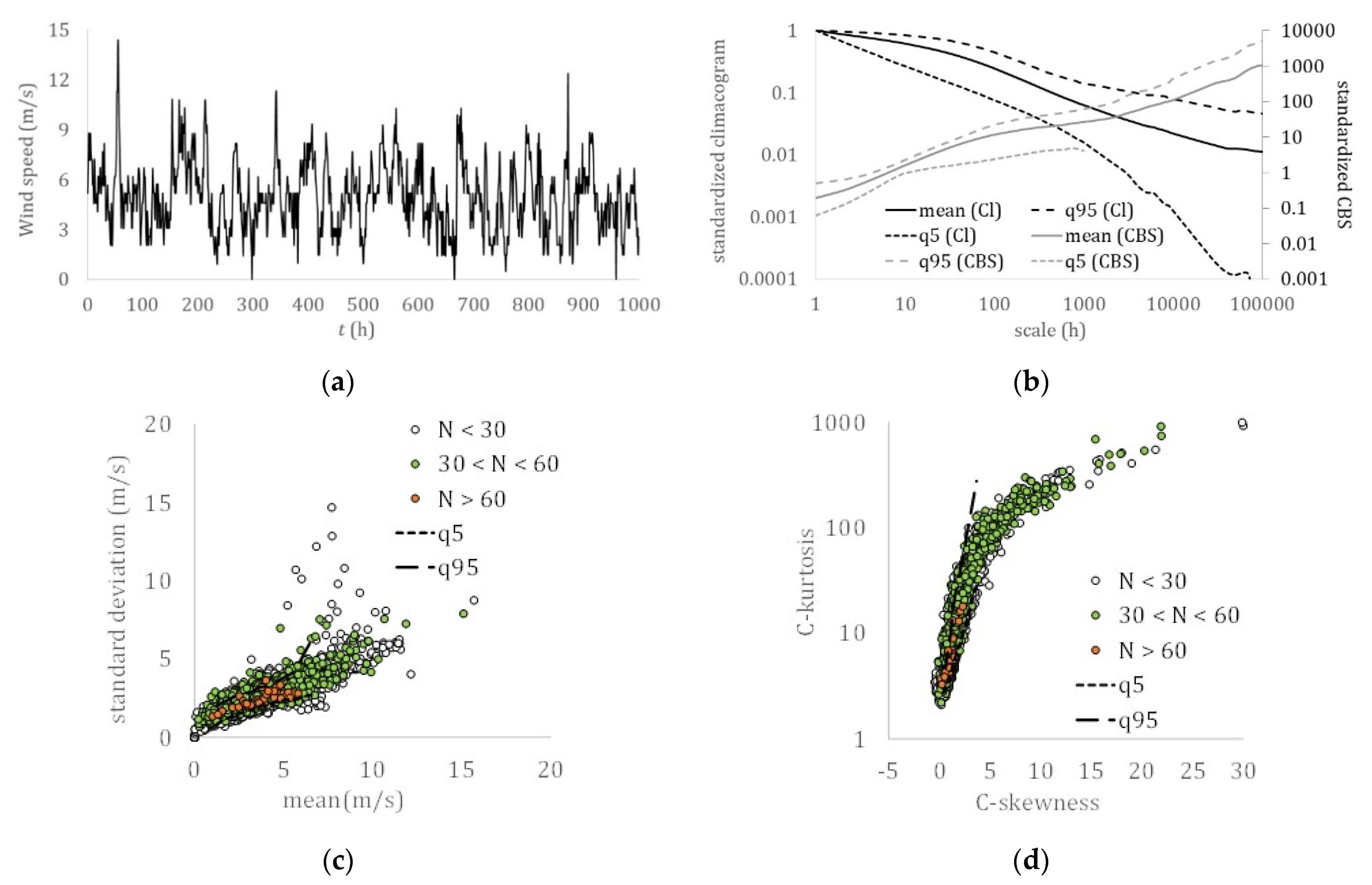
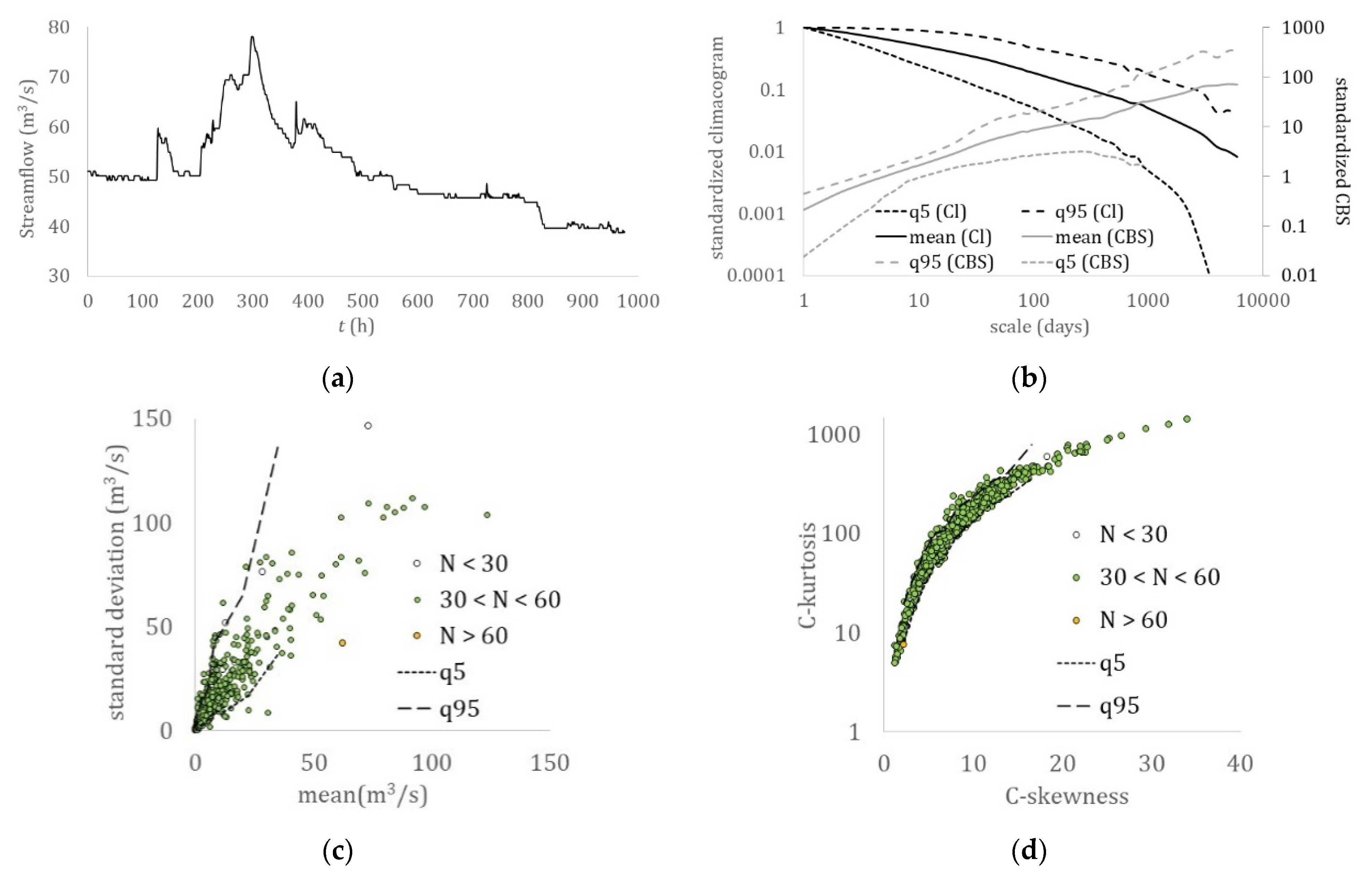
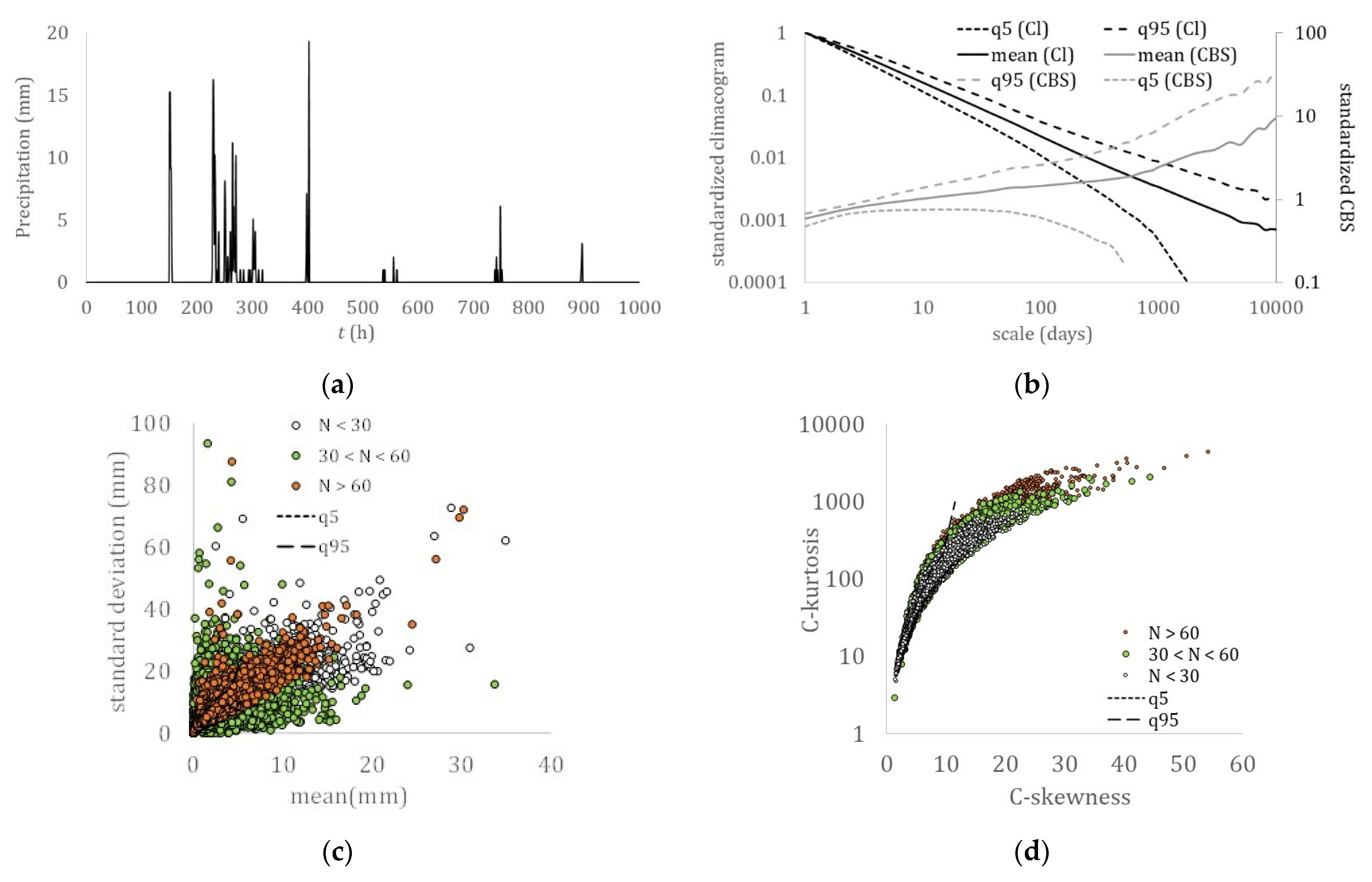
| Near-Surface Temperature | Dew Point | Humidity | Sea Level Pressure | Wind Speed | Precipitation | Streamflow | |
|---|---|---|---|---|---|---|---|
| Temporal resolution | Hourly | hourly | hourly | hourly | hourly | hourly/daily | hourly/daily |
| Total number of stations/time series | 6613 | 5978 | 4025 | 4245 | 6503 | 93,904 | 1815 |
| Total number of data values (×106) | 907.1 | 730.0 | 540.2 | 364.9 | 781.7 | 938.7 | 13.5 |
| Time period | 1938–today | 1938–today | 1940–today | 1939–today | 1939–today | 1778–today | 1900–today |
| Near-Surface Temperature | Relative Humidity | Dew Point | Sea Level Pressure | Wind Speed | Streamflow | Precipitation | |
|---|---|---|---|---|---|---|---|
| Mean | 14.6 (9.3) | 0.68 (0.1) | 8.3 (8.1) | 1013.9 (3.3) | 3.7 (1.2) | 1498.7 * | 2.3 (1.5) |
| 12.6 (3.6) | 0.72 (0.2) | 9.0 (2.3) | 1013.9 (187) | 3.51 (0.9) | 9.5 (1.5) | 2.5 (1.9) | |
| 15.3 (3.1) | 0.71 (0.1) | 6.3 (1.9) | 1014.1 (158) | 3.53 (0.8) | 7.6 (0.2) | 2.8 (2.0) | |
| Standard deviation | 8.2 (3.2) | 0.2 (0.04) | 8.0 (3.2) | 7.1 (2.9) | 2.4 (0.5) | 1007.0 * | 7.2 (4.0) |
| 7.3 (2.1) | 0.2 (0.04) | 6.6 (1.8) | 7.4 (1.6) | 2.5 (0.6) | 16.3 (2.2) | 7.4 (4.8) | |
| 8.8 (1.9) | 0.2 (0.04) | 8.0 (1.6) | 8.0 (1.3) | 2.4 (0.5) | 17.9 (0.5) | 7.8 (5.0) | |
| C-skewness | −0.2 (0.3) | −0.3 (0.5) | −0.6 (0.4) | −0.1 (0.3) | 0.9 (0.5) | 2.3 * | 7.7 (3.8) |
| −0.2 (0.2) | −0.4 (0.2) | −0.8 (0.2) | −0.4 (0.2) | 2.1 (0.5) | 8.5 (0.7) | 6.6 (3.7) | |
| −0.2 (0.1) | −0.4 (0.1) | −0.5 (0.1) | −0.2 (0.2) | 1.1 (0.4) | 9.0 (0.2) | 5.5 (3.1) | |
| C-kurtosis | 3.3 (0.6) | 3.3 (0.7) | 4.0 (1.5) | 4.0 (2.7) | 5.9 (3.3) | 7.5 * | 136 (218) |
| 6.7 (3.4) | 3.9 (0.9) | 10.2 (3.4) | 20.8 (8.0) | 30.2 (10.8) | 160.7 (17.6) | 93 (115) | |
| 5.2 (3.0) | 3.6 (0.7) | 4.6 (1.5) | 6.5 (6.1) | 9.6 (7.6) | 160.8 (3.2) | 53 (50) | |
| L-skewness | −0.04 (0.05) | −0.05 (0.09) | −0.1 (0.06) | −0.02 (0.04) | 0.1 (0.07) | 0.4 * | 0.7 (0.1) |
| −0.03 (0.01) | −0.07 (0.03) | −0.09 (0.02) | −0.04 (0.01) | 0.2 (0.04) | 0.05 (0.04) | 0.7 (0.3) | |
| −0.04 (0.01) | −0.08 (0.02) | −0.09 (0.02) | −0.03 (0.01) | 0.1 (0.03) | 0.6 (0.01) | 0.7 (0.3) | |
| L-kurtosis (modified) | 1.3 (0.01) | 1.3 (0.02) | 1.3 (0.02) | 1.3 (0.01) | 1.3 (0.02) | 1.4 * | 1.6 (0.1) |
| 1.3 (0.3) | 1.3 (0.3) | 1.3 (0.3) | 1.3 (0.2) | 1.3 (0.3) | 1.5 (0.1) | 1.6 (0.7) | |
| 1.3 (0.3) | 1.3 (0.2) | 1.3 (0.2) | 1.3 (0.2) | 1.3 (0.3) | 1.6 (0.02) | 1.6 (0.8) | |
| K-skewness | −0.1 (0.2) | −0.1 (0.3) | −0.3 (0.2) | −0.07 (0.1) | 0.4 (0.2) | 1.5 * | 1.7 (0.1) |
| −0.1 (0.05) | −0.2 (0.1) | −0.3 (0.07) | −0.1 (0.04) | 0.6 (0.1) | 1.6 (0.1) | 1.7 (0.7) | |
| −0.1 (0.04) | −0.2 (0.1) | −0.3 (0.06) | −0.1 (0.04) | 0.5 (0.1) | 1.6 (0.02) | 1.7 (0.8) | |
| K-kurtosis | 2.1 (0.05) | 2.1 (0.07) | 2.1 (0.07) | 2.1 (0.02) | 2.1 (0.05) | 2.1 * | 2.7 (0.1) |
| 2.1 (0.5) | 2.1 (0.5) | 2.1 (0.5) | 2.2 (0.4) | 2.2 (0.5) | 2.7 (0.2) | 2.6 (1.1) | |
| 2.1 (0.4) | 2.1 (0.4) | 2.1 (0.4) | 2.1 (0.3) | 2.1 (0.4) | 2.7 (0.04) | 2.6 (1.2) |
| q (h) | Fractal Parameter (M) | LTP Parameter (H) | |
|---|---|---|---|
| Near-surface temperature | 135.1 (9.2–323.1) | 0.16 (0.01–0.22) | 0.81 (0.61–0.82) |
| Relative humidity | 17.4 (5.6–57.3) | 0.23 (0.2–0.27) | 0.83 (0.62–0.85) |
| Dew point | 120.3 (16.4–213.2) | 0.23 (0.15–0.46) | 0.77 (0.58–0.79) |
| Sea level pressure | 36.5 (10.0–67.2) | 0.36 (0.25–0.55) | 0.7 (0.53–0.77) |
| Wind speed | 9.1 (0.1–25.9) | 0.15 (0.07–0.3) | 0.85 (0.69–0.86) |
| Streamflow | 96.5 (16.8–533.1) | 0.43 (0.2–0.46) | 0.78 (0.67–0.86) |
| Precipitation | 2.1 (0.1–3.0) | 0.25 (0.18–0.67) | 0.61 (0.52–0.69) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimitriadis, P.; Koutsoyiannis, D.; Iliopoulou, T.; Papanicolaou, P. A Global-Scale Investigation of Stochastic Similarities in Marginal Distribution and Dependence Structure of Key Hydrological-Cycle Processes. Hydrology 2021, 8, 59. https://doi.org/10.3390/hydrology8020059
Dimitriadis P, Koutsoyiannis D, Iliopoulou T, Papanicolaou P. A Global-Scale Investigation of Stochastic Similarities in Marginal Distribution and Dependence Structure of Key Hydrological-Cycle Processes. Hydrology. 2021; 8(2):59. https://doi.org/10.3390/hydrology8020059
Chicago/Turabian StyleDimitriadis, Panayiotis, Demetris Koutsoyiannis, Theano Iliopoulou, and Panos Papanicolaou. 2021. "A Global-Scale Investigation of Stochastic Similarities in Marginal Distribution and Dependence Structure of Key Hydrological-Cycle Processes" Hydrology 8, no. 2: 59. https://doi.org/10.3390/hydrology8020059
APA StyleDimitriadis, P., Koutsoyiannis, D., Iliopoulou, T., & Papanicolaou, P. (2021). A Global-Scale Investigation of Stochastic Similarities in Marginal Distribution and Dependence Structure of Key Hydrological-Cycle Processes. Hydrology, 8(2), 59. https://doi.org/10.3390/hydrology8020059









