Development of a Regional Gridded Runoff Dataset Using Long Short-Term Memory (LSTM) Networks
Abstract
1. Introduction
2. Data
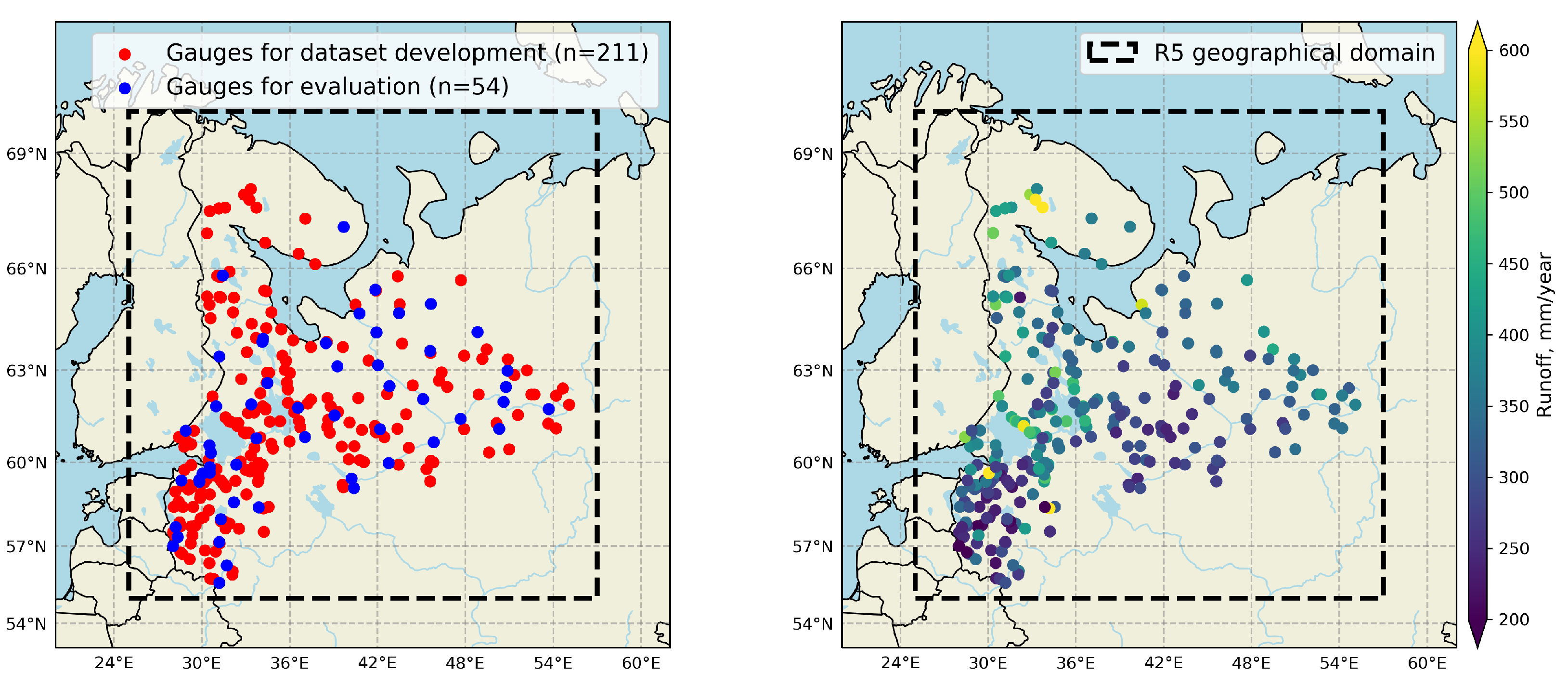
2.1. Streamflow Observations
2.2. Meteorological Forcing Data
3. Methods
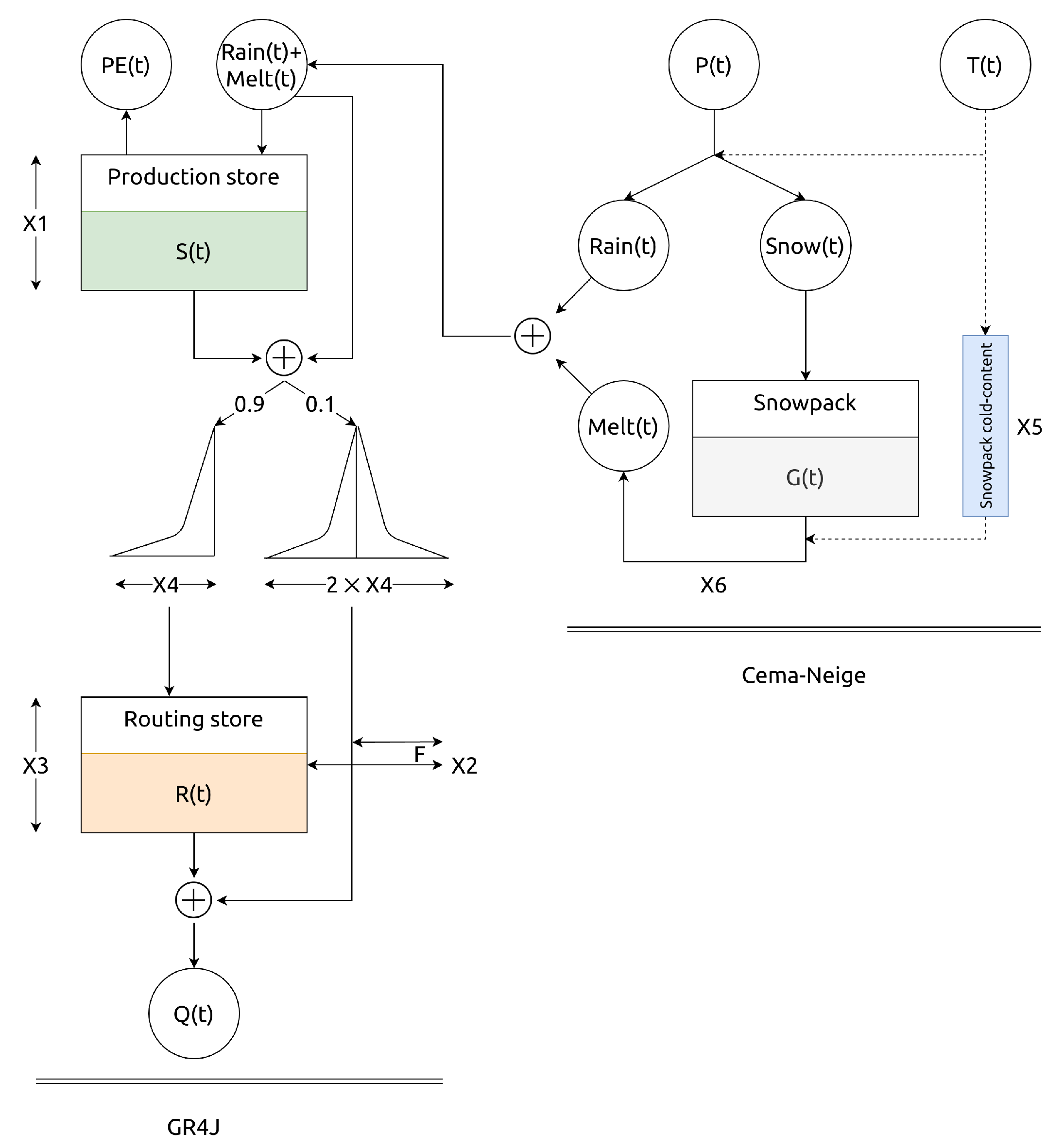
3.1. Hydrological Models
3.1.1. GR4J
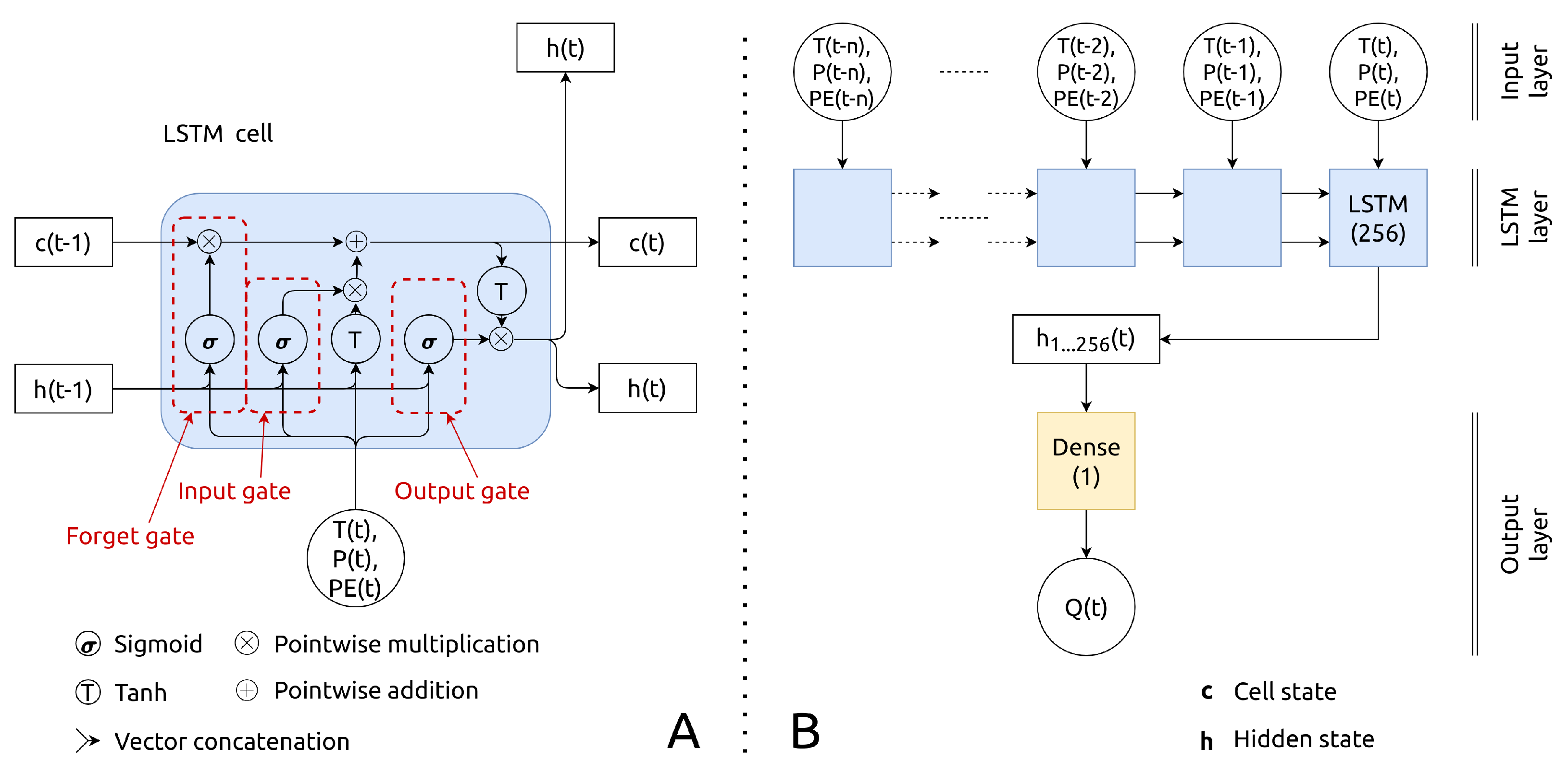
3.1.2. LSTM
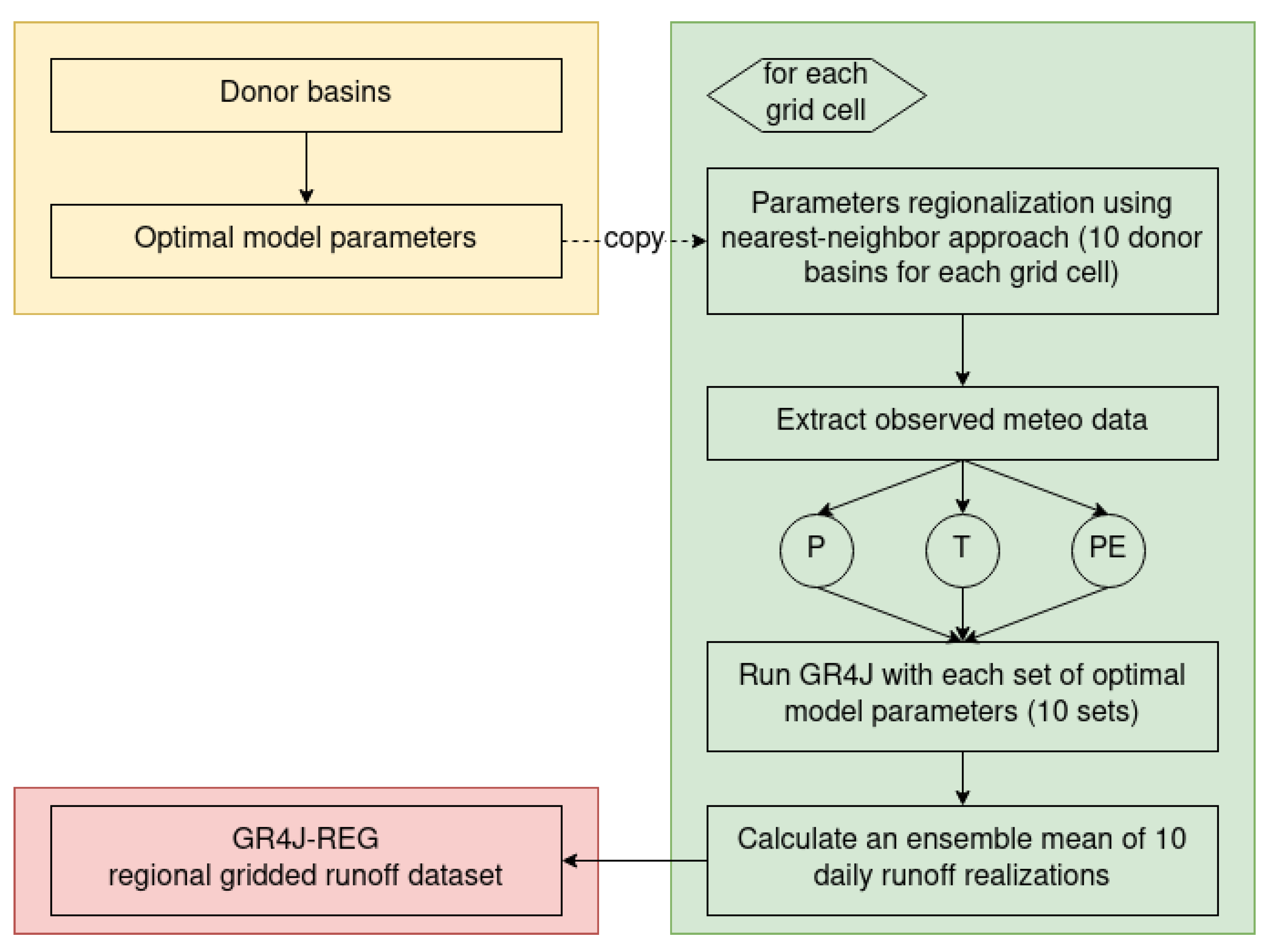
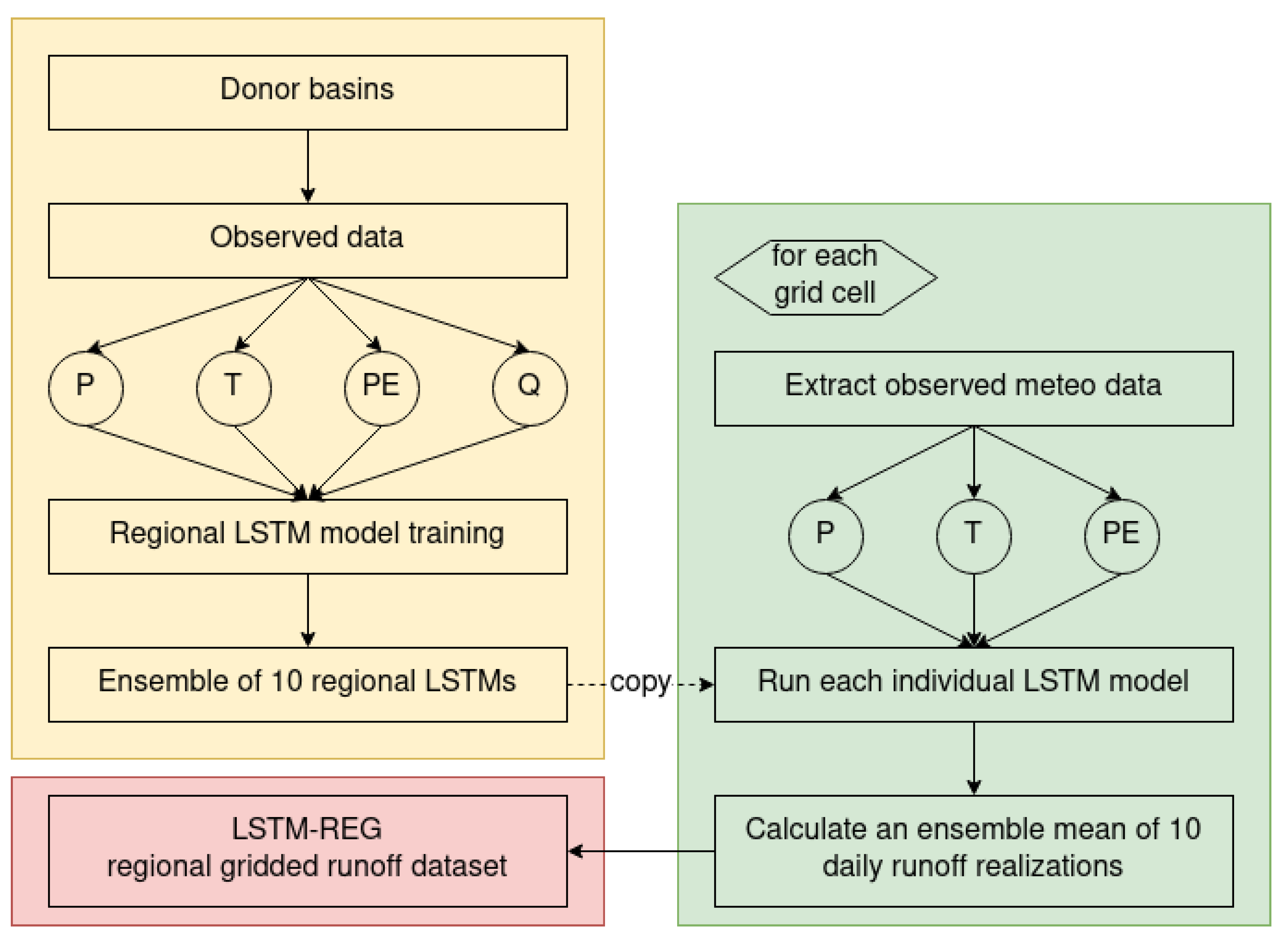
3.2. Gridded Runoff Dataset Development Workflows
3.2.1. Selection of Donor Basins
3.2.2. GR4J-REG
3.2.3. LSTM-REG
3.3. Performance Evaluation
4. Results and Discussion
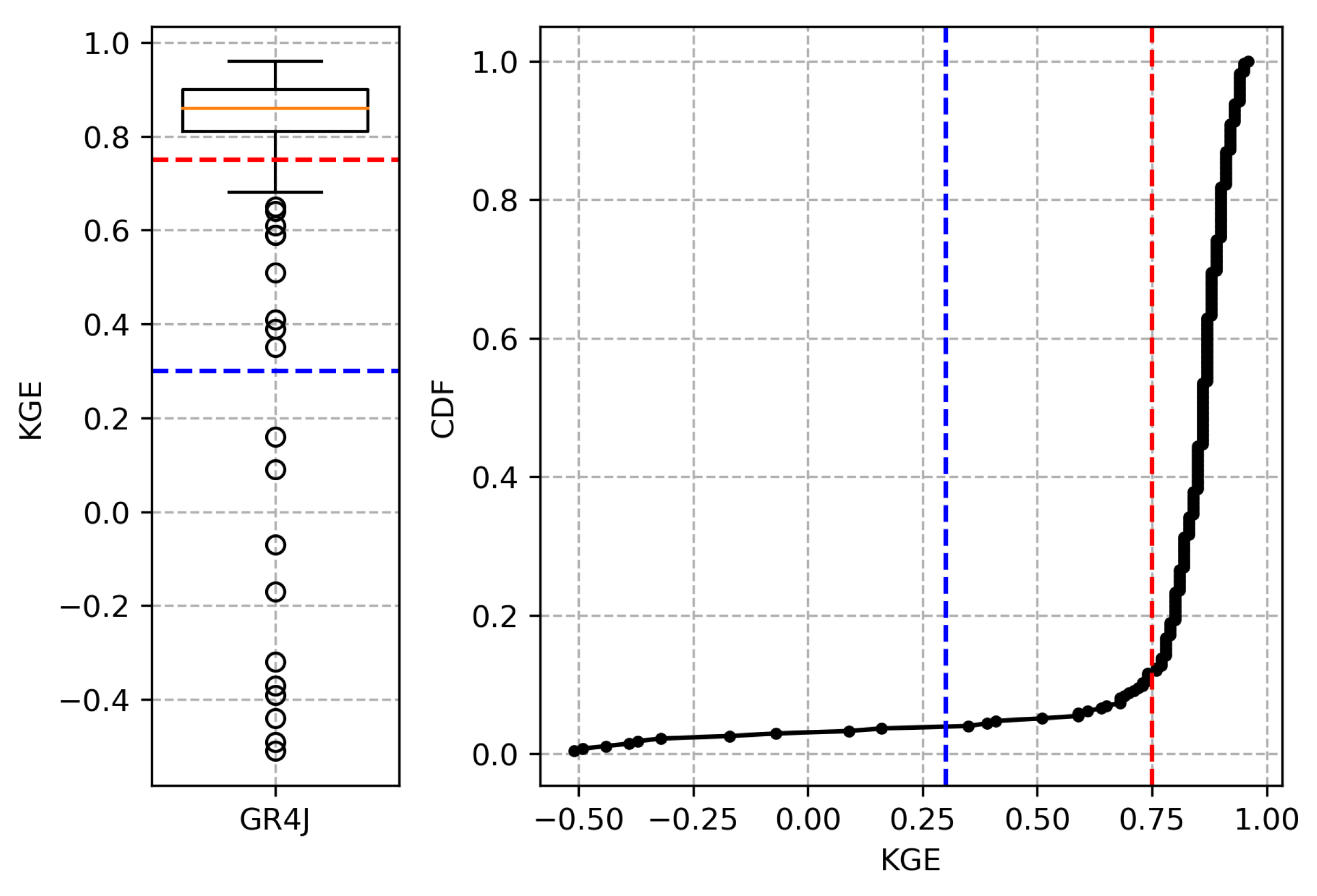
4.1. GR4J Model Calibration and Donor Basin Selection
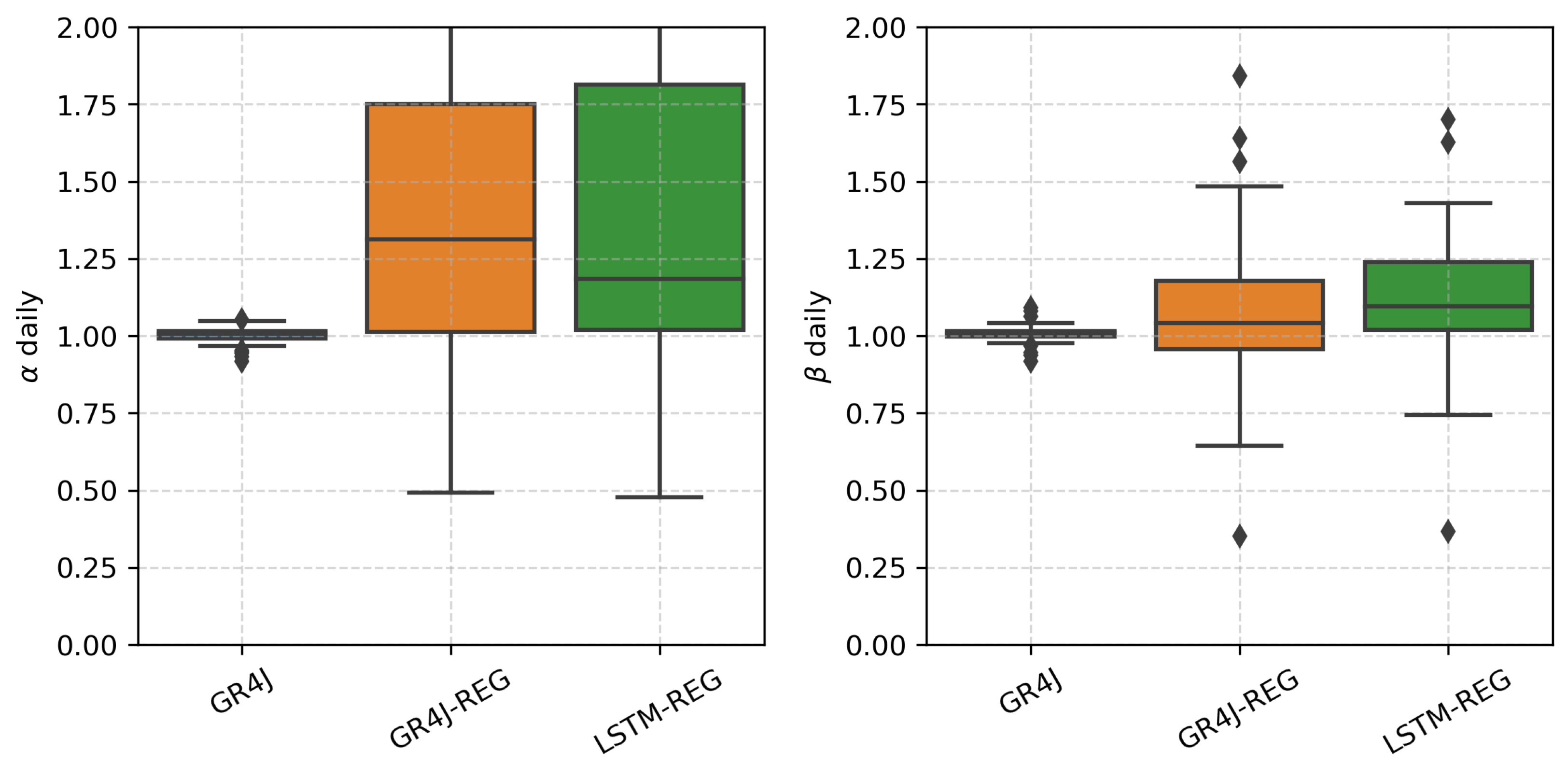
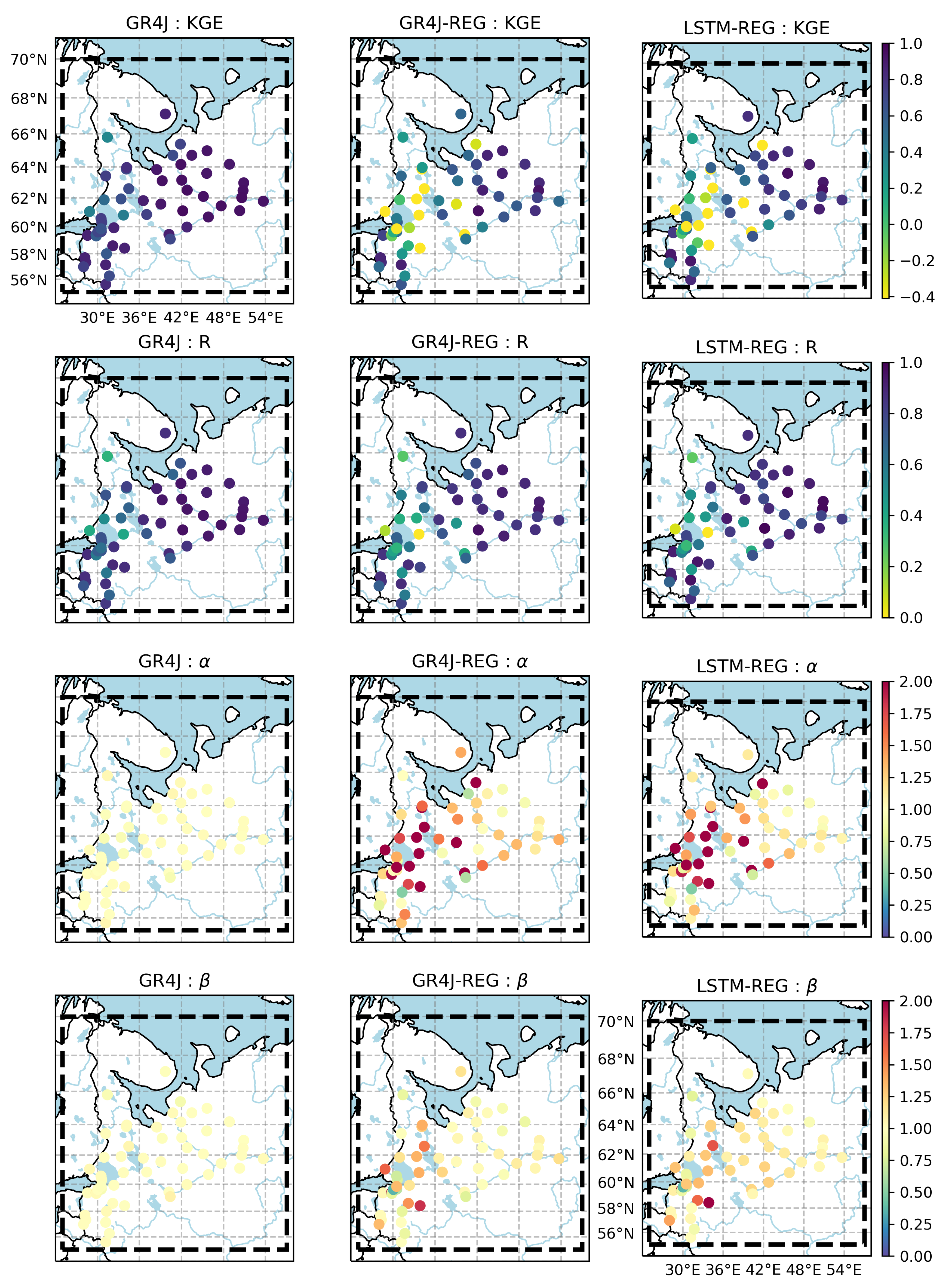
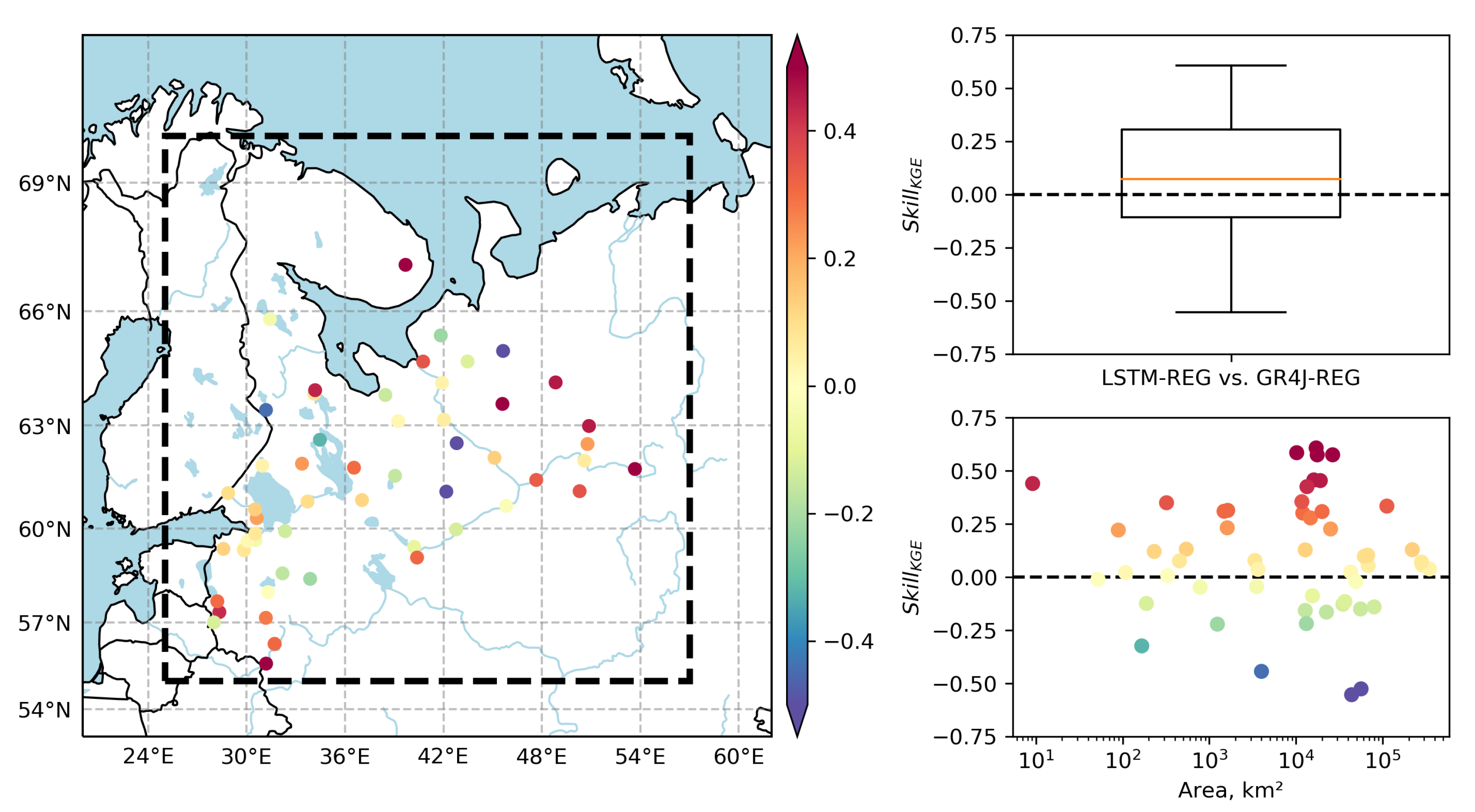
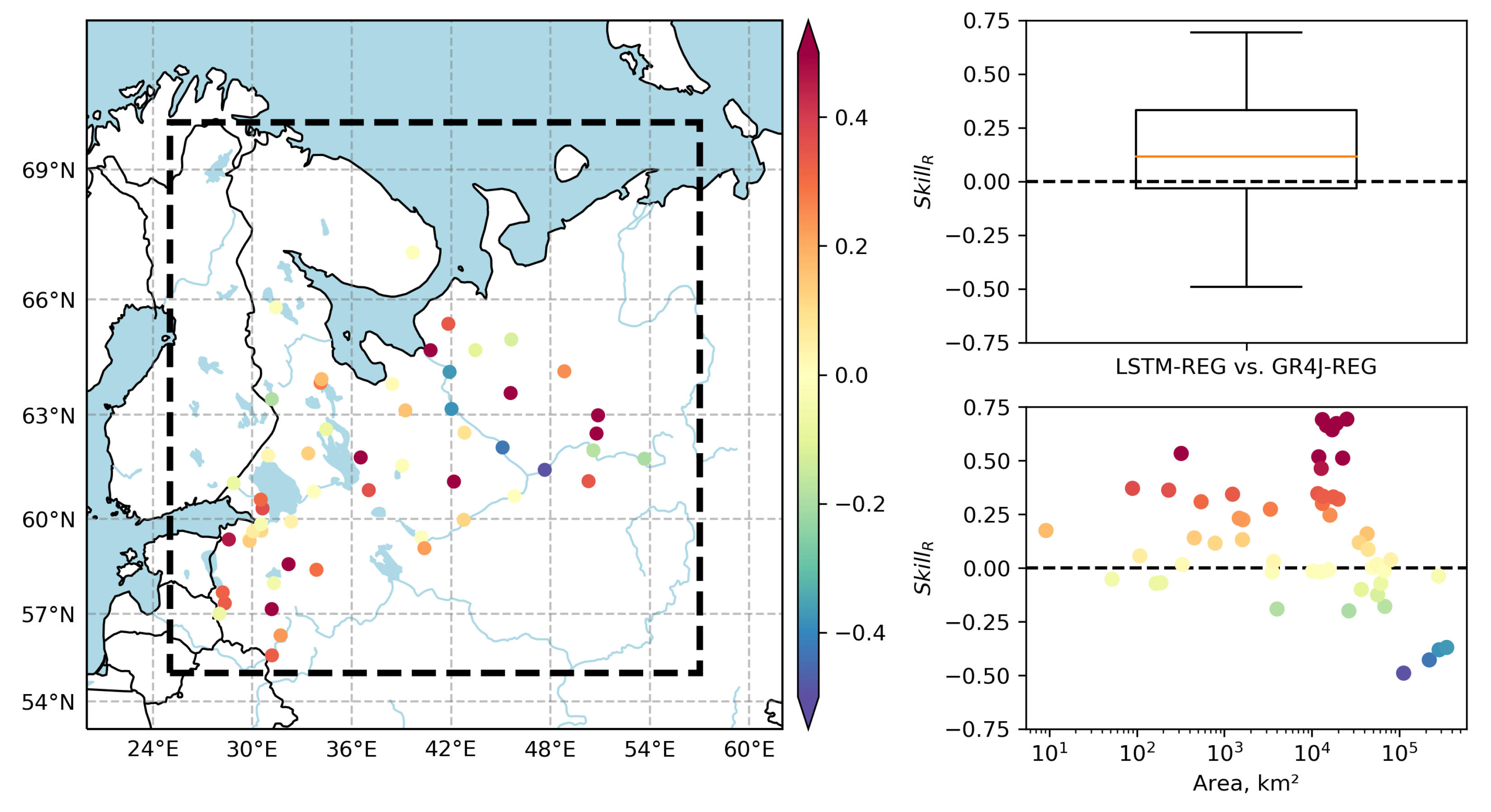
4.2. Performance of the Developed Gridded Runoff Datasets
5. Conclusions and Outlook
6. Data Availability
Author Contributions
Funding
Conflicts of Interest
References
- Vörösmarty, C.J.; McIntyre, P.B.; Gessner, M.O.; Dudgeon, D.; Prusevich, A.; Green, P.; Glidden, S.; Bunn, S.E.; Sullivan, C.A.; Liermann, C.R.; et al. Global threats to human water security and river biodiversity. Nature 2010, 467, 555–561. [Google Scholar] [CrossRef] [PubMed]
- Blöschl, G.; Hall, J.; Viglione, A.; Perdigão, R.A.; Parajka, J.; Merz, B.; Lun, D.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; et al. Changing climate both increases and decreases European river floods. Nature 2019, 573, 108–111. [Google Scholar] [CrossRef] [PubMed]
- Van Loon, A.F. Hydrological drought explained. Wiley Interdiscip. Rev. Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Fekete, B.M.; Looser, U.; Pietroniro, A.; Robarts, R.D. Rationale for Monitoring Discharge on the Ground. J. Hydrometeorol. 2012, 13, 1977–1986. [Google Scholar] [CrossRef]
- Brunner, M.I.; Tallaksen, L.M. Proneness of European Catchments to Multiyear Streamflow Droughts. Water Resour. Res. 2019, 2019WR025903. [Google Scholar] [CrossRef]
- Blöschl, G.; Kiss, A.; Viglione, A.; Barriendos, M.; Böhm, O.; Brázdil, R.; Coeur, D.; Demarée, G.; Llasat, M.C.; Macdonald, N.; et al. Current European flood-rich period exceptional compared with past 500 years. Nature 2020, 583, 560–566. [Google Scholar] [CrossRef] [PubMed]
- Fekete, B.M.; Robarts, R.D.; Kumagai, M.; Nachtnebel, H.P.; Odada, E.; Zhulidov, A.V. Time for in situ renaissance. Science 2015, 349, 685–686. [Google Scholar] [CrossRef] [PubMed]
- Gudmundsson, L.; Seneviratne, S.I. Observation-based gridded runoff estimates for Europe (E-RUN version 1.1). Earth Syst. Sci. Data 2016, 8, 279–295. [Google Scholar] [CrossRef]
- Hannah, D.M.; Demuth, S.; van Lanen, H.A.J.; Looser, U.; Prudhomme, C.; Rees, G.; Stahl, K.; Tallaksen, L.M. Large-scale river flow archives: Importance, current status and future needs. Hydrol. Process. 2011, 25, 1191–1200. [Google Scholar] [CrossRef]
- Stokstad, E. Scarcity of Rain, Stream Gages Threatens Forecasts. Science 1999, 285, 1199–1200. [Google Scholar] [CrossRef]
- Shiklomanov, A.I.; Lammers, R.B.; Vörösmarty, C.J. Widespread decline in hydrological monitoring threatens Pan-Arctic Research. EOS Trans. Am. Geophys. Union 2002, 83, 13. [Google Scholar] [CrossRef]
- Ghiggi, G.; Humphrey, V.; Seneviratne, S.I.; Gudmundsson, L. GRUN: An observation-based global gridded runoff dataset from 1902 to 2014. Earth Syst. Sci. Data 2019, 11, 1655–1674. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Luo, Y.Q.; Randerson, J.T.; Abramowitz, G.; Bacour, C.; Blyth, E.; Carvalhais, N.; Ciais, P.; Dalmonech, D.; Fisher, J.B.; Fisher, R.; et al. A framework for benchmarking land models. Biogeosciences 2012, 9, 3857–3874. [Google Scholar] [CrossRef]
- Beck, H.E.; Wood, E.F.; Pan, M.; Fisher, C.K.; Miralles, D.G.; Van Dijk, A.I.; McVicar, T.R.; Adler, R.F. MSWEP V2 global 3-hourly 0.1 precipitation: Methodology and quantitative assessment. Bull. Am. Meteorol. Soc. 2019, 100, 473–500. [Google Scholar] [CrossRef]
- Ayzel, G. Runoff predictions in ungauged Arctic basins using conceptual models forced by reanalysis data. Water Resour. 2018, 45, 1–7. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; de Roo, A.; Dutra, E.; Fink, G.; Orth, R.; Schellekens, J. Global evaluation of runoff from 10 state-of-the-art hydrological models. Hydrol. Earth Syst. Sci. 2017, 21, 2881–2903. [Google Scholar] [CrossRef]
- Schellekens, J.; Dutra, E.; Martínez-de la Torre, A.; Balsamo, G.; van Dijk, A.; Sperna Weiland, F.; Minvielle, M.; Calvet, J.C.; Decharme, B.; Eisner, S.; et al. A global water resources ensemble of hydrological models: The eartH2Observe Tier-1 dataset. Earth Syst. Sci. Data 2017, 9, 389–413. [Google Scholar] [CrossRef]
- Frieler, K.; Lange, S.; Piontek, F.; Reyer, C.P.O.; Schewe, J.; Warszawski, L.; Zhao, F.; Chini, L.; Denvil, S.; Emanuel, K.; et al. Assessing the impacts of 1.5° global warming—Simulation protocol of the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP2b). Geosci. Model Dev. 2017, 10, 4321–4345. [Google Scholar] [CrossRef]
- Barbarossa, V.; Huijbregts, M.A.; Beusen, A.H.; Beck, H.E.; King, H.; Schipper, A.M. FLO1K, global maps of mean, maximum and minimum annual streamflow at 1 km resolution from 1960 through 2015. Sci. Data 2018, 5, 180052. [Google Scholar] [CrossRef]
- Ayzel, G.; Izhitskiy, A. Climate change impact assessment on freshwater inflow into the Small Aral Sea. Water 2019, 11, 2377. [Google Scholar] [CrossRef]
- Ayzel, G.; Kurochkina, L.; Zhuravlev, S. The influence of regional hydrometric data incorporation on the accuracy of gridded reconstruction of monthly runoff. Hydrol. Sci. J. 2020, 1–12. [Google Scholar] [CrossRef]
- Do, H.X.; Westra, S.; Leonard, M. A global-scale investigation of trends in annual maximum streamflow. J. Hydrol. 2017, 552, 28–43. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources. Water 2019, 11, 910. [Google Scholar] [CrossRef]
- Jiang, S.; Zheng, Y.; Babovic, V.; Tian, Y.; Han, F. A computer vision-based approach to fusing spatiotemporal data for hydrological modeling. J. Hydrol. 2018, 567, 25–40. [Google Scholar] [CrossRef]
- Minns, A.W.; Hall, M.J. Artificial neural networks as rainfall-runoff models. Hydrol. Sci. J. 1996, 41, 399–417. [Google Scholar] [CrossRef]
- Shen, C.; Laloy, E.; Elshorbagy, A.; Albert, A.; Bales, J.; Chang, F.J.; Ganguly, S.; Hsu, K.L.; Kifer, D.; Fang, Z.; et al. HESS Opinions: Incubating deep-learning-powered hydrologic science advances as a community. Hydrol. Earth Syst. Sci. 2018, 22, 5639–5656. [Google Scholar] [CrossRef]
- Shen, C. A trans-disciplinary review of deep learning research and its relevance for water resources scientists. Water Resour. Res. 2018. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Towards learning universal, regional, and local hydrological behaviors via machine learning applied to large-sample datasets. Hydrol. Earth Syst. Sci. 2019, 23, 5089–5110. [Google Scholar] [CrossRef]
- Ayzel, G. Does Deep Learning Advance Hourly Runoff Predictions. In Proceedings of the V International Conference Information Technologies and High-Performance Computing (ITHPC-2019), Khabarovsk, Russia, 16–19 September 2019; pp. 16–19. [Google Scholar]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Sampson, A.K.; Hochreiter, S.; Nearing, G.S. Towards Improved Predictions in Ungauged Basins: Exploiting the Power of Machine Learning. Water Resour. Res. 2019, 2019WR026065. [Google Scholar] [CrossRef]
- Ayzel, G.; Kurochkina, L.; Kazakov, E.; Zhuravlev, S. Streamflow prediction in ungauged basins: Benchmarking the efficiency of deep learning. E3S Web Conf. 2020, 163, 01001. [Google Scholar] [CrossRef]
- Kao, I.F.; Zhou, Y.; Chang, L.C.; Chang, F.J. Exploring a Long Short-Term Memory based Encoder-Decoder framework for multi-step-ahead flood forecasting. J. Hydrol. 2020, 583, 124631. [Google Scholar] [CrossRef]
- Gauch, M.; Mai, J.; Lin, J. The proper care and feeding of CAMELS: How limited training data affects streamflow prediction. Environ. Model. Softw. 2021, 135, 104926. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Lange, S. Bias correction of surface downwelling longwave and shortwave radiation for the EWEMBI dataset. Earth Syst. Dyn. 2018, 9, 627–645. [Google Scholar] [CrossRef]
- Lange, S. Trend-preserving bias adjustment and statistical downscaling with ISIMIP3BASD (v1.0). Geosci. Model Dev. 2019, 12, 3055–3070. [Google Scholar] [CrossRef]
- Lange, S. EartH2Observe, WFDEI and ERA-Interim Data Merged and Bias-Corrected for ISIMIP (EWEMBI); V. 1.1; GFZ Data Services: The GFZ German Research Centre for Geosciences: Potsdam, Germany, 2019. [Google Scholar] [CrossRef]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall–runoff model?: Part 2—Towards a simple and efficient potential evapotranspiration model for rainfall–runoff modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Döll, P.; Trautmann, T.; Gerten, D.; Schmied, H.M.; Ostberg, S.; Saaed, F.; Schleussner, C.F. Risks for the global freshwater system at 1.5 °C and 2 °C global warming. Environ. Res. Lett. 2018, 13, 044038. [Google Scholar] [CrossRef]
- Gelfan, A.; Kalugin, A.; Krylenko, I.; Nasonova, O.; Gusev, Y.; Kovalev, E. Does a successful comprehensive evaluation increase confidence in a hydrological model intended for climate impact assessment? Clim. Chang. 2020. [Google Scholar] [CrossRef]
- Valéry, A.; Andréassian, V.; Perrin, C. ‘As simple as possible but not simpler’: What is useful in a temperature-based snow-accounting routine? Part 1—Comparison of six snow accounting routines on 380 catchments. J. Hydrol. 2014, 517, 1166–1175. [Google Scholar] [CrossRef]
- Valéry, A.; Andréassian, V.; Perrin, C. ‘As simple as possible but not simpler’: What is useful in a temperature-based snow-accounting routine? Part 2—Sensitivity analysis of the Cemaneige snow accounting routine on 380 catchments. J. Hydrol. 2014, 517, 1176–1187. [Google Scholar] [CrossRef]
- Coron, L.; Thirel, G.; Delaigue, O.; Perrin, C.; Andréassian, V. The suite of lumped GR hydrological models in an R package. Environ. Model. Softw. 2017, 94, 166–171. [Google Scholar] [CrossRef]
- Arsenault, R.; Brissette, F.; Martel, J.L. The hazards of split-sample validation in hydrological model calibration. J. Hydrol. 2018, 566, 346–362. [Google Scholar] [CrossRef]
- Tarek, M.; Brissette, F.P.; Arsenault, R. Evaluation of the ERA5 reanalysis as a potential reference dataset for hydrological modelling over North America. Hydrol. Earth Syst. Sci. 2020, 24, 2527–2544. [Google Scholar] [CrossRef]
- Raimonet, M.; Oudin, L.; Thieu, V.; Silvestre, M.; Vautard, R.; Rabouille, C.; Moigne, P.L. Evaluation of Gridded Meteorological Datasets for Hydrological Modeling. J. Hydrometeorol. 2017, 18, 3027–3041. [Google Scholar] [CrossRef]
- Oudin, L.; Andréassian, V.; Perrin, C.; Michel, C.; Le Moine, N. Spatial proximity, physical similarity, regression and ungaged catchments: A comparison of regionalization approaches based on 913 French catchments. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Rojas-Serna, C.; Lebecherel, L.; Perrin, C.; Andréassian, V.; Oudin, L. How should a rainfall-runoff model be parameterized in an almost ungauged catchment? A methodology tested on 609 catchments. Water Resour. Res. 2016, 52, 4765–4784. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical note: Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling—Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Ratner, B. The correlation coefficient: Its values range between +1/−1, or do they? J. Target. Meas. Anal. Mark. 2009, 17, 139–142. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 7 January 2021).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:cs.LG/1412.6980. [Google Scholar]
- Maier, H.; Dandy, G. Neural network based modelling of environmental variables: A systematic approach. Math. Comput. Model. 2001, 33, 669–682. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; de Roo, A.; Miralles, D.G.; McVicar, T.R.; Schellekens, J.; Bruijnzeel, L.A. Global-scale regionalization of hydrologic model parameters. Water Resour. Res. 2016. [Google Scholar] [CrossRef]
- van Dijk, A.I.J.M.; Peña-Arancibia, J.L.; Wood, E.F.; Sheffield, J.; Beck, H.E. Global analysis of seasonal streamflow predictability using an ensemble prediction system and observations from 6192 small catchments worldwide. Water Resour. Res. 2013, 49, 2729–2746. [Google Scholar] [CrossRef]
- Veldkamp, T.I.E.; Zhao, F.; Ward, P.J.; Moel, H.D.; Aerts, J.C.J.H.; Schmied, H.M.; Portmann, F.T.; Masaki, Y.; Pokhrel, Y.; Liu, X.; et al. Human impact parameterizations in global hydrological models improve estimates of monthly discharges and hydrological extremes: A multi-model validation study. Environ. Res. Lett. 2018, 13, 055008. [Google Scholar] [CrossRef]
- Chadalawada, J.; Babovic, V. Review and comparison of performance indices for automatic model induction. J. Hydroinformatics 2019, 21, 13–31. [Google Scholar] [CrossRef]
- Beck, H.E.; Pan, M.; Roy, T.; Weedon, G.P.; Pappenberger, F.; van Dijk, A.I.J.M.; Huffman, G.J.; Adler, R.F.; Wood, E.F. Daily evaluation of 26 precipitation datasets using Stage-IV gauge-radar data for the CONUS. Hydrol. Earth Syst. Sci. 2019, 23, 207–224. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Schaefli, B.; Gupta, H.V. Do Nash values have value? Hydrol. Process. 2007, 21, 2075–2080. [Google Scholar] [CrossRef]
- Mizukami, N.; Rakovec, O.; Newman, A.J.; Clark, M.P.; Wood, A.W.; Gupta, H.V.; Kumar, R. On the choice of calibration metrics for “high-flow” estimation using hydrologic models. Hydrol. Earth Syst. Sci. 2019, 23, 2601–2614. [Google Scholar] [CrossRef]
- Pappenberger, F.; Ramos, M.H.; Cloke, H.L.; Wetterhall, F.; Alfieri, L.; Bogner, K.; Mueller, A.; Salamon, P. How do I know if my forecasts are better? Using benchmarks in hydrological ensemble prediction. J. Hydrol. 2015, 522, 697–713. [Google Scholar] [CrossRef]
- Harrigan, S.; Prudhomme, C.; Parry, S.; Smith, K.; Tanguy, M. Benchmarking ensemble streamflow prediction skill in the UK. Hydrol. Earth Syst. Sci. 2018, 22, 2023–2039. [Google Scholar] [CrossRef]
- Bennett, J.C.; Wang, Q.J.; Robertson, D.E.; Schepen, A.; Li, M.; Michael, K. Assessment of an ensemble seasonal streamflow forecasting system for Australia. Hydrol. Earth Syst. Sci. 2017, 21, 6007–6030. [Google Scholar] [CrossRef]
- Razavi, T.; Coulibaly, P. Streamflow Prediction in Ungauged Basins: Review of Regionalization Methods. J. Hydrol. Eng. 2013, 18, 958–975. [Google Scholar] [CrossRef]
- Parajka, J.; Viglione, A.; Rogger, M.; Salinas, J.L.; Sivapalan, M.; Blöschl, G. Comparative assessment of predictions in ungauged basins—Part 1: Runoff-hydrograph studies. Hydrol. Earth Syst. Sci. 2013, 17, 1783–1795. [Google Scholar] [CrossRef]
- Zaherpour, J.; Gosling, S.N.; Mount, N.; Schmied, H.M.; Veldkamp, T.I.E.; Dankers, R.; Eisner, S.; Gerten, D.; Gudmundsson, L.; Haddeland, I.; et al. Worldwide evaluation of mean and extreme runoff from six global-scale hydrological models that account for human impacts. Environ. Res. Lett. 2018, 13, 065015. [Google Scholar] [CrossRef]
- Schewe, J.; Gosling, S.N.; Reyer, C.; Zhao, F.; Ciais, P.; Elliott, J.; Francois, L.; Huber, V.; Lotze, H.K.; Seneviratne, S.I.; et al. State-of-the-art global models underestimate impacts from climate extremes. Nat. Commun. 2019, 10, 1005. [Google Scholar] [CrossRef]
- Chadalawada, J.; Herath, H.M.V.V.; Babovic, V. Hydrologically Informed Machine Learning for Rainfall-Runoff Modeling: A Genetic Programming-Based Toolkit for Automatic Model Induction. Water Resour. Res. 2020, 56, e2019WR026933. [Google Scholar] [CrossRef]
- Herath, H.M.V.V.; Chadalawada, J.; Babovic, V. Hydrologically Informed Machine Learning for Rainfall-Runoff Modelling: Towards Distributed Modelling. Hydrol. Earth Syst. Sci. Discuss. 2020, 2020, 1–42. [Google Scholar] [CrossRef]
- Beven, K. Deep learning, hydrological processes and the uniqueness of place. Hydrol. Process. 2020, 34, 3608–3613. [Google Scholar] [CrossRef]
- Nearing, G.S.; Kratzert, F.; Sampson, A.K.; Pelissier, C.S.; Klotz, D.; Frame, J.M.; Prieto, C.; Gupta, H.V. What Role Does Hydrological Science Play in the Age of Machine Learning? Water Resour. Res. 2020, e2020WR028091. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayzel, G.; Kurochkina, L.; Abramov, D.; Zhuravlev, S. Development of a Regional Gridded Runoff Dataset Using Long Short-Term Memory (LSTM) Networks. Hydrology 2021, 8, 6. https://doi.org/10.3390/hydrology8010006
Ayzel G, Kurochkina L, Abramov D, Zhuravlev S. Development of a Regional Gridded Runoff Dataset Using Long Short-Term Memory (LSTM) Networks. Hydrology. 2021; 8(1):6. https://doi.org/10.3390/hydrology8010006
Chicago/Turabian StyleAyzel, Georgy, Liubov Kurochkina, Dmitriy Abramov, and Sergei Zhuravlev. 2021. "Development of a Regional Gridded Runoff Dataset Using Long Short-Term Memory (LSTM) Networks" Hydrology 8, no. 1: 6. https://doi.org/10.3390/hydrology8010006
APA StyleAyzel, G., Kurochkina, L., Abramov, D., & Zhuravlev, S. (2021). Development of a Regional Gridded Runoff Dataset Using Long Short-Term Memory (LSTM) Networks. Hydrology, 8(1), 6. https://doi.org/10.3390/hydrology8010006




