WaterbalANce, a WebApp for Thornthwaite–Mather Water Balance Computation: Comparison of Applications in Two European Watersheds
Abstract
1. Introduction
2. Materials and Methods
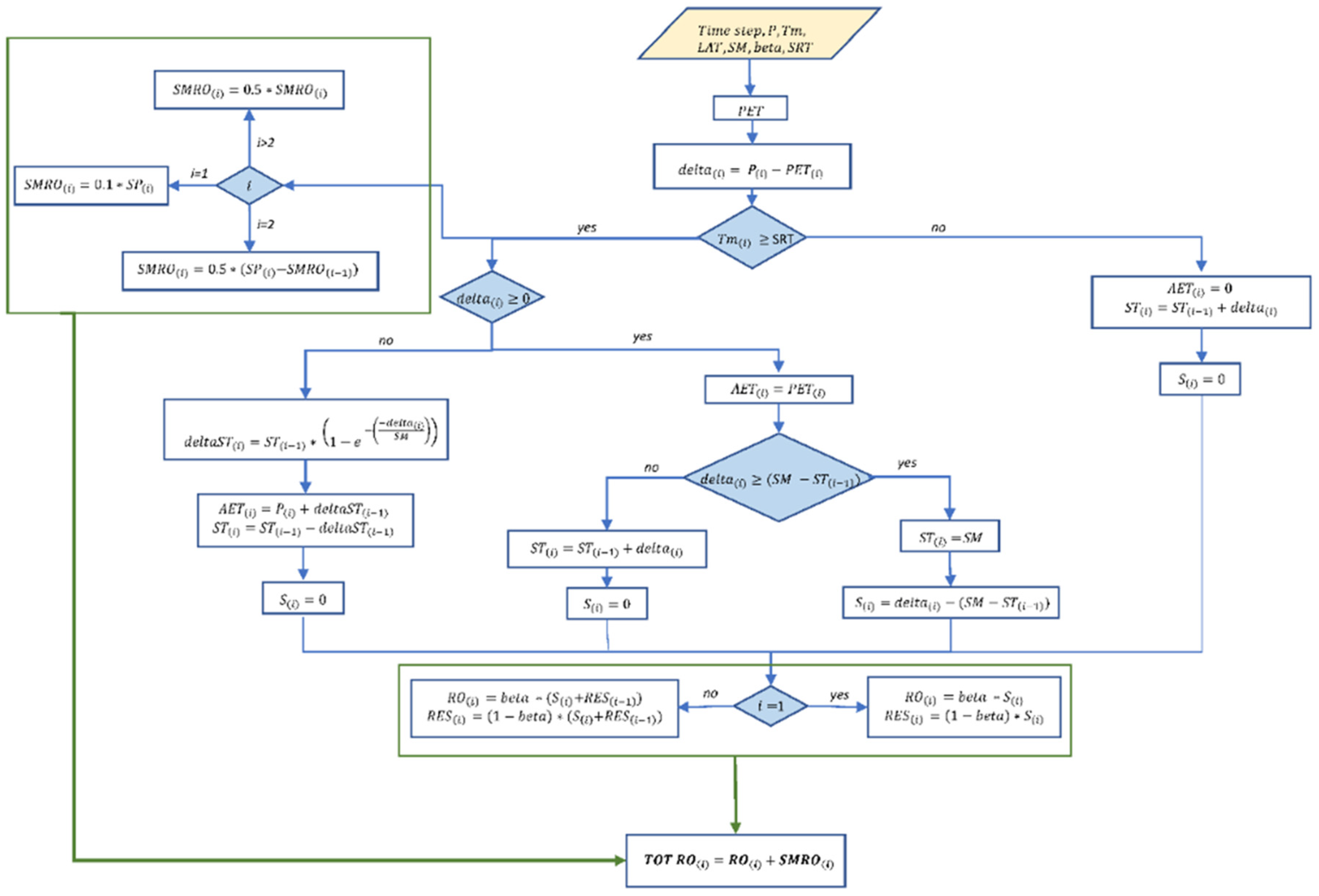
2.1. Outline of the Method
2.2. Exporting Algorithm to the Cloud
2.3. The Practical Case of the Reno at Pracchia Watershed (Northern Apennines, Central Italy)
2.4. The Practical Case of the Savica at Ukanc Watershed (Northwestern Slovenia)
3. Results and Discussion
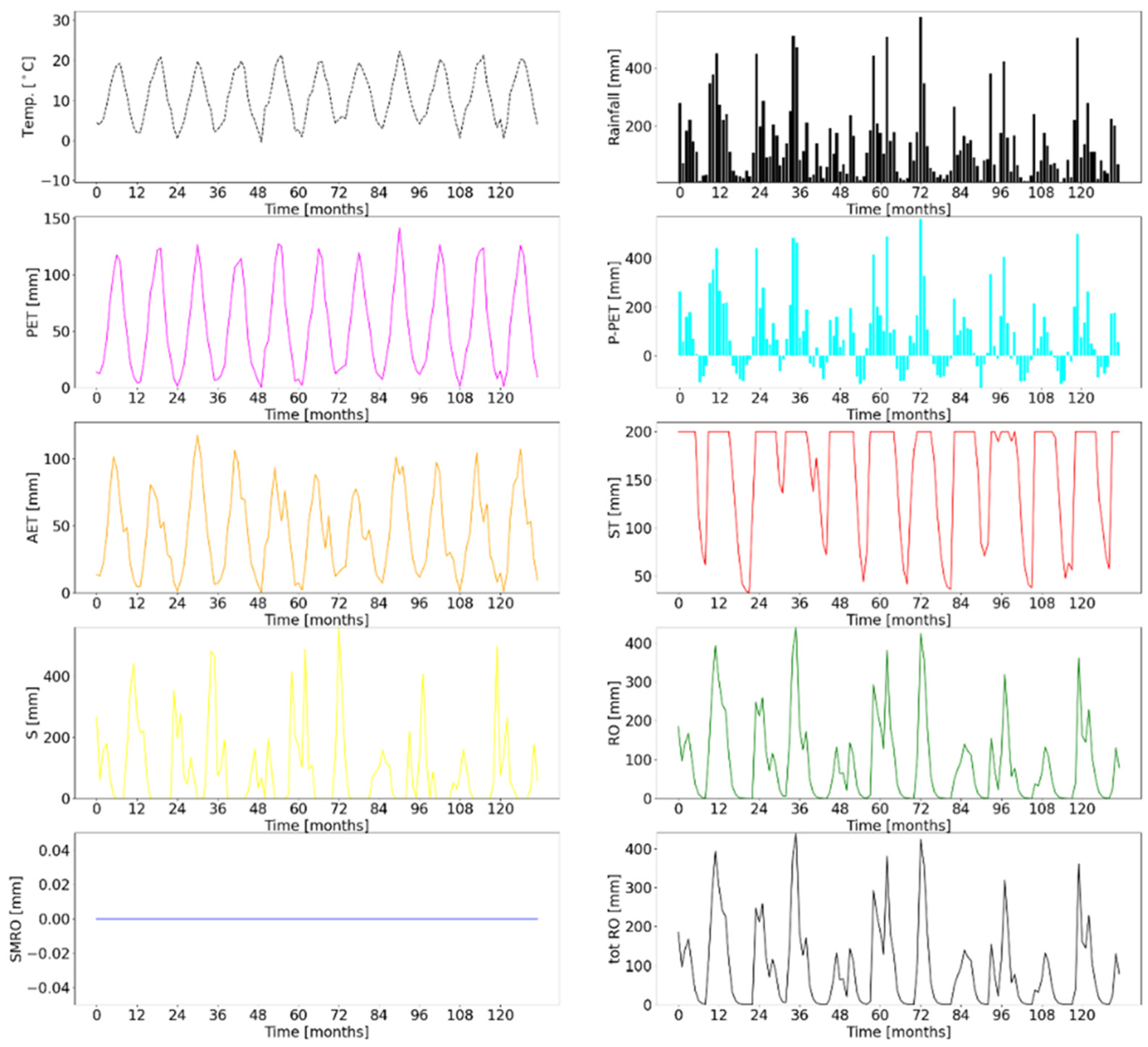
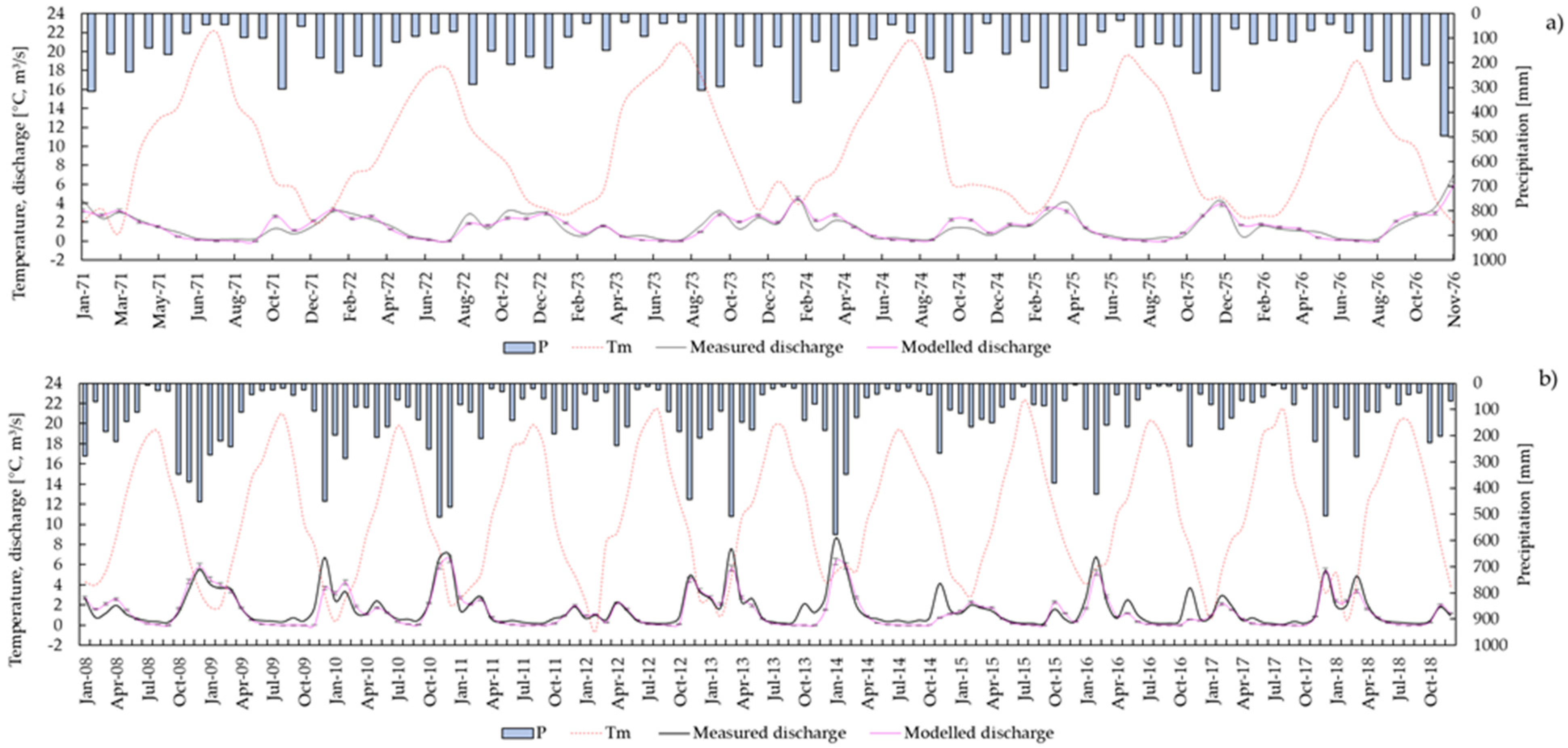
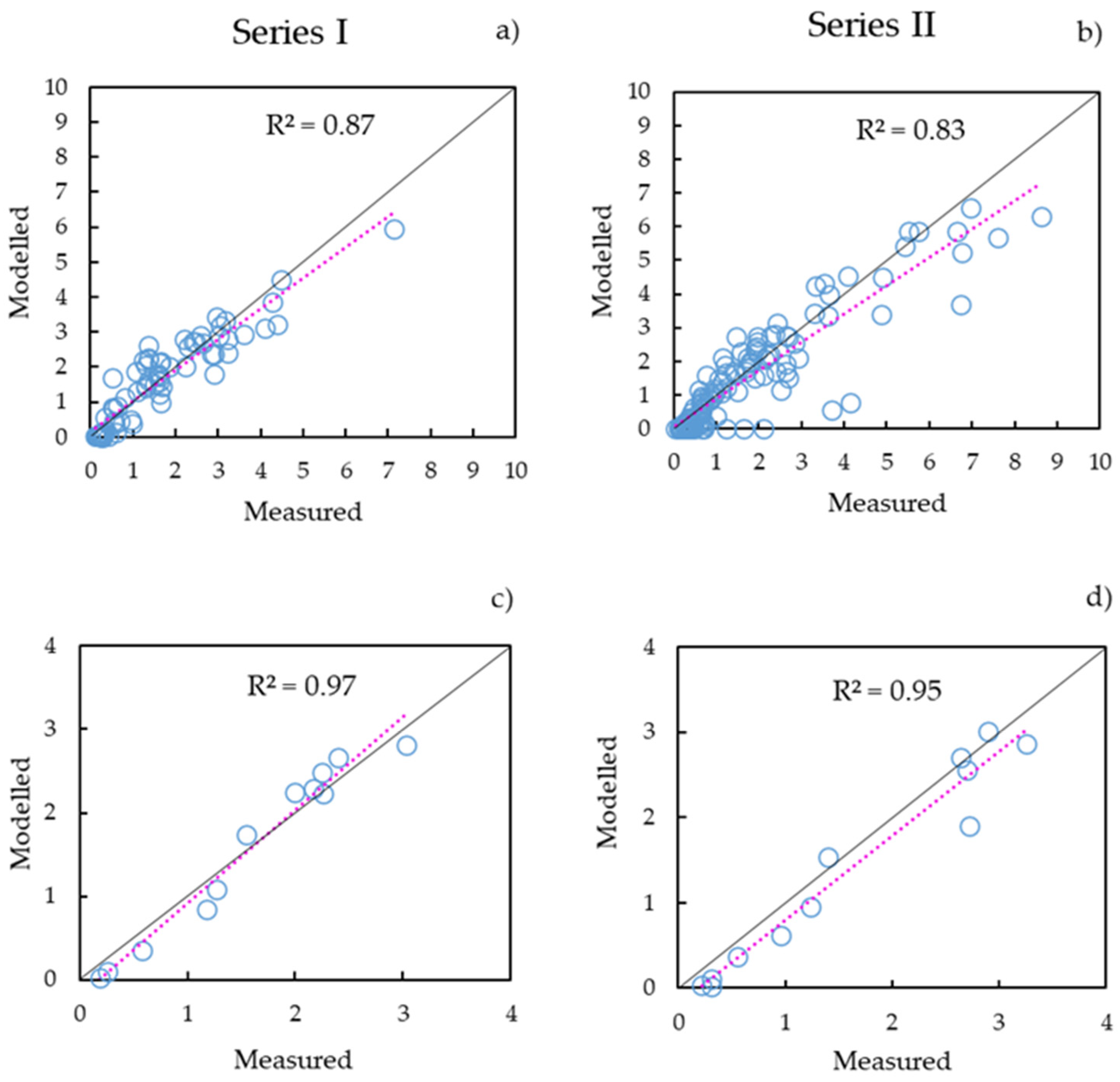
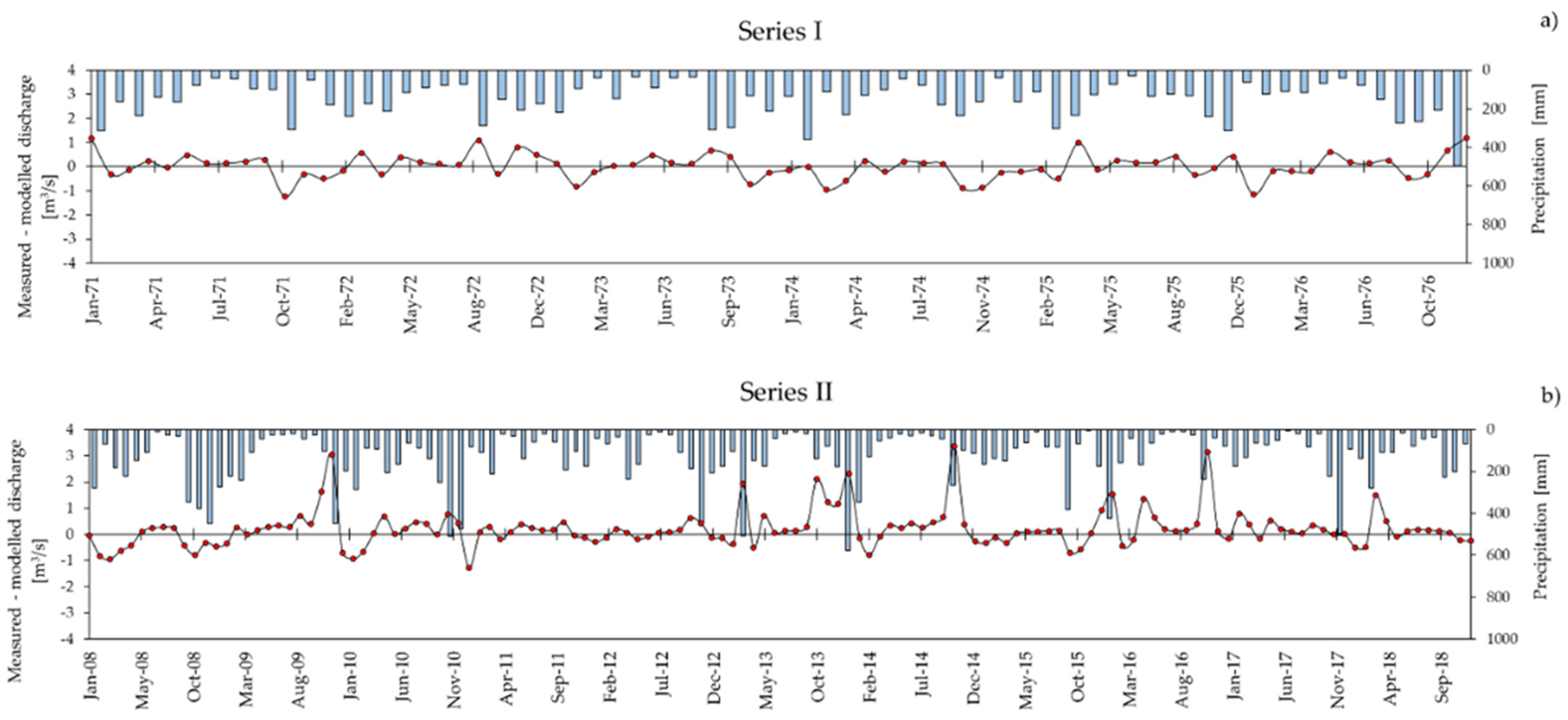
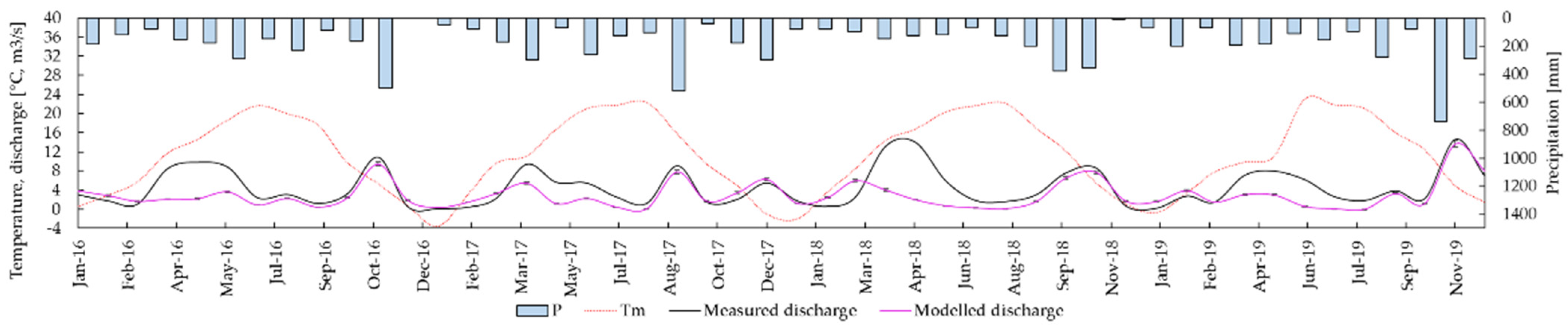
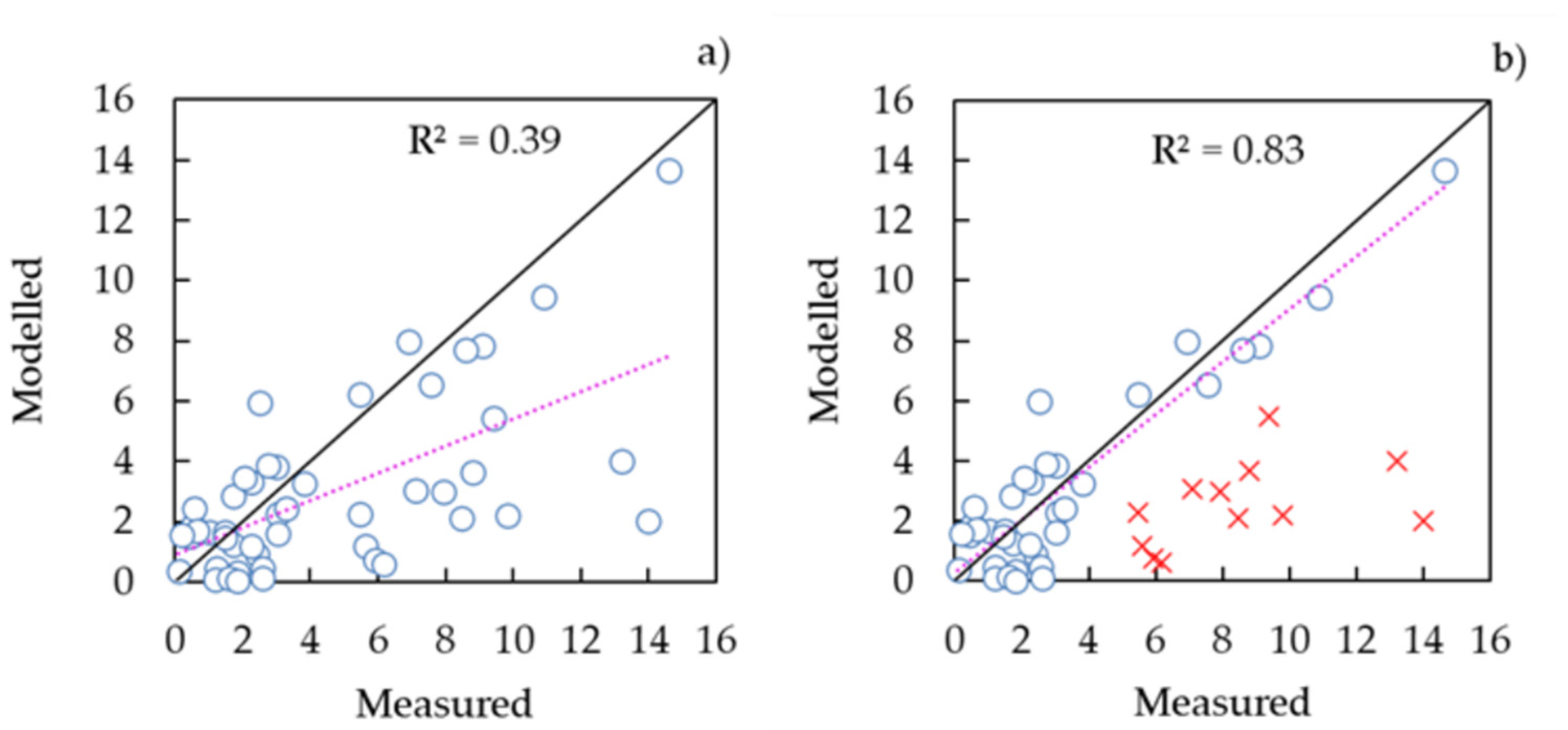
3.1. Reno at Pracchia Watershed
3.2. Savica at Ukanc Watershed
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Donker, N.H.W. WTRBLN: A computer program to calculate water balance. Comput. Geosci. 1987, 13, 95–122. [Google Scholar] [CrossRef]
- Thornthwaite, C.W.; Mather, J.R. The Water Balance; Laboratory in Climatology, Johns Hopkins University: Baltimore, MD, USA, 1955; Volume 8, pp. 1–104. [Google Scholar]
- Thornthwaite, C.W.; Mather, J.R. Instructions and Tables for Computing Potential Evapotranspiration and the Water Balance; Laboratory in Climatology, Johns Hopkins University: Baltimore, MD, USA, 1957; Volume 10, pp. 181–311. [Google Scholar]
- Sepaskhah, A.R.; Razzaghi, F. Evaluation of the adjusted Thornthwaite and Hargreaves-Samani methods for estimation of daily evapotranspiration in a semi-arid region of Iran. Arch. Agron. Soil Sci. 2009, 55, 51–66. [Google Scholar] [CrossRef]
- Bonacci, O.; Andrić, I. Karst spring catchment: An example from Dinaric karst. Environ. Earth Sci. 2015, 74, 6211–6223. [Google Scholar] [CrossRef]
- Pelton, W.L.; King, K.M.; Tanner, C.B. An Evaluation of the Thornthwaite and Mean Temperature Methods for Determining Potential Evapotranspiration 1. Agron. J. 1960, 52, 387–395. [Google Scholar] [CrossRef]
- Pruitt, W.O. Evapotranspiration: A guide to irrigation. Calif. Turfgrass Cult. 1964, 14, 27–32. [Google Scholar]
- Doorenbos, J.; Pruitt, W.O. Crop Water Requirements; FAO Irrigation and Drainage Paper No. 24; FAO: Rome, Italy, 1977; pp. 34–37. [Google Scholar]
- Hashemi, F.; Habibian, M.T. Limitations of temperature-based methods in estimating crop evapotranspiration in arid-zone agricultural development projects. Agric. Meteorol. 1979, 20, 237–247. [Google Scholar] [CrossRef]
- Malek, E. Comparison of alternative methods for estimating ETp and evaluation of advection in the Bajgah area, Iran. Agric. For. Meteorol. 1987, 39, 185–192. [Google Scholar] [CrossRef]
- Camargo, A.P.; Marin, F.R.; Sentelhas, P.C.; Picini, A.G. Adjust of the Thornthwaite’s method to estimate the potential evapotranspiration for arid and superhumid climates, based on daily temperature amplitude. Rev. Bras. Agrometeorol. 1999, 7, 251–257. [Google Scholar]
- Scozzafava, M.; Tallini, M. Net infiltration in the Gran Sasso Massif of central Italy using the Thornthwaite water budget and curve-number method. Hydrogeol. J. 2001, 9, 461–475. [Google Scholar] [CrossRef]
- Nanni, T.; Rusi, S. Idrogeologia del massiccio carbonatico della montagna della Majella (Appennino centrale). Bollettino-Società Geologica Italiana 2003, 122, 173–202. [Google Scholar]
- Sellinger, C.E. Computer Program for Estimating Evapotranspiration Using the Thornthwaite Method; NOAA Technical Memorandum ERL GLERL-101; United States Department of Commerce: Washington, DC, USA, 1996.
- Armiraglio, S.; Cerabolini, B.; Gandellini, F.; Gandini, P.; Andreis, C. Calcolo informatizzato del bilancio idrico del suolo. Nat. Brescia. Ann. Mus. Civ. Sci. Nat. Brescia 2003, 33, 209–216. [Google Scholar]
- McCabe, G.J.; Markstrom, S.L. A Monthly Water-Balance Model Driven by a Graphical User Interface (Vol. 1088); US Geological Survey: Reston, VA, USA, 2007.
- Hamon, W. Estimating potential evapotranspiration. Trans. Am. Soc. Civ. Eng. 1963, 128, 324–338. [Google Scholar] [CrossRef]
- Di Matteo, L.; Dragoni, W. Climate change and water resources in limestone and mountain areas: The case of Firenzuola Lake (Umbria, Italy). In Proceedings of the 8th Conference on Limestone Hydrogeology, Neuchatel, Switzerland, 21–23 September 2006. [Google Scholar]
- Di Matteo, L.; Dragoni, W.; Maccari, D.; Piacentini, S.M. Climate change, water supply and environmental problems of headwaters: The paradigmatic case of the Tiber, Savio and Marecchia rivers (Central Italy). Sci. Total Environ. 2017, 598, 733–748. [Google Scholar] [CrossRef] [PubMed]
- Portela, M.M.; Santos, J.; de Carvalho Studart, T.M. Effect of the Evapotranspiration of Thornthwaite and of Penman-Monteith in the Estimation of Monthly Streamflows Based on a Monthly Water Balance Model. In Current Practice in Fluvial Geomorphology-Dynamics and Diversity; IntechOpen: Rijeka, Croatia, 2019. [Google Scholar]
- Vandewiele, G.L.; Win, N.L. Monthly water balance models for 55 basins in 10 countries. Hydrol. Sci. J. 1998, 43, 687–699. [Google Scholar] [CrossRef]
- Mather, J.R. The Climatic Water Budget in Environmental Analysis; Free Press: Wong Chuk Hang, Hong Kong, 1978. [Google Scholar]
- Mather, J.R. Use of the climatic water budget to estimate streamflow. In Use of the Climatic Water Budget in Selected Environmental Water Problems; Elmer, N.J., Ed.; C.W. Thornthwaite Associates, Laboratory of Climatology: Centerton, NJ, USA, 1979; Volume 32, pp. 1–52. [Google Scholar]
- McCabe, G.J.; Wolock, D.M. Independent effects of temperature and precipitation on modeled runoff in the conterminous United States. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Pinna, M. Climatologia, XV ed.; UTET: Torino, Italy, 1977; p. 442. [Google Scholar]
- Dooge, J.C.I. The rational method for estimating flood peaks. Engineering 1957, 184, 311–313, 374–377. [Google Scholar]
- Schaake, J.C.; Geyer, J.C.; Knapp, J.W. Experimental examination of the rational method. J. Hydraul. Div. 1967, 93, 353–370. [Google Scholar] [CrossRef]
- Boughton, W.C. Evaluating Partial Areas of Watershed runoff. J. Irrig. Drain. Eng. 1987, 113, 356–366. [Google Scholar] [CrossRef]
- Longobardi, A.; Villani, P.; Grayson, R.B.; Western, A.W. On the relationship between runoff coefficient and catchment initial conditions. In Proceedings of the MODSIM, Townsville, Australia, 14–17 July 2003; pp. 867–872. [Google Scholar]
- Ferguson, R.I. Snowmelt runoff models. Prog. Phys. Geogr. 1999, 23, 205–227. [Google Scholar] [CrossRef]
- Spillner, J.; Mateos, C.; Monge, D.A. Faaster, better, cheaper: The prospect of serverless scientific computing and hpc. In Proceedings of the Latin American High-Performance Computing Conference, Buenos Aires, Argentina, 20–22 September 2017; Springer: Cham, Switzerland, 2017; pp. 154–168. [Google Scholar]
- Pawlik, M.; Figiela, K.; Malawski, M. Performance considerations on execution of large-scale workflow applications on cloud functions. arXiv 2019, arXiv:1909.03555. [Google Scholar]
- Cervi, F.; Corsini, A.; Doveri, M.; Mussi, M.; Ronchetti, F.; Tazioli, A. Characterizing the recharge of fractured aquifers: A case study in a flysch rock mass of the northern Apennines (Italy). In Engineering Geology for Society and Territory-Volume 3; Springer: Cham, Switzerland, 2015; pp. 563–567. [Google Scholar]
- Tazioli, A.; Cervi, F.; Doveri, M.; Mussi, M.; Deiana, M.; Ronchetti, F. Estimating the isotopic altitude gradient for hydrogeological studies in mountainous areas: Are the low-yield springs suitable? Insights from the northern Apennines of Italy. Water 2019, 11, 1764. [Google Scholar] [CrossRef]
- Valigi, D. La Simulazione Delle Portate Mensili nei Bacini in Facies di Flysch dell’Appennino Centro-Settentrionale con Particolare Riguardo al F. Nestore. Ph.D. Thesis, Università degli Studi di Perugia, Perugia, Italy, 1995. [Google Scholar]
- Brenčič, M.; Vreča, P. Hydrogeological and isotope mapping of the karstic River Savica in NW Slovenia. Environ. Earth Sci. 2016, 75, 651. [Google Scholar] [CrossRef]
- Ogrinc, N.; Kanduč, T.; Stichler, W.; Vreča, P. Spatial and seasonal variations in δ18O and δD values in the River Sava in Slovenia. J. Hydrol. 2008, 359, 303–312. [Google Scholar] [CrossRef]
- Buser, S. Basic geological map of SFRJ 1:100,000. In Guidebook of Sheets Tolmin and Videm (Udine): L 33–63, 33–64; Zvezni Geološki Zavod, Beograd: Ljubljana, Slovenian, 1986. [Google Scholar]
- Trišič, N.; Bat, M.; Polajnar, J.; Pristov, J. Water balance investigations in the Bohinj region. In Tracer Hydrology 97, Proceedings of the 7th International Symposium on Water Tracing, Portorož, Slovenia, 26–31 May 1997; CRC Press: Boca Raton, FL, USA, 1997; pp. 26–31. [Google Scholar]
- Urbanc, J.; Brancelj, A. Tracing experiment in lake Jezero v Ledvici, valley Triglavska jezera. Geologija 1999, 42, 207–214. [Google Scholar] [CrossRef]
- Bat, M. Hidrološke raziskave ARSO na območju Bohinja. Dela 2007, 165–181. [Google Scholar] [CrossRef]
- Brenčič, M.; Vreča, P. Influence of snow thawing regime changes on the outflow from karstic aquifer. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 7–12 April 2013. [Google Scholar]
- Dourado-Neto, D.; Jong van Lier, Q.D.; Metselaar, K.; Reichardt, K.; Nielsen, D.R. General procedure to initialize the cyclic soil water balance by the Thornthwaite and Mather method. Sci. Agric. 2010, 67, 87–95. [Google Scholar] [CrossRef]
- Dragoni, W.; Giontella, C.; Melillo, M.; Cambi, C.; Di Matteo, L.; Valigi, D. Possible response of two water systems in Central Italy to climatic changes. Adv. Watershed Hydrol. 2015, 397–424. [Google Scholar]
- Guardiola-Albert, C.; Martos-Rosillo, S.; Pardo-Igúzquiza, E.; Duran Valsero, J.J.; Pedrera, A.; Jiménez-Gavilán, P.; Linan Baena, C. Comparison of recharge estimation methods during a wet period in a karst aquifer. Groundwater 2015, 53, 885–895. [Google Scholar] [CrossRef]
- Legates, D.R.; Bogart, T.A. Estimating the proportion of monthly precipitation that falls in solid form. J. Hydrometeorol. 2009, 10, 1299–1306. [Google Scholar] [CrossRef]


| Series I (January 1971–December 1976 Period) | Series II (January 2008–December 2018 Period) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Min | Max | Std | Median | Mean | Min | Max | Std | Median | |
| Modelled discharge (m3/s) | 1.572 | 0.004 | 5.945 | 1.285 | 1.621 | 1.389 | 0.000 | 6.550 | 1.633 | 0.827 |
| Measured discharge (m3/s) | 1.591 | 0.108 | 7.145 | 1.362 | 1.345 | 1.599 | 0.050 | 8.610 | 1.771 | 0.845 |
| Tm (°C) | 9.9 | 0.9 | 22.0 | 6.0 | 8.85 | 10.9 | −0.5 | 22.3 | 6.2 | 10.7 |
| P (mm) | 155.4 | 27.9 | 496.4 | 94.5 | 133.7 | 136.4 | 4.6 | 576.8 | 127.8 | 96.85 |
| Mean | Min | Max | Std | Median | |
|---|---|---|---|---|---|
| Modelled discharge (m3/s) | 2.957 | 0.023 | 13.683 | 2.814 | 2.155 |
| Measured discharge (m3/s) | 4.544 | 0.098 | 14.610 | 3.886 | 2.876 |
| Tm (°C) | 11.2 | −3.5 | 23.1 | 7.8 | 11.2 |
| P (mm) | 179.4 | 0.0 | 739.0 | 140.4 | 150 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mammoliti, E.; Fronzi, D.; Mancini, A.; Valigi, D.; Tazioli, A. WaterbalANce, a WebApp for Thornthwaite–Mather Water Balance Computation: Comparison of Applications in Two European Watersheds. Hydrology 2021, 8, 34. https://doi.org/10.3390/hydrology8010034
Mammoliti E, Fronzi D, Mancini A, Valigi D, Tazioli A. WaterbalANce, a WebApp for Thornthwaite–Mather Water Balance Computation: Comparison of Applications in Two European Watersheds. Hydrology. 2021; 8(1):34. https://doi.org/10.3390/hydrology8010034
Chicago/Turabian StyleMammoliti, Elisa, Davide Fronzi, Adriano Mancini, Daniela Valigi, and Alberto Tazioli. 2021. "WaterbalANce, a WebApp for Thornthwaite–Mather Water Balance Computation: Comparison of Applications in Two European Watersheds" Hydrology 8, no. 1: 34. https://doi.org/10.3390/hydrology8010034
APA StyleMammoliti, E., Fronzi, D., Mancini, A., Valigi, D., & Tazioli, A. (2021). WaterbalANce, a WebApp for Thornthwaite–Mather Water Balance Computation: Comparison of Applications in Two European Watersheds. Hydrology, 8(1), 34. https://doi.org/10.3390/hydrology8010034









