Abstract
In this research work, an analysis is conducted concerning the impact on rainfall-runoff simulations of utilizing rain gauge precipitation measurements against weather radar quantitative precipitation estimates. The study area is the Sarantapotamos river basin, a peri-urban basin located in the greater area of Athens, and measurements from a newly installed X-Band weather radar system, referred to as rainscanner, along with ground rain gauge stations were used. Rainscanner, in contrast to rain gauges, is able to provide with higher resolution surface precipitation datasets, but due to signal errors, uncertainty is involved, and thus proper calibration and evaluation of these estimates must be first performed. In this context, this research work evaluates the impact of adopting different precipitation datasets and interpolation methods for generating runoff, through the use of a lumped based rainfall-runoff model. Initially, the analysis focuses on the correlation between the rain gauge and the rainscanner estimations for each station, as well as for the calculated mean areal precipitation. The results of the rainfall-runoff simulations show that even though a different spatial and temporal variability of the rainfall field is calculated through the two datasets, in a lumped-based scheme, the most important factor that dictates the runoff generation is the amount of total precipitation.
1. Introduction
Rainfall-runoff modelling depends mainly on the precipitation measurements. The most used and traditional system of recording precipitation are rain gauge stations. Rain gauge stations provide with point measurement of precipitation and therefore a suitable network of such stations is usually implemented over a large area. In hydrology, the study is usually performed on a specified basin scale, therefore a network of such rain gauge stations that are properly distributed throughout is essential in order to accurately describe the spatial variability of a rainfall event. General guidelines by the World Meteorological Organization for implementing such networks are provided, however this is not usually the case, since due to installation costs and orography, the distribution of rain gauges, especially on high elevations, is lacking. Moreover, the current demand on quick data has raised the maintenance costs of ground stations, which require constant powering, connection to internet and security. For these reasons, more efficient ways, involving telemetric measurements of precipitation, such as weather radars and satellites, have gained increased attention [1]. Weather radars have long been implemented and are considered among the best precipitation data source for modelling [2], while satellite data were only recently implemented and are gaining ground [3]. These systems feature imminent high spatial and temporal quantitative precipitation estimates (QPE). These benefits, however, come at a price, since they are subject to quantitate errors [4]. There is a large number of factors that affect the quality of the QPE, such as systematic errors due to improper calibration of the rainscanner system, signal attenuation issues and the use of a proper radar reflectivity, Z, to rainfall intensity, R relationship, also known as Z–R relationship, among others [5]. The Z–R relationship is among the most crucial parameters to be configured since it transforms the measured reflectivity fields, Z (mm6/m3), to rainfall intensity, R (mm/h). The relationship is a power law relation in the form of, Z = aRb, where a and b parameters vary depending on the rain droplets’ size distribution of an event [6]. Therefore, the Z–R relationship is a static relationship but varies in time and space. The most common approaches are to calibrate the Z–R relationship for use on a specific weather radar based on measurements of a distrometer [7,8,9], an equipment for measuring the drop size distribution, or the correlation of the QPE with rain gauge measurements [3,10,11,12]. Nevertheless, the parameters of the Z–R relationship should be evaluated for use with only specific storm characteristics, being for instance either convective or stratiform. Only few studies deal with the variability of the Z–R relationship in time space [13,14], while the majority of studies tend to use a one-at-a-time derived Z–R relationship and then apply bias corrections in real time.
Regarding rainfall-runoff modelling, the use of radar datasets tends to increase the quality of runoff modelling [15,16], however the raw QPE provided by these systems should be first adjusted based on the rain gauge measurements, since it tends to lead to better accuracy, compared to raw unadjusted radar estimates [17,18]. Gridded datasets tend to perform well with fully distributed models, but semi-distributed and lumped models can be implemented by calculating the Mean Areal Precipitation (MAP) over a basin. One important factor in all studies is the spatial and temporal scale of the analysis. While the spatial scale can be easily configured through modelling, the temporal aspect must not be ignored since weather radar measurements tend to have better correlation with rain gauge measurements when the analysis is performed on coarser scales [2,19,20]. Therefore, it is important to notice that the use of higher spatial and temporal resolution datasets does not always translate into more accurate estimations [21,22].
In this study, a validation of a newly installed X-Band weather radar, also referred to as rainscanner, is evaluated through performing a comparative analysis between rain gauge measurements and the rainscanner estimates for a peri-urban basin, in the greater region of Athens, in Greece. The rainscanner is located in the facilities of the National Technical University of Athens (NTUA) near the center of Athens, Greece, and features high spatial and temporal scales, with up to 100 × 100 m2 spatial resolution in two min time intervals [23]. This analysis focuses on the generated uncertainty by estimating the rainfall field through different interpolating methods and temporal scales and assessing their impact on the generated hydrographs through rainfall-runoff modelling.
2. Materials and Methods
2.1. Study Area
The study area is the rural part of the Sarantapotamos basin, located in the west part of the Attica region, in Greece, as shown in Figure 1. The Sarantapotamos basin is surrounded by mount Kithairon in the northwest, mount Pastras on the north, mount Parnitha in the northeast and mount Pateras in the west. The main stream is the Sarantapotamos river, which flows throw the valley of Inoi and the Thriasion plain, up to the sea, the Gulf of Elefsis. Other notable sub-streams are Ag. Vlassios, as well as the Soures and Ag. Aikaterini streams that flow within the Mandra settlement and only meet up with Sarantapotamos at Elefsina, just before the sea.
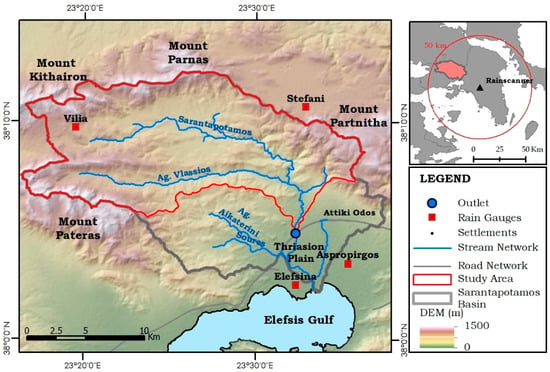
Figure 1.
The Sarantapotamos basin, the study area and the rain gauge network.
The basin is a peri-urban basin case, where the north and largest part of the basin has rural characteristics, while at the south part of the basin, below the Attiki Odos Motorway and the Mandra settlement, extensive urban development is observed. The result of this urbanization has led to the occurrence of numerous flood events, with the most recent and catastrophic being the event of the 14 November 2017, where an intense flash flood event resulted in a total of 24 casualties and huge economic damages within and near the settlement of Mandra [24,25,26]. Since then, storm water management systems have been designed and implemented for the settlement of Mandra. For this cause, the study area is set in the rural part of the basin, which is defined by the cross-section between the Sarantapotamos stream and the Attiki Odos motorway, covering a total area of 231 km2, with a maximum and mean elevation of 1270 and 470 m, respectively. Within this part, the most notable settlements are Vilia, Oinoi, Pournari and Lefka, located near the banks of Sarantapotamos, and Ag. Georgios and Paleochori located near the banks of Ag. Vlassios. The study area is the largest rural basin within the region of Attiki, where data from the newly installed rainscanner are available.
The land cover of the region is mostly forest-based, with agricultural activity found in the plains of Oinoi and Lefka. Sarantapotamos stream has a total length of 38 km, where 28 km lies within the study area. The first 20 km have a west to east direction, only to switch to a southern direction for the remainder. This direction tends to have an impact on the generation of high runoff peaks, since in most cases, the storm movement in the region also has the same direction, and thus the accumulation of runoff is accelerated.
2.2. Data Used
For this study, a rainfall event that occurred in November 2019 from 21:40 UTC+2 of the 24th up until 06:00 UTC+2 of the 25th, was studied. The event resulted in a low barometric pressure that was created on 24 November 2019, over Italy, and a cold front extending almost throughout southwestern Greece. The barometric system was strengthened as it moved to the east over the Ionian Sea and continued to deepen for the next six hours and moved quickly to the east, affecting central Greece and Attica. The system produced high-intensity rainfall events, with large sums of cumulative rain with strong winds. By applying well-known and used Intensity Duration Frequency (IDF) curves derived for the Mandra station [27], the studied event had a 5- to 10-year return period.
Two sets of rainfall measurements were used in this study. The first are ground rain gauge stations, as well as gridded precipitation datasets acquired from the NTUA rainscanner system. The rain gauge stations used in this study are part of the National Observatory of Athens Automatic Network (NOAAN), which provides with high-quality 10 min precipitation height datasets with good coverage of the entire Hellenic continent [28]. The network is constantly updating with the addition of new stations, but for the studied event, only one station, the Vilia station, is located within the study area. Three more stations, the Stefani, the Aspropirgos and the Elefsina stations, in close proximity to the basin, were therefore used, in order to properly calculate the MAP within the basin. As seen in Figure 1, the rain gauge distribution within the basin is not optimal, since only the Vilia station is located in high elevation, whereas Aspropirgos and Elefsina are located further away, near the coast. The Stefani station is located near the basin, and will therefore contribute substantially to the MAP, but is located on the other side of mount Partnitha, which will most likely have a negative effect of MAP estimations, since due to orography and storm movement, the west part will record higher precipitation values than the east. By applying the Thiessen polygons interpolation method, the corresponding station weights were calculated as 54%, 43%, 2% and 1% for stations Vilia, Stefani, Elefsina and Aspropirgos, respectively.
On the other hand, the NTUA rainscanner estimates are based on measurements of reflectivity in a gridded format of a 100 m × 100 m pixel size and 2 min temporal scale. Proper ground clutter corrections were applied, and the datasets were aggregated into 10 min intervals to match the rain gauges scale. In order to utilize the datasets, a suitable Z–R relationship must first be used in order to transform the reflectivity values (Z) into rain rate (R) based on the expression, Z = aRb, where the values of parameters a and b depend upon the droplets’ size distribution of the specific event. Since such measurements were not available, two set of parameters were used based on previous studies. First, the well-known Marshal n’ Palmer equation, Z = 200R1.6, was used [6], which is suitable for general use, as well as the equation Z = 261R1.52, which was derived by analyzing distrometer measurements of rainfall events within the area of Athens [7].
2.3. Rainfall-Runoff Model
As is the case in the majority of subbasins in the region, the study area is an ungauged basin, and no discharge datasets were available. For estimating the generated runoff, the synthetic Soil Conservation Service (SCS) dimensionless United Hydrograph (UH) was used, which due to its simplicity and low data requirements, has been used with success in various studies in Greece [29]. The model has one parameter, the basin lag, i.e., the time difference between the center of mass of rainfall excess and the peak of the UH. The parameter can be evaluated as a fraction of the time of concentration, with 0.6 as the suggested value, plus half the time interval step. The time of concentration can be calculated through the empirical relationships, such as the Giandotti equation, which is reported to have better results in Mediterranean basins than other empirical methods [30,31]. The concentration time was calculated, equal to 6.70 h.
Precipitation losses were calculated through the use of the Soil Conservation Service-Curve Number (SCS-CN) method [32]. The SCS-CN method is a widely used and efficient method for estimating precipitation losses in ungauged basins since it only requires two parameters, i.e., the CN that specifies the soil storage capacity, S, and the initial abstraction, which is expressed as a percentage of S, with 0.2 as the suggested value [30]. The derivation of CN was performed using Geographical Information Systems (GIS) tools, by combining the Corine Land Cover (CLC) of 2018, geological maps and respected CN tables [33]. In Figure 2, the above raster maps are presented. For the CLC map, although shown for classification level one, the analysis was performed on CLC level two. Since a lumped approach was taken for the simulations, the mean value of the CN raster was calculated as the sole CN for the entire basin. In order to evaluate the hydrological condition of soils before the event, the seven days antecedent precipitation index (API) and the normalized antecedent precipitation index (NAPI) [34] were calculated for each station. The API value for stations Vilia, Elefsina, Asporirgos and Stefani was 31.96, 21.80, 20.60 and 28.47 mm, while the NAPI was calculated at 2.94, 2.3, 2.30 and 1.77 mm, respectively. Considering the location of each station, i.e., the high coverage of the study area by stations Vilia and Stefani, averaging at 97% through the Thiessen polygon method, the values indicate that wet antecedent conditions were present prior to the event, and thus the Antecedent Moisture Conditions (AMC), AMC-III was calculated through AMC-II. The mean CN used in the simulations was 83. Finally, regarding baseflow, as in the case of most streams in the Attica region, Sarantapotamos does not feature any form of baseflow. All simulations were performed using the Hydrologic Engineering Center-Hydrologic Modelling System (HEC-HMS) model. HEC-HMS is a rainfall-runoff modelling platform developed by the United States (US) Army Corps of Engineers [35], which integrates the use of sub-models, in order to model different aspects of the rainfall-runoff process, and has been applied with success in various studies in Greece [36,37,38].

Figure 2.
Geomorphological analysis—Curve Number (CN) map derivation process, (a) Corine Land Cover (CLC), classification level one, (b) hydrological groups, (c) CN raster map.
2.4. Mean Areal Precipitation Calculation Methods
When adopting a lumped basin rainfall-runoff scheme, the rain gauge precipitation datasets must be first converted into MAP. Regarding rain gauges, as point measurements, there are several methods by which this can be achieved. The most common method is by applying weights into each station’s measurements and calculating the MAP as the sum of the weighted precipitation. The easiest way to calculate these weights is through the calculation of the Thiessen polygons, which dictate the area of influence of each station within a specified basin. The percentage of the area to the total area of the basin is the actual weight used for MAP calculation. The method dictates that every point within the area of a designated stations’ Thiessen polygon would have the same precipitation value as that of the station. While the method is rather simple, when good distribution of the station’s location within the basin is present, the method performs well.
In cases where bad distribution or a limited number of stations are present, the results may not be representative. Therefore, other interpolation methods can be utilized, such as the inverse distance weighting (IDW) or more complex methods such as ordinary Kriging. In IDW, a gridded precipitation dataset is constructed, utilizing weights based upon the inverse squared distance of each cell for all stations. Following the creation of this dataset, the MAP is easily calculated as the mean value of the raster dataset for each time interval. Finally, regarding the rainscanner measurements, being gridded datasets, the MAP is calculated as in the case of IDW.
3. Results and Discussion
3.1. Precipitation Analysis
First a correlation analysis is performed between each individual station’s timeseries and the timeseries derived from the rainscanner. The 10 min datasets were aggregated into 30 min and 1 h intervals, in order to assess the temporal influence. In Figure 3, the scatter plots are shown, for time intervals of 30 min and 1 h, while in Table 1, the correlation coefficient values for each time interval are presented. It is obvious that by assessing the datasets in high temporal scale, such as 10 min, low correlation is observed, but by aggregating, up to 1 h, the correlation is getting stronger. In the stations’ scale, the correlations on the 10 min datasets are lower than 0.10, while on the 30 min datasets, they are between 0.11 and 0.25, and on the 1 h scale, the correlation is approximately 0.40, apart from station Vilia which reports low correlation in all cases. As seen in Figure 3, it seems that an overestimation is performed by the rainscanner in low precipitation values, while an underestimation is performed on higher values.
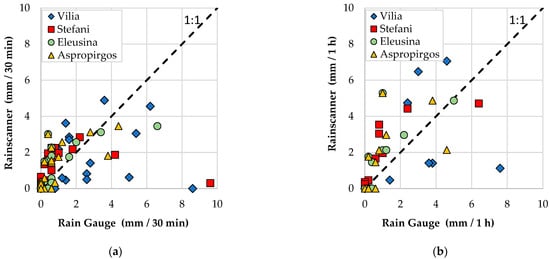
Figure 3.
Rainscanner and rain gauge scatter plots, (a) on a 30 min temporal scale, and (b) on a 1 h temporal scale.

Table 1.
Correlation coefficient for different time interval scales.
In Figure 4, the timeseries of the MAP derived from the IDW method for the rain gauges and the Z = 200R1.6 relationship for the radar measurements are presented in bar plots along with the precipitation accumulation timeseries in lines. MAP derived from the Thiessen method and the Z = 261R1.52 relationship were highly correlated with the above results, and therefore they were not plotted for visualization purposes. While for both sets, the accumulative precipitation is equal at 42 mm, there is a difference in the temporal variability of the rainfall field. In the rainscanner case, a near linear accumulation is observed, whereas in the case of the rain gauges, less precipitation is recorded in the first hours, only to peak at approximately 04:30 until 06:00. In the same time period, the rainscanner measures little to no data, which is evidence of abnormal behavior. Since the rain gauge measurements’ quality is not in question, the most stand out cause of this error would most likely be in radar signal errors, such as signal attenuation or overshooting of the actual storm cloud. The study area is located near the limit of the rainscanner range, thus with a preset 2 degrees of the radar beam angle, the measurements are taken as high as 2 km difference altitude compared to those in the ground surface. X-Band radar systems have weaker signals, thus in some cases, where a storm cloud is in between the rainscanner and further targeted locations, heavy underestimation of the rainfall field in that area may occur. By removing the specific time interval, the correlation in all stations and the MAP increases, above 0.6 in most cases, as seen in Table 2. This indicates that overall, the rainscanner measurements are correlated, but sensitive applications on locations at the rainscanner ranges should be avoided, or work in conjunction with rain gauge measurements. Regardless, in this research work, the datasets were used “as is”, in order to validate the current measurements and their impact on the rainfall-runoff simulations.

Figure 4.
Mean areal precipitation and accumulative precipitation (Acc) for the rain gauge and radar estimations through the IDW and Z = 200R1.6 precipitation products.

Table 2.
Main characteristics of the generated hydrographs.
Regarding the total precipitation recorded by both measurements, 44, 41, 42 and 39 mm were calculated for the for the rain gauge Thiessen, IDW methods and the rainscanner Z = 261R1.52 and Z = 200R1.6, respectively. While the Thiessen and IDW methods do not show any significant difference, the impact of the Z–R relationship is crucial. Lower values of parameters a and b lead to higher precipitation estimates, while higher values of a are usually better suited in convective type storms. Finally, in Figure 5, the spatial distribution of the total precipitation is shown, for rain gauge MAP through the IDW method and the rainscanner estimates through relationship Z = 200R1.6. In the rain gauges case, the spatial distribution of rainfall is dictated only by the station’s locations and their corresponding measurements, thus the maximum precipitation is found at Vilia station, located on the northwest part of the basin. In the rainscanner case, the distribution is affected by the actual storm cloud movement, thus the maximum total precipitation occurred in the southwest, and specifically over the mount Pateras. This difference can have an impact on rainfall-runoff simulations where a semi-distributed or fully distributed approach is considered, which is not the case of this work. However, the error of applying rain gauge measurements as the sole datasets of precipitation is highlighted. Rainscanner and weather radar measurements in general may involve increased uncertainty, but the added value of the spatial variability of rainfall cannot be denied.
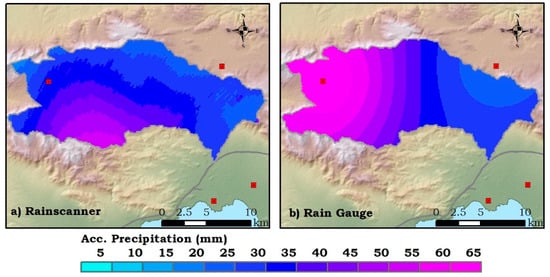
Figure 5.
Accumulative precipitation, (a) rainscanner estimates through Z = 200R1.6, (b) rain gauges through IDW.
3.2. Rainfall-Runoff Simulations
In Figure 6, the simulated hydrographs for all precipitation estimates are presented, along with their respective rainfall timeseries. Specifically, the simulations were performed for four datasets of precipitation, two based on rain gauge measurements, i.e., MAP derived by Thiessen polygons and IDW methods, and two based on rainscanner estimations, i.e., by applying two different Z–R relationships, Z = 200R1.6 and Z = 261R1.52. The simulations were performed in 30 min time steps. In Table 2, the main characteristics of the flood hydrographs are presented. In Figure 6, the individual hydrographs for each dataset are shown, along with their corresponding precipitation and losses. The difference in the temporal variability of rainfall is obvious between the rain gauge simulations, Figure 6a,b, and those from derived from the rainscanner, Figure 6c,d.
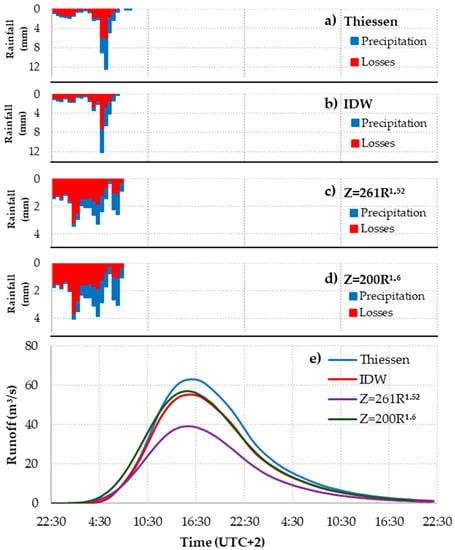
Figure 6.
Rainfall-runoff simulations for each dataset. Rainfall timeseries for each dataset are shown in, (a) Thiessen; (b) IDW; (c) Z = 200R1.6; (d) Z = 261R1.52; (e) simulated hydrographs.
A small deviation is observed in all hydrographs. Overall, all precipitation datasets showed equal hydrographs, except in the case of the first Z–R relationship, where the peak discharge and runoff volume is lower than in the other cases. Concerning the two MAP products derived from the rain gauge measurements, the difference between the Thiessen and the IDW methods was 7.70 m3/s on the peak discharge, which resulted in an only 3 mm difference on total precipitation, while the time to peak was slightly lower in the IDW case. The difference in the Z–R relationship results lie in the difference in the amount of precipitation, since by using the relationship Z = 200R1.6, more precipitation is estimated. By using Z = 200R1.6, the total precipitation was calculated at 7 mm, i.e., 20%, more than the precipitation estimated by using Z = 261R1.52, which resulted in 17.90 m3/s, i.e., 46%, more peak discharge and runoff volume generation.
Finally, comparing the rain gauge measurements with the rainscanner, it seems that the best correlation is seen when utilizing IDW for MAP based on the rain gauge measurements, with the Z = 200R1.6 relationship. The difference between these two sets was less than 3% on the generated peak discharge and runoff volume. It is found that when a lumped scheme is used, the most important factor for achieving the best correlation between the two datasets is the total amount of precipitation, regardless of the temporal and spatial correlation of the precipitation timeseries. Regarding the temporal distribution of rainfall, it is estimated that any difference found between the datasets is actually diminished through the calculation of precipitation losses, even in the case of wet AMC-III conditions, where the least number of losses was calculated. Nevertheless, it is important to notice that the effect of the Z–R relationship upon the generated hydrograph is rather significant, therefore increased attention should be made when applying a specific Z–R relationship. It is suggested that the combined use of rainscanner and rain gauge measurements should be used, in order to obtain the best spatial detail of the rainfall field from the rainscanner measurements and the quality of the rain gauge station datasets.
4. Conclusions
In this study the impact of adopting different mean areal precipitation calculations and their impact on generated hydrographs was performed. The comparisons were performed on a peri-urban basin, the Sarantapotamos river basin, known for its recent catastrophic flood events. The analysis was performed on two areas, first involving a correlation analysis between the different precipitation products, derived from the rain gauge and rainscanner measurements, and secondly regarding their impact on the generated hydrograph through rainfall-runoff modelling.
It was shown that the correlation between the rainscanner and rain gauge datasets is affected by the temporal scale of the analysis, where at fine scales of 10 min, the correlation is not good, whereas at larger scales of 30 min to 1 h, the datasets showed better correlation. However, on average, the rainscanner measurements tended to overestimate low precipitation values, and underestimate high values. It is therefore suggested that weather radar bias corrections should only be applied on the time scale of the proposed analysis. Concerning the estimated total MAP for the studied event, it was found that higher values are estimated through the use of the Thiessen polygons method, in contrast with IDW, although the difference was a few mm of precipitation. However, the Thiessen method failed to recreate the spatial variability of the rainfall field, and as such, the IDW is considered a better estimate. Regarding the rainscanner measurements, it was shown that by using a different Z–R relationship, even with small changes in the parameter values, a significant difference of up to 20 mm was found on the total MAP, which highlights the impact of the used Z–R relationship. The best correlation between the two datasets was found when using the IDW method for the rain gauges and the Z = 200R1.6 relationship. In this case, although the total MAP was equally estimated, the spatial variability of the rainfall field was different in each case, since in the IDW method, it is dictated by the station’s location and measurements, whereas in the rainscanner, it concerns actual rainfall. In the studied event, the IDW method calculated the maximum rainfall in the northwest part of the basin, whereas in the rainscanner, the maximum was located in the southwest.
Finally, regarding the impact on rainfall-runoff simulations, it was found that when a lumped scheme was used, the main parameter that led to equal runoff volume generation was the total precipitation, regardless of its temporal and spatial variability between the two datasets. While a certain amount of temporal correlation between the two datasets is always met, since they are measuring the same rainfall volume, the impact of it is diminished through the calculation of precipitation losses. Results showed that for the studied event, the best correlation between the two datasets was met when adopting the IDW and the Z = 200R1.6, since they feature the same total precipitation values. Finally, the difference between the two Z–R relationships should also be mentioned, since, as stated, a small change in the values of parameters a and b can lead to up to a 20% difference in the estimated total precipitation, which led to a 46% difference on the calculated peak discharge. The usage of an inappropriate Z–R relationship can lead to wrong rainfall estimates, which in turn multiply the extent of the errors generated in the runoff calculations.
Future research will focus on evaluating the spatial variability of the rainfall fields on the generated hydrograph through implementation of semi-distributed and fully distributed rainfall-runoff models for multiple events measured in the region. Observed runoff, if available, should be utilized to calibrate and validate the used model, in order to minimize any uncertainty generated by the added parameters. Finally, a rain gauge–rainscanner error correction scheme could also be evaluated. Through this study, it is also acknowledged that the overall quality and correlation of the rainscanner estimates with rain gauge data depend heavily on the spatial and temporal scale of the analysis, thus the investigation of Z–R relationship calibration and bias corrections in such small scales could be considered important for highly detailed early warning systems.
Author Contributions
Conceptualization, A.B. and E.B.; methodology, A.B.; software, A.B.; validation, A.B. and E.B.; formal analysis, A.B.; investigation, A.B.; resources, A.B. and E.B.; data curation, A.B.; writing—original draft preparation, A.B.; writing—review and editing, A.B. and E.B.; visualization, A.B.; supervision, E.B.; project administration, E.B.; funding acquisition, A.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research is co-financed by Greece and the European Union (European Social Fund-ESF) through the Operational Programme “Human Resources Development, Education and Lifelong Learning” in the context of the project “Strengthening Human Resources Research Potential via Doctorate Research” (MIS-5000432), implemented by the State Scholarships Foundation (ΙΚΥ).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
Authors would like to thank the Institute of Environmental Research and Sustainable Development of the National Observatory of Athens for the supply of the rain gauge precipitation measurements in the study area. This research was conducted in the framework of the corresponding author’s PhD study funded by the Greek State Scholarships Foundation (IKY).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Berenguer, M.; Corral, C.; Sánchez-Diezma, R.; Sempere-Torres, D. Hydrological Validation of a Radar-Based Nowcasting Technique. J. Hydrometeor. 2005, 6, 532–549. [Google Scholar] [CrossRef][Green Version]
- Price, K.; Purucker, S.T.; Kraemer, S.R.; Babendreier, J.E.; Knightes, C.D. Comparison of Radar and Gauge Precipitation Data in Watershed Models across Varying Spatial and Temporal Scales. Hydrol. Process. 2014, 28, 3505–3520. [Google Scholar] [CrossRef]
- Gilewski, P.; Nawalany, M. Inter-Comparison of Rain-Gauge, Radar, and Satellite (IMERG GPM) Precipitation Estimates Performance for Rainfall-Runoff Modeling in a Mountainous Catchment in Poland. Water 2018, 10, 1665. [Google Scholar] [CrossRef]
- Villarini, G.; Krajewski, W.F. Review of the Different Sources of Uncertainty in Single Polarization Radar-Based Estimates of Rainfall. Surv. Geophys. 2010, 31, 107–129. [Google Scholar] [CrossRef]
- Pathak, C.; Curtis, D.; Kitzmiller, D.; Vieux, B. Identifying and Resolving the Barriers and Issues in Using Radar-Derived Rainfall Estimating Technology. J. Hydrol. Eng. 2013, 18, 1193–1199. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M.K. The Distribution of Raindrops with Size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Baltas, E.A.; Panagos, D.S.; Mimikou, M.A. An Approach for the Estimation of Hydrometeorological Variables Towards the Determination of Z-R Coefficients. Environ. Process. 2015, 2, 751–759. [Google Scholar] [CrossRef]
- Baltas, E.A.; Mimikou, M.A. The Use of the Joss-Type Disdrometer for the Derivation of ZR Relationships. In Proceedings of the 2nd European Conference on Radar in Meteorology and Hydrology (ERAD), Delft, The Netherlands, 18–22 November 2002; Volume 291. [Google Scholar]
- Feloni, E.; Baltas, E.; Kotsifakis, K.; Dervos, N.; Giavis, G. Analysis of Joss-Waldvogel Disdrometer Measurements in Rainfall Events. In Proceedings of the Fifth International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2017), Paphos, Cyprus, 6 September 2017; Papadavid, G., Hadjimitsis, D.G., Michaelides, S., Ambrosia, V., Themistocleous, K., Schreier, G., Eds.; SPIE: Paphos, Cyprus, 2017; p. 60. [Google Scholar]
- Sahlaoui, Z.; Mordane, S. Radar Rainfall Estimation in Morocco: Quality Control and Gauge Adjustment. Hydrology 2019, 6, 41. [Google Scholar] [CrossRef]
- Qiu, Q.; Liu, J.; Tian, J.; Jiao, Y.; Li, C.; Wang, W.; Yu, F. Evaluation of the Radar QPE and Rain Gauge Data Merging Methods in Northern China. Remote Sens. 2020, 12, 363. [Google Scholar] [CrossRef]
- Hasan, M.M.; Sharma, A.; Mariethoz, G.; Johnson, F.; Seed, A. Improving Radar Rainfall Estimation by Merging Point Rainfall Measurements within a Model Combination Framework. Adv. Water Resour. 2016, 97, 205–218. [Google Scholar] [CrossRef]
- Wang, G.; Liu, L.; Ding, Y. Improvement of Radar Quantitative Precipitation Estimation Based on Real-Time Adjustments to Z-R Relationships and Inverse Distance Weighting Correction Schemes. Adv. Atmos. Sci. 2012, 29, 575–584. [Google Scholar] [CrossRef]
- Libertino, A.; Allamano, P.; Claps, P.; Cremonini, R.; Laio, F. Radar Estimation of Intense Rainfall Rates through Adaptive Calibration of the Z-R Relation. Atmosphere 2015, 6, 1559–1577. [Google Scholar] [CrossRef]
- Grek, E.; Zhuravlev, S. Simulation of Rainfall-Induced Floods in Small Catchments (the Polomet’River, North-West Russia) Using Rain Gauge and Radar Data. Hydrology 2020, 7, 92. [Google Scholar] [CrossRef]
- Ajami, N.K.; Gupta, H.; Wagener, T.; Sorooshian, S. Calibration of a Semi-Distributed Hydrologic Model for Streamflow Estimation along a River System. J. Hydrol. 2004, 298, 112–135. [Google Scholar] [CrossRef]
- Borga, M. Accuracy of Radar Rainfall Estimates for Streamflow Simulation. J. Hydrol. 2002, 267, 26–39. [Google Scholar] [CrossRef]
- Zhang, X.; Srinivasan, R. GIS-Based Spatial Precipitation Estimation Using next Generation Radar and Raingauge Data. Environ. Model. Softw. 2010, 25, 1781–1788. [Google Scholar] [CrossRef]
- Paschalis, A.; Molnar, P.; Fatichi, S.; Burlando, P. A Stochastic Model for High-Resolution Space-Time Precipitation Simulation. Water Resour. Res. 2013, 49, 8400–8417. [Google Scholar] [CrossRef]
- Schleiss, M.; Olsson, J.; Berg, P.; Niemi, T.; Kokkonen, T.; Thorndahl, S.; Nielsen, R.; Nielsen, J.E.; Bozhinova, D.; Pulkkinen, S. The Accuracy of Weather Radar in Heavy Rain: A Comparative Study for Denmark, the Netherlands, Finland and Sweden. Hydrol. Earth Syst. Sci. 2020, 24, 3157–3188. [Google Scholar] [CrossRef]
- Seo, B.-C.; Dolan, B.; Krajewski, W.F.; Rutledge, S.A.; Petersen, W. Comparison of Single-and Dual-Polarization–Based Rainfall Estimates Using NEXRAD Data for the NASA Iowa Flood Studies Project. J. Hydrometeorol. 2015, 16, 1658–1675. [Google Scholar] [CrossRef]
- Cunha, L.K.; Smith, J.A.; Krajewski, W.F.; Baeck, M.L.; Seo, B.-C. NEXRAD NWS Polarimetric Precipitation Product Evaluation for IFloodS. J. Hydrometeorol. 2015, 16, 1676–1699. [Google Scholar] [CrossRef]
- Bournas, A.; Baltas, E. Application of a Rainscanner System for Quantitative Precipitation Estimates in the Region of Attica. In Proceedings of the Sixth International Symposium on Green Chemistry, Sustainable Development and Circular Economy Conference on Environmental Science and Technology, Thessaloniki, Greece, 20–23 September 2020; p. 8. [Google Scholar]
- Diakakis, M.; Andreadakis, E.; Nikolopoulos, E.I.; Spyrou, N.I.; Gogou, M.E.; Deligiannakis, G.; Katsetsiadou, N.K.; Antoniadis, Z.; Melaki, M.; Georgakopoulos, A.; et al. An Integrated Approach of Ground and Aerial Observations in Flash Flood Disaster Investigations. The Case of the 2017 Mandra Flash Flood in Greece. Int. J. Disaster Risk Reduct. 2019, 33, 290–309. [Google Scholar] [CrossRef]
- Feloni, E.G.; Baltas, E.A.; Nastos, P.T.; Matsangouras, I.T. Implementation and Evaluation of a Convective/Stratiform Precipitation Scheme in Attica Region, Greece. Atmos. Res. 2019, 220, 109–119. [Google Scholar] [CrossRef]
- Pereira, S.; Diakakis, M.; Deligiannakis, G.; Zêzere, J.L. Comparing Flood Mortality in Portugal and Greece (Western and Eastern Mediterranean). Int. J. Disaster Risk Reduct. 2017, 22, 147–157. [Google Scholar] [CrossRef]
- Special Secretariat for Water. Ministry of Environment and Energy Flood Risk Management Plan; Stage I, Phase 1st, Deliverable 2. Intensity-Duration-Frequency Curves; Ministry of Environment and Energy: Athens, Greece, 2017. [Google Scholar]
- Lagouvardos, K.; Kotroni, V.; Bezes, A.; Koletsis, I.; Kopania, T.; Lykoudis, S.; Mazarakis, N.; Papagiannaki, K.; Vougioukas, S. The Automatic Weather Stations NOANN Network of the National Observatory of Athens: Operation and Database. Geosci. Data J. 2017, 4, 4–16. [Google Scholar] [CrossRef]
- Myronidis, D.; Ioannou, K. Forecasting the Urban Expansion Effects on the Design Storm Hydrograph and Sediment Yield Using Artificial Neural Networks. Water 2019, 11, 31. [Google Scholar] [CrossRef]
- Efstratiadis, A.; Koussis, A.D.; Koutsoyiannis, D.; Mamassis, N. Flood Design Recipes vs. Reality: Can Predictions for Ungauged Basins Be Trusted? Nat. Hazards Earth Syst. Sci. 2014, 14, 1417–1428. [Google Scholar] [CrossRef]
- Michailidi, E.M.; Antoniadi, S.; Koukouvinos, A.; Bacchi, B.; Efstratiadis, A. Timing the Time of Concentration: Shedding Light on a Paradox. Hydrol. Sci. J. 2018, 63, 721–740. [Google Scholar] [CrossRef]
- US Department of Agriculture. Urban Hydrology for Small Watersheds. U.S. Dep. Agric. Tech. Release 1986, 55, 164. [Google Scholar]
- NRCS, U. National Engineering Handbook: Part 630—Hydrology; USDA Soil Conservation Service: Washington, DC, USA, 2004. [Google Scholar]
- Heggen, R.J. Normalized Antecedent Precipitation Index. J. Hydrol. Eng. 2001, 6, 377–381. [Google Scholar] [CrossRef]
- US Army Corps of Engineers (USACE). Hydrologic Modeling System HEC-HMS: User’s Manual; No 4.3; Hydrologic Engineering Center: Davis, CA, USA, 2018; Available online: https://www.hec.usace.army.mil/software/hec-hms/documentation/HEC-HMS_Users_Manual_4.3.pdf (accessed on 9 February 2021).
- Bournas, A.; Feloni, E.; Bertsioy, M.; Baltas, E. Hydrological and Hydraulic Modelling for a Severe Flood Event in Sperchios River Basin. In Proceedings of the 16th International Conference on Environmental Science and Technology, Rhodes, Greece, 4–7 September 2019. [Google Scholar]
- Kotsifakis, K.; Psomas, A.; Feloni, E.; Baltas, E. Rainfall-Runoff Modeling in an Experimental Watershed in Greece. In Proceedings of the 14th International Conference on Environmental Science and Technology, Rhodes, Greece, 3–5 September 2015. [Google Scholar]
- Kastridis, A.; Stathis, D. Evaluation of Hydrological and Hydraulic Models Applied in Typical Mediterranean Ungauged Watersheds Using Post-Flash-Flood Measurements. Hydrology 2020, 7, 12. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).