Abstract
In order to select suitable rainwater harvesting sites within the study area, rainwater harvesting criteria needed to be determined, defined, and structured. Several criteria played an important role in selecting the most suitable rainwater harvesting sites. A multicriteria analysis (MCA) approach, which is widely used to classify potential rainwater harvesting sites, was chosen to help select potential sites in the Wadi Horan region of Iraq. An MCA approach offered a systematic methodology focused on mathematics as well as professional expertise to organize and evaluate complex decisions. Unfortunately, there is no method for choosing among them the most appropriate for a given decision problem, as the choice remains a subjective task. This study used a geographic information system (GIS)-based approach with remote sensing to identify the optimal sites for rainwater harvesting. Four indices: evaporation, cost–benefit, sediment, and hydrology were selected in order to compare the potential sites. The analytic hierarchy process (AHP), fuzzy AHP, and rank order method (ROM) were used to assign weight to the study criteria. The results were then compared using a statistical (variance inverse (VI)) method. A sensitivity analysis was done to test the uncertainties and robustness of the results for each method. The results showed that the ROM and VI methods affected the ranking priority and considered all of the criteria that were sensitive to impact in the ranking process at the different levels compared to the methods of AHP and fuzzy AHP.
1. Introduction
The Western Desert of Iraq is a large arid region that has suffered from severe water shortage, not only due to its climatic conditions but also due to a lack of water resource planning and management [1,2]. This area experiences brief, high-intensity rainfall that occurs mainly within a short period of time [3]. Evaporation further diminishes the already insufficient water supply [4]. Rainwater harvesting has emerged as an important tool for water conservation. Rainwater harvesting can provide safe, accessible, and affordable water for drinking, agriculture, livestock, small industries, and domestic uses [5,6].
There are six important factors that should be considered when selecting a rainwater harvesting site: hydrology (rainfall–runoff relationships and intermittent watercourses), climate (rainfall), soil (texture, structure, and depth), agronomy (crop characteristics), topography (land slope), and socio-economic conditions (population density, workforce, people’s priorities, people’s experiences with rainwater harvesting, land tenure, water laws, accessibility, and related costs) [7]. Trying to take all of these factors into account makes selecting a site more difficult and time consuming, especially when a large watershed is involved [8]. The selection of any rainwater harvesting site is a decision-making process that involves analyzing large data sets. In general, data related to the environment and water resources are geospatial [9,10]. Therefore, the comprehensive use of a geographic information system (GIS) can provide the tools needed to facilitate information integration [11]. The process of site selection using GIS techniques focuses on combining specific maps based on predetermined criteria [12]. The combination of data processing and visual representations of this data in GIS can help with multicriteria decision analysis (MCDA) and help decision makers make important choices [13,14]. Geospatial data and GIS techniques are integrated in multicriteria analysis (MCA), which has been used in many studies that have focused on selecting optimal sites for rainwater harvesting (RWH) in arid and semi-arid regions [15,16,17,18,19,20,21,22,23,24,25].
Many MCA approaches entail selecting, ranking, and comparing the most suitable policy options according to the chosen criteria. These approaches differ in the type of data they can handle (quantitative, qualitative, or mixed) and the decision rule they follow (compensatory, partial-compensatory, and non-compensatory) [26]. Several researchers have used comparative studies of MCDA to address problems in water resource management. These studies have shown that multicriteria decision analysis is an effective method to use when making decisions about water resource management, and researchers found that there was no benefit to using one MCDA method over another. Unfortunately, there is no guideline to follow when deciding which method to use for a given problem—the choice remains subjective. Furthermore, each method may produce different rankings [27]. Given these drawbacks, researchers should use more than one MCDM method in order to enhance the selection process [28]. The robustness of an MCA result depends on the (un)certainty of the information being used for the selected criteria, on the priorities given to the criteria (the weights or importance), and the extent to which these weights are commonly agreed upon by stakeholders. Sensitivity analysis can be used to check the robustness of the result for changes in scores and/or weights.
The main objective of this study was to present a methodology based on geospatial data and GIS integrated with the AHP, fuzzy AHP, ROM, and variance inverse methods to aid in selecting optimum sites for rainwater harvesting in the Wadi Horan and improve the decision-making process. To assess the uncertainty and robustness of the output results, a sensitivity analysis was carried out to define the success of the application in ranking potential rainwater harvesting sites. Thus, the sensitivity analysis was used to determine the reliability of the models by assessing uncertainties in the output results. The highlight of this methodology is that the area–volume curve for the RWH sites was developed using GIS to extract four main indexes: evaporation, cost–benefit, sediment, and hydrology.
2. Materials and Methods
2.1. Study Area
The Wadi Horan is the main wadi in the West Desert of Iraq. It represents the main wadi that receives a large amount of rainfall during the rainy season. Beginning at the Saudi border, the wadi extends from the Jordanian border in the southwest to the Syrian border in the northwest. The Wadi Horan is located south of the Euphrates River, with the coordinates 32°10′44″ to 34°11′00″ North, 39°20′00″ to 42°30′00″ East, as shown in Figure 1. An important characteristic of the rainfall regime in the study area, which is usually common for all arid regions, is a high variability of rainfall recorded from year to year and from region to region.
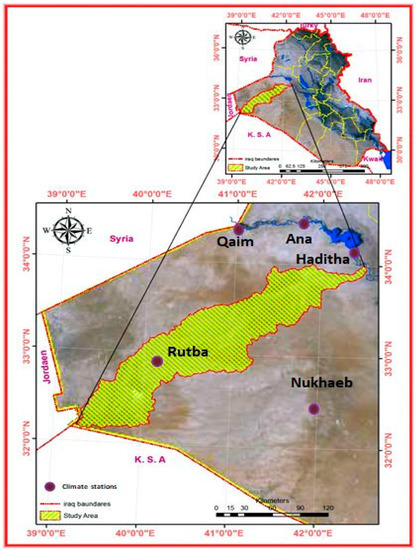
Figure 1.
Area of study: the Wadi Horan in the western part of Iraq and the rain stations available for the region.
The spatial distribution of the average annual rainfall, as shown in Figure 2, indicates the lowest rainfall (below 115 mm) recorded in the south-west region of the study area. With this rainfall distribution, it is worth mentioning that, in spite of the increasing altitude from east to west in the area considered, the rate of rainfall does not increase, owing to its entrance into a purely desert area [2]. In the eastern part of this area, the rate of rainfall increases from south to north. The rainy season takes place from winter to spring (October to May), while the dry season occurs in summer (June to September). The average annual rainfall for this catchment is 115 mm, with 49.5% occurring in winter, 36.3% in spring, and 14.2% in fall [5].
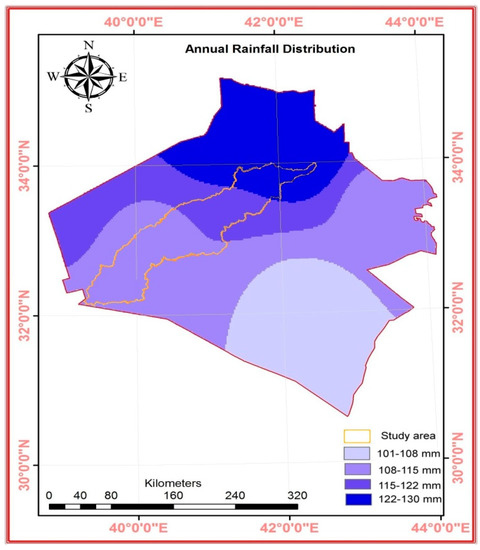
Figure 2.
The spatial distribution of average annual rainfall in the study area from 1980–2018.
RWH in this region is essential to increase the accessibility and affordability of water, thus improving the quality of life in this area. Understandably, rainfall is considered to be one of the most valuable natural resources in this region. The area of study is a very important area in Iraq’s West Desert; it represents the main valley, which receives a large amount of rainfall during the rainy season.
2.2. Data Collection
The description of these data and their main sources are shown in Table 1. We adopted such data since the United States Geological Survey( USGS) website freely downloads these data. These data are available, readily managed and manipulated in contemporary GIS software for regional-scale rainwater harvesting planning and decision support in developing regions.

Table 1.
The data type, source, year, and description.
2.3. Methodology
GIS integration was used to develop thematic maps of area–volume curves with Digital elevation model (DEM) extracted from Shuttle Radar Topographic Mission (SRTM), as shown in Figure 3. This Figure shows the different layers in the final thematic map, which represents water levels at different depths for one site selected in the study area. For every two meters, the area and volume were calculated using ArcGIS software with the spatial analyst model. From the area of the reservoir and the depth of water at each point, the storage of water was calculated (assuming the water level reached the top of the dam). Evaporation losses might be extremely high and will increase with an increasing surface area of the stored water. Therefore, the optimal dam heights with maximum storage of water and minimum surface area of reservoir are required, especially in arid regions with high evaporation losses. In addition, the capacity of the reservoir that can be estimated by computing the surface area and reservoir depth at any level is a vital concern in reservoir operation and management.
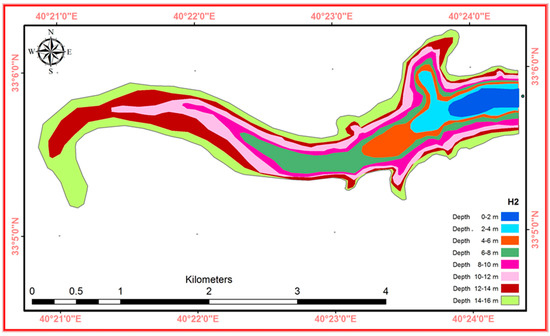
Figure 3.
Area–volume curve, area, and volume thematic map calculated for every two meters.
A comparison between sites was conducted using four main indices: evaporation index, cost–benefit index, sediment index, and hydrology index. The choice of these indices was based on a variation of the key parameters, which were physically dependent. The indices were extracted based on the area–volume curve and the geometric properties of each RWH location. The intersection of the area–volume curve denotes the optimal height for a possible dam, which directly affected all indices.
• Evaporation Index
The evaporation index is defined as the mean ratio at any level between the storage volume and the surface area. The main merit of this assessment was in determining the shape of the reservoir body and the shape’s effects on the evaporation process, which becomes extremely high with increasing surface area of the stored water. The reservoir capacity is the volume of a pyramid at any level, with its base being the water’s surface [29]. The main factors associated with evaporation are water depth and water surface area. Therefore, any constructed reservoir should be deep and narrow to reduce losses from evaporation [30]. The climate criteria: rainfall, wind speed, temperature, sunshine, and relative humidity remained fairly constant in the study area. Hence, for the evaporation index, only surface area and depth were considered.
• Cost–Benefit Index
The cost–benefit index defines the ratio of the potential volume of storage to the volume of the RWH structure. Therefore, the parameter quantitatively represents the quality of the narrows. Water storage represents the benefit, while the cost of the RWH system is a function of the volume of the embankment. A skilled labor force resides in this area, which has limited financial resources and infrastructure. Any structure should be simple, such as earthwork and stonework, since expensive engineering structures, such as concrete dams are not included in the description of the potential rainwater harvesting systems for this study area [31]. The overall estimate of the cost–benefit ratio associated with achieving the structure can be represented by this parameter (the cost to cost ratio). The cost–benefit index calculation procedure was configured based on the area equations of the cross-section and the longitudinal bridge [30].
• Sediment Index
The sedimentation is the result of erosion in watersheds. Sedimentation is affected by several fluctuating factors, such as soil type, slope, land cover/use, rainfall intensity, geological formations, and watershed size. Sediments are a potential concern for any RWH system, since they can reduce storage area and increase maintenance costs. The Al-Furat center (1994) reported that the total annual sediment in the study area is 60 tons / km2 [32]. Therefore, this parameter must be included in the site classification and evaluation. The sediment index represents the ratio of the total storage volume to sediment quantity (ton/year).
• Hydrology Index
The depth of effective rainfall is an important index for site classification, as it is a direct index of the amount of rainfall that can be harvested at each site. Moreover, it is also an indicator of the potential for the resulting reservoir to fill to capacity. In this case, the inverse depth of the rainfall of the hydrology index is reversed where the minimum rainfall depth is sufficient to fill the dam storage and represents the highest value of the hydrological index. The hydrological index is affected by watershed events, such as floods, severe storms, and droughts. The rainfall frequency plays an important role in determining the hydrological indicator value. It is important to give an idea of how the dam was managed over the years and how it was operated. For example, the rainfall rate for the study area in the Wadi Horan was less than 10 mm / h and occurred 27 times in 1975 and 7 times in 1976 [33].
2.3.1. Standardization of Criteria Weight
The criteria were calculated using various scales. Therefore, the site scores need to be specified by standardizing the scale before applying calculations. As shown in Equation (1), the minimum and maximum values of the standard criteria were used as scaling points.
where: xi is the score of the criteria after standardization. Ri is the score of the criteria. Rmin is the minimum score, and Rmax is the maximum score.
Equation (1) allows for the reorganization of the criteria values from different scales to a standard scale.
2.3.2. Selecting Criteria Weight
Four methods of weighting criteria have been used for the ranking process: the analytic hierarchy process (AHP), fuzzy-AHP, rank order method (ROM), and variance inverse. These methods were chosen to allow site ranking, where weight must be given to each index. Information concerning the relative importance of the criteria is very important for decision makers. Multicriteria decision making entails weighing factors of various importance. The weight of each factor is relative and determined by the individual decision maker [34,35].
2.3.3. Analytical Hierarchy Process (AHP)
AHP, first proposed by Saaty (1980), is a multicriteria decision method that uses hierarchical structures. The AHP is a multicriteria decision-making method, providing a structured technique for organizing and analyzing complex decisions based on mathematics and expert knowledge [36]. The main principle of AHP is representing the elements of any problem hierarchically to show the relationships between each level. The weights for the decision-making criteria are derived from the pairwise comparisons of the relative importance between each two criteria [37]. The steps of the AHP procedure are: “define the unstructured problem, develop the AHP hierarchy, perform pairwise comparison, calculate the relative weights, check the consistency, and obtain the total weights and overall rating” [38]. The precision of pairwise comparison is evaluated via the calculation of the consistency ratio (CR). CR is the ratio between the consistency index (CI) and the random index (RI). If the result of the CR is less than 10%, the comparison between the factors is considered to be acceptable. Otherwise, the consistency ratio allows for re-evaluation comparisons. The RI can be found in the specific table prepared by Saaty (1980), depending on the order of the matrix.
After the pairwise comparison, to find out the weight for each criteria and the CR, we solved the pairwise matrixes mathematically. It is a complex process taking a lot of time if done manually, therefore we used online calculations (BPMSG) to solve all matrixes, thus saving time and ensuring high accuracy, as shown in Table 2. The resulting weights were based on the principle eigenvector of the decision matrix.

Table 2.
Pairwise comparison matrix and weight using analytic hierarchy process (AHP).
2.3.4. Fuzzy-AHP
Fuzzy-AHP is another method that is based on the fuzzy set theory proposed by Zadeh (1965). The fuzzy approach allows decision makers to give interval judgments, which can capture a human‘s appraisal of ambiguity when complex multi-attribute decision-making problems, such as water reservoir siting, are considered [39]. According to [40,41], integrating fuzzy logic into the AHP process will give a much better and more accurate representation between criteria and alternatives. Different methods have been proposed to determine weights of criteria in the fuzzy comparison matrix. For this research, the fuzzy extent analysis (FEA) method proposed by Chang (1996) [42] was used.
The weight calculation for each index in the hierarchy is presented in the last column in Table 3.

Table 3.
Pairwise comparison matrix and weight using fuzzy-AHP.
2.3.5. Rank Order Method
Due to the decision maker’s preference, each criterion weight under analysis can be organized in rank order. This is considered to be the easiest way to evaluate the significance of criteria weight for which the ranking may be ascending or descending. Stillwell et al. (1981) showed that there are several approaches for a set of rank-order criteria, i.e., rank sum, rank reciprocal, and rank exponent [43]. They conclude that rank-based methods produce higher correlations with the true weights than equal weights do. The results also shown that rank sum outperforms the others in most scenarios and every measure. Therefore, only the rank sum method was used in this study.
Following Equation (2), the results of the analysis are provided in Table 4.
where W is the weight value, i is the rank position of the criterion, and n is the number of criteria.

Table 4.
Assessing weight using the ranking procedure.
2.3.6. Variance Inverse
Logically, we can conclude that the difference between the best value and value per site for each criterion will have a small standard deviation or variance and, therefore, should be weighed more (retained closer to its value) [44].
Variance inverse is a statistical method applied to give weight to criteria based on inverse variance values. This method defines the variance as the difference between the criteria value of each site and the best criteria value for all sites. With this reasoning, it was concluded that the relative weights were inversely proportional to variances following Equation (3):
where Wc is the weight of a criterion, which has a variance of .
For the current study, the summation of the variance for all sites for each criterion was calculated based on the values extracted after standardization of the criteria to avoid the scaling problem. Results are shown in Table 5.

Table 5.
Assessing weight using the variance inverse procedure.
2.4. Sensitivity Analysis
Choosing the best alternative among a number of opposing alternatives is a major challenge in multicriteria decision making. Therefore, each alternative has been described in terms of a set of evaluative criteria. These criteria were connected by weighting their importance, and it is essential to distinguish the idea of criticality with that importance. The term ‘critical’ here means that a criterion that had a small change in its weight may result in a significant change in the final solution [45,46]. There is the probability of lower-weight criteria being more critical in specific situations than those of greater weight. Sensitivity analysis may shed light on unexpected issues at the beginning of a study. This, in turn, may greatly improve the effectiveness of the initial study and help in the successful implementation of the final solution. Therefore, sensitivity analysis is the process of determining the successful application of the decision model in choosing potential rainwater harvesting sites. Moreover, this analysis is to investigate how sensitive the ranking of the alternatives is to any changes in the importance of the criteria [47]. There are five types of sensitivity analysis, i.e., performance, dynamic, gradient, two-dimensional, and difference. The simplest way to approach sensitivity analysis is to vary each factor one at a time. The big advantage is that any changes (including model failure) observed can be ascribed to the change in that one factor. While one factor is being varied, the others are usually kept at their nominal or baseline values, so that each change is affected regarding a certain model ‘base space’. In this research, sensitivity analysis was performed by changing each of the input criteria by ±5 percent increments. This method is known as ‘one at a time’, better known as the OAT method. It is easy to implement, computationally cheap, and has been frequently applied in various fields where models are employed.
This analysis examines the sensitivity of the order of alternatives to any changes in the importance of criteria. Sensitivity analysis is, therefore, used to determine the reliability of models by assessing uncertainties in output outcomes.
3. Results and Discussion
In Table 6, the decision maker’s opinion is compared for each of the four main criteria: “Eva,” “Ben,” “Sed,” and “Hyd”. The “Eva” criterion was given vital importance in AHP, fuzzy-AHP, ROM, and variance inverse (VI) and weighted 60%, 45%, 40%, and 34%, respectively. The “Ben,” criterion was given weights of 20% in AHP, 24% in fuzzy-AHP, 30% in ROM, and 28% in VI. The “Sed” criterion was weighted 11% in AHP, 18% in fuzzy-AHP, 20% in ROM, and 20% in VI, while the “Hyd” criterion was given less importance as compared to other criteria: 9% in AHP, 13% in fuzzy-AHP, 10% in ROM, and 18% in VI. It should be noted that the evaporation index had the highest weight followed by the cost–benefit, sediment, and hydrology index, as presented in all methods (Table 6). This was reasonable because it represented the nature of the study area, where evaporation was the major issue in the arid region. Table 7 also showed that the difference between the best value and value per site for evaporation criterion will have a small standard deviation or variance and, therefore, should be weighted more (retained closer to its value in the evaporation indexes).

Table 6.
Index weights for AHP, ROM, fuzzy-AHP, and variance inverse depending on the decision maker’s opinion.

Table 7.
Indices and locations of the 7 potential dam sites.
A description of the results is given in Table 7. Table 7 shows that the value of the indices was not on the same scale. Therefore, once all the values were standardized, these methods were weighted. Standardization or normalization was calculated by assigning the same dimensionless continuous scale (from 0 to 1). In the first method, equal weight was assigned to all indices in the ranking process. This method was simple and used to compare the AHP, fuzzy-AHP, ROM, and VI methods.
Index value summation refers to the score of each site, giving the ranking where the highest summation was ranked first. Table 8 shows that site no. 6 is the best location for rainwater harvesting structures. ROM, AHP, fuzzy-AHP, and VI gave similar results for site ranking order. However, the AHP results were closer to the ROM result as compared to the other methods. Table 8 also shows good consistency of indices for all sites. Although there was an agreement between AHP, fuzzy-AHP, ROM, and VI in the priority sequence of indices, it was still necessary to determine the optimal weight selection. The VI is a statistical method, which determines the weight based on the value of each index and is more appropriate than AHP, fuzzy-AHP, and ROM for site ranking. AHP, fuzzy-AHP, and ROM are methods that depend on the decision maker’s judgment, which has some underlying uncertainties.

Table 8.
Ranking of the 7 potential dam sites with different weighting methods.
Sensitivity analysis was performed to define the reliability of models by assessing uncertainty in outputs. The plot of sensitivity analysis against the rank is illustrated in Figure 4.
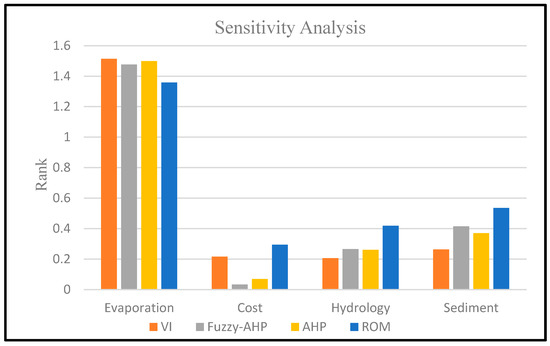
Figure 4.
Analysis against the rank for each criterion according to each method.
For all methods, evaporation was more effective than other indicators, as shown in Figure 5. The “Eva” criterion showed significant effectiveness in AHP (68%), fuzzy-AHP (67%), ROM (52%), and VI (69%). These results reflect the nature of the arid study area where evaporation was the major issue. The “Sed” criterion gave less effectiveness than “Eva” were the values were 17% for AHP, 19% for fuzzy-AHP, 21% for ROM, and 12% for VI. Meanwhile, the “Hyd” criterion gave the effectiveness of 12% for AHP, 12% for fuzzy-AHP, 16% for ROM, and 9% for VI. Although the AHP and fuzzy-AHP approaches gave the “Ben” criterion weights of 20% and 24%, respectively, these methods provided less effectiveness for the “Ben” criterion in the ranking process—3% and 2%, respectively. This is because the criticality may cause a major change in the final solution. As shown in Table 7, the difference between the best value and value per site for "Ben” criterion will have a small standard deviation or variance, as compared to “Hyd” and the “Eva", and therefore, it has more effectiveness for the “Ben” criterion in the ranking process for the VI method and less effectiveness in the AHP and fuzzy-AHP approaches for the ranking process. The ROM and VI methods affected the ranking priority and considered all the criteria that were sensitive in affecting the different levels in the ranking process, as compared to the AHP and fuzzy-AHP methods. Therefore, the statistical method was the most appropriate method for the study criteria that were sensitive in affecting the different levels in the ranking process, compared to the AHP and fuzzy-AHP methods. Therefore, the statistical method is the most appropriate method for this study.

Figure 5.
Ranking effectiveness of each criterion based on AHP, ROM, fuzzy-AHP, and VI. “Eva” was more efficient than other indicators for all methods, whereas the "Ben" criterion was the least efficient.
4. Conclusions
This research presented a case study integrating GIS and four methods of multicriteria analysis: AHP, fuzzy-AHP, ROM, and the statistical (variance inverse) method in identifying potential sites for rainwater harvesting. The present study found that ArcGIS was a very useful tool for integrating diverse information to find suitable sites for harvesting rainwater. ArcGIS was a flexible, time-saving, and cost-effective tool for screening large areas for their suitability of RWH intervention. Sensitivity analysis was carried out to determine the reliability of models by assessing uncertainty in outputs. The “Eva” criterion showed significant effectiveness in AHP (68%), fuzzy-AHP (67%), ROM (52%), and VI (69%). The “Sed” criterion showed less effectiveness than “Eva” where these values were 17% for AHP, 19% for fuzzy-AHP, 21% for ROM, and 12% for VI. Meanwhile, the “Hyd” criterion showed the effectiveness of 12% for AHP, 12% for fuzzy-AHP, 16% for ROM, and 9% for VI. Although the AHP and fuzzy-AHP approaches gave the “Ben” criterion weights of 20% and 24%, respectively, these methods provided less effectiveness for the “Ben” criterion in the ranking process—3% and 2%, respectively. This is because the criticality may cause a major change in the final solution. The ROM and VI methods affected the ranking priority and considered all the criteria that were sensitive in affecting the different levels in the ranking process, as compared to the AHP and fuzzy-AHP methods. Therefore, the statistical method is the most appropriate method for this study.
Finally, the use of GIS and remote sensing (RS) in water resource planning and management is significant in the development of remote areas and should use more than one MCDM method to enhance the selection process. Sensitivity analysis also proved that the proposed method is suitable to be used for RWH site selection in arid regions.
The analysis as presented, however, provides a valuable initial screening of large areas and can easily be modified to incorporate other criteria or information with other spatial resolutions.
Author Contributions
K.S. designed the model and the computational framework and carried out the analysis covered in the methodology section. A.A. developed the main theory of the research and participated in performing the computations. C.J.R. developed the theoretical framework and revised the final version of the manuscript for submission. K.S. and A.A. wrote the manuscript with input from all authors. All authors discussed the results and contributed to the final manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
Special thanks are due for Iraqi Public Authority for meteorological and seismic monitoring for the facilitation of data collection process. Great thanks to Robin Palmer (Palmer English Consulting), for the English reviewing and supporting.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sulaiman, S.; Kamel, A.; Sayl, K.; Alfadhel, M. Water resources management and sustainability over the Western desert of Iraq. Environ. Earth Sci. 2019, 78, 495. [Google Scholar] [CrossRef]
- Ammar, A.; Khamis, N.S.; Rasha, A.; Mohamed, A.A.; Jan, G.W.; Michel, R.; Luuk, F.; Usama, K.; Coen, J.R. A GIS-based approach for identifying potential sites for harvesting rainwater in the Western Desert of Iraq. Int. Soil Water Conserv. Res. 2018, 6, 297–304. [Google Scholar]
- Agarwal, A.; Narain, S.; Khurana, I. Making Water Everybody’s Business: Practice and Policy of Water Harvesting; Centre for Science and Environment: New Delhi, India, 2001; p. 456. [Google Scholar]
- Haddad, N. Characteristics of the Steppe in WANA with an Emphasis on Jordan. Water Benchmarks 2006. Available online: https://www.researchgate.net/publication/267025543_Characteristics_of_benchmark_research_agroecosystems_in_WANA_rainfed_irrigated_and_marginal_drylands (accessed on 31 July 2020).
- Ammar, A.; Jan, G.W.; Rasha, A.; Michel, R.; Mohamed, O.; Coen, J.R. Assessing the impact of climate change on rainwater harvesting in the Oum Zessar watershed in Southeastern Tunisia. Agric. Water Manag. 2019, 221, 131–140. [Google Scholar]
- Samra, J.S.; Sharda, V.N.; Sikka, A.K. Water Harvesting and Recycling: Indian Experiences; Central Soil & Water Conservation Research and Training Institute: Dehradun, India, 2002; p. 347. [Google Scholar]
- Campisano, A.; Butler, D.; Ward, S.; Burns, M.J.; Friedler, E.; DeBusk, K.; Fisher-Jeffes, L.N.; Ghisi, E.; Rahman, A.; Furumai, H.; et al. Urban rainwater harvesting systems: Research, implementation and future perspectives. Water Res. 2017, 115, 195–209. [Google Scholar] [CrossRef] [PubMed]
- Musayev, S.; Burgess, E.; Mellor, J. Global performance assessment of rainwater harvesting under different climates. Resour. Conserv. Recycl. 2018, 132, 62–70. [Google Scholar] [CrossRef]
- FAO Training Course on Water Harvesting. Land and Water Digital Media Series; Food and Agriculture Organization of the United Nations: Rome, Italy, 2003. [Google Scholar]
- Kopp, S. GIS For water resources: Now and into the future. Southwest Hydrol. 2004, 22–23. [Google Scholar]
- Johnson, L.E. Geographical Information Systems in Water Resources Engineering; CRC Press Taylor & Francis Group: New York, NY, USA, 2009. [Google Scholar]
- Malczewski, J. GIS-based land-use suitability analysis: A critical overview. Prog Plann. 2004, 62, 3–65. [Google Scholar] [CrossRef]
- Carver, S.J. Integrating multi-criteria evaluation with geographical information systems. Int. J. Geogr. Inf. Syst. 1991, 5, 321–339. [Google Scholar] [CrossRef]
- Sayl, K.N.; Muhammad, N.S.; Yaseen, Z.M.; El-shafie, A. Estimation the Physical Variables of Rainwater Harvesting System Using Integrated GIS-Based Remote Sensing Approach. Water Resour. Manag. 2016, 30, 3299–3313. [Google Scholar] [CrossRef]
- Krois, J.; Schulte, A. GIS-based multi-criteria evaluation to identify potential sites for soil and water conservation techniques in the Ronquillo watershed, northern Peru. Appl Geogr. 2014, 51, 131–142. [Google Scholar] [CrossRef]
- Kadam, A.K.; Kale, S.S.; Pande, N.N.; Pawar, N.J.; Sankhua, R.N. Identifying potential rainwater harvesting sites of a semi-arid, basaltic region of western India, using SCS-CN method. Water Resour Manag. 2012, 26, 2537–2554. [Google Scholar] [CrossRef]
- Jamali, I.A.; Mörtberg, U.; Olofsson, B.; Shafique, M. A spatial multicriteria analysis approach for locating suitable sites for construction of subsurface dams in northern Pakistan. Water Resour. Manag. 2014, 28, 5157–5174. [Google Scholar] [CrossRef]
- Jasrotia, A.S.; Majhi, A.; Singh, S. Water balance approach for rainwater harvesting using remote sensing and GIS techniques, Jammu Himalaya, India. Water Resour. Manag. 2009, 23, 3035–3055. [Google Scholar] [CrossRef]
- Bulcock, L.M.; Jewitt, G.P.W. Key physical characteristics used to assess water harvesting suitability. Phys. Chem. Earth 2013, 66, 89–100. [Google Scholar] [CrossRef]
- Al-Adamat, R. The combination of indigenous knowledge and geoinformatics for water harvesting siting in the Jordanian Badia. J. Geogr. Inf. Syst. 2012, 4, 366–376. [Google Scholar] [CrossRef]
- Winnaar, G.; Jewitt, G.P.W.; Horan, M. A GIS-based approach for identifying potential runoff harvesting sites in the Thukela River basin, South Africa. Phys. Chem. Earth. 2007, 32, 1058–1067. [Google Scholar] [CrossRef]
- Sekar, I.; Randhir, T.O. Spatial assessment of conjunctive water harvesting potential in watershed systems. J. Hydrol. 2007, 334, 39–52. [Google Scholar] [CrossRef]
- Sayl, K.N.; Muhammad, N.S.; El-Shafie, A. Robust approach for optimal positioning and ranking potential rainwater harvesting structure (RWH): A case study of Iraq. Arab. J. Geosci. 2017, 10, 413. [Google Scholar] [CrossRef]
- Sayl, K.N.; Muhammad, N.S.; El-Shafie, A. Identification of potential sites for runoff water harvesting. Proceedings of the Institution of Civil Engineers. Water Manag. 2019, 172, 135–148. [Google Scholar] [CrossRef]
- Sayl, K.N.; Mohammed, A.S.; Ahmed, A.D. GIS-based approach for rainwater harvesting site selection. IOP Conf. Ser. Mater. Sci. Eng. 2020, 012246. [Google Scholar] [CrossRef]
- Greco, S.; Matarazzo, B.; Slowinski, R. Decision Rule Approach. In Multiple Criteria Decision Analysis: State of the Art Surveys; Figueira, J., Greco, S., Ehrgott, M., Eds.; Springer: London, UK, 2005; pp. 507–562. [Google Scholar]
- Mahmoud, M.R.; Garcia, L.A. Comparison of different multicriteria evaluation methods for the Red Bluff diversion dam. Environ. Model. Softw. 2000, 15, 471–478. [Google Scholar] [CrossRef]
- Duckstein, L.; Treichel, W.; Magnouni, S.E. Ranking ground-water management alternatives by multicriterion analysis. J. Water Resour. Plan. Manag. 1994, 120, 546–565. [Google Scholar] [CrossRef]
- Sawunyama, T.; Senzanje, A.; Mhizha, A. Estimation of small reservoir storage capacities in Limpopo River Basin using geographical information systems (GIS) and remotely sensed surface areas: Case of Mzingwane catchment. Phys. Chem. Earth 2006, 31, 935–943. [Google Scholar] [CrossRef]
- Stephens, T. Manual on Small Earth Dams, A Guide to Siting, Design and Construction; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2010. [Google Scholar]
- Critchley, W.; Siegert, K.; Chapman, C.; Finket, M. Water Harvesting: A Manual for the Design and Construction of Water Harvesting Schemes for Plant Production; Scientific Publishers: Jodhpur, India, 2013. [Google Scholar]
- AL-Furat center for studies and designs of irrigation projects. Western desert dams design report of horan dam H-2. 1994.
- Kamel, A.; Mohammed, A. Determination of water harvesting regions in Iraqi western desert using GIS system. Iraqi J. Desert Stud. 2010, 2, 1994–7801. [Google Scholar]
- Drobne, S.; Lisec, A. Multi-attribute Decision Analysis in GIS: Weighted Linear Combination and Ordered Weighted Averaging. Informatica 2005, 33, 459–474. [Google Scholar]
- Al-Ansari, N.; Ezz-Aldeen, M.; Knutsson, S.; Zakaria, S. Water Harvesting and Reservoir Optimization in Selected Areas of South Sinjar Mountain, Iraq. J. Hydrol. Eng. 2012, 18, 1607–1616. [Google Scholar] [CrossRef]
- Adham, A.; Michel, R.; Mohamed, O.; Coen, J.R. A methodology to assess and evaluate rainwater harvesting techniques in (semi-) arid regions. Water 2016, 8, 198. [Google Scholar] [CrossRef]
- Saaty. The Analytic Hierarchy Process. McGraw-Hill Internationa; New York International Book Company: New York, NY, USA, 1980. [Google Scholar]
- Safari, M.; Ataei, M.; Khalokakaie, R.; Karamozian, M. Mineral processing plant location using the analytic hierarchy process—a case study: The Sangan iron ore mine (phase 1). Min. Sci. Technol. 2010, 20, 691–695. [Google Scholar] [CrossRef]
- Tsiko, R.G.; Haile, T.S. Integrating Geographical Information Systems, Fuzzy Logic and Analytical Hierarchy Process in Modelling Optimum Sites for Locating Water Reservoirs. A Case Study of the Debub District in Eritrea. Water 2011, 3, 254–290. [Google Scholar] [CrossRef]
- Akbari, V.; Rajabi, M.A.; Chavoshi, S.H.; Shams, R. Landfill site selection by combining GIS and Fuzzy Multi Criteria Decision Analysis, case study: Bandar Abbas, Iran. World Appl. Sci. J. 2008, 3, 39–47. [Google Scholar]
- Ocalir, E.V.; Ercoskun, O.Y.; Tur, R. An integrated model of GIS and fuzzy logic (FMOTS) for location decisions of taxicab stands. Expert Syst. Appl. 2010, 37, 4892–4901. [Google Scholar] [CrossRef]
- Chang, D. Applications of the extent analysis method on fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Stillwell, W.G.; Seaver, D.A.; Edwards, W. A Comparison of Weight Approximation Techniques in Multiattribute Utility Decision Making. Organ. Behav. Hum. Perform. 1981, 28, 62–77. [Google Scholar] [CrossRef]
- Wolf, P.; Ghilani, C. Elementary Surveying—An Introduction to Geomatics; Pearson Education: Upper Saddle River, NJ, USA, 2012. [Google Scholar]
- Chen, Y.; Yu, J.; Shahbaz, K.; Xevi, E. A GIS-based sensitivity analysis of multi-criteria weights. In Proceedings of the 18th World IMACS/MODSIM Congress, Cairns, Australia, 13–17 July 2009. [Google Scholar]
- Crosetto, M.; Tarantola, S. Uncertainty and sensitivity analysis: Tools for GIS—based model implementation. Int. J. Geogr. Inf. Sci. 2001, 15, 415–437. [Google Scholar] [CrossRef]
- Hashim, H.Q.; Sayl, K.N. The Application of Radial Basis Network Model, GIS, and Spectral Reflectance Band Recognition for Runoff Calculation. Int. J. Des. Nat. Ecodynamics 2020, 15, 441–447. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).