Analysis of Stage–Discharge Relationship Stability Based on Historical Ratings
Abstract
:1. Introduction
2. Study Area
2.1. River Morphology
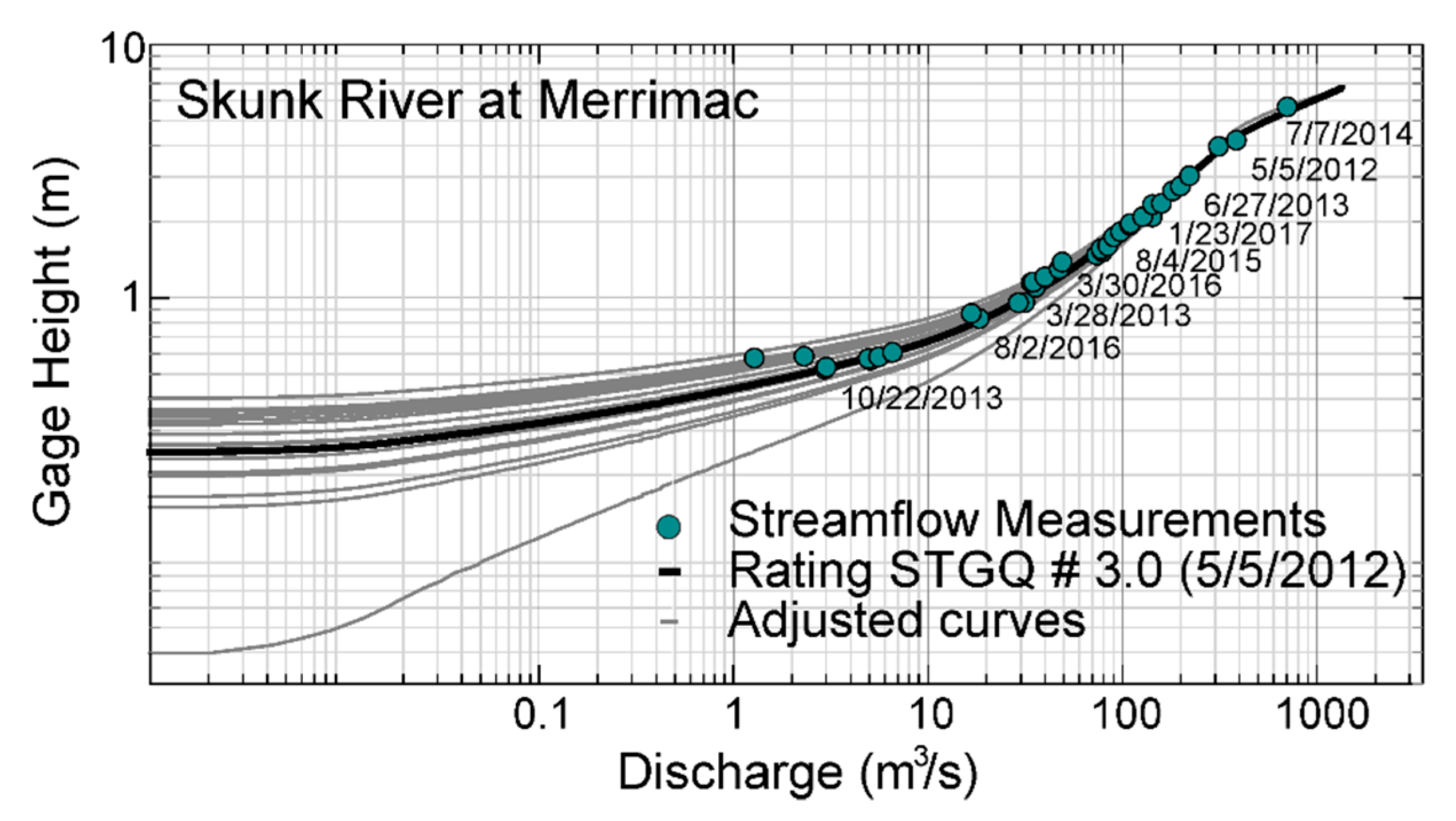
2.2. Rating Curve Information
3. Materials and Methods
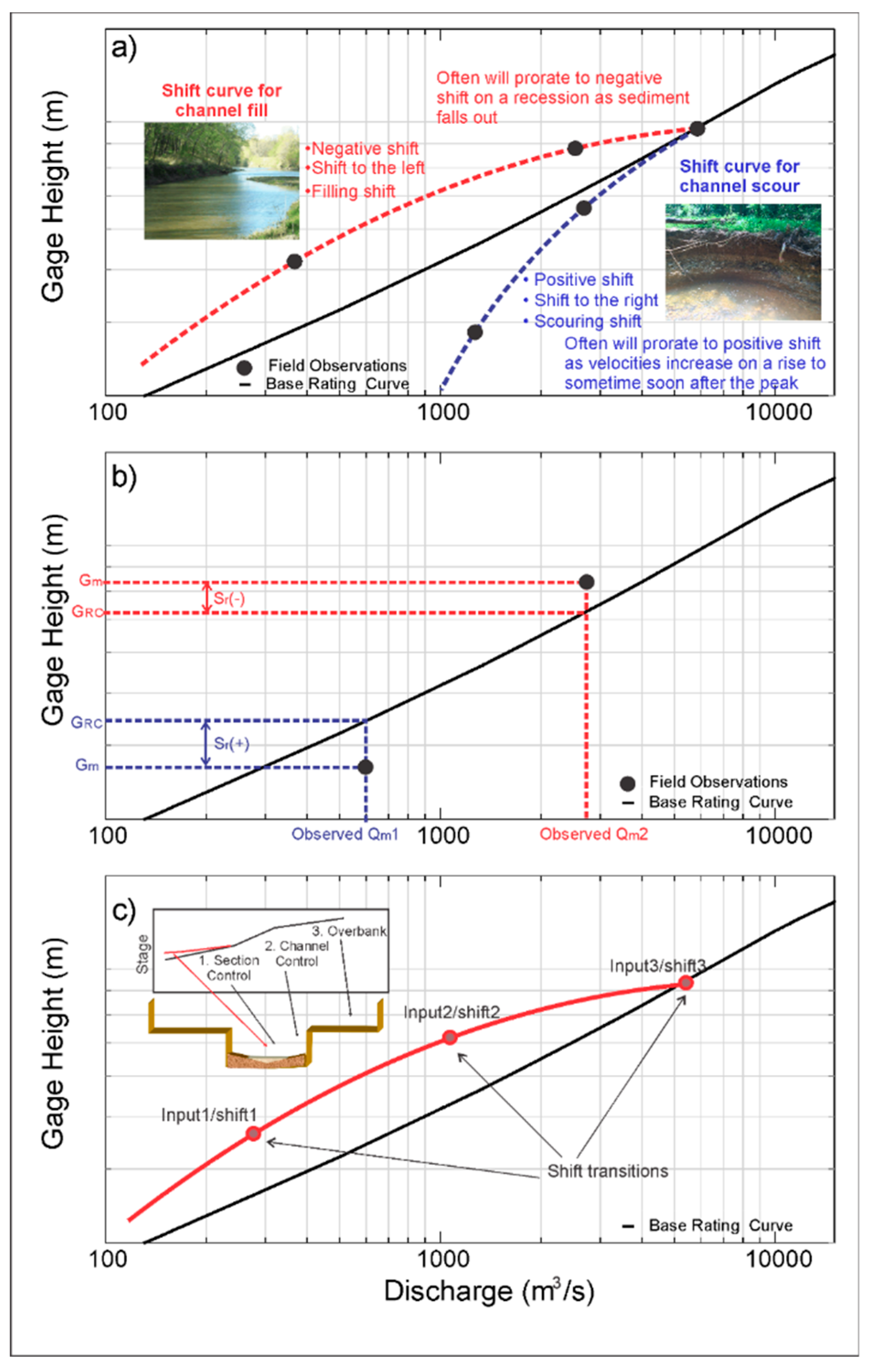
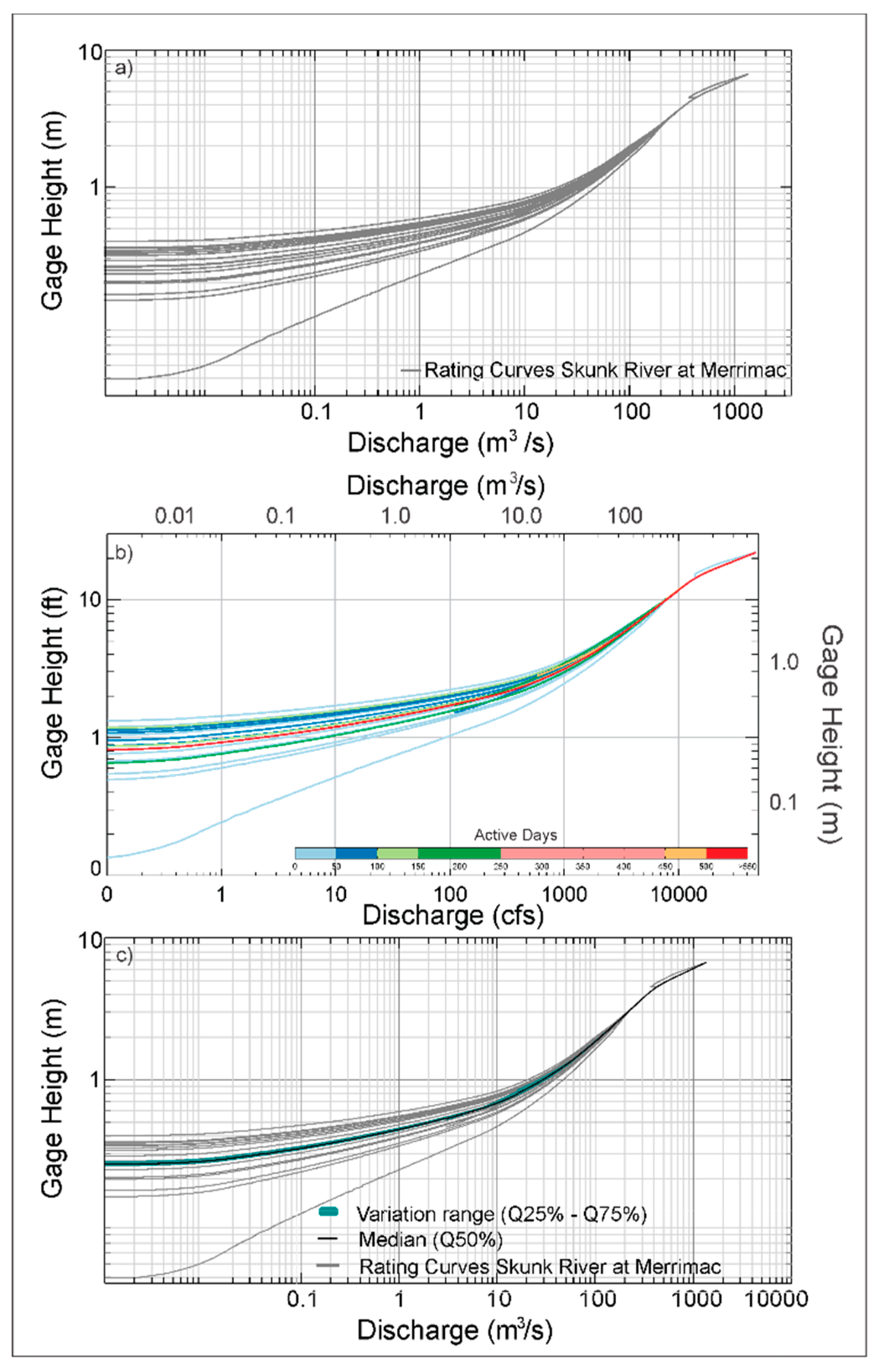
3.1. Obtaining Adjusted Rating Curves from Shifts (Shifts for Stage–Discharge Ratings)
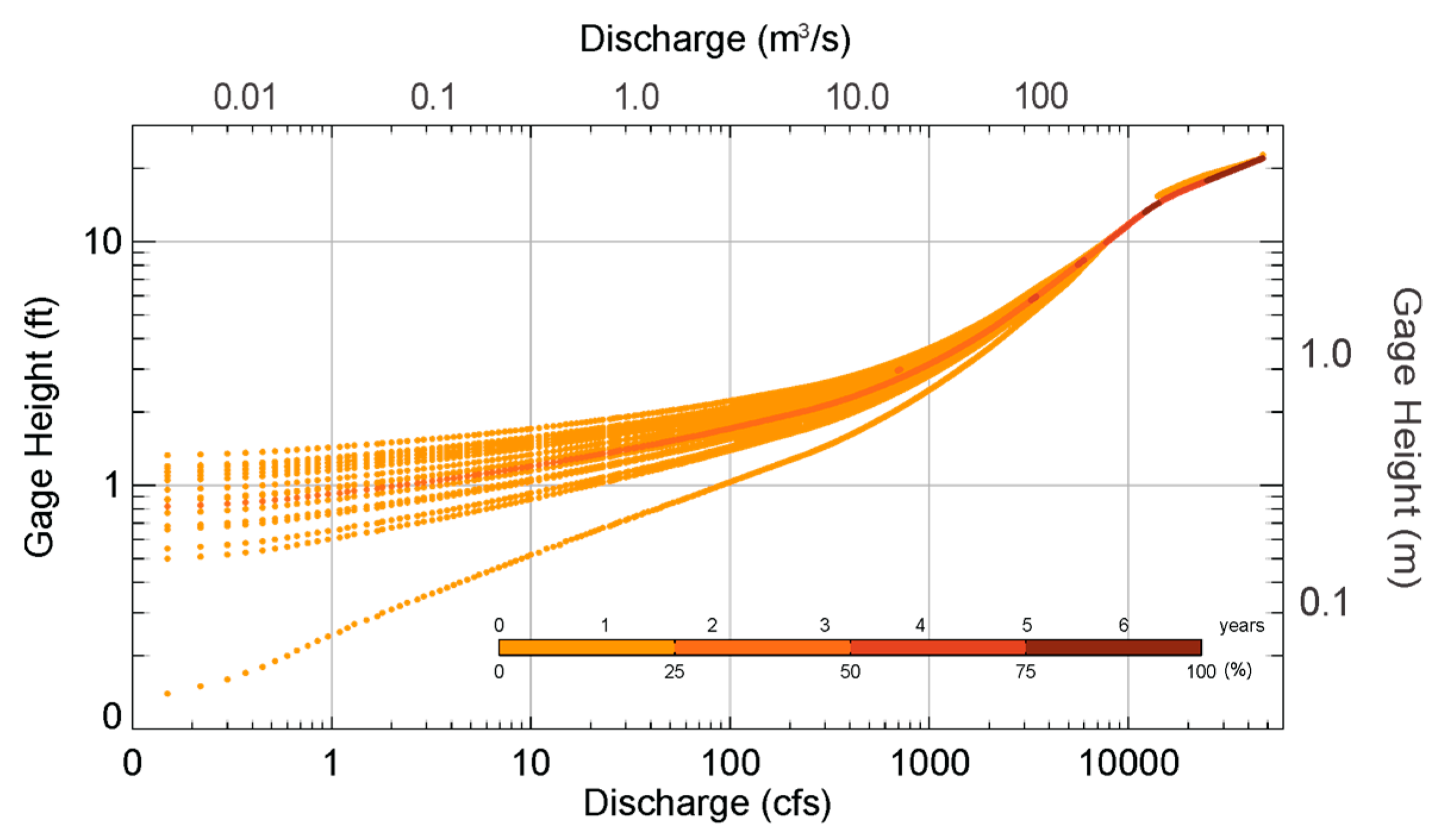
3.2. Rating Curve Variability Analysis
4. Results and Discussion
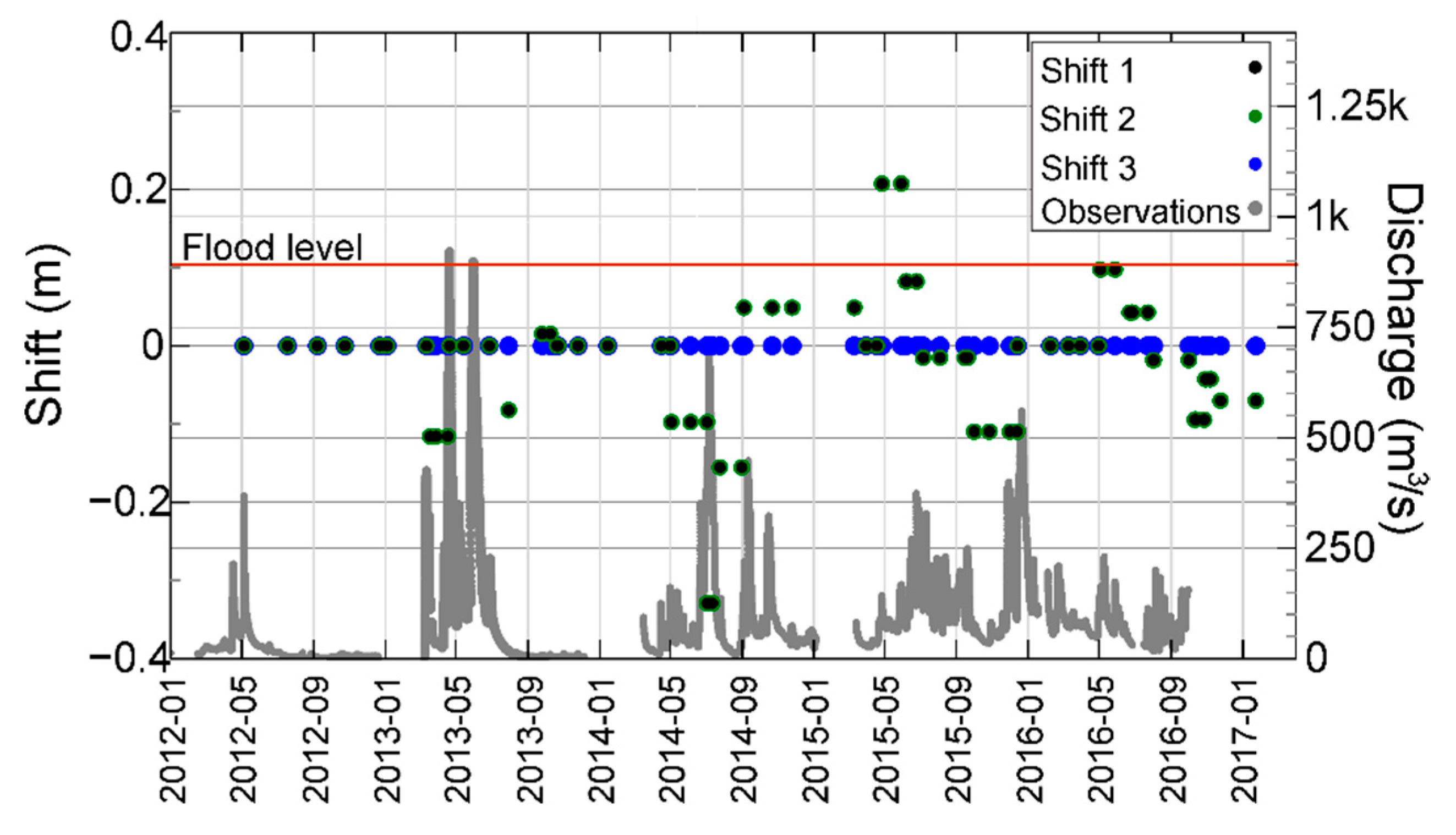
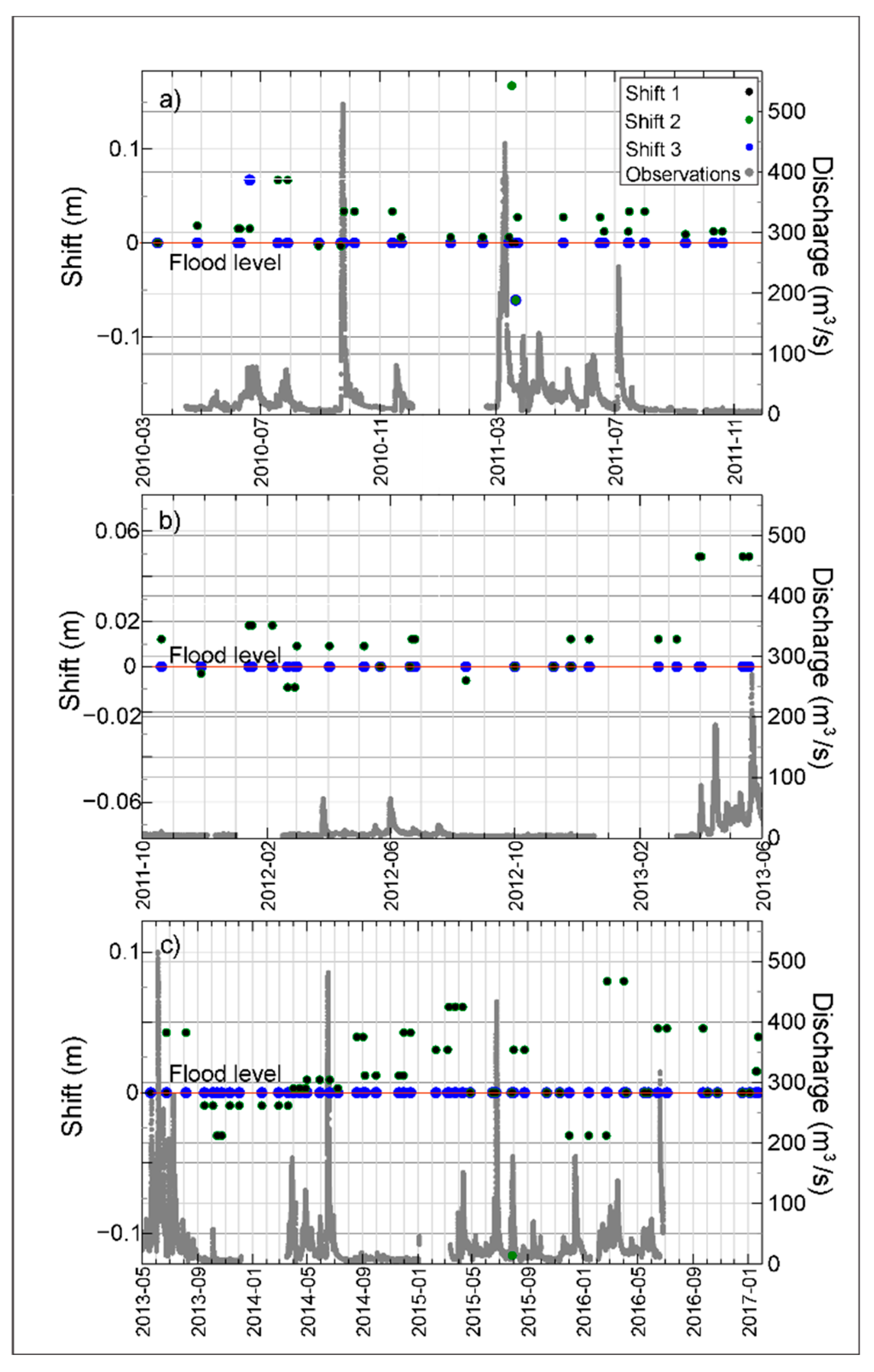
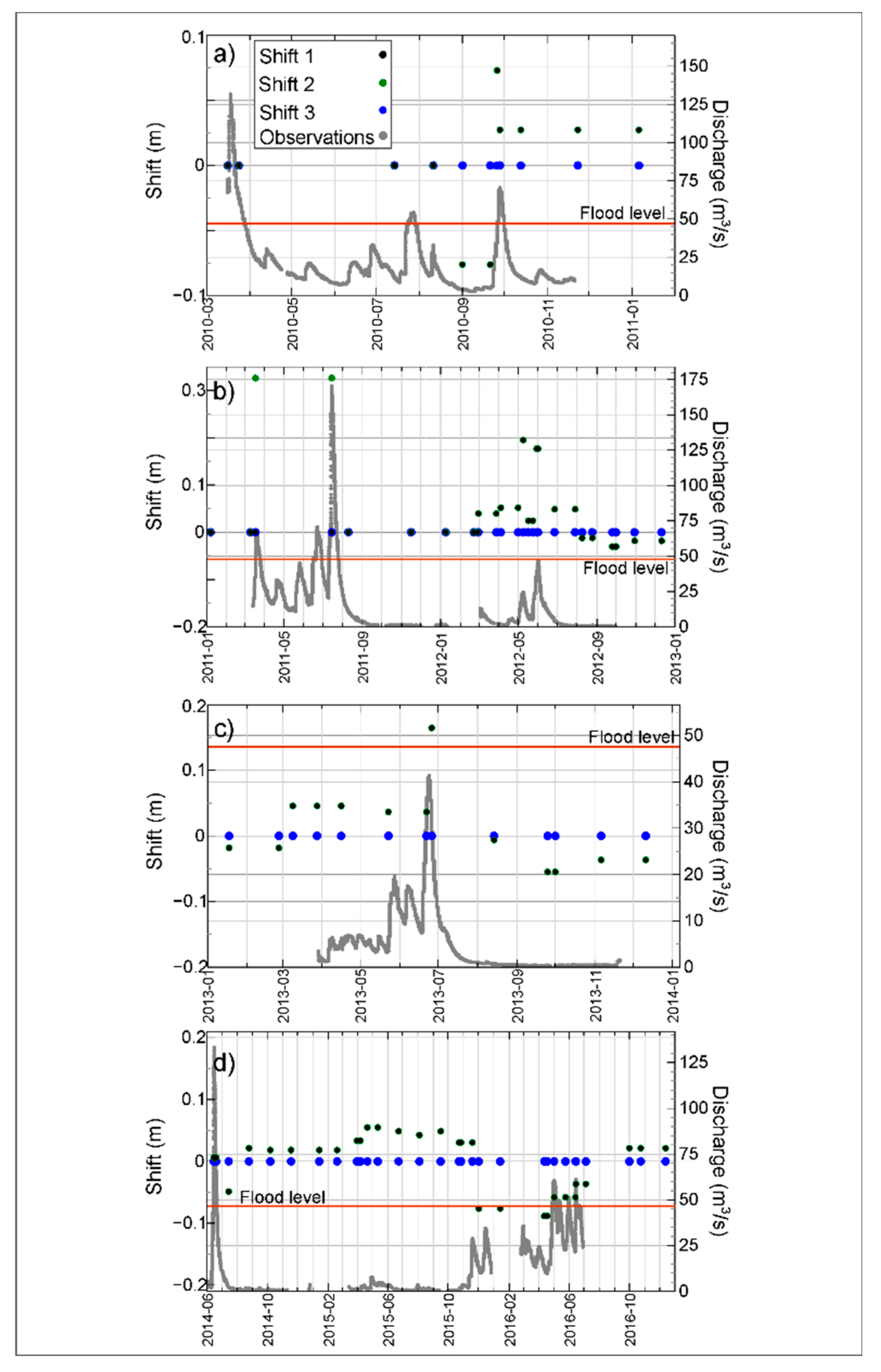
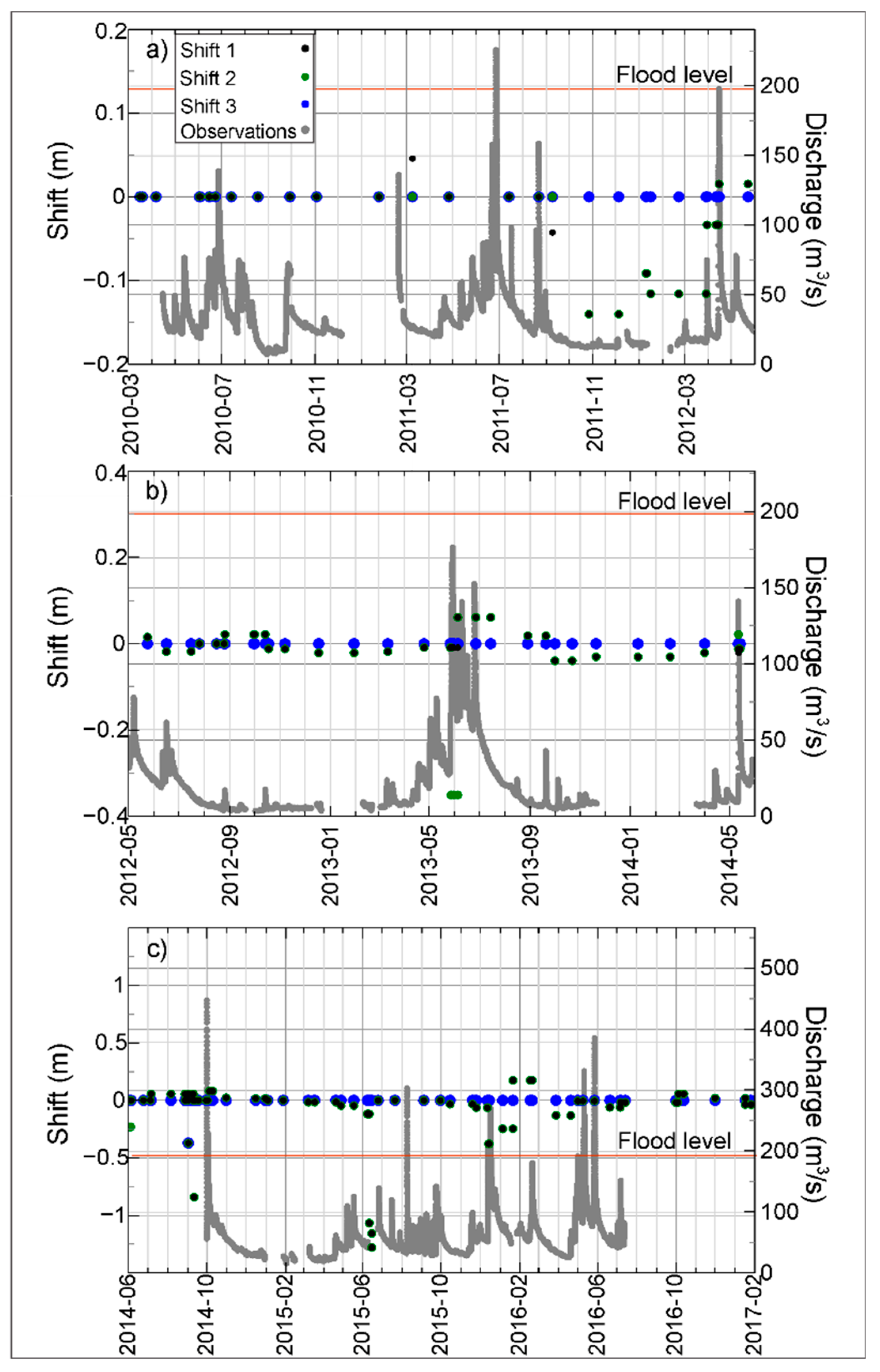
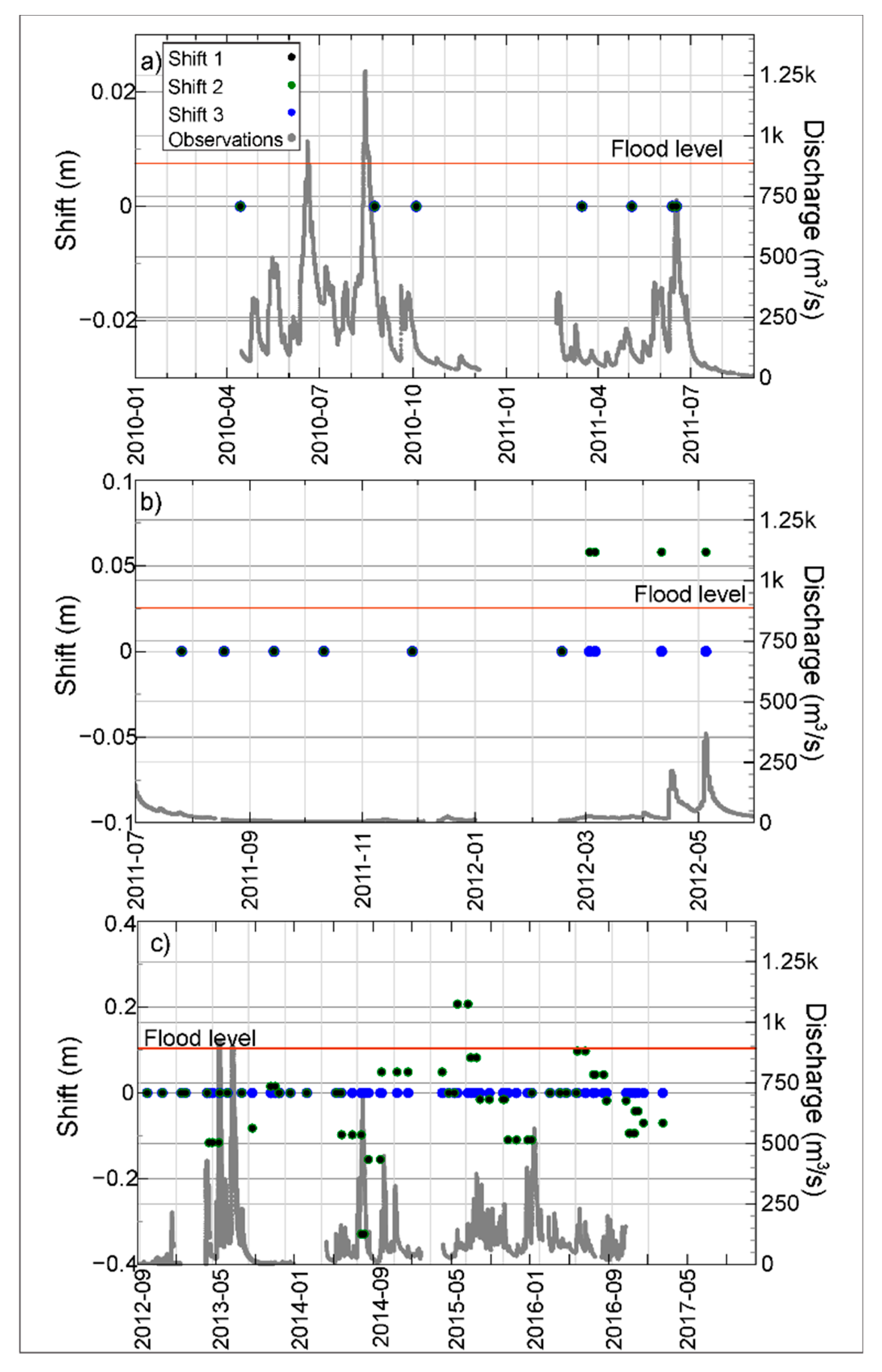
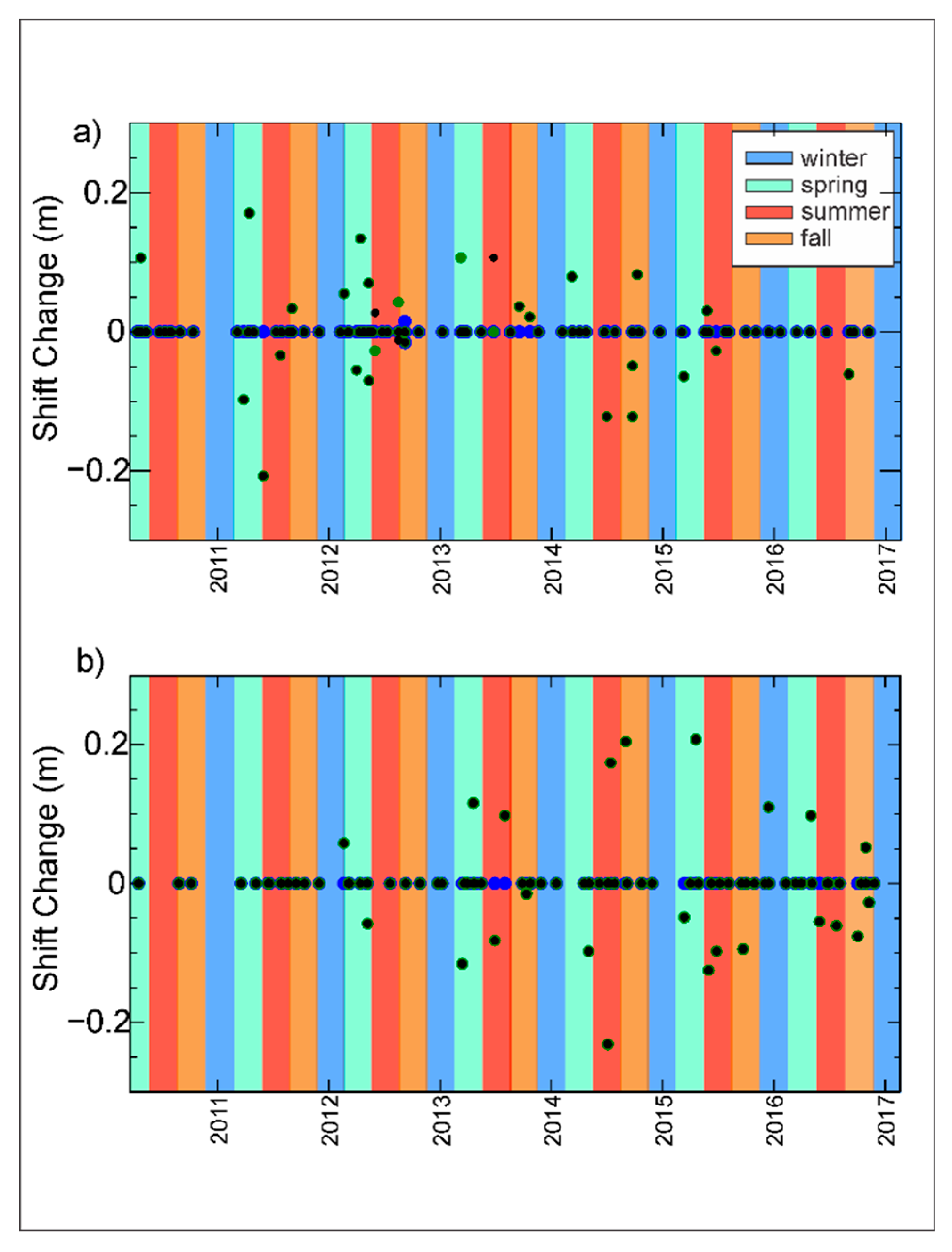
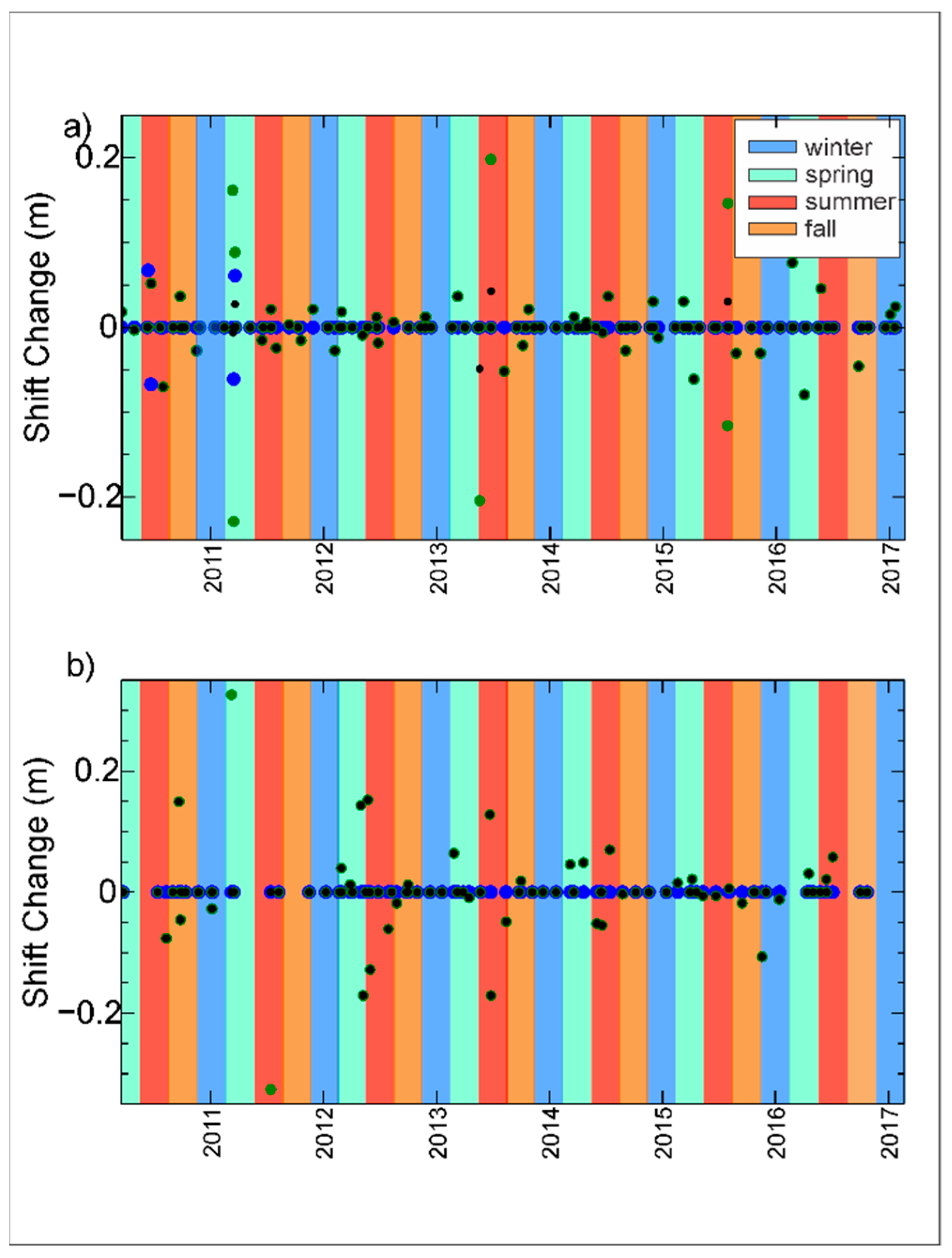
4.1. Shift Rating and Flow Events
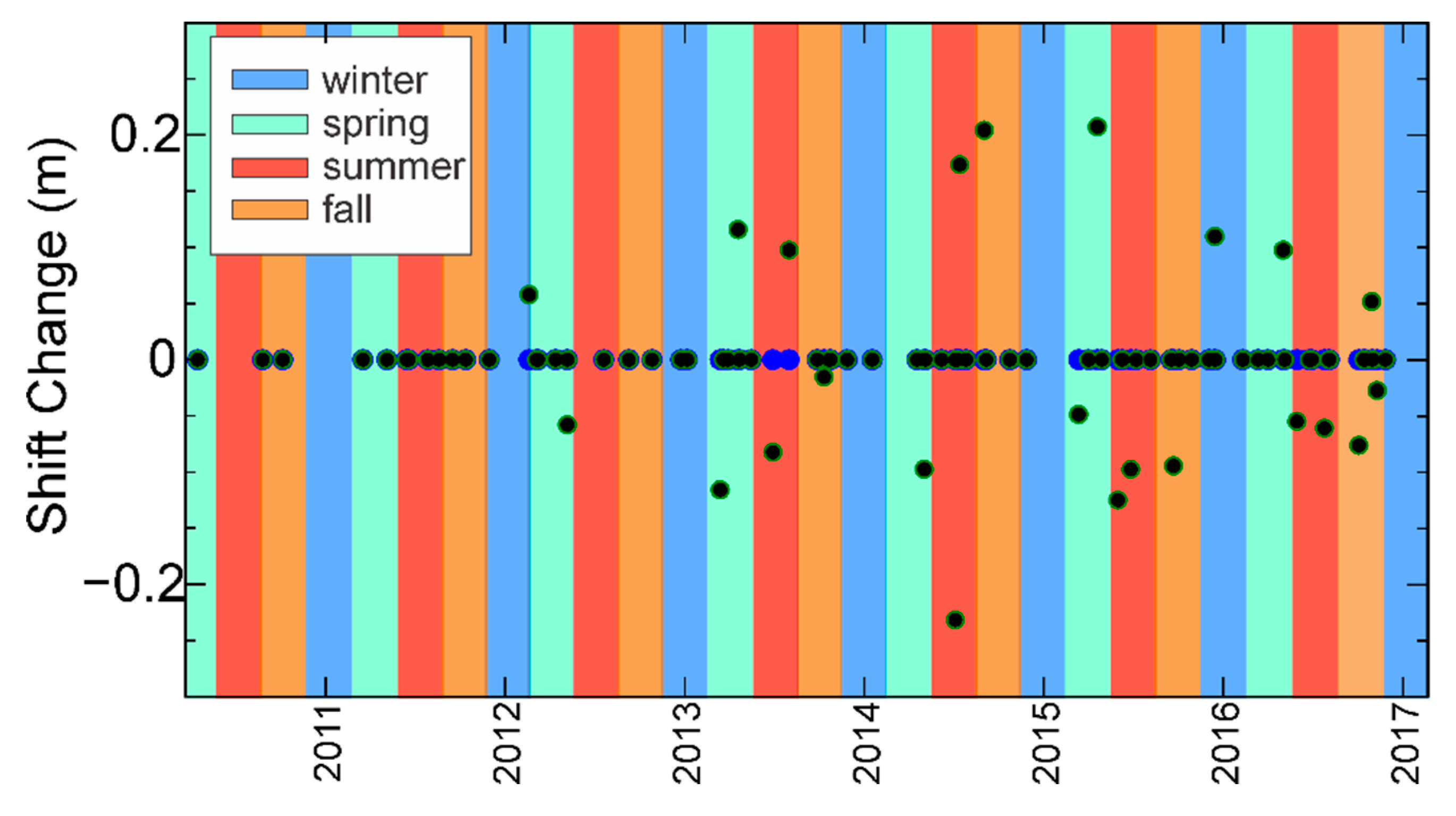
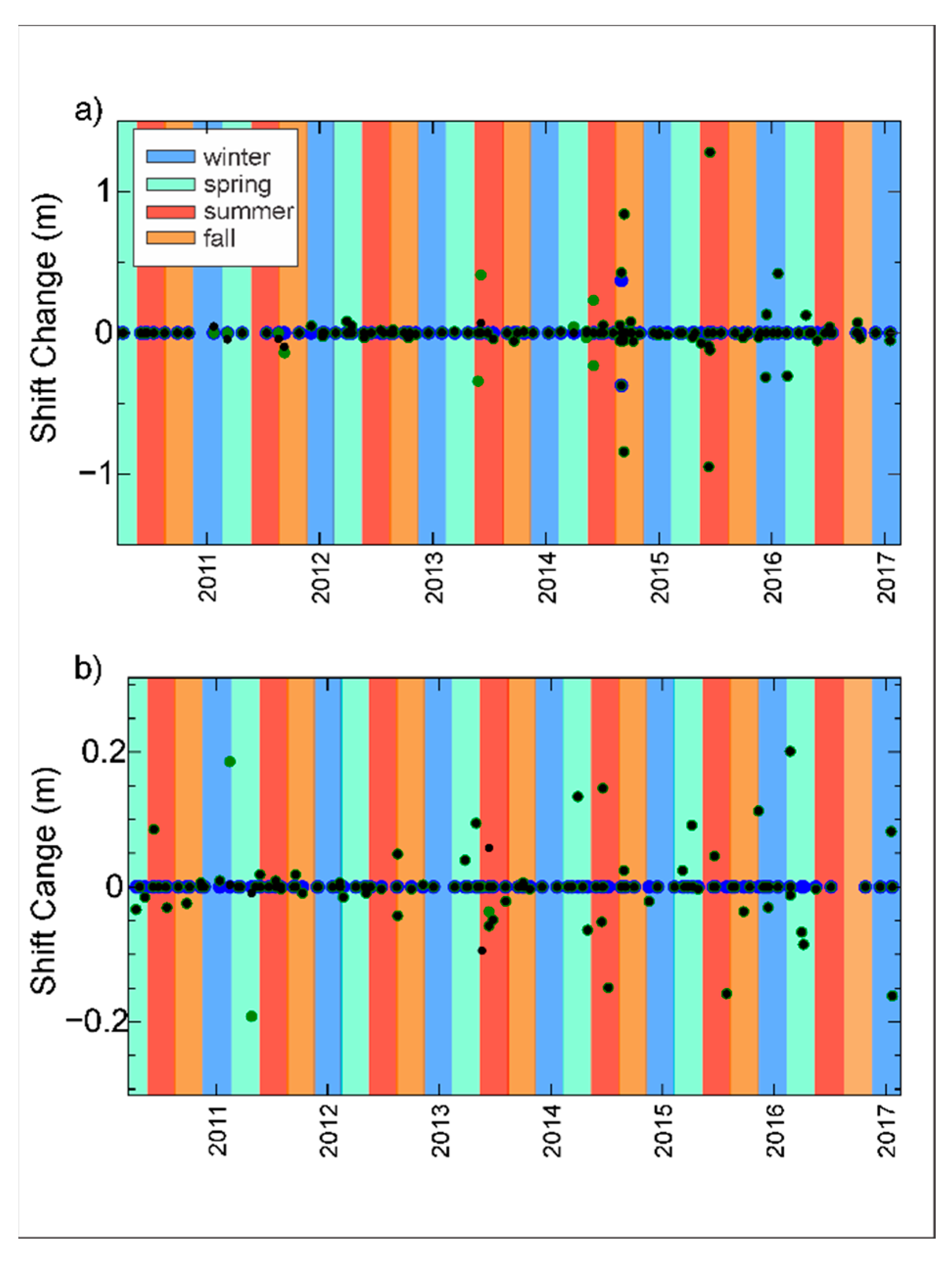
4.2. Seasonal Changes of Rating Shifts
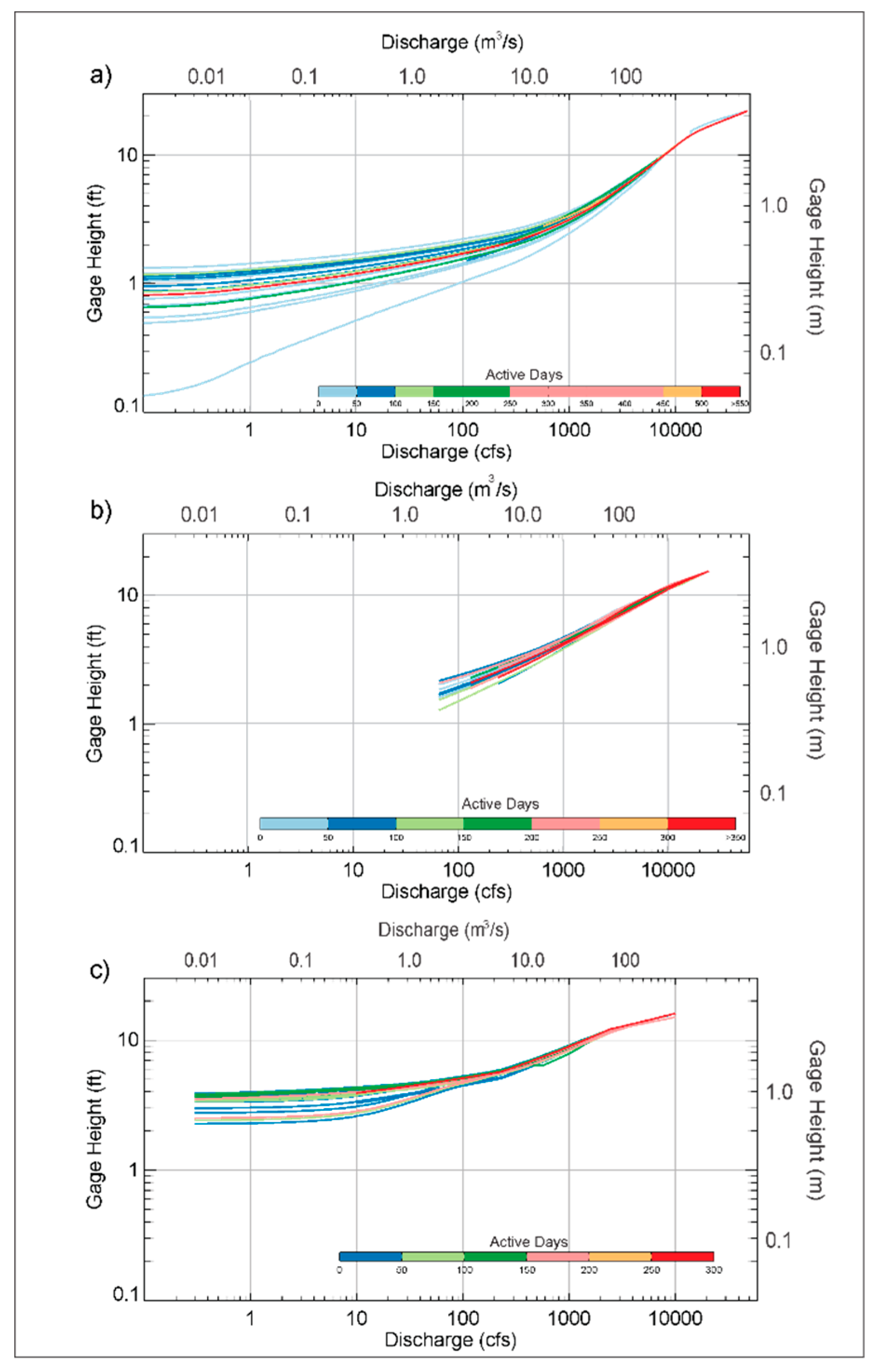
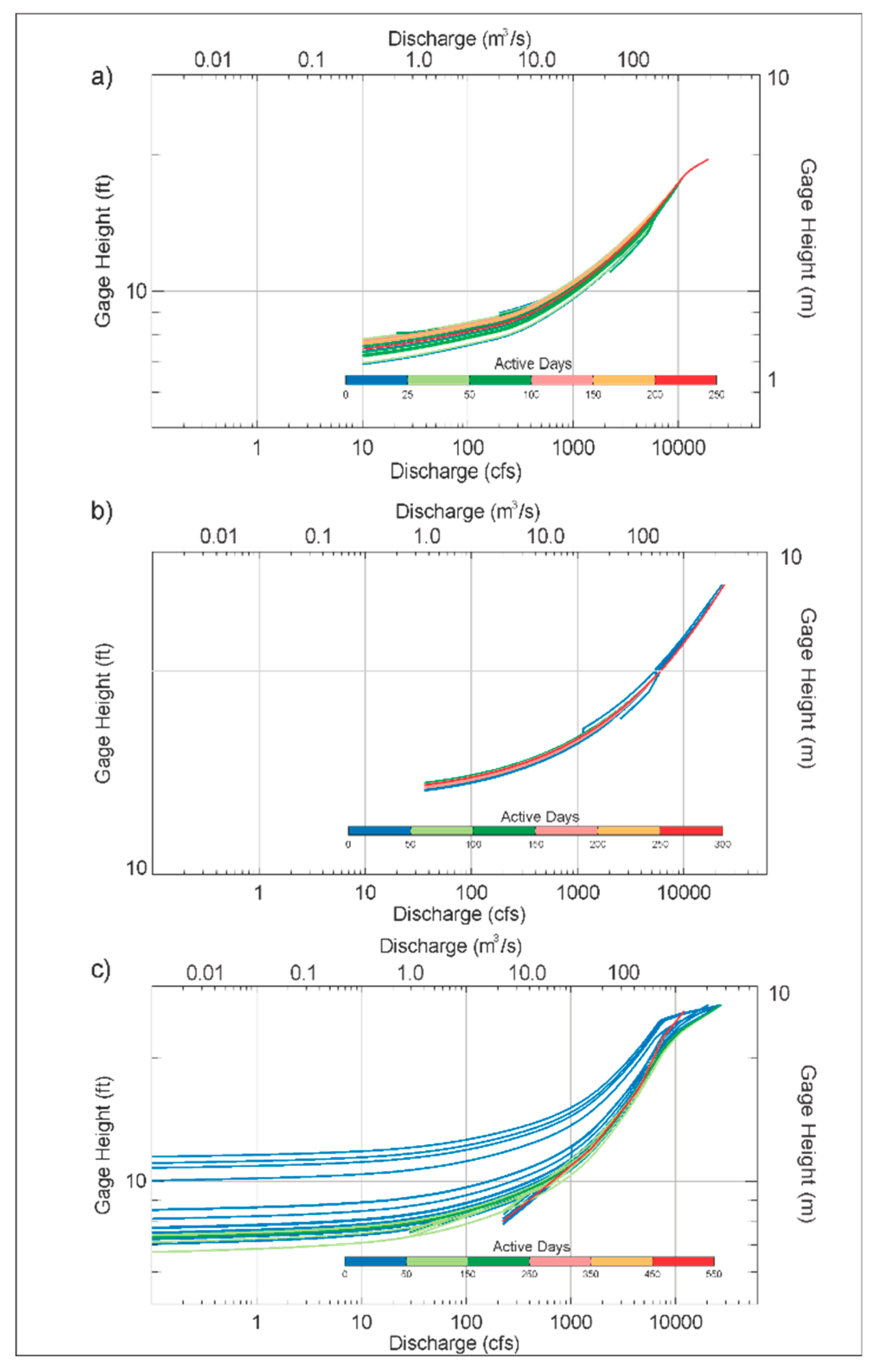
4.3. Rating Curve Variations Over Time
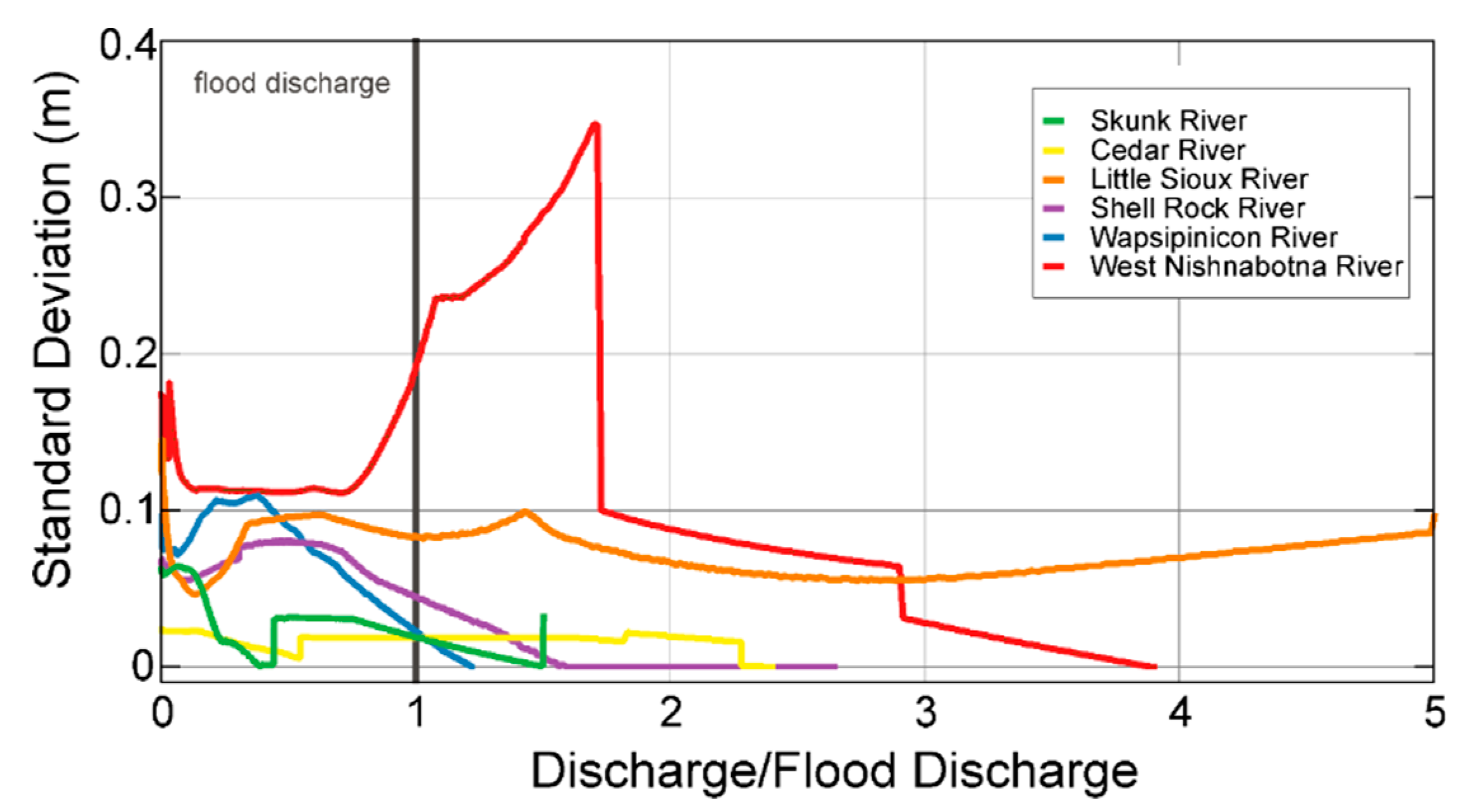
4.4. Stage Variation and Standard Deviation
5. Conclusions
- Additional data is required to conclude about the relation between rating curve stability and the material of the stream bed. The physical characteristics of the six study sites are very similar. The material of the stream bed is basically silty loam soil and, in most of them, the land use of the floodplain for the last 10 years has been cultivation. The main differences between these sites is the drainage area. Channels with larger areas are more prone to present more changes in their geometry than channels with smaller drainage areas, especially during flow changes. This is reflected in the variations of the shift values.
- The sediment transport and erosion processes that take place during large streamflow events lead to modifications in channel geometry that manifest as positive and negative changes in the rating shifts. We also found that during dry periods, little alteration of the channel geometry generally occurs; this is manifested as small or no change in the shift values.
- Adjustments in the rating curve occur through all seasons, but they are more prone to happen during spring and summer, the seasons with more rainfall in Iowa. The increase of rainfall and growing vegetation during spring and summer produces changes in the flow conditions, changes in the roughness of terrain, and ultimately, changes to the channel geometry.
- The greater stage variability in the stage–discharge relationship is observed for lower values of discharge. As discharge increases, the stage has less variation, and the duration of the stage–discharge relation is longer. This is the consequence of the frequent variation of the shift at section and channel control areas, and less variation at the overbank control area. The proposed comparison between stage deviation and discharge–flood ratio provides elements to determine if the stage–discharge relationship at one site is stable.
- For the 6 cases analyzed in our study, the site located in Cedar River at Osage, is the best candidate to use a synthetic rating curve instead of traditional ratings, as this site presents more stability for the entire ranges of discharge. The shift changes in Cedar River were very few and low probably because its small drainage area compared to the other study sites, which favors stability in channel geometry even during large flow events.
- A good alternative to rating curve maintenance is continuous water level monitoring coupled with use of synthetic rating curves. The Iowa Flood Center (IFC) developed and maintains a statewide network of stream stage sensors (around 250 along the state of Iowa) designed to measure stream height and transmit data automatically every 15 min to the Iowa Flood Information System (IFIS), where one can view the sensor locations and data in real time. This kind of information could help to complement the use of synthetic rating curves at a much lower cost.
- The results of the proposed methodology can support the decision to use synthetic rating curves instead of traditional ratings at streamflow gauges.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Herschy, R.W.; Herschy, R.W. Hydrometry: Principles and Practices, 2nd ed.; Wiley: Chichester, UK, 1999; p. 376. [Google Scholar]
- Sauer, V.B. Standards for the Analysis and Processing of Surface-Water Data and Information Using Electronic Methods. US Geol. Surv. Water Resour. Investig. 2002, 1, 106. [Google Scholar] [CrossRef]
- Fontaine, R.A.; Moss, M.; Smath, J.; Thomas, W. Cost-Effectiveness of the Stream-Gaging Program in Maine: A Prototype for Nationwide Implementation; Department of the Interior, US Geological Survey: Alexandria, VA, USA, 1984; Volume 2244. [CrossRef]
- Church, M. Channel Stability: Morphodynamics and the Morphology of Rivers. In Recent Trends in Environmental Hydraulics; Springer Science and Business Media LLC: Cham, Switzerland, 2015; pp. 281–321. [Google Scholar]
- Kennedy, E. Computation of continuous records of streamflow. Tech. Water Resour. Investig. U.S. Geol. Surv. 1983, 53. [Google Scholar] [CrossRef]
- Kennedy, E.J. Discharge Ratings at Gaging Stations; Department of the Interior, US Geological Survey: Alexandria, VA, USA, 1984; p. 58. [CrossRef]
- Fenton, J.D.; Keller, R.J. The Calculation of Streamflow from Measurements of Stage; Tech. Rep. 01/6; Cooperative Research Centre for Catchment Hydrology: Clayton, Victoria, Australia, 2001; p. 77. [Google Scholar]
- Pelletier, P.M. Uncertainties in the single determination of river discharge: A literature review. Can. J. Civ. Eng. 1988, 15, 834–850. [Google Scholar] [CrossRef]
- Prior, J.C. Landforms of Iowa; University of Iowa Press: Iowa City, IA, USA, 1991; ISBN 1587291959. [Google Scholar]
- Torbick, N.; Lusch, D.; Qi, J.; Moore, N.; Olson, J.; Ge, J. Developing land use/land cover parameterization for climate–land modelling in East Africa. Int. J. Remot. Sens. 2006, 27, 4227–4244. [Google Scholar] [CrossRef]
- Rantz, S.E. Measurement and Computation of Streamflow: Volume 2. Computation of Discharge; Department of the Interior, US Geological Survey: Washington, DC, USA, 1982; Volume 2, p. 389.
- U.S. Geological Survey. Available online: https://waterdata.usgs.gov/nwisweb/local/state/ca/text/whatisarating.html (accessed on 1 March 2019).
- Hillacker, H.J. The Drought of 2012 in Iowa Climatology Summary; Iowa Department of Agriculture and Land Stewardship: Desmoines, IA, USA, 2012; p. 6. [Google Scholar]
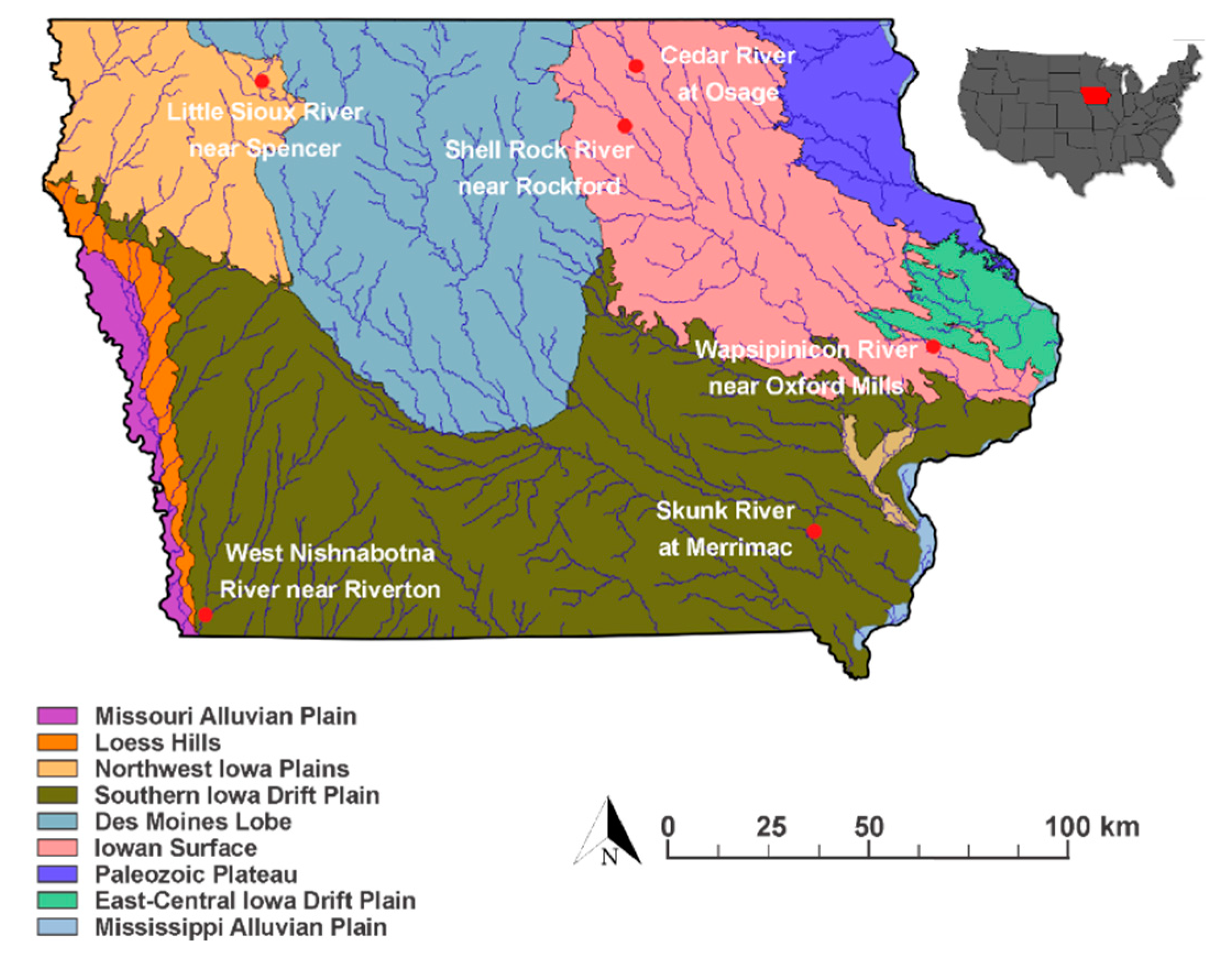

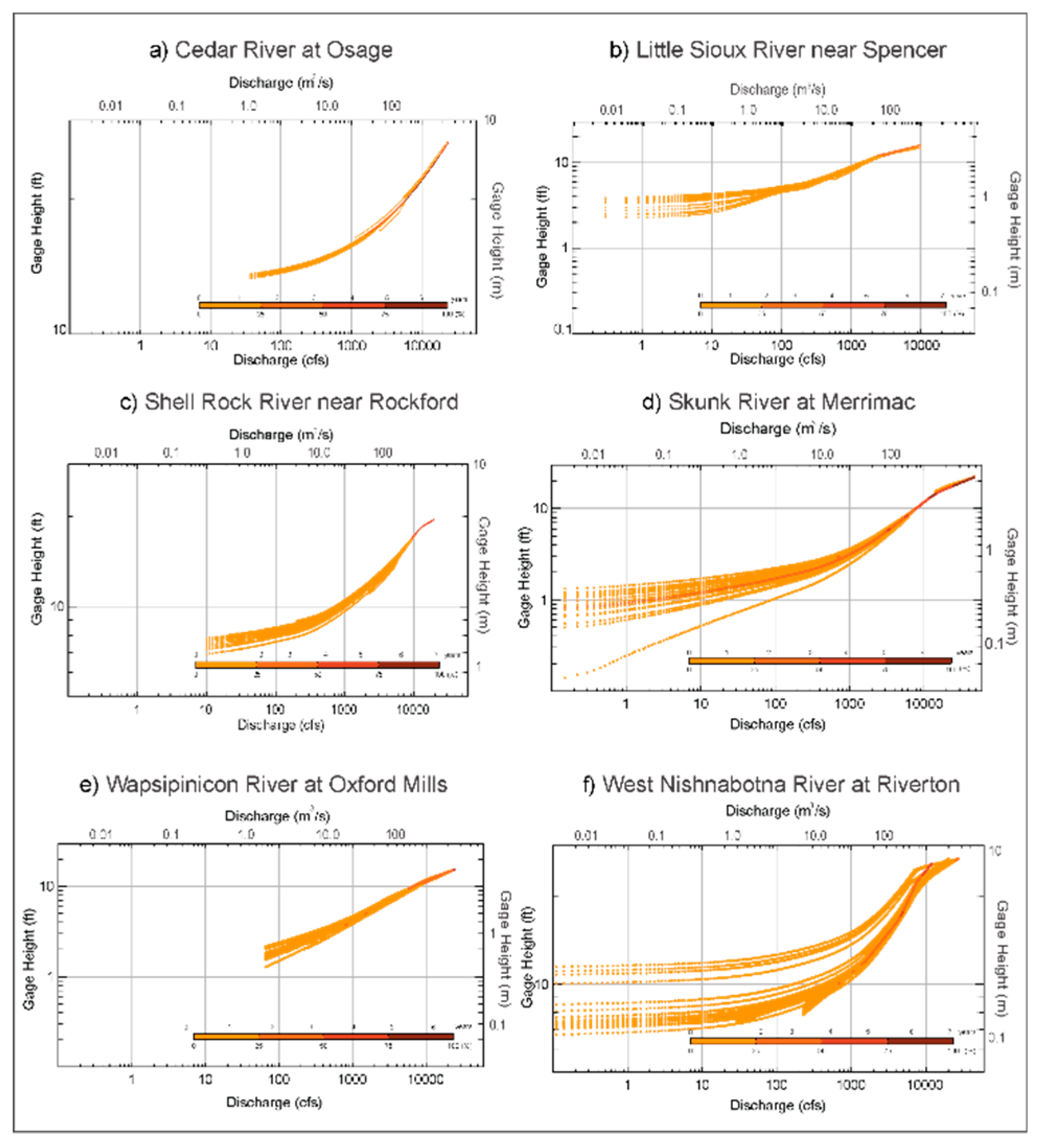
| Name (USGS Code) | Period of Study | Area (km2) | Soil Texture (Bed Material) | Land Use (Flood Plain) [10] |
|---|---|---|---|---|
| Skunk River at Merrimac (05473065) | April 2010–January 2017 | 8360 | silt loam | Cultivated Crops |
| Wapsipinicon River at Oxford Mills (05421760) | April 2010– January 2017 | 4628 | loam | Woody Wetlands/Developed, Open Space |
| Cedar River at Osage (05457505) | March 2010– January 2017 | 2168 | loam | Pasture/Hay/Deciduous Forest |
| Little Sioux River near Spencer (06604440) | March 2010–December 2016 | 1350 | loam | Cultivated Crops |
| Shell Rock River near Rockford (05460400) | April 2010–January 2017 | 3230 | loam | Cultivated Crops |
| West Nishnabotna River at Riverton (06808820) | March 2010–January 2017 | 4254 | silt loam | Emergent Herbaceous Wetlands/Cultivated Crops |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rojas, M.; Quintero, F.; Young, N. Analysis of Stage–Discharge Relationship Stability Based on Historical Ratings. Hydrology 2020, 7, 31. https://doi.org/10.3390/hydrology7020031
Rojas M, Quintero F, Young N. Analysis of Stage–Discharge Relationship Stability Based on Historical Ratings. Hydrology. 2020; 7(2):31. https://doi.org/10.3390/hydrology7020031
Chicago/Turabian StyleRojas, Marcela, Felipe Quintero, and Nathan Young. 2020. "Analysis of Stage–Discharge Relationship Stability Based on Historical Ratings" Hydrology 7, no. 2: 31. https://doi.org/10.3390/hydrology7020031
APA StyleRojas, M., Quintero, F., & Young, N. (2020). Analysis of Stage–Discharge Relationship Stability Based on Historical Ratings. Hydrology, 7(2), 31. https://doi.org/10.3390/hydrology7020031





