Effects of Aquifer Bed Slope and Sea Level on Saltwater Intrusion in Coastal Aquifers
Abstract
1. Introduction
2. Materials and Methods
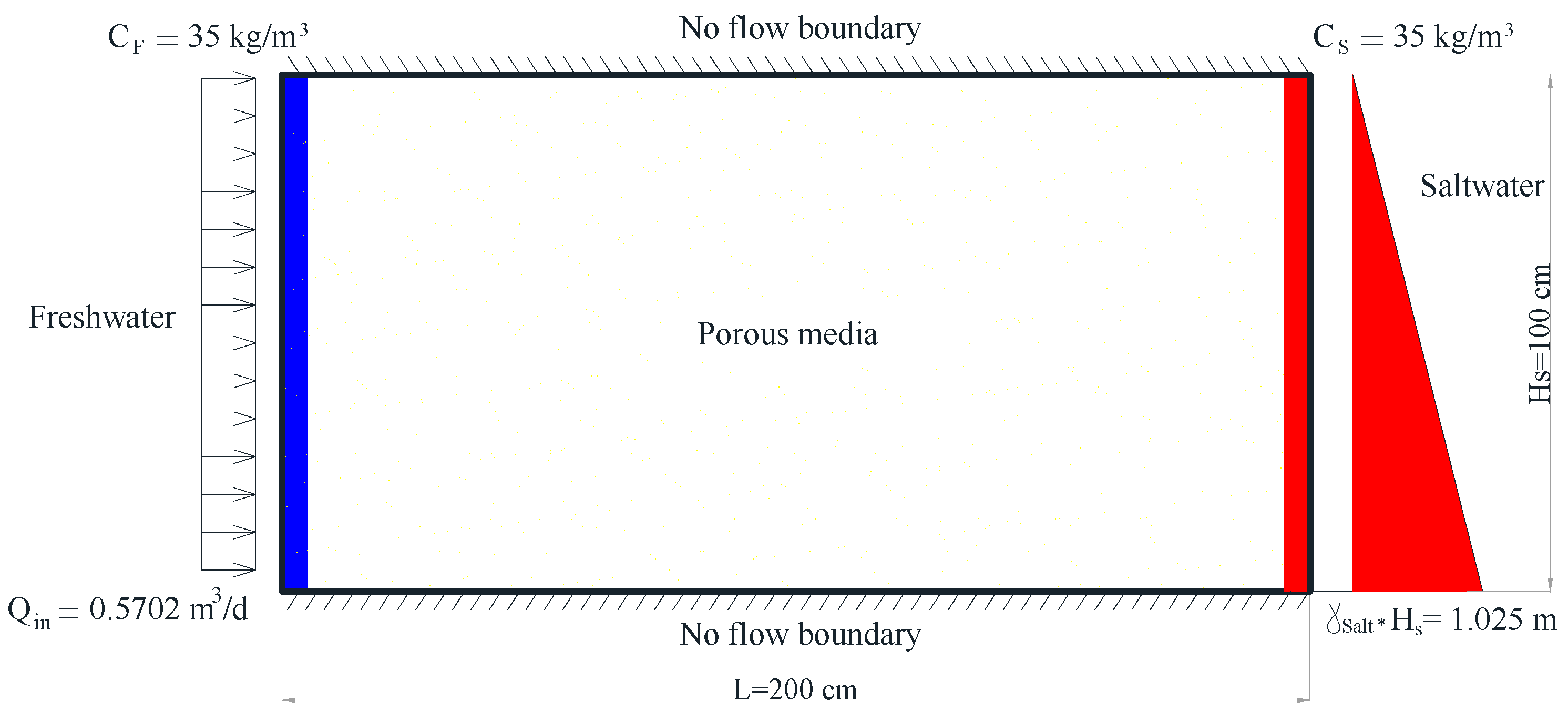
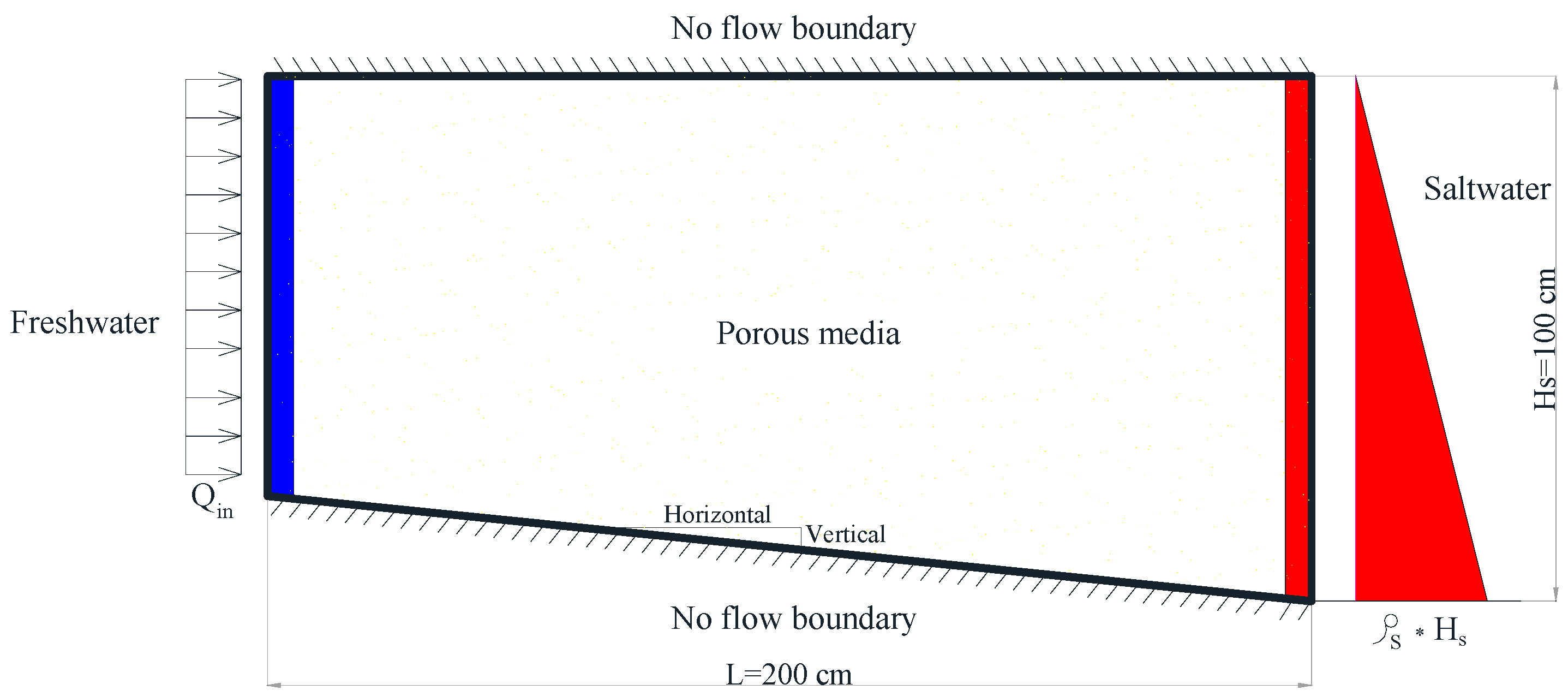
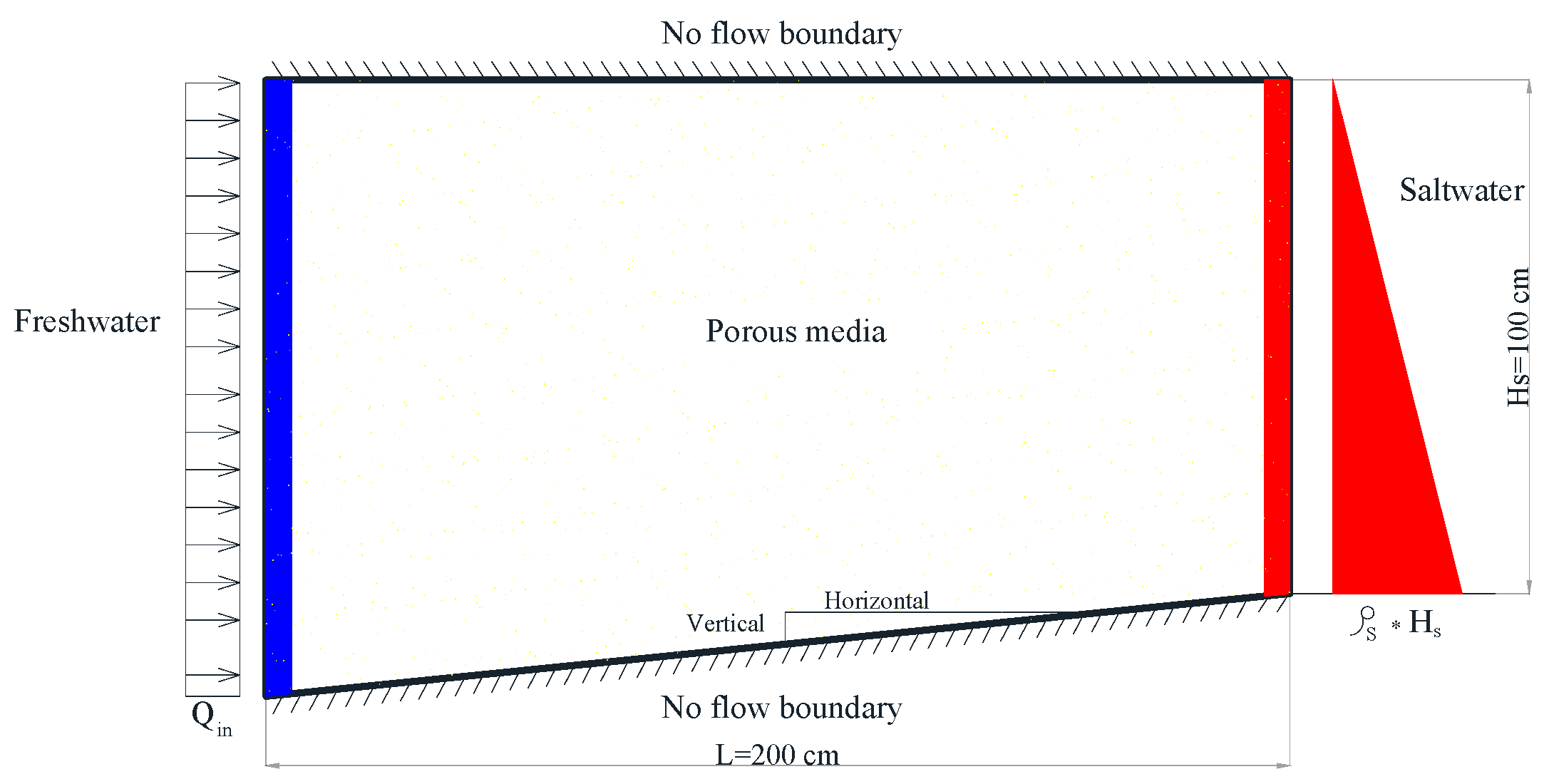
2.1. Numerical Model
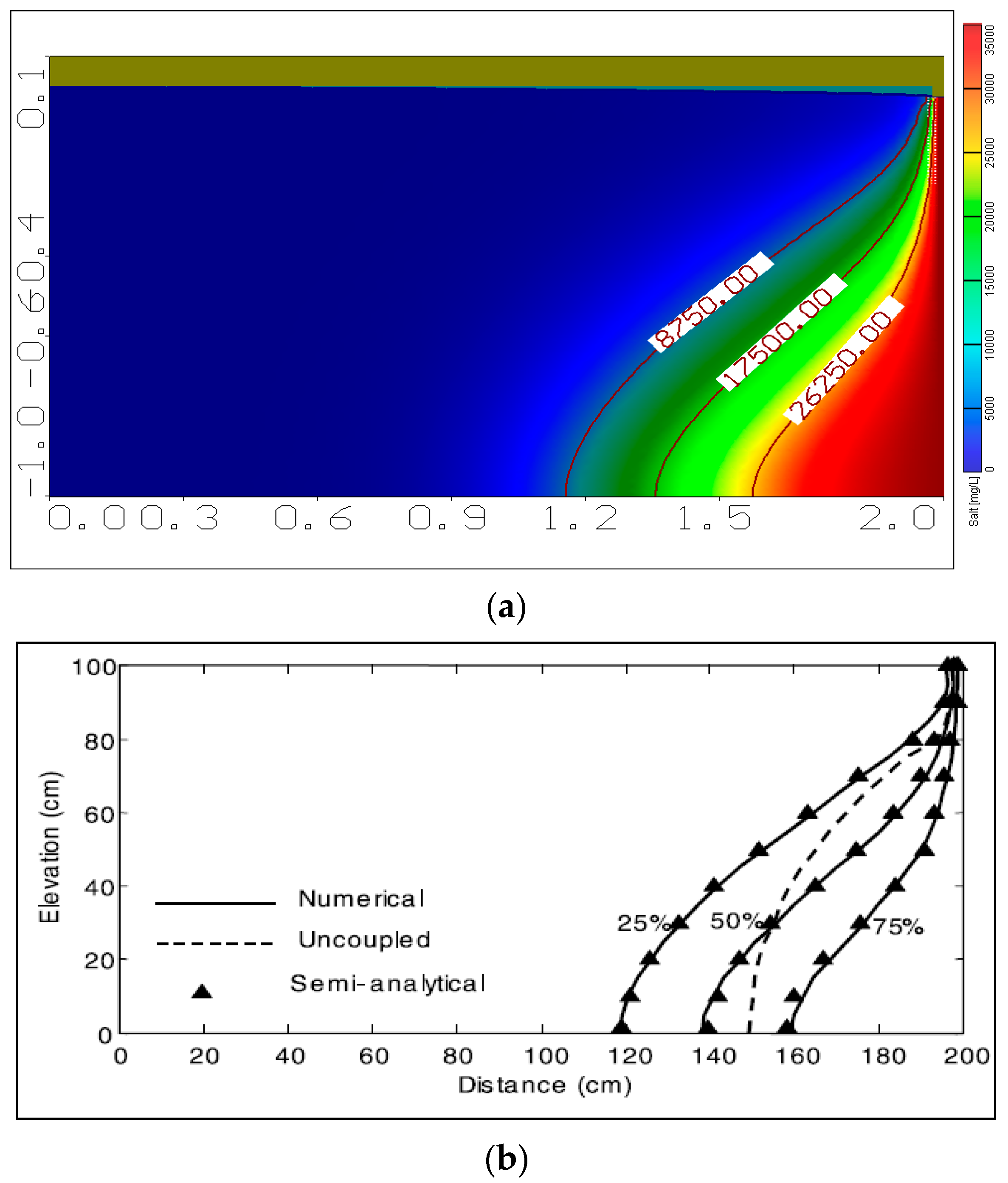
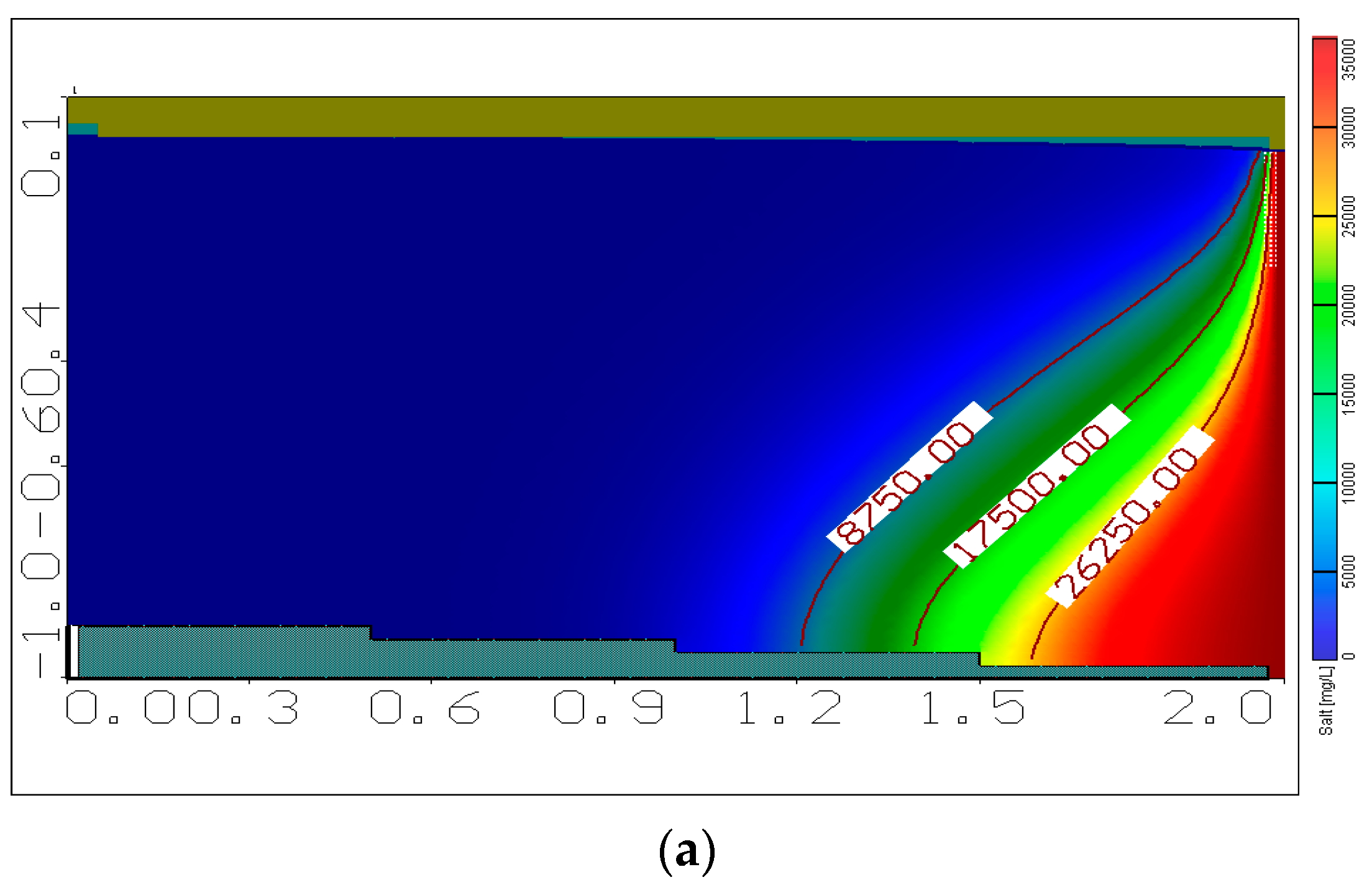
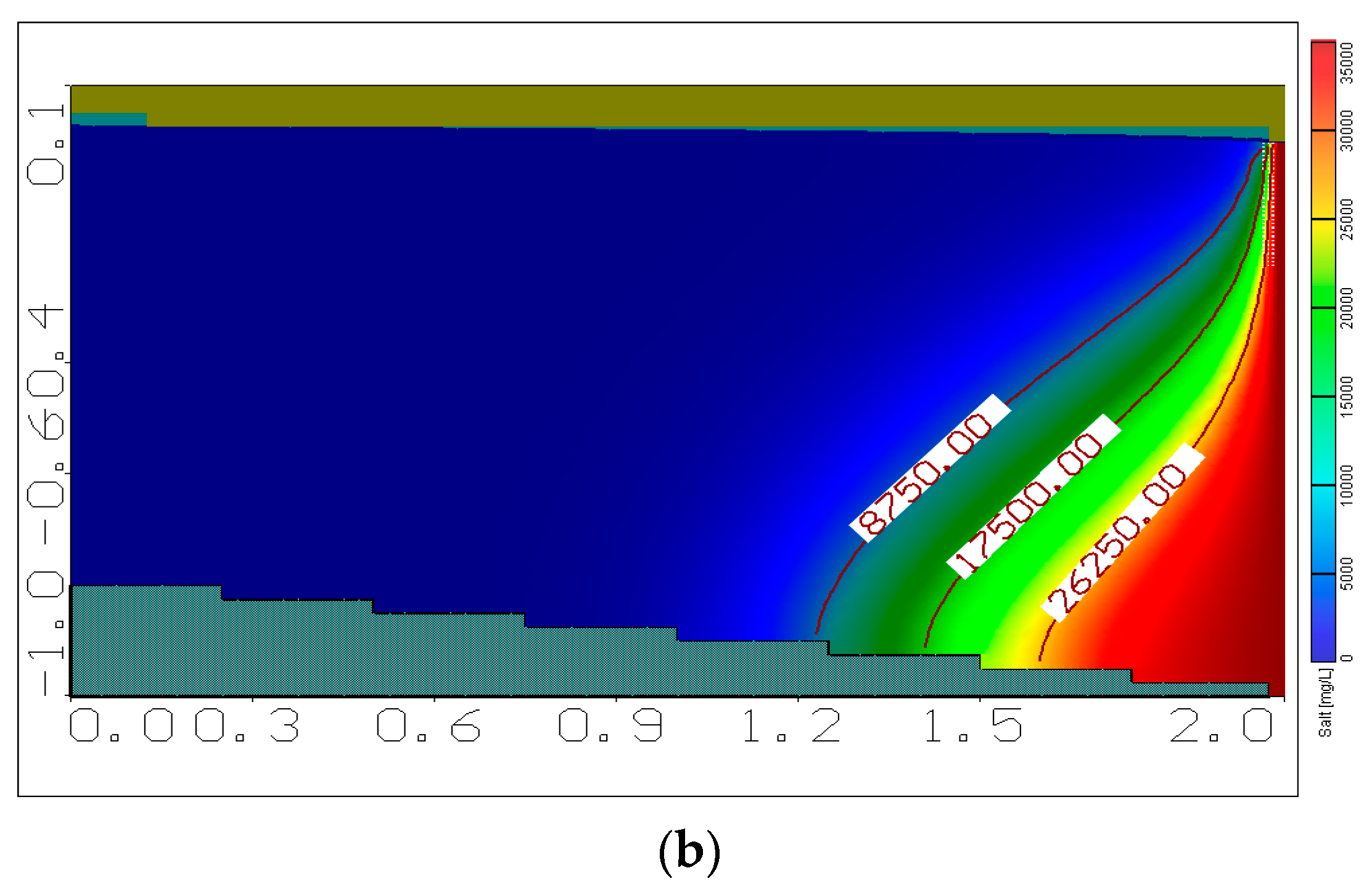
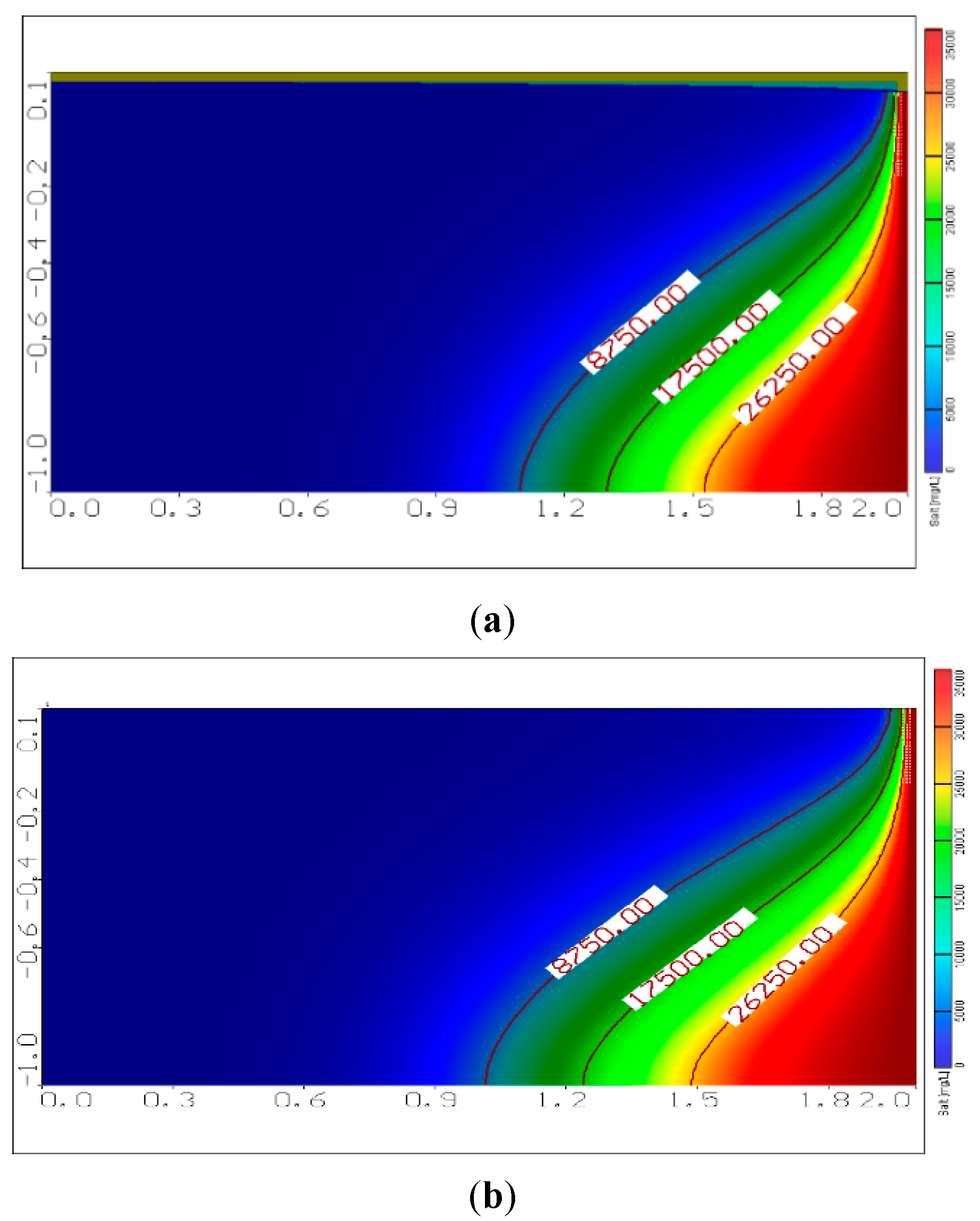
2.2. Model Verification
3. Results
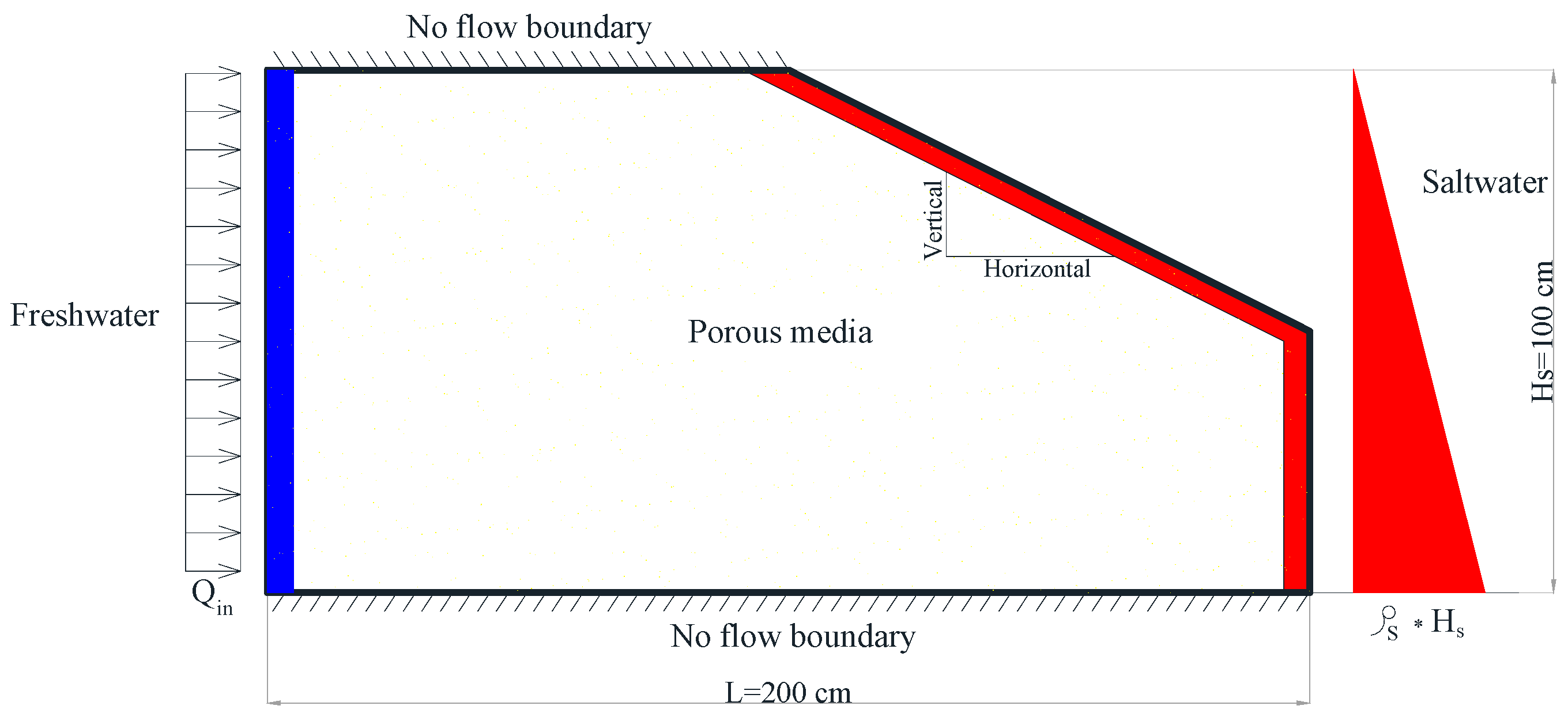
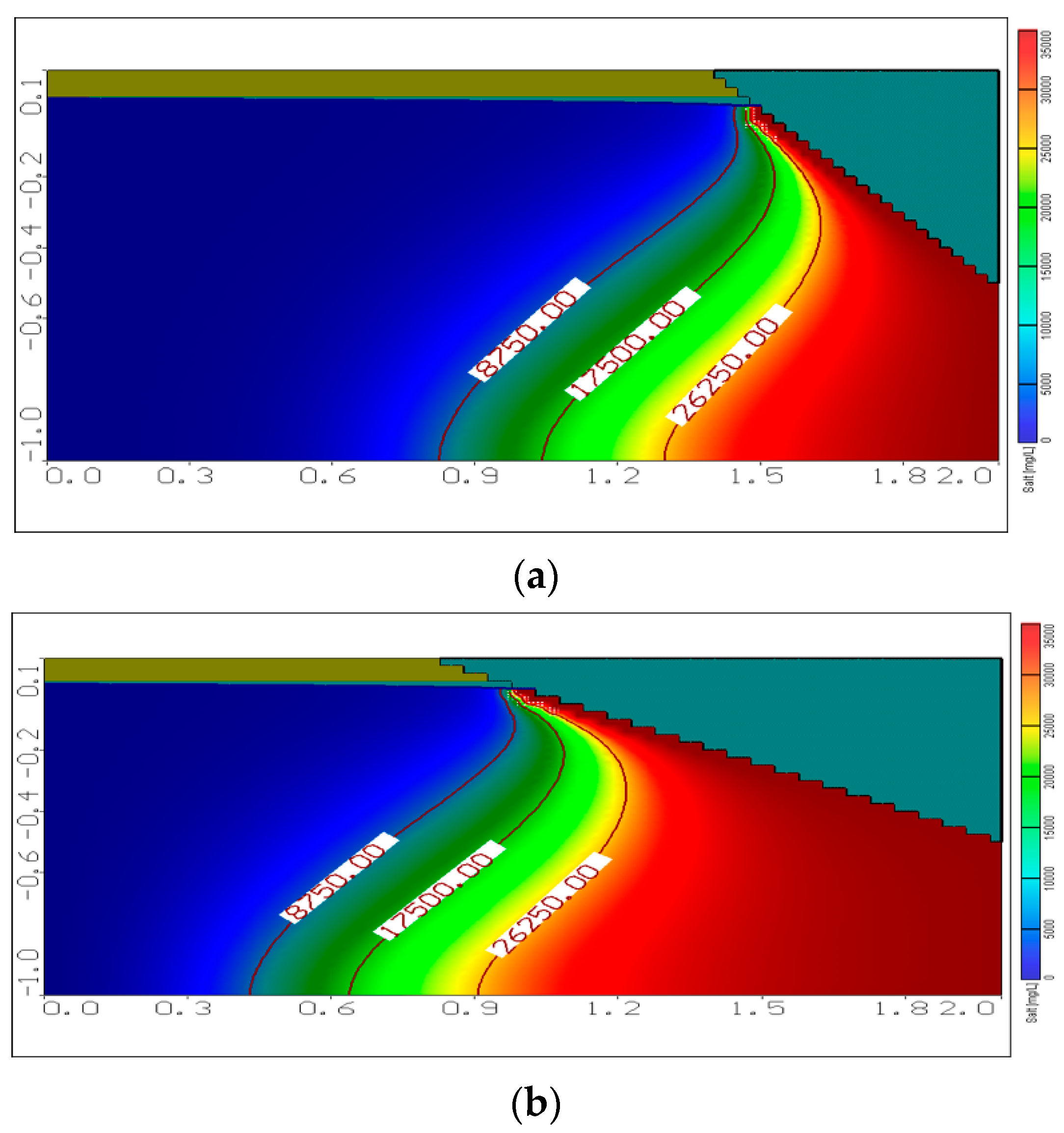
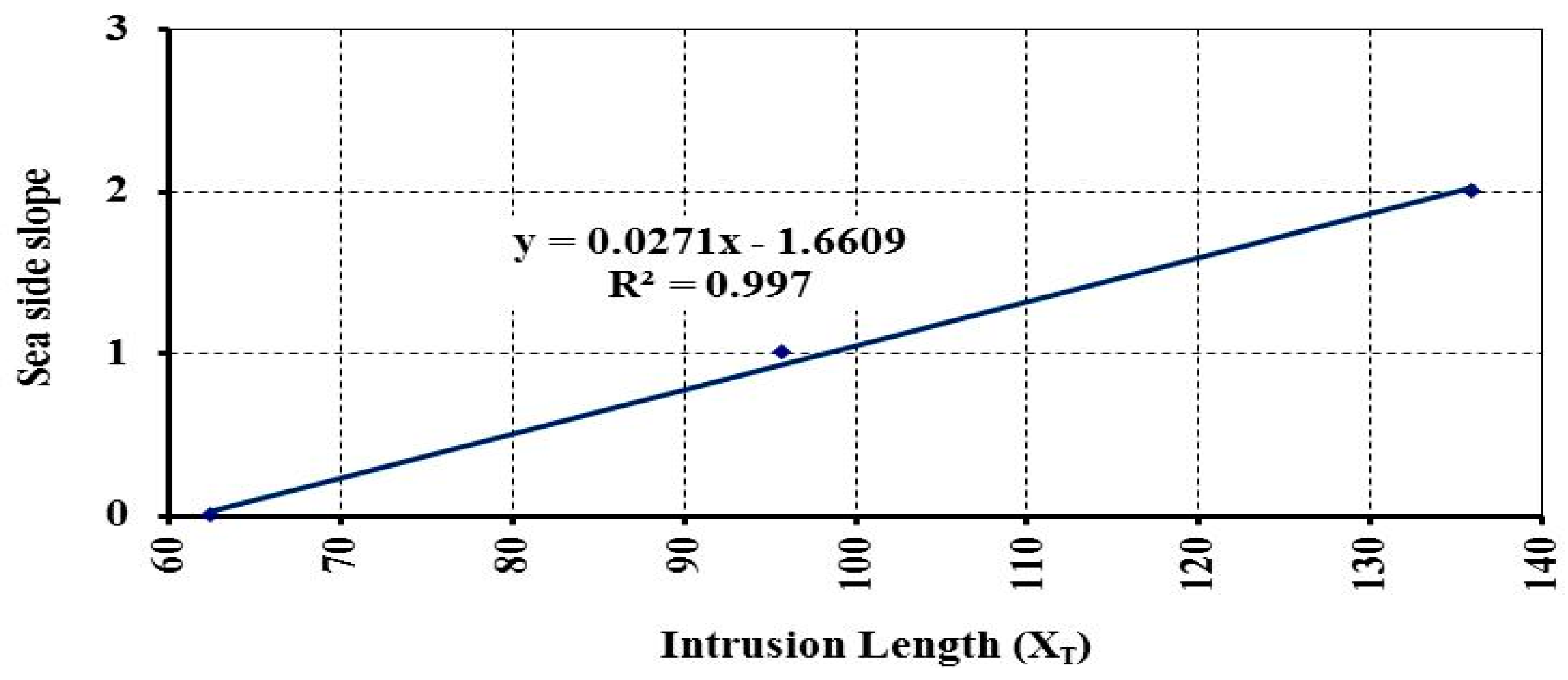
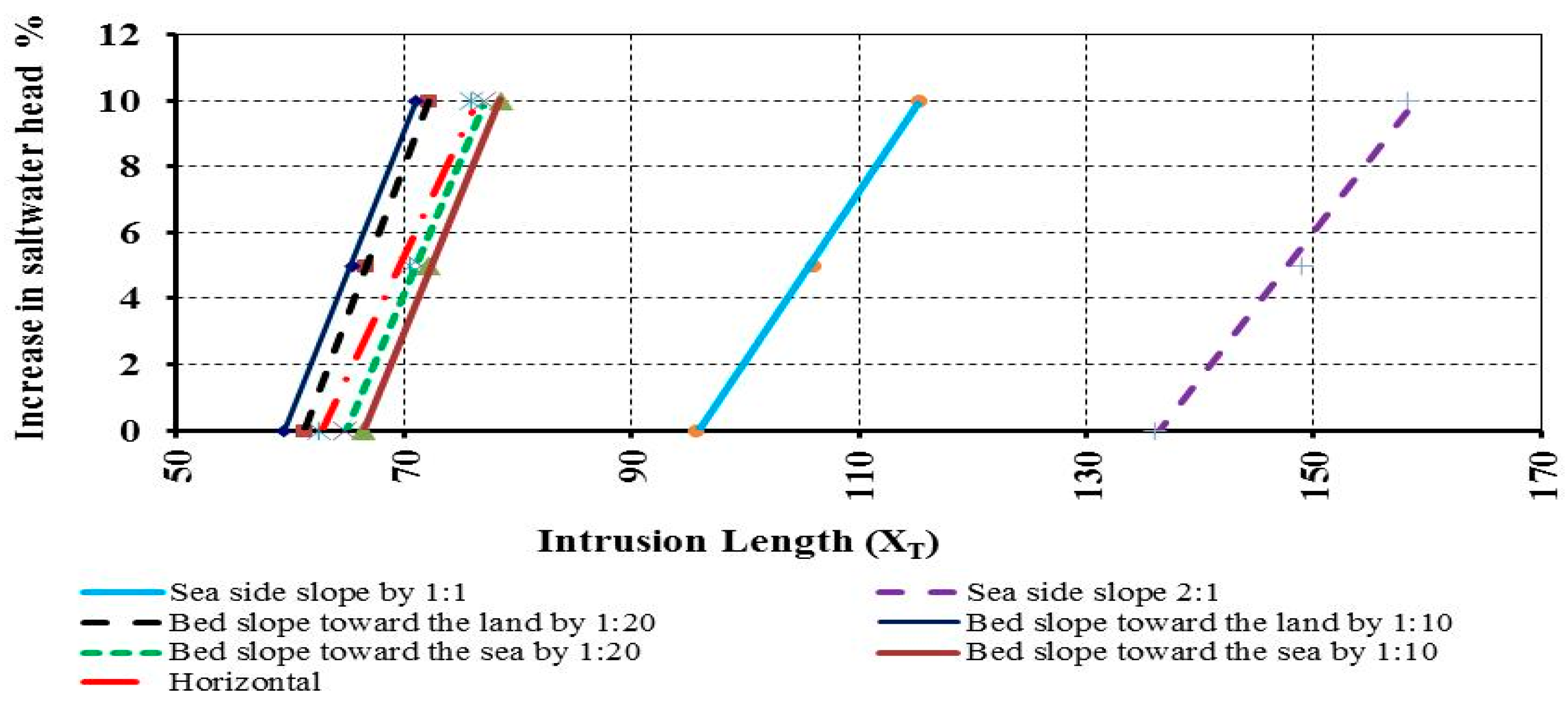
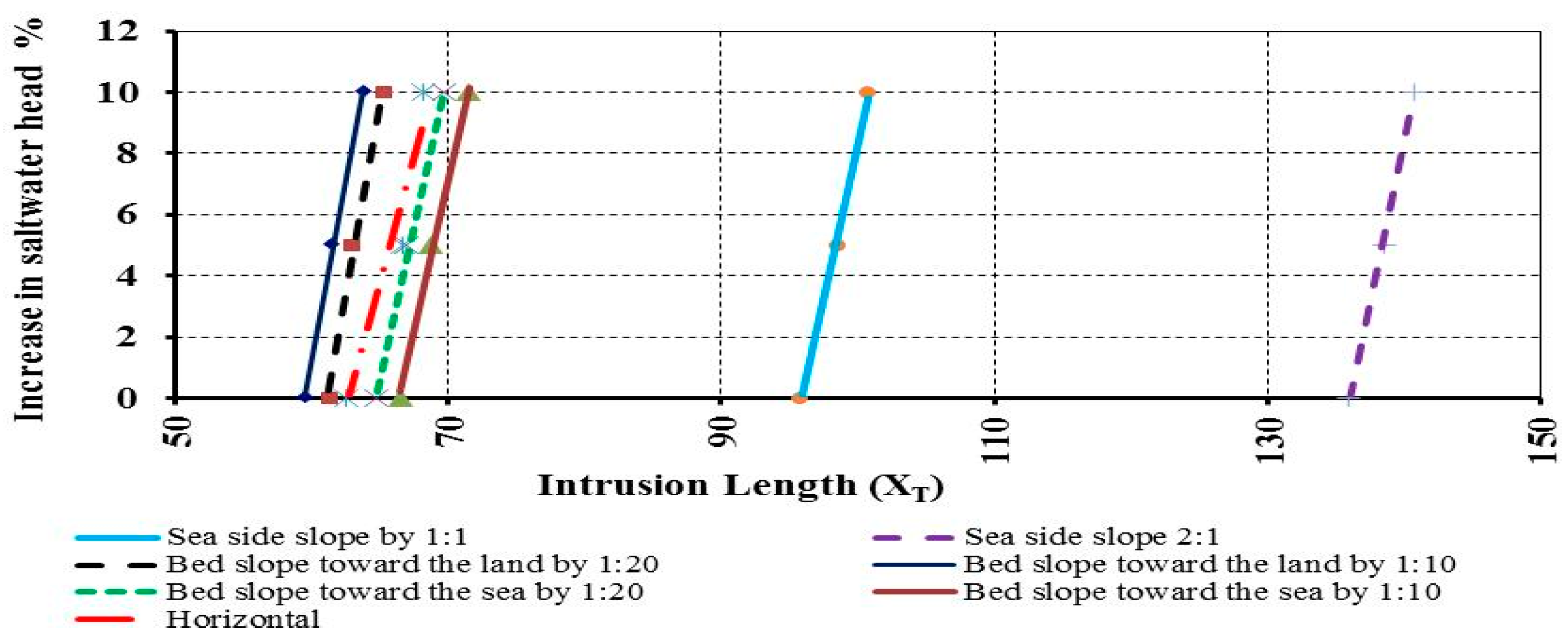
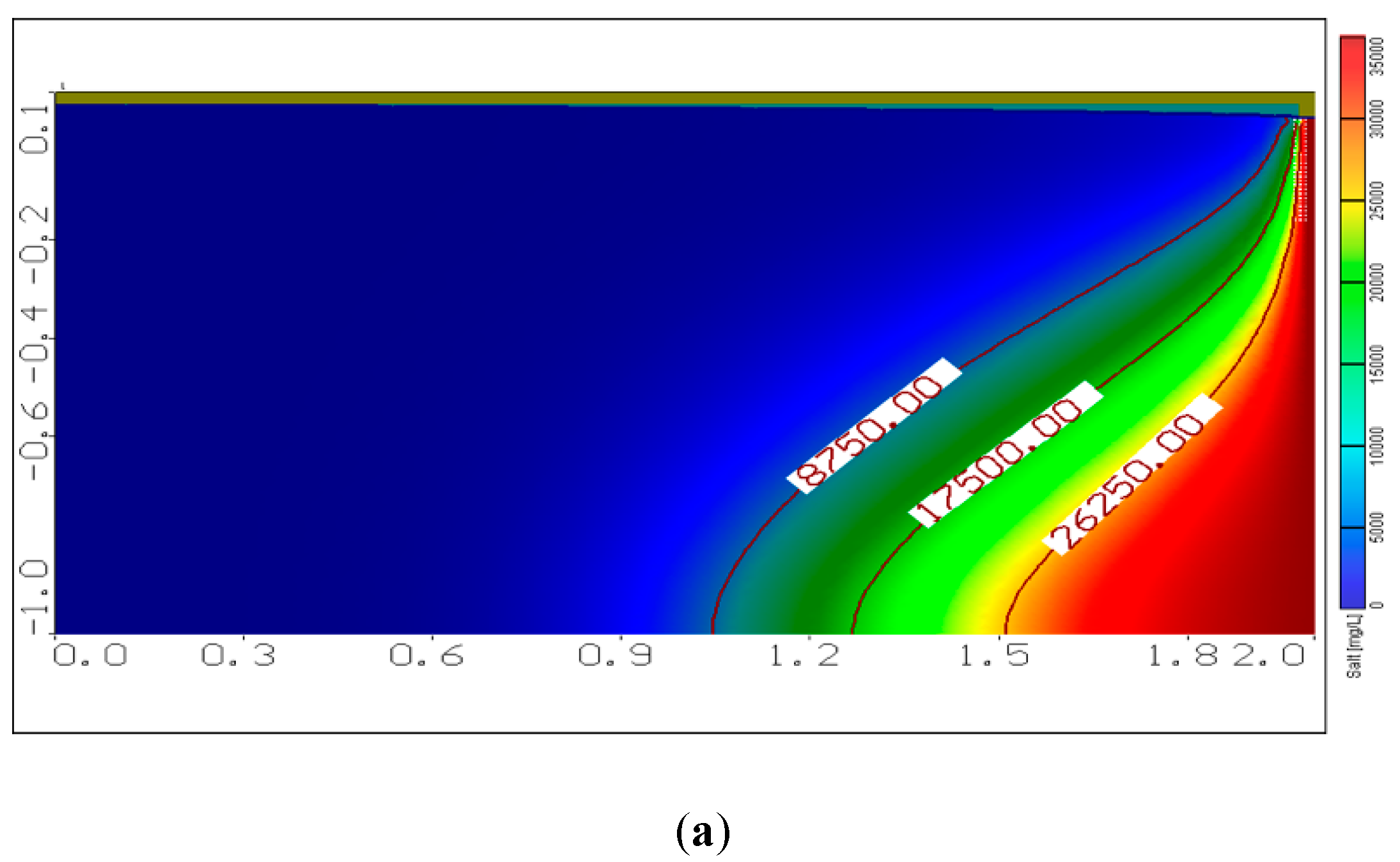
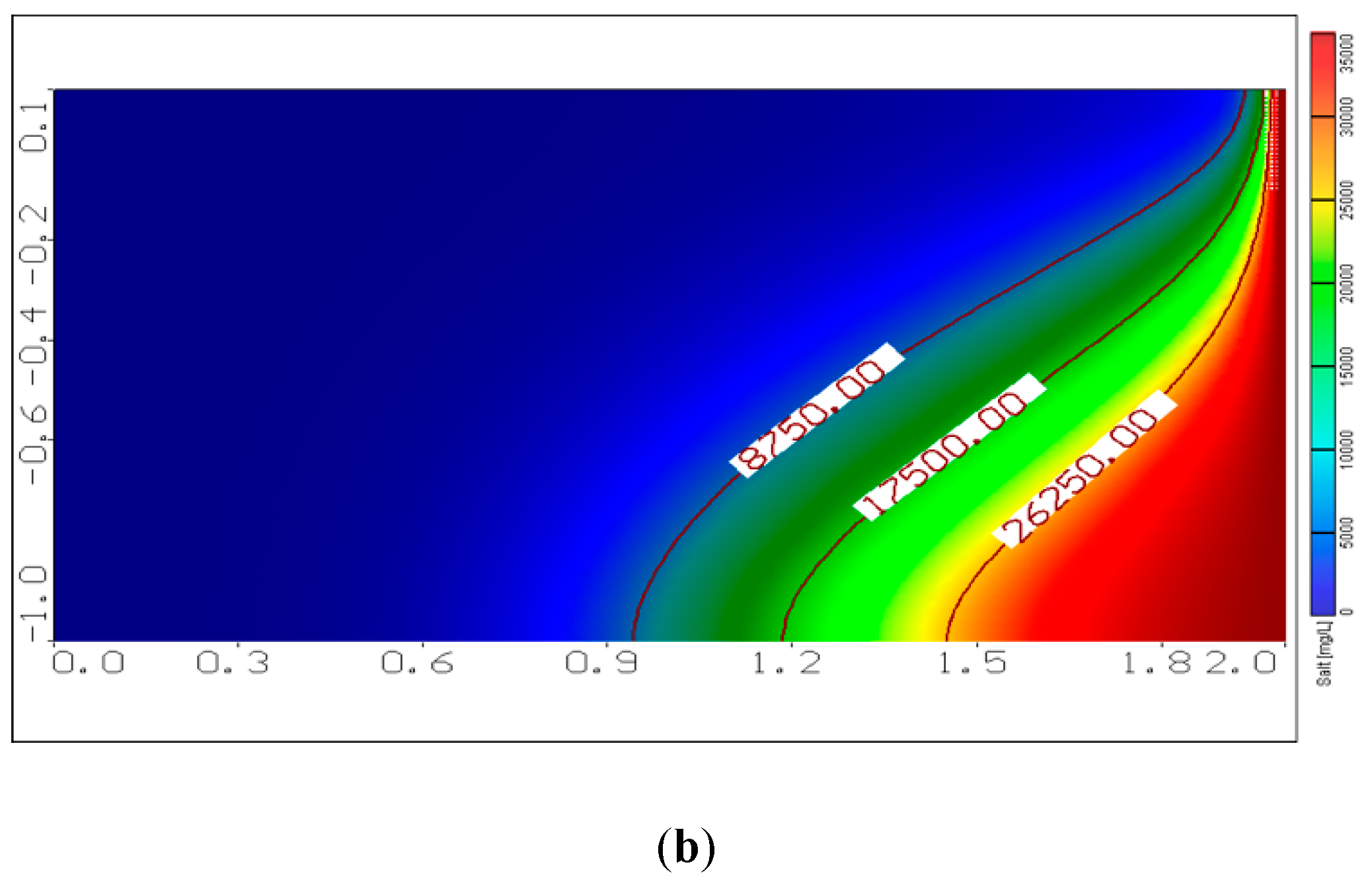
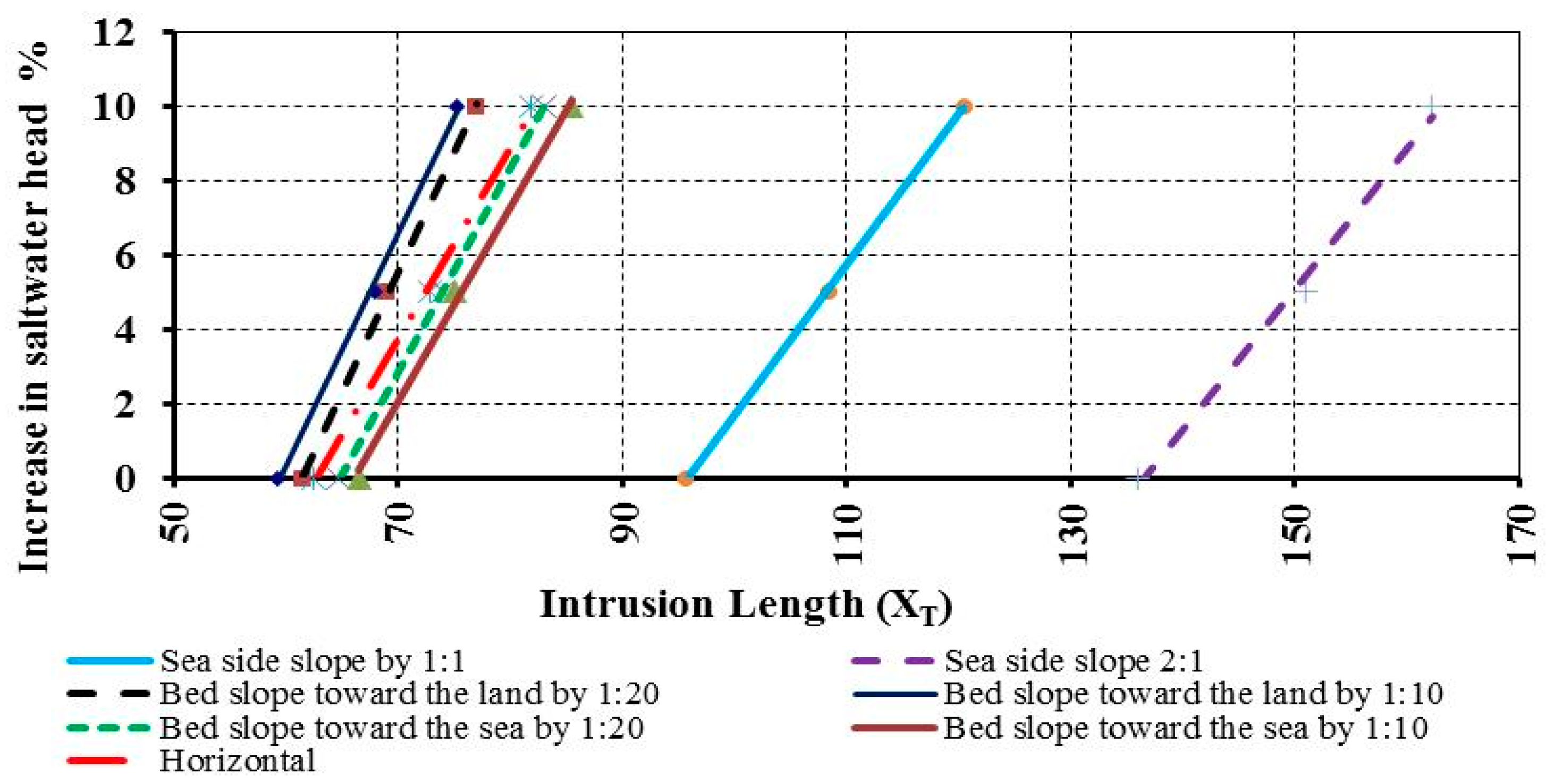
3.1. Effect of Changing Seaside Slope on SWI
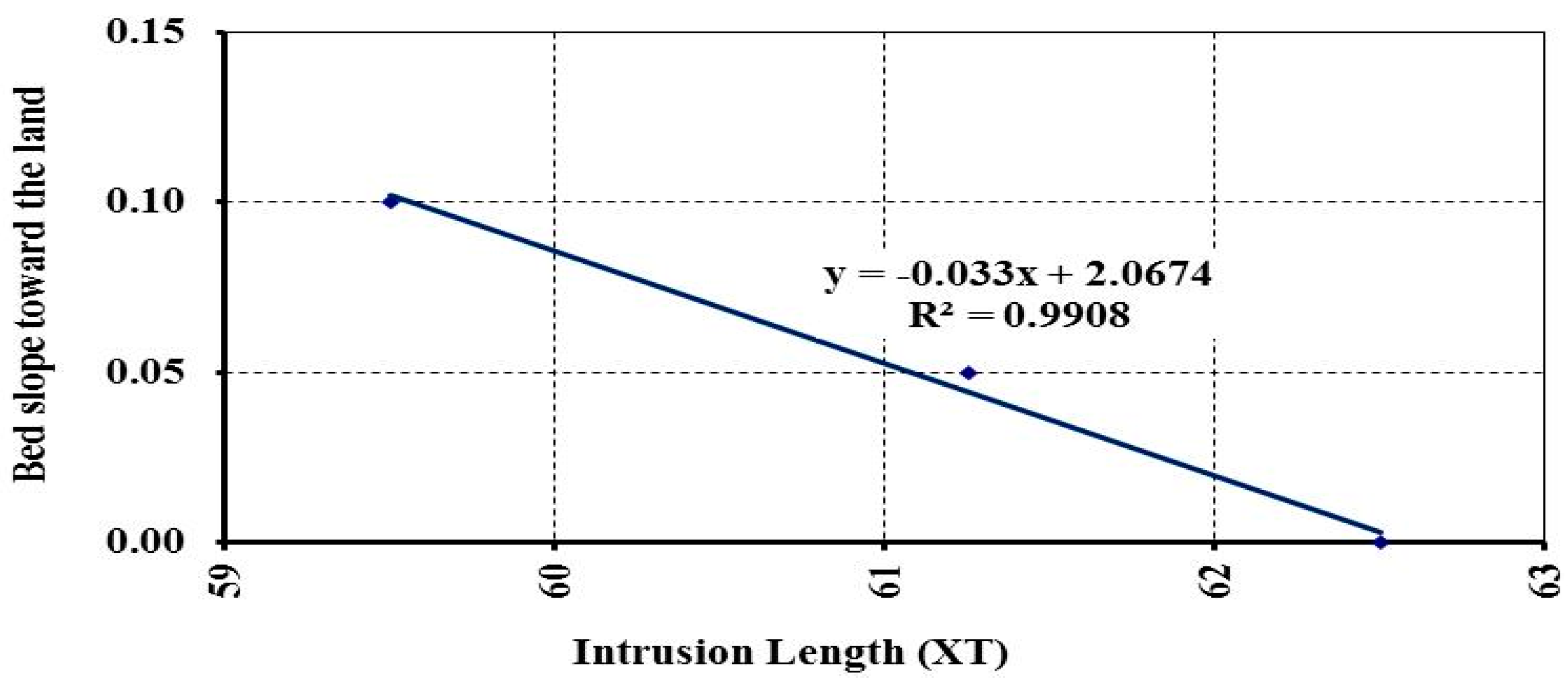
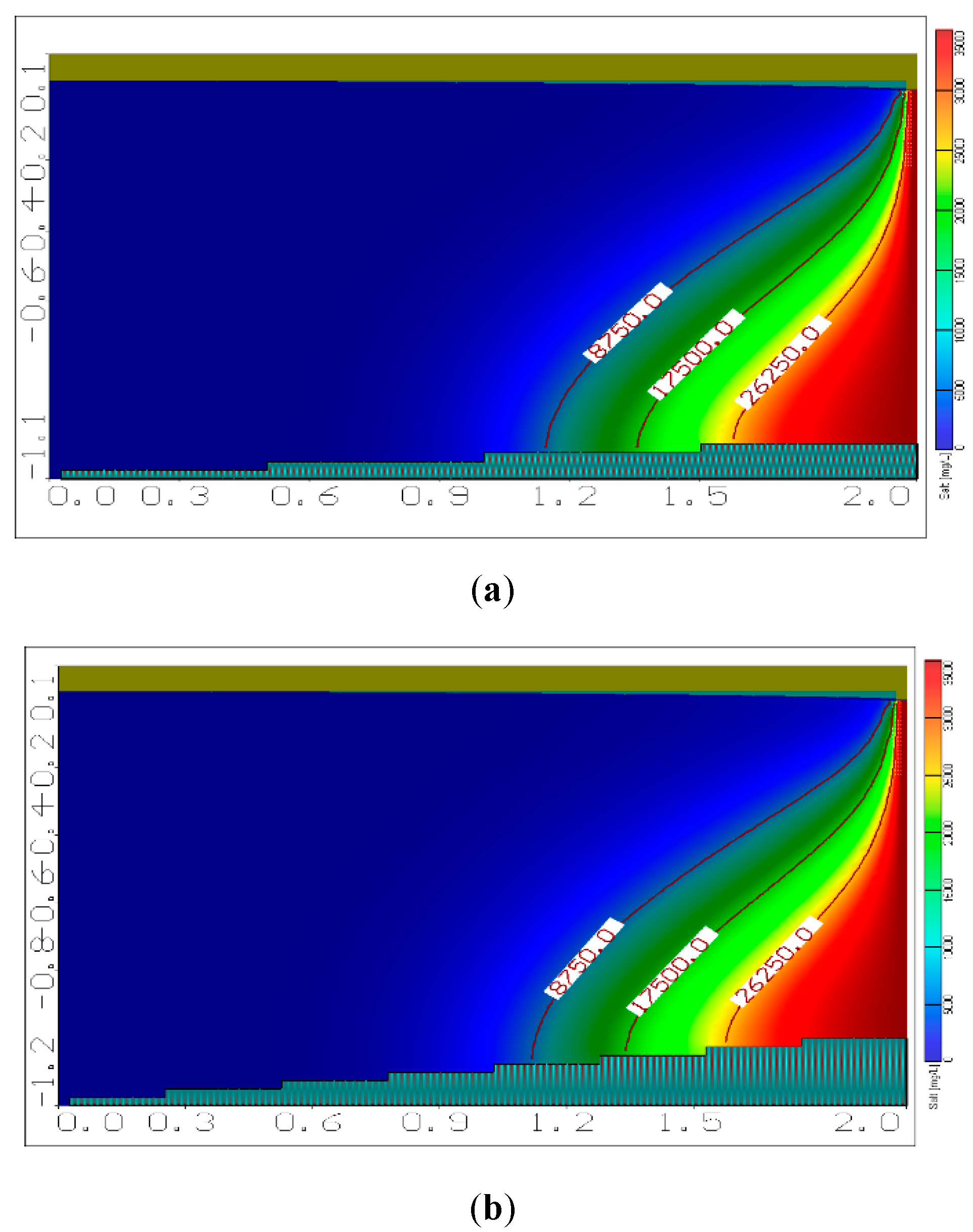
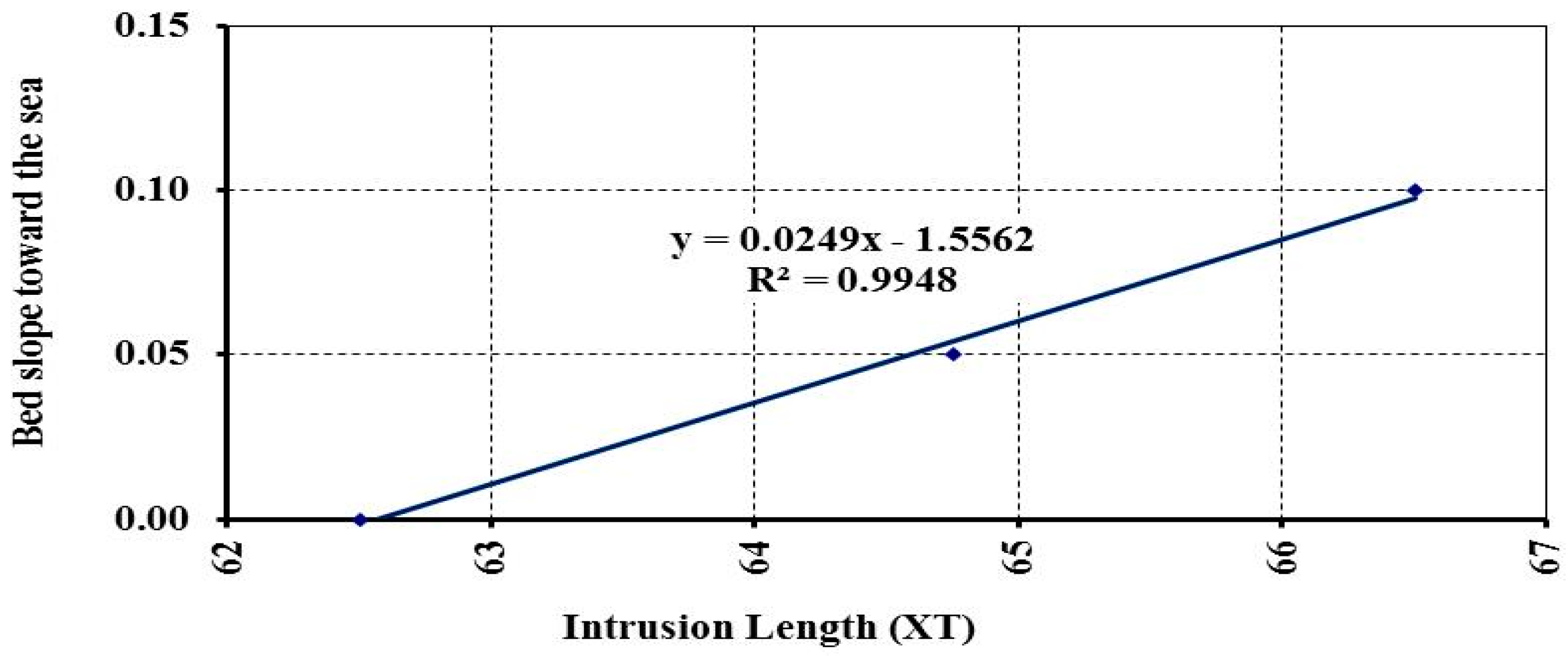
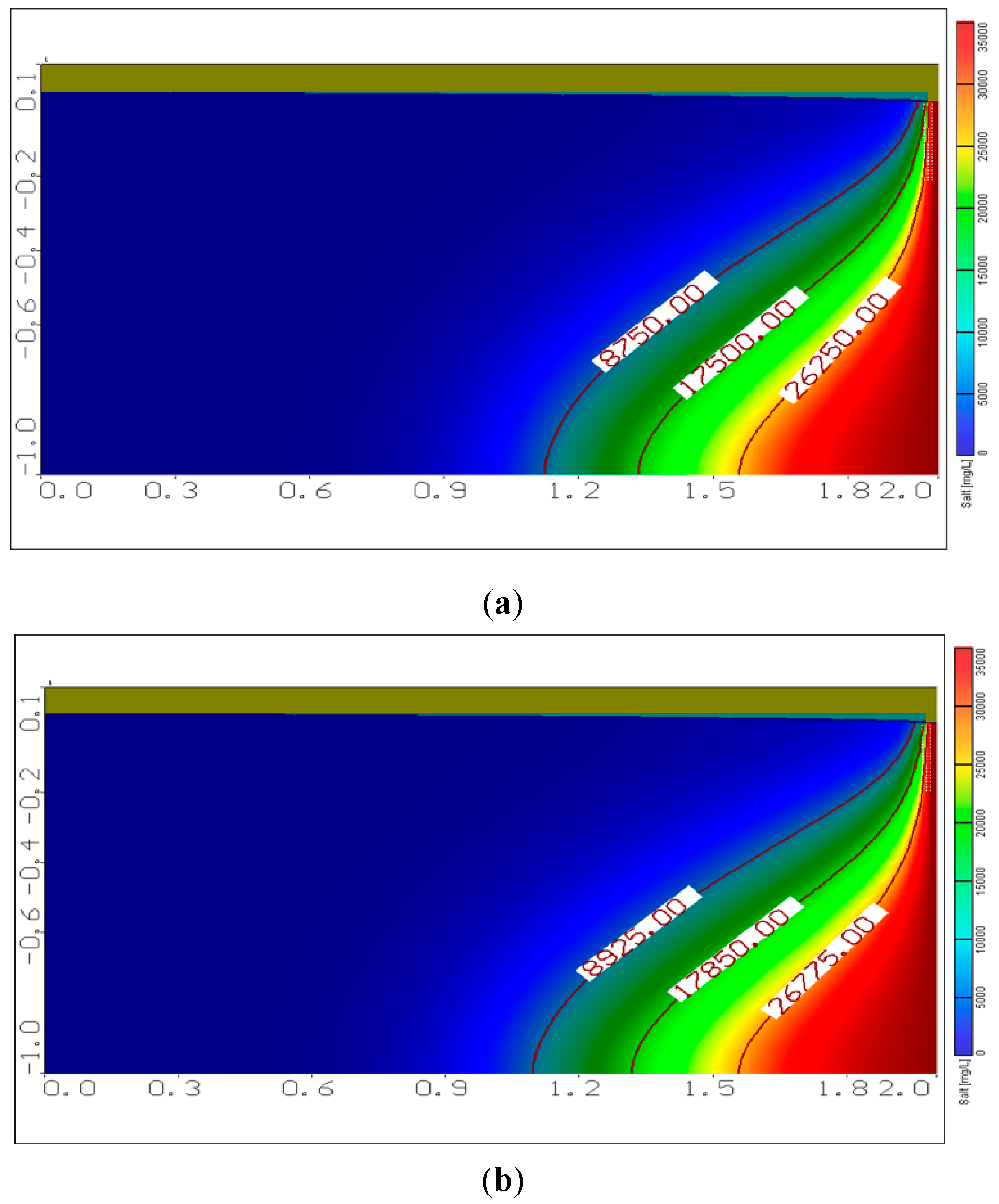
3.2. Effect of Changing Aquifer Bed Slope on SWI
3.3. Effect of Changing Sea Level on SWI
3.4. Effect of Reducing the Landside Recharge
3.5. Combined Effect of Increasing Sea Level and Decreasing Landside Recharge
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bear, J.; Cheng, A.H.; Sorek, S.; Quazar, D.; Herrera, I. Seawater Intrusion in Coastal Aquifers, Concepts, Methods and Practices; Kluwer Academic Publisher: Dordrecht, The Netherlands, 1999; ISBN 0-7923-5573-3. [Google Scholar]
- Sefelnasr, A.; Sherif, M.M. Impacts of seawater rise on seawater intrusion in the Nile Delta Aquifer, Egypt. Groundwater 2014, 52, 264–276. [Google Scholar] [CrossRef] [PubMed]
- Harman, C. The Effect of Basement on Heterogeneity on Saltwater Wedge—Aphysical and Numerical Modelling Approach; The University of Western Australia: Crawley, Australia, 2002. [Google Scholar]
- Abdelhamid, H.; Javadi, A.A.; Abd-Elaty, I.; Sherif, M.M. Simulation of seawater intrusion in the Nile Delta aquifer under the condition of climate change. Hydrol. Res. 2016, 47, 1198–1210. [Google Scholar] [CrossRef]
- Ghyben, B.W. Nota in Verband Met de Voorgenomen put Boring Nabij Amsterdam. Tydscrift Van Het Koninkyky Institute Van Ingenieurs 1889, 21, 8–22. [Google Scholar]
- Herzberg, A. Die wasserversorgung Einnger Nordsecbader. J. Gasbeleucht. U. Wasservesurg 1901, 815–819. [Google Scholar]
- Strack, O.D.L. Single-potential Solution for Regional Interface Problems in Coastal Aquifers. Water Resour. Res. 1976, 12, 1165–1174. [Google Scholar] [CrossRef]
- Henry, H.R. Saltwater intrusion into coastal aquifers. Int. Assoc. Sci. Hydrol. Publ. 1960, 2, 478–487. [Google Scholar]
- Taylor, A.; Hulme, P.; Hughes, A.; Foot, S. Benchmarking of Variable Density Model Codes against Henry’s Problem. In Proceedings of the 1st International Conference and Workshop on Saltwater Intrusion and Coastal Aquifers, Monitoring, Modelling, and Management, Essaouira, Morocco, 23–25 April 2001. [Google Scholar]
- Kacimov, A.R.; Obnosove, Y.V.; Sherif, M.M.; Perret, J.S. Analytical Solutions to a Sea-water Intrusion Problem with a Fresh Water Zone Tapering to a Triple Point. J. Eng. Math. 2006, 54, 197–210. [Google Scholar] [CrossRef]
- Hamza, K.I. Numerical Analysis of Saltwater Upconing below a Pumping Well. In Proceedings of the 18th Salt Water Intrusion Meeting, Cartagena, Spain, 31 May–3 June 2004. [Google Scholar]
- Sherif, M.M.; Sefelnasr, A.; Javadi, A. Areal Simulation of Seawater Intrusion In The Nile Delta Aquifer. ASCE World Environ. Water Resour. Congr. 2012. [Google Scholar] [CrossRef]
- Sherif, M.M.; Singh, V.P. Effect of groundwater pumping on seawater intrusion in coastal aquifers. J. Agric. Mar. Sci. 2002, 7, 61–67. [Google Scholar] [CrossRef]
- Sherif, M.M.; Singh, V.P. Effect of Climate Changes on Seawater Intrusion in Coastal Aquifers. Hydrol. Process. 1999, 13, 1277–1287. [Google Scholar] [CrossRef]
- Lakfifi, L.; Larabi, A.; Bzioui, M.; Benbiba, M.; Lahmouri, A. Regional Model for Seawater Intrusion in the Chaouia Coastal Aquifer (Morocco). In Proceedings of the 18th Saltwater Intrusion Meeting, Cartagena, Spain, 31 May–3 June 2004. [Google Scholar]
- Goswami, R.R.; Clement, T.P. Laboratory-scale investigation of saltwater intrusion dynamics. Water Resour. Res. 2007, 43, W04418. [Google Scholar] [CrossRef]
- Freydoon, V.; Abolghasemi, H. Investigation of Sea and Groundwater Level Changes on Seawater Intrusion in an unconfined Coastal Aquifer. J. Middle East Appl. Sci. Technol. 2014, 20, 684–688. [Google Scholar]
- Abdelaty, I.; Abd-Elhamid, H.F.; Javadi, A. Numerical analysis of the effects of changing hydraulic parameters on saltwater intrusion in coastal aquifers. Eng. Comput. J. 2016, 33, 2546–2564. [Google Scholar] [CrossRef]
- Ketabchi, H.; Mahmoodzadeh, D.; Ataie-Ashtiani, B.; Simmons, C.T. Sea-level rise impacts on seawater intrusion in coastal aquifers: Review and integration. J. Hydrol. 2016, 535, 235–255. [Google Scholar] [CrossRef]
- Thomas, A.; Eldho, T.I.; Rastogi, A.K. Simulation of Seawater Intrusion in Coastal Confined Aquifer Using a Point Collocation Method Based Mesh Free Model. J. Water Resour. Prot. 2016, 8, 534–549. [Google Scholar] [CrossRef]
- Fahs, M.; Koohbor, B.; Belfort, B.; Ataie-Ashtiani, B.; Simmons, C.T.; Younes, A.; Ackerer, P. A Generalized Semi-Analytical Solution for the Dispersive Henry Problem: Effect of Stratification and Anisotropy on Seawater Intrusion. Water 2018, 10, 230. [Google Scholar] [CrossRef]
- Guo, W.; Langevin, C.D. User’s Guide to SEAWAT: A Computer Program for Simulation of Three-Dimensional Variable-Density Groundwater Flow. In Techniques of Water-Resources Investigations 06-A7; USGS: Reston, VA, USA, 2002; p. 77. [Google Scholar]
- Lee, C.H.; Cheng, R.T. Seawater Encroachment in Coastal Aquifer. Water Resour. Res. 1974, 10, 1039–1043. [Google Scholar] [CrossRef]
- Segol, G.; Pinder, G.F.; Gray, W.G. A Galerkin Finite Element Technique for Calculating the Transition Position of the Saltwater Front. Water Resour. Res. 1975, 11, 343–347. [Google Scholar] [CrossRef]
- Huyakorn, P.S.; Anderson, P.F.; Mercer, J.W.; White, H.O. Saltwater Intrusion in Aquifers Development and Testing of a Three-dimensional Finite Element Model. Water Resour. Res. 1987, 23, 293–312. [Google Scholar] [CrossRef]
- Frind, E.O. Simulation of long-term transient density-dependent transport in groundwater. Water Resour. Res. 1982, 5, 73–88. [Google Scholar] [CrossRef]
- Cheng, J.; Strobl, R.O.; Yeh, G.; Lin, H.; Choi, W. Modelling of 2D Density-Dependent Flow and Transport in the Subsurface. J. Hydrol. Eng. 1998, 3, 248–257. [Google Scholar] [CrossRef]
- Rastogi, A.K.; Choi, G.W.; Ukarande, S.K. Diffused interface model to prevent ingress of seawater in multi-layer coastal aquifers. J. Spat. Hydrol. 2004, 4, 1–31. [Google Scholar]
- Simpson, M.J.; Clement, T.B. Improving the worthiness of the Henry problem as A benchmark for Density-Dependent Groundwater Flow Models. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Church, J.A.; Clark, P.U. Sea Level Change, In Climate Change 2013: The Physical Science Basis, Contribution of Working Group 1 to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2013. [Google Scholar]
- U.S. Global Change Research Program. Climate Science Special Report: Fourth National Climate Assessment; Wuebbles, D.J., Fahey, D.W., Hibbard, K.A., Dokken, D.J., Stewart, B.C., Maycock, T.K., Eds.; USGCRP: Washington, DC, USA, 2017; Volume 1, p. 470.
| Parameter | Values | Units |
|---|---|---|
| Porosity (n) | 0.30 | Dimensionless |
| Inland Freshwater Flux (qin) | 5.702 | (m3/day/m) |
| Saltwater head (hs) | 1.00 | (m) |
| Freshwater density (ρf) | 1000 | (kg/m3) |
| Saltwater density (ρs) | 1025 | (kg/m3) |
| Saltwater concentration (C) | 35,000 | (mg/L) |
| Hydraulic conductivity (k) (Isotropic) | 864 | (m/day) |
| Specific Storage | 0 | (1/m) |
| Longitudinal dispersivity (αL) | 0 | (m) |
| Transverse dispersivity (αT) | 0 | (m) |
| Molecular diffusion coefficient(D*) | 1.6295 | (m2/day) |
| Case | Slope | Base Case | SLR | Reduction in Recharge | Combination | |||
|---|---|---|---|---|---|---|---|---|
| 5% | 10% | 5% | 10% | 5% | 10% | |||
| Slandered Henry (Horizontal slope) | 0 | 62.50 | 70.50 | 76 | 66.70 | 68.15 | 72.90 | 81.50 |
| Seaside bed slope | 1:1 | 95.75 | 106 | 115.25 | 98.50 | 100.75 | 108.50 | 120.50 |
| 2:1 | 136 | 149 | 158.25 | 138.50 | 140.75 | 151 | 162.25 | |
| Bed slope toward the land | 1:20 | 61.25 | 66.60 | 72.25 | 63 | 65.25 | 69 | 77 |
| 1:10 | 59.50 | 65.50 | 71 | 61.50 | 63.75 | 68 | 75.25 | |
| Bed slope toward the sea | 1:20 | 64.75 | 71.50 | 77 | 67 | 69.75 | 74 | 83 |
| 1:10 | 66.50 | 72.25 | 78.75 | 68.75 | 71.5 | 75 | 85.50 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abd-Elhamid, H.F.; Abd-Elaty, I.; Sherif, M.M. Effects of Aquifer Bed Slope and Sea Level on Saltwater Intrusion in Coastal Aquifers. Hydrology 2020, 7, 5. https://doi.org/10.3390/hydrology7010005
Abd-Elhamid HF, Abd-Elaty I, Sherif MM. Effects of Aquifer Bed Slope and Sea Level on Saltwater Intrusion in Coastal Aquifers. Hydrology. 2020; 7(1):5. https://doi.org/10.3390/hydrology7010005
Chicago/Turabian StyleAbd-Elhamid, Hany F., Ismail Abd-Elaty, and Mohsen M. Sherif. 2020. "Effects of Aquifer Bed Slope and Sea Level on Saltwater Intrusion in Coastal Aquifers" Hydrology 7, no. 1: 5. https://doi.org/10.3390/hydrology7010005
APA StyleAbd-Elhamid, H. F., Abd-Elaty, I., & Sherif, M. M. (2020). Effects of Aquifer Bed Slope and Sea Level on Saltwater Intrusion in Coastal Aquifers. Hydrology, 7(1), 5. https://doi.org/10.3390/hydrology7010005






