Lake Volume Data Analyses: A Deep Look into the Shrinking and Expansion Patterns of Lakes Azuei and Enriquillo, Hispaniola
Abstract
1. Introduction
2. Materials and Methods
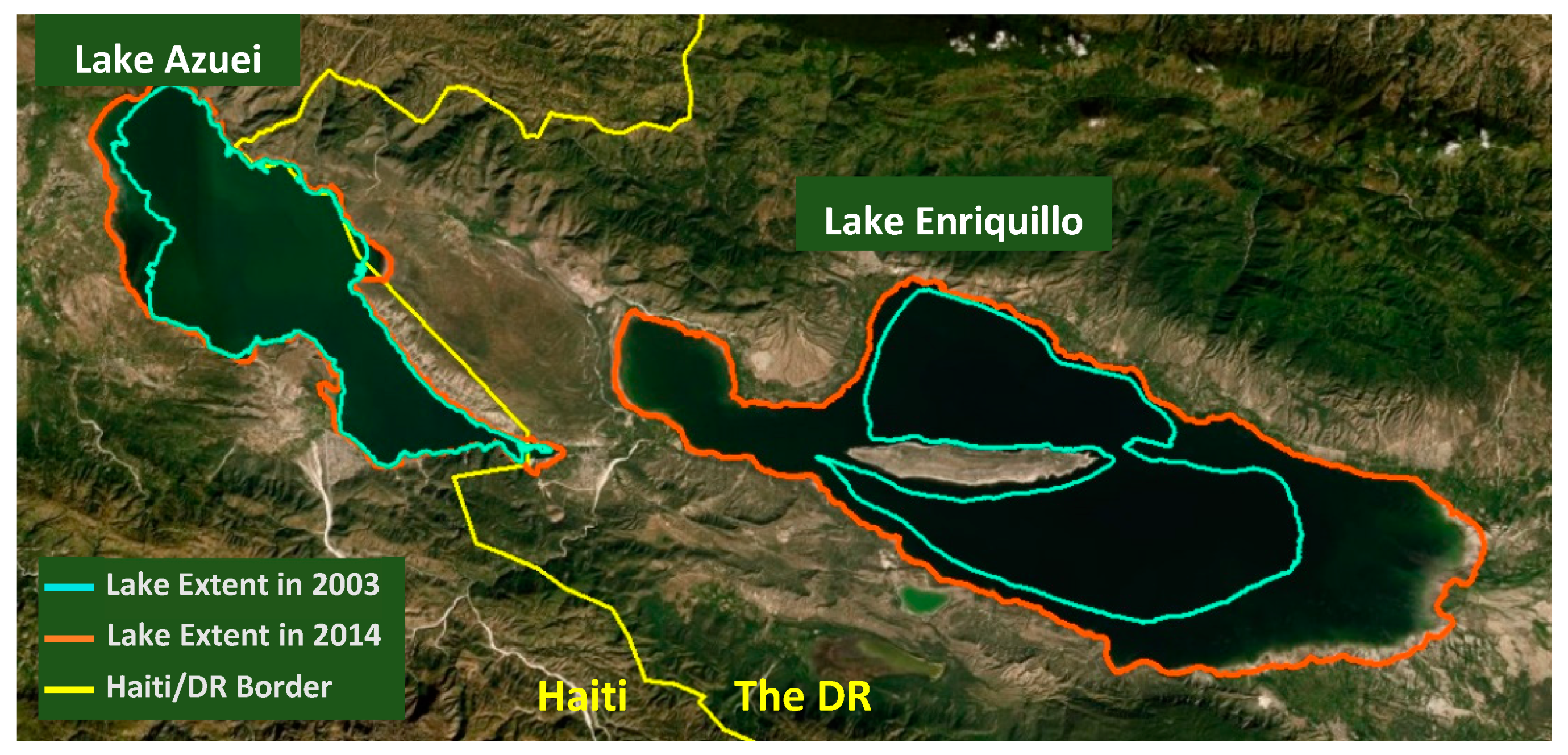
2.1. Data Acquisition and Observational Volume Time Series
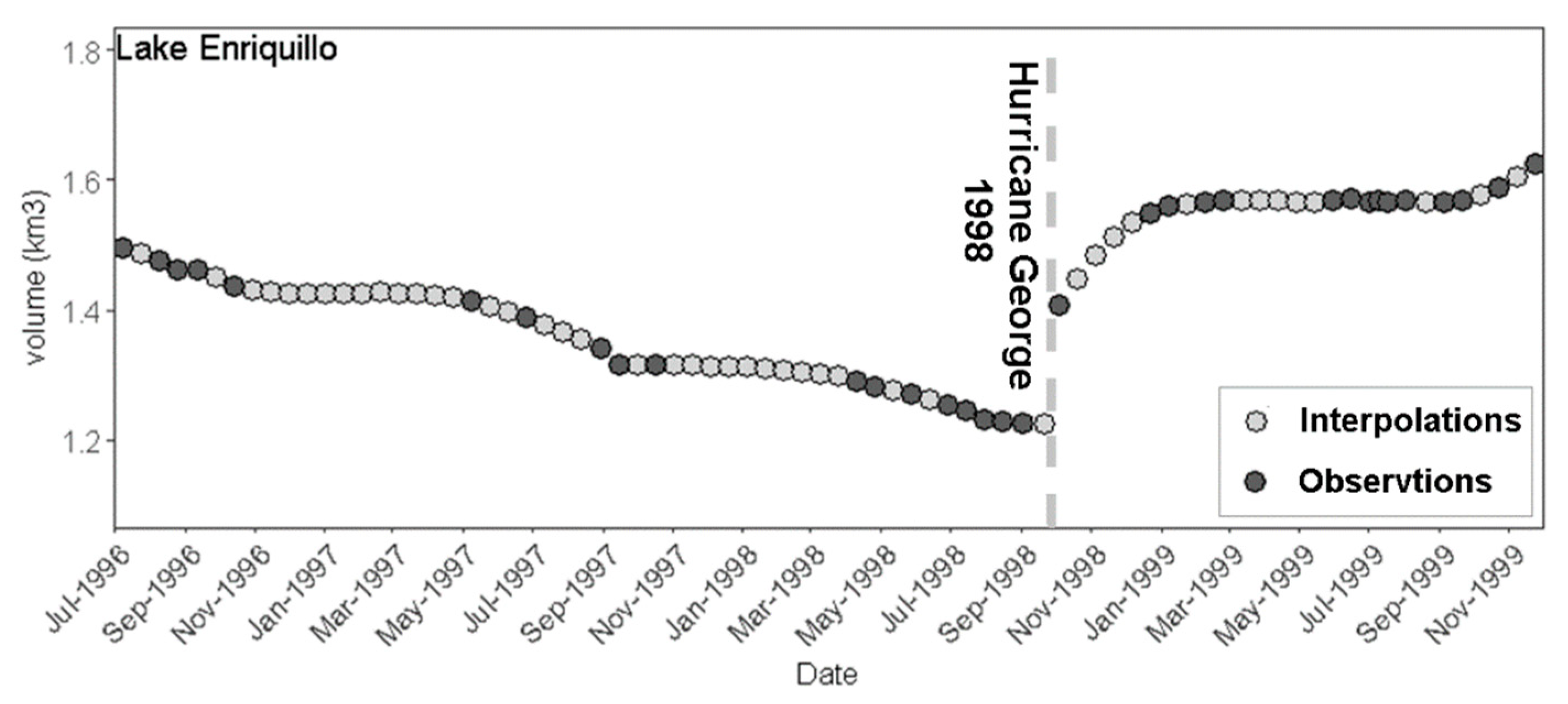
2.2. Missing Data Imputation
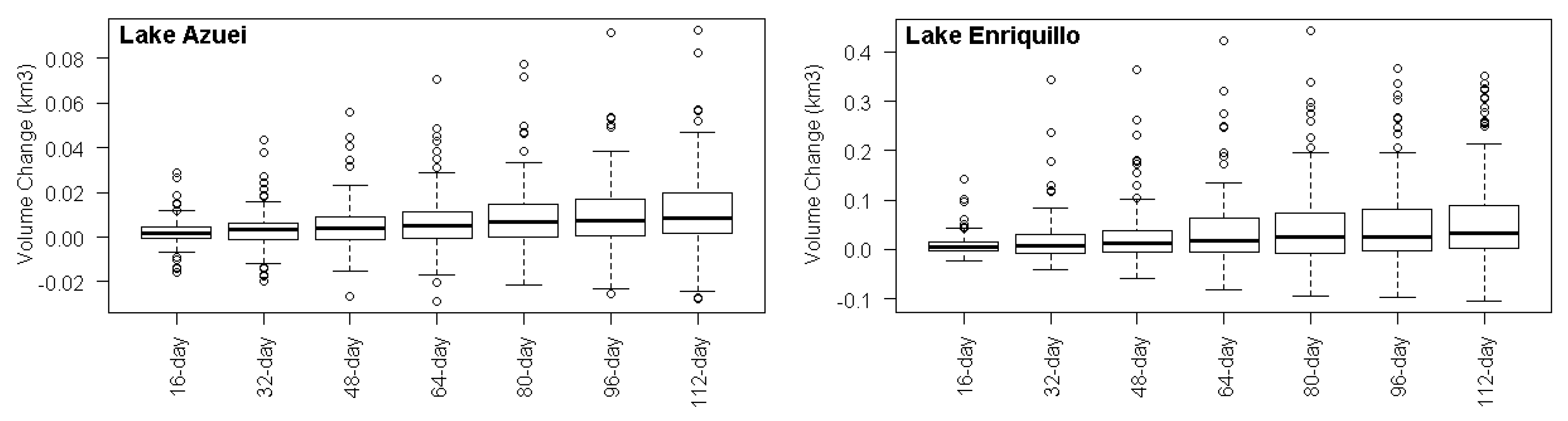
2.2.1. Alternative Observational ∆V Datasets and the Characteristics of Sudden Changes
2.2.2. Evenly Spaced Time Series Construction
2.3. Time Series Analysis
3. Results
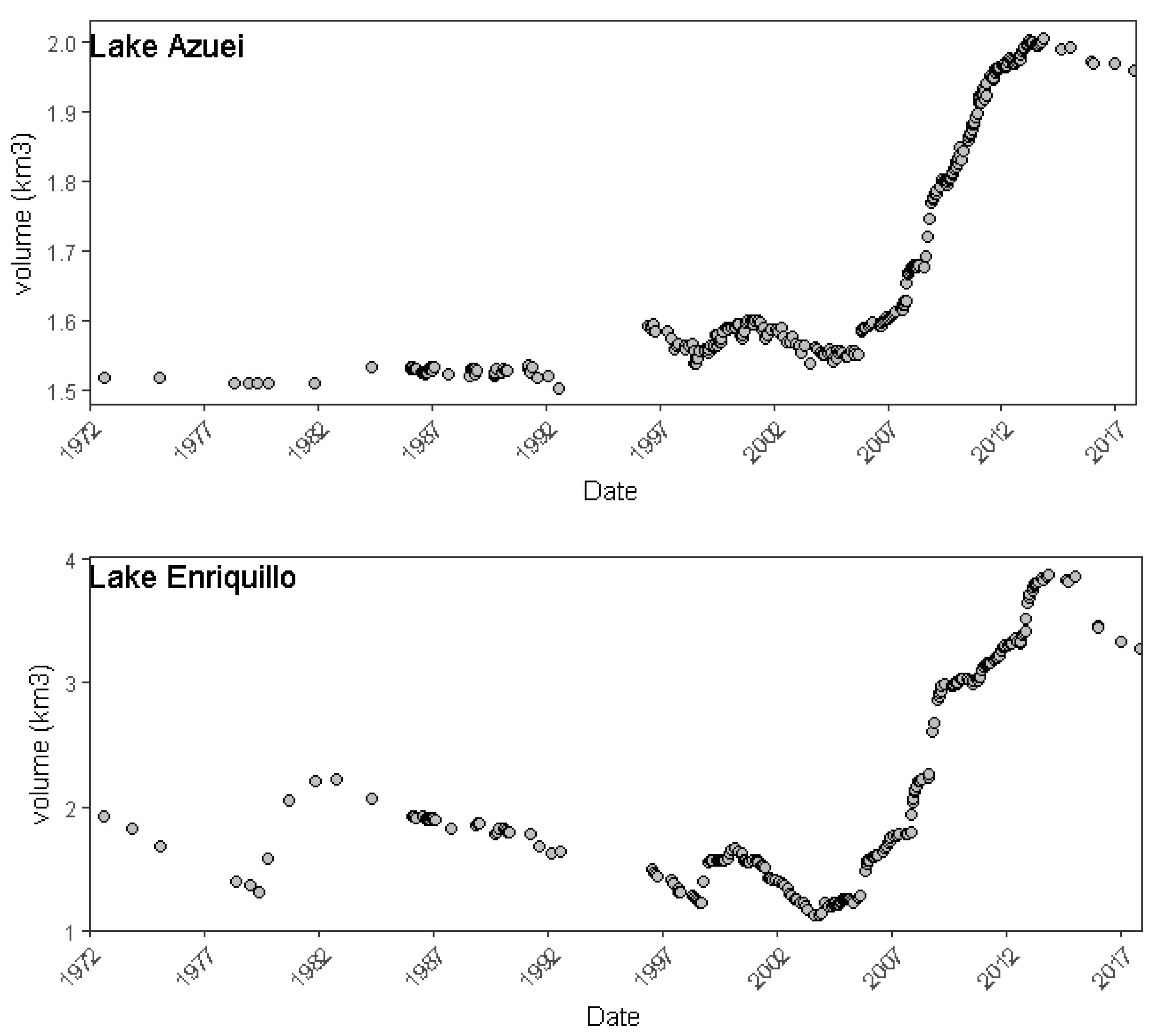
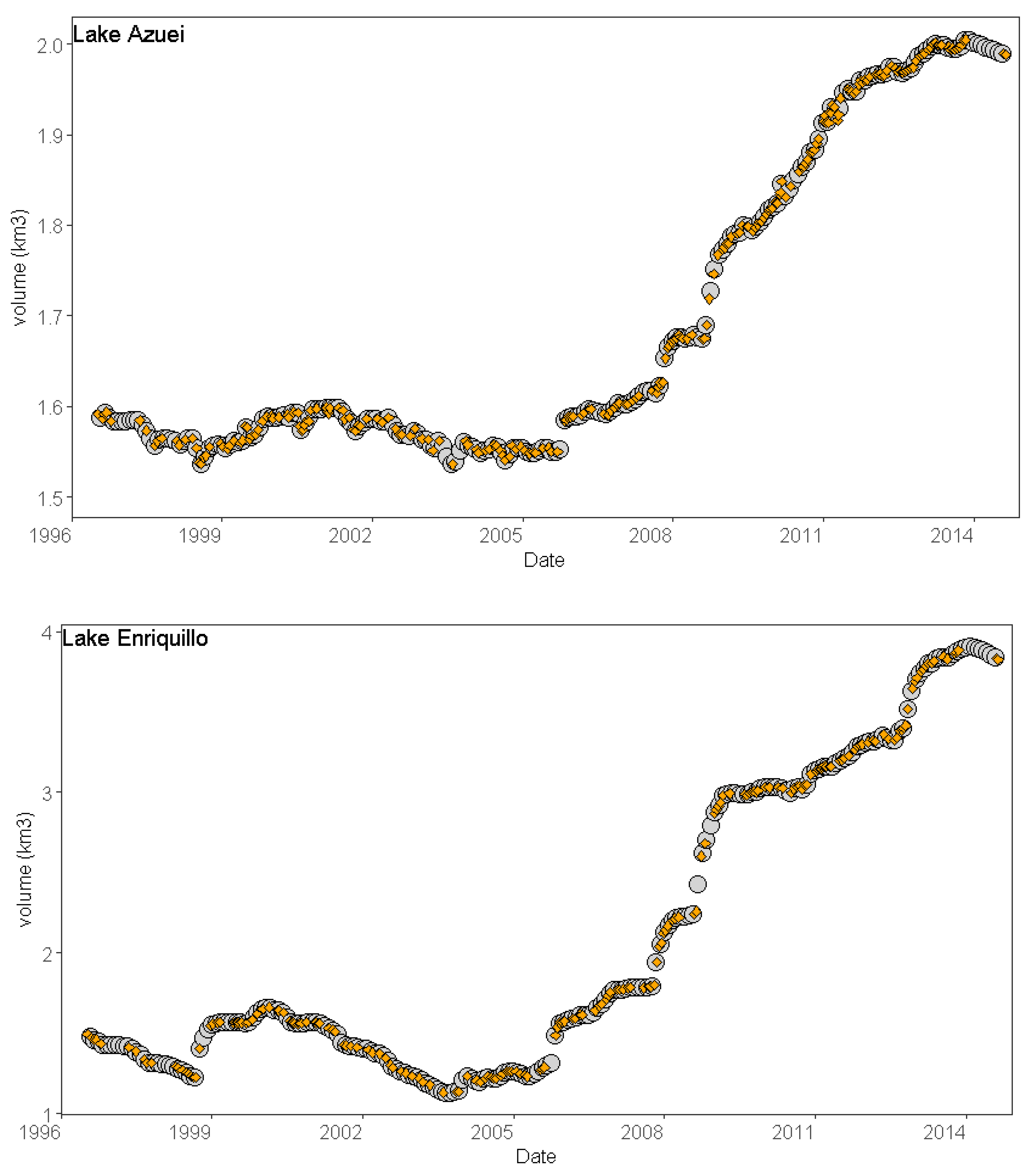
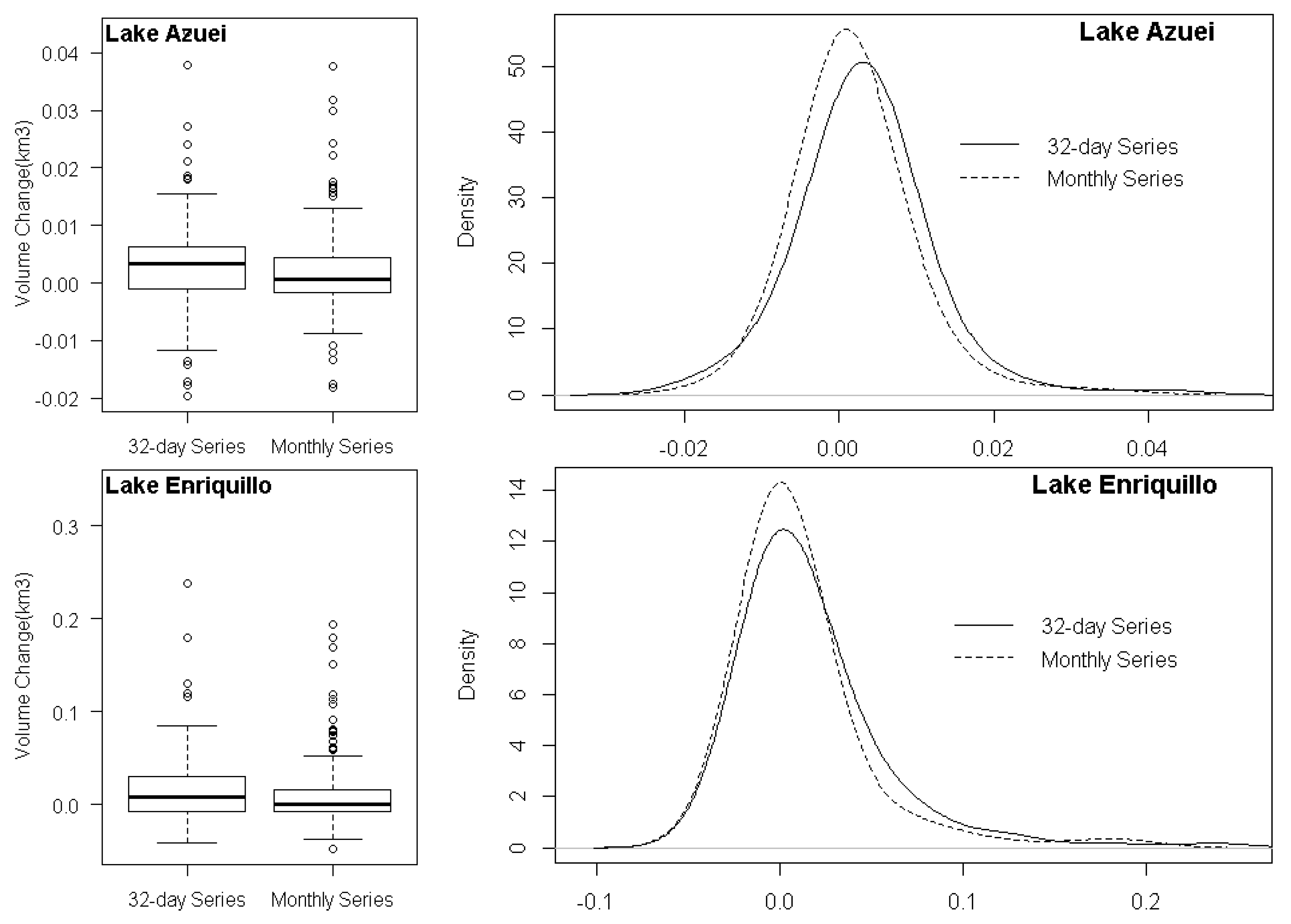
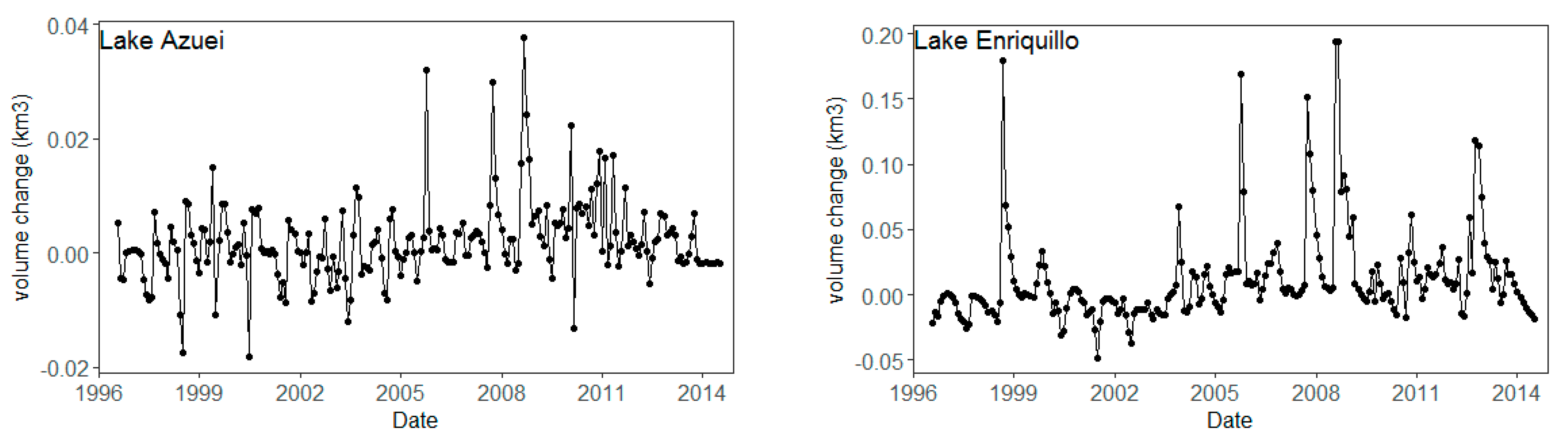
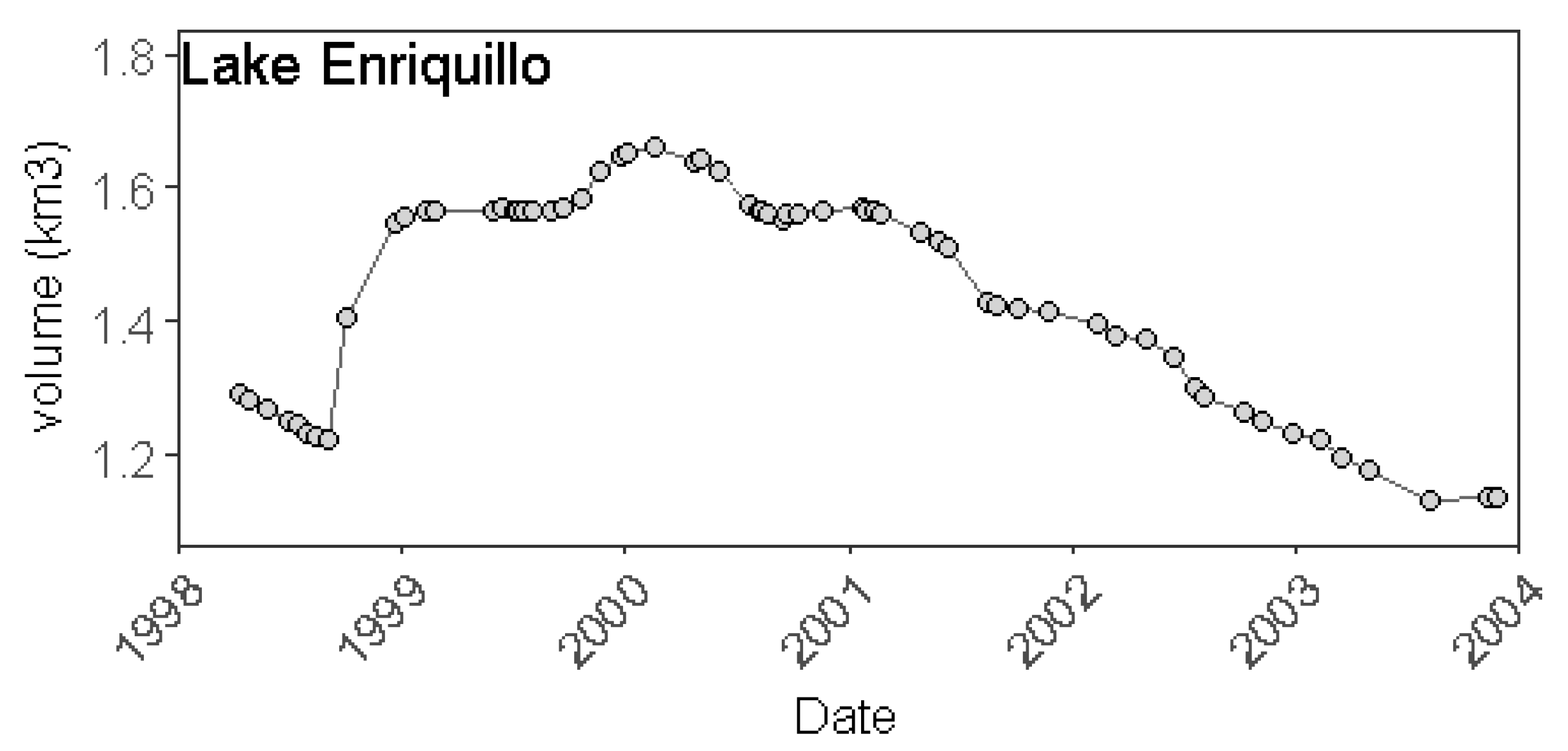
3.1. Monthly Imputed Volume and Volume Change Time Series
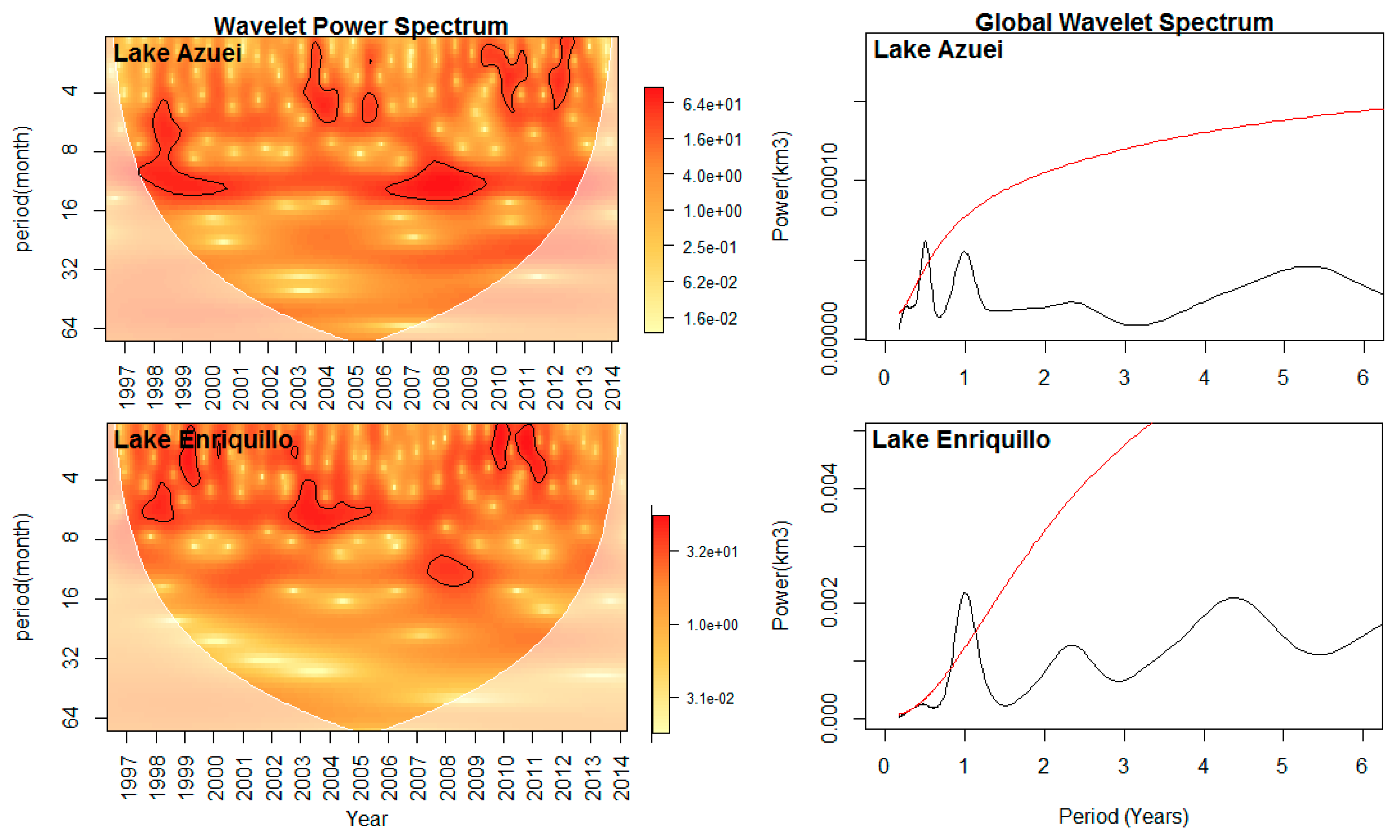
3.2. Periodicity Detection: Wavelet Transform
3.3. Change Point Detection: Pettitt Test
3.4. Trend Test: Mann-Kendall Test and Linear Regression Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sheller, M.; León, Y.M. Uneven socio-ecologies of Hispaniola: Asymmetric capabilities for climate adaptation in Haiti and the Dominican Republic. Geoforum 2016, 73, 32–46. [Google Scholar] [CrossRef]
- Kushner, J. The Relentless Rise of Two Caribbean Lakes Baffles Scientists. 2016. Available online: https://www.nationalgeographic.com/news/2016/03/160303-haiti-dominican-republic-lakes/ (accessed on 3 March 2016).
- Aldenberg, T.; Janse, J.H.; Kramer, P.R.G. Fitting the dynamic model PCLake to a multi-lake survey through Bayesian Statistics. Ecol. Model. 1995, 78, 83–99. [Google Scholar] [CrossRef]
- Kieniewicz, J.M.; Smith, J.R. Paleoenvironmental reconstruction and water balance of a mid-Pleistocene pluvial lake, Dakhleh Oasis, Egypt. Bull. Geol. Soc. Am. 2009, 121, 1154–1171. [Google Scholar] [CrossRef]
- Collins, G.S.; Artemieva, N.; Wünnemann, K.; Bland, P.A.; Reimold, W.U.; Koeberl, C. Evidence that Lake Cheko is not an impact crater. Terra Nov. 2008, 20, 165–168. [Google Scholar] [CrossRef]
- Sivakumar, B. Chaos in Hydrology: Bridging Determinism and Stochasticity, 1st ed.; Springer: Dordrecht, The Netherlands, 2017; pp. 29–62. [Google Scholar]
- Medwedeff, W.G.; Roe, G.H. Trends and variability in the global dataset of glacier mass balance. Clim. Dyn. 2017, 48, 3085–3097. [Google Scholar] [CrossRef]
- Barbosa, S.M.; Donner, R.V. Long-term changes in the seasonality of Baltic sea level. Tellus A Dyn. Meteorol. Oceanogr. 2016, 68, 30540. [Google Scholar] [CrossRef]
- Khelifa, S.; Gourine, B.; Rami, A.; Taibi, H. Assessment of nonlinear trends and seasonal variations in global sea level using singular spectrum analysis and wavelet multiresolution analysis. Arab. J. Geosci. 2016, 9, 1–8. [Google Scholar] [CrossRef]
- Moon, Y.I.; Lall, U. Atmospheric flow indices and interannual Great Salt Lake variability. J. Hydrol. Eng. 1995, 1, 55–62. [Google Scholar] [CrossRef]
- Moon, Y.I.; Lall, U.; Kwon, H.H. Non-parametric short-term forecasts of the Great Salt Lake using atmospheric indices. Int. J. Climatol. 2007, 4, 1549–1555. [Google Scholar] [CrossRef]
- Moknatian, M.; Piasecki, M. Observational Time Series for Lakes Azuei and Enriquillo: Surface Area, Volume, and Elevation; CUNY Academic Works: New York, NY, USA, 2019. [Google Scholar]
- Moknatian, M.; Piasecki, M.; Gonzalez, J. Development of geospatial and temporal characteristics for Hispaniola’s Lake Azuei and Enriquillo using Landsat imagery. Remote Sens. 2017, 9, 510. [Google Scholar] [CrossRef]
- Piasecki, M.; Moknatian, M.; Moshary, F.; Cleto, J.; Leon, Y.; Gonzalez, J.; Comarazamy, D. Bathymetric Survey for Lakes Azuei and Enriquillo, Hispaniola; CUNY Academic Works: New York, NY, USA, 2016. [Google Scholar]
- Piasecki, M.; Moknatian, M. Bathymetry Data for Lakes Azuei and Enriquillo; CUNY Academic Works: New York, NY, USA, 2018. [Google Scholar]
- Moknatian, M.; Piasecki, M.; Moshary, F.; Gonzalez, J. Development of digital bathymetry maps for Lakes Azuei and Enriquillo using sonar and remote sensing techniques. Trans. Gis 2019, 23, 841–859. [Google Scholar] [CrossRef]
- Teegavarapu, R.S.V.; Chandramouli, V. Improved weighting methods, deterministic and stochastic data-driven models for estimation of missing precipitation records. J. Hydrol. 2005, 312, 191–206. [Google Scholar] [CrossRef]
- Teegavarapu, R.S.V. Statistical corrections of spatially interpolated missing precipitation data estimates. Hydrol. Process. 2014, 28, 3789–3808. [Google Scholar] [CrossRef]
- Junninen, H.; Niska, H.; Tuppurainen, K.; Ruuskanen, J.; Kolehmainen, M. Methods for imputation of missing values in air quality data sets. Atmos. Environ. 2004, 38, 2895–2907. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
- Shen, H.; Li, X.; Cheng, Q.; Zeng, C.; Yang, G.; Li, H.; Zhang, L. Missing Information Reconstruction of Remote Sensing Data: A Technical Review. IEEE Geosci. Remote Sens. Mag. 2015, 3, 61–85. [Google Scholar] [CrossRef]
- Simolo, C.; Brunetti, M.; Maugeri, M.; Nanni, T. Improving estimation of missing values in daily precipitation series by a probability density function-preserving approach. Int. J. Climatol. 2010, 30, 1564–1576. [Google Scholar] [CrossRef]
- Pappas, C.; Papalexiou, S.M.; Koutsoyiannis, D. A quick gap-filling of missing hydrometeorological data. J. Geophys. Res. Atmos. 2014, 119, 9290–9300. [Google Scholar] [CrossRef]
- Elshorbagy, A.; Simonovic, S.P.; Panu, U.S. Estimation of missing streamflow data using principles of chaos theory. J. Hydrol. 2002, 255, 123–133. [Google Scholar] [CrossRef]
- Rubin, D.B. Inference and missing data. Biometrika 1976, 63, 581–592. [Google Scholar] [CrossRef]
- Moritz, S.; Bartz-Beielstein, T. imputeTS: Time series missing value imputation in R. R J. 2017, 9, 207–218. [Google Scholar] [CrossRef]
- Moritz, S.; Sardá, A.; Bartz-Beielstein, T.; Zaefferer, M.; Stork, J. Comparison of Different Methods for Univariate Time Series Imputation in R. arXiv 2015, arXiv:1510.03924. [Google Scholar]
- Barnett, V.; Lewis, T. Outliers in Statistical Data, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1980; p. 2434. [Google Scholar]
- González-Rouco, J.F.; Jiménez, J.L.; Quesada, V.; Valero, F. Quality control and homogeneity of precipitation data in the Southwest of Europe. J. Clim. 2001, 14, 964–978. [Google Scholar] [CrossRef]
- Chen, S.; Li, Y.; Kim, J.; Kim, S.W. Bayesian change point analysis for extreme daily precipitation. Int. J. Climatol. 2017, 37, 3123–3137. [Google Scholar] [CrossRef]
- Afshari, S.; Fekete, B.M.; Dingman, S.L.; Devineni, N.; Bjerklie, D.M.; Khanbilvardi, R.M. Statistical filtering of river survey and streamflow data for improving At-A-Station hydraulic geometry relations. J. Hydrol. 2017, 547, 443–454. [Google Scholar] [CrossRef]
- Langbein, W.B. Salinity and Hydrology of Closed Lakes; U.S. Geological Survey Professional Paper 412; U.S. Goverment Printing Office: Washington, DC, USA, 1961.
- Street-Perrott, F.A.; Roberts, N. Fluctuations in closed-basin lakes as an indicator of past atmospheric circulation patterns. Var. Glob. Water Budg. 1983, 331–345. [Google Scholar]
- Mason, I.M.; Guzkowska, M.A.J.; Rapley, C.G.; Street-Perrott, F.A. The response of lake levels and areas to climatic change. Clim. Chang. 1994, 27, 161–197. [Google Scholar] [CrossRef]
- Addison, P.S. The Illustrated Wavelet Transform. Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance, 2nd ed.; CRC Press, Taylor & Francis: Boca Raton, FL, USA, 2002; pp. 6–64. [Google Scholar]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Elsanabary, M.H.; Gan, T.Y. Wavelet analysis of seasonal rainfall variability of the Upper Blue Nile Basin, its teleconnection to global sea Surface temperature, and its forecasting by an artificial neural network. Mon. Weather Rev. 2014, 142, 1771–1791. [Google Scholar] [CrossRef]
- Morales-Pineda, M.; Cõzar, A.; Laiz, I.; Úbeda, B.; Gálvez, J.A. Daily, biweekly, and seasonal temporal scales of pCO2 variability in two stratified Mediterranean reservoirs. J. Geophys. Res. Biogeosci. 2014, 119, 509–520. [Google Scholar] [CrossRef]
- Yu, H.L.; Lin, Y.C. Analysis of space-time non-stationary patterns of rainfall-groundwater interactions by integrating empirical orthogonal function and cross wavelet transform methods. J. Hydrol. 2015, 525, 585–597. [Google Scholar] [CrossRef]
- Elsanabary, M.H.; Gan, T.Y.; Mwale, D. Application of wavelet empirical orthogonal function analysis to investigate the nonstationary character of Ethiopian rainfall and its teleconnection to nonstationary global sea surface temperature variations for 1900–1998. Int. J. Climatol. 2014, 34, 1798–1813. [Google Scholar] [CrossRef]
- Jiang, R.; Gan, T.Y.; Xie, J.; Wang, N. Spatiotemporal variability of Alberta’s seasonal precipitation, their teleconnection with large-scale climate anomalies and sea surface temperature. Int. J. Climatol. 2014, 34, 2899–2917. [Google Scholar] [CrossRef]
- Najibi, N.; Devineni, N.; Lu, M. Hydroclimate drivers and atmospheric teleconnections of long duration floods: An application to large reservoirs in the Missouri River Basin. Adv. Water Resour. 2017, 100, 153–167. [Google Scholar] [CrossRef]
- Cook, R.D. Assessment of local influence. J. R. Stat. Soc. 1986, 48, 133–169. [Google Scholar] [CrossRef]
- Jönsson, C.A.; Tarukoski, E. How Does an Appointed CEO Influence the Stock Price? A Multiple Regression Approach; KTH Royal Institute of Technology, School of Engineering Sciences: Stockholm, Sweden, 2017. [Google Scholar]
- Lawrance, A.J. Deletion influence and masking in regression. J. R. Stat. Soc. 1995, 58, 267–288. [Google Scholar] [CrossRef]
- Cazelles, B.; Cazelles, K.; Chavez, M. Wavelet analysis in ecology and epidemiology: Impact of statistical tests. J. R. Soc. Interface 2014, 11, 20130585. [Google Scholar] [CrossRef]
- Mallakpour, I.; Villarini, G. Investigating the relationship between the frequency of flooding over the central United States and large-scale climate. Adv. Water Resour. 2016, 92, 159–171. [Google Scholar] [CrossRef]
- Mosqueiro, T.; Strube-Bloss, M.; Tuma, R.; Pinto, R.; Smith, B.H.; Huerta, R. Non-parametric change point detection for spike trains. In Proceedings of the 2016 Annual Conference on Information Science and Systems (CISS), Princeton, NJ, USA, 16–18 March 2016; pp. 545–550. [Google Scholar]
- Basseville, M.; Nikiforov, I.V. Detection of Abrupt Changes: Theory and Application; Prentice Hall, Inc.: Englewood Cliffs, NJ, USA, 1993; pp. 25–66. [Google Scholar]
- Matteson, D.S.; James, N.A. A nonparametric approach for multiple change point analysis of multivariate data. J. Am. Stat. Assoc. 2014, 109, 334–345. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change-point problem. Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Ha, K.J.; Ha, E. Climatic change and interannual fluctuations in the long-term record of monthly precipitation for Seoul. Int. J. Climatol. 2006, 26, 607–618. [Google Scholar] [CrossRef]
- Ma, Z.; Kang, S.; Zhang, L.; Tong, L.; Su, X. Analysis of impacts of climate variability and human activity on streamflow for a river basin in arid region of northwest China. J. Hydrol. 2008, 352, 239–249. [Google Scholar] [CrossRef]
- Figura, S.; Livingstone, D.M.; Hoehn, E.; Kipfer, R. Regime shift in groundwater temperature triggered by the Arctic Oscillation. Geophys. Res. Lett. 2011, 38, L23401. [Google Scholar] [CrossRef]
- Li, D.; Xie, H.; Xiong, L. Temporal change analysis based on data characteristics and nonparametric test. Water Resour. Manag. 2014, 28, 227–240. [Google Scholar] [CrossRef]
- Li, J.; Tan, S.; Wei, Z.; Chen, F.; Feng, P. A new method of change point detection using variable fuzzy sets under environmental change. Water Resour. Manag. 2014, 28, 5125–5138. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, X.; Mu, X.; Wang, F.; Li, R.; Zhang, X. Trend and change-point analyses of streamflow and sediment discharge in the Yellow River during 1950–2005. Hydrol. Sci. J. 2010, 55, 275–285. [Google Scholar] [CrossRef]
- Xuedong, L.; Yili, Z.; Zhijun, Y.; Tongliang, G.; Hong, W.; Duo, C.; Linshan, L.; Fei, Z. The trend on runoff variations in the Lhasa River Basin. J. Geogr. Sci. 2008, 18, 95–106. [Google Scholar]
- Liu, D.; Chen, X.; Lian, Y.; Lou, Z. Impacts of climate change and human activities on surface runoff in the Dongjiang River basin of China. Hydrol. Process. 2010, 24, 1487–1495. [Google Scholar] [CrossRef]
- Kisi, O.; Ay, M. Comparison of Mann-Kendall and innovative trend method for water quality parameters of the Kizilirmak River, Turkey. J. Hydrol. 2014, 513, 362–375. [Google Scholar] [CrossRef]
- Bates, B.C.; Chandler, R.E.; Bowman, A.W. Trend estimation and change point detection in individual climatic series using flexible regression methods. J. Geophys. Res. Atmos. 2012, 117, D16106. [Google Scholar] [CrossRef]
- Tomozeiu, R.; Lazzeri, M.; Cacciamani, C. Precipitation fluctuations during the winter season from 1960 to 1995 over Emilia-Romagna, Italy. Theor. Appl. Climatol. 2002, 72, 221–229. [Google Scholar] [CrossRef]
- Ahmad, I.; Tang, D.; Wang, T.; Wang, M.; Wagan, B. Precipitation trends over time using Mann-Kendall and spearman’s Rho tests in swat river basin, Pakistan. Adv. Meteorol. 2015, 2015, 431860. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Glob. Planet. Chang. 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend detection in hydrologic data: The Mann-Kendall trend test under the scaling hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Tarhule, A.; Woo, M.K. Changes in rainfall characteristics in Northern Nigeria. Int. J. Climatol. 1998, 18, 1261–1271. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B. Canadian streamflow trend detection: Impacts of serial and cross-correlation. Hydrol. Sci. J. 2003, 48, 51–63. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Allison, P.D. Missing Data; Sage University Papers Series on Quantitive Applications in the Social Sciences: Thousand Oaks, CA, USA, 2001; Volume 07–136. [Google Scholar]
- Little, R.J.A.; Rubin, D.B. Statistical Analysis with Missing Data, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002; pp. 246–252. [Google Scholar]
- Li, J.; Heap, A.D. A Review of Spatial Interpolation Methods for Environmental Scientists; Record 2008/23; Geoscience Australia: Canberra, Australia, 2008; 137p.
- Stineman, R.W. A consistently well behaved method of interpolation. Creat. Comput. 1980, 6, 54–57. [Google Scholar]
- Leclercq, P.W.; Oerlemans, J. Global and hemispheric temperature reconstruction from glacier length fluctuations. Clim. Dyn. 2012, 38, 1065–1079. [Google Scholar] [CrossRef]
- Szesztay, K. Water balance and water level fluctuations of lakes. Hydrol. Sci. J. 1974, 19, 73–84. [Google Scholar] [CrossRef]
- Gates, D.J.; Diesendorf, M. On the fluctuations in levels of closed lakes. J. Hydrol. 1977, 33, 267–285. [Google Scholar] [CrossRef]
- Rapley, C.G.; Griffiths, H.D.; Squire, V.A.; Oliver, J.G.; Birks, A.R.; Cooper, A.P.R.; Cowan, A.M.; Drewry, D.J.; Gorman, M.R.; Guzkowska, M.; et al. Applications and Scientific Uses of ERS-1 Radar Altimeter Data; ESA Report 5684/83/NL/BI; ESA: Paris, France, 1985. [Google Scholar]
- Roe, G.H.; O’Neal, M.A. The response of glaciers to intrinsic climate variability: Observations and models of late-Holocene variations in the Pacific Northwest. J. Glaciol. 2009, 55, 839–854. [Google Scholar] [CrossRef]
- Morrill, C.; Small, E.E.; Sloan, L.C. Modeling orbital forcing of lake level change: Lake Gosiute (Eocene), North America. Glob. Planet. Chang. 2001, 29, 57–76. [Google Scholar] [CrossRef]
- Todhunter, P.E. Mean hydroclimatic and hydrological conditions during two climatic modes in the Devils Lake Basin, North Dakota (USA). Lakes Reserv. Res. Manag. 2016, 21, 338–350. [Google Scholar] [CrossRef]
- Rising Water Levels at Lake Enriquillo, Dominican Republic: Advice on Potential Causes and Pathways Forward. Available online: https://iciwarm.info/wp-content/uploads/2018/01/Lake_Enriquillo_report_1-26-2012.pdf (accessed on 26 January 2012).
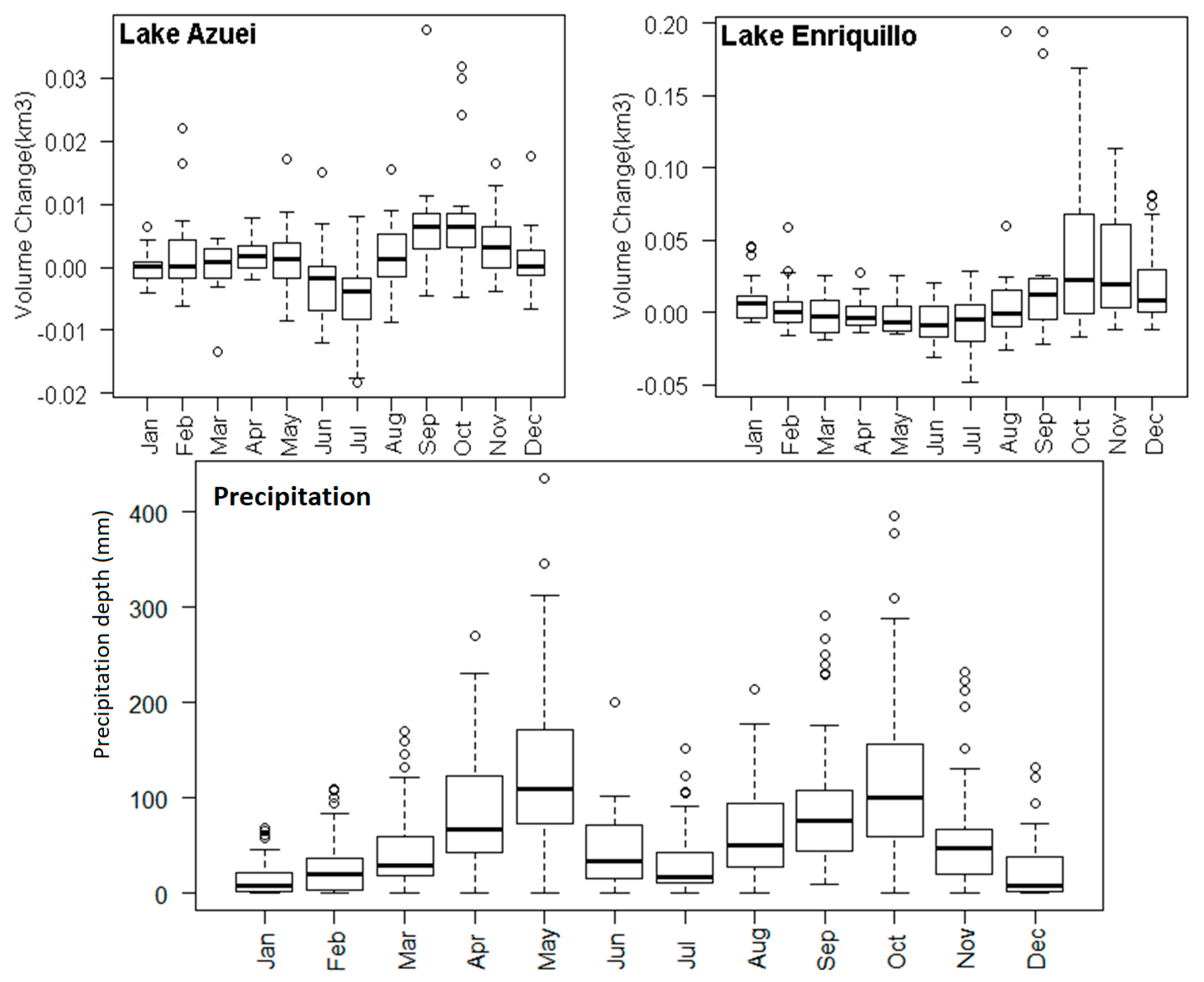
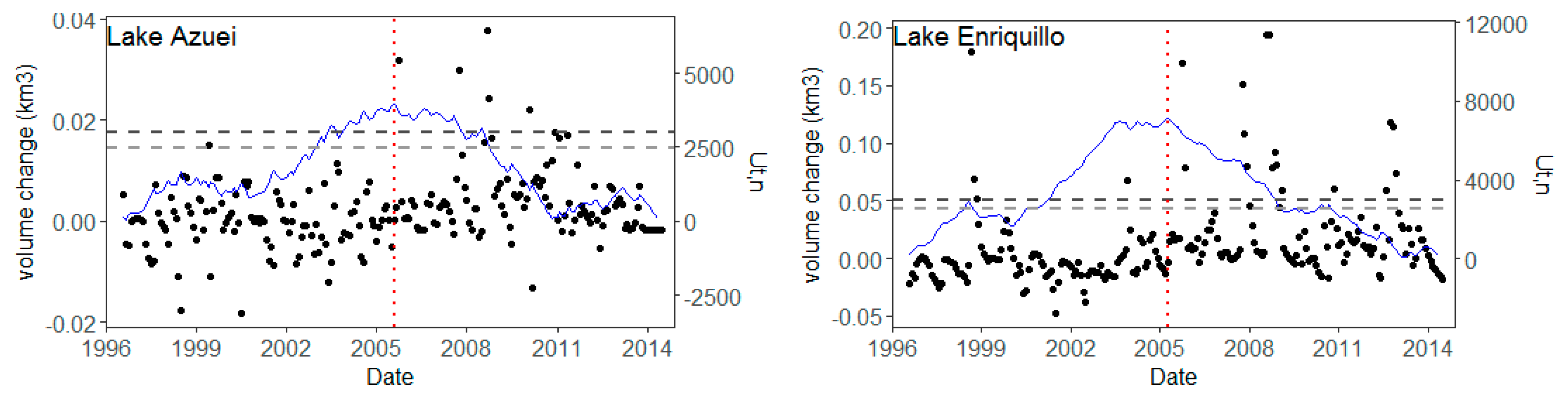
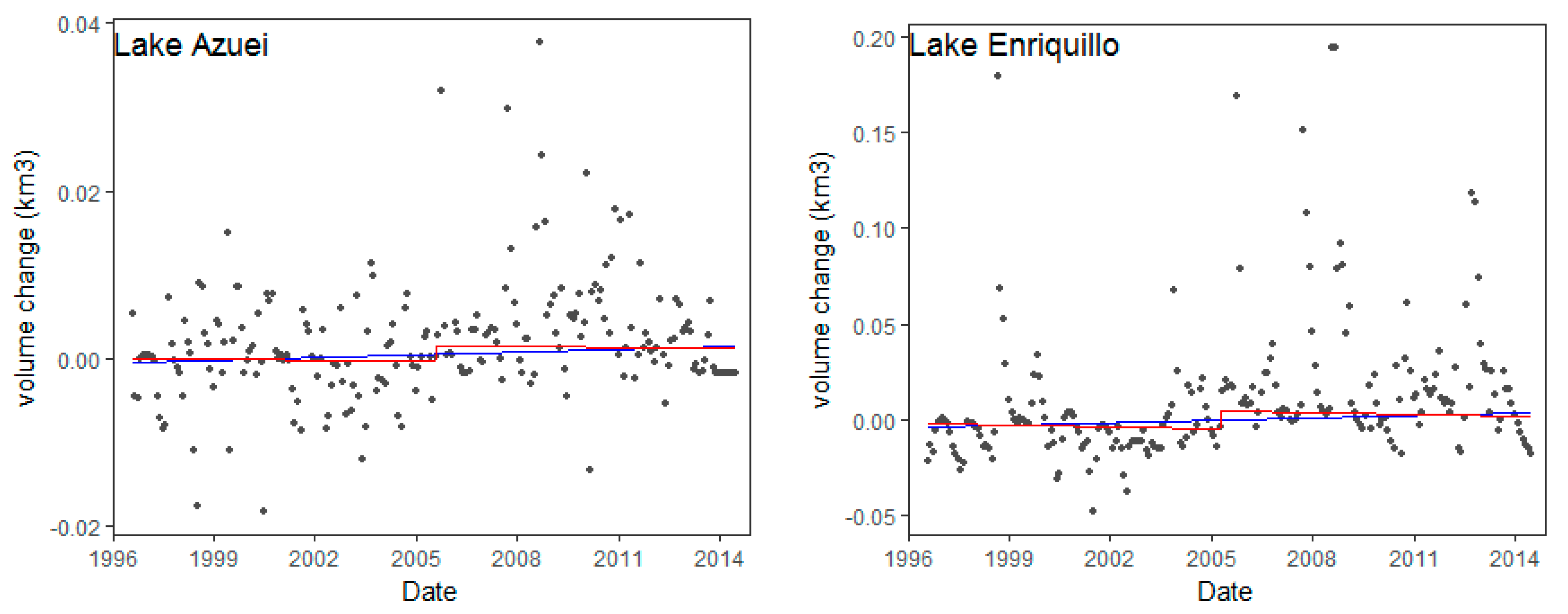
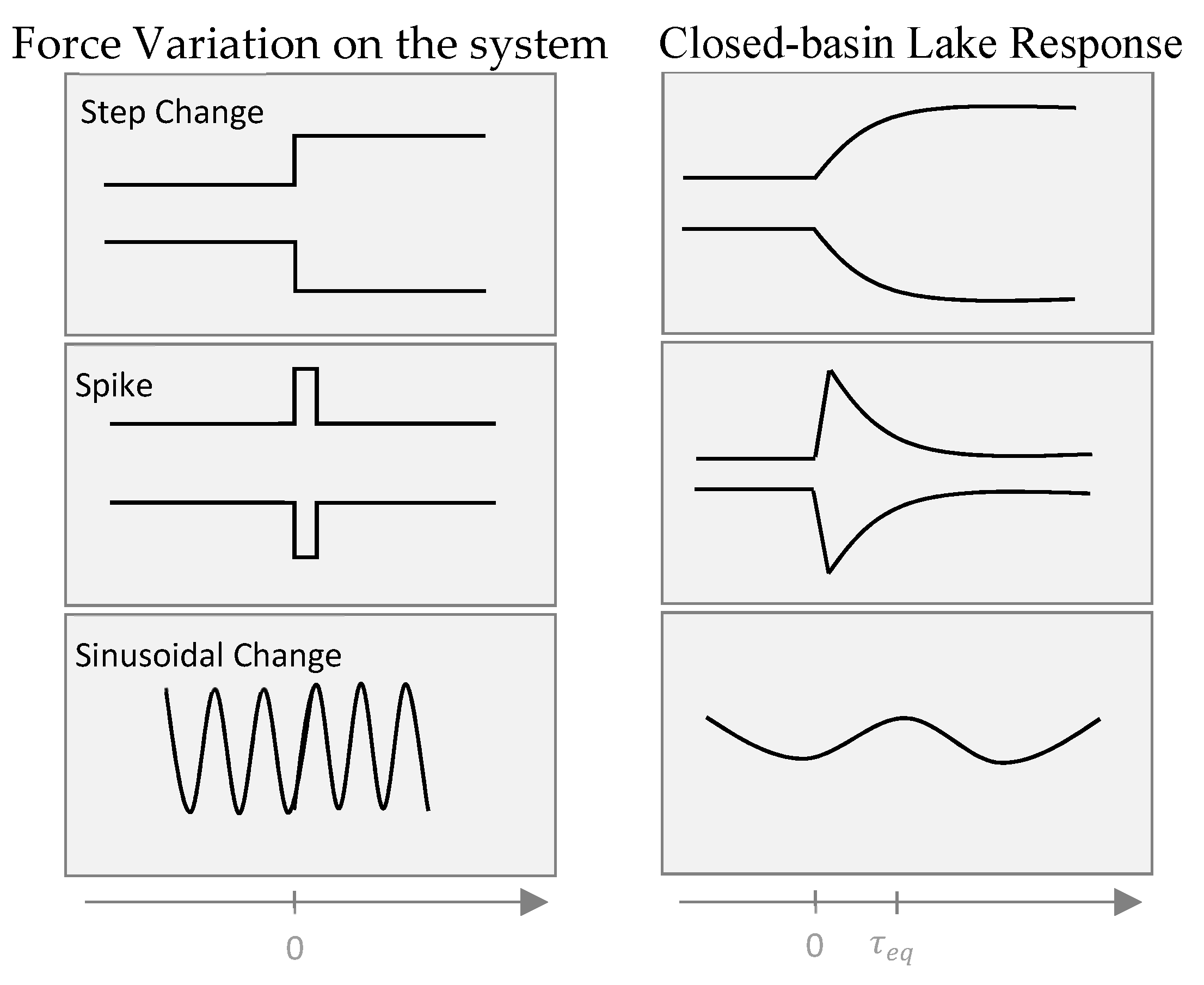
| NRMSE | ||||||
|---|---|---|---|---|---|---|
| Imputation Method | Lake Azuei | Lake Enriquillo | ||||
| 1996–2000 | 2000–2001 | 2001–2014 | 1996–2000 | 2000–2001 | 2001–2014 | |
| Linear Interpolation | 0.272 | 0.380 | 0.020 | 0.108 | 0.056 | 0.018 |
| spline Interpolation | 0.412 | 0.694 | 0.027 | 0.178 | 0.120 | 0.029 |
| Stineman Interpolation | 0.269 | 0.375 | 0.019 | 0.094 | 0.048 | 0.016 |
| Kalman Smoothing using Structural Model | 0.282 | 5.865 | 0.068 | 0.105 | 0.206 | 0.089 |
| Kalman Smoothing using ARIMA State Space Representation | 0.295 | 6.135 | 0.070 | 0.110 | 0.215 | 0.093 |
| Simple Moving Average | 0.327 | 0.475 | 0.031 | 0.191 | 0.137 | 0.034 |
| Linear Weighted Moving Average | 0.306 | 0.434 | 0.027 | 0.171 | 0.121 | 0.029 |
| Exponential Weighted Moving Average | 0.295 | 0.438 | 0.026 | 0.158 | 0.121 | 0.027 |
| Random Value Sample | 1.478 | 1.809 | 1.442 | 1.723 | 1.735 | 1.536 |
| Seasonally Decomposition by Linear Interpolation | 0.271 | 0.381 | 0.020 | 0.111 | 0.055 | 0.018 |
| Seasonally Decomposition by Random | 1.599 | 1.633 | 1.405 | 1.470 | 1.818 | 1.579 |
| Seasonally Decomposition by Weighted Moving Average | 0.297 | 0.429 | 0.026 | 0.156 | 0.122 | 0.027 |
| Seasonally Split by Linear Interpolation | 0.272 | 0.379 | 0.020 | 0.110 | 0.056 | 0.018 |
| Seasonally Split by Random | 1.739 | 1.698 | 1.426 | 1.659 | 1.733 | 1.399 |
| Seasonally Split by Weighted Moving Average | 0.293 | 0.433 | 0.025 | 0.158 | 0.127 | 0.027 |
| Lake | Series | No. Points | Min | 1st Qu | Median | Mean | 3rd Qu | Max | SD |
|---|---|---|---|---|---|---|---|---|---|
| Enriquillo | 32-day dataset | 112 | −0.0415 | −0.0072 | 0.0084 | 0.0221 | 0.0320 | 0.3437 | 0.0509 |
| Monthly imputed | 216 | −0.0483 | −0.0073 | 0.0009 | 0.0109 | 0.0165 | 0.1943 | 0.0362 | |
| Azuei | 32-day dataset | 165 | −0.0197 | −0.0014 | 0.0032 | 0.0029 | 0.0061 | 0.0435 | 0.0083 |
| Monthly imputed | 216 | −0.0183 | −0.0017 | 0.0007 | 0.0019 | 0.0044 | 0.0377 | 0.0070 |
| Sub-Period before Shift | Sub-Period after Shift | |||||
|---|---|---|---|---|---|---|
| Series | Z Statistic | p-Value | Z Statistic | p-Value | ||
| Lake Enriquillo | 0.013 | 0.848 | N | −0.100 | 0.122 | N |
| Lake Azuei | 0.013 | 0.840 | N | −0.082 | 0.211 | N |
| Lake Enriquillo | Lake Azuei | |||||
|---|---|---|---|---|---|---|
| Series | t Statistic | p-Value | t Statistic | p-Value | ||
| Trend | −0.423 | 0.673 | N | −0.524 | 0.601 | N |
| Change Point | 2.596 | 0.010 | * | 0.631 | 0.043 | * |
| 6-month periodicity | 0.413 | 0.680 | N | 3.610 | 0.0004 | *** |
| Annual periodicity | 4.787 | 3.62 × 10−6 | *** | 2.742 | 0.0067 | ** |
| NO | Year | Month | Name | Type | Distance to Watershed (km) | Monthly Rainfall at Jimani Station |
|---|---|---|---|---|---|---|
| 1 | 1979 | Jul | CLAUDETTE | Tropical Storm | 18.8 | 123.4 |
| 2 | 1979 | Sep | DAVID | Category 1 Hurricane | 51.0 | 170.7 |
| 3 | 1998 | Sep | GEORGES | Category 3 Hurricane | 28.2 | 230 |
| 4 | 2005 | Oct | ALPHA | Tropical Storm | 0.0 | 257.4 |
| 5 | 2007 | Oct | NOEL | Tropical Storm | 48.8 | 225.8 |
| 6 | 2008 | Aug | FAYE | Tropical Storm | 3.7 | 214.4 |
| 7 | 2008 | Aug | GUSTAV | Tropical Storm | 71.5 | 214.4 |
| 8 | 2012 | Aug | ISAAC | Tropical Storm | 53.1 | 115.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moknatian, M.; Piasecki, M. Lake Volume Data Analyses: A Deep Look into the Shrinking and Expansion Patterns of Lakes Azuei and Enriquillo, Hispaniola. Hydrology 2020, 7, 1. https://doi.org/10.3390/hydrology7010001
Moknatian M, Piasecki M. Lake Volume Data Analyses: A Deep Look into the Shrinking and Expansion Patterns of Lakes Azuei and Enriquillo, Hispaniola. Hydrology. 2020; 7(1):1. https://doi.org/10.3390/hydrology7010001
Chicago/Turabian StyleMoknatian, Mahrokh, and Michael Piasecki. 2020. "Lake Volume Data Analyses: A Deep Look into the Shrinking and Expansion Patterns of Lakes Azuei and Enriquillo, Hispaniola" Hydrology 7, no. 1: 1. https://doi.org/10.3390/hydrology7010001
APA StyleMoknatian, M., & Piasecki, M. (2020). Lake Volume Data Analyses: A Deep Look into the Shrinking and Expansion Patterns of Lakes Azuei and Enriquillo, Hispaniola. Hydrology, 7(1), 1. https://doi.org/10.3390/hydrology7010001






