‘Teflon Basin’ or Not? A High-Elevation Catchment Transit Time Modeling Approach
Abstract
1. Introduction
- The estimation of catchment transit time and mobile storage by coupling of a surface energy-balance snow and ice melt model with a lumped parameter transit time model,
- The estimation of the Fyw with delayed input of snow and ice melt using the sine wave approach and,
- The comparison of the TTD and the Fyw.
2. Materials and Methods
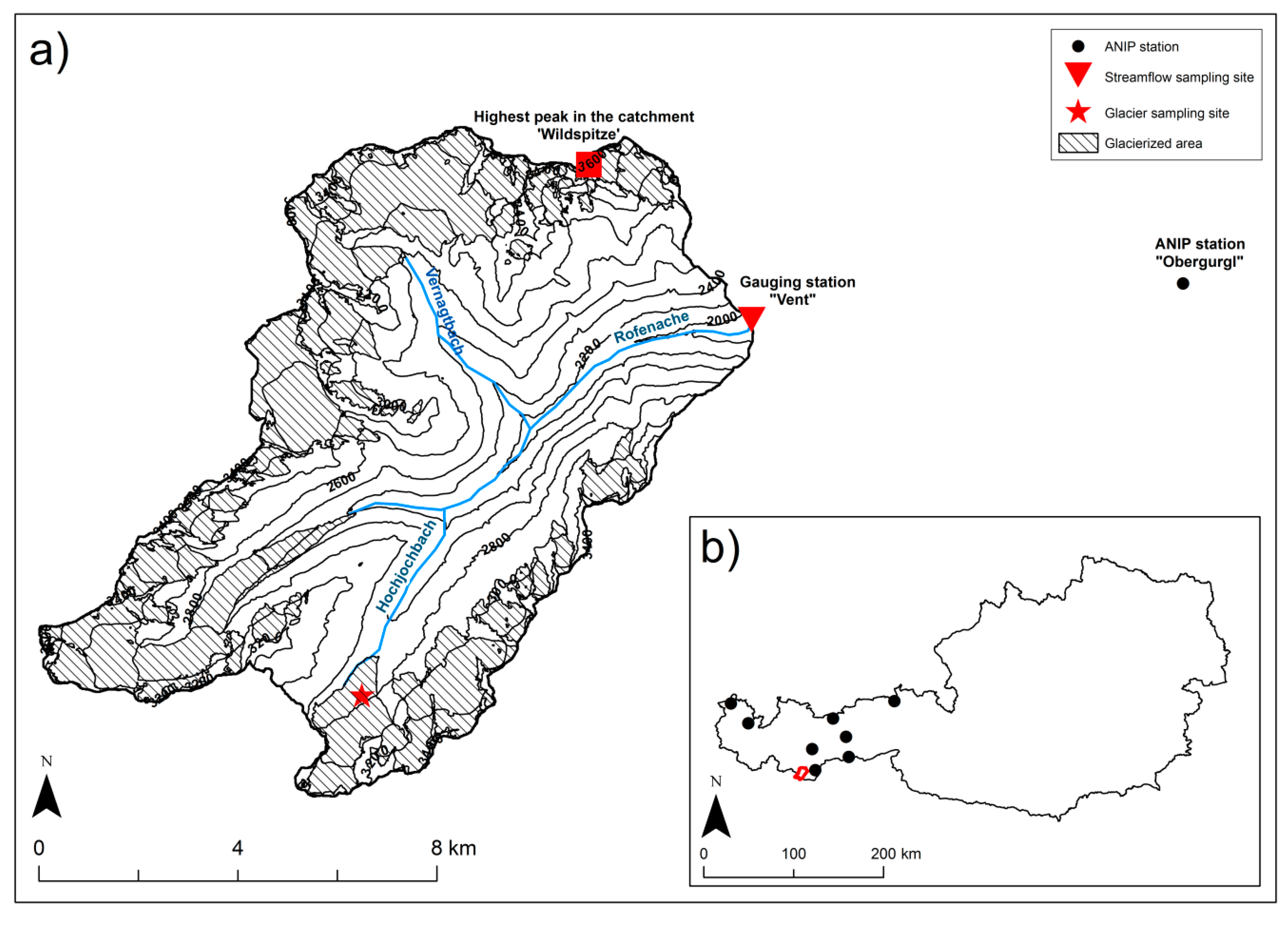
2.1. Study Area
2.2. Data
2.3. The Surface Energy-Balance Model ESCIMO
2.4. The Lumped Parameter Transit Time Model TRANSEP
2.5. Estimating the Young Water Fraction with the Sine Wave Approach
3. Results
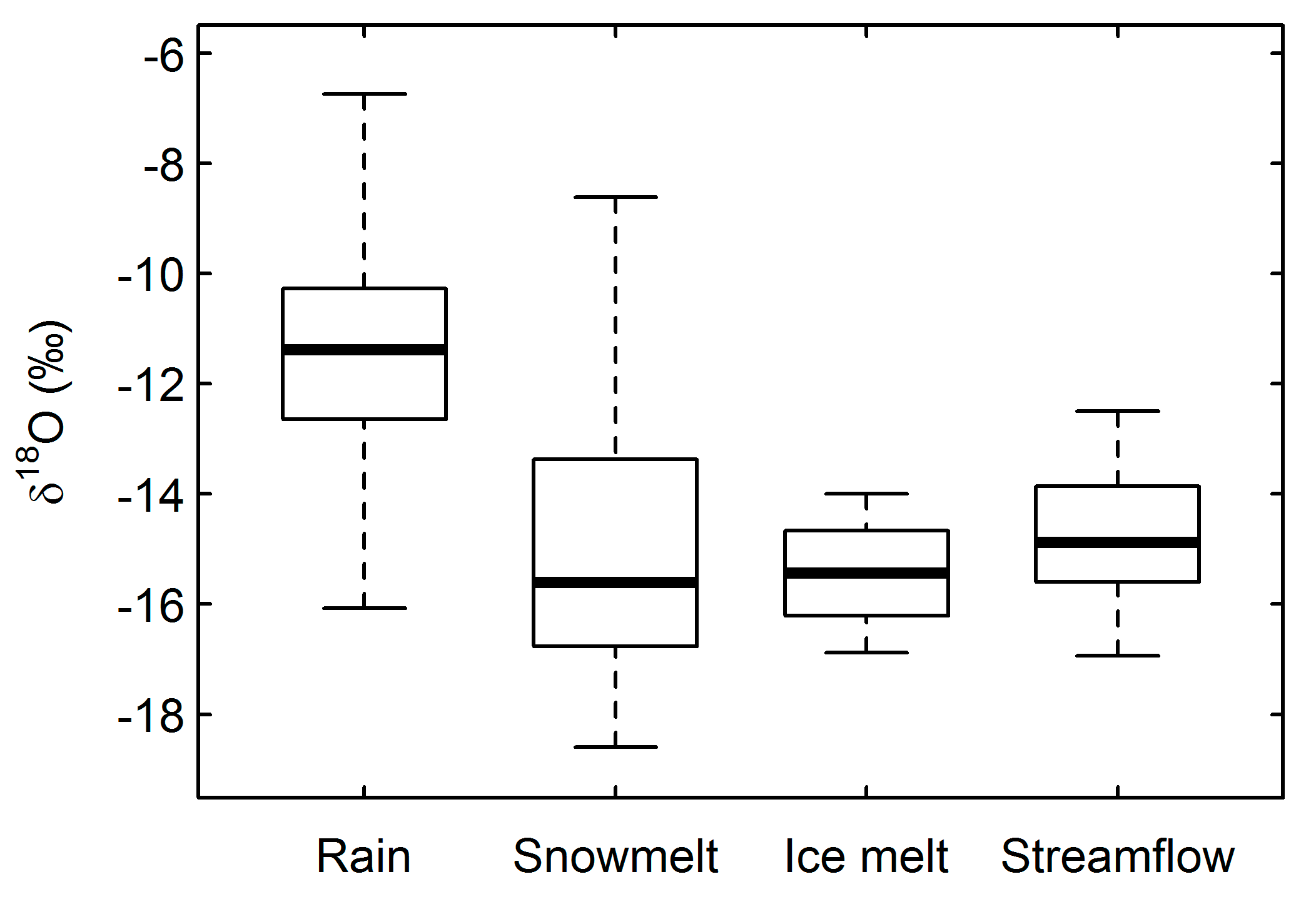
3.1. δ18O Values of Various Water Types in the Rofental for the Period 2014 to 2017
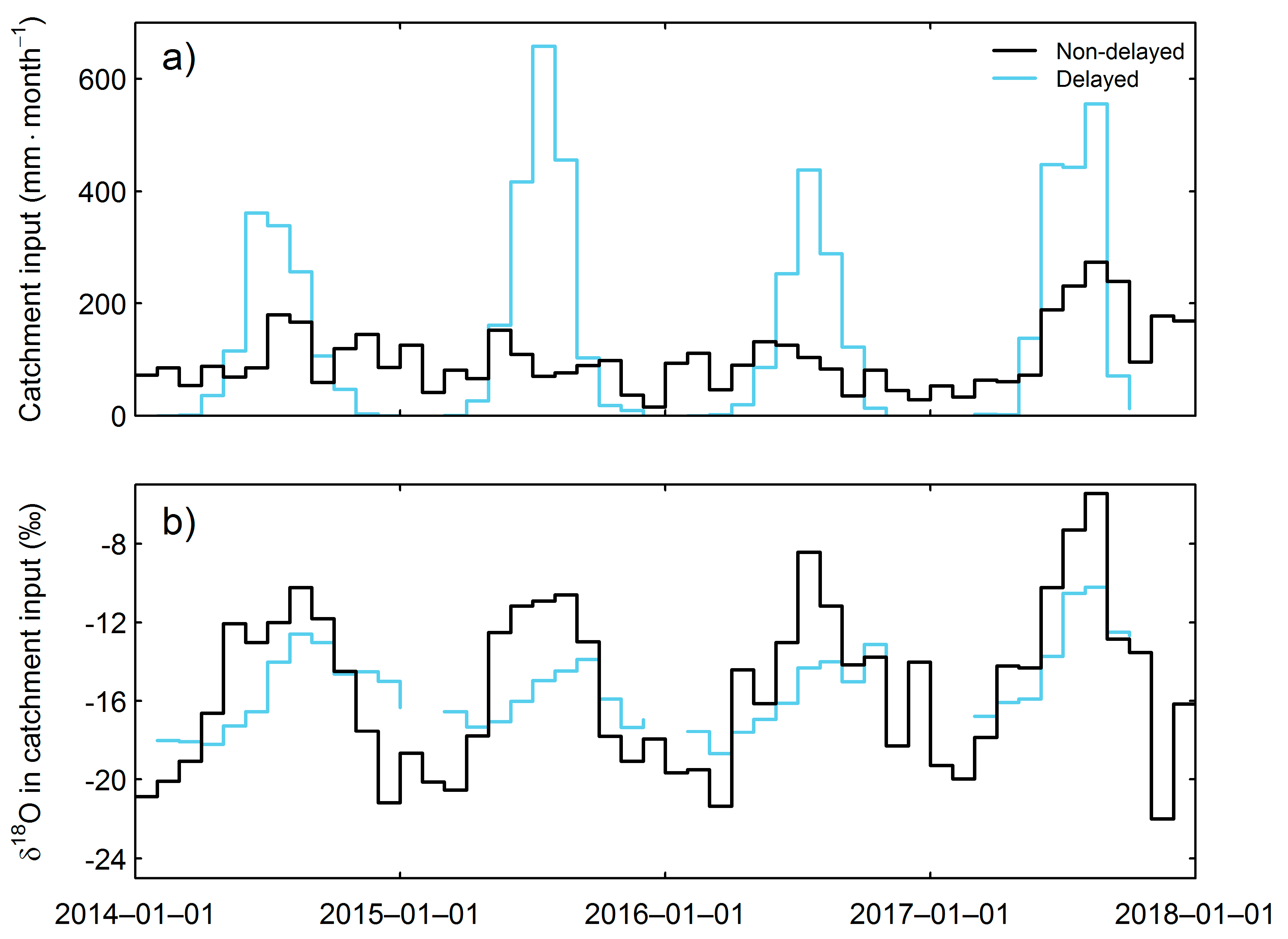
3.2. Flux and δ18O of Water Input into the Rofenache Catchment
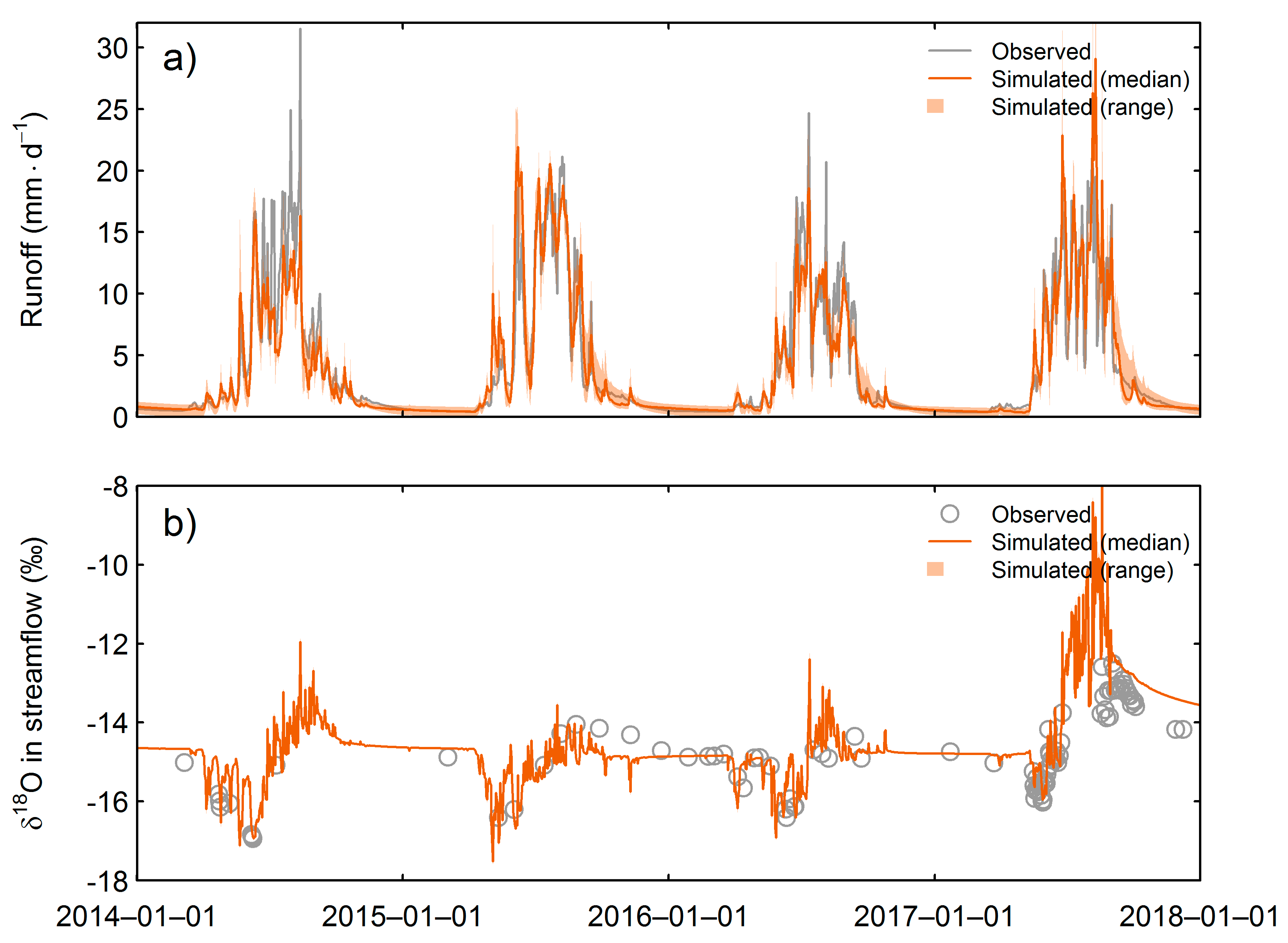
3.3. Runoff and δ18O in Streamflow of the Rofenache at the Gauging Station in Vent
3.4. Streamflow Water Age and Subsurface Storage
3.4.1. Young Water Fraction Estimated with the Sine Wave Approach
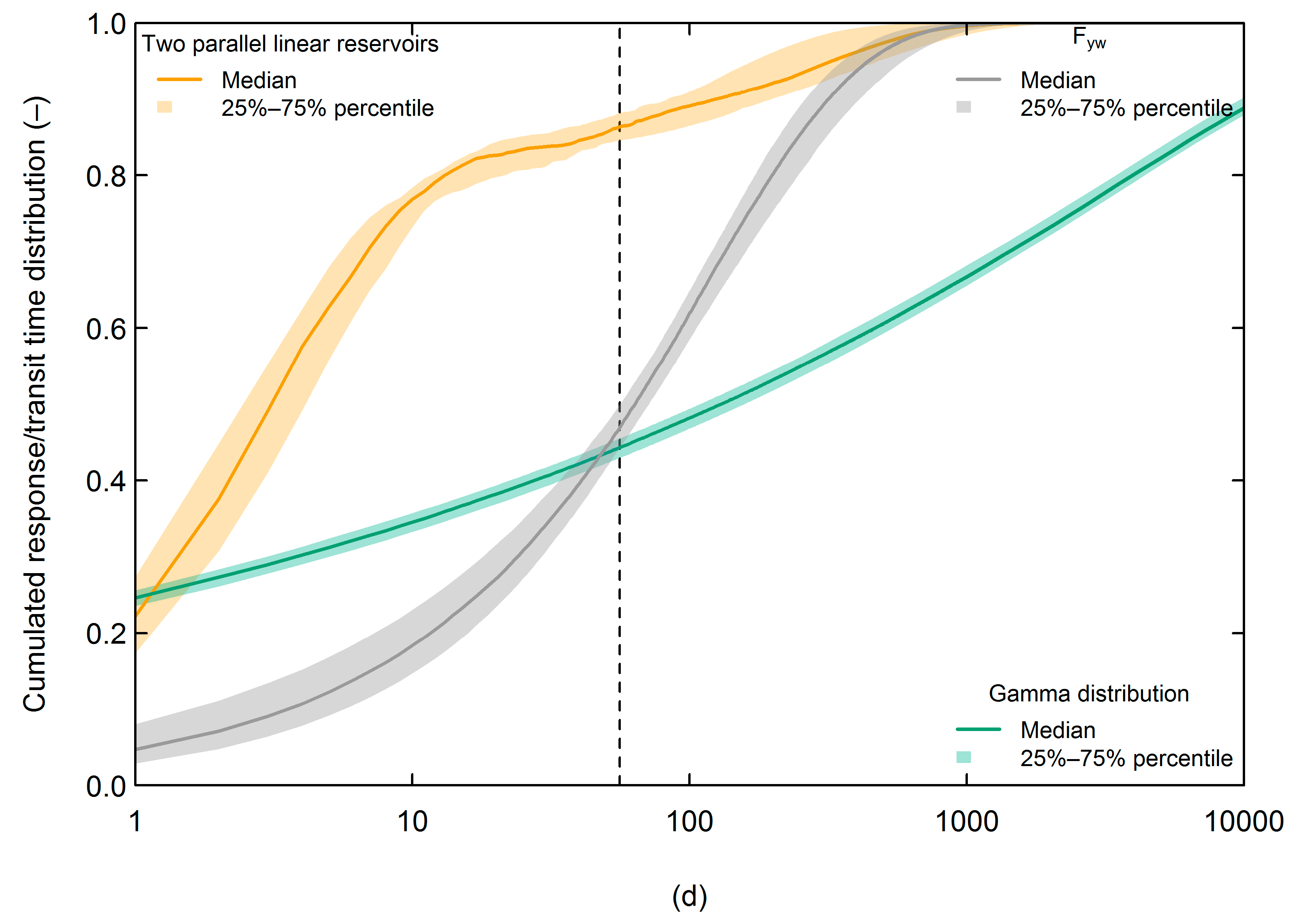
3.4.2. Age Distribution and Subsurface Storage Potential
4. Discussion
4.1. How Large is the Subsurface Storage Potential?
4.2. How Old is Streamflow?
4.3. Methodological Implications
4.3.1. Modeling Catchment Water Input and its δ18O Value with ESCIMO
4.3.2. The Young Water Fraction of a Glacierized High-Elevation Catchment
4.3.3. TRANSEP Applied in Glacierized High-Elevation Catchment
- Structural uncertainty: We used a top-down modeling approach including a pre-defined model structure and tested it in our complex study catchment. The transfer functions were chosen by prior modeling experiments and the TPLR for runoff and the flexible GM for streamflow δ18O were used. The latter allows for both, fast tracer throughputs and relatively long transit times [76], and did not assume a well-mixed reservoir, which was suitable for application in our catchment. Both transfer functions were proved best regarding the objective functions.
- Parameter uncertainty: Three out of five TRANSEP parameters were well-constrained during the Monte Carlo simulation (φ, τf and α). τs and β were less well-constrained, leading to the observed uncertainty of the TTD, RTD and storage estimates (see Figure 5 and Table 2). The physical interpretation of the low α suggests a highly non-linear streamflow tracer response (Table 2, [77]).
- Input uncertainty: We used a single ESCIMO run as input data for TRANSEP and focused on the applicability of and the uncertainty within TRANSEP, but input uncertainty should be investigated in future studies as this represents an important source of uncertainty in TTD modeling, e.g., [68].
- Uncertainty due to the optimization procedure: The choice of the objective function was arbitrary, but after initial model experiments it became apparent that the splitting of the streamflow δ18O time series, as well as the higher weighted flow variability term (as used for the KGE), were relevant.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Williams, M.W.; Hood, E.; Molotch, N.P.; Caine, N.; Cowie, R.; Liu, F. The ‘teflon basin’ myth: Hydrology and hydrochemistry of a seasonally snow-covered catchment. Plant Ecol. Divers. 2015, 8, 639–661. [Google Scholar] [CrossRef]
- Frenierre, J.L.; Mark, B.G. A review of methods for estimating the contribution of glacial meltwater to total watershed discharge. Prog. Phys. Geogr. 2014, 38, 173–200. [Google Scholar] [CrossRef]
- Frisbee, M.D.; Tolley, D.G.; Wilson, J.L. Field estimates of groundwater circulation depths in two mountainous watersheds in the western u.S. And the effect of deep circulation on solute concentrations in streamflow. Water Resour. Res. 2017, 53, 2693–2715. [Google Scholar] [CrossRef]
- Staudinger, M.; Stoelzle, M.; Seeger, S.; Seibert, J.; Weiler, M.; Stahl, K. Catchment water storage variation with elevation. Hydrol. Process. 2017, 31, 2000–2015. [Google Scholar] [CrossRef]
- Spence, C. A paradigm shift in hydrology: Storage thresholds across scales influence catchment runoff generation. Geogr. Compass 2010, 4, 819–833. [Google Scholar] [CrossRef]
- Buttle, J.M. Dynamic storage: A potential metric of inter-basin differences in storage properties. Hydrol. Process. 2016, 30, 4644–4653. [Google Scholar] [CrossRef]
- McNamara, J.P.; Tetzlaff, D.; Bishop, K.; Soulsby, C.; Seyfried, M.; Peters, N.E.; Aulenbach, B.T.; Hooper, R. Storage as a metric of catchment comparison. Hydrol. Process. 2011, 25, 3364–3371. [Google Scholar] [CrossRef]
- Stoelzle, M.; Schuetz, T.; Weiler, M.; Stahl, K.; Tallaksen, L.M. Beyond binary baseflow separation: Delayed flow index as a fresh perspective on streamflow contributions. Hydrol. Earth Syst. Sci. Discuss. 2019, 2019, 1–30. [Google Scholar] [CrossRef]
- Cochand, M.; Christe, P.; Ornstein, P.; Hunkeler, D. Groundwater storage in high alpine catchments and its contribution to streamflow. Water Resour. Res. 2019, 55, 2613–2630. [Google Scholar] [CrossRef]
- Schmieder, J.; Garvelmann, J.; Marke, T.; Strasser, U. Spatio-temporal tracer variability in the glacier melt end-member — how does it affect hydrograph separation results? Hydrol. Process. 2018, 32, 1828–1843. [Google Scholar] [CrossRef]
- Jasechko, S.; Kirchner, J.W.; Welker, J.M.; McDonnell, J.J. Substantial proportion of global streamflow less than three months old. Nat. Geosci. 2016, 9, 126–129. [Google Scholar] [CrossRef]
- Hood, J.L.; Hayashi, M. Characterization of snowmelt flux and groundwater storage in an alpine headwater basin. J. Hydrol. 2015, 521, 482–497. [Google Scholar] [CrossRef]
- Käser, D.; Hunkeler, D. Contribution of alluvial groundwater to the outflow of mountainous catchments. Water Resour. Res. 2016, 52, 680–697. [Google Scholar] [CrossRef]
- Frisbee, M.D.; Phillips, F.M.; Campbell, A.R.; Liu, F.; Sanchez, S.A. Streamflow generation in a large, alpine watershed in the southern rocky mountains of colorado: Is streamflow generation simply the aggregation of hillslope runoff responses? Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Andermann, C.; Longuevergne, L.; Bonnet, S.; Crave, A.; Davy, P.; Gloaguen, R. Impact of transient groundwater storage on the discharge of himalayan rivers. Nat. Geosci. 2012, 5, 127–132. [Google Scholar] [CrossRef]
- Clow, D.W.; Schrott, L.; Webb, R.; Campbell, D.H.; Torizzo, A.; Dornblaser, M. Ground water occurrence and contributions to streamflow in an alpine catchment, colorado front range. Ground Water 2003, 41, 937–950. [Google Scholar] [CrossRef]
- Liu, F.; Williams, M.W.; Caine, N. Source waters and flow paths in an alpine catchment, colorado front range, united states. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Harrington, J.S.; Mozil, A.; Hayashi, M.; Bentley, L.R. Groundwater flow and storage processes in an inactive rock glacier. Hydrol. Process. 2018, 32, 3070–3088. [Google Scholar] [CrossRef]
- Penna, D.; Engel, M.; Bertoldi, G.; Comiti, F. Towards a tracer-based conceptualization of meltwater dynamics and streamflow response in a glacierized catchment. Hydrol. Earth Syst. Sci. 2017, 21, 23–41. [Google Scholar] [CrossRef]
- Engel, M.; Penna, D.; Bertoldi, G.; Dell’Agnese, A.; Soulsby, C.; Comiti, F. Identifying run-off contributions during melt-induced run-off events in a glacierized alpine catchment. Hydrol. Process. 2016, 30, 343–364. [Google Scholar] [CrossRef]
- Berghuijs, W.R.; Woods, R.A.; Hrachowitz, M. A precipitation shift from snow towards rain leads to a decrease in streamflow. Nat. Clim. Chang. 2014, 4, 583–586. [Google Scholar] [CrossRef]
- Musselman, K.N.; Clark, M.P.; Liu, C.; Ikeda, K.; Rasmussen, R. Slower snowmelt in a warmer world. Nat. Clim. Chang. 2017, 7, 214. [Google Scholar] [CrossRef]
- McGuire, K.J.; McDonnell, J.J. A review and evaluation of catchment transit time modeling. J. Hydrol. 2006, 330, 543–563. [Google Scholar] [CrossRef]
- McDonnell, J.J.; McGuire, K.; Aggarwal, P.; Beven, K.J.; Biondi, D.; Destouni, G.; Dunn, S.; James, A.; Kirchner, J.; Kraft, P.; et al. How old is streamwater? Open questions in catchment transit time conceptualization, modelling and analysis. Hydrol. Process. 2010, 24, 1745–1754. [Google Scholar] [CrossRef]
- Kirchner, J.W. Aggregation in environmental systems—Part 1: Seasonal tracer cycles quantify young water fractions, but not mean transit times, in spatially heterogeneous catchments. Hydrol. Earth Syst. Sci. 2016, 20, 279–297. [Google Scholar] [CrossRef]
- Kirchner, J.W. Aggregation in environmental systems—Part 2: Catchment mean transit times and young water fractions under hydrologic nonstationarity. Hydrol. Earth Syst. Sci. 2016, 20, 299–328. [Google Scholar] [CrossRef]
- Stockinger, M.P.; Bogena, H.R.; Lücke, A.; Stumpp, C.; Vereecken, H. Time-variability of the fraction of young water in a small headwater catchment. Hydrol. Earth Syst. Sci. Discuss. 2019, 2019, 1–25. [Google Scholar] [CrossRef]
- Stockinger, M.P.; Bogena, H.R.; Lücke, A.; Diekkrüger, B.; Cornelissen, T.; Vereecken, H. Tracer sampling frequency influences estimates of young water fraction and streamwater transit time distribution. J. Hydrol. 2016, 541, 952–964. [Google Scholar] [CrossRef]
- Tetzlaff, D.; Piovano, T.; Ala-Aho, P.; Smith, A.; Carey, S.K.; Marsh, P.; Wookey, P.A.; Street, L.E.; Soulsby, C. Using stable isotopes to estimate travel times in a data-sparse arctic catchment: Challenges and possible solutions. Hydrol. Process. 2018, 32, 1936–1952. [Google Scholar] [CrossRef]
- Tetzlaff, D.; Buttle, J.; Carey, S.K.; McGuire, K.; Laudon, H.; Soulsby, C. Tracer-based assessment of flow paths, storage and runoff generation in northern catchments. Hydrol. Process. 2014, 16, 3475–3490. [Google Scholar] [CrossRef]
- von Freyberg, J.; Allen, S.T.; Seeger, S.; Weiler, M.; Kirchner, J.W. Sensitivity of young water fractions to hydro-climatic forcing and landscape properties across 22 swiss catchments. Hydrol. Earth Syst. Sci. 2018, 22, 3841–3861. [Google Scholar] [CrossRef]
- Seeger, S.; Weiler, M. Reevaluation of transit time distributions, mean transit times and their relation to catchment topography. Hydrol. Earth Syst. Sci. 2014, 18, 4751–4771. [Google Scholar] [CrossRef][Green Version]
- Song, C.; Wang, G.; Liu, G.; Mao, T.; Sun, X.; Chen, X. Stable isotope variations of precipitation and streamflow reveal the young water fraction of a permafrost watershed. Hydrol. Process. 2017, 31, 935–947. [Google Scholar] [CrossRef]
- Schmieder, J.; Hanzer, F.; Marke, T.; Garvelmann, J.; Warscher, M.; Kunstmann, H.; Strasser, U. The importance of snowmelt spatiotemporal variability for isotope-based hydrograph separation in a high-elevation catchment. Hydrol. Earth Syst. Sci. 2016, 20, 5015–5033. [Google Scholar] [CrossRef]
- Strasser, U.; Marke, T.; Braun, L.; Escher-Vetter, H.; Juen, I.; Kuhn, M.; Maussion, F.; Mayer, C.; Nicholson, L.; Niedertscheider, K.; et al. The rofental: A high alpine research basin (1890–3770 m a.S.L.) in the ötztal alps (austria) with over 150 years of hydrometeorological and glaciological observations. Earth Syst. Sci. Data 2018, 10, 151–171. [Google Scholar] [CrossRef]
- Keller, R. The international hydrological decade—The international hydrological programme. Geoforum 1976, 7, 139–143. [Google Scholar] [CrossRef]
- Schmieder, J.; Marke, T.; Strasser, U. Wo kommt das wasser her? Tracerbasierte analysen im rofental (ötztaler alpen, österreich). Österreichische Wasser Und Abfallwirtsch. 2018, 70, 507–514. [Google Scholar] [CrossRef][Green Version]
- Hanzer, F.; Helfricht, K.; Marke, T.; Strasser, U. Multilevel spatiotemporal validation of snow/ice mass balance and runoff modeling in glacierized catchments. Cryosphere 2016, 10, 1859–1881. [Google Scholar] [CrossRef]
- Hanzer, F.; Förster, K.; Nemec, J.; Strasser, U. Projected cryospheric and hydrological impacts of 21st century climate change in the ötztal alps (austria) simulated using a physically based approach. Hydrol. Earth Syst. Sci. 2018, 22, 1593–1614. [Google Scholar] [CrossRef]
- Strasser, U. Modelling of the mountain snow cover in the berchtesgaden national park. Forschungsberichte des Nationalpark Berchtesgaden 2008, 55, 1–184. [Google Scholar]
- Maier, F. Young Water Fraction in a High-Elevation Catchment: Temporal Variability and Relation to Meteorological and Glacio-Hydrological Proxies for Climate Change. Master’s Thesis, University of Innsbruck, Innsbruck, Austria, 2017. [Google Scholar]
- Schmieder, J.; Marke, T.; Strasser, U. Tracerhydrologische Untersuchungen im Rofental (ötztaler alpen/österreich). Available online: https://www.uibk.ac.at/geographie/igg/berichte/2017/pdf/7_schmieder_etal.pdf (accessed on 20 October 2019).
- Strasser, U.; Marke, T. ESCIMO.spread—A spreadsheet-based point snow surface energy balance model to calculate hourly snow water equivalent and melt rates for historical and changing climate conditions. Geosci. Model Dev. 2010, 3, 643–652. [Google Scholar] [CrossRef]
- Marke, T.; Mair, E.; Förster, K.; Hanzer, F.; Garvelmann, J.; Pohl, S.; Warscher, M.; Strasser, U. Escimo.Spread (v2): Parameterization of a spreadsheet-based energy balance snow model for inside-canopy conditions. Geosci. Model Dev. 2016, 9, 633–646. [Google Scholar] [CrossRef]
- Krinner, G.; Derksen, C.; Essery, R.; Flanner, M.; Hagemann, S.; Clark, M.; Hall, A.; Rott, H.; Brutel-Vuilmet, C.; Kim, H.; et al. Esm-snowmip: Assessing snow models and quantifying snow-related climate feedbacks. Geosci. Model Dev. 2018, 11, 5027–5049. [Google Scholar] [CrossRef]
- He, Z.; Unger-Shayesteh, K.; Vorogushyn, S.; Weise, S.M.; Kalashnikova, O.; Gafurov, A.; Duethmann, D.; Barandun, M.; Merz, B. Constraining hydrological model parameters using water isotopic compositions in a glacierized basin, central asia. J. Hydrol. 2019, 571, 332–348. [Google Scholar] [CrossRef]
- Weiler, M.; McGlynn, B.L.; McGuire, K.J.; McDonnell, J.J. How does rainfall become runoff? A combined tracer and runoff transfer function approach. Water Resour. Res. 2003, 39, 1315. [Google Scholar] [CrossRef]
- Roa-García, M.C.; Weiler, M. Integrated response and transit time distributions of watersheds by combining hydrograph separation and long-term transit time modeling. Hydrol. Earth Syst. Sci. 2010, 14, 1537–1549. [Google Scholar] [CrossRef]
- Segura, C.; James, A.L.; Lazzati, D.; Roulet, N.T. Scaling relationships for event water contributions and transit times in small-forested catchments in eastern quebec. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Mizukami, N.; Rakovec, O.; Newman, A.J.; Clark, M.P.; Wood, A.W.; Gupta, H.V.; Kumar, R. On the choice of calibration metrics for “high-flow” estimation using hydrologic models. Hydrol. Earth Syst. Sci. 2019, 23, 2601–2614. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424, 264–277. [Google Scholar] [CrossRef]
- Klug, C.; Rieg, L.; Ott, P.; Mössinger, M.; Sailer, R.; Stötter, J. A multi-methodological approach to determine permafrost occurrence and ground surface subsidence in mountain terrain, tyrol, austria. Permafr. Periglac. Process. 2017, 28, 249–265. [Google Scholar] [CrossRef]
- McGuire, K.J.; McDonnell, J.J.; Weiler, M.; Kendall, C.; McGlynn, B.L.; Welker, J.M.; Seibert, J. The role of topography on catchment-scale water residence time. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Stewart, M.K.; Morgenstern, U.; McDonnell, J.J.; Pfister, L. The ‘hidden streamflow’ challenge in catchment hydrology: A call to action for stream water transit time analysis. Hydrol. Process. 2012, 26, 2061–2066. [Google Scholar] [CrossRef]
- Stewart, M.K.; Morgenstern, U.; McDonnell, J.J. Truncation of stream residence time: How the use of stable isotopes has skewed our concept of streamwater age and origin. Hydrol. Process. 2010, 24, 1646–1659. [Google Scholar] [CrossRef]
- Stewart, M.K.; Mehlhorn, J.; Elliott, S. Hydrometric and natural tracer (oxygen-18, silica, tritium and sulphur hexafluoride) evidence for a dominant groundwater contribution to pukemanga stream, new zealand. Hydrol. Process. 2007, 21, 3340–3356. [Google Scholar] [CrossRef]
- Behrens, H.; Moser, H.; Oerter, H.; Rauert, W.; Stichler, W.; Ambach, W. Models for the Runoff from a Glaciated Catchment Area Using Measurements of Environmental Isotope Contents. Available online: https://epic.awi.de/id/eprint/25026/1/Behrens_etal_1978.pdf (accessed on 20 October 2019).
- McDonnell, J.J.; Bonell, M.; Stewart, M.K.; Pearce, A.J. Deuterium variations in storm rainfall: Implications for stream hydrograph separation. Water Resour. Res. 1990, 26, 455–458. [Google Scholar] [CrossRef]
- Hager, B.; Foelsche, U. Stable isotope composition in austria. Austrian J. Earth Sci. 2015, 108, 2–13. [Google Scholar]
- Beria, H.; Larsen, J.R.; Ceperley, N.C.; Michelon, A.; Vennemann, T.; Schaefli, B. Understanding snow hydrological processes through the lens of stable water isotopes. WIREs Water 2018, 5, e1311. [Google Scholar] [CrossRef]
- Zuecco, G.; Carturan, L.; De Blasi, F.; Seppi, R.; Zanoner, T.; Penna, D.; Borga, M.; Carton, A.; Dalla Fontana, G. Understanding hydrological processes in glacierized catchments: Evidence and implications of highly variable isotopic and electrical conductivity data. Hydrol. Process. 2019, 33, 816–832. [Google Scholar] [CrossRef]
- Engel, M.; Penna, D.; Bertoldi, G.; Vignoli, G.; Tirler, W.; Comiti, F. Controls on spatial and temporal variability in streamflow and hydrochemistry in a glacierized catchment. Hydrol. Earth Syst. Sci. 2019, 23, 2041–2063. [Google Scholar] [CrossRef]
- Ala-aho, P.; Tetzlaff, D.; McNamara, J.P.; Laudon, H.; Soulsby, C. Using isotopes to constrain water flux and age estimates in snow-influenced catchments using the starr (spatially distributed tracer-aided rainfall–runoff) model. Hydrol. Earth Syst. Sci. 2017, 21, 5089–5110. [Google Scholar] [CrossRef]
- Piovano, T.I.; Tetzlaff, D.; Carey, S.K.; Shatilla, N.J.; Smith, A.; Soulsby, C. Spatially distributed tracer-aided runoff modelling and dynamics of storage and water ages in a permafrost-influenced catchment. Hydrol. Earth Syst. Sci. 2019, 23, 2507–2523. [Google Scholar] [CrossRef]
- Ala-aho, P.; Tetzlaff, D.; McNamara, J.P.; Laudon, H.; Kormos, P.; Soulsby, C. Modeling the isotopic evolution of snowpack and snowmelt: Testing a spatially distributed parsimonious approach. Water Resour. Res. 2017, 53, 5813–5830. [Google Scholar] [CrossRef] [PubMed]
- Ambach, W.; Elsässer, M.; Behrens, H.; Moser, H. Studie zum schmelzwasserabfluss aus dem akkumulationsgebiet eines alpengletschers (hintereisferner, ötztaler alpen). Z. Für Gletsch. Und Glazialgeol. 1974, 10, 181–187. [Google Scholar]
- Behrens, H.; Löschhorn, U.; Ambach, W.; Moser, H. Studie zum schmelzwasserabfluss aus dem akkumulationsgebiet eines alpengletschers (hintereisfern, ötztaler alpen). Z. Für Gletsch. Und Glazialgeol. 1976, 12, 69–74. [Google Scholar]
- Duvert, C.; Stewart, M.K.; Cendón, D.I.; Raiber, M. Time series of tritium, stable isotopes and chloride reveal short-term variations in groundwater contribution to a stream. Hydrol. Earth Syst. Sci. 2016, 20, 257–277. [Google Scholar] [CrossRef]
- Birkel, C.; Soulsby, C.; Tetzlaff, D.; Dunn, S.; Spezia, L. High-frequency storm event isotope sampling reveals time-variant transit time distributions and influence of diurnal cycles. Hydrol. Process. 2012, 26, 308–316. [Google Scholar] [CrossRef]
- Birkel, C.; Soulsby, C.; Tetzlaff, D. Conceptual modelling to assess how the interplay of hydrological connectivity, catchment storage and tracer dynamics controls nonstationary water age estimates. Hydrol. Process. 2015, 29, 2956–2969. [Google Scholar] [CrossRef]
- Benettin, P.; Volkmann, T.H.M.; von Freyberg, J.; Frentress, J.; Penna, D.; Dawson, T.E.; Kirchner, J.W. Effects of climatic seasonality on the isotopic composition of evaporating soil waters. Hydrol. Earth Syst. Sci. Discuss. 2018, 2018, 1–16. [Google Scholar] [CrossRef]
- Benettin, P.; Kirchner, J.W.; Rinaldo, A.; Botter, G. Modeling chloride transport using travel time distributions at plynlimon, wales. Water Resour. Res. 2015, 51, 3259–3276. [Google Scholar] [CrossRef]
- Benettin, P.; van der Velde, Y.; van der Zee, S.E.A.T.M.; Rinaldo, A.; Botter, G. Chloride circulation in a lowland catchment and the formulation of transport by travel time distributions. Water Resour. Res. 2013, 49, 4619–4632. [Google Scholar] [CrossRef]
- McDonnell, J.J.; Beven, K. Debates-the future of hydrological sciences: A (common) path forward? A call to action aimed at understanding velocities, celerities and residence time distributions of the headwater hydrograph. Water Resour. Res. 2014, 50, 5342–5350. [Google Scholar] [CrossRef]
- Rinaldo, A.; Beven, K.J.; Bertuzzo, E.; Nicotina, L.; Davies, J.; Fiori, A.; Russo, D.; Botter, G. Catchment travel time distributions and water flow in soils. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Kirchner, J.W.; Feng, X.; Neal, C. Fractal stream chemistry and its implications for contaminant transport in catchments. Nature 2000, 403, 524–527. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Soulsby, C.; Tetzlaff, D.; Malcolm, I.A.; Schoups, G. Gamma distribution models for transit time estimation in catchments: Physical interpretation of parameters and implications for time-variant transit time assessment. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Lutz, S.R.; Krieg, R.; Müller, C.; Zink, M.; Knöller, K.; Samaniego, L.; Merz, R. Spatial patterns of water age: Using young water fractions to improve the characterization of transit times in contrasting catchments. Water Resour. Res. 2018, 54, 4767–4784. [Google Scholar] [CrossRef]
| Method | AE (‰) | As (‰) | τyw (d) | α (–) | ϕS–ϕE (rad) | Fyw (–) |
|---|---|---|---|---|---|---|
| Delayed daily input | 3.1 (3.01–3.2) | 1.44 (1.37–1.54) | 56 (52–60) | 0.59 (0.47–0.72) | 0.76 (0.65–0.87) | 0.47 (0.45–0.5) |
| Delayed monthly input | 2.69 (2.48–3.07) | 1.44 (1.36–1.55) | 44 (NA) | 0.25 (NA) | 0.37 (0.18–0.54) | 0.54 (0.47–0.6) |
| Non-delayed monthly input | 5.43 (5.22–5.66) | 1.44 (1.37–1.55) | 67 (63–71) | 0.93 (0.8–1.07) | 1.24 (1.11–1.36) | 0.28 (0.26–0.3) |
| Metric | 25th Percentile | 50th Percentile | 75th Percentile |
|---|---|---|---|
| α [–] | 0.14 | 0.14 | 0.15 |
| β (d) | 20606 | 24451 | 27266 |
| MTT (d) | 2994 | 3462 | 3847 |
| Mobile storage (mm) | 11975 | 13846 | 15382 |
| τf (d) | 2 | 3 | 4 |
| τs (d) | 117 | 263 | 435 |
| Φ (–) | 0.76 | 0.81 | 0.84 |
| MRT (d) | 28 | 49 | 71 |
| Dynamic storage (mm) | 110 | 195 | 284 |
| Fyw (–) | 0.43 | 0.44 | 0.45 |
| Fow (–) | 0.26 | 0.28 | 0.29 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmieder, J.; Seeger, S.; Weiler, M.; Strasser, U. ‘Teflon Basin’ or Not? A High-Elevation Catchment Transit Time Modeling Approach. Hydrology 2019, 6, 92. https://doi.org/10.3390/hydrology6040092
Schmieder J, Seeger S, Weiler M, Strasser U. ‘Teflon Basin’ or Not? A High-Elevation Catchment Transit Time Modeling Approach. Hydrology. 2019; 6(4):92. https://doi.org/10.3390/hydrology6040092
Chicago/Turabian StyleSchmieder, Jan, Stefan Seeger, Markus Weiler, and Ulrich Strasser. 2019. "‘Teflon Basin’ or Not? A High-Elevation Catchment Transit Time Modeling Approach" Hydrology 6, no. 4: 92. https://doi.org/10.3390/hydrology6040092
APA StyleSchmieder, J., Seeger, S., Weiler, M., & Strasser, U. (2019). ‘Teflon Basin’ or Not? A High-Elevation Catchment Transit Time Modeling Approach. Hydrology, 6(4), 92. https://doi.org/10.3390/hydrology6040092





