Flood Frequency Analysis Using Participatory GIS and Rainfall Data for Two Stations in Narok Town, Kenya
Abstract
1. Introduction
2. Materials and Methods
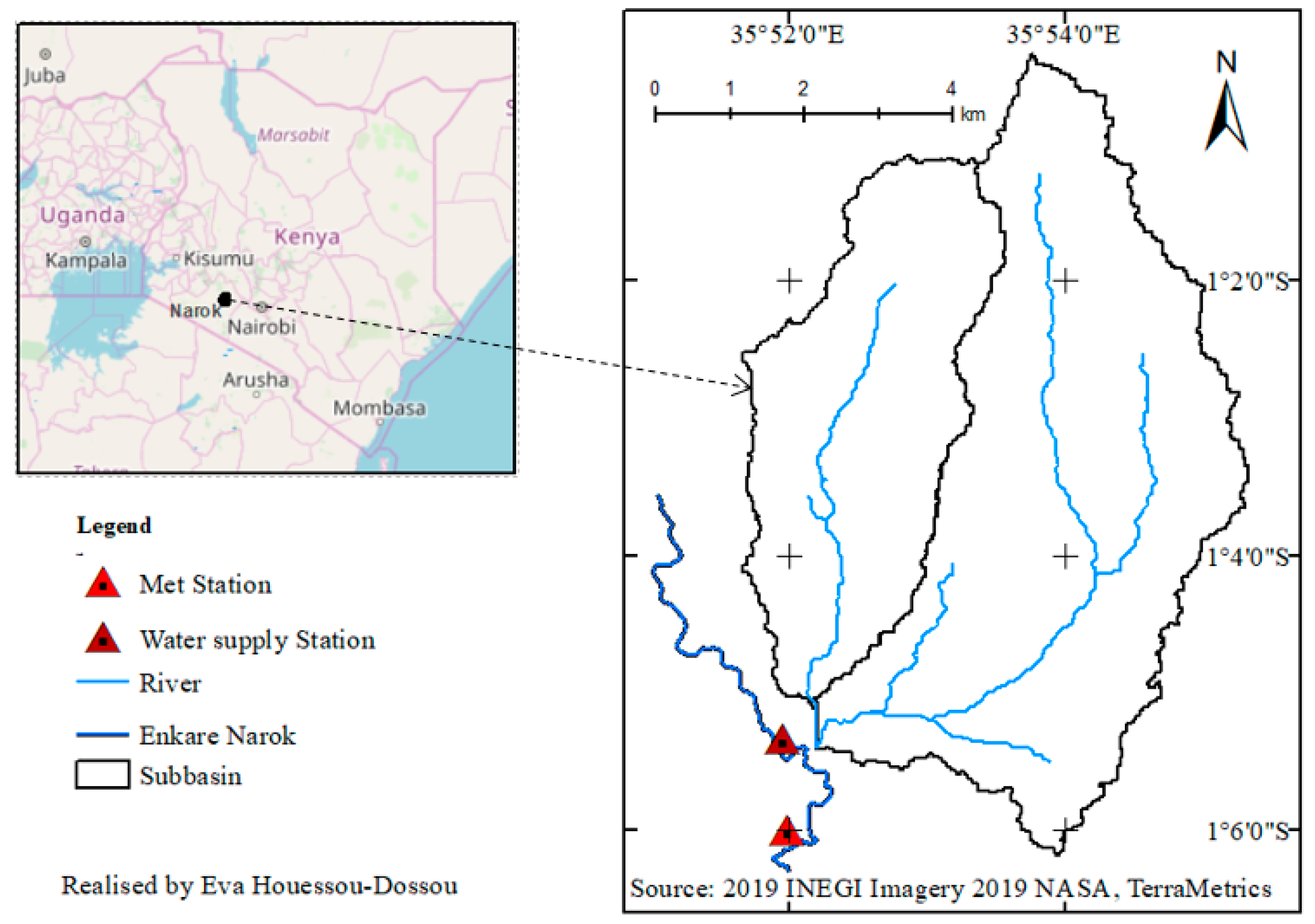
2.1. Study Area
2.2. PGIS
2.3. Flood Frequency Analysis
3. Results and Discussion
3.1. Selection of the Best-Fitted Distribution
3.2. 5, 10, 25, 50, and 100 Years Return Period Calculation
3.3. The Return Period of the Significant Flood Event
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Oosterbaan, R.J. Frequency and Regression Analysis of Hydrologic Data, Part II: Regression Analysis, Chapter 6. Drainage Principles and Applications, Publication, 16; ILRI: Wageningen, The Netherland, 1994. [Google Scholar]
- Singla, S.; Halder, R.; Khosa, R.; Singla, R.; Rajeev, R. Frequency analysis of annual one day to five consecutive days maximum rainfall for Gandak river basin. Int. J. Eng. Technol. 2014, 3, 93. [Google Scholar] [CrossRef][Green Version]
- Dalinsky, J.S. An unconventional approach to flood frequency analysis. Int. Assoc. Sci. Hydrol. Bull. 1970, 15, 55–59. [Google Scholar] [CrossRef]
- Izinyon, O.C.; Ihimekpen, N.; Igbinoba, G.E. Flood Frequency Analysis of Ikpoba River Catchment at Benin City Using Log Pearson Type III Distribution. J. Emerg. Trends Eng. Appl. Sci. 2011, 2, 50–55. [Google Scholar]
- BV, D.C.; Hydraulics, D. How to Analyse Rainfall Data; 2002. Available online: https://www.mahahp.gov.in/old_mahahp.org/resource/modules/12%20How%20to%20analyse%20rainfall%20data.pdf (accessed on 2 September 2019).
- Hailegeorgis, T.T.; Alfredsen, K. Regional flood frequency analysis and prediction in ungauged basins including estimation of major uncertainties for mid-Norway. J. Hydrol. Reg. Stud. 2017, 9, 104–126. [Google Scholar] [CrossRef]
- Kandpal, A.; Kanwal, S.; Gosain, A. Estimation of Consecutive Days Maximum Rainfall using Different Probability Distributions and Their Comparsion. In Proceedings of the National Conference on Innovative Research in Agriculture, Food Science, Forestry, Horticulture, Aquaculture, Animal Sciences, Biodiversity, Environmental Engineering and Climate Change (AFHABEC-2015), New Delhi, India, November 2015. [Google Scholar]
- Tabish, M.; Ahsan, M.J.; Mishra, A. Probability Analysis for Prediction of Annual Maximum Rainfall of One to Seven Consecutive Days for Ambedkar Nagar Uttar Pradesh. IJASR 2015, 6, 47–54. [Google Scholar]
- Chapin, M.; Lamb, Z.; Threlkeld, B. Mapping Indigenous Lands. Annu. Rev. Anthropol. 2005, 34, 619–638. [Google Scholar] [CrossRef]
- Poole, P. Indigenous Peoples, Mapping & Biodiversity Conservation: An Analysis of Current Activities and Opportunities for Applying Geomatics Technologies (No. 333.95 P822); Biodiversity Support Program; EUA: Washington, DC, USA, 1995. [Google Scholar]
- Ouma, Y.O.; Tateishi, R. Urban Flood Vulnerability and Risk Mapping Using Integrated Multi-Parametric AHP and GIS: Methodological Overview and Case Study Assessment. Water 2014, 6, 1515–1545. [Google Scholar] [CrossRef]
- Lassueur, T.; Joost, S.; Randin, C.F. Very high resolution digital elevation models: Do they improve models of plant species distribution? Ecol. Model. 2006, 198, 139–153. [Google Scholar] [CrossRef]
- Musungu, K.; Motala, S.; Smit, J. A Participatory Approach to Data Collection for GIS for Flood Risk Management in Informal Settlements of Cape Town. In Proceedings of the AfricaGEO Conference, Cape Town, South Africa, 1–2 June 2011. [Google Scholar]
- Abbot, J.; Chambers, R.; Dunn, C.; Harris, T.; Merode, E.D.; Porter, G.; Weiner, D. Participatory GIS: Opportunity or oxymoron. PLA Notes 1998, 33, 27–33. [Google Scholar]
- Guarín, G.P.; Westen, C.J.; Montoya, L. Community-Based Flood Risk Assessment Using GIS for the Town of San Sebastian, Guatemala; International Institute for Geoinformation Science and Earth Observation (ITC): Enschede, The Netherlands, 2004. [Google Scholar]
- Hunter, A.P.G.; Bishop, A.P.I. Introduction to GIS Definition of GIS. System 1–13. Available online: https://aqua.wisc.edu/CPR/IntroductiontoGeographicInformationSystemsGIS/tabid/78/Default.aspx (accessed on 2 September 2019).
- Cinderby, S. Participatory Geographic Information Systems (GIS): The future of environmental GIS. Int. J. Environ. Pollut. 1999, 11, 304–315. [Google Scholar] [CrossRef]
- McCall, M. Precision for whom? Mapping ambiguity and certainty in (Participatory) GIS. Particip. Learn. Action 2006, 54, 114–119. [Google Scholar]
- Corbett, J.; Rambaldi, G.; Kyem, P.; Weiner, D.; Olson, R.; Muchemi, J.; McCall, M.; Chambers, R. Mapping for Change: The emergence of a new Participatory GIS practice. Particip. Learn. Action 2006, 13–19. Available online: Ftp://ftp.itc.nl/pub/pgis/PGIS%20Articles/Intro%20New%20PGIS.PDF (accessed on 2 September 2019).
- Tripathi, N.; Bhattarya, S. Integrating Indigenous Knowledge and GIS for Participatory Natural Resource Management: State-of-the-Practice. Electron. J. Inf. Syst. Dev. Ctries. 2004, 17, 1–13. [Google Scholar]
- Rinner, C.; Bird, M. Evaluating community engagement through argumentation maps-A public participation GIS case study. Environ. Plan. B Plan. Des. 2009, 36, 588–601. [Google Scholar] [CrossRef]
- Ghanbarpour, M.R.; Salimi, S.; Saravi, M.M.; Zarei, M. Calibration of river hydraulic model combined with GIS analysis using ground-based observation data. Res. J. Appl. Sci. Eng. Technol. 2011, 3, 456–463. [Google Scholar]
- Citation, S. Improving American River Flood Frequency Analyses; The National Academies Press: Washington, DC, USA, 1999. [Google Scholar]
- Gilleland, E.; Ribatet, M.; Stephenson, A.G. A software review for extreme value analysis. Extremes 2013, 16, 103–119. [Google Scholar] [CrossRef]
- Raes, D.; Mallants, D.; Song, Z. Rainbow: A software package for analysing hydrologic data. WIT Trans. Ecol. Environ. 1970, 18. [Google Scholar] [CrossRef]
- Flynn, K.M.; Kirby, W.H.; Hummel, P.R. User′s Manual for Program PeakFQ, Annual Flood-Frequency Analysis Using Bulletin 17B Guidelines; (No. 4-B4); 2006. Available online: https://pubs.er.usgs.gov/publication/tm4B4 (accessed on 2 September 2019).
- Kozanis, S.; Christofides, A.; Mamassis, N.; Efstratiadis, A.; Koutsoyiannis, D. Hydrognomon–open source software for the analysis of hydrological data. In Proceedings of the European Geosciences Union General Assembly 2010, Vienna, Austria, 2–7 May 2010; Volume 12, p. 12419. [Google Scholar]
- Adlouni, E.S.B.; Bobée, B. Hydrological frequency analysis using HYFRAN-PLUS software. In Chaire Indusrielle Hydro-Québec/CRSNG en Hydrologie Statistique/Institut National de la Recherche Scientifique (INRS)/Centre Eau; Terre et Environnement: Montréal, QC, Canada, 2015; p. 71. [Google Scholar]
- Garba, H.; Ismail, A.; Olusoga, F.; Oriola, P. Calibration of Hydrognomon Model for Simulating the Hydrology of Urban Catchment. Open J. Mod. Hydrol. 2013, 3, 75–78. [Google Scholar] [CrossRef][Green Version]
- Garba, H.; Ibrahim, A.; Ahmed, S.; Faustinus, B. Hydrological Modeling of the Impact Of Climate Change On A Tropical Perennial River Flooding By. Res. Inven. Int. J. Eng. Sci. 2013, 3, 30–35. [Google Scholar]
- Alam, M.A.; Emura, K.; Farnham, C.; Yuan, J. Best-Fit Probability Distributions and Return Periods for Maximum Monthly Rainfall in Bangladesh. Climate 2018, 6, 9. [Google Scholar] [CrossRef]
- Wuensch, K.L. Chi-Square Tests. Int. Encycl. Stat. Sci. 2011, 252–253. [Google Scholar] [CrossRef]
- Romman, Z.A.; Al-Bakri, J.T.; al Kuisi, M.M. Estimation of Rainfall Missing Data in an Arid Area using Spatial and EM Methods. J. Softw. Eng. Appl. 2019, 9, 76–80. [Google Scholar]
- Simolo, C.; Brunetti, M.; Maugeri, M.; Nanni, T. Improving estimation of missing values in daily precipitation series by a probability density function-preserving approach. Int. J. Climatol. 2010, 30, 1564–1576. [Google Scholar] [CrossRef]
- Oosterbaan, R.J. Frequency and Regression Analysis of Hydrologic Data. Part I: Frequency Analysis. Drainage Principles and Applications, Publication 16. Chapter 6; Ritzema, H.P., Ed.; International Institute for Land Reclamation and Improvement (ILRI): Wageningen, The Netherlands, 1994. [Google Scholar]
- Chen, T.; Ren, L.; Yuan, F.; Yang, X.; Jiang, S.; Tang, T.; Liu, Y.; Zhao, C.; Zhang, L. Comparison of Spatial Interpolation Schemes for Rainfall Data and Application in Hydrological Modeling. Water 2017, 9, 342. [Google Scholar] [CrossRef]
- Al-Amri, N.S.; Subyani, A.M. Analysis of Rainfall, Missing Data, Frequency and PMP in Al-Madinah Area, Western Saudi Arabia. In Arabian Plate and Surroundings: Geology, Sedimentary Basins and Georesources; Springer: Cham, Germany, 2020; pp. 235–248. [Google Scholar]
- World Meteorological Organization Communications and Public Affairs Office Hydrology and Water Resources Branch Climate and Water Department. Manual On Flood Forecasting and Warning; P-ClW_102107; World Meteorological Organization: Geneva, Switzerland, 2011; No. 1072. [Google Scholar]
- Keblouti, M.; Ouerdachi, L.; Boutaghane, H. Spatial Interpolation of Annual Precipitation in Annaba-Algeria—Comparison and Evaluation of Methods. Energy Procedia 2012, 18, 468–475. [Google Scholar] [CrossRef]
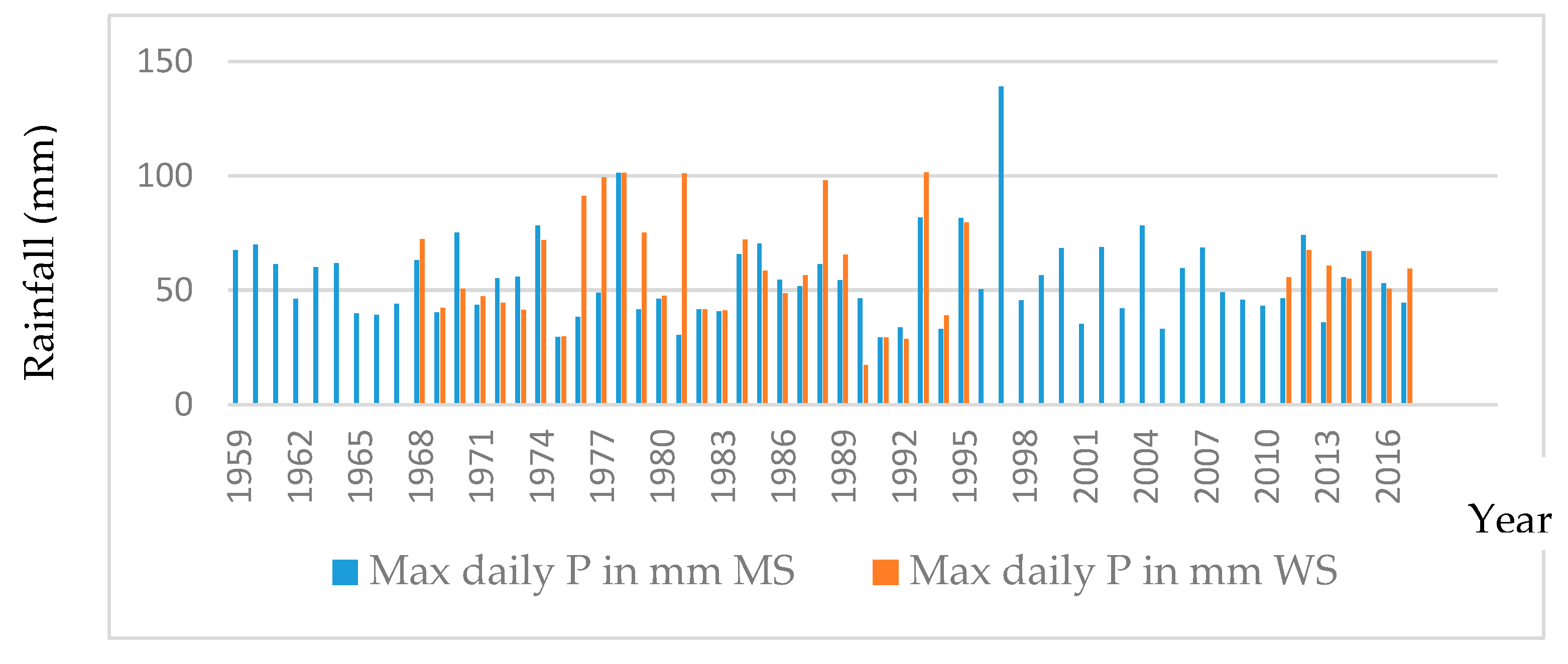
| Year | Max Daily P in mm | Year | Max Daily P in mm | Year | Max Daily P in mm | |||
|---|---|---|---|---|---|---|---|---|
| MS | WS | MS | WS | MS | WS | |||
| 1959 | 67.3 | - | 1979 | 41.7 | 75.1 | 1999 | 56.5 | - |
| 1960 | 69.9 | - | 1980 | 46.2 | 47.5 | 2000 | 68.2 | - |
| 1961 | 61.2 | - | 1981 | 30.3 | 101 | 2001 | 35.2 | - |
| 1962 | 46.2 | - | 1982 | 41.6 | 41.6 | 2002 | 68.8 | - |
| 1963 | 60 | - | 1983 | 40.7 | 41.1 | 2003 | 42 | - |
| 1964 | 61.6 | - | 1984 | 65.6 | 72 | 2004 | 78.2 | - |
| 1965 | 39.9 | - | 1985 | 70.3 | 58.5 | 2005 | 33.1 | - |
| 1966 | 39.1 | - | 1986 | 54.4 | 48.7 | 2006 | 59.4 | - |
| 1967 | 44 | - | 1987 | 51.5 | 56.4 | 2007 | 68.6 | - |
| 1968 | 63 | 72.3 | 1988 | 61.2 | 98 | 2008 | 49.1 | - |
| 1969 | 40.3 | 42.3 | 1989 | 54.2 | 65.5 | 2009 | 45.8 | - |
| 1970 | 75 | 50.5 | 1990 | 46.5 | 17.3 | 2010 | 43.1 | - |
| 1971 | 43.6 | 47.3 | 1991 | 29.2 | 29.3 | 2011 | 46.5 | 55.5 |
| 1972 | 55 | 44.5 | 1992 | 33.8 | 28.7 | 2012 | 74 | 67.4 |
| 1973 | 55.7 | 41.4 | 1993 | 81.7 | 101.5 | 2013 | 36 | 60.5 |
| 1974 | 78.2 | 71.8 | 1994 | 33 | 39 | 2014 | 55.6 | 54.8 |
| 1975 | 29.6 | 29.7 | 1995 | 81.4 | 79.5 | 2015 | 67 | 67 |
| 1976 | 38.2 | 91 | 1996 | 50.2 | - | 2016 | 52.8 | 50.5 |
| 1977 | 48.9 | 99.3 | 1997 | 139 | - | 2017 | 44.5 | 59.2 |
| 1978 | 101.2 | 101.2 | 1998 | 45.5 | - | |||
| Water Supply Station | |||||
|---|---|---|---|---|---|
| Max 1 Day | Max 2 Days | Max 3 Days | |||
| K–S | Chi-Square | K–S | Chi-Square | K–S | Chi-Square |
| LP III (0.08) | LP III (0.33) | Gal (0.09) | Gal (4.33) | Norm L- mom (0.07) | Norm L- mom (0.33) |
| Par (0.08) | Par (2.33) | Pear III (0.09) | Pear III (4.33) | EV3 (0.07) | EV3 (0.07) |
| GEV L-mom (0.08) | GEV L-mom (2.33) | Gam (0.09) | Gam (4.00) | GEV (0.07) | GEV (1.00) |
| EV1 L-mom (0.08) | EV1 L-mom (0.33) | GEV (0.09) | GEV (3.33) | GEV L-mom (0.07) | GEV L-mom (1.00) |
| Par (0.08) | Par (2.33) | GEV L-mom (0.08) | GEV L-mom (3.00) | EV3 L-mom (0.07) | EV3 L-mom (1.00) |
| GEV L-mom k specified (0.09) | GEV L-mom k specified (0.33) | Par L-mom (0.07) | Par L-mom (1.7) | Par L-mom (0.07) | Par L-mom (0.67) |
| Meteorological Station | |||||
|---|---|---|---|---|---|
| Max 1 Day | Max 2 Days | Max 3 Days | |||
| k–s | Chi-Square | k–s | Chi-Square | k–s | Chi-Square |
| LN (0.06) | LN (0.92) | LN (0.06) | LN (4.71) | LN (O.06) | LN (2.34) |
| Gal (0.05) | Gal (3.29) | Gal (0.06) | Gal (06.14) | Gam (0.06) | Gam (1.62) |
| LP III (O.05) | LP III (2.10) | LP III (0.06) | LP III (5.19) | LP III (0.05) | LP III (3.53) |
| EV1 (0.06) | EV1 (1.15) | EV1 (0.06) | EV1 (4.71) | EV1 (0.06) | EV1 (3.29) |
| GEV (0.06) | GEV (3.05) | GEV (0.06) | GEV (6.14) | EV1 L-mom (0.05) | EV1 L-mom (2.10) |
| GEV L-mom (0.04) | GEV L-mom (1.15) | GEV L-mom (0.06) | GEV L-mom (4.71) | GEV L-mom (0.05) | GEV L-mom (2.10) |
| WS | MS | ||
|---|---|---|---|
| Max 1 Day | Max 1 Day | ||
| Gumbel L-moment | GEV Min L-moment | ||
| Return period (year) | Max daily Rainfall (mm) | Return period (year) | Max daily Rainfall (mm) |
| 5 | 78.8022 | 5 | 68.8304 |
| 10 | 92.8842 | 10 | 80.0689 |
| 25 | 110.677 | 25 | 93.4172 |
| 50 | 123.876 | 50 | 102.734 |
| 100 | 131.592 | 100 | 111.55 |
| Max 2 Days | Max 2 Days | ||
| Pareto L-moment | Gumbel Max | ||
| Return period (year) | Rainfall (mm) | Return period (year) | Rainfall (mm) |
| 5 | 106.007 | 5 | 88.5849 |
| 10 | 118.705 | 10 | 101.557 |
| 25 | 128.513 | 25 | 117.948 |
| 50 | 132.789 | 50 | 130.107 |
| 100 | 135.464 | 100 | 142.177 |
| Max 3 Days | Max 3 Days | ||
| EV3-Min (Weibull) | gamma | ||
| Return period (year) | Rainfall (mm) | Return period (year) | Rainfall (mm) |
| 5 | 113.632 | 5 | 101.115 |
| 10 | 125.974 | 10 | 114.296 |
| 25 | 138.729 | 25 | 129.526 |
| 50 | 146.741 | 50 | 140.024 |
| 100 | 153.797 | 100 | 149.916 |
| MS Rainfall in mm | WS Rainfall in mm | Date | MS Rainfall in mm | WS Rainfall in mm | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Date | One Day | 2 Days | 3 Days | One Day | 2 Days | 3 Days | One Day | 2 Days | 3 Days | One Day | 2 Days | 3 Days | |
| 1/1/1993 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 5/1/2013 | 0.0 | 3.6 | 5.3 | 5 | 5 | 5 |
| 1/2/1993 | 0.1 | 0.1 | 0.1 | 0 | 0 | 0 | 5/2/2013 | 31.9 | 31.9 | 35.5 | 0 | 5 | 5 |
| 1/3/1993 | 0.0 | 0.1 | 0.1 | 0 | 0 | 0 | 5/3/2013 | 0.0 | 31.9 | 31.9 | 37 | 37 | 42 |
| 1/4/1993 | 2.1 | 2.1 | 2.2 | 1.9 | 1.9 | 1.9 | 5/4/2013 | 0.0 | 0.0 | 31.9 | 0 | 37 | 37 |
| 1/5/1993 | 0.0 | 2.1 | 2.1 | 0 | 1.9 | 1.9 | 5/5/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 37 |
| 1/6/1993 | 0.0 | 0.0 | 2.1 | 0 | 0 | 1.9 | 5/6/2013 | 4.3 | 4.3 | 4.3 | 4.6 | 4.6 | 4.6 |
| 1/7/1993 | 0.6 | 0.6 | 0.6 | 0.9 | 0.9 | 0.9 | 5/7/2013 | 0.8 | 5.1 | 5.1 | 0 | 4.6 | 4.6 |
| 1/8/1993 | 5.8 | 6.4 | 6.4 | 5.7 | 6.6 | 6.6 | 5/8/2013 | 2.7 | 3.5 | 7.8 | 0 | 0 | 4.6 |
| 1/9/1993 | 1.4 | 7.2 | 7.8 | 1.9 | 7.6 | 8.5 | 5/9/2013 | 5.3 | 8.0 | 8.8 | 10.6 | 10.6 | 10.6 |
| 1/10/1993 | 0.0 | 1.4 | 7.2 | 0 | 1.9 | 7.6 | 5/10/2013 | 7.3 | 12.6 | 15.3 | 9.1 | 19.7 | 19.7 |
| 1/11/1993 | 0.0 | 0.0 | 1.4 | 0 | 0 | 1.9 | 5/11/2013 | 0.0 | 7.3 | 12.6 | 0 | 9.1 | 19.7 |
| 1/12/1993 | 21.7 | 21.7 | 21.7 | 22.7 | 22.7 | 22.7 | 5/12/2013 | 0.0 | 0.0 | 7.3 | 0 | 0 | 9.1 |
| 1/13/1993 | 8.4 | 30.1 | 30.1 | 8.1 | 30.8 | 30.8 | 5/13/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/14/1993 | 6.7 | 15.1 | 36.8 | 12.8 | 20.9 | 43.6 | 5/14/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/15/1993 | 2.5 | 9.2 | 17.6 | 3.3 | 16.1 | 24.2 | 5/15/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/16/1993 | 39.7 | 42.2 | 48.9 | 40.8 | 44.1 | 56.9 | 5/16/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/17/1993 | 10.8 | 50.5 | 53.0 | 5.3 | 46.1 | 49.4 | 5/17/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/18/1993 | 0.0 | 10.8 | 50.5 | 0 | 5.3 | 46.1 | 5/18/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/19/1993 | 26.6 | 26.6 | 37.4 | 27.5 | 27.5 | 32.8 | 5/19/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/20/1993 | 81.7 | 108.3 | 108.3 | 101.5 | 129 | 129 | 5/20/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/21/1993 | 0.0 | 81.7 | 108.3 | 0 | 101.5 | 129 | 5/21/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/22/1993 | 2.7 | 2.7 | 84.4 | 33.1 | 33.1 | 134.6 | 5/22/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/23/1993 | 29.1 | 31.8 | 31.8 | 0 | 33.1 | 33.1 | 5/23/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/24/1993 | 0.0 | 29.1 | 31.8 | 0 | 0 | 33.1 | 5/24/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/25/1993 | 0.0 | 0.0 | 29.1 | 0 | 0 | 0 | 5/25/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/26/1993 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 5/26/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/27/1993 | 0.6 | 0.6 | 0.6 | 0 | 0 | 0 | 5/27/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/28/1993 | 0.8 | 1.4 | 1.4 | 1.4 | 1.4 | 1.4 | 5/28/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/29/1993 | 0.0 | 0.8 | 1.4 | 0 | 1.4 | 1.4 | 5/29/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/30/1993 | 16.9 | 16.9 | 17.7 | 14.2 | 14.2 | 15.6 | 5/30/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 1/31/1993 | 0.0 | 16.9 | 16.9 | 0.5 | 14.7 | 14.7 | 5/31/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 3/1/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 4/1/2015 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 3/2/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 4/2/2015 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 3/3/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 4/3/2015 | 8.0 | 8.0 | 8.0 | 0 | 0 | 0 |
| 4/3/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 4/4/2015 | 0.0 | 8.0 | 8.0 | 8 | 8 | 8 |
| 3/5/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 4/5/2015 | 0.0 | 0.0 | 8.0 | 0 | 8 | 8 |
| 3/6/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 4/6/2015 | 3.0 | 3.0 | 3.0 | 0 | 0 | 8 |
| 3/7/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 4/7/2015 | 1.0 | 4.0 | 4.0 | 3 | 3 | 3 |
| 3/8/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 4/8/2015 | 0.0 | 1.0 | 4.0 | 1 | 4 | 4 |
| 3/9/2013 | 13.5 | 13.5 | 13.5 | 0 | 0 | 0 | 4/9/2015 | 0.0 | 0.0 | 1.0 | 0 | 1 | 4 |
| 3/10/2013 | 0.5 | 14.0 | 14.0 | 0 | 0 | 0 | 4/10/2015 | 32.8 | 32.8 | 32.8 | 0 | 0 | 1 |
| 3/11/2013 | 0.0 | 0.5 | 14.0 | 14.2 | 14.2 | 14.2 | 4/11/2015 | 0.0 | 32.8 | 32.8 | 32.8 | 32.8 | 32.8 |
| 3/12/2013 | 0.0 | 0.0 | 0.5 | 0 | 14.2 | 14.2 | 4/12/2015 | 0.0 | 0.0 | 32.8 | 0 | 32.8 | 32.8 |
| 3/13/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 14.2 | 4/13/2015 | 0.0 | 0.0 | 0.0 | 0 | 0 | 32.8 |
| 3/14/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 4/14/2015 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 3/15/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 4/15/2015 | 1.6 | 1.6 | 1.6 | 0 | 0 | 0 |
| 3/16/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 4/16/2015 | 0.0 | 1.6 | 1.6 | 1.6 | 1.6 | 1.6 |
| 3/17/2013 | 7.6 | 7.6 | 7.6 | 0 | 0 | 0 | 4/17/2015 | 12.4 | 12.4 | 14.0 | 0 | 1.6 | 1.6 |
| 3/18/2013 | 2.1 | 9.7 | 9.7 | 0 | 0 | 0 | 4/18/2015 | 4.4 | 16.8 | 16.8 | 12.4 | 12.4 | 14 |
| 3/19/2013 | 0.0 | 2.1 | 9.7 | 12.4 | 12.4 | 12.4 | 4/19/2015 | 8.4 | 12.8 | 25.2 | 4.4 | 16.8 | 16.8 |
| 3/20/2013 | 0.0 | 0.0 | 2.1 | 2.7 | 15.1 | 15.1 | 4/20/2015 | 0.0 | 8.4 | 12.8 | 8.4 | 12.8 | 25.2 |
| 3/21/2013 | 0.0 | 0.0 | 0.0 | 0 | 2.7 | 15.1 | 4/21/2015 | 10.8 | 10.8 | 19.2 | 0 | 8.4 | 12.8 |
| 3/22/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 2.7 | 4/22/2015 | 1.0 | 11.8 | 11.8 | 10.8 | 10.8 | 19.2 |
| 3/23/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 4/23/2015 | 16.8 | 17.8 | 28.6 | 1 | 11.8 | 11.8 |
| 3/24/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 4/24/2015 | 1.6 | 18.4 | 19.4 | 16.8 | 17.8 | 28.6 |
| 3/25/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 4/25/2015 | 6.8 | 8.4 | 25.2 | 1.6 | 18.4 | 19.4 |
| 3/26/2013 | 14.8 | 14.8 | 14.8 | 0 | 0 | 0 | 4/26/2015 | 16.0 | 22.8 | 24.4 | 6.8 | 8.4 | 25.2 |
| 3/27/2013 | 2.7 | 17.5 | 17.5 | 0 | 0 | 0 | 4/27/2015 | 14.0 | 30.0 | 36.8 | 16 | 22.8 | 24.4 |
| 3/28/2013 | 0.0 | 2.7 | 17.5 | 18.5 | 18.5 | 18.5 | 4/28/2015 | 33.2 | 47.2 | 63.2 | 14 | 30 | 36.8 |
| 3/29/2013 | 27.5 | 27.5 | 30.2 | 0 | 18.5 | 18.5 | 4/29/2015 | 4.6 | 37.8 | 51.8 | 33.2 | 47.2 | 63.2 |
| 3/30/2013 | 33.6 | 61.1 | 61.1 | 0 | 0 | 18.5 | 4/30/2015 | 34.2 | 38.8 | 72.0 | 4.6 | 37.8 | 51.8 |
| 3/31/2013 | 0.0 | 33.6 | 61.1 | 29.8 | 29.8 | 29.8 | 5/1/2015 | 3.5 | 37.7 | 42.3 | 34.2 | 38.8 | 72 |
| 4/1/2013 | 1.1 | 1.1 | 34.7 | 0 | 29.8 | 29.8 | 5/2/2015 | 0.0 | 3.5 | 37.7 | 3.5 | 37.7 | 42.3 |
| 4/2/2013 | 0.0 | 1.1 | 1.1 | 0 | 0 | 29.8 | 5/3/2015 | 0.0 | 0.0 | 3.5 | 0 | 3.5 | 37.7 |
| 4/3/2013 | 0.0 | 0.0 | 1.1 | 0 | 0 | 0 | 5/4/2015 | 10.2 | 10.2 | 10.2 | 0 | 0 | 3.5 |
| 4/4/2013 | 6.9 | 6.9 | 6.9 | 7.8 | 7.8 | 7.8 | 5/5/2015 | 0.0 | 10.2 | 10.2 | 10.2 | 10.2 | 10.2 |
| 4/5/2013 | 4.0 | 10.9 | 10.9 | 6.6 | 14.4 | 14.4 | 5/6/2015 | 67.0 | 67.0 | 77.2 | 0 | 10.2 | 10.2 |
| 4/6/2013 | 7.8 | 11.8 | 18.7 | 40.5 | 47.1 | 54.9 | 5/7/2015 | 2.8 | 69.8 | 69.8 | 67 | 67 | 77.2 |
| 4/7/2013 | 23.0 | 30.8 | 34.8 | 60.5 | 101 | 107.6 | 5/8/2015 | 0.0 | 2.8 | 69.8 | 2.8 | 69.8 | 69.8 |
| 4/8/2013 | 14.0 | 37.0 | 44.8 | 19.2 | 79.7 | 120.2 | 5/9/2015 | 0.0 | 0.0 | 2.8 | 0 | 2.8 | 69.8 |
| 4/9/2013 | 15.6 | 29.6 | 52.6 | 12 | 31.2 | 91.7 | 5/10/2015 | 5.9 | 5.9 | 5.9 | 0 | 0 | 2.8 |
| 4/10/2013 | 0.0 | 15.6 | 29.6 | 0 | 12 | 31.2 | 5/11/2015 | 8.1 | 14.0 | 14.0 | 5.9 | 5.9 | 5.9 |
| 4/11/2013 | 1.3 | 1.3 | 16.9 | 0 | 0 | 12 | 5/12/2015 | 14.3 | 22.4 | 28.3 | 8.1 | 14 | 14 |
| 4/12/2013 | 30.8 | 32.1 | 32.1 | 57.7 | 57.7 | 57.7 | 5/13/2015 | 16.9 | 31.2 | 39.3 | 14.3 | 22.4 | 28.3 |
| 4/13/2013 | 11.8 | 42.6 | 43.9 | 16.8 | 74.5 | 74.5 | 5/14/2015 | 0.0 | 16.9 | 31.2 | 16.9 | 31.2 | 39.3 |
| 4/14/2013 | 6.8 | 18.6 | 49.4 | 6.4 | 23.2 | 80.9 | 5/15/2015 | 0.0 | 0.0 | 16.9 | 0 | 16.9 | 31.2 |
| 4/15/2013 | 0.0 | 6.8 | 18.6 | 0 | 6.4 | 23.2 | 5/16/2015 | 0.0 | 0.0 | 0.0 | 0 | 0 | 16.9 |
| 4/16/2013 | 27.8 | 27.8 | 34.6 | 27.6 | 27.6 | 34 | 5/17/2015 | 0.8 | 0.8 | 0.8 | 0 | 0 | 0 |
| 4/17/2013 | 0.0 | 27.8 | 27.8 | 0 | 27.6 | 27.6 | 5/18/2015 | 0.0 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
| 4/18/2013 | 24.4 | 24.4 | 52.2 | 23.2 | 23.2 | 50.8 | 5/19/2015 | 0.0 | 0.0 | 0.8 | 0 | 0.8 | 0.8 |
| 4/19/2013 | 7.7 | 32.1 | 32.1 | 7.9 | 31.1 | 31.1 | 5/20/2015 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0.8 |
| 4/20/2013 | 0.0 | 7.7 | 32.1 | 0 | 7.9 | 31.1 | 5/21/2015 | 1.8 | 1.8 | 1.8 | 0 | 0 | 0 |
| 4/21/2013 | 1.0 | 1.0 | 8.7 | 0 | 0 | 7.9 | 5/22/2015 | 1.0 | 2.8 | 2.8 | 1.8 | 1.8 | 1.8 |
| 4/22/2013 | 14.3 | 15.3 | 15.3 | 21.9 | 21.9 | 21.9 | 5/23/2015 | 0.0 | 1.0 | 2.8 | 1 | 2.8 | 2.8 |
| 4/23/2013 | 4.3 | 18.6 | 19.6 | 1.7 | 23.6 | 23.6 | 5/24/2015 | 0.0 | 0.0 | 1.0 | 0 | 1 | 2.8 |
| 4/24/2013 | 1.4 | 5.7 | 20.0 | 0 | 1.7 | 23.6 | 5/25/2015 | 0.0 | 0.0 | 0.0 | 0 | 0 | 1 |
| 4/25/2013 | 0.0 | 1.4 | 5.7 | 0 | 0 | 1.7 | 5/26/2015 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 4/26/2013 | 0.0 | 0.0 | 1.4 | 0 | 0 | 0 | 5/27/2015 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 4/27/2013 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 | 5/28/2015 | 0.0 | 0.0 | 0.0 | 0 | 0 | 0 |
| 4/28/2013 | 36.0 | 36.0 | 36.0 | 39.5 | 39.5 | 39.5 | 5/29/2015 | 0.5 | 0.5 | 0.5 | 0 | 0 | 0 |
| 4/29/2013 | 1.7 | 37.7 | 37.7 | 0 | 39.5 | 39.5 | 5/30/2015 | 0.8 | 1.3 | 1.3 | 0.5 | 0.5 | 0.5 |
| 4/30/2013 | 3.6 | 5.3 | 41.3 | 0 | 0 | 39.5 | 5/31/2015 | 0.0 | 0.8 | 1.3 | 0.8 | 1.3 | 1.3 |
| Date | Daily Rainfall in mm | Forecast T in Years |
|---|---|---|
| 1/20/1993 | 81.7 | 6 |
| 3/30/2013 | 33.6 | 1 |
| 4/18/2013 | 24.4 | 1 |
| 4/28/2015 | 33.2 | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Houessou-Dossou, E.A.Y.; Mwangi Gathenya, J.; Njuguna, M.; Abiero Gariy, Z. Flood Frequency Analysis Using Participatory GIS and Rainfall Data for Two Stations in Narok Town, Kenya. Hydrology 2019, 6, 90. https://doi.org/10.3390/hydrology6040090
Houessou-Dossou EAY, Mwangi Gathenya J, Njuguna M, Abiero Gariy Z. Flood Frequency Analysis Using Participatory GIS and Rainfall Data for Two Stations in Narok Town, Kenya. Hydrology. 2019; 6(4):90. https://doi.org/10.3390/hydrology6040090
Chicago/Turabian StyleHouessou-Dossou, Eva Audrey Yessito, John Mwangi Gathenya, Mugwima Njuguna, and Zachary Abiero Gariy. 2019. "Flood Frequency Analysis Using Participatory GIS and Rainfall Data for Two Stations in Narok Town, Kenya" Hydrology 6, no. 4: 90. https://doi.org/10.3390/hydrology6040090
APA StyleHouessou-Dossou, E. A. Y., Mwangi Gathenya, J., Njuguna, M., & Abiero Gariy, Z. (2019). Flood Frequency Analysis Using Participatory GIS and Rainfall Data for Two Stations in Narok Town, Kenya. Hydrology, 6(4), 90. https://doi.org/10.3390/hydrology6040090





