Doing Hydrology Backwards—Analytic Solution Connecting Streamflow Oscillations at the Basin Outlet to Average Evaporation on a Hillslope
Abstract
1. Introduction
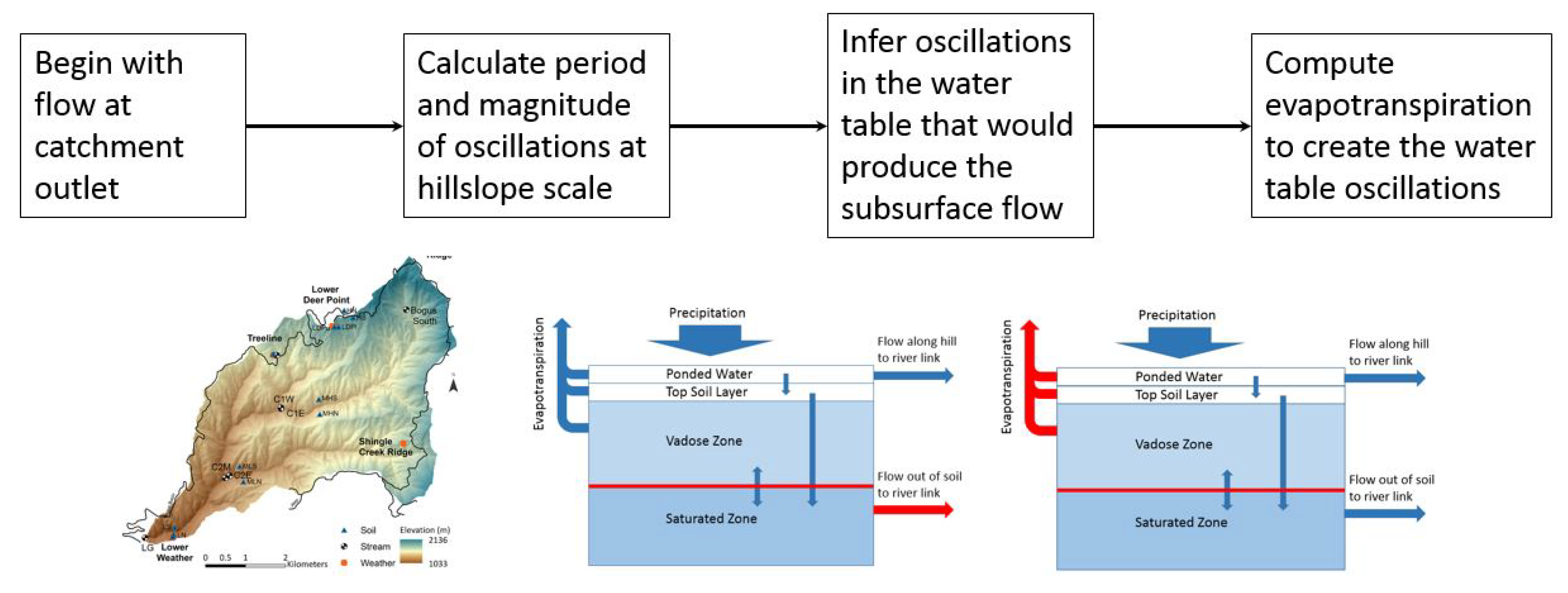
2. Hydrology Across Scales—Using Catchment Streamflow to Determine Hillslope Runoff
3. Damping Oscillatory Runoff Patterns and Hillslope Scale Physical Processes
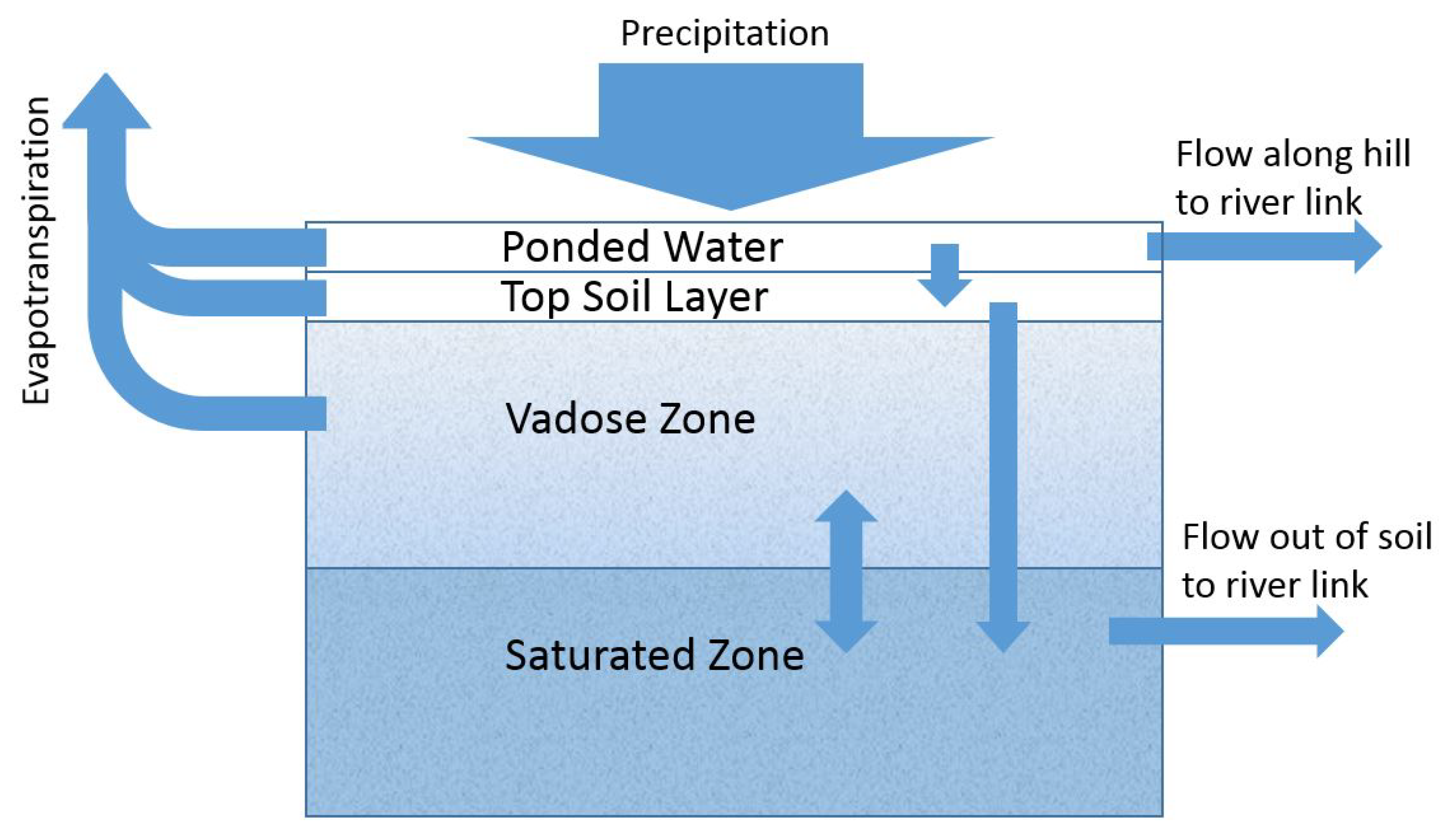
3.1. Model to Describe Water
3.2. Expected Subsurface Characteristics That Lead to Observed Fluctuating Runoff Patterns
3.3. The Modified Hillslope Model
4. Using the Subsurface Model and Subsurface Flow to Determine Evapotranspiration
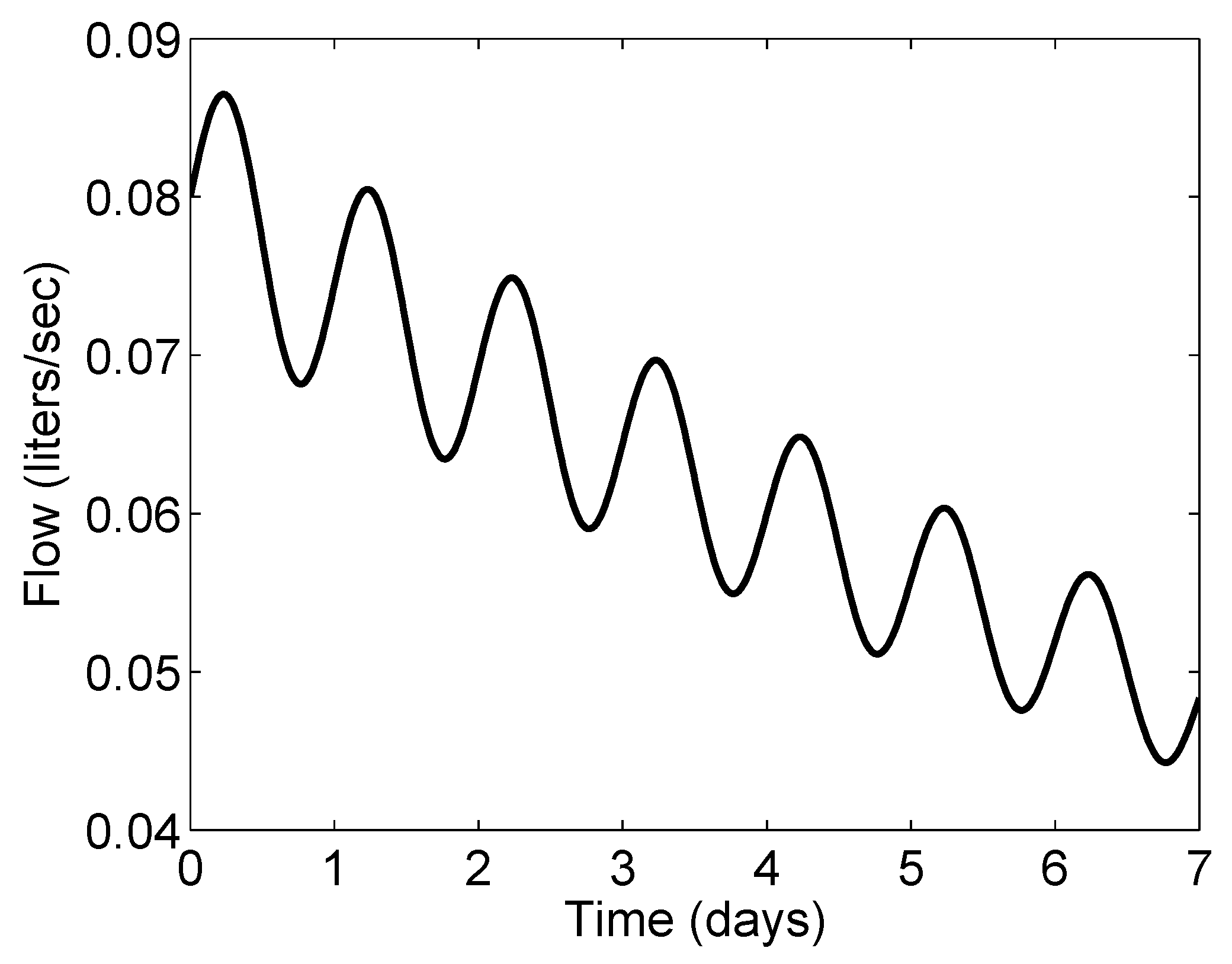
4.1. Application to a Decaying Oscillatory Runoff
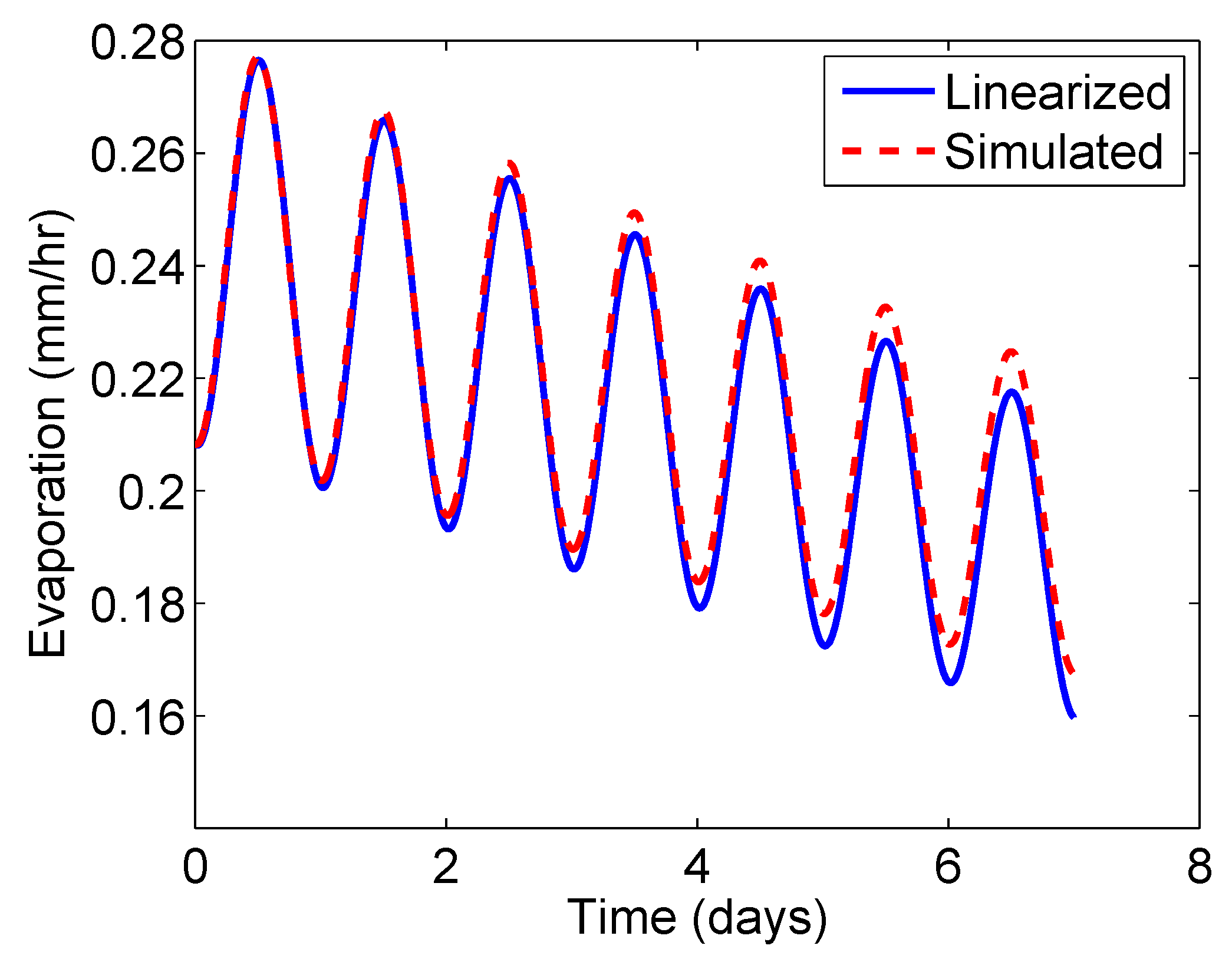
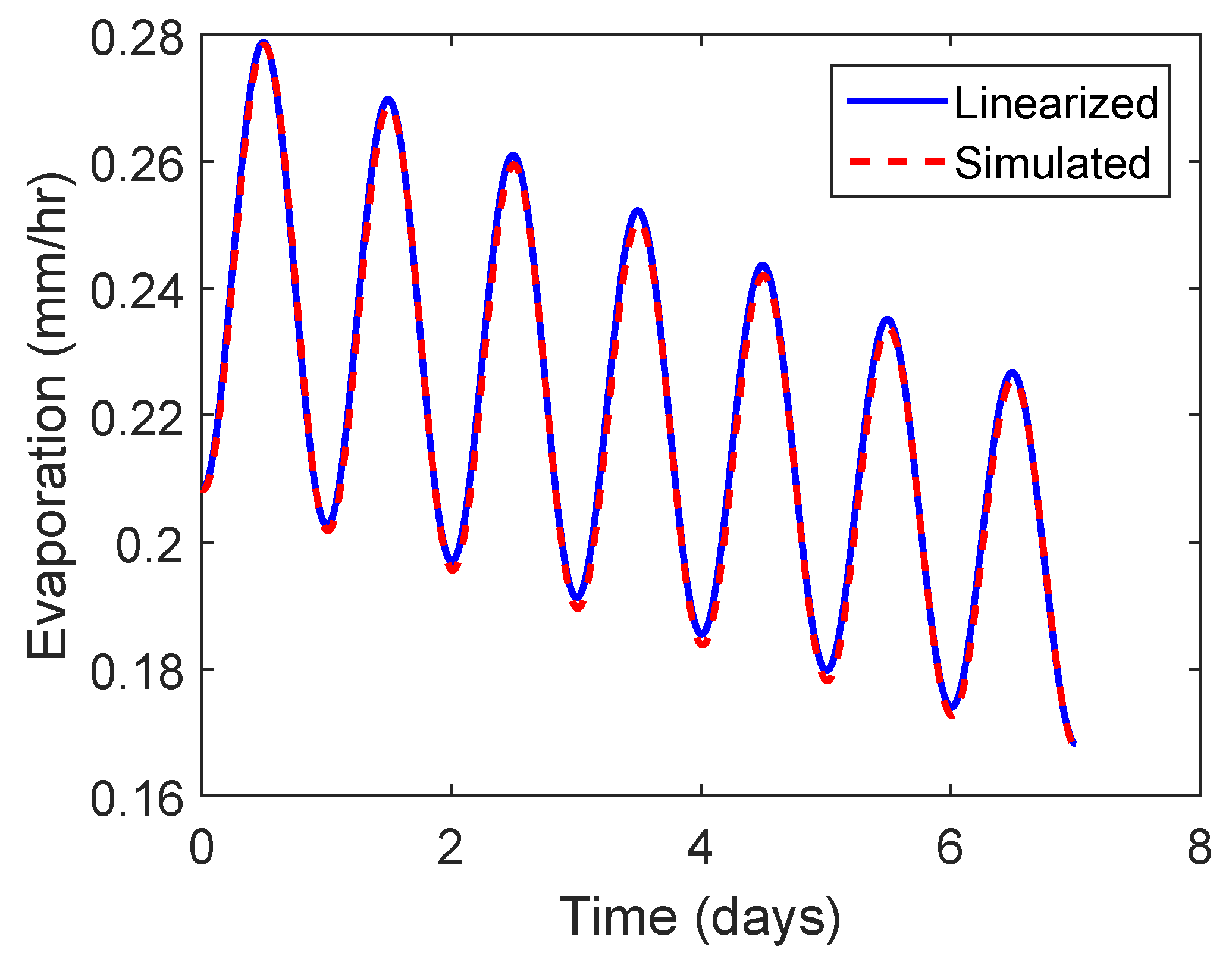
4.2. Finding the Evapotranspiration Solution by Linearizing About the Average Evapotranspiration
5. Numerical Example—Doing Hydrology Backwards on a Realistic Catchment
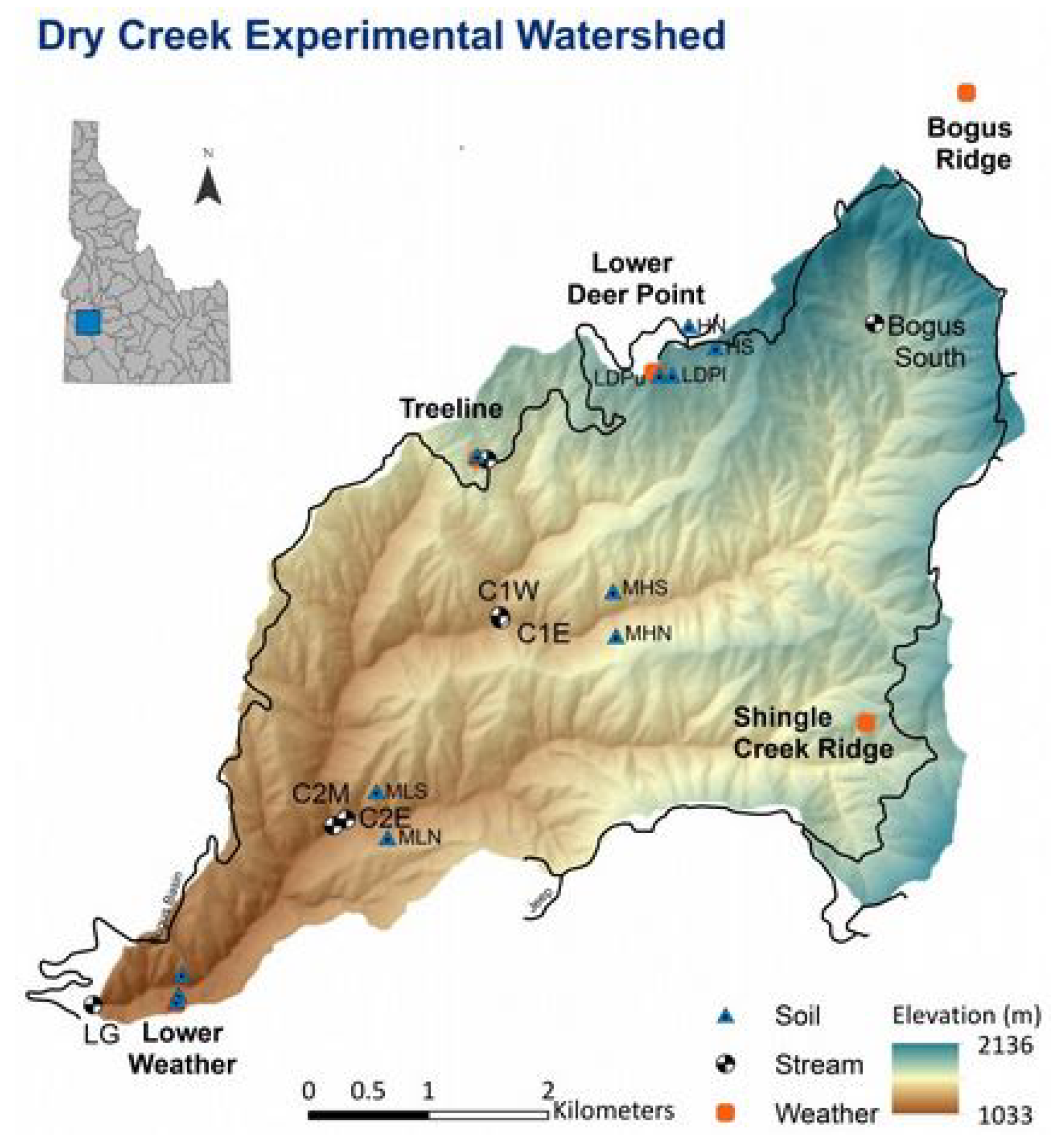
5.1. Available Data
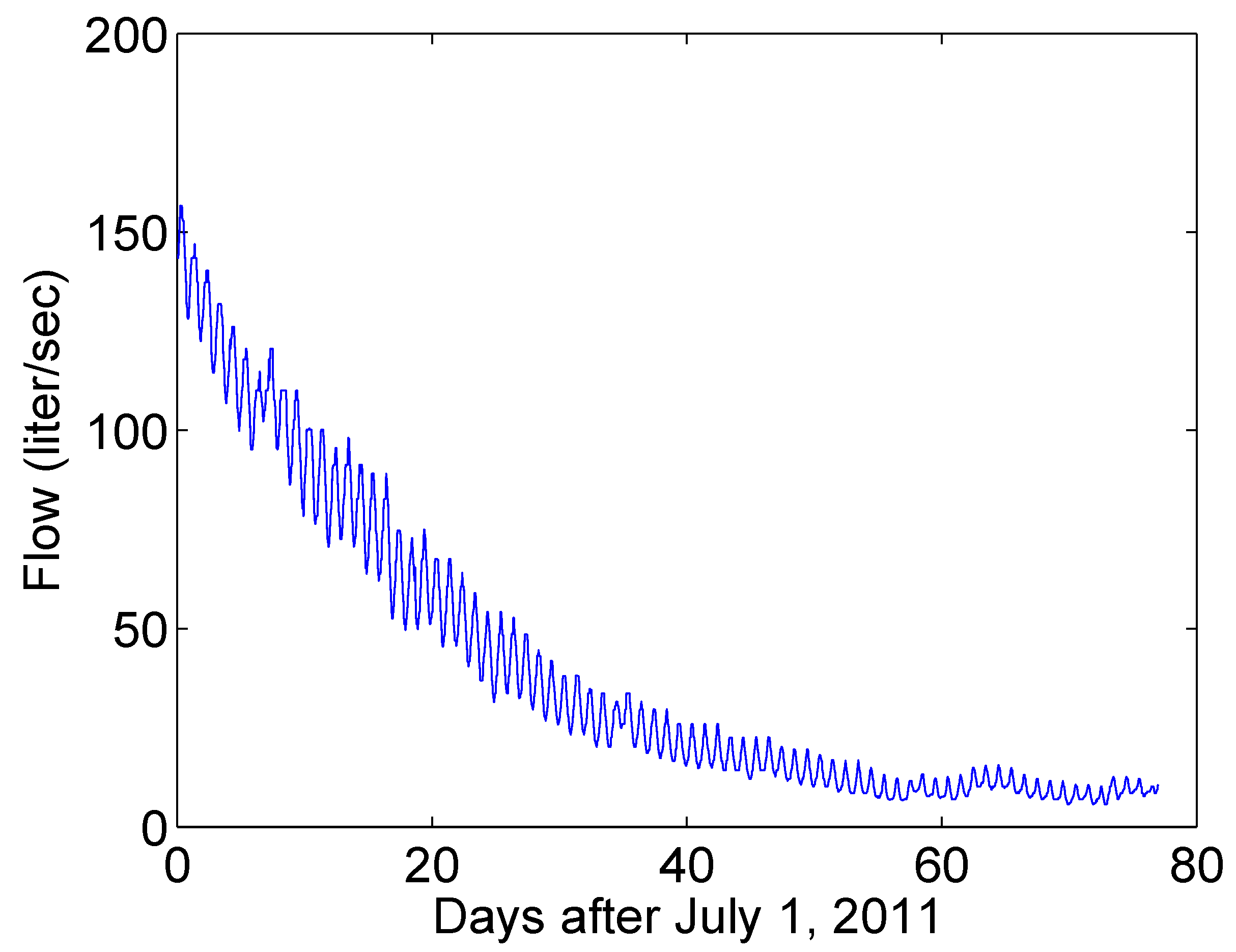
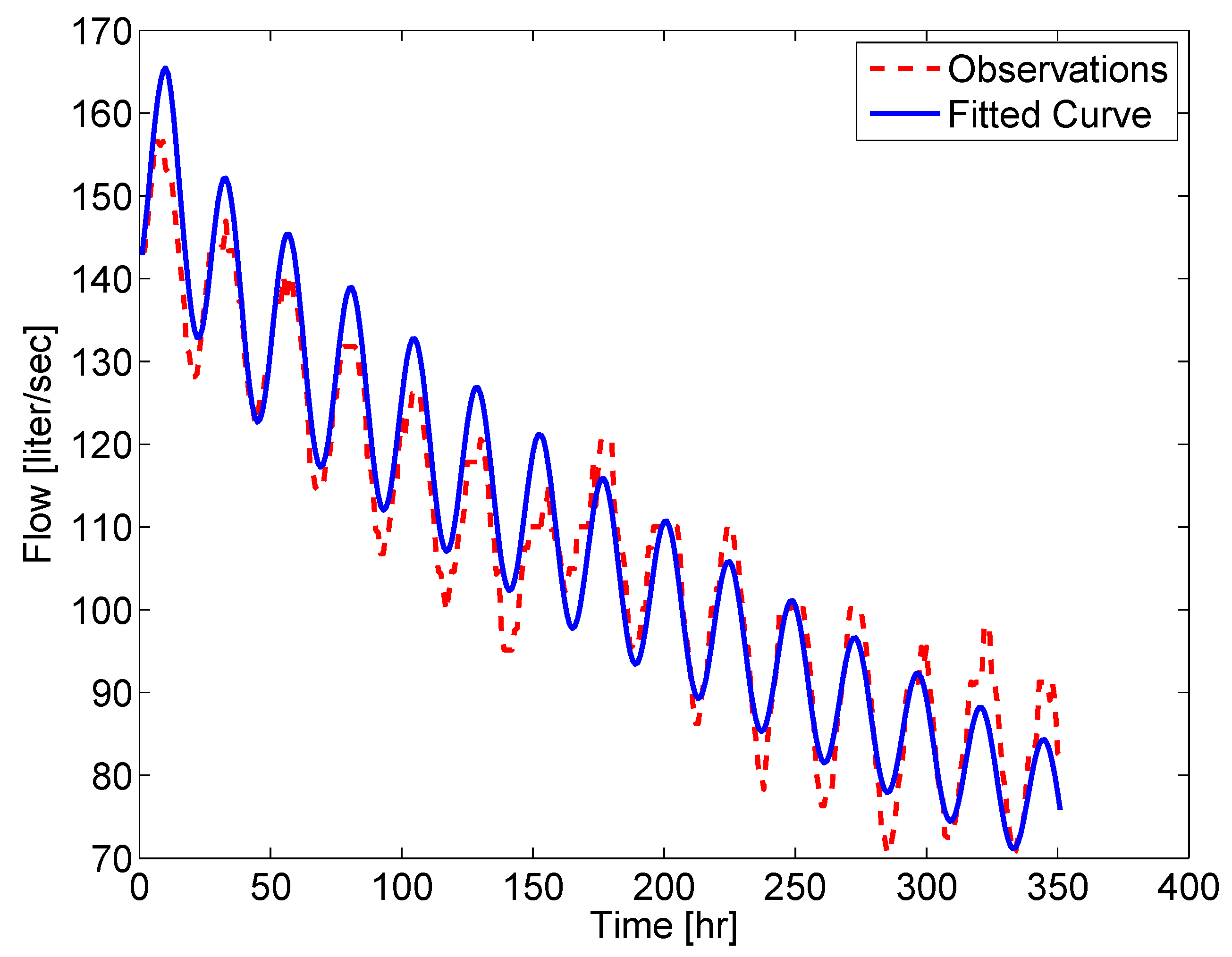
5.2. Determining Hillslope Runoff from Streamflow at The Outlet
5.3. Finding the Evapotranspiration Required to Produce Prescribed Runoff Pattern
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. An Approximate Solution for Evapotranspiration by Linearization about the Equilibrium
Appendix A.1. A Particular Choice for the Soil Moisture Function
Appendix A.2. First Order Linear Approximation of the Solution
References
- Martina, M.L.V.; Entekhabi, D. Identification of runoff generation spatial distribution using conventional hydrology gauge time series. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Kirchner, J.W. Catchments as simple dynamical systems: Catchment characterization, rainfall-runoff modeling, and doing hydrology backward. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Krier, R.; Matgen, P.; Goergen, K.; Pfister, L.; Hoffmann, L.; Kirchner, J.W.; Uhlenbrook, S.; Savenije, H.H.G. Inferring catchment precipitation by doing hydrology backward: A test in 24 small and mesoscale catchments in Luxembourg. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W. A new method for rainfall estimation through soil moisture observations. Geophys. Res. Lett. 2013, 40, 853–858. [Google Scholar] [CrossRef]
- Kretzschmar, A.; Tych, W.; Chappell, N.A. Reversing hydrology: Estimation of sub-hourly rainfall time-series from streamflow. Environ. Model. Softw. 2014, 60, 290–301. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J.F.; Clark, M.P.; Hyman, J.M.; Robinson, B.A. Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov chain Monte Carlo simulation. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Fahle, M.; Dietrich, O. Estimation of evapotranspiration using diurnal groundwater level fluctuations: Comparison of different approaches with groundwater lysimeter data. Water Resour. Res. 2014, 50, 273–286. [Google Scholar] [CrossRef]
- Habib, E.; Krajewski, W.F.; Kruger, A. Sampling errors of tipping-bucket rain gauge measurements. J. Hydrol. Eng. 2001, 6, 129–166. [Google Scholar] [CrossRef]
- Walter, I.A.; Allen, R.G.; Elliott, R.; Jensen, M.E.; Itenfisu, D.; Mecham, B.; Howell, T.A.; Snyder, R.; Brown, P.; Echings, S.; et al. ASCE’s standarized reference evapotranspiration equation. In Proceedings of the Watershed Management and Operations Management Conferences 2000, Fort Collins, CO, USA, 20–24 June 2000; pp. 1–11. [Google Scholar]
- Jin, R.; Li, X.; Liu, S.M. Understanding the Heterogeneity of Soil Moisture and Evapotranspiration Using Multiscale Observations From Satellites, Airborne Sensors, and a Ground-Based Observation Matrix. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2132–2136. [Google Scholar] [CrossRef]
- Mantilla, R.; Gupta, V.K. A GIS numerical framework to study the process basis of scaling statistics in river networks. IEEE Geosci. Remote Sens. Lett. 2005, 2. [Google Scholar] [CrossRef]
- Reggiani, P.; Sivapalan, M.; Hassandizadeh, S.M.; Gray, W.G. Coupled equations for mass and momentum balance in a stream network: Theoretical derivation and computational experiments. Proc. R. Soc. A 2001, 457. [Google Scholar] [CrossRef]
- Wondzell, S.; Gooseff, M.; McGlynn, B. Flow velocity and the hydrologic behavior of streams during baseflow. Geophys. Res. Lett. 2007, 34, L24404. [Google Scholar] [CrossRef]
- Gupta, V.K.; Waymire, E. Spatial variability and scale invariance in hydrologic regionalization. Scale Depend. Scale Invariance Hydrol. 1998, 88–135. [Google Scholar]
- Menabde, M.; Sivapalan, M. Linking space-time variability of rainfall and runoff fields on a river network: A dynamic approach. Adv. Water Resour. 2001, 24, 1001–1014. [Google Scholar] [CrossRef]
- Mantilla, R. Physical Basis of Statistical Scaling in Peak Flows and Stream Flow Hydrographs for Topologic and Spatially Embedded Random Self-Similiar Channel Networks. Ph.D. Thesis, University of Colorado at Boulder, Boulder, CO, USA, 2007. [Google Scholar]
- Krajewski, W.F.; Ceynar, D.; Demir, I.; Goska, R.; Kruger, A.; Langel, C.; Mantilla, R.; Niemeier, J.; Quintero, F.; Seo, B.C.; et al. Real-Time Flood Forecasting and Information System for the State of Iowa. Bull. Am. Meteorol. Soc. 2017, 98, 539–554. [Google Scholar] [CrossRef]
- Ayalew, T.B.; Krajewski, W.F.; Mantilla, R. Connecting the power-law scaling structure of peak-discharges to spatially variable rainfall and catchment physical properties. Adv. Water Resour. 2014, 71, 32–43. [Google Scholar] [CrossRef]
- Fonley, M.; Mantilla, R.; Small, S.; Curtu, R. On the propagation of diel signals in river networks using analytic solutions of flow equations. Hydrol. Earth Syst. Sci. 2016, 20, 2899–2912. [Google Scholar] [CrossRef]
- Burt, T.P. Diurnal variations in stream discharge and throughflow during a period of low flow. J. Hydrol. 1979, 41, 291–301. [Google Scholar] [CrossRef]
- Duffy, C.J. A two-state integral-balance model for soil moisture and groundwater dynamics in complex terrain. Water Resour. Res. 1996, 32, 2421–2434. [Google Scholar] [CrossRef]
- Qu, Y.; Duffy, C.J. A semidiscrete finite volume formulation for multiprocess watershed simulation. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Curtu, R.; Mantilla, R.; Fonley, M.; Cunha, L.K.; Small, S.; Jay, L.; Krajewski, W.F. An integral-balance nonlinear model to simulate changes in soil moisture, groundwater and surface runoff dynamics at the hillslope scale. Adv. Water Resour. 2014, 71, 125–139. [Google Scholar] [CrossRef]
- Bond, B.; Jones, J.; Moore, G.; Phillips, N.; Post, D.; McDonnell, J. The zone of vegetation influence on baseflow revealed by diel patterns of streamflow and vegetation water use in a headwater basin. Hydrol. Process. 2002, 16, 1671–1677. [Google Scholar] [CrossRef]
- Graham, C.; Barnard, H.; Kavanagh, K.; McNamara, J. Catchment scale controls the temporal connection of transpiration and diel fluctuations in streamflow. Hydrol. Process. 2013, 27, 2541–2556. [Google Scholar] [CrossRef]
- Ayalew, T.B.; Krajewski, W.F.; Mantilla, R. Exploring the effect of reservoir storage on peak discharge frequency. J. Hydrol. Eng. 2013, 18, 1697–1708. [Google Scholar] [CrossRef]
- Gribovszki, Z.; Kalicz, P.; Szilágyi, J.; Kucsara, M. Riparian zone evapotranspiration estimation from diurnal groundwater level fluctuations. J. Hydrol. 2008, 349, 6–17. [Google Scholar] [CrossRef]
- Wondzell, S.M.; Gooseff, M.N.; McGlynn, B.L. An analysis of alternative conceptual models relating hyporheic exchange flow to diel fluctuations in discharge during baseflow recession. Hydrol. Process. 2010, 24, 686–694. [Google Scholar] [CrossRef]
- Dry Creek Experimental Watershed, Lower Gauge Streamflow Data; Boise State University: Boise, ID, USA, 2015.
- MATLAB and Optimization Toolbox Release; The MathWorks, Inc.: Natick, MA, USA, 2012.
| Flux | Physical Meaning |
|---|---|
| The flux from ponded water into the | |
| top layer of subsurface | |
| The flux from water in the top layer of | |
| subsurface to the saturated layer of subsurface | |
| The flux between the vadose zone | |
| and the saturated zone | |
| Overland flow from ponded water to | |
| river link | |
| Flow from saturated subsurface to river link | |
| Soil moisture determined by evaporation |
| Expression | Physical Meaning |
|---|---|
| Evaporation from the ponded water (m/min) | |
| Evaporation from the top layer of subsurface (m/min) | |
| Temperature-driven transpiration from the vadose zone | |
| (m/min) | |
| Common units for evapotranspiration are (mm/h). | |
| We convert to (m/min) with the conversion factor | |
| Divides the evapotranspiration into three portions | |
| The proportion of evapotranspiration from the ponded | |
| water depends directly upon the amount of water in the | |
| ponded zone | |
| The proportion of evapotranspiration from the top layer | |
| depends on the proportion of the top layer containing | |
| water | |
| The proportion of evapotranspiration from the vadose | |
| zone depends on the proportion of the vadose zone | |
| containing water |
| Parameter | Value | Units | Physical Meaning |
|---|---|---|---|
| 0.1 | meter | Depth of top layer of subsurface | |
| 0.4 | meter | Depth of bottom layer of subsurface | |
| Includes vadose and saturated zones | |||
| Rate of movement to link | |||
| Rate of movement using preferential flow | |||
| Rate of infiltration | |||
| Rate of flow exiting subsurface | |||
| 0.1 | Unitless | Residual soil moisture at night | |
| 0.9 | Unitless | Residual soil moisture during day |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fonley, M.; Mantilla, R.; Curtu, R. Doing Hydrology Backwards—Analytic Solution Connecting Streamflow Oscillations at the Basin Outlet to Average Evaporation on a Hillslope. Hydrology 2019, 6, 85. https://doi.org/10.3390/hydrology6040085
Fonley M, Mantilla R, Curtu R. Doing Hydrology Backwards—Analytic Solution Connecting Streamflow Oscillations at the Basin Outlet to Average Evaporation on a Hillslope. Hydrology. 2019; 6(4):85. https://doi.org/10.3390/hydrology6040085
Chicago/Turabian StyleFonley, Morgan, Ricardo Mantilla, and Rodica Curtu. 2019. "Doing Hydrology Backwards—Analytic Solution Connecting Streamflow Oscillations at the Basin Outlet to Average Evaporation on a Hillslope" Hydrology 6, no. 4: 85. https://doi.org/10.3390/hydrology6040085
APA StyleFonley, M., Mantilla, R., & Curtu, R. (2019). Doing Hydrology Backwards—Analytic Solution Connecting Streamflow Oscillations at the Basin Outlet to Average Evaporation on a Hillslope. Hydrology, 6(4), 85. https://doi.org/10.3390/hydrology6040085