Hydrological hazard estimation for the municipality of Yautepec de Zaragoza, Morelos, Mexico
Abstract
1. Introduction
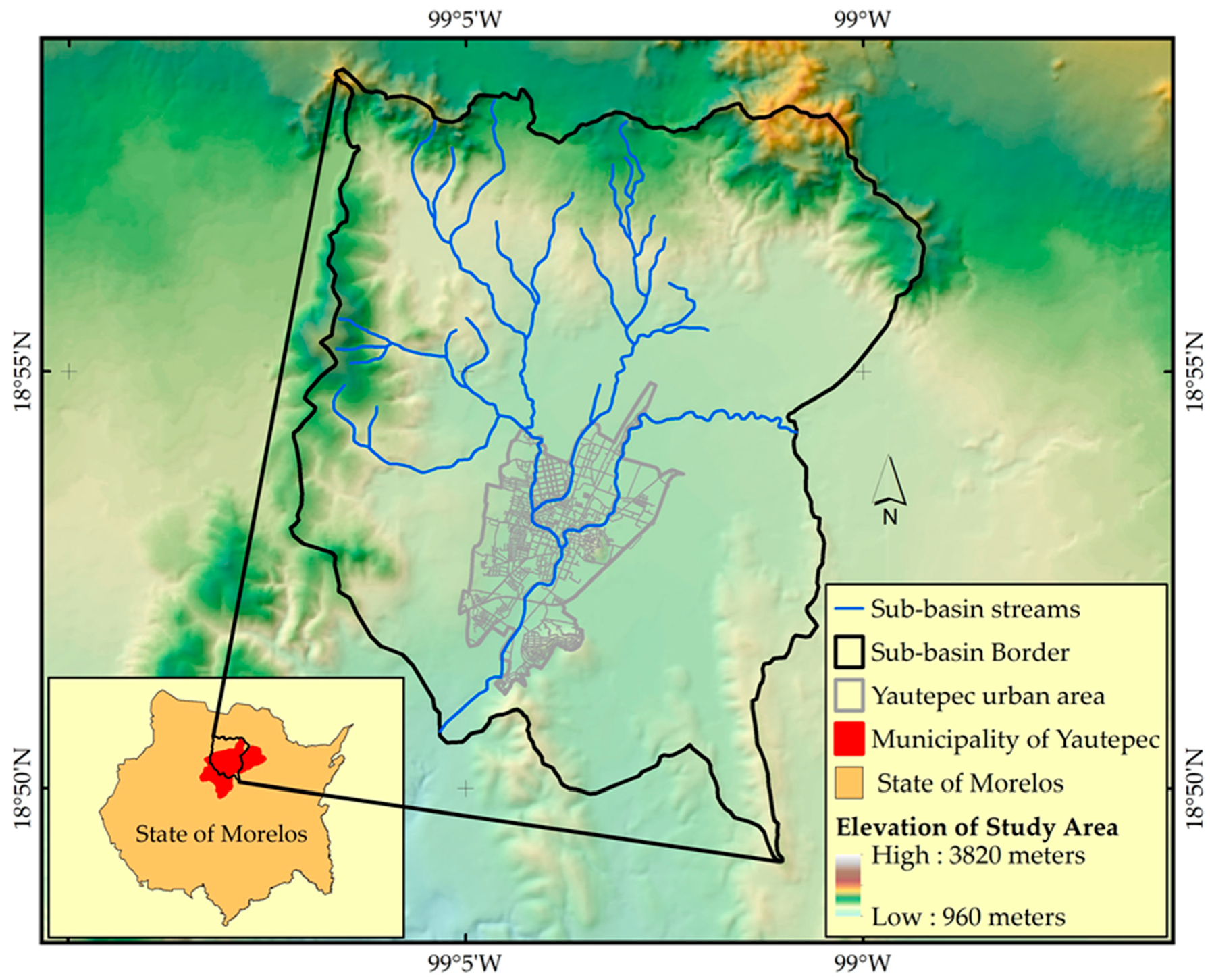
2. Study Area
3. Materials and Methods
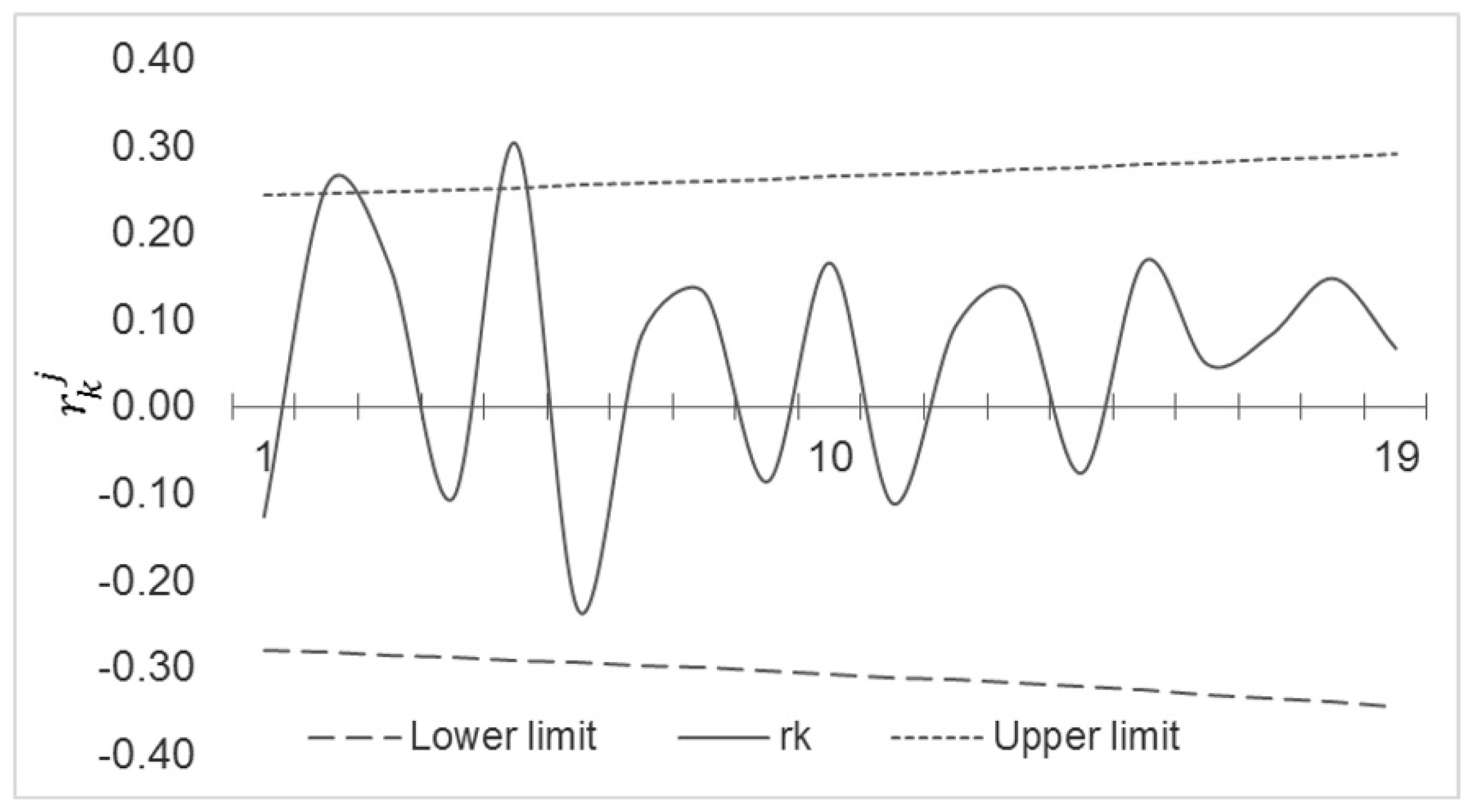
3.1. Statistical Analysis
- = Blocks of size w = 60 and w = 30
- = Total sample size
- = /S
- S = Standard deviation of total sample size
- j = Sampled data.
- k = Delay time.
- = Number of data.
- = Sample mean of j.
- n = Sample size.
- m = Registration order number considering a determined return period.
- includes the events ordered from the highest to the lowest values with an assigned Rp of and a probability of non-exceedance given by [47]:
- = Length in years of the analyzed record.
- M = Registration order number.
- = Events estimated with a certain probability distribution for Rp assigned to the ordered sample .
- Mp = Number of parameters of the adjusted distribution.
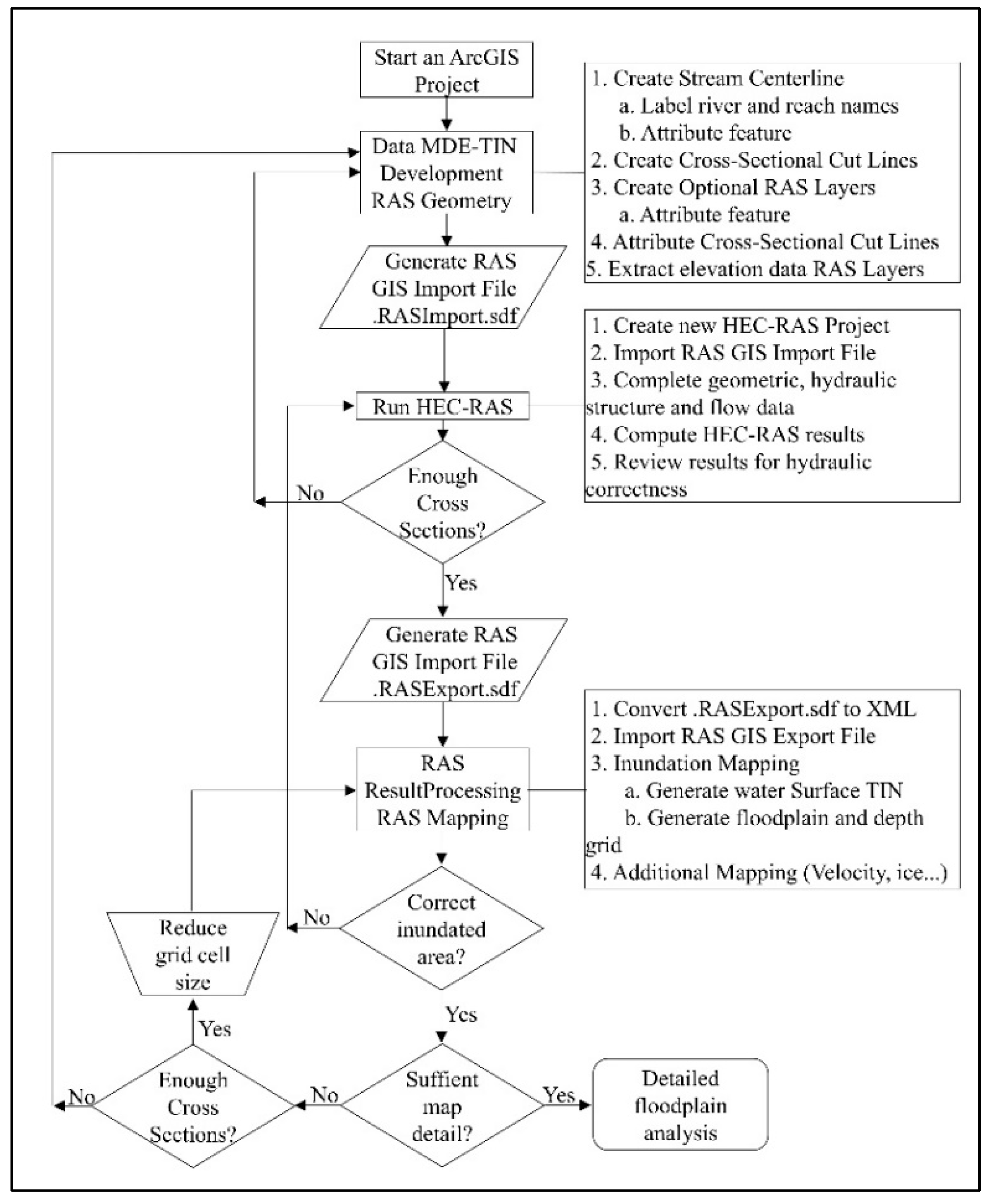
3.2. Hydraulic Flow Model for the Yautepec River Sub-Basin
4. Results
4.1. Statistical Analysis
- v = (w = 60 + w = 30) − 2
- α = 0.05
- = Student’s t-distribution quantiles
- v = Location
- β = Shape
- α = Scale > 0.
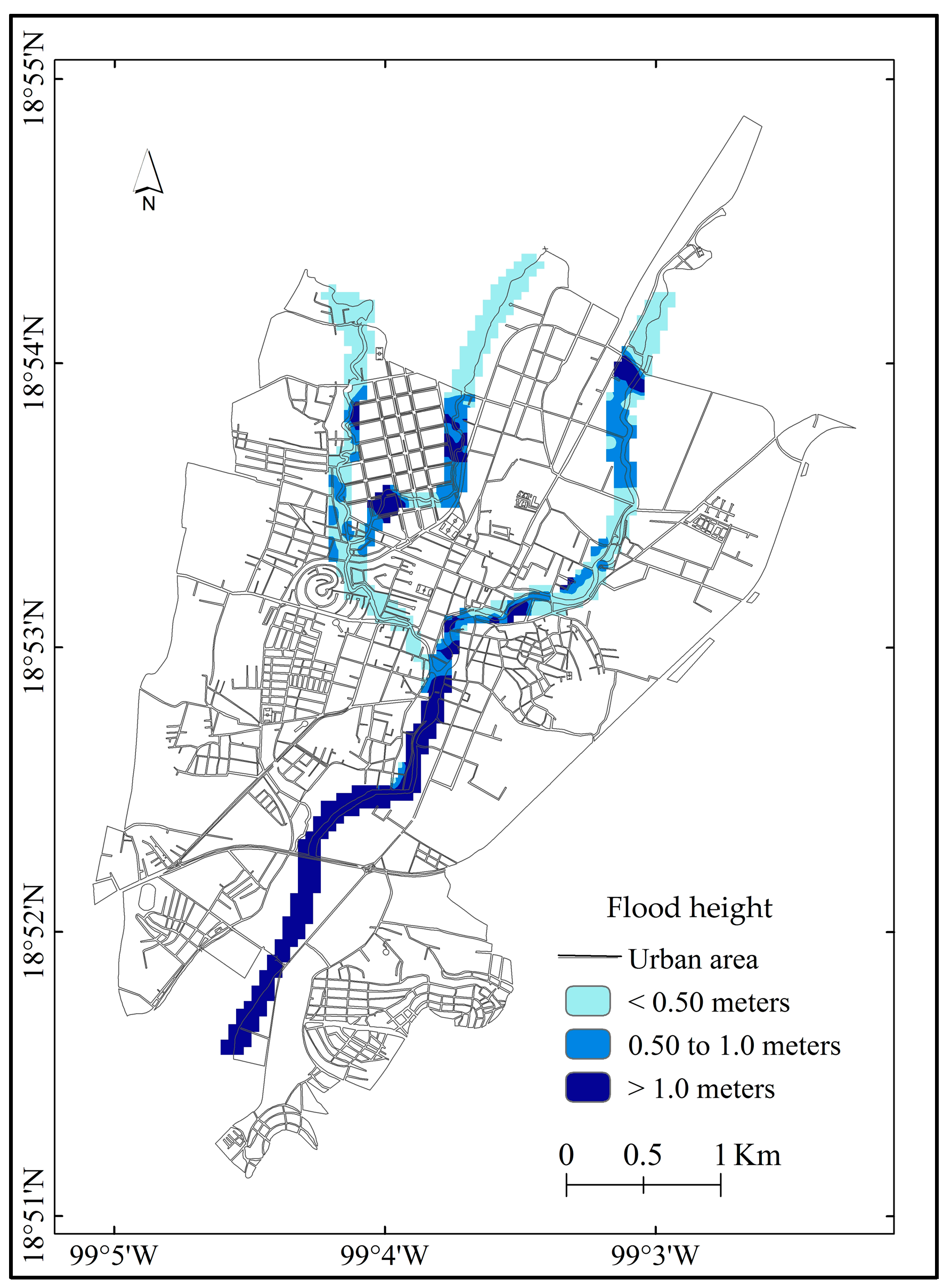
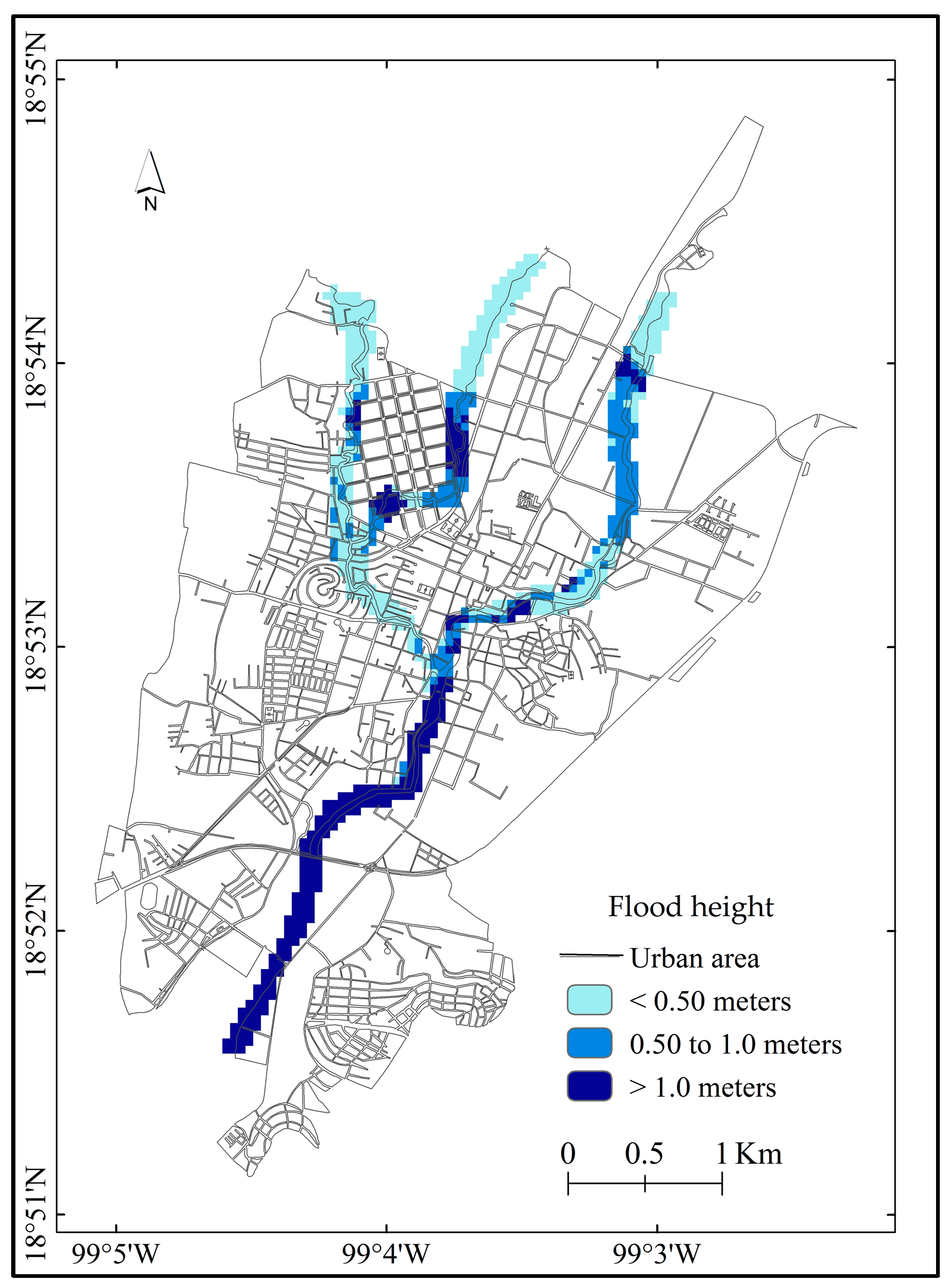
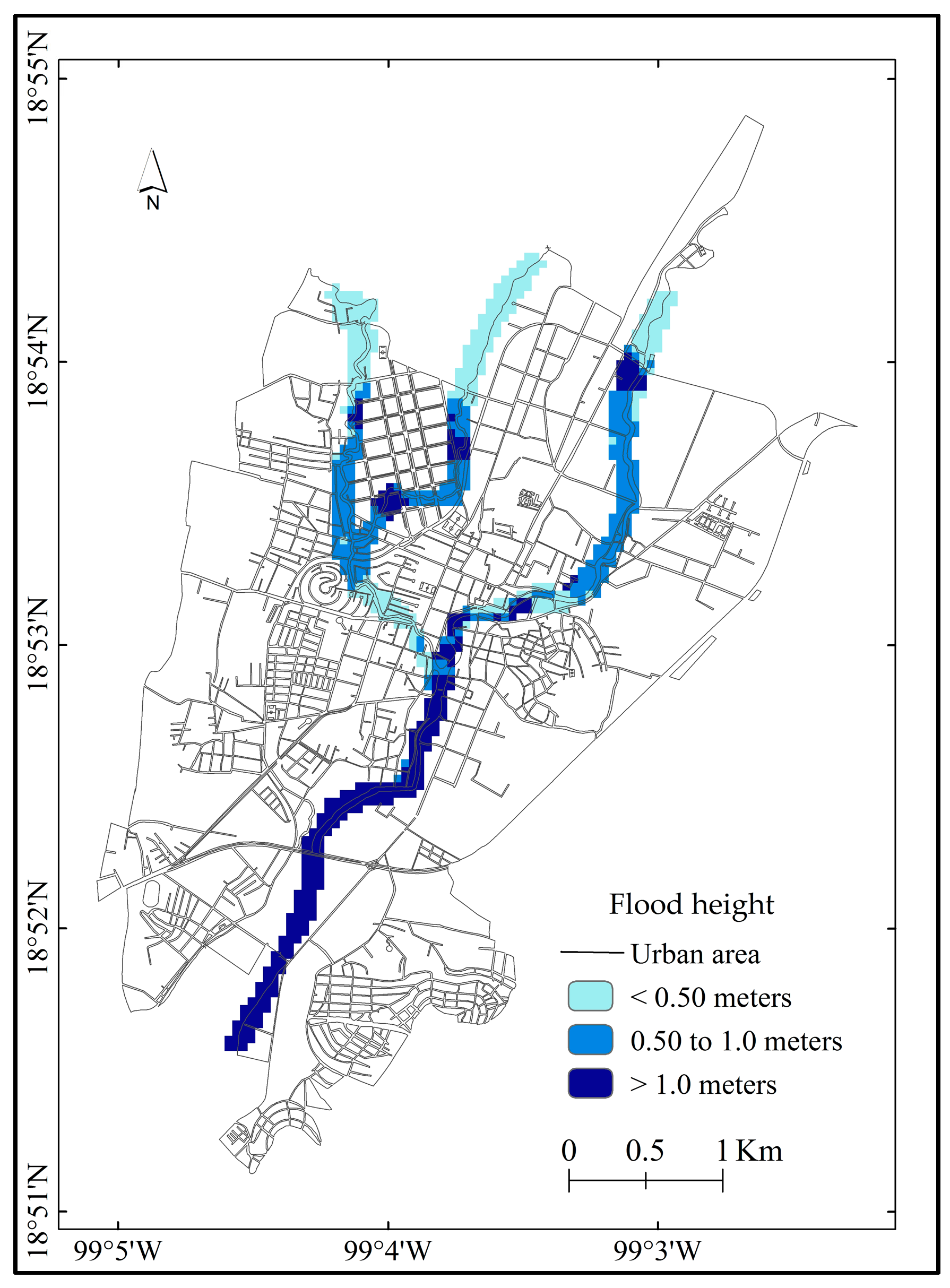
4.2. Hydraulic Modeling
- High: Flood height > 1 m. Expected losses in infrastructure and population. They are infrequent events.
- Moderate: Flood height > 50 cm and < 1 m. Moderate damage and some losses in infrastructure with low impact to local people. They are events of moderate frequency.
- Low: Flood height < 50 cm. Minimal impact to infrastructure and population. They are high frequency events.
- For Rp 50 years, 10% (1.5 km2) of the total community area will be flooded: Of this flooded area, 65% will be covered with a water level ≤ 50 cm; 15.5% between 0.50 cm and 1.0 m; and 19.5% > 1.0 m.
- For Rp 100 years, 12% (1.8 km2) of the total community area will be flooded: of this flooded area, 62% will have a water level ≤ 50 cm; 18.5% from 0.50 cm to 1.0 m and 19.5% > 1.0 m.
- For Rp 500 years, 13.5% (2.1 km2) of the total community area will be flooded: of this flooded area, 59% will reach a water level ≤ 50 cm; 18.4% between of 0.50 cm to 1.0 and 22.6% > 1.0 m.
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jonkman, S.N. Global perspectives on loss of human life caused by floods. Nat. Hazards 2005, 34, 151–175. [Google Scholar] [CrossRef]
- Ahmad, B.; Zakir, H. Hydrological modelling and flood hazard mapping of Nullah Lai. Proc. Pak. Acad. Sci. 2010, 47, 215–226. [Google Scholar]
- Kourgialas, N.N.; Karatzas, G.P. Flood management and a GIS modelling method to assess flood-hazard areas—A case study. Hydrolog. Sci. J. 2011, 56, 212–225. [Google Scholar] [CrossRef]
- Johnson, C.; Blackburn, S. Making Cities Resilient Report 2012: My City Getting Ready! A Global Snapshot of How Local Governments Reduce Disaster Risk; The United Nations International Strategy for Disaster Reduction: Geneva, Switzerland, 2012; ISBN 978-92-1-132036-7. [Google Scholar]
- Munich, R.E.; Kron, W.; Schuck, A. Topics Geo: Natural Catastrophes 2013: Analyses, Assessments, Positions; Munchener Ruckversicherungs-Gesellschaf: Munich, Germany, 2014; Available online: https://www.munichre.com/site/corporate/get/documents_E1043212252/mr/assetpool.shared/Documents/5_Touch/_Publications/302-08121_en.pdf (accessed on 1 January 2019).
- Konrad, C.P. Effects of Urban Development on Floods 2003. Available online: https://pubs.usgs.gov/fs/fs07603/ (accessed on 1 December 2018).
- Douglas, I.; Kobold, M.; Lawson, N. Characterization of Urban Streams and Flooding. Advances in Urban Flood Management; CRC Press: London, UK, 2007; pp. 41–70. Available online: https://doi.org/10.1201/9780203945988 (accessed on 1 December 2018).
- Aragón-Durand, F. Urbanization and Flood Vulnerability in the peri-urban interface of Mexico City. Disasters 2007, 31, 477–497. [Google Scholar] [CrossRef] [PubMed]
- Föster, S.; Kuhlmann, B.; Lindenschmindt, K.; Bronstert, A. Assessing flood risk for rural detention area. Nat. Hazard Earth Syst. Sci. 2008, 8, 311–322. [Google Scholar] [CrossRef]
- Hollis, G.E. The effect of urbanization on floods of different recurrence interval. Water Resour. Res. 1975, 11, 431–435. [Google Scholar] [CrossRef]
- UNISDR. Hyogo framework for action 2005–2015: Building the resilience of nations and communities to disasters. In Proceedings of the World Conference on Disaster Reduction, Kobe, Hyogo, Japan, 18–22 January 2005; The United Nations International Strategy for Disaster Reduction: Geneva, Switzerland, 2005; Volume 380. A/CONF. 206/6. Available online: https://www.unisdr.org/files/1037_hyogoframeworkforactionenglish.pdf (accessed on 1 January 2019).
- Amangabara, G.T.; Gobo, A.E. Factors that influence the flooding of the Middle and Lower Ntamogba stream catchments, Port Harcourt, Nigeria. J. Environ. Hydrol. 2007, 15, 1–15. Available online: http://www.hydroweb.com/protect/pubs/jeh/jeh2007/amanga.pdf (accessed on 1 December 2018).
- Jha, A.K.; Bloch, R.; Lamond, J. Cities and Flooding: A Guide to Integrated Urban Flood Risk Management for the 21st Century; World Bank Publications: Washington, DC, USA, 2012; Available online: http://siteresources.worldbank.org/INTWBEUROPE/Resources/Brief_Guide_to_Urban_Flood_Risk_Management.pdf (accessed on 1 December 2018).
- Zúñiga, E.; Magaña, V. Vulnerability and risk to intense rainfall in Mexico: The effect of land use cover change. Investig. Geogr. 2017, 95, 1–18. [Google Scholar] [CrossRef]
- Areau-Rangel, O.; Cea, L.; Bonasia, R.; Espinoza-Echavarria, V. Impact of Urban Growth and Changes in Land Use on River Flood Hazard in Villahermosa, Tabasco (Mexico). Water 2019, 11, 304. [Google Scholar] [CrossRef]
- Suriya, S.; Mudgai, B. Impact of urbanization on flooding: The Thirusoolam sub watershed—A case study. J. Hydrol. 2012, 412, 210–219. [Google Scholar] [CrossRef]
- Smith, K.; Ward, R.C. Floods: Physical Processes and Human Impacts; Wiley: Chichester, UK, 1998; ISBN 0471952486. [Google Scholar]
- León, P.A. Natural Disasters; Wm. C. Brown Publishers: Dubuque, IA, USA, 1996; ISBN 9780697254931. [Google Scholar]
- Du, J.; Quian, L.; Rui, H.; Zuo, T.; Zheng, D.; Xu, Y.; Xu, C. Assessing the effects of urbanization on annual runoff and flood events using an integrated hydrological modeling system for Qinhuai River basin, China. J. Hydrol. 2012, 464, 127–139. [Google Scholar] [CrossRef]
- Sala, M.; Inbar, M. Some hydrology effects of urbanization in Catalan rivers. Catena 1992, 19, 363–378. [Google Scholar] [CrossRef]
- Nations, U. Terminology on Disaster Risk Reduction; United Nations Office for Disaster Risk Reduction, Report, 2009; International Strategy for Disaster Reduction of the United Nations: Geneva, Switzerland, 2009; Available online: https://www.unisdr.org/we/inform/publications/7817 (accessed on January 2019).
- Li, G.-F.; Xiang, X.-Y.; Tong, Y.-Y.; Wang, H.-M. Impact assessment of urbanization on flood risk in the Yangtze River Delta. Stoch. Environ. Res. Risk Assess. 2013, 27, 1683–1693. [Google Scholar] [CrossRef]
- CENAPRED. Impacto Socioeconómico de Los Principales Desastres Ocurridos En La República Mexicana: Serie Impacto Socioeconómico de Los Desastres En México; Secretaría de Gobernación—CENAPRED: Ciudad de México, México, 2017; Volumes 1–15, Available online: http://www.cenapred.unam.mx/PublicacionesWebGobMX/buscar_buscaSubcategoria?categoria=Series+especiales+%2F&subcategoria=Impacto+Socioecon%26oacute%3Bmico+de+los+desastres+en+M%26eacute%3Bxico&palabraClave=de+los+Desastres+en (accessed on 1 January 2019).
- DesInventar. Sistema de Inventario de Desastres. Available online: https://online.desinventar.org/ (accessed on 1 December 2018).
- Dirección general de protección civil del municipio de Yautepec de Zaragoza. Plan Municipal de Contingencias Hidrometeorológicas; Dirección General de protección civil del municipio de Yautepec de Zaragoza: Yautepec, Morelos, México, Unpublished manuscript; 2007. [Google Scholar]
- Estrada, M. Investigación Hidrológica e Hidrogeológica Para Reducir el Caudal de Escurrimiento en el río Yautepec y Evitar Inundaciones en La Zona Centro de Yautepec, Morelos. Bachelor’s Thesis, Universidad Nacional Autónoma de México, Ciudad de México, México, 2005. Available online: http://oreon.dgbiblio.unam.mx (accessed on 30 November 2018).
- Zúñiga, E. Análisis del Riesgo Por Inundaciones Como Consecuencia del Desbordamiento del Río Yautepec, Morelos, México. Master’s Thesis, Universidad Nacional Autónoma de México, Ciudad de México, México, 2009. Available online: http://oreon.dgbiblio.unam.mx (accessed on 30 October 2018).
- Stelling, G.S.; Verwey, A. Numerical flood simulation. In Encyclopedia of Hydrological Sciences; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Bladé, E.; Gómez-Valentín, M.; Dolz, J.; Aragón-Hernández, J.L.; Corestein, G.; Sánchez-Juny, M. Integration of 1D and 2D finite volume schemes for computations of water flow in natural channels. Adv. Water Resour. 2012, 42, 17–29. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Modell. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Knebl, M.R.; Yang, Z.-L.; Hutchison, K.; Maidment, D.R. Regional scale flood modeling using NEXRAD rainfall, GIS, and HEC-HMS/RAS: A case study for the San Antonio River Basin Summer 2002 storm event. J. Environ. Manag. 2005, 75, 325–336. [Google Scholar] [CrossRef] [PubMed]
- Hicks, F.E.; Peacock, T. Suitability of HEC-RAS for flood forecasting. Can. Water Resour. J. 2005, 30, 159–174. [Google Scholar] [CrossRef]
- Yang, J.; Townsend, R.D.; Daneshfar, B. Applying the HEC-RAS model and GIS techniques in river network floodplain delineation. Can. J. Civ. Eng. 2006, 33, 19–28. [Google Scholar] [CrossRef]
- Mohammed, J.R.; Qasim, J.M. Comparison of One-Dimensional HEC-RAS with Two-Dimensional ADH for Flow over Trapezoidal Profile Weirs. CJSR 2012, 1, 6. Available online: http://www.cjasr.com/images/manuscripts/Jun/CJASR-12-07-18.pdf (accessed on 1 January 2019).
- İcaga, Y.; Tas, E.; Kilit, M. Flood inundation mapping by GIS and a hydraulic model (HEC RAS): A case study of Akarcay Bolvadin subbasin, in Turkey. Acta Geobalcanica 2016, 2, 111–118. [Google Scholar] [CrossRef]
- Khattak, M.S.; Anwar, F.; Saeed, T.U.; Sharif, M.; Sheraz, K.; Ahmed, A. Floodplain mapping using HEC-RAS and ArcGIS: A case study of Kabul River. Arab. J. Sci. Eng. 2016, 41, 1375–1390. Available online: https://link.springer.com/content/pdf/10.1007%2Fs13369-015-1915-3.pdf (accessed on 1 December 2018). [CrossRef]
- Thakur, B.; Parajuli, R.; Kalra, A.; Dunn, C.N.; Van Weele, B.; Ahmad, S.; Gupta, R. Coupling HEC-RAS and HEC-HMS in Precipitation Runoff Modelling and Evaluating Flood Plain Inundation Map. World Environ. Water Resour. Congr. 2017, 240–251. [Google Scholar] [CrossRef]
- Tenzin, J.; Bhaskar, A.S. Modeling of the Precipitation Induced Flash Flood in Sarpang, Bhutan Using Hec-Ras. Rasayan J. Chem. 2017, 12, 195–202. Available online: http://rasayanjournal.co.in/admin/php/upload/158_pdf.pdf (accessed on 1 January 2019). [CrossRef]
- Romali, N.S.; Yusop, Z.; Ismail, A.Z. Application of HEC-RAS and Arc GIS for floodplain mapping in Segamat town. Malays. Int. J. 2018, 14, 125–131. [Google Scholar] [CrossRef]
- Delgado, C.D.; Isuhuaylas, G.V. Análisis de gran visión de las inundaciones en la cuenca alta del río Lerma: Caso de la subcuenca del río Tejalpa, Estado de México, México. Ing. Hidraul. Mex. 2001, 16, 73–86. [Google Scholar]
- Wurl, J.; Martínez, G.; Cynthia, N.; Imaz, L. Caracterización del peligro por inundaciones en el oasis La Purísima, Baja California Sur, México. Investig. Geogr. 2015, 87, 76–87. [Google Scholar] [CrossRef][Green Version]
- Larios-Tlali, H. Riesgo de inundación en la subcuenca del río La Antigua, Veracruz, México. Tecnol. Cienc. Agua 2015, 6, 39–56. Available online: http://www.scielo.org.mx/pdf/tca/v6n3/v6n3a4.pdf (accessed on 1 February 2019).
- Norman, L.M. Flood hazard awareness and hydrologic modelling at Ambos Nogales, United States—Mexico border. J. Flood Risk Manag. 2010, 3, 151–165. [Google Scholar] [CrossRef]
- CONAGUA. Atlas del Agua en México 2015. Available online: http://www.conagua.gob.mx/CONAGUA07/Publicaciones/Publicaciones/ATLAS2015.pdf (accessed on 1 March 2019).
- Vide, J. Ingeniería de Ríos [River Engineering], 2nd ed.; Universidad Politécnica de Catalunya: Barcelona, España, 2007; Volume 9, ISBN 978-84-8301-900-9. [Google Scholar]
- CONAGUA. Banco Nacional de Datos de Aguas Superficiales (BANDAS). Available online: ftp://ftp.conagua.gob.mx/Bandas/Bases_Datos_Bandas (accessed on 1 February 2019).
- Escalante, C.; Reyes, L. Técnicas Estadísticas en Hidrología [Statistical Techniques in Hydrology], 1st ed.; Universidad Nacional Autónoma de México, Facultad de Ingeniería: Ciudad de México, México, 2005; ISBN 970-32-0173-3. [Google Scholar]
- Rao, A.R.; Hamed, K.H. Flood Frequency Analysis. Ing. Agua 2000, 7, 309. Available online: https://www.taylorfrancis.com/books/9780429128813 (accessed on 1 December 2018).
- Chow, V. Hidráulica de Canales Abiertos [Open Channel Hydraulics]; McGraw-Hill: Santafé de Bogotá, Colombia, 1994; ISBN 958-600-228-4. [Google Scholar]
- Salas, J.; Delleur, J.; Yevjevich, V.; Lane, W. Applied Modeling of Hydrological Time Series, 4th ed.; Water Resources Pubications: Highlands Ranch, CO, USA, 1998; p. 484. ISBN 978-091833437-4. [Google Scholar]
- Chow, V.; Maidment, D.; Mays, L. Applied Hydrology; McGraw-Hill: Singapur, Singapur, 1988; ISBN 0-07-010810-2. Available online: http://ponce.sdsu.edu/Applied_Hydrology_Chow_1988.pdf (accessed on 1 March 2019).
- INEGI. Conjunto de Datos Vectoriales Topográficos. Carta E14A59. Escala 1:50,000. Available online: http://www.beta.inegi.org.mx/app/buscador/default.html?q=e14a59 (accessed on 1 January 2019).
- HEC-GeoRAS. Handbook of HecGeoRAS. Available online: http://www.hec.usace.army.mil/software/hec-georas/ (accessed on 1 February 2019).
- ArcGis. ArcGis Tutorials. Available online: http://desktop.arcgis.com/es/arcmap/latest/get-started/introduction/arcgis-tutorials.htm (accessed on February 2019).
- INEGI. Modelo Digital de Elevaciones—Continuo de Elevaciones Mexicana 3.0. Available online: http://www.inegi.org.mx/geo/contenidos/datosrelieve/continental/descarga.aspx (accessed on 1 January 2019).
- Arcement, G.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; U.S. Geological Survey: Denver, CO, USA, 1989; ISBN 88-600129. Available online: https://dpw.lacounty.gov/lacfcd/wdr/files/WG/041615/Guide%20for%20Selecting%20n-Value.pdf (accessed on 1 April 2019).
- Nanía, L.S.; León, A.S.; García, M.H. Hydrologic-hydraulic model for simulating dual drainage and flooding in urban areas: Application to a catchment in the metropolitan area of Chicago. J. Hydrol. Eng. 2014, 20, 04014071. Available online: https://ascelibrary.org/doi/pdf/10.1061/%28ASCE%29HE.1943-5584.0001080 (accessed on 1 April 2019). [CrossRef]
- HEC-RAS. Handbook of HECRAS. Available online: http://www.hec.usace.army.mil/software/hec-ras/ (accessed on 10 January 2017).
- Chow, V.; Maidment, D.; Mays, L. Hidrología Aplicada; McGraw-Hill: Santafé de Bogotá, Colombia, 1994; ISBN 0-07-010810-2. [Google Scholar]
- Hosking, J.R. L-moments: Analysis and estimation of distributions using linear combinations of order statistics. J. Roy. Stat. Soc. Ser. B Methodol. 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Ferrer, J. Análisis Estadístico de Caudales de Avenida; Monografías, M26; Centro de Estudios Hidrográficos (CEDEX, MOPT): Madrid, Spain, 1992; p. 42. ISBN 9788477901402. [Google Scholar]
- Rosique, L. Análisis del Riesgo Por Inundación En La Ciudad de Villahermosa, Tabasco. Master’s Thesis, Universidad Nacional Autónoma de México, Ciudad de México, México, 2010. Available online: http://oreon.dgbiblio.unam.mx (accessed on 30 November 2018).
- Campos, A. Introducción a La Hidrología Urbana [Introduction to Urban Hydrology], 1st ed.; Universitaria Potosina: San Luis Potosí, México, 2010; ISBN -970-95118-1-5. [Google Scholar]
- Herrero, A.D.; Laín-Huerta, L.; Isidro, M.L. Mapas de Peligrosidad Por Avenidas e Inundaciones: Guía Metodológica Para Su Elaboración; IGME: Madrid, Spain, 2008; No. 1; ISBN 978-84-7840-770-5. [Google Scholar]
- Wolfgang, K. Flood risk = Hazard • Values • Vulnerability. Water Int. 2005, 30, 58–68. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.594.999&rep=rep1&type=pdf (accessed on 1 December 2018).
- Merz, B.; Thieken, A.H.; Gocht, M. Flood Risk Mapping at the Local Scale: Concepts and Challenges. In Flood Risk Management in Europe; Springer: Dordrecht, The Netherlands, 2007; pp. 231–251. ISBN 978-1-4020-4199-0. Available online: https://link.springer.com/content/pdf/10.1007%2F978-1-4020-4200-3_13.pdf (accessed on 1 January 2019).
- Federal Emergency Management Agency 10 year/50 year flood zones—DFIRM Flood Maps. Available online: https://fema.ideascale.com/a/dtd/10-Year-50-Year-Flood-Zones-DFIRM-Flood-Maps/315482-14692#idea-tab-comments (accessed on 30 May 2018).
- Novelo-Casanova, D.A.; Rodríguez-Vangort, F. Flood risk assessment. Case of study: Motozintla de Mendoza, Chiapas, Mexico. Geomat. Nat. Hazards. Risk 2016, 7, 1538–1556. [Google Scholar] [CrossRef]
- Wurl, J.; Martínez, G.; Cynthia, N.; Imaz, L. Respuesta hidrológica al cambio climático en regiones áridas: Caso de estudio en los Comondú, Baja California Sur, México. Hidrobiológica 2017, 27, 13–22. Available online: http://www.scielo.org.mx/pdf/hbio/v27n1/0188-8897-hbio-27-01-00013.pdf (accessed on 1 March 2019). [CrossRef]
| Distribution/Parameter | M | M-ML | M-L | ML | HP |
|---|---|---|---|---|---|
| Normal | 11.41 | 11.41 | |||
| Log Normal with two parameters | 16.23 | ||||
| Log Normal with three parameters | 7.95 | ||||
| Exponential with parameter β | 16.91 | 55.53 | 44.72 | ||
| Gamma with two parameters | 8.46 | 7.71 | 7.58 | ||
| Gamma with three parameters | 7.83 | 7.72 | |||
| Log Pearson typo III | 8.32 | ||||
| Extreme Values I (Gumbel) | 8.56 | 7.52 | 7.29 | ||
| General extreme values (GEV) | 7.02 |
| River/ (m3/s) | Rp 50 years | Rp 100 years | Rp 500 years |
|---|---|---|---|
| Yautepec | 288 | 316 | 373 |
| Apanquetzalco | 100.8 | 110.6 | 130.5 |
| Oacalco | 115.2 | 126.4 | 149.2 |
| Flood Level (m). | Hazard Level. | |||
|---|---|---|---|---|
| H | > 1.00 | H | H | H |
| M | 0.51–1.00 | H | M | L |
| L | 0.0–0.50 | M | L | L |
| Rp ≤ 50 | 50 < Rp ≤ 100 | 100 < Rp ≤ 500 | ||
| H | M | L | ||
| Frequency (years) | ||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zúñiga, E.; Novelo-Casanova, D.A. Hydrological hazard estimation for the municipality of Yautepec de Zaragoza, Morelos, Mexico. Hydrology 2019, 6, 77. https://doi.org/10.3390/hydrology6030077
Zúñiga E, Novelo-Casanova DA. Hydrological hazard estimation for the municipality of Yautepec de Zaragoza, Morelos, Mexico. Hydrology. 2019; 6(3):77. https://doi.org/10.3390/hydrology6030077
Chicago/Turabian StyleZúñiga, Emmanuel, and David A. Novelo-Casanova. 2019. "Hydrological hazard estimation for the municipality of Yautepec de Zaragoza, Morelos, Mexico" Hydrology 6, no. 3: 77. https://doi.org/10.3390/hydrology6030077
APA StyleZúñiga, E., & Novelo-Casanova, D. A. (2019). Hydrological hazard estimation for the municipality of Yautepec de Zaragoza, Morelos, Mexico. Hydrology, 6(3), 77. https://doi.org/10.3390/hydrology6030077





