A Long–Term Response-Based Rainfall-Runoff Hydrologic Model: Case Study of The Upper Blue Nile

Abstract

This study develops a response-based hydrologic model for long-term (continuous) rainfall-runoff simulations over the catchment areas of big rivers. The model overcomes the typical difficulties in estimating infiltration and evapotranspiration parameters using a modified version of the Soil Conservation Service curve number SCS-CN method. In addition, the model simulates the surface and groundwater hydrograph components using the response unit-hydrograph approach instead of using a linear reservoir routing approach for routing surface and groundwater to the basin outlet. The unit-responses are Geographic Information Systems (GIS)-pre-calculated on a semi-distributed short-term basis and applied in the simulation in every time step. The unit responses are based on the time-area technique that can better simulate the real routing behavior of the basin. The model is less sensitive to groundwater infiltration parameters since groundwater is actually controlled by the surface component and not the opposite. For that reason, the model is called the SCHydro model (Surface Controlled Hydrologic model). The model is tested on the upper Blue Nile catchment area using 28 years daily river flow data set for calibration and validation. The results show that SCHydro model can simulate the long-term transforming behavior of the upper Blue Nile basin. Our initial assessment of the model indicates that the model is a promising tool for long-term river flow simulations, especially for long-term forecasting purposes due to its stability in performing the water balance.

1. Introduction

In order to simulate the continuous (long-term) rainfall-runoff transforming behavior of big rivers (e.g., the upper Blue Nile), there are many methods and algorithms which can account for the soil moisture balance to produce long-term hydrologic simulations. For example, the Soil Moisture Accounting (SMA) method is one method that can simulate the catchment runoff over long-term, where the SMA approach is considered as a water balance component dividing the basin into storage zones. Each storage zone has different parameters to simulate the water movement. Different SMA algorithms are encompassed in many long-term hydrologic models such as the Hydrologic Engineering Center-Hydrologic Modeling System (HEC-HMS), Soil Moisture Accounting and Routing (SMAR), Sacramento Soil Moisture Accounting Model (SAC-SMA) that is used by the U.S. National Weather Service River Forecast System (NWSRFS), and Nile Forecasting System (NFS). HEC-HMS was applied to different river basins such as Blue Nile River, Vamsadhara River in India and Mkurumudzi River in Kenya respectively [1,2,3]. All these studies showed a satisfactory performance; however, the SMA algorithm, used in the (HEC-HMS), has a linear structure that could be an error source for simulating the non-linear rainfall-runoff [1]. The 12 calibration parameters of the HEC-HMS was enhanced in several studies over the Blue Nile basin [4,5]. A study of the comparative performance of the SMA algorithm used in HEC-HMS and SMAR was conducted over the Blue Nile basin [4] in which SMAR better fitted the whole observed hydrograph. However, HEC-HMS showed better performance in reproducing the overall basin peak. The lumped SAC-SMA model and a spatially variable model, which called modified Interactions Soil–Biosphere–Atmosphere (MISBA), were used to evaluate the hydrologic impact of the climate anomalies on the water availability in the upper Blue Nile basin [6]. In this study [6], the SAC-SMA and MISBA were calibrated and validated, and their outputs were compared with the observed flow data at Diem station. The lumped SAC-SMA model better represented the observed flow than the spatially variable MISBA model. This may be attributed to the lack of accurate data (especially rainfall) to provide proper spatially variable input to MISBA model. The approach used in the water balance model in NFS also follows the SMA concept dividing the soil into upper and lower zones; however, it uses the CN for the first estimate of the maximum soil moisture deficit in the thin upper soil zone, which represents the short-term storm retention [7,8].

The Soil Conservation Service curve number (SCS-CN) is another method that is used for the watersheds modeling, where it considers the effect of the soil moisture condition prior to the storm. Originally, SCS-CN is limitedly developed for computing the direct surface runoff from a single storm without taking into consideration the soil moisture condition (SMC) in its basic formulation. In the original SCS-CN method, the CN is attributed to the antecedent soil moisture state prior to the storm [9,10] instead of the SMC resulting in unrealistic sudden jumps in the CN values and, hence, in the estimated runoff [11,12]. The potential was done by several researchers to modify the SMA procedure in the SCS-CN versions to be applicable for the long-term simulation in order to overcome this limitation of the original SCS-CN, (e.g., [13,14,15,16,17,18,19,20]). The modified SCS-CN versions became more complicated due to the new added parameters [21]. The modified SCS-CN was also used for developing a long-term hydrologic rainfall-runoff simulation by incorporating it with Clark’s unit hydrograph method [22]. The Soil and Water Assessment Tool (SWAT) is another common hydrological model having the capability of continuous simulation for long-term periods operating on a daily time step at river basin scale [23,24]. The SCS-CN method, in SWAT, estimates the surface runoff, where the CN is daily updated depending on the daily SMC or the evapotranspiration [25]. The applicability of the CN within SWAT was tested in three small catchments from the upper Blue Nile [26]. SWAT-CN showed well performance in simulating the surface runoff under low and high rainfall.

A major problematic issue in long-term simulations using the SMA approach is the difficulties encountered in estimating/calibrating the different soil moisture accounting parameters especially infiltration rates and storage capacities. Infiltration rate from the surface to the subsurface zone and the rates from the sub-sequent lower groundwater zones and the storage capacities are the most sensitive parameters that affect both the calculated surface and groundwater hydrograph components. In addition, evapotranspiration is another problematic variable that cannot be estimated precisely since plants actually tend to adjust the water consumption based on the soil moisture available and not only on temperature and humidity. Another issue that can be problematic in large basins is the routing approaches used to route both runoff and groundwater depths to the basin outlet. A linear or non-linear reservoir model is usually used in long-term models to route surface water, while a constant lag value is usually used for groundwater. New research started to implement the synthetic unit hydrograph concept to route surface water in long term analysis [22]. However, the above routing approaches can depart from reality in large basins with different sub-catchments that contribute at the basin outlet at significantly different times. For such large basins, a time-area unit hydrograph (developed on a short-term basis) can better represent the transforming behavior [27,28,29]. This can blend the powerful accuracy of short-term modeling into the required simplicity of the long-term analysis.

The above problematic issues create difficulties in performing robust and accurate (yet simple) long-term simulations. For that reason, this paper aims to overcome these difficulties by developing an easy to use hydrological model for long-term simulations. The developed model incorporates a modified version of the SCS-CN technique for separating the excess rainfall from the total rainfall on the surface. This new approach overcomes the infiltration rates problem by performing the mass balance on the surface using a modified version of SCS-CN. Surface soil moisture capacity in the model varies over time according to the rainfall depths of the previous 10 days using an inverse time-weighted method. To simplify the calculations of evapotranspiration, the calculations are not based on potential evapotranspiration data (i.e., no evapotranspiration data is required as input). Part of evapotranspiration in the model is assumed to be implicitly accounted for in the SCS-CN initial abstraction, while the other part is taken as a continuous component from the root zone. Finally, the separated excess and groundwater depths are convoluted at the basin outlet (routed to the basin outlet) using a time-area unit-response approach that is developed on a short-term basis [27,28,29], which can better simulate the real responses of large basins.

2. Model Description

The model uses a modified version of SCS-CN to perform water balance at the surface interface. The water balance at the surface is responsible for separating the surface and groundwater component depths, in addition to separating part of evapotranspiration. The separated depths are then convoluted later at the outlet (routed to the catchment or sub-catchment outlet) using response functions in order to generate the different flow hydrograph components at the outlet. The surface unit-response is based on arrival times computed by Manning’s equation of the grid two dimensional (2D) cells, while the groundwater responses are based on arrival times computed using seepage velocity of the same 2D cells (considering seepage velocity that is Darcy’s velocity divided by the porosity).

It should be noted that at the early stages of this research, two approaches were considered to choose from for the model design (in the two approaches, the routing to the outlet is based on the same travel time grid).

• Approach-1 (Grid-based mass balance):

This approach performs the mass balance per pixel. The excess/infiltrated depths are calculated per pixel and each excess volume (i.e., depth * cellsize²) is routed to the outlet according to the corresponding travel time grid (whether surface or underground). The excess volume is simply accumulated at the outlet on the timeline at its arrival time. Computationally this is not a difficult exercise because the flow at the arrival time is simply retrieved from its one-dimensional memory array then increased by the contributing cell then set back into the array on the fly (no significant computer memory is needed). The advantage of this approach is that it allows spatially variable rainfall input, and all other model parameters/coefficients including the curve number can be input as spatially variables. However, a problem of that approach exists actually in its advantages; that the user must enter the model parameters/coefficients as spatially variable grids (or polygons to be rasterized later by the model), which can be very difficult during calibration and the user will have at the end of the day to assume uniform parameters to do the calibration. On the other side, rainfall will have to be entered spatiotemporally variable (a grid at each time step). Another problem with this approach is that it cannot accommodate hydraulic structures inside the grid.

• Approach-2: (Catchment/Sub-catchment based mass balance):

Water balance here is performed on the catchment or sub-catchments (not the cell) using spatially uniform mass balance parameters and rainfall. In case there is significant spatial variability in the mass-balance parameters or rainfall or in case there are hydraulic structures or lakes/reservoirs, the user sub-divides the catchment into a network of sub-catchments (the typical hydrologic networks) and performs the mass-balance on the divisions (separate mass balance per each sub-catchment). After the mass balance is done, the excess/infiltrated depths (per catchment or sub-catchment) are transformed to hydrographs at the outlets using unit hydrographs (developed from the same travel time grid used in the previous approach). The hydrographs entering the network nodes are then combined/routed across the network until the outlet. This approach is much simpler computationally and in term of data requirements and yet flexible for installing hydraulic structures and reservoirs/lakes.

Hence, approach-2 (i.e., catchment/sub-catchment based mass balance) was chosen for the model design for the following reasons:

• Simple to use and can be programmed even over a spreadsheet (after the unit hydrographs have been obtained);
• Calibrating spatially variable (unknown) grids for the coefficients is very difficult and one will have to assume uniform parameters (so, no benefit of allowing grid-based mass balance in the first place);
• The target usage of the model is to be implemented for long-term forecasting applications (this is what initiated the research). A long-term forecast of rainfall (e.g., from Global Climate Models (GCMs)) is needed as input to the model to produce long-term forecasts for the runoff hydrographs. GCMs rainfall is almost uniform over the basin (the whole basin covers 1-2 GCM cells (i.e., the rainfall input that will be used for forecasting is already uniform);
• This approach can accommodate lakes/reservoirs and hydraulic structures. Taking a reservoir as an example: If the basin is represented in a network of sub-catchments, a hydrologic reservoir component (level pool) can be installed through the network. However, if the whole basin is used as one unit that geographically contains the lake/reservoir (lumped mass balance as used in the case study), then the reservoir area must be subtracted from the whole basin area in mass balance. In this case, the mass balance of the lake is calculated separately and added at the basin outlet at its corresponding arrival time.

Hence, the developed hydrological model is considered lumped over a catchment or sub-catchment (in terms of doing the water balance) and semi-distributed (in terms of routing to the catchment or sub-catchment outlet). However, the model can be applied in a network mode (across a hydrologic network of connected sub-catchments where each sub-catchment has uniformity in the parameter). Using that network mode makes the model semi-distributed in terms of water balance (since the balance is done on each sub-catchment separately and the developed hydrographs from the sub-catchments are routed across the network using any reach/reservoir routing method).

Two main sub-modules are combined in the model; the first one is a water balance sub-module (for surface and groundwater) and the second one is the transforming sub-module (for surface and groundwater).

2.1. The Water Balance Sub-Module

The water balance is mainly controlled by the surface interface at which a modification of the soil conversation service (SCS-CN) loss method is used to model the surface interface. The surface interface separates the water depths that are transformed into surface and groundwater.

2.1.1. Water Balance at the Surface

The original SCS-CN method (originally made for event-based short-term) assumes that there is a constant potential maximum soil moisture retention (S₀ in mm), which can be determined from a constant curve number CN₀ (a dimensionless number that varies from 0 to 100) as follows:

$$S_0=\frac{25400}{C{N}_0}-254$$

(1)

In the original SCS-CN, both S₀ and CN₀ are temporally constant. The long-term formulation of the SCS-CN method (used in SCHydro) considers that there are temporal variations in S (denoted S_act(t)) or, in other words, the curve number of the soil is also variable with time (not temporally constant as in the original SCS-CN formulation). S_act(t) depends on the antecedent rainfall (P_ant(t)) [16,30]. The term antecedent can cover a period from 5 to 30-days [9,10,31]. P_ant is temporally interpolated at any day from the previous days (10 days are used in this study) using an inverse time-weighted approach. Hence, the calculations sequence used in SCHydro at any time step can be explained as follows:

$$P_{ant\left(t\right)}=\frac{{{\displaystyle \sum }}_{i=1}^{i=10}\frac{P_{\left(t-i\right)}}{i^2}}{{{\displaystyle \sum }}_{i=1}^{i=10}\frac{1}{i^2}}$$

(2)

$$SM{C}_t=\mathsf{\beta }\sqrt{P_{ant\left(t\right)}}$$

(3)

$$S_{act\left(t\right)}=\frac{S_0{}^2}{SM{C}_t+S_0}$$

(4)

$$I_{a_t}=\{\begin{array}{c} P_t \left(P_t\le \lambda S_{act\left(t\right)}\right)\\ \lambda S_{act\left(t\right)} \left(Else\right)\end{array}$$

(5)

$$P_{e_t}=P_t-I_{a_t}$$

(6)

$$R{O}_t=\{\begin{array}{c} 0 \left(P_t\le \lambda S_{act\left(t\right)}\right)\\ \frac{P_e{{}_t}^2}{P_{e_t}+S_{act\left(t\right)}} \left(Else\right)\end{array}$$

(7)

$$F_t=P_t-I_{a_t}-R{O}_t$$

(8)

where:

$$\begin{array}{l}{P}_{ant\left(t\right)} = \mathrm{The} \mathrm{antecedent} \mathrm{rainfall} \mathrm{during} \mathrm{time} \mathrm{step} t.\\ P_t = \mathrm{Rainfall} \mathrm{depth} \mathrm{during} \mathrm{time} \mathrm{step} t.\\ SM{C}_t = \mathrm{Surface} \mathrm{soil} \mathrm{moisture} \mathrm{condition} \mathrm{at} \mathrm{time} \mathrm{step} t.\\ \beta = \mathrm{Coefficient} \mathrm{of} \mathrm{soil} \mathrm{moisture} (\mathrm{to} \mathrm{be} \mathrm{alibrated}).\\ S_{act\left(t\right)} = \mathrm{Modified} \mathrm{potential} \mathrm{maximum} \mathrm{retention} \mathrm{at} \mathrm{time} t.\\ S_0 = \mathrm{Normal} \left(\mathrm{constant}\right) \mathrm{potential} \mathrm{maximum} \mathrm{soil} \mathrm{moisture} \mathrm{retention}.\\ I_a{}_t = \mathrm{Initial} \mathrm{abstraction} \mathrm{at} \mathrm{time} t (\mathrm{the} \mathrm{first} \mathrm{evapotranspiration} \mathrm{part}).\\ \lambda = \mathrm{Initial} \mathrm{abstraction} \mathrm{coefficient} (\mathrm{taken} \mathrm{constant} = 0.2).\\ P_{e_t} = \mathrm{Effective} \mathrm{rainfall} \mathrm{during} \mathrm{time} \mathrm{step} t (\mathrm{exceeding} \mathrm{initial} \mathrm{abstraction}).\\ R{O}_t = \mathrm{Runoff} \mathrm{depth} \mathrm{during} \mathrm{time} \mathrm{step} t.\\ F_t = \mathrm{Infiltration} \mathrm{depth} \mathrm{during} \mathrm{time} \mathrm{step} t.\end{array}$$

Equation (2) is the standard inverse weighted interpolation (IDW) that is usually applied for spatial interpolation [32] (note that time replaces distance here). Based on Equation (2), the far precipitation occurs in the past 10 days, the less contribution it has in the surface moisture condition of the current day (i.e., the closer to a dry CN). Equations (3) and (4) relate the potential maximum soil moisture retention to the antecedent rainfall (refer to [30] for the details). Equation (7) is the basic formula of the SCS-CN method [9,10].

Accordingly, SCHydro starts the simulation with an initial value of S (i.e., $S_0$) then modifies it at each time step according to the variation in the surface soil moisture. It should be noted that the SCS method (Equation (8)) implicitly considers wet-evapotranspiration in its initial abstraction. While the time depletion in P_ant (as modeled in the inverse time-weighted approach) considers the change in the surface curve number due to the moisture condition.

2.1.2. Groundwater Balance

As described in the introduction section, evapotranspiration in the model is divided into two components. The first component is the wet-evapotranspiration (extra plant consumption during wet conditions due to plant tendency to store water when available in addition to evaporation from the surface due to the availability of ponded water), which occurs near the surface interface. This first evapotranspiration component is implicitly considered in the SCS-CN initial abstraction (I_a). Note that the initial abstraction of the surface soil occurs mainly due to the suction head of the surface soil, which makes the initial abstraction vulnerable to evapotranspiration. Note also that I_a is affected by the surface moisture condition simulated using the inverse time-weighted method described above (Equation (2)). The second component (TR) is the basic evapotranspiration, which is a continuous small component (for life keeping) that is proportional to the amount of moisture (RZ) in the lower root zone (Equation (9)).

The underground in the model is divided into three zones: (1) The root zone; (2) groundwater1 layer; and (3) groundwater2 layer. In other words, the model contains two groundwater aquifers. Infiltrated water that exceeds the field capacity of the root zone (${\theta }_f$) is divided between the two groundwater aquifers in mass balance. The upper aquifer accounts for the unsaturated/saturated flow, while the underlying aquifer simulates the saturated base flow. Both aquifers contribute back to river flow with different net depths. The net depth that each aquifer contributes back to the river flow is assumed proportional to the rate at which each aquifer is being charged. The net depths are then convoluted into groundwater hydrographs at the basin outlet using specific response functions (i.e., underground unit hydrographs). To explain the calculations of the underground balance, let RZ_t denotes the depth of moisture in the root zone at time t, the underground calculations proceed as follows:

$$T{R}_t=C_1\ast R{Z}_t$$

(9)

$$D{R}_t=C_2\ast \left(R{Z}_t-{\theta }_f\right)$$

(10)

$$GW{1}_t=C_3\ast D{R}_t$$

(11)

$$P{R}_t=\left(1-C_3\right)\ast D{R}_t$$

(12)

$$DS{P}_t={\left(P{R}_t\right)}^E$$

(13)

$$GW{2}_t=C_4\ast DS{P}_t$$

(14)

where, during time step t, the depths (mm) of the different components are:

$$\begin{array}{l}T{R}_t = \mathrm{Basic} \mathrm{evapotranspiration} (\mathrm{for} \mathrm{life} \mathrm{keeping}).\\ {\theta }_f = \mathrm{Constant} \mathrm{field} \mathrm{capacity} \mathrm{of} \mathrm{the} \mathrm{root} \mathrm{zone}.\\ D{R}_t = \mathrm{Drainage} \mathrm{from} \mathrm{the} \mathrm{root} \mathrm{zone} \mathrm{to} \mathrm{the} \mathrm{upper} \mathrm{groundwater} \mathrm{layer}. \\ GW{1}_t = \mathrm{Contribution} \mathrm{of} \mathrm{upper} \mathrm{groundwater} \mathrm{linear} \mathrm{aquifer} \mathrm{to} \mathrm{the} \mathrm{river}.\\ P{R}_t = \mathrm{Percolation} \mathrm{from} \mathrm{upper} \mathrm{groundwater} \mathrm{aquifer} \mathrm{to} \mathrm{lower} \mathrm{aquifer}.\\ DS{P}_t = \mathrm{Deep} \mathrm{seepage} \mathrm{from} \mathrm{the} \mathrm{lower} \text{non-linear} \mathrm{aquifer}.\\ GW{2}_t = \mathrm{Base} \mathrm{flow} \mathrm{from} \mathrm{lower} \mathrm{aquifer} \mathrm{that} \mathrm{contributes} \mathrm{back} \mathrm{to} \mathrm{the} \mathrm{river}.\\ C_1,C_2,C_3,C_4, \mathrm{and} E \mathrm{are} \mathrm{model} \mathrm{coefficients} \mathrm{to} \mathrm{be} \mathrm{calibrated}.\end{array}$$

Hence, the model starts in the initialization with initial condition S_o for the surface interface and RZ₀ for the moisture in the root zone and updates S_act(t) (Equation (4) above) and updates the moisture storage (mm) in the root zone in each next time step as follows:

$$R{Z}_t=R{Z}_{t-1}+F_{t-1}-T{R}_{t-1}-D{R}_{t-1}=F_{t-1}+R{Z}_{t-1}\left(1-C_1-C_2\right)+C_2{\theta }_f$$

(15)

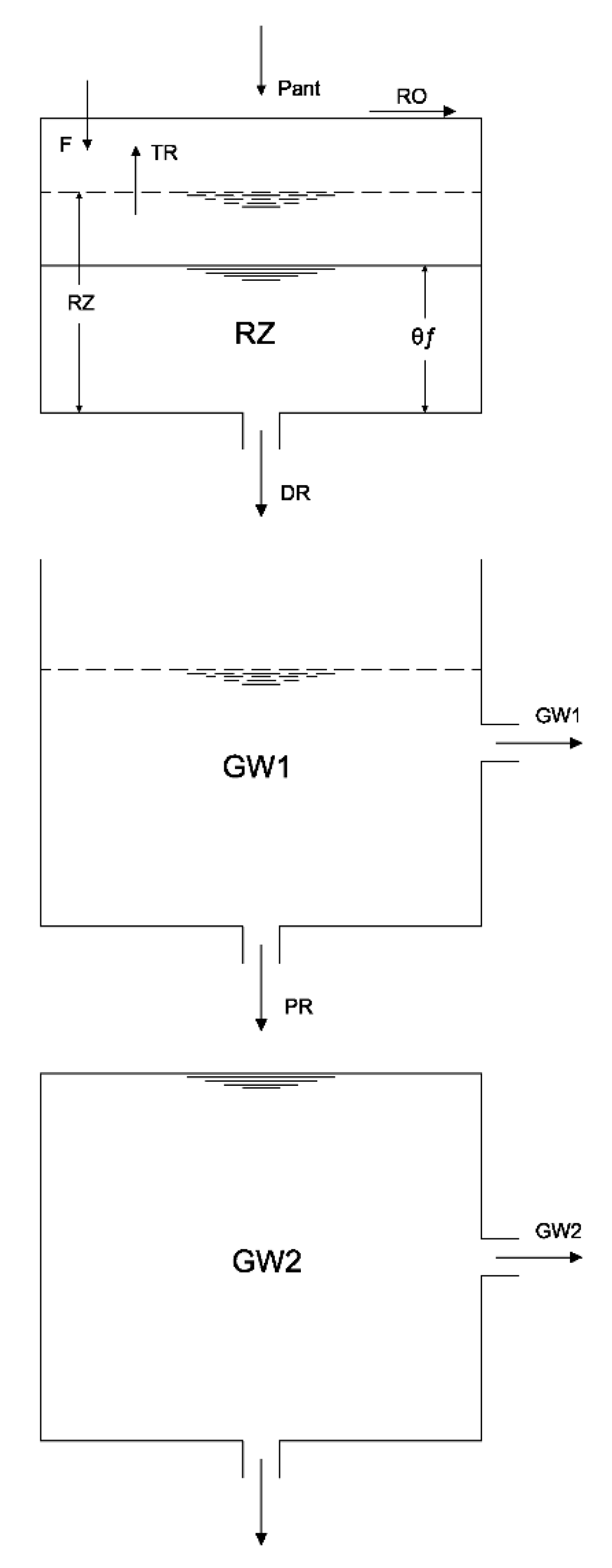
Accordingly, the surface components (Equations from (2) to (8)) and underground components (Equations from (9) to (14)) are calculated in each time step t from S_act(t) and RZ_t, at the same time step respectively. Figure 1 presents the concept used for water balance.

2.2. The Transforming Sub-Module

The transforming functions (response functions) using which the surface and groundwater depths (RO, GW1, and GW2) are transformed into three components hydrographs at the outlet follow the unit hydrograph principle. The response functions are developed using the time-area approach. This approach can precisely capture the real response of the basin to transform the three contributing depths in a semi-distributed sense in which the different grid cells of the model contribute at different arrival times at the outlet. Python-GIS is used programmatically to extract these responses by determining a travel time grid for each of the three component depths. The surface water travel time grid is calculated using Manning’s formula, while groundwater travel time is determined using Darcy’s formula (considering seepage velocity equals Darcy velocity divided by the porosity) until it reaches back to the surface. All the flow properties such as velocity and travel time are programmatically calculated in GIS environment on grid-basis as described below.

2.2.1. Surface Response

The approach used is similar to the one described in [27,28,29]. This approach depends on a stream power formulation in which the hydraulic radius at each grid cell is related to the upstream catchment area (i.e., the GIS flow accumulation value at the grid cell). The flow velocity is then calculated from Manning’s formula in which the slope is determined along the flow directions. To illustrate the approach, let i denotes a grid cell in the model, the calculations of the surface response (as shown in Equation (20) for 1 mm runoff depth) proceeds as follows:

$$R_i=0.072 {\left(A_{us\left(i\right)}\right)}^{0.23}$$

(16)

$$V_{s\left(i\right)}=\frac{24\ast 3600}{n_i} {\left(R_i\right)}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.} \sqrt{S_i}$$

(17)

$$d{t}_{s\left(i\right)}=\frac{d{l}_i}{V_{s\left(i\right)}}=d{l}_i\times \frac{1}{V_{s\left(i\right)}}$$

(18)

where

$$\begin{array}{l}{R}_i = \mathrm{Hydraulic} \mathrm{radius} \mathrm{at} \mathrm{the} \mathrm{grid} \mathrm{cell} i \left(\mathrm{m}\right).\\ A_{us\left(i\right)} = \mathrm{Upstream} \mathrm{area} \mathrm{contributing} \mathrm{at} \mathrm{cell} \mathrm{i} \left({\mathrm{km}}^2\right) = \mathit{the} \mathit{GIS} \mathit{flow} \mathit{accumulation} \left(i\right)\times {\mathit{cellsize}}^2.\\ n_i = \mathrm{Manning}’\mathrm{s} \mathrm{Coefficient} \mathrm{at} \mathrm{grid} \mathrm{cell} \mathrm{i}.\\ S_i = \mathrm{Longitudinal} \mathrm{slope} \mathrm{at} \mathrm{grid} \mathrm{cell} i (\mathrm{m}/\mathrm{m}).\\ V_{s\left(i\right)} = \mathrm{Surface} \mathrm{flow} \mathrm{velocity} \mathrm{at} \mathrm{the} \mathrm{grid} \mathrm{cell} i (\mathrm{m}/\mathrm{d}).\\ d{l}_i = \mathrm{Flow} \mathrm{length} \mathrm{across} \mathrm{cell} i (\mathrm{cellsize} \mathrm{for} \mathrm{orthogonal} \mathrm{direction} \mathrm{and} 1.414 \mathrm{cellsize} \mathrm{for} \mathrm{the} \mathrm{diagonal} \mathrm{flow} \mathrm{direction}).\\ d{t}_{si} = \mathrm{Surface} \mathrm{mini}-\mathrm{travel} \mathrm{time} \mathrm{though} \mathrm{grid} \mathrm{cell} i (\mathrm{m}/\mathrm{d}).\end{array}$$

The surface travel time grid (times to the outlet) can then be obtained by calculating the arrival times of all grid cells to the outlet. The arrival time (T_si) of any grid cell i at the outlet is calculated by accumulating the mini travel times of all its downstream cells until the outlet. This can simply be accomplished via the weighted flow length GIS-built-in function [33] using (1/V_si) as weight along flow direction to the outlet as follows:

$$T_{si}={\displaystyle \sum }_i^{outlet}(d{l}_i\times \frac{1}{V_{s\left(i\right)}})\left[along flow direction\right]$$

(19)

The surface response function (i.e., the surface unit hydrograph due to 1 mm runoff depth) is then determined by counting the cells (i.e., the surface area) that arrives at the outlet within each time step (i.e., having the same travel time to the outlet rounded to the nearest integer) as follows:

$$u_{s\left(j\right)}={10}^{-3}\times cellsiz{e}^2\times n_{\left(T_{si}=j\right)}$$

(20)

where

$$\begin{array}{l}{u}_{s\left(j\right)} = \mathrm{Ordinate} \mathrm{number} j (\mathrm{e}.\mathrm{g}., \mathrm{j} \mathrm{days}) \mathrm{of} \mathrm{the} \mathrm{surface} \mathrm{unit} \mathrm{hydrograph} ({\mathrm{m}}^3/\mathrm{time} \mathrm{step}).\\ n_{\left(T_{si}=j\right)} = \mathrm{Number} \mathrm{of} \mathrm{cells} \mathrm{having} \mathrm{arrival} \mathrm{time} T_{si} = j (\mathrm{where} T_{si}\mathrm{is} \mathrm{rounded} \mathrm{to} \mathrm{integer}).\\ cellsize = \mathrm{Grid} \mathrm{resolution} \mathrm{in} \left(\mathrm{m}\right).\end{array}$$

Hence, all ordinates of the surface unit hydrograph can be determined. For complete details on the time-area approach and its literature history refer to [27,28,29].

2.2.2. Groundwater Responses

In the modeling of groundwater flows, for the sake of simplicity and since no precise information on the groundwater gradients is usually available, it is assumed here that the gradient vectors of groundwater ($i_{i,z}$) in both layers are proportional to the slope vectors ($S_i$) of surface water (where z stands for groundwater aquifer layer no.). This is not a bad assumption since groundwater is also gravity induced and the slope of bedrocks in the lower aquifer can be approximated proportional to the surface topography. In other words, the hydraulic gradient vectors in Darcy’s law are considered proportional to the slope vectors along the surface. Hence, Darcy law can be applied as follows:

$${V^{\prime }}_{g\left(i,z\right)}=K_{i,z}\left(i_{i,z}\right)=K_{i,z} B_z\left(S_i\right)$$

(21)

where

$$\begin{array}{l}{V^{\prime }}_{g\left(i,z\right)} = \mathrm{Groundwater} \mathrm{flow} \mathrm{velocity} \mathrm{at} \mathrm{grid} \mathrm{cell} i \mathrm{in} \mathrm{at} \mathrm{layer} \mathrm{no}.z (\mathrm{m}/\mathrm{d}).\\ K_{i,z} = \mathrm{Hydraulic} \mathrm{conductivity} \mathrm{divided} \mathrm{by} \mathrm{porosity} \mathrm{of} \mathrm{the} \mathrm{aquifer} \mathrm{at} \mathrm{grid} \mathrm{cell} i \mathrm{in} \mathrm{layer} \mathrm{no}. \mathrm{z} (\mathrm{m}/\mathrm{d}).\\ i_i = \mathrm{Groundwater} \mathrm{hydraulic} \mathrm{gradient} \mathrm{at} \mathrm{grid} \mathrm{cell} i \mathrm{in} \mathrm{layer} \mathrm{no}. z (\mathrm{m}/\mathrm{m}).\\ B_z = \mathrm{Proportionality} \mathrm{constant} \mathrm{for} \mathrm{aquifer} \mathrm{layer} \mathrm{no}. z (\mathrm{where} B_z < 1).\end{array}$$

Since groundwater flows in both aquifers can intersect surface water before reaching the outlet, a velocity grid of groundwater should actually be a blend between the groundwater velocity grid and the surface water velocity grid. After groundwater intersects the surface, the velocity of flow of groundwater is set the same as the velocity of flow of the surface water. In order to make this mix, first, a stream grid is developed from the flow accumulation grid. A stream grid has a value of 1 at streams and 0 elsewhere (1 where flow accumulation exceeds a threshold catchment area and 0 for upstream cells). The GIS map algebra condition function (“con function”) [33] is used to make the mix $V_{g\left(i,z\right)}$ between ground and surface velocities as follows:

$$V_{g\left(i,z\right)}=\{\begin{array}{c}{V^{\prime }}_{g\left(i,z\right)} \left(if stream ==0\right)\\ V_{s\left(i\right)} \left(else where\right)\end{array}$$

(22)

Now the groundwater travel time grids (a grid for each aquifer) can be developed in a similar GIS procedure than that of surface water (using the weighted flow length function):

$$T_{g\left(i,z\right)}={\displaystyle \sum }_i^{outlet}(d{l}_i\times \frac{1}{V_{g\left(i,z\right)}}) \left[along flow direction\right]$$

(23)

where $T_{g\left(i,z\right)}$ denotes the arrival time of cell i in aquifer z at the outlet. The response function (unit hydrograph) of each aquifer is then determined from the travel time grids as follows:

$$u_{g\left(j,z\right)}={10}^{-3}\times cellsiz{e}^2\times n_{\left(T_{g\left(i,z\right)}=j\right)}$$

(24)

where

$$\begin{array}{l}{u}_{g\left(j,z\right)} = \mathrm{Ordinate} \mathrm{number} j (\mathrm{e}.\mathrm{g}., j \mathrm{days}) \mathrm{of} \mathrm{the} \mathrm{unit} \mathrm{hydrograph} \mathrm{of} \mathrm{aquifer} \mathrm{no}. \mathrm{z}.\\ n_{\left(T_{g\left(i,z\right)}=j\right)} = \mathrm{Number} \mathrm{of} \mathrm{cells} \mathrm{having} \mathrm{arrival} \mathrm{time} \mathrm{Tg}(\mathrm{i},\mathrm{z}) = \mathrm{j} (\mathrm{where} \mathrm{Tg}(\mathrm{i},\mathrm{z}) \mathrm{is} \mathrm{rounded} \mathrm{to} \mathrm{the} \mathrm{nearest} \mathrm{integer} \mathrm{in} \mathrm{days}).\\ cellsize = \mathrm{Grid} \mathrm{resolution} \mathrm{in} \left(\mathrm{m}\right). \end{array}$$

2.3. Hydrograph Convolution

The three response functions (i.e., unit hydrographs) developed in the previous section (Section 2.2) are used to convolute the contributing water depths into corresponding component hydrographs. The three contributing water depths are RO, GW1, and GW2 (refer to Section 2.1). The three components of the hydrograph are subsequently added using convolution to develop the resulting outflow hydrograph from the basin:

$$\begin{gathered} Q_t=Q_{s\left(t\right)}+Q_{gw1\left(t\right)}+ Q_{gw2\left(t\right)} \\ ={\displaystyle \sum }_{j=1}^{n_{js}}(R{O}_{\left(t-j\right)}{u}_{s\left(j\right)})+{\displaystyle \sum }_{j=1}^{n_{jg1}}(GW{1}_{\left(t-j\right)}{u}_{g\left(j,1\right)})+{\displaystyle \sum }_{j=1}^{n_{jg2}}\left(GW{2}_{\left(t-j\right)}{u}_{g\left(j,2\right)}\right) \end{gathered}$$

(25)

where

$$\begin{array}{l}{n}_{js} = \mathrm{Number} \mathrm{of} \mathrm{ordinates} \mathrm{of} \mathrm{surface} \mathrm{unit} \mathrm{hydrograph}.\\ n_{jg1} = \mathrm{Number} \mathrm{of} \mathrm{ordinates} \mathrm{of} \mathrm{upper} \mathrm{aquifer} \mathrm{unit} \mathrm{hydrograph}.\\ n_{jg2} = \mathrm{Number} \mathrm{of} \mathrm{ordinates} \mathrm{of} \mathrm{lower} \mathrm{aquifer} \mathrm{unit} \mathrm{hydrograph}.\end{array}$$

In other words, n_j denotes the base time of each unit hydrograph in number time steps (i.e., days in this research). Figure 2 presents a schematic chart depicting the run sequence of the different modules in SCHydro model.

3. Case Study

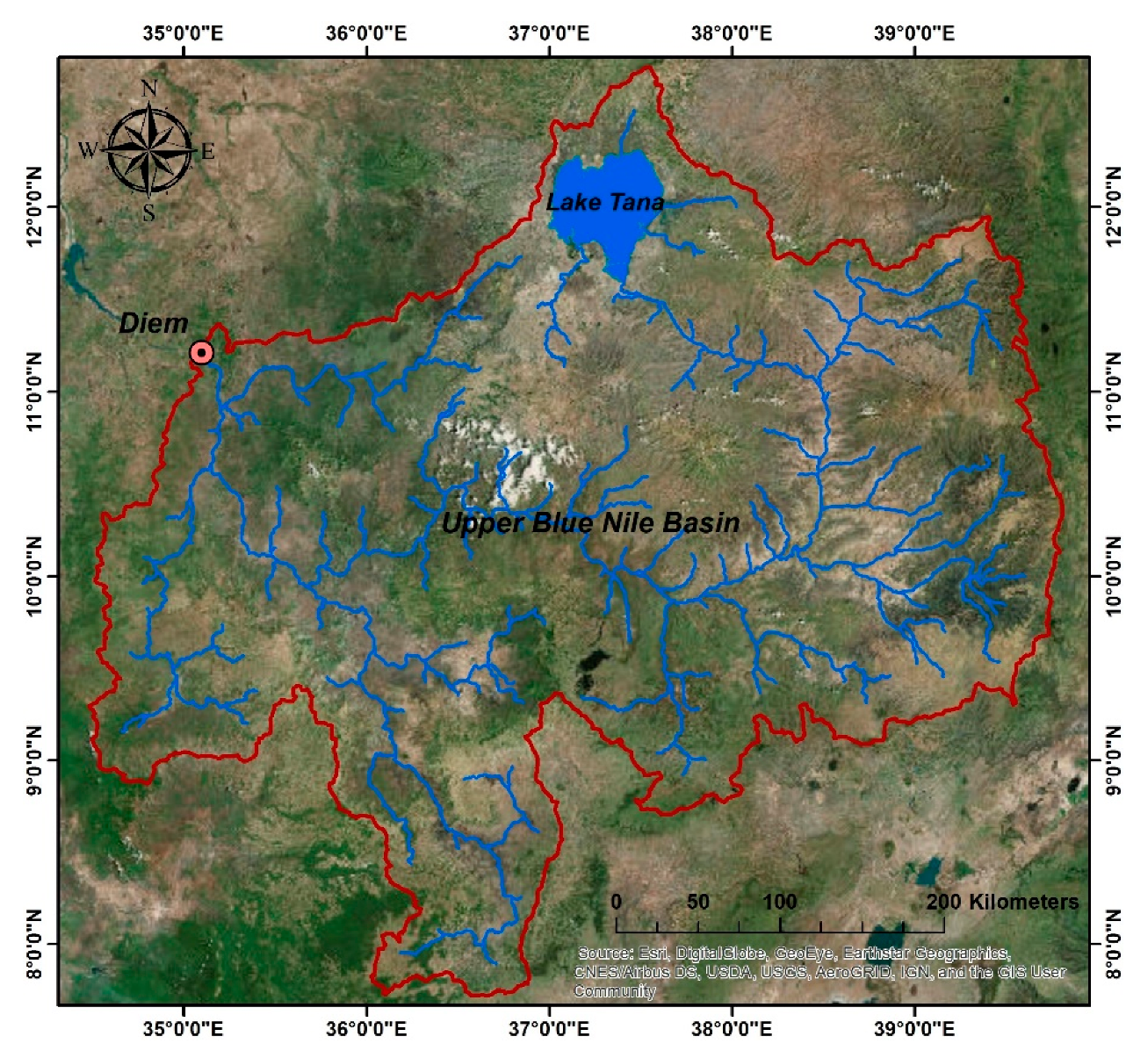
The upper Blue Nile is the largest river basin in terms of volume of discharge and second largest river in terms of area in Ethiopia [34]. It is the most important tributary of the Nile as it is contributing about 60% of the total Nile flow. The reliable rainfall-runoff modeling over the upper Blue Nile to estimate the flow can help the decision making process for better planning and water resources management. The case study focuses on the area up to the Diem station located at the Ethiopian-Sudanese borders with 179,000 km² area. Figure 3 shows the upper Blue Nile basin map. This basin is characterized by a highly seasonal rainfall pattern with most of the rainfall falling in four months (June to September), where the peak occurs during the period (July-August). The mean annual rainfall and potential evapotranspiration (PET) for this basin are 1200 mm and 1400 mm respectively [35]. The mean annual flow at Diem station during the period (1990–2017) estimated to be 52 BCM/year (Billion Cubic Meters per year).

The rainfall data used in this study was obtained from the NFS pre-processor (PP6), which is responsible for converting the rainfall gauge data to distributed gridded data [36]. The daily Mean Areal Precipitation (MAP) was calculated from PP6, over the upper Blue Nile basin, for the period (1990–2017) that will be used as input to the developed hydrological model. However, it should be noted that this data set is insufficient to provide a representable daily areal rainfall average during some periods. This is because the original source of the rain-gauge data is the data summaries provided by the data exchanged under the World Meteorological Organization (WMO) World Weather Watch Program (i.e., the global surface summary of day product produced by the National Climatic Data Center in Asheville, NC). The upper Blue Nile Basin is covered by 7 rain-gauges of this dataset (3 in the middle and 4 at the boundaries). The reason why this data set lacks accuracy is that the records of the rain-gauges contain significant periods of zero readings but there is still a possibility that rainfall occurred but not reported (as mentioned in the data manual available for free from the internet). Hence, the treatment of such zero reading gauges reduces the accuracy. In case zero records are considered (or spatially interpolated using weights developed from long-term averages) at a certain day, this can significantly alter (mainly reduce) the calculated areal average in this day. While if these zero-record-gauges are excluded at a certain day, this reduces the number of gauges used to produce the areal average at this day (to one or 2 gauges only at some days), which can miss significant rainfall producing a non-representing areal average.

The daily observed flow data was collected at Diem station during the period (1990–2017), from Ministry of Water Resources and Irrigation (MWRI), in order to be used in the calibration and validation processes.

A SRTM (Shuttle Radar Topography Mission) Digital Elevation Model (DEM) for the upper Blue Nile region is used to model topography (grid resolution used is 200 m).

3.1. Model Calibration

SCHydro requires a spatially uniform rainfall hyetograph as input for the catchment (or different hyetographs for the sub-catchments in case the model is applied in a hydrologic network). The total number of parameters required are 12 parameters per sub-catchment. 9 parameters are spatially uniform over each sub-catchment, while three parameters are “allowed” to be entered as spatially variable grids.

Table 1. Model parameters and their calibration domains.

Parameter Name	Symbol	Search Domain	Units
Initial curve number (spatially uniform)	$C{N}_0$	60–90	-
Antecedent moisture coefficient (spatially uniform)	$\beta$	0–300	mm0.5
Basic transpiration coefficient (spatially uniform)	$C_1$	0–1	-
Root zone drainage coefficient (spatially uniform)	$C_2$	0–1	-
GW1 contributing coefficient (spatially uniform)	$C_3$	0–1	-
Field capacity of the root zone (spatially uniform)	${\theta }_f$	0–200	mm
Exponent of lower aquifer (spatially uniform)	$E$	0–1	-
GW2 contributing coefficient (spatially uniform)	$C_4$	0–1	-
Initial root zone soil storage (spatially uniform)	$R{Z}_o$	0–200	mm
Manning’s Coefficient (spatially variable)	$n$i	0.02–0.1	-
Conductivity of upper aquifer (spatially variable)	K(i,1)	0–50	m/d
Conductivity of lower aquifer (spatially variable)	K(i,2)	0–50	m/d

shows the parameters and their definitions and calibration domains used (ranges). For the sake of simplifying the calibration and to provide average parameters values that can be used later as an initial guess for the upper Blue Nile sub-catchments, the model is applied in a lumped mode (i.e., the whole catchment of the upper Blue Nile is considered as one unit in performing the mass balance). In addition, Manning roughness and the hydraulic conductivities are approximated as spatially uniform in determining the response functions of the basin. The consideration of the spatial variability (i.e., the use of hydrologic networks in performing the mass balance and the use of spatially variable roughness and conductivity) can improve the accuracy of SCHydro output. However, the initial calibration made in this paper for the whole basin provides the average values of the parameters to start with when calibrating the basin in a network mode (sub-catchment parameters shall be taken around the calibrated average values according to the spatial information that may be available in the future).

The parameters of SCHydro were calibrated using 20 years observed daily flow data from 1990 until 2009. The root mean square error (between the observed and the simulated daily discharges), as well as the standard deviation of the error, were used as two separate objective functions to be minimized in order to select the optimum values of the parameters. It should be noted that the optimum solution found minimized both objective functions (i.e., a composite objective function using the score and weight approach was not needed).

Due to the big number of coefficients to be optimized (i.e., run-time limitations to perform a full search using 12 nested loops), a heuristic approach, that includes both manual and automated searches, was used to search for the optimum parameters. Table 1 shows the search domain used for each parameter, while

Table 2. The optimum model parameters in lumped mode.

Parameter	Value	Unit
$C{N}_0$	82	-
$\beta$	40	mm0.5
$C_1$	0.001	-
$C_2$	0.04	-
$C_3$	0.36	-
${\theta }_f$	70	mm
$E$	0.30	-
$C_4$	0.10	-
$R{Z}_o$	60	mm
$n_i$	0.082	-
K(i,1)	20	m/d
K(i,2)	10	m/d

shows the optimized values of the 12 parameters.

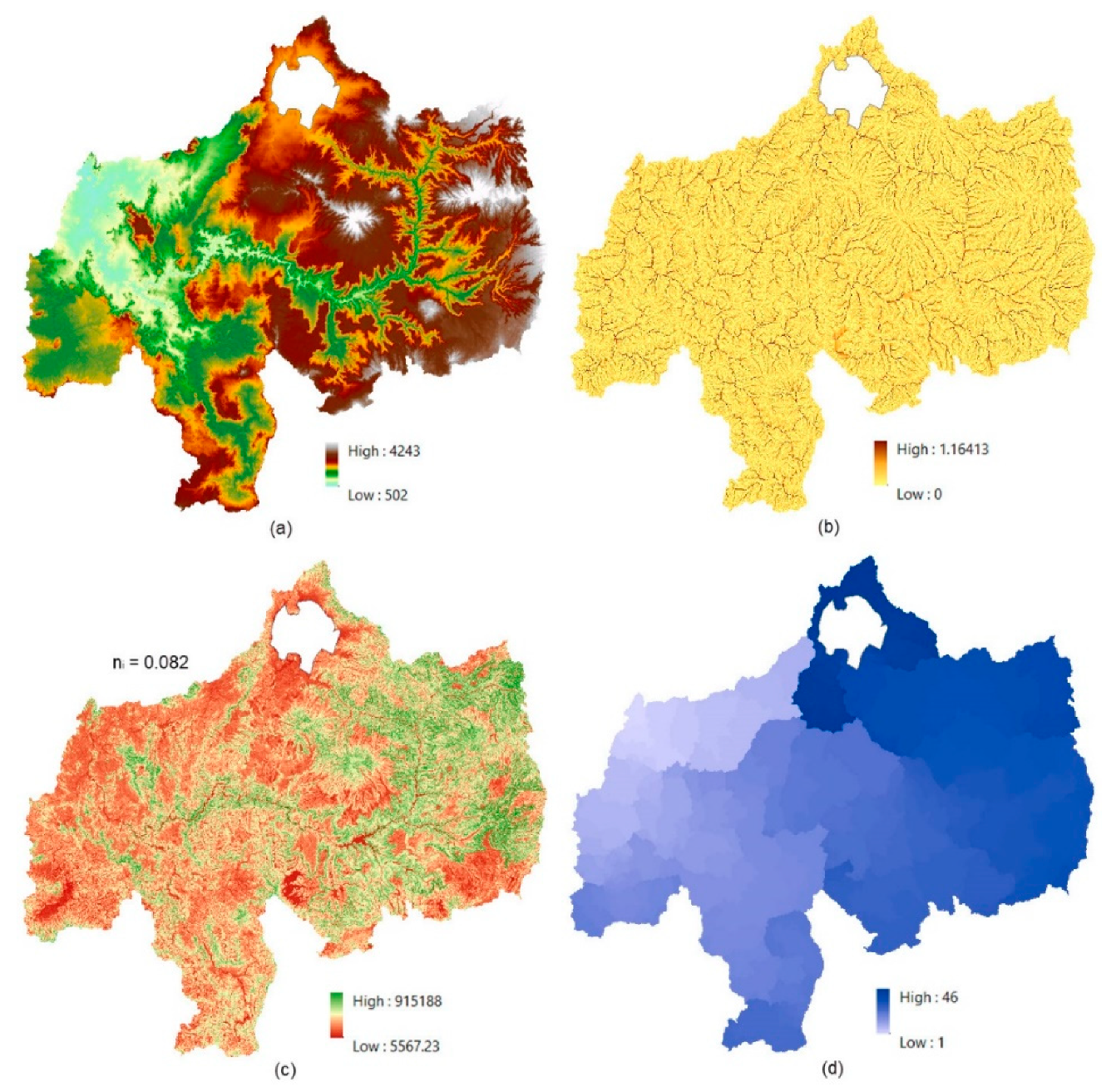
It should be noted that during the calibration of the parameters, it was found that some parameters are more sensitive than the others. The parameters (CN_o, $n$, $\beta$, $C_1$, $C_3$, and $C_4$) have more influence on the simulated flow more than the remaining parameters. The parameter $n$ affects the spatially variable surface response function, as it is related to the travel time of the basin surface water, which affects the spread and peak of the surface hydrograph component.

Figure 4 and Figure 5 show sample grids through the calculations of the arrival time grids (surface and groundwater) using the optimum parameters, while Figure 6 presents the derived response functions based on the corresponding arrival times grids.

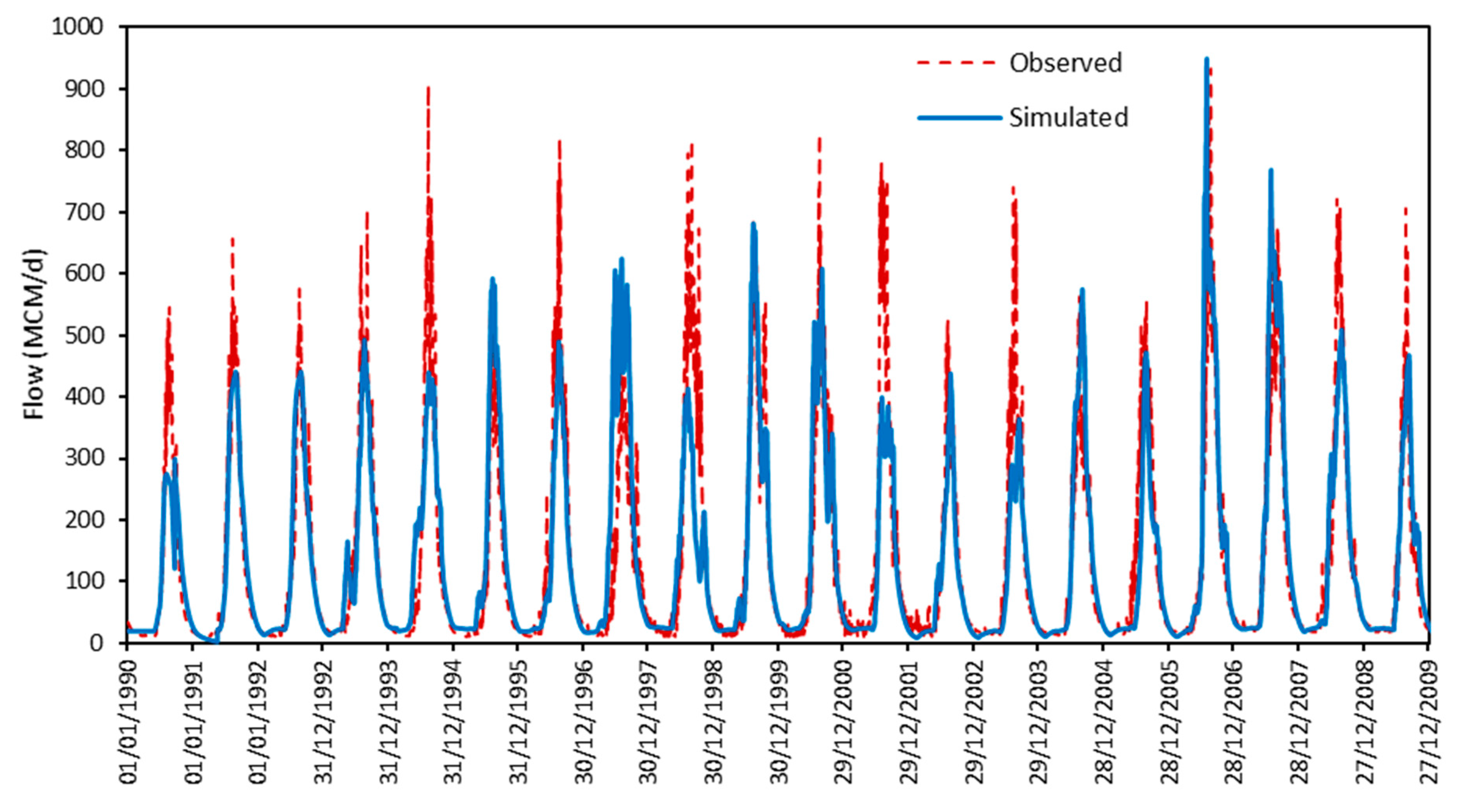
Figure 7 shows the simulated and observed flow discharges for the calibration period. It should be noted that the simulated flow peaks are underestimated in general; however, they are captured in years 1999, 2004, and 2006, and slightly overestimated in years 1995, 1997, and 2007. This difference may be attributed to the lack of precise areal average rainfall on the catchment due to the reason described above (at the beginning of Section 3). Figure 8 shows the mean monthly flow at Diem station. The hydrograph shape of the mean monthly flow has a slight overestimation in the rising limb especially from May to July, while there is a relative match in the falling limb.

3.2. Model Validation and Assessment

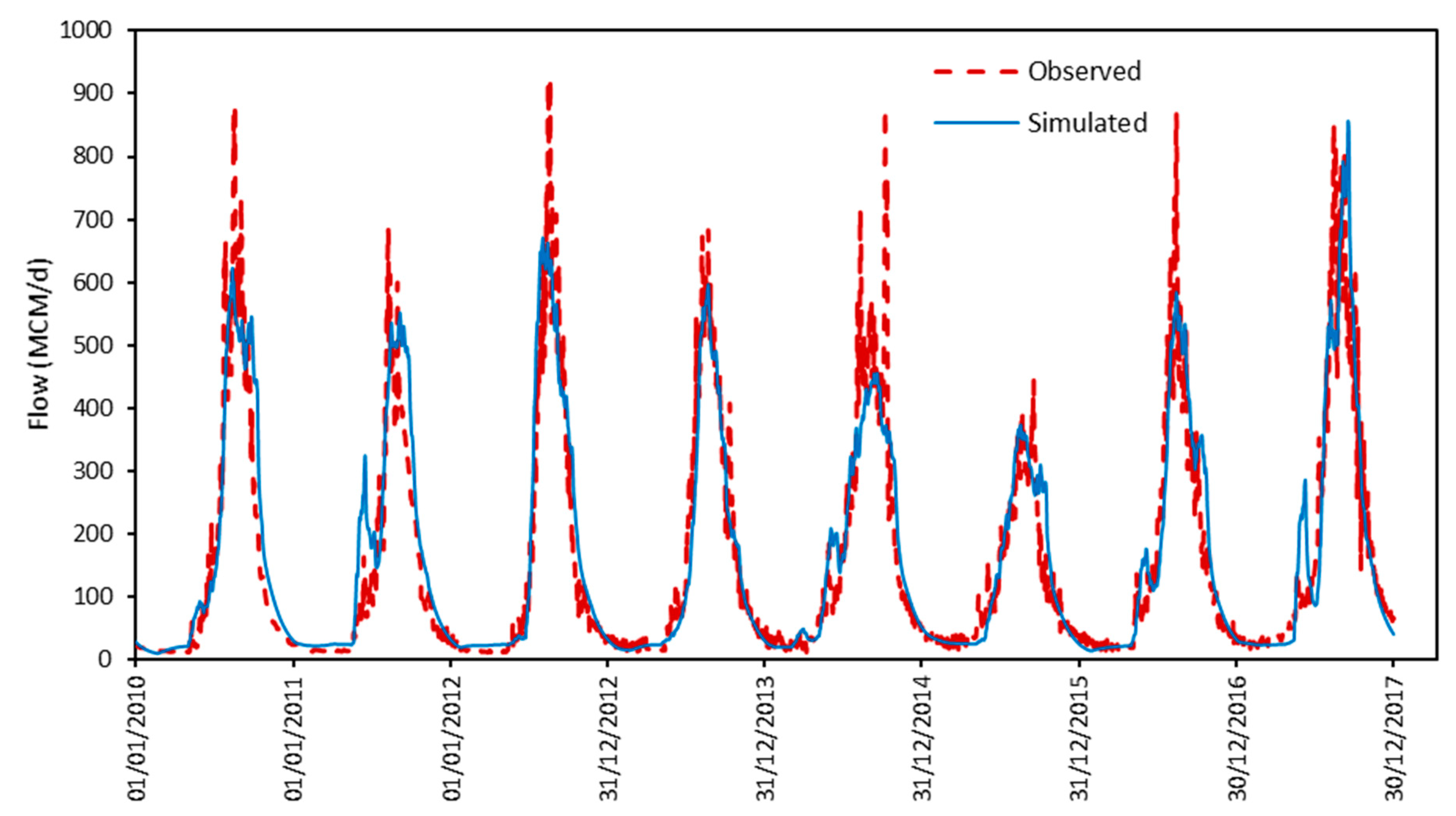
The model validation was done on the period from 2010 to 2017 using the calibrated parameters. Figure 9 shows the simulated and observed flow hydrographs for the validation period that spans low, moderate, and high flooding years. It can be noticed that the model could succeed to simulate the period. A slight underestimation is noticed in the flow peaks at years 2011, 2013, and 2015 but a significant underestimation is showed at years 2010, 2014, and 2015. Again, this may be attributed to the poor resolution of the available rain gauges to provide a representative areal average rainfall. 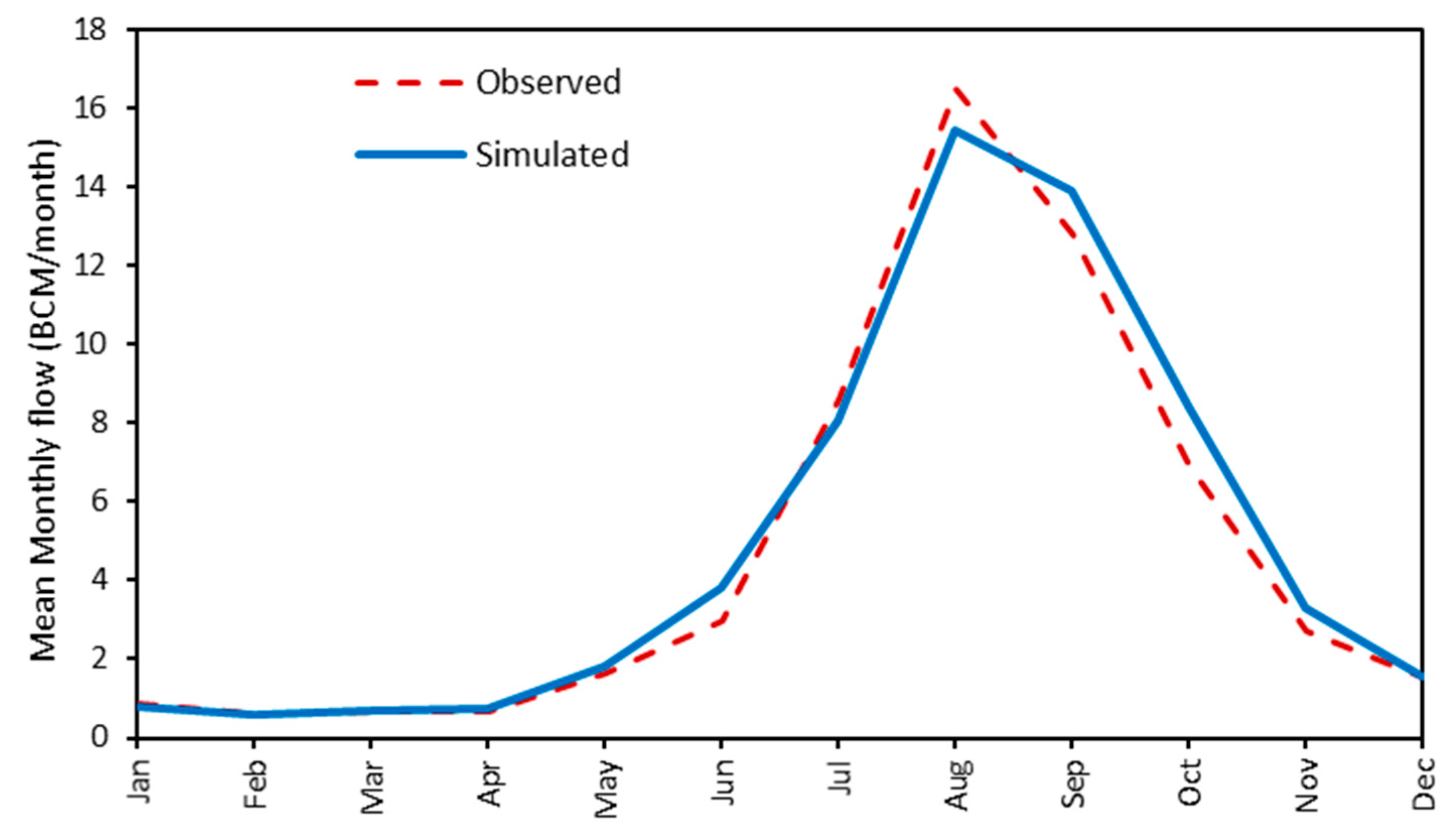Figure 10 shows the mean monthly flow for the validated period at Diem station. It is noticed that the rising limb of the simulated hydrograph relatively matches the observed hydrograph, whereas there is an overestimation in the falling limb. For the rising limb of the simulated hydrograph, a slight overestimation is obvious from May to July.

In order to assess the model performance, the simulated and observed flow are statistically compared. The Nash-Sutcliffe Efficiency (NSE), and the Absolute Error (%AE) of the calculated annual volume (as a percentage of the annual observed volume) are calculated for the whole simulation period (1990–2017). The NSE value is 0.80, which is classified as a very good performance based on Moriasi [37]. The average% AE is 14.30 ± 12.80% in the calculated annual volume (where 12.80 is the standard deviation).

3.3. Analysis of the Hydrologic Components in SCHydro

The purpose of this section is to analyze the different hydrologic components involved in the long-term hydrologic simulation of SCHydro. On top of these components is the evapotranspiration. SCHydro represents evapotranspiration in two parts. The first part is determined implicitly inside the initial abstraction of the modified SCS-CN method, while the second part is small but continuous consumption from the root zone (refer to Section 2). The sum of the two parts (i.e., the total evapotranspiration EVTR) can be calculated by adding the two components.

$$EVT{R}_t=I_{a_t}+T{R}_t$$

(26)

It should be noted that the same total evapotranspiration can also be obtained using the backward mass balance of a control volume containing both the surface interface and the root zone together as follows:

$$EVT{R}_t=P_t-R{O}_t-D{R}_t-∆RZ$$

(27)

where:

$$\begin{array}{l}∆RZ = \mathrm{The} \mathrm{Change} \mathrm{in} \mathrm{Root} \mathrm{Zone} \mathrm{Moisture} in mm=(R{Z}_{t+1}- R{Z}_t).\\ EVT{R}_t = \mathrm{Total} \mathrm{evapotranspiration} \mathrm{during} \mathrm{time} \mathrm{step} t.\end{array}$$

Note that Equation (27) can be obtained from Equation (26) by substitution from Equations (8) and (16) into Equation (26).

In order to assess the different hydrologic processes including evapotranspiration (in comparison with precipitation) as calculated by SCHydro, the different monthly component depths representing the different hydrologic processes are plotted in Figure 11 for the whole period of study, while Figure 12 shows their averages. Note that the two figures show the depths of surface and groundwater before transformation into hydrographs.

Figure 11 and Figure 12 show that evapotranspiration increases with the availability of precipitation. This can be explained by the high evaporation due to the availability of water ponded on the surface (the full potential evaporation occurs) in addition to the tendency of plants to consume and store water in wet periods (this is mainly modeled via the first evapotranspiration part using the SCS-CN method). While in dry periods, the continuous second part (Equation (9)) dominates evapotranspiration (i.e., capillarity evaporation from the root zone and life keeping minimum transpiration). The percentage of total evapotranspiration varies from 80–40% in the wet season with a yearly average of 61%, which agrees with [38]. While in the dry periods, the evapotranspiration/precipitation ratio can significantly exceed 100% in severe dry months due to the second component. 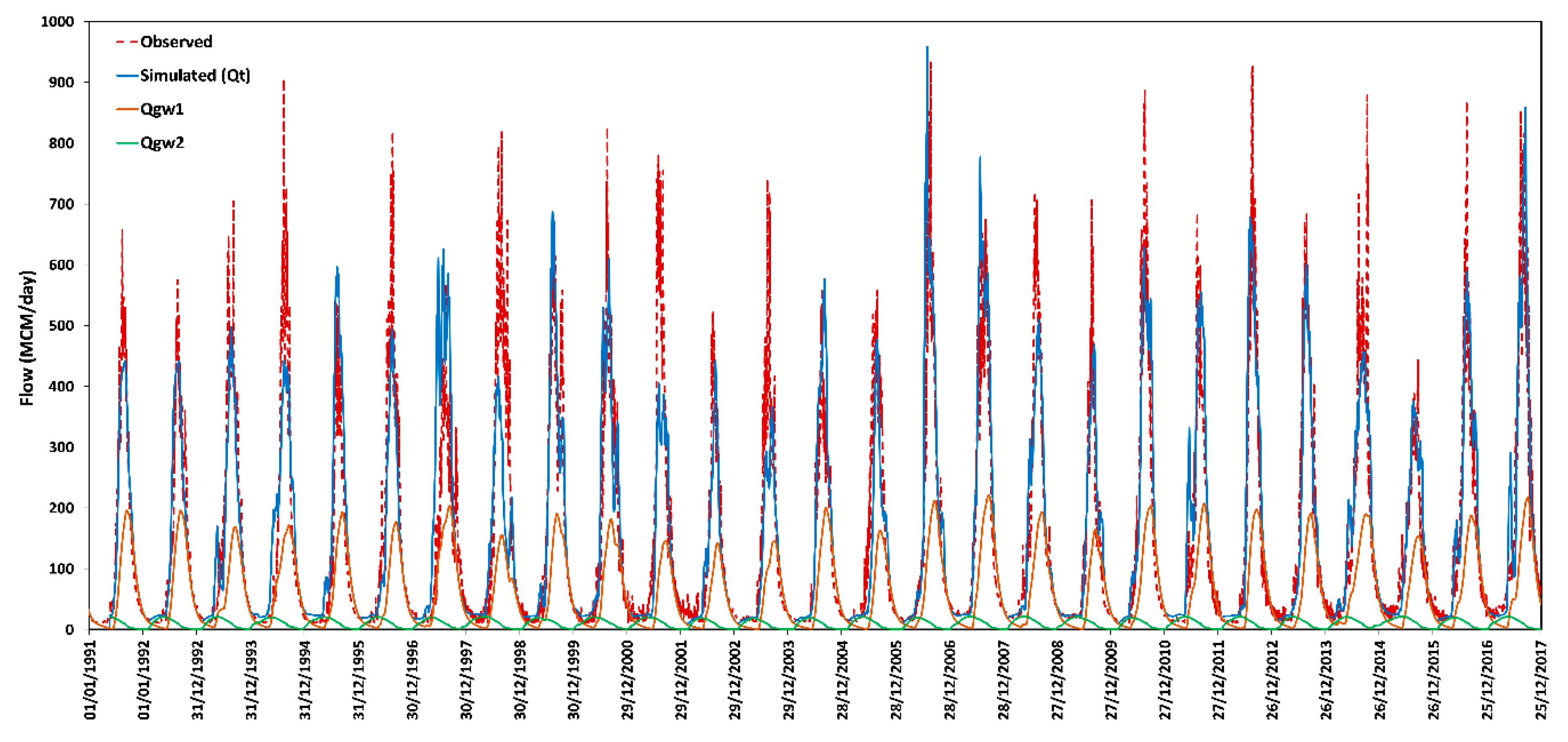It should be noted that the average runoff coefficient of the basin is 12%, while the contribution of groundwater from the upper aquifer is significantly higher than the contribution of the deep aquifer as shown in Figure 11, Figure 12 and Figure 13.

Figure 13 presents the different components of the hydrograph, which indicates also that the contribution of the deep aquifer is relatively lagged and is mainly responsible for the base flow of the river in the dry season.

3.4. Technical Comparison with Other Models

Comparing SCHydro with HEC-HMS-SMA, HEC-HMS-SMA algorithm has a linear structure, while SCHydro takes into consideration the non-linearity of the saturated store through the deep groundwater layer. In addition, HEC-HMS-SMA parameters are very difficult to be calibrated due to model sensitivity to the infiltration rates between zones as well as the storage capacities of the layers, while SCHydro is much simpler to be calibrated since it is controlled by the surface curve number.

In comparison with SWAT model, despite the popularity of SWAT application in the Blue Nile basin, it is considered a complicated parameterization and calibration model due to its large number of input comparing with other long-term models including SCHydro. SWAT needs moisture and energy inputs such as daily precipitation, maximum/minimum air temperature, solar radiation, wind speed, and relative humidity that control the water balance [24], while SCHydro requires only the daily precipitation as input data. Similarly, both the developed model and SWAT-CN considers the initial CN as a calibrated parameter.

The NFS hydrological model and SCHydro have a similar concept of the water balance; however, the NFS equations use the soil moisture deficit rather than the soil moisture. The NFS water balance component divides the basin into two soil layers; an upper layer for short-term storm retention, and a lower deeper layer representing the saturated and unsaturated subsurface zone [8,39]. The surface excess depth is also estimated using a similar approach of SCHydro by using a similar logic of the CN method [7,8]. The difference between the mass balances of both models is the estimation of the evapotranspiration. For the NFS, the evapotranspiration is estimated based on the minimum of the potential evapotranspiration and the available in the soil moisture storage, while for SCHydro, it is related to the soil moisture implicitly inside the calculations of the modified SCS-CN method. SCHydro requires only one input data series (daily rainfall data), while NFS needs the daily precipitation and the potential evapotranspiration to simulate the basin flow.

It should be noted that the most important feature of SCHydro that is not available in other models is the use of response functions in routing excess/groundwater depths. The response functions are based on the time-area approach that reflects the real transforming behavior of the basin (instead of the linear reservoir concept implemented in other models).

4. Conclusions and Discussion

A new response-based approach was used to develop a long-term hydrological model (called SCHydro) to simulate large catchment areas. The new approach consists of surface balance sub-module based on a long-term modification of the SCS-CN method and routing sub-module based on time-area (TA) unit hydrograph. The surface long-term SCS-CN sub-module with a revised soil moisture condition approach considers temporally variable surface SMC (Soil Moisture Condition). The advantage of the developed SCS-CN surface balance approach is its dependence on only one parameter (CN₀). The water balance accordingly is controlled at the surface, which ensures accurate surface hydrograph (the main component of the total hydrograph) that does not depend on underground parameters. In addition, the approach considers implicitly a component of evapotranspiration into the initial abstraction of the SCS-CN. This is a good assumption because the initial abstraction of the surface soil occurs mainly due to the suction head of the surface soil, which makes the initial abstraction vulnerable to evapotranspiration. This provides the missing link between the SCS-CN method (developed originally for single event analysis) and long-term simulations. The routing sub-module is based on TA unit hydrographs produced using the Geographic Information Systems (GIS) (developed on a short-term basis). The routing sub-module automatically calculates the surface and underground travel time grids from readily available digital elevation models (DEMs). In addition, the routing sub-module produces quick unit hydrographs for the large catchment areas like the upper Blue Nile basin. It should be noted that the usage of TA basin responses blends the powerful accuracy of short-term routing with the required simplicity of long-term modeling. The developed model was successfully calibrated and validated on the upper Blue Nile basin, where the simulated flow showed a good capture for the observed hydrograph. The Nash-Sutcliffe Efficiency (NSE) value is 0.80, which is classified as a very good performance based on Moriasi [37]. The absolute error of the calculated annual volumes% AE is 14.30 ± 12.80% (as a percentage of the observed annual volumes). The developed hydrological model has a potential for flood forecasting applications (i.e., using rainfall forecasts as input) since the model is robust and less sensitive to groundwater parameterization. This is because the water balance is controlled at the surface. In addition, one of the important simplified features of the model is that it does not require potential evapotranspiration data. This simplicity raises its applicability for ungauged basins (subject to more verification studies) as well as for forecasting purposes.

The use of the response time-area concept in computing both surface and groundwater hydrographs constitutes one of the main novelty of this research. It must be noted that although the response functions (i.e., unit hydrographs) are calculated in SCHydro in a semi-distributed sense, but the model is lumped over the catchment/sub-catchment in terms of mass balance. The convolution at the outlet is performed for spatially uniform rainfall depths over the basin/sub-catchment. In cases where there is significant spatial variability in the mass-balance parameters or rainfall, or in case there are hydraulic structures or lakes/reservoirs, the basin must be divided into a hydrologic network of sub-catchments (the typical hydrologic networks). The mass balance and transformation, in that case, is performed on the divisions (separate mass balance and separate unit hydrograph for each sub-catchment). The sub-catchments hydrographs across the network can then be combined/routed across the network nodes until the outlet. The network approach can enable spatially variable input for the hydrologic variables (rainfall and balance parameters for each sub-catchment), which can increase model accuracy. We believe that such network approach together with more accurate daily rainfall fields may explain the remaining differences between the observed and modeled hydrographs in this research for the upper Blue Nile. It should be noted also that the calibrated parameters presented in the paper are limited to the upper Blue Nile only. The application of SCHydro in a network mode is a very interesting topic for future research when more accurate long-term spatiotemporally variable rainfall data is available.