Long Term Historic Changes in the Flow of Lesser Zab River, Iraq
Abstract
1. Introduction
2. Study Area and Datasets
3. Methodology
3.1. Distributional Analysis
3.2. Estimation of Magnitude of Change
3.3. Mann–Kendall Trend Tests
4. Result and Discussion
4.1. Distributional Analysis
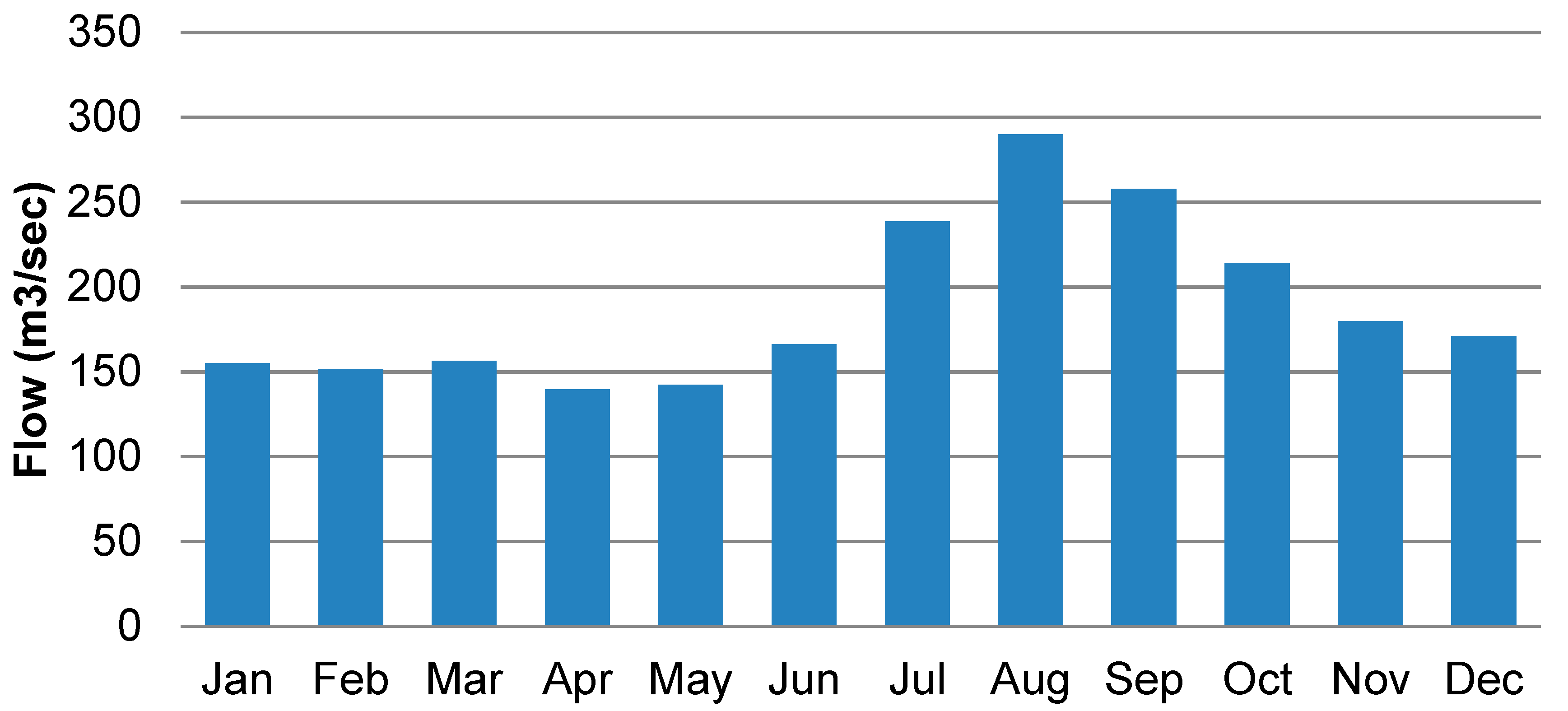
4.2. Seasonal Distribution of Flow
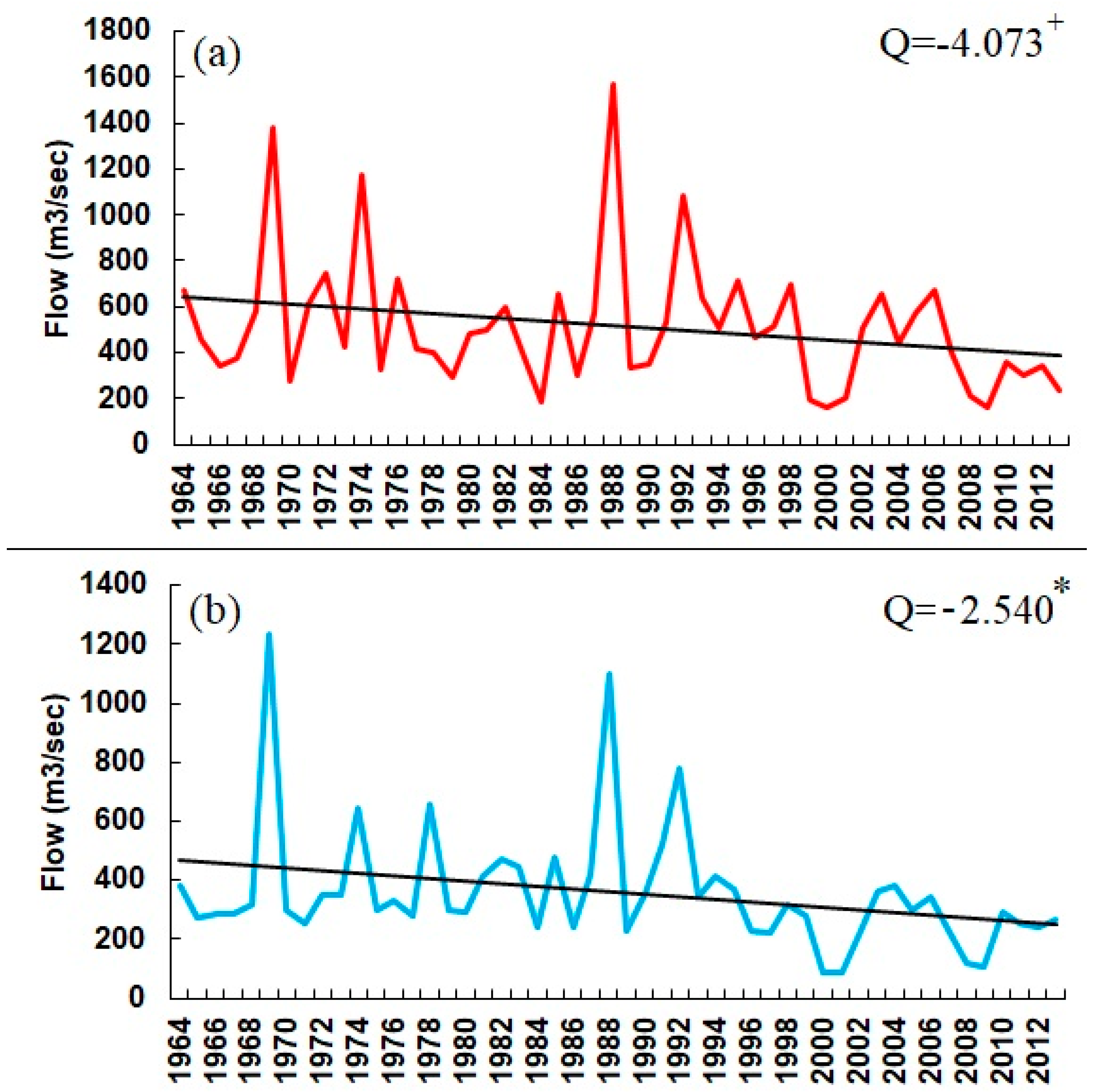
4.3. Trends in Monthly and Annual Flow
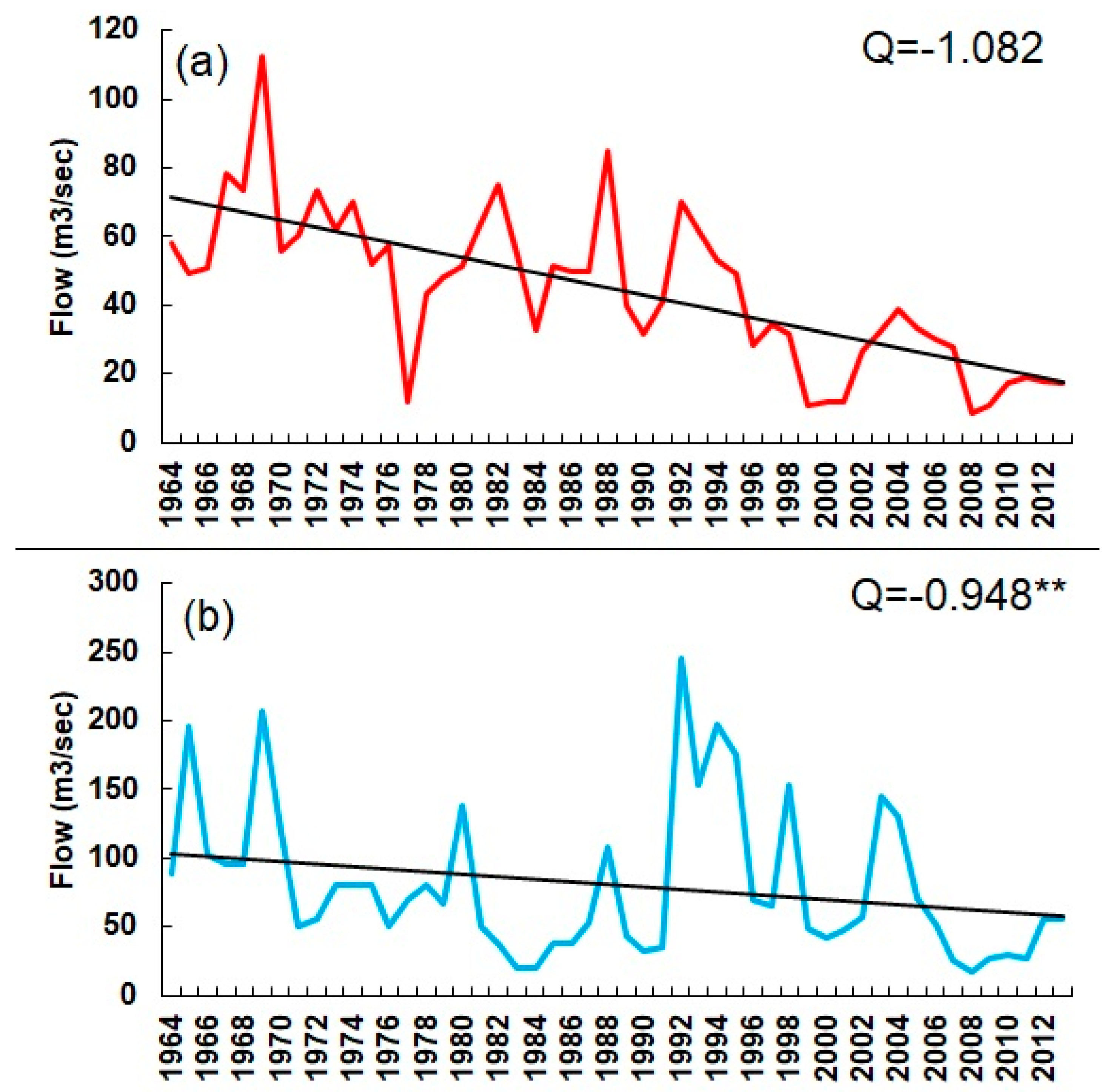
4.4. Trends in Maximum Annual Flow
4.5. Trends in Minimum Annual Flow
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karl, T.R.; Trenberth, K.E. Modern Global Climate Change. Science 2003, 302, 1719–1723. [Google Scholar] [CrossRef]
- Crawford, J.; Venkataraman, K.; Booth, J. Developing climate model ensembles: A comparative case study. J. Hydrol. 2019, 568, 160–173. [Google Scholar] [CrossRef]
- Ahmed, K.; Chung, E.-S.; Song, J.-Y.; Shahid, S. Effective Design and Planning Specification of Low Impact Development Practices Using Water Management Analysis Module (WMAM): Case of Malaysia. Water 2017, 9, 173. [Google Scholar] [CrossRef]
- Moazenzadeh, R.; Mohammadi, B.; Shamshirband, S.; Chau, K.-W. Coupling a firefly algorithm with support vector regression to predict evaporation in northern Iran. Eng. Appl. Comput. Fluid Mech. 2018, 12, 584–597. [Google Scholar] [CrossRef]
- Stagl, J.; Mayr, E.; Koch, H.; Hattermann, F.F.; Huang, S. Effects of climate change on the hydrological cycle in central and eastern Europe. In Managing Protected Areas in Central and Eastern Europe Under Climate Change; Springer: Dordrecht, The Netherlands, 2014; pp. 31–43. [Google Scholar]
- Wang, Y.; Wang, D.; Lewis, Q.W.; Wu, J.; Huang, F. A framework to assess the cumulative impacts of dams on hydrological regime: A case study of the Yangtze River. Hydrol. Process. 2017, 31, 3045–3055. [Google Scholar] [CrossRef]
- Iqbal, Z.; Shahid, S.; Ahmed, K.; Ismail, T.; Nawaz, N. Spatial distribution of the trends in precipitation and precipitation extremes in the sub-Himalayan region of Pakistan. Theor. Appl. Climatol. 2019. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Chung, E.-S.; Wang, X.-J.; Harun, S.B. Climate Change Uncertainties in Seasonal Drought Severity-Area-Frequency Curves: Case of Arid Region of Pakistan. J. Hydrol. 2019. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, K.-W.; Sivakumar, B. Neural network river forecasting through baseflow separation and binary-coded swarm optimization. J. Hydrol. 2015, 529, 1788–1797. [Google Scholar] [CrossRef]
- Sa’adi, Z.; Shahid, S.; Ismail, T.; Chung, E.-S.; Wang, X.-J. Trends analysis of rainfall and rainfall extremes in Sarawak, Malaysia using modified Mann–Kendall test. Meteorol. Atmos. Phys. 2017, 1–15. [Google Scholar] [CrossRef]
- Ahmad, I.; Tang, D.; Wang, T.; Wang, M.; Wagan, B. Precipitation Trends over Time Using Mann-Kendall and Spearman’s rho Tests in Swat River Basin, Pakistan. Adv. Meteorol. 2015, 2015, 15. [Google Scholar] [CrossRef]
- Asfaw, A.; Simane, B.; Hassen, A.; Bantider, A. Variability and time series trend analysis of rainfall and temperature in northcentral Ethiopia: A case study in Woleka sub-basin. Weather Clim. Extremes 2018, 19, 29–41. [Google Scholar] [CrossRef]
- Meshram, S.G.; Singh, V.P.; Meshram, C. Long-term trend and variability of precipitation in Chhattisgarh State, India. Theor. Appl. Climatol. 2017, 129, 729–744. [Google Scholar] [CrossRef]
- Schmidhuber, J.; Tubiello, F.N. Global food security under climate change. Proc. Natl. Acad. Sci. USA 2007, 104, 19703–19708. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, K.; Shahid, S.; Harun, S.B.; Wang, X.-J. Characterization of seasonal droughts in Balochistan Province, Pakistan. Stoch. Environ. Res. Risk Assess. 2015, 30, 747–762. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Nawaz, N. Impacts of climate variability and change on seasonal drought characteristics of Pakistan. Atmos. Res. 2018, 214, 364–374. [Google Scholar] [CrossRef]
- Ezzine, H.; Bouziane, A.; Ouazar, D. Seasonal comparisons of meteorological and agricultural drought indices in Morocco using open short time-series data. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 36–48. [Google Scholar] [CrossRef]
- Cigizoglu, H.; Bayazit, M.; Önöz, B. Trends in the maximum, mean, and low flows of Turkish rivers. J. Hydrometeorol. 2005, 6, 280–290. [Google Scholar] [CrossRef]
- Ehsanzadeh, E.; Adamowski, K. Trends in timing of low stream flows in Canada: Impact of autocorrelation and long-term persistence. Hydrol. Process. 2010, 24, 970–980. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend detection in hydrologic data: The Mann–Kendall trend test under the scaling hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Kumar, S.; Merwade, V.; Kam, J.; Thurner, K. Streamflow trends in Indiana: Effects of long term persistence, precipitation and subsurface drains. J. Hydrol. 2009, 374, 171–183. [Google Scholar] [CrossRef]
- Zhang, X.; Harvey, K.D.; Hogg, W.; Yuzyk, T.R. Trends in Canadian streamflow. Water Resour. Res. 2001, 37, 987–998. [Google Scholar] [CrossRef]
- Gajbhiye, S.; Meshram, C.; Singh, S.K.; Srivastava, P.K.; Islam, T. Precipitation trend analysis of Sindh River basin, India, from 102-year record (1901–2002). Atmos. Sci. Lett. 2016, 17, 71–77. [Google Scholar] [CrossRef]
- Meshram, S.G.; Singh, S.K.; Meshram, C.; Deo, R.C.; Ambade, B. Statistical evaluation of rainfall time series in concurrence with agriculture and water resources of Ken River basin, Central India (1901–2010). Theor. Appl. Climatol. 2018, 134, 1231–1243. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W. Rainfall–runoff modeling using artificial neural network coupled with singular spectrum analysis. J. Hydrol. 2011, 399, 394–409. [Google Scholar] [CrossRef]
- Luković, J.; Bajat, B.; Blagojević, D.; Kilibarda, M. Spatial pattern of recent rainfall trends in Serbia (1961–2009). Region. Environ. Chang. 2014, 14, 1789–1799. [Google Scholar] [CrossRef]
- Liuzzo, L.; Bono, E.; Sammartano, V.; Freni, G. Analysis of spatial and temporal rainfall trends in Sicily during the 1921–2012 period. Theor. Appl. Climatol. 2015, 1–17. [Google Scholar] [CrossRef]
- Wickramagamage, P. Spatial and temporal variation of rainfall trends of Sri Lanka. Theor. Appl. Climatol. 2015, 1–12. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Sulaiman, S.O.; Deo, R.C.; Chau, K.-W. An enhanced extreme learning machine model for river flow forecasting: State-of-the-art, practical applications in water resource engineering area and future research direction. J. Hydrol. 2019, 569, 387–408. [Google Scholar] [CrossRef]
- Chau, K.-W. Use of Meta-Heuristic Techniques in Rainfall-Runoff Modelling. Water 2017, 9, 186. [Google Scholar] [CrossRef]
- Salman, S.A.; Shahid, S.; Ismail, T.; Chung, E.-S.; Al-Abadi, A.M. Long-term trends in daily temperature extremes in Iraq. Atmos. Res. 2017, 198, 97–107. [Google Scholar] [CrossRef]
- Salman, S.A.; Shahid, S.; Ismail, T.; Rahman, N.B.A.; Wang, X.; Chung, E.-S. Unidirectional trends in daily rainfall extremes of Iraq. Theor. Appl. Climatol. 2017, 1–13. [Google Scholar] [CrossRef]
- Shubbar, R.M.; Salman, H.H.; Lee, D.I. Characteristics of climate variation indices in Iraq using a statistical factor analysis. Int. J. Climatol. 2017, 37, 918–927. [Google Scholar] [CrossRef]
- Yousuf, M.; Rapantova, N.; Younis, J. Sustainable Water Management in Iraq (Kurdistan) as a Challenge for Governmental Responsibility. Water 2018, 10, 1651. [Google Scholar] [CrossRef]
- Abbas, N.; Wasimi, S.; Al-Ansari, N.; Nasrin Baby, S. Recent Trends and Long-Range Forecasts of Water Resources of Northeast Iraq and Climate Change Adaptation Measures. Water 2018, 10, 1562. [Google Scholar] [CrossRef]
- Issa, I.; Al-Ansari, N.; Sherwany, G.; Knutsson, S. Trends and future challenges of water resources in the Tigris–Euphrates Rivers basin in Iraq. Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 14617–14644. [Google Scholar] [CrossRef]
- Khan, N.; Shahid, S.; Ismail, T.; Ahmed, K.; Nawaz, N. Trends in heat wave related indices in Pakistan. Stoch. Environ. Res. Risk Assess. 2018, 1–16. [Google Scholar] [CrossRef]
- Khan, N.; Shahid, S.; Ismail, T.B.; Wang, X.-J. Spatial distribution of unidirectional trends in temperature and temperature extremes in Pakistan. Theor. Appl. Climatol. 2018. [Google Scholar] [CrossRef]
- Preethi, B.; Mujumdar, M.; Kripalani, R.; Prabhu, A.; Krishnan, R. Recent trends and tele-connections among South and East Asian summer monsoons in a warming environment. Clim. Dyn. 2016, 1–17. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S. Spatial distribution of unidirectional trends in climate and weather extremes in Nile river basin. Theor. Appl. Climatol. 2018, 1–19. [Google Scholar] [CrossRef]
- Chandniha, S.K.; Meshram, S.G.; Adamowski, J.F.; Meshram, C. Trend analysis of precipitation in Jharkhand State, India. Theor. Appl. Climatol. 2017, 130, 261–274. [Google Scholar] [CrossRef]
- Ezz-Aldeen, M.; Hassan, R.; Ali, A.; Al-Ansari, N.; Knutsson, S. Watershed Sediment and Its Effect on Storage Capacity: Case Study of Dokan Dam Reservoir. Water 2018, 10, 858. [Google Scholar] [CrossRef]
- Hassan, R.; Al-Ansari, N.; Ali, S.S.; Ali, A.A.; Abdullah, T.; Knutsson, S. Dukan Dam Reservoir Bed Sediment, Kurdistan Region, Iraq. Engineering 2016, 8, 582–596. [Google Scholar] [CrossRef]
- Pilesjo, P.; Al-Juboori, S.S. Modelling the effects of climate change on hydroelectric power in Dokan, Iraq. Int. J. Energy Power Eng. 2016, 5, 7–12. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Feddema, J.J. Estimating continental and terrestrial precipitation averages from rain-gauge networks. Int. J. Climatol. 1994, 14, 403–414. [Google Scholar] [CrossRef]
- Teegavarapu, R.S.; Chandramouli, V. Improved weighting methods, deterministic and stochastic data-driven models for estimation of missing precipitation records. J. Hydrol. 2005, 312, 191–206. [Google Scholar] [CrossRef]
- Eischeid, J.K.; Pasteris, P.A.; Diaz, H.F.; PLantico, M.S.; Lott, N.J. Creating a serially complete, national daily time series of temperature and precipitation for the western United States. J. Appl. Meteorol. 2000, 39, 1580–1591. [Google Scholar] [CrossRef]
- Wallis, J.R.; Lettenmaier, D.P.; Wood, E.F. A daily hydroclimatological data set for the continental United States. Water Resour. Res. 1991, 27, 1657–1663. [Google Scholar] [CrossRef]
- Coulibaly, P.; Evora, N. Comparison of neural network methods for infilling missing daily weather records. J. Hydrol. 2007, 341, 27–41. [Google Scholar] [CrossRef]
- Ali Ghorbani, M.; Kazempour, R.; Chau, K.-W.; Shamshirband, S.; Taherei Ghazvinei, P. Forecasting pan evaporation with an integrated artificial neural network quantum-behaved particle swarm optimization model: A case study in Talesh, Northern Iran. Eng. Appl. Comput. Fluid Mech. 2018, 12, 724–737. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B Methodol. 1977, 39, 1–38. [Google Scholar] [CrossRef]
- McLachlan, G.; Krishnan, T. The EM Algorithm and Extensions; John Wiley & Sons: Hoboken, NJ, USA, 1997; Volume 382. [Google Scholar]
- Ahmed, K.; Shahid, S.; Ali, R.O.; Harun, S.B.; Wang, X.-J. Evaluation of the performance of gridded precipitation products over Balochistan Province, Pakistan. Desalination 2017, 79, 73–86. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Ismail, T.; Nawaz, N.; Wang, X.-J. Absolute homogeneity assessment of precipitation time series in an arid region of Pakistan. Atmósfera 2018, 31, 301–316. [Google Scholar] [CrossRef]
- Noor, M.; Ismail, T.; Chung, E.-S.; Shahid, S.; Sung, J. Uncertainty in Rainfall Intensity Duration Frequency Curves of Peninsular Malaysia under Changing Climate Scenarios. Water 2018, 10, 1750. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Chung, E.-S.; Ismail, T.; Wang, X.-J. Spatial distribution of secular trends in annual and seasonal precipitation over Pakistan. Clim. Res. 2017, 74, 95–107. [Google Scholar] [CrossRef]
- Souvignet, M.; Laux, P.; Freer, J.; Cloke, H.; Thinh, D.Q.; Thuc, T.; Cullmann, J.; Nauditt, A.; Flügel, W.-A.; Kunstmann, H.; et al. Recent climatic trends and linkages to river discharge in Central Vietnam. Hydrol. Process. 2014, 28, 1587–1601. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, X.; Liu, Z.; Wang, D. Trend analysis of precipitation in the Jinsha River Basin in China. J. Hydrometeorol. 2013, 14, 290–303. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Sonali, P.; Nagesh Kumar, D. Review of trend detection methods and their application to detect temperature changes in India. J. Hydrol. 2013, 476, 212–227. [Google Scholar] [CrossRef]
- Salman, S.A.; Shahid, S.; Ismail, T.; Ahmed, K.; Chung, E.-S.; Wang, X.-J. Characteristics of Annual and Seasonal Trends of Rainfall and Temperature in Iraq. Asia-Pacif. J. Atmos. Sci. 2019. [Google Scholar] [CrossRef]
- Hassan, R.; Al-Ansari, N.; Ali, A.A.; Ali, S.S.; Knutsson, S. Bathymetry and siltation rate for Dokan Reservoir, Iraq. Lakes Reserv. Sci. Policy Manag. Sustain. Use 2017, 22, 179–189. [Google Scholar] [CrossRef]


| Month/Season | Upstream Gauge | Downstream Gauge | ||||
|---|---|---|---|---|---|---|
| Gamma | Gen. Extreme Value | Normal | Gamma | Gen. Extreme Value | Normal | |
| Jan | 0.071 | 0.072 | 0.150 | 0.136 | 0.146 | 0.190 |
| Feb | 0.063 | 0.067 | 0.118 | 0.065 | 0.071 | 0.151 |
| Mar | 0.123 | 0.092 | 0.202 | 0.207 | 0.113 | 0.232 |
| Apr | 0.051 | 0.063 | 0.103 | 0.325 | 0.071 | 0.276 |
| May | 0.089 | 0.076 | 0.142 | 0.253 | 0.077 | 0.285 |
| Jun | 0.082 | 0.073 | 0.153 | 0.109 | 0.065 | 0.142 |
| Jul | 0.093 | 0.074 | 0.139 | 0.089 | 0.080 | 0.130 |
| Aug | 0.115 | 0.105 | 0.127 | 0.128 | 0.103 | 0.120 |
| Sep | 0.098 | 0.076 | 0.096 | 0.130 | 0.097 | 0.101 |
| Oct | 0.071 | 0.072 | 0.150 | 0.139 | 0.071 | 0.078 |
| Nov | 0.153 | 0.096 | 0.090 | 0.088 | 0.065 | 0.095 |
| Dec | 0.090 | 0.055 | 0.184 | 0.131 | 0.088 | 0.092 |
| Mean Annual | 0.095 | 0.085 | 0.116 | 0.107 | 0.097 | 0.121 |
| Maximum Flow | 0.109 | 0.081 | 0.141 | 0.203 | 0.122 | 0.216 |
| Minimum Flow | 0.152 | 0.103 | 0.088 | 0.095 | 0.085 | 0.180 |
| Time Series | Upstream Gauge | Downstream Gauge | ||||
|---|---|---|---|---|---|---|
| Test Z | Significance | Q | Test Z | Significance | Q | |
| Jan | −1.44 | −1.31 | −2.27 | * | −1.6019 | |
| Feb | −1.07 | −1.65 | −2.36 | * | −2.0343 | |
| Mar | −1.42 | −2.67 | −2.28 | * | −1.5108 | |
| Apr | −2.38 | * | −5.09 | −2.22 | * | −1.2254 |
| May | −2.48 | * | −2.70 | −1.36 | −0.6374 | |
| Jun | −3.58 | −2.02 | 0.77 | 0.73651 | ||
| Jul | −4.89 | −1.33 | −0.45 | −0.3925 | ||
| Aug | −6.74 | −1.41 | −2.87 | ** | −2.495 | |
| Sep | −6.51 | −1.57 | −4.32 | −4.3828 | ||
| Oct | −5.25 | −1.31 | −4.05 | −3.7975 | ||
| Nov | −2.48 | * | −1.06 | −2.35 | * | −2.0692 |
| Dec | −1.66 | + | −1.17 | −1.94 | + | −1.7103 |
| Annual | −2.59 | ** | −1.91 | −2.91 | ** | −1.8038 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, R.; Ismael, A.; Heryansyah, A.; Nawaz, N. Long Term Historic Changes in the Flow of Lesser Zab River, Iraq. Hydrology 2019, 6, 22. https://doi.org/10.3390/hydrology6010022
Ali R, Ismael A, Heryansyah A, Nawaz N. Long Term Historic Changes in the Flow of Lesser Zab River, Iraq. Hydrology. 2019; 6(1):22. https://doi.org/10.3390/hydrology6010022
Chicago/Turabian StyleAli, Rawshan, Arez Ismael, Arien Heryansyah, and Nadeem Nawaz. 2019. "Long Term Historic Changes in the Flow of Lesser Zab River, Iraq" Hydrology 6, no. 1: 22. https://doi.org/10.3390/hydrology6010022
APA StyleAli, R., Ismael, A., Heryansyah, A., & Nawaz, N. (2019). Long Term Historic Changes in the Flow of Lesser Zab River, Iraq. Hydrology, 6(1), 22. https://doi.org/10.3390/hydrology6010022





