A Correlation–Scale–Threshold Method for Spatial Variability of Rainfall
Abstract
:1. Introduction
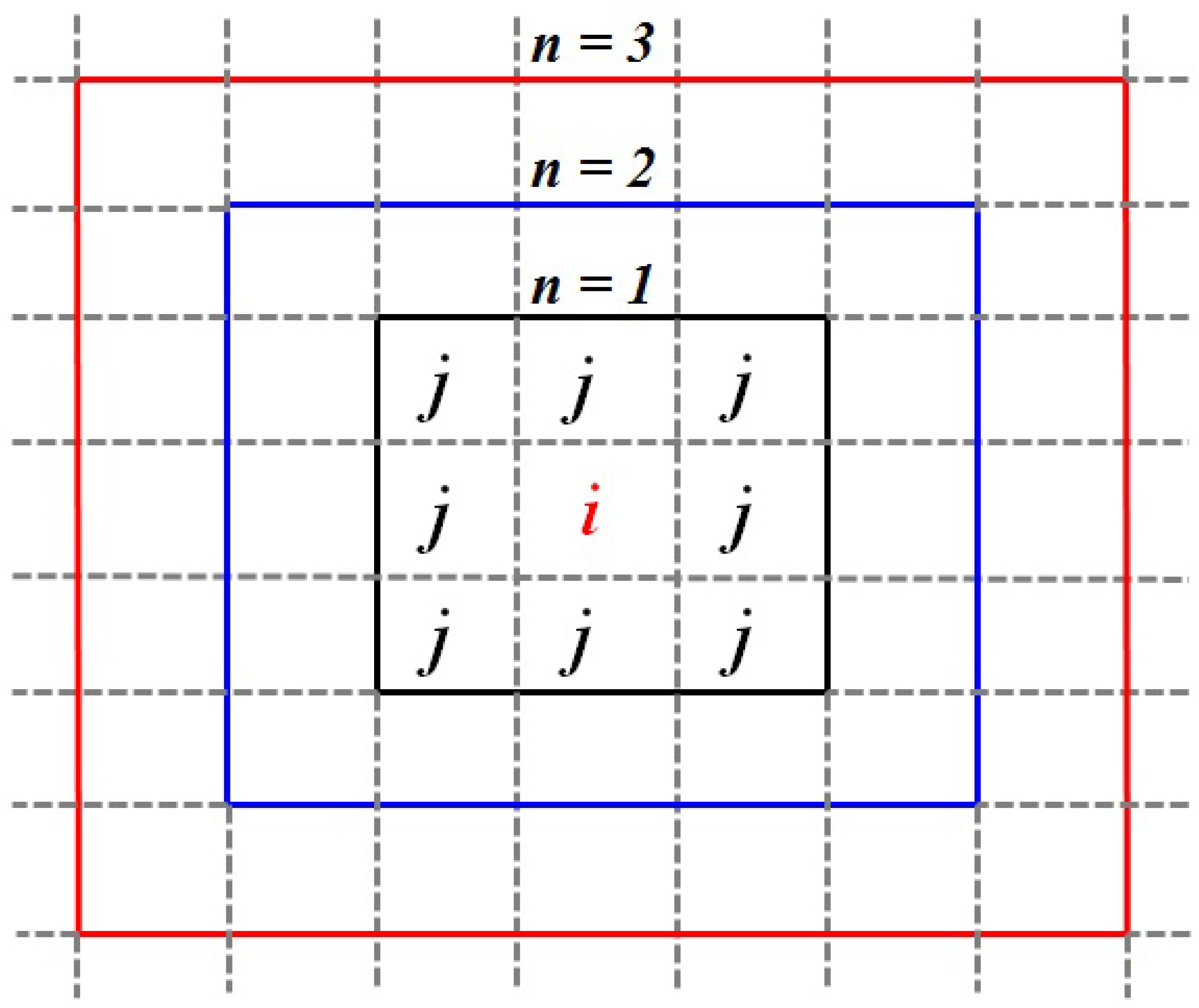
2. Methodology
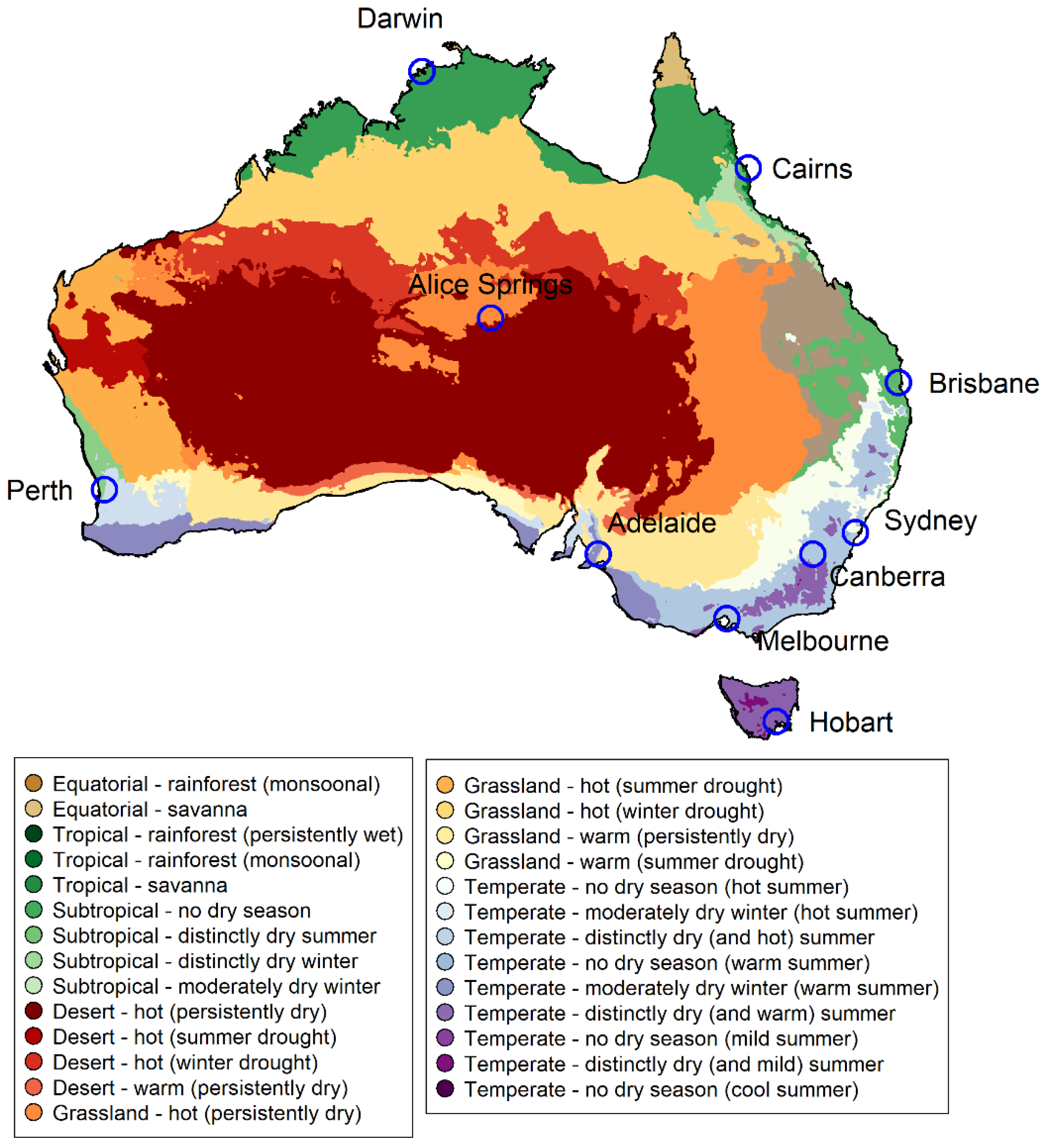
3. Study Area and Data
4. Analysis, Results, and Discussion
4.1. Analysis
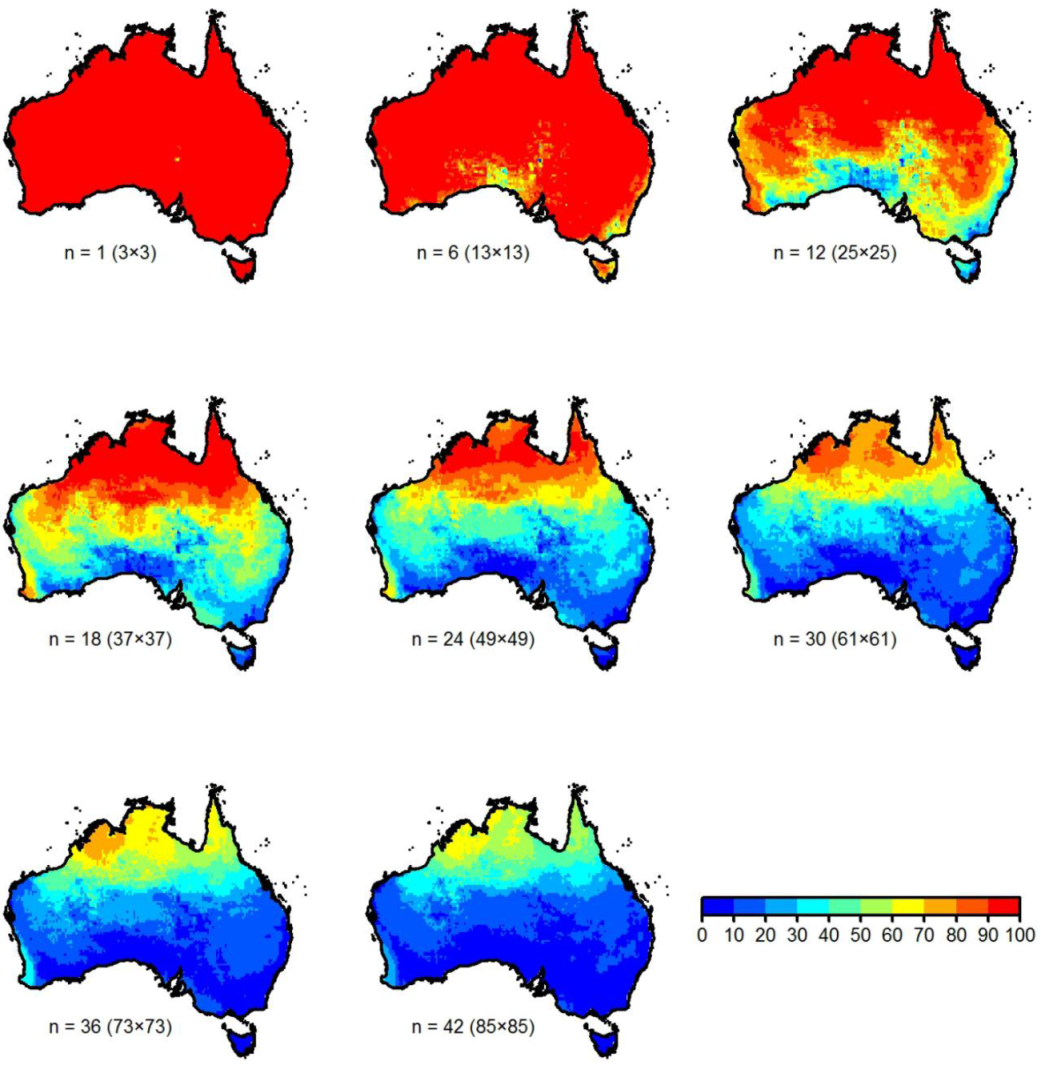
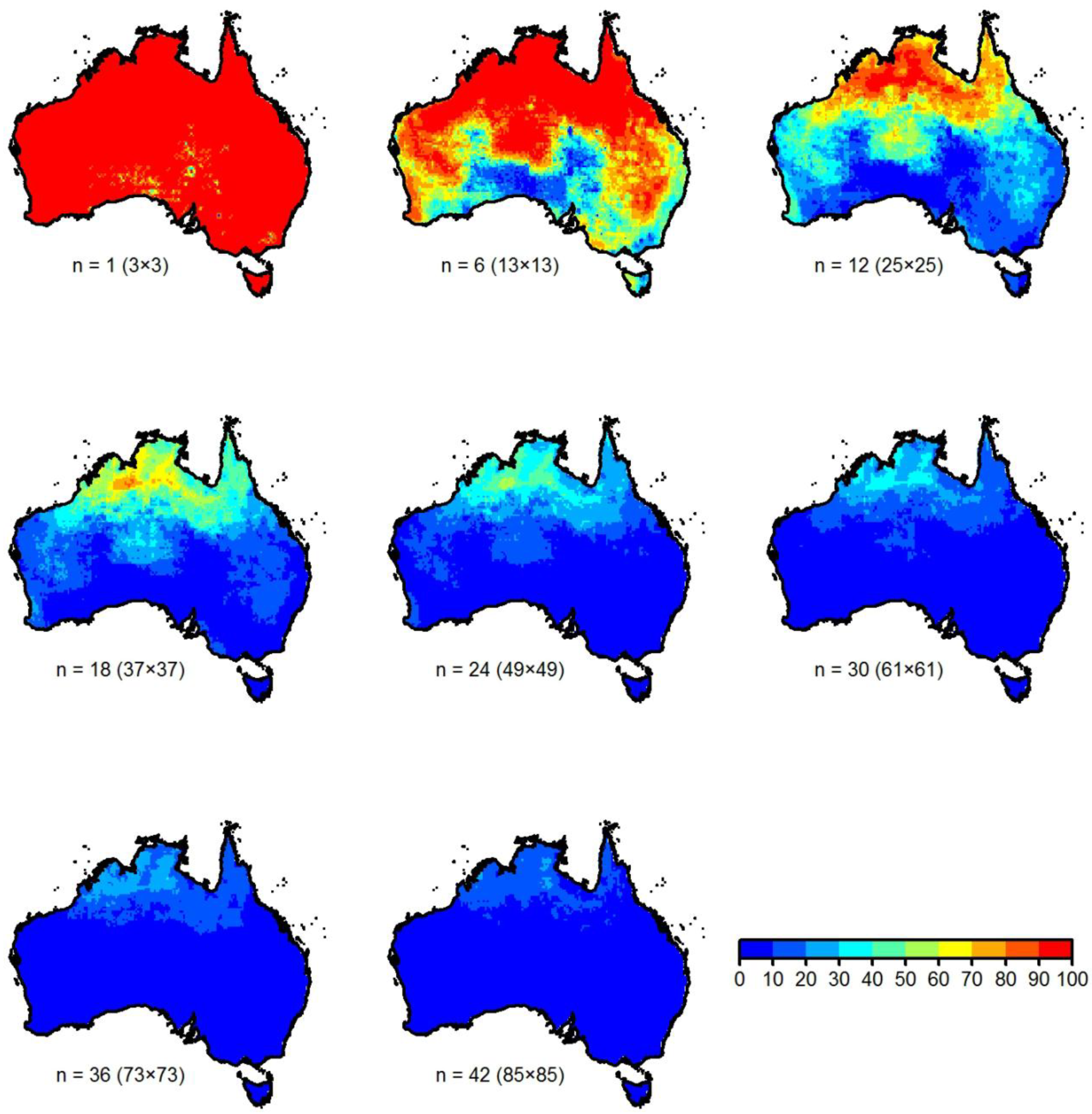
4.2. Results for Australia-Wide Analysis
- When the box size is too small (e.g., n = 1), the spatial correlations are high all across Australia (i.e., almost all grids have rainfall correlations exceeding 0.6).
- When the box size is too large (e.g., n = 42), the spatial correlations are generally low (i.e., only 0–30% of grids have rainfall correlations exceeding 0.6), except in the northern region (where about 30–70% of grids have correlations exceeding T = 0.6).
- As expected, spatial rainfall correlation decreases as the box size increases (and vice versa) all across Australia. However, very clear changes are observed at/across certain box sizes, with “pockets of regions” having similar (or different) spatial correlations emerging; see, for instance, the changes in results for south and southeast Australia when n = 12 and for western Australia when n = 18 (when compared to those when n = 1).
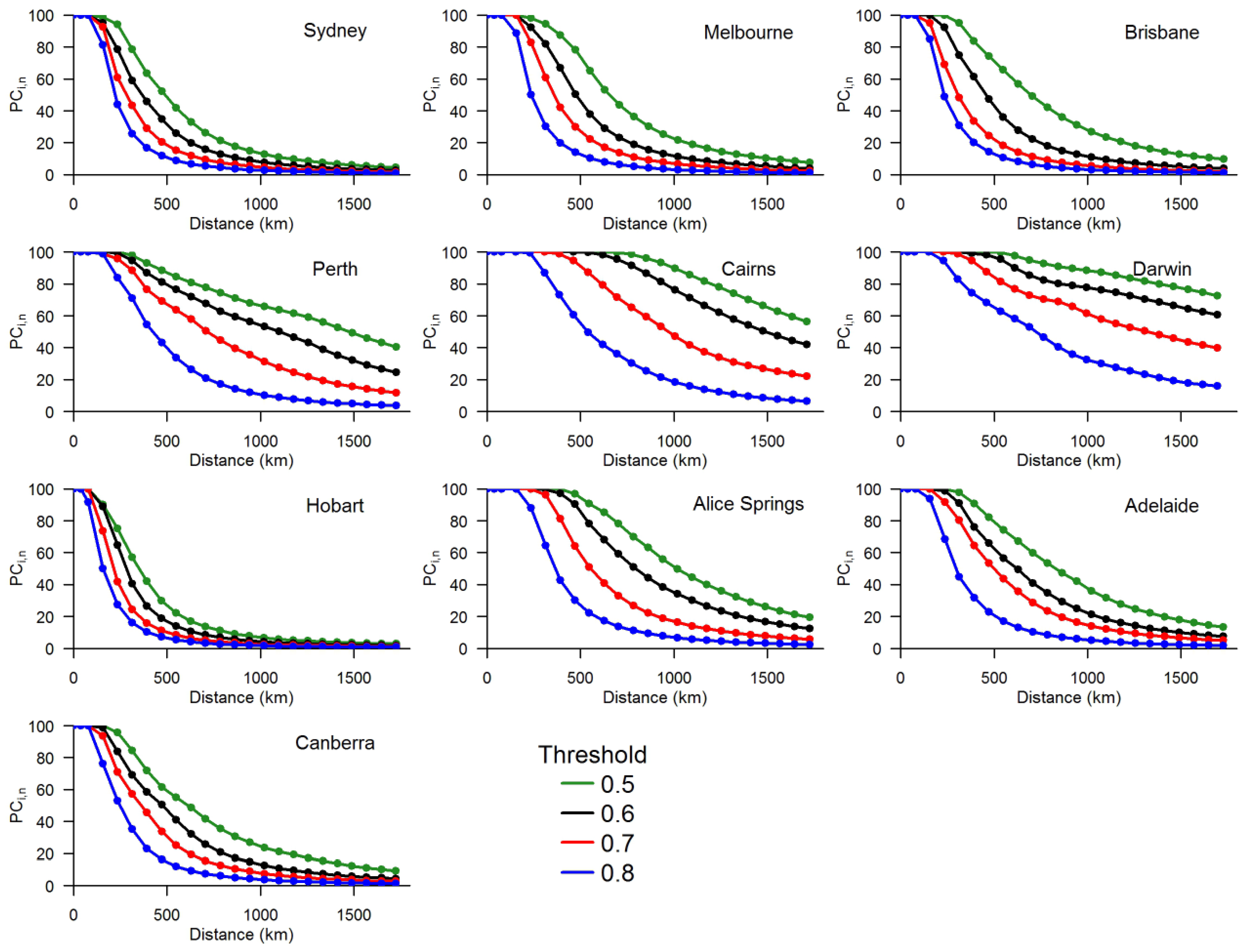
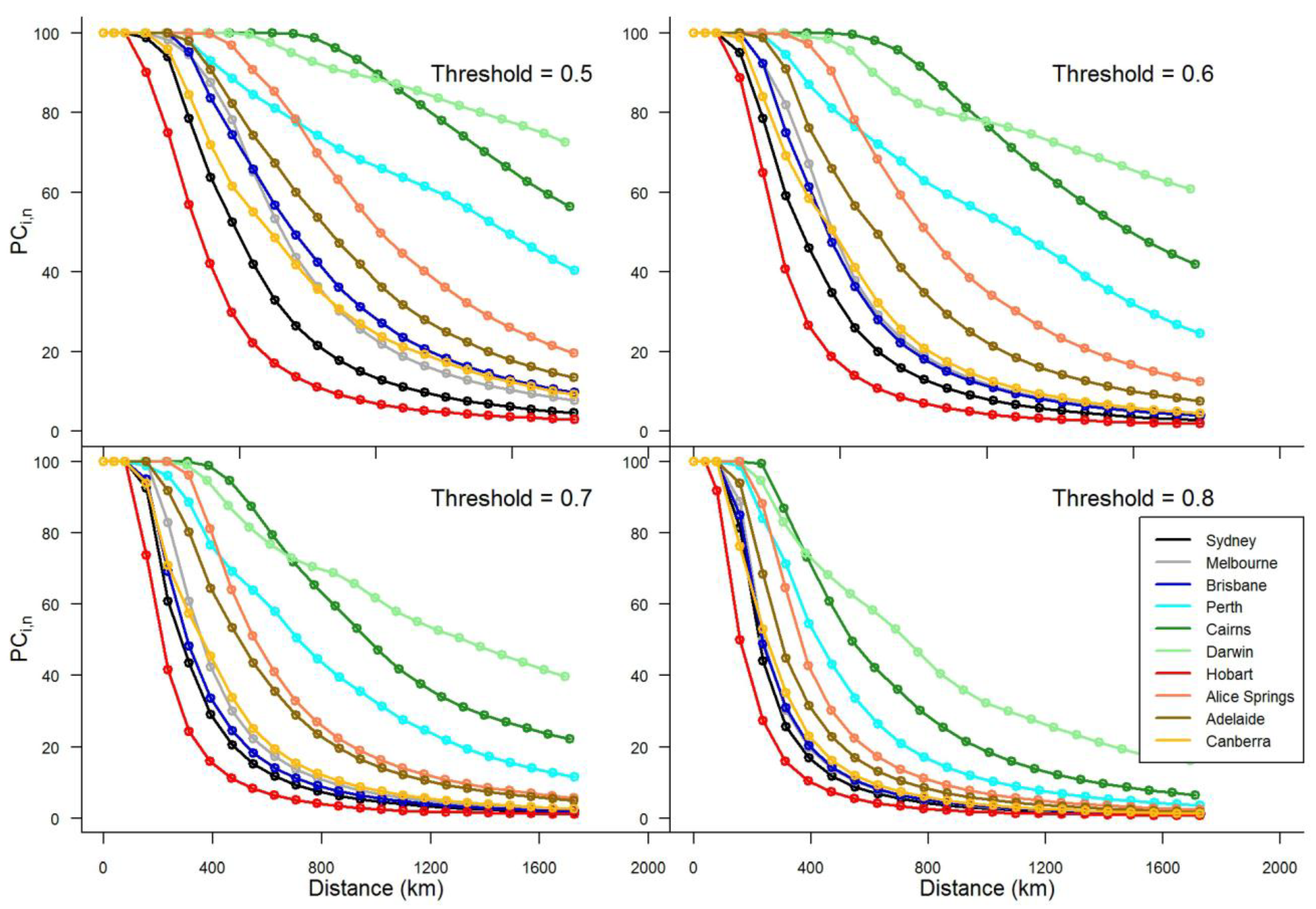
4.3. Results for Ten Major Cities
- Rainfall in Darwin and Cairns shows very significant correlations among grids for any threshold up to about 300 km or greater. Even in the most stringent case (T = 0.8), about 90–100% of grids have rainfall correlations exceeding the correlation threshold. It is relevant to note that these two cities have a tropical climate, with tropical savannah in Darwin and tropical rainforest (monsoonal) in Cairns.
- Rainfall in Hobart and Sydney shows particularly low correlations among grids for any of the threshold levels, with Hobart showing the worst results. In the most stringent case (T = 0.8), the distance up to which 90–100% of grids exceed the correlation threshold is only about 100 km. Even in the most relaxed case, i.e., “average” threshold of 0.5, 90–100% of grids exceed the threshold only up to about 250 km, especially for Hobart. It is relevant to note that these two cities have a temperate, no dry season climate, with a mild summer in Hobart and a hot summer in Sydney.
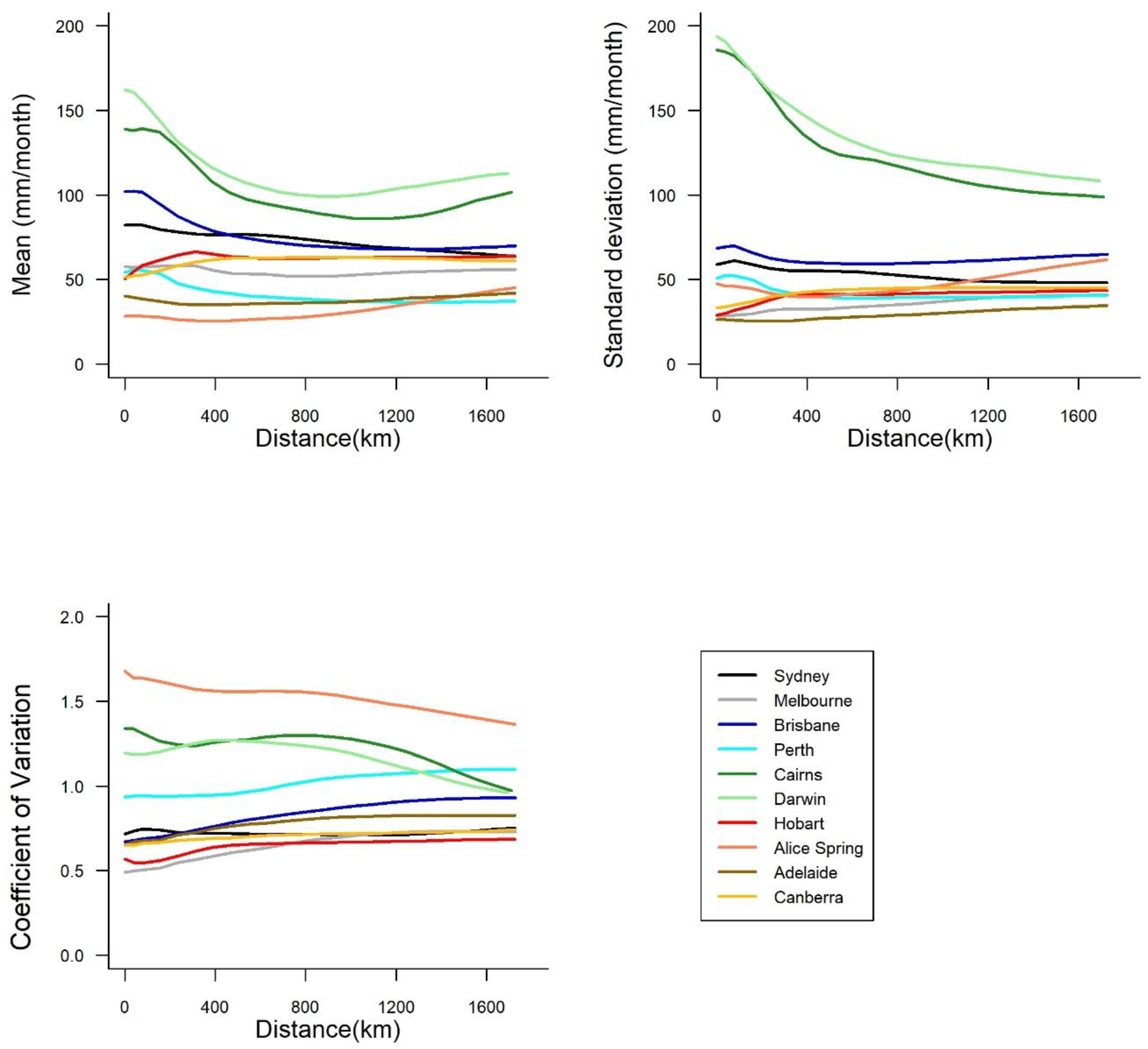
- Between Darwin and Cairns on one hand (tropical climate) and Hobart and Sydney on the other (temperate, no dry season climate), rainfall correlations among grids show a decreasing trend for, in order, Perth, Alice Springs, Adelaide, Canberra, Melbourne, and Brisbane, although some differences exist for different thresholds. These results also seem to suggest that spatial rainfall correlations among grids decrease from a temperate (no dry season) climate to a grassland (persistently dry) climate to a subtropical (distinctly dry summer) climate, with others in between. Nevertheless, there can certainly be exceptions to this interpretation. This is because, even if the climates in two cities are approximately similar, possible bias in spatial rainfall correlations may also occur due to many other factors that influence rainfall both within and surrounding the cities. On the other hand, rainfall statistical properties in two cities can be significantly different even when the cities have approximately similar climates. A comparison of the spatial rainfall correlation results in Figure 6 with the rainfall statistics (mean, standard deviation, and coefficient of variation—standard deviation/mean) in Figure 7 for the ten cities seems to suggest the possible inconsistencies and complications that may arise in interpreting the spatial rainfall correlation results and/or rainfall statistics; see, for instance, the results for Alice Springs and Adelaide. Therefore, proper care needs to be exercised in interpreting the spatial rainfall correlations and rainfall statistics, towards rainfall interpolation/extrapolation. We will examine these issues in more detail in a future study.
5. Study Implications and Further Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Thiessen, A.H. Precipitation averages for large areas. Mon. Weather Rev. 1911, 39, 1082–1084. [Google Scholar] [CrossRef]
- Eagleson, P.S. Optimum density of rainfall networks. Water Resour. Res. 1967, 3, 1021–1033. [Google Scholar] [CrossRef]
- Zawadzki, I.I. Statistical properties of precipitation patterns. J. Appl. Meteorol. 1973, 12, 459–472. [Google Scholar] [CrossRef]
- Berndtsson, R. Temporal variability in spatial correlation of daily rainfall. Water Resour. Res. 1988, 24, 1511–1517. [Google Scholar] [CrossRef]
- Krstanovic, P.F.; Singh, V.P. Evaluation of rainfall networks using entropy: I. Theoretical development. Water Resour. Manag. 1992, 6, 279–293. [Google Scholar] [CrossRef]
- Krstanovic, P.F.; Singh, V.P. Evaluation of rainfall networks using entropy: II. Application. Water Resour. Manag. 1992, 6, 295–314. [Google Scholar] [CrossRef]
- McCollum, J.R.; Krajewski, W.F. Uncertainty of monthly rainfall estimates from rain gauges in the global precipitation climatology project. Water Resour. Res. 1998, 34, 2647–2654. [Google Scholar] [CrossRef]
- Garcia, M.; Peters-Lidard, C.D.; Goodrich, D.C. Spatial interpolation of precipitation in a dense gauge network for monsoon storm events in the southwestern united states. Water Resour. Res. 2008, 44, W05S13. [Google Scholar] [CrossRef]
- Mishra, A.K.; Coulibaly, P. Hydrometric network evaluation for canadian watersheds. J. Hydrol. 2010, 380, 420–437. [Google Scholar] [CrossRef]
- Sivakumar, B.; Woldemeskel, F.M. A network-based analysis of spatial rainfall connections. Environ. Model. Softw. 2015, 69, 55–62. [Google Scholar] [CrossRef]
- Shi, H.; Li, T.; Wei, J.; Fu, W.; Wang, G. Spatial and temporal characteristics of precipitation over the three-river headwaters region during 1961–2014. J. Hydrol. Reg. Stud. 2016, 6, 52–65. [Google Scholar] [CrossRef]
- Lakew, H.B.; Mogus, S.A.; Asfaw, D.H. Hydrological evaluation of satellite and reanalysis precipitation products in the Upper Blue Nile Basin: A case study of Gilgel Abbay. Hydrology 2017, 4, 39. [Google Scholar] [CrossRef]
- Chen, A.; Chen, D.; Azorin-Molina, C. Assessing reliability of precipitation data over the Mekong River Basin: A comparison of ground-based, satellite, and reanalysis data sets. Int. J. Climatol. 2018, 38, 4314–4334. [Google Scholar] [CrossRef]
- Wang, W.; Wang, D.; Singh, V.P.; Wang, Y.; Wu, J.; Wang, L.; Zou, X.; Liu, J.; Zou, Y.; He, R. Optimization of rainfall networks using information entropy and temporal variability analysis. J. Hydrol. 2018. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Rudolf, B.; Schneider, U.; Keehn, P.R. Global precipitation estimates based on a technique for combining satellite-based estimates, rain gauge analysis, and NWP model precipitation information. J. Clim. 1995, 8, 1284–1295. [Google Scholar] [CrossRef]
- Li, M.; Shao, Q. An improved statistical approach to merge satellite rainfall estimates and raingauge data. J. Hydrol. 2010, 385, 51–64. [Google Scholar] [CrossRef]
- Woldemeskel, F.M.; Sivakumar, B.; Sharma, A. Merging gauge and satellite rainfall with specification of associated uncertainty across australia. J. Hydrol. 2013, 499, 167–176. [Google Scholar] [CrossRef]
- Shi, H.; Li, T.; Wei, J. Evaluation of the gridded CRU TS precipitation dataset with the point raingauge records over the Three-River Headwaters region. J. Hydrol. 2017, 548, 322–332. [Google Scholar] [CrossRef]
- Sivakumar, B.; Sorooshian, S.; Gupta, H.V.; Gao, X. A chaotic approach to rainfall disaggregation. Water Resour. Res. 2001, 37, 61–72. [Google Scholar] [CrossRef]
- Li, J.; Bárdossy, A.; Guenni, L.; Liu, M. A copula based observation network design approach. Environ. Model. Softw. 2011, 26, 1349–1357. [Google Scholar] [CrossRef]
- Niu, J. Precipitation in the Pearl River basin, South China: Scaling, regional patterns, and influence of large-scale climate anomalies. Stoch. Environ. Res. Risk Assess. 2013, 27, 1253–1268. [Google Scholar] [CrossRef]
- Jha, S.K.; Sivakumar, B. Complex networks for rainfall modeling: Spatial connections, temporal scale, and network size. J. Hydrol. 2017, 554, 482–489. [Google Scholar] [CrossRef]
- Kummerow, C.; Simpson, J.; Thiele, O.; Barnes, W.; Chang, A.T.C.; Stocker, E.; Adler, R.F.; Hou, A.; Kakar, R.; Wentz, F.; et al. The status of Tropical Rainfall Measuring Mission (TRMM) after two years in orbit. J. Appl. Meteorol. 2000, 39, 1965–1982. [Google Scholar] [CrossRef]
- Fleming, K.; Awange, J.L.; Kuhn, M.; Featherstone, W.E. Evaluating the TRMM 3B43 monthly precipitation product using gridded raingauge data over Australia. J. South. Hemisph. Earth Syst. Sci. 2011, 61, 171–184. [Google Scholar] [CrossRef]
- Taschetto, A.S.; England, M.H. An analysis of late twentieth century trends in australian rainfall. Int. J. Clim. 2009, 29, 791–807. [Google Scholar] [CrossRef]
- Stern, H.; De Hoedt, G.; Ernst, J. Objective classification of Australian climates. Aust. Meteorol. Mag. 2000, 49, 87–96. [Google Scholar]
- Guo, D.; Westra, S.; Maier, R.H. Sensitivity of potential evapotranspiration to changes in climate variables for different Australian climate zones. Hydrol. Earth Syst. Sci. 2017, 21, 2107–2126. [Google Scholar] [CrossRef]
- Jeffrey, S.J.; Carter, J.O.; Moodie, K.B.; Beswick, A.R. Using spatial interpolation to construct a comprehensive archive of Australian climate data. Environ. Model. Softw. 2001, 16, 309–330. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Young, W.J.; Cai, W.; Teng, J. Current drought and future hydroclimate projections in southeast australia and implications for water resources management. Stoch. Environ. Res. Risk Assess. 2010, 25, 601–612. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Potter, N.J.; Vaze, J.; Petheram, C.; Zhang, L.; Teng, J.; Post, D.A. Observed hydrologic non-stationarity in far south-eastern australia: Implications for modelling and prediction. Stoch. Environ. Res. Risk Assess. 2014, 28, 3–15. [Google Scholar] [CrossRef]
- Sivakumar, B.; Woldemeskel, F.M.; Puente, C.E. Nonlinear analysis of rainfall variability in australia. Stoch. Environ. Res. Risk Assess. 2014, 28, 17–27. [Google Scholar] [CrossRef]
- Chokngamwong, R.; Chiu, L.S. Thailand daily rainfall and comparison with trmm products. J. Hydrometeorol. 2008, 9, 256–266. [Google Scholar] [CrossRef]
- Chiu, L.S.; Liu, Z.; Vongsaard, J.; Morain, S.; Budge, A.; Neville, P.; Bales, C. Comparison of trmm and water district rain rates over new mexico. Adv. Atmospheric Sci. 2006, 23, 1–13. [Google Scholar] [CrossRef]
- Hughes, D.A. Comparison of satellite rainfall data with observations from gauging station networks. J. Hydrol. 2006, 327, 399–410. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Nasrollahi, N.; Habib, E. Accounting for uncertainties of the TRMM satellite estimates. Remote Sens. 2009, 1, 606–619. [Google Scholar] [CrossRef]
- Guofeng, Z.; Dahe, Q.; Yuanfeng, L.; Fenli, C.; Pengfei, H.; Dongdong, C.; Kai, W. Accuracy of trmm precipitation data in the southwest monsoon region of china. Theor. Appl. Clim. 2016. [Google Scholar] [CrossRef]
- Grimes, D.I.; Pardo-Igúzquiza, E.; Bonifacio, R. Optimal areal rainfall estimation using raingauges and satellite data. J. Hydrol. 1999, 222, 93–108. [Google Scholar] [CrossRef]
- Collischonn, B.; Collischonn, W.; Tucci, C.E.M. Daily hydrological modeling in the amazon basin using trmm rainfall estimates. J. Hydrol. 2008, 360, 207–216. [Google Scholar] [CrossRef]
- Su, F.; Hong, Y.; Lettenmaier, D.P. Evaluation of trmm multisatellite precipitation analysis (tmpa) and its utility in hydrologic prediction in the La Plata basin. J. Hydrometeorol. 2008, 9, 622–640. [Google Scholar] [CrossRef]
- Yong, B.; Hong, Y.; Ren, L.-L.; Gourley, J.J.; Huffman, G.J.; Chen, X.; Wang, W.; Khan, S.I. Assessment of evolving trmm-based multisatellite real-time precipitation estimation methods and their impacts on hydrologic prediction in a high latitude basin. J. Geophys. Res. Atmos. 2012, 117, D09108. [Google Scholar] [CrossRef]
- Naufan, I.; Sivakumar, B.; Woldemeskel, F.M.; Raghavan, S.V.; Wu, M.T.; Liong, S.-Y. Spatial connections in regional climate model rainfall outputs at different temporal scales: Application of network theory. J. Hydrol. 2018, 556, 1232–1243. [Google Scholar] [CrossRef]
- Kurtzman, D.; Navon, S.; Morin, E. Improving interpolation of daily precipitation for hydrologic modelling: Spatial patterns of preferred interpolators. Hydrol. Process. 2009, 23, 3281–3291. [Google Scholar] [CrossRef]
- Jha, S.K.; Zhao, H.; Woldemeskel, F.M.; Sivakumar, B. Network theory and spatial rainfall connections: An interpretation. J. Hydrol. 2015, 527, 13–19. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sivakumar, B.; Woldemeskel, F.M.; Vignesh, R.; Jothiprakash, V. A Correlation–Scale–Threshold Method for Spatial Variability of Rainfall. Hydrology 2019, 6, 11. https://doi.org/10.3390/hydrology6010011
Sivakumar B, Woldemeskel FM, Vignesh R, Jothiprakash V. A Correlation–Scale–Threshold Method for Spatial Variability of Rainfall. Hydrology. 2019; 6(1):11. https://doi.org/10.3390/hydrology6010011
Chicago/Turabian StyleSivakumar, Bellie, Fitsum M. Woldemeskel, Rajendran Vignesh, and Vinayakam Jothiprakash. 2019. "A Correlation–Scale–Threshold Method for Spatial Variability of Rainfall" Hydrology 6, no. 1: 11. https://doi.org/10.3390/hydrology6010011
APA StyleSivakumar, B., Woldemeskel, F. M., Vignesh, R., & Jothiprakash, V. (2019). A Correlation–Scale–Threshold Method for Spatial Variability of Rainfall. Hydrology, 6(1), 11. https://doi.org/10.3390/hydrology6010011




