Development of Monsoonal Rainfall Intensity-Duration-Frequency (IDF) Relationship and Empirical Model for Data-Scarce Situations: The Case of the Central-Western Hills (Panchase Region) of Nepal
Abstract
1. Introduction
1.1. Background
1.2. Rationale
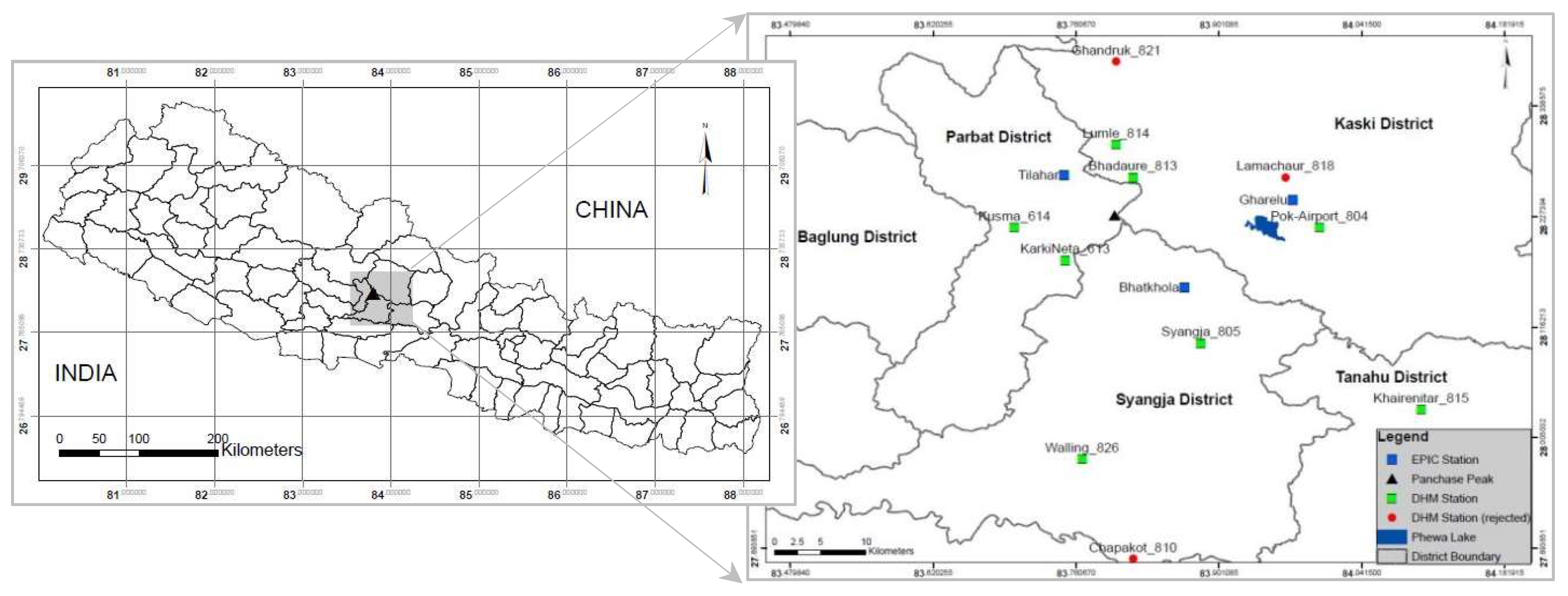
1.3. The Panchase Region
2. Methods
2.1. Data Quality and Rainfall Variability
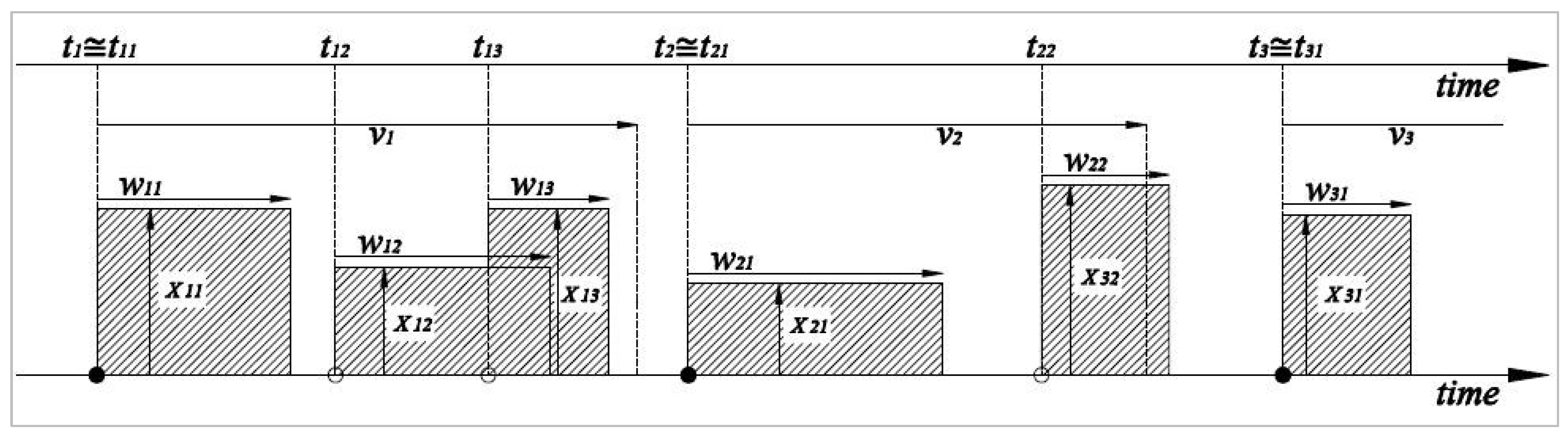
2.2. Disaggregation of Daily Rainfall
- The occurrence of random storm events (ti) is assumed to be modelled as a Poisson process with rate and each event i is associated with a random number of cells.
- Each storm event tij, is assumed as a precipitation rectangular pulse with random duration td and the origin of storm events tij of each cell j occurs following a second Poisson process with rate . The inter-arrival time of two subsequent storm events (i.e., successive cells) is independent, identically distributed and follows an exponential distribution.
- The cell-generation process terminates after time span of following the exponential distribution rate . Also, the number of cells per storm contains a geometric distribution of mean .
- The random precipitation rectangular pulse duration td is modelled as wij and also follows exponential distribution with rate .
- Finally, the cell intensity xij is assumed to be exponentially distributed with mean .
2.3. Evaluation of Disaggregation Model
2.4. Fitting of Probability Distribution Function and Construction of Reference Intensity-Duration-Frequency (IDF)
2.5. Estimation of IDF for Ungauged Location
- Screening of data through discordancy measure;
- Identification of homogeneous regions;
- Selection of regional distribution and goodness of fit measure;
- Estimation of regional growth curve using index-flood procedure.
2.5.1. Screening of Data and Discordancy Measure
2.5.2. Identification of Homogeneous Region
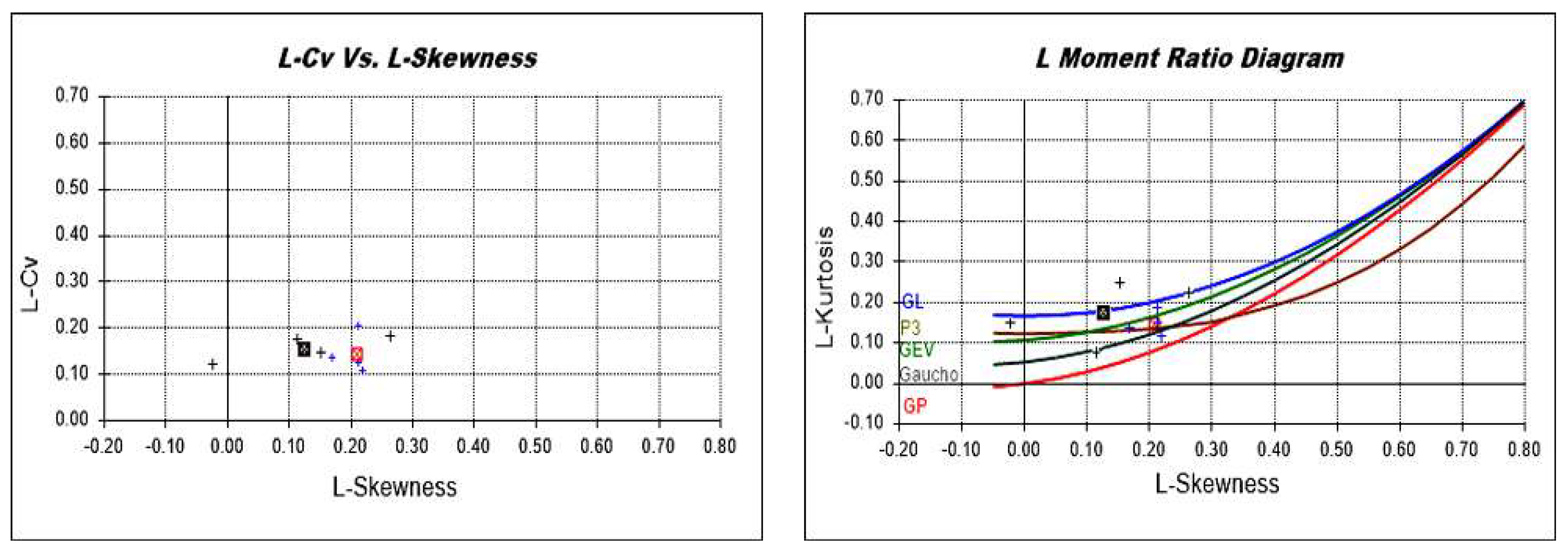
2.5.3. Selection of Regional Distribution and Goodness of Fit
2.5.4. Estimation of Regional Growth Curves using Index-Flood Procedure
3. Results
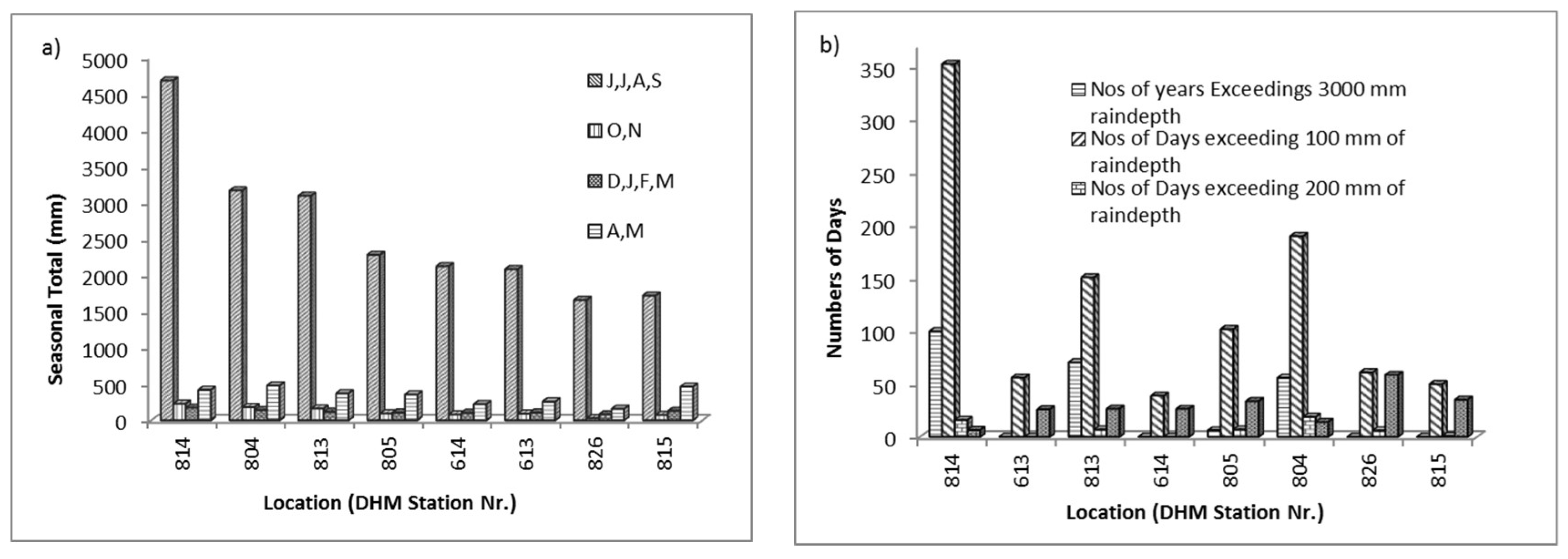
3.1. Data Quality and Rainfall Variability
3.2. Disaggregation of Daily Rainfall Depth
3.3. Evaluation of Disaggregation Model
3.4. Selection of Probability Distribution Function (PDF) and Parameter Estimation
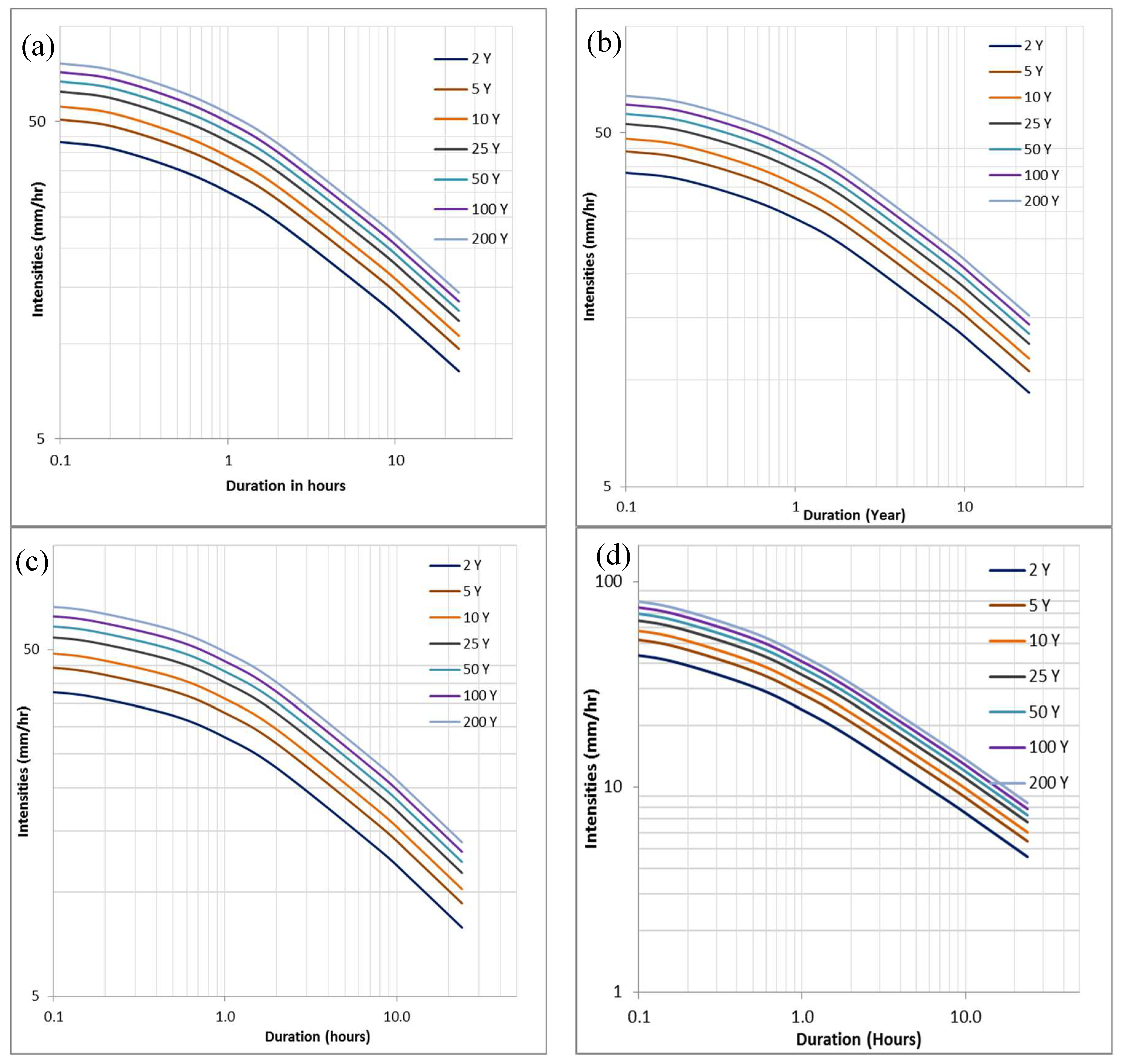
3.5. Construction of Reference and Empirical IDF Relationship
3.6. Evaluation of the IDF Relationship and Development of Empirical Model
3.7. Reganalization of IDF for Ungauged Locations
3.8. Rainfall Intensity in the Region
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- ADPC. Nepal Hazard Risk Assessment, Part 1; Asian Disaster Preparedness Center (ADPC): Bangkok, Thailand, 2010; p. 114. [Google Scholar]
- MoHA; DPNeT. Nepal Disaster Report 2015; DPNeT: Kathmandu, Nepal, 2015; p. 147. [Google Scholar]
- MoENV. National Adaptation Porgramme of Action (NAPA); Ministry of Environment: Kathmandu, Nepal, 2010; p. 165.
- Petley, D.N.; Hearn, G.J.; Hart, A.; Rosser, N.; Dunning, S.; Oven, K.; Mitchell, W. Trends in Landslide occurrence in Nepal. Nat. Hazards 2007, 43, 23–44. [Google Scholar] [CrossRef]
- Petley, D.N. On the impact of climate change and population growth on the occurrence of landslides in Asia. Q. J. Eng. Geol. Hydrogeol. 2010, 43, 487–496. [Google Scholar] [CrossRef]
- CBS. Compendium of Environment Statistics of Nepal 2015; Government of Nepal: Kathmandu, Nepal, 2015; p. 176.
- Haigh, M.; Rawat, J.S. Landslide causes: Human impacts on a Himalayan landslide swarm, Belgeo. Rev. Balge Geogr. 2011, 201–220. [Google Scholar] [CrossRef]
- Cruden, D.M.; Varnes, D.J. Landslide Types and Processes. In Landslide: Investigation and Mitigation; Transportation Research Board: Denver, CO, USA, 1996; Volume 247, pp. 36–75. [Google Scholar]
- Sudmeier-Rieux, K.; Jaquet, S.; Derron, M.-H.; Jaboyedoff, M.; Devkota, S. A Case Study of Landslides and Coping Strategies in Two Villages of Central-Eastern Nepal. J. Appl. Geogr. 2011, 32, 680–690. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Derron, M.H.; Voumard, J.; Leibundgut, G.; Sudmeier-Rieux, K.; Nadim, F.; Leroi, E. Human-Induced Landslides: Toward the Analysis of Anthropogenic Changes of the Slope Environment; CRC Press: Bocaton, FL, USA, 2016. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: New York, NY, USA, 1997. [Google Scholar]
- Rakhecha, P.R.; Singh, V.P. Applied Hydrometeorology; Springer: Dordrecht, The Netherlands; Capital Publishing Company: New Delhi, India, 2009. [Google Scholar]
- Rana, A.; Bengtsson, L.; Jothiprakash, V. Development of IDF-curves for tropical India by random cascade modelling. Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 4709–4738. [Google Scholar] [CrossRef]
- WMO-UNESCO-IAHS. Design of Water Resources Projects with inadequate data. In Proceedings of the Madrid Symposium, Madrid, Spain, 4–6 June 1973. [Google Scholar]
- Ganguli, P.; Paulin, C. Does nonstationarity in rainfall require nonstationary intensity–duration–frequency curves? Hydrol. Earth Syst. Sci. 2017, 21, 6461. [Google Scholar] [CrossRef]
- Nhat, L.M.; Tachikawa, Y.; Taka, K. Establishment of Intensity-Duration-frequency Curves for Precipitaiton in the Monsoon area of Vietnam. Ann. Disaster Prev. Res. 2006, 49, 93–103. [Google Scholar]
- Van de Vyver, H.; Demaree, G.R. Construction of Intensity-Duration-frequency (IDF) curves for precipitation at Lubumabashi, Congo, under the hypothesis of inadequate data. Hydrol. Sci. J. 2010, 55, 555–564. [Google Scholar] [CrossRef]
- Dahal, R.K.; Hasegawa, S. Representative rainfall thresholds for landslides in the Nepal Himalayas. Geomorphology 2008, 100, 429–443. [Google Scholar] [CrossRef]
- Langousis, A.; Veneziano, D. Intensity-Duration-frequency curves from scaling representation of rainfall. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Van Asch, T.W.J.; Buma, J.; Van Beek, L.P.H. A view on some hydrological triggering system in landslides. Geomorphology 1999, 30, 25–32. [Google Scholar] [CrossRef]
- Gerold, L.A.; Watkins, D.W. Short Duration Rainfall Frequency Analysis in Michigan Using Scale-Invariance Assumptions. J. Hydrol. Eng. 2005, 10, 450–457. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A mathematical framework for studying rainfall intensity-duration-frequency relationship. J. Hydrol. 1998, 208, 118–235. [Google Scholar] [CrossRef]
- Afrin, S.; Islam, M.M.; Rahman, M.M. Development of IDF Curves for Dhaka City based on Scaling Theory under future precipitation variability due to climate change. Int. J. Environ. Sci. Dev. 2015, 6, 332–335. [Google Scholar] [CrossRef]
- Cardoso, C.O.; Bertol, I.; de Paiva Sampaio, C.A. Generation of Intensity Duration frequency Curves and Intensity temporal variability Pattern of Intense rainfall for Lages. Braz. Arch. Biol. Technol. 2013, 57, 274–283. [Google Scholar] [CrossRef]
- Verhoest, N.; Troch, P.A.; De Troch, F.P. On the applicability of Bartlett-Lewis rectangular pulses models in the modelling of design storms at a point. J. Hydrol. 1997, 202, 108–120. [Google Scholar] [CrossRef]
- Chen, C.L. Rainfall-Intensity-Duration Formulas. ASCE J. Hydrol. Eng. 1983, 109, 1603–1621. [Google Scholar] [CrossRef]
- Baghirathan, V.R.; Shaw, E.M. Rainfall depth-duration-frequency studies for Sri Lanka. J. Hydrol. 1978, 37, 223–239. [Google Scholar] [CrossRef]
- Gert, A.; Wall, D.J.; White, E.L.; Dunn, C.N. Regional Rainfall Intensity-Duration-Frequency Curves For Pennsylvania. J. Am. Water Resour. 1987, 23, 479–485. [Google Scholar]
- Kothyari, U.C.; Grade, R.J. Rainfall intensity duration frequency formula for India. J. Hydraul. Eng. 1992, 118, 323–336. [Google Scholar] [CrossRef]
- Yu, P.S.; Chen, C.L. regional analysis of rainfall intensity-duration-frequency relationship. J. Chin. Inst. Eng. 1996, 19, 523–532. [Google Scholar] [CrossRef]
- Madsen, H.; Mikkelsen, P.S.; Rosbjerg, D.; Harremoes, P. Regional estimation of rainfall intensity-duration-frequency curves using generalized least squares regression of partial duration series statistics. Water Resour. Res. 2002, 38, 21–31. [Google Scholar] [CrossRef]
- Willems, P. Compound intensity-duration-frequency relationships of extreme precipitation for two seasons and two storm types. J. Hydrol. 2000, 233, 189–205. [Google Scholar] [CrossRef]
- Yu, P.-S.; Yang, T.-C.; Lin, C.-S. Regional rainfall intensity formulas based on scaling property of rainfall. J. Hydrol. 2004, 295, 108–123. [Google Scholar] [CrossRef]
- Dalrymple, T. Flood-Frequency Analyses, Mannual of Hydrology; USGS: Leston, VA, USA, 1960; p. 80. [Google Scholar]
- Ariff, N.M.; Jemain, A.A.; Bakar, M.A.A. Regionalization of IDF Curves with L-Moments for Storm Events. Int. J. Math. Comput. Sci. 2016, 10, 217–223. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R.; Wood, E.F. An appraisal of the regional frequency analysis. Hydrol. Sci. J. 1985, 30, 85–109. [Google Scholar]
- Gaume, E.; Mouhous, N.; Andrieu, H. Rainfall stochastic disaggregation models: Calibration and validation of a multiplicative cascade model. Adv. Water Resour. 2007, 30, 1301–1319. [Google Scholar] [CrossRef]
- Glasbey, C.A.; Cooper, G.; McGechan, M.B. Disaggregation of daily rainfall by conditional simulation of point-process model. J. Hydrol. 1995, 165, 1–9. [Google Scholar] [CrossRef]
- Kaczmarska, J.; Isham, V.; Onof, C. Point process models for fine-resolution rainfall. Hydrol. Sci. J. 2014, 59, 1972–1991. [Google Scholar] [CrossRef]
- Kilsby, C.D.G.; Jones, P.D.; Burton, A.; Ford, A.C.; Fowler, H.J.; Harpham, C.; James, P.; Smith, A.; Wilby, R.L. A daily weather generator for use in climate change studies. J. Environ. Model. Softw. 2007, 22, 1705–1719. [Google Scholar] [CrossRef]
- Kossieris, P.; Makropoulos, C.; Onof, C.; Koutsoyiannis, D. A rainfall disaggregation scheme for sub-hourly time scales: Coupling a Bartlett-Lewis based model with adjusting procedures. J. Hydrol. 2016, 556, 980–992. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. A stochastic disaggregation method for design storm and flood synthesis. J. Hydrol. 1994, 156, 193–225. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Onof, C. A computer program for temporal rainfall disaggregation using adjusting procedures (HYETOS). In Proceedings of the XXV General Assembly of European Geophysical Society, Nice, France, 25–29 April 2010. [Google Scholar]
- Koutsoyiannis, D.; Onof, C. Rainfall disaggregation using adjusting procedures on a Poisson cluster model. J. Hydrol. 2001, 246, 109–122. [Google Scholar] [CrossRef]
- Kaczmarska, J. Further Development of Barlett-Lewis Model for Fine-Resolution Rainfall; Department of Statistical Science, University College London: London, UK, 2011. [Google Scholar]
- Shrestha, M.L. Inter-annual variation of summer monsoon rainfall over Nepal and its relation to Southern Oscillation Index. Meteorol. Atmos. Phys. 2000, 75, 21–28. [Google Scholar] [CrossRef]
- Chalise, S.R.; Khanal, N.R. An introduction to climate, hydrology and landslide hazards in the Hindu Kush-Himalayan region. In Landslide Hazard Mitigation in the Hindu Kush-Himalaya; ICIMOD: Kathmandu, Nepal, 2001; pp. 51–62. [Google Scholar]
- Leibundgut, G.; Sudmeier-Rieux, K.; Devkota, S.; Jaboyedoff, M.; Derron, M.-H.; Penna, I.; Nguyen, L. Rural earthen roads impact assessment in Phewa watershed, Western region, Nepal. Geoenviron. Disasters 2016, 3, 13. [Google Scholar] [CrossRef]
- Devkota, S.; Adhikari, B.R. Development of Ecosystem Based Sediment Control Techniques and Design of Siltation Dam to Protect Phewa Lake, Kaski District, Nepal; GOVN/UNDP/IUCN: Kathmandu, Nepal, 2015; p. 46. [Google Scholar]
- Fleming, B.; Felming, P.J. A watershed conservation success story in Nepal: Land use changes over 30 years. Waterlines 2009, 28, 29–46. [Google Scholar] [CrossRef]
- Gurung, H. Pokhara Valley: A Field Study in Regional Geography; University of Edingurg: Edingurg, UK, 1965. [Google Scholar]
- JICA. The Development Study on the Environmental Conservation of Phewa Lake; Unpublished Project Report; JICA: Kathmandu, Nepal, 2002. [Google Scholar]
- Thapa, G.B.; Weber, K.E. Status and management of watersheds in the upper Pokhara valley, Nepal. Environ. Manag. 1995, 19, 497–513. [Google Scholar] [CrossRef]
- Buishand, T.A. Some methods for testing the homogeneity of rainfall records. Hydrology 1982, 58, 11–27. [Google Scholar] [CrossRef]
- Wijngaard, J.B.; Klein Tank, A.M.G.; Können, G.P. Homogeneity of 20th century European daily temperature and precipitation series. Int. J. Climatol. 2003, 23, 679–692. [Google Scholar] [CrossRef]
- Raes, D.; Willems, P.; GBaguidi, F. RAINBOW—A software package for analyzing data and testing the homogeneity of historical data sets. In Proceedings of the 4th International Workshop on ‘Sustainable management of marginal drylands’, Islamabad, Pakistan, 27–31 January 2006. [Google Scholar]
- RClimTool. RClimTool: A Free Application for Analyzing Climatic Series; Clima y Sector Agropecuario Colombiano: Palmira, Colombia, 2014. [Google Scholar]
- XLSTAT. XLSTAT Getting Started Manual; XLSTAT: Paris, France, 2016. [Google Scholar]
- Devkota, S.; Lal, A.C. Local Knowledge for Addressing Climate Change Risks at Local level. In Identifying Emerging Issues in Disaster Risk Reduction, Migration, Climate Change and Sustainable Development; Sudmeier-Rieux, K., Fernandez, M., Penna, I.M., Jaboyedoff, M., Gaillard, J.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Manetas, A. Simple disaggregation by accurate adjusting procedures. Water Resour. Res. 1996, 32, 2105–2117. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Cox, D.R.; Isham, V. Some models for rainfall based on stochastic point processes. Proc. R. Soc. Lond. A 1987, 410, 269–288. [Google Scholar] [CrossRef]
- Onof, C.; Wheater, H.S. Improvement to the modelling of British rainfall using a modified random parameter Bartlett-Lewis rectangular Pulses Model. J. Hydrol. 1994, 157, 177–195. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Cox, D.R.; Isham, V. A point process model for rainfall: Further developments. Proc. R. Soc. Lond. A 1988, 417, 283–298. [Google Scholar] [CrossRef]
- Abdellatif, M.; Atherton, W.; Alkhaddar, R. Application of the stochastic model for temporal rainfall disaggregation for hydrological studies in north western England. J. Hydroinf. 2013. [Google Scholar] [CrossRef]
- Cowpertwait, P.S.P.; O’Connel, P.E.; Matcalfe, A.V.; Mawdsley, J.A. Stochastic point process modelling of rainfall, I, Single site fitting and validation. J. Hydrol. 1996, 176, 17–46. [Google Scholar] [CrossRef]
- Cowpertwait, P.S.P.; O’Connel, P.E.; Matcalfe, A.V.; Mawdsley, J.A. Stochastic point process modelling of rainfall. II, Regionalization and disaggregation. J. Hydrol. 1996, 176, 47–65. [Google Scholar] [CrossRef]
- Islam, D.; Entekhabi, D.; Bras, R.L. Parameter-estimation and sensitivity analysis for the modified Bartlett-Lweis rectangular pulses model of rainfall. J. Geophys. Res. 1990, 95, 2093–2100. [Google Scholar] [CrossRef]
- Onof, C.; Wheater, H.S. Modelling of British rainfall using a random parameter Bartlett-Lewis rectangular Pulse Model. J. Hydrol. 1993, 149, 67–95. [Google Scholar] [CrossRef]
- Onof, C.; Wheater, H.S. Improved fitting of the Bartlett-Lewis Rectangular Pulse Model for hourly rainfall. Hydrol. Sci. J. 1994, 39, 663–680. [Google Scholar] [CrossRef]
- Pui, A.; Sharma, A.; Mehrotra, R.; Sivakumar, B.; Jeremiah, E. A comparison of alternatives for daily to sub-daily rainfall disaggregation. J. Hydrol. 2012, 470–471, 138–157. [Google Scholar] [CrossRef]
- Yusop, H.Z.; Yusof, F. The use of BLRP Model for Disaggregating Daily Rainfall Affected by Monsoon in Peninsular Malaysia. Sains Malays. 2016, 45, 87–97. [Google Scholar]
- Kossieris, P.; Koutsoyiannis, D.; Onof, C.; Tyralis, H.; Efstratiadis, A. ‘HyetosMinute’ Rainfall Disaggregation Software Plug in Package of R: Temporal Stochastic Simulation of Rainfall at Fine Time Scale; European Geosciences Union: Vienna, Austria, 2012. [Google Scholar]
- Ghosh, S.; Roy, M.K.; Biswas, S.C. Determination of the best fit probability distribution for monthly rainfall data in Bangladesh. Am. J. Math. Stat. 2016, 6, 170–174. [Google Scholar]
- Hanson, L.S.; Vogel, R. The Probability Distribution of Daily Rainfall in the United States; World Environmental and Water Resources Congress: Honolulu, HI, USA, 2008. [Google Scholar]
- Millington, N.; Das, S.; Simonovic, S.P. The Comparison of GEV, Log-Pearson Type 3 and Gumbel Distributions in the Upper Thames River Watershed under Global Climate Models; The University Of Western Ontario Department Of Civil And Environmental Engineering: London, ON, Canada, 2011. [Google Scholar]
- Svensson, C.; Jones, D.A. Review of rainfall frequency estimation methods. J. Flood Risk Manag. 2010, 3, 296–313. [Google Scholar] [CrossRef]
- Win, N.L.; Win, K.M. The Probability Distributions of Daily Rainfall for Kuantan River Basin in Malaysia. Int. J. Sci. Res. 2014, 3, 977–983. [Google Scholar]
- EasyFit. Data Analysis and Simulation, Distribution Fitting Tutorials. Available online: http://www.mathwave.com/company.html (accessed on 14 May 2018).
- Gamage, S.H.P.W.; Hewa, G.A.; Beecham, S. Probability distributions for explaining hydrological losses in South Australian catchments. Hydrol. Earth Syst. Sci. 2013, 17, 4541–4553. [Google Scholar] [CrossRef]
- Misic, B. Communication in Large Scale Basin Networks in Theory and Application; University of Toronto: Toronto, ON, Canada, 2014. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R.; Wood, E.F. Estimation of the generalized extreme-value distribution by the method of probability-weighted moments. Technometric 1985, 27, 251–261. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Vogel, R.M.; Foufoula-Georgiou, E. Frequency analysis of extreme events. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Koutsoyiannis, D. Statistics of extremes and estimation of extreme rainfall, Theoretical investigation. Hydrol. Sci. J. 2004, 49, 575–590. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Statistics of extremes and estimation of extreme rainfall, Empirical investigation of long rainfall records. Hydrol. Sci. J. 2004, 49, 591–610. [Google Scholar] [CrossRef]
- Wilson, E.M. Engineering Hydrology, 4th ed.; Macmillan: London, UK, 1990. [Google Scholar]
- Benabdesselam, T.; Amarchi, H. Regional approach for the estimation of extreme daily precipitation on North-east area of Algeria. Int. J. Water Resour. Environ. Eng. 2013, 5, 573–583. [Google Scholar]
- Burn, D.H. Evaluation of regional Flood Frequency Analysis with a region of Influence Approach. Water Resour. Res. 1990, 26, 2257–2265. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Landwehr, J.M.; Matalas, N.C.; Wallis, J.R. Probability weighted moments: Definition and relation to parameters of several distributions expressible in inverse form. Water Resour. Res. 1979, 15, 1049–1054. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. R. Stat. Soc. Ser. B 1990, 52, 105–124. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Some statistics useful in regional frequency analysis. Water Resour. Res. 1993, 29, 271–281. [Google Scholar]
- Villani, V.; di Serafino, D.; Rianna, G.; Mercogliano, P. Stochastic Models for the Disaggregation of Precipitation Time Series on Sub-Daily Scale: Identification of Parameters by Global Optimization. Centro Euro-mediterraneo sui Cambiamenti Climatici: CMCC Research Paper No. RP0256. Available online: http://dx.doi.org/10.2139/ssrn.2602889 (accessed on 14 May 2018).
- AlHassoun, A.S. Developing an empirical formulae to estimate rainfall intensity in Riyadh region. J. King Saud Univ. Eng. Sci. 2011, 23, 81–88. [Google Scholar] [CrossRef]
- DePaola, F.; Giugni, M.; Topa, M.E.; Bucchignani, E. Intensity-Duration-Frequency (IDF) Curves, for data series and climate projection in African cities. Springerplus 2014, 3, 133. [Google Scholar] [CrossRef] [PubMed]
- Connolly, R.D.; Schirmer, J.; Dunn, P.K. A daily rainfall disaggregation model. Agric. For. Meteorol. 1998, 92, 105–177. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Onof, C.; Wheater, H.S. Multivariate rainfall disaggregation at a fine timescale. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Apel, H.; Thieken, H.A.; Merz, B.; Blöschl, G. A Probabilistic Modelling System for Assessing Flood Risks. Nat. Hazards 2006, 38, 79–100. [Google Scholar] [CrossRef]
- Solomon, O.; Prince, O. Flood Frequency Analysis using Gumbel’s Distribution. Civ. Environ. Res. 2013, 3, 51. [Google Scholar]
| Location | Department of Hydrology and Meteorology (DHM) Station Number (Nr.) | Altitude (masl) | Years of Records | Annual (mean) Rainfall (mm) | Monsoonal (mean) Rainfall (mm) | Nr. of Storms > 100 mm in 24 h | Nr. of Storms > 200 mm in 24 h | Mean (Extreme) Daily Rainfall (mm/day) | Missing Values | Homogeneity (Rejected at 95%) |
|---|---|---|---|---|---|---|---|---|---|---|
| GHANDRUK | 821 | 1960 | 1982–2014 | 3384 | 2642 | 47 | 0 | 7.5 | >5% | Yes |
| LUMLE | 814 | 1740 | 1982–2014 | 5504 | 4681 | 352 | 17 | 15.1 | <5% | No |
| KARKI-NETA | 613 | 1720 | 1982–2014 | 2543 | 2047 | 56 | 0 | 7 | <5% | No |
| BHADAURE-DEURALI | 813 | 1600 | 1984–2015 | 3744 | 3093 | 150 | 7 | 11.3 | <5% | No |
| LAMACHAUR | 818 | 1070 | 1982–2014 | 4220 | 3380 | 204 | 10 | 10.5 | >5% | Yes |
| KUSHMA | 614 | 891 | 1982–2014 | 2531 | 2122 | 39 | 0 | 7.3 | <5% | No |
| SYANGJA | 805 | 868 | 1982–2014 | 2840 | 2280 | 101 | 7 | 7.8 | <5% | No |
| POKHARA-AIRPORT | 804 | 827 | 1982–2015 | 3969 | 3160 | 189 | 19 | 10.9 | <5% | No |
| WALLING | 826 | 750 | 1989–2012 | 1929 | 1658 | 61 | 6 | 5.4 | <5% | No |
| KHAIRINITAR | 815 | 500 | 1982–2012 | 2384 | 1719 | 50 | 1 | 6.6 | <5% | No |
| CHAPAKOT | 810 | 460 | 1982–2012 | 1878 | 1451 | 59 | 2 | 7.8 | >5% | Yes |
| Location | Weather Station | (day−1) | (day) | (mm/day) | |||
|---|---|---|---|---|---|---|---|
| Gharelu | EPIC:1 | 1.4805 | 6.9398 | 0.1534 | 1.9181 | 0.2615 | 105.98 |
| SN | Location | DHM (Nr.) | (day−1) | (day) | (mm/day) | Hourly (Extreme) Mean (mm/h) | |||
|---|---|---|---|---|---|---|---|---|---|
| 1 | Lumle | 814 | 2.282 | 4.039 | 0.105 | 1.651 | 0.246 | 63.287 | 38.36 |
| 2 | Karki-Neta | 613 | 0.939 | 4.327 | 0.186 | 0.251 | 0.101 | 83.702 | 17.4 |
| 3 | Bhadaure-Deurali | 813 | 1.087 | 3.511 | 0.103 | 1.303 | 0.1493 | 55.347 | 27.89 |
| 4 | Kusma | 614 | 1.031 | 9.904 | 0.47 | 0.577 | 0.171 | 68.614 | 17.46 |
| 5 | Syangja | 805 | 0.863 | 5.797 | 0.224 | 1.145 | 0.201 | 68.704 | 18.63 |
| 6 | Pokhara Airport | 804 | 1.601 | 4.505 | 0.304 | 1.022 | 0.686 | 74.703 | 25.81 |
| 7 | Walling | 826 | 0.423 | 6.816 | 0.2 | 1.895 | 0.129 | 58.762 | 14.27 |
| 8 | Khairenitar | 815 | 0.423 | 6.816 | 0.2 | 1.895 | 0.129 | 58.762 | 13.59 |
| Month | En | En′ | Varn | Varn′ | Skewn | Skewn′ |
|---|---|---|---|---|---|---|
| June | 15.41 | 15.41 | 461.53 | 461.52 | 1.644 | 1.644 |
| July | 46.07 | 46.07 | 2459.81 | 2459.79 | 1.105 | 1.105 |
| August | 28.50 | 28.50 | 1873.35 | 1873.36 | 1.831 | 1.831 |
| September | 45.67 | 45.67 | 1925.78 | 1925.77 | 0.966 | 0.966 |
| S. N. | Location | Parameter: Monsoonal Daily Time Series | Test Statistics | Parameter: Monsoonal Annual Extremes | Test Statistics | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K-S | A-D | K-S | A-D | |||||||||||
| 1 | Lumle | GEV | 0.22 | 18.59 | 23.28 | 0.09 | 41.79 | 161.35 | 0.11 | 183.24 | 28.163 | 0.081 | 0.274 | 1.284 |
| EV I | - | 20.28 | 31.34 | 0.148 | 78.32 | 138.42 | - | 185.11 | 30.59 | 0.108 | 0.407 | 2.744 | ||
| 2 | Karki Neta | GEV | 0.37 | 6.84 | 11.26 | 0.137 | 160.39 | 350.25 | −0.3 | 104.32 | 26.43 | 0.105 | 0.497 | 1.522 |
| EV I | - | 7.67 | 20.97 | 0.229 | 183.24 | 252.72 | - | 101.87 | 21.33 | 0.154 | 0.875 | 0.563 | ||
| 3 | Bhadaure Deurali | GEV | 0.26 | 11.64 | 17.65 | 0.136 | 99.08 | 456.92 | 0.1 | 131.91 | 42.13 | 0.068 | 0.202 | 1.147 |
| EV I | - | 12.96 | 25.86 | 0.192 | 115.48 | 187.68 | - | 134.16 | 46.13 | 0.08 | 0.254 | 0.214 | ||
| 4 | Kusma | GEV | 0.35 | 6.11 | 10.36 | 0.144 | 133.95 | 460.62 | −0.3 | 106.06 | 24.33 | 0.101 | 0.377 | 0.313 |
| EV I | - | 7.12 | 17.91 | 0.226 | 190.73 | 262.53 | - | 103.19 | 18.72 | 0.104 | 1.06 | 0.383 | ||
| 5 | Syangja | GEV | 0.45 | 5.12 | 9.83 | 0.178 | 182.59 | 762.43 | −0.1 | 139.27 | 41.64 | 0.073 | 0.246 | 0.382 |
| EV I | - | 5.59 | 22.6 | 0.278 | 286.99 | 329.4 | - | 139.01 | 36.81 | 0.087 | 0.313 | 0.199 | ||
| 6 | Pokhara Airport | GEV | 0.38 | 8.92 | 14.45 | 0.132 | 99.27 | 411.95 | 0.05 | 170.89 | 33.81 | 0.104 | 0.574 | 4.124 |
| EV I | - | 9.87 | 27.62 | 0.238 | 212.39 | 276.32 | - | 171.13 | 36.1 | 0.111 | 0.584 | 4.118 | ||
| 7 | Walling | GEV | 0.61 | 2.05 | 5.47 | 0.326 | 356.66 | 1804.8 | 0.11 | 126.09 | 33.66 | 0.134 | 0.372 | 0.08 |
| EV I | - | 1.3 | 21.29 | 0.323 | 381.37 | 586.36 | - | 127.57 | 37.86 | 0.129 | 0.388 | 0.873 | ||
| 8 | Khairenitar | GEV | 0.49 | 3.46 | 7.02 | 0.19 | 197.91 | 986.36 | 0.05 | 112.62 | 26.34 | 0.085 | 0.263 | 0.325 |
| EV I | - | 3.56 | 18.35 | 0.297 | 318.15 | 520.36 | - | 113.45 | 27.68 | 0.088 | 0.277 | 0.643 | ||
| SN | Location | DHM (Nr.) | ||||
|---|---|---|---|---|---|---|
| 1 | Lumle | 814 | 31.335 | 20.284 | 21.889 | 0.943 |
| 2 | Karki-Neta | 613 | 20.97 | 7.673 | 4.226 | 0.959 |
| 3 | Bhadaure-Deurali | 813 | 25.857 | 12.961 | 8.428 | 0.988 |
| 4 | Kusma | 614 | 17.91 | 7.125 | 4.38 | 0.98 |
| 5 | Syangja | 805 | 22.599 | 5.589 | 5.125 | 0.865 |
| 6 | Pokhara-Airport | 804 | 27.623 | 9.866 | 8.977 | 0.957 |
| 7 | Walling | 826 | 21.292 | 1.298 | 0.99 | 0.5 |
| 8 | Khairenitar | 815 | 18.354 | 3.564 | 0.988 | 0.472 |
| S. N. | Location | DHM Station Number (Nr.) | Before Calibration | After Calibration | Region | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Standard Error of Prediction (SEP) | Chi-Square Test Statistics (alpha at 0.05 = 12.59) | Standard Error of Prediction (SEP) | Chi-square Test Statistics (alpha at 0.05 = 12.59) | ||||||||
| 1 h | 24 h | 1 h | 24 h | 1 h | 24 h | 1 h | 24 h | ||||
| 1 | Lumle | 814 | 6.59 | 8.22 | 7.55 | 24.36 | 0.10 | 0.00 | 0.00 | 0.00 | N-W hill range |
| 2 | Karki-Neta | 613 | 3.19 | 2.10 | 1.81 | 3.55 | 2.05 | 0.00 | 0.72 | 0.00 | Western part |
| 3 | Bhadaure-Deurali | 813 | 6.10 | 1.95 | 11.47 | 4.00 | 5.70 | 0.56 | 0.17 | 0.05 | Eastern part |
| 4 | Kusma | 614 | 0.77 | 0.28 | 0.14 | 0.09 | 0.29 | 0.00 | 0.02 | 0.00 | Western part |
| 5 | Syangja | 805 | 1.27 | 0.52 | 0.24 | 0.21 | 0.00 | 0.87 | 0.00 | 0.60 | Western part |
| 6 | Pokhara-Airport | 804 | 1.37 | 1.21 | 0.36 | 0.97 | 0.60 | 0.90 | 0.06 | 0.55 | Eastern part |
| 7 | Walling | 826 | 9.27 | 2.21 | 17.41 | 3.05 | 0.87 | 1.10 | 0.19 | 1.02 | Western part |
| 8 | Khairenitar | 815 | 4.98 | 0.44 | 3.96 | 0.14 | 0.64 | 0.63 | 6.55 | 8.77 | Eastern part |
| S. N. | Location | DHM Nr. | Empirical Model |
|---|---|---|---|
| 1 | Khairenitar | 815 | |
| 2 | Pokhara Airport | 804 | |
| 3 | Bhadaure-Deurali | 813 | |
| 4 | Lumle | 814 | |
| 5 | Kusma | 614 | |
| 6 | Karki-neta | 613 | |
| 7 | Syangja | 805 | |
| 8 | Walling | 826 |
| S. N. | Distribution | ZDIST-Statistics/GoF | Remarks | |
|---|---|---|---|---|
| Eastern Region | Western Region | |||
| 1 | Pearson Type III | −0.19 | −1.31 | accept |
| 2 | Gen. Normal | 0.35 | −1.10 | accept |
| 3 | Gaucho | −0.48 | −2.37 | accept/reject |
| 4 | Gen. Extreme Value | 0.61 | −1.12 | accept |
| 5 | Gen. Logistic | 1.6 | 0.11 | accept |
| 6 | Gen. Pareto | −1.66 | −3.67 | reject |
| S. N. | Distribution | Parameters | Region | ||||
|---|---|---|---|---|---|---|---|
| Location () | Scale () | Shape () | |||||
| 1 | Gen. Logistics (GLO) | 0.98 | 0.388 | −0.085 | 0.09 | 0.39 | western |
| 2 | Gen. Extreme Value (GEV) | 0.877 | 0.191 | −0.06126 | 0.51 | 0.40 | eastern |
| S. N. | Location | DHM Station Number (Nr.) | Before Calibration | After Calibration | Region | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Standard Error of Prediction (SEP) | Chi-square Test Statistics (alpha at 0.05 = 12.59) | Standard Error of Prediction (SEP) | Chi-Square Test Statistics (alpha at 0.05 = 12.59) | ||||||||
| 1 h | 24 h | 1 h | 24 h | 1 h | 24 h | 1 h | 24 h | ||||
| 1 | Khairenitar | 815 | 117.6 | 24.8 | 0 | 0 | 8.69 | 1.11 | 0.19 | 0.98 | eastern |
| 2 | Pokhara- Airport | 804 | 1.53 | 0.37 | 0.95 | 0.99 | no adjustment | eastern | |||
| 3 | Bhadaure-Deurali | 813 | 6.1 | 1.95 | 11.47 | 4 | eastern | ||||
| 4 | Lumle | 814 | 37.15 | 17.43 | 0 | 0.01 | 9.34 | 0.11 | 0.16 | 0.99 | eastern |
| 5 | Syangja | 805 | 1.27 | 0.52 | 0.24 | 0.84 | no adjustment | western | |||
| 6 | Kusma | 614 | 1.37 | 1.21 | 0.36 | 0.86 | western | ||||
| 7 | Karki-Neta | 613 | 9.27 | 2.21 | 17.41 | 0.85 | western | ||||
| 8 | Walling | 826 | 37.54 | 8.52 | 0 | 0.20 | 24.60 | 3.60 | 0 | 0.73 | western |
| S. N. | Area (Distribution) | DHM Nr. | Empirical Model | Region/Sub-Region |
|---|---|---|---|---|
| 1 | Khairenitar (GEV) | 815 | eastern-1 | |
| 2 | Pokhara Airport & Bhadaure-Deurali (GEV) | 804/813 | eastern-2 | |
| 3 | Lumle (GEV) | 814 | eastern-3 | |
| 4 | Kusma/Karki-Neta & Syangja (GLO) | 614/613/805 | western-1 | |
| 5 | Walling (GLO) | 826 | western-2 |
| Return Period (Tr in Year) | Duration (td in h) | Region/Sub-Region | |||
|---|---|---|---|---|---|
| 0.5 | 1 | 2 | 24 | ||
| 5 | 31.61 | 26.10 | 20.77 | 7.95 | eastern-1 |
| 25 | 45.48 | 37.56 | 29.88 | 11.44 | |
| 100 | 57.85 | 47.77 | 38.01 | 14.55 | |
| 5 | 28.89 | 24.57 | 20.03 | 8.04 | eastern-2 |
| 25 | 45.40 | 38.60 | 31.47 | 12.63 | |
| 100 | 54.70 | 46.51 | 37.92 | 15.22 | |
| 5 | 43.28 | 36.59 | 29.00 | 8.89 | eastern-3 |
| 25 | 55.90 | 47.25 | 37.45 | 11.48 | |
| 100 | 67.35 | 56.93 | 45.12 | 13.83 | |
| 5 | 32.88 | 25.88 | 20.08 | 7.74 | western-1 |
| 25 | 50.56 | 39.79 | 30.87 | 11.90 | |
| 100 | 66.57 | 52.40 | 40.65 | 15.67 | |
| 5 | 29.74 | 23.41 | 18.40 | 7.72 | western-2 |
| 25 | 47.10 | 37.08 | 29.14 | 12.23 | |
| 100 | 61.62 | 48.51 | 38.13 | 16.01 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Devkota, S.; Shakya, N.M.; Sudmeier-Rieux, K.; Jaboyedoff, M.; Van Westen, C.J.; Mcadoo, B.G.; Adhikari, A. Development of Monsoonal Rainfall Intensity-Duration-Frequency (IDF) Relationship and Empirical Model for Data-Scarce Situations: The Case of the Central-Western Hills (Panchase Region) of Nepal. Hydrology 2018, 5, 27. https://doi.org/10.3390/hydrology5020027
Devkota S, Shakya NM, Sudmeier-Rieux K, Jaboyedoff M, Van Westen CJ, Mcadoo BG, Adhikari A. Development of Monsoonal Rainfall Intensity-Duration-Frequency (IDF) Relationship and Empirical Model for Data-Scarce Situations: The Case of the Central-Western Hills (Panchase Region) of Nepal. Hydrology. 2018; 5(2):27. https://doi.org/10.3390/hydrology5020027
Chicago/Turabian StyleDevkota, Sanjaya, Narendra Man Shakya, Karen Sudmeier-Rieux, Michel Jaboyedoff, Cees J. Van Westen, Brian G. Mcadoo, and Anu Adhikari. 2018. "Development of Monsoonal Rainfall Intensity-Duration-Frequency (IDF) Relationship and Empirical Model for Data-Scarce Situations: The Case of the Central-Western Hills (Panchase Region) of Nepal" Hydrology 5, no. 2: 27. https://doi.org/10.3390/hydrology5020027
APA StyleDevkota, S., Shakya, N. M., Sudmeier-Rieux, K., Jaboyedoff, M., Van Westen, C. J., Mcadoo, B. G., & Adhikari, A. (2018). Development of Monsoonal Rainfall Intensity-Duration-Frequency (IDF) Relationship and Empirical Model for Data-Scarce Situations: The Case of the Central-Western Hills (Panchase Region) of Nepal. Hydrology, 5(2), 27. https://doi.org/10.3390/hydrology5020027






