Next Article in Journal
Groundwater Condition and Management in Kano Region, Northwestern Nigeria
Previous Article in Journal
The Climate Change Vulnerability and Risk Management Matrix for the Coastal Zone of The Gambia
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Hydrology
Volume 5
Issue 1
10.3390/hydrology5010015
hydrology-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Quantifying Processes Governing Nutrient Concentrations in a Coastal Aquifer via Principal Component Analysis

by
Alanna L. Lecher
1,*,
Joseph Murray
2 and
Adina Paytan
3
1
Department of Natural and Applied Science, Lynn University, 2519 N Military Trail, Boca Raton, FL 33431, USA
2
Department of Ocean Sciences, University of California Santa Cruz, 1156 High Street, Santa Cruz, CA 95064, USA
3
Institute of Marine Sciences, University of California Santa Cruz, 1156 High Street, Santa Cruz, CA 95064, USA
*
Author to whom correspondence should be addressed.
Hydrology 2018, 5(1), 15; https://doi.org/10.3390/hydrology5010015
Submission received: 28 December 2017 / Revised: 1 February 2018 / Accepted: 5 February 2018 / Published: 7 February 2018
Browse Figures
Versions Notes

Abstract

:
Submarine groundwater discharge (SGD) is an important source of nutrients to coastal ecosystems. The flux of nutrients associated with SGD is governed by the volumetric discharge of groundwater and the concentrations of nutrients in groundwater within the coastal aquifer. Nutrient concentrations in the coastal aquifer, in turn, are controlled by processes such as mixing, precipitation, adsorption-desorption, the decay of organic material, and nitrogen-fixation/denitrification. In this study, Principal Component Analysis (PCA) was applied to groundwater and ocean water nutrient concentration data from Monterey Bay, California, to identify and rank processes controlling coastal aquifer nutrient concentrations. Mixing with seawater, denitrification, the decay of organic matter, and desorption of phosphate were determined to be the three most important processes accounting for 39%, 19%, 14%, and 12% of the variability, respectively. This study shows how PCA can be applied to SGD studies to quantify the relative contribution of different processes controlling nutrient concentrations in coastal aquifers.

1. Introduction

Submarine groundwater discharge (SGD) occurs along the coastline and the continental shelf in every ocean basin and is a major source of nutrients to the coastal ocean [1,2,3]. Best estimates suggest that SGD water input to the ocean is equivalent to 60–400% of riverine water flux [1,4]. Nutrients transported to the ocean through SGD have been shown to affect marine biota, specifically the abundance and productivity of phytoplankton, macro-algae, and seagrasses, which have implications for organisms in higher trophic levels [5,6,7,8,9]. SGD is comprised of fresh groundwater, seawater that has circulated through the coastal aquifer, or a mixture of both water types [10,11,12]. When fresh groundwater and circulating sea water mix in the coastal aquifer, several processes can occur that increase or decrease the concentration of nutrients in the groundwater [13,14]. Therefore, nutrient fluxes to the coastal ocean including nitrate (NO3), ammonium (NH4), phosphate (PO4), and silicate (SiO4), can be modulated by these processes. Quantifying the relative contribution of each of the governing processes within the coastal aquifer is required to ensure accurate extrapolation of SGD-related solute fluxes regionally and globally [13]. Recent attempts to upscale SGD fluxes have excluded the associated solute (nutrients, gases, carbon, etc.) fluxes, due to the difficulty of constraining their concentrations in the coastal aquifer [1,4]. As the scientific community moves toward regional and global SGD flux estimates and SGD-associated solute fluxes to the ocean, quantitative methods are needed to constrain processes that regulate solute concentrations in the coastal aquifer across regional scales [13].
Nutrient concentrations in coastal aquifers are modulated by conservative mixing, oxidation of ammonium, nitrification/denitrification of nitrate, adsorption, desorption, precipitation and other processes (Table 1); [10,12]. These processes have been qualitatively described at small spatial scales [14,15,16,17]. However, quantification of these processes within a coastal aquifer has not previously been achieved, especially at the regional scales where it is most needed for assessing solute fluxes to the coastal ocean and predicting how such fluxes might change with climate change and other environmental perturbations. SGD water volume fluxes have been calculated at the basin scale in the North Atlantic [4], Northwestern Pacific [18], Mediterranean Sea [19], and globally [1,20] but associated solute fluxes cannot be determined at the basin scale until a better understanding and more quantitative description of the processes that govern solute concentrations at larger scales is achieved.
Principal component analysis (PCA) has been previously used to quantify processes that govern groundwater quality, including at the regional scale [21,22,23,24,25,26,27]. PCA is an exploratory statistical technique that can be used to identify and rank factors contributing to the variance in datasets [28]. Previous PCA-based groundwater studies have been largely confined to systems where flow rates are low and processes other than conservative mixing regulate concentrations of groundwater solutes. Coastal aquifers often have high flow rates and nutrient concentrations can be heavily modulated by mixing with seawater [10,11,12]. Here, conservative mixing and other processes in the coastal aquifer of Monterey Bay, CA, an area where SGD was identified as an important nutrient source to the coastal ocean [6,29], are quantified. Data collected at four different locations along the coast of Monterey Bay were analyzed via PCA to provide an overall view of the relative importance of processes in the coastal aquifer that may affect the nutrient loads associated with SGD in the region.

2. Materials and Methods

2.1. Study Approach

The goal of this study was to identify and rank processes in the coastal aquifer at spatial scales larger than a single beach. Hence, the study encompassed data collected at four beaches (coastal aquifers) and from two coastal wells located in the alluvial and Aromas Sand aquifers (Figure 1). The study area is bordered on the north by the Santa Cruz Mountains and the hilly San Andreas Fault to the east, with a mix of hills and coastal plains underlying most of the study area. The Aromas Sand aquifer underlies most of the land in the study area and consists of the upper Aromas Sand (confined) and lower Aromas Sand (confined), with the alluvial aquifer topping the Aromas Sand (unconfined) [30]. Both the Aromas Sand and alluvial aquifers consist of coarse-grained marine and terrestrial deposits and are separated by fine-grained deposits that act as aquitards [30]. The coarse-grained deposits combined with over-pumping allowed for extensive seawater intrusion into all layers of the aquifers at the coast [30]. The alluvial aquifer is generally above sea level, with the upper Aromas Sand intersecting sea level, and the lower Aromas Sand occurring mostly below sea level [30]. Recharge to all aquifers consists of deep percolation of infiltration and infiltration from stream flow, with high nitrate concentrations in streamflow contributing to high nitrate concentrations in the aquifer [30]. The dominant land-use in the area is year-round agriculture [30].
The intermediary coastal aquifer is limited to the beach (generally <30 m wide) that encircles the bay, and is an unconfined system of mostly quartz sand with groundwater ranging from saline to fresh, with salinity largely controlled by tides [29]. A previous study showed nitrate, silicate, and phosphate concentrations in the coastal aquifer range from seawater concentrations up to 400 µM, 500 µM, and 10 µM respectively [29]. The source of silicate to the coastal aquifer was determined to be dissolution of aquifer substrate while the sources of nitrate and phosphate were undetermined [29]. SGD flux from the coastal aquifer was determined to be an important source of nutrients to the coastal waters throughout the year, but especially during the late summer/early fall (dry season) when other sources of nutrients to the bay, river discharge and upwelling, were limited [6,29]. SGD fluxes were similar year-round and modulated by tides and wave ramp-up [6,29].
Samples were analyzed for several water quality parameters that can be indicative of processes occurring within the coastal aquifer, namely salinity, nitrate (NO3), silicate (SiO4), ammonium (NH4), soluble reactive phosphate (PO4), δ15NNO3, and δ18ONO3. The data from these samples were first analyzed using more commonly used statistical methods (including averaging, boxplots, and regressions) to illuminate processes occurring in the coastal aquifer outlined in Table 1. The data were then analyzed via PCA to determine the relative contribution of each of these processes (i.e., determine what percentage each process contributed to the variance of the data). The analysis integrated data from both the dry and wet seasons, which in turn gave an average contribution of each process integrated over the course of a year. A previous study found salinity and some nutrient concentrations to be largely influenced by tides and wave-ramp up, which do not vary significantly throughout the year [29]. Therefore, processes within the coastal aquifer were not expected to vary throughout the year either [29]. This is further supported by similar nutrient concentrations and regressions of salinity and nutrient concentrations across the wet and dry seasons in the coastal aquifer [29].

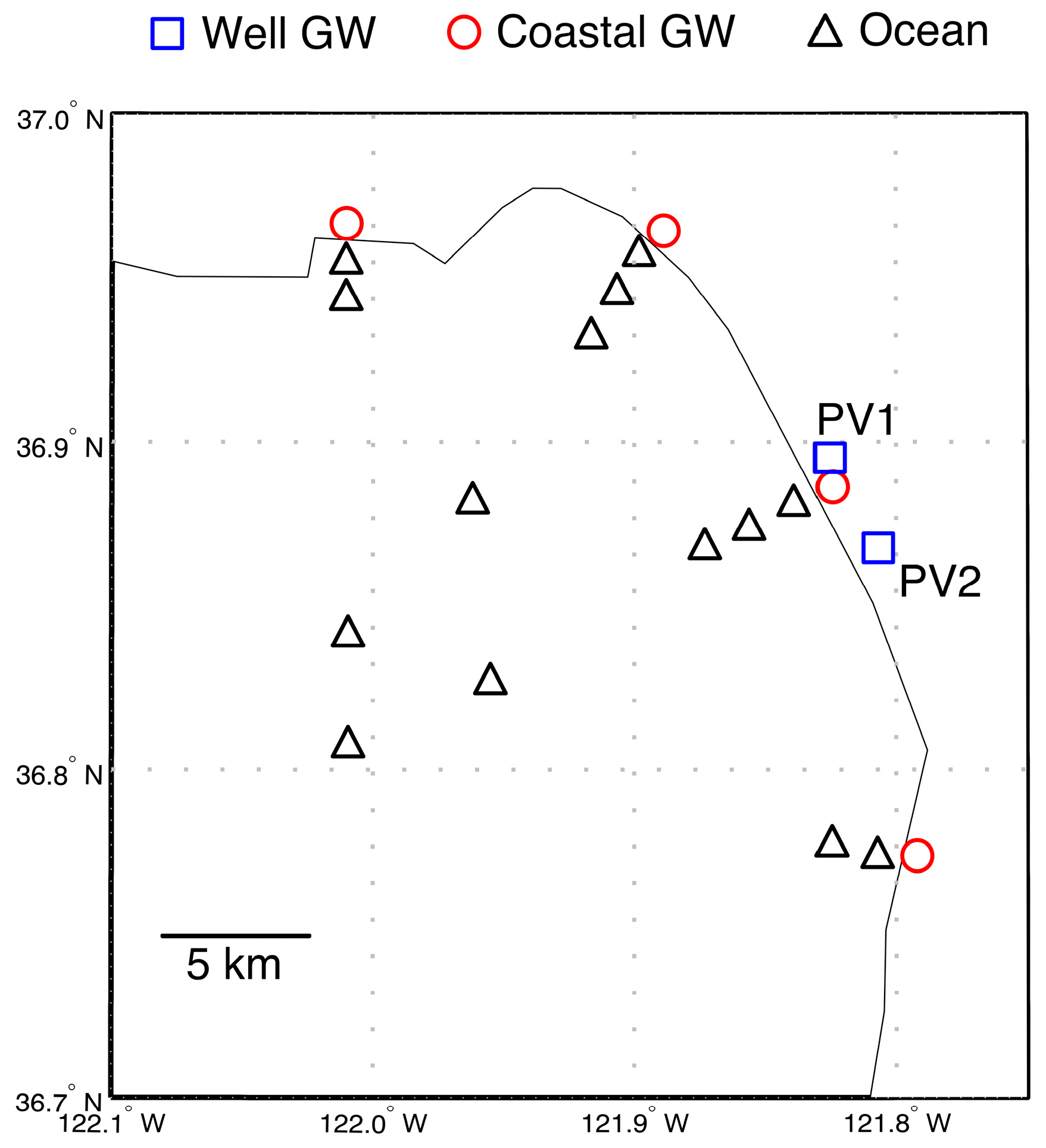
2.2. Sample Collection

Samples were collected in June 2012 (end of wet season), October 2012 (end of dry season), and February 2014 (mid-wet season). The samples from June 2012 and October 2012 represent a subset of samples from previous studies that reported on the fluxes, impacts, and regional distribution of SGD in the bay, although new analyses were performed, namely δ15NNO3 and δ18ONO3 and PCA [6,29]. In all, the water quality data collected included salinity, nitrate, silicate, ammonium, soluble reactive phosphate, δ15NNO3, and δ18ONO3. Samples collected in Monterey Bay (Figure 1) consisted of groundwater retrieved from established monitoring wells (hereafter referred to as well groundwater, which represents the terrestrial end-member), groundwater collected from the beach face (hereafter referred to as coastal groundwater and intermediary water), and ocean water collected from Monterey Bay (the oceanic end-member). The monitoring wells PV1 and PV3 were screened in the upper and lower Aromas Sand aquifer (brackish) and alluvium (fresh) aquifer [6,30]. The alluvial aquifer was generally above sea level, the upper Aromas Sand aquifer generally coincided with sea level, and the lower Aromas Sand aquifer was below sea level [30]. These wells were chosen due to their location close to the ocean (within 0.5 km of the shore), and we assumed that they are representative of close to shore groundwater in the region. Coastal aquifer groundwater samples were collected at sea level at the beach face from multiple screened temporary PVC well points of a depth of <2 m at 4 locations using submersible pumps (Figure 1). At each sampling location, 4–6 PVC well points were installed in a transect leading from the shoreline at regular intervals (~2 m long) towards the back of the beach. As the PVC well points were screened the full length of the well point, the coastal groundwater samples represent an integration across the full saturated zone that intersected with the well points. Coastal groundwater sampling was limited by depth to water, as locations where the water table was deeper than 2 m could not be sampled due to the length of the well points. Ocean water samples were collected from Monterey Bay either by wading or using a small boat from a depth of <1 m representing conditions above the thermocline in the mixed layer (Figure 1) [29].

2.3. Analytical Methods

Water was collected for nutrient concentration analysis in 500 mL HDPE acid-cleaned bottles and stored on ice in a cooler until filtering at the end of the day. Aliquots (40 mL) were filtered (0.45 μm) into acid-cleaned centrifuge tubes and frozen until analysis. Nitrate, silicate, ammonium, and soluble reactive phosphate were measured by colorimetric methods on a Flow Injection Auto Analyzer (FIA, Lachat Instruments Model QuickChem 8000) [31]. Salinity was measured with a YSI hand-held Pro 30 probe.
An additional 250 mL of water was filtered for stable nitrogen and oxygen isotopic composition of dissolved nitrate (δ15NNO3, δ18ONO3) and stored frozen until analysis. δ15NNO3 and δ18ONO3 were prepared using the azide reduction method [32,33] and were measured on a modified Thermo Finnigan GasBench II and Delta-Plus XP mass spectrometer. International nitrate isotopic standards USGS 34 (δ15N = −1.8‰, δ18O = −27.9‰), USGS 35 (δ15N = +2.7‰, δ18O = +57.5‰) and IAEA-N3 (δ15N = +4.7‰, δ18O = +25.6‰) were analyzed to correct for blanks, drift, and oxygen isotopic exchange. δ15NNO3 values are referenced against air N2 and δ18ONO3 values are referenced against Vienna Standard Mean Ocean Water (VSMOW). Analytical precision (1σ) was generally better than 0.3‰ for δ15NNO3 and 0.6‰ for δ18ONO3. Only samples with nitrate concentrations > 1 μM and nitrite concentrations < 5% of the total NOx pool (nitrate + nitrite) were analyzed to avoid nitrite interference.

2.4. Statistical Analyses

Statistical differences between water types (well groundwater, coastal groundwater, and ocean water) were determined via ANOVA and Tukey-Kramer (p < 0.05). To determine the relative contribution of different processes affecting nutrient concentrations, salinity, δ15NNO3, and δ18ONO3 of well groundwater, coastal groundwater, and ocean water, a Euclidian distance-based PCA was used. Only samples for which all data were collected (the greatest limiting factor was δ15NNO3 and δ18ONO3 analysis as nitrate concentrations of some samples were below the detection limit or error was large) were included in the analyses. In all, with this limitation, the data include 29 ocean samples, 41 coastal groundwater samples, and 9 well groundwater samples.

3. Results

Boxplots of salinity (A), nitrate (B), ammonium (C), silicate (D), phosphate (E), δ15NNO3 (F), and δ18ONO3 (G) for each sample type: well groundwater (right box in each panel), coastal groundwater (middle box in each panel), and ocean water (left box in each panel) are shown in Figure 2. Parameters that decreased in concentration from well groundwater to ocean water included nitrate (from 200 ± 70 μM to 10 ± 1 μM) and silicate (390 ± 30 μM to 13 ± 2 μM). Only silicate concentrations when considering all water types were statistically different from each other. Both groundwater types were statically higher in nitrate concentration than ocean water but were not different from each other. Salinity, δ15NNO3, and δ18ONO3 increased from well water to ocean water (from 13 ± 4 to 33.0 ± 0.1, from 5.6 ± 0.2 ‰ to 10.2 ± 0.4 ‰, and from 0.0 ± 0.4 ‰ to 10.7 ± 0.8 ‰, respectively). Each water type was statistically different from the others with respect to δ18ONO3. However, the only statistical difference with respect to δ15NNO3 was that well groundwater had lower δ15NNO3 than the other two water types. Ocean water salinity was statistically higher than both groundwater types. Phosphate and ammonium were highest in the coastal groundwater (6.8 ± 1.7 μM and 4.4 ± 0.9 μM), and lower in the well groundwater (2.0 ± 0.4 μM and 0.6 ± 0.3 μM) and ocean water (0.9 ± 0.1 μM and 3.6 ± 0.7 μM). For phosphate concentrations, coastal groundwater was statistically different from ocean water, and neither ocean water nor coastal groundwater was different from the well groundwater. No sample types were statistically different for ammonium.
Silicate concentrations were considered to be conservative in these analyses because of the distinct differences between the terrestrial (silicate = 390 ± 30 μM) and oceanic (silicate = 13 ± 2 μM) end members and the limited reactivity of silicate in groundwater. Conservative mixing behavior of silicate in similar settings has been observed previously [34]. At this location, silicate displays a more conservative behavior than salinity because seawater intrusion resulted in well groundwater with high salinity. To determine if the other parameters were mixed conservatively, each parameter was plotted against silicate in Figure 3, and linear correlations were fitted. There were no strong linear correlations (R2 < 0.25) with silicate concentration for any of the parameters examined here. While not exhibiting simple mixing between the end members (e.g., a linear trend), nitrate concentrations increased with increasing silicate concentrations, and δ18ONO3 decreased with increasing silicate concentrations. Ammonium and phosphate concentrations and δ15NNO3 were highest in the mid-range (20–200 μM) of silicate concentrations.
Ammonium, δ18ONO3, and δ15NNO3 plotted against nitrate concentration are shown in Figure 4A–C. Ammonium concentrations, δ18ONO3, and δ15NNO3 increased as nitrate concentration decreased. Ocean water data clustered in the low nitrate and high ammonium/δ18ONO3/δ15NNO3 portion of the graph, and well groundwater data clustered in the high nitrate and low ammonium/δ18ONO3/δ15NNO3 area. Coastal groundwater data displayed the most variation, encompassing both these end-members and the area in between. Also shown in Figure 4D is δ15NNO3 plotted against δ18ONO3. In Figure 4D, well groundwater and ocean water data are distinct, particularly with respect to δ18ONO3. Coastal groundwater exhibited more variation with much of the data plotting either between ocean water and well groundwater data or along a near 2 δ15NNO3:1 δ18ONO3 trend (~0.5 slope), a trend typical of denitrification in groundwater.
Figure 5 shows the results of the PCA. Components 1, 2, 3, and 4 accounted for 39%, 19%, 14%, and 12%, of the variability respectively. The length of the vectors with respect to each component represent the relative contribution of that parameter (nutrient concentrations, salinity, δ15NNO3, or δ18ONO3) to that component. That is, the longer the vector with respect to a given component, the more that parameter (nitrate concentrations, salinity, etc.) correlated with or contributed to that component. Vectors that extend similarly (e.g., the same direction and length) indicate those parameters correlated with each other. Nitrate and silicate concentrations correlated with component 1 and with each other, indicating that as one of these parameters increased so did the other. Conversely, δ15NNO3, δ18ONO3, and salinity negatively correlated with component 1. This indicates as nitrate and silicate increased δ15NNO3, δ18ONO3, and salinity decreased. Ocean water samples clustered at the most negative portion of component 1, while well groundwater clustered in the most positive portion of component 1. Coastal groundwater fell between well groundwater and ocean water.
δ15NNO3 correlated most strongly with component 2. Well groundwater clustered at the negative end of component 2, and coastal groundwater had the most variance, reaching from the most negative to most positive data along this component. Ocean water data clustered around 0, indicating there was less variation in ocean water with respect to this component compared to well and coastal groundwater. Ammonium strongly correlated with component 3 while phosphate correlated to a lesser degree. Component 3 was most influenced by coastal groundwater as these data extend the full length of component 3. Ocean water and well groundwater cluster near 0, indicating those data had little influence on component 3. Phosphate correlated most strongly with component 4.

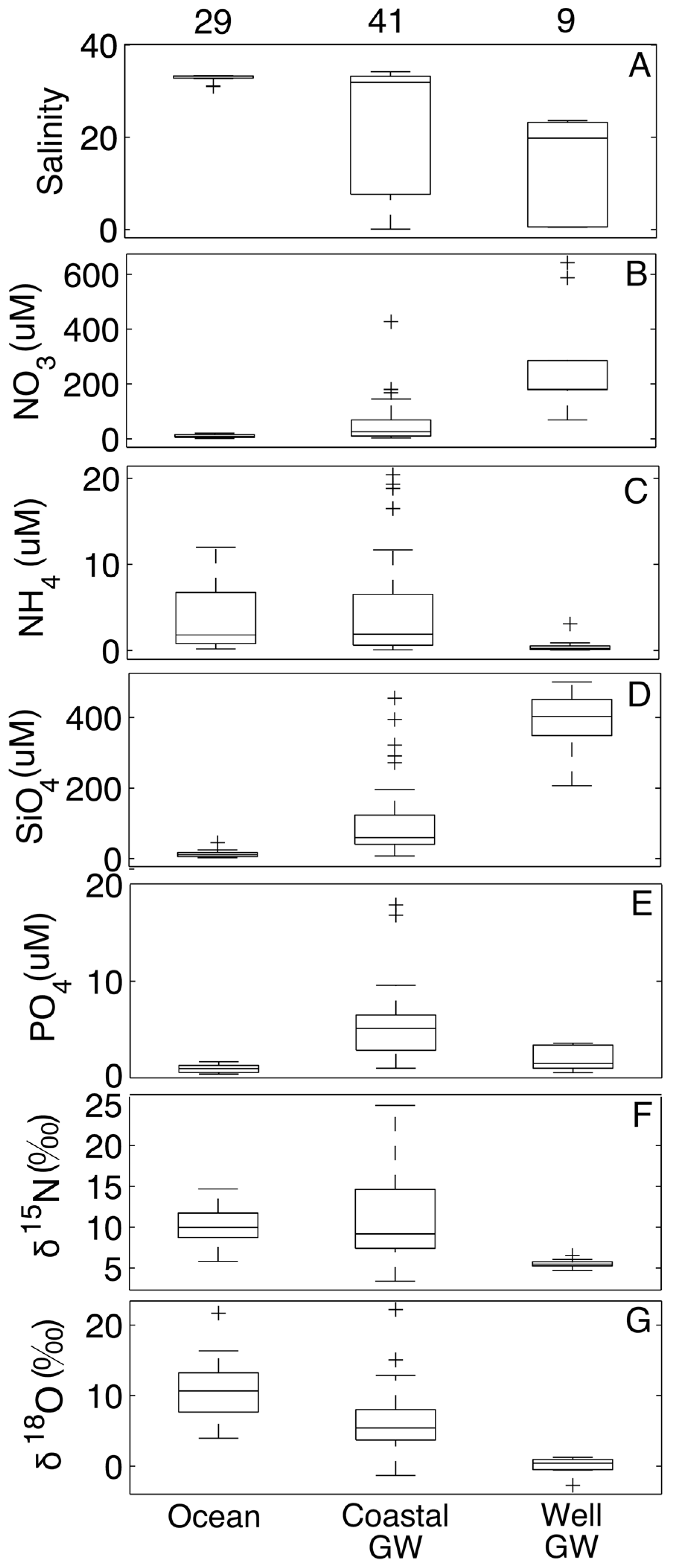
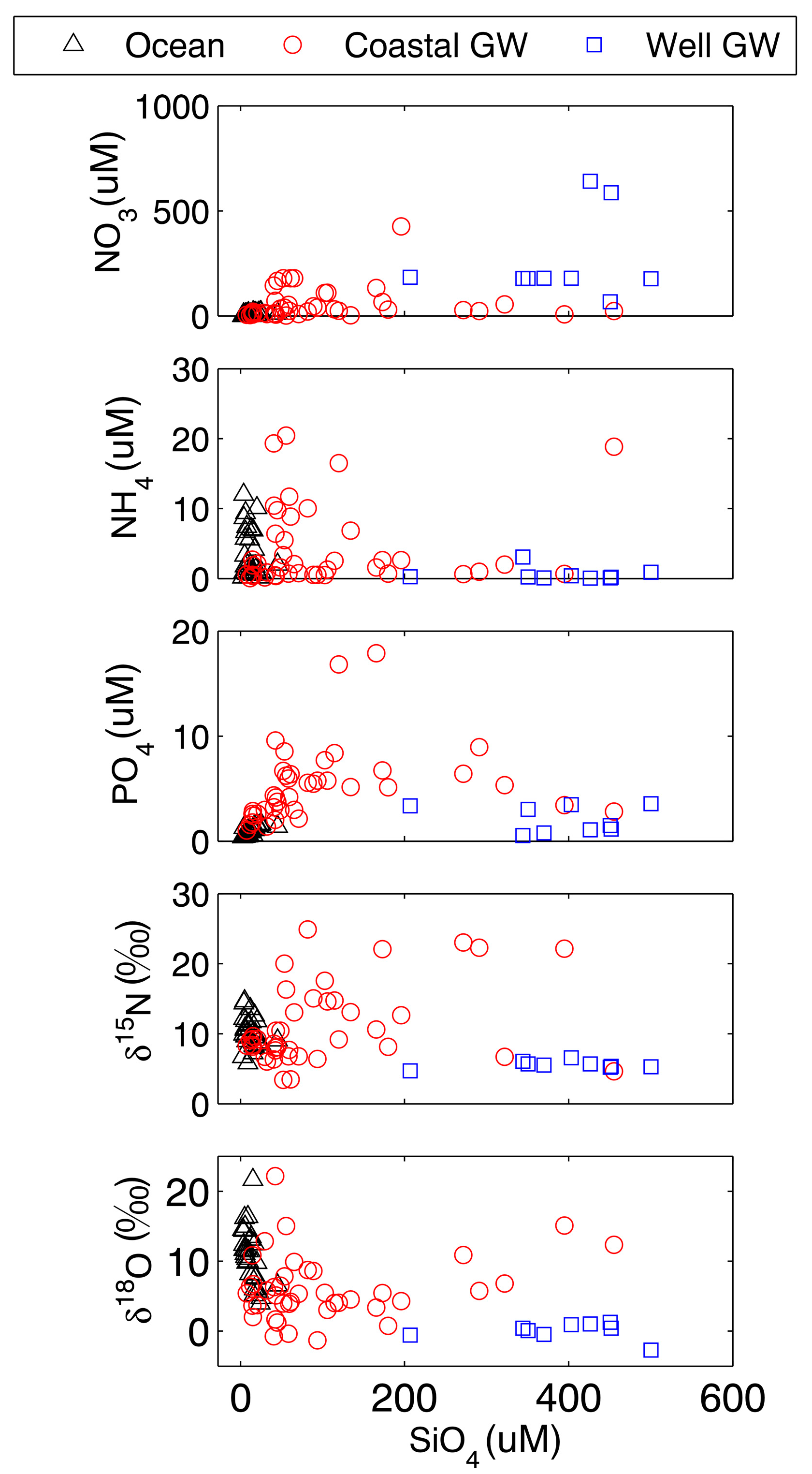
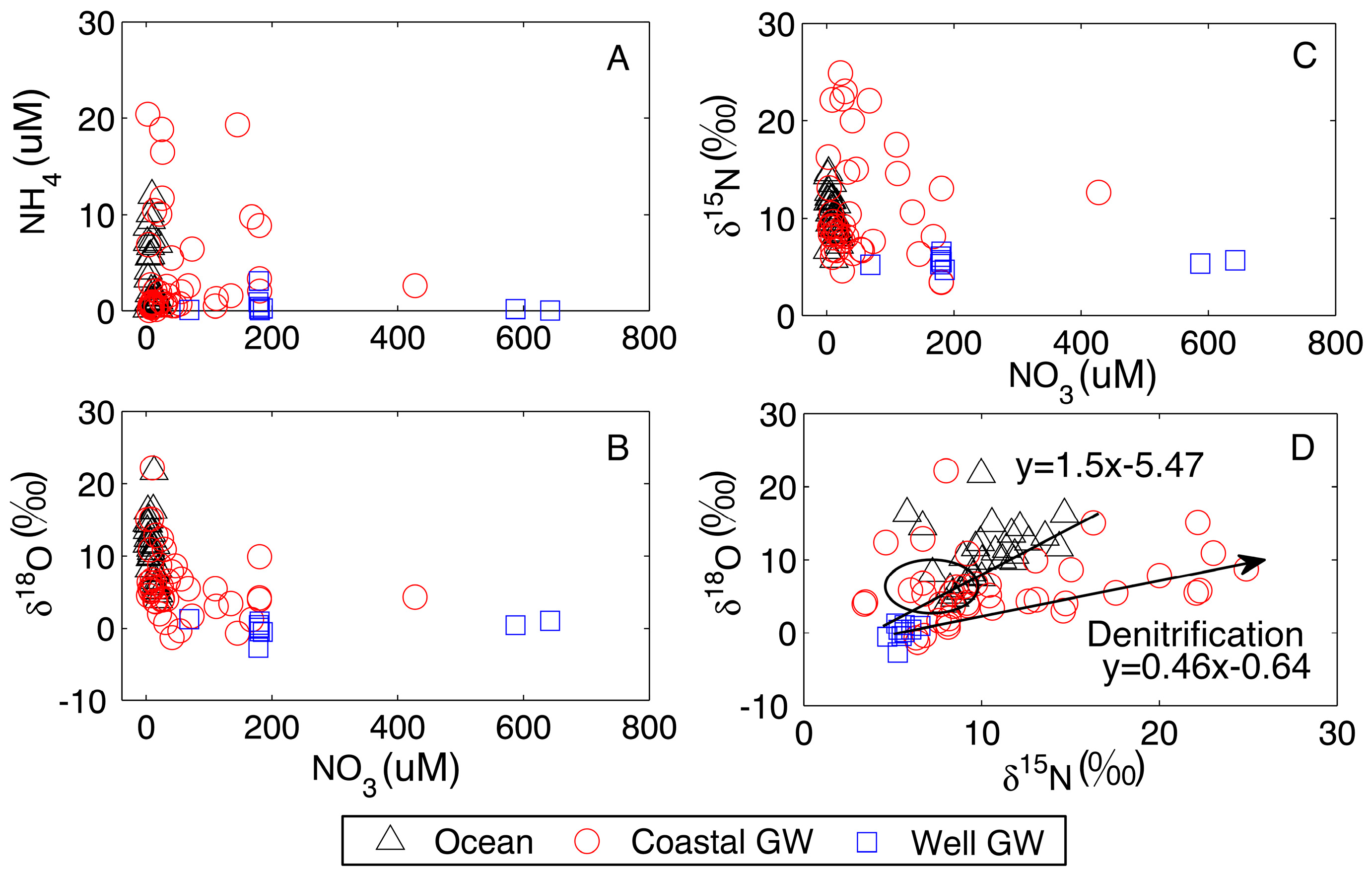
4. Discussion

4.1. Processes Observed in the Coastal Aquifer

Several processes controlling solute concentrations and isotopic values of nitrate appeared to be occurring in the coastal aquifer of Monterey Bay. One of these processes was mixing of well groundwater water high in concentrations of nitrate and silicate and with low values of δ18ONO3 and δ15NNO3 with ocean water with low concentrations of nitrate and silicate and high values of δ18ONO3 and δ15NNO3. This is consistent with the observation that the well groundwater and ocean water data were statistically different for all these parameters. The high silicate concentrations in the well groundwater were due to the dissolution of aquifer substrate, while the high nitrate concentrations and low δ18ONO3 and δ15NNO3 values were consistent with nitrate input from agricultural fertilizer use in the basin (Figure 2). However, a lack of a linear trend with a strong correlation between silicate and nitrate concentrations in Figure 3 suggested that additional processes affected the concentration of nitrate in the coastal groundwater.
In the groundwater (both well and coastal), some samples showed increasing δ15NNO3 with decreasing nitrate concentrations. This is indicative of a process that consumes nitrate resulting in isotopic fractionation that enriches the nitrate residue with heavy isotopes. Indeed, this signal was apparent in the δ18ONO3 data as well (Figure 4B). Specifically, a general trend of increasing δ15NNO3 with increasing δ18ONO3 was apparent for all data (Figure 4D), although with two distinct relationships. Some coastal groundwater data plotted between the well groundwater data and ocean data on a slope of 1.5. This slope of 1.5 could be indicative of mixing, although other processes such as nitrification can also result in a similar distribution. This trend was not indicative of denitrification in seawater as denitrification in seawater is represented by a slope of 1 [36], and the seawater at this location is well oxygenated. Another trend on the same plot, overlain by much of the coastal groundwater data and well groundwater data, exhibited a slope of ~0.5. The ~0.5 slope was indicative of denitrification in groundwater [37]. δ15NNO3 and δ18ONO3 in this study were more heterogeneous than those reported in a previous study of Monterey Bay seawater (Figure 4D), but that study was conducted offshore where the direct impact of coastal groundwater discharge is less prominent and isotopes therein are more homogeneous [35].
Ammonium concentrations are likewise affected by multiple processes. Ammonium concentrations increased with decreasing silicate concentrations (e.g., indicative of mixing between high silica/low ammonium groundwater with low silica/higher ammonium ocean water). However, the highest ammonium concentrations were in coastal groundwater (Figure 4A), suggesting a local source within the coastal aquifer. The decay of organic material (Table 1) increases ammonium concentrations and could have caused the high ammonium concentrations in the coastal aquifer. Similarly, dissimilatory nitrate reduction to ammonium (DNRA), also known as nitrate/nitrite ammonification, attributed to anaerobic respiration by chemoorganoheterotrophic microbes using nitrate as an electron acceptor for respiration can increase ammonium levels in the anoxic portions of the coastal aquifer.
Like ammonium, the highest concentrations of phosphate were present in coastal groundwater. Salinization of an aquifer can cause an increase in phosphate concentrations [13]. This is due to the increased concentrations of ions in the groundwater causing phosphate to desorb from the aquifer substrate. Reduction of iron oxides also increases phosphate concentrations without impacting ammonium concentrations. It is possible that decay of organic material caused the high phosphate concentrations as well as the high ammonium concentrations [13]. A mixture of salinization, reduction of iron oxides, and organic material decay could also account for the high phosphate and ammonium concentrations, processes that can be elucidated by PCA.

4.2. Principal Component Analysis

Once the processes were identified they could be ranked: their relative importance in controlling nutrient concentrations in the coastal aquifer determined. This was achieved by determining which of the PCA components were indicative of each process, the processes being mixing, denitrification, salinization increasing desorption of phosphate or reduction of iron oxides, and organic matter decomposition (aerobic and anaerobic). Component 1 accounted for 39% of the variance in the data and was consistent with characteristics of mixing observed in Figure 2 and described in Table 1. Well groundwater was highest in nitrate and silicate concentrations, while ocean water was the lowest. Conversely, ocean water was highest in salinity and well groundwater was lowest. Indeed the nitrate and silicate vectors correlated with component 1 in the PCA (Figure 5). Also, they were located near the well groundwater data and opposite the salinity vector and ocean water data with respect to component 1. Thus, mixing accounted for 39% of the variance in the nutrient data.
Component 2 accounted for 19% of the variance in the data and was consistent with denitrification. δ15NNO3 positively correlated with component 2 (Figure 5, Table 1). Higher δ15NNO3 values were associated with denitrification (Figure 4D). As with δ15NNO3, δ18ONO3 increased with denitrification, although the shift in δ18ONO3 is only half that of δ15NNO3 due to the 2 δ15NNO3:1 δ18ONO3 shift denitrification typically induces in groundwater. In the PCA, δ18ONO3 also correlated with component 2, although only half as much as δ15NNO3. This manifests on the plot as the δ18ONO3 coefficient vector only extending half as long along component 2 as the δ15NNO3 coefficient vector. Furthermore, nitrate concentrations decreased as denitrification progressed (Figure 4B,C), and the nitrate concentrations negatively correlated with δ15NNO3 (opposite the δ15NNO3 vector). Thus, denitrification accounted for 19% of the data variation in the coastal aquifer.
Component 3 accounted for 14% of the variance in the data and was most consistent with organic matter decomposition (Table 1). Ammonium correlated strongly with component 3. Phosphate correlated with component 3, but not as strongly as ammonium. Both nutrients increase in concentration when organic matter is oxidized, especially ammonium, which was the longer of the two coefficient vectors with respect to component 3. Coastal groundwater had the most variance with respect to component 3, indicating that rates of organic matter decomposition in the coastal aquifer vary spatially as they would depend on specific conditions such as whether the aquifer is oxic or anoxic and the concentration of nitrate and organic matter. Thus, we hypothesized organic matter decomposition accounted for 14% of the data variation in the coastal aquifer. We surmise organic matter decomposition accounted for component 3 as the data best fit the presence of this process, but more data on whether reducing conditions in the aquifer are needed to confirm this hypothesis.
Component 4 accounted for 12% of the variability and was most consistent with reductions of iron oxides or desorption due to salinization, which would increase phosphate concentrations, but not ammonium (Table 1). Phosphate strongly correlated with component 4 (Figure 5), and these processes are differentiated from organic matter oxidation as phosphate increases via this mechanism but not ammonium, which was not strongly correlated with component 4. Additionally, phosphate concentrations were highest in coastal groundwater (Figure 2), thus excluding mixing as an explanation for the high phosphate concentrations in the coastal aquifer. Therefore, we hypothesized reduction of iron oxides or desorption due to salinization accounted for 12% of the data variability in the coastal aquifer. Confirming which of these processes is represented by component 4 would require data on dissolved iron concentrations or adsorption of phosphate to mineral/organic surfaces, which are unavailable. Therefore, further study is needed to confirm this hypothesis. As the PCA incorporates data from several sites, the percentages here show the relative importance of processes on a regional scale, where conditions (oxic or anoxic) could differ between the sites.

4.3. Conclusions

The PCA revealed both the processes governing nutrient concentrations in the coastal aquifer (mixing, denitrification, organic matter oxidation, and desorption of phosphate) and their relative importance (39%, 19%, 14% and 12%, respectively). Mixing was the most important factor in governing the nutrient concentrations in this case study, and this is often observed to be the case in coastal aquifers [12,38]. However, as apparent in Figure 3, which showed low R2 values for the correlations with silicate, the most conservative solute, indicated other processes were also contributing to the variability within the aquifer. Denitrification was observed as indicated in Figure 4D, although only encompassing some coastal groundwater samples, and the PCA showed only 19% of the variability could be attributed to denitrification, approximately half that of mixing. The last two processes suggested by the PCA, organic matter decomposition and phosphate desorption (due to salinization or Fe-Mn oxides reduction), contributed only 14% and 12% in this system. Without the PCA, these processes would not have been identified, because the only indication of their presence was higher concentrations in the coastal groundwater than ocean or well groundwater in Figure 2 and Figure 3 for ammonium. Indeed, in a previous study, the governing processes of phosphate in the coastal aquifer of this area could only be speculated [29].
This type of analysis is limited to sites where accurate end-member data can be acquired, and enough data from the coastal aquifer exist to fully encompass heterogeneity within the aquifer. Benefits of this analysis beyond more common methods (simple regression, bar plots, etc.) lie in that minor contributing processes (such as organic matter decomposition and phosphate desorption) can be identified, and that the relative importance of all process can be quantified. Although in this study the scope was limited to understanding the processes controlling nutrient concentrations, PCA could be adapted to study other solutes within the coastal aquifer including gasses and metals.

Acknowledgments

This project was funded by the California Sea Grant award 035-CONT-N to A.P. We would like to thank all the undergraduate, graduate students, and post-doctoral researchers who assisted in sampling and Katherine Roberts, who assisted in sample analysis. Additionally, we would like to thank the Pajaro Valley Water Management District for allowing us access to their monitoring wells.

Author Contributions

Lecher and Paytan conceived and designed the experiments; Lecher and Murray performed the experiments; Lecher, Murray and Paytan analyzed the data; Paytan contributed reagents/materials/analysis tools; Lecher wrote the paper; Paytan and Murray edited and revised the paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Kwon, E.; Kim, G.; Primeau, F.; Moore, W.; Cho, H.-M.; DeVries, T.; Sarmiento, J.; Charette, M.; Cho, Y.-K. Global Estimate of Submarine Groundwater Discharge Based on an Observationally Constrained Radium Isotope Model. Geophys. Res. Lett. 2014, 62–68. [Google Scholar] [CrossRef]
  2. Lecher, A.L. Groundwater Discharge in the Arctic: A Review of Studies and Implications for Biogeochemistry. Hydrology 2017, 4, 41. [Google Scholar] [CrossRef]
  3. Taniguchi, M.; Burnett, W.C.; Cable, J.E.; Turner, J.V. Investigation of submarine groundwater discharge. Hydrol. Process. 2002, 16, 2115–2129. [Google Scholar] [CrossRef]
  4. Moore, W.S.; Sarmiento, J.L.; Key, R.M. Submarine groundwater discharge revealed by 228Ra distribution in the upper Atlantic Ocean. Nat. Geosci. 2008, 1, 309–311. [Google Scholar] [CrossRef]
  5. Hosono, T.; Ono, M.; Burnett, W.C.; Tokunaga, T.; Taniguchi, M.; Akimichi, T. Spatial distribution of submarine groundwater discharge and associated nutrients within a local coastal area. Environ. Sci. Technol. 2012, 46, 5319–5326. [Google Scholar] [CrossRef] [PubMed]
  6. Lecher, A.L.; Mackey, K.R.M.; Kudela, R.; Ryan, J.; Fisher, A.; Murray, J.; Paytan, A. Nutrient Loading through Submarine Groundwater Discharge and Phytoplankton Growth in Monterey Bay, CA. Environ. Sci. Technol. 2015, 49, 6665–6673. [Google Scholar] [CrossRef] [PubMed]
  7. Valiela, I.; Foreman, K.; LaMontagne, M.; Hersh, D.; Costa, J.; Peckol, P.; DeMeo-Andreson, B.; D’Avanzo, C.; Babione, M.; Sham, C.-H.; et al. Couplings of Watersheds and Coastal Waters: Sources and Consequences of Nutrient Enrichment in Waquoit Bay, Massachusetts. Estuaries 1992, 15, 443. [Google Scholar] [CrossRef]
  8. Carruthers, T.J.B.; Van Tussenbroek, B.I.; Dennison, W.C. Influence of submarine springs and wastewater on nutrient dynamics of Caribbean seagrass meadows. Estuar. Coast. Shelf Sci. 2005, 64, 191–199. [Google Scholar] [CrossRef]
  9. Lecher, A.L.; Mackey, K.R.M.; Paytan, A. River and submarine groundwater discharge effects on diatom phytoplankton abundance in the Gulf of Alaska. Hydrology 2017, 4, 61. [Google Scholar] [CrossRef]
  10. Knee, K.; Paytan, A. 4.08 Submarine Groundwater Discharge: A Source of Nutrients, Metals, and Pollutants to the Coastal Ocean. Treatise Estuar. Coast. Sci. 2011, 4, 205–234. [Google Scholar] [CrossRef]
  11. Moore, W.S. The subterranean estuary: A reaction zone of ground water and sea water. Mar. Chem. 1999, 65, 111–125. [Google Scholar] [CrossRef]
  12. Lecher, A.L.; Chien, C.; Paytan, A. Submarine groundwater discharge as a source of nutrients to the North Pacific and Arctic coastal ocean. Mar. Chem. 2016, 186, 167–177. [Google Scholar] [CrossRef]
  13. Slomp, C.P.; Van Cappellen, P. Nutrient inputs to the coastal ocean through submarine groundwater discharge: Controls and potential impact. J. Hydrol. 2004, 295, 64–86. [Google Scholar] [CrossRef]
  14. Erler, D.V.; Santos, I.R.; Zhang, Y.; Tait, D.R.; Befus, K.M.; Hidden, A.; Li, L.; Eyre, B.D. Nitrogen transformations within a tropical subterranean estuary. Mar. Chem. 2014, 164, 38–47. [Google Scholar] [CrossRef]
  15. Kroeger, K.D.; Charette, M.A. Nitrogen biogeochemistry of submarine groundwater discharge. Limnol. Oceanogr. 2008, 53, 1025–1039. [Google Scholar] [CrossRef]
  16. Charette, M.A.; Sholkovitz, E.R. Trace element cycling in a subterranean estuary: Part 2. Geochemistry of the pore water. Geochim. Cosmochim. Acta 2006, 70, 811–826. [Google Scholar] [CrossRef]
  17. Charette, M.A.; Sholkovitz, E.R.; Hansel, C.M. Trace element cycling in a subterranean estuary: Part 1. Geochemistry of the permeable sediments. Geochim. Cosmochim. Acta 2005, 69, 2095–2109. [Google Scholar] [CrossRef]
  18. Kim, J.; Cho, H.-M.; Kim, G. 228Ra flux in the northwestern Pacific marginal seas: Implications for disproportionally large submarine groundwater discharge. Ocean Sci. J. 2015, 50, 195–202. [Google Scholar] [CrossRef]
  19. Rodellas, V.; Garcia-Orellana, J.; Masqué, P.; Feldman, M.; Weinstein, Y. Submarine groundwater discharge as a major source of nutrients to the Mediterranean Sea. Proc. Natl. Acad. Sci. USA 2015, 112, 3926–3930. [Google Scholar] [CrossRef] [PubMed]
  20. Le Gland, G.; Mémery, L.; Aumont, O.; Resplandy, L. Improving the inverse modeling of a trace isotope: How precisely can radium-228 fluxes toward the ocean and submarine groundwater discharge be estimated? Biogeosciences 2017, 14, 3171–3189. [Google Scholar] [CrossRef]
  21. Sánchez-Martos, F.; Jiménez-Espinosa, R.; Pulido-Bosch, A. Mapping groundwater quality variables using PCA and geostatistics: A case study of Bajo Andarax, southeastern Spain. Hydrol. Sci. J. 2001, 46, 227–242. [Google Scholar] [CrossRef]
  22. Guggenmos, M.R.; Daughney, C.J.; Jackson, B.M.; Morgenstern, U. Regional-scale identification of groundwater-surface water interaction using hydrochemistry and multivariate statistical methods, Wairarapa Valley, New Zealand. Hydrol. Earth Syst. Sci. 2011, 15, 3383–3398. [Google Scholar] [CrossRef]
  23. Chen, K.; Jiao, J.J.; Huang, J.; Huang, R. Multivariate statistical evaluation of trace elements in groundwater in a coastal area in Shenzhen, China. Environ. Pollut. 2007, 147, 771–780. [Google Scholar] [CrossRef] [PubMed]
  24. De Andrade, E.M.; Palácio, H.A.Q.; Souza, I.H.; de Oliveira Leão, R.A.; Guerreiro, M.J. Land use effects in groundwater composition of an alluvial aquifer (Trussu River, Brazil) by multivariate techniques. Environ. Res. 2008, 106, 170–177. [Google Scholar] [CrossRef] [PubMed]
  25. Cloutier, V.; Lefebvre, R.; Therrien, R.; Savard, M.M. Multivariate statistical analysis of geochemical data as indicative of the hydrogeochemical evolution of groundwater in a sedimentary rock aquifer system. J. Hydrol. 2008, 353, 294–313. [Google Scholar] [CrossRef]
  26. Lee, J.M.; Woo, N.C.; Lee, C.J.; Yoo, K. Characterising bedrock aquifer systems in Korea using paired water-level monitoring data. Water 2017, 9, 420. [Google Scholar] [CrossRef]
  27. Abou Zakhem, B.; Al-Charideh, A.; Kattaa, B. Using principal component analysis in the investigation of groundwater hydrochemistry of Upper Jezireh Basin, Syria. Hydrol. Sci. J. 2017, 62, 2266–2279. [Google Scholar] [CrossRef]
  28. Paliy, O.; Shankar, V. Application of multivariate statistical techniques in microbial ecology. Mol. Ecol. 2016, 25, 1032–1057. [Google Scholar] [CrossRef] [PubMed]
  29. Lecher, A.L.; Fisher, A.T.; Paytan, A. Submarine groundwater discharge in Northern Monterey Bay, California: Evaluation by mixing and mass balance models. Mar. Chem. 2016, 179, 44–55. [Google Scholar] [CrossRef]
  30. Hanson, R. Geohydrologic Framework of Recharge and Seawater Intrusion in the Pajaro Valley, Santa Cruz and Monterey Counties, California; US Geological Survey: Washington, DC, USA, 2003.
  31. Hansen, H.P.; Koroleff, F. Determination of nutrients. In Methods of Seawater Analysis: Third, Completely Revised and Extended Edition; Minister of Supply and Services Canada: Ottawa, ON, Canada, 2007; pp. 159–228. ISBN 9783527613984. [Google Scholar]
  32. McIlvin, M.R.; Altabet, M.A. Chemical conversion of nitrate and nitrite to nitrous oxide for nitrogen and oxygen isotopic analysis in freshwater and seawater. Anal. Chem. 2005, 77, 5589–5595. [Google Scholar] [CrossRef] [PubMed]
  33. Ryabenko, E. Effect of chloride on the chemical conversion of nitrate to nitrous oxide for δ 15 N analysis. Limnol. Oceanogr. Methods 2009, 7, 545–552. [Google Scholar] [CrossRef] [Green Version]
  34. Street, J.H.; Knee, K.L.; Grossman, E.E.; Paytan, A. Submarine groundwater discharge and nutrient addition to the coastal zone and coral reefs of leeward Hawai′i. Mar. Chem. 2008, 109, 355–376. [Google Scholar] [CrossRef]
  35. Wankel, S.D.; Kendall, C.; Pennington, J.T.; Chavez, F.P.; Paytan, A. Nitrification in the euphotic zone as evidenced by nitrate dual isotopic composition: Observations from Monterey Bay, California. Glob. Biogeochem. Cycles 2007, 21. [Google Scholar] [CrossRef]
  36. Sigman, D.M.; Granger, J.; DiFiore, P.J.; Lehmann, M.M.; Ho, R.; Cane, G.; van Geen, A. Coupled nitrogen and oxygen isotope measurements of nitrate along the eastern North Pacific margin. Glob. Biogeochem. Cycles 2005, 19. [Google Scholar] [CrossRef]
  37. Chen, D.J.Z.; MacQuarrie, K.T.B. Correlation of delta N-15 and delta O-18 in NO3- during denitrification in groundwater. J. Environ. Eng. Sci. 2005, 4, 221–226. [Google Scholar] [CrossRef]
  38. Knee, K.; Street, J.H.; Grossman, E.G.; Paytan, A. Nutrient inputs to the coastal ocean from submarine groundwater discharge in a groundwater-dominated system: Relation to land use (Kona coast, Hawaii, U.S.A.). Limnol. Oceanogr. 2010, 55, 1105–1122. [Google Scholar] [CrossRef]
Hydrology 05 00015 g001 550
Figure 1. Sampling locations in Monterey Bay, CA. Samples were collected from monitoring wells (Well GW, PV1 and PV2), the coastal aquifer (Coastal GW), and Monterey Bay itself (Ocean). Symbols are consistent across all figures.
Figure 1. Sampling locations in Monterey Bay, CA. Samples were collected from monitoring wells (Well GW, PV1 and PV2), the coastal aquifer (Coastal GW), and Monterey Bay itself (Ocean). Symbols are consistent across all figures.
Hydrology 05 00015 g001
Hydrology 05 00015 g002 550
Figure 2. Box plots of salinity (A), nitrate (B), ammonium (C), silicate (D), and phosphate (E) concentrations, and δ15NNO3 (F) and δ18ONO3 (G) data from monitoring wells (Well GW), groundwater from the beach face (Coastal GW), or Monterey Bay itself (Ocean). Numbers at the top indicate the number of samples per group. Silicate concentrations and δ18ONO3 were statistically different between all three water types (Tukey-Kramer, p < 0.05).
Figure 2. Box plots of salinity (A), nitrate (B), ammonium (C), silicate (D), and phosphate (E) concentrations, and δ15NNO3 (F) and δ18ONO3 (G) data from monitoring wells (Well GW), groundwater from the beach face (Coastal GW), or Monterey Bay itself (Ocean). Numbers at the top indicate the number of samples per group. Silicate concentrations and δ18ONO3 were statistically different between all three water types (Tukey-Kramer, p < 0.05).
Hydrology 05 00015 g002
Hydrology 05 00015 g003 550
Figure 3. Nutrient concentrations and δ15NNO3 and δ18ONO3 plotted against silicate concentrations, the solute best indicative of conservative mixing. Fits of linear regressions were low (R2 < 0.25).
Figure 3. Nutrient concentrations and δ15NNO3 and δ18ONO3 plotted against silicate concentrations, the solute best indicative of conservative mixing. Fits of linear regressions were low (R2 < 0.25).
Hydrology 05 00015 g003
Hydrology 05 00015 g004 550
Figure 4. Nitrate concentrations plotted against ammonium (A), δ18ONO3 (B), and δ15NNO3 (C) and δ15NNO3 plotted against δ18ONO3 (D). In D the circle represents the range of data found in Monterey Bay ocean water by [35]. The arrow displays what a 2 δ15NNO3:1 δ18ONO3 denitrification trend would look like. The line is a regression of well groundwater and ocean water.
Figure 4. Nitrate concentrations plotted against ammonium (A), δ18ONO3 (B), and δ15NNO3 (C) and δ15NNO3 plotted against δ18ONO3 (D). In D the circle represents the range of data found in Monterey Bay ocean water by [35]. The arrow displays what a 2 δ15NNO3:1 δ18ONO3 denitrification trend would look like. The line is a regression of well groundwater and ocean water.
Hydrology 05 00015 g004
Hydrology 05 00015 g005a 550Hydrology 05 00015 g005b 550
Figure 5. Results of the Principal Component Analysis (PCA). Components 1 and 2 (A) and 3 and 4 (B) accounted for 39%, 19%, 14%, and 12%, of the variability respectively. Coefficient vectors represent how much each parameter (salinity, nutrient concentrations, etc.) contributed to the component, with the longer vectors contributing more than the shorter vectors.
Figure 5. Results of the Principal Component Analysis (PCA). Components 1 and 2 (A) and 3 and 4 (B) accounted for 39%, 19%, 14%, and 12%, of the variability respectively. Coefficient vectors represent how much each parameter (salinity, nutrient concentrations, etc.) contributed to the component, with the longer vectors contributing more than the shorter vectors.
Hydrology 05 00015 g005aHydrology 05 00015 g005b
Table
Table 1. Summary of processes that affect nutrient concentrations in coastal aquifers.
Table 1. Summary of processes that affect nutrient concentrations in coastal aquifers.
ProcessNutrients AffectedIndicators of Presence
MixingAllDistinct end-members in the ocean and inland groundwater and good correlation with a conservative tracer like salinity or silicate
DenitrificationNitrateConcentrations of nitrate decrease as δ15NNO3 and δ18ONO3 increase
NitrificationNitrateConcentrations of nitrate increase as δ15NNO3 and δ18ONO3 decrease
Decay of Organic MaterialPhosphate and AmmoniumIncreasing concentrations of phosphate and ammonium
SalinizationPhosphateIncreased salinity and phosphate concentrations as cations cause desorption from aquifer substrate
Precipitation of OxidesPhosphateDecreasing phosphate concentrations under oxic conditions
Nutrient UptakeAllDecreasing concentrations of nutrients paired with increasing isotopic signatures
Reduction of Iron OxidesIron and PhosphateIncreasing phosphate concentrations and dissolved iron and manganese under anoxic conditions

Share and Cite

MDPI and ACS Style

Lecher, A.L.; Murray, J.; Paytan, A. Quantifying Processes Governing Nutrient Concentrations in a Coastal Aquifer via Principal Component Analysis. Hydrology 2018, 5, 15. https://doi.org/10.3390/hydrology5010015

AMA Style

Lecher AL, Murray J, Paytan A. Quantifying Processes Governing Nutrient Concentrations in a Coastal Aquifer via Principal Component Analysis. Hydrology. 2018; 5(1):15. https://doi.org/10.3390/hydrology5010015

Chicago/Turabian Style

Lecher, Alanna L., Joseph Murray, and Adina Paytan. 2018. "Quantifying Processes Governing Nutrient Concentrations in a Coastal Aquifer via Principal Component Analysis" Hydrology 5, no. 1: 15. https://doi.org/10.3390/hydrology5010015

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop