Water Balance Analysis over the Niger Inland Delta-Mali: Spatio-Temporal Dynamics of the Flooded Area and Water Losses
Abstract
1. Introduction
2. Materials and Methods
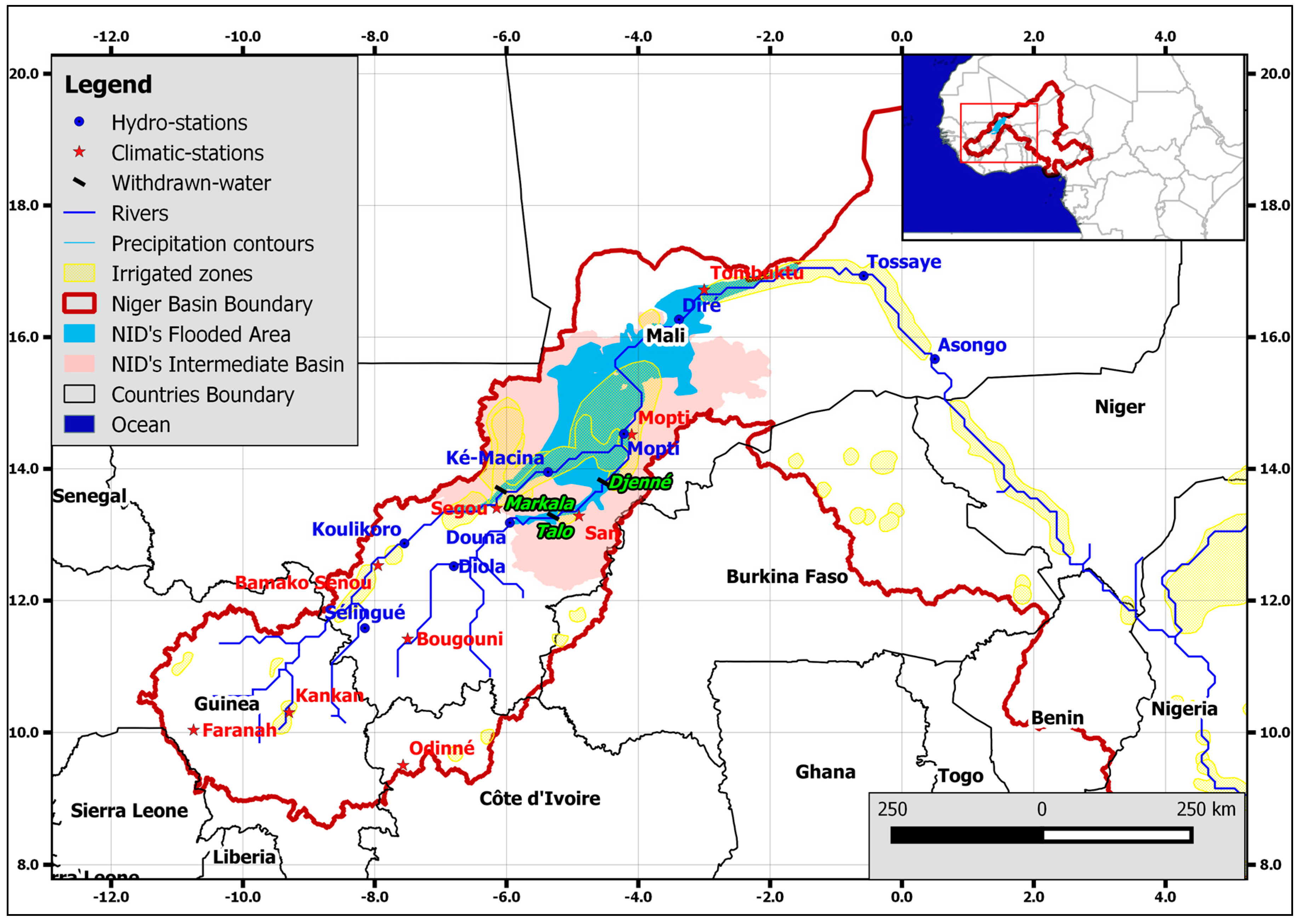
2.1. Study Area
2.2. Data
2.2.1. Remote Sensing (RS) Data
2.2.2. Hydro-Meteorological Data
2.2.3. Field Irrigation Data
2.3. Methods
2.3.1. Land Cover Mapping and Flooded Areas Assessment
Supervised Classification of Landsat 7 Images
SeaWinds Classification
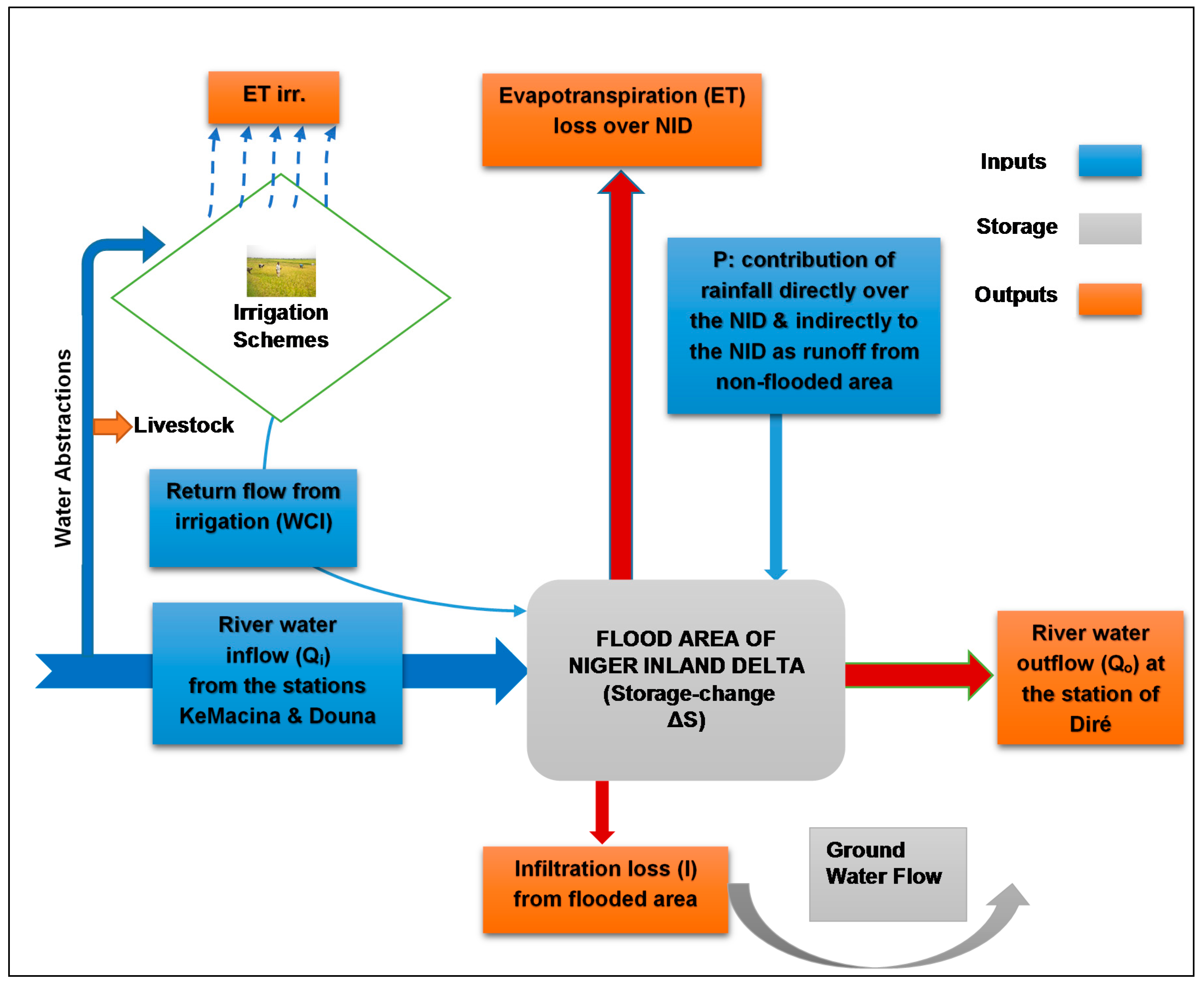
2.3.2. Water Balance of the NID
- = change of storage,
- Qi = river water inflow, calculated as the sum of discharge measured at the stations KeMacina and Douna,
- P = Rainfall contribution (directly on the flooded area and indirectly as runoff from areas in the NID’s catchment that drain to the flooded areas),
- ET = evapotranspiration loss over the NID,
- I = infiltration loss from flooded area,
- WCI = return flow from irrigation to the NID’s water balance,
- Qo = river water outflow at the station of Diré, and,
- t = time.
- All units are in (km3·month−1).
2.3.3. Estimation of Water Balance Terms
Evaporation (ET) Loss Computation
Precipitation (P) Contribution to the NID
Return Flow from Irrigated Fields (WCI)
- = net irrigation water requirement,
- = water requirement (),
- = depth of water for soil condition (data collected from the “Office du Niger”),
- = Infiltration rate (refers to percolation losses) within the irrigation scheme (Data collected at “Office du Niger); and,
- = effective rainfall (, with as rainfall over the area and as coefficient for effective rainfall).
Change of Storage (∆S) Assessment
- = Average flooded area (km2) between two time intervals,
- = average variation of surface water level (in km) between two time intervals, calculated from the mean water height at the gauging stations (Mopti, Diré & Ké-Macina) between two time intervals.
2.3.4. Analyzing the Water Balance
3. Results
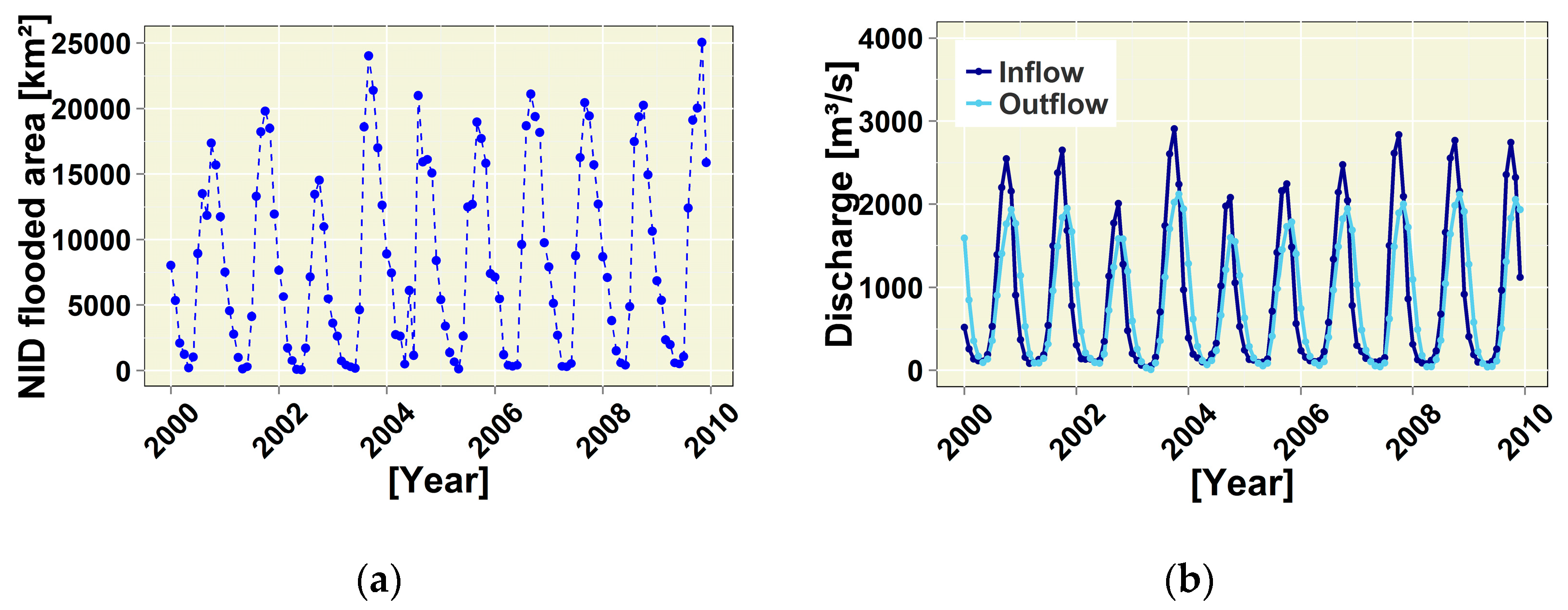
3.1. Assessment of Flooded Area
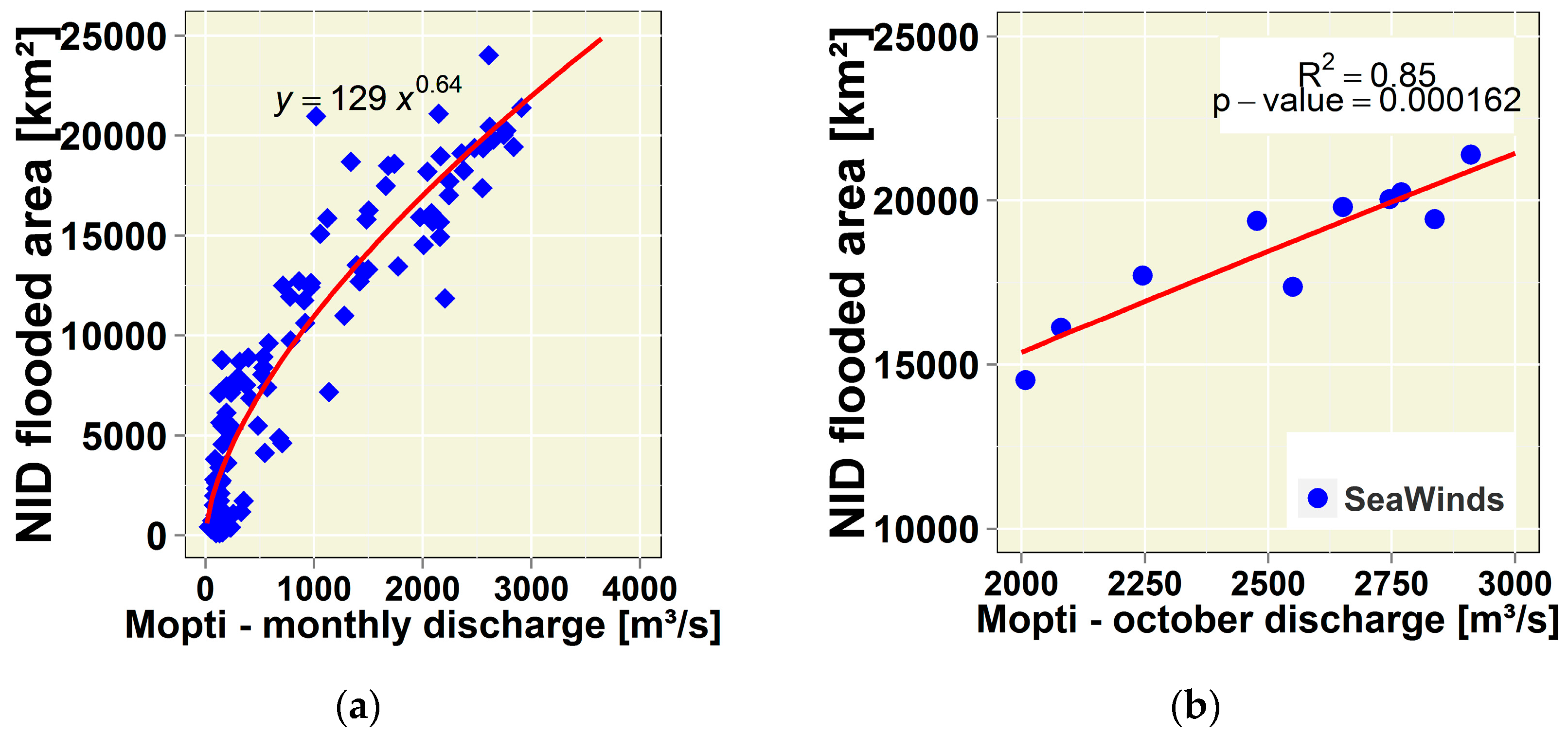
Remotely Sensed Flooded Area Comparison-Discharge and Area Relationship
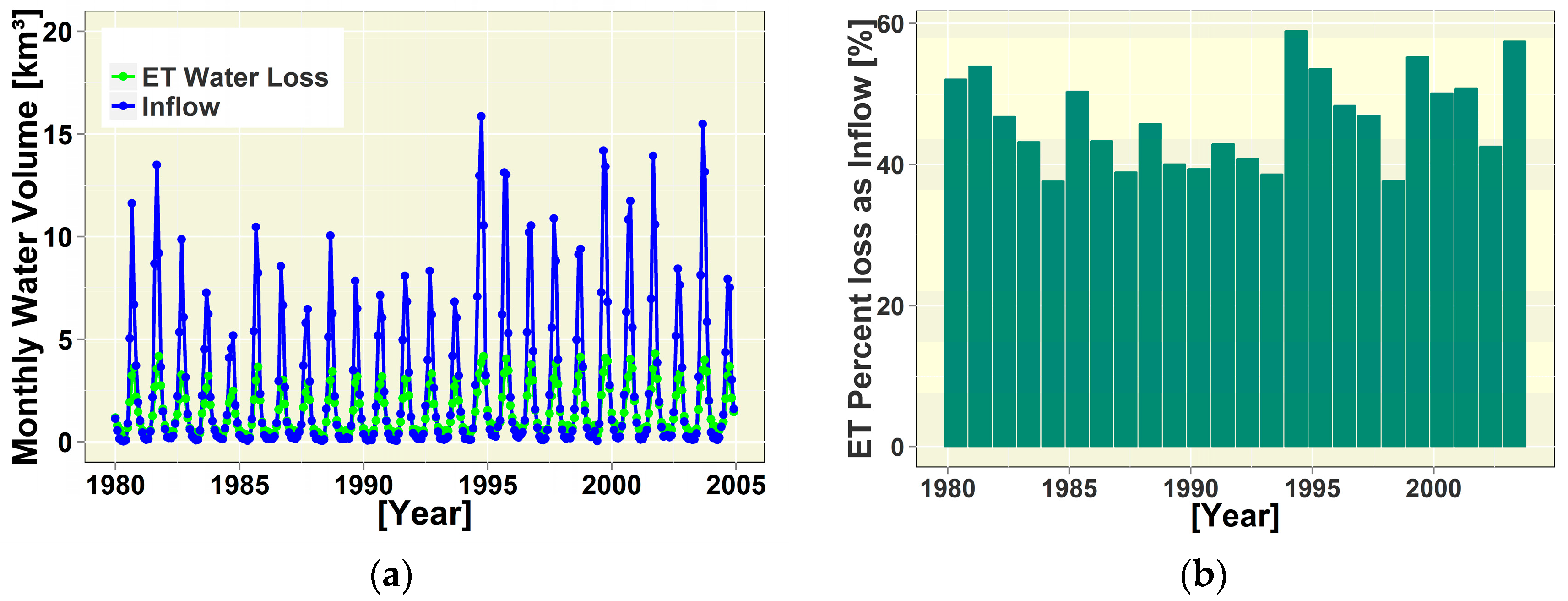
3.2. Water Balance Hydrological Variables Estimations
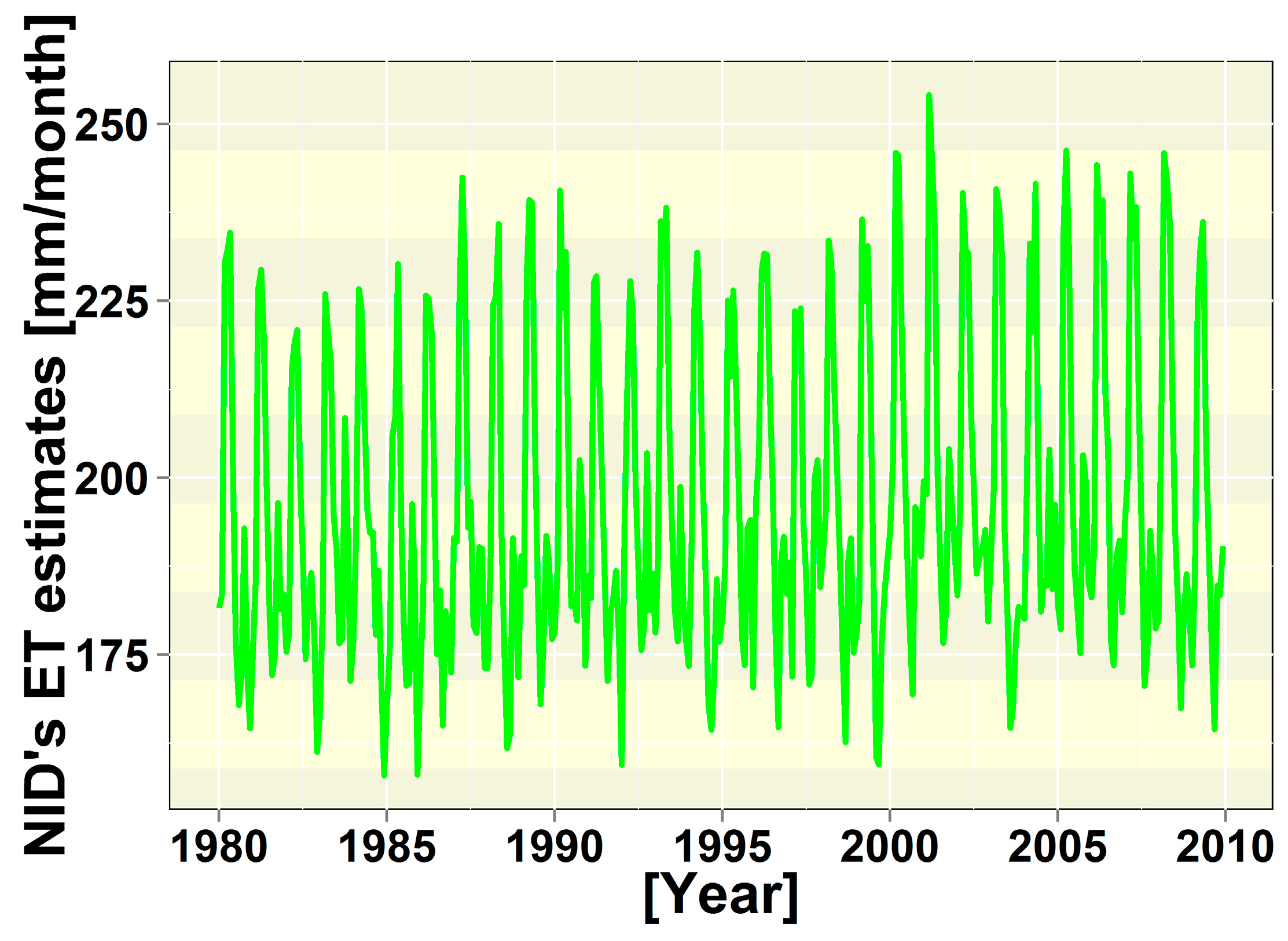
3.2.1. Water Losses (Evaporation (ET)) Estimations over the NID
3.2.2. Accounting for Rainfall and Estimating Return Flow from Irrigation
4. Discussion
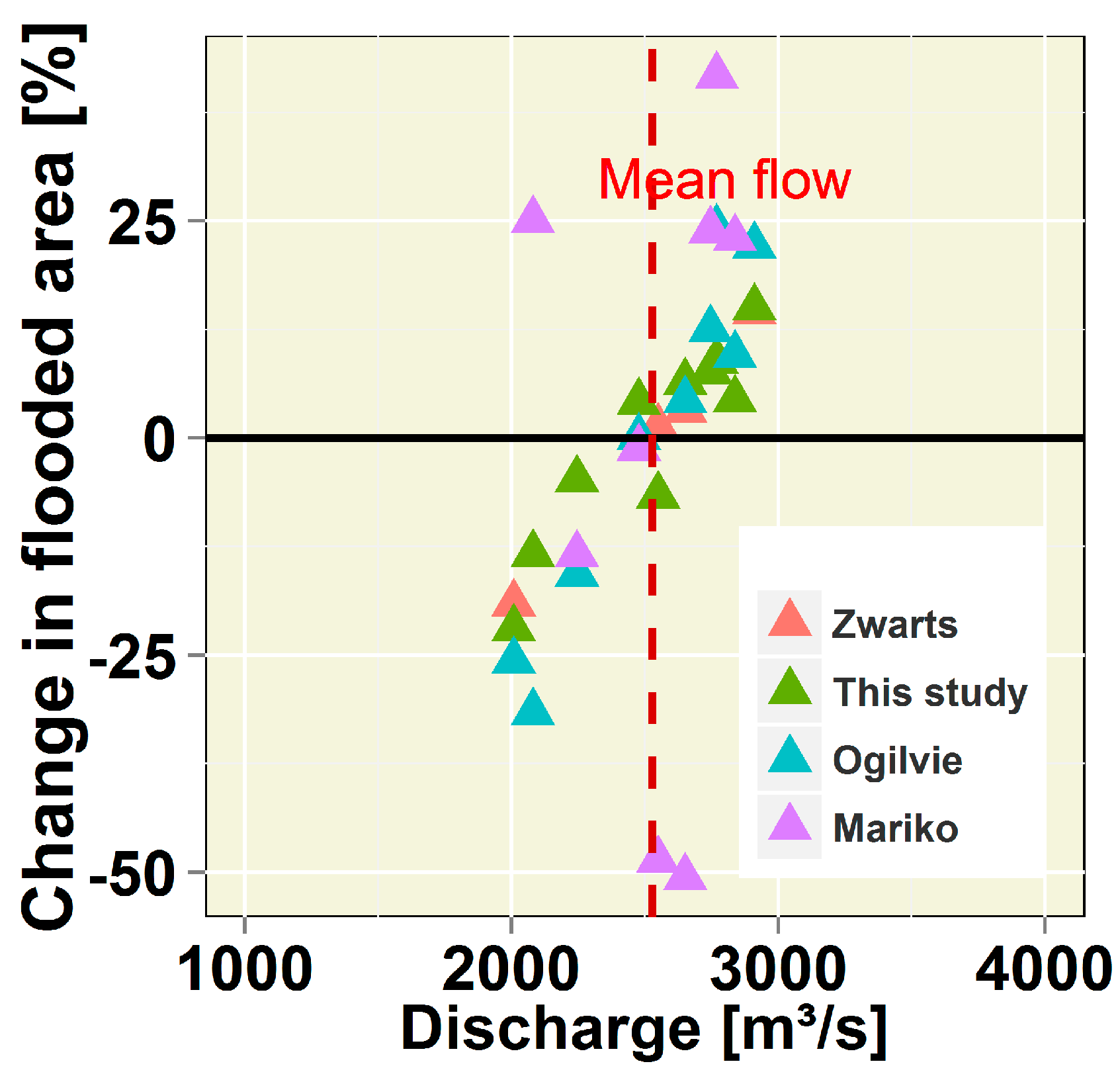
4.1. Comparing Remotely Sensed Flooded Areas with Previous Estimates
4.2. Comparing Water Balance Components with the Previous Studies
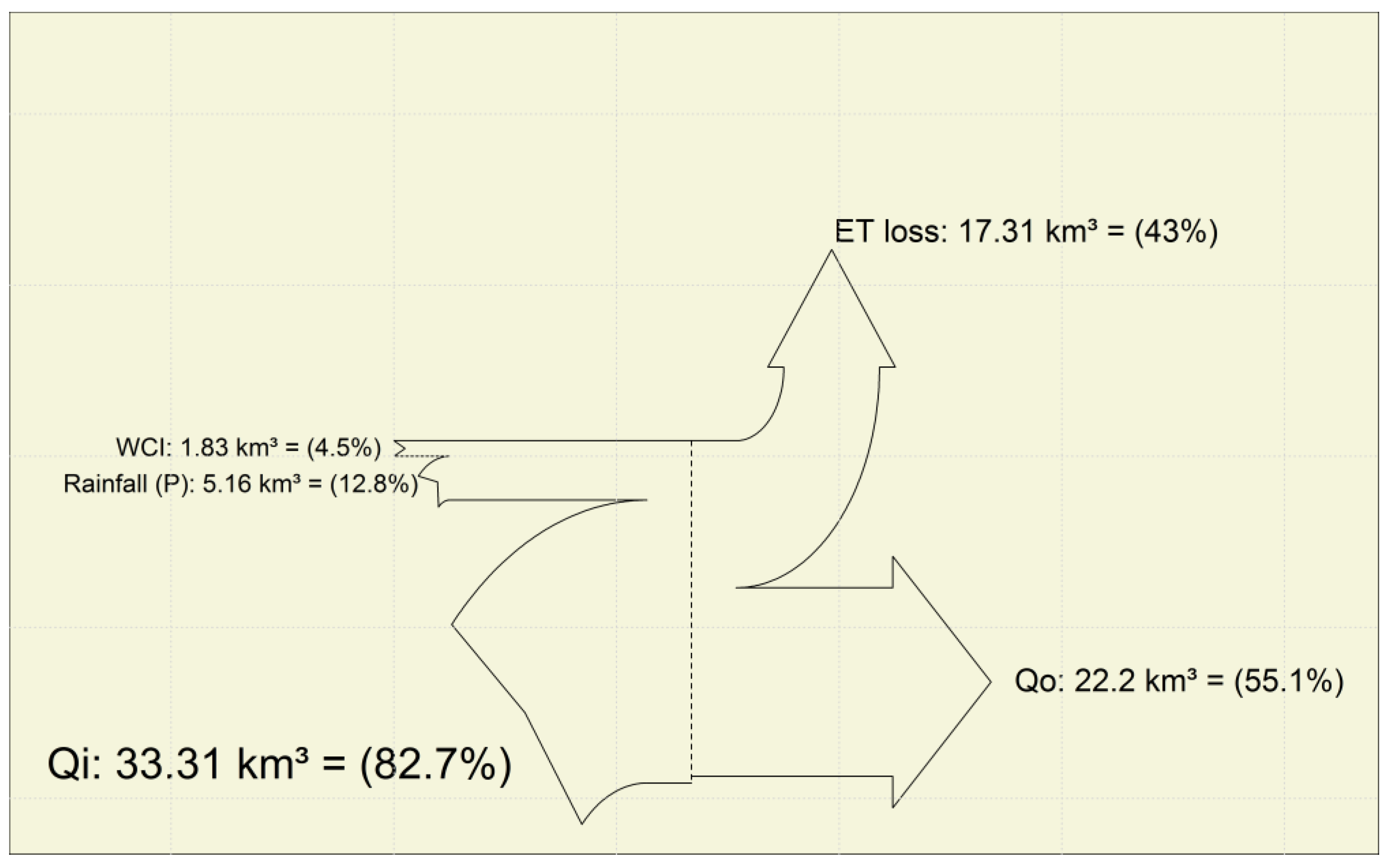
4.3. Water Balance (NIDWat) Analysis
4.4. Uncertainty and Outlook
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ABT | Simple Abtew equation |
| AGRHYMET | Agrometeorology and Operational Hydrology and Their Applications |
| CW | Consumptive Water used |
| DEM | Digital Elevation Models |
| HAM | Hamon evaporation model |
| HARG | Hargreaves evapotranspiration model |
| JULES | Joint UK Land-Environment Simulator |
| MAK | Modified Makkink equation |
| NID | Niger Inland Delta |
| NIDWat | Niger Inland Delta Water balance model |
| NRB | Niger River Basin |
| ON | “Office du Niger” |
| ORM | “Office Riz Mopti” |
| OUD | Oudin evapotranspiration model |
| PET | Potential Evapotranspiration |
| PMO | Penman-Monteith combination equation |
| PRT | Priestley-Taylor method |
| RMSE | Root Mean Square Error |
| RSR | Ratio of RMSE to the standard deviation of the observations |
| TUR | Modified Turc evapotranspiration method |
| WASCAL | West African Science Service Center on Climate Change and Adapted Land Use |
| WU | Withdrawn water |
| WCI | Return flow from irrigated fields |
| ZEF | Center for Development Research |
Appendix A
Appendix A.1. Potential PET Estimation Methods
- PE = rate of potential evapotranspiration in mm per day;
- Re = extraterrestrial radiation in MJ per m2 per day;
- λ = latent heat flux for the vaporization (as 2.45 MJ per kg);
- ρ = density of water (ρ = 995.6502 kg per m3); and
- Ta = air temperature (°C) which correspond to the mean daily air temperature.
- HAM = evapotranspiration, (mm day−1)
- = average number of daylight hours per day during the month
- = saturated vapor pressure at temperature T
- Ta = mean daily air temperature (°C)
Appendix A.2. Calculation of Short and Long-Wave Radiation
References
- Zwarts, L.; Van Beukering, P.; Kone, B.; Wymenga, E. The Niger, a Lifeline. Effective Water Management in the Upper Niger Basin; RIZA/Wetlands International/Institute for Environmental Studies (IVM)/A&W Ecological Consultants: Lelystad, The Netherlands; Sevare, Mali; Amsterdam, The Netherlands; Veenwouden, The Netherlands, 2005; p. 169. [Google Scholar]
- Hoogeveen, J.; Faurès, J.-M.; Peiser, L.; Burke, J.; van de Giesen, N. GlobWat—A global water balance model to assess water use in irrigated agriculture. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 801–838. [Google Scholar] [CrossRef]
- Orange, D.; Mahe, G.; Dembélé, L.; Diakité, C.H.; Kuper, M.; Olivry, J.-C. Hydrologie, agro-écologie et superficies d’inondation dans le delta intérieur du Niger. In Gestion Intégrée des Ressources Naturelles en Zones Inondabless Tropicales; Séminaire International: Bamako, Mali, 2002; pp. 208–228. [Google Scholar]
- IPCC. Climate change 2007: The physical science basis. Intergov. Panel Clim. Chang. 2007, 446, 727–728. [Google Scholar] [CrossRef]
- Mahe, G.; Bamba, F.; Soumaguel, A.; Orange, D.; Olivry, J.C. Water losses in the inner delta of the River Niger: Water balance and flooded area. Hydrol. Process. 2009, 23, 3157–3160. [Google Scholar] [CrossRef]
- Mahé, G.; Lienou, G.; Descroix, L.; Bamba, F.; Paturel, J.E.; Laraque, A.; Khomsi, K. The rivers of Africa: Witness of climate change and human impact on the environment. Hydrol. Process. 2013, 27, 2105–2114. [Google Scholar] [CrossRef]
- Descroix, L.; Mahé, G.; Lebel, T.; Favreau, G.; Galle, S.; Gautier, E.; Sighomnou, D. Spatio-temporal variability of hydrological regimes around the boundaries between Sahelian and Sudanian areas of West Africa: A synthesis. J. Hydrol. 2009, 375, 90–102. [Google Scholar] [CrossRef]
- Kuper, M.; Mullon, C.; Poncet, Y.; Benga, E. Integrated modelling of the ecosystem of the Niger river inland delta in Mali. Ecol. Model. 2003, 164, 83–102. [Google Scholar] [CrossRef]
- Lebel, T.; Ali, A. Recent trends in the Central and Western Sahel rainfall regime (1990–2007). J. Hydrol. 2009, 375, 52–64. [Google Scholar] [CrossRef]
- Wolski, P.; Savenije, H.H.G.; Murray-Hudson, M.; Gumbricht, T. Modelling of the flooding in the Okavango Delta, Botswana, using a hybrid reservoir-GIS model. J. Hydrol. 2006, 331, 58–72. [Google Scholar] [CrossRef]
- Olivry, J.C. Fonctionnement hydrologique de la cuvette lacustre du Niger et essai de la modélisation de l’inondation du delta intérieur. In Grands Bassins Fluviaux; Olivry, J.C., Boulegue, J., Eds.; Actes Du Colloque PEGI, INSU-CNRS-ORSTOM Paris; Colloque et Séminaire: Paris, France, 1994; pp. 267–280. [Google Scholar]
- Dadson, S.J.; Ashpole, I.; Harris, P.; Davies, H.N.; Clark, D.B.; Blyth, E.; Taylor, C.M. Wetland inundation dynamics in a model of land surface climate: Evaluation in the Niger inland delta region. J. Geophys. Res. 2010, 115, 1–7. [Google Scholar] [CrossRef]
- Hughes, D.A.; Tshimanga, R.M.; Tirivarombo, S.; Tanner, J. Simulating wetland impacts on stream flow in southern Africa using a monthly hydrological model. Hydrol. Process. 2014, 28, 1775–1786. [Google Scholar] [CrossRef]
- Mahe, G.; Orange, D.; Mariko, A.; Bricquet, J.P. Estimation of the flooded area of the Inner Delta of the River Niger in Mali by hydrological balance and satellite data. In Hydro-Climatology, Proceedings of Symposium J-H02 Held during IUGG2011 in Melbourne, Australia, July 2011; Franks, S.W., Ed.; IAHS Pub. 344; IAHS Press: Wallingford, UK, 2011; pp. 138–143. [Google Scholar]
- Zwarts, L.; Beukering, P.; Van Koné, B.; Wymenga, E.; Taylor, D. The economic and ecological effects of water management choices in the Upper Niger River: Development of decision support methods. Int. J. Water Resour. Dev. 2006, 22, 135–156. [Google Scholar] [CrossRef]
- Ogilvie, A.; Belaud, G.; Delenne, C.; Bailly, J.-S.; Bader, J.-C.; Oleksiak, A.; Martin, D. Decadal monitoring of the Niger Inner Delta flood dynamics using MODIS optical data. J. Hydrol. 2015, 523, 368–383. [Google Scholar] [CrossRef]
- Schwerdtfeger, J.; Johnson, M.S.; Couto, E.G.; Amorim, R.S.S.; Sanches, L.; Campelo Júnior, J.H.; Weiler, M. Inundation and groundwater dynamics for quantification of evaporative water loss in tropical wetlands. Hydrol. Earth Syst. Sci. Discuss. 2014, 11, 4017–4062. [Google Scholar] [CrossRef]
- Moret, B.; Chaperon, P.; Lamagat, J.P.; Molinier, M. Monographie Hydrologique du fleuve Niger; ORSTOM, Ed.; Tome II—Cuvette Lacustre et Niger Moyen; Monographies Hydrologiques: Paris, France, 1986. [Google Scholar]
- Chelton, D.B.; Freilich, M.H. Scatterometer-based assessment of 10-m wind analyses from the operational ECMWF and NCEP numerical weather prediction models. Am. Meteorol. Soc. 2005, 134, 737–742. [Google Scholar] [CrossRef]
- NASA LP DAAC. Land Cover Type Yearly L3 Global 500 m SIN Grid (MCD12Q1). Version 051. NASA EOSDIS Land Processes DAAC. USGS Earth Resources Observation and Science (EROS) Center: Sioux Falls, South Dakota, 2005. Available online: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mcd12q1 (accessed on 1 January 2014).
- Vandersypen, K.; Keita, A.C.T.; Coulibaly, Y.; Raes, D.; Jamin, J.Y. Formal and informal decision making on water management at the village level: A case study from the Office du Niger irrigation scheme (Mali). Water Resour. Res. 2007, 43, 1–10. [Google Scholar] [CrossRef]
- Vittek, M.; Brink, A.; Donnay, F.; Simonetti, D.; Desclée, B. Land cover change monitoring using landsat MSS/TM satellite image data over west Africa between 1975 and 1990. Remote Sens. 2013, 6, 658–676. [Google Scholar] [CrossRef]
- Mariko, A.; Mahe, G.I.L.; Orange, D. Monitoring flood propagation in the Niger River Inner Delta in Mali: Prospects with the low resolution NOAA/AVHRR data. In Proceedings of the IAHS-IAPSO-IASPEI Assembly, Gothenburg, Sweden, 22–26 July 2013; pp. 101–109, IAHS Publ. 358. [Google Scholar]
- Mayaux, P.; Bartholome, E.; Fritz, S.; Belward, A. A New Land Cover Map of Africa for the Year 2000. J. Biogeogr. 2004, 31, 861–877. [Google Scholar] [CrossRef]
- Ashcraft, I.S.; Long, D.G. The spatial response function of SeaWinds backscatter measurements. Proc. SPIE 2003, 5151, 609–618. [Google Scholar] [CrossRef]
- Weissman, D.E.; Bourassa, M.A.; O’Brien, J.J.; Tongue, J.S. Calibrating the Quikscat/SeaWinds radar for measuring rainrate over the oceans. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2814–2820. [Google Scholar] [CrossRef]
- De Bruin, H.A.R.; Holtslag, A.A.M. A Simple parameterization of the surface fluxes of sensible and latent heat during daytime compared with the penman-monteith concept. J. Appl. Meteorol. 1982, 21, 1610–1621. [Google Scholar] [CrossRef]
- Alazard, M.; Leduc, C.; Travi, Y.; Boulet, G.; Ben Salem, A. Estimating evaporation in semi-arid areas facing data scarcity: Example of the El Haouareb dam (Merguellil catchment, Central Tunisia). J. Hydrol. Reg. Stud. 2015, 3, 265–284. [Google Scholar] [CrossRef]
- Ball, J.E.; Luk, K.C. Modeling spatial variability of rainfall over a catchment. J. Hydrol. Eng. 1998, 3, 122–130. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Requirements; Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998; p. 300. [Google Scholar]
- Mariko, A. Caractérisation et Suivi de la Dynamique de L’inondation et du Couvert Végétal dans le Delta intérieur du Niger (Mali) par Télédétection. Ph.D. Thesis, Université Montpellier II, Paris, France, 2003. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. Am. Soc. Agric. Biol. Eng. 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Aich, V.; Liersch, S.; Vetter, T.; Fournet, S.; Andersson, J.C.M.; Calmanti, S.; Paton, E.N. Flood projections within the Niger River Basin under future land use and climate change. Sci. Total Environ. 2016, 562, 666–677. [Google Scholar] [CrossRef] [PubMed]
- Liersch, S.; Cools, J.; Kone, B.; Koch, H.; Diallo, M.; Reinhardt, J.; Hattermann, F.F. Vulnerability of rice production in the Inner Niger Delta to water resources management under climate variability and change. Environ. Sci. Policy 2013, 34, 18–33. [Google Scholar] [CrossRef]
- Mahé, G.; Bamba, F.; Orange, D.; Fofana, L.; Kuper, M.; Marieu, B.; Cissé, N. Dynamique hydrologique du delta intérieur du Niger (Mali). In Gestion Intégrée des Ressources Naturelles en Zones Inondabless Tropicales; Séminaire International: Bamako, Mali, 2002; pp. 179–195. Available online: http://www.documentation.ird.fr/hor/fdi:010030365 (accesssed on 10 March 2015).
- Oguntunde, P.G.; Abiodun, B.J. The impact of climate change on the Niger River Basin hydroclimatology, West Africa. Clim. Dyn. 2012, 40, 81–94. [Google Scholar] [CrossRef]
- Frenken, K. Irrigation in Africa in Figures, FAO WATER REPORTS 29, AQUASTAT Survey, FAO Land and Water Development Division; Frenken, K., Ed.; FAO: Rome, Italy, 2005. [Google Scholar]
- Marlet, S.; N’Diaye, M.K. Impacts environnementaux de la mise en valeur d’une zone inondable par irrigation Evolution des sols et des eaux à l’Office du Niger (Mali). In Gestion Intégrée des Ressources Naturelles en Zones Inondabless Tropicales; Séminaire International: Bamako, Mali, 2002; pp. 364–374. [Google Scholar]
- Kurtzman, D.; Scanlon, B.R. Groundwater recharge through vertisols: Irrigated cropland vs. natural land, Israel. Vadose Zone J. 2011, 10, 662. [Google Scholar] [CrossRef]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall-runoff model? J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- De Bruin, H.A.R. Evapotranspiration in humid tropical regions. In Hydrology of Humid Tropical Regions with Particular Reference to the Hydrological Effects of Agriculture and Forestry Practice, Proceedings of the Hamburg Symposium, Hambury, Germany, 15–27 August 1983; IAHS Publ.: Hamburg, Germany, 1983; pp. 1–14. [Google Scholar]
- Xu, C.Y.; Singh, V.P. Cross comparison of empirical equations for calculating potential evapotranspiration with data from Switzerland. Water Resour. Manag. 2002, 16, 197–219. [Google Scholar] [CrossRef]
- Glover, J.; McCulloch, J.S.G. The empirical relation between solar radiation and hours of sunshine. Q. J. R. Meteorol. Soc. 1958, 84, 172–175. [Google Scholar] [CrossRef]

| Model Performance Tools | OUD | HAM | TUR | HARG | PMO | ABT | PRT | MAK |
|---|---|---|---|---|---|---|---|---|
| ET Mean values estimates (mm) | 2153 | 2409 | 2549 | 2059 | 2370 | 2760 | 2795 | 2087 |
| Percent Bias (%) | −15.8 | −5.8 | −0.4 | −19.5 | −7.4 | 7.9 | 9.3 | −18.4 |
| RMSE-RSR | 1.98 | 1.11 | 1.04 | 2.34 | 1.23 | 1.30 | 1.38 | 2.24 |
| Pearson coefficient of correlation with observation | 0.30 | 0.27 | 0.01 | 0.60 | 0.73 | 0.68 | 0.72 | 0.64 |
| Average rank | 6 | 3.25 | 2.75 | 7.25 | 2.5 | 3.75 | 4.25 | 6.25 |
| Rank | 6 | 3 | 2 | 8 | 1 | 4 | 5 | 7 |
| J | F | M | A | M | J | J | A | S | O | N | D | Sum | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ON | 0.150 | 0.168 | 0.181 | 0.207 | 0.226 | 0.254 | 0.264 | 0.264 | 0.314 | 0.337 | 0.194 | 0.117 | 2.677 |
| Djenné | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.039 | 0.156 | 0.236 | 0.290 | 0.218 | 0.000 | 0.938 |
| Talo | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.008 | 0.129 | 0.040 | 0.077 | 0.155 | 0.000 | 0.408 |
| Total | 0.150 | 0.168 | 0.181 | 0.207 | 0.226 | 0.254 | 0.311 | 0.549 | 0.589 | 0.704 | 0.567 | 0.117 | 4.024 |
| Months | WU (10−3 km3 Month−1) | CW (10−3 km3 Month−1) | WCI (10−3 km3 Month−1) |
|---|---|---|---|
| January | 151 | 138 | 13 |
| February | 168 | 153 | 15 |
| March | 182 | 163 | 19 |
| April | 207 | 184 | 23 |
| May | 225 | 206 | 19 |
| June | 254 | 224 | 30 |
| July | 312 | 260 | 52 |
| August | 512 | 226 | 286 |
| September | 566 | 236 | 330 |
| October | 833 | 273 | 560 |
| Novenber | 605 | 141 | 464 |
| December | 118 | 102 | 16 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, M.; Wisser, D.; Ali, A.; Diekkrüger, B.; Seidou, O.; Mariko, A.; Afouda, A. Water Balance Analysis over the Niger Inland Delta-Mali: Spatio-Temporal Dynamics of the Flooded Area and Water Losses. Hydrology 2017, 4, 40. https://doi.org/10.3390/hydrology4030040
Ibrahim M, Wisser D, Ali A, Diekkrüger B, Seidou O, Mariko A, Afouda A. Water Balance Analysis over the Niger Inland Delta-Mali: Spatio-Temporal Dynamics of the Flooded Area and Water Losses. Hydrology. 2017; 4(3):40. https://doi.org/10.3390/hydrology4030040
Chicago/Turabian StyleIbrahim, Moussa, Dominik Wisser, Abdou Ali, Bernd Diekkrüger, Ousmane Seidou, Adama Mariko, and Abel Afouda. 2017. "Water Balance Analysis over the Niger Inland Delta-Mali: Spatio-Temporal Dynamics of the Flooded Area and Water Losses" Hydrology 4, no. 3: 40. https://doi.org/10.3390/hydrology4030040
APA StyleIbrahim, M., Wisser, D., Ali, A., Diekkrüger, B., Seidou, O., Mariko, A., & Afouda, A. (2017). Water Balance Analysis over the Niger Inland Delta-Mali: Spatio-Temporal Dynamics of the Flooded Area and Water Losses. Hydrology, 4(3), 40. https://doi.org/10.3390/hydrology4030040





