Field Analysis of Stepwise Effective Thermal Conductivity along a Borehole Heat Exchanger under Artificial Conditions of Groundwater Flow
Abstract
:1. Introduction
2. Materials and Methods
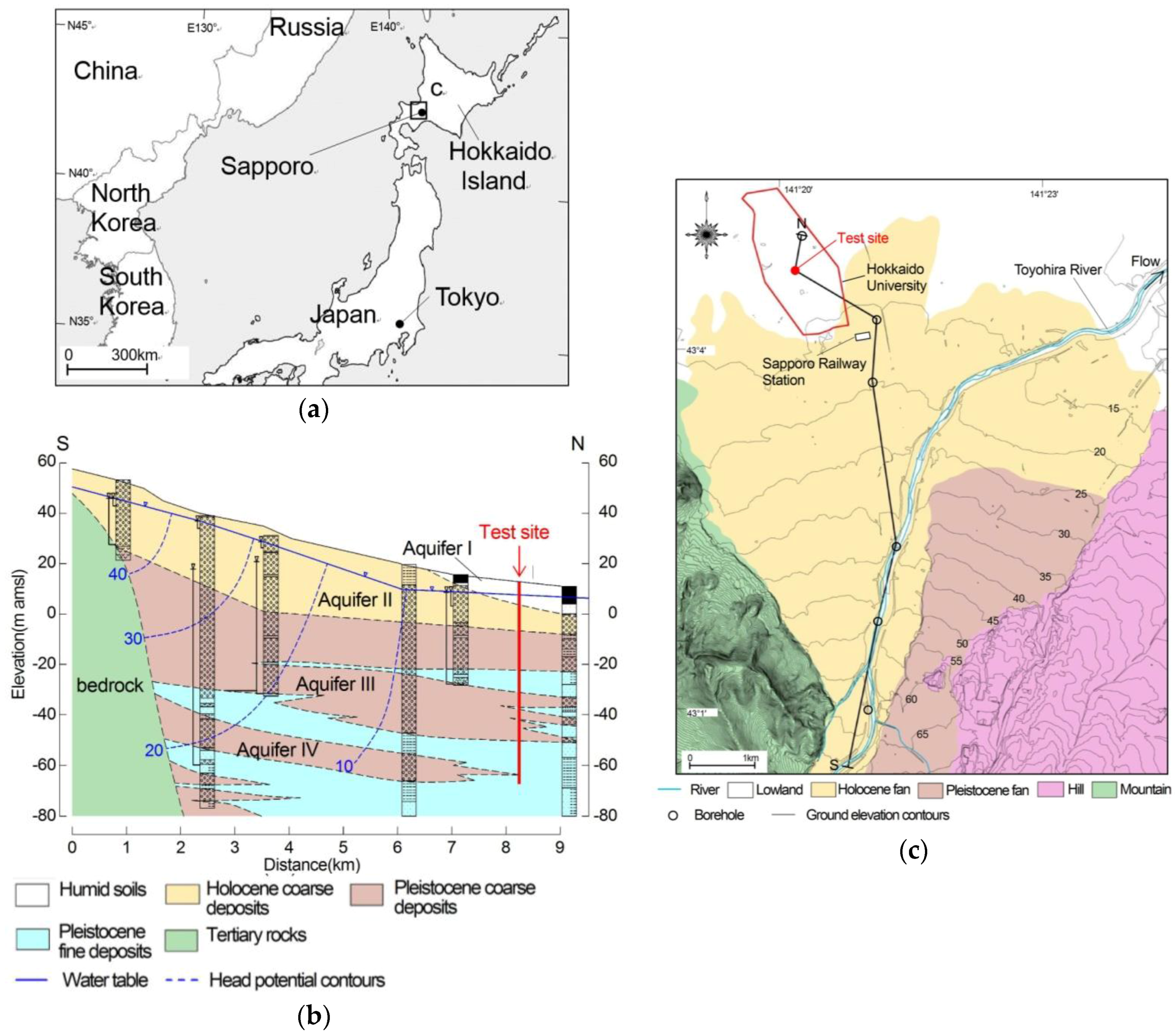
2.1. Site Description
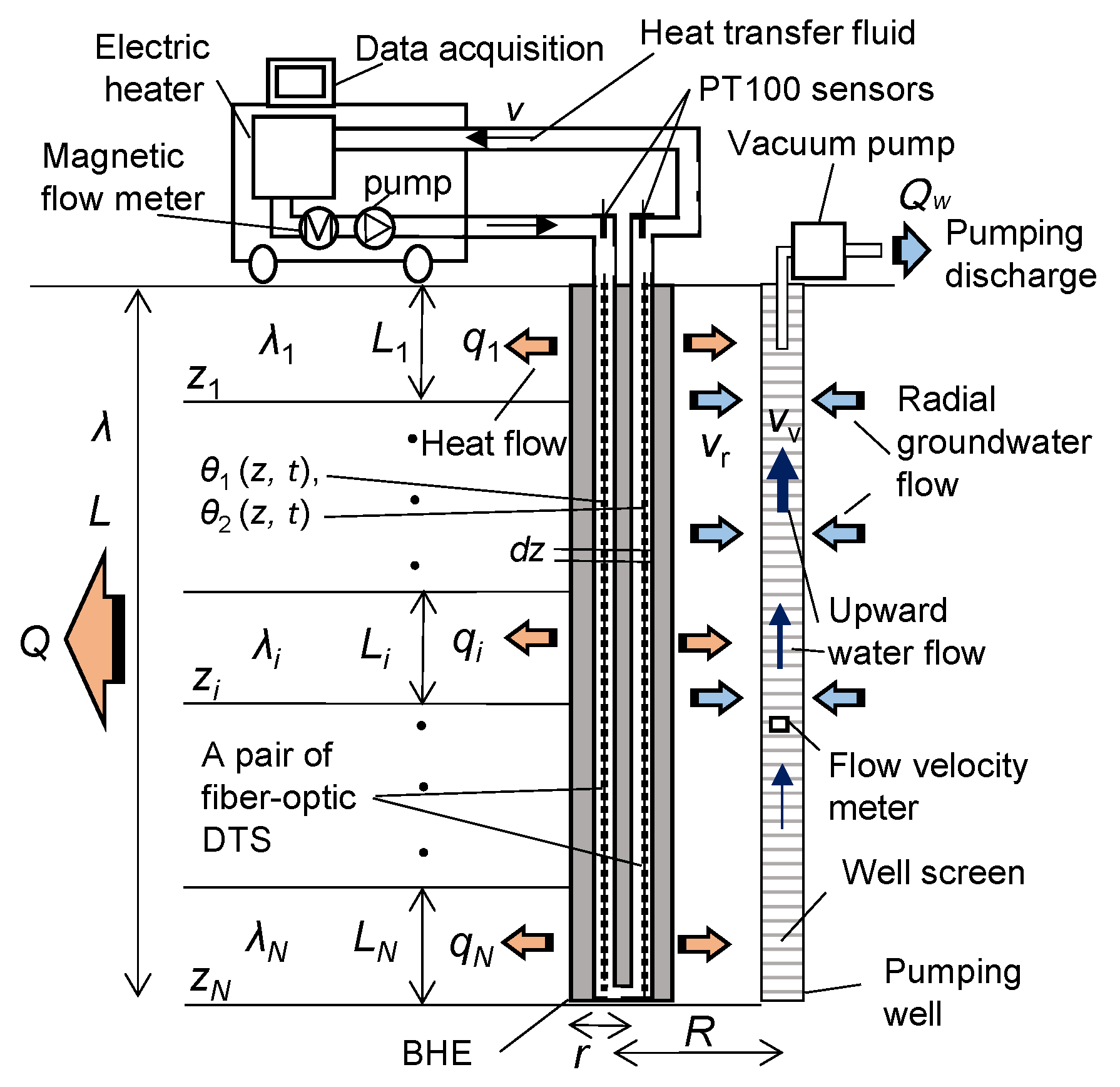
2.2. Thermal Response Tests under Natural and Artificial Conditions of Groundwater Flow
2.3 Analysis of Temperature Profiles to Determine Stepwise Thermal Conductivity
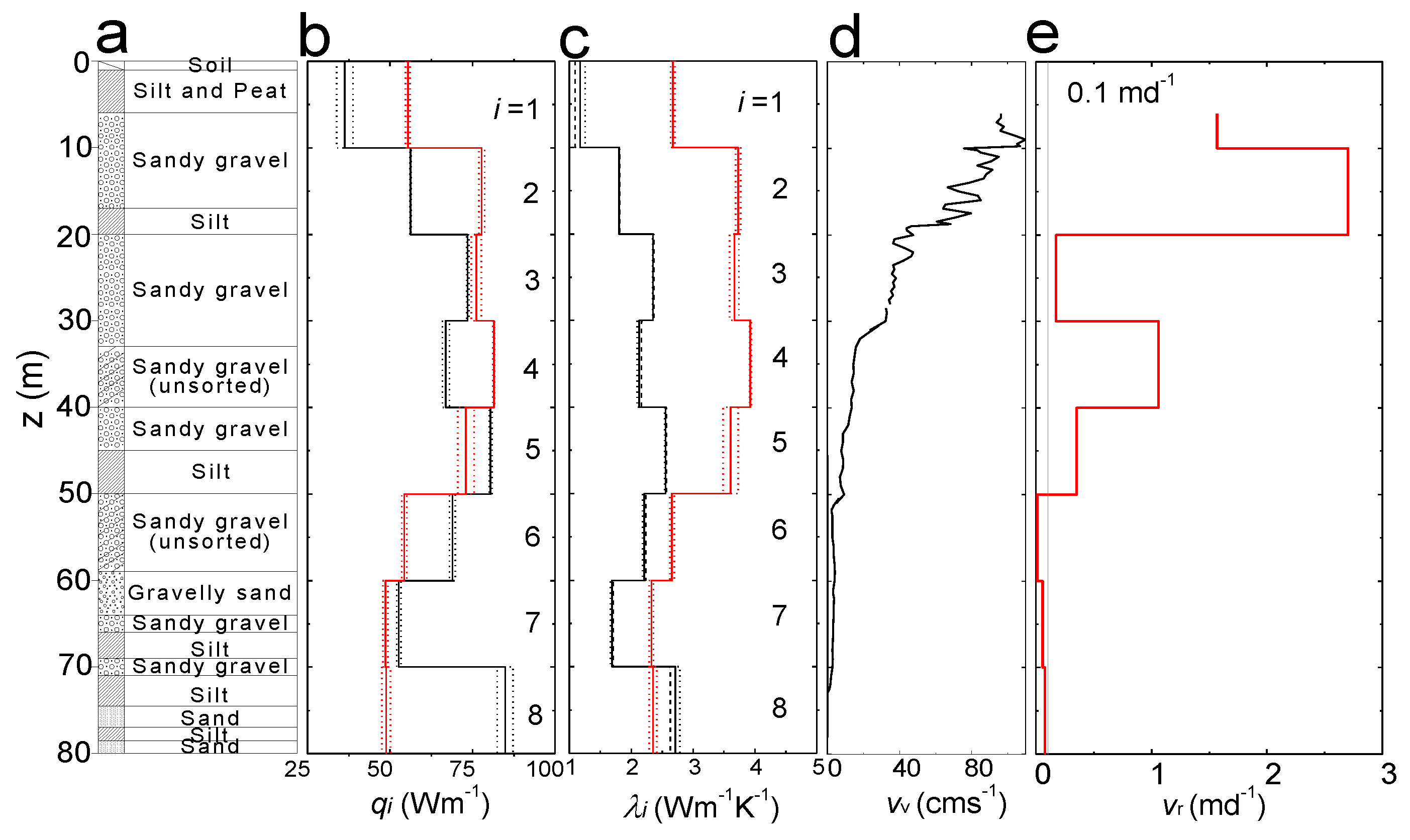
3. Results and Discussion
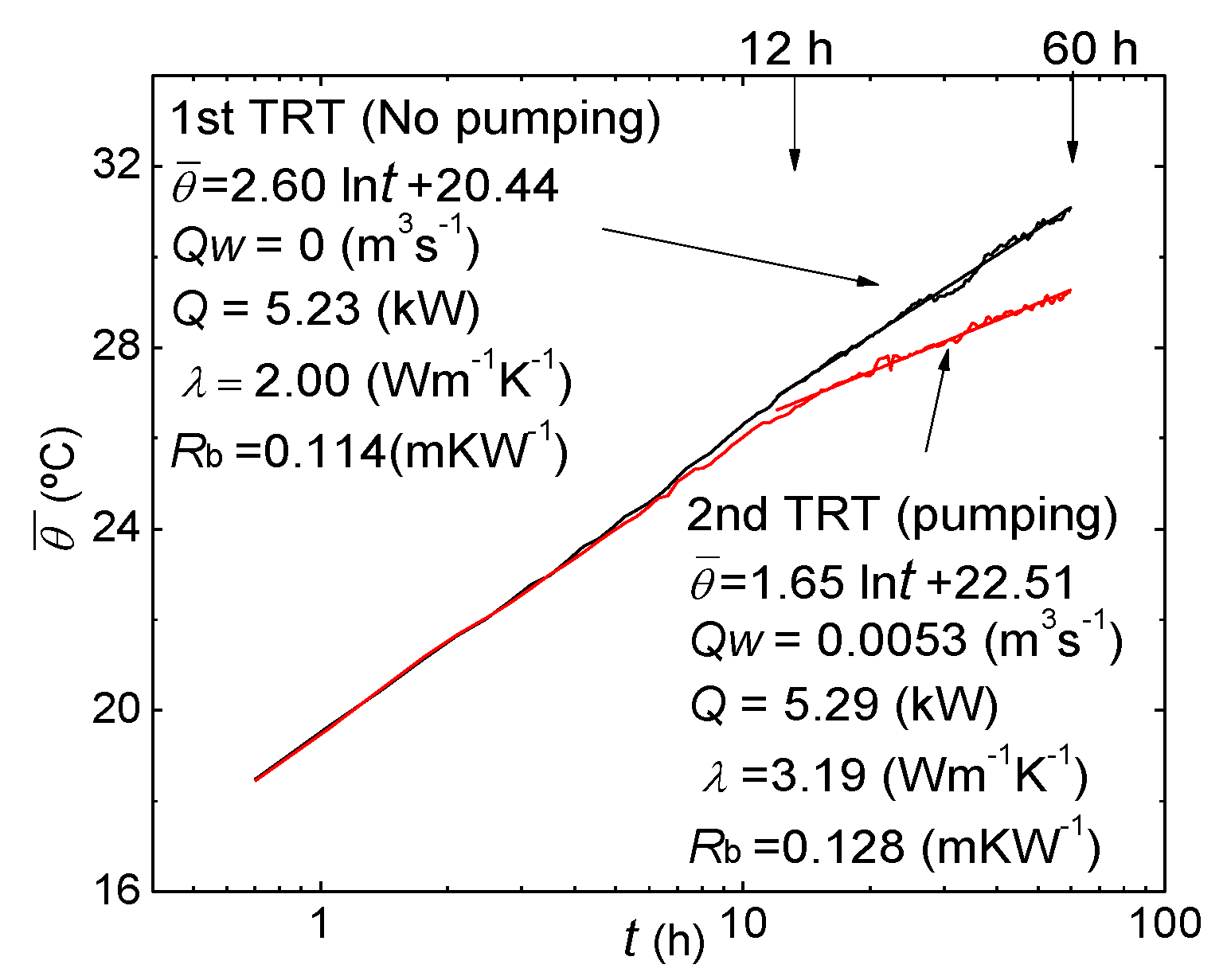
3.1. Standard Test Results
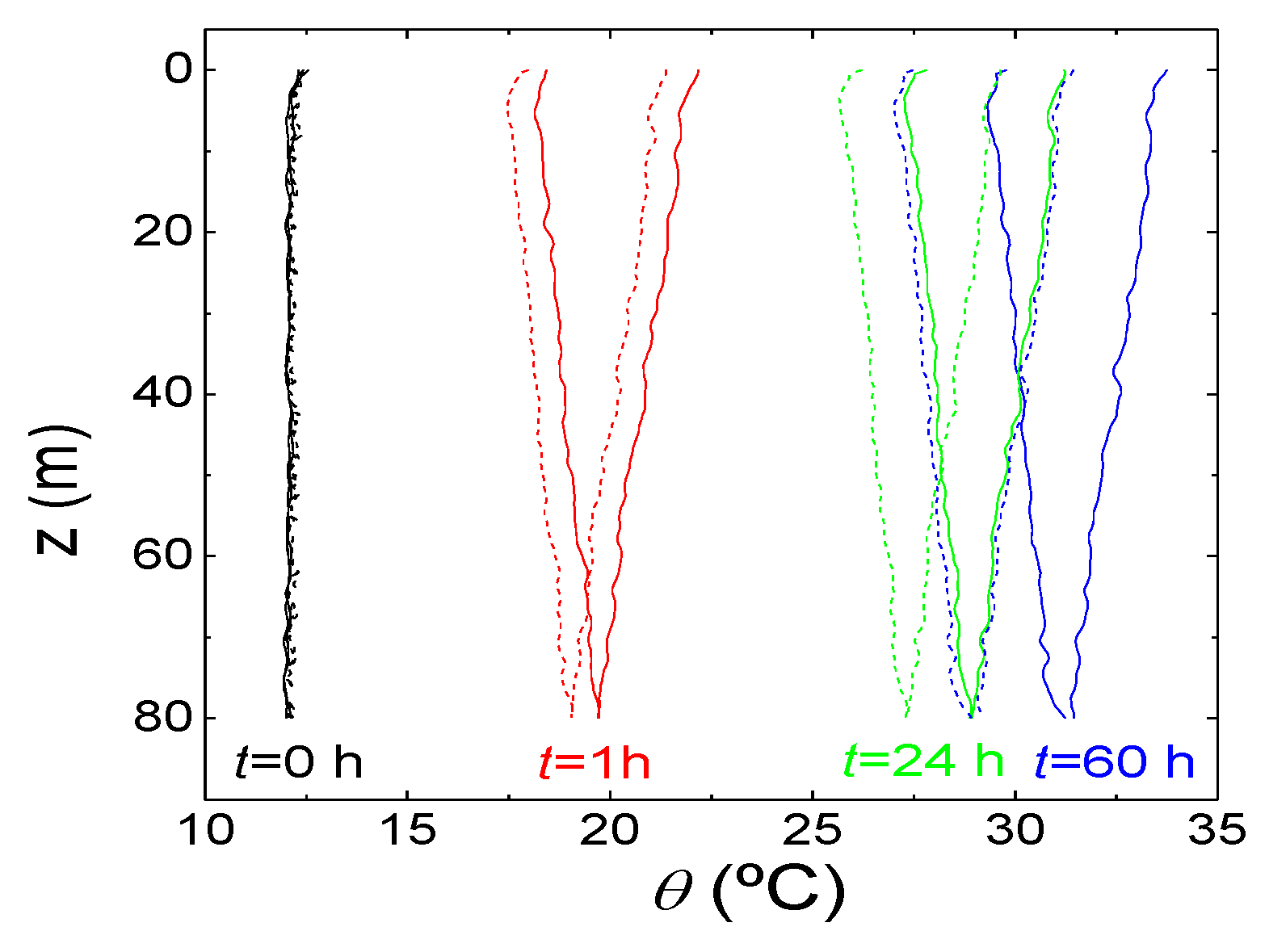
3.2. Profiles of Temperature in the U-Tube
3.3. Comparison of Stepwise Thermal Conductivity under Natural and Artificial Conditions of Groundwater Flow
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Spitler, J.D. Ground-source heat pump system re-search—Past, present and future. HVAC & R Res. 2005, 11, 165–167. [Google Scholar]
- Nagano, K. The progress of GSHP in Japan. IEA Heat Pump Cent. Newsl. 2015, 33, 21–25. [Google Scholar]
- Ingersoll, L.R.; Zobel, O.J.; Ingersoll, A.C. Heat Conduction with Engineering and Geological Applications; McGraw-Hill Book: New York, NY, USA, 1954; pp. 241–245. [Google Scholar]
- Chiasson, A.C.; Rees, S.J.; Spitler, J.D. A preliminary assessment of the effects of ground-water flow on closed-loop ground-source heat pump systems. ASHRAE Trans. 2000, 106, 380–393. [Google Scholar]
- Signorelli, S.; Bassetti, S.; Pahud, D.; Kohl, T. Numerical evaluation of thermal response tests. Geothermics 2007, 36, 141–166. [Google Scholar]
- Angelotti, A.; Alberti, L.; Licata, I.L.; Antelmi, M. Borehole Heat Exchangers: Heat transfer simulation in the presence of a groundwater flow. J. Phys. Conf. Ser. 2014, 501, 1–9. [Google Scholar] [CrossRef]
- Raymond, J.; Therrien, R.; Gosselin, L.; Lefebvre, R. Numerical analysis of thermal response tests with a groundwater flow and heat transfer model. Renew. Energy 2011, 36, 315–324. [Google Scholar] [CrossRef]
- Katsura, T.; Nagano, K.; Nakamura, Y. Development of simulation tool for ground heat exchanger considering multiple geological layer and its Application. Trans. Jpn. Soc. Refrig. Air Cond. Eng. 2015, 32, 335–344. [Google Scholar]
- Mogensen, P. Fluid to duct wall heat transfer in duct system heat storages. Proceeding of the International Conference on Subsurface Heat Storage in Theory and Practice, Stockholm, Sweden, 6–8 June 1983; Swedish Council for Building Research: Stockholm, Sweden, 1983; pp. 1652–6571. [Google Scholar]
- American Society of Heating and Air-Conditioning Engineers (ASHRAE). ASHRAE Handbook Heating, Ventilating and Air-Conditioning Applications; ASHRAE: Atlanta, GA, USA, 2011; p. 34. [Google Scholar]
- IEA ECES Annex 21 Sub-task 4. Standard TRT procedure. In Thermal Response Test Final Report; IEA ECES Annex 21; IEA: Garching, Deutsch, 2013; pp. 1–28. Available online: http://www.iea-eces.org/files/a4.1_iea_eces_annex_21_final_report_1.pdf (accessed on 11 June 2015).
- Bandos, T.V.; Montero, Á.; Fernández, E.; Santander, J.L.G.; Isidro, J.M.; Pérez, J.; Fernández de Córdoba, P.J.; Urchueguía, J.F. Finite line-source model for borehole heat exchangers: Effect of vertical temperature variations. Geothermics 2009, 38, 263–270. [Google Scholar] [CrossRef]
- Bandos, T.V.; Campos-Celador, Á.; López-González, L.M.; Sala-Lizarraga, J.M. Finite cylinder-source model for energy pile heat exchangers: Effects of thermal storage and vertical temperature variations. Energy 2014, 78, 639–648. [Google Scholar] [CrossRef]
- Zarrella, A.; Emmi, G.; Zecchin, R.; De Carli, M. An appropriate use of the thermal response test for the design of energy foundation piles with U-tube circuits. Energy Build. 2017, 134, 259–270. [Google Scholar] [CrossRef]
- Pasquier, P. Stochastic interpretation of thermal response test with TRT-SInterp. Comput. Geosci. 2015, 75, 73–87. [Google Scholar] [CrossRef]
- Lee, C.K. Effects of multiple ground layers on thermal response test analysis and ground-source heat pump simulation. Appl. Energy 2011, 88, 4405–4410. [Google Scholar] [CrossRef]
- Sakata, Y.; Katsura, T.; Zhai, J.; Nagano, K. Estimation of effective thermal conductivities according to multi-layers by thermal response test with a set of fiber optics in a U-tube. J. Jpn. Soc. Civ. Eng. Ser. G 2016, 72, 50–60. [Google Scholar] [CrossRef]
- Daimaru, H. Holocene evolution of the Toyohira River alluvial fan and distal floodplain, Hokkaido, Japan. Geogr. Rev. Jpn. Ser. A 1989, 62, 589–603. [Google Scholar]
- Hu, S.G.; Miyajima, S.; Nagaoka, D.; Koizumi, K.; Mukai, K. Study on the relation between groundwater and surface water in Toyohira-gawa alluvial fan, Hokkaido, Japan. In Groundwater Response to Changing Climate; Taniguchi, M., Holman, I.P., Eds.; CRC Press: London, UK, 2010; pp. 141–158. [Google Scholar]
- Sakata, Y.; Ikeda, R. Regional mapping of vertical hydraulic gradient using uncertain well data: A case study of the Toyohira River alluvial fan, Japan. J. Water Resour. Prot. 2013, 5, 823–834. [Google Scholar] [CrossRef]
- Grattan, K.T.V.; Sun, T. Fiber optic sensor technology: An overview. Sens. Actuators 2000, 82, 40–61. [Google Scholar] [CrossRef]
- Kallio, J.; Leppäharju, N.; Martinkauppi, I.; Nousiainen, M. Geoenergy research and its utilization in Finland. Geol. Surv. Finl. Spec. Pap. 2011, 49, 179–185. [Google Scholar]
- Fujii, H.; Okubo, H.; Nishia, K.; Itoi, R.; Ohyama, K.; Shibata, K. An improved thermal response test for U-tube ground heat exchanger based on optical fiber thermometers. Geothermics 2009, 38, 399–406. [Google Scholar] [CrossRef]
- Acuña, J.; Mogensen, P.; Palm, B. Distributed thermal response test on a U-pipe borehole heat exchanger. In Proceedings of the Effstock—The 11th International Conference on Energy Storage, Stockholm, Sweden, 14–17 June 2009. [Google Scholar]
- Ingersoll, L.R.; Plass, H.J. Theory of the ground pipe heat source for the heat pump. ASHVE Trans. 1948, 54, 167–188. [Google Scholar]
- Witte, H.J.L. Error analysis of thermal response tests. Appl. Energy 2013, 109, 302–311. [Google Scholar] [CrossRef]
- Banks, D. An Introduction to Thermogeology: Ground Source Heating and Cooling, 2nd ed.; Wiley-Blackwell: Oxford, UK, 2008; pp. 285–286. [Google Scholar]
- Nagano, K. Standard Procedure of Standard TRT, version 2.0; Heat Pump and Thermal Storage Technology Center of Japan: Tokyo, Japan, 2011; pp. 1–13. [Google Scholar]
- Diao, N.; Li, Q.; Fang, Z. Heat transfer in ground heat exchangers with groundwater advection. Int. J. Therm. Sci. 2004, 43, 1203–1211. [Google Scholar] [CrossRef]
- Beier, R. Transient heat transfer in a U-tube borehole heat exchanger. Appl. Therm. Eng. 2013, 62, 256–266. [Google Scholar] [CrossRef]

| Instrument | N4385A-008 (A.P. Sensing, Ltd) |
|---|---|
| Maximum distance range | 8 km |
| Spatial resolution | 0.5 m |
| Measurement interval | 1 min |
| Accuracy (Uncertainty) | +/− 0.2 K (moving average per 20 min) |
| Optic fiber | SKF-VP13L404CC140 (NK Systems, Ltd.) |
| Structure | Dual fibers in a single water-proofed tube |
| Diameter | 4 mm (18 mm at the top) |
| Total length | 140 m |
| Temperature range | −10 °C to 85 °C |
| First TRT (no pumping) | Second TRT (pumping) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1Qw | 0 | 0.0053 | |||||||
| 2Q | 5.23 | 5.29 | |||||||
| 3Q* | 5.20 | 5.16 | |||||||
| 4λ | 2.00 | 3.19 | |||||||
| 5λ* | 2.08 | 3.12 | |||||||
| 6i | 7zi | 8qi | 9kti | 10λi | 7zi | 8qi | 9kti | 10λi | 11vr |
| 1 | 10 | 36.4 | 2.46 | 1.18 | 10 | 55.4 | 1.65 | 2.67 | 1.57 |
| 2 | 20 | 56.2 | 2.48 | 1.80 | 20 | 77.8 | 1.66 | 3.73 | 2.70 |
| 3 | 30 | 73.5 | 2.48 | 2.36 | 30 | 76.2 | 1.65 | 3.67 | 0.17 |
| 4 | 40 | 66.9 | 2.50 | 2.13 | 40 | 81.4 | 1.65 | 3.92 | 1.06 |
| 5 | 50 | 80.5 | 2.50 | 2.56 | 50 | 73.0 | 1.61 | 3.61 | 0.35 |
| 6 | 60 | 68.9 | 2.48 | 2.21 | 60 | 54.3 | 1.62 | 2.66 | 0.01 |
| 7 | 70 | 52.7 | 2.48 | 1.69 | 70 | 48.6 | 1.66 | 2.33 | 0.06 |
| 8 | 80 | 84.9 | 2.49 | 2.71 | 80 | 48.9 | 1.65 | 2.35 | 0.08 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakata, Y.; Katsura, T.; Nagano, K.; Ishizuka, M. Field Analysis of Stepwise Effective Thermal Conductivity along a Borehole Heat Exchanger under Artificial Conditions of Groundwater Flow. Hydrology 2017, 4, 21. https://doi.org/10.3390/hydrology4020021
Sakata Y, Katsura T, Nagano K, Ishizuka M. Field Analysis of Stepwise Effective Thermal Conductivity along a Borehole Heat Exchanger under Artificial Conditions of Groundwater Flow. Hydrology. 2017; 4(2):21. https://doi.org/10.3390/hydrology4020021
Chicago/Turabian StyleSakata, Yoshitaka, Takao Katsura, Katsunori Nagano, and Manabu Ishizuka. 2017. "Field Analysis of Stepwise Effective Thermal Conductivity along a Borehole Heat Exchanger under Artificial Conditions of Groundwater Flow" Hydrology 4, no. 2: 21. https://doi.org/10.3390/hydrology4020021
APA StyleSakata, Y., Katsura, T., Nagano, K., & Ishizuka, M. (2017). Field Analysis of Stepwise Effective Thermal Conductivity along a Borehole Heat Exchanger under Artificial Conditions of Groundwater Flow. Hydrology, 4(2), 21. https://doi.org/10.3390/hydrology4020021







