Abstract
Mounding often occurs beneath engineering structures designed to infiltrate reuse water. AQTESOLV software and a spreadsheet solution for Hantush, together with soil moisture water balance (SWAGMAN farm model), were used for quantitatively predicting the height and extent of groundwater mounding underground to assess the groundwater-flow simulations of infiltration from a hypothetical irrigation site. Horizontal and vertical permeability, aquifer thickness, specific yield, and basin geometry are among the aquifer and recharge properties inputs. For 2.2 ha sites, the maximum heights of the simulated groundwater mound ranges up to 0.29 m. The maximum areal extent of groundwater mounding measured from the edge of the infiltration basins of 0.24 m ranges from 0 to 75 m. Additionally, the simulated height and extent of the groundwater mounding associated with a hypothetical irrigation infiltration basin for 2.2 ha development may be applicable to sites of different sizes, using the recharge rate estimated from the SWAGMAN farm model. For example, for a 2.2 ha site with a 0.0002 m/day recharge rate, the irrigation infiltration basin design capacity (and associated groundwater mound) would be the same as for a 1.1 ha site with a 0.0004 m/day recharge rate if the physical characteristics of the aquifer are unchanged. The study claimed that the present modelling approach overcomes the complications of solving the Hantush equation for transient flow. The approach utilised in this study can be applied for other purposes such as measuring the feasibility of infiltrating water, attenuation zone, risk mitigation essential for decision-makers and planning regulators in terms of environmental effects and water use efficiency.
1. Introduction
Concentrating recharge in a small area can cause groundwater mounding that affects the basements of nearby structures. Artificial recharge of groundwater through recharge basins has been conducted for various reasons. In some applications, the goal is to store excess water available seasonally for later use in irrigation. In other applications, the goal is to dispose of treated wastewater. Reuse of treated municipal wastewater for purposes such as agricultural and landscape irrigation reduces the amount of water that needs to be extracted from natural water sources and reduces the discharge of wastewater to the environment [1,2,3,4,5].
There are decades of experience with wastewater irrigation, notably in Spain, Israel, and California (USA), in soil aquifer treatment and managed aquifer recharge [1,6,7]. Studies related to mounding due to infiltration have been a focus of many researchers. Infiltration of irrigation water is a similar application, although the timeframe of infiltration may vary. Meanwhile, infiltration water, stormwater, or wastewater may rise in low hydraulic conductivity layers in the vadose zone and may cause mounding of the water table beneath the infiltration area or the perched mound [8].
Analytical techniques have been used to estimate the magnitude and extent of groundwater mounding beneath infiltration structures [9,10,11,12,13,14]. A number of investigators have presented analytical solutions for the shape of the water table beneath an artificial recharge basin, including [15], and [16] evaluated these solutions. Previous works presented a similar analytical solution to that of [15] that include a variety of different boundary conditions (for example, [17]). For all of the analytical solutions referenced above, it is assumed that flow away from the location of the recharge basin is horizontal and occurs in an isotropic, homogeneous aquifer in which the change in height of the water table is not large (generally less than one-half the aquifer thickness). Although the above analytical solutions have been used to simulate the shape of a groundwater mound beneath hypothetical infiltration basins, they are difficult to apply without numerical integration [18]. Previous researchers found the solution of [15], to be the most accurate and amenable to numerical integration. [19] presents a computer program for solving the [15] equation, and [20] offers a simplified method for solving the Hantush equation, but both of these approaches are used only with steady-state conditions [12,17,21]. The difficulty of solving the Hantush equation for transient flow has prevented it being from widely applied in groundwater mounding applications [4]. To overcome this limitation, the current study combines the soil moisture water balance empirical mode together with AQTESOLV software and [15] via a spreadsheet model solution.
The aim of this paper is to estimate the seasonal accession of deep drainage from irrigation practices to the groundwater level, assess the potential for mounding of the water table and risk of land salinisation, and assess the potential effect on groundwater quality due to irrigation. The hypothetical site (Figure 1) is proposed to be developed for irrigation of a tree plantation using treated sewage effluent.
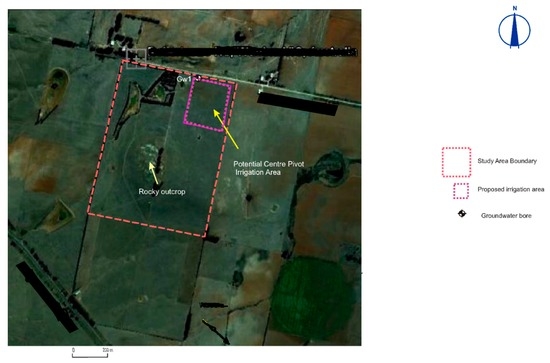
Figure 1.
Aerial photo of the hypothetical study area.
2. Site Description—Background of the Hypothetical Site
The hypothetical site is assumed to be in extensive granite throughout the vicinity of the site, and granite outcrop at the site (Figure 1 and Figure 2) is considered as a potential recharge area to the underlying aquifer at the site due to hydraulic connection. Therefore, based on the current investigation, the rocky granite outcrop in the site is likely to be a groundwater recharge area. Irrigation should be avoided in the area of granite outcrop, which would be the case for practical agronomic reasons.
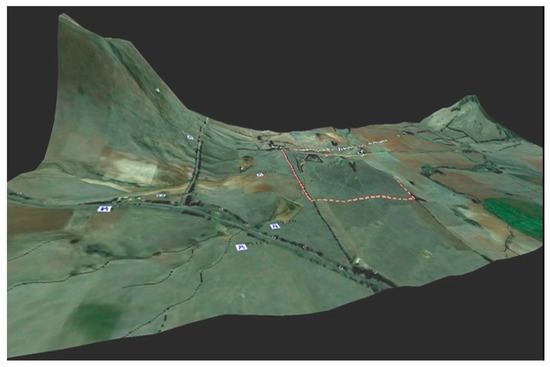
Figure 2.
Local topography of the hypothetical study area and its surroundings, with a granite ridge representing the higher elevation inside the study area, shown with dashed line (viewed to the north).
Groundwater was initially intersected in groundwater bore in a weathered zone at the base of the basalt or top of the granite. Water was struck approximately 12 m deep, and a week later the groundwater level was observed at 2 m Below Ground Level (BGL). This indicates that the aquifer intersected is confined and has a potentiometric surface or level (imaginary water level due to pressure) close to ground level. This is not the water table level, and, assuming that this interpretation applies to the entire irrigation area, the upper volcanic aquifer is unsaturated in this area. The groundwater seems to be discharging from the weathered granite. The degree of connectivity between the upper volcanic aquifer units and the underlying granite aquifer is variable, as the upper volcanic aquifer can be extensively weathered to clay, and the extensive clay/silt capping and deeper ancient buried soil horizons is of variable thickness across the site. It is expected that the natural groundwater flow direction is consistent (Figure 3) with the regional topography (Figure 4) following the contours of the land and water course.
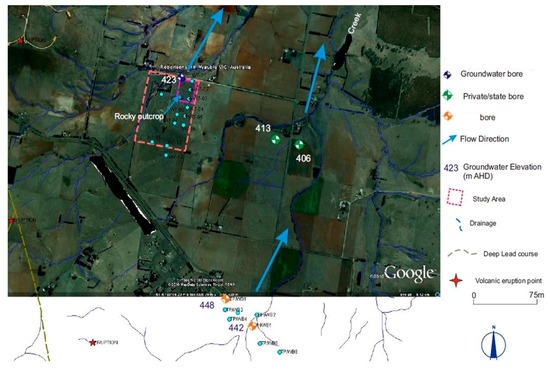
Figure 3.
Groundwater elevation and flow direction.
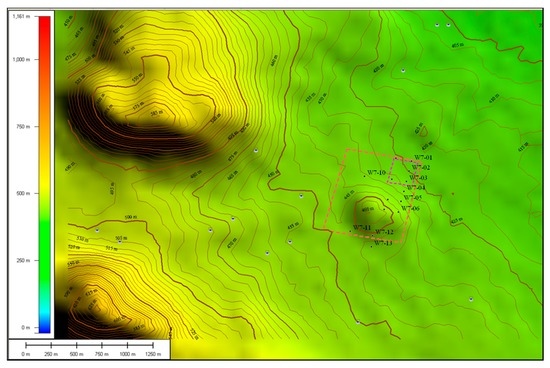
Figure 4.
Topographic contours of the hypothetical study area.
3. Approach
The current study utilised the combination of analytical and soil moisture water balance models. The details of the methods are discussed below.
3.1. Analytical Use of Hantush (1967) Solution to Estimate Groundwater Mounding
Both AQTESOLV software (using the infiltration tool) and a spreadsheet [4] to numerically integrate equations presented by [15] were used to calculate groundwater mounding. The spreadsheet method [4] was used to quantitatively estimate the extent of groundwater mounds near the proposed irrigation basin, and the AQTESOLV software was employed to simulate the height of groundwater mounds. The spreadsheet accepts user-supplied values for horizontal soil permeability, initial saturated aquifer thickness, specific yield, basin length, basin width, and the duration and magnitude of the recharge rate.
3.2. Soil Moisture Water Balance via the SWAGMAN Model to Estimate Net Recharge
Recharge was estimated using soil moisture water balance via the SWAGMAN model. Hantush’s equations define the shape of groundwater mounds beneath rectangular (including square) or round infiltration basins, and are based on several simplifying assumptions, including that the aquifer has a homogeneous and isotropic flow. The SWAGMAN Farm modeling system is a farm scale for water and salt balance within irrigation areas. The model considers the distribution of soils within the farm, potential land uses, crop evaporative requirements, current irrigation practices, leaching requirements, annual rainfall, rainfall runoff, leakage to deeper aquifers, depth to water tables, capillary upflow from shallow water tables, the salt concentration of the irrigation water, groundwater, and rainwater, and the economic returns of potential land use. The quantitative net recharge information is crucial when examining options that aim to balance irrigation profitability with natural resource management and to increase water use efficiency at the farm level [22,23,24,25].
4. Analysis and Result
An assessment of the potential for irrigation of treated effluent to impact local groundwater quality was undertaken. The most important factors that control the risk groundwater pollution are the depth to the groundwater and the nature of the vadose zone, the net recharge (including the impact of vadose zone and soil type), and the topography. In this study, the depth to groundwater refers to the top of the aquifer, where the aquifer is confined. The depth to water table and the nature of the vadose zone is primarily important because it determines the depth of the material through which a contaminant must travel before reaching the aquifer. The depth to water is also important because it provides the maximum opportunity for the adsorption of metals or the biodegradation of organic contaminants. In general, there is a greater chance for attenuation to occur as the depth to groundwater increases because deeper water levels infer longer travel times of contaminants travelling from the land surface.
Assuming the aquifer is confined with a potentiometric surface at 2 m BGL, the vadose zone is approximately 11 m thick. The material in the vadose zone includes clay and weathered basalt as well as fresh basalt fractured rock. This provides ample opportunity for the attenuation of contaminants originating from irrigation at the land surface.
In areas where the aquifer is unconfined, recharge to the aquifer usually occurs more readily, and the potential for contamination of groundwater is greater than in areas with a confined aquifer. The principal recharge areas for confined aquifers are often remote from the point of observation (many kilometres away). The granite ridge within the site could be a recharge area, but it is not proposed as an irrigation area.
The net recharge is estimated from excess precipitation, which is when the precipitation exceeds the evapotranspiration. At our site, this occurs between about May to August (potential for recharge to the groundwater). Irrigation practices can result in the increased percolation of water to the shallower aquifer (artificial recharge). An additional factor must be considered since irrigation uses the wastewater. This requires an estimation of the seasonal accession of deep drainage from irrigation to the water table. The SWAGMAN (Salt Water and Groundwater Management) farm model was used to estimate the net recharge to the groundwater using the equation below:
Net recharge = Irrigation + Rainfall + Capillary upflow − (Evapotranspiration + leakage + runoff + change in soil content).
The model accounts for the initial soil water condition and changes in soil water content during cropping and fallow periods and associated recharge to groundwater. When the water table is deeper than 1.5 m to 2 m, most land uses show negligible capillary upflows.
The water balance modeling previously undertaken has been used to estimate the amount of recycled water that will be available for irrigation. The maximum quantity of water reused when fully developed will be 11 ×106 L/year, which can service up to 60 properties. This study estimated net recharge using the SWAGMAN model.
The proposed irrigation area is a 2.2 ha farm. The farm has an annual allocation of 11 × 106 L, with an assumed depth to water level at 2 m and a groundwater salinity of 3000 µS/cm. Using monthly climate data from the irrigation area, the reference evapotranspiration data calculated is adjusted with a crop coefficient. Optimisation of available farm land with crop types was carried out to match water use as much as possible to crop water needs in order to minimise wastage and excessive groundwater recharge.
The SWAGMAN model combines not only crop water use, but also a complex range of other information including soils, current irrigation practices, leaching requirements, rainfall, depth to water tables, capillary upflow, the salt concentration of irrigation water, and groundwater. The SWAGMAN model results of this scenario show that, with average irrigation efficiency, in an average rainfall year, the water table can rise by about 0.21 m (after contributing a net recharge of 1.87 ×106 L (0.85 ×106 L/ha).
4.1. Seasonal Accession to Groundwater (Net Recharge)
The soil moisture water balance result using the SWAGMAN farm model indicates that there is less net recharge (estimated about 0.0002 m/day) to the groundwater. There will be less influence to the groundwater level if the proposed irrigation area is underlain by a thick unsaturated zone (>11 m) and an extensive/continuous confining layer throughout the site.
4.2. Estimate of Ground Mounding Effect
The net recharge estimated using the SWAGMAN farm model was used to assess its effect in relation to groundwater mounding. AQTESOLV software was used to simulate groundwater mounding beneath the irrigation area (for 4 months irrigation) with an analytical solution by [15]. This is based on the assumption that there is a shallow water table beneath the site. Similarly, a spreadsheet model that uses [15] was used to simulate groundwater mounding in relation to distance from the centre of the basin. The spreadsheet calculates the height of a groundwater mound beneath a hypothetical stormwater infiltration basin. The macro uses the Excel function “Goal seek” to converge on a solution where the estimated and calculated water levels are within 0.0001 [4,25]. Physical variables affecting height and extent of groundwater mounding includes soil permeability, aquifer thickness, specific yield, design irrigation, basin shape, and depth to water tables.
The required input values are summarised below.
4.2.1. Aquifer Properties
Horizontal hydraulic conductivity (k) = 0.0005 m/day. Vertical hydraulic conductivity is assumed to be one-tenth horizontal hydraulic conductivity.
- Specific yield (Sy) = 0.1;
- Initial saturated thickness (h(0)) = 2 m;
- Half-length of basin (X direction) = 50 m;
- Half-length of basin (Y direction) = 50 m.
4.2.2. Recharge Area Properties
- Recharge rate = 0.0002 m/day (= (1.87 × 106 L/2.2 ha) per year);
- Simulation time (t) = 120 days;
- Time when recharge stops, (t(0)) = 36,500 days;
- Initial thickness of saturated zone = 10 m.
The last consideration at the discharge sites is the potential that the increase in the groundwater mound would result in undesirable effects on the surrounding area: if the water table mound rises above basements, foundations, or other structures in the area, there could be potentially serious consequences that would disqualify any affected site as a useful discharge area. The groundwater mounding result (Table 1) shows that the groundwater level could rise by approximately 0.3 m (annually). Given the current interpretation of the aquifer being confined, this rise would be insignificant as the host rock/aquifer is unsaturated at the site.

Table 1.
Transient water table rise.
Mounding was modelled at peak discharge/percolation for the site, and it was concluded that there will be no problems with mounding at the site/in the vicinity. The maximum thickness of the saturated thickness beneath the centre of the basin at the end of the infiltration period will increase by 0.24 m (Figure 5), and the impact of the (lateral spreading) mounding will be insignificant/nil past 75 m from the centre of the basin.
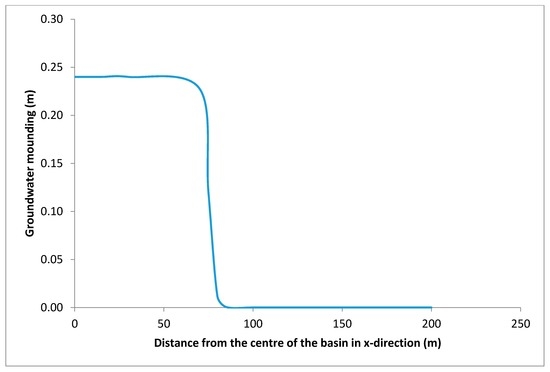
Figure 5.
Groundwater mounding in meter versus distance from the centre of the basin.
4.3. Effect on Groundwater Quality
According to EPA regulations, governing discharge facilities for small wastewater treatment facilities, the minimum depth to mounded water table is 1.5 m at the discharge site [26]. Given that the aquifer is deep and confined by clay and weathered basalt, there is significant protection of the groundwater quality. As demonstrated in the table above, the groundwater table does not mound enough to be a concern at any site. The surrounding land uses, nearby potential sources of contamination, and sensitive receptors are assessed in relation to the effect of mounding. If the modelled effluent volume was actually discharged, nearby homes and structures could be substantially affected by the increased groundwater table. This could lead to treated effluent leaking into the basements of nearby homes, or permanent damage to the substructure of roads in the area.
4.4. Attenuation Zone
These data for hydraulic conductivity (K) indicate that the productivity of the aquifer in the hypothetical site area is likely to be low [27,28]. However, the productivity of the aquifers is likely to be enhanced within closer proximity to the recharge point (e.g., toward the granite outcrop). The average linear seepage velocity (V) is calculated using the equation below:
where K = Hydraulic conductivity, i = Hydraulic gradient, and n = effective porosity
The K-value ranges from 0.0005 to 0.0006 m/day, which falls within the general range for fractured and/or weathered granites [27]. The average linear seepage velocity (groundwater flow rate based on Equation (2)) ranges from 7.3 × 10−3 to 8.8 × 10−3 m/year (an assumed porosity of 0.25 and a hydraulic gradient value of ~0.01) [29] provides for an “attenuation zone” around certain types of contamination source facilities, namely, landfills, evaporation basins (ash ponds), and wastewater irrigation. The policy allows for the beneficial uses of groundwater to be precluded by contamination within the attenuation zone but not extending beyond the site boundary.
4.5. The Potential Impact of Water Reuse on Groundwater Beneficial Uses
The proposed wastewater reuse of the site will not have any significant impact on the groundwater quality at the site because the thickness of the unsaturated zone and the presence of thick clay soils provide protection for the underlying aquifer in the event of the release of contaminants at the land surface. Meanwhile, given that the hypothetical site is a “confined aquifer” condition (with a thick vadose zone), it is possible that a perched water table aquifer occurs at the site. Further monitoring bores should be installed as part of the reuse facility to monitoring for this phenomenon.
4.6. Risk Management Measure
The only management measures considered prudent to manage the residual risk of impact on groundwater by irrigation would be to monitor the groundwater for mounding or quality impacts in a series of purpose-built monitoring bores and to periodically consider the potential need for an attenuation zone in general accordance with current industry standards and groundwater quality guidelines [26,29]. In the case of the hypothetical site, the indicted low risk of any impact on the groundwater suggests that an attenuation zone would not be necessary. However, it is recommended that the irrigation reuse operator undertake a periodic review of the groundwater monitoring data, and studies aiming to determine the potential need for a groundwater quality attenuation zone should be conducted.
The treated effluent proposed to irrigate the site is to have the salinity of approximately 1400 mg/L Total Dissolved Solutes (TDS), which is less than the local groundwater salinity of approximately 1600 mg/L. The effluent nutrient would tend to be taken up by the irrigated crop if the effluent nutrient values are not high (less than the local groundwater salinity).
5. Discussion and Conclusions
This paper present a modelling approach to simulate the groundwater mounding due to irrigation practices. The purpose of this method was to provide preliminary data on the suitability of a hypothetical site for irrigation purposes using wastewater and the consequent implications for groundwater quality. The current study demonstrates the combination use of analytical and empirical models. It combines AQTESOLV software and a spreadsheet solution for [15] to overcome the difficulty of solving the Hantush equation for transient flow, which has prevented it from being widely applied in groundwater mounding applications. Net recharge was estimated using a soil moisture water balance and the SWAGMAN farm model, which was an input to the Hantush solution to simulate the maximum height of groundwater mounding and the maximum extent of groundwater mounding. Based on the estimated net recharge, the mounding potential was estimated to be 0.3 m annually. This mound would reduce after the irrigation season. While the overall risk of mounding, causing a shallow water table and salinisation effects, are minimal at this site, the uncertainty around the potential for a perched water table aquifer indicates the need to incorporate a groundwater monitoring system in the final facility. This approach can help to estimate the seasonal accession of deep drainage from irrigation to the water table (site water balance), assess the potential for mounding of the water table and the risk of land salinisation, and assess the potential effect on groundwater quality due to irrigation.
The analytical solution predicts mounding with relatively less execution time. The extended application of such an approach includes assessing the effect on groundwater quality, the attenuation zone, and the risking mitigation measure [30,31]. The model can be used to assist decision-makers in choosing techniques or formulating strategies to manage infiltration and planning regulators. The outcome can help to provide preliminary recommendations on the potential impacts of the wastewater reuse (irrigation) on the water or land environments at the site and can provide the approval assessment of a treated effluent reuse in relation to on-site and off-site impacts. However, when there is potential for problematic mounding in a heterogeneous and anisotropic site condition, the use of a numerical model is appropriate for representing the vertical component of the flow. Although an over-prediction of the mound height or extent could result if the layer is assumed to be continuous, a discontinuous layer exists because some of the wastewater travels between the discontinuous low-permeability zones and does not mound in these areas.
The study demonstrates a method of assessing the net recharge from irrigation by estimates of soil moisture surplus contributing to groundwater, by estimates of potential groundwater mounding effect, and by estimates of worst-case impacts on quality due to effluent reuse. The result presented in this study can be readily transferred to other geographical settings and may assist in extending the current state of knowledge or practice. This method can be applied elsewhere for other purposes, such as the feasibility of infiltrating water via a trench/gallery where there is shallow groundwater such that water can infiltrate into an aquifer via the additional head generated.
Acknowledgments
The author acknowledges the contribution from anonymous reviewers. The manuscript has benefitted from reviewers’ and editors’ comments.
Conflicts of Interest
The author declares no conflict of interest.
References
- Andreas, N.; Angelakis, A.N.; Snyder, S.A. Wastewater Treatment and Reuse: Past, Present, and Future. Water 2015, 7, 4887–4895. [Google Scholar]
- Yihdego, Y.; Al-Weshah, R. Engineering and environmental remediation scenarios due to leakage from the Gulf War oil spill using 3-D numerical contaminant modellings. J. Appl. Water Sci. 2016. [Google Scholar] [CrossRef]
- Al-Weshah, R.; Yihdego, Y. Modelling of Strategically Vital Fresh Water Aquifers, Kuwait. Env. Earth Sci. 2016, 75, 1315. [Google Scholar] [CrossRef]
- Carleton, G.B. Simulation of Groundwater Mounding Beneath Hypothetical Stormwater Infiltration Basins: U.S. In Geological Survey Scientific Investigations Report 2010–5102; USGS: Reston, VA, USA, 2010; p. 64. [Google Scholar]
- Yihdego, Y.; Al-Weshah, R. Gulf war contamination assessment for optimal monitoring and remediation cost –benefit analysis, Kuwait. Env. Earth Sci. 2016, 75, 1234. [Google Scholar] [CrossRef]
- Dismore, W.A.; Moran, A.P.; Vasallo, K.A. Modeling, Analysis and Design of Effluent Disposal to Reduce Estuarine Nitrogen Levels in Mashpee, MA, USA; E-Project-030508-144909; Worcester Polytechnic Institute, Civil and Environmental Engineering: Mashpee, MA, USA, 2008. [Google Scholar]
- Pedrero, F.; Ioannis, K.; Alarcón, J.J.; Asano, T. Use of treated municipal wastewater in irrigated agriculture-Review of some practices in Spain and Greece. Agric. Water Manag. 2010, 97, 1233–1241. [Google Scholar] [CrossRef]
- Poeter, E.; McCray, J.E.; Thyne, G.; Siegrist, R. Guidance for Evaluation of Potential Groundwater Mounding Associated with Cluster and High-Density Wastewater Soil Absorption Systems; Project No. WU-HT-02–45; Washington University: St. Louis, MO, USA, 2005. [Google Scholar]
- Poeter, E.; David, A. Multi-model ranking and inference in groundwater modelling. Groundwater 2005, 43, 597–605. [Google Scholar] [CrossRef] [PubMed]
- Yihdego, Y. Engineering and enviro-management value of radius of influence estimate from mining excavation. J. Appl. Water Eng. Res. 2017. [Google Scholar] [CrossRef]
- Yihdego, Y.; Al-Weshah, R. Assessment and prediction of saline sea water transport in groundwater using using 3-D numerical modelling. Environ. Process. J. 2016, 89, 144–154. [Google Scholar] [CrossRef]
- Poeter, E.; McCray, J.E. Modelling water table mounding to design cluster and high-density wastewater soil absorption systems. ASCE J. Hydrol. Eng. 2008, 13, 702–709. [Google Scholar]
- Yihdego, Y. Evaluation of Flow Reduction due to Hydraulic Barrier Engineering Structure: Case of Urban Area Flood, Contamination and Pollution Risk Assessment. J. Geotech. Geol. Eng. 2016, 34, 1643–1654. [Google Scholar] [CrossRef]
- Yihdego, Y.; Webb, J.A.; Vaheddoost, B. Highlighting the Role of Groundwater in Lake—Aquifer Interaction to Reduce Vulnerability and Enhance Resilience to Climate Change. J. Hydrol. 2017, 4, 10. [Google Scholar] [CrossRef]
- Hantush, M.S. Growth and decay of groundwater mounds in response to uniform percolation. Water Resour. Res. 1967, 3, 227–234. [Google Scholar] [CrossRef]
- Warner, J.W.; Molden, D.J.; Chehata, M.; Sunada, D.K. Mathematical analysis of artificial recharge from basins. Water Resour Bull. 1989, 25, 401–411. [Google Scholar] [CrossRef]
- Manglik, A.; Rai, S.N.; Singh, R.N. Modelling of aquifer response to time varying recharge and pumping from multiple basins and wells. J. Hydrol. 2003, 292, 23–29. [Google Scholar] [CrossRef]
- Yihdego, Y.; Drury, L. Mine water supply assessment and evaluation of the system response to the designed demand in a desert region, central Saudi Arabia. Environ. Monit. Assess. J. 2016, 188, 619. [Google Scholar] [CrossRef] [PubMed]
- Finnemore, E.J. A program to calculate ground-water mound heights. Ground Water 1995, 33, 139–143. [Google Scholar] [CrossRef]
- Zomorodi, K. Simplified solutions for groundwater mounding under stormwater infiltration facilities. In Proceedings of the American Water Resources Association 2005 annual Water Resources Conference, Seattle, WA, USA, 7–10 November 2005; American Society of Civil Engineers: Kansas City, MO, USA, 2005; p. 4. [Google Scholar]
- Latinopoulos, P. The response of groundwater to artificial recharge schemes. Water Resour. Res. 1981, 17, 1712–1714. [Google Scholar] [CrossRef]
- Yihdego, Y. Water Reuse in Hilly Urban Area. In Urban Water Reuse Handbook (UWRH); Eslamian, S., Ed.; Francis and Taylor, CRC Group: Burlington, MA, USA, 2015; Chapter 70; pp. 903–913. [Google Scholar]
- Swagman Model Farm 2016. Available online: http://www.colyirr.com.au/swagmanfarm/allUser/SwagFarm.asp (accessed on 15 March 2016).
- Yihdego, Y. Water Reuse and Recreational Waters. In Urban Water Reuse Handbook (UWRH); Eslamian, S., Ed.; Francis and Taylor, CRC Group: Burlington, MA, USA, 2015; Chapter 78; pp. 1029–1039. [Google Scholar]
- Yihdego, Y.; Reta, G.; Becht, R. Hydrological analysis as a technical tool to support strategic and economic development: Case of Lake Navaisha, Kenya. Water Environ. J. 2016, 30, 40–48. [Google Scholar] [CrossRef]
- United States Environmental Protection Agency. Groundwater Sampling Guidelines Wastewater Technology Factsheets; Publication 669, EPA 832-F-02-12; United States Environment Protection Agency Authority, Municipal Technology Branch: Ada, OK, USA, 2002.
- Freeze, A.; Cherry, J. Groundwater; Prentice Hall Publishers: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Yihdego, Y. Hydraulic In situ Testing for Mining and Engineering Design: Packer Test Procedure, Preparation, Analysis and Interpretation. J. Geotech. Geol. Eng. 2016, 35, 29–44. [Google Scholar]
- Marker, R.B. Contaminants in the Subsurface: Source Zone Assessment and Remediation, National Research Council; The National Academies Press: Washington, DC, USA, 2007; p. 358. [Google Scholar]
- Khan, S.; Xevi, E.; O’Çonnell, N.; Madden, J.C.; Zhou, F. A farm scale hydrologic economic optimisation model to manage water logging and salinity in irrigation area. In Proceedings of the Fourth Biennial Engineering Mathematics and Applications Conference, EMAC 2000, RMIT University, Melbourne, Australia, 10–13 September 2000; pp. 179–182. [Google Scholar]
- Manglik, A.; Rai, S.N.; Singh, R.N. Response of an unconfined aquifer induced by time varying recharge from a rectangular basin. Water Resour. Manag. 1997, 11, 185–196. [Google Scholar] [CrossRef]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).