Meteorological Knowledge Useful for the Improvement of Snow Rain Separation in Surface Based Models
Abstract
:1. Introduction
2. Atmospheric Interactions during Phase Change
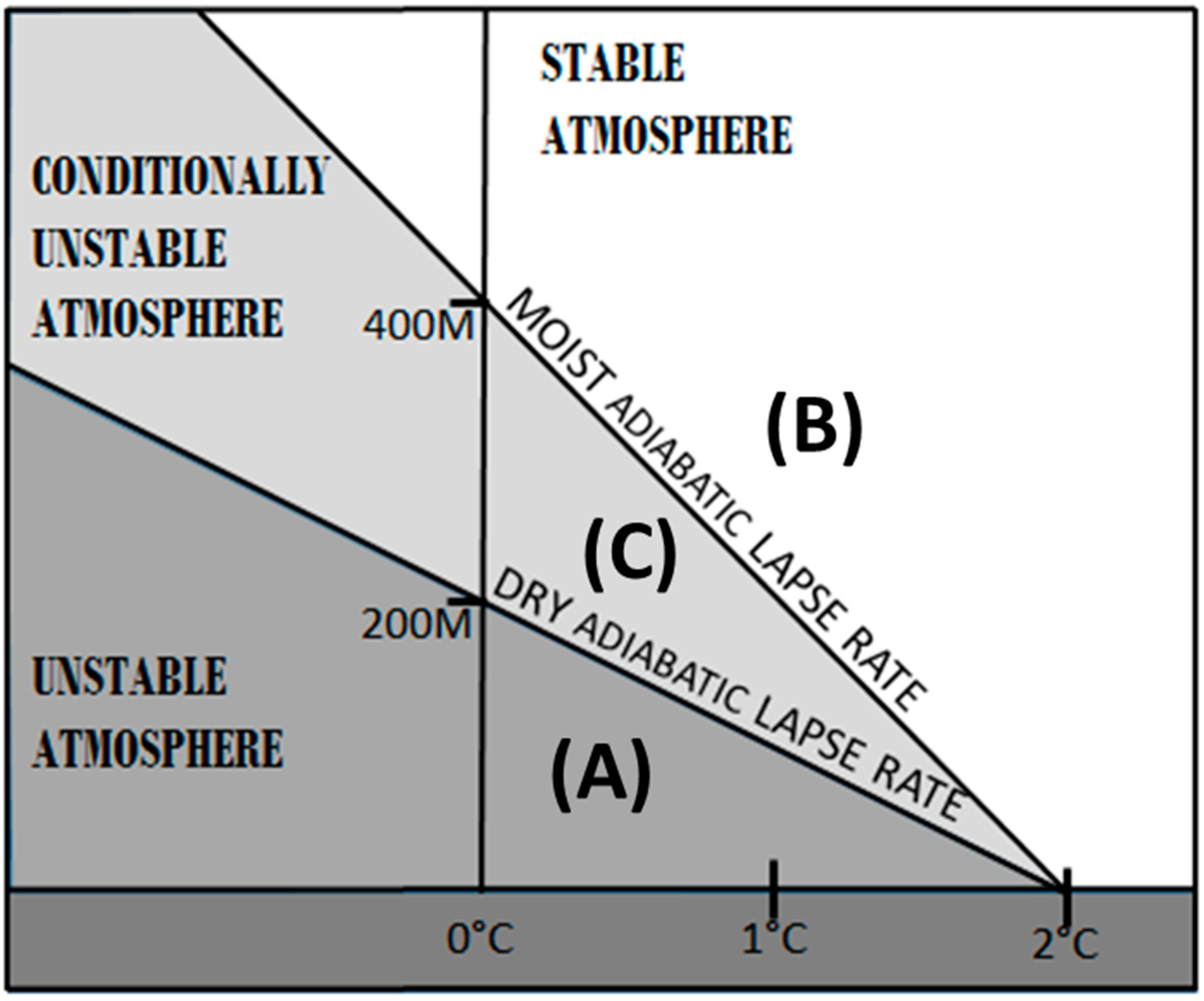
2.1. Lapse Rates
2.2. Deviations from Average Lapse Rates
2.2.1. Air Mass Boundaries
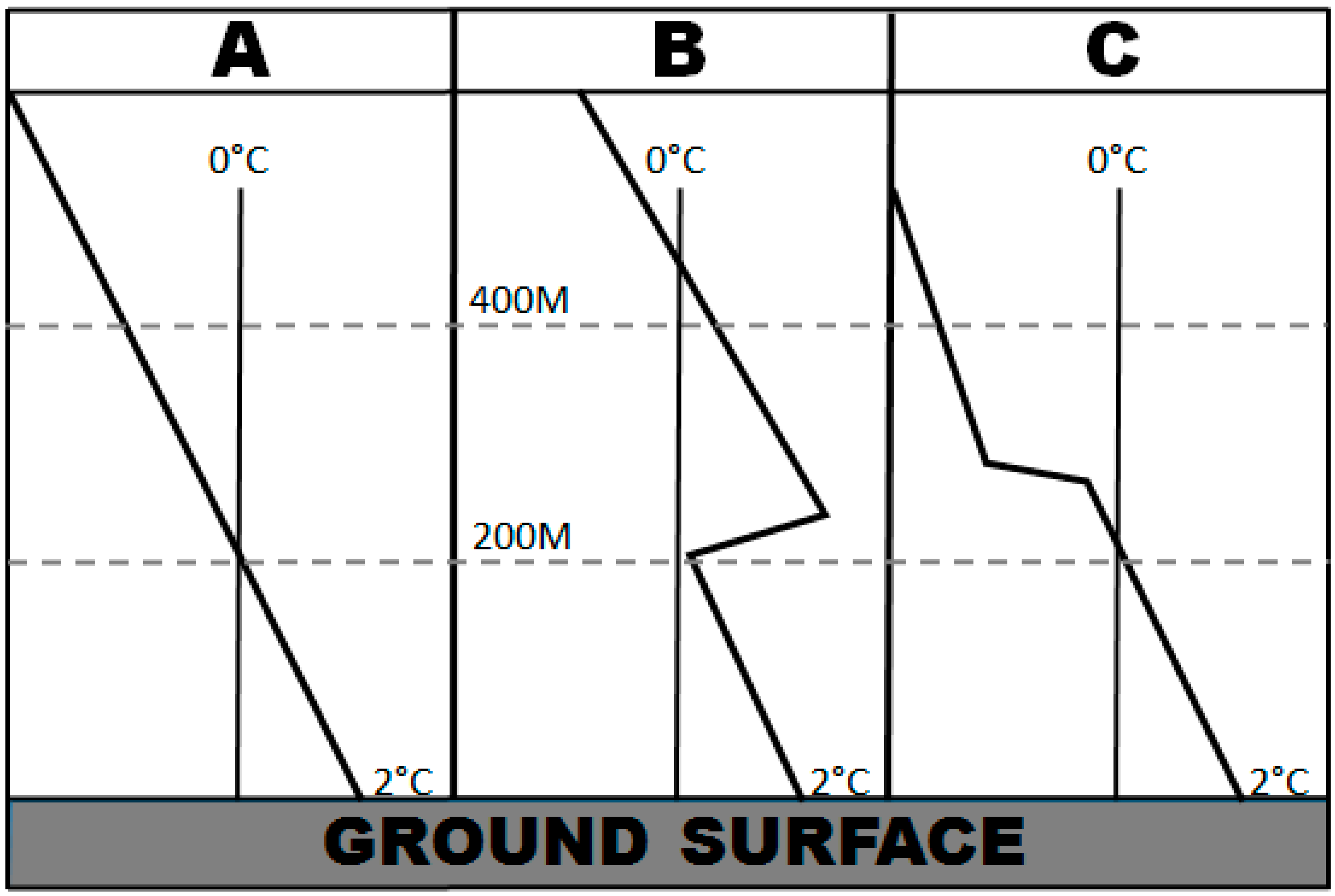
2.2.2. Isothermal Layers
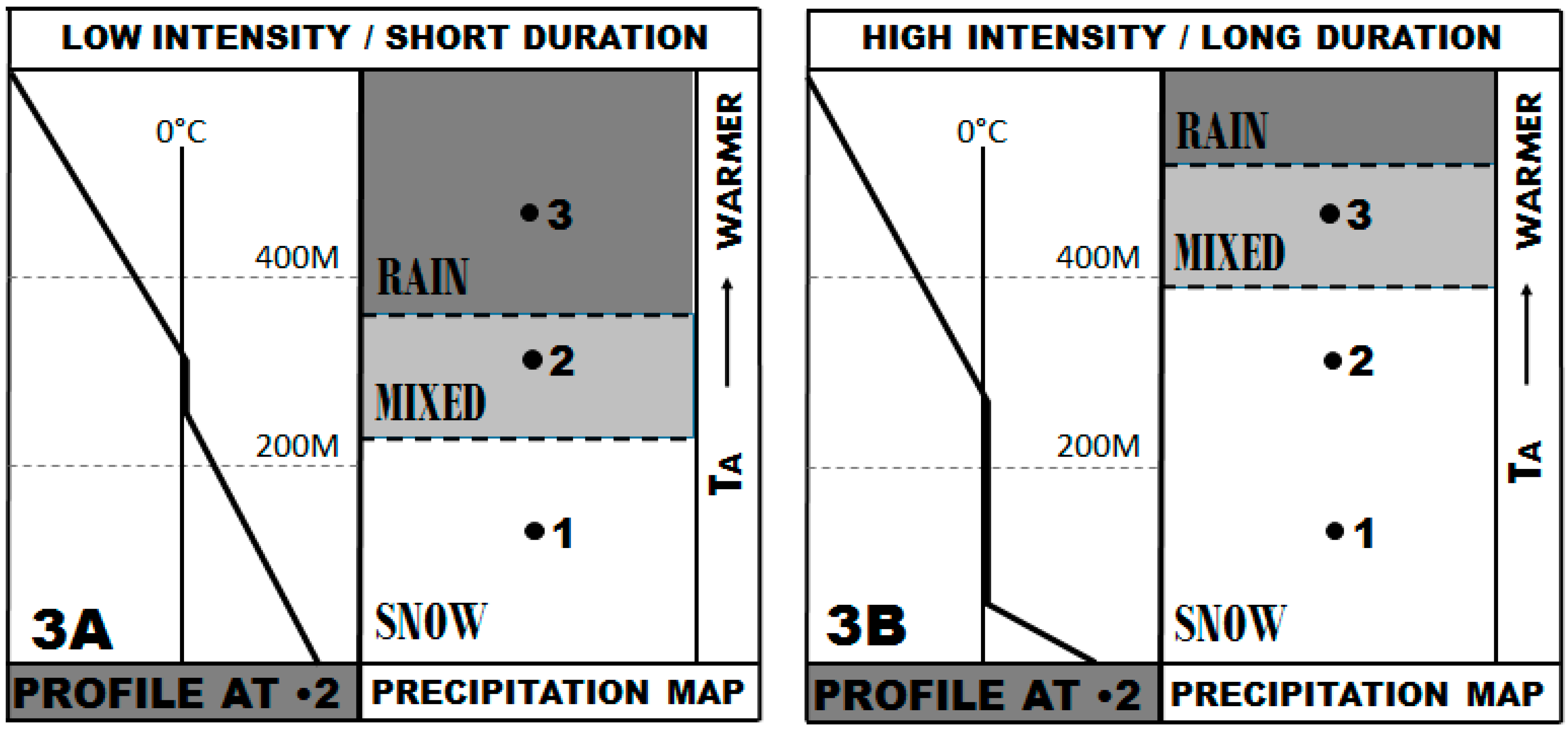
2.2.3. Precipitation Intensity and Duration
2.2.4. Evaporation, Sublimation and Condensation
2.2.5. Hydrometeor Interactions
2.2.6. Terrain Influence

3. Atmospheric Precipitation Phase Determination
3.1. Bulk Microphysical Schemes
| Microphysical Scheme | Precipitation Types | Allows Mixed Phase Processes |
|---|---|---|
| Morrison 2-Moment | 10 | Yes |
| Thompson | 7 | Yes |
| Goddard | 6 | Yes |
| Purdue Lin | 6 | Yes |
| WSM6 | 6 | Yes |
| WSM5 | 5 | No |
| WSM3 | 3 | No |
| Kessler | 3 | No |
| Eta GCP | 2 | Yes |
3.2. Empirical Phase Determination Schemes
3.2.1. Thickness Values

3.2.2. Freezing Levels
| Freezing Layer Height (m)* | 0 | 95 | 200 | 280 | 365 |
|---|---|---|---|---|---|
| Snow Probability (%) | 100 | 90 | 70 | 50 | 0 |
4. Surface Based Precipitation Phase Determination
4.1. Time Step Dependence
4.2. Regional Variance
4.3. Variations Caused by Threshold Determination Method
| Model Name, Reference | TRS °C | Applied Region | TRS Method |
|---|---|---|---|
| CLM Community Land Model [2] | 2.5 | French Alps | M |
| WRF_CLM Weather Research and Forecasting CLM [2] | 2.5 | French Alps | M |
| BATS Biosphere–Atmosphere Transfer Scheme [49] | 2.2 | Former Soviet Union | M |
| Dai [18] | 1.9 | Ocean; world wide | DO |
| 1.2 | Land; world wide | ||
| Feiccabrino et al. [21] | 1.0 | Sweden | DO |
| Feiccabrino et al. [48] | 1.0 | Northern US | DO |
| L’hôte et al. [51] | 0.75–1.25 | Andes | IO |
| L’hôte et al. [51] | 0.50–1.00 | Switzerland | DO |
| Ye et al. [1] | 0.5–1.0 | European Russia | DO |
| Ye et al. [1] | 1.5–2.5 | South-central Siberia | DO |
| HBV Braun and Lang [52] Hottelet et al. [53] | 0.5, −0.8, 1.0 | Switzerland, low Alpine Czech Republic, sub-alpine | M M |
| EALCO Ecological Assimilation of Land and Climate Observations [54] | 0.0 | Northern Canada | M |
| ISBA Interactions between Soil, Biosphere and Atmosphere [55] | −1.5 | Tropical Andes Cordillera, | M |
4.4. Air Temperature Threshold Schemes
4.4.1. Critical Air Temperature Threshold Schemes
4.4.2. Dual Air Temperature Threshold Schemes
4.4.3. Air Mass Boundary Scheme
4.5. Temperature Schemes Including Humidity
4.5.1. Dew Point Temperature Schemes
4.5.2. Wet-Bulb Temperature Schemes
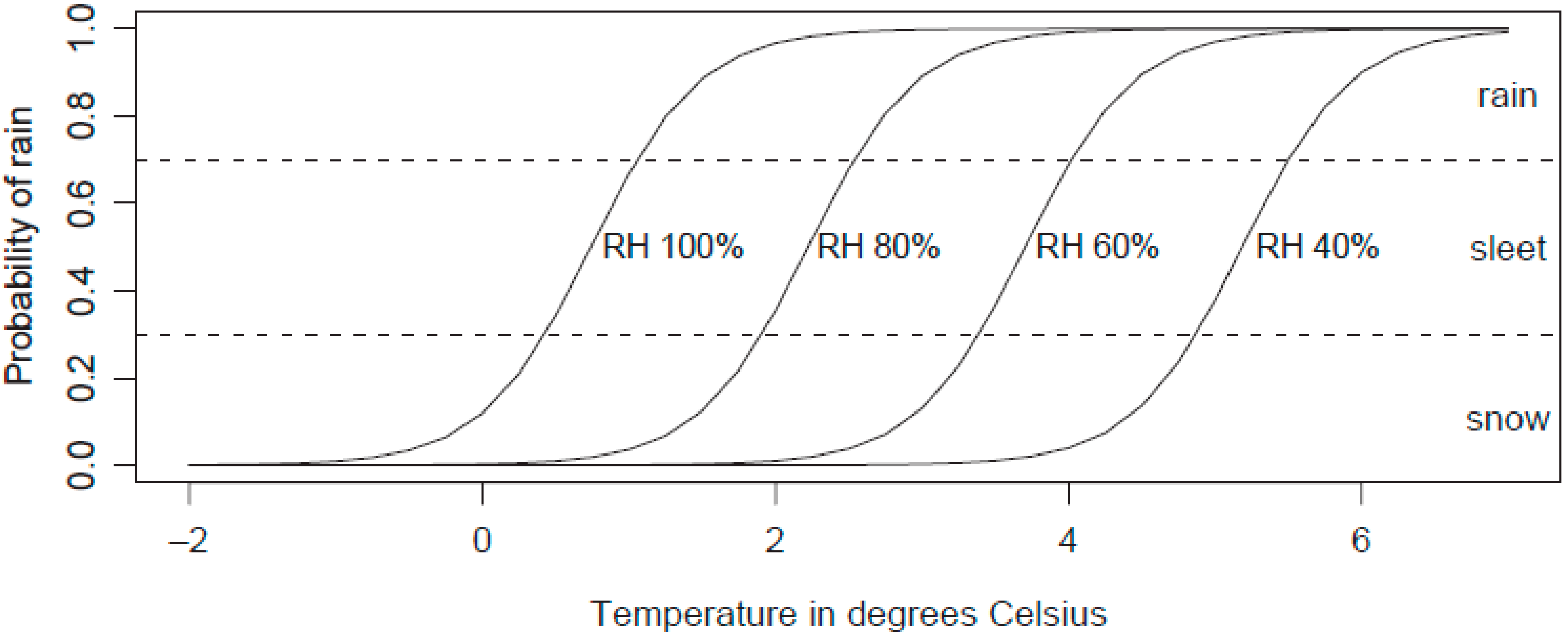
4.5.3. Relative Humidity Schemes

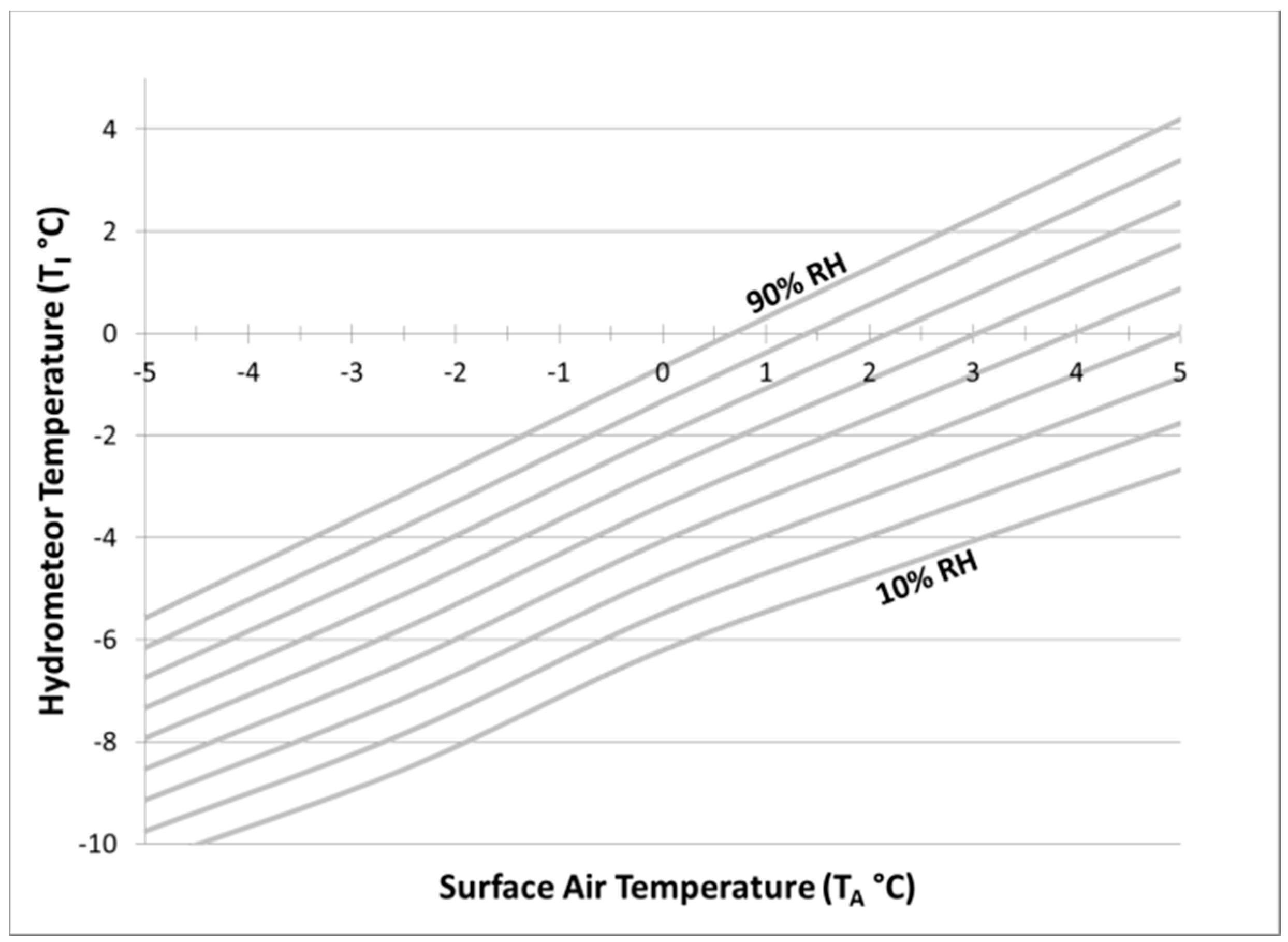
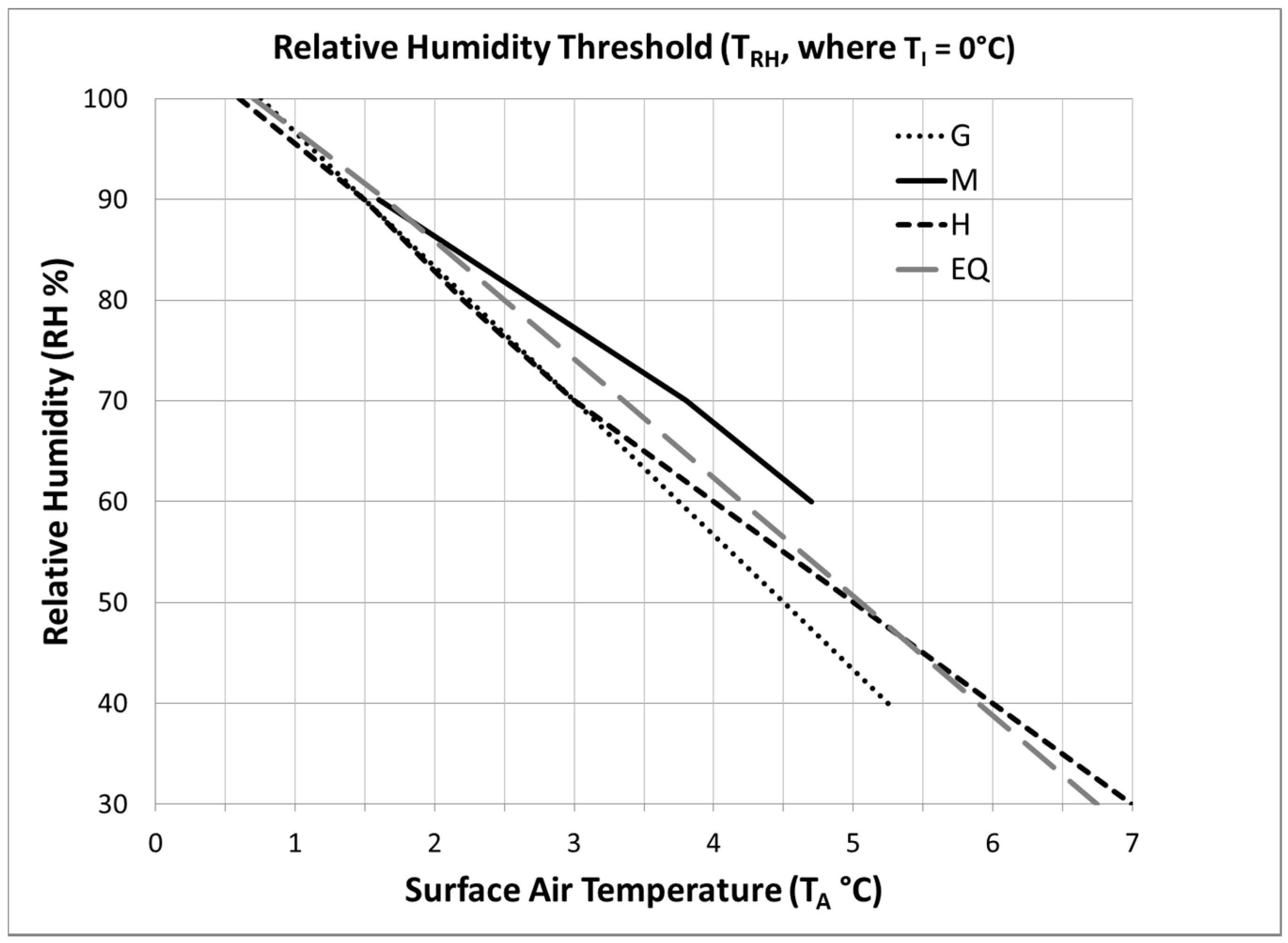
5. Summary
- Using a shorter a time-step:
- Introducing single (or dual rain/snow) thresholds which vary with relative humidity RH (%):
- Identification of air mass boundaries:
- Inclusion of precipitation intensity and/or duration:
- Seasonal and/or terrain dependent lapse rates:
6. Conclusions
- Cold frontal passage
- Locations over or near large ice free water bodies
- Low relative humidity
- Long duration or high intensity precipitation events
- Locations on the windward side of mountains (caused by increased precipitation intensity)
Author Contributions
Conflict of Interest
Abbreviations
| PPDS | precipitation phase determination scheme |
| AOS | automated observing system |
| Dmelt. | depth of the near-freezing isothermal layer (in the atmosphere) |
| DP | difference in (atmospheric) pressure |
| DZ | difference in (atmospheric) height |
| RH | surface relative humidity |
| SF | snow fraction |
| TA | surface air temperature |
| TAG | above ground air temperature |
| TD | surface dew point temperature |
| Ti | hydrometeor temperature |
| TR | rain temperature threshold (all precipitation warmer is rain) |
| TRS | single rain/snow threshold temperature |
| TS | snow temperature threshold (all precipitation colder is snow) |
| TW | surface wet bulb temperature |
| ZS | snow elevation (lowest at which snow falls) |
| Z0 °C | height of the 0 °C isotherm |
References
- Ye, H.; Cohen, J.; Rawlins, M. Discrimination of solid from liquid precipitation over northern Eurasia using surface atmospheric conditions. J. Hydrometeorol. 2013, 14, 1345–1355. [Google Scholar] [CrossRef]
- Wen, L.; Nagabhatla, N.; Lü, S.; Wang, S.Y. Impact of rain snow threshold temperature on snow depth simulation in land surface and regional atmospheric models. Adv. Atmos. Sci. 2013, 30, 1449–1460. [Google Scholar] [CrossRef]
- Thériault, J.M.; Rasmussen, R.; Ikeda, K.; Landolt, S. Dependence of snow gauge collection efficiency on snowflake characteristics. J. Appl. Meteorol. Climatol. 2012, 51, 745–762. [Google Scholar] [CrossRef]
- Bartlett, P.A.; MacKay, M.D.; Verseghy, D.L. Modified snow algorithms in the Canadian land surface scheme: Model runs and sensitivity analysis at three Boreal forest stands. Atmos. Ocean 2006, 43, 207–222. [Google Scholar] [CrossRef]
- Coudrain, A.; Francou, B.; Kundzewicz, Z.W. Glacier shrinkage in the Andes and consequences for water resources—Editorial. Hydrol. Sci. J. 2005, 50, 925–932. [Google Scholar]
- Lundberg, A.; Fieccabrino, J. Sea ice growth, modeling of precipitation phase. In Proceedings of the 20th International Conference on Port and Ocean Engineering under Arctic Conditions, Lulea, Sweden, 9–12 June 2009.
- Davis, R.E.; Lowit, M.B.; Knappenberger, P.C.; Legates, D.R. A climatology of snowfall-temperature relationships in Canada. J. Geophys. Res. Atmos. 1999, 104, 11985–11994. [Google Scholar] [CrossRef]
- Bellaire, S.; Jamieson, B. Forecasting the formation of critical snow layers using a coupled snow cover and weather model. Cold Reg. Sci. Technol. 2013, 94, 37–44. [Google Scholar] [CrossRef]
- Lundberg, A.; Nakai, Y.; Thunehed, H.; Halldin, S. Snow accumulation in forests from ground and remote-sensing data. Hydrol. Process. 2004, 18, 1941–1955. [Google Scholar] [CrossRef]
- Lundberg, A.; Feiccabrino, J.; Westerlund, C.; Al-Ansari, N. Urban snow deposits versus snow cooling plants in northern Sweden: A quantitative analysis of snow melt pollutant releases. Water Qual. Res. J. Can. 2014, 49, 32–42. [Google Scholar] [CrossRef]
- Stewart, T.R.; Pielke, R., Jr.; Nath, R. Understanding user decision making and the value of improved precipitation forecasts lessons from a case study. Bull. Am. Meteorol. Soc. 2004, 85, 223–235. [Google Scholar] [CrossRef]
- Gray, D.M.; Toth, B.; Zhao, L.; Pomeroy, J.W.; Granger, R.J. Estimating areal snowmelt infiltration into frozen soils. Hydrol. Process. 2001, 15, 3095–3111. [Google Scholar] [CrossRef]
- Ecke, F.; Christensen, P.; Rentz, R.; Nilsson, M.; Sandström, P.; Hörnfeldt, B. Landscape structure and the long-term decline of cyclic grey-sided voles in Fennoscandia. Landsc. Ecol. 2010, 25, 551–560. [Google Scholar] [CrossRef]
- Braun, L.N. Modeling of the snow-water equivalent in the mountain environment. In Snow in Hydrology and Forests in High Alpine Areas; Bergmann, H., Lang, H., Frey, W., Issler, D., Salm, B., Eds.; IAHS Press: Wallingford, UK, 1991; pp. 3–17. [Google Scholar]
- Sivapalan, M.; Takeuchi, K.; Franks, S.W.; Gupta, V.K.; Karambiri, H.; Lakshmi, V.; Liang, X.; McDonnell, J.J.; Mendiondo, E.M.; O’Connell, P.E.; et al. IAHS decade on Predictions in Ungauged Basins (PUB), 2003–2012: Shaping an exciting future for the hydrological sciences. Hydrol. Sci. J. 2003, 48, 857–880. [Google Scholar] [CrossRef]
- Fang, X.; Pomeroy, J.W.; Ellis, C.R.; MacDonald, M.K.; DeBeer, C.M.; Brown, T. Multi-variable evaluation of hydrological model predictions for a headwater basin in the Canadian Rocky Mountains. Hydrol. Earth Syst. Sci. 2013, 17, 1635–1659. [Google Scholar] [CrossRef]
- Minder, J.R.; Durran, D.R.; Roe, G.H. Mesoscale controls on the mountainside snow line. J. Atmos. Sci. 2011, 68, 2107–2127. [Google Scholar] [CrossRef]
- Dai, A. Temperature and pressure dependence of the rain-snow phase transition over land and ocean. Geophys. Res. Lett. 2008. [Google Scholar] [CrossRef]
- Feiccabrino, J. A cross sectional study of rain/snow threshold changes from the North Sea across the Scandinavian Mountains to the Bay of Bothnia. In Proceedings of the 20th International Northern Research Basins Symposium and Workshop, Kuusamo, Finland, 16–21 August 2015; pp. 4–13.
- Marks, D.; Winstral, A.; Reba, M.; Pomeroy, J.; Kumar, M. An evaluation of methods for determining during-storm precipitation phase and the rain/snow transition elevation at the surface in a mountain basin. Adv. Water Resour. 2013, 55, 98–110. [Google Scholar] [CrossRef]
- Feiccabrino, J.; Gustafsson, D.; Lundberg, A. Surface-based precipitation phase determination methods in hydrological models. Hydrol. Res. 2013, 44, 44–57. [Google Scholar] [CrossRef]
- Kongoli, C.E.; Bland, W.L. Long-term snow depth simulations using a modified atmosphere-land exchange model. Agric. For. Meteorol. 2000, 104, 273–287. [Google Scholar] [CrossRef]
- United States Army Corps of Engineers (USACE). Snow Hydrology: Summary Report of the Snow Investigations; United States Army Corps of Engineers North Pacific Division: Portland, OR, USA, 1956; p. 437. [Google Scholar]
- Kane, D.L.; Stuefer, S. Reflecting on the status of precipitation data collection in Alaska: A case study. Hydrol. Res. 2015, 46, 478–493. [Google Scholar] [CrossRef]
- Stewart, R.E. Precipitation types in the transition region of winter storms. Bull. Am. Meteorol. Soc. 1992, 73, 287–296. [Google Scholar] [CrossRef]
- Thériault, J.M.; Stewart, R.E. A parameterization of the microphysical processes forming many types of winter precipitation. J. Atmos. Sci. 2010, 67, 1492–1508. [Google Scholar] [CrossRef]
- Matsuo, T.; Sato, Y.; Sasyo, Y. Relationship between types of precipitation on the ground and surface meteorological elements. J. Meteorol. Soc. Jpn. 1981, 59, 462–475. [Google Scholar]
- Lundquist, J.D.; Neiman, P.J.; Martner, B.; White, A.B.; Gottas, J.D.; Ralph, F.M. Rain versus snow in the Sierra Nevada, California: Comparing Doppler profiling radar and surface observations of melting level. J. Hydrometeorol. 2008, 9, 194–211. [Google Scholar] [CrossRef]
- Harder, P.; Pomeroy, J. Estimating precipitation phase using a psychrometric energy balance method. Hydrol. Process. 2013, 27, 1901–1914. [Google Scholar] [CrossRef]
- Ólafsson, H.; Haraldsdóttir, S.H. Diurnal, seasonal, and geographical variability of air temperature limits of snow and rain. In Proceedings of the International Conference on Alpine Meteorology (ICAM 2003), Brig, Switzerland, 19–23 May 2003; pp. 473–476.
- Kienzle, S.W. A new temperature based method to separate rain and snow. Hydrol. Process. 2008, 22, 5067–5085. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Kouwen, N.; Soulis, E.D. Surface temperature adjustments to improve weather radar representation of multi-temporal winter precipitation accumulations. J. Hydrol. 2001, 253, 148–168. [Google Scholar] [CrossRef]
- Gjertsen, U.; Ødegaard, V. The water phase of precipitation—A comparison between observed, estimated and predicted values. Atmos. Res. 2005, 77, 218–231. [Google Scholar] [CrossRef]
- Davison, B. Snow Accumulation in a Distributed Hydrological Model. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2003. [Google Scholar]
- NOAA National Weather Service Radiosonde Observations. Available online: http://www.ua.nws.noaa.gov/factsheet.htm (accessed on 23 September 2015).
- Kain, J.S.; Goss, S.M.; Baldwin, M.E. The melting effect as a factor in precipitation-type forecasting. Weather Forecast 2000, 15, 700–714. [Google Scholar] [CrossRef]
- Fujibe, F. On the near-0 °C frequency maximum in surface air temperature under precipitation: A statistical evidence for the melting effect. J. Meteorol. Soc. Jpn. 2001, 79, 731–739. [Google Scholar] [CrossRef]
- Lackmann, G.M.; Keeter, K.; Lee, L.G.; Ek, M.B. Model representation of freezing and melting precipitation: Implications for winter weather forecasting. Weather Forecast 2002, 17, 1016–1033. [Google Scholar] [CrossRef]
- Mitra, S.K.; Vohl, O.; Ahr, M.; Pruppacher, H.R. A wind tunnel and theoretical study of the melting behavior of atmospheric ice particles IV: Experiment and theory for snowflakes. J. Atmos. Sci. 1990, 47, 584–591. [Google Scholar] [CrossRef]
- Chen, S.H.; Sun, W.Y. A one-dimensional time dependent cloud model. J. Meteorol. Soc. Jpn. 2002, 80, 99–118. [Google Scholar] [CrossRef]
- Hong, S.Y.; Lim, J.O.J. The WRF single-moment 6-class microphysics scheme (WSM6). J. Korean Meteorol. Soc. 2006, 42, 129–151. [Google Scholar]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; NCAR Tech. Note. NCAR/TN-475+ STR; National Center for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Venne, M.G.; Jasperson, W.H.; Venne, D.E. Difficult Weather: A Review of Thunderstorms, Fog, and Stratus, and Winter Precipitation Forecasting; AIRFM Command Tech. Report #A246633; Augsburg Coll Minneapolis MN Center for Atmospheric and Space Sciences: Minneapolis, MN, USA, 1997. [Google Scholar]
- McNulty, R.P. Winter Precipitation Type; NWS Central Region Tech. Attach. 88–4; National Weather Service: Kansas City, MO, USA, 1988.
- Ruddell, A.R.; Budd, W.F.; Smith, I.N.; Keage, P.L.; Jones, R. The South East Australian Alpine Climate Study: A report by the Meteorology Department, University of Melbourne, for the Alpine Resorts Commissions; Department of Meteorology, University of Melbourne: Melbourne, Australia, 1990; p. 115. [Google Scholar]
- Schreider, S.Y.; Whetton, P.H.; Jakeman, A.J.; Pittock, A.B. Runoff modelling for snow-affected catchments in the Australian alpine region, eastern Victoria. J. Hydrol. 1997, 200, 1–23. [Google Scholar] [CrossRef]
- Sælthun, N.R. “The Nordic” HBV Model, Description and Documentation of the Model Version Developed for the Project ‘Climate Change and Energy Production’; Norwegian Water Resources and Energy Administration (NVE): Oslo, Norway, 1996. [Google Scholar]
- Feiccabrino, J.; Lundberg, A.; Gustafsson, D. Improving surface-based precipitation phase determination through air mass boundary identification. Hydrol. Res. 2012, 43, 179–191. [Google Scholar]
- Yang, Z.L.; Dickinson, R.E.; Robock, A.; Vinnikov, K.Y. Validation of the snow submodel of the biosphere-atmosphere transfer scheme with Russian snow cover and meteorological observational data. J. Clim. 1997, 10, 353–373. [Google Scholar] [CrossRef]
- Motoyama, H. Simulation of seasonal snowcover based on air temperature and precipitation. J. Appl. Meteorol. 1990, 29, 1104–1110. [Google Scholar] [CrossRef]
- L’hôte, Y.; Chevallier, P.; Coudrain, A.; Lejeune, Y.; Etchevers, P. Relationship between precipitation phase and air temperature: Comparison between the Bolivian Andes and the Swiss Alps. Hydrol. Sci. J. 2005, 50, 989–997. [Google Scholar]
- Braun, L.N.; Lang, H. Simulation of snowmelt runoff in lowland and lower alpine regions of Switzerland. In Proceedings of the Budapest Symposium, Budapest, Hungary, 2–10 July 1986; pp. 125–140.
- Hottelet, C.; Blažková, Š.; Blčík, M. Application of the ETH snow model to three basins of different character in Central Europe. Nord. Hydrol. 1994, 25, 113–128. [Google Scholar]
- Zhang, Y.; Wang, S.; Barr, A.G.; Black, T.A. Impact of snow cover on soil temperature and its simulation in a boreal aspen forest. Cold Reg. Sci. Technol. 2008, 52, 355–370. [Google Scholar] [CrossRef]
- Caballero, Y.; Chevallier, P.; Gallaire, R.; Pillco, R. Flow modelling in a high mountain valley equipped with hydropower plants: Rio Zongo Valley, Cordillera Real, Bolivia. Hydrol. Process. 2004, 18, 939–957. [Google Scholar] [CrossRef]
- Baun, S.D. Frequency Mapping of Maximum Snow Water Equivalent of March Snow Cover over Minnesota and the Eastern Dakotas; NWS Central Region Tech. Memo. CR-113; National Weather Service: Silver Spring, MD, USA, 1998.
- Pomeroy, J.W.; Gray, D.M.; Brown, T.; Hedstrom, N.R.; Quinton, W.L.; Granger, R.J.; Carey, S.K. The cold regions hydrological model: A platform for basing process representation and model structure on physical evidence. Hydrol. Process. 2007, 21, 2650–2667. [Google Scholar] [CrossRef]
- Daly, S.F.; Davis, R.; Ochs, E.; Pangburn, T. An approach to spatially distributed snow modelling of the Sacramento and San Joaquin basins, California. Hydrol. Process. 2000, 14, 3257–3271. [Google Scholar] [CrossRef]
- Auer, A.H., Jr. The rain versus snow threshold temperatures. Weatherwise 1974. [Google Scholar] [CrossRef]
- Bjerknes, J. On the structure of moving cyclones. Mon. Weather Rev. 1919, 47, 95–99. [Google Scholar] [CrossRef]
- Oliver, V.J.; Oliver, M.B. Weather analysis from single-station data. In Handbook of Meteorology; Berry, F.A., Bolay, E., Beers, N.R., Eds.; McGraw-Hill Book Co.: New York, NY, USA, 1945; pp. 858–879. [Google Scholar]
- Fraedrich, K.; Bach, R.; Naujokat, N. Single station climatology of central European fronts Number, time and precipitation statistics. Beitr. Phys. Atmos. 1986, 59, 54–65. [Google Scholar]
- Sanders, F. A proposed method of surface map analysis. Mon. Weather Rev. 1999, 127, 945–955. [Google Scholar] [CrossRef]
- Schultz, D.M. A review of cold fronts with prefrontal troughs and wind shifts. Mon. Weather Rev. 2005, 133, 2449–2472. [Google Scholar] [CrossRef]
- Lundberg, A.; Halldin, S. Evaporation of intercepted snow: Analysis of governing factors. Water Resour. Res. 1994, 30, 2587–2598. [Google Scholar] [CrossRef]
- Nuti, R.; Wong, K. Instruments and Observing Methods; WMO/TD-No.1544; World Meteorological Organization: Geneva, Switzerland, 2010. [Google Scholar]
- Boudala, F.S.; Rasmussen, R.; Isaac, G.A.; Scott, B. Performance of hot plate for measuring solid precipitation in complex terrain during the 2010 Vancouver Winter Olympics. J. Atmos. Ocean. Technol. 2014, 31, 437–446. [Google Scholar] [CrossRef]
- Grazioli, J.; Tuia, D.; Monhart, S.; Schneebeli, M.; Raupach, T.; Berne, A. Hydrometeor classification from two dimensional video disdrometer data. Atmos. Meas. Tech. 2014, 7, 2869–2882. [Google Scholar] [CrossRef]
- Thériault, J.M.; Rasmussen, R.; Petro, E.; Trépanier, J.Y.; Colli, M.; Lanza, L.G. Impact of Wind Direction, Wind Speed, and Particle Characteristics on the Collection Efficiency of the Double Fence Intercomparison Reference. J. Appl. Meteorol. Climatol. 2015, 54, 1918–1930. [Google Scholar] [CrossRef]
- Yang, D. Double fence intercomparison reference DFIR vs bush gauge for “true” snowfall measurement. J. Hydrol. 2014, 509, 94–100. [Google Scholar] [CrossRef]
- Garvelmann, J.; Pohl, S.; Weiler, M. From observation to the quantification of snow processes with a time-lapse camera network. Hydrol. Earth Syst. Sci. 2013, 17, 1415–1429. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feiccabrino, J.; Graff, W.; Lundberg, A.; Sandström, N.; Gustafsson, D. Meteorological Knowledge Useful for the Improvement of Snow Rain Separation in Surface Based Models. Hydrology 2015, 2, 266-288. https://doi.org/10.3390/hydrology2040266
Feiccabrino J, Graff W, Lundberg A, Sandström N, Gustafsson D. Meteorological Knowledge Useful for the Improvement of Snow Rain Separation in Surface Based Models. Hydrology. 2015; 2(4):266-288. https://doi.org/10.3390/hydrology2040266
Chicago/Turabian StyleFeiccabrino, James, William Graff, Angela Lundberg, Nils Sandström, and David Gustafsson. 2015. "Meteorological Knowledge Useful for the Improvement of Snow Rain Separation in Surface Based Models" Hydrology 2, no. 4: 266-288. https://doi.org/10.3390/hydrology2040266
APA StyleFeiccabrino, J., Graff, W., Lundberg, A., Sandström, N., & Gustafsson, D. (2015). Meteorological Knowledge Useful for the Improvement of Snow Rain Separation in Surface Based Models. Hydrology, 2(4), 266-288. https://doi.org/10.3390/hydrology2040266







