Skill Assessment of Water Supply Outlooks in the Colorado River Basin
Abstract
:1. Introduction
2. Methods and Data
2.1. Skill Measures
| Skill Measure | Equation a |
|---|---|
| Mean Absolute Error (MAE) | |
| Mean Square Error (MSE) | |
| MAE skill score | SSMAE = 1 − MAE/MAEcl where MAEcl = |
| MSE skill score b | SSMSE = 1 − MSE/MSEcl where MSEcl = |
| Observed | Not Observed | |
|---|---|---|
| Forecast | a | b |
| Not forecast | c | d |
| Measure | Explanation | Equation | Range |
|---|---|---|---|
| Probability of Detection (POD) | Correct forecasts divided by observations | a/(a + c) | 0–1 (perfect) |
| False Alarm Rate (FAR) | Incorrect forecasts divided by forecasts | b/(a + b) | 1–0 (perfect) |
| Bias | Correct and non-correct forecasts divided by observations | (a + b)/(a + c) | >1 over; and <1 under forecast |
| Threat Score or Critical Success Index (TS) | Correct forecasts divided by the forecasts plus non-forecast observations | a/(a + b + c) | 0–1 (perfect) |
| Hit Rate (HR) | Correct forecasts and correct non-forecasts, divided by total forecasts and observations | (a + d)/(a + b + c + d) | 0–1 (perfect) |
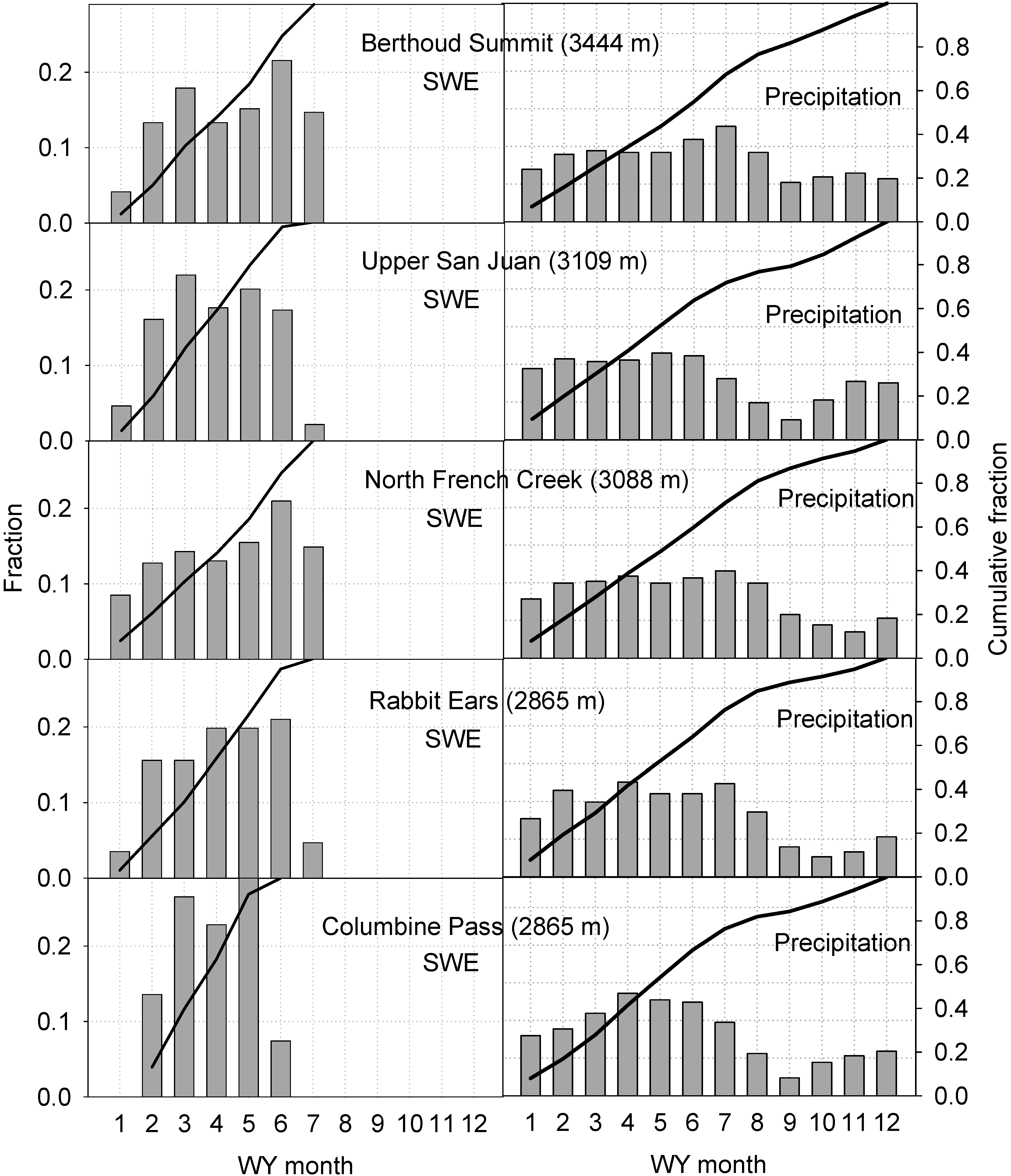
2.2. Source of Data
| Year | Forecast Month | Forecast Flow | Observed Flow |
|---|---|---|---|
| 2011 | January | 195 | 105.1 |
| 2011 | February | 180 | 105.1 |
| 2011 | March | 196 | 105.1 |
| 2011 | April | 150 | 105.1 |
| 2011 | May | 124 | 105.1 |
| 2012 | January | 335 | 507.2 |
| 2012 | February | 335 | 507.2 |
| 2012 | March | 350 | 507.2 |
| 2012 | April | 415 | 507.2 |
| 2012 | May | 495 | 507.2 |
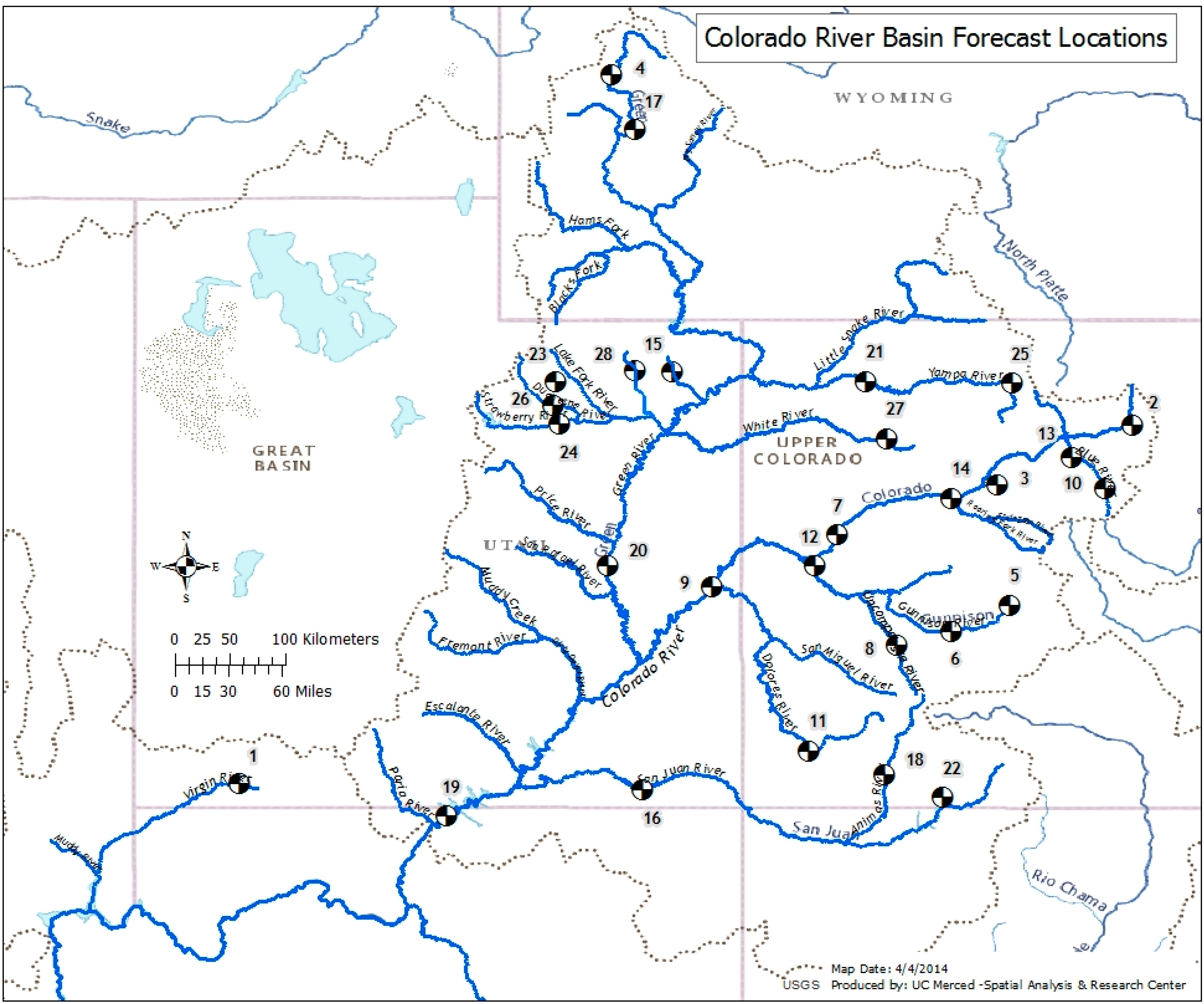
2.3. Watershed Characteristics
| No. | Location–Runoff Type | NWS/USGS | Lat/Lon | Runoff Records | Median Elev., m | Area, km2 | Mean April–July Runoff, million m3 |
|---|---|---|---|---|---|---|---|
| 1 | Virgin River at Virgin, UT–O | VIRU1/9406000 | 37.204/113.180 | 1958–2012 | 1984 | 2476 | 72 |
| 2 | Colorado River below Lake Granby, CO–N | GBYC2/9019000 | 40.140/105.835 | 1954–2013 | 3120 | 808 | 273 |
| 3 | Eagle River below Gypsum, CO–N | GPSC2/9070000 | 39.649/106.953 | 1975–2012 | 2971 | 2445 | 414 |
| 4 | Green River at Warren Bridge, near Daniel, WY–O | WBRW4/9188500 | 43.019/110.119 | 1958–2012 | 2768 | 1212 | 299 |
| 5 | East River at Almont, CO–N | ALEC2/9112500 | 38.664/106.848 | 1957–2012 | 3135 | 749 | 225 |
| 6 | Gunnison River inflow to Blue Mesa Reservoir, CO–N | BMDC2/9124800 | 38.451/107.332 | 1972–2012 | 3023 | 9091 | 834 |
| 7 | Colorado River near Cameo, CO–N | CAMC2/9095500 | 39.239/108.266 | 1957–2012 | 2776 | 20,850 | 2906 |
| 8 | Uncompahgre River at Colona, CO–N | CLOC2/9147500 | 38.331/107.779 | 1954–2012 | 2807 | 1160 | 168 |
| 9 | Colorado River near Cisco, UT–N | CLRU1/9180500 | 38.811/109.293 | 1957–2012 | 2636 | 62,419 | 5475 |
| 10 | Blue River inflow to Dillon Reservoir, CO–N | DIRC2/9050700 | 39.626/106.066 | 1972–2012 | 3364 | 868 | 200 |
| 11 | Dolores River at Dolores, CO–O | DOLC2/9166500 | 37.473/108.497 | 1954–2012 | 2984 | 1305 | 304 |
| 12 | Gunnison River near Grand Junction, CO–N | GINC2/9152500 | 38.983/108.450 | 1954–2012 | 2783 | 20,534 | 1822 |
| 13 | Blue River inflow to Green Mountain Reservoir, CO–N | GMRC2/9057500 | 39.880/106.333 | 1954–2012 | 3260 | 1551 | 339 |
| 14 | Roaring Fork at Glenwood Springs, CO–N | GWSC2/9085000 | 39.544/107.329 | 1954–2012 | 3026 | 3763 | 853 |
| 15 | Ashley Creek near Vernal, UT–O | ASHU1/9266500 | 40.578/109.621 | 1954–2012 | 2746 | 262 | 61 |
| 16 | San Juan River near Bluff, UT–N | BFFU1/9379500 | 37.147/109.864 | 1957–2012 | 1985 | 59,570 | 1350 |
| 17 | New Fork River near Big Piney, WY–O | BPNW4/9205000 | 42.567/109.929 | 1975–2012 | 2452 | 3186 | 438 |
| 18 | Animas River at Durango, CO–O | DRGC2/9361500 | 37.279/107.880 | 1954–2012 | 3167 | 1792 | 514 |
| 19 | Lake Powell at Glen Canyon Dam, AZ–N | GLDA3/9379900 | 36.937/111.483 | 1964–2012 | 2135 | 289,303 | 8822 |
| 20 | Green River at Green River, UT–N | GRVU1/9315000 | 38.986/110.151 | 1957–2012 | 2135 | 116,162 | 3650 |
| 21 | Yampa River near Maybell, CO–N | MBLC2/9251000 | 40.503/108.033 | 1957–2012 | 2316 | 8832 | 1154 |
| 22 | Piedra River near Arboles, CO–O | PIDC2/9349800 | 37.088/107.397 | 1972–2012 | 2604 | 1629 | 258 |
| 23 | Rock Creek near Mtn Home, UT–N | ROKU1/9279000 | 40.493/110.578 | 1965–2012 | 3121 | 381 | 109 |
| 24 | Strawberry River near Duchesne, UT–N | STAU1/9288180 | 40.155/110.554 | 1954–2012 | 2435 | 2375 | 154 |
| 25 | Yampa River at Steamboat Springs, CO–N | STMC2/9239500 | 40.484/106.832 | 1954–2012 | 2695 | 1471 | 318 |
| 26 | Duchesne River near Tabiona, UT–N | TADU1/9277500 | 40.300/110.602 | 1954–2012 | 2707 | 914 | 133 |
| 27 | White River near Meeker, CO–O | WRMC2/9304500 | 40.034/107.862 | 1954–2012 | 2763 | 1955 | 343 |
| 28 | Whiterocks River near Whiterocks, UT–O | WTRU1/9299500 | 40.594/109.932 | 1954–2012 | 3194 | 282 | 67 |
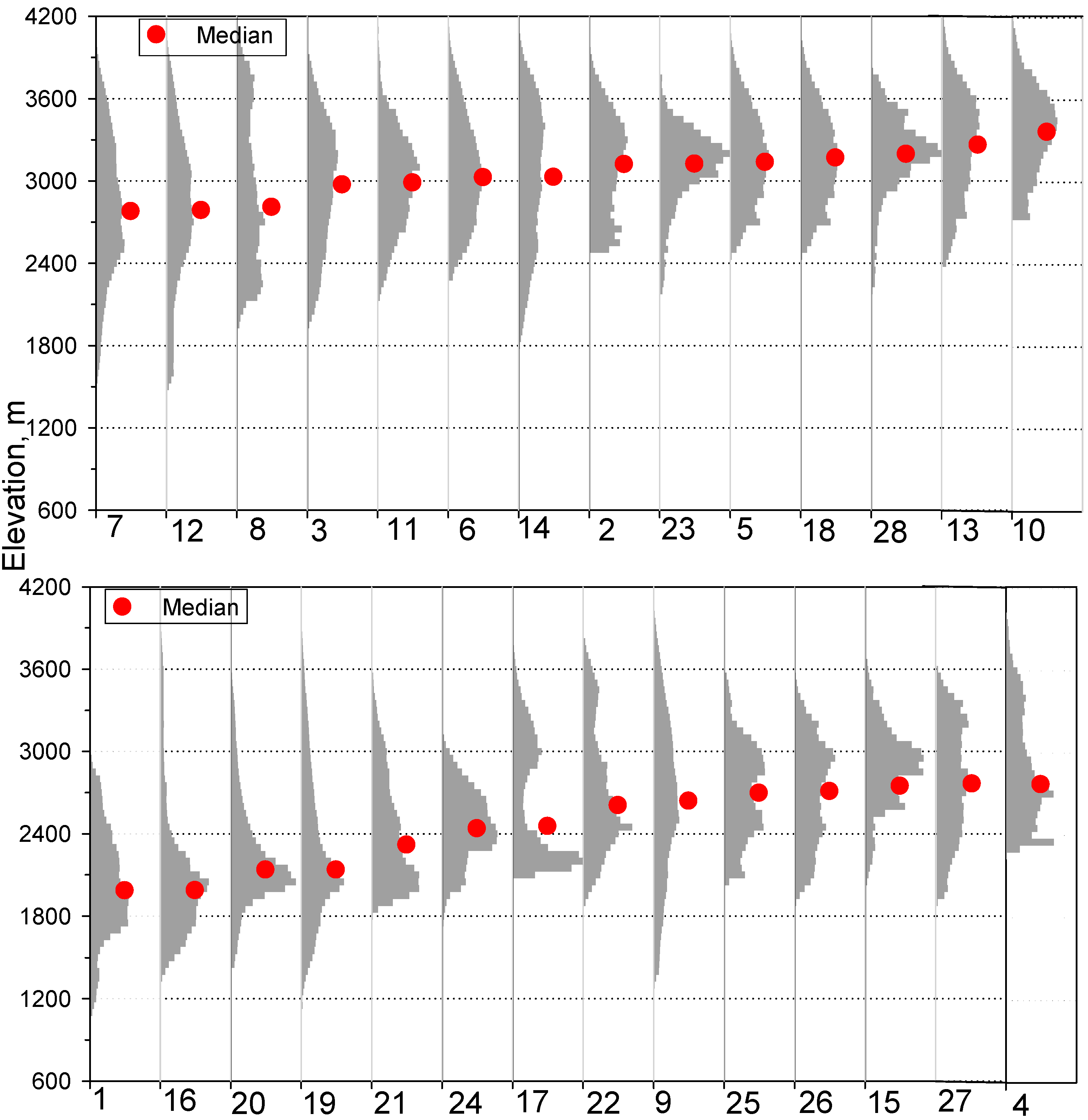
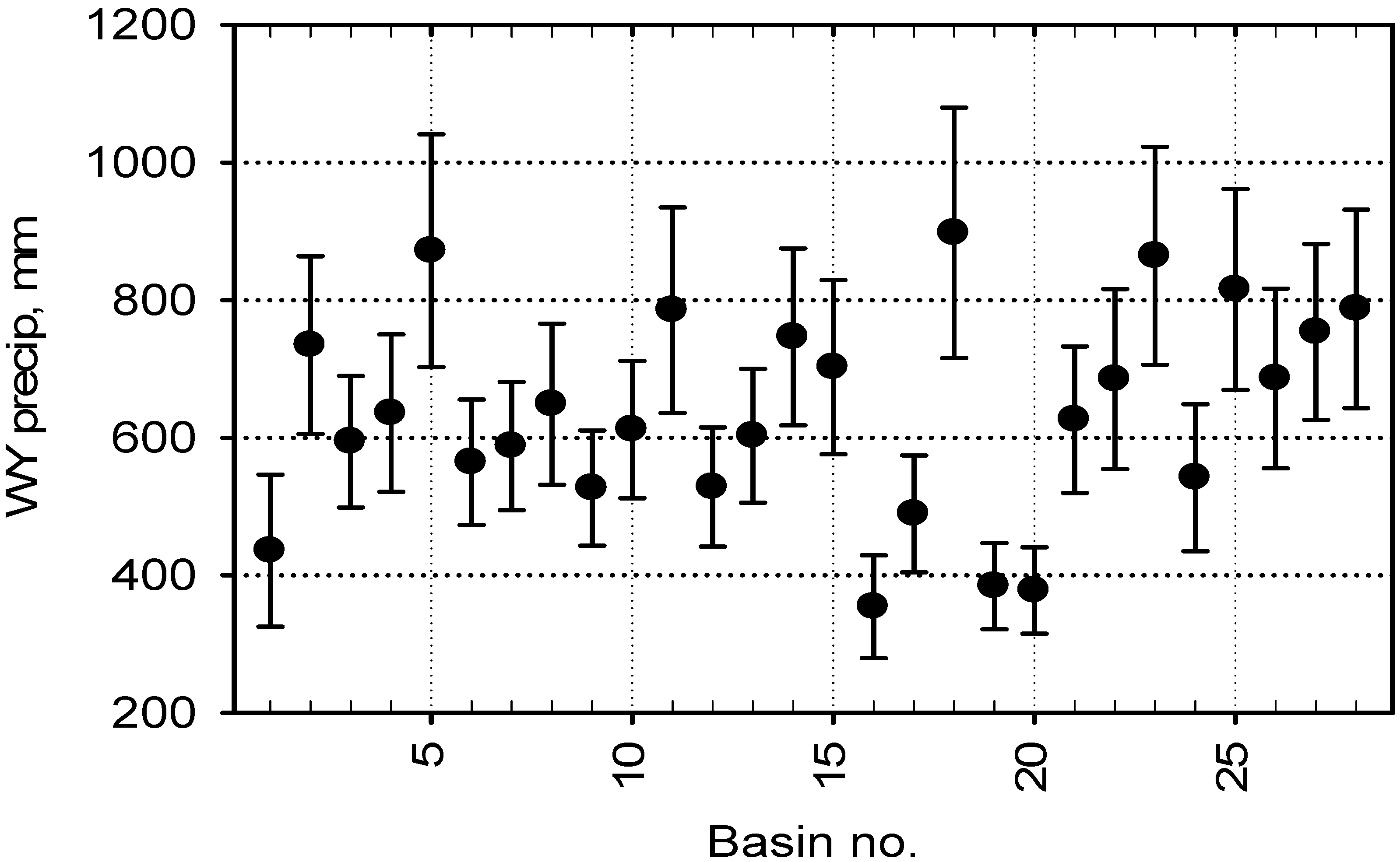
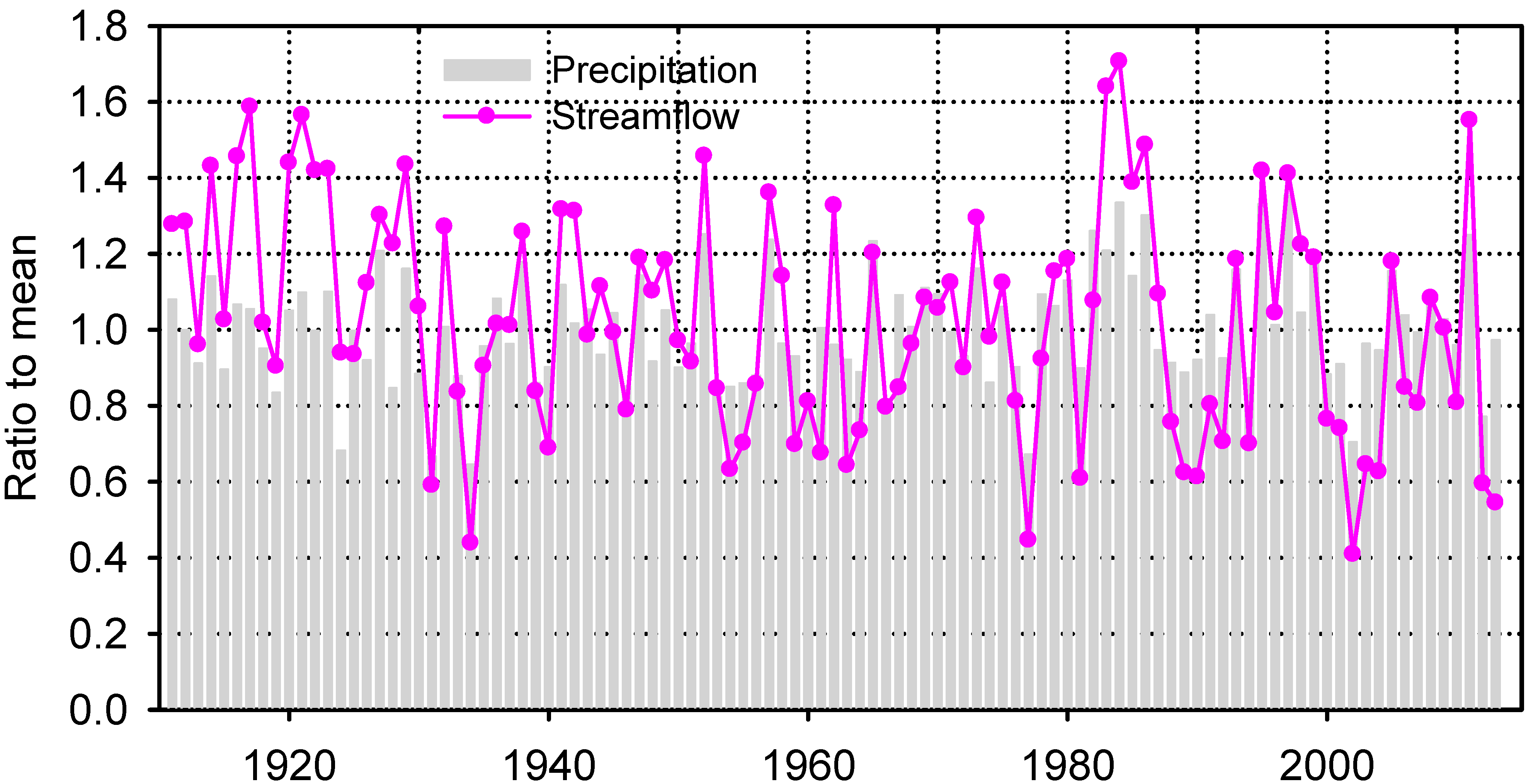
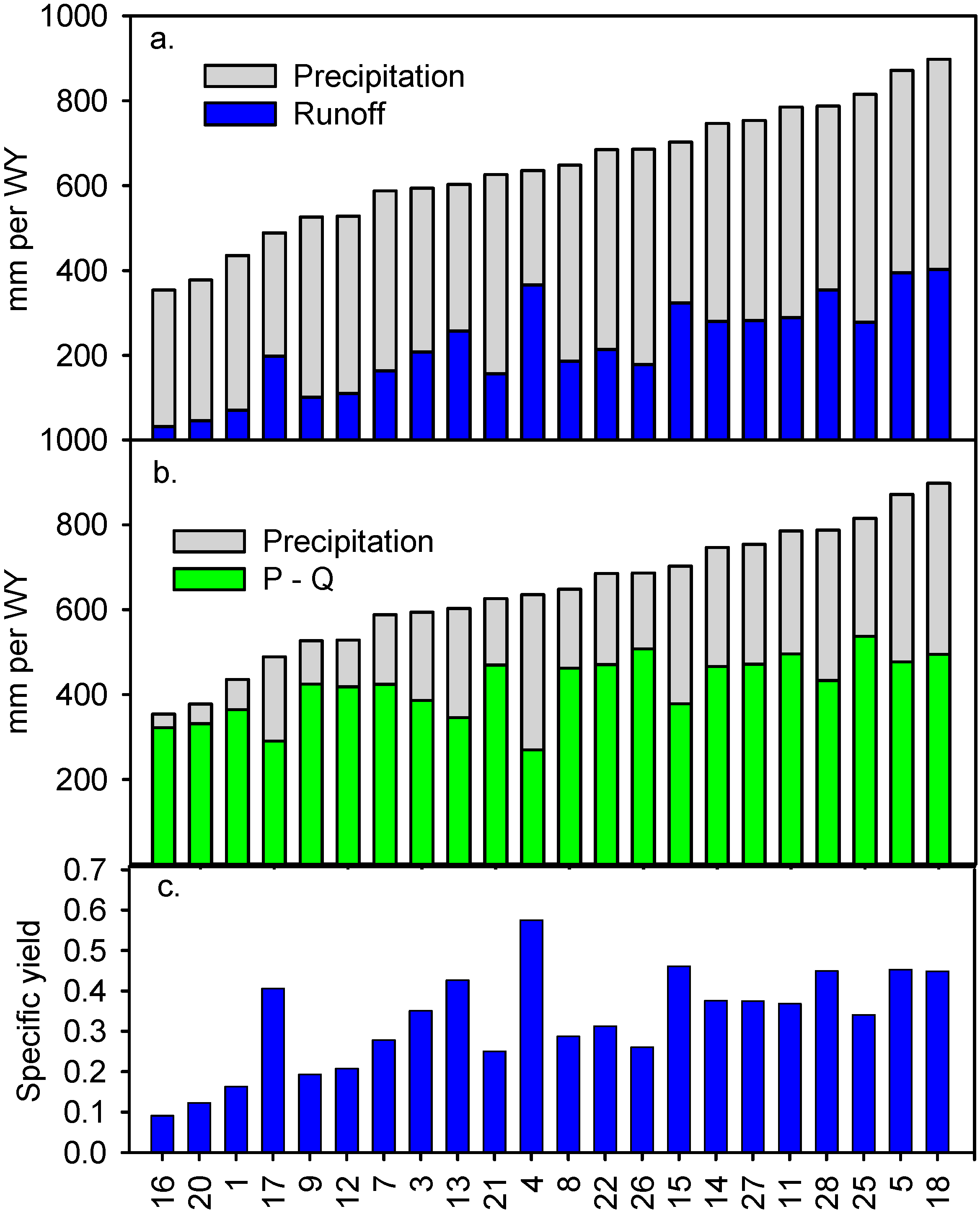
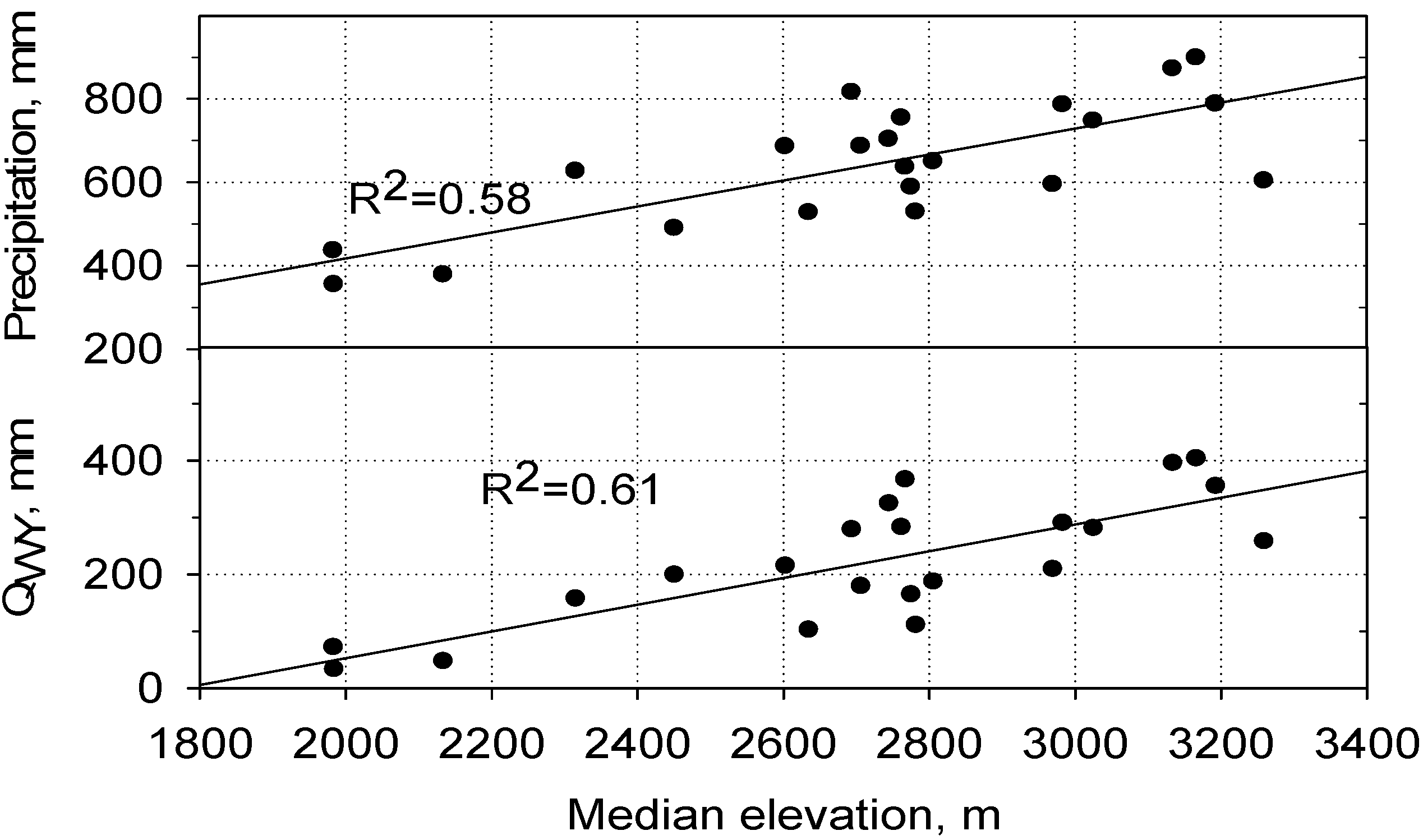
3. Results
3.1. Forecast Skill—Summary and Correlation Measures
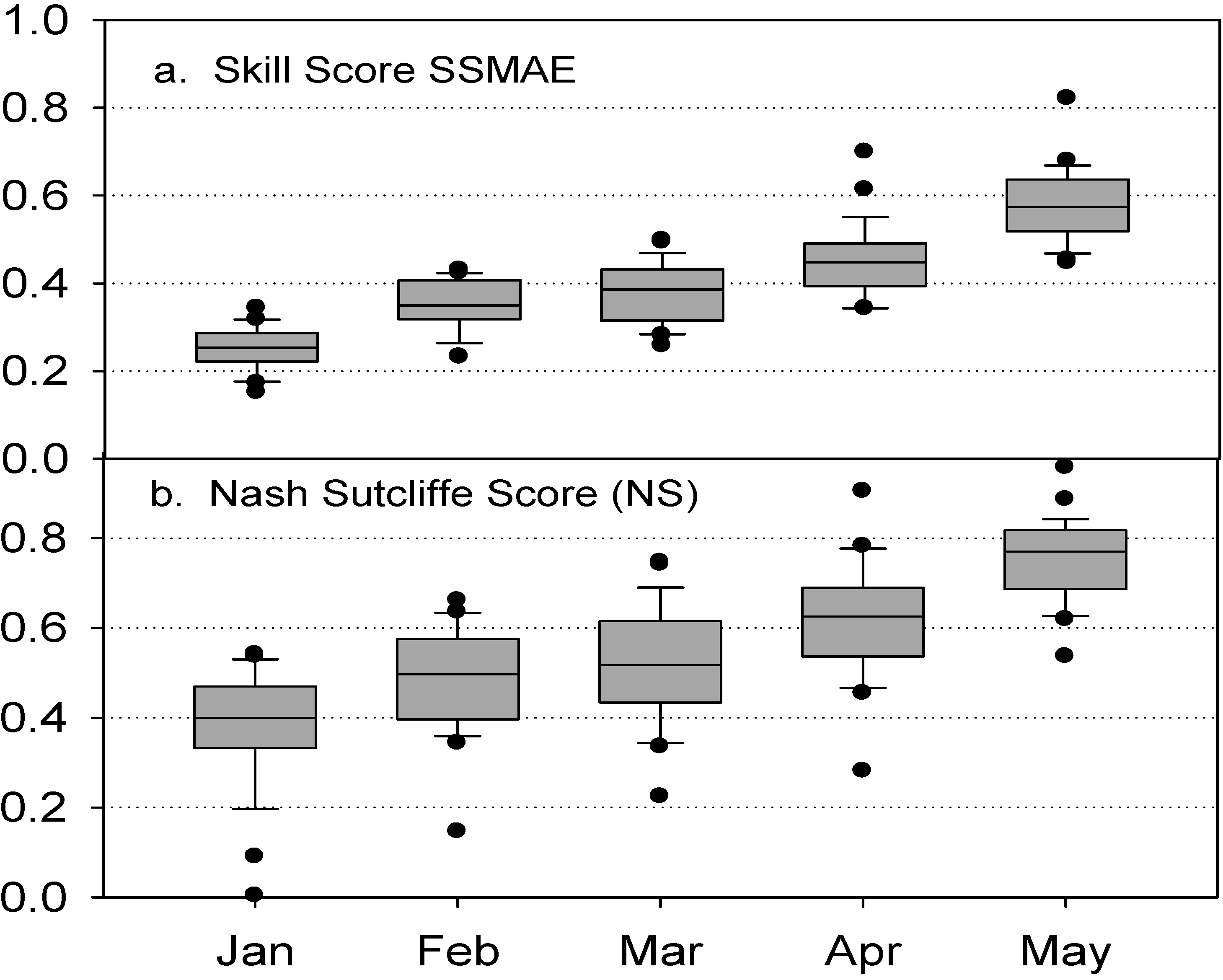
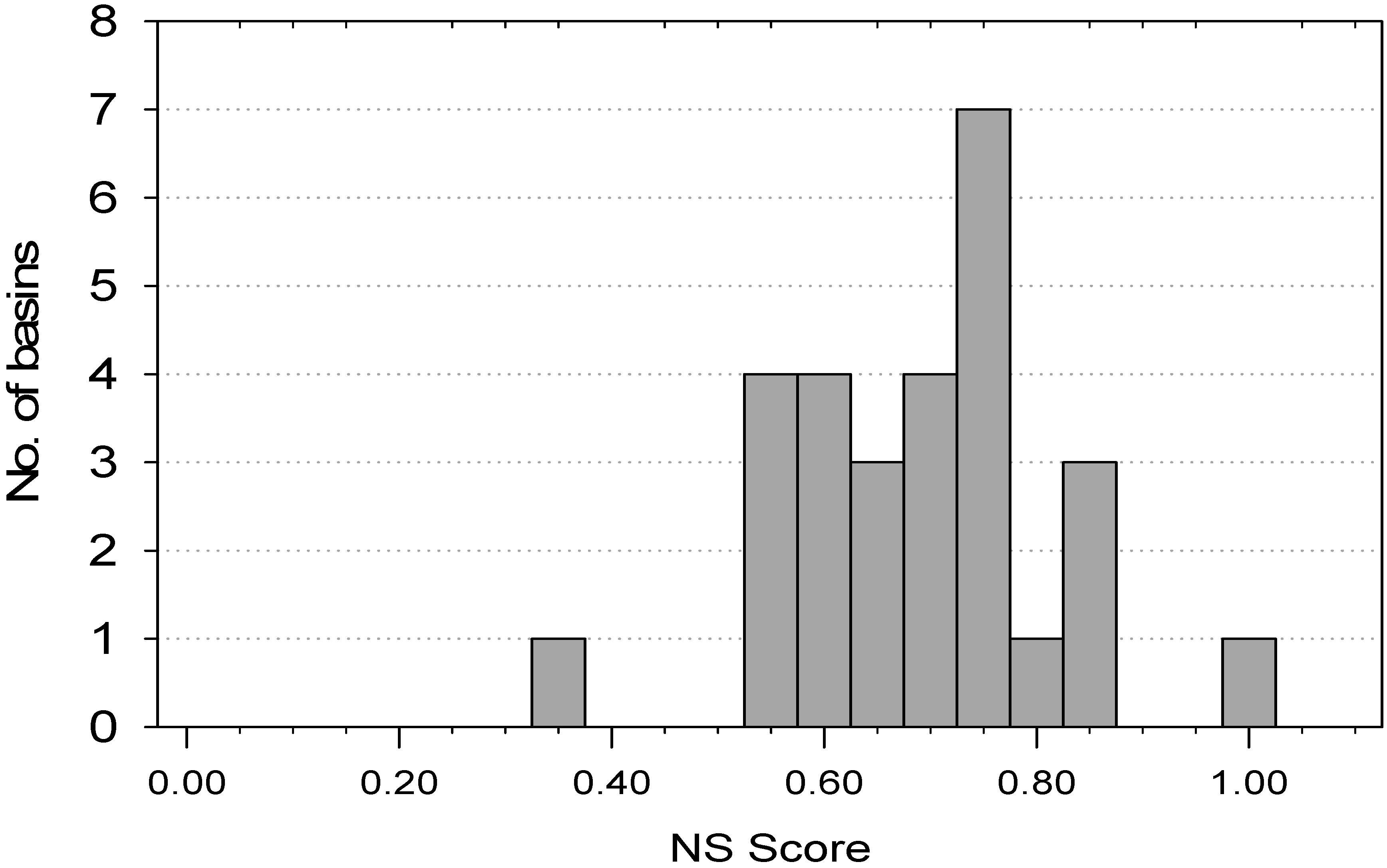
3.2. Forecast Skill—Categorical Measures
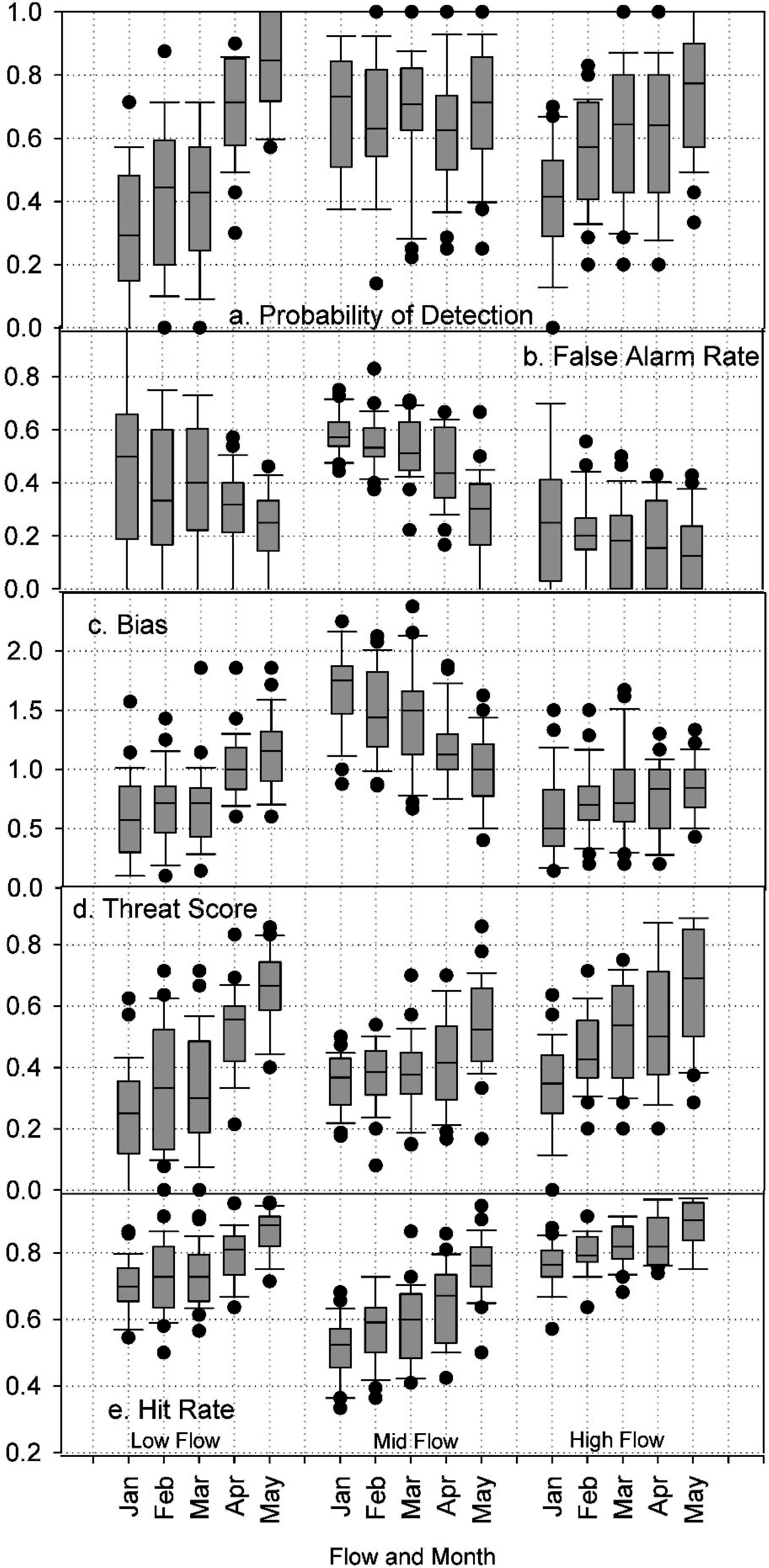
4. Discussion

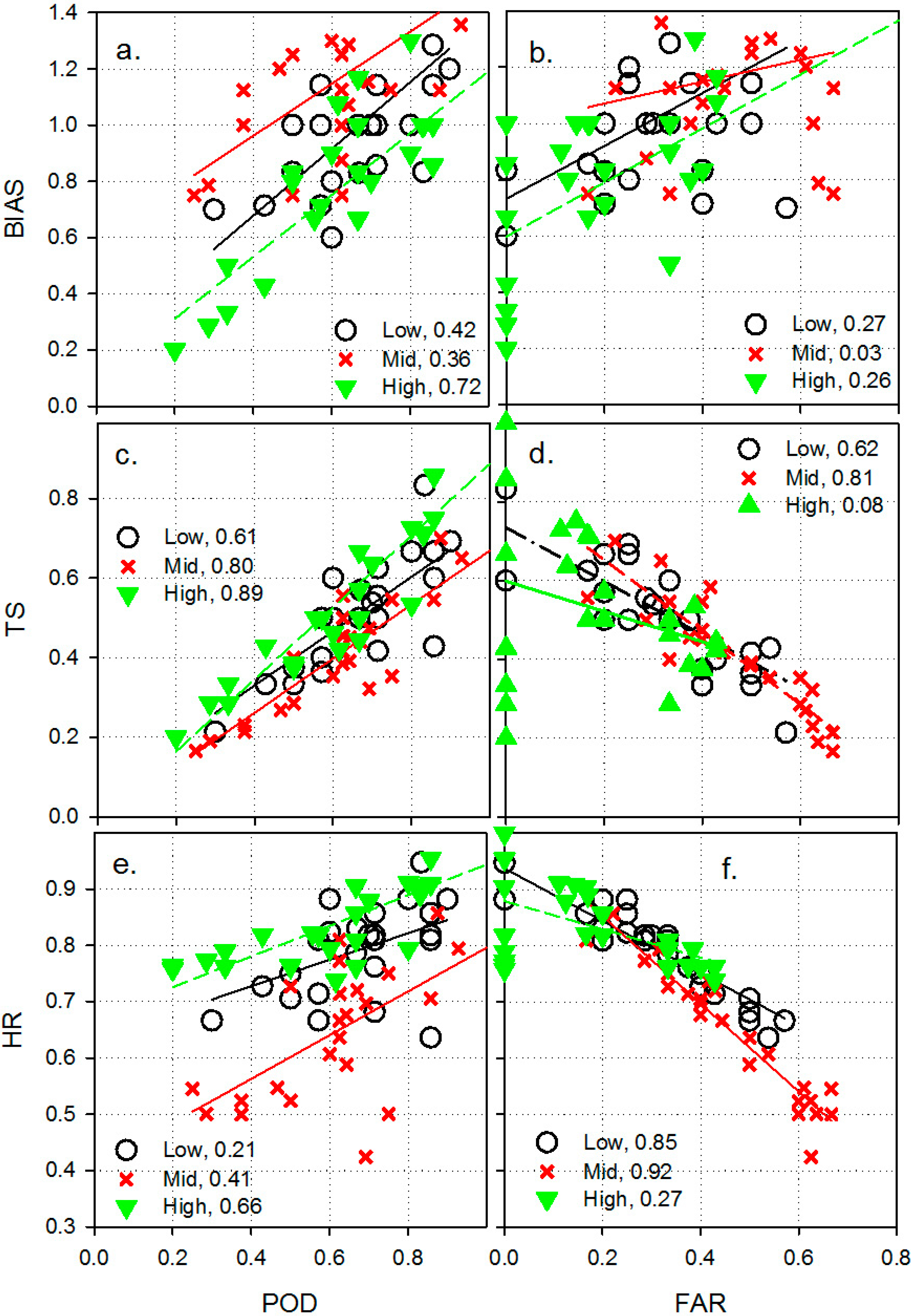
5. Conclusions
Acknowledgments
Author Contributions
Conflict of Interest
References
- Pagano, T.; Garen, D.; Sorooshian, S. Evaluation of official western US seasonal water supply outlooks, 1922–2002. J. Hydrometeorol. 2004, 5, 896–909. [Google Scholar] [CrossRef]
- Bender, S.; Colorado Basin River Forecast Center, Salt Lake City, UT, USA. Personal communication, 2013.
- Work, R.A.; Beaumont, R.T. Basic data characteristics in relation to runoff forecast accuracy. In Proceedings of Western Snow Conference, Bozeman, MT, USA, 16–18 April 1958; pp. 45–53.
- Kohler, M.A. Preliminary report on evaluating the utility of water supply forecasts. In Proceedings of Western Snow Conference, Reno, NV, USA, 21–23 April 1959; pp. 26–33.
- Shafer, B.A.; Huddleston, J.M. Analysis of seasonal volume streamflow forecast errors in the western United States. In Proceedings of A Critical Assessment of Forecasting in Water Quality Goals in Western Water Resource Management, Bethesda, MD, USA, 11–13 June 1984; pp. 117–126.
- Schaake, J.C.; Peck, E.L. Analysis of water supply forecasts. In Proceedings of Western Snow Conference, Boulder, CO, USA, 16–18 April 1985; pp. 44–53.
- Dracup, J.A.; Haynes, D.L.; Abramson, S.D. Accuracy of hydrologic forecasts. In Proceedings of Western Snow Conference, Boulder, CO, USA, 16–18 April 1985; pp. 13–24.
- Hartmann, H.C.; Bales, R.; Sorooshian, S. Weather, climate, and hydrologic forecasting for the US southwest: A survey. Clim. Res. 2002, 21, 239–258. [Google Scholar] [CrossRef]
- Franz, K.J.; Hartmann, H.C.; Sorooshian, S.; Bales, R. Verification of national weather service ensemble streamflow predictions for water supply forecasting in the colorado river basin. J. Hydrometeorol. 2003, 4, 1105–1118. [Google Scholar] [CrossRef]
- Hartmann, H.C.; Morrill, J.C.; Bales, R. A Baseline for Identifying Improvements in Hydrologic Forecasts: Assessment of Water Supply Outlooks for the Colorado River Basin. In Proceedings of AGU Fall Meeting, San Francisco, CA, USA, 11–15 December 2006. Abstract H53C-0649.
- Morrill, J.C.; Hartmann, H.C.; Bales, R.C. An Assessment of Seasonal Water Supply Outlooks in the Colorado River Basin; Working Paper; Dept. of Hydrology and Water Resources, University of Arizona: Tucson, AZ, USA, 2007. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Elsevier: Oxford, UK, 2011. [Google Scholar]
- USGS National Water Information System. Available online: http://waterdata.usgs.gov/nwis (accessed on 3 March 2014).
- PRISM, PRISM Climate Group, Oregon State University. Available online: http://prism.oregonstate.edu (accessed on 15 September 2014).
- Harrison, B.; Bales, R. Skill assessment of water supply forecasts for western Sierra Nevada watersheds. J. Hydrol. Eng. 2015. submitted. [Google Scholar]
- NRCS Snotel Data. Available online: www.wcc.nrcs.usda.gov/snow (accessed on 11 December 2014).
- Decision-Support Experiments and Evaluations using Seasonal-to-Interannual Forecasts and Observational Data: A Focus on Water Resources. Available online: http://downloads.globalchange.gov/sap/sap5-3/sap5-3-final-all.pdf (accessed on 8 July 2015).
- Harrison, B.; Bales, R. Percent bias assessment of water supply outlooks in the Colorado River basin. In Proceedings of 82nd Annual Western Snow Conference, Durango, CO, USA, 14–17 April 2014; pp. 91–100.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harrison, B.; Bales, R. Skill Assessment of Water Supply Outlooks in the Colorado River Basin. Hydrology 2015, 2, 112-131. https://doi.org/10.3390/hydrology2030112
Harrison B, Bales R. Skill Assessment of Water Supply Outlooks in the Colorado River Basin. Hydrology. 2015; 2(3):112-131. https://doi.org/10.3390/hydrology2030112
Chicago/Turabian StyleHarrison, Brent, and Roger Bales. 2015. "Skill Assessment of Water Supply Outlooks in the Colorado River Basin" Hydrology 2, no. 3: 112-131. https://doi.org/10.3390/hydrology2030112
APA StyleHarrison, B., & Bales, R. (2015). Skill Assessment of Water Supply Outlooks in the Colorado River Basin. Hydrology, 2(3), 112-131. https://doi.org/10.3390/hydrology2030112





