Seismic Performance Assessment of Gravity Dams for Urban Flood Risk Mitigation Using the Scaled Boundary Finite Element Method (SBFEM)
Abstract
1. Introduction
2. Methodology
2.1. Overview of the SBFEM Framework
2.2. Polygonal Finite Elements for Dam Bodies
2.3. Modeling of Dam–Water Interaction
2.4. Modeling of Dam–Foundation Interaction
2.5. Time-Domain Seismic Input and Solution Procedure
2.6. Computational Efficiency of SBFEM
3. Numerical Model Setup
3.1. Geometry and Material Properties of the Dam
3.2. Reservoir and Foundation Modeling
3.3. Seismic Input and Time Discretization
3.4. Mass Matrix Formulation and Natural Frequency Evaluation
4. Analysis of Dam–Water Interaction
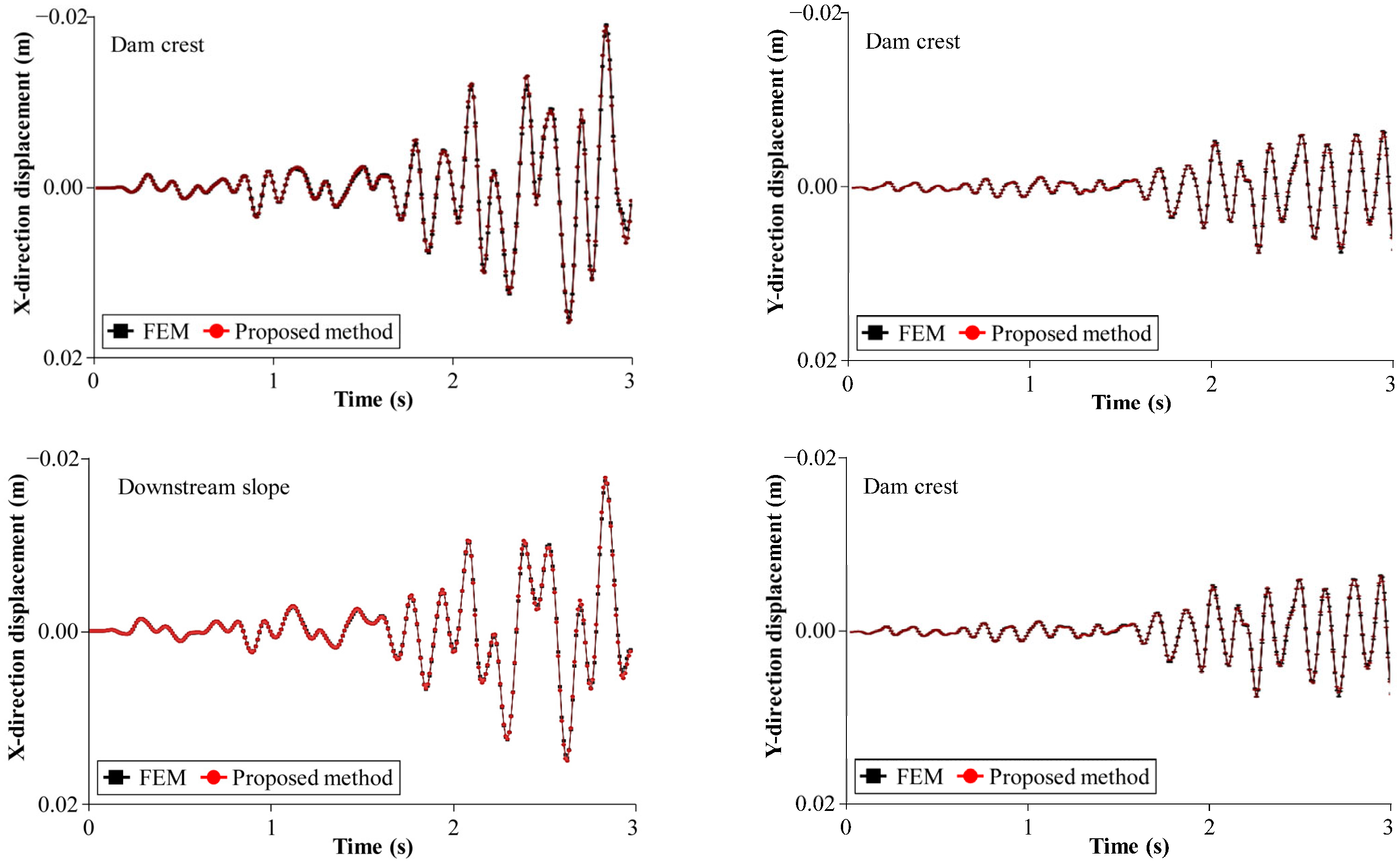
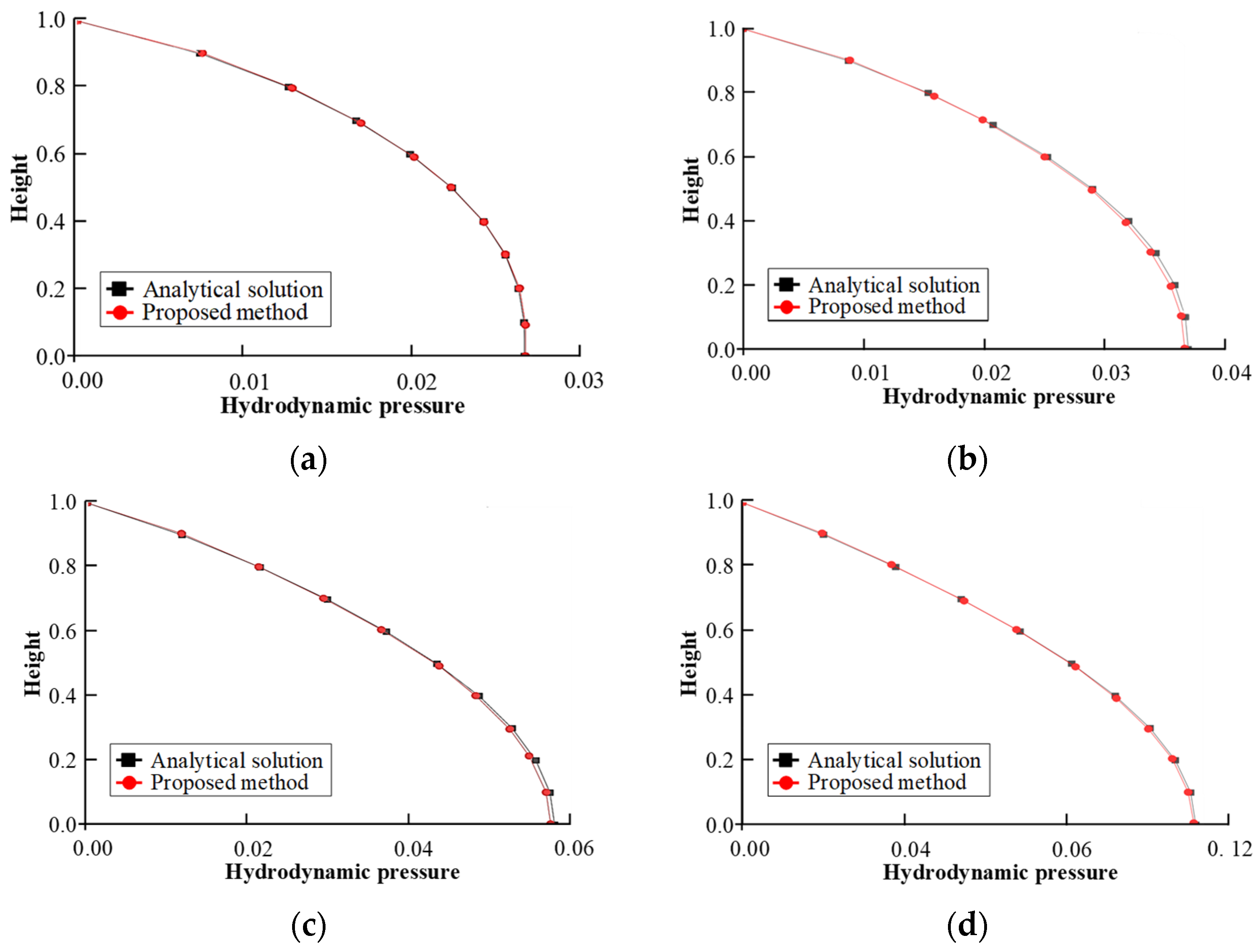
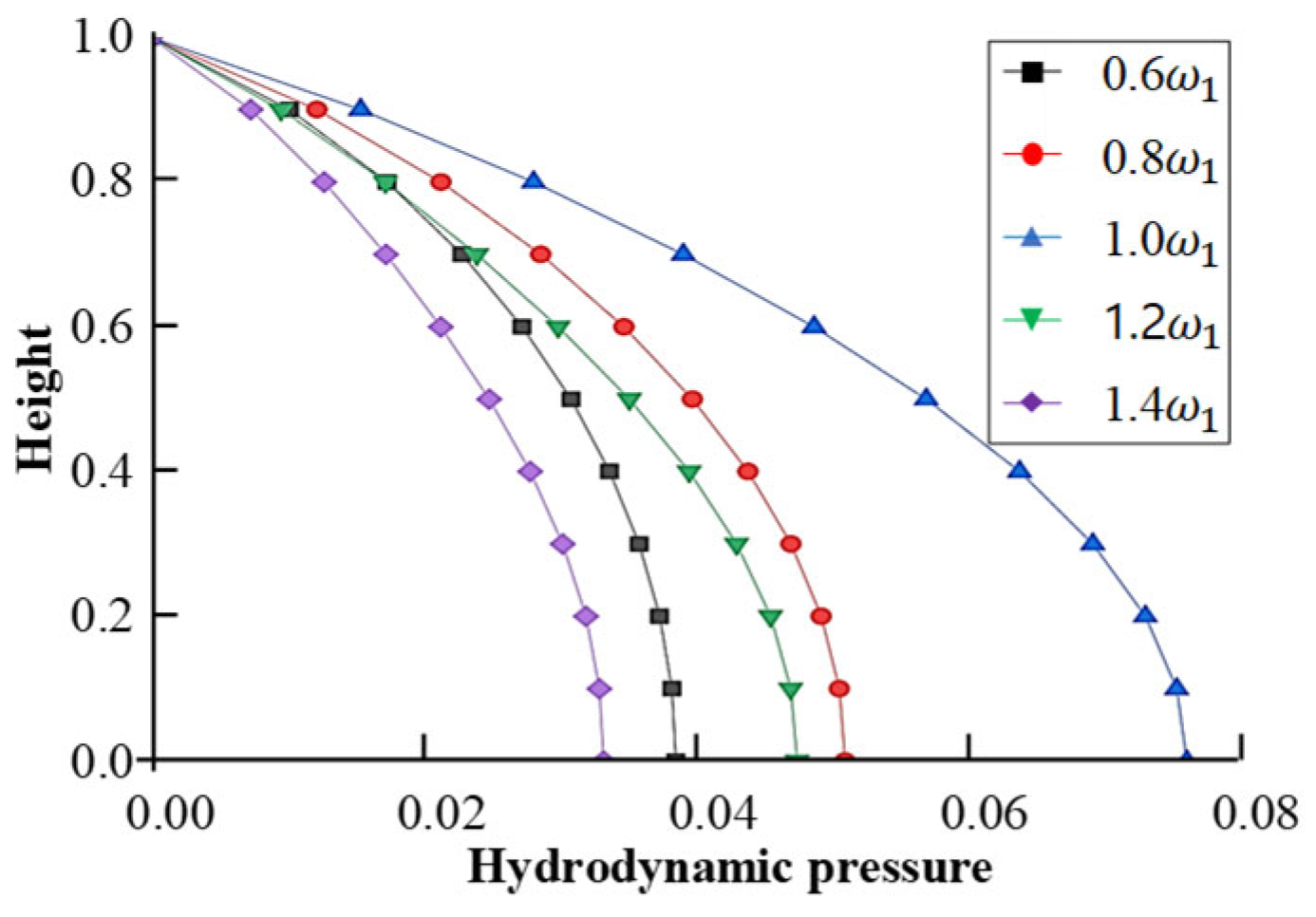
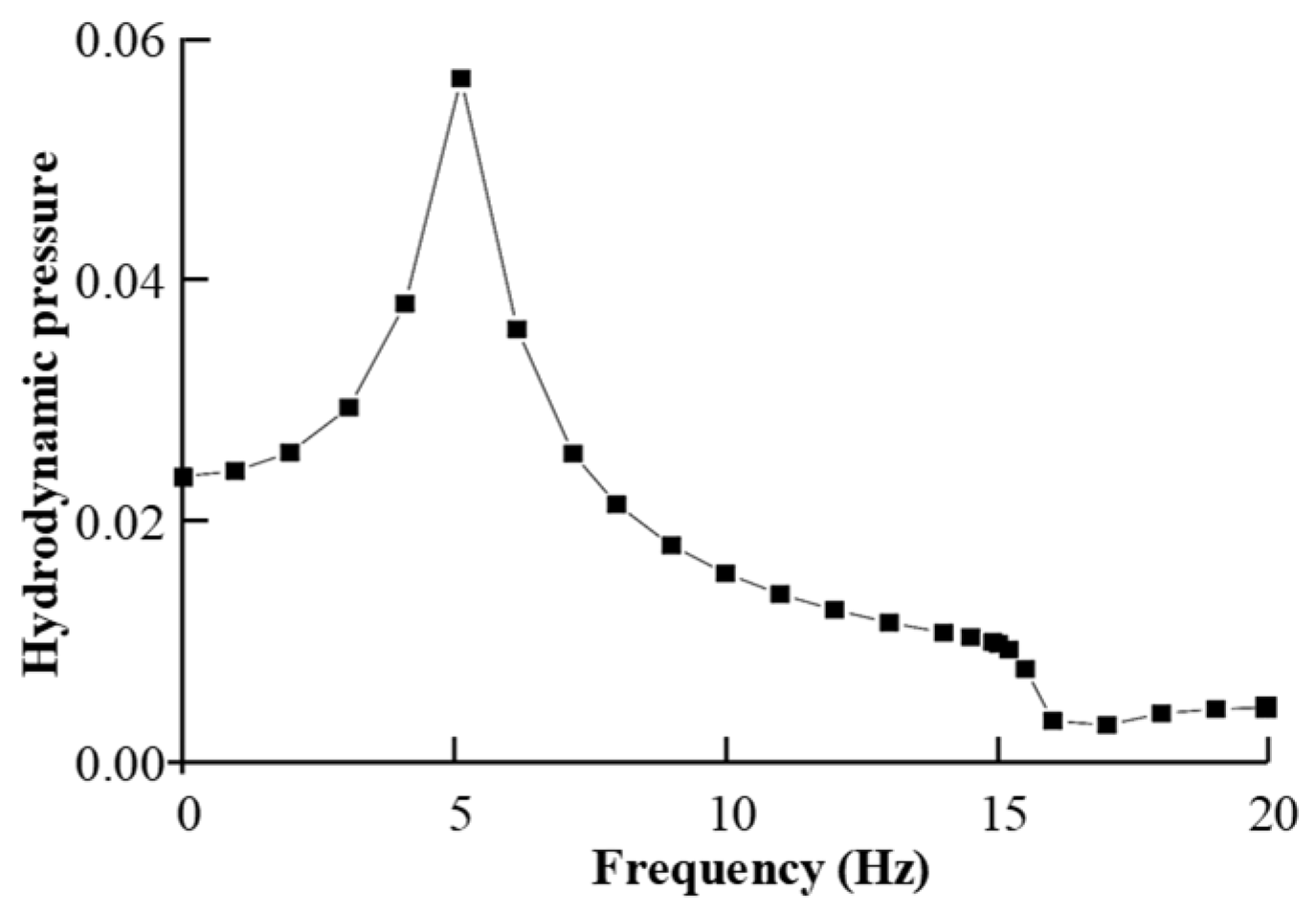
4.1. Uttarakhand Gravity Dam, India
4.2. Koyna Gravity Dam, India
5. Analysis of Dam–Foundation Interaction
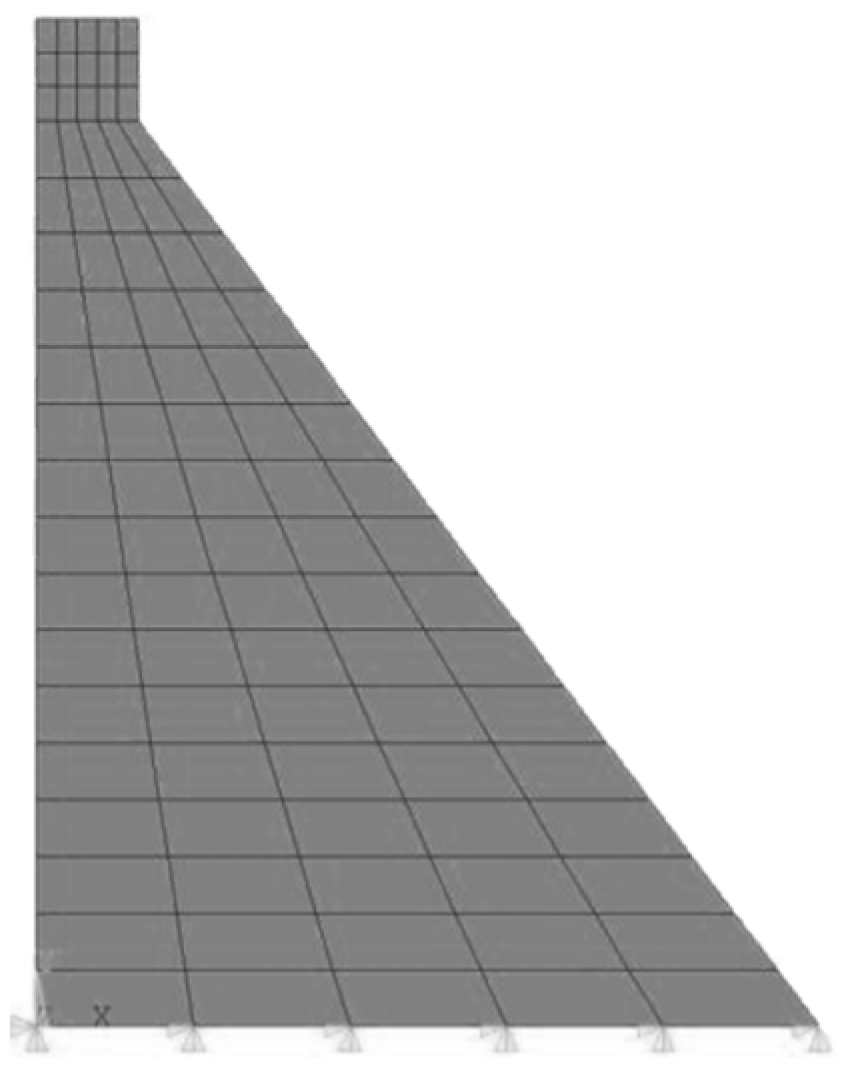
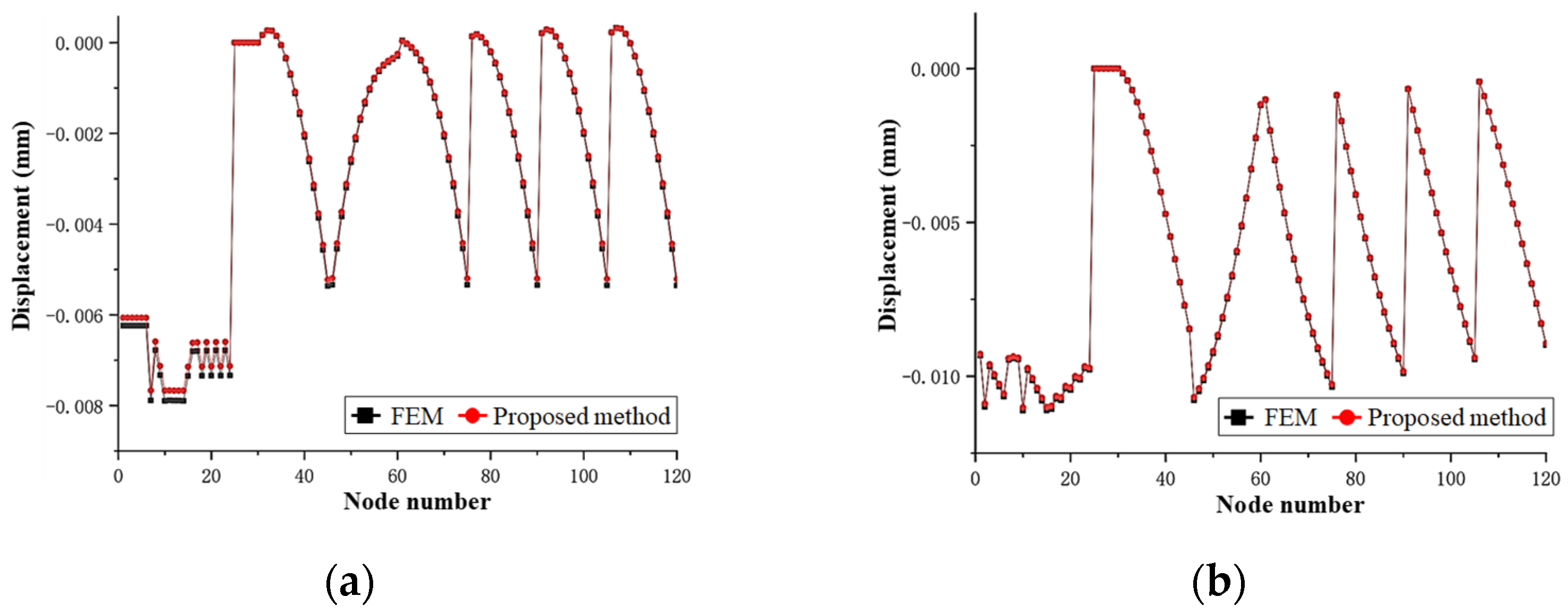
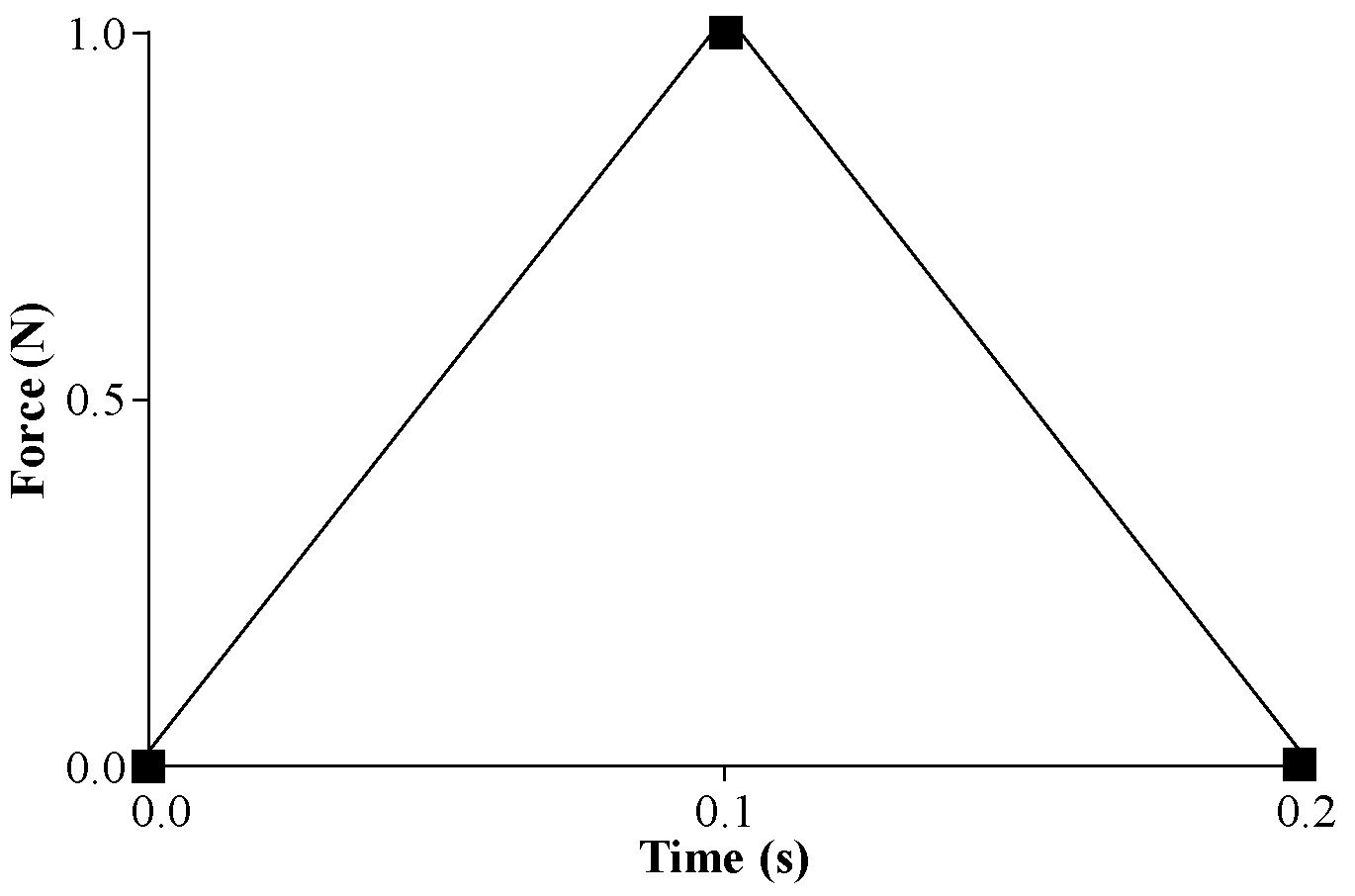
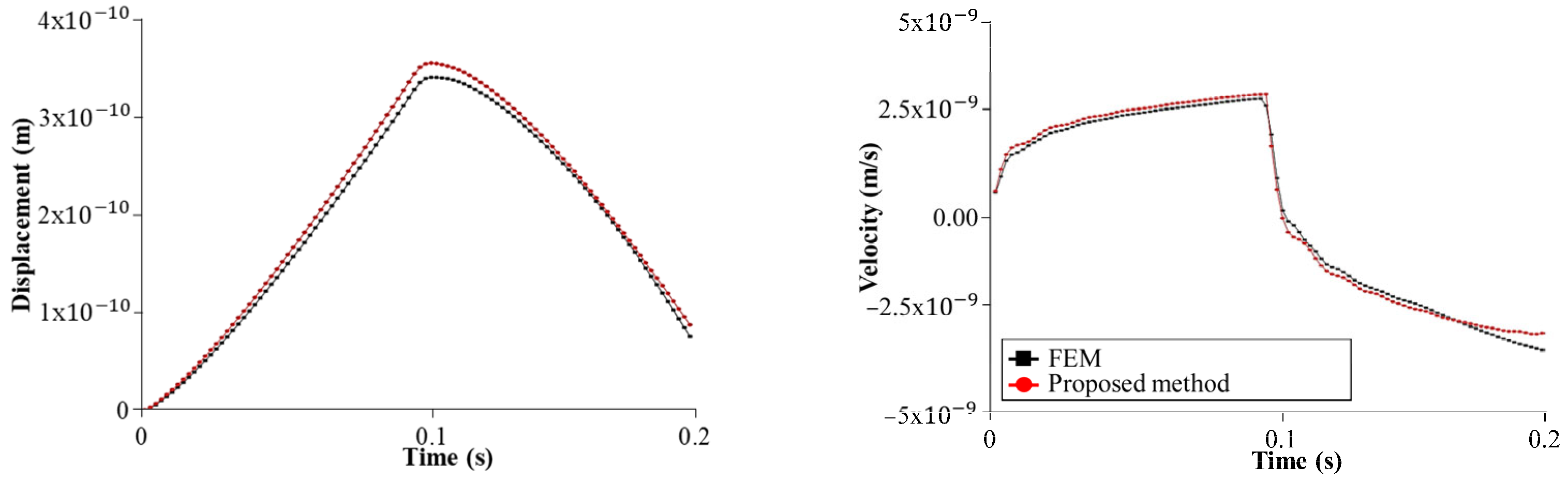
5.1. Infinite Foundation Under Impulse Loading
5.2. Scattering Problem in a Semi-Circular Valley
6. Hydrological Implications and Urban Resilience
6.1. Role of Gravity Dams in Urban Flood Mitigation
6.2. Compound Effects Under Climate-Driven Extremes
6.3. Toward Integrated Hydrological and Structural Analyses
6.4. Implications for Policy, Design Codes, and Future Research
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K. Flood risk and climate change: Global and regional perspectives. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef]
- Zhou, Q.; Mikkelsen, P.S.; Halsnæs, K. Framework for economic pluvial flood risk assessment considering climate change effects and adaptation benefits. J. Hydrol. 2012, 414–415, 539–549. [Google Scholar] [CrossRef]
- Vitter, J.S.; Webber, M. Water event categorization using sub-metered water and coincident electricity data. Water 2018, 10, 714. [Google Scholar] [CrossRef]
- Salvadore, E.; Bronders, J.; Batelaan, O. Hydrological modelling of urbanized catchments: A review and future directions. J. Hydrol. 2015, 529, 62–81. [Google Scholar] [CrossRef]
- Smith, J.; Brown, L. The impact of climate change on dam overtopping flood risk: A case study of 18 Australian dams. Hydrol. Earth Syst. Sci. Discuss. 2025. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, J.; Wang, D.; Song, C. Scaled boundary finite element method for seismic safety assessment of concrete gravity dams. Appl. Math. Model. 2023, 120, 747–763. [Google Scholar] [CrossRef]
- Bevacqua, E.; Maraun, D.; Vousdoukas, M.I.; Voukouvalas, E.; Vrac, M.; Mentaschi, L.; Widmann, M. Higher probability of compound flooding from precipitation and storm surge in Europe under anthropogenic climate change. Sci. Adv. 2019, 5, eaaw5531. [Google Scholar] [CrossRef]
- Ridder, N.N.; Pitman, A.J.; Westra, S.; Ukkola, A.; Do, H.X.; Bador, M.; Hirsch, A.L.; Evans, J.P.; Luca, A.D.; Zscheischler, J. Global hotspots for the occurrence of compound events. Nat. Commun. 2020, 11, 5956. [Google Scholar] [CrossRef]
- Zscheischler, J.; Westra, S.; van den Hurk, B.J.J.M.; Seneviratne, S.I.; Ward, P.J.; Pitman, A.; AghaKouchak, A.; Bresch, D.N.; Leonard, M.; Wahl, T.; et al. Future climate risk from compound events. Nat. Clim. Chang. 2018, 8, 469–477. [Google Scholar] [CrossRef]
- Chopra, A.K.; Chakrabarti, P. The Koyna earthquake and the damage to Koyna Dam. Bull. Seismol. Soc. Am. 1973, 63, 381–397. [Google Scholar] [CrossRef]
- Jansen, R. Dams and Public Safety; U.S. Department of the Interior, Bureau of Reclamation: Denver, CO, USA, 1980. [Google Scholar]
- Xu, H.; Xu, Y.; Dai, H.; Li, D. Seismic performance of concrete gravity dams under combined reservoir water levels and ground motions. Soil Dyn. Earthq. Eng. 2019, 116, 538–552. [Google Scholar] [CrossRef]
- Dasgupta, P.; Das, J.; Roy, S. Impact of climate change on flood frequency and intensity in the Indian subcontinent. J. Hydrol. 2020, 590, 125223. [Google Scholar]
- Bathe, K.J. Finite Element Procedures; Prentice Hall: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Li, S. Coupled finite element–scaled boundary finite element method for transient analysis of dam–reservoir interaction. In Computational Science and Its Applications—ICCSA 2011; Murgante, B., Gervasi, O., Iglesias, A., Taniar, D., Apduhan, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 26–34. [Google Scholar] [CrossRef]
- Xu, H.; Xu, J.; Yan, D.; Chen, K.; Zou, D. An efficient dynamic coupling calculation method for dam–reservoir systems based on FEM. Water 2023, 15, 3095. [Google Scholar] [CrossRef]
- Song, C.; Wolf, J.P. The scaled boundary finite-element method—Alias consistent infinitesimal finite-element cell method—For elastodynamics. Comput. Methods Appl. Mech. Eng. 1997, 147, 329–355. [Google Scholar] [CrossRef]
- Zhao, L.H. Seismic Response Analysis of Arch Dams with Transverse Joints Considering Dam-Reservoir-Foundation Interaction. Ph.D. Thesis, Hohai University, Nanjing, China, 2006. [Google Scholar]
- Yaseri, A.; Konrad, J.-M. Computation of amplification functions of earth dam–flexible canyon systems by the hybrid FEM–SBFEM technique. Earthq. Eng. Struct. Dyn. 2021, 50, 2883–2902. [Google Scholar] [CrossRef]
- Wang, J.; Song, C. Scaled boundary finite element analysis of dam-reservoir interaction in layered half-space. Soil Dyn. Earthq. Eng. 2020, 135, 106189. [Google Scholar] [CrossRef]
- Hallegatte, S.; Green, C.; Nicholls, R.J.; Corfee-Morlot, J. Future flood losses in major coastal cities. Nat. Clim. Chang. 2013, 3, 802–806. [Google Scholar] [CrossRef]
- UNDRR. Global Assessment Report on Disaster Risk Reduction 2019; United Nations Office for Disaster Risk Reduction: Geneva, Switzerland, 2019; Available online: https://gar.undrr.org/ (accessed on 30 June 2025).
- IPCC. Climate Change 2021: Impacts, Adaptation and Vulnerability; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2021; Available online: https://www.ipcc.ch/report/ar6/wg2/ (accessed on 30 June 2025).
- Zhang, L.; Liu, Y.; Song, C. A scaled boundary finite element method for dynamic analysis of dam-reservoir systems under earthquake excitation. Eng. Struct. 2019, 197, 109402. [Google Scholar] [CrossRef]
- Chen, D.; Chen, K.; Zou, D. High-resolution numerical modeling of dam–reservoir–foundation systems using SBFEM. J. Comput. Phys. 2021, 429, 110018. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Saouma, V.E. Seismic fragility analysis of concrete dams: A state-of-the-art review. Eng. Struct. 2016, 128, 374–399. [Google Scholar] [CrossRef]
- Arheimer, B.; Lindström, G. Climate impact on floods: Changes in high flows in Sweden in the past and the future (1911–2100). Hydrol. Earth Syst. Sci. 2015, 19, 771–784. [Google Scholar] [CrossRef]
- Blöschl, G.; Hall, J.; Viglione, A.; Perdigão, R.A.P.; Parajka, J.; Merz, B.; Lun, D.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; et al. Changing climate both increases and decreases European river floods. Nature 2019, 573, 108–111. [Google Scholar] [CrossRef] [PubMed]

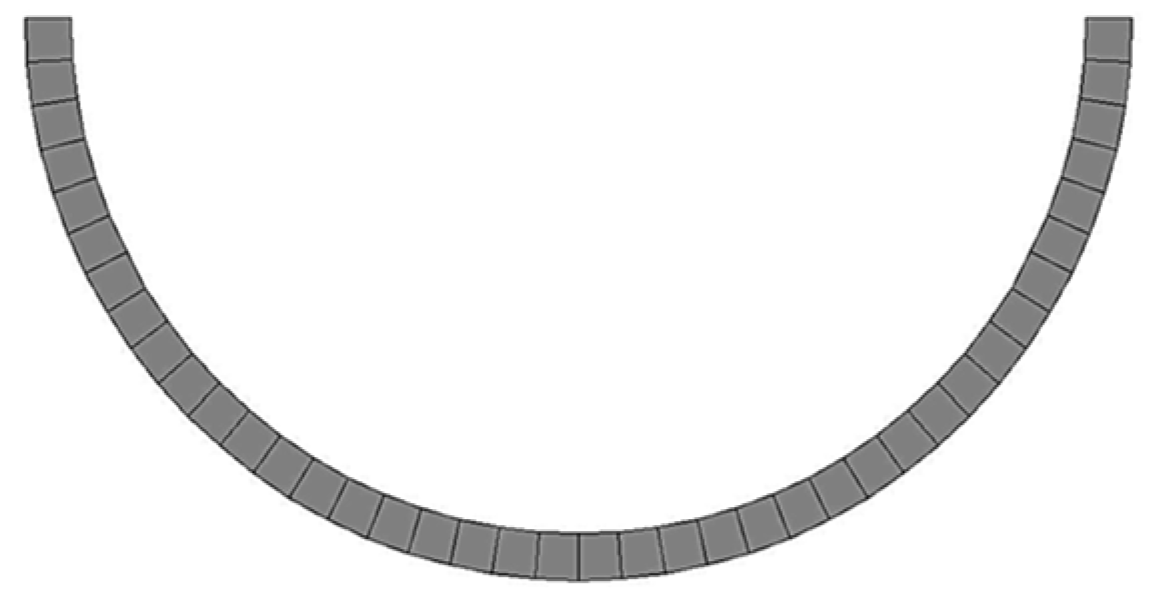
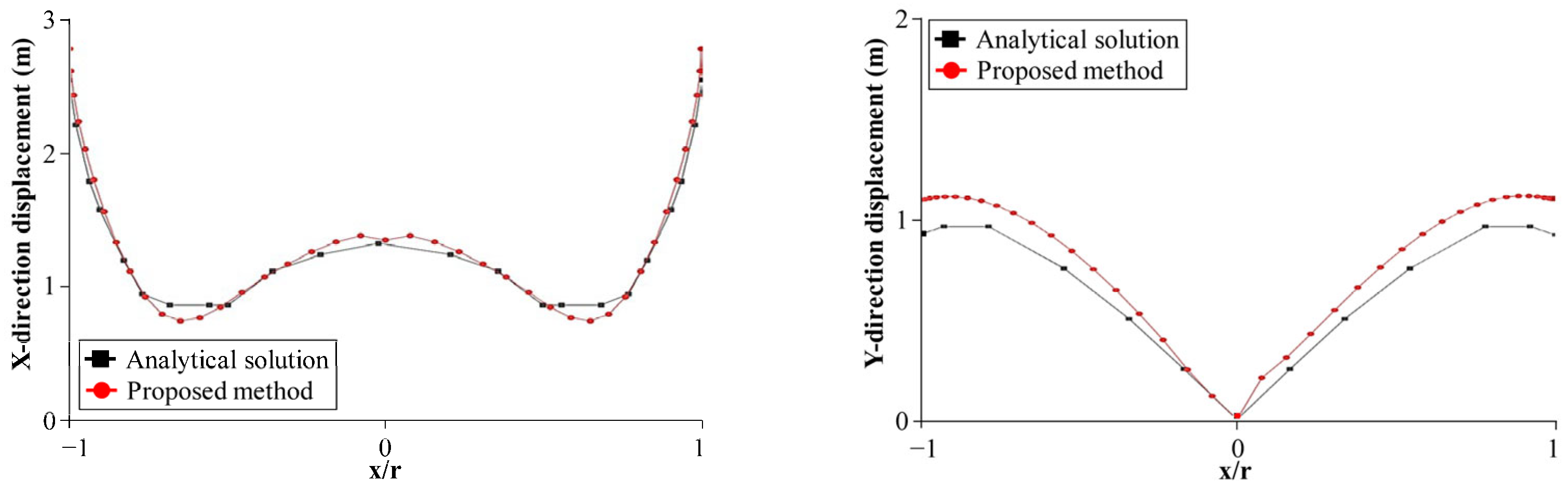
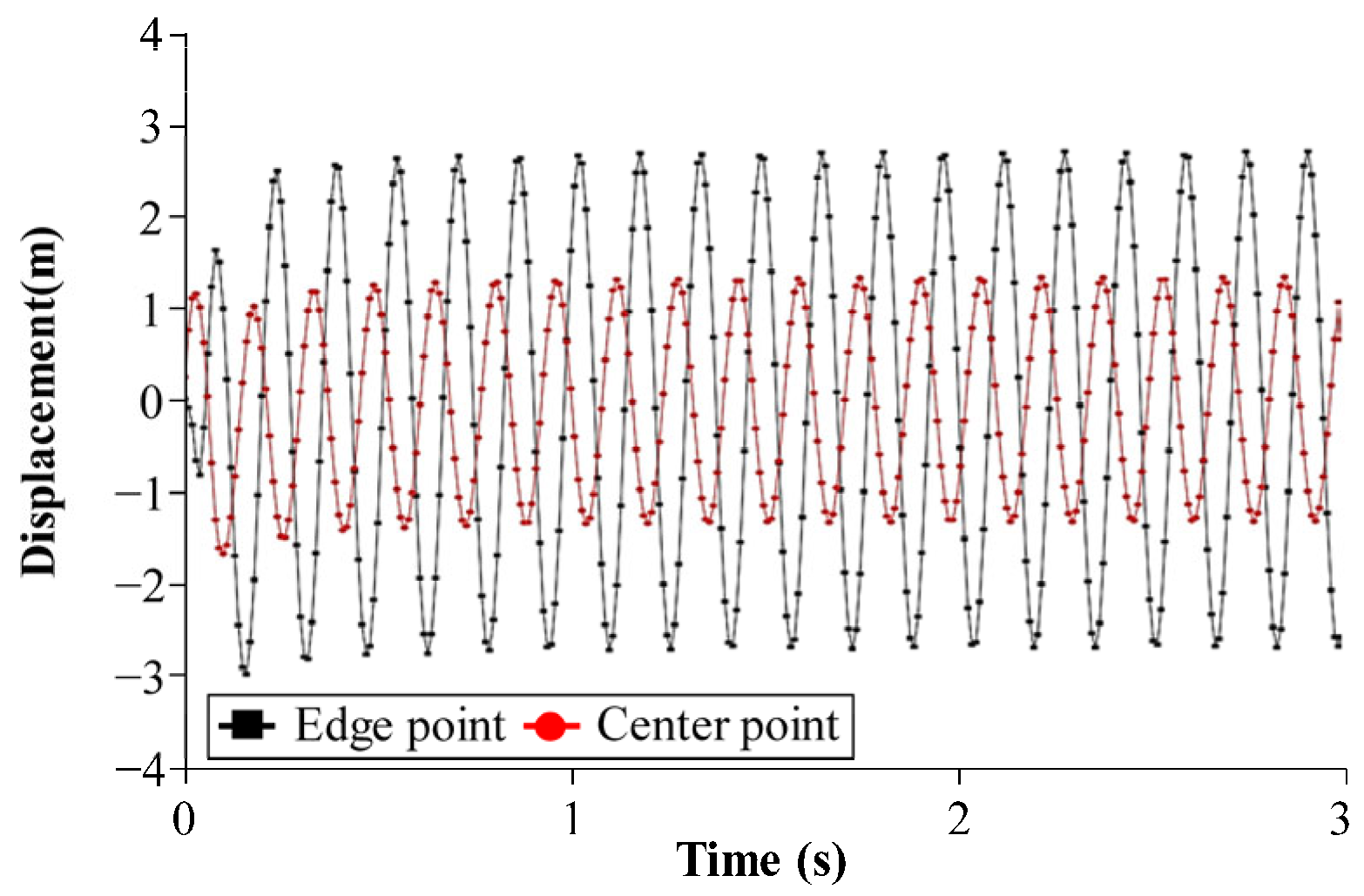
| Case Study | Method | Nodes | Elements | CPU Time (s) | Memory Usage (MB) |
|---|---|---|---|---|---|
| Koyna Dam | SBFEM | 82 | 40 | 120 | 50 |
| FEM | 1200 | 1100 | 300 | 500 | |
| Semi-circular Valley | SBFEM | 82 | 40 | 100 | 45 |
| FEM | 1407 | 1320 | 200 | 550 |
| Property | Value | Unit |
|---|---|---|
| Elastic modulus | 28.5 | GPa |
| Poisson’s ratio | 0.167 | – |
| Density | 2400 | kg/m3 |
| Tensile strength | 1.96 | MPa |
| Compressive strength | 17.5 | MPa |
| Dilation coefficient | 0.3 | – |
| Property | Value | Unit |
|---|---|---|
| Elastic modulus | 10 | GPa |
| Poisson’s ratio | 0.25 | – |
| Density | 2000 | kg/m3 |
| Shear wave velocity | 1414 | m/s |
| Property | Value |
|---|---|
| Total simulation time | 3.0 s |
| Time step | 0.01 s |
| Number of steps | 300 |
| Order | Consistent Mass Matrix | Concentrated Mass Matrix | ||||
|---|---|---|---|---|---|---|
| Proposed Method | FEM | Error | Proposed Method | FEM | Error | |
| 1 | 14.99489 | 14.70902 | 1.94% | 14.93761 | 14.70902 | 1.55% |
| 2 | 34.89665 | 34.2373 | 1.93% | 34.58361 | 34.2373 | 1.01% |
| 3 | 41.53249 | 40.84575 | 1.68% | 41.43663 | 40.84575 | 1.45% |
| 4 | 61.04594 | 59.65121 | 2.34% | 59.87308 | 59.65121 | 0.37% |
| 5 | 89.77952 | 88.08956 | 1.92% | 87.75917 | 88.08956 | 0.38% |
| 6 | 94.48564 | 92.69908 | 1.93% | 92.50532 | 92.69908 | 0.21% |
| 7 | 118.8139 | 117.6998 | 0.95% | 114.4989 | 117.6998 | 2.72% |
| 8 | 123.1543 | 120.2494 | 2.42% | 116.8022 | 120.2494 | 2.87% |
| 9 | 130.9144 | 129.3366 | 1.22% | 125.4198 | 129.3366 | 3.03% |
| 10 | 148.2714 | 144.911 | 2.32% | 135.8962 | 144.911 | 6.22% |
| Scenario | Reservoir Level Increase (m) | Frequency of High Reservoir Events (%) |
|---|---|---|
| RCP 4.5 | +5 | +20 |
| RCP 8.5 | +10 | +45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, M.-k.; Xu, D. Seismic Performance Assessment of Gravity Dams for Urban Flood Risk Mitigation Using the Scaled Boundary Finite Element Method (SBFEM). Hydrology 2025, 12, 209. https://doi.org/10.3390/hydrology12080209
Kim M-k, Xu D. Seismic Performance Assessment of Gravity Dams for Urban Flood Risk Mitigation Using the Scaled Boundary Finite Element Method (SBFEM). Hydrology. 2025; 12(8):209. https://doi.org/10.3390/hydrology12080209
Chicago/Turabian StyleKim, Min-koan, and Dai Xu. 2025. "Seismic Performance Assessment of Gravity Dams for Urban Flood Risk Mitigation Using the Scaled Boundary Finite Element Method (SBFEM)" Hydrology 12, no. 8: 209. https://doi.org/10.3390/hydrology12080209
APA StyleKim, M.-k., & Xu, D. (2025). Seismic Performance Assessment of Gravity Dams for Urban Flood Risk Mitigation Using the Scaled Boundary Finite Element Method (SBFEM). Hydrology, 12(8), 209. https://doi.org/10.3390/hydrology12080209







