The Characteristics and Trend Prediction of Water and Sediment Evolution at the Toudaoguai Station on the Yellow River from 1960 to 2019
Abstract
1. Introduction
2. Overview of the Research Area and Research Methodology
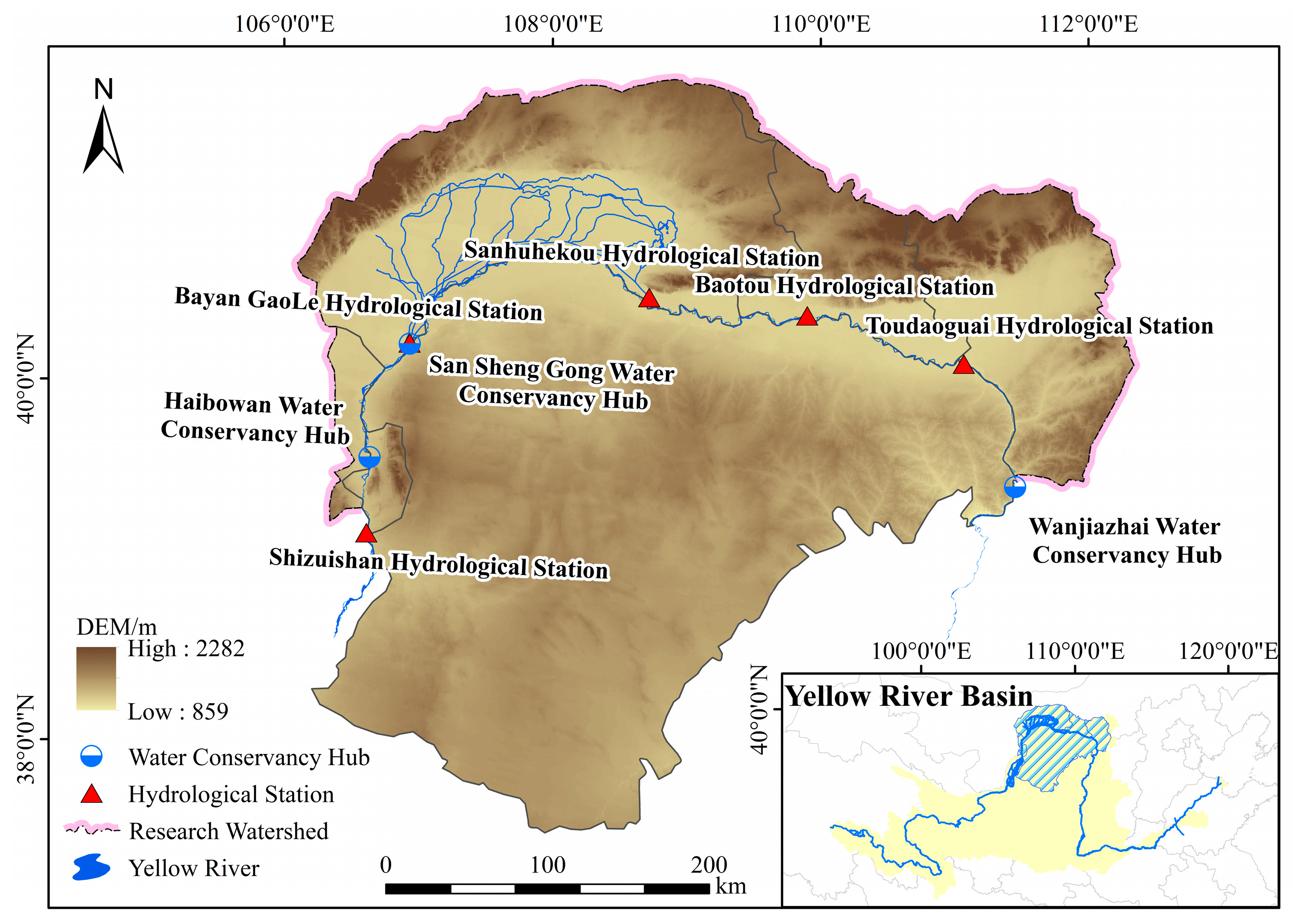
2.1. Overview of the Research Area
2.2. Methodology
2.2.1. M–K Method
2.2.2. Cumulative Anomaly Method
2.2.3. Wavelet Analysis Method
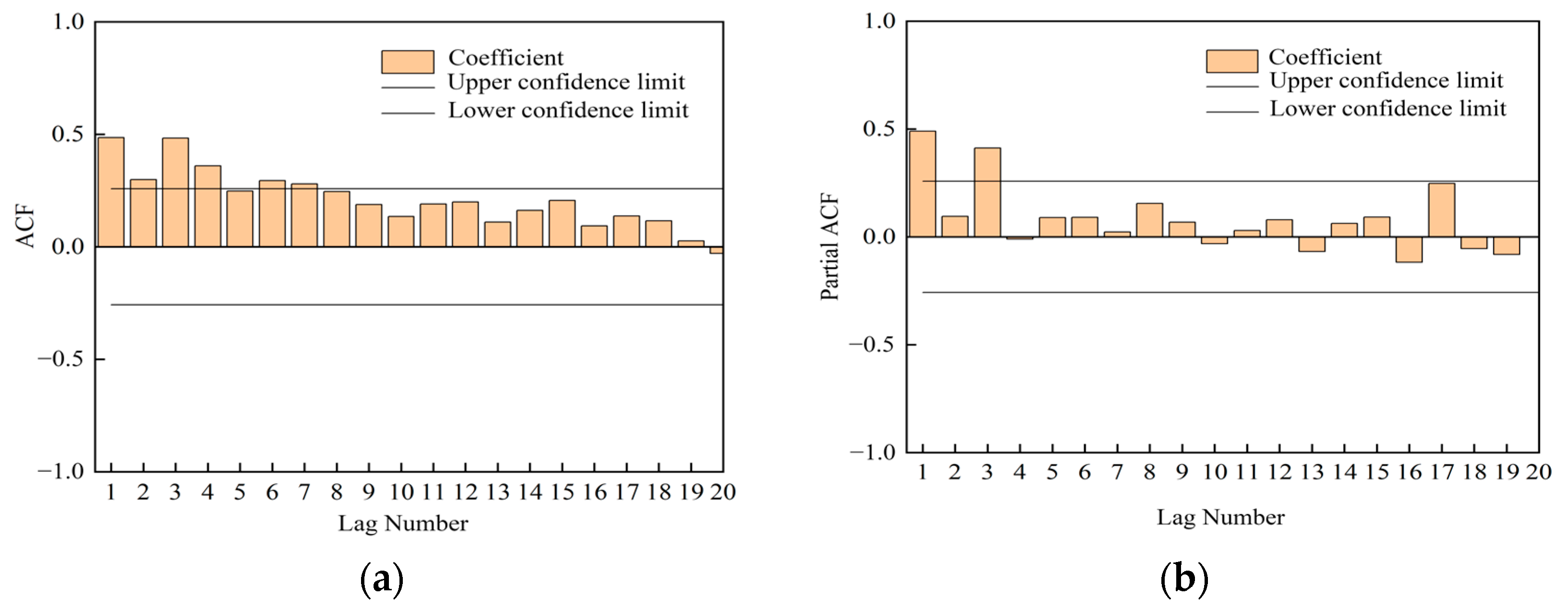
2.2.4. Methods for Simulation of Water–Sediment Evolution and Trend Prediction
- (1)
- Forward Propagation Process:
- (2)
- Backpropagation Process:
- (3)
- ARIMA-BP Coupled Model:
3. Analysis of Water and Sediment Evolution Characteristics at the Toudaoguai Hydrometric Station Cross-Section in the Inner Mongolia Reach of the Yellow River
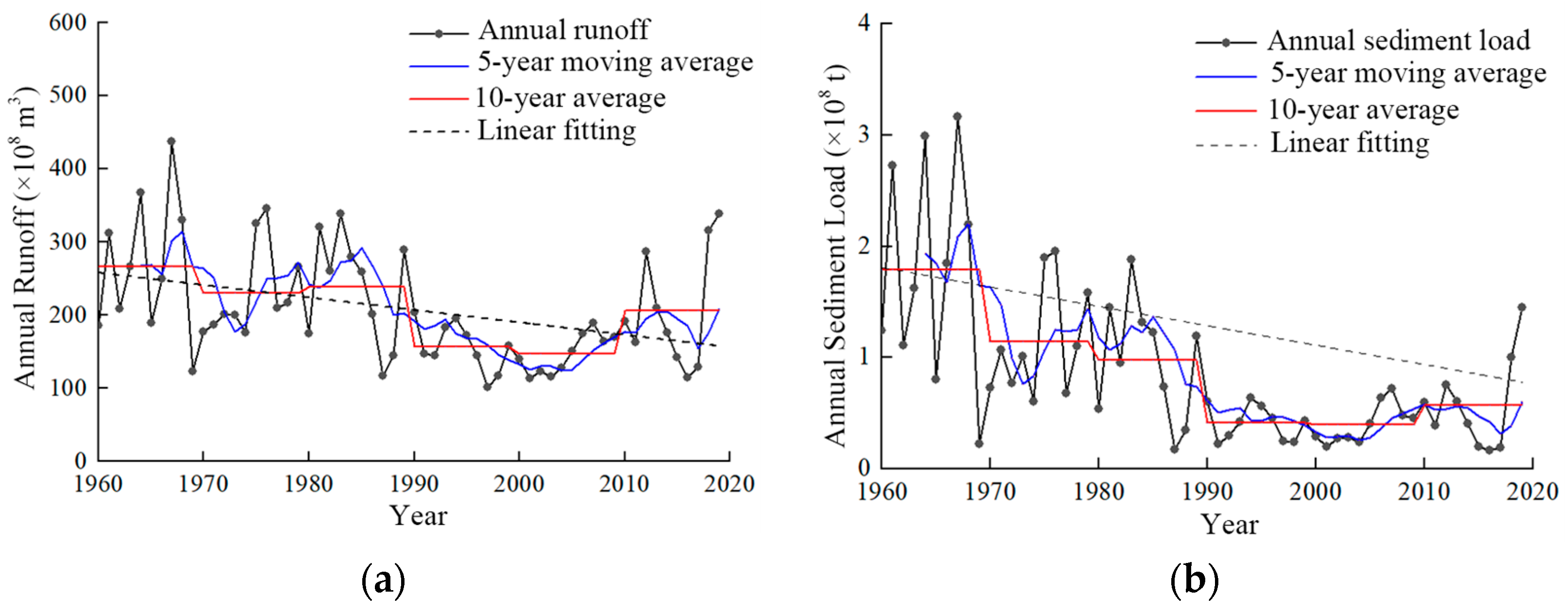
3.1. Interannual Trend of Water and Sediment Evolution
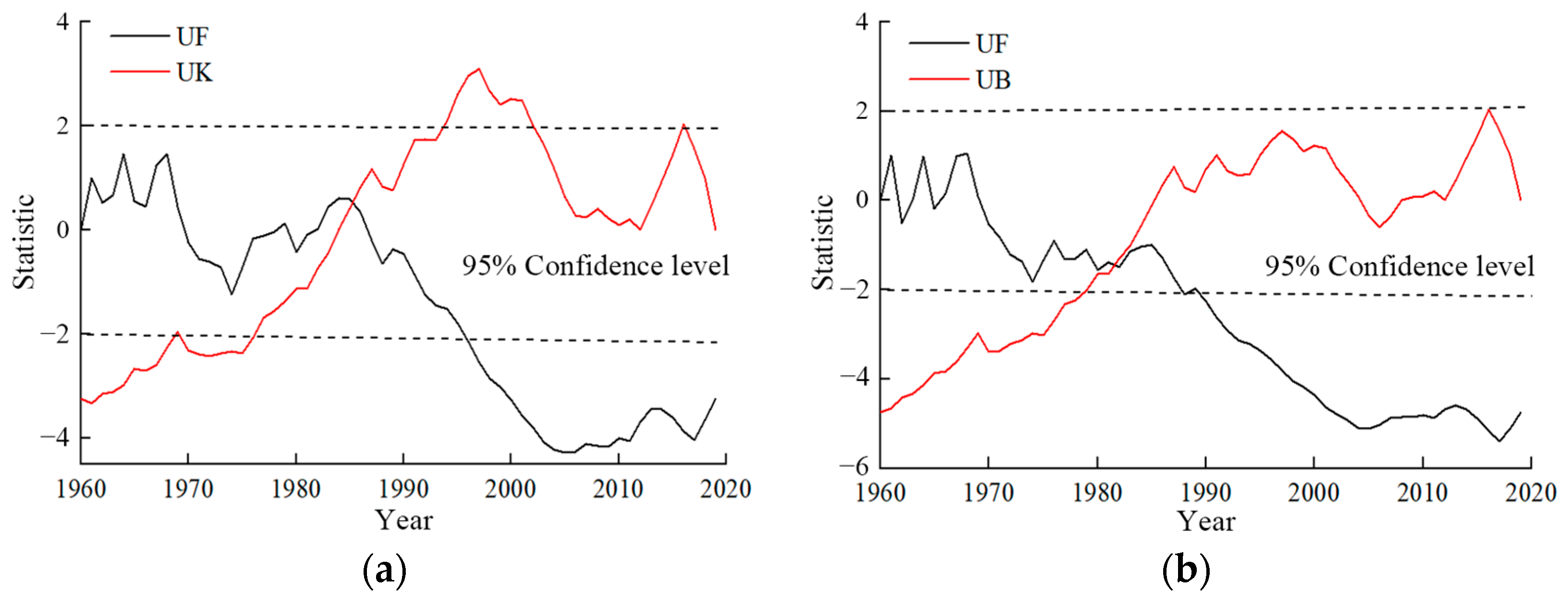
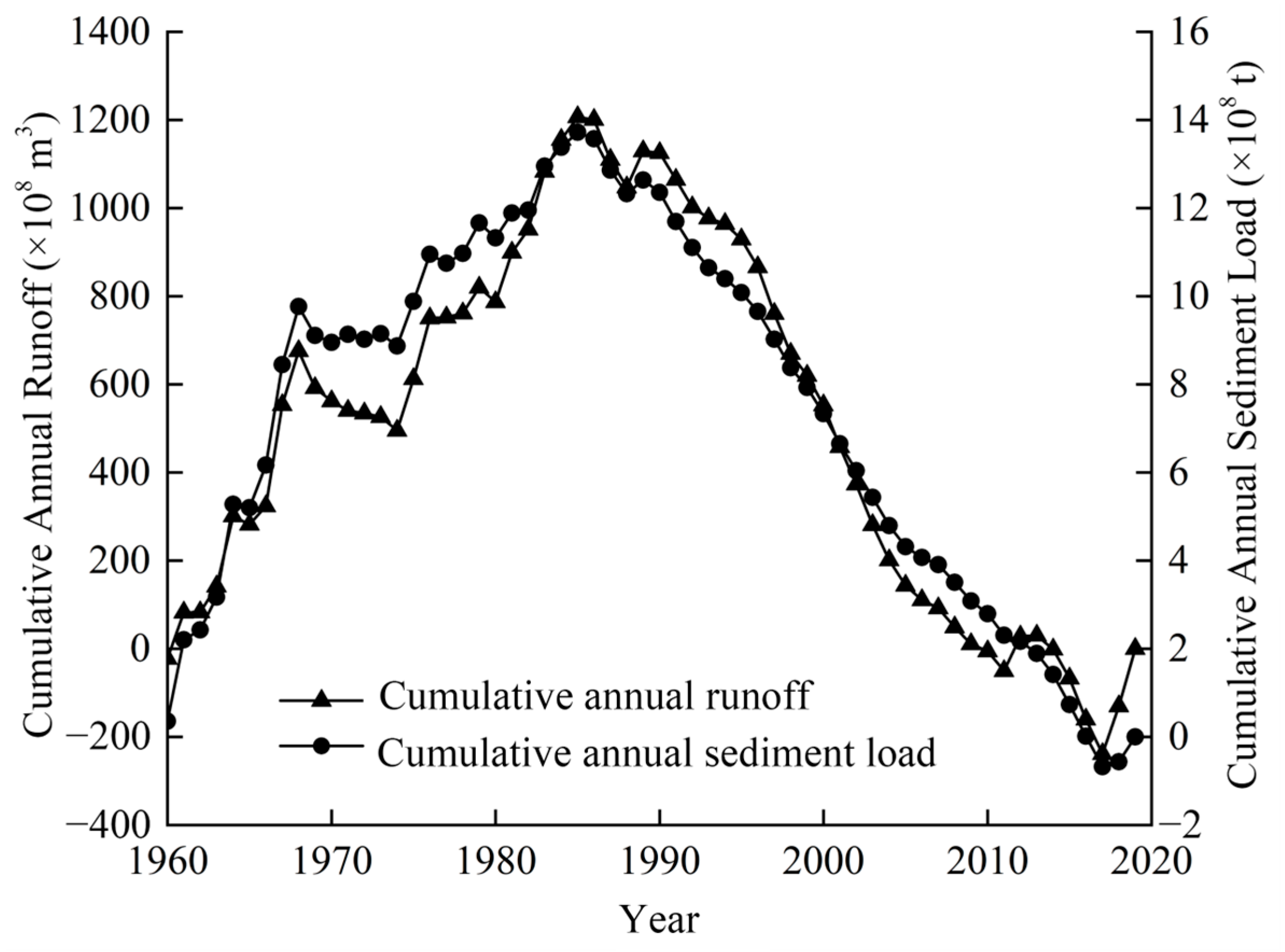
3.2. Abruptness of Water and Sediment Evolution
3.3. Periodicity of Water–Sediment Evolution
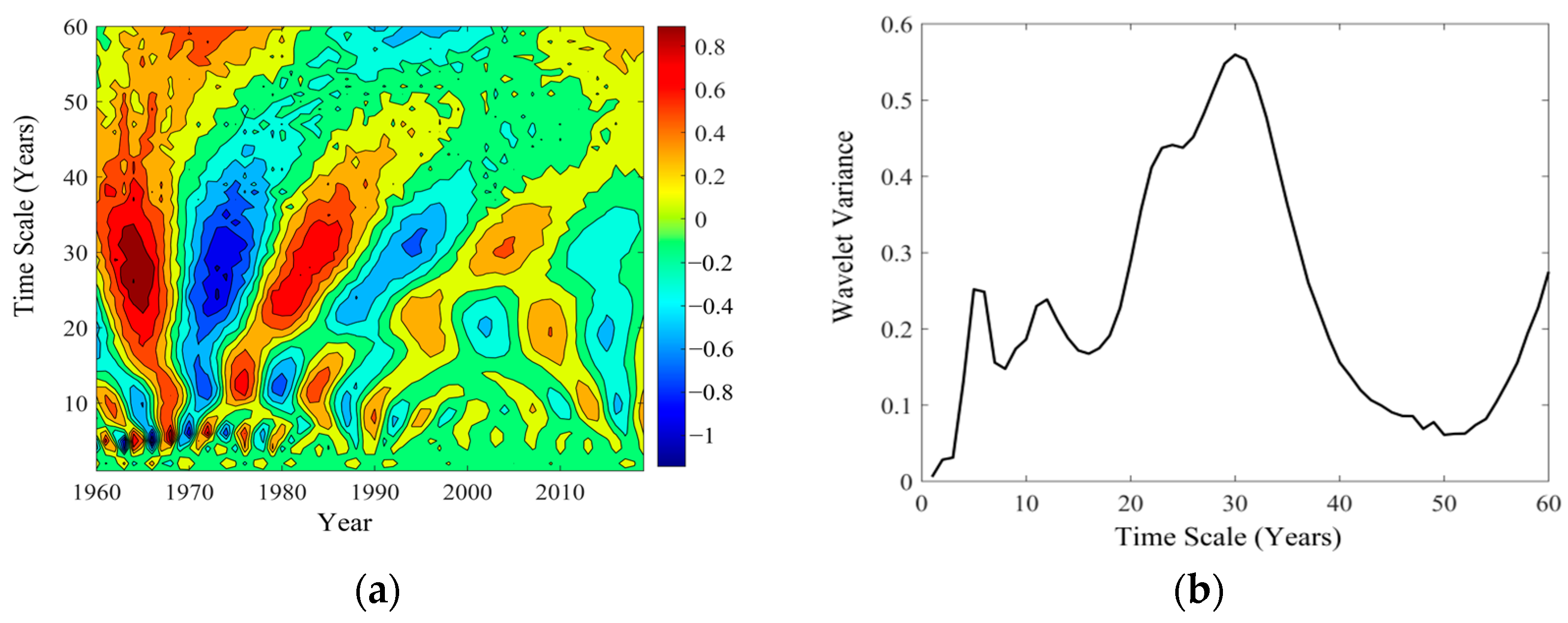
3.3.1. Periodic Analysis of Annual Runoff
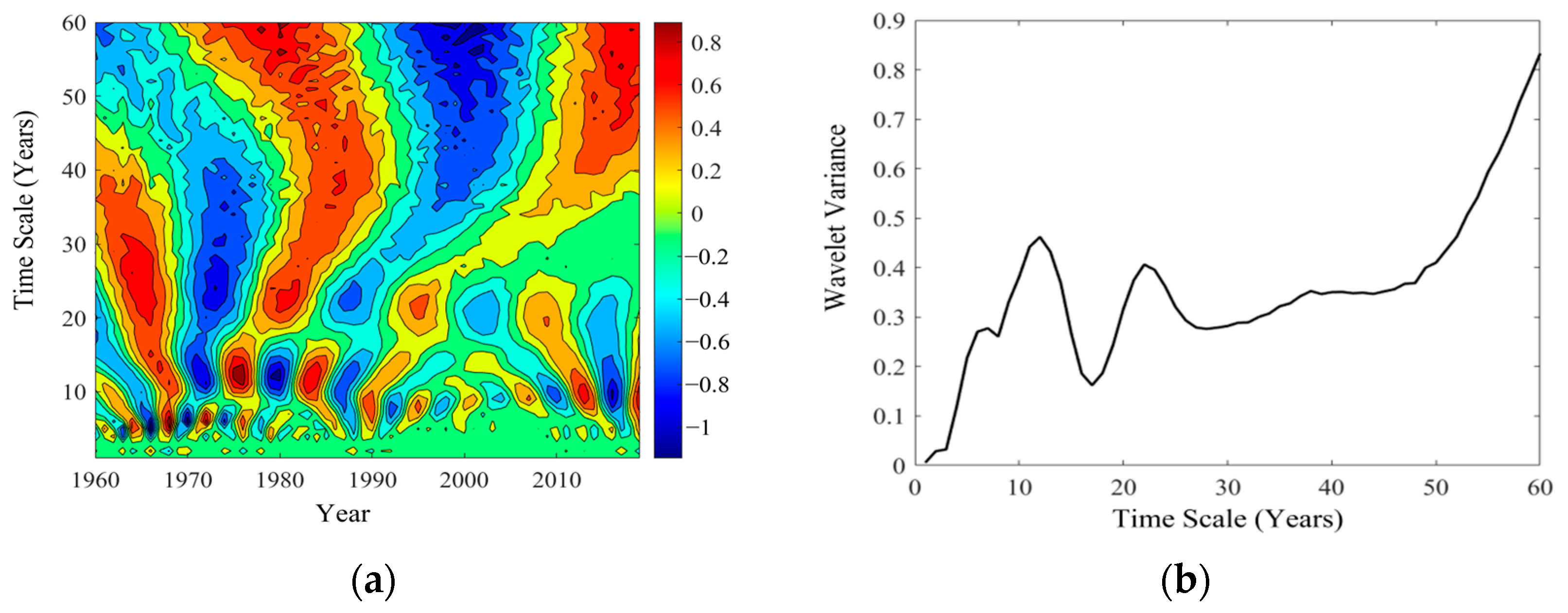
3.3.2. Periodic Analysis of Annual Sediment Load
4. Simulation and Prediction of Water–Sediment Evolution at the Toudaoguai Hydrological Station of the Yellow River
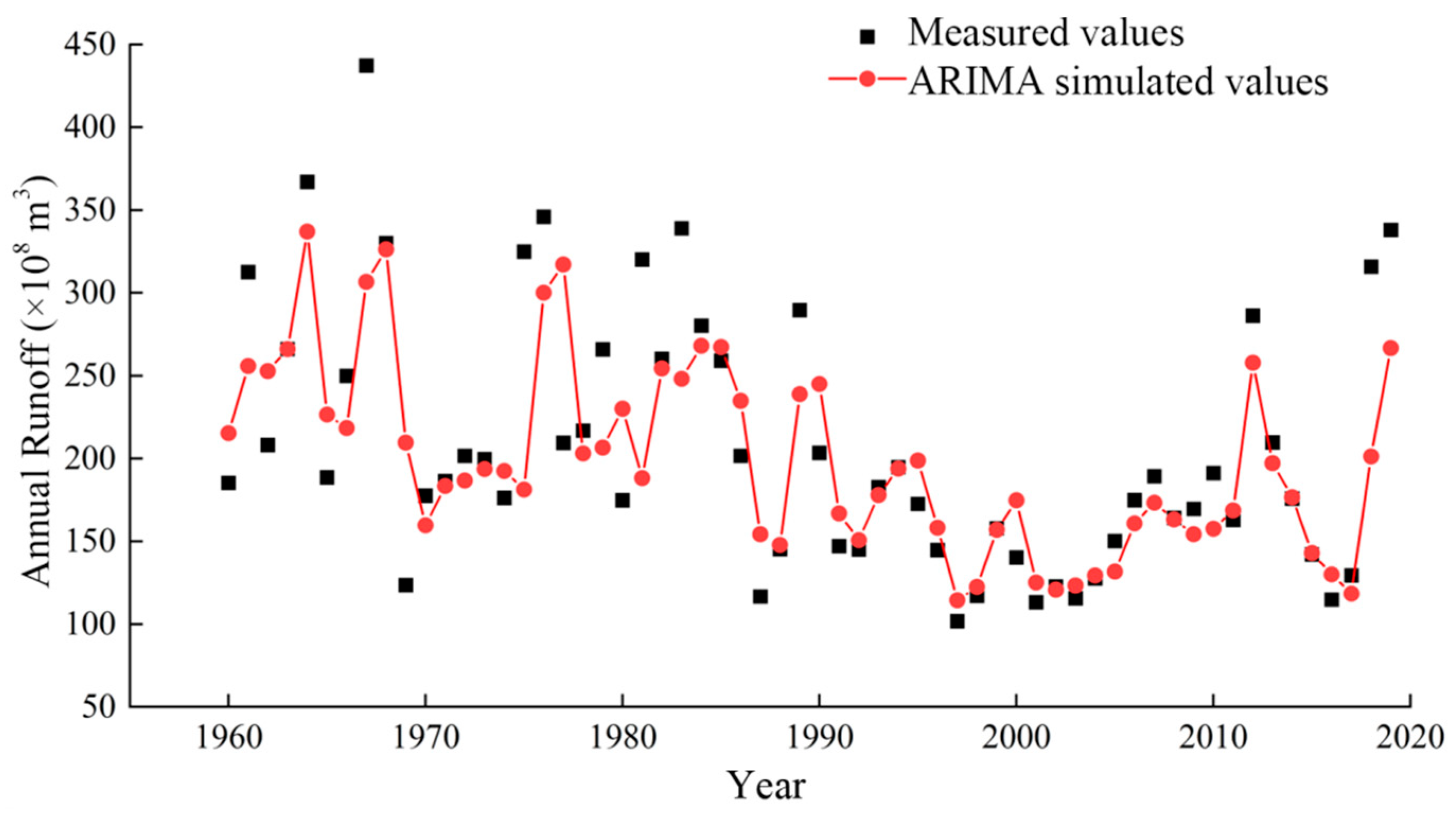
4.1. Simulation of Water–Sediment Evolution Process Based on the ARIMA Model
4.1.1. Simulation of the Evolution Process of Annual Runoff
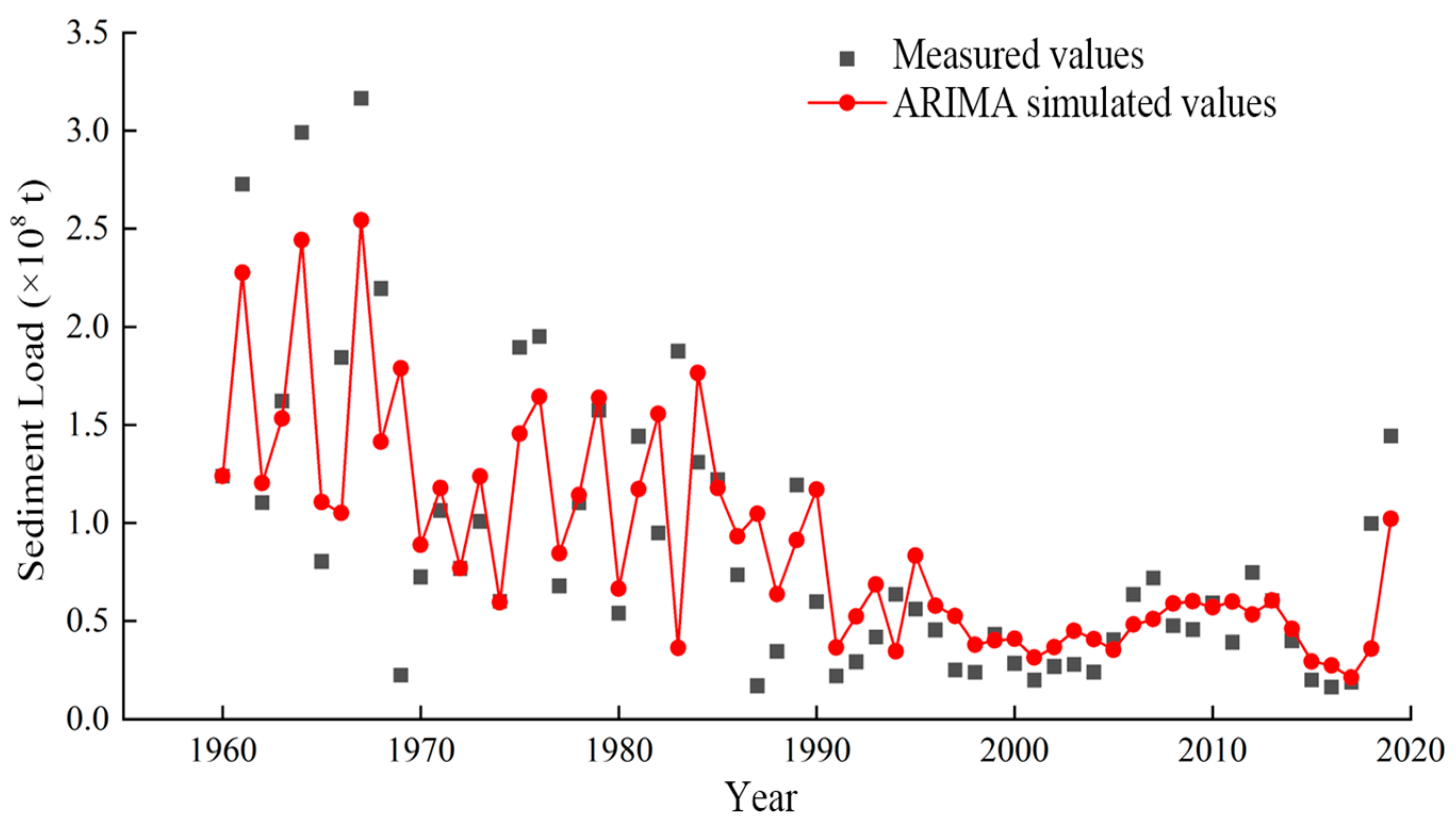
4.1.2. Prediction of Annual Sediment Transport by the ARIMA Model
4.2. Simulation of Water and Sediment Evolution Processes Using BP Neural Networks
4.2.1. Simulation of Annual Runoff Volume
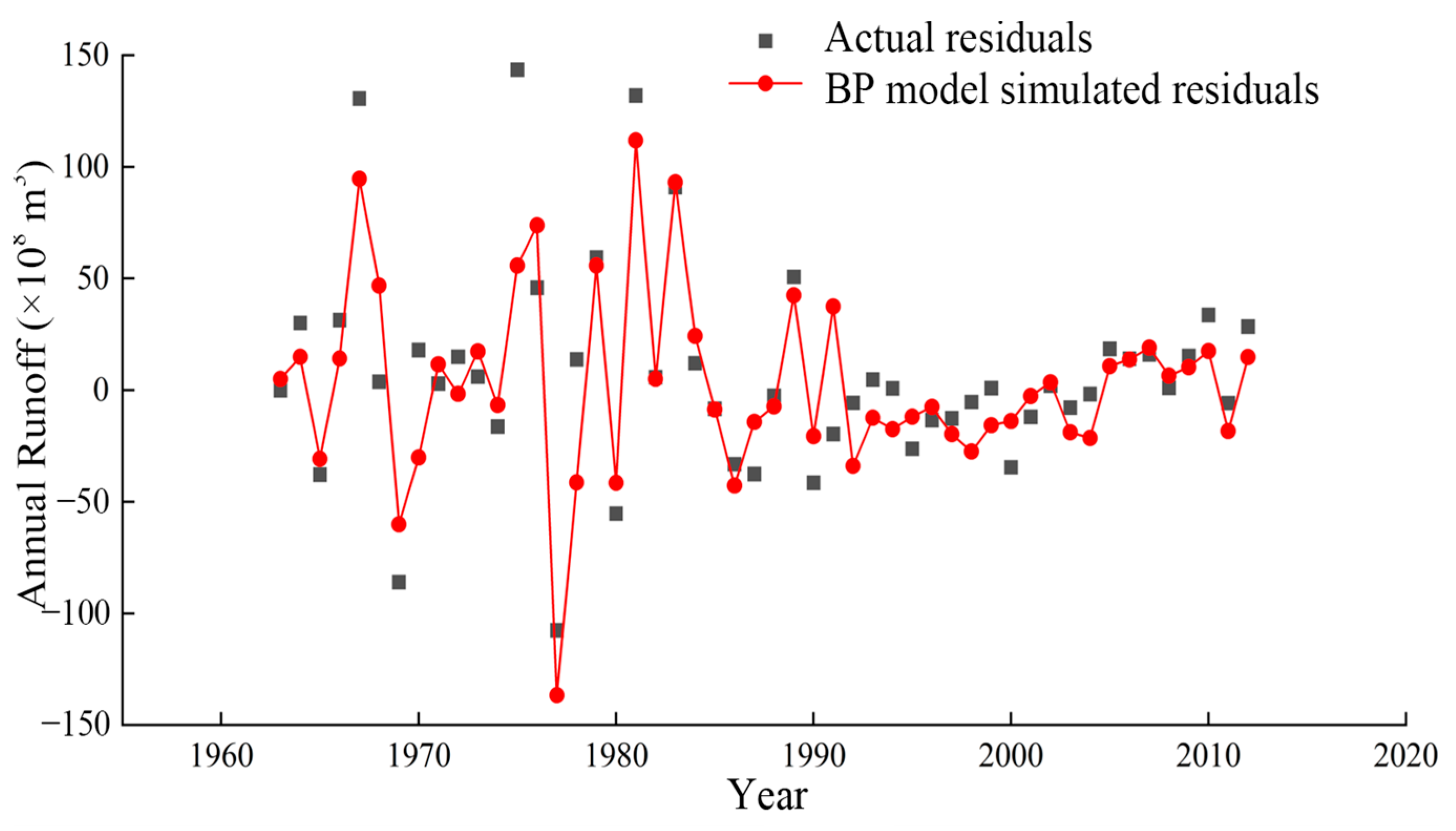
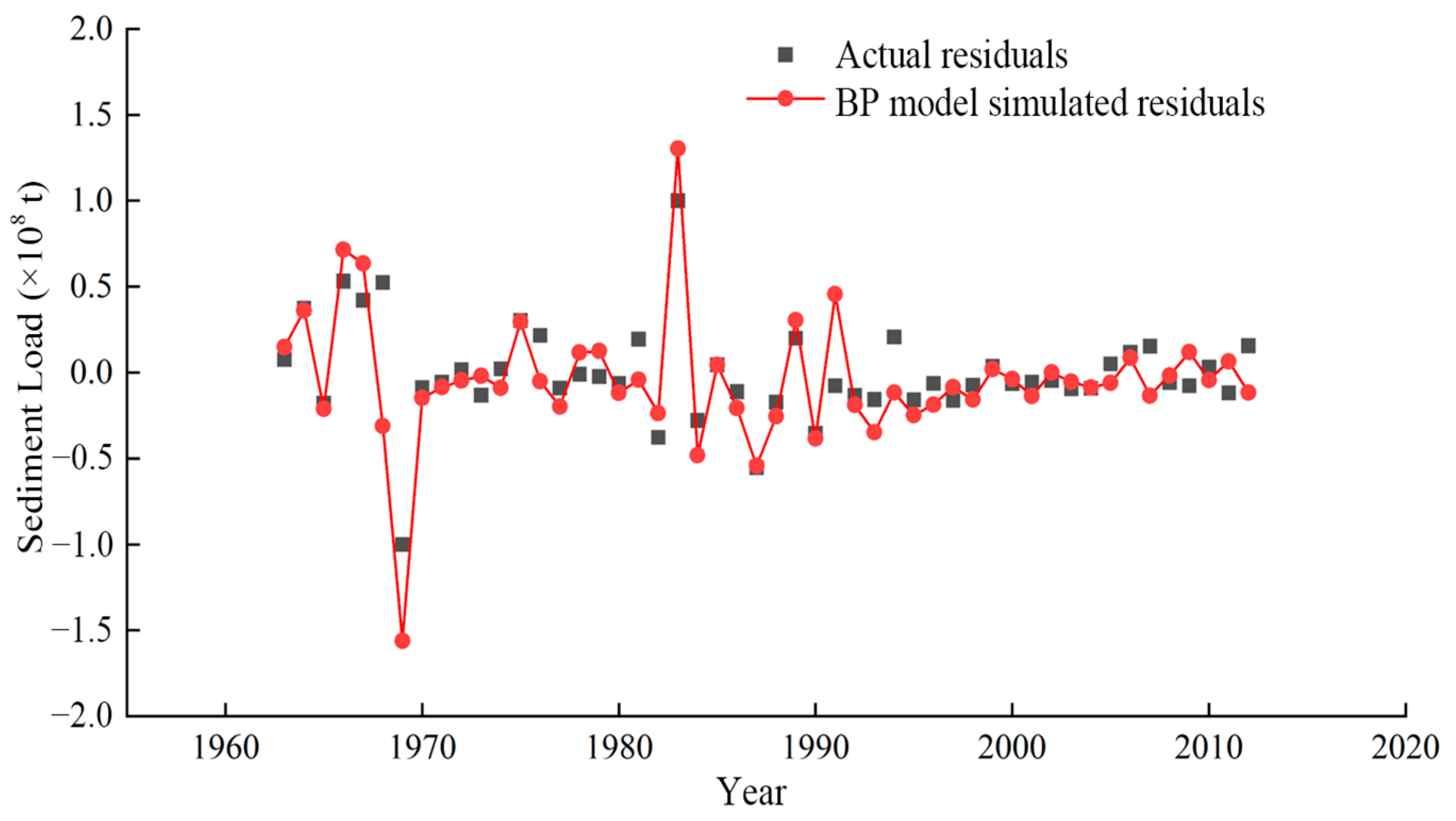
4.2.2. Prediction of Residuals in Annual Sediment Transport Using BP Neural Networks
4.3. Simulation of Water and Sediment Evolution Based on the ARIMA-BP Coupled Model
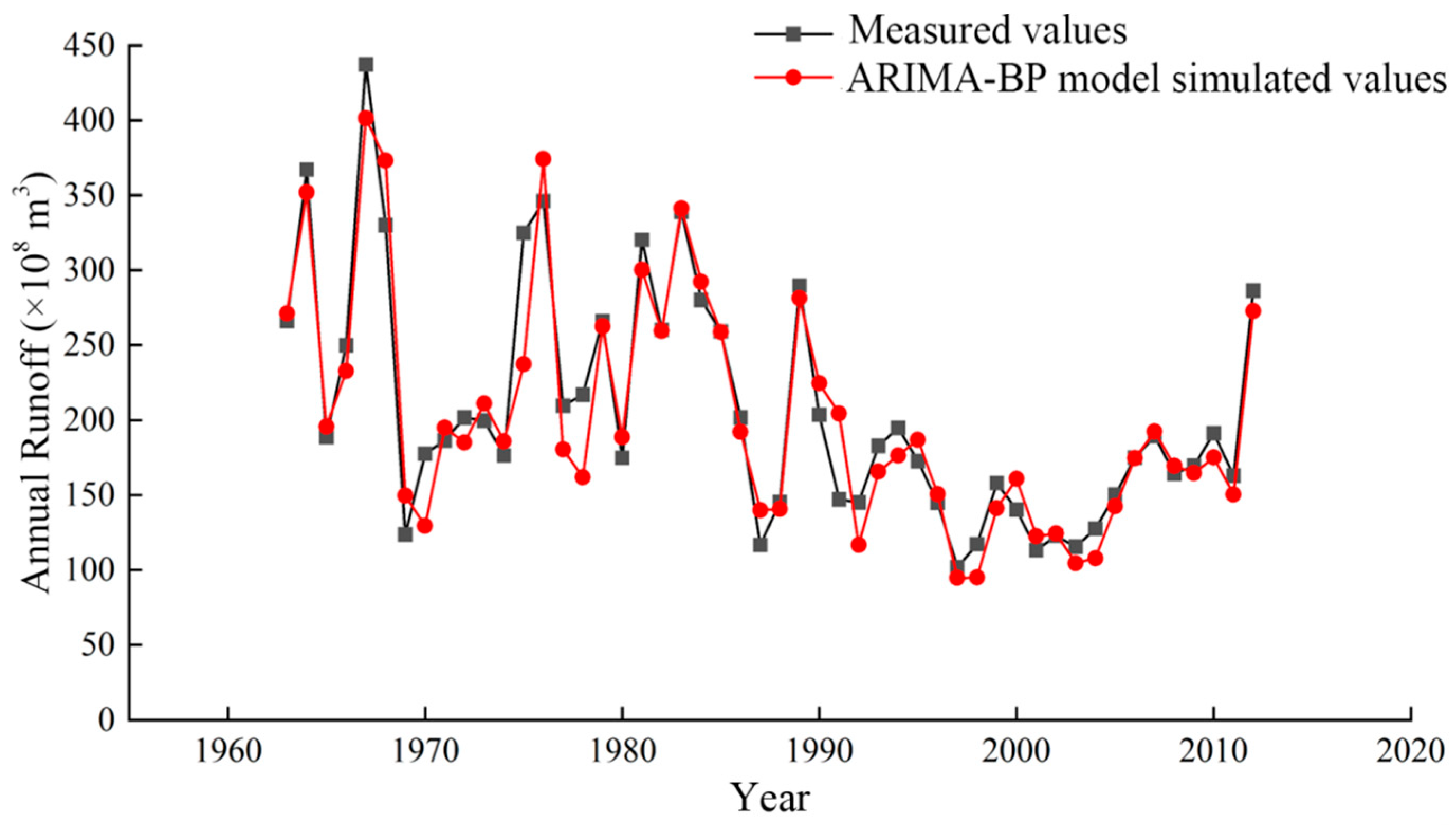
4.3.1. Fitting and Simulation of Annual Runoff
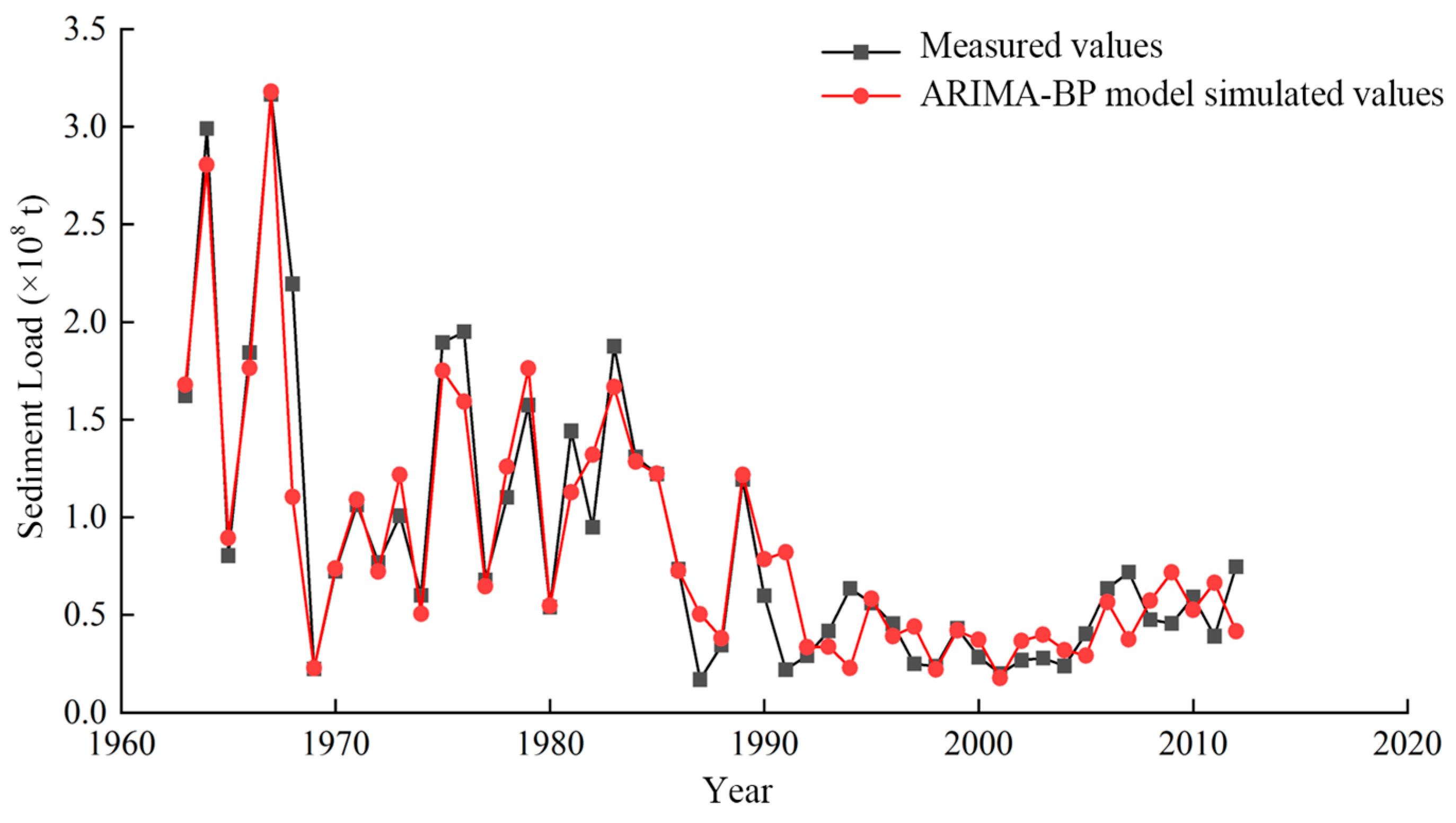
4.3.2. Fitting and Simulation of Annual Sediment Load
4.4. Comparative Analysis of Simulation Accuracy Among Different Models
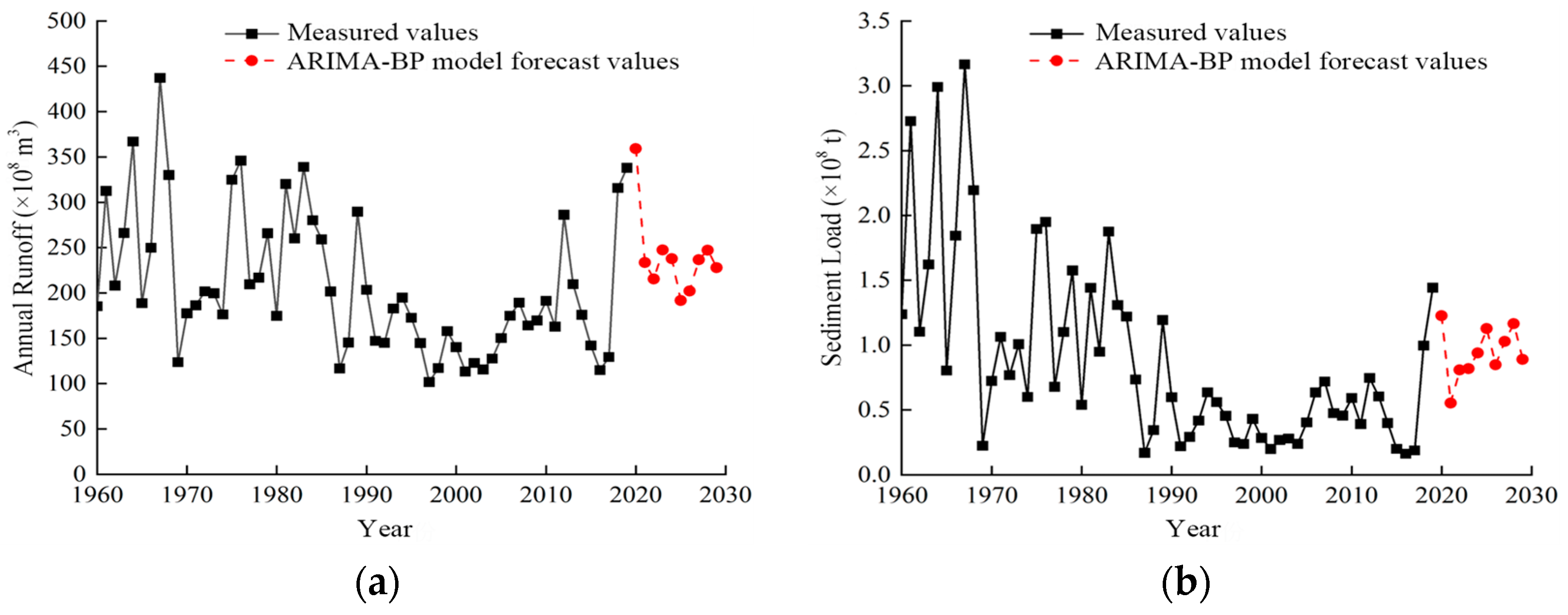
4.5. Prediction of Water and Sediment Variation Trends for the Next Decade
5. Analysis of the Causes of the Evolution Process and Trends of Water and Sediment
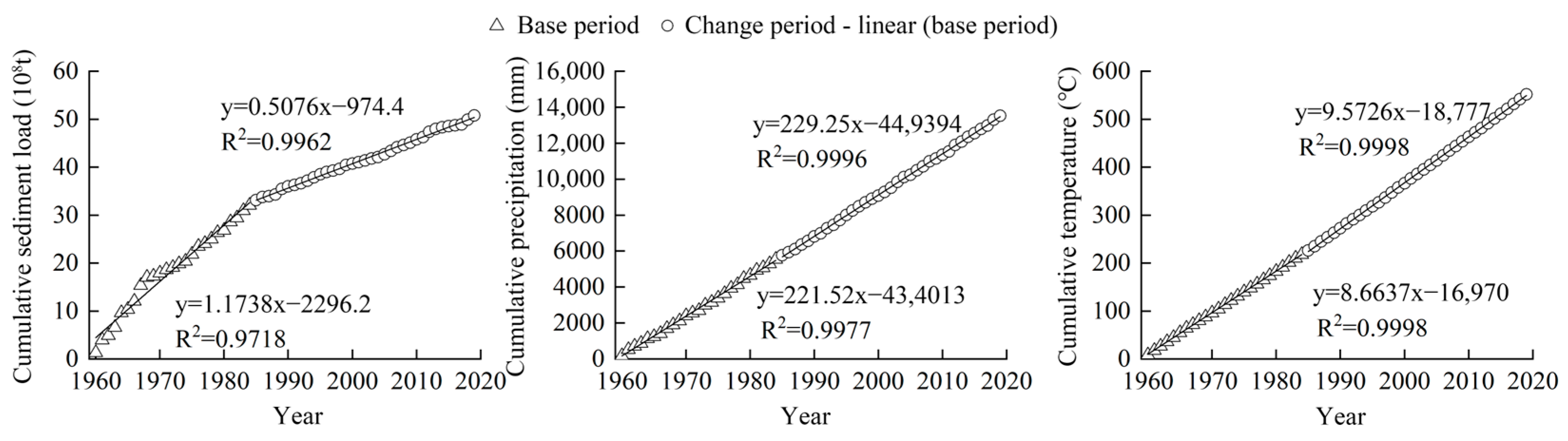
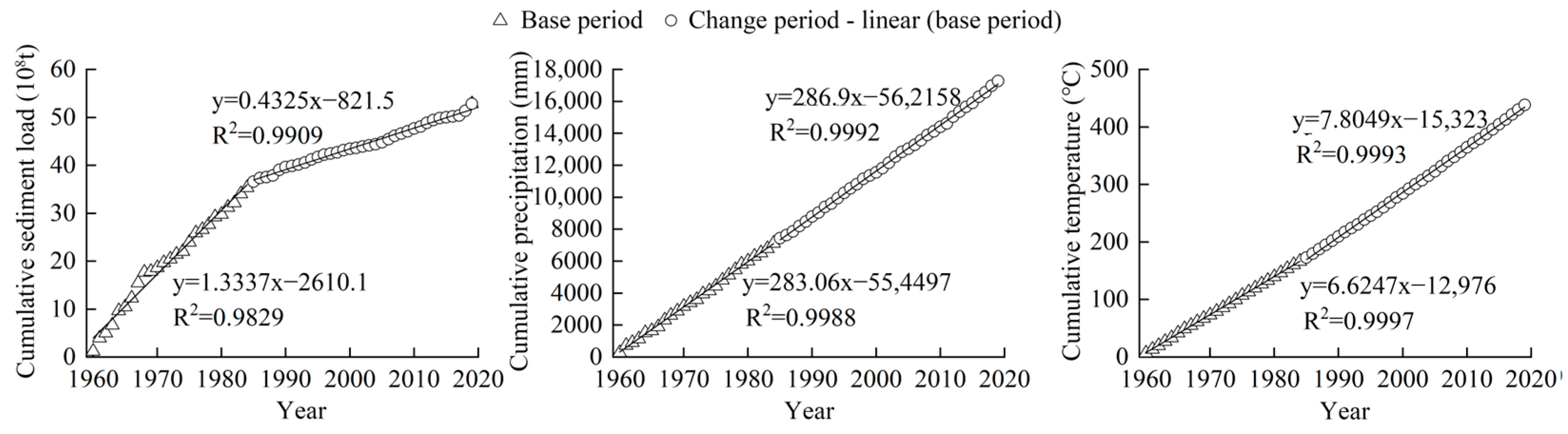
5.1. Discussion of Effect Factors
5.2. Discussion of the Contribution Rates of Influencing Factors to the Evolution of Water and Sediment
6. Conclusions
- (1)
- From 1960 to 2019, both annual runoff and sediment load at the Toudaoguai Station exhibited a declining trend. A significant abrupt change in annual runoff occurred in 1986, while a similar change in annual sediment load occurred in 1984. The first dominant cycle in the evolution of annual runoff was 12 years, and that of annual sediment load was 31 years.
- (2)
- The simulation accuracy of the ARIMA-BP coupled model was significantly superior to that of the BP neural network model and the ARIMA model. The model predicts that the runoff and sediment load at the Toudaoguai Hydrological Station will continue to follow a decreasing trend from 2020 to 2029.
- (3)
- The contribution rate of natural factors to the runoff at the Toudaoguai hydrological station is 75.14%, while the impact of human activities on the sediment load is 75.59%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jing, E.H. Significant Scientific and Technological Progress and Trend of Sediment Research in the Yellow River. J. Water Resour. Archit. Eng. 2020, 18, 1–9. [Google Scholar] [CrossRef]
- Fan, X.L.; Shi, C.X.; Zhou, Y.Y.; Shao, W.W. Sediment rating curves in the Ningxia-Inner Mongolia reaches of the upper Yellow River and their implications. Quat. Int. 2012, 282, 152–162. [Google Scholar] [CrossRef]
- Jiong, X. Decreasing trend of sediment transfer function of the Upper Yellow River, China, in response to human ac-tivity and climate change. Hydrol. Sci. J. 2015, 60, 311–325. [Google Scholar] [CrossRef]
- Zhang, X.H.; Zheng, Y.S.; Shang, H.X.; Feng, Q. Sedimentation characteristics of the reach from Bayangaole to Toudaoguai of the Yellow River. Hydro-Sci. Eng. 2022, 03, 41–49. [Google Scholar] [CrossRef]
- Ran, D.C.; Yao, W.Y.; Shen, Z.Z.; Ni, Y.; Dong, F. Analysis on the contribution rate of driving factors for the annual water and sediment variations at the Toudaoguai hydrological station in the Yellow River. Adv. Water Sci. 2015, 22, 769–778. [Google Scholar] [CrossRef]
- Chen, L.H.; Lv, Q.; Wang, Z.G. Processes of bed-forming flow and its driving factors at Toudaoguai Hydrological Station in the main stream of the Yellow River. J. Sediment Res. 2023, 48, 45–51. [Google Scholar] [CrossRef]
- Shi, F.X.; Gao, G.M.; Wang, Y.J.; Ma, W.M.; Chen, R.X. Analysis of Inflow and Sediment Change of the Lower Yellow River Based on th-e Degree of Incoordination. Yellow River 2020, 42, 52–55+61. [Google Scholar] [CrossRef]
- Zhao, S.X.; Wang, W.J.; Quan, D.; Li, C.; Wu, Y.J.; Quan, Q.; Sun, Z.H. Characteristics and Impacting Factors of Flow-Sediment Movement at Toudao-guai Hydrological Station of the Yellow River. J. Soil Water Conserv. 2021, 35, 125–131. [Google Scholar] [CrossRef]
- Shen, G.Q.; Zhang, Y.F.; Shang, H.X.; Li, X.P. Sedimentation and cross-section regulation in different periods in the Low-er Yellow River. J. Sediment Res. 2005, 03, 30–34. [Google Scholar] [CrossRef]
- Hu, C.H.; Zhang, X.M.; Zhao, Y. Cause analysis of the centennial trend and recent fluctuation of the Yellow River se-diment load. Adv. Water Sci. 2020, 31, 725–733. [Google Scholar] [CrossRef]
- Yao, W.Y.; Ran, D.C.; Chen, J.N. Recent changes in runoff and sediment regimes and future projections in the Yello-w River basin. Adv. Water Sci. 2013, 24, 607–616. [Google Scholar] [CrossRef]
- Hu, C.H.; Zhang, X.M. Several key questions in the researches of runoff and sediment changes and trend predictions in the Yellow River. Shui Li Xue Bao 2018, 49, 1028–1039. [Google Scholar] [CrossRef]
- Bao, Z.X.; Zhang, J.Y.; Wang, G.Q.; He, R.; Jin, J.; Wang, J.; Wu, H. Quantitative assessment of the attribution of runoff and sediment change ba-sed on hydrologic model and machine learning: A case study of the Kuye River in the Middle Yellow River basin. Adv. Water Sci. 2021, 32, 485–496. [Google Scholar] [CrossRef]
- Li, C.Y.; Li, C.; Shi, X.H.; Zhang, S. River Ice Evolution of Yellow River in Inner Mongolia and Its Numerical Simulation; Science Press: Beijing, China, 2018; pp. 9–10. [Google Scholar]
- Xiao, Y.; Yang, S.F.; Shao, X.J. Trends of temporal variation of the flow-sediment discharges into the Three Gorges Reservoir. J. Sediment Res. 2017, 42, 22–27. [Google Scholar] [CrossRef]
- Qi, F.; Zhang, C.Q.; Liu, X.; Yu, H.P.; Zhao, C.P.; Wu, A.; Jia, M. Spatiotemporal Variation Trend Analysis of Rainfall Erosivity in Yimeng Mountain Region Based on M-K Test and Geostatistical Analysis. Bullentin Soil Water Conserv. 2021, 41, 146–153. [Google Scholar] [CrossRef]
- Wei, X.T.; Huang, S.Z.; Huang, Q.; Wang, H.; Li, P.; Liu, D. Quantitative Decomposition of Contributions of Climate Change and Human Activities to Seasonal Runoff Variability. J. Soil Water Conserv. 2019, 33, 182–189. [Google Scholar] [CrossRef]
- Xie, Z.B.; Mu, X.M.; Gao, P.; Qiu, D.X. Variation Characteristics of Runoff in the Upper Reaches of Beiluo River Based on R/S and Morlet Wavelet Analysis. J. Soil Water Conserv. 2022, 29, 139–144. [Google Scholar] [CrossRef]
- Zhang, X.; Tuo, W.; Song, C. Application of MEEMD-ARIMA combining model for annual runoff prediction in the Lower Yellow River. J. Water Clim. Change 2019, 11, 865–876. [Google Scholar] [CrossRef]
- Han, Y.G.; Han, L.; Huang, X.Y.; Gao, Y. Prediction of vapor pressure deficit in Northwest China based on exponential and ARIMA models. Arid Zone Res. 2021, 38, 303–313. [Google Scholar] [CrossRef]
- Zhu, Y.J. Application of Composite Single Sand Model for Sediment Monitoring Based on BP Neural Network in Xi-jiang River: A Case Study of Wuzhou Hydrometric Station. J. China Hydrol. 2024, 44, 36–40. [Google Scholar] [CrossRef]
- Chen, N.; Cao, Z.; Cui, H.; Xu, L.J.; Zhao, W.J. Evolution of Water and Sediment Situation in the Inner Mongolia Reach of the Yellow River in Recent 60 Years. Yellow River 2021, 43, 46–51. [Google Scholar] [CrossRef]
- Chen, H.T.; Mu, X.Y.; Luo, H.C.; Ji, H.L.; Liu, X.M. Analysis and Prediction of Runoff and Sediment Flux Characteristics at the Toudaoguai Hydrological Station of the Yellow River from 1958 to 2022. Res. Soil Water Conserv. 2024, 31, 10–21. [Google Scholar]
- Wang, H.X.; Yang, K.F.; Liu, J.H.; Hu, P.F. Evolution and influencing factors analysis of water and sediment evolution in the upper Yellow River in recent 60 years. China Rural Water Hydropower 2022, 03, 86–93. [Google Scholar]
- Zhao, Y.; Hu, C.H.; Zhang, X.M.; Wang, Y.S.; Cheng, C.; Yin, X.L.; Xie, M. Analysis on runoff and sediment regimes and its causes of the Yellow River in recent 70 years. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2018, 34, 112–119. [Google Scholar] [CrossRef]
- Chen, L.H. Analysis of Influencing Factors of Runoff and Sediment Variation and Riverbed Evolution in Ning-Meng Reach of Upper Yellow River. Master’s Thesis, Hebei University of Engineering, Handan, China, 2022. [Google Scholar]
- Zhai, Q.M.; Ning, Y.X.; Liu, S. Analysis of Sediment Change and Its Influence in the Middle and Lower Reaches of the Yellow River. Henan Sci. Technol. 2020, 16, 78–80. [Google Scholar]
- Deng, A.J.; Chen, J.G.; Hu, H.H.; Zhang, G.S. Analysis of reservoir siltation in China. J. Hydraul. Eng. 2022, 53, 325–332. [Google Scholar] [CrossRef]
- Zhu, J.S.; Li, J.R.; Huang, S.F.; Zang, W.B. Remote Sensing Survey and Analysis of the Spatial Changes in Vegetation Cover in the Last 30 Years in the Ten Major Gullies Basin. Soil Water Conserv. China 2015, 07, 68–70. [Google Scholar] [CrossRef]
- Wang, X.; Wu, J.X. Rating curves based on wavelet analyses: A case study at Datong station in the lower Changjiang River. J. Mar. Sci. 2009, 27, 16–22. [Google Scholar]
- Li, L.; Gong, H.L.; Guo, L.; Zhu, L.; Chen, B. Research advances on hydrologic time series analysis methods. J. Geo-Inf. Sci. 2024, 26, 927–945. [Google Scholar] [CrossRef]
- Du, Y.; Ma, R.Y. Application of Different Improved ARIMA Models in the Prediction of Hydrological Time Series. Water Power 2018, 44, 12–14+28. [Google Scholar]
- Liu, X.Y.; Dang, S.Z.; Zhang, H. Possible Incoming Sediment Amount of the Yellow River Under the Extreme Rainfall Scenarios in the Future. Yellow River 2016, 38, 13–17. [Google Scholar] [CrossRef]
- Yellow River Conservancy Commission of the Ministry of Water Resources. Comprehensive Plan for the Yellow River Basin (2012–2030); Yellow River Publishing House: Zhengzhou, China, 2013; pp. 11–12. [Google Scholar]
- Xu, W.L.; Zhao, G.J.; Mu, C.M.; Gao, P.; Sun, W.Y. Variation of runoff and sediment load in the upper reaches of the Yellow R-iver over the past 60 years. Sci. Soil Water Conserv. 2018, 16, 38–47. [Google Scholar] [CrossRef]
- Wang, S.; Yan, Y.; Yan, M.; Zhao, X. Contributions of Precipitation and Human Activities to the Runoff Change of the Huangfuchuan Drainage Basin: Application of Comparative Method of the Slope Changing Ratio of Cumulative Quantity. Acta Geogr. Sin. 2012, 67, 388–397. [Google Scholar]
- Wang, S.J.; Li, L.; Yan, M. The contributions of climate change and human activities to the runoff yield changes in the middle Yellow River Basin. Geogr. Res. 2013, 32, 395–402. [Google Scholar]


| Cv | Statistical Measure Z | Variation Trend | Significance | |
|---|---|---|---|---|
| Runoff | 0.35 | −3.22 | Decrease | 0.01 |
| sediment load | 0.80 | −4.73 | Decrease | 0.01 |
| Year | Measured | Predicted | Absolute Error | Relative Error |
|---|---|---|---|---|
| Billion m3 | Billion m3 | Billion m3 | % | |
| 2013 | 209.714 | 197.1452 | 12.5688 | 5.99% |
| 2014 | 175.806 | 174.6440 | 1.1620 | 0.66% |
| 2015 | 142.058 | 142.9123 | 0.8543 | 0.60% |
| 2016 | 114.876 | 129.9725 | 15.0965 | 13.14% |
| 2017 | 129.343 | 118.4548 | 10.8882 | 8.42% |
| 2018 | 315.807 | 201.3660 | 114.4410 | 36.24% |
| 2019 | 337.971 | 266.6469 | 71.3231 | 21.10% |
| Mean Value | 203.653 | 175.8773 | 32.3334 | 12.31% |
| Year | Measured | Predicted | Absolute Error | Relative Error |
|---|---|---|---|---|
| Billion t | Billion t | Billion t | % | |
| 2013 | 0.604 | 0.6022 | 0.0022 | 0.37% |
| 2014 | 0.399 | 0.4609 | 0.0615 | 15.40% |
| 2015 | 0.199 | 0.2942 | 0.0945 | 47.31% |
| 2016 | 0.162 | 0.2738 | 0.1109 | 68.10% |
| 2017 | 0.188 | 0.2116 | 0.0236 | 12.52% |
| 2018 | 0.996 | 0.3601 | 0.6365 | 63.87% |
| 2019 | 1.443 | 1.0214 | 0.4216 | 29.22% |
| Mean Value | 0.571 | 0.461 | 0.192 | 33.83% |
| Year | Actual Residuals | Predicted Residuals | Absolute Error | Relative Error |
|---|---|---|---|---|
| Billion m3 | Billion m3 | Billion m3 | % | |
| 2013 | 19.416 | 12.568 | 6.848 | 54.48% |
| 2014 | 2.9377 | 1.162 | 1.775 | 152.82% |
| 2015 | 5.687 | −0.854 | 6.541 | 765.80% |
| 2016 | −11.395 | −15.096 | 3.701 | 24.52% |
| 2017 | 17.885 | 10.888 | 6.997 | 64.26% |
| 2018 | 51.118 | 114.441 | 63.322 | 55.33% |
| 2019 | 65.688 | 71.323 | 5.634 | 7.90% |
| Mean Value | 21.619 | 27.776 | 13.545 | 160.73 |
| Year | Actual Residuals | Predicted Residuals | Absolute Error | Relative Error |
|---|---|---|---|---|
| Billion t | Billion t | Billion t | % | |
| 2013 | 0.0022 | 0.0004 | 0.0018 | 80.96% |
| 2014 | −0.0615 | −0.0907 | 0.0292 | 47.41% |
| 2015 | −0.0945 | −0.0848 | 0.0097 | 10.25% |
| 2016 | −0.1109 | −0.0061 | 0.1048 | 94.47% |
| 2017 | −0.0236 | −0.0365 | 0.0129 | 54.95% |
| 2018 | 0.6365 | 0.2199 | 0.4166 | 65.45% |
| 2019 | 0.4216 | 0.3338 | 0.0878 | 20.83% |
| Mean Value | 0.1099 | 0.048 | 0.0946 | 53.47% |
| Year | Measured | Simulated | Absolute Error | Relative Error |
|---|---|---|---|---|
| Billion m3 | Billion m3 | Billion m3 | % | |
| 2013 | 209.714 | 216.5620 | 6.8480 | 3.27% |
| 2014 | 175.806 | 177.5817 | 1.7757 | 1.01% |
| 2015 | 142.058 | 148.5999 | 6.5419 | 4.61% |
| 2016 | 114.876 | 118.5771 | 3.7011 | 3.22% |
| 2017 | 129.343 | 136.3402 | 6.9972 | 5.41% |
| 2018 | 315.807 | 252.4849 | 63.3221 | 20.05% |
| 2019 | 337.97 | 332.3355 | 5.6345 | 1.67% |
| Mean Value | 203.653 | 197.497 | 13.545 | 5.61% |
| Year | Measured | Simulated | Absolute Error | Relative Error |
|---|---|---|---|---|
| Billion t | Billion t | Billion t | % | |
| 2013 | 0.6044 | 0.6049 | 0.0004 | 0.07% |
| 2014 | 0.3993 | 0.3702 | 0.0292 | 7.30% |
| 2015 | 0.1997 | 0.2094 | 0.0097 | 4.85% |
| 2016 | 0.1629 | 0.2677 | 0.1048 | 64.33% |
| 2017 | 0.1880 | 0.1751 | 0.0129 | 6.88% |
| 2018 | 0.9966 | 0.5801 | 0.4166 | 41.80% |
| 2019 | 1.4430 | 1.3552 | 0.0878 | 6.09% |
| Mean Value | 0.571 | 0.508 | 0.0944 | 18.76% |
| Model | RMSE | MAE | R2 |
|---|---|---|---|
| ARIMA | 51.6724 | 32.3334 | 0.6157 |
| BP | 56.4424 | 48.1080 | 0.5414 |
| ARIMA-BP | 24.4860 | 13.5458 | 0.9137 |
| Model | RMSE | MAE | R2 |
|---|---|---|---|
| ARIMA | 0.2948 | 0.1927 | 0.5725 |
| BP | 0.2518 | 0.2222 | 0.6881 |
| ARIMA-BP | 0.1662 | 0.0945 | 0.8642 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Guo, J.; Guo, X.; Fu, H. The Characteristics and Trend Prediction of Water and Sediment Evolution at the Toudaoguai Station on the Yellow River from 1960 to 2019. Hydrology 2025, 12, 174. https://doi.org/10.3390/hydrology12070174
Li C, Guo J, Guo X, Fu H. The Characteristics and Trend Prediction of Water and Sediment Evolution at the Toudaoguai Station on the Yellow River from 1960 to 2019. Hydrology. 2025; 12(7):174. https://doi.org/10.3390/hydrology12070174
Chicago/Turabian StyleLi, Chao, Jing Guo, Xinlei Guo, and Hui Fu. 2025. "The Characteristics and Trend Prediction of Water and Sediment Evolution at the Toudaoguai Station on the Yellow River from 1960 to 2019" Hydrology 12, no. 7: 174. https://doi.org/10.3390/hydrology12070174
APA StyleLi, C., Guo, J., Guo, X., & Fu, H. (2025). The Characteristics and Trend Prediction of Water and Sediment Evolution at the Toudaoguai Station on the Yellow River from 1960 to 2019. Hydrology, 12(7), 174. https://doi.org/10.3390/hydrology12070174






