Predictive Modeling of Flood Frequency Utilizing an Analysis of the Casimcea River in Romania
Abstract
1. Introduction
2. Area Under Study and Data Collection Methodology
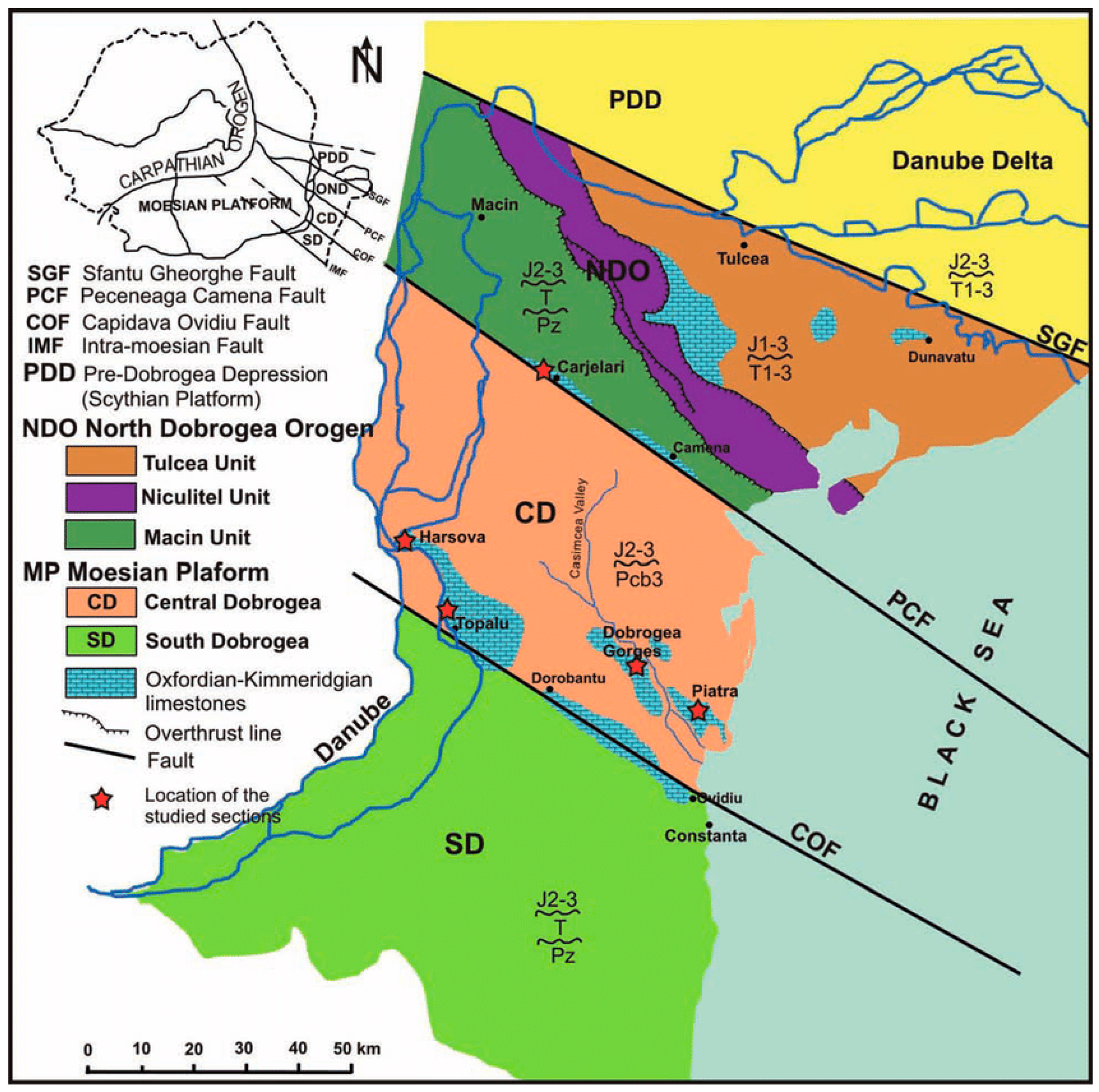
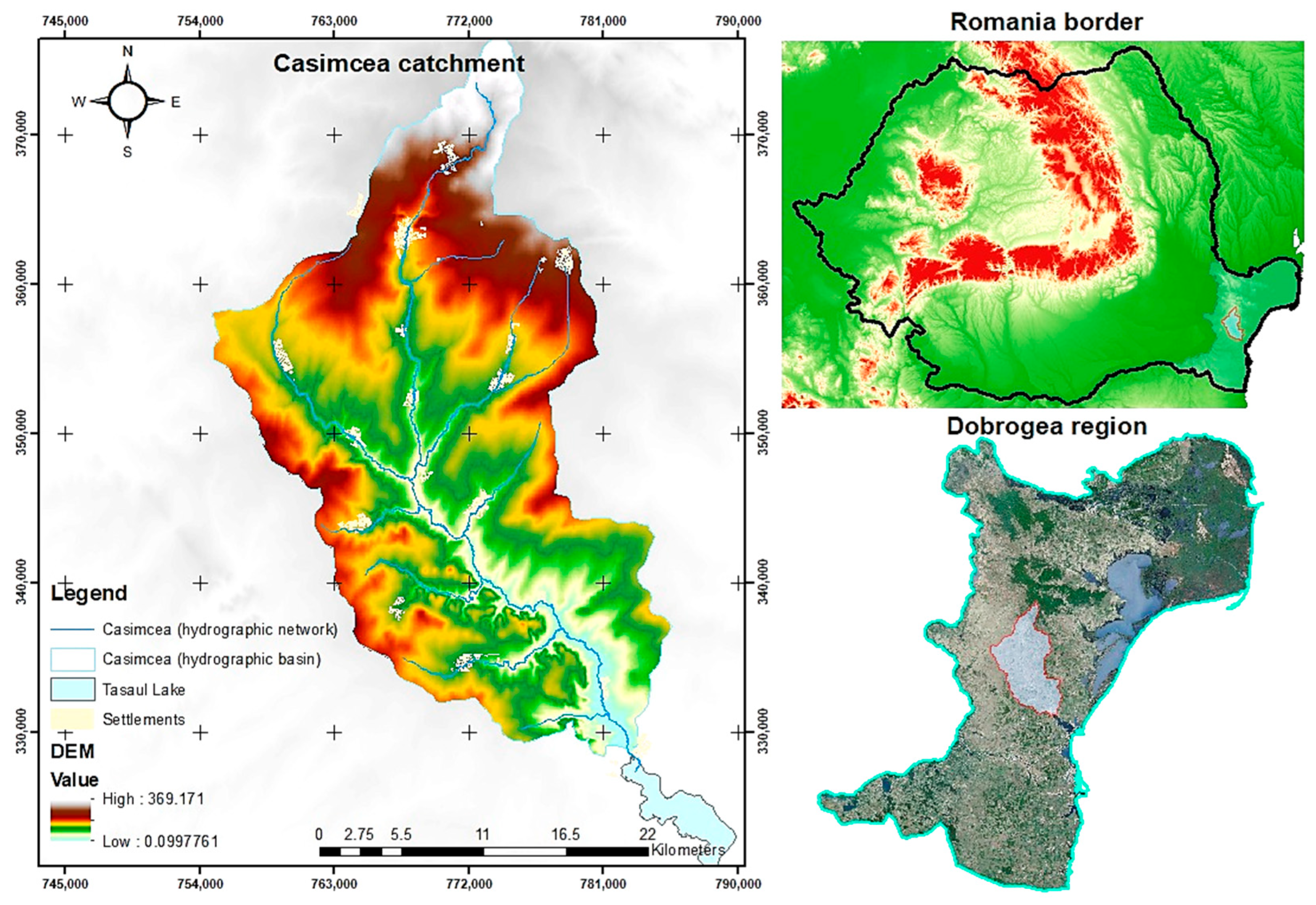
2.1. Study Area
2.2. Materials and Methods
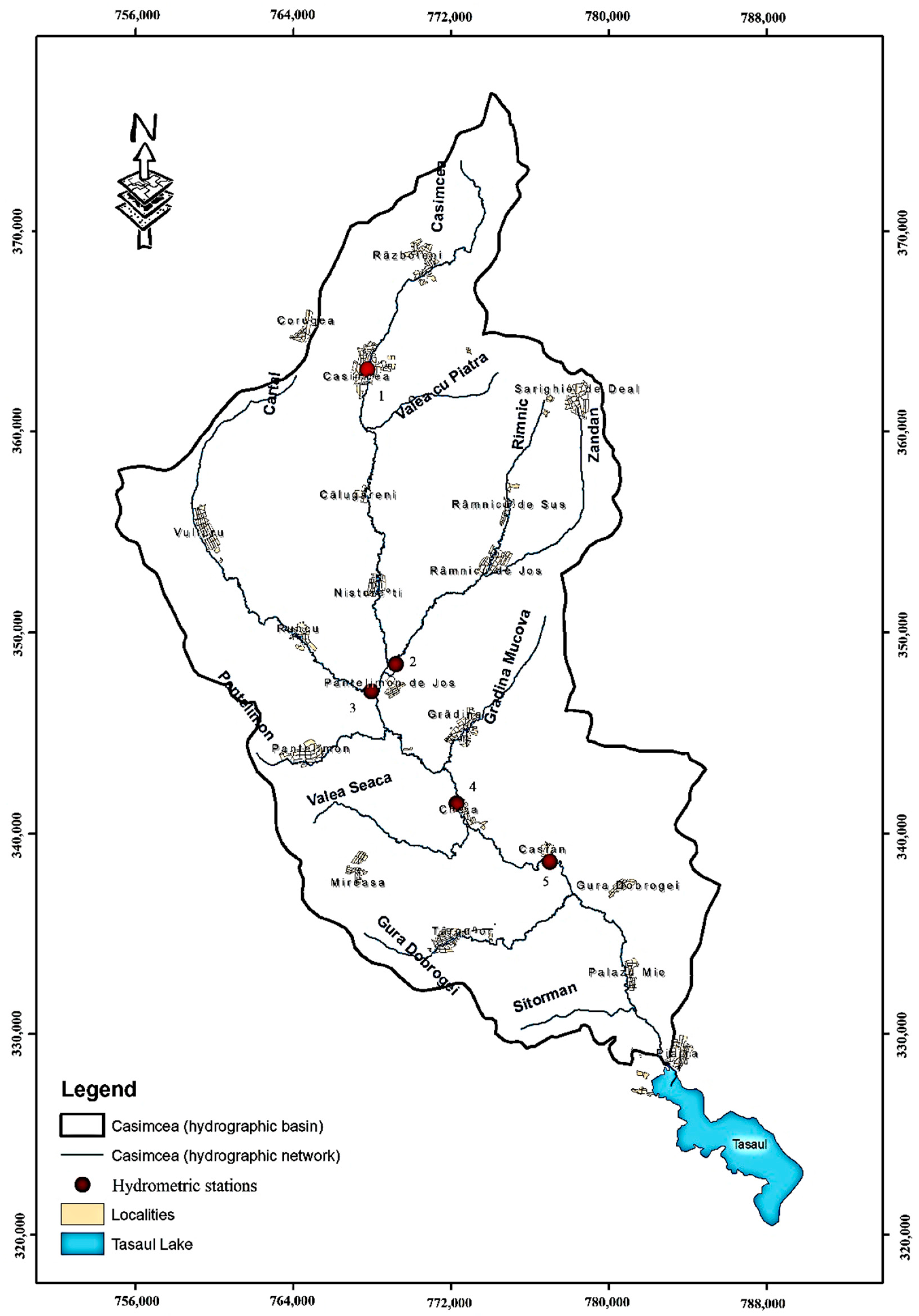
2.3. Data Collection
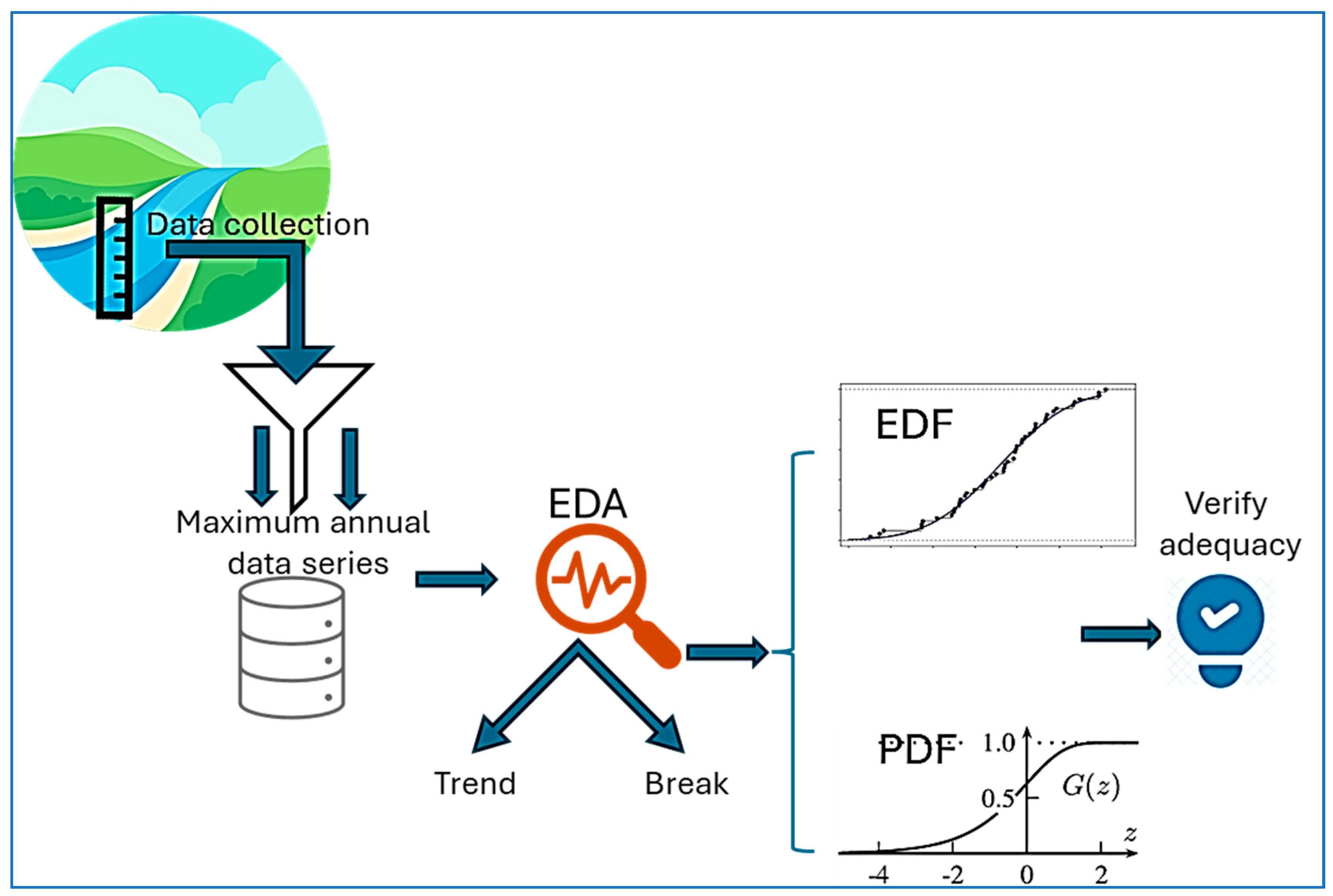
3. Analytical Methods
4. Results and Discussion
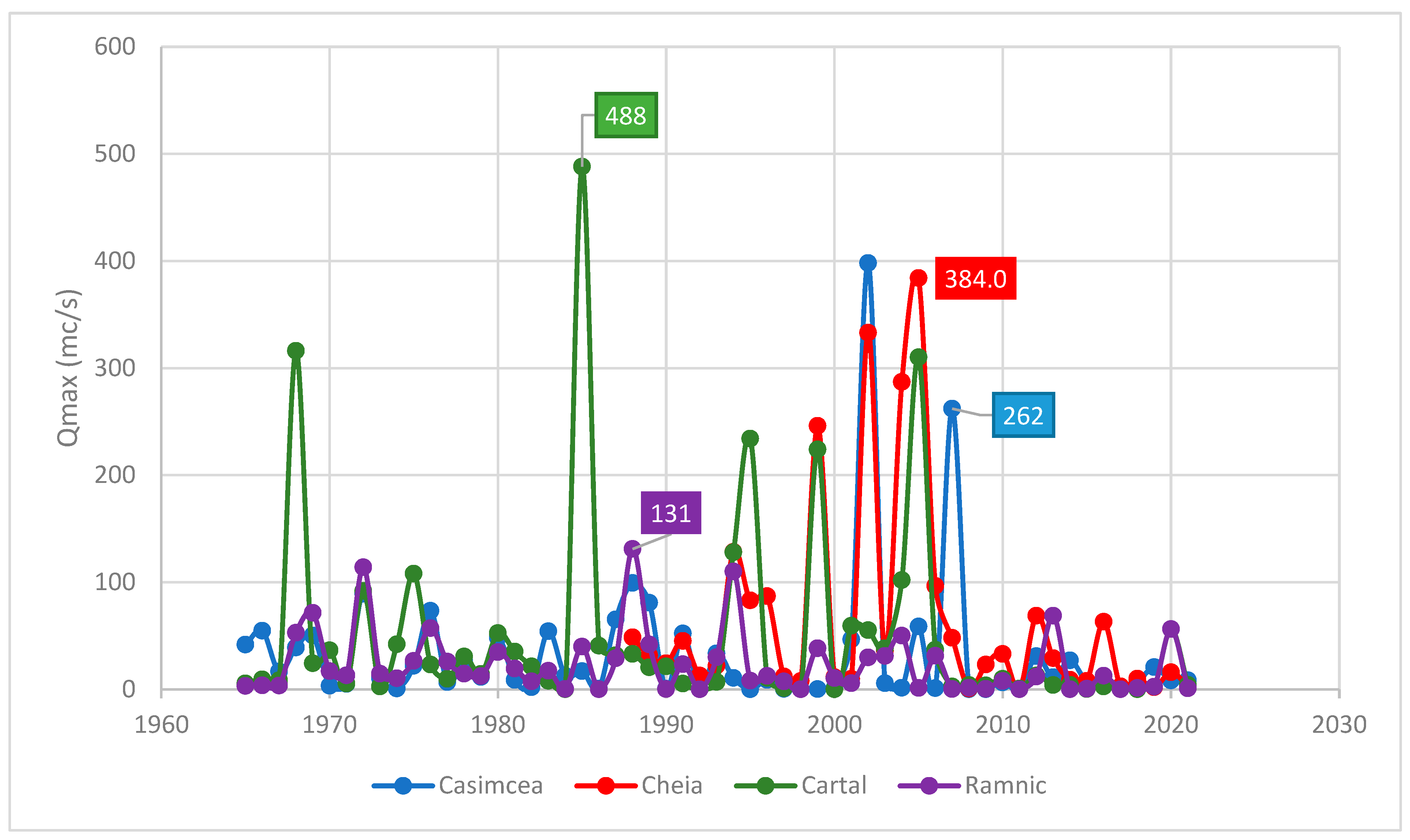
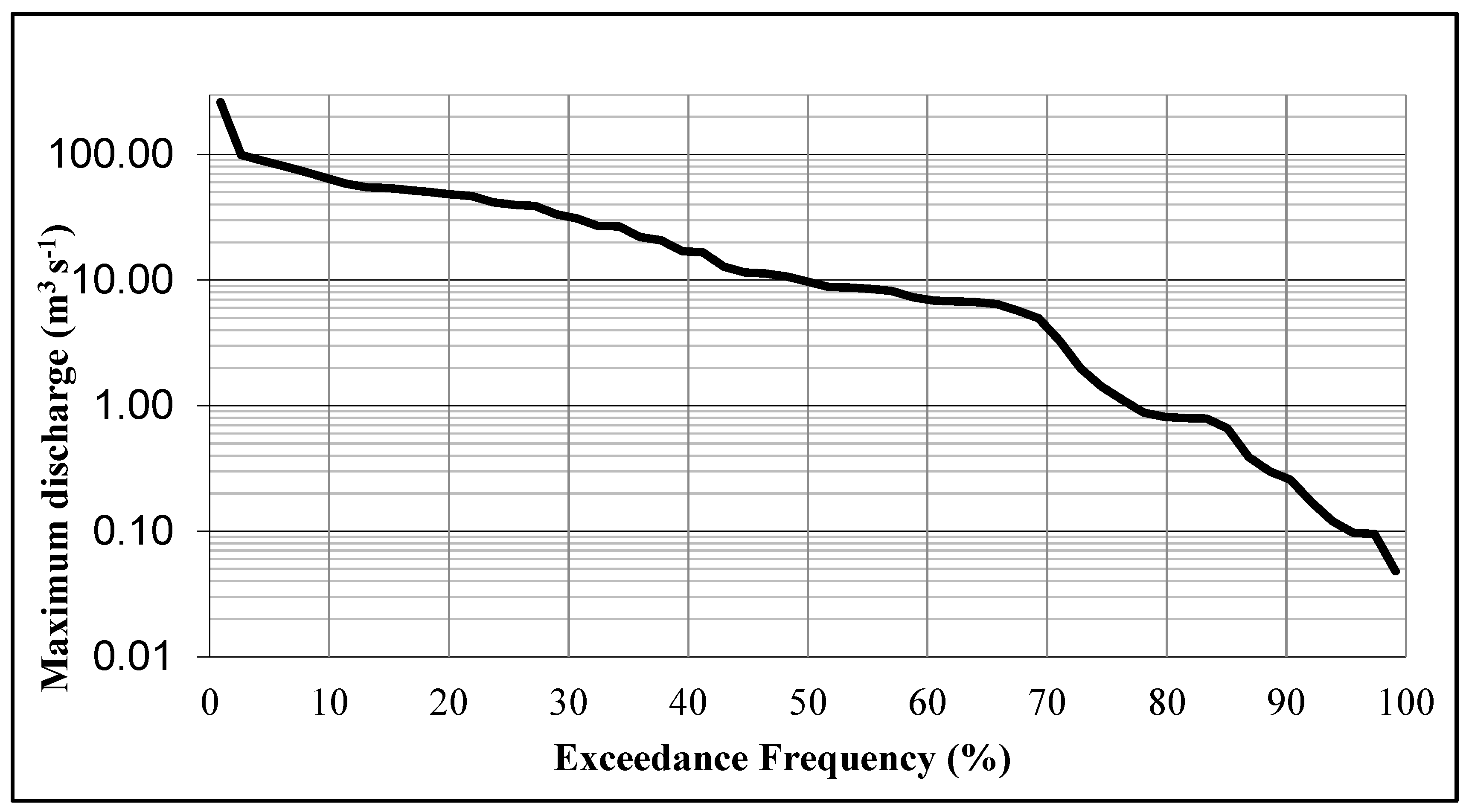
4.1. Floods Inventory
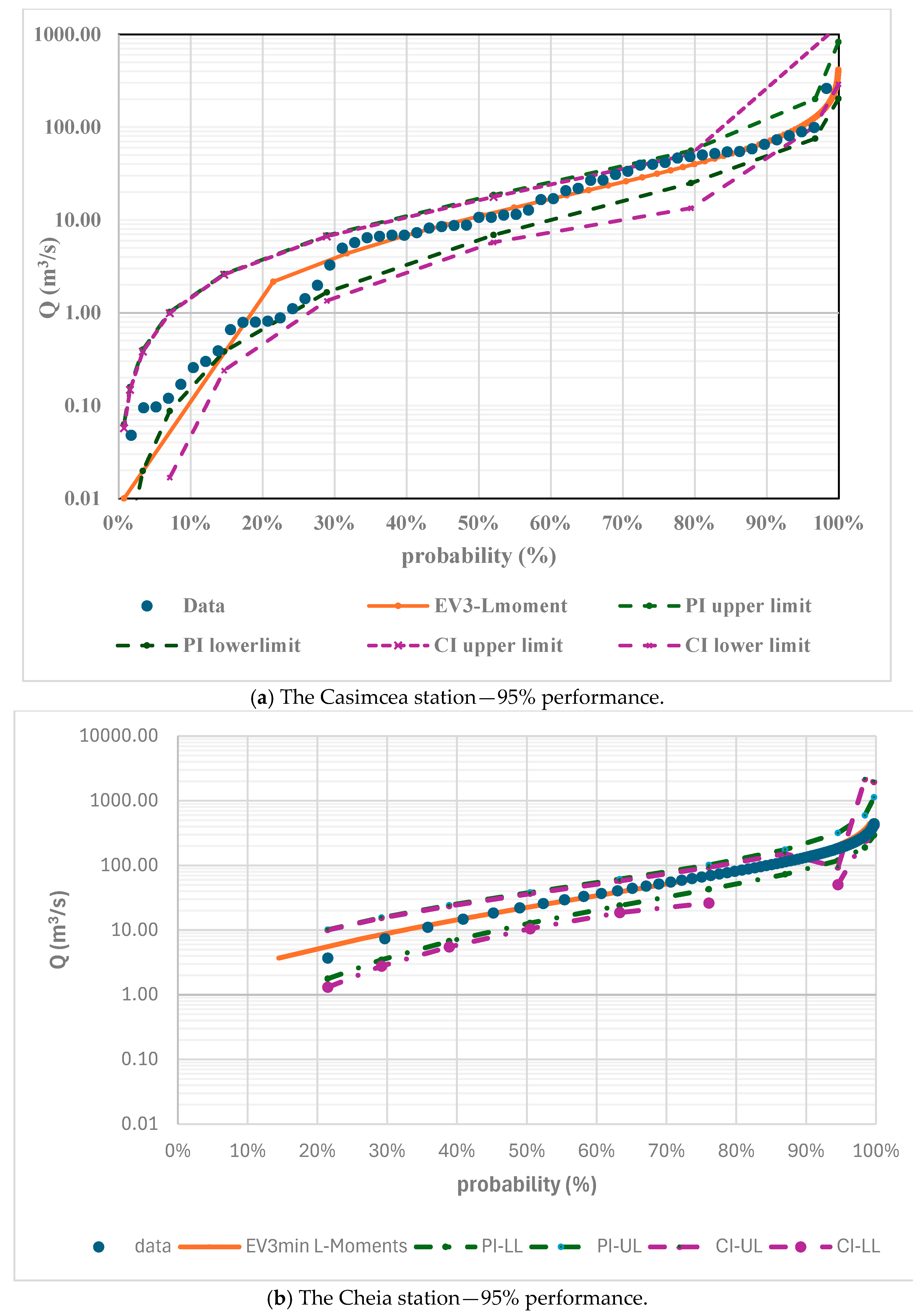
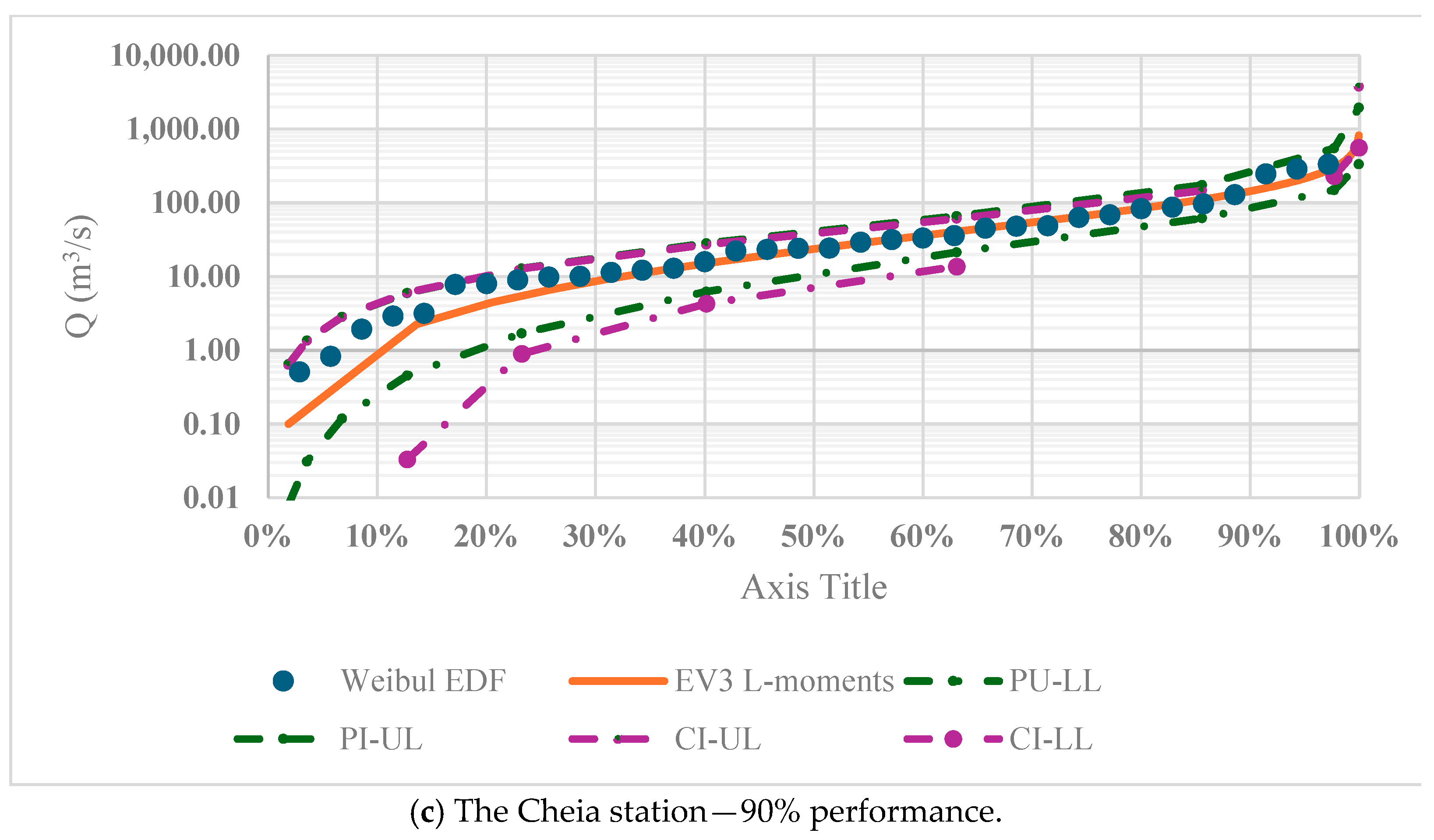
4.2. Frequency Analysis Results
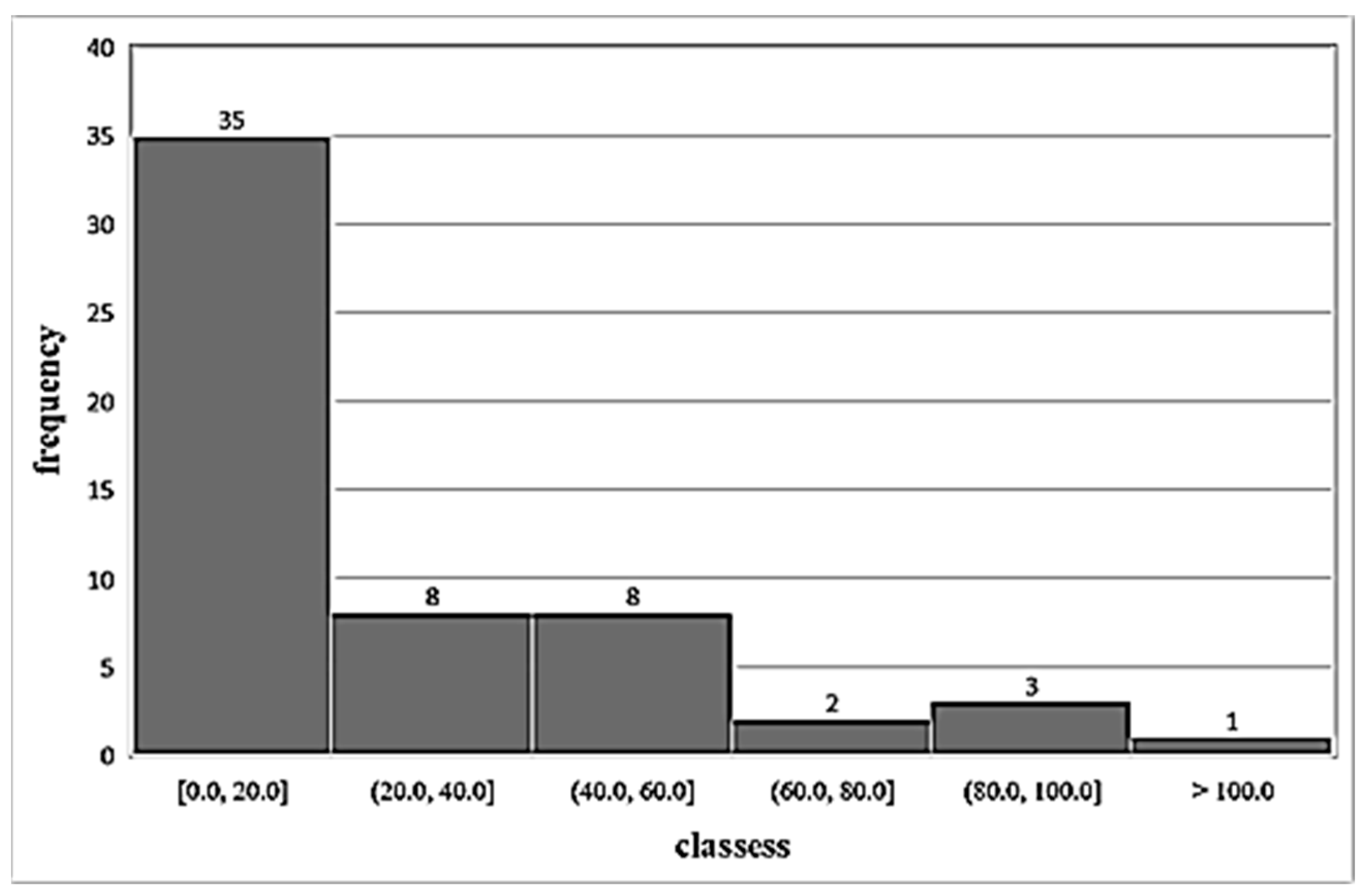
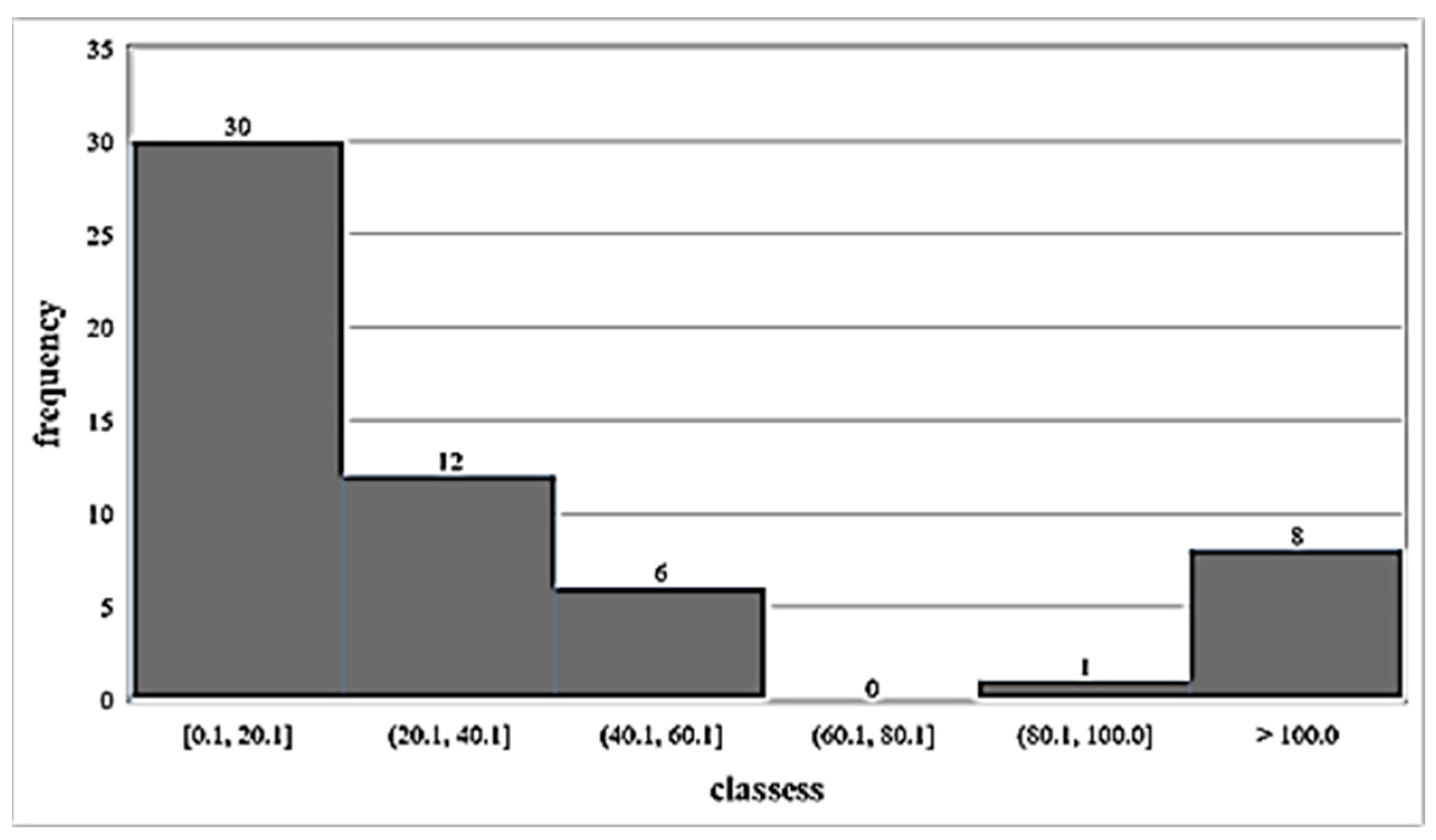
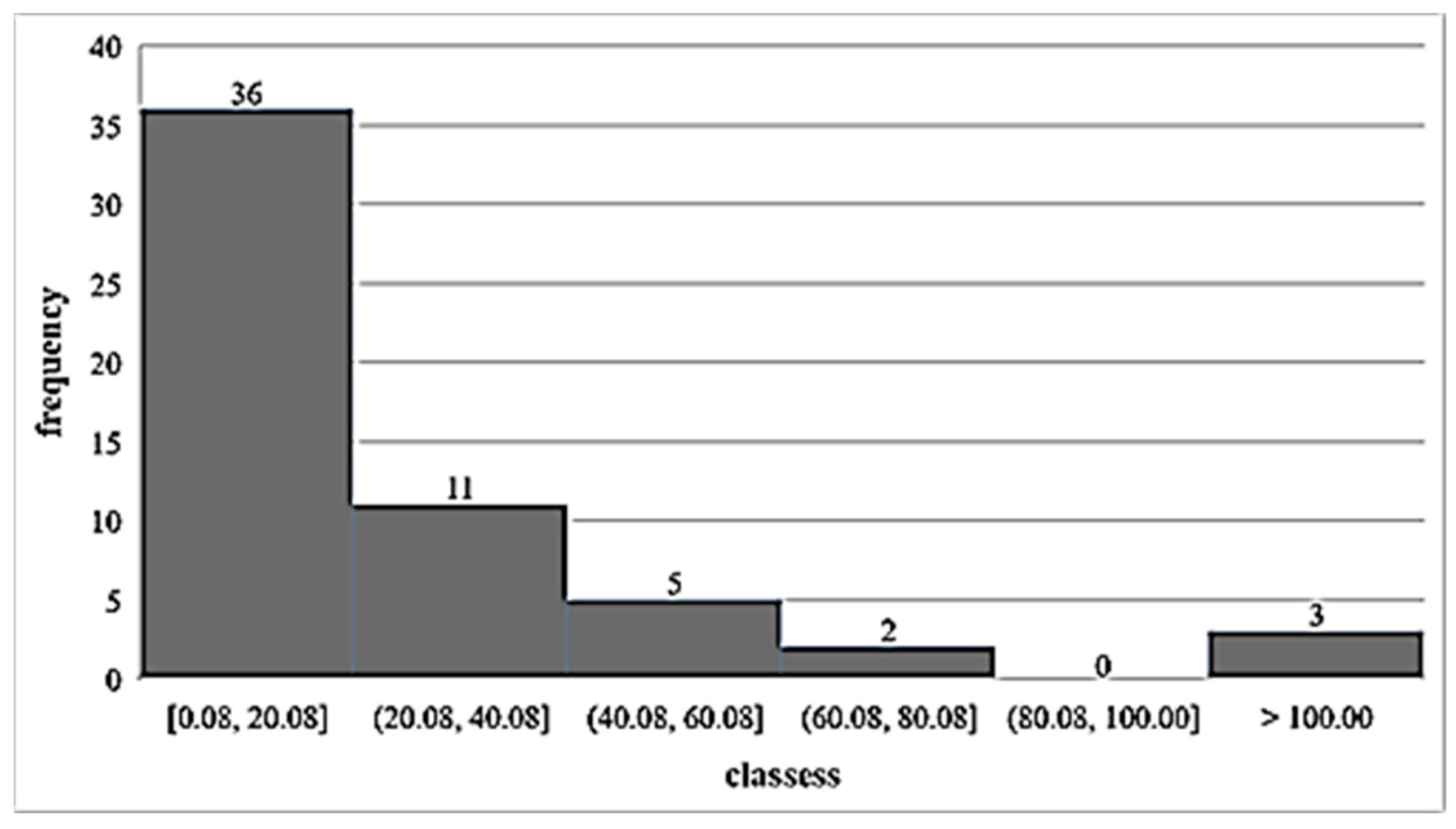
4.3. Results of Adequacy Tests
4.4. Results of the ELECTRE Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Jurisdictional Claims
References
- EEA. Climate Change, Impacts and Vulnerability in Europe 2012; European Environment Agency: Copenhagen, Denmark, 2012. [Google Scholar]
- Modeling and Monitoring Extreme Hydrometeorological Events; Maftei, C., Muntean, R., Vaseashta, A., Eds.; Advances in Environmental Engineering and Green Technologies; IGI Global: Hershey, PA, USA, 2023; ISBN 978-1-66848-771-6. [Google Scholar]
- The European Parliament. Directive; The European Parliament: Strasbourg, France, 2007; Volume 288. [Google Scholar]
- Hall, J.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; Boháč, M.; Bonacci, O.; Borga, M.; Burlando, P.; Castellarin, A.; Chirico, G.B.; et al. A European Flood Database: Facilitating Comprehensive Flood Research beyond Administrative Boundaries. Proc. IAHS 2015, 370, 89–95. [Google Scholar] [CrossRef]
- EEA. Flood Risks and Environmental Vulnerability—Exploring the Synergies Between Floodplain Restoration, Water Policies and Thematic Policies; European Environment Agency: Copenhagen, Denmark, 2016. [Google Scholar]
- Kundzewicz, Z.W.; Krysanova, V.; Dankers, R.; Hirabayashi, Y.; Kanae, S.; Hattermann, F.F.; Huang, S.; Milly, P.C.D.; Stoffel, M.; Driessen, P.P.J.; et al. Differences in Flood Hazard Projections in Europe—Their Causes and Consequences for Decision Making. Hydrol. Sci. J. 2017, 62, 1–14. [Google Scholar] [CrossRef]
- Alfieri, L.; Bisselink, B.; Dottori, F.; Naumann, G.; De Roo, A.; Salamon, P.; Wyser, K.; Feyen, L. Global Projections of River Flood Risk in a Warmer World: RIVER FLOOD RISK IN A WARMER WORLD. Earth’s Future 2017, 5, 171–182. [Google Scholar] [CrossRef]
- Statista. Deadliest Floods in Europe 2021. 2023. Available online: https://www.statista.com/statistics/1295966/deadliest-floods-in-europe/ (accessed on 2 August 2023).
- Kundzewicz, Z.W.; Pińskwar, I.; Brakenridge, G.R. Changes in River Flood Hazard in Europe: A Review. Hydrol. Res. 2017, 49, 294–302. [Google Scholar] [CrossRef]
- Paprotny, D.; Morales-Nápoles, O.; Jonkman, S.N. HANZE: A Pan-European Database of Exposure to Natural Hazards and Damaging Historical Floods since 1870. Earth Syst. Sci. Data 2018, 10, 565–581. [Google Scholar] [CrossRef]
- Maftei, C.; Papatheodorou, K. Flash Flood Prone Area Assessment Using Geomorphological and Hydraulic Model. J. Environ. Prot. Ecol. 2015, 16, 63–73. [Google Scholar]
- Maftei, C.; Papatheodorou, K. Mathematical Models Used for Hydrological Floodplain Modeling. In Extreme Weather and Impacts of Climate Change on Water Resources in the Dobrogea Region; IGI Global: Hershey, PA, USA, 2016; pp. 69–100. ISBN 978-1-4666-8438-6. [Google Scholar]
- Gumbel, E.J. On the Frequency Distribution of Extreme Values in Meteorological Data. Bull. Am. Meteorol. Soc. 1942, 3, 95–105. [Google Scholar] [CrossRef]
- Raynal, J.A.; Salas, J.D. Estimation Procedures for the Type-1 Extreme Value Distribution. J. Hydrol. 1986, 3–4, 315–336. [Google Scholar] [CrossRef]
- El Adlouni, S.; Bobée, B.; Ouarda, T.B.M.J. On the Tails of Extreme Event Distributions in Hydrology. J. Hydrol. 2008, 355, 16–33. [Google Scholar] [CrossRef]
- De Gusmão, F.R.S.; Ortega, E.M.M.; Cordeiro, G.M. The Generalized Inverse Weibull Distribution. Stat Pap. 2011, 52, 591–619. [Google Scholar] [CrossRef]
- Weibull, W. A Statistical Distribution Function of Wide Applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Cerneagă, C.; Maftei, C. Flood Frequency Analysis of Casimcea River. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1138, 012014. [Google Scholar] [CrossRef]
- Maftei, C.; Barbulescu, A. Statistical Analysis of Climate Evolution in Dobrudja Region. In Proceedings of the World Congress on Engineering, London, UK, 2–4 July 2008. [Google Scholar]
- Koutsoyiannis, D. Statistics of Extremes and Estimation of Extreme Rainfall: I. Theoretical Investigation/Statistiques de Valeurs Extrêmes et Estimation de Précipitations Extrêmes: I. Recherche Théorique. Hydrol. Sci. J. 2004, 49, 3. [Google Scholar] [CrossRef]
- Balkema, A.A.; De Haan, L. Residual Lifetime at Great Age. Ann. Probab. 1974, 2, 792–804. [Google Scholar] [CrossRef]
- Pickands, J. Statistical Inference Using Extreme Order Statistics. Ann. Stat. 1975, 3, 119–131. [Google Scholar]
- Berbecariu, A.; Vespremeanu-Stroe, A. In Search of Marine Terraces from Central Dobrogea (Casimcea Plateau, Western Black Sea). Preliminary Inquiries on Distribution, Extension and Vertical Crustal Movements. Rev. De Geomorfol. 2020, 22, 87–97. [Google Scholar] [CrossRef]
- Maftei, C.; Barbulescu, A. Statistical Analysis of Precipitation Time Series in Dobrudja Region. Mausam 2012, 63, 553–564. [Google Scholar] [CrossRef]
- Ciulache, S.; Torică, V. Clima Dobrogei (Dobrogea Climate). In Analele Universității București, Seria Geografie (Annals of the University of Bucharest – Geography Series); University of Bucharest: București, Romania, 2003; pp. 83–107. [Google Scholar]
- Schweitzer, C.E.; Lazăr, I.; Feldmann, R.M.; Stoica, M.; Frantescu, O. Decapoda (Anomura; Brachyura) from the Late Jurassic of Dobrogea, Romania. Neues Jahrb. Für Geol. Und Paläontol. Abh. 2017, 286, 207–228. [Google Scholar] [CrossRef]
- Meylan, P.; Musy, A. Hydrologie Fréquentielle; HGA: Bucureşti, Romania, 1999; ISBN 973-98954-5-X. [Google Scholar]
- Kundzewicz, Z.W.; Robson, A. Detecting Trend and Other Changes in Hydrological Data; WMO: Geneva, Switzerland, 2000. [Google Scholar]
- Zaiontz, C. Sen’s Slope Mann-Kendall Text; 2024.
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. J. R. Stat. Society. Ser. C (Appl. Stat.) 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Buishand, T.A. Tests for Detecting a Shift in the Mean of Hydrological Time Series. J. Hydrol. 1984, 73, 51–69. [Google Scholar] [CrossRef]
- Lee, A.F.S.; Heghinian, S.M. A Shift Of The Mean Level In A Sequence Of Independent Normal Random Variables—A Bayesian Approach. Technometrics 1977, 19, 503–506. [Google Scholar] [CrossRef]
- Hubert, P. The Segmentation Procedure as a Tool for Discrete Modeling of Hydrometeorological Regimes. Stoch. Environ. Res. Risk Assess. 2000, 14, 297–304. [Google Scholar] [CrossRef]
- Kozanis, S.; Christofides, A.; Mamassis, N.; Efstratiadis, A.; Koutsoyiannis, D. Hydrognomon—Open Source Software for the Analysis of Hydrological Data. In Proceedings of the European Geosciences Union General Assembly 2010, Vienna, Austria, 2 May 2010. [Google Scholar]
- Kozanis, S.; Christofides, A.; Efstratiadis, A. Scientific Documentation of the Hydrogram Software Version 4; Department of Water Resources and Environmental Engineering, National Technical University of Athens: Athens, Greece, 2010; p. 173. [Google Scholar]
- Das, S. Goodness-of-Fit Tests for Generalized Normal Distribution for Use in Hydrological Frequency Analysis. Pure Appl. Geophys. 2018, 175, 3605–3617. [Google Scholar] [CrossRef]
- Moriasi, D.; Gitau, M.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. ASABE (Am. Soc. Agric. Biol. Eng.) 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Singh, J.; Knapp, H.; Arnold, J.; Misganaw, D. Hydrologic Modeling of the Iroquois River Watershed Using HSPF and SWAT. JAWRA J. Am. Water Resour. Assoc. 2005, 41, 343–360. [Google Scholar] [CrossRef]
- Abdolazimi, A.; Momeni, M.; Montazeri, M. Comparing ELECTRE and Linear Assignment Methods in Zoning Shahroud-Bastam Watershed for Artificial Recharge of Groundwater with GIS Technique. Mod. Appl. Sci. 2014, 9, p68. [Google Scholar] [CrossRef][Green Version]
- Figueira, J.R.; Greco, S.; Roy, B.; Slowinski, R. Electre Methods: Main Features and Recent Developments. In Handbook of Multicriteria Analysis; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Rosu, L.; Maftei, C.; Dobre, M.; Serban, A.; Iordache, G. ELECTRE Method Used in the Economical Analysis of Romanian Irrigation Systems; Bogazici University: Istanbul, Turkey, 2004; pp. 1358–1367. [Google Scholar]
- Taherdoost, H.; Madanchian, M. A Comprehensive Overview of the ELECTRE Method in Multi Criteria Decision-Making. J. Manag. Sci. Eng. Res. 2023, 6, 5–16. [Google Scholar] [CrossRef]
- Das, S. An Assessment of Using Subsampling Method in Selection of a Flood Frequency Distribution. Stoch. Environ. Res. Risk Assess. 2017, 31, 2033–2045. [Google Scholar] [CrossRef]
- Telteu, C.-E.; Stan, F.-I.; Brănescu, E.; Berghezan, A. Maximum Flow Variability and Floods Characteristics in the Central and North Dobrogea. Lucr. Semin. Geogr. Dimitrie Cantemir 2013, 36, 73–84. [Google Scholar]
- Traore, V.B.; Ndiaye, M.L.; Mbow, C.; Malomar, G.; Sarr, J.; Beye, A.C.; Diaw, A.T. Khronostat Model as Statistical Analysis Tools in Low Casamance River Basin, Senegal. World Environ. 2017, 7, 10–22. [Google Scholar]
- Ma, L.; Liu, D.; Huang, Q.; Guo, F.; Zheng, X.; Zhao, J.; Luan, J.; Fan, J.; Ming, G. Identification of a Function to Fit the Flow Duration Curve and Parameterization of a Semi-Arid Region in North China. Atmosphere 2023, 14, 116. [Google Scholar] [CrossRef]
- Jenkinson, A.F. Estimation Of Maximum Floods; WMO: Geneva, Switzerland, 1969; p. 288. [Google Scholar]
- Vivekanandan, N. Flood Frequency Analysis Using Method of Moments and L-Moments of Probability Distributions. Cogent Eng. 2015, 2, 1018704. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Kuczera, G. Comprehensive At-site Flood Frequency Analysis Using Monte Carlo Bayesian Inference. Water Resour. Res. 1999, 35, 1551–1557. [Google Scholar] [CrossRef]

| α | Defining Equation | Name (Proponent) |
|---|---|---|
| 0 | Weibull (probability unbiased) | |
| 0.3 | Cegodaev (empirical) | |
| 0.4 | Cunnane (empirical) | |
| 0.5 | Hazen (empirical) |
| Hydrometric Station | Length of Record Years | Q Mean (m3/s) | Q max/Data (m3/s) | Q min (m3/s) | Standard Deviation | Skewness | Drainage Area (km2) | Average Elevation (m) |
|---|---|---|---|---|---|---|---|---|
| Casimcea | 57 | 32.43 | 398/2002 | 0.048 | 64.54 | 4.27 | 78 | 263 |
| Cheia | 34 | 65.9 | 384/2005 | 0.5 | 99.70 | 2.18 | 500 | 158 |
| Cartal | 56 | 49.9 | 488/1985 | 0.1 | 92.86 | 3.06 | 128 | 150 |
| Ramnic | 56 | 23.5 | 131/1988 | 0.076 | 29.61 | 1.98 | 89 | 166 |
| No | River | Hydrometric Station/Discharge Equivalent to the Alert Thresholds * in (m3/s) | Date | The Maximum Discharge Qmax (m3/s) | Precipitation Causing the Qmax | |||
|---|---|---|---|---|---|---|---|---|
| On the Day of the Flood (mm) | Precipitation During the 10 Previous Days (mm) * | |||||||
| 1 | Casimcea | Casimcea | ||||||
| Qa | Qi | Qp | ||||||
| 1.0 | 5.00 | 28.0 | 23.10.1964 | 104 | – | – | ||
| 13.06.1988 | 99.3 | 74 | – | |||||
| 03.06.1972 | 89.3 | – | – | |||||
| 30.05.2002 | 398 | 94 | ||||||
| 03–04.07 2005 | 58.6 | 91 (73 in 3 h) | ||||||
| 2 | Casimcea | Cheia | ||||||
| Qa | Qi | Qp | ||||||
| 5.0 | 72.0 | – | 03.07.2005 | 384 | 44 | 27 | ||
| 31.05.2002 | 333 | 10 | 27 | |||||
| 28.08.2004 | 287 | 77 | 25 | |||||
| 17.06.2007 | 262 | |||||||
| 3 | Cartal | Cartal | ||||||
| Qa | Qi | Qp | ||||||
| 6.9 | 16.4 | 80.0 | 11.06.1985 | 488 | – | – | ||
| 24.09.1968 | 316 | – | – | |||||
| 03.07.2005 | 310 | 59 (24 in 30 min) | – | |||||
| 4 | Râmnic | Ramnic | ||||||
| Qa | Qi | Qp | ||||||
| 6.7 | 60.9 | – | 22.05.1988 | 131 | 25 | – | ||
| 04.06.1972 | 114 | – | – | |||||
| 11.06.1994 | 110 | 12 | 33 | |||||
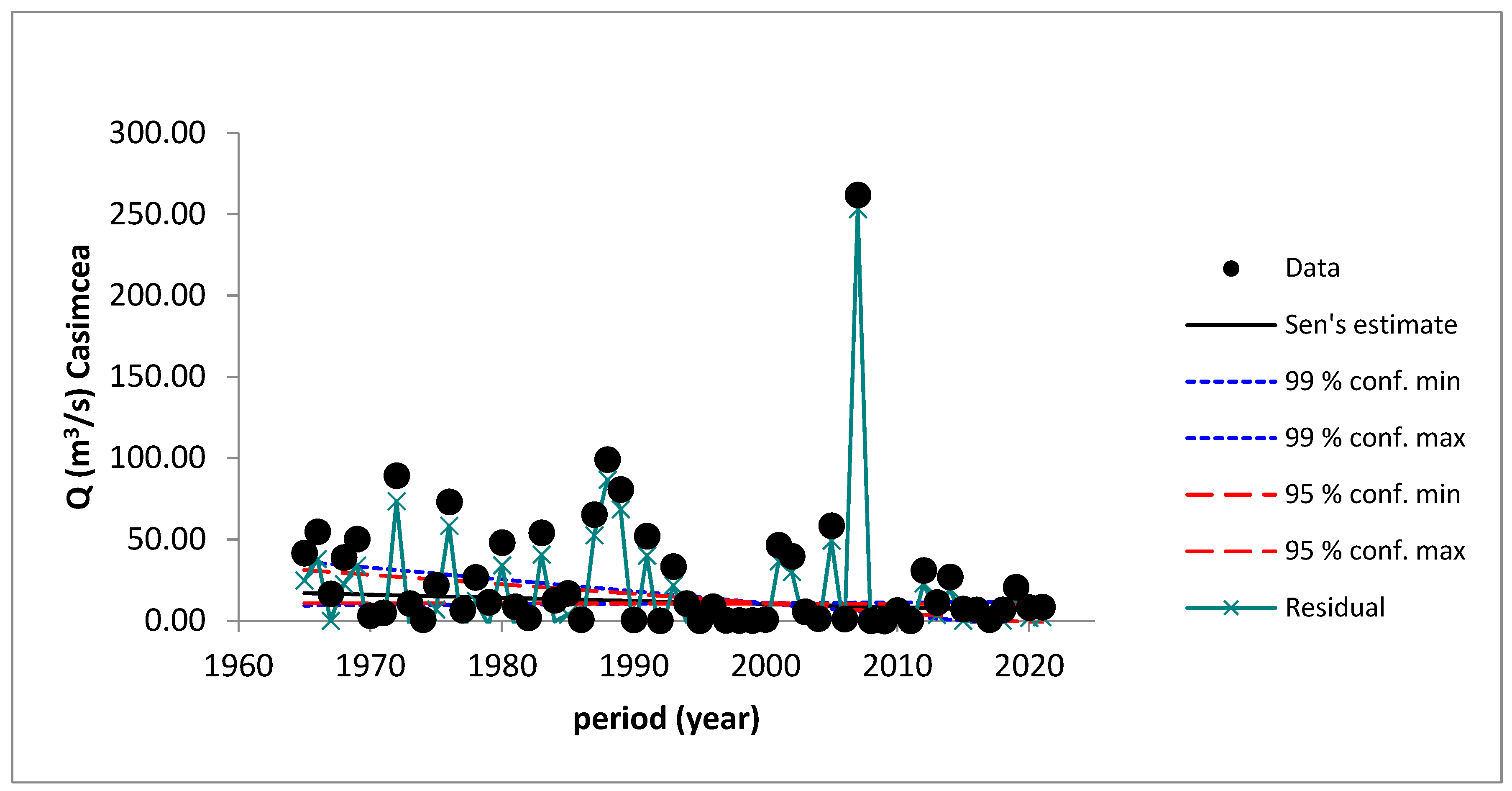
| Time Series | First Year | Last Year | n | Test Z | Signific. | Sen’s Slope Estimate |
|---|---|---|---|---|---|---|
| Q Casimcea | 1965 | 2021 | 57 | −2.13 | 0.05 | −0.194 |
| Q Cheia | 1988 | 2021 | 34 | −2.31 | 0.05 | −0.908 |
| Q Cartal | 1965 | 2021 | 57 | −2.24 | 0.05 | −0.247 |
| Q Ramnic | 1965 | 2021 | 57 | −2.11 | 0.05 | −0.232 |
| Hydrometric Station | Period (Years) | Mean (m3/s) | Khronostat Results for Independence | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Rank Correlation | Buishard | Pettitt | Lee & Heghinian | Hubert | |||||
| Results | Year | Results | Year | ||||||
| Casimcea | 57 | 26.03 | rejected at 95% confid. | rejected at 90% confid. | rejected at 95% confid. | 1989 | rejected Ho | 1989 | accepted |
| Cheia | 34 | 55.0 | rejected at 95% confid. | rejected at 95% confid. | rejected at 95% confid. | 2007 | rejected Ho | 2007 | accepted |
| Cartal | 57 | 50.8 | rejected at 95% confid. | rejected at 95% confid. | rejected at 95% confid. | 2006 | rejected Ho | 2006 | accepted |
| Ramnic | 57 | 23.9 | rejected at 90% confid. | rejected at 95% confid. | rejected at 90% confid. | 2006 | rejected Ho | 2006 | accepted |
| Maximum Discharge (m3/s) | ||||||
|---|---|---|---|---|---|---|
| EDF | Hazen | |||||
| Return period (year) Hydrometric station | 100 | 50 | 20 | 10 | 5 | 2 |
| Casimcea | 262 | 157.87 | 89.3 | 65.4 | 50.3 | 10.7 |
| Cheia | no | 377.92 | 310 | 128 | 56.2 | 12.9 |
| Cartal | 333 | 324.72 | 287 | 246 | 83.1 | 24.3 |
| Ramnic | 131 | 119.85 | 110 | 57.2 | 39.8 | 12.6 |
| EDF | Weibull | |||||
| Casimcea | 262 | 224.35 | 99.3 | 73.3 | 50.3 | 10.7 |
| Cheia | no | 333 | 297.87 | 246 | 83.1 | 24.3 |
| Cartal | 488 | 460.48 | 316 | 224 | 56.2 | 12.9 |
| Ramnic | 131 | 128.12 | 114.00 | 68.8 | 39.8 | 12.6 |
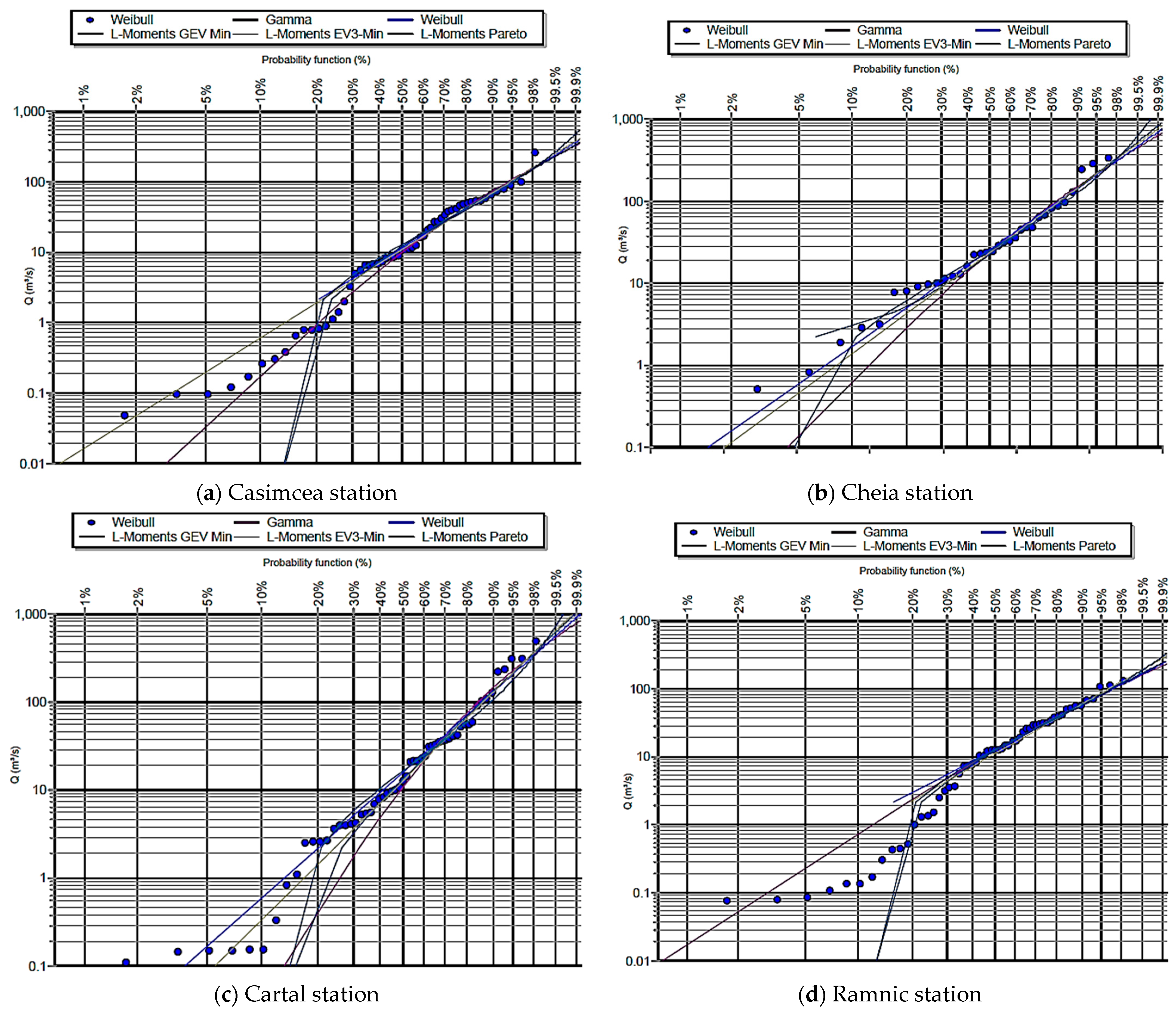
| Kolmogorov–Smirnov Test | a = 1% | Rank | Dmax |
|---|---|---|---|
| Gamma | ACCEPT | 1 | 0.0796 |
| Pearson-III | ACCEPT | 2 | 0.0831 |
| GEV-Min | ACCEPT | 3 | 0.0847 |
| EV3-Min (Weibull, L-moments) | ACCEPT | 4 | 0.098 |
| EV3-Min (Weibull) | ACCEPT | 5 | 0.1052 |
| Pareto (L-moments) | ACCEPT | 6 | 0.1200 |
| GEV-Min (L-moments) | ACCEPT | 7 | 0.1215 |
| Gamma | Pearson-III | GEV-Min | EV3-Min (Weibull, L-Moments) | EV3-Min (Weibull) | Pareto (L-Moments) | GEV-Min (L-Moments) | GEV-Max (L-Moments) | Log Pearson-III | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Hydrometric Station | ||||||||||
| Casimcea | 1 | 2 | 3 | 4 | 5 | 6 | 7 | x | x | |
| Cheia | 7 | x | x | 6 | 3 | 1 | 4 | 2 | 5 | |
| Cartal | 7 | x | 6 | 2 | 1 | 5 | 5 | 4 | 3 | |
| Ramnic | 2 | x | x | 5 | 6 | 3 | 4 | 1 | x | |
| Return Period (T) Hydrometric Station and PDF’s | 1000 | 100 | 50 | 20 | 10 | 5 | 2 |
|---|---|---|---|---|---|---|---|
| Casimcea—Qmax (m3/s) | |||||||
| Gamma | 323.522 | 193.42 | 155.808 | 107.943 | 73.8253 | 42.6248 | 9.93832 |
| EV3-Min (Weibull, L-Moments) | 376.839 | 201.90 | 157.07 | 104.162 | 69.4718 | 40.0324 | 10.9478 |
| EV3-Min (Weibull) | 361.019 | 196.20 | 153.516 | 102.766 | 69.1782 | 40.3687 | 11.3719 |
| Pareto (L-Moments) | 469.357 | 200.59 | 149.699 | 96.6856 | 65.1675 | 39.5258 | 12.8146 |
| GEV-Min (L-Moments) | 331.602 | 187.72 | 149.211 | 102.364 | 70.4469 | 42.146 | 11.9543 |
| EDF | 262 | 157.8 | 89.3 | 65.4 | 50.3 | 10.7 | |
| Hazen | Weibull | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rank | r | RMSE | NSE | R2 | r | RMSE | NSE | R2 | |
| Casimcea | |||||||||
| Gamma | 1 | 0.96 | 29.40 | 0.87 | 0.92 | 0.98 | 39.87 | 0.81 | 0.92 |
| EV3-Min (Weibull, L-Moments) | 2 | 0.97 | 25.68 | 0.90 | 0.95 | 0.98 | 37.15 | 0.84 | 0.95 |
| EV3-Min (Weibull) | 3 | 0.97 | 27.82 | 0.89 | 0.94 | 0.98 | 39.74 | 0.81 | 0.94 |
| Pareto (L-Moments) | 4 | 0.98 | 25.86 | 0.90 | 0.97 | 0.99 | 39.87 | 0.81 | 0.97 |
| GEV-Min (L-Moments) | 5 | 0.97 | 31.24 | 0.86 | 0.94 | 0.98 | 43.30 | 0.78 | 0.94 |
| Cheia | |||||||||
| Pareto (L-Moments) | 1 | 0.87 | 73.34 | 0.62 | 0.76 | 0.93 | 56.67 | 0.74 | 0.87 |
| EV3-Min (Weibull) | 2 | 0.90 | 80.06 | 0.55 | 0.80 | 0.94 | 56.91 | 0.74 | 0.88 |
| GEV-Min (L-Moments) | 3 | 0.92 | 52.44 | 0.81 | 0.85 | 0.93 | 53.70 | 0.77 | 0.86 |
| EV3-Min (Weibull, L-Moments) | 4 | 0.90 | 60.02 | 0.75 | 0.81 | 0.82 | 172.03 | −1.40 | 0.67 |
| Gamma | 5 | 0.90 | 60.02 | 0.75 | 0.81 | 0.94 | 53.91 | 0.76 | 0.88 |
| Cartal | |||||||||
| EV3-Min (Weibull) | 1 | 0.98 | 49.00 | 0.92 | 0.80 | 0.97 | 79.97 | 0.81 | 0.93 |
| EV3-Min (Weibull, L-Moments) | 2 | 0.98 | 38.52 | 0.75 | 0.81 | 0.98 | 67.81 | 0.86 | 0.92 |
| Pareto (L-Moments) | 3 | 0.96 | 58.72 | 0.62 | 0.76 | 0.96 | 92.35 | 0.74 | 0.86 |
| GEV-Min (L-Moments) | 4 | 0.97 | 45.35 | 0.81 | 0.85 | 0.97 | 72.52 | 0.84 | 0.91 |
| Gamma | 5 | 0.99 | 40.54 | 0.75 | 0.81 | 0.99 | 68.58 | 0.86 | 0.96 |
| Râmnic | |||||||||
| Gamma | 1 | 0.86 | 37.36 | 0.29 | 0.74 | 0.83 | 38.43 | 0.28 | 0.70 |
| Pareto (L-Moments) | 2 | 0.79 | 68.69 | −1.41 | 0.62 | 0.75 | 69.22 | −1.33 | 0.57 |
| GEV-Min (L-Moments) | 3 | 0.87 | 34.92 | 0.38 | 0.76 | 0.82 | 46.06 | −0.03 | 0.67 |
| EV3-Min (Weibull, L-Moments) | 4 | 0.82 | 61.21 | −0.91 | 0.68 | 0.79 | 44.37 | −0.84 | 0.63 |
| EV3-Min (Weibull) | 5 | 0.84 | 43.35 | 0.04 | 0.71 | 0.81 | 61.55 | 0.04 | 0.66 |
| Performance | r | RMSE/STDEV | NSE | R2 |
|---|---|---|---|---|
| very good | 0.80–1 | 0.0–0.5 | 0.80–1 | 0.80–1 |
| good | 0.6–0.8 | 0.5–0.6 | 0.70–0.80 | 0.6–0.8 |
| satisfactory | 0.4–0.6 | 0.6–0.7 | 0.5–0.70 | 0.4–0.6 |
| unsatisfactory | <0.4 | >0.7 | <0.5 | <0.4 |
| Criteria | Achieved a | r | RRS | NSE | R2 |
|---|---|---|---|---|---|
| weight | 0.50 | 0.12 | 0.13 | 0.13 | 0.12 |
| Model (M) | Net Superior Value | Rank | Net Superior Value | Rank | Observation |
|---|---|---|---|---|---|
| Casimcea | |||||
| M1 (Gamma) | 0.390 | 3 | −2.862 | 2 | E |
| M2 (EV3-Min-Weibull, L-Moments) | 2.650 | 1 | −3.057 | 1 | |
| M3 (EV3-Min Weibull) | 0.000 | 4 | 0.036 | 3 | E |
| M4 (Pareto-L-Moments) | 0.480 | 2 | 1.883 | 4 | E |
| M5 (GEV-Min-L-Moments) | −3.520 | 5 | 4.000 | 5 | |
| Cheia | |||||
| M1 (Pareto-L-Moments) | 0.130 | 2 | −0.729 | 2 | |
| M2 (EV3-Min-Weibull) | −0.130 | 3 | 0.050 | 3 | |
| M3 (GEV-Min-L-Moments) | 2.000 | 1 | −1.296 | 1 | |
| M4 (EV3-Min Weibull, L-Moments) | −0.500 | 4 | 1.000 | 5 | E |
| M5 (Gamma) | −1.500 | 5 | 0.975 | 4 | E |
| Cartal | |||||
| M1 (EV3-Min-Weibull) | 1.510 | 2 | −2.956 | 2 | |
| M2 (EV3-Min-Weibull, L-Moments) | 2.260 | 1 | −2.976 | 1 | |
| M3 (Pareto-L-Moments) | −2.000 | 5 | 0.731 | 3 | E |
| M4 (GEV-Min-L-Moments) | −0.500 | 3 | 1.614 | 4 | E |
| M5 (Gamma) | −1.270 | 4 | 3.588 | 5 | E |
| Ramnic | |||||
| M1 (Gamma) | 1.130 | 2 | −2.320 | 1 | |
| M2 (Pareto-L-Moments) | 0.130 | 3 | 1.966 | 4 | |
| M3 (GEV-Min-L-Moments) | 2.000 | 1 | −2.267 | 2 | |
| M4 (EV3-Min-Weibull, L-Moments) | −1.260 | 4 | 0.282 | 3 | |
| M5 (EV3-Min-Weibull) | −2.000 | 5 | 2.339 | 5 | |
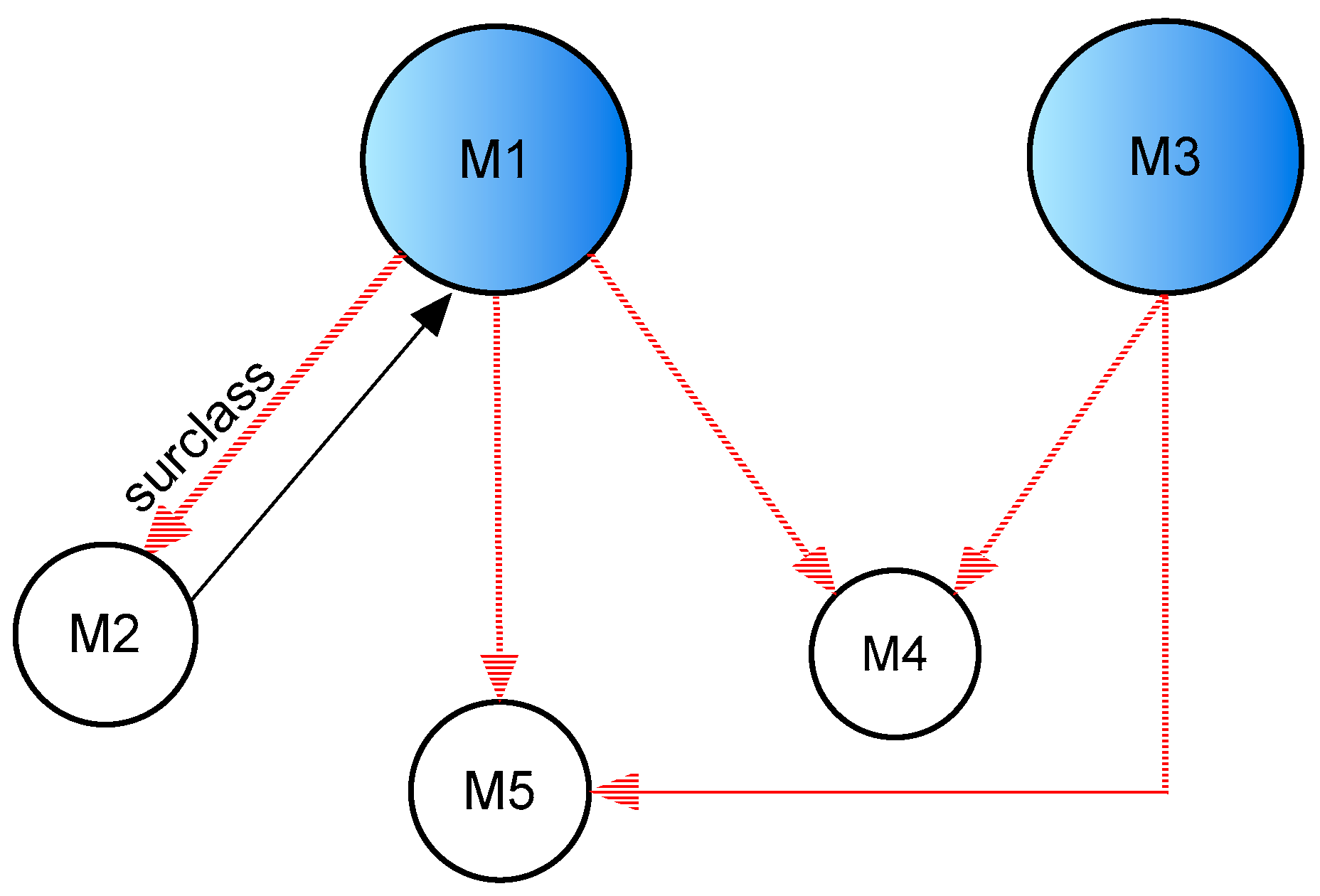
| Cartal | M1 | M2 | M3 | M4 | M5 |
|---|---|---|---|---|---|
| M1 | 0 | 1 | 0 | 1 | 1 |
| M2 | 1 | 0 | 0 | 0 | 0 |
| M3 | 0 | 0 | 0 | 1 | 1 |
| M4 | 0 | 0 | 0 | 0 | 0 |
| M5 | 0 | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maftei, C.; Cerneaga, C.; Vaseashta, A. Predictive Modeling of Flood Frequency Utilizing an Analysis of the Casimcea River in Romania. Hydrology 2025, 12, 172. https://doi.org/10.3390/hydrology12070172
Maftei C, Cerneaga C, Vaseashta A. Predictive Modeling of Flood Frequency Utilizing an Analysis of the Casimcea River in Romania. Hydrology. 2025; 12(7):172. https://doi.org/10.3390/hydrology12070172
Chicago/Turabian StyleMaftei, Carmen, Constantin Cerneaga, and Ashok Vaseashta. 2025. "Predictive Modeling of Flood Frequency Utilizing an Analysis of the Casimcea River in Romania" Hydrology 12, no. 7: 172. https://doi.org/10.3390/hydrology12070172
APA StyleMaftei, C., Cerneaga, C., & Vaseashta, A. (2025). Predictive Modeling of Flood Frequency Utilizing an Analysis of the Casimcea River in Romania. Hydrology, 12(7), 172. https://doi.org/10.3390/hydrology12070172







