Triangular Fuzzy Finite Element Solution for Drought Flow of Horizontal Unconfined Aquifers
Abstract
1. Introduction
2. Materials and Methods
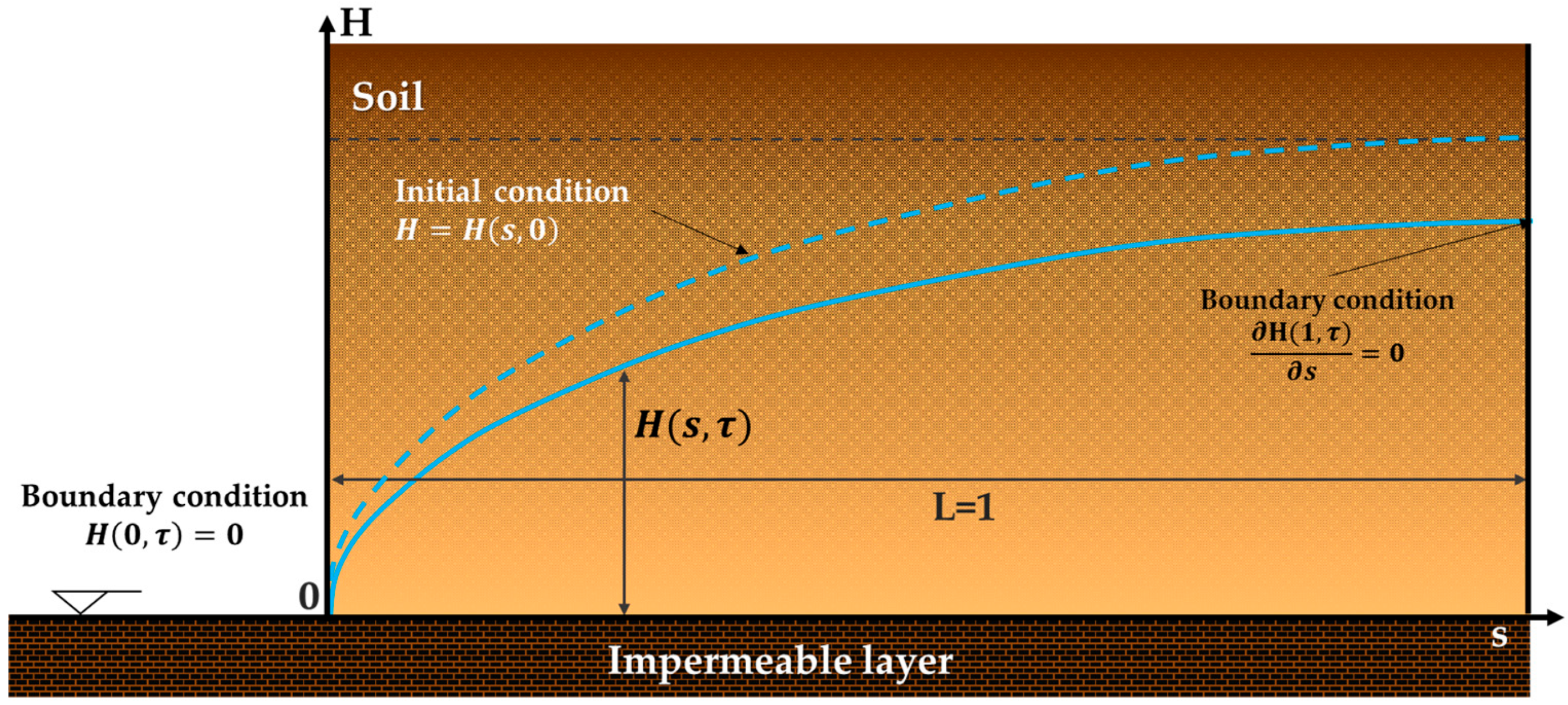
2.1. Crisp Model
Numerical Method
2.2. Fuzzy Model Definitions
2.2.1. Fuzzy Theory Definitions
- (a)
- is increasing, is decreasing as functions of α, and ;
- (b)
- is decreasing, is increasing as functions of α, and .
- is (i)-gH-differentiable at if
- (i)
- ;
- is (ii)-gH-differentiable at if
- (i)
- .
- is [(i)-p]-differentiable with respect to x at ( if
- is [(ii)-p]-differentiable with respect to x at ( if
2.2.2. Possibility Theory Definitions
2.3. Fuzzy Finite Elements and Corresponding Systems
2.3.1. Fuzzy Model
- Boundary conditions
- Initial condition
- System (1, 1):
- System (1, 2):
- System (1, 3):
- System (1, 4):
- System (2, 1):
- System (2, 2):
- System (2, 3):
- System (2, 4):
- Case a
- Case b
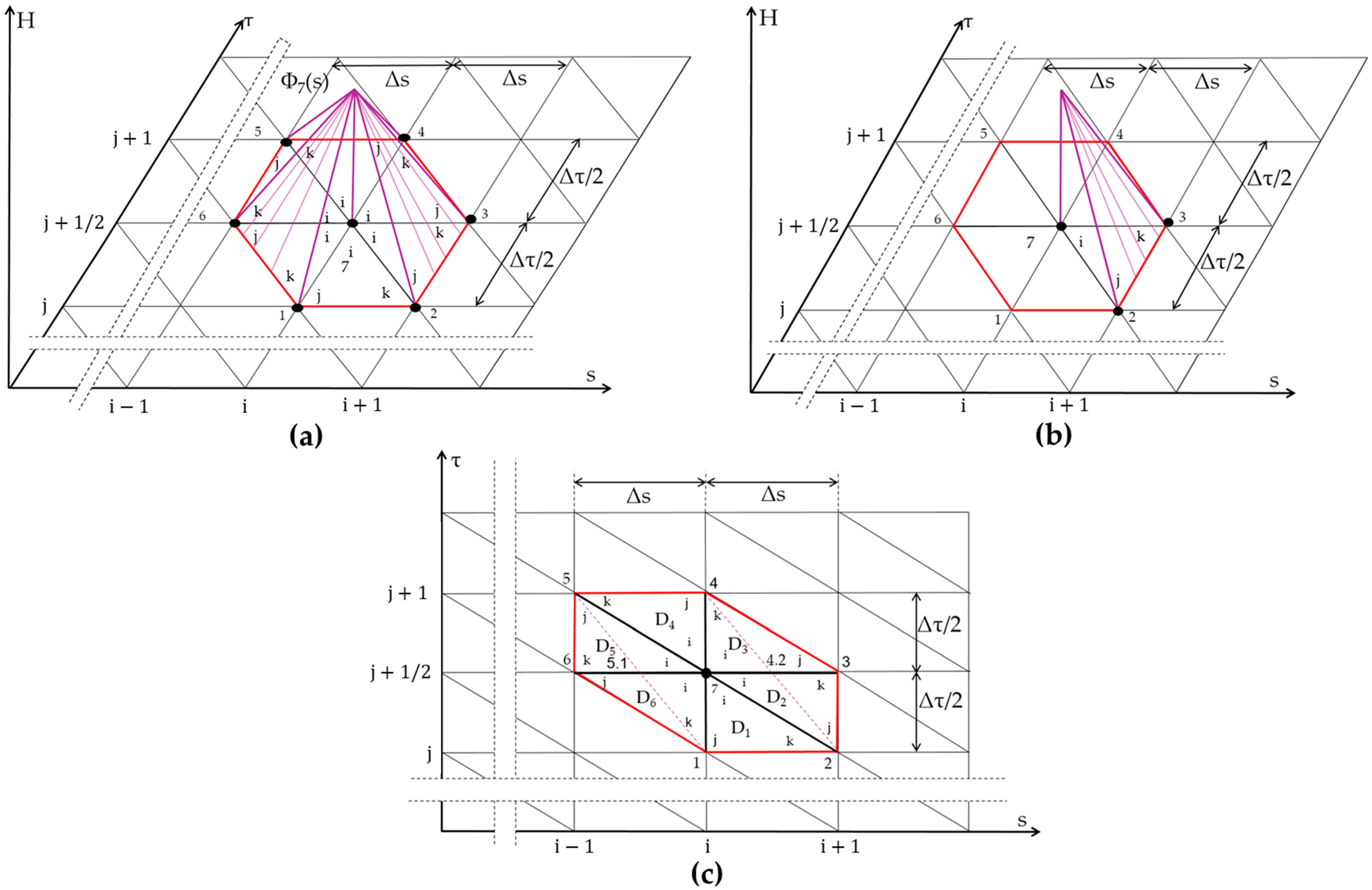
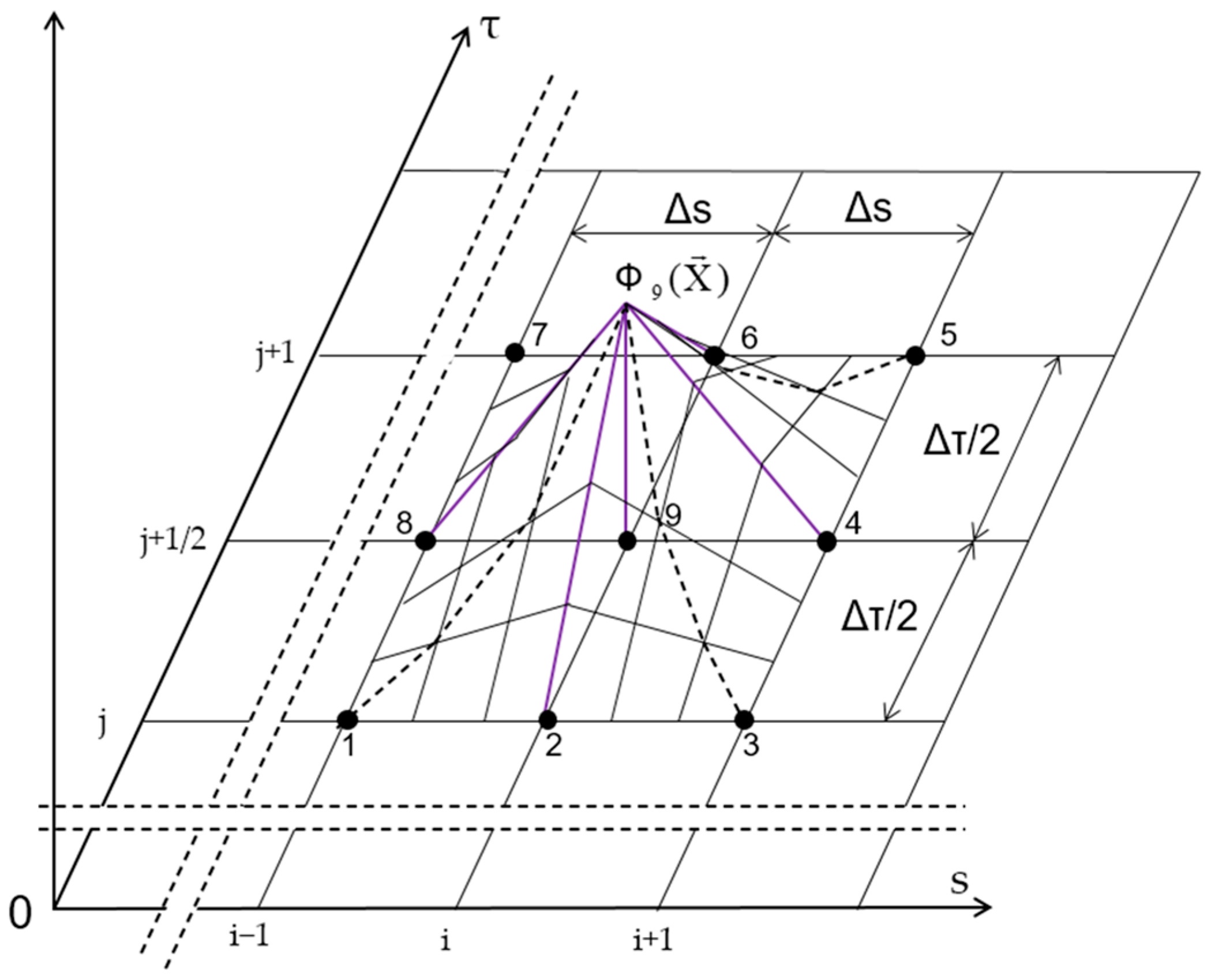
2.3.2. The Proposed Fuzzy Triangular Finite Element Solution
2.3.3. Outflow Volumes
2.4. Proposed Method for Solving the Crisp and Fuzzy Cases of Non-Dimensional Variables
| Algorithem 1 A pseudocode solving process | |
| Step 1: | τ = 0 The interval [s0, sN] is divided into N equal parts: |
| Step 2: | τ = τ+Δτ, |
| Step 3: | Initial values H(sr,0) sr, r = 1,2,…N + 1 |
| Step 4: | Boundary values H(0,τ) = h0, |
| Step 5: | Find coefficients |
| Step 6: | Solve the tridiagonal system [36,37] |
| Step 7: | Put HNEW into HINITIAL |
| Step 8: | Compute outflow volume V(HNEW) |
| Step 9: | Print τ, V(τ), HΝΕW values |
| Step 10: | If go to 2 |
| end | |
3. Results
3.1. Boussinesq Analytical Solution
- (a)
- Neglecting the effect of capillary rise above the water table;
- (b)
- Accepting the Dupuit–Forcheimer approximation, i.e., the hydraulic head is independent of depth and therefore the streamlines are assumed to be approximately parallel to the bed;
- (c)
- His solution is valid when t is large, that is, when the water table at x = L is below the aquifer depth h0 (See Figure 1).
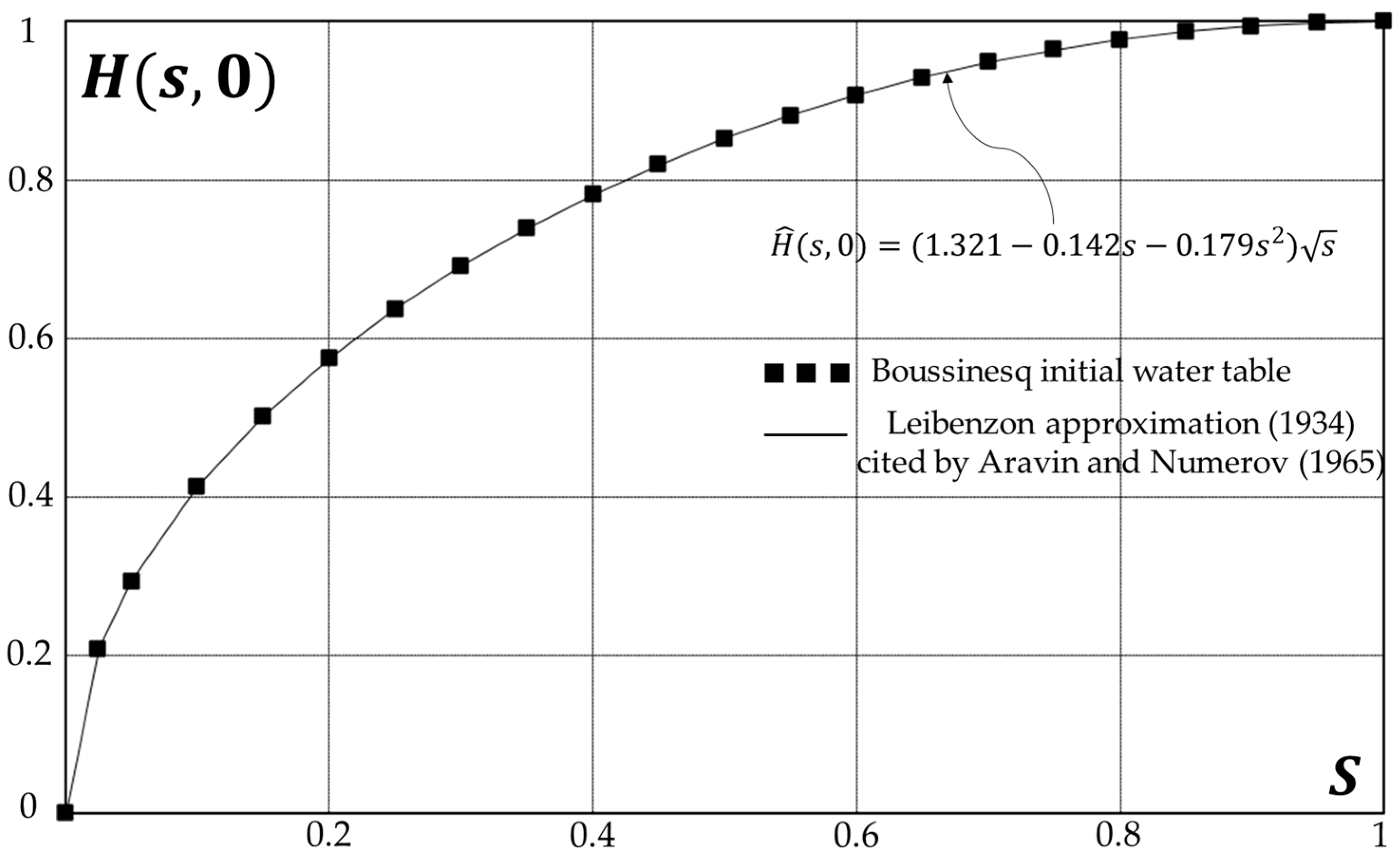
3.2. Initial Water Table
3.3. Storativity and Discharge
3.3.1. Dimensional Storativity
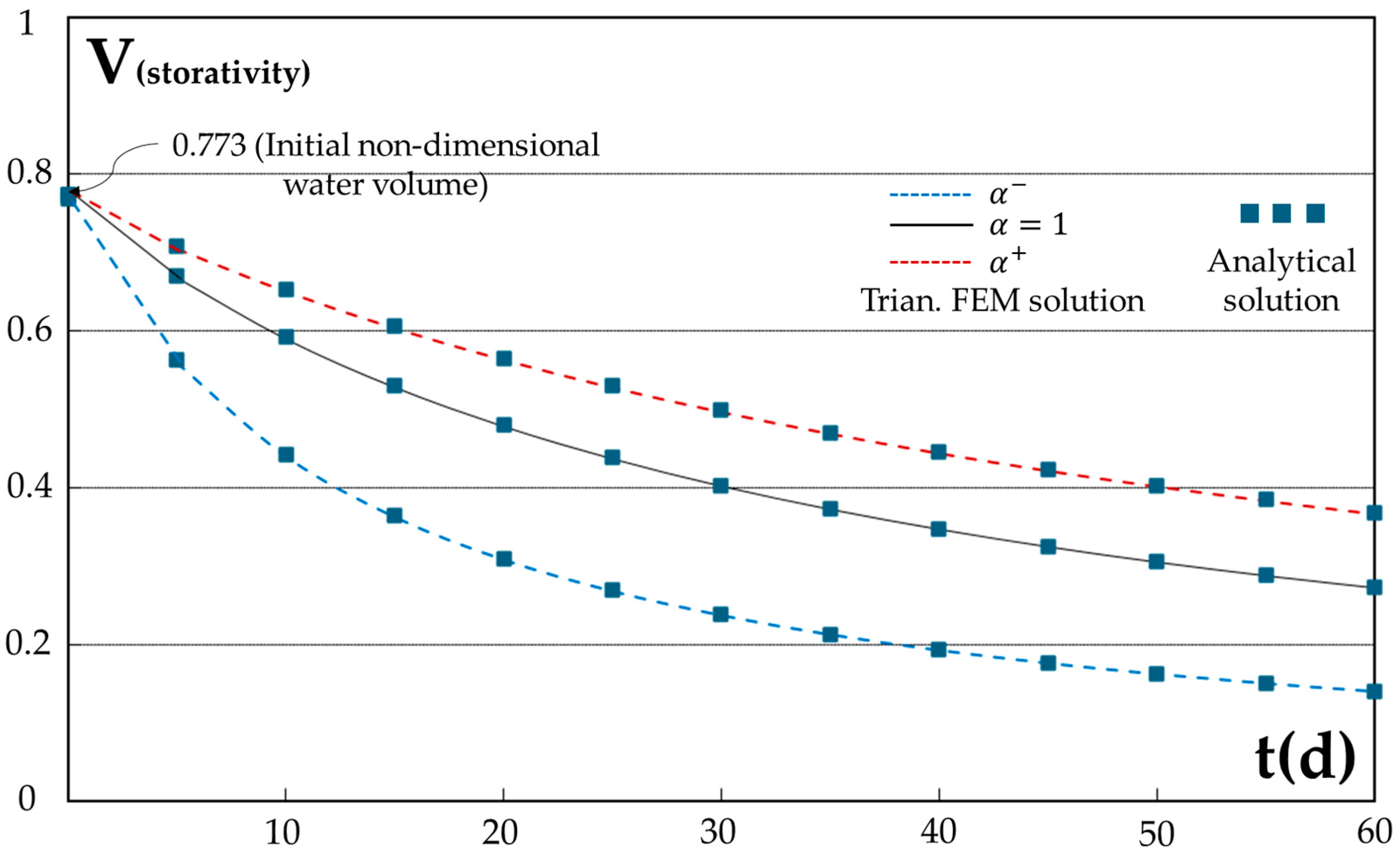
3.3.2. Non-Dimensional Storativity
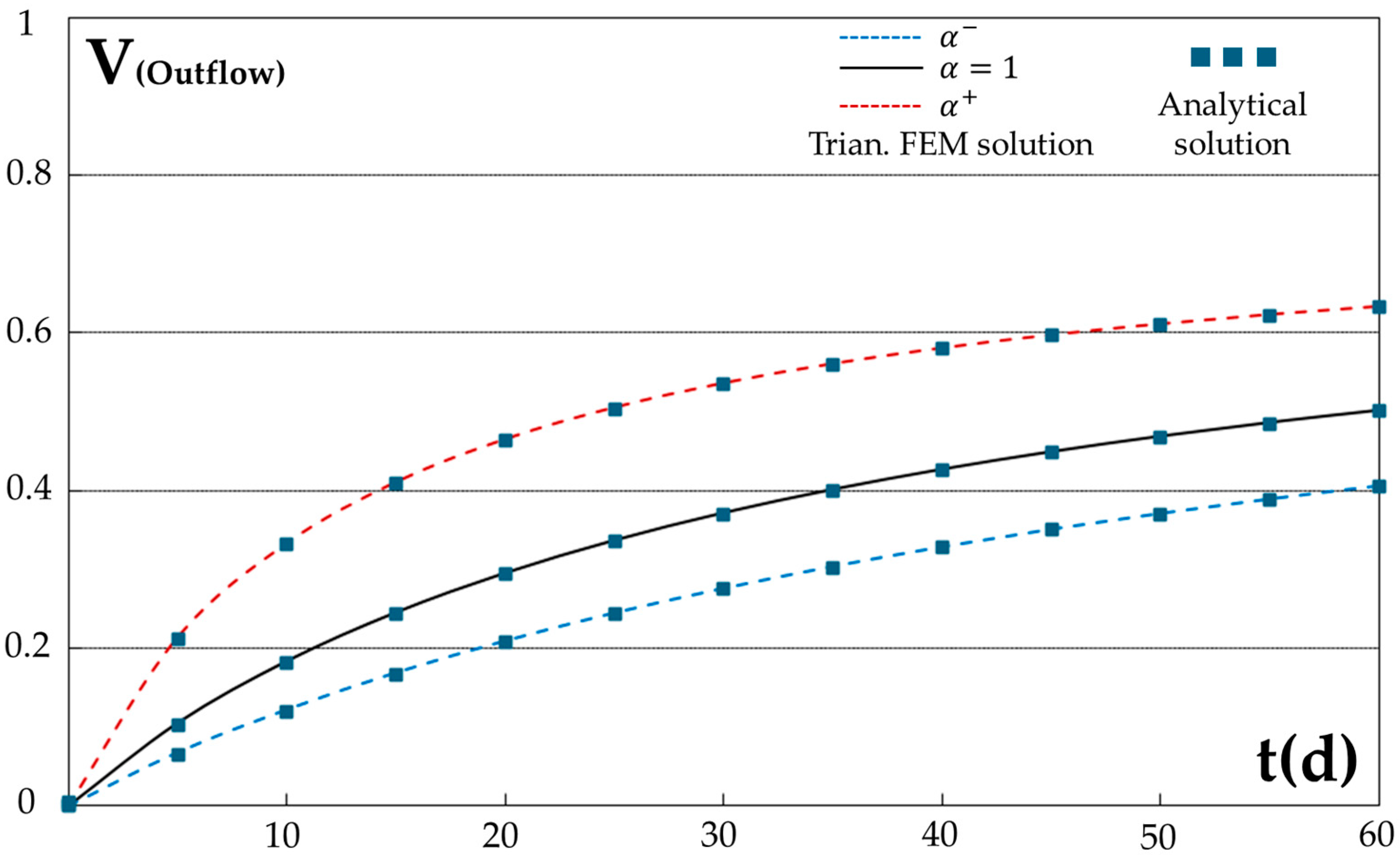
3.3.3. Discharge
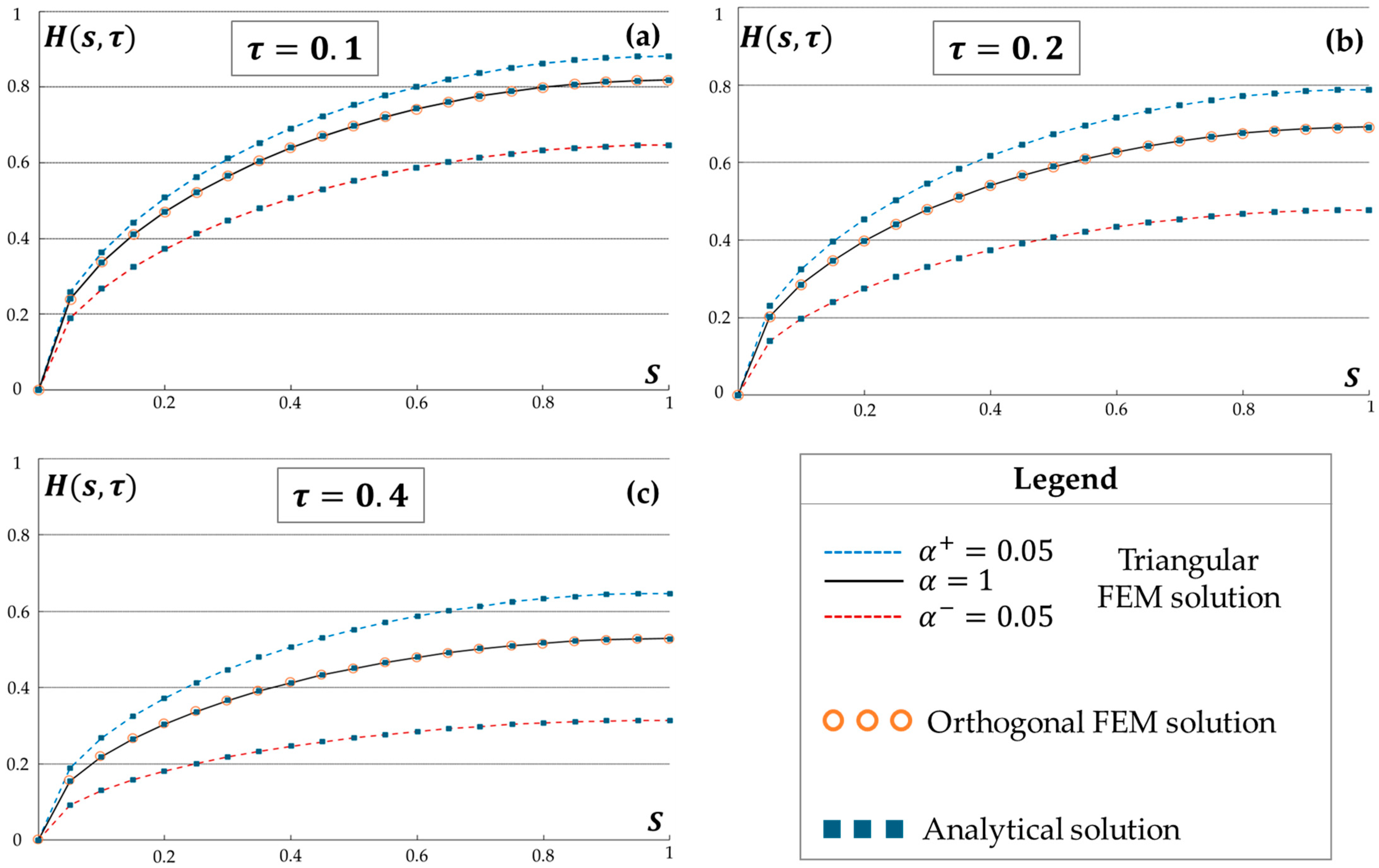
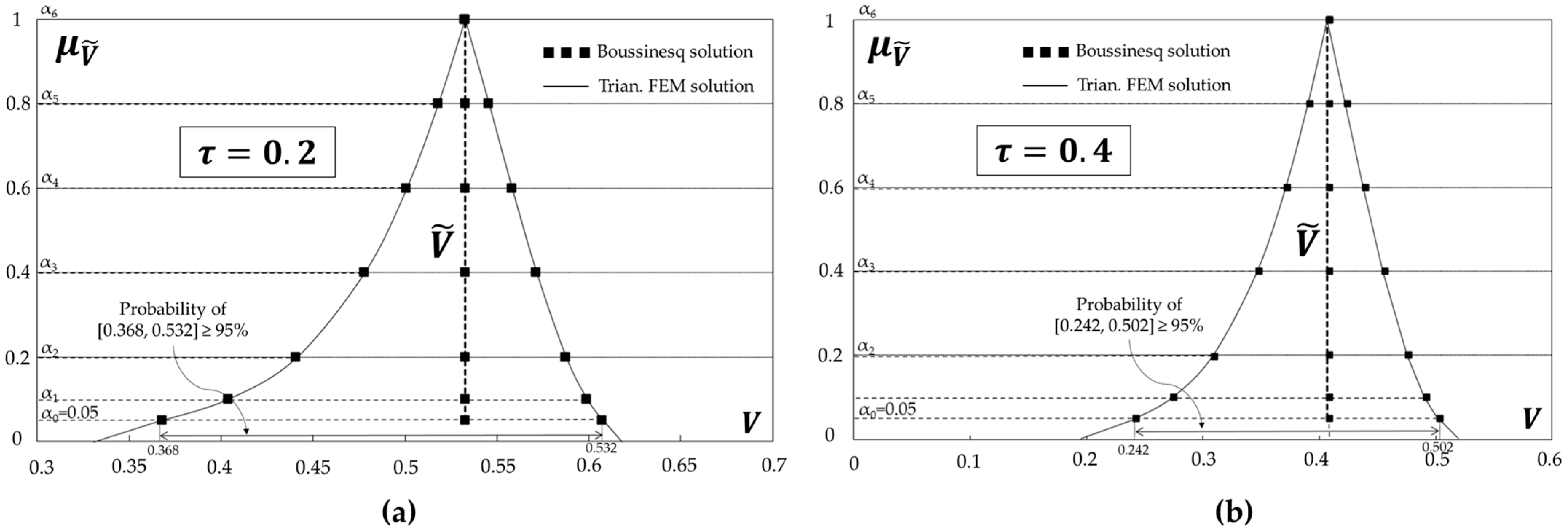
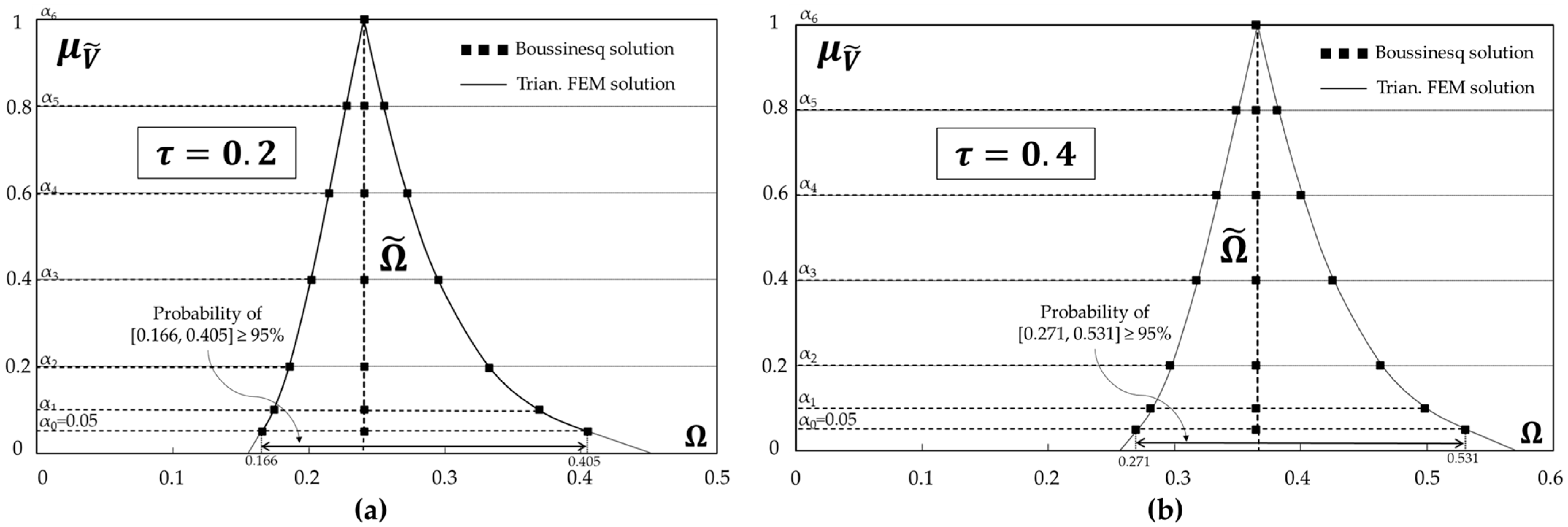
3.4. Fuzzy Triangular Finite Element Method Application and Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FDM | Finite Difference Method |
| FEM | Finite Element Method |
| FVM | Finite Volume Method |
| gH | Generalized Hukuhara |
| XFEM | Extended Finite Element Method |
Appendix A

- Gelerkin’s Method
References
- Hall, F.R. Base-Flow Recessions—A Review. Water Resour. Res. 1968, 4, 973–983. [Google Scholar] [CrossRef]
- Boussinesq, J. Recherches Theoriques Sur l’ecoulement Des Nappes d’eau Infiltrees Dans Le Sol et Sur Le Debit Des Sources. J. Math. Pures Appl. 1904, 10, 5–78. [Google Scholar]
- Brutsaert, W.; Nieber, J.L. Regionalized Drought Flow Hydrographs from a Mature Glaciated Plateau. Water Resour. Res. 1977, 13, 637–643. [Google Scholar] [CrossRef]
- Troch, P.A.; De Troch, F.P.; Brutsaert, W. Effective Water Table Depth to Describe Initial Conditions Prior to Storm Rainfall in Humid Regions. Water Resour. Res. 1993, 29, 427–434. [Google Scholar] [CrossRef]
- Szilagyi, J.; Parlange, M.B.; Albertson, J.D. Recession Flow Analysis for Aquifer Parameter Determination. Water Resour. Res. 1998, 34, 1851–1857. [Google Scholar] [CrossRef]
- Troch, P.A.; van Loon, A.H.; Hilberts, A.G.J. Analytical Solution of the Linearized Hillslope-storage Boussinesq Equation for Exponential Hillslope Width Functions. Water Resour. Res. 2004, 40, W08601. [Google Scholar] [CrossRef]
- Troch, P.A.; Berne, A.; Bogaart, P.; Harman, C.; Hilberts, A.G.J.; Lyon, S.W.; Paniconi, C.; Pauwels, V.R.N.; Rupp, D.E.; Selker, J.S.; et al. The Importance of Hydraulic Groundwater Theory in Catchment Hydrology: The Legacy of Wilfried Brutsaert and Jean-Yves Parlange. Water Resour. Res. 2013, 49, 5099–5116. [Google Scholar] [CrossRef]
- Bartlett, M.S.; Porporato, A. A Class of Exact Solutions of the Boussinesq Equation for Horizontal and Sloping Aquifers. Water Resour. Res. 2018, 54, 767–778. [Google Scholar] [CrossRef]
- Akylas, E.; Gravanis, E. Approximate Solutions of the Boussinesq Equation for Horizontal Unconfined Aquifers During Pure Drainage Phase. Water 2024, 16, 2984. [Google Scholar] [CrossRef]
- Richtmyer, R.D.; Morton, K.W. Difference Methods for Initial-Value Problems; John Wiley & Sons: New York, NY, USA; London, UK; Sidney, Australia, 1967. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 2018; ISBN 9781315275130. [Google Scholar]
- Argyris, J.H. Energy Theorems and Structural Analysis. Aircr. Eng. Aerosp. Technol. 1954, 26, 383–394. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Cheung, Y.K. Finite Element Method in Structural & Continuum Mechanics Hardcover, 1st ed.; McGraw Hill: London, UK, 1967. [Google Scholar]
- Oden, J.T. Finite Elements of Nonlinear Continua; Dover Publications: New York, NY, USA, 1972. [Google Scholar]
- Oden, J.T. Historical Comments on Finite Elements. In A History of Scientific Computing; ACM: New York, NY, USA, 1990; pp. 152–166. [Google Scholar]
- Tzimopoulos, C. Solution de l’équation de Boussinesq par une méthode des éléments finis. J. Hydrol. 1976, 30, 1–18. [Google Scholar] [CrossRef]
- Galerkin, B.G. Rods and Plates: Series in Some Questions of Elastic Equilibrium of Rods and Plates; National Technical Information Service: Springfield, VA, USA, 1968. [Google Scholar]
- Frangakis, C.N.; Tzimopoulos, C. Unsteady Groundwater Flow on Sloping Bedrock. Water Resour. Res. 1979, 15, 176–180. [Google Scholar] [CrossRef]
- Tzimopoulos, C.; Tolikas, P. ICID Bulletin (International Commission on Irrigation and Drainage); ICID: New Delhi, India, 1980; pp. 40–44. [Google Scholar]
- Tber, M.H.; El Alaoui Talibi, M. A Finite Element Method for Hydraulic Conductivity Identification in a Seawater Intrusion Problem. Comput. Geosci. 2007, 33, 860–874. [Google Scholar] [CrossRef]
- Mohammadnejad, T.; Khoei, A.R. An Extended Finite Element Method for Hydraulic Fracture Propagation in Deformable Porous Media with the Cohesive Crack Model. Finite Elem. Anal. Des. 2013, 73, 77–95. [Google Scholar] [CrossRef]
- Yang, D.; Zhou, Y.; Xia, X.; Gu, S.; Xiong, Q.; Chen, W. Extended Finite Element Modeling Nonlinear Hydro-Mechanical Process in Saturated Porous Media Containing Crossing Fractures. Comput. Geotech. 2019, 111, 209–221. [Google Scholar] [CrossRef]
- Aslan, T.A.; Temel, B. Finite Element Analysis of the Seepage Problem in the Dam Body and Foundation Based on the Galerkin’s Approach. Eur. Mech. Sci. 2022, 6, 143–151. [Google Scholar] [CrossRef]
- Puri, M.L.; Ralescu, D.A. Differentials of Fuzzy Functions. J. Math. Anal. Appl. 1983, 91, 552–558. [Google Scholar] [CrossRef]
- Hukuhara, M. Integration Des Applications Measurables Dont La Valeur Est Un Compact Convexe. Funkc. Ekvacioj 1967, 10, 205–233. [Google Scholar]
- Kaleva, O. Fuzzy Differential Equations. Fuzzy Sets Syst. 1987, 24, 301–307. [Google Scholar] [CrossRef]
- Seikkala, S. On the Fuzzy Initial Value Problem. Fuzzy Sets Syst. 1987, 24, 319–330. [Google Scholar] [CrossRef]
- Vorobiev, D.; Seikkala, S. Towards the Theory of Fuzzy Differential Equations. Fuzzy Sets Syst. 2002, 125, 231–237. [Google Scholar] [CrossRef]
- Nieto, J.J.; Rodríguez-López, R. Bounded Solutions for Fuzzy Differential and Integral Equations. Chaos Solitons Fractals 2006, 27, 1376–1386. [Google Scholar] [CrossRef]
- Diamond, P. Brief Note on the Variation of Constants Formula for Fuzzy Differential Equations. Fuzzy Sets Syst. 2002, 129, 65–71. [Google Scholar] [CrossRef]
- Bede, B.; Gal, S.G. Generalizations of the Differentiability of Fuzzy-Number-Valued Functions with Applications to Fuzzy Differential Equations. Fuzzy Sets Syst. 2005, 151, 581–599. [Google Scholar] [CrossRef]
- Bede, B. A Note on “Two-Point Boundary Value Problems Associated with Non-Linear Fuzzy Differential Equations”. Fuzzy Sets Syst. 2006, 157, 986–989. [Google Scholar] [CrossRef]
- Stefanini, L. A Generalization of Hukuhara Difference and Division for Interval and Fuzzy Arithmetic. Fuzzy Sets Syst. 2010, 161, 1564–1584. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Gouyandeh, Z.; Armand, A.; Hasanoglu, A. On Fuzzy Solutions for Heat Equation Based on Generalized Hukuhara Differentiability. Fuzzy Sets Syst. 2015, 265, 1–23. [Google Scholar] [CrossRef]
- Tzimopoulos, C.; Papadopoulos, K.; Samarinas, N.; Papadopoulos, B.; Evangelides, C. Fuzzy Finite Elements Solution Describing Recession Flow in Unconfined Aquifers. Hydrology 2024, 11, 47. [Google Scholar] [CrossRef]
- Thomas, L.H. Elliptic Problems in Linear Difference Equations over a Network; Watson Scientific Computing Laboratory at Columbia University: New York, NY, USA, 1949. [Google Scholar]
- Samarinas, N.; Tzimopoulos, C.; Evangelides, C. An Efficient Method to Solve the Fuzzy Crank–Nicolson Scheme with Application to the Groundwater Flow Problem. J. Hydroinformatics 2022, 24, 590–609. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Negoita, C.V.; Ralescu, D.A. REPRESENTATION THEOREMS FOR FUZZY CONCEPTS. Kybernetes 1975, 4, 169–174. [Google Scholar] [CrossRef]
- Goetshel, R.; Voxman, W. Elementary Fuzzy Calculus. Fuzzy Sets Syst. 1986, 18, 31–43. [Google Scholar] [CrossRef]
- Bede, B.; Stefanini, L. Generalized Differentiability of Fuzzy-Valued Functions. Fuzzy Sets Syst. 2013, 230, 119–141. [Google Scholar] [CrossRef]
- Khastan, A.; Nieto, J.J. A Boundary Value Problem for Second Order Fuzzy Differential Equations. Nonlinear Anal. Theory Methods Appl. 2010, 72, 3583–3593. [Google Scholar] [CrossRef]
- Dubois, D.; Foulloy, L.; Mauris, G.; Prade, H. Probability-Possibility Transformations, Triangular Fuzzy Sets, and Probabilistic Inequalities. Reliab. Comput. 2004, 10, 273–297. [Google Scholar] [CrossRef]
- Mylonas, N. Applications in Fuzzy Statistic and Approximate Reasoning. Ph.D. Thesis, Dimokritos University of Thrace, Komotini, Greece, 2022. [Google Scholar]
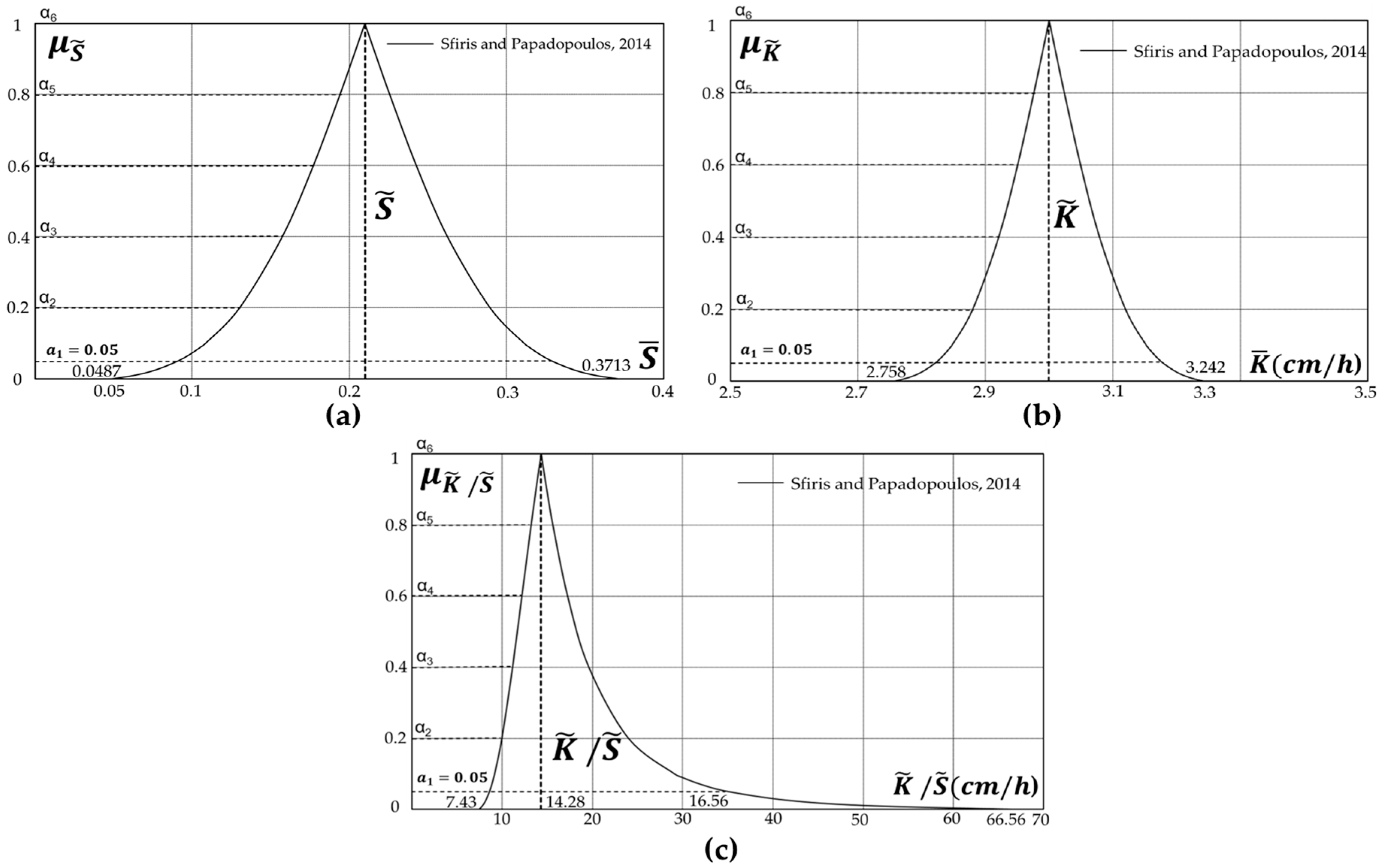
- Sfiris, D.S.; Papadopoulos, B.K. Non-Asymptotic Fuzzy Estimators Based on Confidence Intervals. Inf. Sci. 2014, 279, 446–459. [Google Scholar] [CrossRef]
- Tzimopoulos, C.; Papadopoulos, K.; Evangelides, C.; Papadopoulos, B. Fuzzy Solution to the Unconfined Aquifer Problem. Water 2018, 11, 54. [Google Scholar] [CrossRef]
- Domenico, P.A.; Schwartz, F.W. Physical and Chemical Hydrogeology, 2nd ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 1990. [Google Scholar]
- Aravin, V.I.; Numerov, S.N. Theory of Fluid Flow in Deformable Porous Media; Israel Program for Scientific Translation: Jerusalem, Israel, 1948. [Google Scholar]
- Samarinas, N.; Tzimopoulos, C.; Evangelides, C. Fuzzy Numerical Solution to Horizontal Infiltration. Int. J. Circuits Syst. Signal Process. 2018, 12, 326–332. [Google Scholar]
- Samarinas, N.; Tzimopoulos, C.; Evangelides, C. Fuzzy Numerical Solution to the Unconfined Aquifer Problem under the Boussinesq Equation. Water Supply 2021, 21, 3210–3224. [Google Scholar] [CrossRef]
| ORTH Fuzzy FEM | TRIAN Fuzzy FEM | Boussinesq | |||||||
|---|---|---|---|---|---|---|---|---|---|
| a/a | 0.48959 | 0.20000 | 0.12002 | 0.48959 | 0.20000 | 0.12002 | 0.48959 | 0.20000 | 0.12002 |
| 0.00 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| 0.05 | 0.13991 | 0.20232 | 0.23077 | 0.13991 | 0.20240 | 0.23077 | 0.14041 | 0.20311 | 0.23169 |
| 0.10 | 0.19702 | 0.28490 | 0.32496 | 0.19702 | 0.28501 | 0.32496 | 0.19729 | 0.28541 | 0.32555 |
| 0.15 | 0.23987 | 0.34686 | 0.39564 | 0.23987 | 0.34700 | 0.39564 | 0.23990 | 0.34703 | 0.39586 |
| 0.20 | 0.27500 | 0.39766 | 0.45358 | 0.27500 | 0.39781 | 0.45357 | 0.27482 | 0.39758 | 0.45349 |
| 0.25 | 0.30493 | 0.44094 | 0.50294 | 0.30493 | 0.44111 | 0.50294 | 0.30460 | 0.44068 | 0.50263 |
| 0.30 | 0.33095 | 0.47856 | 0.54585 | 0.33095 | 0.47875 | 0.54585 | 0.33052 | 0.47815 | 0.54541 |
| 0.35 | 0.35382 | 0.51164 | 0.58358 | 0.35382 | 0.51184 | 0.58358 | 0.35335 | 0.51113 | 0.58308 |
| 0.40 | 0.37405 | 0.54089 | 0.61695 | 0.37405 | 0.54110 | 0.61695 | 0.37358 | 0.54039 | 0.61645 |
| 0.45 | 0.39197 | 0.56681 | 0.64651 | 0.39197 | 0.56703 | 0.64651 | 0.39152 | 0.56639 | 0.64606 |
| 0.50 | 0.40783 | 0.58974 | 0.67266 | 0.40784 | 0.58997 | 0.67266 | 0.40742 | 0.58935 | 0.67230 |
| 0.55 | 0.42182 | 0.60996 | 0.69572 | 0.42182 | 0.61020 | 0.69572 | 0.42146 | 0.60968 | 0.69547 |
| 0.60 | 0.43406 | 0.62766 | 0.71591 | 0.43406 | 0.62790 | 0.71591 | 0.43376 | 0.62746 | 0.71576 |
| 0.65 | 0.44467 | 0.64300 | 0.73341 | 0.44467 | 0.64325 | 0.73341 | 0.44442 | 0.64288 | 0.73336 |
| 0.70 | 0.45373 | 0.65610 | 0.74835 | 0.45373 | 0.65635 | 0.74835 | 0.45353 | 0.65609 | 0.74838 |
| 0.75 | 0.46130 | 0.66705 | 0.76083 | 0.46130 | 0.66731 | 0.76083 | 0.46113 | 0.66708 | 0.76093 |
| 0.80 | 0.46744 | 0.67593 | 0.77096 | 0.46744 | 0.67619 | 0.77096 | 0.46729 | 0.67600 | 0.77109 |
| 0.85 | 0.47219 | 0.68279 | 0.77878 | 0.47219 | 0.68305 | 0.77878 | 0.47203 | 0.68285 | 0.77892 |
| 0.90 | 0.47556 | 0.68767 | 0.78435 | 0.47556 | 0.68793 | 0.78435 | 0.47539 | 0.68769 | 0.78446 |
| 0.95 | 0.47759 | 0.69060 | 0.78769 | 0.47759 | 0.69087 | 0.78769 | 0.47740 | 0.69059 | 0.78777 |
| 1.00 | 0.47772 | 0.69087 | 0.78804 | 0.47772 | 0.69113 | 0.78804 | 0.47806 | 0.69156 | 0.78887 |
| ORTH Fuzzy FEM | TRIAN Fuzzy FEM | Boussinesq | |||||||
|---|---|---|---|---|---|---|---|---|---|
| a/a | 0.97917 | 0.40000 | 0.24004 | 0.97917 | 0.40000 | 0.24004 | 0.97917 | 0.40000 | 0.24004 |
| 0.00 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| 0.05 | 0.09194 | 0.15466 | 0.19058 | 0.09194 | 0.15466 | 0.19058 | 0.09225 | 0.15523 | 0.19130 |
| 0.10 | 0.12947 | 0.21779 | 0.26836 | 0.12947 | 0.21779 | 0.26836 | 0.12963 | 0.21813 | 0.26880 |
| 0.15 | 0.15763 | 0.26515 | 0.32673 | 0.15763 | 0.26515 | 0.32673 | 0.15763 | 0.26522 | 0.32685 |
| 0.20 | 0.18071 | 0.30398 | 0.37457 | 0.18071 | 0.30399 | 0.37457 | 0.18057 | 0.30386 | 0.37444 |
| 0.25 | 0.20038 | 0.33707 | 0.41534 | 0.20038 | 0.33707 | 0.41534 | 0.20014 | 0.33680 | 0.41501 |
| 0.30 | 0.21748 | 0.36583 | 0.45078 | 0.21748 | 0.36583 | 0.45078 | 0.21717 | 0.36543 | 0.45033 |
| 0.35 | 0.23251 | 0.39112 | 0.48194 | 0.23251 | 0.39112 | 0.48194 | 0.23217 | 0.39064 | 0.48143 |
| 0.40 | 0.24581 | 0.41348 | 0.50949 | 0.24581 | 0.41348 | 0.50949 | 0.24546 | 0.41300 | 0.50898 |
| 0.45 | 0.25759 | 0.43329 | 0.53390 | 0.25759 | 0.43329 | 0.53390 | 0.25725 | 0.43288 | 0.53343 |
| 0.50 | 0.26801 | 0.45082 | 0.55551 | 0.26801 | 0.45082 | 0.55551 | 0.26770 | 0.45042 | 0.55510 |
| 0.55 | 0.27720 | 0.46628 | 0.57455 | 0.27720 | 0.46628 | 0.57455 | 0.27692 | 0.46596 | 0.57423 |
| 0.60 | 0.28524 | 0.47981 | 0.59122 | 0.28525 | 0.47981 | 0.59122 | 0.28501 | 0.47955 | 0.59099 |
| 0.65 | 0.29222 | 0.49154 | 0.60567 | 0.29222 | 0.49154 | 0.60567 | 0.29201 | 0.49133 | 0.60551 |
| 0.70 | 0.29817 | 0.50155 | 0.61801 | 0.29817 | 0.50155 | 0.61801 | 0.29799 | 0.50143 | 0.61792 |
| 0.75 | 0.30315 | 0.50992 | 0.62833 | 0.30315 | 0.50992 | 0.62833 | 0.30299 | 0.50983 | 0.62828 |
| 0.80 | 0.30719 | 0.51671 | 0.63669 | 0.30719 | 0.51671 | 0.63669 | 0.30704 | 0.51665 | 0.63667 |
| 0.85 | 0.31031 | 0.52196 | 0.64315 | 0.31031 | 0.52196 | 0.64315 | 0.31015 | 0.52188 | 0.64313 |
| 0.90 | 0.31253 | 0.52569 | 0.64775 | 0.31253 | 0.52569 | 0.64775 | 0.31236 | 0.52558 | 0.64771 |
| 0.95 | 0.31386 | 0.52793 | 0.65051 | 0.31386 | 0.52793 | 0.65051 | 0.31368 | 0.52780 | 0.65044 |
| 1.00 | 0.31392 | 0.52809 | 0.65075 | 0.31392 | 0.52809 | 0.65075 | 0.31411 | 0.52854 | 0.65134 |
| TRIAN Fuzzy FEM vs. Boussinesq | |||
|---|---|---|---|
| 0.0000011292 | 0.0000011775 | 0.0000011763 | |
| 0.0000012431 | 0.0000012289 | 0.0000011372 | |
| 0.0000013667 | 0.0000011672 | 0.0000011166 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzimopoulos, C.; Samarinas, N.; Papadopoulos, K.; Evangelides, C. Triangular Fuzzy Finite Element Solution for Drought Flow of Horizontal Unconfined Aquifers. Hydrology 2025, 12, 128. https://doi.org/10.3390/hydrology12060128
Tzimopoulos C, Samarinas N, Papadopoulos K, Evangelides C. Triangular Fuzzy Finite Element Solution for Drought Flow of Horizontal Unconfined Aquifers. Hydrology. 2025; 12(6):128. https://doi.org/10.3390/hydrology12060128
Chicago/Turabian StyleTzimopoulos, Christos, Nikiforos Samarinas, Kyriakos Papadopoulos, and Christos Evangelides. 2025. "Triangular Fuzzy Finite Element Solution for Drought Flow of Horizontal Unconfined Aquifers" Hydrology 12, no. 6: 128. https://doi.org/10.3390/hydrology12060128
APA StyleTzimopoulos, C., Samarinas, N., Papadopoulos, K., & Evangelides, C. (2025). Triangular Fuzzy Finite Element Solution for Drought Flow of Horizontal Unconfined Aquifers. Hydrology, 12(6), 128. https://doi.org/10.3390/hydrology12060128