Abstract
A concise model, utilizing the threshold values of closed depressions, the convergence index, and the leaf area index (LAI) that play a significant role in modeling vegetation–atmosphere interactions and understanding the impact of vegetation on the hydrological cycle, was employed to pinpoint potential aquifer recharge centroids. The LAI index served as a geographic mask, linking centroid locations to soil vegetation cover. Analyzing a paired subsample of 500 centroids for each strata (true and false), we observed that maximum values of true centroids, indicating potential groundwater recharge, correlated with the presence of abundant vegetation (0.074 < LAI < 0.639). Conversely, lower LAI values were associated with sparse vegetation in false centroids (0.01 < LAI < 0.590). The study’s findings hold promising implications for aquifer management, biodiversity conservation, hydric planning, and land use protection, making a substantial contribution to the field. The recharge hypothesis is theoretically sound and empirically supported to propose that areas of high topographic convergence and closed depressions are potential water recharge zones, and these locations may exhibit permanent or denser vegetation, reflected as higher LAI values. This happens because water accumulates or lingers in these zones, soil moisture is maintained more consistently, and plant roots access water for longer periods, even during dry seasons. Vegetation becomes more resilient and persistent (possibly even forming phreatophytes—plants accessing groundwater). Additionally, there is potential for expanding the research by incorporating field observations, including tracking the routes of surface and subsurface runoff and determining arrival times to the aquifer. Such studies are increasingly vital for addressing contemporary environmental and water resource challenges.
1. Introduction
Groundwater is stored in geological reservoirs (aquifers) made of rocks and deposits from different geological ages and types [1]. Aquifers consisting mainly of carbonate and evaporite rocks with unconsolidated sediments that originate from the deposition of geological material through weathering are referred to as karst aquifers [2,3]. A parsimonious model can be explained in essence as an explanatory model that forecasts on the basis of as few variables as possible. This indicates that the model being developed or used in the research is intentionally kept simple and straightforward. A parsimonious model typically includes only the most essential variables and parameters necessary to achieve the research objectives. The aim is to avoid unnecessary complexity while still obtaining meaningful results.
The systematic classification of geo relief, its components and associations, and its regional structuring is one of the prerequisites for understanding geoscientific systems in different temporal and spatial dimensions [4]. In this sense, it is a two-dimensional surface in three-dimensional space [5]. On the other hand, the geo-relief can be understood as the surface of a body formed by the near-surface subsurface, which the authors of [6] called a three-dimensional geomorphospheric complex. A useful tool in the interpretation of several properties of geo relief exhibited by natural networks results in a convergence index. In geomorphology, geo relief is understood as the interface between the lithosphere/pedosphere and the atmosphere/hydrosphere dimensions [4]. In any of its forms, water is a valuable resource for life and its use is vital for sustainable development. Affording assured water resources for agricultural and domestic activities is a seemingly tough task in areas of scarce water sources and uneven rainfall distribution [6,7]. The hydrogeological conditions of Chiapas are as varied and complex as its topography. The state’s geology, climate, and relief create a mosaic of surface water systems and groundwater regimes. Groundwater varies by region, with productive alluvial aquifers in the Central Depression, limited fractured-rock systems in the highlands, and complex karst aquifers in the north.
Groundwater is a renewable source and the most important hydric resource for the sustainability of current and future generations. It is the stabilizing factor of production chains, especially in areas with rainfall deficits and limited water storage infrastructure, and it is essential to improve socio-economic development in rural and urban areas. A report from UNESCO [8] stated that about 2.5 billion people around the world depend merely on groundwater sources in many activities, such as domestic use and industrial and agricultural purposes. The variability in groundwater recharge affects freshwater availability [9]. The spatiotemporal assessment of groundwater recharge is becoming a critical concern due to data scarcity in different climatic regions [10]. Recharging becomes effective if the infiltration is concentrated at a given time and space [11]. Groundwater recharge requires detailed assessments of scientific principles governing groundwater flow processes [12]. Groundwater recharge is focused in topographic depressions, which receive lateral inputs of snowmelt runoff in addition to vertical inputs of precipitation [13]. The growth in population and the corresponding increase in water demand will lead to much higher groundwater consumption [14], so aquifer sustainable management is mandatory.
The assessment of groundwater recharge (i.e., the downward movement that crosses the vadose zone and enters the saturated zone) is a key element of water resources management [15,16], but its response to extreme climate change has a large degree of uncertainty [17,18]. In most regions, rainfall events have been observed as randomness, with strong spatial variation in frequency and intensity. All of these could affect runoff and infiltration [19], and subsequently groundwater recharge. Previous studies on climate change impacts on groundwater recharge were mostly conducted in temperate regions [20,21,22], with a few exceptions in tropical regions—for example, in Mexico. Hence, there is a need to advance our understanding of climate change effects on groundwater recharge in tropical regions.
Groundwater recharge rate depends on several geological and climatic factors, including soil infiltration capacity, the porosity and permeability of the water-bearing geological formations, the spatial−temporal distribution, frequency and intensity of rainfall events, air and soil temperature, wind conditions prevailing in the area, and the composition of biotic communities. The spatial distribution of recharge is largely dependent on the balance between infiltration and evapotranspiration [13]. In humid regions, where precipitation exceeds potential evaporation, recharge can occur over wide areas within the landscape, and it is considered “direct” [23]. In contrast, in arid and semi-arid regions, where potential evaporation exceeds precipitation, recharge is restricted to localized areas [13]. In these areas, the lateral transfer of surface water increases infiltration in localized areas such as ephemeral ponds [24] and intermittent streams [25]. This mode of recharge is called “localized” or “focused” [26]. Focused recharge may occur in humid regions, but it is most dominant in arid and semi-arid regions. What is appreciated is that it may be associated with the geographic location of sites with geologic properties that facilitate the rate of aquifer recharge. The relevance of knowing the value of the rate of water recharge to the aquifer, can achieve a greater added value when associated with the coordinate pair of geological permeability properties, which would facilitate estimating how relevant the site is to facilitate the rate of aquifer recharge.
Enclosed topographic depressions can occur in virtually any lithology. These ground depressions are regarded as the most common landforms of karst in many landscapes. They can have varied genetic origins ranging from a single basic genetic process (dissolution) especially in the formation of dolines (or sinkholes, the smallest) in karst terrains because of the relative high solubility of carbonates, gypsum and evaporites [27] to a complex polygenetic origin. They range in diameter from centimeters, a few meters to hundreds of meters, exhibiting the well-known functions of storing runoff water, recharging soil moisture, shallow groundwater, and providing food and habitat for many organisms [28,29].
The kilometric-scale depressions as reported in [30], include inter alia, rift basins, volcanic fault depressions, fault depressions [31], large-scale playa lakes [32,33], salt weathering in desert environments [34], tectonic basins created by reverse faults [35], lithospheric flexural subsidence basins [36], intra-montane basins [37] and large poljes [38].
Closed depressions that are intermediate between dolines and solution pans are covered in [39]. Larger depressions are uvalas (coalescence of dolines) and poljes [40]. Collapse and subsidence are two other common processes in the formation of dolines [29]. Tiankengs are large collapse pits (giant collapse dolines) and their origin implies mechanical instability and the chemical removal of collapsed rock [41]. Collapse dolines [42] have the same origin but they are smaller in size. Potholes or entrance pits are usually formed by the collapse of cave roofs [43].
The convergence index is a terrain parameter which shows the structure of the relief as a set of convergent areas (channels) and divergent areas (ridges) [44]; it is a measure of how the flow in a cell diverges (convergence index in negative and positive values). It represents the agreement of aspect direction of the surrounding cells with the theoretical matrix direction. The convergence index is the mean (or weighted mean, if weights are used) aspect difference between real aspect and theoretical maximum divergent direction matrix representing the ideal peak. The convergence index is very useful for the analysis of lineaments, especially those represented by ridges or channel systems as well as a valley recognition tool.
The aim of this manuscript is to delineate potential aquifer recharge centroids by utilizing the degree of spatial organization within a convergence/divergence matrix, the closed depressions and vegetation expression. This approach allows us to predict the likely locations of aquifer recharge zones. The significance and potential impact of this study is also highlighted, as follows, (a) aquifer management: this research will provide valuable insights for aquifer management. Identifying potential recharge centroids can assist in optimizing the use and preservation of groundwater resources, which is crucial for sustainable water management. (b) Biodiversity conservation. Understanding the relationships between landscape features, such as closed depressions and aquifer recharge zones, can contribute to biodiversity conservation efforts. These findings may help protect ecosystems that depend on groundwater resources. (c) Hydric planning: the study has implications for hydric planning, particularly in regions where water resources are limited or subject to stress. Predicting aquifer recharge locations is essential for effective water resource planning. (d) Land use protection: the information provided can inform land use planning decisions. Identifying areas with high potential for aquifer recharge can influence land use policies to prevent activities that might compromise water quality or quantity. (e) Baseline information: this research establishes a baseline of critical information that can be used for various environmental and land management programs. This baseline is essential for future monitoring, assessment, and decision-making.
2. Materials and Methods
2.1. Description of the Study Area
The state of Chiapas, located in southeastern, Mexico, has some of the most varied and dramatic topographic relief in the country, ranging from sea level to volcanic peaks over 4000 m above sea level (masl) in the Northern Mountains and Sierra Madre de Chiapas. This relief contributes to its diverse ecosystems and climate expression (Figure 1).
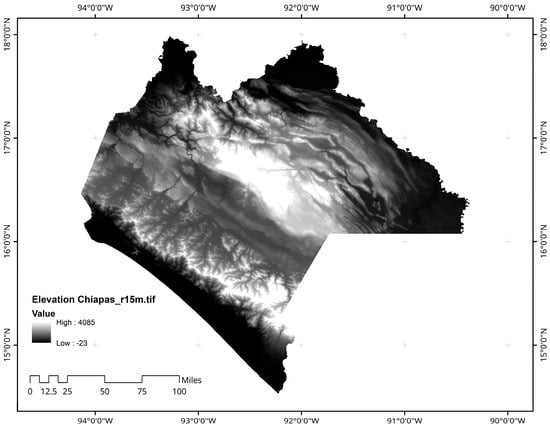
Figure 1.
Digital elevation model of the state of Chiapas [45].
Chiapas spans an area of 73,612 km2. Two major rivers, the Usumacinta and Grijalva, traverse the state, effectively dividing it into seven distinct biodiverse areas [46]. These areas exhibit variations in terms of climate, land quality, economic activities, and demographics. Chiapas is known for its diverse economy, influenced by its varied geography and natural resources. The state is a significant producer of hydroelectric energy, generating approximately 50% of Mexico’s hydroelectric power through seven dams: La Angostura, Malpaso, Peñitas, Chicoasén, Bombaná, Schoina, and José Cecilio Valle [47]. Agriculture plays a pivotal role in Chiapas, with the state being the leading producer of coffee and bananas in Mexico. It also ranks second in the production of papaya, mango, and cocoa, as well as third in tobacco production. Chiapas is the third-largest beef producer and the fourth-largest honey producer in Mexico.
Geographically situated in the tropical zone, Chiapas experiences a wide range of climates due to its orographic configuration. These climates vary from sub-humid temperate to warm humid, and the region receives rainfall throughout the year. Overall, Chiapas is a region of great ecological diversity and economic significance in Mexico. Its varied geography, coupled with its abundant natural resources, plays a crucial role in shaping its unique climatic conditions and supporting a wide range of economic activities, particularly in agriculture and energy production.
The geology of the State of Chiapas (Figure 2) has been described by several authors as consisting of a pre-Mesozoic metamorphic and sedimentary basement, a sequence of Mesozoic sedimentary rocks and a sequence of volcanic and Cenozoic sedimentary and igneous rocks [48]. The oldest of the pre-Mesozoic units are Proterozoic granites, diorites, and gneisses [49,50,51]. These units are covered by a sequence of sedimentary deposits, and metamorphic rocks (serpentinites, schists, quarzites and gneisses) [50,51,52]. These rocks are in turn intruded by gabbros, granodiorite, diorite and granite rocks of the Chiapas Batholith (or granitic Chiapas Massif), which outcrops mainly in the southwest portion of Chiapas [51]. The Mesozoic units are composed of a sequence of marine and continental clastic-carbonate deposits from Triassic–Jurassic to Upper Cretaceous in age. These deposits outcrop in the north-central part of the State forming steep mountains [52]. The Cenozoic sequence (Paleocene to Pliocene) rests on Mesozoic rocks and consists principally of igneous and sedimentary rocks. Rock permeability is delineated in Table 1.
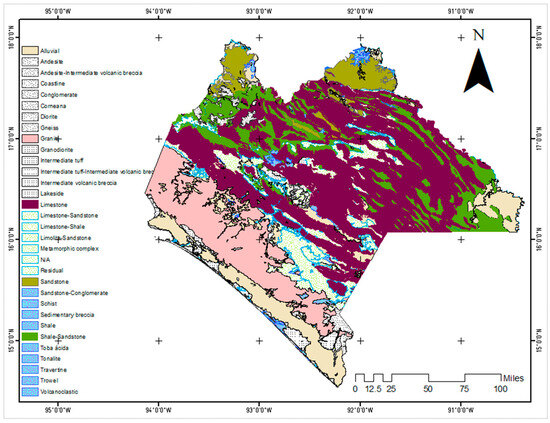
Figure 2.
The geologic map of the study area, classified by type.

Table 1.
The geology of rocks plays a crucial role in groundwater recharge. The ability of rocks to transmit water, known as permeability, is generally associated with facilitating groundwater recharge.
According with Figure 2, there are 32 types of geology that prevail. Classified by area (ha) with respect to the total area (7.26 Mha), limestone (37.13%), granite (14.67%), sandstone shale (12.95), alluvial (12.82%), sandstone-siltstone (6.09%), and sandstone (4.90%) dominate the geologic landscape. The rest of the strata represented on Figure 1 fulfil the remaining 11.43% of the total.
2.2. Topographic Indices and Leaf Area Index (LAI)
Groundwater potential recharge (GWPR) is highlighted as a crucial factor that supports various activities, including domestic, agriculture, and industrial activities [53]. It accomplishes this by allowing rainwater to infiltrate the ground, replenishing groundwater resources. This is a critical aspect of water resource management. The lithological (related to rock and soil types) and land use characteristics in the region under study are described as having low variability. This suggests that the geological and land use features in the area may be relatively uniform (Figure 2 and Figure 3). The closed depression index identifies pits or depressions in the terrain where water may accumulate but cannot drain out (i.e., they are surrounded by higher elevation). Closed depression features are usually considered to be primarily phenomena of the vadose zone [41]. With this constraint, deep air-filled depressions are only possible in regions with deep water tables. The horizontal transport system at the base of large collapse structures may be a free surface stream, but it could also be a conduit in the phreatic zone through model runoff retention, flood zones or temporary lakes. There exist water-filled closed depression features such as the cenotes of the Yucatan Peninsula in eastern Mexico, which may have originated as vadose zone features, before being flooded by post-Pleistocene sea level rise. An exceptional feature is Zacatón in Tamaulipas, Mexico [54]. The general use of the closed depression index is to detect sinks, potholes, or kettle holes.
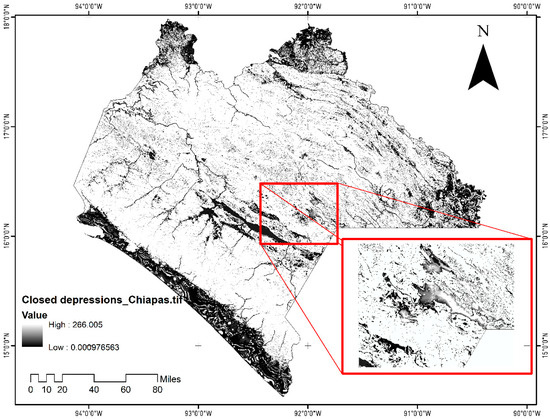
Figure 3.
The closed depressions within the study area. A closed depression is defined as an area surrounded by higher ground in all directions [30]. This geographical feature can have significant implications for water drainage and runoff patterns to improve hydrological modelling in a digital elevation model (DEM). The inset image is a close-up of the area.
From Figure 3, closed depressions in the landscape are typically areas where water can accumulate, often forming small ponds or wetlands. These depressions can serve as natural collection points for precipitation, allowing water to slowly infiltrate into the underlying aquifers and also to explode a vegetation patch. Understanding the geological characteristics of an area is essential for assessing its groundwater recharge potential. Geological surveys, hydrogeological studies, and the analysis of aquifer properties provide valuable insights into the role of rocks in groundwater recharge. Close depression maps are useful for evaluating geomorphological diversity and can be integrated into geomorphological maps as part of a geodiversity inventory [55]. Geodiversity assessments help in understanding the geological and geomorphological richness of a region. A commonly used form of the closed depression index is as follows:
where Zs = elevation of the lowest saddle or spill point surrounding the depression, stands for the elevation of the pit or lowest point inside the depression. This difference gives the depth of the depression before it can overflow. In some GIS-based implementations, CDI is computed over raster cells, and a threshold is used to filter out insignificant depressions (e.g., noise due to DEM resolution). To secure the representativeness of CDI index, the domain was “filled” using the Planchon–Darboux fill algorithm. The method applied is based on a radically different approach that first adds a thick layer of water over all the DEM and then drains excess water [56].
The convergence index (CI) also known as topographic wetness index (TWI) in certain contexts, is slightly different (Figure 4). The CI is designed to quantify how much terrain converges or diverges at a specific point—i.e., how likely it is for water to accumulate or disperse there. A high convergence stands for valleys, channels, and potential flow accumulation zones, whilst low or negative convergence represent ridges, hilltops, or dispersal zones. A general form of CI is as follows:
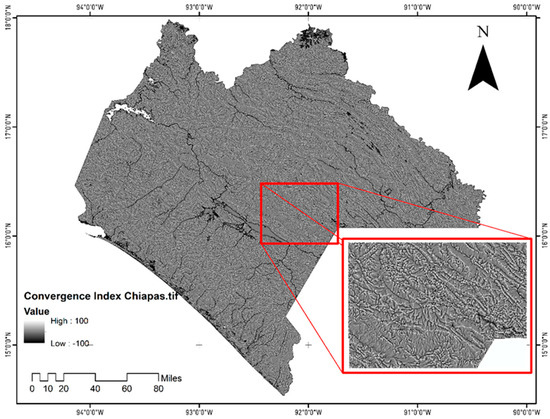
Figure 4.
This figure displays the convergence/divergence index within the study area. The convergence index value indicates the direction of surface runoff. According to [53], different values on the convergence index represent various runoff scenarios. (a) Peak (convergence index value = 100). This suggests a high level of convergence in surface runoff. (b) Slope of uniform exposure (convergence index value = 0). This indicates a situation where surface runoff is uniform and not strongly converging or diverging. (c) The deepest point of the depression outflow (convergence index value = −100). This signifies a situation where surface runoff is directed toward the deepest point within a depression. The inset image is a close-up of the area.
This is effectively the Laplacian of the elevation field z, representing the second spatial derivative. In essence, it measures curvature: whether a surface is bowl-shaped (positive convergence) or dome-shaped (negative convergence).
The convergence index is a measure that indicates how surface water flows or converges within a particular area. A high convergence index suggests that water is likely to flow toward a central point, which can be indicative of potential recharge areas.
The LAI is a dimensionless quantity that represents the leaf surface area per unit ground area.
It is a strong proxy for vegetation density, transpiration, biomass, and photosynthetic activity. High LAI values suggest lush, dense vegetation; low values suggest sparse or seasonal vegetation. LAI is defined as the one-sided green leaf area per unit ground area in broadleaf canopies and as one-half the total needle surface area per unit ground area in coniferous canopies [57]. According to [58], the LAI values range between 0.0 (bare land, ploughed fields, urban areas, and rock) and about 0.8 (deciduous/mixed forest). For biotic studies, the combination of LAI and the fraction of photosynthetic active radiation (fPAR; 400–700 nm) absorbed by the green elements of a vegetation canopy [59] is relevant and, in theory, its values maximize the presence of vegetation patches which coincide with runoff convergence points.
2.3. Model’s Parameters
QGIS (v. 3.30.3-‘s-Hertogenbosch), is a widely used open-source geographic information system (GIS) software that is valuable for geospatial data analysis and mapping. The raster calculator tool in QGIS allows users to perform mathematical operations on raster data, making it a valuable tool for spatial analysis and modeling. The model’s expression follows the SQL (structured query language). This suggests that SQL-like queries or expressions are being used to manipulate and analyze spatial data in the GIS environment. Four specific models are being used, and they are based on different combinations of minimum and maximum threshold values for closed depressions and the convergence index. These models likely serve different analytical purposes or scenarios. The technical approach involves using a script, which is likely a mathematical or algorithmic representation of the models. Threshold values for closed depressions and the convergence index are provided in Table 2.

Table 2.
These thresholds likely determine the criteria for feature selection or classifying data in the models. Cells that meet these pre-defined criteria may unveil the presence of spatial patterns.
The structure likely contains the mathematical expression SQL used in the models, which specify how the model’s parameters are named. Threshold, also known as a threshold (cutoff), is the value used as a reference for the selected feature. The choice of threshold values is crucial and can significantly affect output results. Sensitivity analysis by varying the thresholds can provide insights into the robustness of our results.
2.4. Model Outputs
A graphical summary–research process to locate the centroids of potential recharge points is presented in Figure 5.
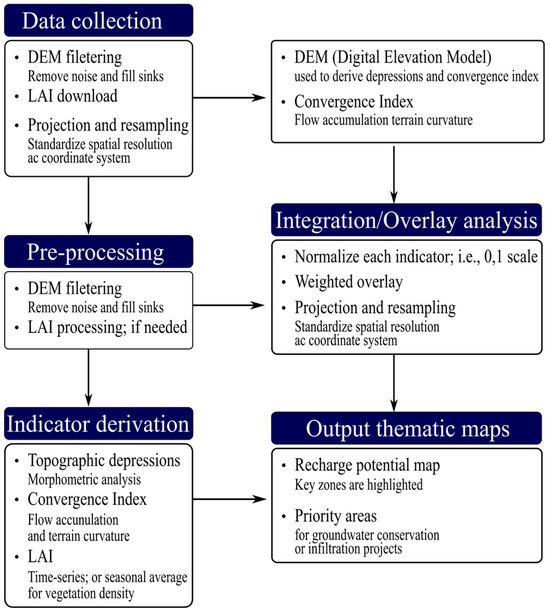
Figure 5.
Graphical summary to obtain potential recharge points for groundwater conservation or infiltration projects. The arrows in the flowchart represent process direction, logical dependency, or data flow. DEM filtering → means that closed depressions and convergence index was extracted from the Digital Elevation Model (DEM) using topographic algorithms (e.g., depression filling or pit detection). DEM → Flow Direction/Convergence Index, indicates that flow accumulation and direction are computed from the DEM to derive the convergence index, showing where water is likely to accumulate. Satellite Imagery → LAI, shows the derivation of the Leaf Area Index. LAI represents vegetative canopy density and indirectly, water availability. Depressions + Convergence Index → Potential Recharge Zones (Terrain-Based), suggests a combination of topographic variables (depressions and convergence) to identify areas of high surface water retention potential. Output thematic maps → Recharge potential map and priority areas. The last arrow leads to the generation of a spatially explicit map, integrating all three indicators to highlight priority zones.
3. Results
The outputs of the proposed models are thematic maps in TIFF format. These thematic maps are binary, containing values of either 0 or 1. A value of 0 indicates a “false” model output. This means that the pixel or location in the map does not meet the specified conditions or criteria set by the model. A value of 1 indicates a “true” model output. In this case, the pixel or location on the map satisfies the conditions or criteria defined by the model. This approach is common in spatial analysis to delineate areas of interest or significance based on specified criteria.
The results of the four models indicate variations in the presence of false (0 s) and true values (1 s). Models 2, 3, and 4 dropped all false values, meaning that they did not classify any pixels as meeting the model criteria. Model 1, on the other hand, yielded both false and positive results. It included the largest closed depressions and the peak concentration of surface runoff. The total number of pixels where the models were run was 1,733,076. Of this total, the output of Model 1 was 13,848 centroids (Figure 6).
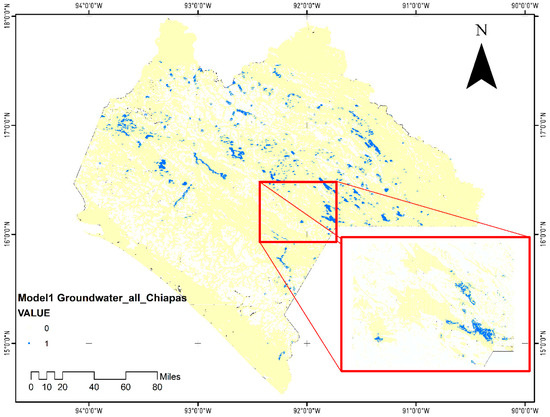
Figure 6.
The model output, where yellow pixels represent zeros (false), and blue pixels represent true values. The inner black lines on the map represent water bodies, indicating the presence of water features within the study area. The inset image is a close-up of the area.
The thematic map depicted in Figure 6 serves two main purposes. (1) Evaluation of geomorphological diversity; the map represents the closed depressions, which are a key component of geomorphological diversity and geodiversity [30]. Geodiversity is the diversity of geological and geomorphological features within an area. (2) Surface runoff location; this also indicates where surface runoff coincides with the presence of closed depressions.
3.1. Model Clarification Conditions
The clarification conditions of the model pertain to the explicit criteria or rules employed by the proposed models to decide whether a pixel or cell on the output map should be assigned a value of 1 (true) or 0 (false). Integrating LAI with CI and CDI, which stand for: identifying areas of potential water accumulation due to terrain-driven flow (CI), identifying isolated pits where water may collect and stagnate (no outlet; CDI). In essence, mapping hydrological sinks or convergence zones. These areas are, by nature, more hydrologically favorable—they are more likely to retain water, leading to higher soil moisture, particularly in semi-arid or seasonally dry environments. These conditions hinge on the amalgamation of threshold values for closed depressions and the convergence index, as previously discussed. The LAI was incorporated into the analysis to associate the coordinate data of the centroids with the condition of the soil cover vegetation. The serial database of 241 days (1 January 2023 to 30 August 2023) was generated. The origin of this index is the MODIS product MCD15A2H v006. The MCD15A2H Level 4, is an 8-day composite dataset with 500 m pixel size [58]. The algorithm chooses the best pixel available from all the acquisitions of both MODIS sensors located on NASA’s Terra and Aqua satellites from within the 8-day period.
To analyze the patterns within the dataset, we partitioned the entire dataset into consistent samples of 500 elements for both false and true centroids, as illustrated in Figure 5. While the sample size may not have been determined for statistical representativeness, our assumption was that all centroids adhered to the categorization generated by Model 1. Subsequently, we computed overall statistics, encompassing minimum, maximum, and average values, based on this subset of data.
3.2. Random Selection Points
Associating the outcomes of Model 1, both true and false values, with the LAI is pertinent. We can presume that the LAI is correlated with soil moisture concentration and soil vegetation cover. The thematic map of the 500 records subsampled of each condition is presented in Figure 7.
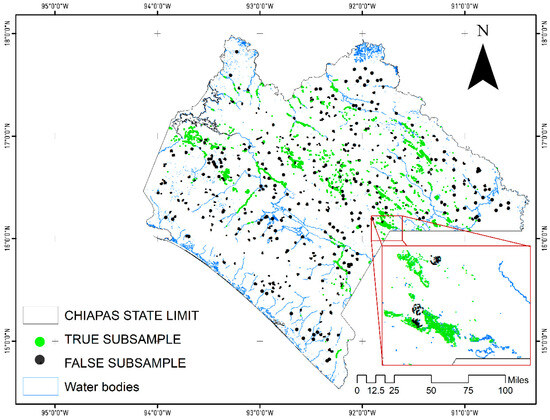
Figure 7.
Subsample selection points. The subsample is proportional to both strata, it accounts for variability within false and true centroids; it was obtained through randomness to avoid introducing bias. The inset image is a close-up of the area.
Figure 7 illustrates the selection points for the subsample. This subsample is proportionate to both strata, capturing variability within false and true centroids. It was generated randomly to prevent the introduction of bias, and the distribution of water bodies was considered in the process. Although there is not a specific number ensuring the subsample’s representativeness, given the exploratory nature of this manuscript, this sample size is deemed adequate. As depicted in Figure 6, a significant portion of false coordinate pairs are situated at a distance from water bodies. In contrast, true centroids are predominantly located on or very close to bodies of water
In Table 3, a snapshot of the statistical data is presented.

Table 3.
Statistics are associated with the LAI index, including minimum, maximum, and average values from the subsampled data.
From Table 3, the first six strata, which are those that occupy the largest geographic area, are located in the upper rows of the table. It is also worth noting that geologic strata of smaller geographic coverage (i.e., andesite, sandstone conglomerate, metamorphic complex, shale, granodiorite and lake) did not correspond to the true output of the model, but only to the false one (“NO DATA”). It is important to highlight the differences between the centroids that met the model specifications and those that did not (Figure 8) in the context of vegetation cover. The comparison between false/true centroids for LAI is represented in Figure 9.
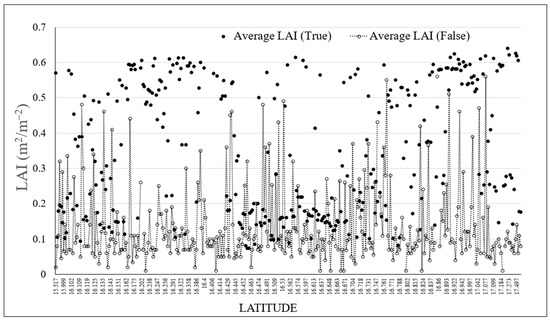
Figure 8.
Comparison of the average value of leaf area index according to the implementation of Model 1.
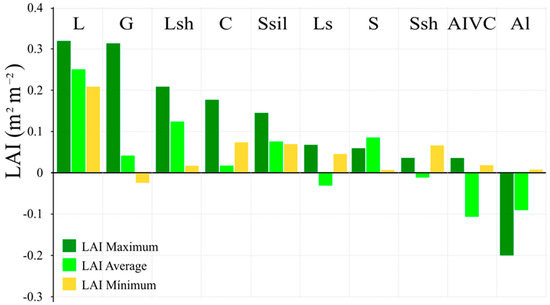
Figure 9.
Estimated differences in the relationship LAI/geologic strata between false and true centroids on a sample of 1000 centroids (500 each). Negative differences stand for higher plant cover in false centroids.
In Figure 8, the contrast between the true and false centroids is evident. Of the sample centroids (397), 79% resulted in average minimum and maximum values with a positive difference; that is, for the true centroids, the minimum average of the data series was 0.074 and the maximum 0.639. On the other hand, in the set of false centroids (107), the minimum and maximum values were between 0.01 and 0.59, respectively. A comparison of the differences in LAI between minimum, maximum and mean by geologic strata is presented in Figure 9.
From Figure 9, the most conspicuous correlation between geologic strata and plant coverage manifested in the LAI:L stratum. Notably, all significant disparities in the minimum, average, and maximum values of LAI between true and false centroids were evident for the L substrate (0.21, 0.25, and 0.32, respectively).
4. Discussion
The recharge hypothesis is theoretically sound and empirically supported to propose that areas of high topographic convergence and closed depressions are potential water recharge zones, and these locations may exhibit permanent or denser vegetation, reflected as higher LAI values. This happens because water accumulates or lingers in these zones, soil moisture is maintained more consistently, and plant roots access water for longer periods, even during dry seasons. Vegetation becomes more resilient and persistent (possibly even forming phreatophytes—plants accessing groundwater). The permeability properties of parent material is quite contrasting. According to [60], the parent material plays a major role in the development of a soil and its physical and chemical properties. Limestone materials have a particularly significant influence on soil morphology, which is because of their high base saturation and calcium content, their tendency to produce alkaline soils, and their solubility in weak acids (ibidem). Despite the evidence of this relationship, we are well aware that due to the exploratory nature of this manuscript, and the subsample data, it is not feasible to reach a conclusion to support the claim that vegetation cover and permeability properties are fully related, as it would be necessary to perform complementary studies with ground measuring devices. Geology and lithology may control the long-term recharge pathways (e.g., fractured basalts or karst vs. clay), essential for understanding deep infiltration and aquifer structure. However, they do not indicate where the water enters the ground. Other indices like the topographic water index (TWI), the soil hydraulic conductivity/permeability index (SHC/P), and the geology/lithology index (G/L) are easier to compute, to predict the vertical water movement toward the aquifer, and control long-term recharge pathways. However, the TWI index is useful for runoff concentration, but weak in reflecting actual infiltration/recharge unless used in conjunction with soil and land cover data. The SHC/P index must be interpreted spatially and contextually (e.g., soil compaction from agriculture may not be reflected in soil maps). And the G/L index is foundational, especially for regional-scale studies, but needs to be combined with surface and soil indicators for local accuracy.
Karst limestone aquifers exhibit hydrological and hydrochemical heterogeneity, with common point source recharge occurring through sinkholes and fissures [61]. The observed heterogeneity in pinpointing GWPRs prompts the exploration of additional research questions. Beyond discerning their locations, researchers could delve into inquiries related to field methods for mapping both surface and subsurface runoff, thereby evaluating potential charge points and employing quantitative field methods to trace the route of subsurface runoff. While this perspective extends beyond the objectives of the current manuscript, it opens up a spectrum of options for future exploration. Based on the parsimonious nature of this study, using minimum, maximum, and average data to characterize a large dataset can provide some valuable insights, but the validity of this approach is tight on the goals of the study and characteristics of any particular analysis. In Ref. [62], the authors suggest that the minimum, maximum, and average values can help provide a high-level overview of the data’s distribution and central tendency. A general overview or the making of high-level comparisons, or summary statistics can be valid. However, if you need to make precise predictions or detailed inferences, you might need more advanced statistical methods.
They are particularly useful for identifying outliers, understanding data ranges, and getting a sense of the overall data patterns. However, using only these summary statistics can result in a loss of detailed information. They condense a potentially complex dataset into a few values, which might not capture nuances or variations within the data. For some analyses, this loss of detail might be acceptable, while for others, it could be a significant limitation.
Another noteworthy relationship was observed in the LAI:G substrate (−0.03, 0.04, 0.31) and LAI:Al (−0.09, 0.01, −0.20, respectively). Notably, the correlation between LAI and Al is particularly contrasting. Firstly, alluvial soils are sedimentary deposits formed by sand, silt, clay, and gravel transported to natural watercourses, a composition that is not ideal for sustaining plant communities. Secondly, as highlighted by [63], alluvial soils, despite being highly productive, are often covered with tall grasses and forest species, serving as locations for agricultural areas. Our results depict this substrate with negative differences in maximum and average parameters. In this context, alluvial sites exhibit reduced vegetation in response to the true centroids in the model parameters. However, it is essential to note that this observed condition extends beyond the scope of this manuscript, presenting an opportunity for posing new research questions. The LAI integrates vegetation density and type, which strongly influence interception losses, evapotranspiration, and soil structure through root systems, also indirectly reflecting land cover condition, management practices, and soil health.
This manuscript delves into two primary aspects of GWPR. Firstly, it explores the influence of abundant plant cover and the coinciding location of centroids where two topographic indices intersect. Vegetation influences rainfall distribution by means of throughfall and stemflow pathways [64], increases the infiltration capacity of a soil [65] and modifies soil structure [66], which commonly result in a runoff reduction. At this point, the permeability of geological formations emerges as a crucial factor in groundwater dynamics, and it appears to be associated with plant cover. On one hand, permeability determines the speed of water movement through the subsurface, impacting aquifer recharge. As observed in connection with the LAI index, this seems to indicate pronounced differences in plant cover. However, these differences are notably conspicuous in three strata within the study region: LAI:L, LAI:G, and LAI:Al. Limestone, often characterized by high permeability due to the formation of solution channels and fractures, facilitates rapid downward water movement to the aquifer, ensuring a high availability of surface water. In contrast, granite, being an igneous rock with generally low porosity and permeability, is less conducive to swift groundwater recharge. Alluvial deposits, comprising materials like gravel, sand, and silt transported by rivers, are often considered highly permeable, allowing for substantial and relatively swift groundwater recharge. However, our evidence suggests the contrary, indicating that true centroids lack robust vegetation cover. Shale, characterized by its fine-grained nature, is generally less permeable, impeding water movement. Nevertheless, the presence of fractures can enhance permeability. Conglomerate, a sedimentary rock formed from rounded or angular clasts cemented together, exhibits variable permeability. Well-cemented conglomerate may have lower permeability, while less-cemented formations with spaces between clasts could be more permeable. Andesite, an intermediate volcanic rock, demonstrates permeability influenced by factors like porosity, vesicularity (presence of gas bubbles), and degree of alteration. Generally, volcanic rocks like andesite have moderate permeability. Metamorphic rocks, resulting from the alteration of pre-existing rocks under high pressure and temperature, exhibit varying permeability influenced by factors such as the original rock type, degree of metamorphism, and presence of fractures or foliation. Granodiorite, an intrusive igneous rock, and igneous rocks, in general, tend to have lower permeability compared to some sedimentary and volcanic rocks. However, the presence of fractures or other structural features can significantly influence permeability. Critically examined, the integrated proposal of convergence index, closed depression index and LAI locates zones of water concentration, identifies microtopographic zones where water can accumulate and linger, and reflects vegetative cover expression and surface–soil interaction potential.
By combining in a concise model the data of zones of water concentration (closed depressions), zones where water can accumulate and linger (convergence index), and permanent vegetative cover, the potential locations can be found where the topographic relief is favorable for mapping the GWPR. These areas are likely to receive and retain water, allowing it to percolate into the aquifer below. This approach is valuable for aquifer management, as it helps pinpoint areas where natural recharge processes are active. It can guide decisions related to land use, water resource management, and conservation efforts to protect these critical recharge zones.
Despite the reduced number of input variables, the tested Model 1 effectively located areas within the geographic space that are likely to be of high relevance for aquifer recharge. The recharge rate is less sensitive to fluctuations in coarse soil [58]. Recharge rates vary considerably with small changes in fine soil, suggesting that soil texture plays a much bigger role in the recharge (ibidem). Ref. [67] found that soil texture causes slightly larger variations in recharge than land cover, and that the recharge decreases considerably in fine soil for all land cover types. Here are some key points to consider based on this finding. (1) The fact that the model output exhibits spatial congruence with the location of water bodies is significant. It suggests that Model 1 is capturing meaningful patterns and relationships within the landscape. This spatial congruence reinforces the credibility of the model’s predictions. (2) The recharge process is influenced by a multitude of factors, including vegetation, soil properties (chemical and physical), evapotranspiration rate, rainfall events, and many more. While the proposed Model 1 is parsimonious, it is essential to recognize the complexity of the recharge processes. Future research can explore the integration of additional variables to account for these complexities to add robustness to the model. (3) Identifying connected sinkholes on the map is a valuable insight. Sinkholes can indeed serve as important pathways for water to rapidly enter aquifers. Understanding the dynamics of conduit systems within the aquifer is crucial for assessing recharge rates and residence times. (4) The areas highlighted as potential recharge centroids have hydrogeological significance. They represent locations where water is likely to enter the aquifer, which is vital information for groundwater resource management and protection. (5) Briefly, we mention the potential for rapid transport and removal of water in conduit systems, leading to short residence times. This underscores the need for further research to not only identify recharge areas but also understand the dynamics of water movement within aquifers.
Posing New Research Questions
Studies focusing on GWPR are highly relevant, not only for their contributions to understanding hydrological processes but also for the valuable geomorphological information they provide. This research has the potential for continued improvement and expansion. By refining the proposed models, incorporating additional variables, and collaborating with experts to enhance its accuracy, the applicability of these findings in the field of aquifer recharge prediction and management might sound attractive. The definition of threshold values for the CD and CI indices and the insights gained from Model 1 is a valuable approach. It is clear that this research has the potential for further development and enhancement. However, before fully jumping to conclusions, soil type matters, human land use too, vegetation type, and depression size and depth. Some soils retain water better, irrigation or land use management can distort the signal, and some plants thrive in dry conditions with lower LAI. Here are some key points to consider for future studies:
- Defining threshold values for topographic indices was an essential step in this research. Further refinement of these thresholds can lead to more accurate identification of potential aquifer recharge zones. By refining the strata rank, we can explore different threshold values to optimize the model’s performance.
- As mentioned before, expanding the number of classes can provide a more detailed and nuanced understanding of potential recharge areas. This can help differentiate between various degrees of suitability for recharge and can be particularly useful for land management decisions.
- Adding new variables, such as soil moisture values and evapotranspiration, could enrich the analysis. The ET losses generally increase with increasing LAI across the whole soil textural gradient [58], and in combination with the soil moisture data, they can provide valuable information about the ecosystem’s capacity to facilitate groundwater recharge. Researchers have to consider how these variables interact with topographic indices.
- Improving the accuracy of location identification and the spatial distribution of potential recharge areas is a commendable goal. Fine-tuning of Model 1 and incorporating additional data could contribute to achieving this objective.
- It is necessary to validate and calibrate Model 1 using field data and observations. This step could help to ensure that the model’s predictions align with real-world conditions.
- Collaborating with experts from related fields, such as hydrology, ecology, and geology, would provide valuable insights and data sources to strengthen this research.
- The relevance of long-term monitoring to assess the actual effectiveness of identified recharge areas over time. This study can provide critical information for aquifer management and conservation efforts.
5. Conclusions
The combination of convergence, depressions and LAI indices is more dynamic, responsive to terrain conditions, and operationally useful, especially in data-scarce or arid and semi-arid environments.
It would be reasonable to infer that high CI and CDI areas, which represent water accumulation or recharge zones, might correlate with regions of permanent or dense vegetation (high LAI). The presence of such vegetation could indicate that these areas have a consistent water supply, possibly due to groundwater recharge, and would form stable ecological niches. This interplay may be a crucial piece in understanding how landscapes manage water flow and vegetation growth, with LAI helping to map the extent of permanent vegetation in these hydrologically significant zones. The visual expression of permanent vegetation in these areas, if verified, would align with the theory of them being recharge points for the water table. The proposed model, based on CD, CI, and LAI indices, demonstrates the capability to pinpoint potential groundwater recharge areas, presenting a significant contribution to hydrogeology and aquifer management, and reflects the ground-level hydrological reality better than using deep or static variables like geology on their own, especially for mapping entry points or recharge hotspots on the surface.
Our future research endeavors involve enhancing the model’s complexity by incorporating additional variables and collaborating with experts in relevant fields to achieve a more comprehensive understanding of the intricacies of aquifer recharge processes. Historically, accessing and analyzing such information posed limitations, but recent strides in computing resources and advancements in ecosystem interface computing environments have opened new avenues.
The LAI was of great help in documenting the fundamental relationship between vegetation cover and geologic strata. We found evidence of two relevant associations between vegetation cover and geologic substrate—specifically, limestone (L) and alluvial (Al). As documented in numerous research papers, L strata exhibit notable permeable properties that may foster the expansion or, at the very least, stability in vegetation cover.
Contrary to L strata, the Al strata might potentially promote more dense vegetation, but this property was not evident in our study, as it lies far beyond the goals of this manuscript.
Author Contributions
Conceptualization, R.-M.V.M.; methodology, R.-M.V.M.; software, R.-M.V.M.; validation, R.-M.V.M. and K.T.G.; formal analysis, R.-M.V.M.; investigation, R.-M.V.M.; resources, R.-M.V.M. and K.T.G.; data curation, R.-M.V.M.; writing—original draft preparation, R.-M.V.M.; writing—review and editing, R.-M.V.M. and K.T.G.; visualization, R.-M.V.M.; supervision, R.-M.V.M.; project administration, R.-M.V.M.; funding acquisition, R.-M.V.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data is available upon request.
Acknowledgments
The authors agree to express in writing their gratitude and appreciation for the institutional support provided by the National Institute of Forestry, Agricultural and Livestock Research (INIFAP; Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias) through the National Laboratory of Modeling and Remote Sensing (Laboratorio Nacional de Modelaje y Sensores Remotos), for the completion of this manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Perry, E.; Velazquez-Oliman, G.; Marin, L. The Hydrogeochemistry of the Karst Aquifer System of the Northern Yucatan Peninsula, Mexico. Int. Geol. Rev. 2002, 44, 191–221. [Google Scholar] [CrossRef]
- Escolero, O.; Marín, L.E.; Steinich, B.; Pacheco, J.A.; Molina-Maldonado, A.; Anzaldo, J.M. Geochemistry of the hydrogeological reserve of Mérida, Yucatán, Mexico. Geofísica Int. 2005, 44, 301–314. [Google Scholar] [CrossRef]
- Dikau, R.; Schmidt, J. Georeliefklassifikation. In Angewandte Landschaftsökologie; Schneider-Sliwa, R., Gerold, G., Schaub, D., Eds.; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar] [CrossRef]
- Fränzle, O. Physische Geographie als quantitative Landschaftsforschung; Schriften des Geographischen Institutes der Universität Kiel: Kiel, Germany, 1971; Volume 37, pp. 297–312. [Google Scholar]
- Kugler, H. Das Georelief und Seine Kartographische Modellierung. Master’s Thesis, Martin-Luther-Universität Halle-Wittenberg, Halle, Germany, 1974. [Google Scholar]
- Prabhakar, A.; Tiwari, H. Land use and land cover effect on groundwater storage. Model. Earth Syst. Environ. 2015, 1, 45. [Google Scholar] [CrossRef]
- UNESCO World Water Assessment Programme. Facts and Figures; from the United Nations World Water Development Report 4: Managing Water Under Uncertainty and Risk. UNESDOC Digital Library. Available online: https://unesdoc.unesco.org/ark:/48223/pf0000215492 (accessed on 18 May 2025).
- Dile, Y.T.; Tekleab, S.; Ayana, E.K.; Gebrehiwot, S.G.; Worqlul, A.W.; Bayabil, H.K.; Yimam, Y.T.; Tilahun, S.A.; Daggupati, P.; Karlberg, L.; et al. Advances in water resources research in the Upper Blue Nile basin and the way forward: A review. J. Hydrol. 2018, 560, 407–423. [Google Scholar] [CrossRef]
- Chung, I.-M.; Sophocleous, M.A.; Mitiku, D.B.; Kim, N.W. Estimating groundwater recharge in the humid and semi-arid African regions. Geosci. J. 2016, 20, 731–744. [Google Scholar] [CrossRef]
- Nimmo, J.; Stonestrom, D.A.; Healy, R.W. Aquifers: Recharge. In Fresh Water and Watersheds, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2020; pp. 11–15. [Google Scholar]
- Kebede, S. Groundwater in Ethiopia; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-30390-6. [Google Scholar]
- Negm, A.; Abdrakhimova, P.; Hayashi, M.; Rasouli, K. Effects of climate change on depression-focused groundwater recharge in the Canadian Prairies. Vadose Zone J. 2021, 20, e20153. [Google Scholar] [CrossRef]
- Sherif, M.; Sefelnasr, A.; Al Rashed, M.; Alshamsi, D.; Zaidi, F.K.; Alghafli, K.; Baig, F.; Al-Turbak, A.; Alfaifi, H.; Loni Allfouza, O.; et al. A Review of Managed Aquifer Recharge Potential in the Middle East and North Africa Region with Examples from the Kingdom of Saudi Arabia and the United Arab Emirates. Water 2023, 15, 742. [Google Scholar] [CrossRef]
- Pierce, S.A.; Sharp, J.M.; Guillaume, J.H.A.; Mace, R.E.; Eaton, D.J. Aquifer-yield continuum as a guide and typology for science-based groundwater management. Hydrogeol. J. 2013, 21, 331–340. [Google Scholar] [CrossRef]
- Zhou, Y. A critical review of groundwater budget myth, safe yield and sustainability. J. Hydrol. 2009, 370, 207–213. [Google Scholar] [CrossRef]
- Green, T.R.; Taniguchi, M.; Kooi, H.; Gurdak, J.J.; Allen, D.M.; Hiscock, K.M.; Treidel, H.; Aureli, A. Beneath the surface of global change: Impacts of climate change on groundwater. J. Hydrol. 2011, 405, 532–560. [Google Scholar] [CrossRef]
- Holman, I.P. Climate change impacts on groundwater recharge-uncertainty, shortcomings, and the way forward? Hydrogeol. J. 2006, 14, 37–647. [Google Scholar] [CrossRef]
- Sutinen, R.; Hänninen, P.; Venäläinen, A. Effect of mild winter events on soil water content beneath snowpack. Cold Reg. Sci. Technol. 2008, 51, 56–67. [Google Scholar] [CrossRef]
- Crosbie, R.S.; Scanlon, B.R.; Mpelasoka, F.S.; Reedy, R.C.; Gates, J.B.; Zhang, L. Potential climate change effects on groundwater recharge in the High Plains Aquifer, USA. Water Resour. Res. 2013, 49, 3936–3951. [Google Scholar] [CrossRef]
- Eckhardt, K.; Ulbrich, U. Potential impacts of climate change on groundwater recharge and streamflow in a central European low mountain range. J. Hydrol. 2003, 284, 244–252. [Google Scholar] [CrossRef]
- Jyrkama, M.I.; Sykes, J.F. The impact of climate change on spatially varying groundwater recharge in the Grand River watershed. J. Hydrol. 2007, 338, 237–250. [Google Scholar] [CrossRef]
- de Vries, J.J.; Simmers, I. Groundwater recharge: An overview of processes and challenges. Hydrogeol. J. 2002, 10, 5–17. [Google Scholar] [CrossRef]
- Greenwood, W.J.; Buttle, J.M. Land cover controls on depression-focused recharge on the Oak Ridges Moraine, southern Ontario. Canada. Hydrol. Process. 2018, 32, 1909–1926. [Google Scholar] [CrossRef]
- Izbicki, J.A.; Radyk, J.; Michel, R.L. Water movement through a thick unsaturated zone underlying an intermittent stream in the western Mojave Desert, southern California, USA. J. Hydrol. 2000, 238, 194–217. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Keese, K.E.; Flint, A.L.; Flint, L.E.; Gaye, C.B.; Edmunds, W.M.; Simmers, I. Global synthesis of groundwater recharge in semiarid and arid regions. Hydrol. Process. 2006, 20, 3335–3370. [Google Scholar] [CrossRef]
- Ford, D.; Williams, P. Karst Hydrogeology and Geomorphology; John Wiley & Sons: Hoboken, NJ, USA, 2007; 562p. [Google Scholar]
- Abdelkareem, M.; El-Baz, F. Analyses of optical images and radar data reveal structural features and predict groundwater accumulations in the central Eastern Desert of Egypt. Arab. J. Geosci. 2015, 8, 2653–2666. [Google Scholar] [CrossRef]
- Hayashi, M.; van Der Kamp, G.; Schmidt, R. Focused infiltration of snowmelt water in partially frozen soil under small depressions. J. Hydrol. 2003, 270, 214–229. [Google Scholar] [CrossRef]
- Pardo-Igúzquiza, E.; Dowd, P.A. Fractal analysis of karst landscapes. Math. Geosci. 2020, 52, 543–563. [Google Scholar] [CrossRef]
- Wang, D.; Shu, L. Late Mesozoic basin and range tectonics and related magmatism in Southeast China. Geosci. Front. 2012, 3, 109–124. [Google Scholar] [CrossRef]
- Kuzucuoglu, C.; Parish, R.; Karabiyikoglu, M. The dune systems of the Konya plain (Turkey): Their relation to environmental changes in Central Anatolia during the late Pleistocene and Holocene. Geomorphology 1998, 23, 257–271. [Google Scholar] [CrossRef]
- Briere, P.R. Playa, playa lake, sebkha: Proposed definitions for old terms. J. Arid. Environ. 2000, 45, 1–7. [Google Scholar] [CrossRef]
- Aref, M.A.M.; El-Khoriby, E.; Hamdan, M.A. The role of salt weathering in the origin of the Qattara Depression, Western Desert, Egypt. Geomorphology 2002, 45, 181–195. [Google Scholar] [CrossRef]
- Martínez, F.; Gonzalez, R.; Bascuñan, S.; Arriagada, C. Structural styles of the Salar de Punta Negra Basin in the Preandean depression (24°–25°S) of the Central Andes. J. S. Am. Earth Sci. 2018, 87, 188–199. [Google Scholar] [CrossRef]
- García, H.P.A.; Gianni, G.M.; Lupari, M.N.; Sánchez, M.A.; Soler, S.R.; Ruiz, F.; Kinger, F.G.L. Effective elastic thickness in the Central Andes. Correlation to orogenic deformation styles and lower crust high-gravity anomaly. J. S. Am. Earth Sci. 2018, 87, 232–246. [Google Scholar] [CrossRef]
- Leeuw, A.D.; Mandic, O.; Krijgsman, W.; Kuiper, K.; Hrvatovic, H. Paleomagnetic and geochronologic constrains on the geodynamic evolution of the Central Dinarides. Tectonophysics 2012, 530–531, 286–298. [Google Scholar] [CrossRef]
- Bonacci, O. Poljes, ponors and their cathchments. In Treatise on Geomorphology. Karst Geomorphology; Shroder, J.F., Frumkin, A., Eds.; Academic Press: San Diego, CA, USA, 2013; Volume 6, pp. 112–120. [Google Scholar]
- Meneghel, M.; Sauro, U. Dolines of karstic and periglacial origin in the high mountain karst of Pale di San Martino plateau (Dolomites). Z. Geomorphol. Suppl. Issues 2006, 50, 63–76. [Google Scholar] [CrossRef]
- Kranjc, A. Classification of closed depressions in carbonate karst. In Treatise on Geomorphology. Karst Geomorphology; Shroder, J.F., Frumkin, A., Eds.; Academic Press: San Diego, CA, USA, 2013; Volume 6, pp. 104–111. [Google Scholar]
- White, W.B.; White, E.L. Size scales for closed depression landforms: The place of tiankengs. Spelogenesis Evol. Karst Acquifers 2006, 4, 1–10. [Google Scholar]
- Gabrovšek, F.; Stepišnik, U. On the formation of collapse dolines: A modelling perspective. Geomorphology 2011, 134, 23–31. [Google Scholar] [CrossRef]
- Monroe, W.H. A Glossary of Karst Terminology; Water Supply Paper; The US Government Publishing Office: New York, NY, USA, 1972; 29p. [Google Scholar]
- Claps, P.; Fiorentino, M.; Oliveto, G. Informational entropy of fractal river networks. J. Hydrol. 1996, 187, 145–156. [Google Scholar] [CrossRef]
- Instituto Nacional de Estadística, y Geografía (INEGI). Continuo de elevaciones mexicano y modelos digitales de elevación. 2013. Available online: https://www.inegi.org.mx/app/geo2/elevacionesmex/ (accessed on 15 May 2025).
- Comisión para el Conocimiento y Uso de la Biodiversidad (CONABIO). La Biodiversidad en Chiapas: Estudio de Estado. Tuxtla Gutiérrez, Chiapas: Gobierno del Estado de Chiapas. 2013. Available online: https://www.biodiversidad.gob.mx/region/eeb/estudios/ee_chiapas (accessed on 18 May 2025).
- Galicia-Luna, V.J. Cartografías del Deseo en Chiapas: Entre la Conservación y el Extractivismo (Tesis de Maestría). El Colegio de la Frontera Sur, San Cristobal de las Casas, Chiapas. Available online: http://ecosur.repositorioinstitucional.mx/jspui/handle/1017/1519 (accessed on 18 May 2025).
- Mora, J.C.; Jaimes-Viera, M.C.; Garduño-Monroy, V.H.; Layer, P.W.; Pompa-Mera, V.; Godinez, M.L. Geology and geochemistry characteristics of the Chiapanecan Volcanic Arc (Central Area), Chiapas Mexico. J. Volcanol. Geotherm. Res. 2007, 162, 43–72. [Google Scholar] [CrossRef]
- Pantoja-Alor, J. Contribución a la geocronología del Estado de Chiapas: Mexico, D.F. Boletín Asoc. Mex. De Geólogos Petroleros 1974, 26, 29. [Google Scholar]
- López-Ramos, E. Carta Geológica del Estado de Chiapas: Mexico, D.F. Universidad Nacional Autónoma de México, Instituto de Geología, Escala 1:500,000; Universidad Nacional Autónoma de México, Instituto de Geología: Ciudad de Mexico, Mexico, 1975. [Google Scholar]
- Salas, G.P. Carta y Provincias Metalogenéticas de la Republica Mexicana; 21-E; Consejo de Recursos Minerales: Ciudad de Mexico, Mexico, 1975; Volume 21, 242p. [Google Scholar]
- Castro-Mora, J. Monografía Geológico-Minera del Estado de Chiapas; Consejo de Recursos Minerales: Ciudad de Mexico, Mexico, 1999; 178p. [Google Scholar]
- Kadam, A.K.; Umrikar, B.N.; Sankhua, R.N. Assessment of recharge potential zones for groundwater development and management using geospatial and MCDA technologies in semiarid region of Western India. SN Appl. Sci. 2020, 2, 312. [Google Scholar] [CrossRef]
- Gary, M. Understanding Zacatón: Exploration and initial interpretation of the worlds deepest known phreatic sinkhole and related karst features, southern Tamaulipas, Mexico. Karst Waters Inst. Spec. Publ. 2002, 7, 141–145. [Google Scholar]
- Guerra, V.; Lazzari, M. Geomorphological mapping as a tool for geoheritage inventory and geotourism promotion: A case study from the middle vallye of Marecchia river (northen Italy). Géomorphologie 2021, 27, 127–145. [Google Scholar] [CrossRef]
- Planchon, O.; Darboux, F. A fast, simple and versatile algorithm to fill the depressions of digital elevation models. Catena 2001, 46, 159–176. [Google Scholar] [CrossRef]
- Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An Overview of Global Leaf Area Index (LAI): Methods, Products, Validation, and Applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Simic, A.; Fernandes, R.; Wang, S. Assessing the Impact of Leaf Area Index on Evapotranspiration and Groundwater Recharge across a Shallow Water Region for Diverse Land Cover and Soil Properties. J. Water Resour. Hydraul. Eng. 2014, 3, 60–73. [Google Scholar]
- Myneni, R.; Knyazikhin, Y.; Park, T. MOD15A2H MODIS Leaf Area Index/FPAR 8-Day L4 Global 500m SIN Grid V006. NASA EOSDIS Land Processes DAAC. Available online: https://modis.gsfc.nasa.gov/data/dataprod/mod15.php (accessed on 9 September 2023).
- Goldin, A.; Nimios, T. Vegetation Patterns on Limestone and Acid Parent Materials in the Garnet Mountains of Western Montana. Northwest Sci. 1977, 51, 149–160. [Google Scholar]
- Somaratne, N. Characteristics of Point Recharge in Karst Aquifers. Water 2014, 6, 2782–2807. [Google Scholar] [CrossRef]
- Hayes, A. Descriptive Statistics: Definition, Overview, Types, Example. [Revised: 28 September 2023]. 2023. Available online: https://www.investopedia.com/terms/d/descriptive_statistics.asp (accessed on 18 May 2025).
- Dwevedi, A.; Kumar, P.; Kumar, P.; Kumar, Y.; Sharma, Y.K.; Kayastha, A.M. Soil sensors: Detailed insight into research updates, significance, and future prospects. In New Pesticides and Soil Sensors; Academic Press: Cambridge, MA, USA, 2017; pp. 561–594. [Google Scholar] [CrossRef]
- Dingman, S.L. Physical Hydrology; Prentice Hall, Inc.: Englewood Cliffs, NJ, USA, 1994. [Google Scholar]
- Thurow, T.L.; Blackburn, W.H.; Taylor, C.A. Hydrologic characteristics of vegetation types as affected by livestock grazing systems, Edward Plateau, Texas. J. Range Manag. 1986, 39, 505–508. [Google Scholar] [CrossRef]
- Emerson, W.W.; Bond, R.D.; Dexter, A.R. Modification of Soil Structure; John Wiley: New York, NY, USA, 1978. [Google Scholar]
- Batelaan, O.; De Smedt, F. GIS-based recharge estimation by coupling surface-subsurface water balances. J. Hydrol. 2007, 337, 355. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).