Baseflow Index Trends in Iowa Rivers and the Relationships to Other Hydrologic Metrics
Abstract
1. Introduction
2. Materials and Methods
2.1. Regional Setting
2.2. Selection of Stream Gauges
2.3. Calculation of Hydrologic Metrics
2.3.1. Baseflow Separation
2.3.2. Annual Statistics
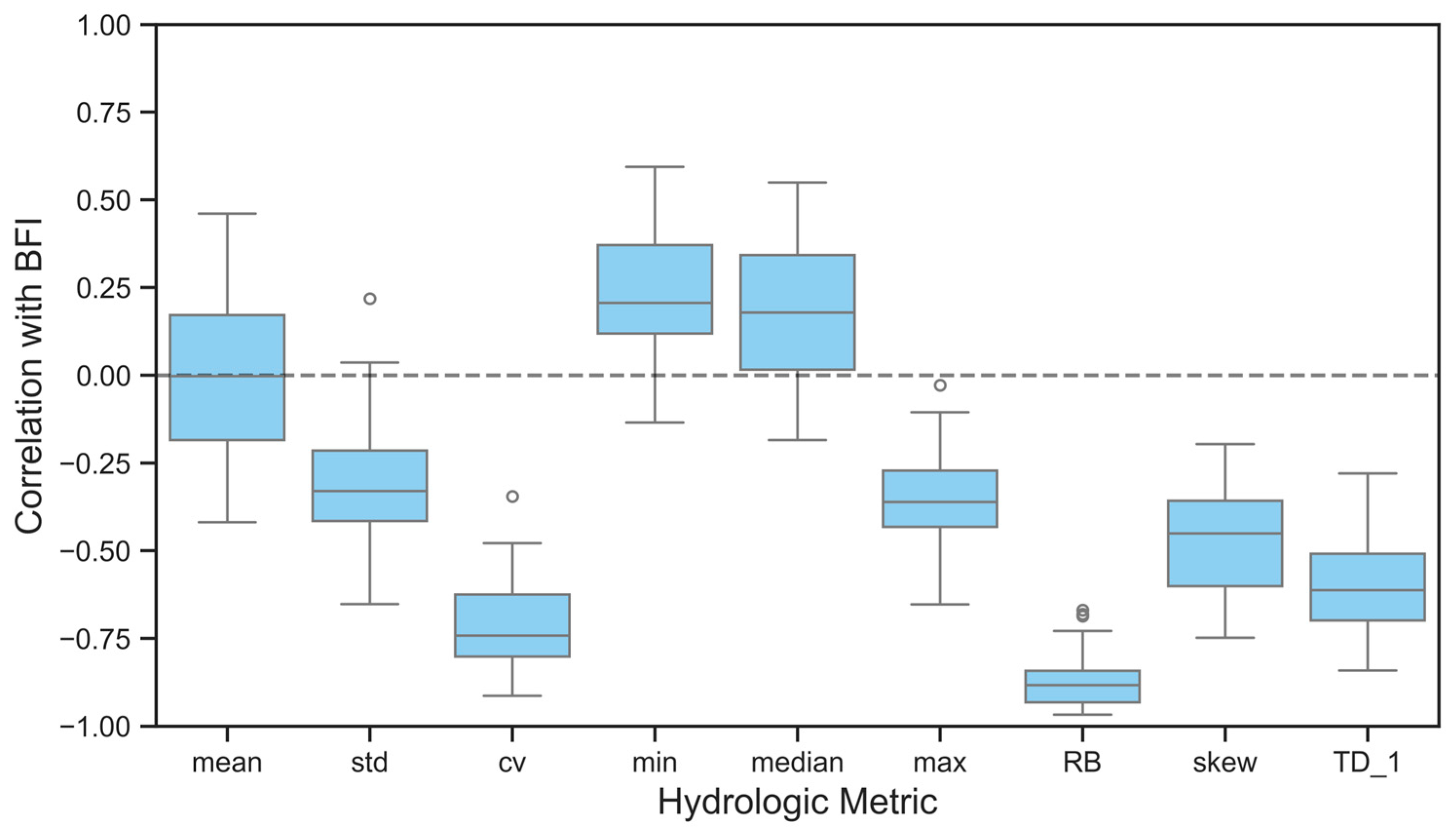
2.3.3. Correlations Between BFI and Other Metrics
2.4. Trend Analysis
2.5. Statewide Analysis
3. Results
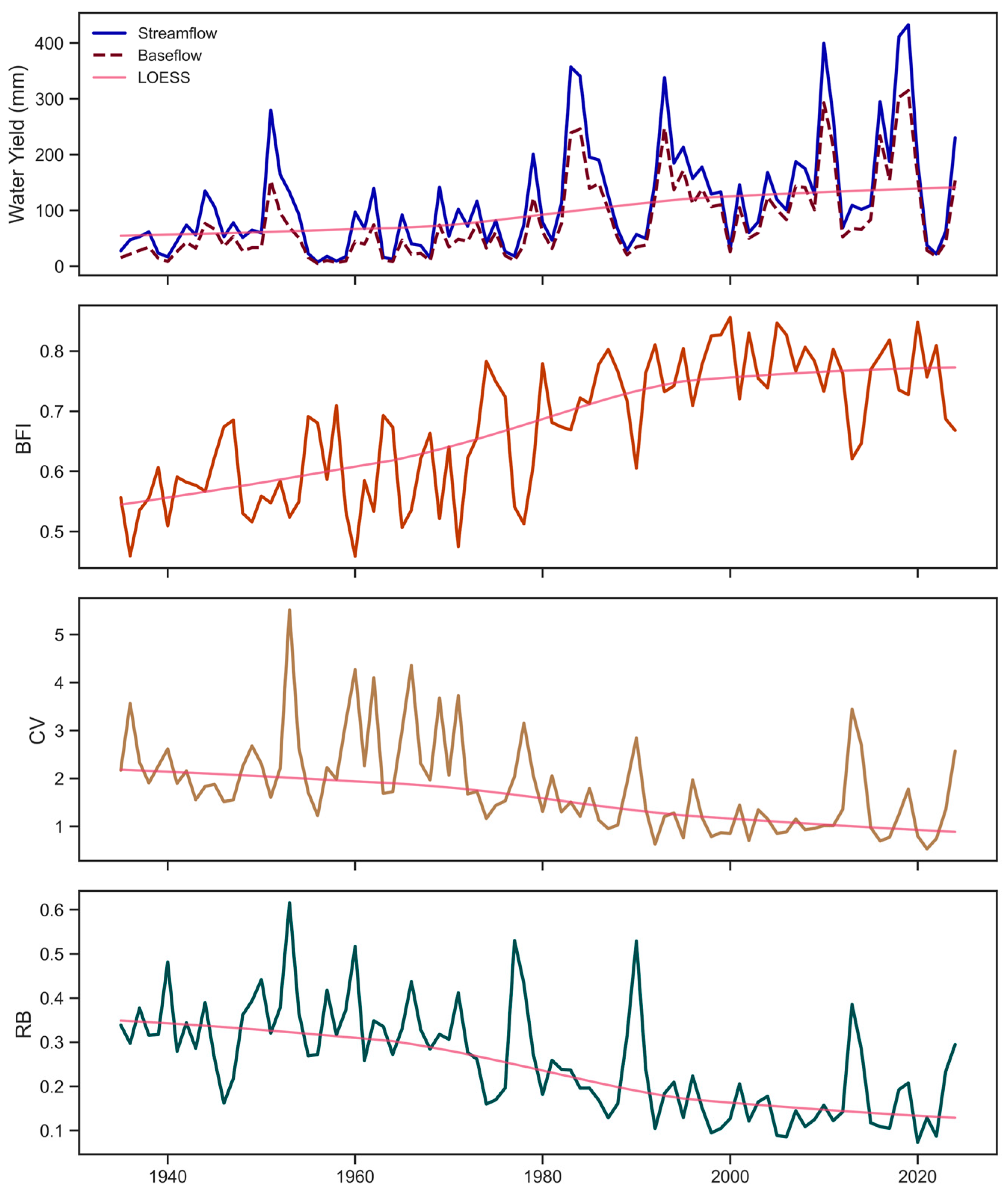
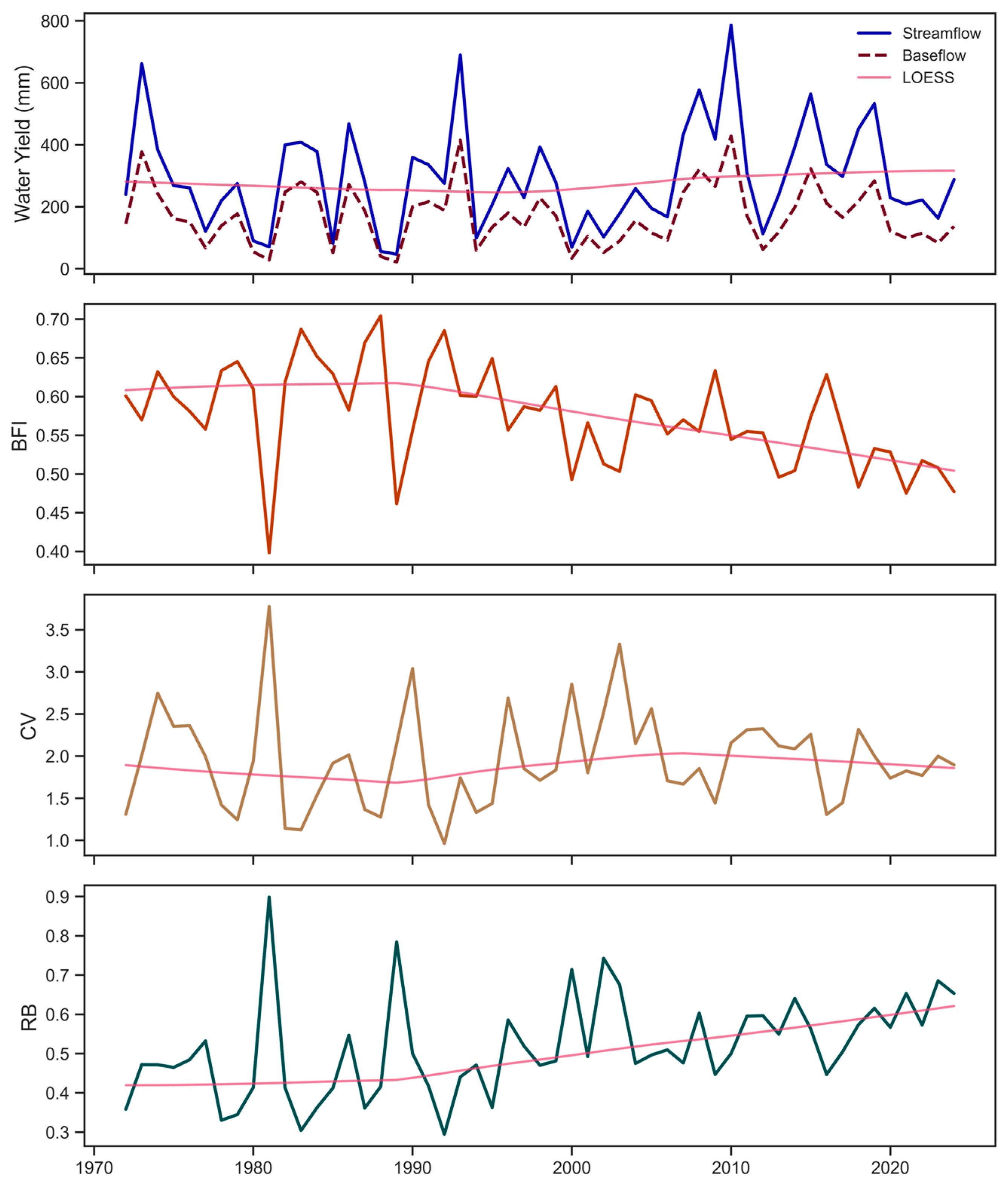
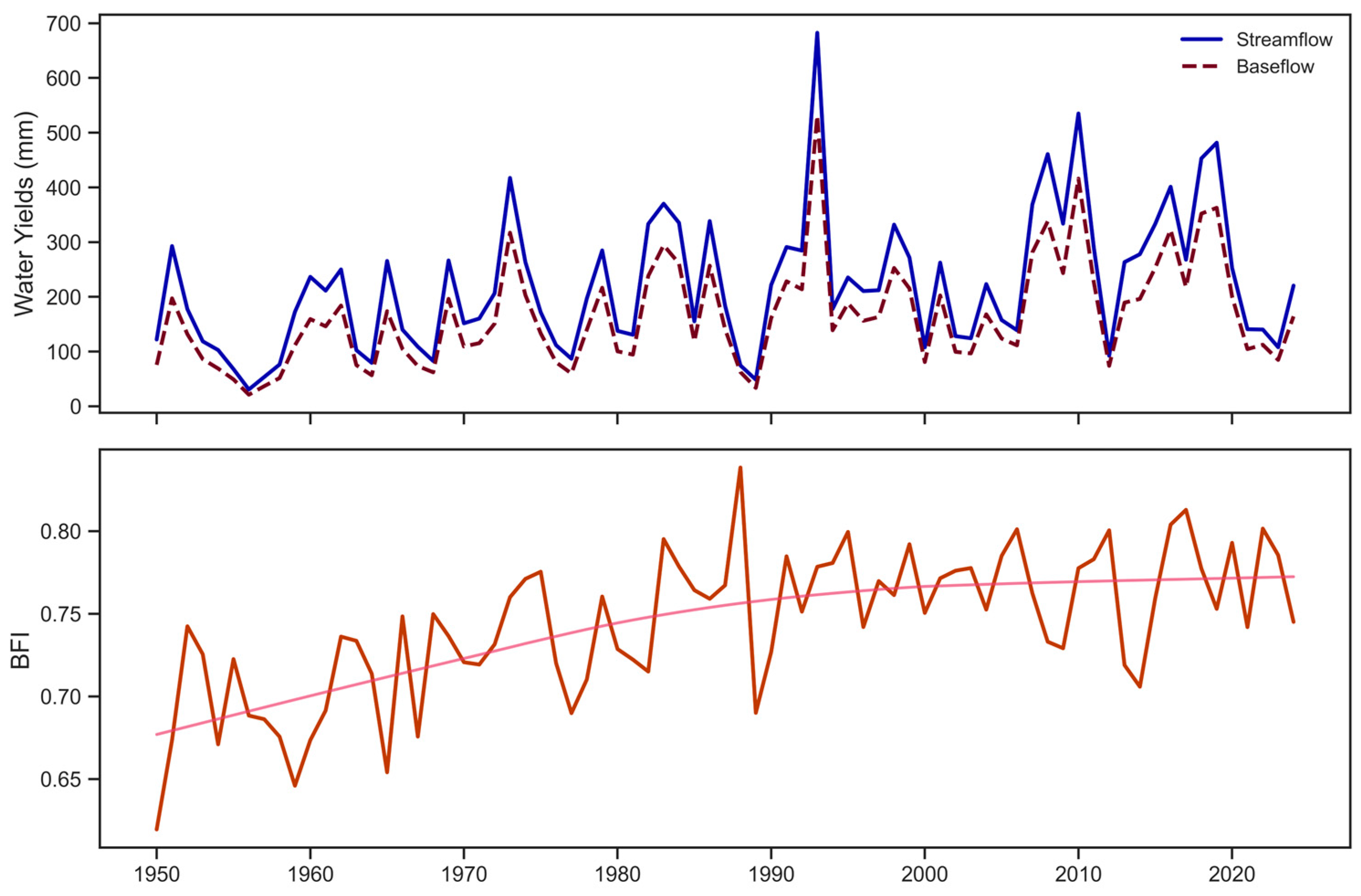
3.1. Hydrologic Metrics
3.2. Trends
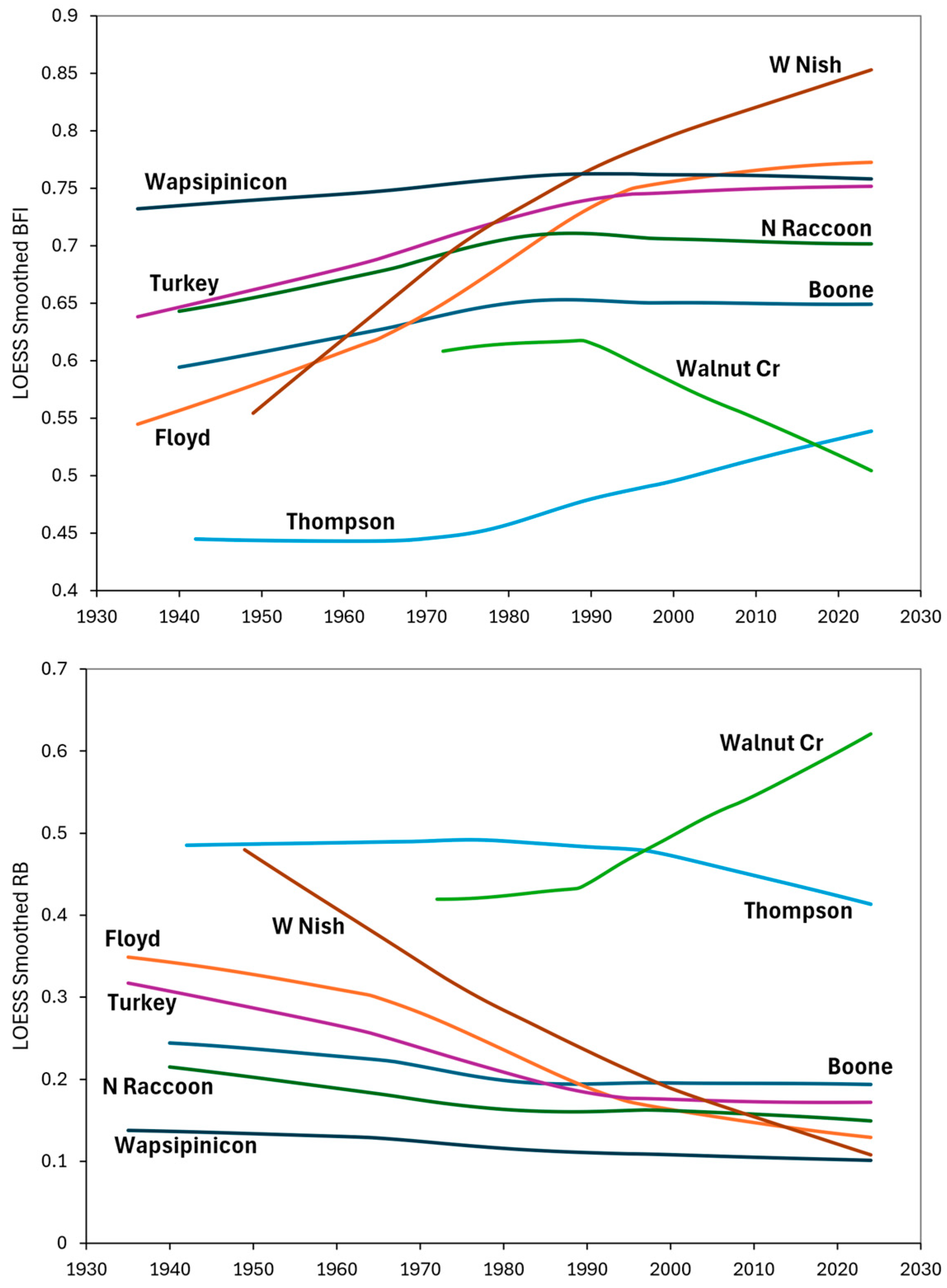
3.2.1. Multi-Decadal Timeframe
3.2.2. 30-Year Periods
3.3. Statewide Values
4. Discussion
4.1. Temporal Patterns in Baseflow Indices
4.2. Interconnectivity of Hydrologic Metrics
4.3. Future Work and Implications of BFI Trends
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BFI | Baseflow Index |
| CV | Coefficient of Variation |
| LOESS | Locally estimated scatterplot smoothing |
| max | Annual maximum streamflow |
| mean | Annual streamflow arithmetic mean |
| min | Annual minimum streamflow |
| MLRA | Major land resource area |
| N | Nitrogen |
| P | Phosphorus |
| RB | Richards–Baker Flashiness Index |
| skew | Skewness |
| std | Standard Deviation |
| TD | Top Days metric |
| TSS | Total Suspended Sediment |
| USGS | United States Geological Survey |
References
- Rantz, S.E. Measurement and Computation of Streamflow; US Department of the Interior, Geological Survey: Reston, VA, USA, 1982; Volume 2175.
- Fenton, J.D.; Keller, R.J. The Calculation of Streamflow from Measurements of Stage. Technical Report Cooperative Research Centre for Catchment Hydrology. 2001. Available online: https://www.ewater.org.au/archive/crcch/archive/pubs/pdfs/technical200106.pdf (accessed on 23 March 2025).
- Fleig, A.K.; Tallaksen, L.M.; Hisdal, H.; Demuth, S. A global evaluation of streamflow drought characteristics. Hydrol. Earth Syst. Sci. 2006, 10, 535–552. [Google Scholar] [CrossRef]
- Carlisle, D.M.; Wolock, D.M.; Meador, M.R. Alteration of streamflow magnitudes and potential ecological consequences: A multiregional assessment. Front. Ecol. Environ. 2011, 9, 264–270. [Google Scholar] [CrossRef]
- Brown, T.C.; Taylor, J.G.; Shelby, B. Assessing the direct affects of streamflow on recreation: A literature review. JAWRA J. Am. Water Resour. Assoc. 1991, 27, 979–989. [Google Scholar] [CrossRef]
- Murphy, J.; Sprague, L. Water-quality trends in US rivers: Exploring effects from streamflow trends and changes in watershed management. Sci. Total Environ. 2019, 656, 645–658. [Google Scholar] [CrossRef]
- Hodgkins, G.; Dudley, R.W.; Aichele, S.S. Historical Changes in Precipitation and Streamflow in the US Great Lakes Basin, 1915–2004; US Geological Survey: Reston, VA, USA, 2007.
- Milly, P.C.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Leonard, M.; Do, H.X.; Westra, S.; Seneviratne, S.I. Observed trends in global indicators of mean and extreme streamflow. Geophys. Res. Lett. 2019, 46, 756–766. [Google Scholar] [CrossRef]
- Lins, H.F.; Slack, J.R. Streamflow trends in the United States. Geophys. Res. Lett. 1999, 26, 227–230. [Google Scholar] [CrossRef]
- Rice, J.S.; Emanuel, R.E.; Vose, J.M.; Nelson, S.A. Continental US streamflow trends from 1940 to 2009 and their relationships with watershed spatial characteristics. Water Resour. Res. 2015, 51, 6262–6275. [Google Scholar] [CrossRef]
- Ahiablame, L.; Sheshukov, A.Y.; Rahmani, V.; Moriasi, D. Annual baseflow variations as influenced by climate variability and agricultural land use change in the Missouri River Basin. J. Hydrol. 2017, 551, 188–202. [Google Scholar] [CrossRef]
- Hamel, P.; Daly, E.; Fletcher, T.D. Source-control stormwater management for mitigating the impacts of urbanisation on baseflow: A review. J. Hydrol. 2013, 485, 201–211. [Google Scholar] [CrossRef]
- Schilling, K.E.; Jindal, P.; Basu, N.B.; Helmers, M.J. Impact of artificial subsurface drainage on groundwater travel times and baseflow discharge in an agricultural watershed, Iowa (USA). Hydrol. Process. 2012, 26, 3092–3100. [Google Scholar] [CrossRef]
- Saedi, J.; Sharifi, M.R.; Saremi, A.; Babazadeh, H. Assessing the impact of climate change and human activity on streamflow in a semiarid basin using precipitation and baseflow analysis. Sci. Rep. 2022, 12, 9228. [Google Scholar] [CrossRef] [PubMed]
- Eckhardt, K. A comparison of baseflow indices, which were calculated with seven different baseflow separation methods. J. Hydrol. 2008, 352, 168–173. [Google Scholar] [CrossRef]
- Rosburg, T.T.; Nelson, P.A.; Bledsoe, B.P. Effects of urbanization on flow duration and stream flashiness: A case study of Puget Sound streams, western Washington, USA. JAWRA J. Am. Water Resour. Assoc. 2017, 53, 493–507. [Google Scholar] [CrossRef]
- Granato, G.E.; Ries, K.G., III; Steeves, P.A. Compilation of Streamflow Statistics Calculated from Daily Mean Streamflow Data Collected During Water Years 1901–2015 for Selected US Geological Survey Streamgages; US Geological Survey: Reston, VA, USA, 2017.
- Ries, K.G.; Atkins, J. The National Streamflow Statistics Program: A Computer Program for Estimating Streamflow Statistics for Ungaged Sites; DIANE Publishing: Darby, PA, USA, 2007. [Google Scholar]
- Reilly, C.F.; Kroll, C.N. Estimation of 7-day, 10-year low-streamflow statistics using baseflow correlation. Water Resour. Res. 2003, 39, 1236. [Google Scholar] [CrossRef]
- Gao, Y.; Vogel, R.M.; Kroll, C.N.; Poff, N.L.; Olden, J.D. Development of representative indicators of hydrologic alteration. J. Hydrol. 2009, 374, 136–147. [Google Scholar] [CrossRef]
- Olden, J.D.; Poff, N. Redundancy and the choice of hydrologic indices for characterizing streamflow regimes. River Res. Appl. 2003, 19, 101–121. [Google Scholar] [CrossRef]
- Loritz, R.; Gupta, H.; Jackisch, C.; Westhoff, M.; Kleidon, A.; Ehret, U.; Zehe, E. On the dynamic nature of hydrological similarity. Hydrol. Earth Syst. Sci. 2018, 22, 3663–3684. [Google Scholar] [CrossRef]
- Peres, D.J.; Cancelliere, A. Environmental flow assessment based on different metrics of hydrological alteration. Water Resour. Manag. 2016, 30, 5799–5817. [Google Scholar] [CrossRef]
- Peñas, F.; Barquín, J.; Álvarez, C. Assessing hydrologic alteration: Evaluation of different alternatives according to data availability. Ecol. Indic. 2016, 60, 470–482. [Google Scholar] [CrossRef]
- Lins, H.F.; Slack, J.R. Seasonal and regional characteristics of US streamflow trends in the United States from 1940 to 1999. Phys. Geogr. 2005, 26, 489–501. [Google Scholar] [CrossRef]
- Gallant, A.L.; Sadinski, W.; Roth, M.F.; Rewa, C.A. Changes in historical Iowa land cover as context for assessing the environmental benefits of current and future conservation efforts on agricultural lands. J. Soil Water Conserv. 2011, 66, 67A–77A. [Google Scholar] [CrossRef]
- Steinwand, A.; Fenton, T. Landscape evolution and shallow groundwater hydrology of a till landscape in central Iowa. Soil Sci. Soc. Am. J. 1995, 59, 1370–1377. [Google Scholar] [CrossRef]
- Steffens, K.J.; Franz, K. Late 20th-century trends in Iowa watersheds: An investigation of observed and modelled hydrologic storages and fluxes in heavily managed landscapes. Int. J. Climatol. 2012, 32, 1373. [Google Scholar] [CrossRef]
- Green, C.; Tomer, M.; Di Luzio, M.; Arnold, J. Hydrologic evaluation of the soil and water assessment tool for a large tile-drained watershed in Iowa. Trans. ASABE 2006, 49, 413–422. [Google Scholar] [CrossRef]
- Kling, C.; Rabotyagov, S.; Jha, M.; Feng, H.; Parcel, J.; Gassman, P.; Campbell, T. Conservation practices in Iowa: Historical investments, water quality, and gaps. In A Report to the Iowa Farm Bureau and Partners. Final Report; Iowa State University Center for Agricultural and Rural Development: Ames, IA, USA, 2007. [Google Scholar]
- Morris, C.; Arbuckle, J.G. Conservation plans and soil and water conservation practice use: Evidence from Iowa. J. Soil Water Conserv. 2021, 76, 457–471. [Google Scholar] [CrossRef]
- Takle, E.S.; Gutowski, W.J. Iowa’s agriculture is losing its Goldilocks climate. Phys. Today 2020, 73, 26–33. [Google Scholar] [CrossRef]
- Schilling, K.E.; Helmers, M. Effects of subsurface drainage tiles on streamflow in Iowa agricultural watersheds: Exploratory hydrograph analysis. Hydrol. Process. Int. J. 2008, 22, 4497–4506. [Google Scholar] [CrossRef]
- Lenhart, C.F.; Peterson, H.; Nieber, J. Increased streamflow in agricultural watersheds of the Midwest: Implications for management. Watershed Sci. Bull. 2011, 2, 25–31. [Google Scholar]
- Slater, L.J.; Villarini, G. Evaluating the Drivers of Seasonal Streamflow in the U.S. Midwest. Water 2017, 9, 695. [Google Scholar] [CrossRef]
- Gupta, S.C.; Kessler, A.C.; Brown, M.K.; Zvomuya, F. Climate and agricultural land use change impacts on streamflow in the upper midwestern United States. Water Resour. Res. 2015, 51, 5301–5317. [Google Scholar] [CrossRef]
- Douglas, E.; Vogel, R.; Kroll, C. Trends in floods and low flows in the United States: Impact of spatial correlation. J. Hydrol. 2000, 240, 90–105. [Google Scholar] [CrossRef]
- Knapp, H.V. Analysis of Streamflow Trends in the Upper Midwest Using Long-Term Flowrecords. In Impacts of Global Climate Change; Illinois State Water Survey: Champaign, IL, USA, 2005; pp. 1–12. [Google Scholar]
- Schilling, K.E.; Libra, R.D. Increased baseflow in Iowa over the second half of the 20th century. JAWRA J. Am. Water Resour. Assoc. 2003, 39, 851–860. [Google Scholar] [CrossRef]
- Zhang, Y.-K.; Schilling, K. Increasing streamflow and baseflow in Mississippi River since the 1940s: Effect of land use change. J. Hydrol. 2006, 324, 412–422. [Google Scholar] [CrossRef]
- Ayers, J.R.; Villarini, G.; Schilling, K.; Jones, C. On the statistical attribution of changes in monthly baseflow across the US Midwest. J. Hydrol. 2021, 592, 125551. [Google Scholar] [CrossRef]
- Ayers, J.R.; Villarini, G.; Jones, C.; Schilling, K. Changes in monthly baseflow across the US Midwest. Hydrol. Process. 2019, 33, 748–758. [Google Scholar] [CrossRef]
- Demaria, E.M.; Palmer, R.N.; Roundy, J.K. Regional climate change projections of streamflow characteristics in the Northeast and Midwest US. J. Hydrol. Reg. Stud. 2016, 5, 309–323. [Google Scholar] [CrossRef]
- Xu, X.; Scanlon, B.R.; Schilling, K.; Sun, A. Relative importance of climate and land surface changes on hydrologic changes in the US Midwest since the 1930s: Implications for biofuel production. J. Hydrol. 2013, 497, 110–120. [Google Scholar] [CrossRef]
- Arnold, J.G.; Allen, P.M. Automated methods for estimating baseflow and ground water recharge from streamflow records. JAWRA J. Am. Water Resour. Assoc. 1999, 35, 411–424. [Google Scholar] [CrossRef]
- Prior, J.C. Landforms of Iowa; University of Iowa Press: Iowa City, IA, USA, 1991. [Google Scholar]
- Austin, M.E. Land resource regions and major land resource areas of the United States (exclusive of Alaska and Hawaii). In Soil Conservation Service; US Department of Agriculture: Washington, DC, USA, 1965. [Google Scholar]
- Jones, C.S.; Schilling, K.E.; Simpson, I.M.; Wolter, C.F. Iowa stream nitrate, discharge and precipitation: 30-year perspective. Environ. Manag. 2018, 62, 709–720. [Google Scholar] [CrossRef]
- Son, J.-Y.; Bell, M.L. Exposure to animal feeding operations including concentrated animal feeding operations (CAFOs) and environmental justice in Iowa, USA. Environ. Res. Health 2022, 1, 015004. [Google Scholar] [CrossRef]
- Falcone, J.A.; Murphy, J.C.; Sprague, L.A. Regional patterns of anthropogenic influences on streams and rivers in the conterminous United States, from the early 1970s to 2012. J. Land Use Sci. 2018, 13, 585–614. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Costa, J.E. US stream flow measurement and data dissemination improve. Eos Trans. Am. Geophys. Union 2004, 85, 197–203. [Google Scholar] [CrossRef]
- Hodson, T.O.; DeCicco, L.A.; Hariharan, J.A.; Stanish, L.F.; Black, S.; Horsburgh, J.S. Reproducibility Starts at the Source: R, Python, and Julia Packages for Retrieving USGS Hydrologic Data. Water 2023, 15, 4236. [Google Scholar] [CrossRef]
- Eckhardt, K. How to construct recursive digital filters for baseflow separation. Hydrol. Process. Int. J. 2005, 19, 507–515. [Google Scholar] [CrossRef]
- Kang, T.; Lee, S.; Lee, N.; Jin, Y. Baseflow separation using the digital filter method: Review and sensitivity analysis. Water 2022, 14, 485. [Google Scholar] [CrossRef]
- Collischonn, W.; Fan, F.M. Defining parameters for Eckhardt’s digital baseflow filter. Hydrol. Process. 2013, 27, 2614–2622. [Google Scholar] [CrossRef]
- Dettinger, M.D.; Diaz, H.F. Global characteristics of stream flow seasonality and variability. J. Hydrometeorol. 2000, 1, 289–310. [Google Scholar] [CrossRef]
- Baker, D.B.; Richards, R.P.; Loftus, T.T.; Kramer, J.W. A new flashiness index: Characteristics and applications to midwestern rivers and streams. JAWRA J. Am. Water Resour. Assoc. 2004, 40, 503–522. [Google Scholar] [CrossRef]
- Gannon, J.; Kelleher, C.; Zimmer, M. Controls on watershed flashiness across the continental US. J. Hydrol. 2022, 609, 127713. [Google Scholar] [CrossRef]
- Adelsperger, S.R.; Ficklin, D.L.; Robeson, S.M. Tile drainage as a driver of streamflow flashiness in agricultural areas of the Midwest, USA. Hydrol. Process. 2023, 37, e15021. [Google Scholar] [CrossRef]
- Leander, R.; Buishand, T.; Tank, A.K. An alternative index for the contribution of precipitation on very wet days to the total precipitation. J. Clim. 2014, 27, 1365–1378. [Google Scholar] [CrossRef]
- Schilling, K.E.; Anderson, E.S.; Mount, J.; Suttles, K.; Gassman, P.W.; Cerkasova, N.; White, M.J.; Arnold, J.G. Evaluation of flood metrics across the Mississippi-Atchafalaya River Basin and their relation to flood damages. PLoS ONE 2024, 19, e0307486. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Tarboton, D.G.; Lall, U. Streamflow simulation: A nonparametric approach. Water Resour. Res. 1997, 33, 291–308. [Google Scholar] [CrossRef]
- Archfield, S.A.; Hirsch, R.M.; Viglione, A.; Blöschl, G. Fragmented patterns of flood change across the United States. Geophys. Res. Lett. 2016, 43, 10232–10239. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Alexander, R.B.; Smith, R.A. Selection of methods for the detection and estimation of trends in water quality. Water Resour. Res. 1991, 27, 803–813. [Google Scholar] [CrossRef]
- McKinney, W.; Perktold, J.; Seabold, S. Time Series Analysis in Python with statsmodels. In Proceedings of the 10th Python in Science Conference, Austin, TX, USA, 11–16 July 2011; pp. 107–113. [Google Scholar]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M.; Ryberg, K.R.; Archfield, S.A.; Gilroy, E.J. Statistical Methods in Water Resources; US Geological Survey: Reston, VA, USA, 2020.
- Theil, H. A rank-invariant method of linear and polynomial regression analysis. Indag. Math. 1950, 12, 173. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Hussain, M.; Mahmud, I. pyMannKendall: A python package for non parametric Mann Kendall family of trend tests. J. Open Source Softw. 2019, 4, 1556. [Google Scholar] [CrossRef]
- Arguez, A.; Vose, R.S. The definition of the standard WMO climate normal: The key to deriving alternative climate normals. Bull. Am. Meteorol. Soc. 2011, 92, 699–704. [Google Scholar] [CrossRef]
- Giorgi, F.; Bi, X.; Pal, J.S. Mean, interannual variability and trends in a regional climate change experiment over Europe. I. Present-day climate (1961–1990). Clim. Dyn. 2004, 22, 733–756. [Google Scholar] [CrossRef]
- Anderson, E.S.; Schilling, K. The speciation of Iowa’s nutrient loads and the implications for midwestern nutrient reduction strategies. J. Soil Water Conserv. 2024, 79, 233–246. [Google Scholar] [CrossRef]
- Anderson, E.S.; Schilling, K.E.; Jones, C.S.; Weber, L.J. Estimating Iowa’s riverine phosphorus concentrations via water quality surrogacy. Heliyon 2024, 10, e37377. [Google Scholar] [CrossRef]
- Jones, C.S.; Davis, C.A.; Drake, C.W.; Schilling, K.E.; Debionne, S.H.; Gilles, D.W.; Demir, I.; Weber, L.J. Iowa statewide stream nitrate load calculated using in situ sensor network. JAWRA J. Am. Water Resour. Assoc. 2018, 54, 471–486. [Google Scholar] [CrossRef]
- Schilling, K.E. Relation of baseflow to row crop intensity in Iowa. Agric. Ecosyst. Environ. 2005, 105, 433–438. [Google Scholar] [CrossRef]
- Hammond, J.C.; Simeone, C.; Hecht, J.S.; Hodgkins, G.A.; Lombard, M.; McCabe, G.; Wolock, D.; Wieczorek, M.; Olson, C.; Caldwell, T. Going beyond low flows: Streamflow drought deficit and duration illuminate distinct spatiotemporal drought patterns and trends in the US during the last century. Water Resour. Res. 2022, 58, e2022WR031930. [Google Scholar] [CrossRef]
- Kam, J.; Sheffield, J. Changes in the low flow regime over the eastern United States (1962–2011): Variability, trends, and attributions. Clim. Change 2016, 135, 639–653. [Google Scholar] [CrossRef]
- Kay, A.L.; Bell, V.; Guillod, B.; Jones, R.G.; Rudd, A.C. National-scale analysis of low flow frequency: Historical trends and potential future changes. Clim. Change 2018, 147, 585–599. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Robeson, S.M.; Knouft, J.H. Impacts of recent climate change on trends in baseflow and stormflow in United States watersheds. Geophys. Res. Lett. 2016, 43, 5079–5088. [Google Scholar] [CrossRef]
- Boland-Brien, S.J.; Basu, N.B.; Schilling, K.E. Homogenization of spatial patterns of hydrologic response in artificially drained agricultural catchments. Hydrol. Process. 2013, 28, 5010–5020. [Google Scholar] [CrossRef]
- Li, C.; Wang, L.; Wanrui, W.; Qi, J.; Linshan, Y.; Zhang, Y.; Lei, W.; Cui, X.; Wang, P. An analytical approach to separate climate and human contributions to basin streamflow variability. J. Hydrol. 2018, 559, 30–42. [Google Scholar] [CrossRef]
- Chang, J.; Zhang, H.; Wang, Y.; Zhu, Y. Assessing the impact of climate variability and human activities on streamflow variation. Hydrol. Earth Syst. Sci. 2016, 20, 1547–1560. [Google Scholar] [CrossRef]
- Burn, D.H.; Elnur, M.A.H. Detection of hydrologic trends and variability. J. Hydrol. 2002, 255, 107–122. [Google Scholar] [CrossRef]
- Varble, S.; Secchi, S.; Druschke, C.G. An examination of growing trends in land tenure and conservation practice adoption: Results from a farmer survey in Iowa. Environ. Manag. 2016, 57, 318–330. [Google Scholar] [CrossRef]
- Weber, L.J.; Muste, M.; Bradley, A.A.; Amado, A.A.; Demir, I.; Drake, C.W.; Krajewski, W.F.; Loeser, T.J.; Politano, M.S.; Shea, B.R. The Iowa Watersheds Project: Iowa’s prototype for engaging communities and professionals in watershed hazard mitigation. Int. J. River Basin Manag. 2018, 16, 315–328. [Google Scholar] [CrossRef]
- Jones, C.S.; Schilling, K.E. From agricultural intensification to conservation: Sediment transport in the Raccoon River, Iowa, 1916–2009. J. Environ. Qual. 2011, 40, 1911–1923. [Google Scholar] [CrossRef]
- Villarini, G.; Schilling, K.E.; Jones, C.S. Assessing the relation of USDA conservation expenditures to suspended sediment reductions in an Iowa watershed. J. Environ. Manag. 2016, 180, 375–383. [Google Scholar] [CrossRef]
- Mitchell, M.E.; Newcomer-Johnson, T.; Christensen, J.; Crumpton, W.; Dyson, B.; Canfield, T.J.; Helmers, M.; Forshay, K.J. A review of ecosystem services from edge-of-field practices in tile-drained agricultural systems in the United States Corn Belt Region. J. Environ. Manag. 2023, 348, 119220. [Google Scholar] [CrossRef]
- Helmers, M.; Christianson, R.; Brenneman, G.; Lockett, D.; Pederson, C. Water table, drainage, and yield response to drainage water management in southeast Iowa. J. Soil Water Conserv. 2012, 67, 495–501. [Google Scholar] [CrossRef]
- Schilling, K.E.; Langel, R.J.; Wolter, C.F.; Arenas-Amado, A. Using baseflow to quantify diffuse groundwater recharge and drought at a regional scale. J. Hydrol. 2021, 602, 126765. [Google Scholar] [CrossRef]
- Cueff, S.; Coquet, Y.; Aubertot, J.-N.; Bel, L.; Pot, V.; Alletto, L. Estimation of soil water retention in conservation agriculture using published and new pedotransfer functions. Soil Tillage Res. 2021, 209, 104967. [Google Scholar] [CrossRef]
- Ford, T.W.; Chen, L.; Schoof, J.T. Variability and transitions in precipitation extremes in the Midwest United States. J. Hydrometeorol. 2021, 22, 533–545. [Google Scholar] [CrossRef]
- Johnson, B.G.; Morris, C.S.; Mase, H.L.; Whitehouse, P.S.; Paradise, C.J. Seasonal flashiness and high frequency discharge events in headwater streams in the North Carolina Piedmont (United States). Hydrol. Process. 2022, 36, e14550. [Google Scholar] [CrossRef]
- Schilling, K.E.; Tomer, M.D.; Gassman, P.W.; Kling, C.L.; Isenhart, T.M.; Moorman, T.B.; Simpkins, W.W.; Wolter, C.F. A tale of three watersheds: Nonpoint source pollution and conservation practices across Iowa. Choices 2007, 22, 87–95. [Google Scholar]
- Hu, X.; McIsaac, G.; David, M.; Louwers, C. Modeling riverine nitrate export from an east-central Illinois watershed using SWAT. J. Environ. Qual. 2007, 36, 996–1005. [Google Scholar] [CrossRef]
- Cowell, C.M.; Urban, M.A. The changing geography of the US water budget: Twentieth-century patterns and twenty-first-century projections. Ann. Assoc. Am. Geogr. 2010, 100, 740–754. [Google Scholar] [CrossRef]
- Schilling, K.E.; Streeter, M.T.; Seeman, A.; Jones, C.S.; Wolter, C.F. Total phosphorus export from Iowa agricultural watersheds: Quantifying the scope and scale of a regional condition. J. Hydrol. 2020, 581, 124397. [Google Scholar] [CrossRef]
- Anderson, E.S.; Schilling, K.; Jones, C.; Weber, L.; Wolter, C. Iowa’s Annual Phosphorus Budget: Quantifying the Inputs and Outputs of Phosphorus Transport Processes. Land 2024, 13, 1483. [Google Scholar] [CrossRef]
- McPhillips, L.; Earl, S.; Hale, R.; Grimm, N. Urbanization in arid central Arizona watersheds results in decreased stream flashiness. Water Resour. Res. 2019, 55, 9436–9453. [Google Scholar] [CrossRef]
- Arnold, J.G.; Muttiah, R.S.; Srinivasan, R.; Allen, P.M. Regional estimation of base flow and groundwater recharge in the Upper Mississippi river basin. J. Hydrol. 2000, 227, 21–40. [Google Scholar] [CrossRef]
- Van Noordwijk, M.; Tanika, L.; Lusiana, B. Flood risk reduction and flow buffering as ecosystem services–Part 1: Theory on flow persistence, flashiness and base flow. Hydrol. Earth Syst. Sci. 2017, 21, 2321–2340. [Google Scholar] [CrossRef]
- Holko, L.; Parajka, J.; Kostka, Z.; Škoda, P.; Blöschl, G. Flashiness of mountain streams in Slovakia and Austria. J. Hydrol. 2011, 405, 392–401. [Google Scholar] [CrossRef]
- Quintero, F.; Krajewski, W.F.; Seo, B.-C.; Mantilla, R. Improvement and evaluation of the Iowa Flood Center Hillslope Link Model (HLM) by calibration-free approach. J. Hydrol. 2020, 584, 124686. [Google Scholar] [CrossRef]
- Politano, M.; Arenas, A.; Weber, L. A process-based hydrological model for continuous multi-year simulations of large-scale watersheds. Int. J. River Basin Manag. 2023, 23, 15–28. [Google Scholar] [CrossRef]
- Feng, D.; Zheng, Y.; Mao, Y.; Zhang, A.; Wu, B.; Li, J.; Tian, Y.; Wu, X. An integrated hydrological modeling approach for detection and attribution of climatic and human impacts on coastal water resources. J. Hydrol. 2018, 557, 305–320. [Google Scholar] [CrossRef]
- Harrigan, S.; Murphy, C.; Hall, J.; Wilby, R.; Sweeney, J. Attribution of detected changes in streamflow using multiple working hypotheses. Hydrol. Earth Syst. Sci. 2014, 18, 1935–1952. [Google Scholar] [CrossRef]
- Whittaker, D.; Shelby, B.; Jackson, W.; Beschta, R. Instream flows for recreation: A handbook on concepts and research methods. In Instream Flows for Recreation: A Handbook on Concepts and Research Methods; National Park Service-RTCA: Washington, DC, USA, 1993; Volume 104. [Google Scholar]
- Meko, D.M.; Woodhouse, C.A. Application of streamflow reconstruction to water resources management. Dendroclimatology Prog. Prospect. 2011, 11, 231–261. [Google Scholar]
- Vogel, R.M.; Sieber, J.; Archfield, S.A.; Smith, M.P.; Apse, C.D.; Huber-Lee, A. Relations among storage, yield, and instream flow. Water Resour. Res. 2007, 43, 5. [Google Scholar] [CrossRef]
- Santhi, C.; Allen, P.; Muttiah, R.; Arnold, J.; Tuppad, P. Regional estimation of base flow for the conterminous United States by hydrologic landscape regions. J. Hydrol. 2008, 351, 139–153. [Google Scholar] [CrossRef]
- Murray, J.; Ayers, J.; Brookfield, A. The impact of climate change on monthly baseflow trends across Canada. J. Hydrol. 2023, 618, 129254. [Google Scholar] [CrossRef]
- Renwick, W.H.; Vanni, M.J.; Zhang, Q.; Patton, J. Water quality trends and changing agricultural practices in a Midwest US watershed, 1994–2006. J. Environ. Qual. 2008, 37, 1862–1874. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Schilling, K.E.; Jones, C.S.; Zhang, Y.-K. Temporal scaling of long-term co-occurring agricultural contaminants and the implications for conservation planning. Environ. Res. Lett. 2021, 16, 094015. [Google Scholar] [CrossRef]
- Lee, J.; Bang, K.; Ketchum Jr, L.; Choe, J.; Yu, M. First flush analysis of urban storm runoff. Sci. Total Environ. 2002, 293, 163–175. [Google Scholar] [CrossRef]
- Mackay, D.M.; Roberts, P.V.; Cherry, J.A. Transport of organic contaminants in groundwater. Environ. Sci. Technol. 1985, 19, 384–392. [Google Scholar] [CrossRef]
- Schilling, K.E.; Zhang, Y.-K. Baseflow contribution to nitrate-nitrogen export from a large, agricultural watershed, USA. J. Hydrol. 2004, 295, 305–316. [Google Scholar] [CrossRef]
- Wang, C.; Chan, K.S.; Schilling, K.E. Total phosphorus concentration trends in 40 Iowa rivers, 1999 to 2013. J. Environ. Qual. 2016, 45, 1351–1358. [Google Scholar] [CrossRef]
- Cruse, R.; Flanagan, D.; Frankenberger, J.; Gelder, B.; Herzmann, D.; James, D.; Krajewski, W.; Kraszewski, M.; Laflen, J.; Opsomer, J. Daily estimates of rainfall, water runoff, and soil erosion in Iowa. J. Soil Water Conserv. 2006, 61, 191–199. [Google Scholar] [CrossRef]
- Schilling, K.E.; Isenhart, T.; Wolter, C.F.; Streeter, M.T.; Kovar, J.L. Contribution of streambanks to phosphorus export from Iowa. J. Soil Water Conserv. 2022, 77, 103–112. [Google Scholar] [CrossRef]
- Schilling, K.E.; Wolter, C.F. Modeling nitrate-nitrogen load reduction strategies for the Des Moines River, Iowa using SWAT. Environ. Manag. 2009, 44, 671–682. [Google Scholar] [CrossRef]
- Ma, D.; Luo, W.; Yang, G.; Lu, J.; Fan, Y. A study on a river health assessment method based on ecological flow. Ecol. Model. 2019, 401, 144–154. [Google Scholar] [CrossRef]
- Neri, A.; Villarini, G.; Napolitano, F. Statistically-based projected changes in the frequency of flood events across the US Midwest. J. Hydrol. 2020, 584, 124314. [Google Scholar] [CrossRef]
- Messner, F.; Meyer, V. Flood damage, vulnerability and risk perception–challenges for flood damage research. In Flood Risk Management: Hazards, Vulnerability and Mitigation Measures; Springer: Berlin, Germany, 2006; pp. 149–167. [Google Scholar]
| Short Name | USGS Site Name | USGS ID | Area (km2) | Lat | Long | Start Year | BFI (1975–2024) |
|---|---|---|---|---|---|---|---|
| Beaver Cr Grimes A | Beaver Creek near Grimes, IA | 05481950 | 927 | 41.6883 | −93.7347 | 1961 | 0.654 |
| Beaver Cr Hartford A | Beaver Creek at New Hartford, IA | 05463000 | 899 | 42.5720 | −92.6183 | 1946 | 0.671 |
| Big Bear Cr A | Big Bear Creek at Ladora, IA | 05453000 | 490 | 41.7494 | −92.1821 | 1946 | 0.641 |
| Boone A | Boone River near Webster City, IA | 05481000 | 2186 | 42.4320 | −93.8059 | 1940 | 0.647 |
| Boyer A,B | Boyer River at Logan, IA | 06609500 | 2256 | 41.6417 | −95.7823 | 1938 | 0.749 |
| Cedar Cr A | Cedar Creek near Bussey, IA | 05489000 | 969 | 41.2190 | −92.9085 | 1948 | 0.382 |
| Cedar Janesville A | Cedar River at Janesville, IA | 05458500 | 4302 | 42.6483 | −92.4652 | 1946 | 0.719 |
| Chariton B | Chariton River near Rathbun, IA | 06903900 | 1422 | 40.8219 | −92.8913 | 1957 | 0.625 |
| Chariton near Char A | Chariton River near Chariton, IA | 06903400 | 471 | 40.9519 | −93.2598 | 1966 | 0.334 |
| Clear Cr A | Clear Creek near Coralville, IA | 05454300 | 254 | 41.6767 | −91.5988 | 1953 | 0.612 |
| Des Moines B | Des Moines River at Keosauqua, IA | 05490500 | 36,358 | 40.7278 | −91.9596 | 1912 | 0.783 |
| E Nish A | East Nishnabotna River at Red Oak, IA | 06809500 | 2315 | 41.0086 | −95.2417 | 1937 | 0.708 |
| EFork DM A | East Fork Des Moines River at Dakota City, IA | 05479000 | 3388 | 42.7236 | −94.1935 | 1940 | 0.744 |
| English A | English River at Kalona, IA | 05455500 | 1487 | 41.4697 | −91.7146 | 1940 | 0.560 |
| Floyd A,B | Floyd River at James, IA | 06600500 | 2295 | 42.5767 | −96.3114 | 1935 | 0.745 |
| Iowa B | Iowa River at Wapello, IA | 05465500 | 32,375 | 41.1781 | −91.1821 | 1915 | 0.806 |
| Iowa Marshalltown A | Iowa River at Marshalltown, IA | 05451500 | 3968 | 42.0658 | −92.9077 | 1933 | 0.733 |
| L Sioux Correctionville A | Little Sioux River at Correctionville, IA | 06606600 | 6475 | 42.4822 | −95.7926 | 1937 | 0.778 |
| Little Sioux B | Little Sioux River near Turin, IA | 06607500 | 9132 | 41.9650 | −95.9723 | 1958 | 0.791 |
| Maple A | Maple River at Mapleton, IA | 06607200 | 1733 | 42.1569 | −95.8100 | 1942 | 0.763 |
| Maquoketa A,B | Maquoketa River near Maquoketa, IA | 05418500 | 4022 | 42.0834 | −90.6329 | 1914 | 0.767 |
| Middle River A | Middle River near Indianola, IA | 05486490 | 1268 | 41.4242 | −93.5874 | 1940 | 0.553 |
| N Raccoon A | North Raccoon River near Jefferson, IA | 05482500 | 4193 | 41.9879 | −94.3771 | 1940 | 0.696 |
| N Skunk A | North Skunk River near Sigourney, IA | 05472500 | 1891 | 41.3008 | −92.2046 | 1946 | 0.624 |
| Nishnabotna B | Nishnabotna River above Hamburg, IA | 06810000 | 7268 | 40.6017 | −95.6450 | 1929 | 0.763 |
| Nodaway A,B | Nodaway River at Clarinda, IA | 06817000 | 1974 | 40.7433 | −95.0142 | 1937 | 0.585 |
| North River A | North River near Norwalk, IA | 05486000 | 904 | 41.4579 | −93.6550 | 1940 | 0.577 |
| Rapid Cr A | Rapid Creek near Iowa City, IA | 05454000 | 66 | 41.7000 | −91.4877 | 1938 | 0.576 |
| Richland Cr A | Richland Creek near Haven, IA | 05451900 | 145 | 41.8994 | −92.4744 | 1950 | 0.632 |
| Rock A,B | Rock River near Rock Valley, IA | 06483500 | 4123 | 43.2144 | −96.2945 | 1949 | 0.705 |
| S Raccoon A | South Raccoon River at Redfield, IA | 05484000 | 2574 | 41.5904 | −94.1512 | 1940 | 0.670 |
| S Skunk A | South Skunk River near Oskaloosa, IA | 05471500 | 4235 | 41.3557 | −92.6574 | 1946 | 0.710 |
| Salt Cr A | Salt Creek near Elberon, IA | 05452000 | 521 | 41.9642 | −92.3132 | 1946 | 0.642 |
| SFork Chariton A | South Fork Chariton River near Promise City, IA | 06903700 | 435 | 40.8006 | −93.1924 | 1968 | 0.317 |
| Skunk B | Skunk River at Augusta, IA | 05474000 | 11,168 | 40.7537 | −91.2771 | 1915 | 0.679 |
| Soldier A,B | Soldier River at Pisgah, IA | 06608500 | 1054 | 41.8305 | −95.9314 | 1940 | 0.738 |
| South River A | South River near Ackworth, IA | 05487470 | 1191 | 41.3372 | −93.4863 | 1940 | 0.420 |
| Thompson A,B | Thompson River at Davis City, IA | 06898000 | 1816 | 40.6403 | −93.8083 | 1942 | 0.485 |
| Timber Cr A | Timber Creek near Marshalltown, IA | 05451700 | 306 | 42.0089 | −92.8524 | 1950 | 0.661 |
| Turkey A,B | Turkey River at Garber, IA | 05412500 | 4002 | 42.7400 | −91.2618 | 1933 | 0.738 |
| Upper Iowa A,B | Upper Iowa River near Dorchester, IA | 05388250 | 1994 | 43.4211 | −91.5088 | 1975 | 0.770 |
| W Nish A | West Nishnabotna River at Randolph, IA | 06808500 | 3434 | 40.8731 | −95.5803 | 1949 | 0.788 |
| Walnut Cr A | Walnut Creek at Des Moines, IA | 05484800 | 203 | 41.5872 | −93.7033 | 1972 | 0.577 |
| Wapsipinicon A,B | Wapsipinicon River near De Witt, IA | 05422000 | 6050 | 41.7670 | −90.5349 | 1935 | 0.750 |
| WFork Cedar A | West Fork Cedar River at Finchford, IA | 05458900 | 2191 | 42.6294 | −92.5435 | 1946 | 0.726 |
| WFork DM A | Des Moines River at Humboldt, IA | 05476750 | 5843 | 42.7194 | −94.2205 | 1965 | 0.789 |
| Stat | Flow | Baseflow | BFI | Mean | Std | CV | Min | Median | Max | Skew | RB | TD1 | TD4 | TD37 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mean | 222 | 138 | 0.629 | 0.602 | 1.08 | 1.91 | 0.056 | 0.286 | 10.8 | 5.16 | 0.345 | 0.054 | 0.151 | 0.491 |
| std | 150 | 96.8 | 0.136 | 0.411 | 0.885 | 0.994 | 0.070 | 0.248 | 11.5 | 2.77 | 0.220 | 0.044 | 0.095 | 0.148 |
| min | 7.16 | 2.99 | 0.158 | 0.020 | 0.023 | 0.400 | 0 | 0 | 0.166 | 0.153 | 0.048 | 0.007 | 0.026 | 0.183 |
| 25% | 104 | 61.6 | 0.548 | 0.284 | 0.478 | 1.21 | 0.010 | 0.096 | 3.83 | 3.04 | 0.171 | 0.024 | 0.083 | 0.375 |
| 50% | 192 | 120 | 0.655 | 0.526 | 0.847 | 1.67 | 0.029 | 0.213 | 7.33 | 4.66 | 0.285 | 0.041 | 0.126 | 0.474 |
| 75% | 298 | 189 | 0.730 | 0.817 | 1.41 | 2.33 | 0.079 | 0.400 | 13.6 | 6.77 | 0.471 | 0.069 | 0.195 | 0.586 |
| max | 1080 | 612 | 0.917 | 2.96 | 11.3 | 8.45 | 0.514 | 1.57 | 195 | 17.6 | 1.39 | 0.407 | 0.675 | 0.975 |
| Stat | Decreasing | Increasing | ||||
|---|---|---|---|---|---|---|
| p < 0.01 | 0.01 ≤ p < 0.05 | p ≥ 0.05 | p < 0.01 | 0.01 ≤ p < 0.05 | p ≥ 0.05 | |
| baseflow | 0 | 0 | 1 | 28 | 6 | 7 |
| BFI | 1 | 0 | 0 | 34 | 1 | 6 |
| CV | 25 | 2 | 12 | 0 | 0 | 3 |
| max | 0 | 2 | 8 | 1 | 3 | 28 |
| mean | 0 | 0 | 0 | 21 | 6 | 15 |
| median | 0 | 0 | 0 | 24 | 8 | 10 |
| min | 0 | 0 | 2 | 27 | 4 | 9 |
| RB | 33 | 4 | 2 | 1 | 0 | 2 |
| skew | 17 | 7 | 13 | 0 | 0 | 5 |
| std | 0 | 1 | 6 | 6 | 2 | 27 |
| TD (1) | 24 | 2 | 11 | 0 | 0 | 5 |
| TD (4) | 25 | 4 | 10 | 0 | 0 | 3 |
| TD (37) | 28 | 3 | 9 | 0 | 0 | 2 |
| Short Name | BFI Slope (1000 *#/Year) | RB Slope (1000 *#/Year) | ||||||
|---|---|---|---|---|---|---|---|---|
| Full Record | 1935–1964 | 1965–1994 | 1995–2024 | Full Record | 1935–1964 | 1965–1994 | 1995–2024 | |
| Beaver Cr Grimes | 0.87 | 3.37 | −0.81 | −0.77 | −2.59 | 0.74 | ||
| Beaver Cr Hartford | 1.03 | 8.41 | 2.54 | −0.28 | −1.79 | −14.3 | −3.02 | 0.03 |
| Big Bear Cr | 2.25 | 3.82 | 1.60 | 1.05 | −3.98 | −6.30 | −2.77 | −2.31 |
| Boone | 0.66 | 0.89 | 1.45 | 0.18 | −0.66 | 2.18 | −1.07 | −0.39 |
| Boyer | 3.80 | 6.93 | 5.31 | 2.07 | −5.06 | −4.23 | −4.78 | −2.58 |
| Cedar Cr | 0.50 | 3.38 | −0.23 | −0.07 | −0.50 | −7.21 | 2.44 | −0.22 |
| Cedar Janesville | 0.91 | 5.26 | 2.24 | −1.37 | −1.03 | −4.11 | −2.31 | 1.36 |
| Chariton near Char | 0.01 | −1.67 | −0.19 | 0.41 | 2.13 | −1.50 | ||
| Clear Cr | 1.98 | 1.47 | −0.20 | −2.77 | −2.83 | 0.06 | ||
| E Nish | 3.28 | 6.52 | 4.81 | 2.02 | −4.06 | −6.74 | −5.78 | −2.74 |
| EFork DM | 0.84 | −1.06 | 2.08 | 0.48 | −0.63 | 1.49 | −0.87 | −0.18 |
| English | 1.34 | −0.36 | 2.54 | 1.76 | −1.24 | 1.15 | −2.47 | −1.94 |
| Floyd | 3.04 | 1.82 | 6.93 | −2.00 | −3.00 | 0.38 | −5.56 | 0.42 |
| Iowa Marshalltown | 0.94 | 0.92 | 4.14 | −1.06 | −1.12 | 1.04 | −2.18 | 0.85 |
| L Sioux Correctionville | 1.13 | −0.51 | 2.95 | −1.27 | −1.06 | 1.09 | −1.83 | 0.40 |
| Maple | 3.14 | 1.98 | 5.94 | 1.15 | −3.71 | −0.45 | −5.36 | −2.16 |
| Maquoketa | 1.51 | 1.45 | 3.55 | 0.69 | −1.96 | −1.95 | −4.61 | −0.64 |
| Middle River | 1.28 | 1.91 | 3.11 | 0.18 | −1.88 | 0.12 | −5.05 | −2.63 |
| N Raccoon | 0.81 | −0.32 | 2.17 | 0.81 | −0.63 | 0.56 | −1.03 | −1.01 |
| N Skunk | 1.88 | 1.99 | 2.40 | 0.57 | −1.83 | −1.59 | −1.49 | −1.35 |
| Nodaway | 2.41 | 6.22 | 3.64 | −0.42 | −2.88 | −6.04 | −4.34 | 1.25 |
| North River | 2.07 | 0.70 | 4.59 | 1.37 | −2.40 | −1.87 | −3.56 | −1.57 |
| Rapid Cr | 2.49 | 0.30 | 3.64 | 0.40 | −4.63 | 0.90 | −7.21 | −0.91 |
| Richland Cr | 2.26 | 3.77 | −1.68 | −4.59 | −5.16 | 1.12 | ||
| Rock | 2.62 | 3.40 | 0.30 | −2.28 | −2.80 | −0.46 | ||
| S Raccoon | 1.56 | 1.49 | 3.53 | 0.52 | −1.91 | −3.87 | −3.45 | −1.97 |
| S Skunk | 1.07 | 2.70 | 2.36 | −0.22 | −0.90 | −0.44 | −1.16 | −0.47 |
| Salt Cr | 2.68 | 6.12 | 1.08 | −1.40 | −4.33 | −13.7 | −0.33 | 0.38 |
| SFork Chariton | 0.92 | 2.59 | 2.27 | −2.49 | −4.10 | −6.99 | ||
| Soldier | 4.64 | 8.51 | 5.21 | 2.11 | −7.35 | −17.5 | −8.02 | −4.80 |
| South River | 1.12 | −0.81 | 3.50 | 0.02 | −1.54 | 2.35 | −6.01 | −2.06 |
| Thompson | 1.36 | −1.51 | 1.31 | 0.67 | −0.98 | −0.51 | −0.71 | −2.25 |
| Timber Cr | 1.82 | 4.83 | −0.72 | −3.71 | −9.02 | 0.27 | ||
| Turkey | 1.49 | 2.10 | 4.52 | −0.34 | −1.98 | −1.86 | −4.61 | 0.93 |
| Upper Iowa | 0.36 | 3.65 | 0.00 | −0.47 | −4.69 | 0.38 | ||
| W Nish | 3.70 | 5.55 | 2.76 | −5.01 | −5.97 | −3.52 | ||
| Walnut Cr | −2.30 | 2.24 | −2.93 | 4.21 | 0.33 | 4.38 | ||
| Wapsipinicon | 0.37 | 0.64 | 0.96 | −0.26 | −0.48 | −0.01 | −1.14 | −0.60 |
| WFork Cedar | 0.79 | 3.48 | 2.75 | 0.00 | −1.09 | −5.05 | −2.37 | −0.57 |
| WFork DM | 0.63 | 1.75 | −0.55 | −0.46 | −0.74 | −0.01 | ||
| White Breast Cr | 0.56 | 0.73 | 1.65 | 0.51 | −0.07 | −2.24 | ||
| Winnebago | 0.97 | 0.51 | 1.79 | −0.77 | −1.08 | −0.41 | −1.17 | 0.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anderson, E.S.; Schilling, K.E. Baseflow Index Trends in Iowa Rivers and the Relationships to Other Hydrologic Metrics. Hydrology 2025, 12, 116. https://doi.org/10.3390/hydrology12050116
Anderson ES, Schilling KE. Baseflow Index Trends in Iowa Rivers and the Relationships to Other Hydrologic Metrics. Hydrology. 2025; 12(5):116. https://doi.org/10.3390/hydrology12050116
Chicago/Turabian StyleAnderson, Elliot S., and Keith E. Schilling. 2025. "Baseflow Index Trends in Iowa Rivers and the Relationships to Other Hydrologic Metrics" Hydrology 12, no. 5: 116. https://doi.org/10.3390/hydrology12050116
APA StyleAnderson, E. S., & Schilling, K. E. (2025). Baseflow Index Trends in Iowa Rivers and the Relationships to Other Hydrologic Metrics. Hydrology, 12(5), 116. https://doi.org/10.3390/hydrology12050116






