Hydrological Modelling and Remote Sensing for Assessing the Impact of Vegetation Cover Changes
Abstract
1. Introduction
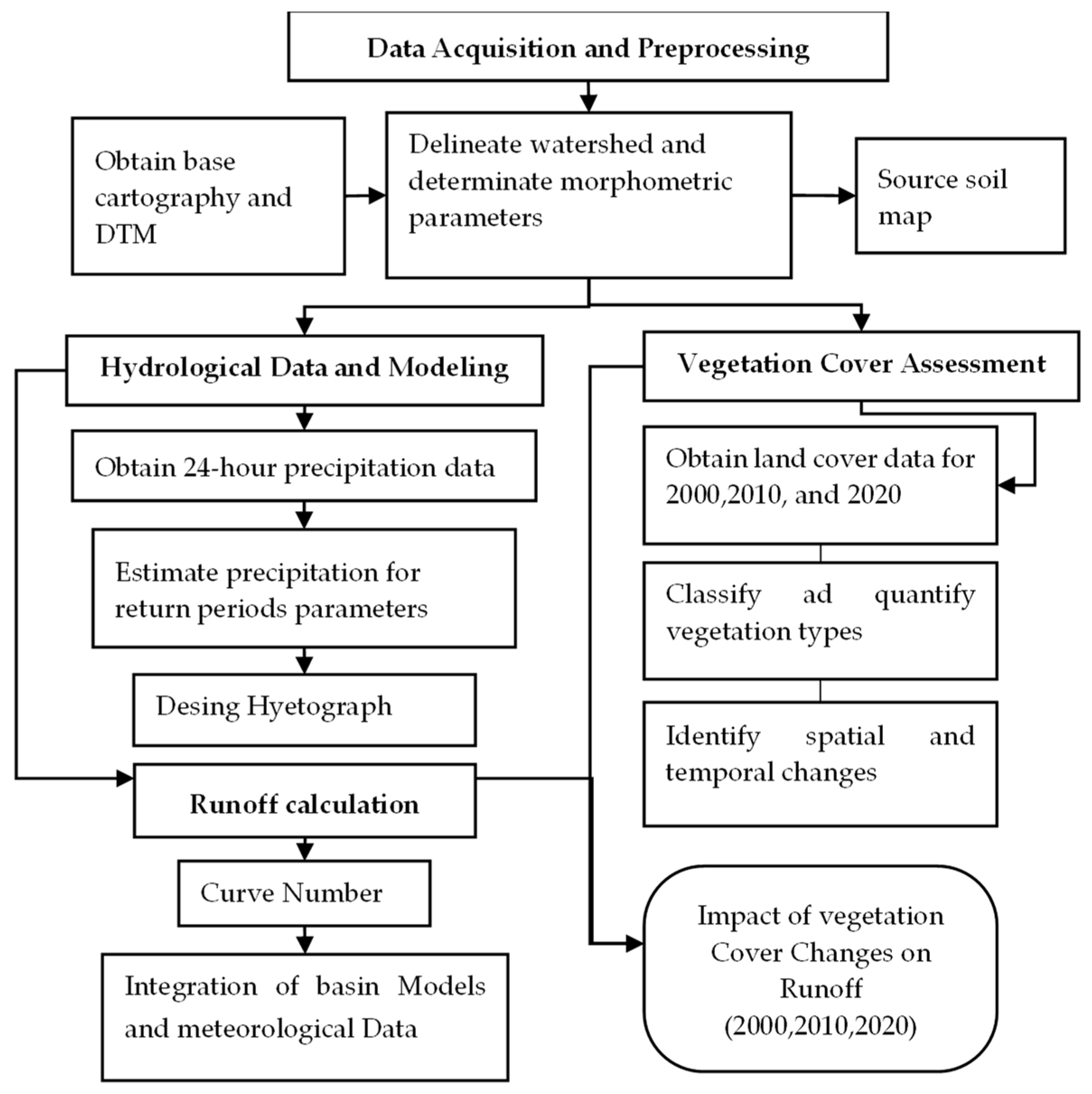
2. Materials and Methods
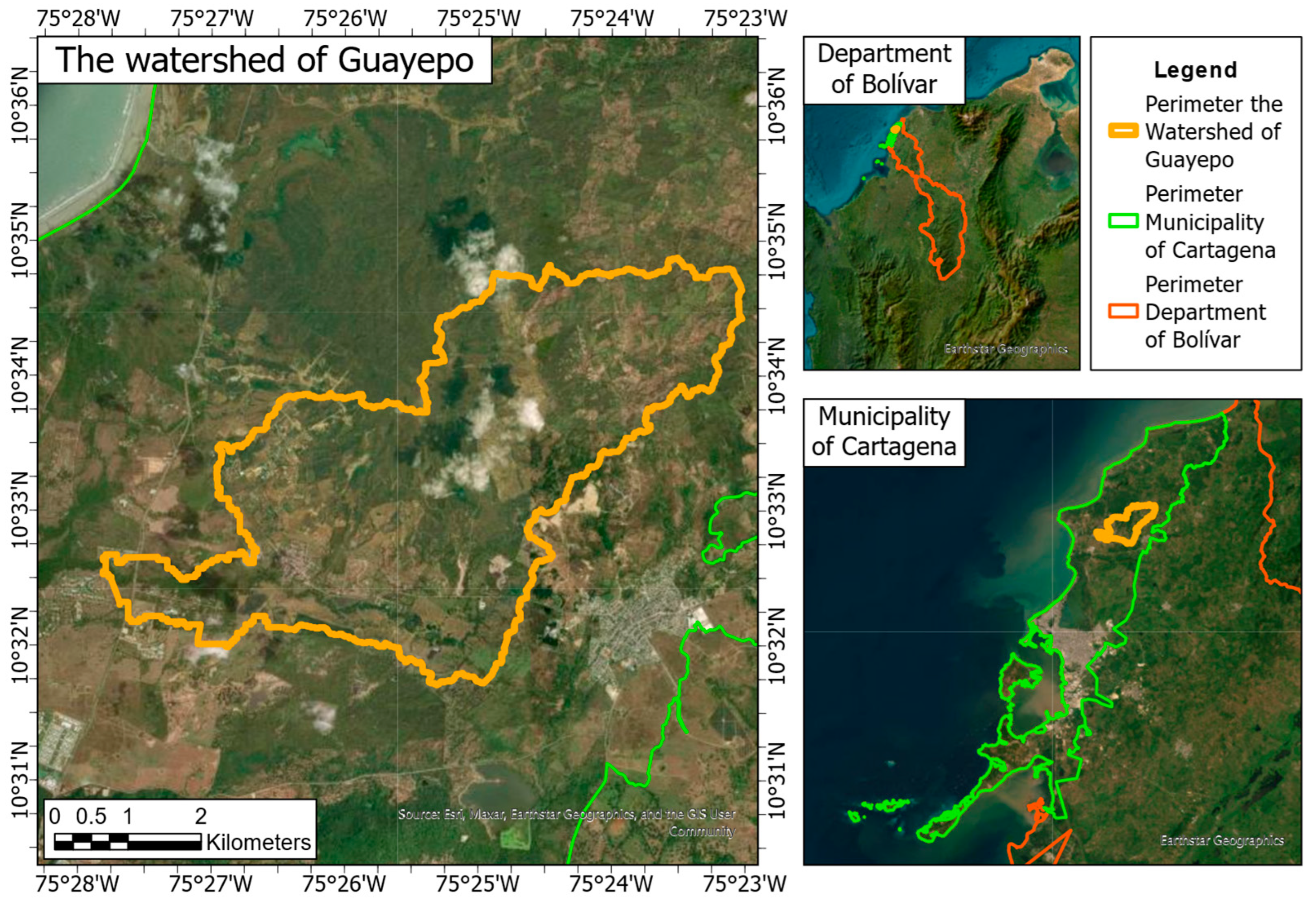
2.1. Data Acquisition and Preprocessing
2.2. Hydrological Data and Modelling
2.3. Vegetation Cover Assessment
2.4. Hydrological Modelling
3. Results
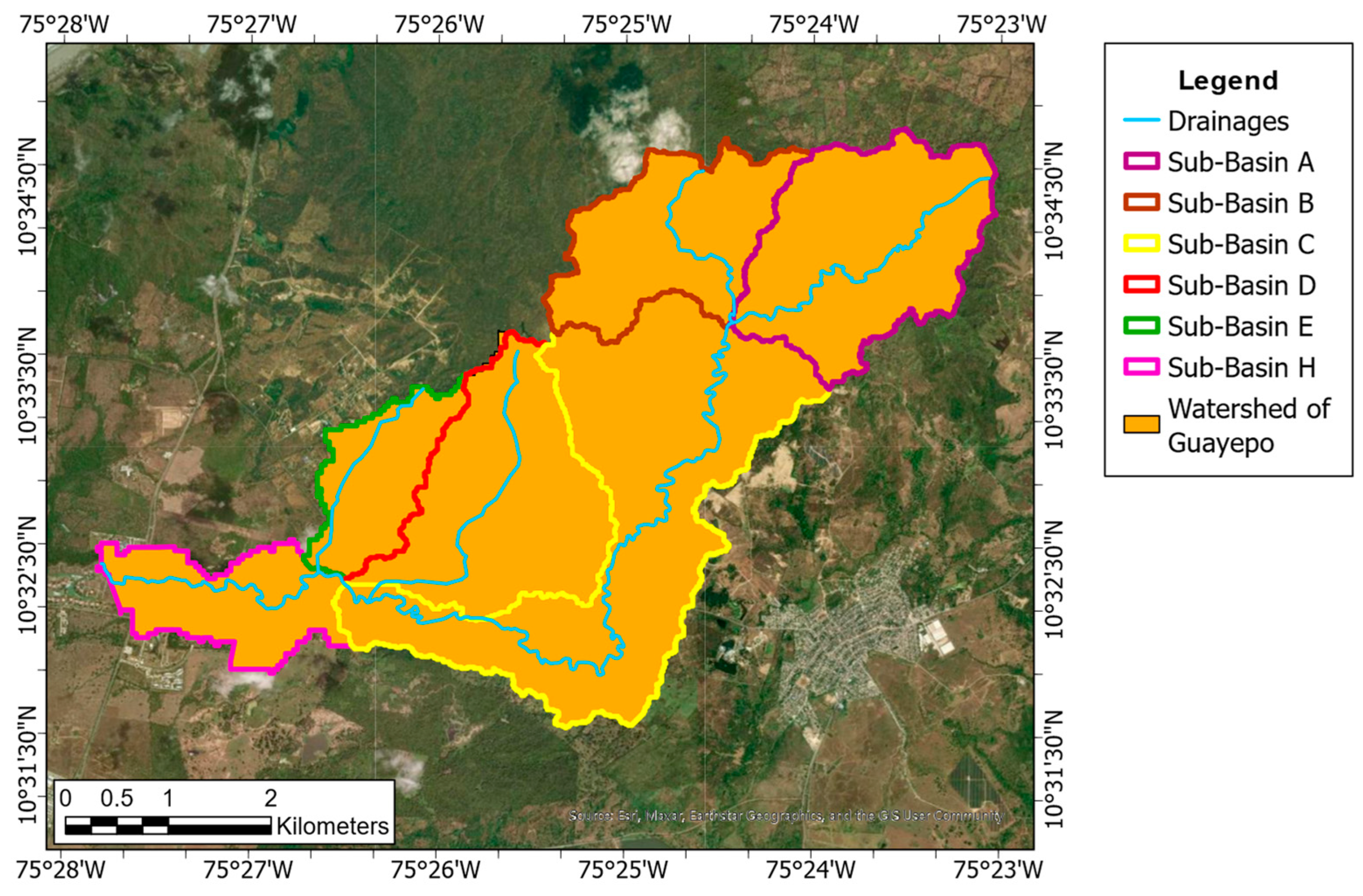
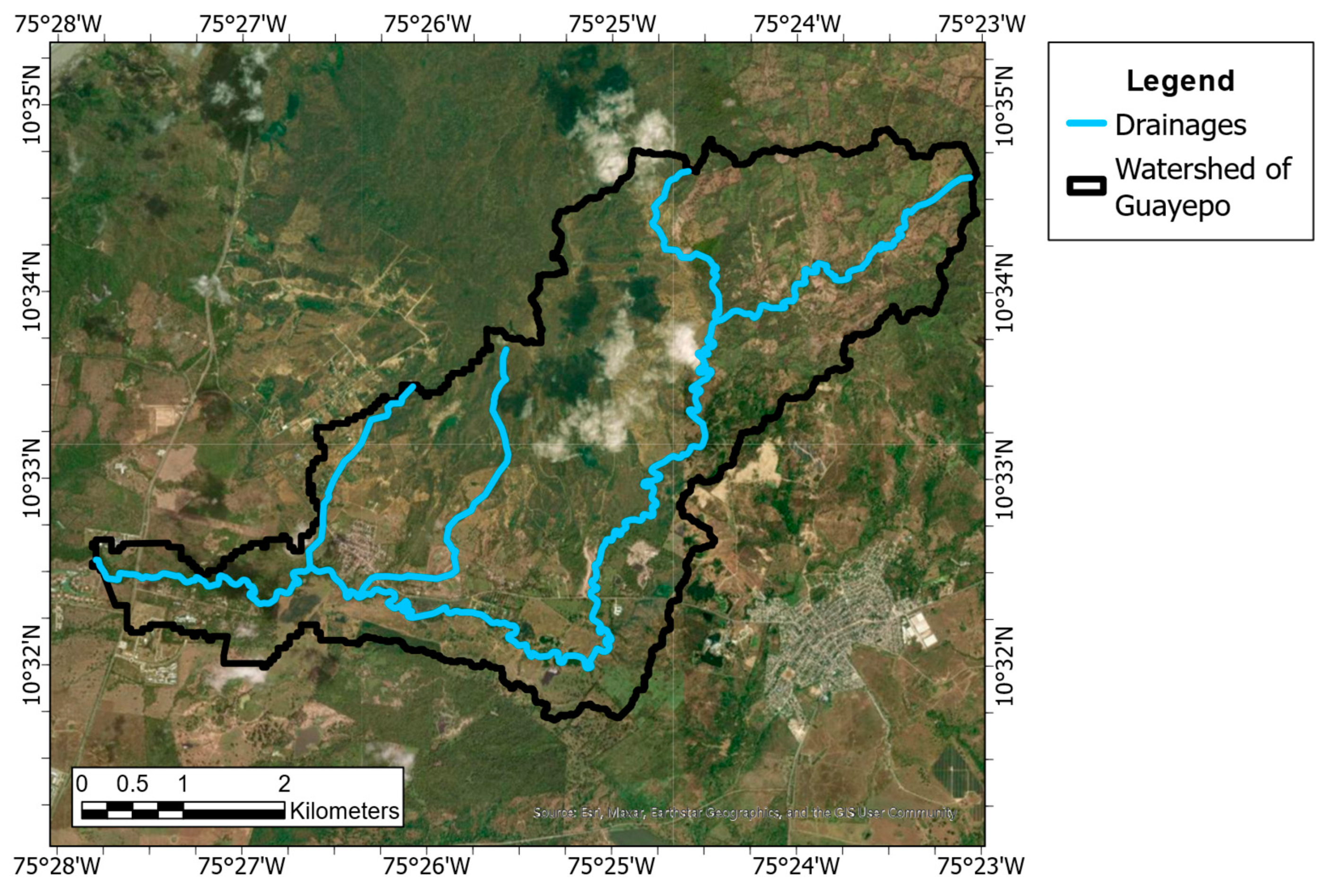
3.1. Data Processing and Preliminary Analysis
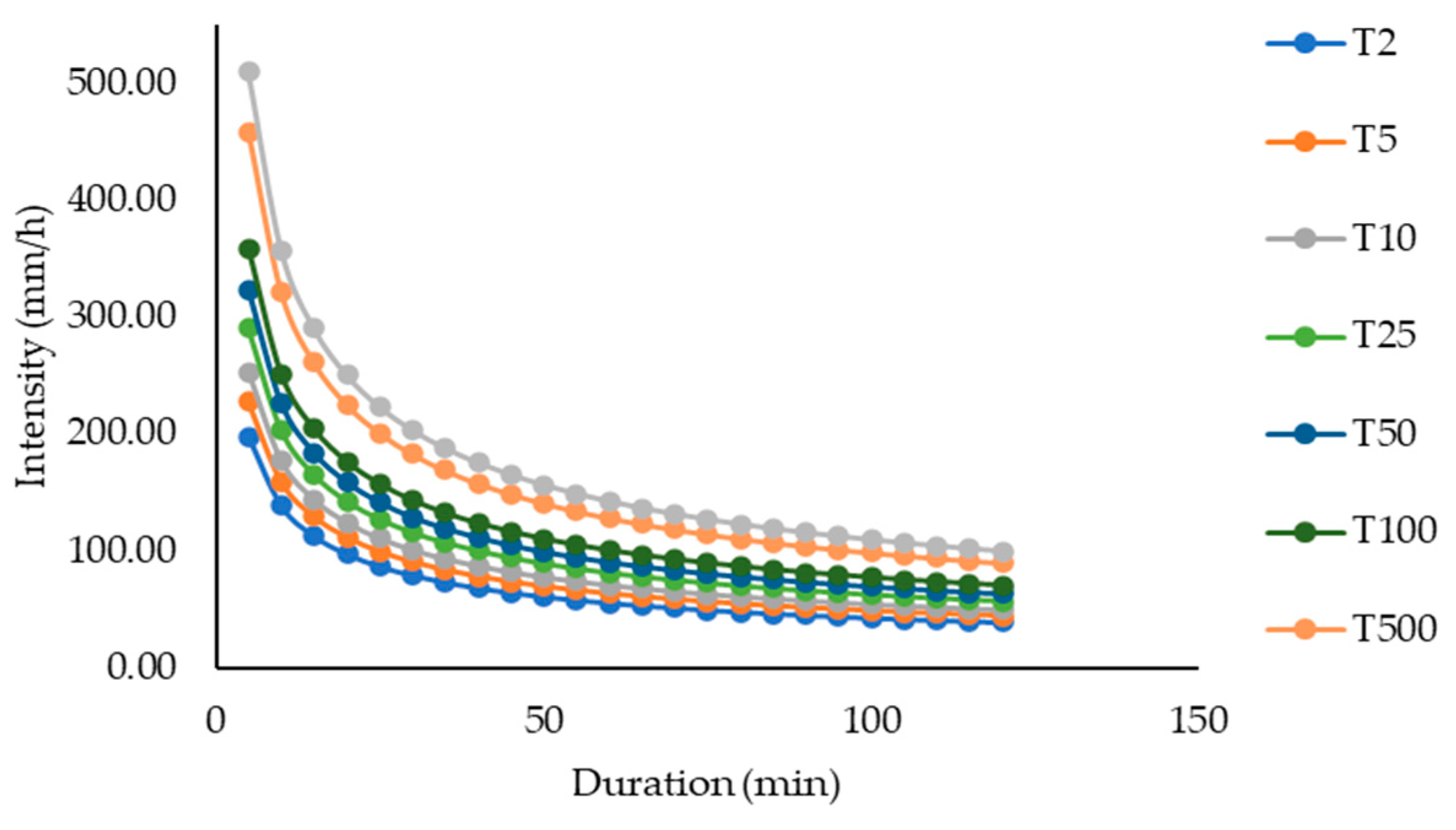
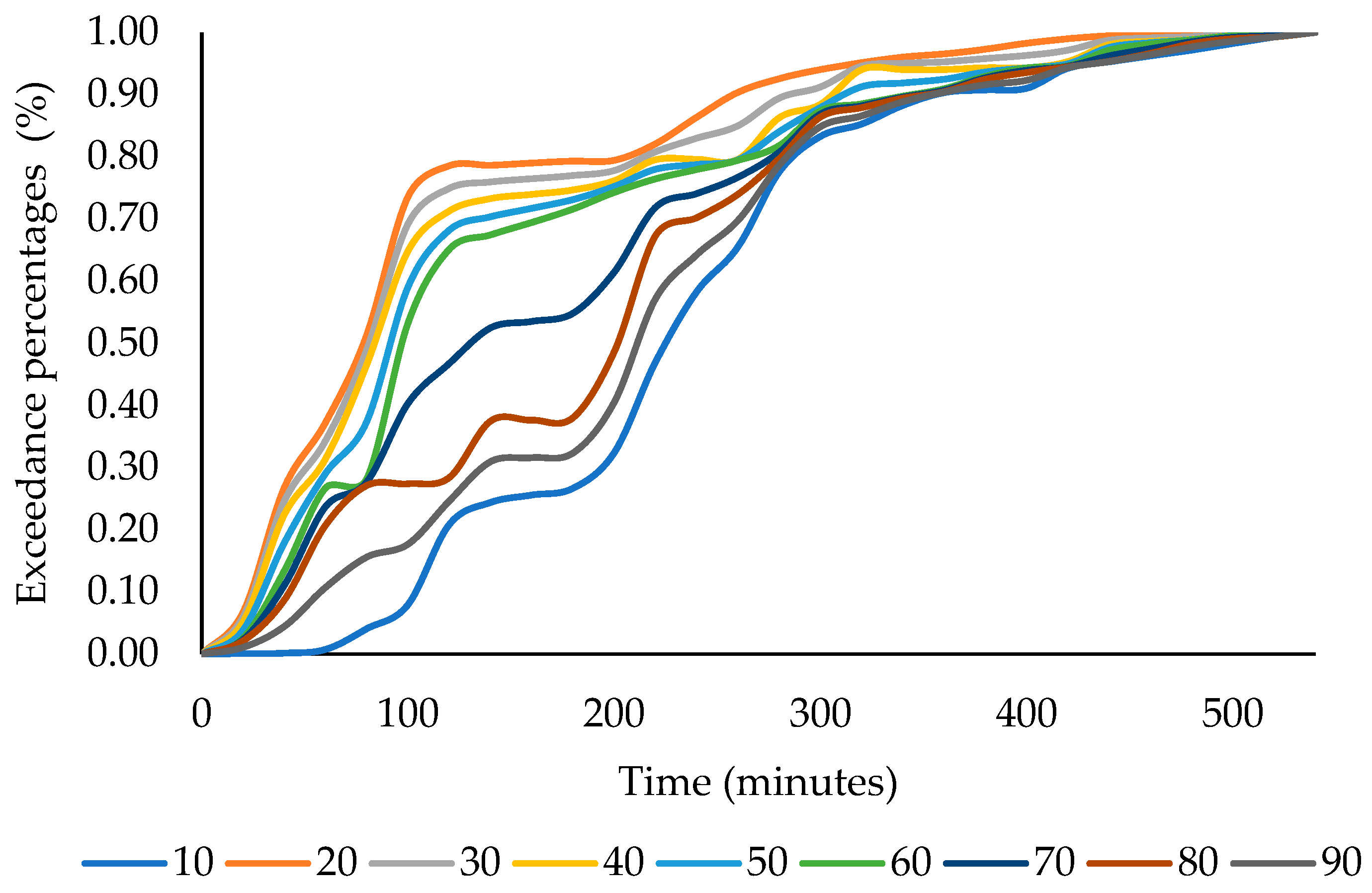
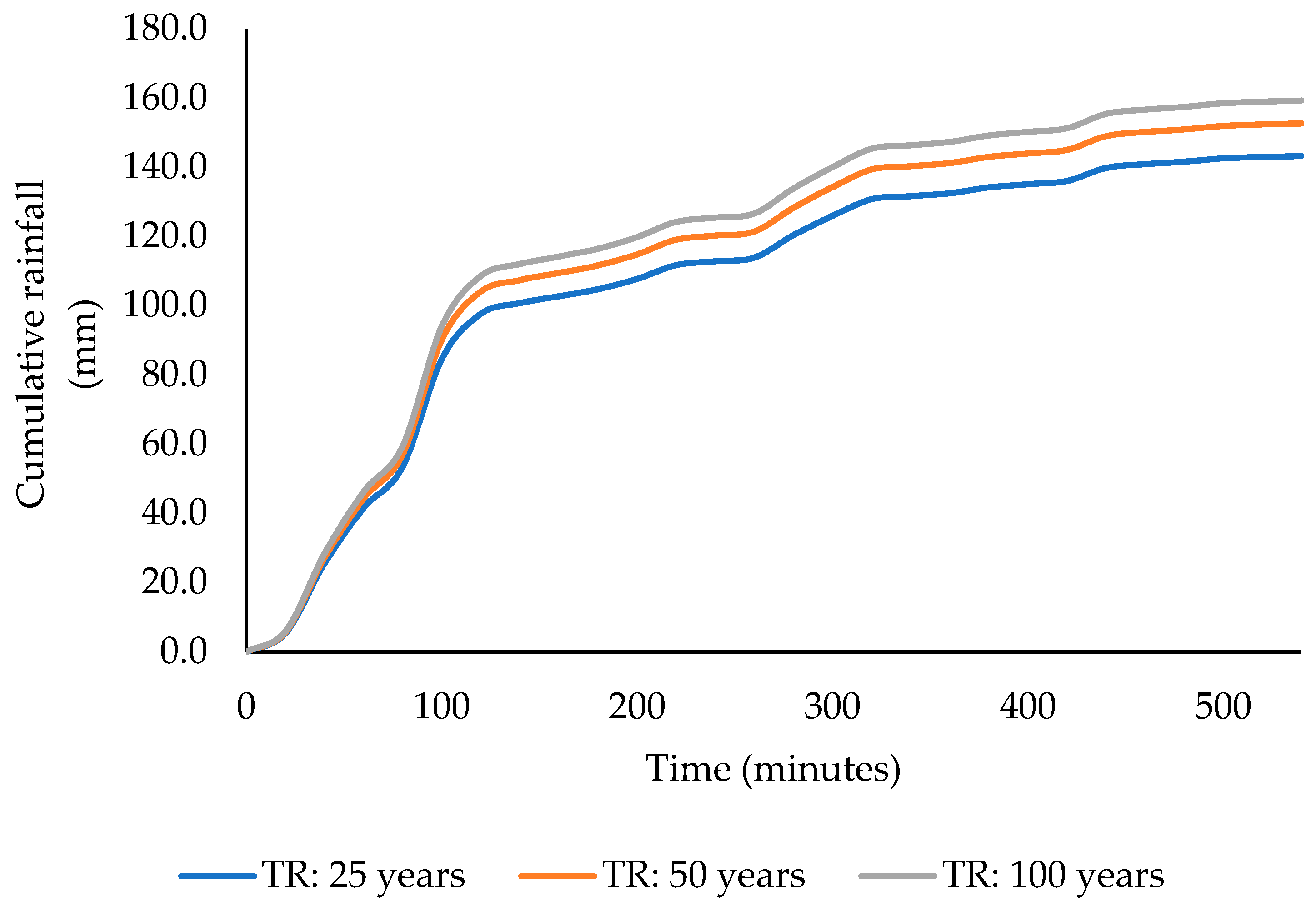
3.2. Precipitation Analysis and IDF Curves
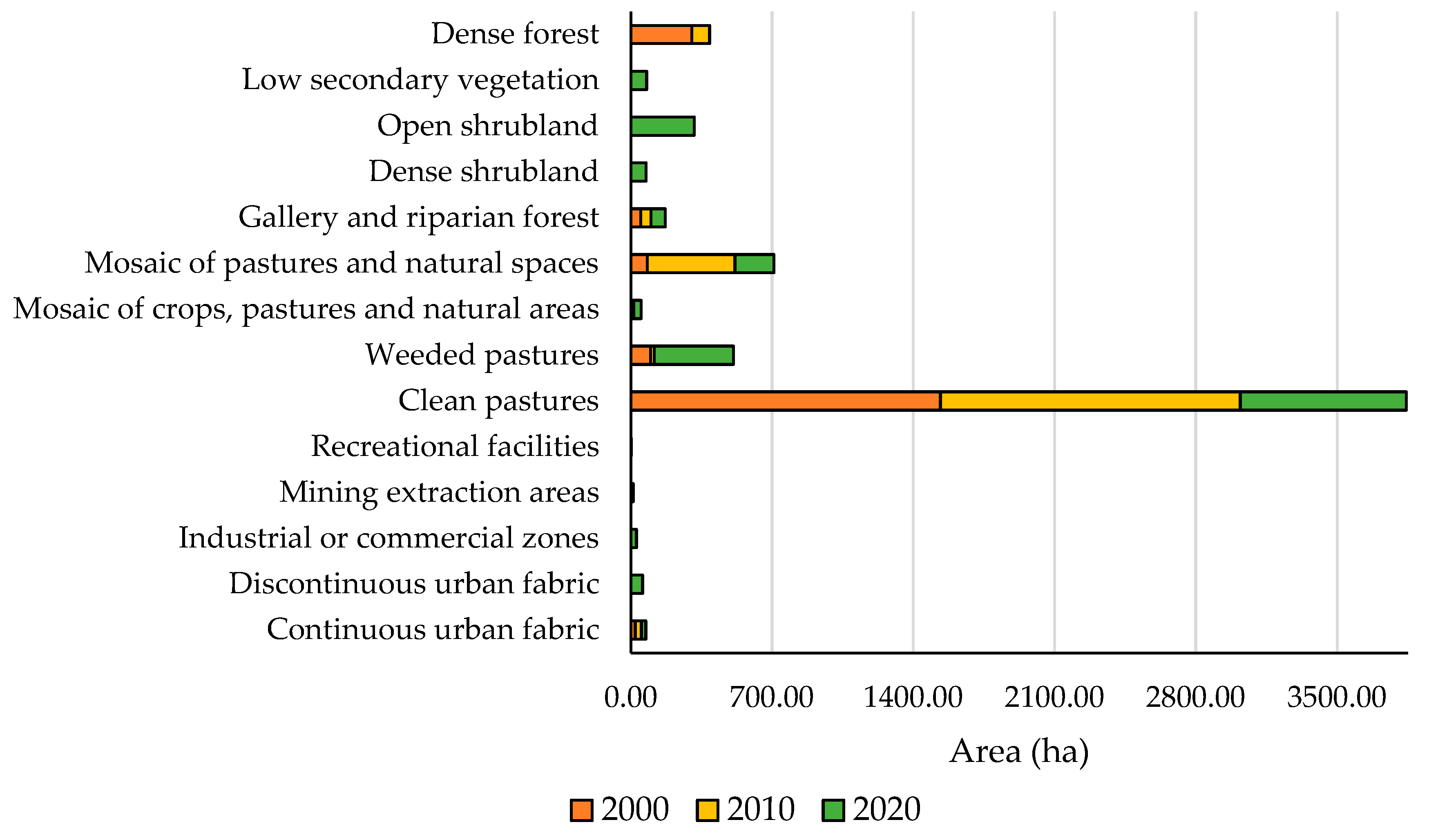
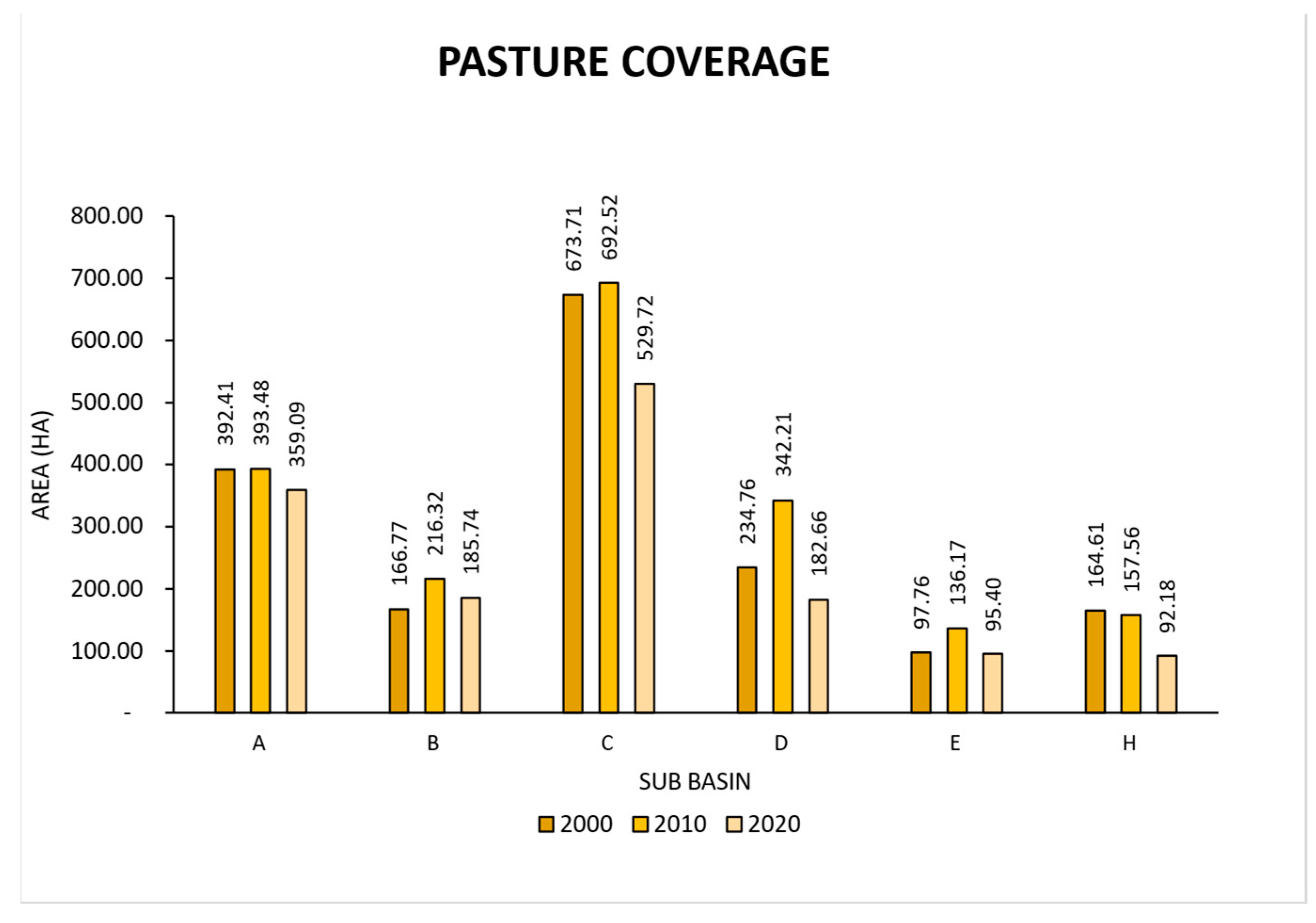
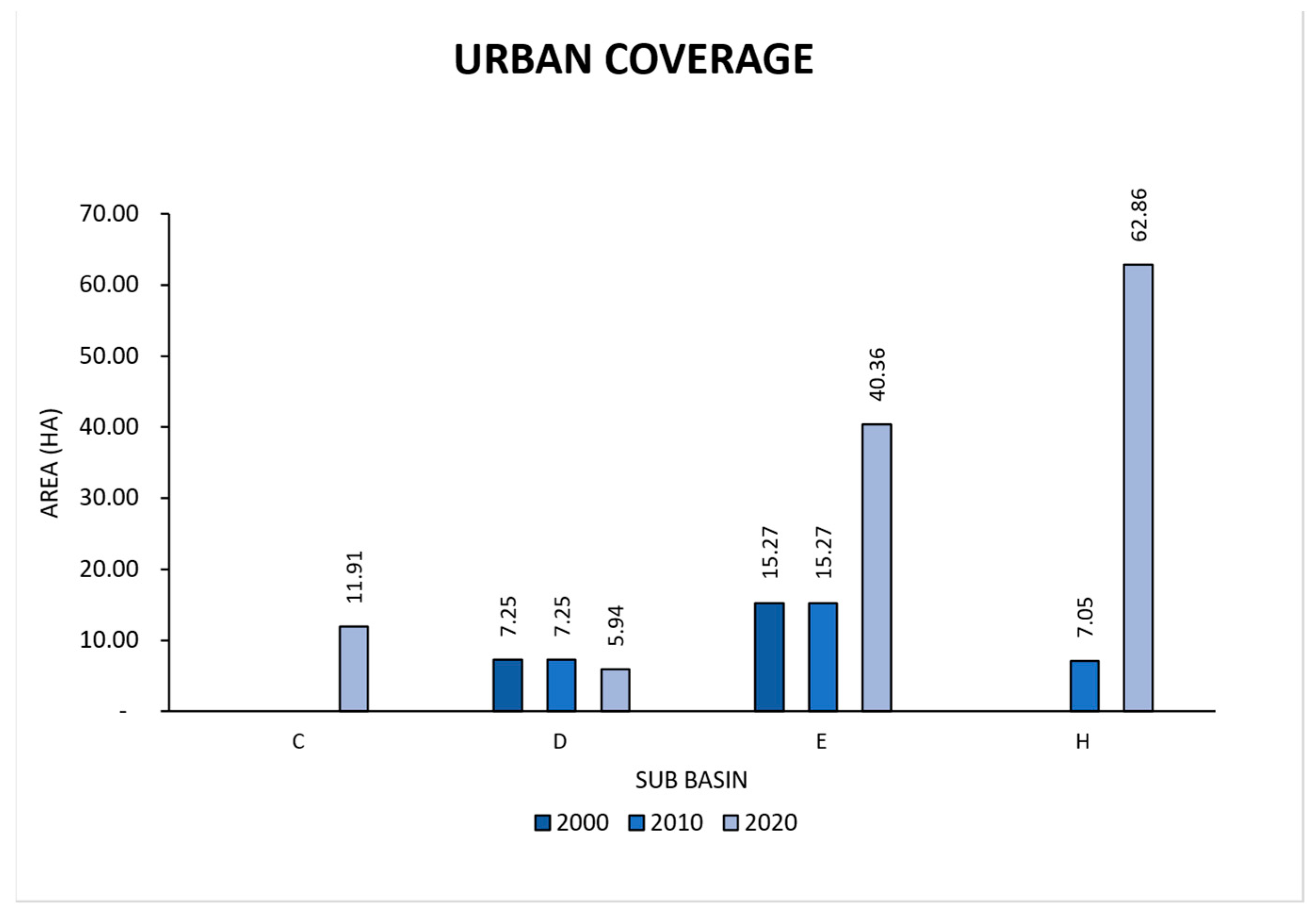
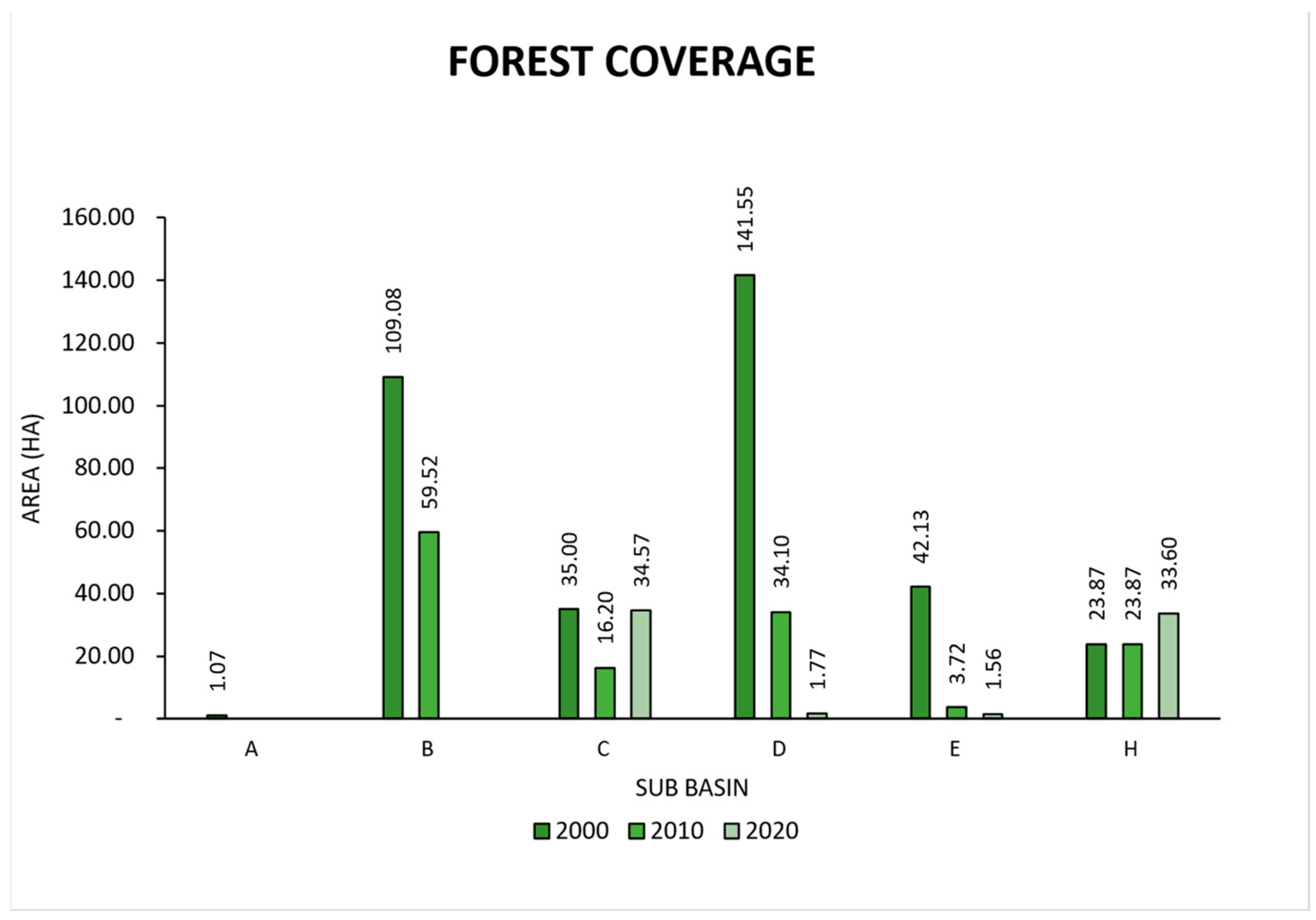
3.3. Vegetation Cover Change Assessment
3.4. Hydrological Simulation Using the HEC-HMS Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Year | Precipitation (mm) | Year | Precipitation (mm) |
|---|---|---|---|
| 1974 | 137 | 1997 | 94 |
| 1975 | 174 | 1998 | 62.5 |
| 1976 | 95 | 1999 | 106 |
| 1977 | 120 | 2000 | 32.5 |
| 1978 | 140 | 2001 | 112.2 |
| 1979 | 140 | 2002 | 90.3 |
| 1980 | 83 | 2003 | 80.5 |
| 1981 | 78.8 | 2004 | 122 |
| 1982 | 52.8 | 2005 | 106 |
| 1983 | 120 | 2006 | 138 |
| 1984 | 84 | 2007 | 122 |
| 1985 | 95.7 | 2008 | 108.5 |
| 1986 | 60.34 | 2009 | 81 |
| 1987 | 72.73 | 2010 | 109.3 |
| 1988 | 150 | 2011 | 75 |
| 1989 | 100 | 2012 | 105.1 |
| 1990 | 137 | 2013 | 56.1 |
| 1991 | 85.5 | 2014 | 132 |
| 1992 | 56.6 | 2015 | 50.5 |
| 1993 | 87.4 | 2016 | 121.8 |
| 1994 | 85 | 2017 | 50 |
| 1995 | 84 | 2018 | 85.4 |
| 1996 | 80 | 2019 | 127 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| P Max 24 h (mm) | 142.55 | 101.7 | 108.5 | 65.1 | 135.3 | 72.4 |
| Factor Reduction Time | 0.89 | 0.94 | 0.92 | 0.92 | 0.99 | 0.99 |
| t (min) | 14-nov-20 | 25-nov-97 | 13-jun-71 | 23-oct-78 | 28-jul-80 | 3-oct-81 |
| 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 20 | 0.09 | 2.00 | 5.10 | 4.00 | 3.40 | 10.20 |
| 40 | 0.19 | 8.30 | 27.00 | 8.00 | 30.10 | 19.10 |
| 60 | 0.93 | 30.00 | 37.20 | 12.40 | 52.60 | 19.10 |
| 80 | 5.15 | 57.30 | 46.50 | 16.90 | 69.00 | 19.40 |
| 100 | 10.11 | 79.30 | 64.80 | 31.90 | 98.90 | 19.60 |
| 120 | 26.51 | 84.50 | 71.20 | 39.00 | 105.60 | 20.30 |
| 140 | 31.03 | 87.50 | 73.20 | 40.40 | 105.70 | 26.80 |
| 160 | 32.54 | 88.10 | 73.90 | 41.60 | 106.20 | 26.90 |
| 180 | 33.90 | 88.30 | 74.60 | 42.90 | 106.60 | 27.20 |
| 200 | 41.22 | 89.20 | 76.10 | 44.50 | 106.80 | 34.80 |
| 220 | 59.70 | 89.90 | 82.00 | 45.80 | 106.90 | 48.10 |
| 240 | 74.13 | 89.90 | 86.30 | 46.70 | 107.00 | 50.20 |
| 260 | 83.31 | 89.90 | 90.30 | 47.60 | 107.00 | 52.90 |
| 280 | 98.66 | 89.90 | 92.50 | 49.00 | 107.10 | 61.70 |
| 300 | 109.87 | 89.90 | 94.00 | 49.90 | 118.90 | 62.50 |
| 320 | 111.80 | 89.90 | 96.00 | 51.10 | 127.90 | 63.30 |
| 340 | 113.73 | 89.90 | 97.10 | 52.90 | 129.10 | 64.20 |
| 360 | 115.66 | 89.90 | 97.30 | 54.20 | 129.80 | 64.60 |
| 380 | 117.59 | 90.20 | 98.40 | 55.70 | 130.80 | 64.90 |
| 400 | 119.00 | 90.20 | 98.70 | 56.50 | 132.10 | 65.10 |
| 420 | 120.14 | 90.50 | 98.90 | 57.10 | 133.30 | 67.40 |
| 440 | 121.28 | 91.10 | 99.40 | 58.20 | 133.80 | 70.10 |
| 460 | 122.42 | 92.40 | 99.70 | 58.80 | 134.00 | 70.50 |
| 480 | 123.59 | 93.90 | 99.90 | 59.20 | 134.20 | 70.70 |
| 500 | 124.92 | 95.20 | 99.90 | 59.60 | 134.30 | 70.80 |
| 520 | 126.25 | 95.40 | 99.90 | 59.80 | 134.40 | 71.00 |
| 540 | 127.16 | 95.60 | 99.90 | 59.90 | 134.40 | 71.50 |
| Return Periods | ||||||
| t (min) | 5 | 10 | 20 | 25 | 50 | 100 |
| 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 20 | 4.4 | 5.0 | 5.4 | 5.5 | 5.8 | 6.1 |
| 40 | 20.7 | 23.2 | 25.1 | 25.6 | 27.3 | 28.5 |
| 60 | 33.7 | 37.8 | 40.8 | 41.6 | 44.3 | 46.3 |
| 80 | 43.3 | 48.6 | 52.5 | 53.5 | 57.1 | 59.5 |
| 100 | 68.5 | 76.8 | 82.9 | 84.6 | 90.2 | 94.1 |
| 120 | 79.0 | 88.7 | 95.7 | 97.7 | 104.1 | 108.6 |
| 140 | 81.5 | 91.5 | 98.8 | 100.8 | 107.4 | 112.0 |
| 160 | 83.1 | 93.3 | 100.7 | 102.7 | 109.5 | 114.2 |
| 180 | 84.8 | 95.1 | 102.7 | 104.8 | 111.7 | 116.5 |
| 200 | 87.2 | 97.8 | 105.6 | 107.8 | 114.8 | 119.8 |
| 220 | 90.4 | 101.4 | 109.5 | 111.7 | 119.1 | 124.2 |
| 240 | 91.3 | 102.5 | 110.6 | 112.8 | 120.3 | 125.5 |
| 260 | 92.2 | 103.4 | 111.7 | 113.9 | 121.4 | 126.7 |
| 280 | 97.4 | 109.3 | 118.0 | 120.4 | 128.3 | 133.8 |
| 300 | 101.9 | 114.4 | 123.5 | 126.0 | 134.2 | 140.0 |
| 320 | 105.8 | 118.7 | 128.2 | 130.7 | 139.3 | 145.4 |
| 340 | 106.5 | 119.5 | 129.1 | 131.6 | 140.3 | 146.4 |
| 360 | 107.2 | 120.3 | 129.9 | 132.5 | 141.2 | 147.3 |
| 380 | 108.6 | 121.8 | 131.5 | 134.2 | 143.0 | 149.2 |
| 400 | 109.3 | 122.7 | 132.5 | 135.1 | 144.0 | 150.2 |
| 420 | 110.1 | 123.5 | 133.4 | 136.1 | 145.0 | 151.3 |
| 440 | 113.1 | 126.9 | 137.0 | 139.8 | 149.0 | 155.4 |
| 460 | 114.0 | 127.9 | 138.1 | 140.9 | 150.2 | 156.7 |
| 480 | 114.6 | 128.6 | 138.8 | 141.6 | 150.9 | 157.4 |
| 500 | 115.4 | 129.4 | 139.8 | 142.6 | 152.0 | 158.5 |
| 520 | 115.7 | 129.8 | 140.1 | 143.0 | 152.4 | 158.9 |
| 540 | 115.9 | 130.0 | 140.4 | 143.2 | 152.7 | 159.2 |
References
- dos Santos, F.M.; De Oliveira, R.P.; Mauad, F.F. Evaluating a Parsimonious Watershed Model versus SWAT to Estimate Streamflow, Soil Loss and River Contamination in Two Case Studies in Tietê River Basin, São Paulo, Brazil. J. Hydrol. Reg. Stud. 2020, 29, 100685. [Google Scholar] [CrossRef]
- Te Chow, V.; Maidment, D.R.; Mays, L.W. Hidrología Aplicada; McGraw-Hill: New York, NY, USA, 1994; ISBN 958-600-171-7. [Google Scholar]
- Aparicio Mijares, F.J. Fundamentos de Hidrología de Superficie; Grupo Noriega, Ed.; Limusa: Cuernavaca, Mexico, 1989; Volume 53, ISBN 9788578110796. [Google Scholar]
- Huntington, T.G. Evidence for Intensification of the Global Water Cycle: Review and Synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Chen, D.; Li, J.; Yang, X.; Zhou, Z.; Pan, Y.; Li, M. Quantifying Water Provision Service Supply, Demand and Spatial Flow for Land Use Optimisation: A Case Study in the YanHe Watershed. Ecosyst. Serv. 2020, 43, 101117. [Google Scholar] [CrossRef]
- Obeysekera, J.; Salas, J.D. Frequency of Recurrent Extremes under Nonstationarity. J. Hydrol. Eng. 2016, 21, 04016005. [Google Scholar] [CrossRef]
- Yazdanfar, Z.; Sharma, A. Urban Drainage System Planning and Design—Challenges with Climate Change and Urbanization: A Review. Water Sci. Technol. 2015, 72, 165–179. [Google Scholar] [CrossRef]
- Spence, C.; Whitfield, P.H.; Pomeroy, J.W.; Pietroniro, A.; Burn, D.H.; Peters, D.L.; St-Hilaire, A. A Review of the Prediction in Ungauged Basins (PUB) Decade in Canada. Can. Water Resour. J. 2013, 38, 253–262. [Google Scholar] [CrossRef]
- Butts, M.B.; Payne, J.T.; Kristensen, M.; Madsen, H. An Evaluation of the Impact of Model Structure on Hydrological Modelling Uncertainty for Streamflow Simulation. J. Hydrol. 2004, 298, 242–266. [Google Scholar] [CrossRef]
- Shin, M.-J.; Kim, C.-S. Analysis of the Effect of Uncertainty in Rainfall-Runoff Models on Simulation Results Using a Simple Uncertainty-Screening Method. Water Resour. 2019, 11, 1361. [Google Scholar] [CrossRef]
- Alipour, M.H. Streamflow Prediction in Ungauged Basins Located within Data-Scarce Areas Using XGBoost: Role of Feature Engineering and Explainability. Int. J. River Basin Manag. 2025, 23, 71–92. [Google Scholar] [CrossRef]
- Sierra-Sánchez, A.; Coronado-Hernandez, O.E.; Paternina-Verona, D.A.; Gatica, G.; Ramos, H.M. Statistical Analysis to Quantify the Impact of Map Type on Estimating Peak Discharge in Non-Instrumented Basins. Trans. Energy Syst. Eng. Appl. 2023, 4, 1–17. [Google Scholar] [CrossRef]
- Genxu, W.; Guangsheng, L.; Chunjie, L. Effects of Changes in Alpine Grassland Vegetation Cover on Hillslope Hydrological Processes in a Permafrost Watershed. J. Hydrol. 2012, 444–445, 22–33. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, Y.; Fang, Y.; Liu, B.; Xia, D. Modeling and Assessing Hydrologic Processes for Historical and Potential Land-Cover Change in the Duoyingping Watershed, Southwest China. Phys. Chem. Earth Parts A/B/C 2012, 53–54, 19–29. [Google Scholar] [CrossRef]
- Jehanzaib, M.; Ajmal, M.; Achite, M.; Kim, T.-W. Comprehensive Review: Advancements in Rainfall-Runoff Modelling for Flood Mitigation. Climate 2022, 10, 147. [Google Scholar] [CrossRef]
- Sahu, M.K.; Shwetha, H.R.; Dwarakish, G.S. State-of-the-Art Hydrological Models and Application of the HEC-HMS Model: A Review. Model. Earth Syst. Environ. 2023, 9, 3029–3051. [Google Scholar] [CrossRef]
- Castro, C.V.; Maidment, D.R. GIS Preprocessing for Rapid Initialization of HEC-HMS Hydrological Basin Models Using Web-Based Data Services. Environ. Model. Softw. 2020, 130, 104732. [Google Scholar] [CrossRef]
- Miyata, S.; Gomi, T.; Sidle, R.C.; Hiraoka, M.; Onda, Y.; Yamamoto, K.; Nonoda, T. Assessing Spatially Distributed Infiltration Capacity to Evaluate Storm Runoff in Forested Catchments: Implications for Hydrological Connectivity. Sci. Total Environ. 2019, 669, 148–159. [Google Scholar] [CrossRef]
- Yu, Y.; Zhu, R.; Ma, D.; Liu, D.; Liu, Y.; Gao, Z.; Yin, M.; Bandala, E.R.; Rodrigo-Comino, J. Multiple Surface Runoff and Soil Loss Responses by Sandstone Morphologies to Land-Use and Precipitation Regimes Changes in the Loess Plateau, China. Catena 2022, 217, 106477. [Google Scholar] [CrossRef]
- Gao, H.; Wu, Z.; Jia, L.; Pang, G. Vegetation Change and Its Influence on Runoff and Sediment in Different Landform Units, Wei River, China. Ecol. Eng. 2019, 141, 105609. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, J.; Li, P.; Li, Z.; Lu, K.; Wang, X.; Wang, F.; Cheng, Y.; Wang, B. Vegetation Restoration Projects and Their Influence on Runoff and Sediment in China. Ecol. Indic. 2018, 95, 233–241. [Google Scholar] [CrossRef]
- Gao, Q.; Yu, M. Forest Cover and Locality Regulate Response of Watershed Discharge to Rainfall Variability in Caribbean Region. Forests 2024, 15, 154. [Google Scholar] [CrossRef]
- Liu, W.; Xu, Z.; Wei, X.; Li, Q.; Fan, H.; Duan, H.; Wu, J. Assessing Hydrological Responses to Reforestation and Fruit Tree Planting in a Sub-Tropical Forested Watershed Using a Combined Research Approach. J. Hydrol. 2020, 590, 125480. [Google Scholar] [CrossRef]
- Liu, Y.F.; Liu, Y.; Wu, G.L.; Shi, Z.H. Runoff Maintenance and Sediment Reduction of Different Grasslands Based on Simulated Rainfall Experiments. J. Hydrol. 2019, 572, 329–335. [Google Scholar] [CrossRef]
- Vargas Garay, L.; Torres Goyeneche, O.D.; Carrillo Soto, G.A. Evaluation of SCS—Unit Hydrograph Model to Estimate Peak Flows in Watersheds of Norte de Santander. Respuestas 2019, 24, 6–15. [Google Scholar] [CrossRef]
- Chantre Velasco, M. Análisis Comparativo de Cambios de Área En Coberturas En La Parte Alta de La Subcuenca Rio Palacé, a Través de Imágenes Landsat Entre 1989 y 2016; Especialización en Sistemas De Información Geográfica, Universidad de Manizales: Manizales, Colombia, 2017. [Google Scholar]
- Yabrudy, H.; Sotomayor, A. Variación Histórica Del Coeficiente de Escorrentía En La Microcuenca Del Canal Ricaurte de La Ciudad de Cartagena; Universidad de Cartagena: Cartagena, Colombia, 2020. [Google Scholar]
- Secretaría de Planeación Distrital de Cartagena de Indias. Documento Técnico de Soporte del Componente General del Plan de Ordenamiento Territorial; Secretaría de Planeación Distrital de Cartagena de Indias: Cartagena, Colombia, 2023. [Google Scholar]
- Diaz Chamorro, I.; Dávila Sinning, J. Estimación de la Influencia de la Infiltración en el Coeficiente de Escorrentía en el Suelo de la Cuenca del Arroyo de Guayepo de Pontezuela Cartagena; Universidad de Cartagena: Cartagena, Colombia, 2020. [Google Scholar]
- Almanza Agámez, L.E.; Martínez Blanco, O.E.; Velásquez Agámez, R.D. Prediseño Del Alcantarillado Pluvial Del Sector de San Vicente de Paúl, Cartagena de Indias; Ingeniería Civil, Universidad de Cartagena: Cartagena de Indias, Colombia, 1995. [Google Scholar]
- Herrera Herrera, J.B.; Llamas Castro, A.d.J. Actualización de las Curvas de Intensidad, Duración y Frecuencia (IDF) para la Estación “Aeropuerto Rafael Núñez” de la Ciudad de Cartagena de Indias D. T. y C. (1970–2016); Ingeniería Civil, Universidad de Cartagena: Cartagena de Indias, Colombia, 2018. [Google Scholar]
- Torne Angulo, L.M. Construcción de Las Curvas de Intensidad, Duración y Frecuencia En El Municipio de Arjona, Bolívar (1999–2020); Ingeniería Civil, Universidad de Cartagena: Cartagena de Indias, Colombia, 2023. [Google Scholar]
- Chang Nieto, G.A.; Bolívar Lovato, M.I. Establecimiento de Relaciones Entre la Precipitación de 24 Horas y las Precipitaciones de Una Duración Diferente Pt para la Estación Metereológica del Aereopuerto Rafael Nuñez de la Ciudad de Cartagena; Ingeniería Civil, Universidad de Cartagena: Cartagena de Indias, Colombia, 1997. [Google Scholar]
- Weiss, L.L. Ratio of True to Fixed-Interval Maximum Rainfall. J. Hydraul. Div. 1964, 90, 77–82. [Google Scholar] [CrossRef]
- Yoo, C.; Jun, C.; Park, C. Effect of Rainfall Temporal Distribution on the Conversion Factor to Convert the Fixed-Interval into True-Interval Rainfall. J. Hydrol. Eng. 2015, 20, 04015018. [Google Scholar] [CrossRef]
- Brakensiek, D.L.; Rawls, W.J.; Stephenson, G.R. Modifying SCS Hydrologic Soil Groups and Curve Numbers for Rangeland Soils; ASAE paper no. PNR-84203; St. Joseph, MI, USA, 1984. [Google Scholar]
- Rawls, W.J.; Brakensiek, D.L.; Saxtonn, K.E. Estimation of Soil Water Properties. Trans. ASAE 1982, 25, 1316–1320. [Google Scholar] [CrossRef]
- Asaeda, T.; García de Jalón, D.; O’Hare, M.; Rahman, M. Sequential Riparian Vegetation Alteration in Japanese River Landscapes. Int. J. River Basin Manag. 2025, 23, 183–195. [Google Scholar] [CrossRef]
- Jähnig, S.C.; Brabec, K.; Buffagni, A.; Erba, S.; Lorenz, A.W.; Ofenböck, T.; Verdonschot, P.F.M.; Hering, D. A Comparative Analysis of Restoration Measures and Their Effects on Hydromorphology and Benthic Invertebrates in 26 Central and Southern European Rivers. J. Appl. Ecol. 2010, 47, 671–680. [Google Scholar] [CrossRef]
- Li, P.; Li, D.; Sun, X.; Chu, Z.; Xia, T.; Zheng, B. Application of Ecological Restoration Technologies for the Improvement of Biodiversity and Ecosystem in the River. Water 2022, 14, 1402. [Google Scholar] [CrossRef]
- Vargas Ríos, O.; Díaz Triana, J.E.; Reyes Bejarano, S.P.; Gómez Ruiz, P.A. Guías Técnicas para la Restauración Ecológica de los Ecosistemas de Colombia; Universidad Nacional de Colombia: Bogotá, Colombia, 2012. [Google Scholar]
| Parameters | Value |
|---|---|
| 21.06 | |
| 38.98 | |
| 22.9 | |
| 13.02 |
| Sub-Basin | Area () | Length of the Channel (m) | Slope (m/m) | |||
|---|---|---|---|---|---|---|
| A | 3.935 | 4067.21 | 0.00836 | 1.76 | 0.456 | 1.18 |
| B | 2.758 | 2283.19 | 0.01577 | 2.06 | 1.221 | 1.14 |
| C | 7.087 | 10,152.77 | 0.00217 | 2.61 | 0.265 | 1.52 |
| D | 3.840 | 3641.75 | 0.01922 | 1.83 | 0.443 | 1.03 |
| E | 1.552 | 2265.42 | 0.01501 | 1.89 | 0.375 | 1.09 |
| H | 1.885 | 3413.16 | 0.00234 | 1.94 | 0.350 | 1.25 |
| Sub-Basin | Tc Kirpich Minutes | Tc California Minutes | Tc Bransby Williams Minutes | Tc Mean Minutes | Lag Time Minutes |
|---|---|---|---|---|---|
| A | 73.88 | 71.77 | 130.31 | 91.99 | 55.19 |
| B | 37.10 | 36.04 | 66.76 | 46.63 | 27.98 |
| C | 251.30 | 244.13 | 401.77 | 299.07 | 179.44 |
| D | 49.25 | 47.84 | 99.02 | 65.37 | 39.22 |
| E | 37.58 | 36.51 | 70.86 | 48.32 | 28.99 |
| H | 105.32 | 102.32 | 151.79 | 119.81 | 71.89 |
| Tr (Years) | Pmax-24 h (mm) | |
|---|---|---|
| Mean * | Confidence Intervals ** | |
| 100 | 169 | 148–190 |
| 50 | 162 | 144–179 |
| 25 | 152 | 138–167 |
| 20 | 149 | 135–163 |
| 10 | 138 | 126–150 |
| 5 | 123 | 113–134 |
| 3 | 110 | 99.9–120 |
| 2 | 96.4 | 86.9–106 |
| Area (%) | |||
|---|---|---|---|
| Coverage | 2000 | 2010 | 2020 |
| Continuous urban fabric | 1.07 | 1.40 | 1.06 |
| Discontinuous urban fabric | 0.00 | 0.00 | 2.77 |
| Industrial or commercial zones | 0.00 | 0.00 | 1.33 |
| Mining extraction areas | 0.00 | 0.00 | 0.57 |
| Recreational facilities | 0.00 | 0.00 | 0.01 |
| Clean pastures | 72.90 | 70.56 | 39.07 |
| Weeded pastures | 4.68 | 0.85 | 18.65 |
| Mosaic of crops, pastures, and natural areas | 0.72 | 0.00 | 1.70 |
| Mosaic of pastures and natural spaces | 3.88 | 20.65 | 9.15 |
| Gallery and riparian forest | 2.37 | 0.00 | 3.39 |
| Dense shrubland | 0.00 | 0.00 | 3.61 |
| Open shrubland | 0.00 | 0.00 | 14.93 |
| Low secondary vegetation | 0.00 | 0.00 | 3.76 |
| Dense forest | 14.38 | 4.16 | 0.00 |
| Gallery and riparian forest | 0.00 | 2.37 | 0.00 |
| The Year 2000 | The Year 2010 | The Year 2020 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Sub-Basins | CN (I) | CN (II) | CN (III) | CN (I) | CN (II) | CN (III) | CN (I) | CN (II) | CN (III) |
| A | 64.48 | 83.10 | 91.87 | 63.04 | 82.13 | 91.36 | 65.33 | 83.66 | 92.17 |
| B | 58.36 | 78.81 | 89.54 | 60.87 | 80.62 | 90.54 | 63.51 | 82.44 | 91.52 |
| C | 60.92 | 80.65 | 90.55 | 63.43 | 82.39 | 91.50 | 65.85 | 84.00 | 92.35 |
| D | 58.94 | 79.23 | 89.77 | 63.78 | 82.63 | 91.62 | 66.94 | 84.71 | 92.72 |
| E | 61.35 | 80.96 | 90.72 | 64.00 | 82.78 | 91.70 | 73.02 | 88.45 | 94.63 |
| H | 59.47 | 79.62 | 89.99 | 60.41 | 80.29 | 90.36 | 68.49 | 85.70 | 93.23 |
| The Year 2000 | The Year 2010 | The Year 2020 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Sub-Basins | CN (I) | CN (II) | CN (III) | CN (I) | CN (II) | CN (III) | CN (I) | CN (II) | CN (III) |
| A | 27.98 | 10.33 | 4.49 | 29.78 | 11.06 | 4.81 | 26.96 | 9.93 | 4.32 |
| B | 36.24 | 13.66 | 5.94 | 32.65 | 12.21 | 5.31 | 29.19 | 10.82 | 4.70 |
| C | 32.59 | 12.19 | 5.30 | 29.29 | 10.86 | 4.72 | 26.35 | 9.68 | 4.21 |
| D | 35.40 | 13.31 | 5.79 | 28.84 | 10.68 | 4.64 | 25.08 | 9.17 | 3.99 |
| E | 32.00 | 11.95 | 5.20 | 28.57 | 10.57 | 4.60 | 18.77 | 6.63 | 2.88 |
| H | 34.62 | 13.00 | 5.65 | 33.29 | 12.47 | 5.42 | 23.37 | 8.48 | 3.69 |
| Year | Return Period (Years) | Flow (m3/s) | |
|---|---|---|---|
| AMC I | AMC II | ||
| 2000 | 25 | 40.20 | 80.70 |
| 50 | 46.00 | 89.20 | |
| 100 | 49.60 | 94.80 | |
| 2010 | 25 | 43.30 | 83.20 |
| 50 | 49.00 | 91.60 | |
| 100 | 52.60 | 97.20 | |
| 2020 | 25 | 49.20 | 93.40 |
| 50 | 54.50 | 101.70 | |
| 100 | 58.90 | 108.80 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno-Pájaro, Á.M.; Osorio-Gastelbondo, A.; Moreno-Egel, D.A.; Coronado-Hernández, O.E.; Narváez-Cuadro, M.A.; Saba, M.; Arrieta-Pastrana, A. Hydrological Modelling and Remote Sensing for Assessing the Impact of Vegetation Cover Changes. Hydrology 2025, 12, 107. https://doi.org/10.3390/hydrology12050107
Moreno-Pájaro ÁM, Osorio-Gastelbondo A, Moreno-Egel DA, Coronado-Hernández OE, Narváez-Cuadro MA, Saba M, Arrieta-Pastrana A. Hydrological Modelling and Remote Sensing for Assessing the Impact of Vegetation Cover Changes. Hydrology. 2025; 12(5):107. https://doi.org/10.3390/hydrology12050107
Chicago/Turabian StyleMoreno-Pájaro, Ángela M., Aldhair Osorio-Gastelbondo, Dalia A. Moreno-Egel, Oscar E. Coronado-Hernández, María A. Narváez-Cuadro, Manuel Saba, and Alfonso Arrieta-Pastrana. 2025. "Hydrological Modelling and Remote Sensing for Assessing the Impact of Vegetation Cover Changes" Hydrology 12, no. 5: 107. https://doi.org/10.3390/hydrology12050107
APA StyleMoreno-Pájaro, Á. M., Osorio-Gastelbondo, A., Moreno-Egel, D. A., Coronado-Hernández, O. E., Narváez-Cuadro, M. A., Saba, M., & Arrieta-Pastrana, A. (2025). Hydrological Modelling and Remote Sensing for Assessing the Impact of Vegetation Cover Changes. Hydrology, 12(5), 107. https://doi.org/10.3390/hydrology12050107







