Selection of a Probability Model Adapted to the Current Climate for Annual Maximum Daily Rainfall in the Benin Mono-Couffo Basin (West Africa)
Abstract
:1. Introduction
| Study | Regions | No. of Stations | Period of Record | Distribution | Estimation Method | Goodness of Fit | Conclusion |
|---|---|---|---|---|---|---|---|
| [25] | Montreal (Canada) | 9 | 1963–1974 | MEXP, EXP, WEB, GAM | ML | , AIC | The mixed exponential was found to be the best model. |
| [26] | Ilorin, Nigeria | 1 | 1955–1995 | LPIII, EV1, LN, EXP, N | - | - | The LPIII distribution best suited the maximum daily rainfall data while the normal distribution best described the maximum monthly rainfall for Ilorin. |
| [27] | Southern Quebec (Canada) | 20 | - | BEK, BEP, GEV, GNO, GPA, GUM, PIII, LPIII, WAK | ML, LM | Q-Q plots, CC, RMSE, RRMSE, MAE, Bootstrap | The GEV was recommended as the most suitable distribution. |
| [28] | Malaysia | 70 | 23 to 28 years | GAM, GNO, GPA, GEV, LPIII, PIII, GUM, WAK | LM | CC, MAE, RMSE, RRMSE | The GEV distribution is the most appropriate distribution for describing the annual maximum rainfall series in Malaysia. |
| [29] | Nigeria | 20 | 54 years (1952–2005) | GUM, LGUM, N, LN, PIII, LPIII | - | , F, CC, | The LP3 distribution performed the best, followed by PIII and LGUM distributions. |
| [30] | Chott-Chergui basin (Algeria) | 27 | 1970–2004 | GEV, GUM, LPIII, LN | ML | GEV law showed a good fit to the series of maximum daily rainfall of the “Chott Chergui” basin. | |
| [31] | India | 4 | Fatehabad and Hansi (1954–2011) Hissar (1969–2011) and Tohana (1951–2011) | GUM, EV2 | LM | , K-S, D-Index | The study shows the GUM distribution is better suited for rainfall estimation for the stations under study. |
| [32] | Brazil | 342 | 2001–2010 (10 years) | GEV, Kappa, GUM, LN | LM | K-S, , Filliben test | The Kappa distribution presented the best performance, followed by the GEV. |
| [33] | Poland | 1 | 1960–2009 (50 years) | GED2, GED3, GAM, GUM, WEB, LN | ML | BIC, RRMSE | GED3, gamma and Weibull distributions were the best for describing. |
| [3] | Benin | 26 | 1921–2001 | GEV, GUM, LN, PIII, LPIII | ML | AIC, BIC | The results showed a predominance of Gumbel and Lognormal laws. |
| [34] | Qatar | 29 | (36 years) | N, LN2, LN3, GAM2, GAM3, GGAM, GUM, LLO, GEV, PIII, LPIII, GPA, Beta, WEB | - | K-S, , | GEV distribution is found to be the best-fit distribution. |
| [11] | Ontario (Canada) | 21 | (63 years) | BEK, BEP, GEV, GLO, GNO, GPA, GUM, LPIII, PIII, WAK | ML, NCMs, LM | Q-Q plots, RMSE, CC, RRMSE, MAE, BIC, AIC, bootstrap | The GEV distribution is the best model for describing the distribution of daily and sub-daily annual maximum rainfalls. |
| [14] | Ivory Coast | 1 | 1961- 2014 | GEV, GUM, LN | ML | AIC, BIC, | The law that best adjusted the annual maximum daily rainfall of the Port-Bouët station (Abidjan) was the law of Gumbel. |
| [12] | Egypt | 31 | - | N, LN, PIII, LPIII, GUM, GEV, GAM, EXP, LO, GLO, GPA, WEB | MOM, ML, LM | Q-Q plot, RMSE, RRMSE, CC, AIC, BIC, BIASr | LN, LPIII and EXP are the top three distributions for the frequency analysis of daily annual extreme rainfalls in Egypt. |
| [35] | lower Ouémé valley (Benin) | 9 | 39 years (1981 to 2019) | GEV, GUM, LN, WEB, GAM | - | AIC, BIC | The results obtained show that the Gumbel, Lognormal, and GEV distributions are the most suitable for the data series in the study area. |
| [36] | Niger | 1 | 1960–2020 | N, GUM, LN | - | K-S, T-S | It was found that the Gumbel model is the most suitable for modeling extreme rainfall and for calculating return periods. |
| [37] | Romania | 14 | - | 14 probability distributions from Beta families | LM, MOM | RME, RAE | The best-fit distributions are the Kumaraswamy, the Generalized Beta Exponential and the Generalized Beta distributions, which presented stability related to both the length of the data and the presence of outliers. |
| [38] | Poland | 51 | 1971–2014 | PIII, WEB, LN, GEV, GUM | ML | RMSE, R2, PWRMSE | The GEV distribution as recommended for calculating the maximum daily precipitation with the specific probability of exceedance. |
2. Materials and Methods
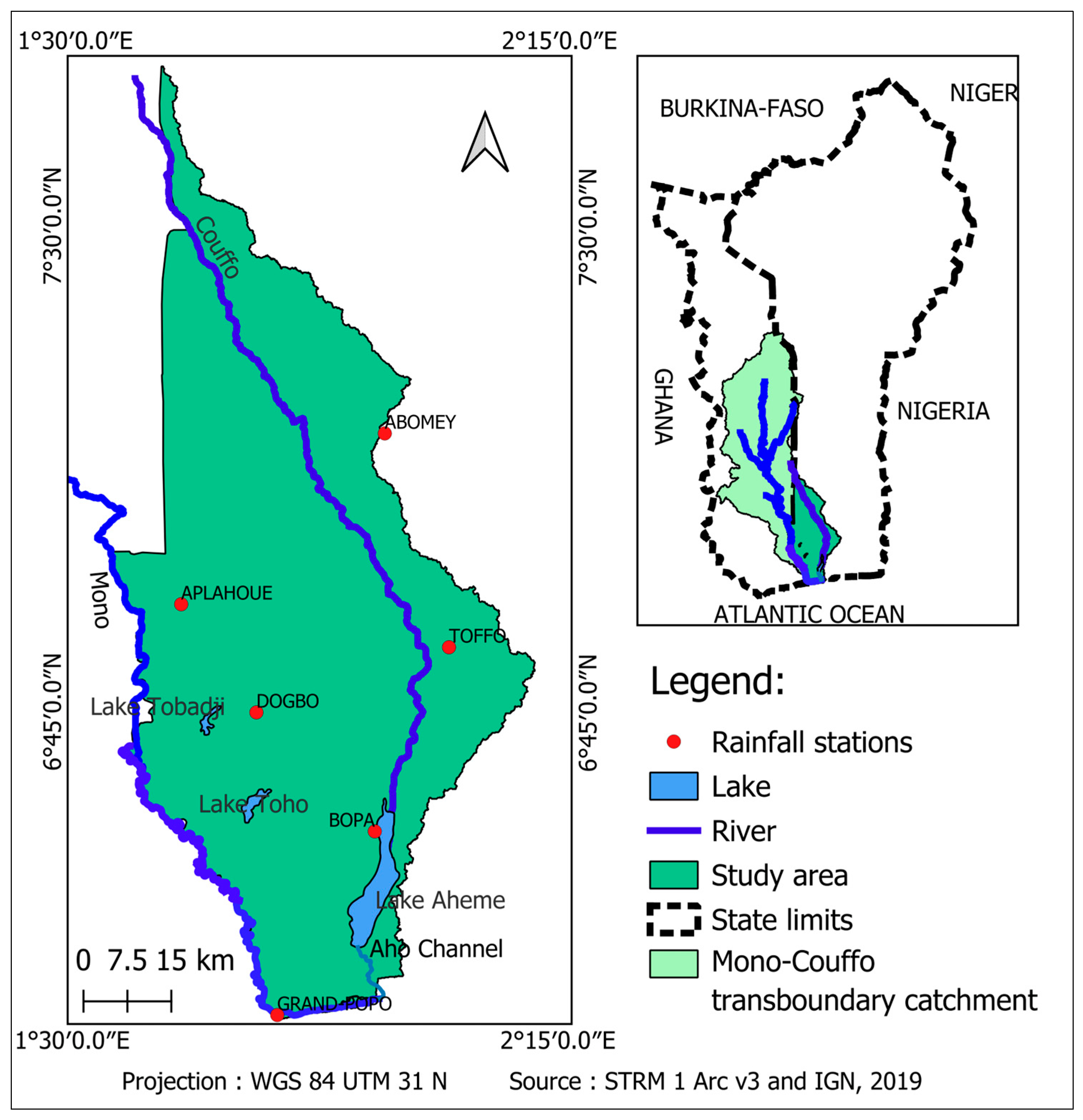
2.1. Study Area
2.2. Data
2.3. Methods
2.3.1. Hypothesis Testing for Frequency Analysis
- Test of independence (Wald–Wolfowitz): This test assesses whether two samples come from the same distribution by verifying the independence of the observations;
- Stationarity test (modified Kendall): This test examines whether data are stationary, i.e., whether their statistical properties (such as mean and variance) do not change over time;
- Annual homogeneity test (Wilcoxon): This test compares the distributions of two samples to determine whether there are significant differences between them.
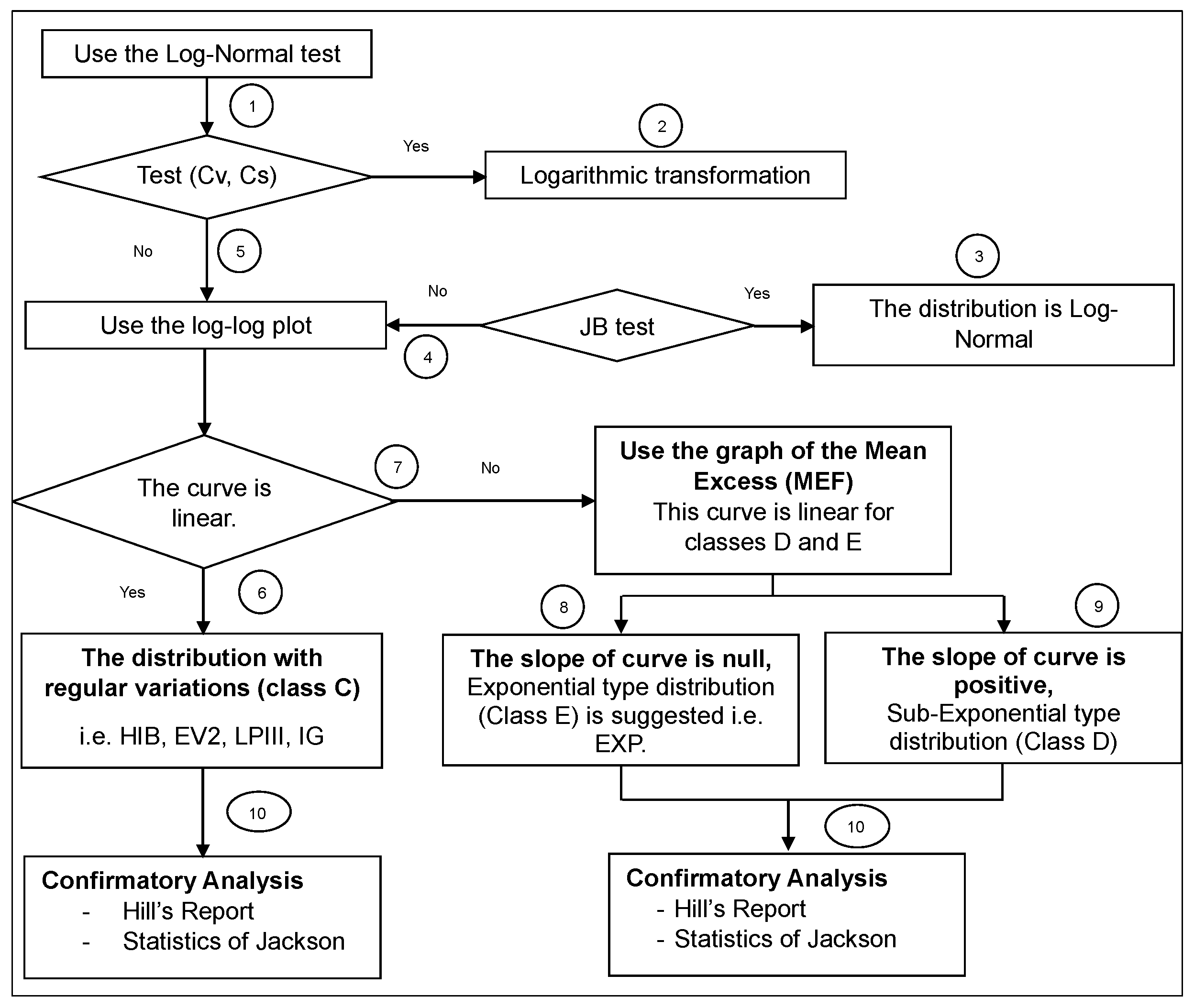
2.3.2. Selecting Distribution Classes
- Class C (regularly varying distributions): Fréchet (EV2), Halphen Inverse type B (HIB), Log-Pearson type III (LPIII) and Inverse Gamma (IG);
- Class D (sub-exponential distributions): Halphen type A (HA), Halphen type B (HB), Gumbel (EV1), Pearson type III (PIII) and Gamma (G);
- class E (exponential law: EXP).
- The Jarque–Bera test: considered for testing Lognormality with a priori selection based on the coefficients of variation and skewness (Cv, Cs) diagram;
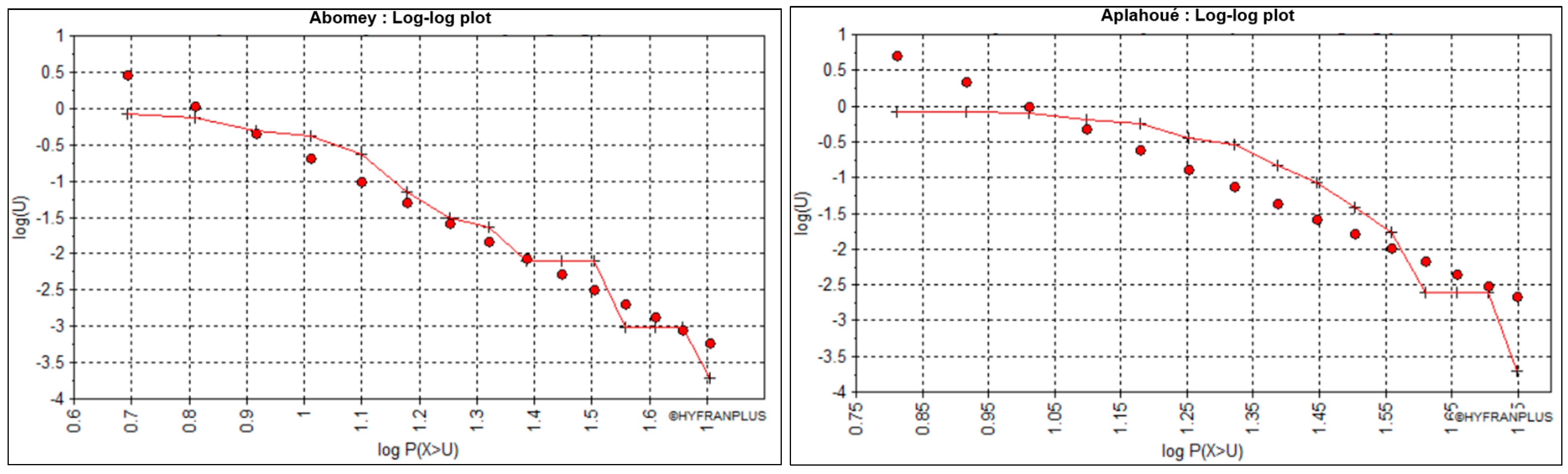
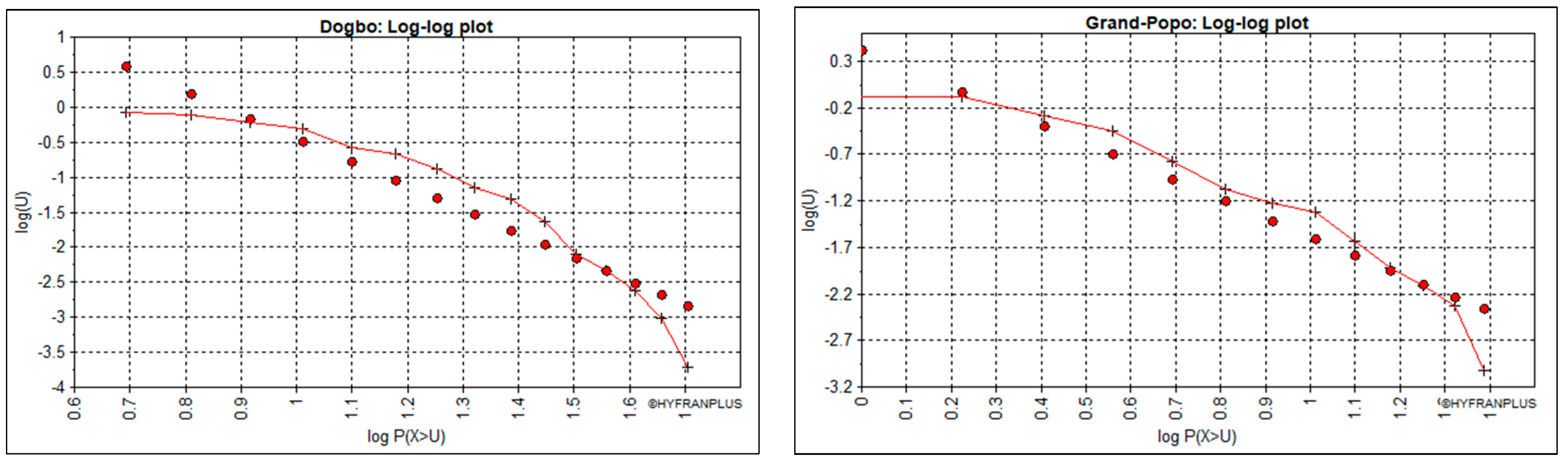
- The Log–Log plot: used to discriminate between class C, on the one hand, and classes E and D, on the other hand;
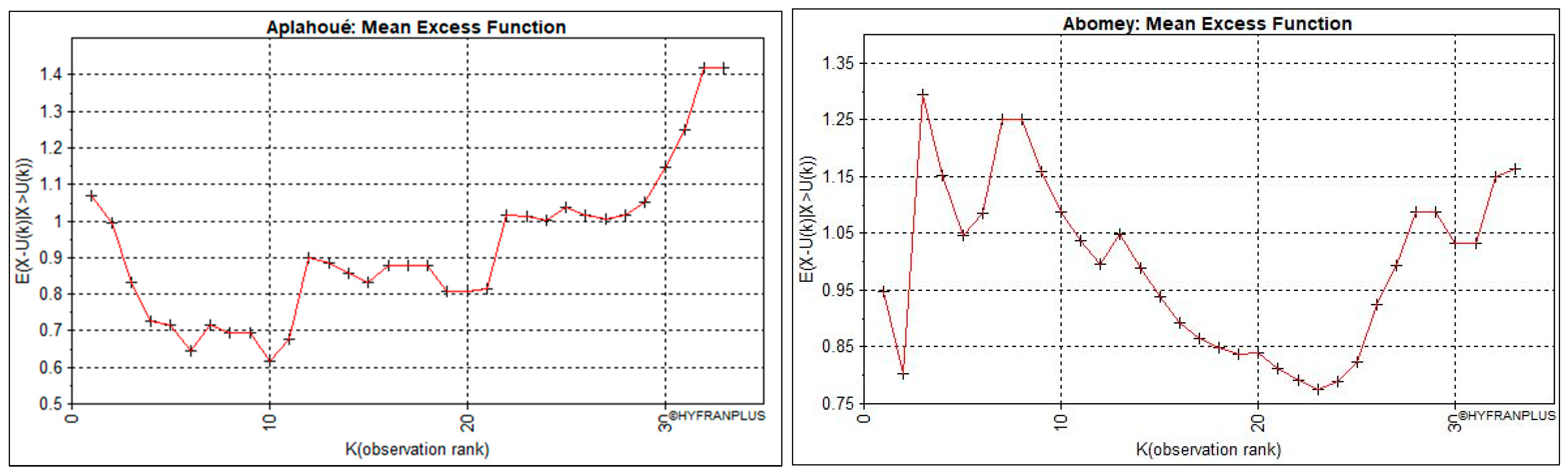
- The Mean Excess Function (MEF) to discriminate between classes D and E;
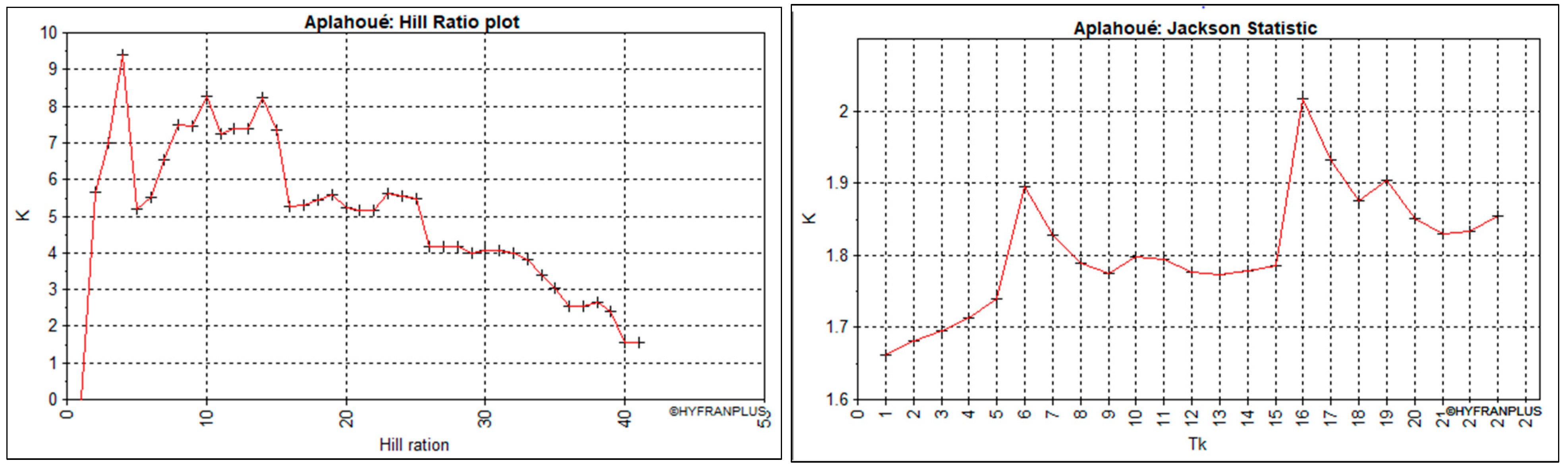
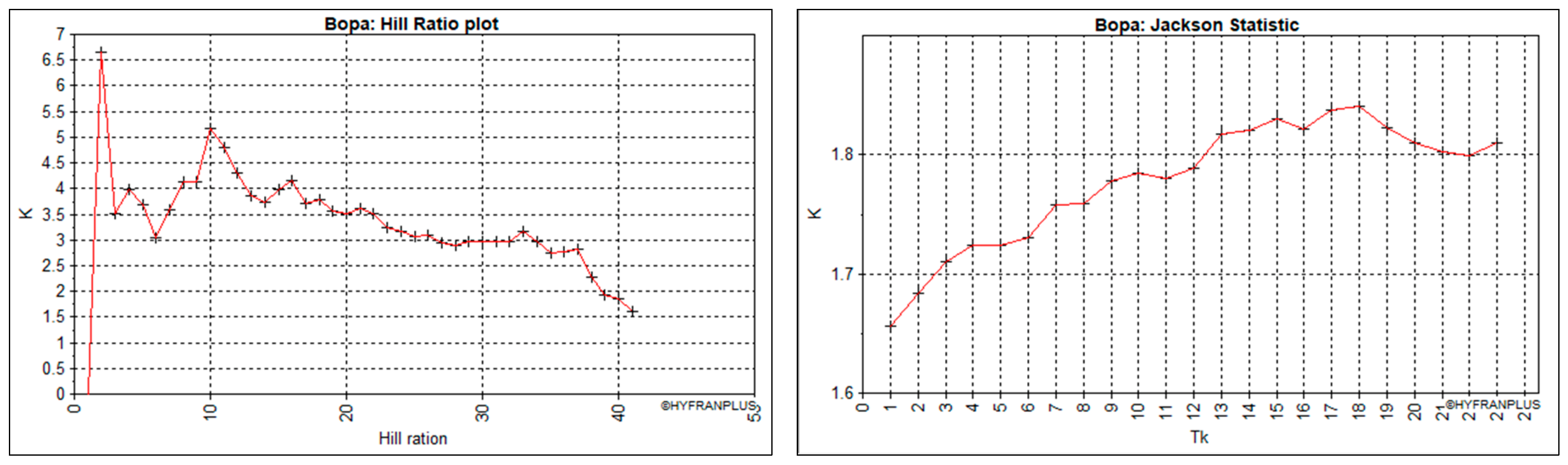
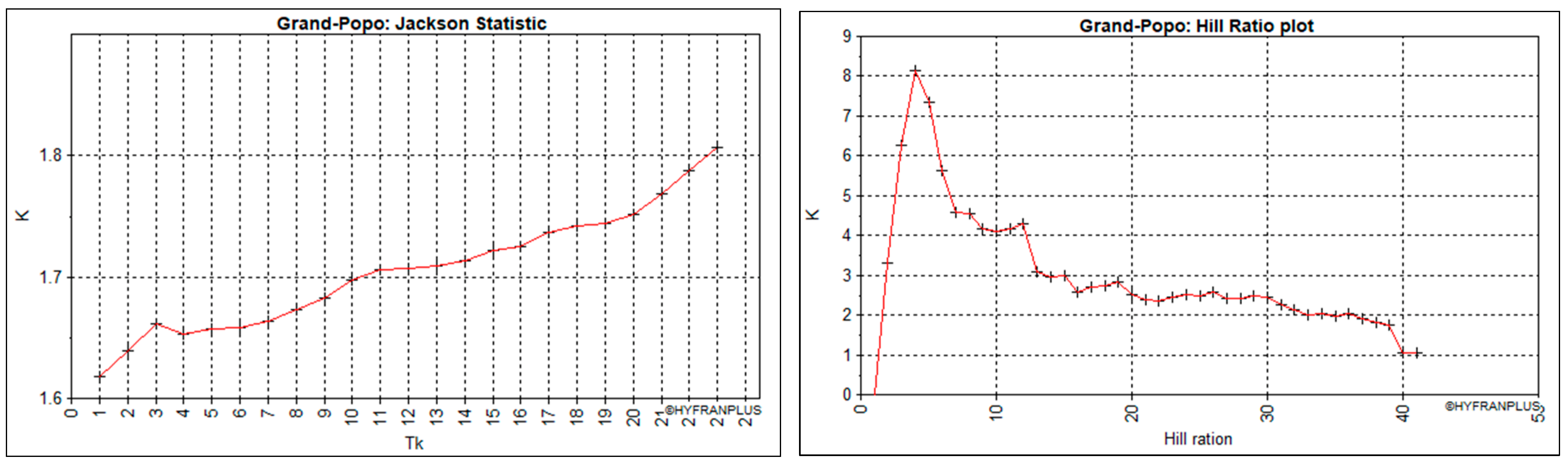
- Two statistics: Hill’s ratio and modified Jackson statistic, for confirmatory analysis of the conclusions suggested by the previous two methods.
2.3.3. Distribution Parameter Estimation Methods
2.3.4. Criteria for Determining the Most Appropriate Probability Model
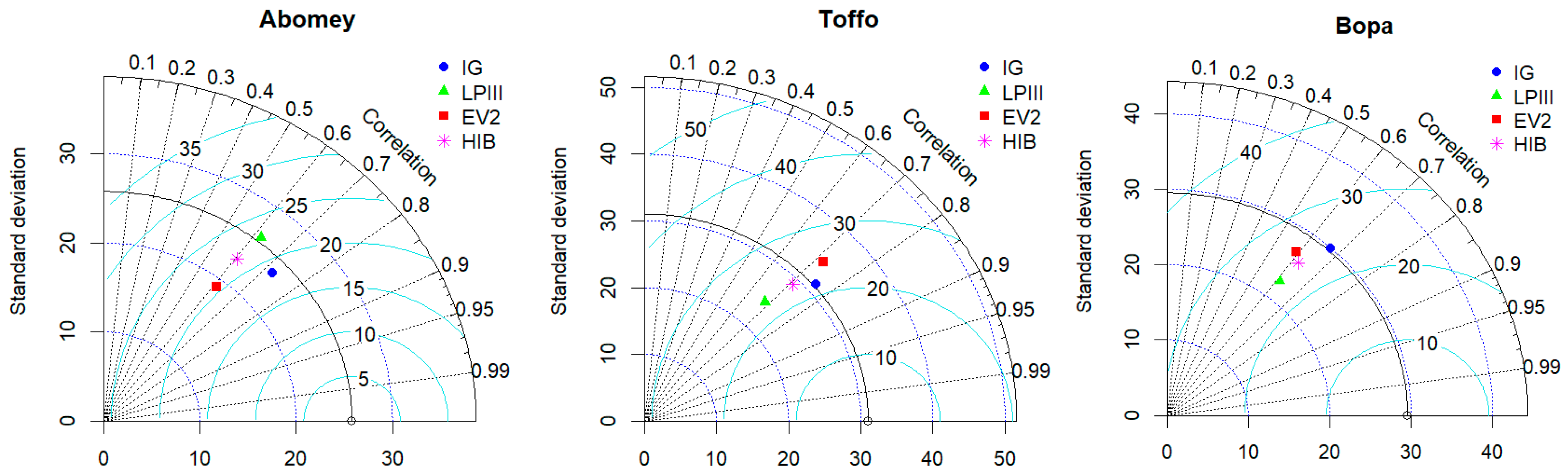
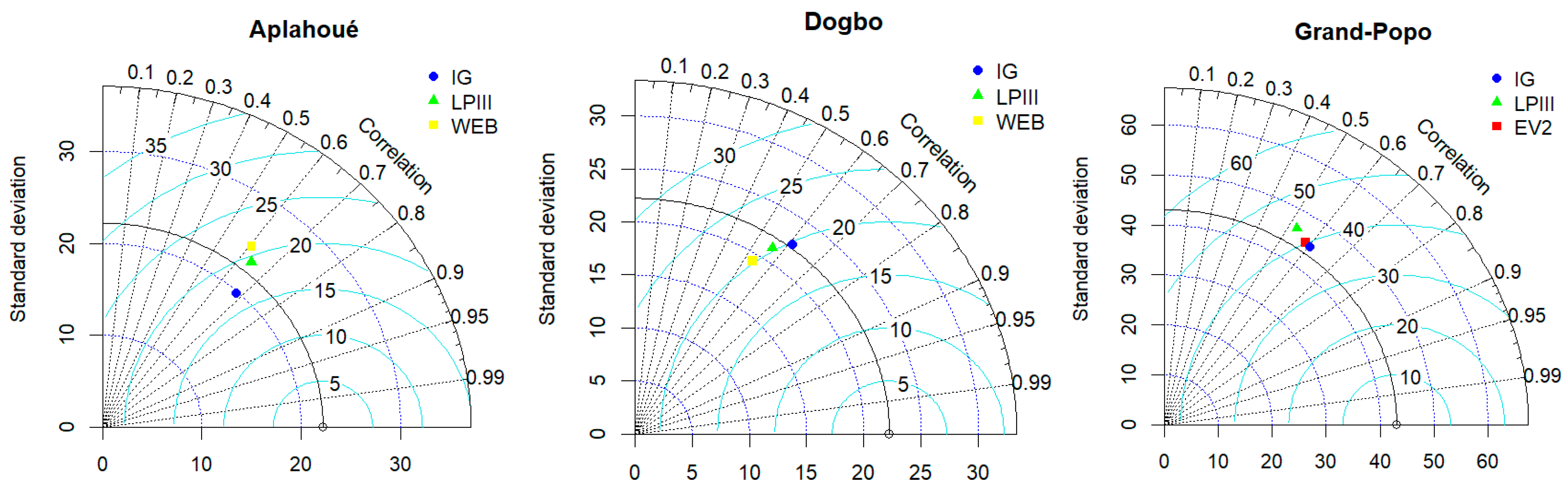
- Taylor Diagram
- A high correlation, close to the horizontal axis;
- A standard deviation close to the circle corresponding to the standard deviation of the observations, indicating that the variability of the model is similar to that of the observed data;
- A low RMSE, close to the observation reference point “circle on the x-axis”, meaning that the model’s error is minimized and its performance is better.
- AIC and BIC criteria
3. Results
3.1. Analysis of Hypothesis Tests Applied to Annual Maximum Daily Rainfall
3.2. Selecting the Most Appropriate Distribution Class
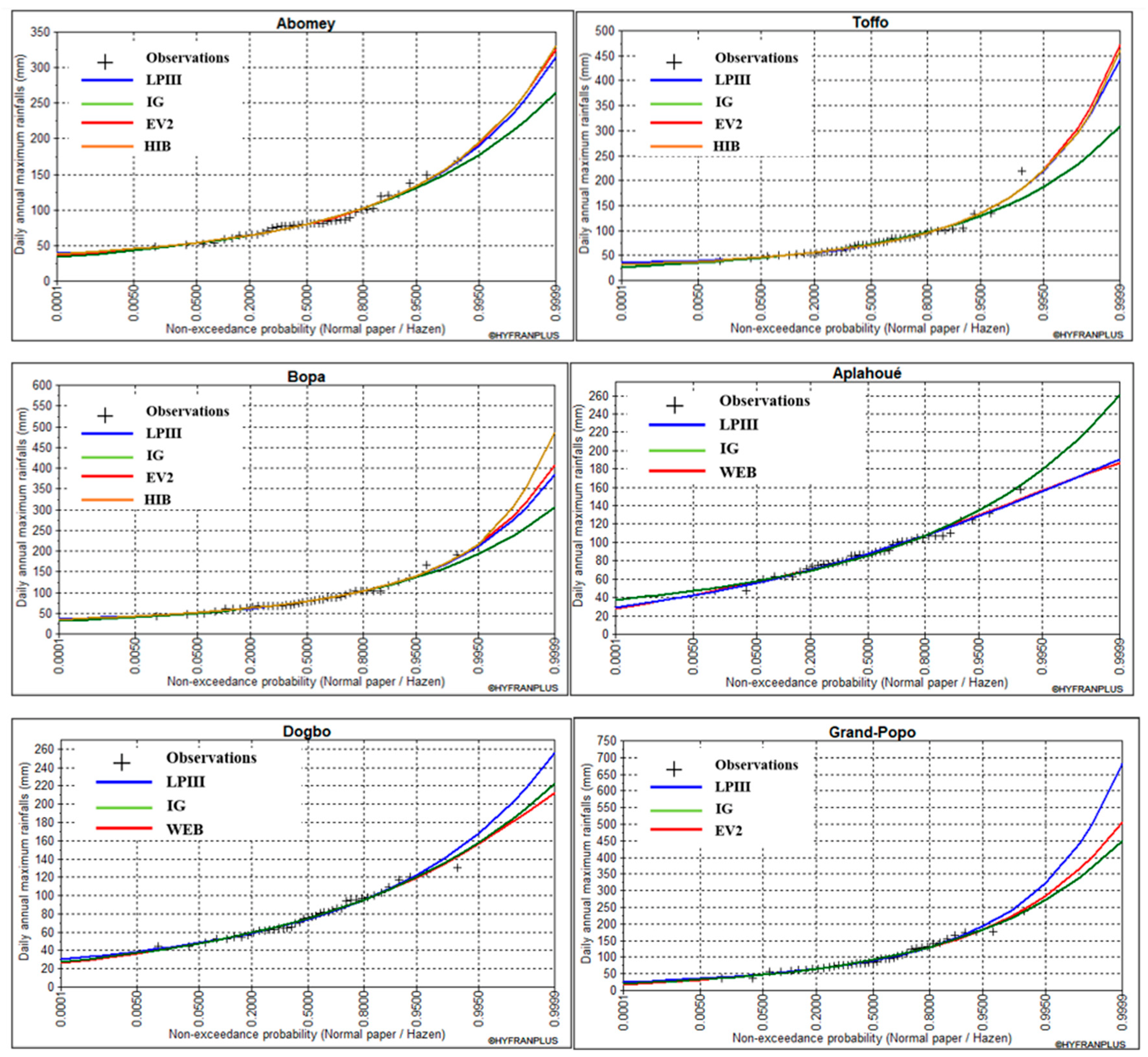
3.3. Selection of Best-Fit Distribution
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
| Station | T = 2 | T = 5 | T = 10 | T = 20 | T = 50 | T = 100 |
|---|---|---|---|---|---|---|
| Dogbo | 74.2 | 94.9 | 109 | 123 | 141 | 154 |
| Grand-Popo | 89.4 | 129 | 160 | 193 | 240 | 280 |
| Aplahoué | 85.6 | 107 | 121 | 135 | 153 | 166 |
| Bopa | 79.1 | 103 | 120 | 136 | 158 | 175 |
| Toffo | 72.8 | 96.5 | 113 | 129 | 152 | 169 |
| Abomey | 80.6 | 102 | 117 | 131 | 149 | 163 |
References
- Bossa, A.Y.; Akpaca, J.d.D.; Hounkpè, J.; Yira, Y.; Badou, D.F. Non-Stationary Flood Discharge Frequency Analysis in West Africa. GeoHazards 2023, 4, 316–327. [Google Scholar] [CrossRef]
- Yuan, J.; Emura, K.; Farnham, C.; Alam, M.A. Frequency Analysis of Annual Maximum Hourly Precipitation and Determination of Best Fit Probability Distribution for Regions in Japan. Urban Clim. 2018, 24, 276–286. [Google Scholar] [CrossRef]
- Agué, A.I.; Afouda, A. Analyse Fréquentielle et Nouvelle Cartographie Des Maxima Annuels de Pluies Journalières Au Bénin. Int. J. Biol. Chem. Sci. 2015, 9, 121–133. [Google Scholar] [CrossRef]
- Nka Nnomo, B. Contribution à l’Actualisation des Normes Hydrologiques en relation avec les Changements Climatiques et Environnementaux en Afrique de l’Ouest. Ph.D. Thesis, Institut International D’ingénierie de L’eau et de L’environnement, Université Pierre et Marie Curie—Paris VI, Paris, France, 2016. [Google Scholar]
- Kouassi, A.M.; Kouao, J.-M.; Kouakou, K.E. Caractérisation intra-annuelle de la variabilité climatique en Côte d’Ivoire. Bull. L’association Géographes Français Géographies 2022, 99, 289–306. [Google Scholar] [CrossRef]
- Amoussou, E.; Vissin, E.; Boko, M. Simulations Des Écoulements Dans Le Bassin Versant Du Fleuve Mono (Afrique de l’ouest) Avec Le Modèle GR2M; Université d’Abomey-Calavi: Cotonou, Benin, 2007; Volume 8, p. 9. [Google Scholar]
- Amoussou, E. Variabilité Pluviométrique et Dynamique Hydro-Sédimentaire du Bassin Versant du Complexe Fluvio-Lagunaire Mono-Ahémé-Couffo (Afrique de L’ouest). Ph.D. Thesis, Université de Bourgogne, Dijon, France, 2010. [Google Scholar]
- Amoussou, E.; Totin Vodounon, S.H.; Clédjo, F.P.; Allagbé, Y.B.S.; Akognongbé, J.S.A.; Houndenou, C.; Mahe, G.; Camberlin, P.; Boko, M.; Pérard, J. Évolution Climatique Du Bénin de 1950 à 2010 et Son Influence Sur Les Eaux de Surface. In Proceedings of the XXIXe Colloque de l’Association Internationale de Climatologie, Lausanne, Besançon, 6–9 July 2016; pp. 231–236. [Google Scholar]
- Amoussou, E.; Tramblay, Y.; Totin, H.S.V.; Mahé, G.; Camberlin, P. Dynamique et Modélisation Des Crues Dans Le Bassin Du Mono à Nangbéto (Togo/Bénin). Hydrol. Sci. J. 2014, 59, 2060–2071. [Google Scholar] [CrossRef]
- Amani, A.; Paturel, J.-E. Le projet de révision des normes hydrologiques en Afrique de l’Ouest et Afrique Centrale. Météorologie 2017, 96, 6–7. [Google Scholar] [CrossRef]
- Nguyen, T.-H.; El Outayek, S.; Lim, S.H.; Nguyen, V.-T.-V. A Systematic Approach to Selecting the Best Probability Models for Annual Maximum Rainfalls—A Case Study Using Data in Ontario (Canada). J. Hydrol. 2017, 553, 49–58. [Google Scholar] [CrossRef]
- Gado, T.; Salama, A.; Zeidan, B. Selection of the Best Probability Models for Daily Annual Maximum Rainfalls in Egypt. Theor. Appl. Climatol. 2021, 144, 1267–1284. [Google Scholar] [CrossRef]
- Griffis, V.W.; Stedinger, J.R. Evolution of Flood Frequency Analysis with Bulletin 17. J. Hydrol. Eng. 2007, 12, 283–297. [Google Scholar] [CrossRef]
- Kouassi, A.M.; Nassa, R.A.-K.; Yao, K.B.; Kouame, K.F.; Biemi, J. Modélisation Statistique Des Pluies Maximales Annuelles Dans Le District d’Abidjan (Sud de La Côte d’Ivoire). Rev. Sci. L’eau/J. Water Sci. 2018, 31, 147–160. [Google Scholar] [CrossRef]
- El Adlouni, S.; Bobée, B.; Ouarda, T.B.M.J. On the Tails of Extreme Event Distributions in Hydrology. J. Hydrol. 2008, 355, 16–33. [Google Scholar] [CrossRef]
- Nerantzaki, S.D.; Papalexiou, S.M. Tails of Extremes: Advancing a Graphical Method and Harnessing Big Data to Assess Precipitation Extremes. Adv. Water Resour. 2019, 134, 103448. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, Q.; Singh, V.P.; Liu, L.; Shi, P. Spatiotemporal Patterns of Annual and Seasonal Precipitation Extreme Distributions across China and Potential Impact of Tropical Cyclones. Int. J. Climatol. 2017, 37, 3949–3962. [Google Scholar] [CrossRef]
- Fontanari, A.; Taleb, N.N.; Cirillo, P. Gini Estimation under Infinite Variance. Phys. A Stat. Mech. Its Appl. 2018, 502, 256–269. [Google Scholar] [CrossRef]
- Fontanari, A.; Cirillo, P.; Oosterlee, C.W. From Concentration Profiles to Concentration Maps. New Tools for the Study of Loss Distributions. Insur. Math. Econ. 2018, 78, 13–29. [Google Scholar] [CrossRef]
- Sartori, M.; Schiavo, S. Connected We Stand: A Network Perspective on Trade and Global Food Security. Food Policy 2015, 57, 114–127. [Google Scholar] [CrossRef]
- Ehsanzadeh, E.; El Adlouni, S.; Bobée, B. Frequency Analysis Incorporating a Decision Support System for Hydroclimatic Variables. J. Hydrol. Eng. 2010, 15, 869–881. [Google Scholar] [CrossRef]
- Nassa, R.A.-K.; Kouassi, A.M.; Toure, M.L. Sensitivity of Statistical Models for Extremes Rainfall Adjustment Regarding Data Size: Case of Ivory Coast. J. Water Resour. Prot. 2021, 13, 654–674. [Google Scholar] [CrossRef]
- Bobée, B. Extreme flood events valuation using frequency analysis: A critical review. La Houille Blanche 1999, 85, 100–105. [Google Scholar] [CrossRef]
- Robson, A.; Reed, D. Statistical Procedures for Flood Frequency Estimation; Flood Estimation Handbook; Centre for Ecology&Hydrology: Lancaster, UK, 1999; Volume 3, ISBN 978-1-906698-03-4. [Google Scholar]
- Nguyen, V.-T.-V.; Mayabi, A. Probabilistic Analysis of Summer Daily Rainfall for the Montreal Region. Can. Water Resour. J./Rev. Can. Ressour. Hydr. 1991, 16, 65–80. [Google Scholar] [CrossRef]
- Ogunlela, A.O. Stochastic Analysis of Rainfall Events in Ilorin, Nigeria. J. Agric. Res. Dev. 2001, 1, 39–50. [Google Scholar] [CrossRef]
- Tao, D.; Nguyen, V.-T.-V.; Bourque, A. On Selection of Probability Distributions for Representing Extreme Precipitations in Southern Quebec. In Proceedings of the Annual Conference of the Canadian Society for Civil Engineering, Montréal, QC, Canada, 5–8 June 2002; Volume 2002, p. 9. [Google Scholar]
- Zalina, M.D.; Desa, M.N.M.; Nguyen, V.-T.-A.; Kassim, A.H.M. Selecting a Probability Distribution for Extreme Rainfall Series in Malaysia. Water Sci. Technol. 2002, 45, 63–68. [Google Scholar] [CrossRef]
- Olofintoye, O.O.; Sule, B.F.; Salami, A.W. Best–Fit Probability Distribution Model for Peak Daily Rainfall of Selected Cities in Nigeria. N. Y. Sci. J. 2009, 2, 1–12. [Google Scholar]
- Habibi, B.; Meddi, M.; Boucefiane, A. Analyse Fréquentielle Des Pluies Journalières Maximales Cas Du Bassin Chott-Chergui. Nat. Technol. 2013, 8, 41–48. [Google Scholar]
- Vivekanandan, N. Rainfall Frequency Analysis Using Order Statistics Approach of Extreme Value Distributions. Int. J. Civ. Eng. 2014, 1, 6–12. [Google Scholar] [CrossRef]
- Beskow, S.; Caldeira, T.L.; de Mello, C.R.; Faria, L.C.; Guedes, H.A.S. Multiparameter Probability Distributions for Heavy Rainfall Modeling in Extreme Southern Brazil. J. Hydrol. Reg. Stud. 2015, 4, 123–133. [Google Scholar] [CrossRef]
- Kaźmierczak, B.; Kotowski, A. The Suitability Assessment of a Generalized Exponential Distribution for the Description of Maximum Precipitation Amounts. J. Hydrol. 2015, 525, 345–351. [Google Scholar] [CrossRef]
- Mamoon, A.A.; Rahman, A. Selection of the Best Fit Probability Distribution in Rainfall Frequency Analysis for Qatar. Nat. Hazards 2016, 86, 281–296. [Google Scholar] [CrossRef]
- Avossè, A.D.; Sintondji, L.O.; Bessou, J.; Bossa, A.; Bodjrènou, R.; Gbaguidi, B. Characterization of the Frequency of Hydroclimatic Extremes in the Lower Ouémé Valley. Int. J. Eng. Res. Appl. 2022, 12, 20–27. [Google Scholar]
- Amadou Abdou, M.A.; Sidi Zakari, I.; Abdourhamane Toure, A.; Garba, Z. Modélisation statistique des évènements extrêmes de pluies dans le district de la station de Niamey Aéroport. Afr. Sci. 2023, 22, 70–86. [Google Scholar]
- Ilinca, C.; Anghel, C.G. Frequency Analysis of Extreme Events Using the Univariate Beta Family Probability Distributions. Appl. Sci. 2023, 13, 4640. [Google Scholar] [CrossRef]
- Młyński, D.; Wałęga, A.; Petroselli, A.; Tauro, F.; Cebulska, M. Estimating Maximum Daily Precipitation in the Upper Vistula Basin, Poland. Atmosphere 2019, 10, 43. [Google Scholar] [CrossRef]
- Azandégbé, J.E.V. Nouvelle Méthode De Formalisation Des Terres Au Benin: Perceptions Des Acteurs Fonciers De La Moyenne Vallée Du Mono. Int. J. Progress. Sci. Technol. 2023, 39, 346. [Google Scholar] [CrossRef]
- Kouton, G.A. Répartition Spatio-Temporelle des Pluies Extrêmes dans le Département de l’Atacora au Bénin: Trajectoire et Vulnérabilité des Etablissements Humains. Ph.D. Thesis, Université d’Abomey-Calavi, Cotonou, Benin, 2022. [Google Scholar]
- El Adlouni, S.; Bobée, B. Analyse Fréquentielle Avec le Logiciel HYFRAN-PLUS; Université de Monctone: Moncton, NB, Canada, 2014; p. 71. [Google Scholar]
- El Adlouni, S.; Bobée, B. Decision Support System for Hydrological Risk Assessment. IAHS-AISH Publ. 2010, 340, 25–31. [Google Scholar]
- Haddad, K.; Rahman, A. Selection of the Best Fit Flood Frequency Distribution and Parameter Estimation Procedure: A Case Study for Tasmania in Australia. Stoch. Environ. Res. Risk Assess. 2011, 25, 415–428. [Google Scholar] [CrossRef]
- Gado, T.A.; Nguyen, V.-T.-V. An At-Site Flood Estimation Method in the Context of Nonstationarity II. Statistical Analysis of Floods in Quebec. J. Hydrol. 2016, 535, 722–736. [Google Scholar] [CrossRef]
- Bobée, B.; Ashkar, F. Sundry Averages Method (Sam) for Estimating Parameters of the Log-Pearson Type 3 Distribution; INRS-Eau: rue de la Couronne, QC, Canada, 1988; ISBN 978-2-89146-248-8. [Google Scholar]
- Taylor, K.E. Summarizing Multiple Aspects of Model Performance in a Single Diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- dos Santos Silva, F.D.; da Costa, C.P.W.; dos Santos Franco, V.; Gomes, H.B.; da Silva, M.C.L.; dos Santos Vanderlei, M.H.G.; Costa, R.L.; da Rocha Júnior, R.L.; Cabral Júnior, J.B.; dos Reis, J.S.; et al. Intercomparison of Different Sources of Precipitation Data in the Brazilian Legal Amazon. Climate 2023, 11, 241. [Google Scholar] [CrossRef]
- Andrade-Velázquez, M.; Montero-Martínez, M.J. Statistical Downscaling of Precipitation in the South and Southeast of Mexico. Climate 2023, 11, 186. [Google Scholar] [CrossRef]
- Wadoux, A.M.J.-C.; Walvoort, D.J.J.; Brus, D.J. An Integrated Approach for the Evaluation of Quantitative Soil Maps through Taylor and Solar Diagrams. Geoderma 2022, 405, 115332. [Google Scholar] [CrossRef]
- Gupta, N.; Chavan, S.R. A Comprehensive Decision Support System for the Characterization of Probability Distribution Tails for Daily Precipitation. J. Hydrol. 2023, 626, 130282. [Google Scholar] [CrossRef]
- Wietzke, L.M.; Merz, B.; Gerlitz, L.; Kreibich, H.; Guse, B.; Castellarin, A.; Vorogushyn, S. Comparative Analysis of Scalar Upper Tail Indicators. Hydrol. Sci. J. 2020, 65, 1625–1639. [Google Scholar] [CrossRef]
- Gupta, N.; Chavan, S.R. Characterizing the Tail Behaviour of Daily Precipitation Probability Distributions over India Using the Obesity Index. Int. J. Climatol. 2022, 42, 2543–2565. [Google Scholar] [CrossRef]
- El Adlouni, S.; Bobée, B.; Ouarda, T.B.M.J. Caractérisation des Distributions à Queue Lourde pour L’analyse des Crues; Université de Québec: rue de la Couronne, QC, Canada, 2007; p. 82. [Google Scholar]
- Moccia, B.; Papalexiou, S.M.; Russo, F.; Napolitano, F. Spatial Variability of Precipitation Extremes over Italy Using a Fine-Resolution Gridded Product. J. Hydrol. Reg. Stud. 2021, 37, 100906. [Google Scholar] [CrossRef]
- Allé, U. Analyse de la Gestion des Changements Climatiques par les Producteurs de Maïs sur le Plateau d’Allada au Sud-Bénin. Ph.D. Thesis, Université d’Abomey-Calavi, Cotonou, Benin, 2014. [Google Scholar]
- Seydou, W. Vulnérabilité du Paysannat aux Changements Climatiques dans la Dépression Médiane au Sud-Bénin. Ph.D. Thesis, Université d’Abomey-Calavi, Cotonou, Benin, 2020. [Google Scholar]
- Nakou, R.T.; Worou, N.C.; Bacharou, T.; Codo, F.d.P.; Sintondji, L.O.; Alassane, A.; Yalo, N. Analyse Spatio-Temporelle Des Sècheresses et Humidités Dans La Portion Béninoise Du Bassin Du Fleuve Mono, Basse Vallée. Rev. Ivoir. Sci. Technol. 2022, 40, 248–264. [Google Scholar]
- Kouassi, A.M.; Nassa, R.A.-K.; Kouakou, K.E.; Kouame, K.F.; Biemi, J. Analyse des impacts des changements climatiques sur les normes hydrologiques en Afrique de l’Ouest: Cas du district d’Abidjan (sud de la Côte d’Ivoire). Rev. Sci. L’eau/J. Water Sci. 2019, 32, 207–220. [Google Scholar] [CrossRef]
- El Adlouni, S.; Bobée, B.; Samoud, O. Guide Pour Les Méthodes Du Système d’Aide à La Décision (SAD) de Hyfran-Plus; Water Resources Publication: Littleton, CO, USA, 2012; p. 12. [Google Scholar]
| Distributions | Parameters | ||
|---|---|---|---|
| GEV | (1) | ||
| IG | (2) | ||
| LPIII | (3) | ||
| HIB | (4) | ||
| Rain Gauge Station | Independence Test | Stationarity Test | Homogeneity Test | |||
|---|---|---|---|---|---|---|
| U | P (α = 5%) | K | P (α = 5%) | W | P (α = 5%) | |
| Dogbo | 1.46 | 0.14 | 1.22 | 0.22 | 1.29 | 0.19 |
| Grand-Popo | 2.28 | 0.02 | 1.2 | 0.23 | 0.38 | 0.70 |
| Aplahoué | 0.59 | 0.55 | 0.10 | 0.92 | 1.13 | 0.26 |
| Bopa | 0.65 | 0.51 | 1.33 | 0.18 | 1.32 | 0.19 |
| Toffo | 1.23 | 0.22 | 1.68 | 0.09 | 0.98 | 0.33 |
| Abomey | 0.11 | 0.91 | 1.62 | 0.11 | 1.03 | 0.30 |
| Distributions | Stations | ||||||
|---|---|---|---|---|---|---|---|
| Abomey | Toffo | Dogbo | Grand-Popo | Bopa | Aplahoué | ||
| Log-Normal (LN) | X | X | X | X | X | X | |
| Class C | Fréchet (EV2) | V | V | V | V | V | V |
| Halphen Type B Inverse (HIB) | V | V | V | V | V | V | |
| Log-Pearson Type III (LPIII) | V | V | V | V | V | V | |
| Inverse Gamma (IG) | V | V | V | V | V | V | |
| Class E | Exponential (EXP) | V | V | X | X | X | V |
| Class D | Halphen Type A (HA) | X | X | X | X | X | X |
| Gamma | X | X | X | X | X | X | |
| Pearson Type III (PIII) | X | X | X | X | X | X | |
| Halphen Type B (HB) | X | X | X | X | X | X | |
| Gumbel (GMB) | X | X | X | X | X | X | |
| Tests | Log-Normal test | NA | NA | NA | NA | NA | NA |
| JB Test | NA | NA | NA | NA | NA | NA | |
| Log-log plot | C | C | C | C | C | NA | |
| Mean Excess Function (MEF) | E | E | NA | NA | NA | E | |
| Hill ratio plot | C | C | C | C | C | C | |
| Jackson Statistic | D-E | D-E | C | C | C | D-E | |
| Results | Class | C-E | C-E | C | C | C | C-E |
| Percentage (%) | C | 67 | 67 | 100 | 100 | 100 | 33 |
| D | 0 | 0 | 0 | 0 | 0 | 0 | |
| E | 33 | 33 | 0 | 0 | 0 | 67 | |
| Stations | Model | Parameters | ||
|---|---|---|---|---|
| Location | Scale | Shape | ||
| Dogbo | GEV | 68.13 | 18.26 | 0.03 |
| LPIII | −1.68 | 240.16 | 854.89 | |
| IG | 938.30 | 12.97 | ||
| Grand-Popo | GEV | 79.70 | 30.79 | −0.08 |
| LPIII | −3.73 | 177.68 | 1011.60 | |
| IG | 515.85 | 6.09 | ||
| Aplahoué | GEV | 80.16 | 20.15 | 0.13 |
| LPIII | 2.72 | −65.16 | 51.04 | |
| IG | 1297.30 | 15.48 | ||
| Bopa | GEV | 70.75 | 19.13 | −0.13 |
| LPIII | 1.46 | 24.76 | 11.08 | |
| IG | 862.87 | 11.24 | ||
| HIB | 132.38 | 0.29 and 2.96 | ||
| Toffo | GEV | 64.52 | 18.13 | −0.172 |
| LPIII | 1.49 | 18.25 | 6.83 | |
| IG | 714.09 | 10.13 | ||
| HIB | 127.05 | 1.43 and 2.25 | ||
| Abomey | GEV | 72.94 | 17.93 | −0.08 |
| LPIII | 1.45 | 32.04 | 14.87 | |
| IG | 1085.46 | 13.79 | ||
| HIB | 148.83 | 0.20 and 3.64 | ||
| Stations | GEV | Log-Pearson Type III | Inverse Gamma (IG) | Halphen Type B Inverse (HIB) | ||||
|---|---|---|---|---|---|---|---|---|
| BIC | AIC | BIC | AIC | BIC | AIC | BIC | AIC | |
| Dogbo | 377.75 | 372.61 | 377.64 | 372.5 | 374.03 | 370.60 | - | - |
| Grand-Popo | 425.74 | 420.60 | 425.69 | 420.55 | 422.68 | 419.25 | - | - |
| Aplahoué | 379.99 | 374.85 | 379.93 | 374.79 | 378.12 | 374.69 | - | - |
| Bopa | 388.54 | 383.40 | 388.67 | 383.53 | 385.45 | 382.03 | 388.58 | 383.44 |
| Toffo | 386.07 | 380.92 | 386.07 | 380.93 | 383.23 | 379.80 | 386.01 | 380.87 |
| Abomey | 381.32 | 376.18 | 381.32 | 376.18 | 378.10 | 374.68 | 381.35 | 376.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alofa, V.M.; Hounsou, M.B.; Houeffa, G.-D.; N’tcha M’po, Y.; Ahoton, D.H.; Vissin, E.; Agbossou, E. Selection of a Probability Model Adapted to the Current Climate for Annual Maximum Daily Rainfall in the Benin Mono-Couffo Basin (West Africa). Hydrology 2025, 12, 86. https://doi.org/10.3390/hydrology12040086
Alofa VM, Hounsou MB, Houeffa G-D, N’tcha M’po Y, Ahoton DH, Vissin E, Agbossou E. Selection of a Probability Model Adapted to the Current Climate for Annual Maximum Daily Rainfall in the Benin Mono-Couffo Basin (West Africa). Hydrology. 2025; 12(4):86. https://doi.org/10.3390/hydrology12040086
Chicago/Turabian StyleAlofa, Voltaire Midakpo, Mathieu B. Hounsou, Grâce-Désirée Houeffa, Yèkambèssoun N’tcha M’po, David Houéwanou Ahoton, Expédit Vissin, and Euloge Agbossou. 2025. "Selection of a Probability Model Adapted to the Current Climate for Annual Maximum Daily Rainfall in the Benin Mono-Couffo Basin (West Africa)" Hydrology 12, no. 4: 86. https://doi.org/10.3390/hydrology12040086
APA StyleAlofa, V. M., Hounsou, M. B., Houeffa, G.-D., N’tcha M’po, Y., Ahoton, D. H., Vissin, E., & Agbossou, E. (2025). Selection of a Probability Model Adapted to the Current Climate for Annual Maximum Daily Rainfall in the Benin Mono-Couffo Basin (West Africa). Hydrology, 12(4), 86. https://doi.org/10.3390/hydrology12040086