Simulating Nonpoint Source Pollution Impacts in Groundwater: Three-Dimensional Advection–Dispersion Versus Quasi-3D Streamline Transport Approach
Abstract
1. Introduction
2. Materials and Methods
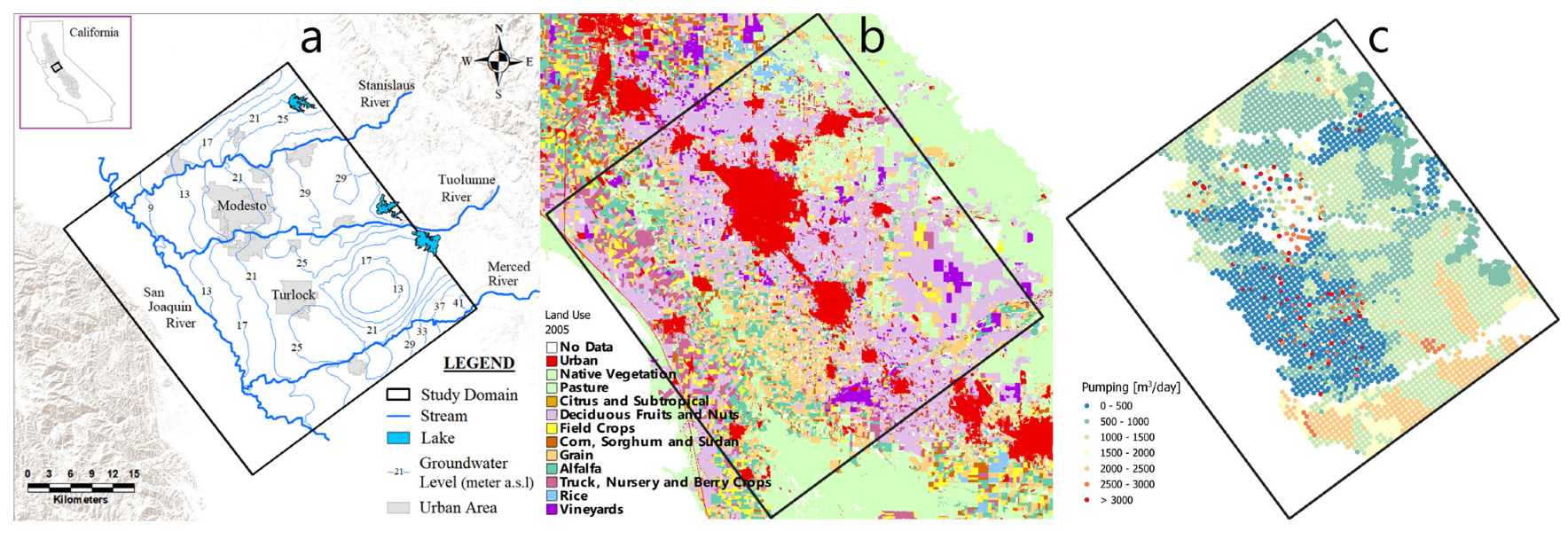
2.1. Description of the Study Area
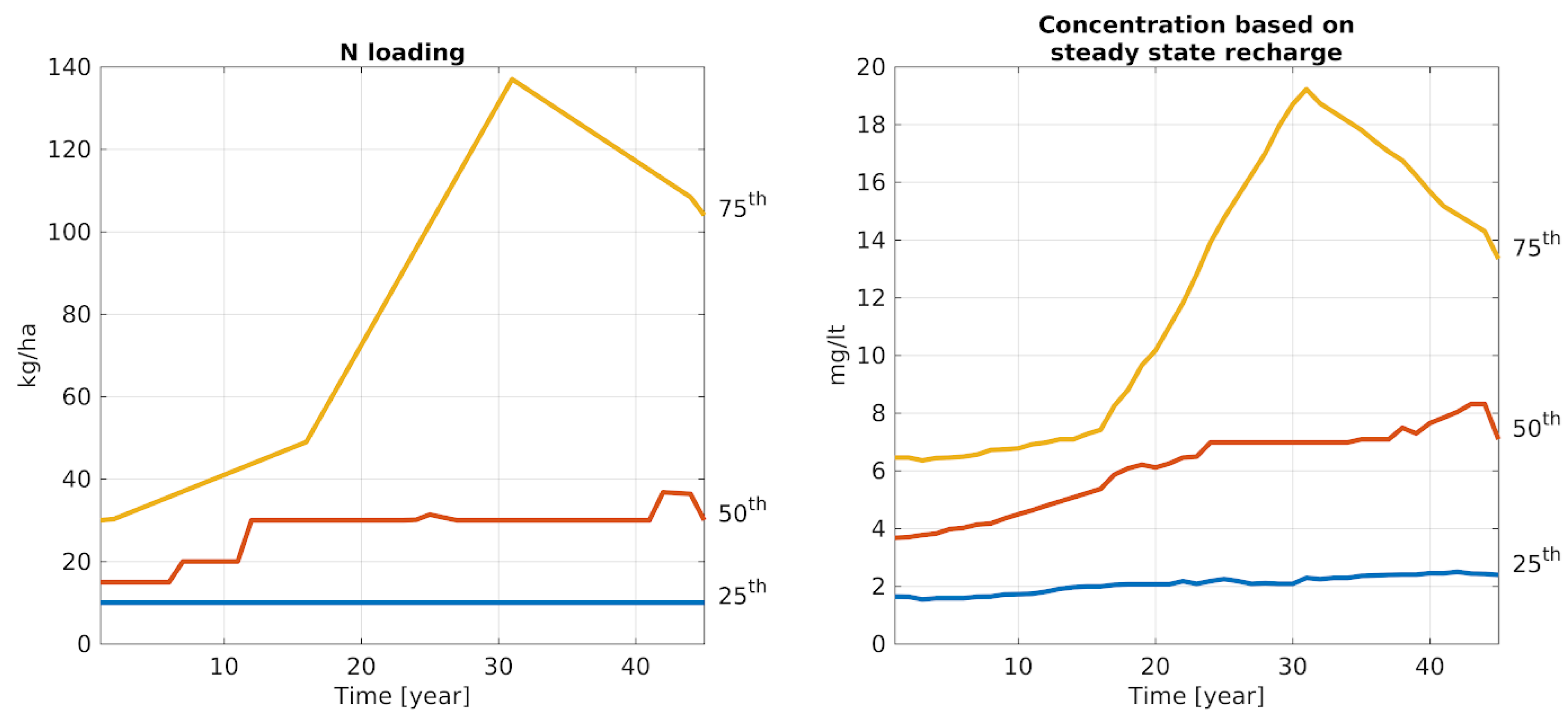
2.2. Nitrate Loading to Groundwater
2.3. Numerical Methods: Mathematical Problem
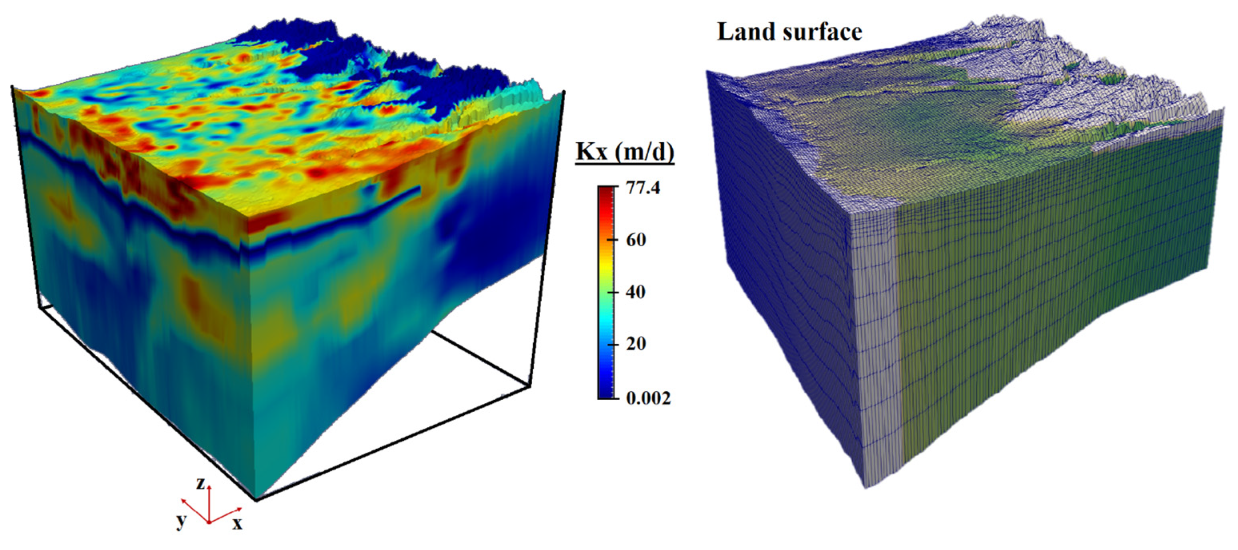
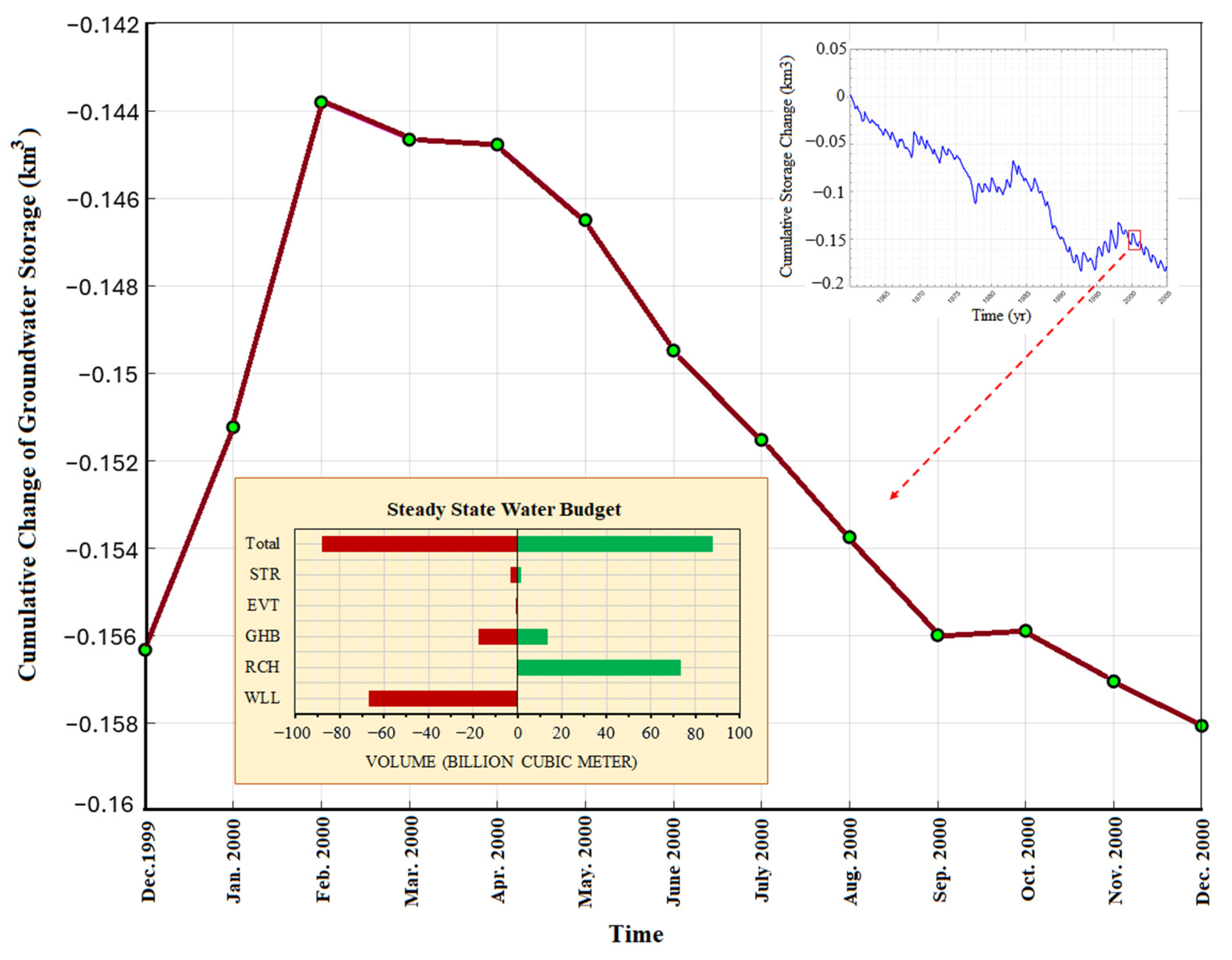
2.4. Numerical Methods: Transient and Steady-State Groundwater Flow Models
2.5. Numerical Methods: Fully 3D ADE-Based Transport Model (MT3D)
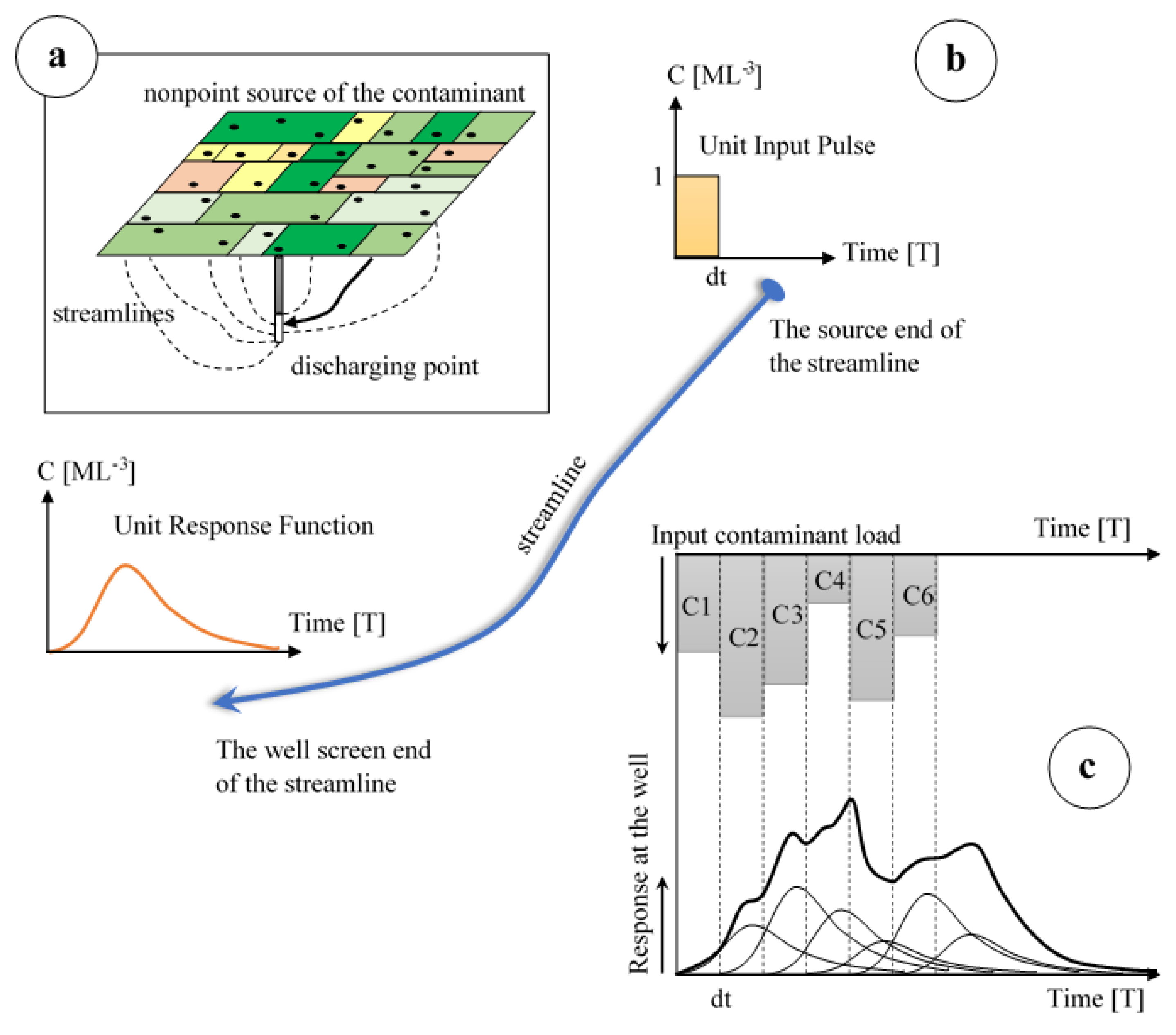
2.6. Numerical Methods: High-Resolution Flow with Quasi-3D URF-Based Transport Simulation
- Simulation of the groundwater flow field;
- Backward particle tracking from the points of interest (compliance surfaces/well screens);
- Streamline transport simulation with unit step/unit input loading to derive the streamline unit response functions (URFs);
- Convolution of the URFs with a nitrate loading history scenario.
2.7. Statistical Analysis for Shallow and Deep Aquifer Model Comparison
3. Results
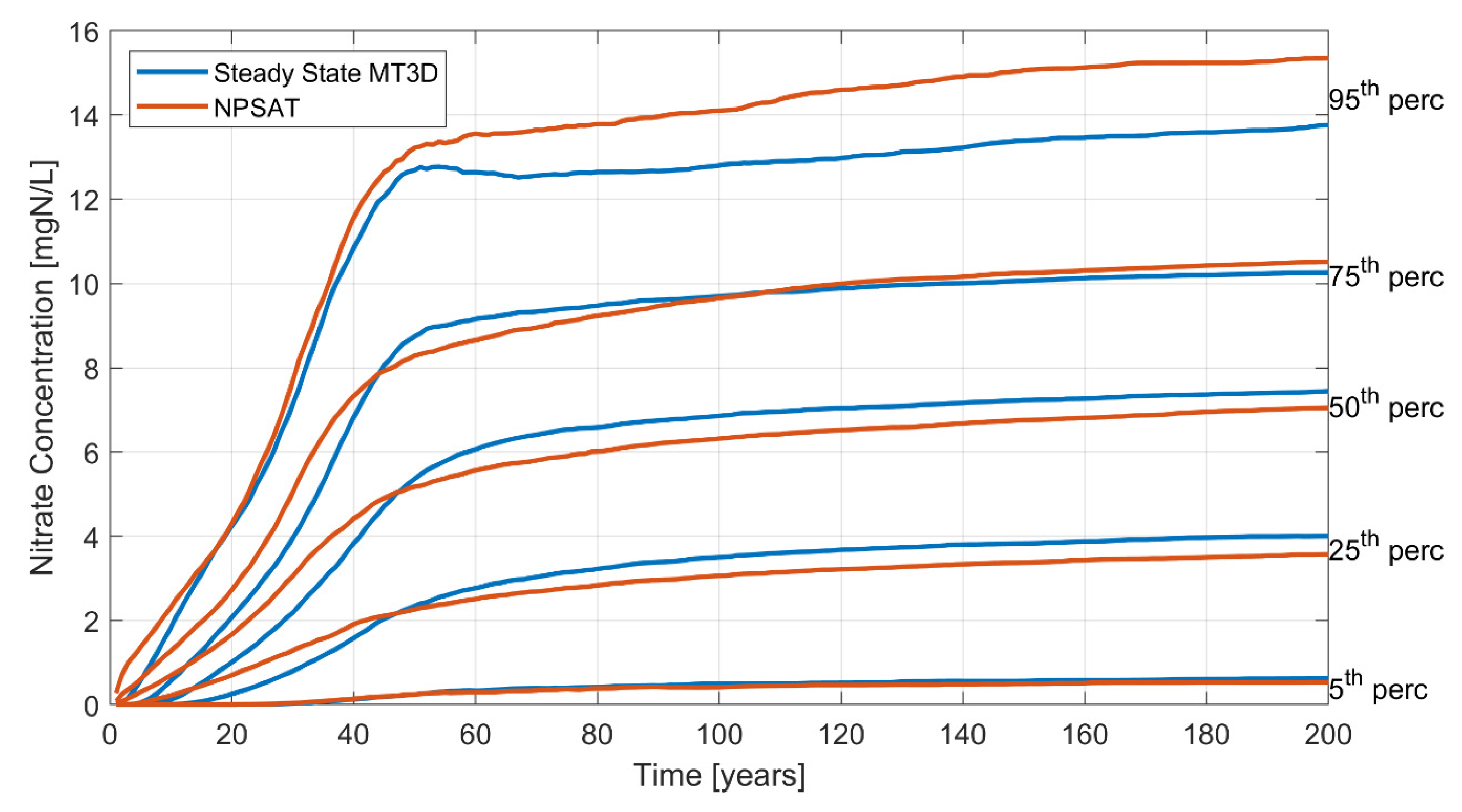
3.1. Business-as-Usual Simulations
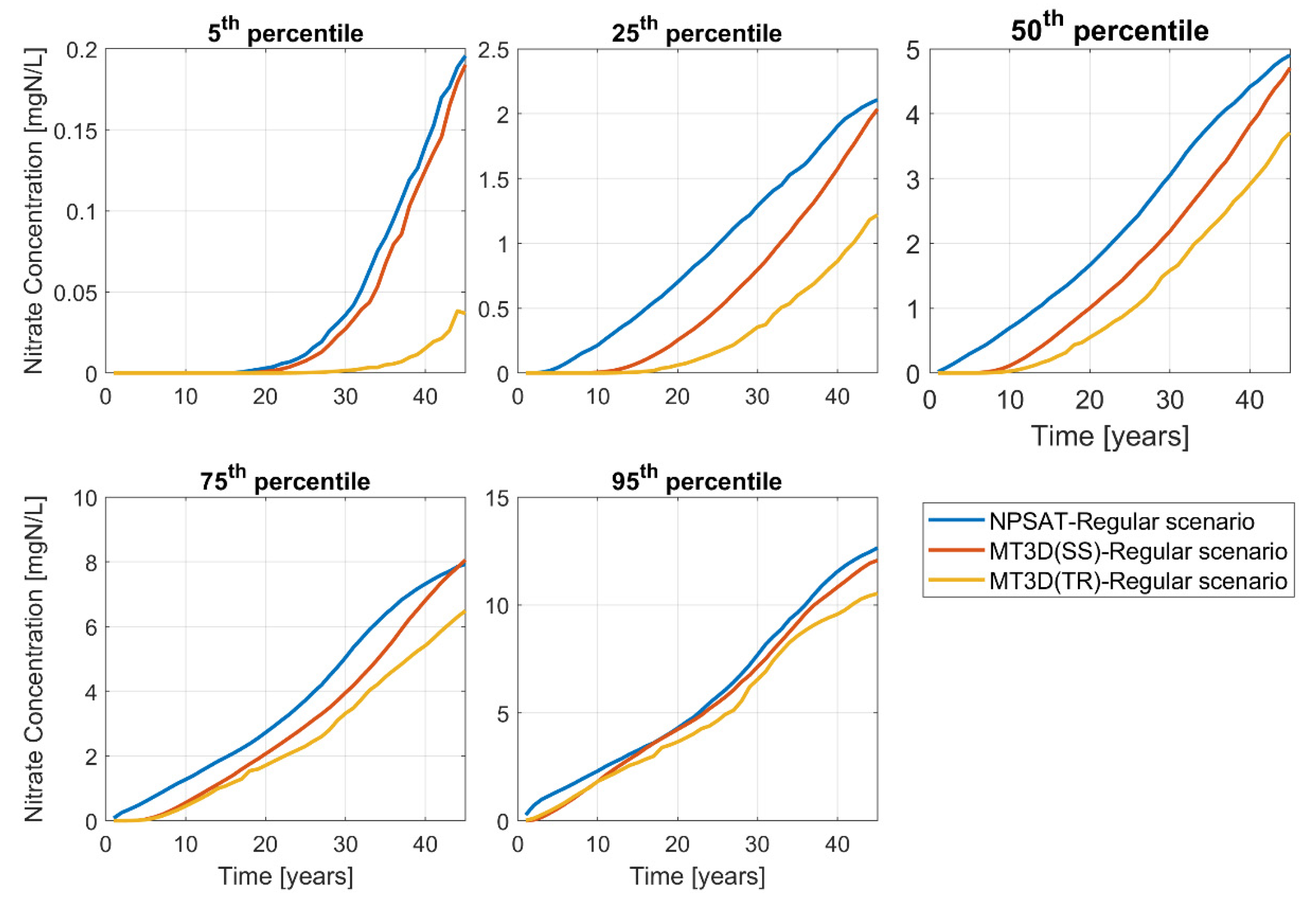
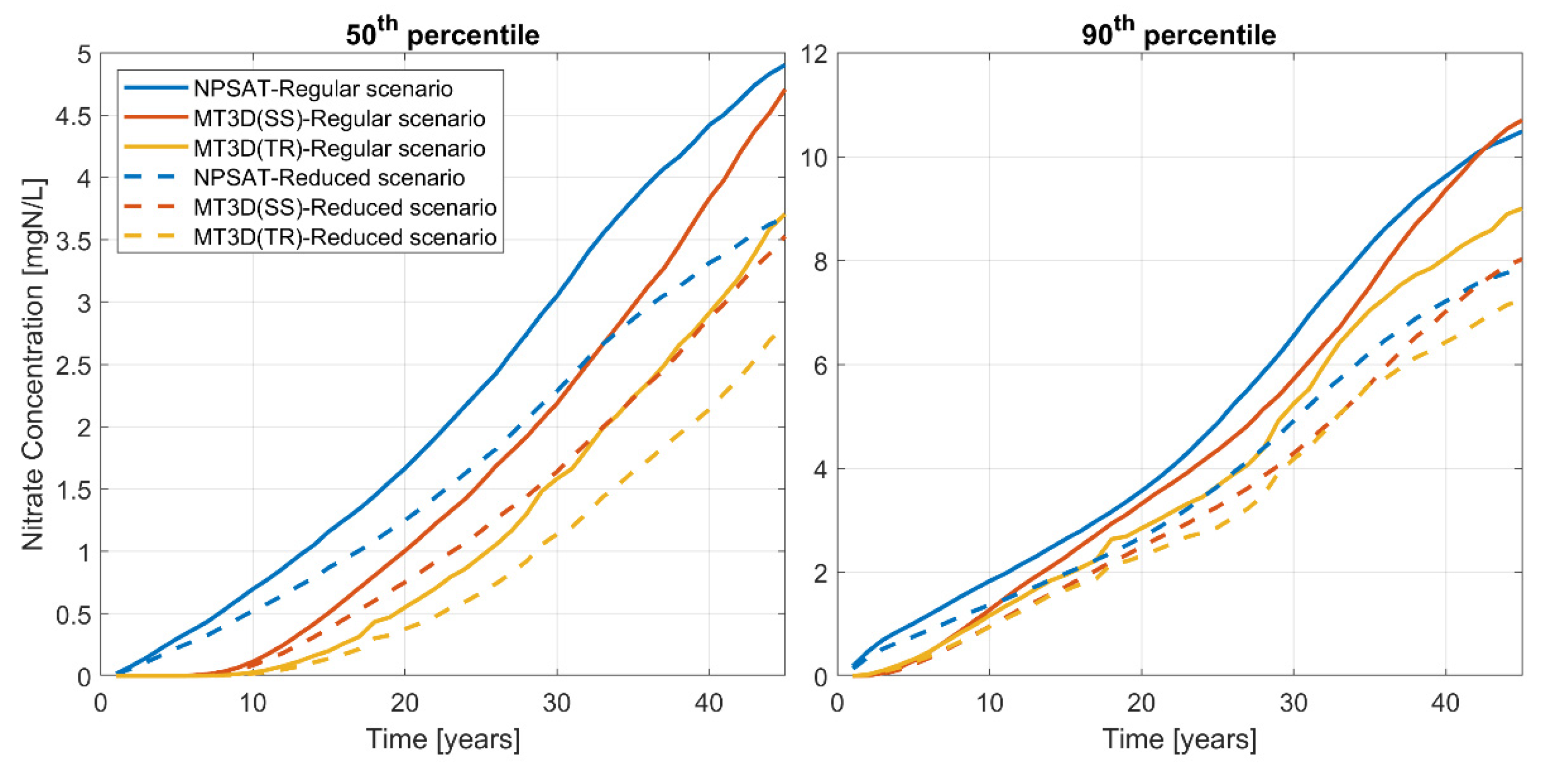
3.2. Predicting Relative Future Changes
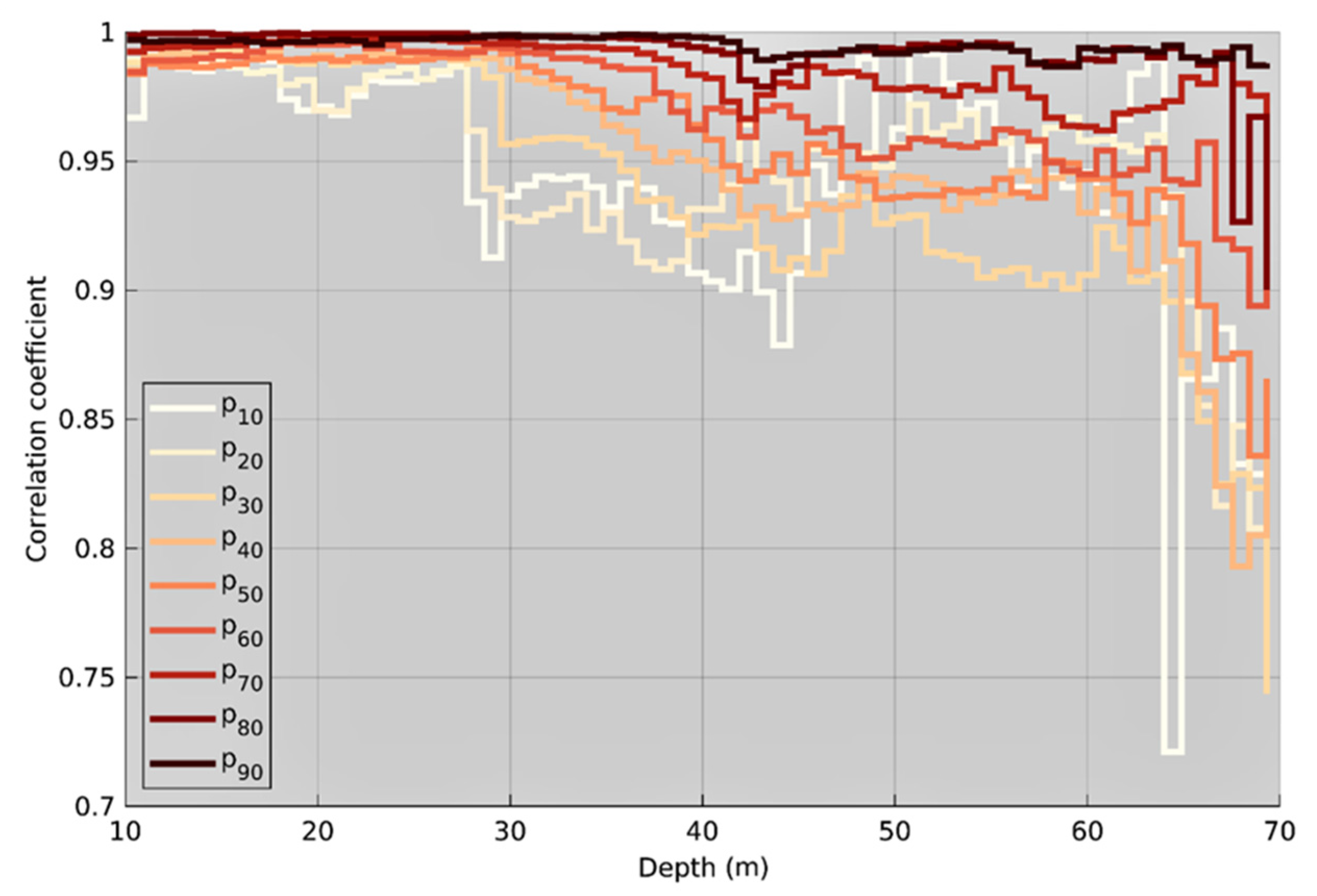
3.3. Depth-Dependent Correlation of NPSAT and MT3D Results
4. Discussion
Computational Efficiency of the URF-Based Transport Simulator
5. Conclusions
- Albeit lacking transverse dispersion, the URF-based method shows very good agreement with the 3D ADE solution, when both are based on a steady-state flow field (maximum discrepancies are 10%, observed for the most contaminated fraction of wells).
- Similarly, the 3D ADE solution based on a significantly coarser grid around wells than the URF-based framework proposed has an only slightly reduced spread of concentration percentiles across the ensemble of wells, relative to the URF-based framework.
- Using the steady-state approximation of the cyclically transient flow field yields similar disagreements to the 3D-ADE-based solution with the transient flow field, whether using the 3D-ADE- or the URF-based transport model. The 3D-ADE-based solution for a steady flow field is closer to that for a transient flow field than the URF-based solution, possibly due to the lack of difference in the discretization of the flow-field between the 3-ADE solutions for steady and transient flow.
- The URF-based transport solution in the case study (evaluation of nitrate BTCs at 3900 wells over a 45-year simulation period) maintains at least three-order-of-magnitude gains in computational efficiency for nitrate loading scenario evaluation.
- The URF-based transport solution is applicable to a wide range of solutes as it retains the ability to also account for reactive transport of contaminants or tracers subject to retardation (sorption) and/or first-order degradation.
- Model agreement was shown to depend on the vertical location of the well screen. The correlation of the predictions between the models is higher between the URF-based and 3D ADE models for the shallow wells. For deep wells, differences between travel path length in the high-resolution, URF-based framework and the lower-resolution 3D ADE framework lead to smaller spread of travel time in the latter approach.
- The results suggest that diffusion, transverse dispersion, and cyclical transiency of the velocity field have relatively small effects on the ensemble statistical outcome of contaminant concentration across a large group of CSs (wells, stream reaches) in a region with diverse, contiguous nonpoint sources of evolving strength. The observed variability of concentration between CSs is predominantly driven by (i) the variability among source concentrations emitted across the landscape to the water table and (ii) the variability across CSs with respect to the number and diversity of sources mixed into the waters of an individual CS (e.g., within a well screen).
- The efficiency of the URF-based approach makes it appropriate for decision-makers and stakeholders. However, future research is needed to identify suitable methods and tools to incorporate the modeling framework into a suitable tool, e.g., web-based or server applications that can be used by policy makers and planners.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, Y.; Khu, S.-T.; Xi, B.; Su, J.; Hao, F.; Wu, J.; Huo, S. Status and Challenges of Water Pollution Problems in China: Learning from the European Experience. Environ. Earth Sci. 2014, 72, 1243–1254. [Google Scholar] [CrossRef]
- Adimalla, N.; Qian, H. Groundwater Quality Evaluation Using Water Quality Index (WQI) for Drinking Purposes and Human Health Risk (HHR) Assessment in an Agricultural Region of Nanganur, South India. Ecotoxicol. Environ. Saf. 2019, 176, 153–161. [Google Scholar] [CrossRef] [PubMed]
- Armour, J.D.; Nelson, P.N.; Daniells, J.W.; Rasiah, V.; Inman-Bamber, N.G. Nitrogen Leaching from the Root Zone of Sugarcane and Bananas in the Humid Tropics of Australia. Agric. Ecosyst. Environ. 2013, 180, 68–78. [Google Scholar] [CrossRef]
- Biggs, J.S.; Thorburn, P.J.; Crimp, S.; Masters, B.; Attard, S.J. Interactions between Climate Change and Sugarcane Management Systems for Improving Water Quality Leaving Farms in the Mackay Whitsunday Region, Australia. Agric. Ecosyst. Environ. 2013, 180, 79–89. [Google Scholar] [CrossRef]
- Van Grieken, M.E.; Roebeling, P.C.; Bohnet, I.C.; Whitten, S.M.; Webster, A.J.; Poggio, M.; Pannell, D. Adoption of Agricultural Management for Great Barrier Reef Water Quality Improvement in Heterogeneous Farming Communities. Agric. Syst. 2019, 170, 1–8. [Google Scholar] [CrossRef]
- Lockhart, K.M.; King, A.M.; Harter, T. Identifying sources of groundwater nitrate contamination in a large alluvial groundwater basin with highly diversified intensive agricultural production. J. Contam. Hydrol. 2013, 151, 140–154. [Google Scholar] [CrossRef]
- Yang, A.L.; Raghuram, N.; Adhya, T.K.; Porter, S.D.; Panda, A.N.; Kaushik, H.; Jayaweera, A.; Nissanka, S.P.; Anik, A.R.; Shifa, S.; et al. Policies to Combat Nitrogen Pollution in South Asia: Gaps and Opportunities. Environ. Res. Lett. 2022, 17, 025007. [Google Scholar] [CrossRef]
- Hansen, B.; Thorling, L.; Schullehner, J.; Termansen, M.; Dalgaard, T. Groundwater Nitrate Response to Sustainable Nitrogen Management. Sci. Rep. 2017, 7, 8566. [Google Scholar] [CrossRef]
- Platjouw, F.M.; Nesheim, I.; Enge, C. Policy Coherence for the Protection of Water Resources against Agricultural Pollution in the EU and Norway. Rev. Eur. Comp. Int. Environ. Law 2023, 32, 485–500. [Google Scholar] [CrossRef]
- Velthof, G.L.; Lesschen, J.P.; Webb, J.; Pietrzak, S.; Miatkowski, Z.; Pinto, M.; Kros, J.; Oenema, O. The Impact of the Nitrates Directive on Nitrogen Emissions from Agriculture in the EU-27 during 2000–2008. Sci. Total Environ. 2014, 468–469, 1225–1233. [Google Scholar] [CrossRef]
- Kallis, G.; Butler, D. The EU Water Framework Directive: Measures and Implications. Water Policy 2001, 3, 125–142. [Google Scholar] [CrossRef]
- California State of Sustainable Groundwater Management Act (SGMA). Available online: https://water.ca.gov/Programs/Groundwater-Management/SGMA-Groundwater-Management (accessed on 17 February 2025).
- Lubell, M.; Blomquist, W.; Beutler, L. Sustainable Groundwater Management in California: A Grand Experiment in Environmental Governance. Soc. Nat. Resour. 2020, 33, 1447–1467. [Google Scholar] [CrossRef]
- Salt Program. CV SALTS. Available online: https://www.cvsalinity.org/ (accessed on 17 February 2025).
- Quinn, N.W.T.; Oster, J.D. Innovations in Sustainable Groundwater and Salinity Management in California’s San Joaquin Valley. Sustainability 2021, 13, 6658. [Google Scholar] [CrossRef]
- Bastani, M.; Harter, T. Source Area Management Practices as Remediation Tool to Address Groundwater Nitrate Pollution in Drinking Supply Wells. J. Contam. Hydrol. 2019, 226, 103521. [Google Scholar] [CrossRef] [PubMed]
- McMahon, P.B.; Böhlke, J.K.; Kauffman, L.J.; Kipp, K.L.; Landon, M.K.; Crandall, C.A.; Burow, K.R.; Brown, C.J. Source and Transport Controls on the Movement of Nitrate to Public Supply Wells in Selected Principal Aquifers of the United States. Water Resour. Res. 2008, 44, W04401. [Google Scholar] [CrossRef]
- McMahon, P.B.; Burow, K.R.; Kauffman, L.J.; Eberts, S.M.; Böhlke, J.K.; Gurdak, J.J. Simulated Response of Water Quality in Public Supply Wells to Land Use Change. Water Resour. Res. 2008, 44, W00A06. [Google Scholar] [CrossRef]
- Kuai, P.; Li, W.; Liu, N. Evaluating the Effects of Land Use Planning for Non-Point Source Pollution Based on a System Dynamics Approach in China. PLoS ONE 2015, 10, e0135572. [Google Scholar] [CrossRef]
- Zhang, H.; Hiscock, K.M. Modelling Response of Groundwater Nitrate Concentration in Public Supply Wells to Land-Use Change. Q. J. Eng. Geol. Hydrogeol. 2016, 49, 170–182. [Google Scholar] [CrossRef]
- Kourakos, G.; Klein, F.; Cortis, A.; Harter, T. A Groundwater Nonpoint Source Pollution Modeling Framework to Evaluate Long-Term Dynamics of Pollutant Exceedance Probabilities in Wells and Other Discharge Locations. Water Resour. Res. 2012, 48, W00L13. [Google Scholar] [CrossRef]
- Hansen, B.; Dalgaard, T.; Thorling, L.; Sørensen, B.; Erlandsen, M. Regional Analysis of Groundwater Nitrate Concentrations and Trends in Denmark in Regard to Agricultural Influence. Biogeosciences 2012, 9, 3277–3286. [Google Scholar] [CrossRef]
- Boyle, D.; King, A.; Kourakos, G.; Lockhart, K.; Mayzelle, M.; Fogg, G.; Harter, T. Groundwater Nitrate Occurrence. Technical Report 4 in: Addressing Nitrate in California’s Drinking Water with a Focus on Tulare Lake Basin and Salinas Valley Groundwater; Report for the State Water Resources Control Board Report to the Legislature; Center for Watershed Sciences, University of California: Davis, CA, USA, 2012. [Google Scholar]
- Turkeltaub, T.; Kurtzman, D.; Dahan, O. Real-Time Monitoring of Nitrate Transport in the Deep Vadose Zone under a Crop Field—Implications for Groundwater Protection. Hydrol. Earth Syst. Sci. 2016, 20, 3099–3108. [Google Scholar] [CrossRef]
- Ransom, K.M.; Nolan, B.T.A.; Traum, J.; Faunt, C.C.; Bell, A.M.; Gronberg, J.A.M.; Wheeler, D.C.Z.; Rosecrans, C.; Jurgens, B.; Schwarz, G.E.; et al. A Hybrid Machine Learning Model to Predict and Visualize Nitrate Concentration throughout the Central Valley Aquifer, California, USA. Sci. Total Environ. 2017, 601–602, 1160–1172. [Google Scholar] [CrossRef] [PubMed]
- Rosecrans, C.Z.; Nolan, B.T.; Gronberg, J.M. Prediction and Visualization of Redox Conditions in the Groundwater of Central Valley, California. J. Hydrol. 2017, 546, 341–356. [Google Scholar] [CrossRef]
- Milnes, E.; Perrochet, P. Simultaneous Identification of a Single Pollution Point-Source Location and Contamination Time under Known Flow Field Conditions. Adv. Water Resour. 2007, 30, 2439–2446. [Google Scholar] [CrossRef]
- Zhou, Y.; Jiang, Y.; An, D.; Ma, Z.; Xi, B.; Yang, Y.; Li, M.; Hao, F.; Lian, X. Simulation on Forecast and Control for Groundwater Contamination of Hazardous Waste Landfill. Environ. Earth Sci. 2014, 72, 4097–4104. [Google Scholar] [CrossRef]
- Abd-Elaty, I.; Zelenakova, M.; Straface, S.; Vranayová, Z.; Abu-hashim, M. Integrated Modelling for Groundwater Contamination from Polluted Streams Using New Protection Process Techniques. Water 2019, 11, 2321. [Google Scholar] [CrossRef]
- Colman, J.A.; Masterson, J.P. Transient Simulations of Nitrogen Load for a Coastal Aquifer and Embayment, Cape Cod, MA. Environ. Sci. Technol. 2008, 42, 207–213. [Google Scholar] [CrossRef]
- Yager, R.M.; Heywood, C.E. Simulation of the Effects of Seasonally Varying Pumping on Intraborehole Flow and the Vulnerability of Public-Supply Wells to Contamination. Groundwater 2014, 52, 40–52. [Google Scholar] [CrossRef]
- Bexfield, L.M.; Jurgens, B.C. Effects of Seasonal Operation on the Quality of Water Produced by Public-Supply Wells. Groundwater 2014, 52, 10–24. [Google Scholar] [CrossRef]
- Hiscock, K.; Lovett, A.; Saich, A.; Dockerty, T.; Johnson, P.; Sandhu, C.; Sünnenberg, G.; Appleton, K.; Harris, B.; Greaves, J. Modelling Land-Use Scenarios to Reduce Groundwater Nitrate Pollution: The European Water4All Project. Q. J. Eng. Geol. Hydrogeol. 2007, 40, 417–434. [Google Scholar] [CrossRef]
- Carle, S.F.; Esser, B.K.; Moran, J.E. High-Resolution Simulation of Basin-Scale Nitrate Transport Considering Aquifer System Heterogeneity. Geosphere 2006, 2, 195–209. [Google Scholar] [CrossRef]
- Lin, L.; Yang, J.-Z.; Zhang, B.; Zhu, Y. A Simplified Numerical Model of 3-D Groundwater and Solute Transport at Large Scale Area. J. Hydrodyn. 2010, 22, 319–328. [Google Scholar] [CrossRef]
- Prommer, H.; Barry, D.A.; Davis, G.B. Modelling of Physical and Reactive Processes during Biodegradation of a Hydrocarbon Plume under Transient Groundwater Flow Conditions. J. Contam. Hydrol. 2002, 59, 113–131. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Sykes, J.F.; Normani, S.D. Impacts of Spatial and Temporal Recharge on Field-Scale Contaminant Transport Model Calibration. J. Hydrol. 2015, 527, 77–87. [Google Scholar] [CrossRef]
- Zheng, C.; Wang, P.P. A Field Demonstration of the Simulation Optimization Approach for Remediation System Design. Groundwater 2002, 40, 258–266. [Google Scholar] [CrossRef]
- Bastani, M.; Harter, T. Effects of Upscaling Temporal Resolution of Groundwater Flow and Transport Boundary Conditions on the Performance of Nitrate-Transport Models at the Regional Management Scale. Hydrogeol. J. 2020, 28, 1299–1322. [Google Scholar] [CrossRef]
- Martin, J.C.; Wegner, R.E. Numerical Solution of Multiphase, Two-Dimensional Incompressible Flow Using Stream-Tube Relationships. Soc. Pet. Eng. J. 1979, 19, 313–323. [Google Scholar] [CrossRef]
- Matringe, S.F.; Juanes, R.; Tchelepi, H.A. Robust Streamline Tracing for the Simulation of Porous Media Flow on General Triangular and Quadrilateral Grids. J. Comput. Phys. 2006, 219, 992–1012. [Google Scholar] [CrossRef]
- Robinson, B.A.; Dash, Z.V.; Srinivasan, G. A Particle Tracking Transport Method for the Simulation of Resident and Flux-Averaged Concentration of Solute Plumes in Groundwater Models. Comput. Geosci. 2010, 14, 779–792. [Google Scholar] [CrossRef]
- Valocchi, A.J.; Herrera, P.; Viswanathan, H. Incorporating Transverse Mixing into Streamline-Based Simulation of Transport in Heterogeneous Aquifers. In Groundwater Quality Modeling and Management Under Uncertainty; American Society of Civil Engineers: Reston, VA, USA, 2003; pp. 294–304. [Google Scholar] [CrossRef]
- Henri, C.V.; Harter, T. Denitrification in Heterogeneous Aquifers: Relevance of Spatial Variability and Performance of Homogenized Parameters. Adv. Water Resour. 2022, 164, 104168. [Google Scholar] [CrossRef]
- Kourakos, G.; Harter, T. Vectorized Simulation of Groundwater Flow and Streamline Transport. Environ. Model. Softw. 2014, 52, 207–221. [Google Scholar] [CrossRef]
- Kourakos, G.; Harter, T. Parallel Simulation of Groundwater Non-Point Source Pollution Using Algebraic Multigrid Preconditioners. Comput. Geosci. 2014, 18, 851–867. [Google Scholar] [CrossRef]
- Henri, C.; Harter, T. Stochastic Assessment of Nonpoint Source Contamination: Joint Impact of Aquifer Heterogeneity and Well Characteristics on Management Metrics. Water Resour. Res. 2019, 55, 6773–6794. [Google Scholar] [CrossRef]
- Brunetti, G.F.A.; Maiolo, M.; Fallico, C.; Severino, G. Unraveling the Complexities of a Highly Heterogeneous Aquifer under Convergent Radial Flow Conditions. Eng. Comput. 2024, 40, 3115–3130. [Google Scholar] [CrossRef]
- Severino, G.; Fallico, C.; Brunetti, G.F.A. Correlation Structure of Steady Well-Type Flows Through Heterogeneous Porous Media: Results and Application. Water Resour. Res. 2024, 60, e2023WR036279. [Google Scholar] [CrossRef]
- Dowd, B.M.; Press, D.; Huertos, M.L. Agricultural Nonpoint Source Water Pollution Policy: The Case of California’s Central Coast. Agric. Ecosyst. Environ. 2008, 128, 151–161. [Google Scholar] [CrossRef]
- Dinar, A.; Quinn, N.W.T. Developing a Decision Support System for Regional Agricultural Nonpoint Salinity Pollution Management: Application to the San Joaquin River, California. Water 2022, 14, 2384. [Google Scholar] [CrossRef]
- Davis, G.H.; Green, J.H.; Olmsted, F.H.; Brown, D.W. Ground-Water Conditions and Storage Capacity in the San Joaquin Valley California; Prepared in cooperation with the California Department of Water Resources; USGS: Washington, DC, USA, 1959. [Google Scholar] [CrossRef]
- Phillips, S.P.; Green, C.T.; Burow, K.R.; Shelton, J.L.; Rewis, D.L. Simulation of Multiscale Ground-Water Flow in Part of the Northeastern San Joaquin Valley, California; USGS: Reston, VA, USA, 2007; p. 43. [Google Scholar] [CrossRef]
- Paschke, S.S. (Ed.) Hydrogeologic Settings and Ground-Water Flow Simulations for Regional Studies of the Transport of Anthropogenic and Natural Contaminants to Public-Supply Wells—Studies Begun in 2001; U.S. Geological Survey: Reston, VA, USA, 2007; p. 244. [Google Scholar] [CrossRef]
- Harter, T.; Dzurella, K.; Kourakos, G.; Hollander, A.; Bell, A.; Santos, N.; Hart, Q.; A.King, J.Q.; Lampinen, G.; Liptzin, D.; et al. Nitrogen Fertilizer Loading to Groundwater in the Central Valley. In Final Report to the Fertilizer Research Education Program, Projects 11-0301 and 15-0454; California Department of Food and Agriculture, University of California Davis: Davis, CA, USA, 2017; p. 333. [Google Scholar]
- Harbaugh, A.W. MODFLOW-2005, the U.S. Geological Survey Modular Ground-Water Model—The Ground-Water Flow Process. In U.S. Geological Survey Techniques and Methods; 6–A16; USGS: Reston, VA, USA, 2005. [Google Scholar] [CrossRef]
- Zheng, C.; Bennett, G.D. Applied Contaminant Transport Modeling; Wiley: Hoboken, NJ, USA, 2002; ISBN 978-0-471-38477-9. [Google Scholar]
- Hanson, R.T.; Boyce, S.E.; Schmid, W.; Hughes, J.D.; Mehl, S.W.; Leake, S.A.; Iii, T.M.; Niswonger, R.G. One-Water Hydrologic Flow Model (MODFLOW-OWHM); U.S. Geological Survey Techniques and Methods 6–A51, 120 p; USGS: Reston, VA, USA, 2014. [Google Scholar] [CrossRef]
- Phillips, S.P.; Rewis, D.L.; Traum, J.A. Hydrologic Model of the Modesto Region, California, 1960–2004; U.S. Geological Survey Scientific Investigations Report, 2015–5045: Reston, VA, USA, 2015; p. 69. [Google Scholar] [CrossRef]
- Kourakos, G.; Harter, T. Simulation of Unconfined Aquifer Flow Based on Parallel Adaptive Mesh Refinement. Water Resour. Res. 2021, 57, e2020WR029354. [Google Scholar] [CrossRef]
- Zheng, C.; Wang, P.P. MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems; Documentation and User’s Guide; U.S. Army Corps of Engineers: Washington, DC, USA, 1990; p. 170. [Google Scholar]
- Davis, S.N.; Hall, F.R. Water Quality of Eastern Stanislaus and Northern Merced Counties; Stanford University: Stanford, CA, USA, 1959; Volume 6. [Google Scholar]
- Phillips, S.P.; Burow, K.R.; Rewis, D.L.; Shelton, J.; Jurgens, B. Hydrogeologic Settings and Ground-Water Flow Simulations of the San Joaquin Valley Regional Study Area, California. In Hydrogeologic Settings and Ground-Water Flow Simulations for Regional Studies of the Transport of Anthropogenic and Natural Contaminants to Public-Supply Wells—Studies Begun in 2001; Paschke, S.S., Ed.; U.S. Geological Survey Professional Paper; U.S. Geological Survey: Reston, VA, USA, 2007; pp. 4-1–4-31. [Google Scholar]
- Schulze-Makuch, D. Longitudinal Dispersivity Data and Implications for Scaling Behavior. Groundwater 2005, 43, 443–456. [Google Scholar] [CrossRef]
- Liu, Y.; Kitanidis, P.K. A Mathematical and Computational Study of the Dispersivity Tensor in Anisotropic Porous Media. Adv. Water Resour. 2013, 62, 303–316. [Google Scholar] [CrossRef]
- McMillan, L.A.; Rivett, M.O.; Tellam, J.H.; Dumble, P.; Sharp, H. Influence of Vertical Flows in Wells on Groundwater Sampling. J. Contam. Hydrol. 2014, 169, 50–61. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers, 7th ed.; Wiley: Hoboken, NJ, USA, 2018; ISBN 978-1-119-40036-3. [Google Scholar]
- Sudicky, E.A.; Huyakorn, P.S. Contaminant Migration in Imperfectly Known Heterogeneous Groundwater Systems. Rev. Geophys. 1991, 29, 240–253. [Google Scholar] [CrossRef]
- Nakagawa, K.; Jinno, K. Evaluation of the Transition Characteristics of Macroscopic Dispersion and Estimation of the Non-Uniform Hydrogeological Structure. In Calibration and Reliability in Groundwater Modelling: Coping with Uncertainty, Proceedings of the ModelCare’99 Conference Held in Zurich, Switzerland, 20–23 September 1999, 265th ed.; Stauffer, F., Kinzelbach, W., Kovar, K., Hoehn, E., Eds.; IAHS-AISH Publication; IAHS Press: Wallingford, UK, 2000; pp. 110–116. [Google Scholar]
- Fogg, G.E.; Zhang, Y. Debates—Stochastic Subsurface Hydrology from Theory to Practice: A Geologic Perspective. Water Resour. Res. 2016, 52, 9235–9245. [Google Scholar] [CrossRef]
- Burow, K.R.; Jurgens, B.C.; Kauffman, L.J.; Phillips, S.P.; Dalgish, B.A.; Shelton, J.L. Simulations of Ground-Water Flow and Particle Pathline Analysis in the Zone of Contribution of a Public-Supply Well in Modesto, Eastern San Joaquin Valley, California; U.S. Geological Survey Scientific Investigations Report 2008–5035, 41 p; U.S. Geological Survey: Reston VA, USA, 2008. [Google Scholar]
- Green, C.T.; Zhang, Y.; Jurgens, B.C.; Starn, J.J.; Landon, M.K. Accuracy of Travel Time Distribution (TTD) Models as Affected by TTD Complexity, Observation Errors, and Model and Tracer Selection. Water Resour. Res. 2014, 50, 6191–6213. [Google Scholar] [CrossRef]
- Green, C.T.; Jurgens, B.C.; Zhang, Y.; Starn, J.J.; Singleton, M.J.; Esser, B.K. Regional Oxygen Reduction and Denitrification Rates in Groundwater from Multi-Model Residence Time Distributions, San Joaquin Valley, USA. J. Hydrol. 2016, 543, 155–166. [Google Scholar] [CrossRef]
- Fogg, G.E.; LaBolle, E.M. Motivation of Synthesis, with an Example on Groundwater Quality Sustainability. Water Resour. Res. 2006, 42, W03S05. [Google Scholar] [CrossRef]
- Somura, H.; Goto, A.; Matsui, H.; Ali Musa, E. Impacts of Nutrient Management and Decrease in Paddy Field Area on Groundwater Nitrate Concentration: A Case Study at the Nasunogahara Alluvial Fan, Tochigi Prefecture, Japan. Hydrol. Process. 2008, 22, 4752–4766. [Google Scholar] [CrossRef]
- Howden, N.J.K.; Burt, T.P.; Worrall, F.; Mathias, S.; Whelan, M.J. Nitrate Pollution in Intensively Farmed Regions: What Are the Prospects for Sustaining High-Quality Groundwater? Water Resour. Res. 2011, 47, W00L02. [Google Scholar] [CrossRef]

| Land Use | Nitrate Load as N (kg/ha/yr) | |||
|---|---|---|---|---|
| 1960 | 1975 | 1990 | 2005 | |
| Urban | 20 | 20 | 20 | 20 |
| Natural vegetation | 15 | 15 | 15 | 15 |
| Almond | 29 | 49 | 137 | 104 |
| Alfalfa | 30 | 30 | 30 | 30 |
| Vineyard | 41 | 46 | 23 | 22 |
| Corn | 61 | 64 | 153 | 87 |
| Truck crops | 83 | 134 | 186 | 124 |
| Field crops | 63 | 76 | 79 | 53 |
| Rice | 8 | 20 | 39 | 36 |
| Pasture | 0 | 0 | 0 | 0 |
| Grain | 73 | 49 | 89 | 57 |
| Fallow | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kourakos, G.; Bastani, M.; Harter, T. Simulating Nonpoint Source Pollution Impacts in Groundwater: Three-Dimensional Advection–Dispersion Versus Quasi-3D Streamline Transport Approach. Hydrology 2025, 12, 42. https://doi.org/10.3390/hydrology12030042
Kourakos G, Bastani M, Harter T. Simulating Nonpoint Source Pollution Impacts in Groundwater: Three-Dimensional Advection–Dispersion Versus Quasi-3D Streamline Transport Approach. Hydrology. 2025; 12(3):42. https://doi.org/10.3390/hydrology12030042
Chicago/Turabian StyleKourakos, Georgios, Mehrdad Bastani, and Thomas Harter. 2025. "Simulating Nonpoint Source Pollution Impacts in Groundwater: Three-Dimensional Advection–Dispersion Versus Quasi-3D Streamline Transport Approach" Hydrology 12, no. 3: 42. https://doi.org/10.3390/hydrology12030042
APA StyleKourakos, G., Bastani, M., & Harter, T. (2025). Simulating Nonpoint Source Pollution Impacts in Groundwater: Three-Dimensional Advection–Dispersion Versus Quasi-3D Streamline Transport Approach. Hydrology, 12(3), 42. https://doi.org/10.3390/hydrology12030042






