Abstract
This paper presents a novel methodology to generate Digital Elevation Models (DEMs) in flat areas, incorporating river channels from relatively coarse initial data. The technique primarily utilizes filtered dense point clouds derived from SfM-MVS (Structure from Motion-Multi-View Stereo) photogrammetry of available crewed aerial imagery datasets. The methodology operates under the assumption that the aerial survey was carried out during low-flow or drought conditions so that the dry (or almost dry) riverbed is detected, although in an imprecise way. Direct interpolation of the detected elevation points yields unacceptable river channel bottom profiles (often exhibiting unrealistic artifacts) and even distorts the floodplain. In our Fluvial Domain Method, channel bottoms are represented like “highways”, perhaps overlooking their (unknown) detailed morphology but gaining in general topographic consistency. For instance, we observed an 11.7% discrepancy in the river channel long profile (with respect to the measured cross-sections) and a 0.38 m RMSE in the floodplain (with respect to the GNSS-RTK measurements). Unlike conventional methods that utilize active sensors (satellite and airborne LiDAR) or classic topographic surveys—each with precision, cost, or labor limitations—the proposed approach offers a more accessible, cost-effective, and flexible solution that is particularly well suited to cases with scarce base information and financial resources. However, the method’s performance is inherently limited by the quality of input data and the simplification of complex channel morphologies; it is most suitable for cases where high-resolution geomorphological detail is not critical or where direct data acquisition is not feasible. The resulting DEM, incorporating a generalized channel representation, is well suited for flood hazard modeling. A case study of the Ranchería river delta in the Northern Colombian Caribbean demonstrates the methodology.
1. Introduction
Terrain modeling is a cornerstone of Earth Sciences, increasingly supported by indirect geomatics techniques such as satellite remote sensing [1,2]. The precise generation of altimetric information, represented in geospatial products like Digital Elevation Models (DEMs) that exclusively refer to ground elevations, as well as Digital Surface Models (DSMs) that include all surface features [3,4], is essential for various geoscientific disciplines dedicated to representing terrain morphology [5,6]. In particular, DEMs are crucial for a wide range of applications in water resources management, such as hydraulic modeling and flood risk assessment [4,7,8,9,10,11,12,13,14,15]. Traditionally, DEM generation in data-scarce regions has relied on methods based on classical field surveying and conventional aerial photogrammetry. More recently, state-of-the-art DEM generation derived from active sensors like airborne LiDAR (Light Detection and Ranging) and radar altimeters on satellites has been widely utilized in geosciences and hydrology [16]. Each of these options has its own limitations in terms of accuracy, cost, and logistics [17,18]. Satellite methods, although offering broad global coverage, typically provide limited spatial resolution, while active technologies like airborne LiDAR, despite their high precision and detail, involve significant costs and logistical resources [8,19,20]. Field measurements, on the other hand, are laborious and difficult to conduct over extensive areas, especially in hard-to-reach or environmentally hazardous zones [12,21,22].
Depending on sensor altitude, remote sensing technologies for altimetric data acquisition vary in spatial resolution, coverage, and applicability: Radar altimetry provides extensive spatial coverage and is valuable for large-scale hydrological studies, but its relatively coarse resolution limits its ability to capture fine-scale topographic variations, particularly in low-relief areas [23]. While airborne LiDAR, the state-of-the-art for remote sensing elevation data, penetrates vegetation and is valuable for flood modeling and river channel morphology studies, its high cost, logistical constraints, and partial penetration of deep, turbid waters limit its use in data-scarce regions [10,24]. More recently, UAV-based photogrammetry has emerged as a cost-effective and flexible alternative for high-resolution topographic mapping, particularly in riverine and floodplain environments [25]. Despite demonstrating significant potential for hydrological and hydraulic applications [12], UAV-derived elevation data remain sensitive to vegetation cover, water surface reflectance, and the dependence on external control data to enhance accuracy [26,27,28,29].
In this context, researchers and modelers increasingly turn to photogrammetric DEMs derived from various platforms, including satellites, airborne systems, and crewed and unmanned aerial vehicles (UAVs) [10,12,22,30,31]. Digital photogrammetry techniques, integrated into Structure from Motion by Multi-View Stereo (SfM-MVS) workflows, have revolutionized and democratized the acquisition and availability of high-resolution topographic data from RGB images [20,21,32,33,34,35]. The SfM-MVS workflow generates dense point clouds that, once filtered, provide terrain information, producing vector or grid-based DEMs, which are fundamental inputs for hydrological and/or hydrodynamic applications [36,37,38,39,40,41,42].
In this regard, recent studies have shown the potential to enhance DEM accuracy in data-scarce regions using freely accessible geospatial data and innovative algorithms. For instance, Monteiro et al. (2018) [43] demonstrated that combining low-resolution STRM DEMs with OpenStreetMap vectors can improve drainage network delineation. Similarly, Li et al. (2023) [44] evaluated several approaches for near-real-time flood mapping using satellite imagery and available DEMs, offering new insights into using multiple sources in data-scarce contexts. These approaches highlight the importance of leveraging available geospatial data in regions with limited topographic information.
However, one of the critical aspects of producing DEMs for hydrological and hydraulic modeling applications in floodplains is related to the representation of the river channels [45,46,47,48,49]. Data acquisition in river channels, characterized in most cases by challenging conditions such as dense riparian vegetation, shadows, and high-water turbidity (which hinders seeing the riverbed), introduces significant inconsistencies in their topo-bathymetric reconstruction from SfM-MVS point clouds [50,51]. Within river channels and their adjacent zones in the DEMs, these irregularities compromise the generation of accurate altimetric products [52]. Additionally, the conversion of point clouds into rasterized products generates artifacts that distort the general terrain trend within and outside the channel [51,53,54].
To address channel representation, enhancement techniques such as hydro-flattering [55] or DEM-Burning [56,57] are commonly employed. There are also solutions based on hydrodynamic modeling for geometric reconstruction of the channel [58,59], as well as the generation of bathymetries from multispectral [60] and hyperspectral images [61]. Despite these advances, representing river channels in data-scarce contexts remains a critical gap in the hydrological and hydraulic modeling literature. While the above-mentioned techniques can allow for channel correction, they do not solve all problems, as they might underestimate the channel depth and not adequately capture its topography, limiting the applicability of the derived DEMs. Although SfM-MVS photogrammetry has proven useful in generating high-resolution DEMs in floodplains [20,62], the precise reconstruction of river channels under conditions of dense vegetation or water turbidity remains a significant challenge [21,32,54,63,64], representing an active line of research.
Nevertheless, few studies have focused on maximizing the potential of SfM-MVS point clouds to represent river channels in data-limited conditions. To address this gap, this paper introduces a novel approach—the Fluvial Domain Method—designed to incorporate river channels into DEMs in flat areas with limited data, specifically using SfM-MVS altimetric information. This approach avoids distorting the flat area topography and the typical longitudinal profile artifacts resulting from bathymetric surface interpolation while also allowing for the integration of sporadic field measurements.
This article is structured into four sections: Section 2 describes the study area (Ranchería River, Colombian Caribbean), the data used (aerial images for SfM-MVS processing and topographic data), and the proposed method explanation. The Section 3 present the evaluation of the method’s accuracy, comparing it to reference topographic data using error statistics. The Section 4 analyzes the effectiveness of the method compared to traditional techniques, exploring its application in flood management and detailing its advantages and limitations. Finally, the Conclusions summarize the main findings and propose future work.
2. Materials and Methods
2.1. Study Area Description
The lower basin of the Ranchería River, located in the La Guajira Peninsula (next to Riohacha Town, Colombia Caribbean locality), was selected as the study area owing to its ecological and socioeconomic importance (Figure 1). The analyzed stretch spans 26 km, from the “Aremasain” flow measurement station to the end of the arm, colloquially known as “Riito”, in Riohacha. The selection of the “Riito” arm is based on the greater availability of validation data in this sector compared to the other arms of the delta.
Generally, the area of interest is located in a semi-arid region with a bimodal precipitation regime typical of the Caribbean, with marked alternations between dry and flood periods and an annual average of 541 mm of precipitation in the coastal town of Riohacha, concentrated mainly between September and October and, to a lesser extent, during April and May [65]. The predominant vegetation includes tropical dry forest and mangroves near the coast, as well as xerophytic scrub and scattered dry forest along the riverbed (known as “bosque de galleria”). Areas with higher water availability support denser vegetation. The Ranchería River (see Figure 2), in its lowermost reaches, exhibits a pronounced meandering planform and a mainly unconfined channel, with several geomorphic units in the floodplain, like oxbows, paleochannels, and wetlands, suggesting a highly dynamic character, although possibly in a previous period. The dense riparian vegetation, while indicative of a relatively healthy ecosystem, hinders direct observation of the riverbed.
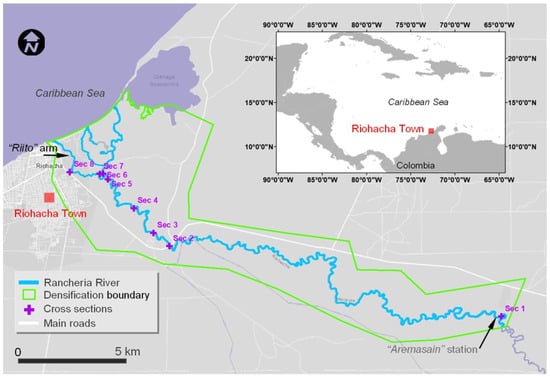
Figure 1.
Study area: lower Ranchería River basin sector (green polygon), Riohacha (Colombia). The study reach focuses on the main channel from the “Aremasain” station to the branch named “Riito”.
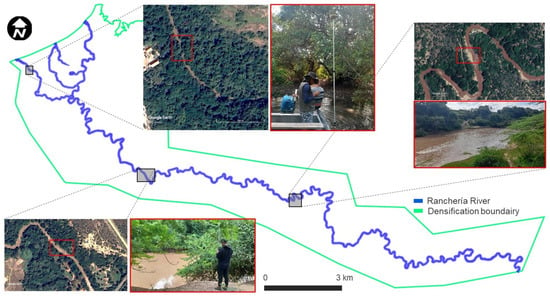
Figure 2.
Dense vegetation context along the studied river reach.
The terrain is characterized by a gentle slope, averaging approximately 0.1%, slightly decreasing to 0.02% near the delta coastline. Geomorphologically, the final stretch of the river, the true delta, runs over recent alluvial deposits and between old fluvial terraces, with a system of meandering channels, sandbanks, emergent bars, and intermittently flooded riparian zones [66]. Temporary waterlogged areas and peripheral, coastal lagoons are also found. A large portion of the delta is designated as a conservation area. Nevertheless, a serious flood risk problem exists owing to the presence of dispersed settlements, mainly indigenous. The combination of flat topography, low-permeability soils, and active fluvial dynamics poses a significant challenge for terrain modeling and accurate flood risk estimation, demanding the development of methods capable of generating DEMs with adequate altimetric resolution and robust hydraulic representation of the channel.
2.2. Datasets
Three types of geospatial data were used: aerial imagery, field data such as cross-sections, and elevation measurements in the floodplain for altimetric reference. Additional topographic measurements were collected to refine the method’s outputs.
2.2.1. Aerial Imagery for SfM-MVS Photogrammetric DEM Generation
This dataset consists of aerial imagery acquired by a national government risk agency during the 2017 dry season (before the March–April rainy season) using manned photogrammetric flights [67,68]. The image dataset was captured using UltraCam® sensors (Vexcel Imaging, Denver, USA) at an approximate height of 1200 m, georeferenced externally with centimeter-level accuracy. According to the contractor’s report, the images have a ground sampled distance (GSD) of 20 cm/pixel and an approximate frontal overlap of 75%, captured with two models of large-format cameras (Table 1). The dataset of approximately 1400 images comprehensively covers the 279 km2 area of interest, the green polygon shown in Figure 1.

Table 1.
Main intrinsic parameters of the photogrammetric sensors used.
2.2.2. Validation Topographic Field Data
Two sets of topographic data were used to validate the method’s output: one for the river channel and another for the floodplain zones. The first set consisted of eight topographic cross-sections of the channel surveyed in the 2015 dry season, using geometric leveling (see purple cross, Figure 1). These cross-sections were obtained under low-flow conditions [69], when the water level was shallow enough to allow direct measurement of the bed elevations without significant challenges. The resulting cross-section profiles (leveling survey), referenced to an arbitrary elevation (100 m.a.s.l.), have been recalculated for this study as channel depth profiles (h), allowing for a direct standardized comparison with the profiles derived from the final DEM of the proposed method. The second dataset consisted of a floodplain survey conducted in 2022 (red triangles in Figure 3), obtained through direct observations using differential GNSS corrections in real time, serving as altimetric (Z) checkpoints (GNSS-RTK Topcon HiPer V Dual-Frequency GNSS Receiver). The concentration of points in the lower part of the study area is justified by the importance of obtaining high precision in these areas where the main human settlements are located for future flood mapping purposes and due to accessibility and safety factors. Outliers (points deviating more than 1 m from the generated DEM) and closely spaced points were removed from the verification dataset (n = 593 altimetric points used). Validation error statistics for the channel and floodplain areas are presented in Section 2.5.
2.2.3. Topographic Field Data for Final Altimetric Refinements
These data are used for final refinements of the proposed method results (final DEM) for the floodplain and river channel. Figure 3 (gray circle markers, n = 31) presents a set of field GNSS-RTK data used for subsequent altimetric adjustments after the SfM-MVS processing.
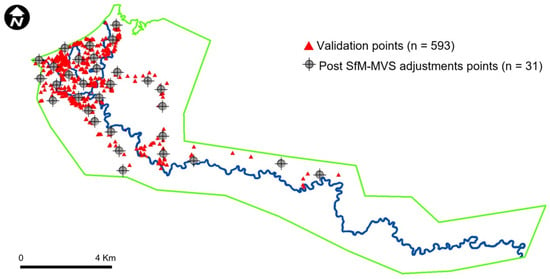
Figure 3.
Deployment of GNSS-RTK points (gray dots) used for subsequent DEM adjustments from the photogrammetric process and validation (red triangles) of DSM/DEM products.
These floodplain data were collected during the same GNSS-RTK validation campaign, aiming for uniform coverage of the area of interest (green perimeter, Figure 3). The number of survey points used for post-SfM-MVS control was deemed sufficient, as increasing it does not always improve altimetric accuracy, according to the literature [70,71].
An additional 28 elevation points of the channel bottom were collected in 2023 along the final stretch (Riito arm) near the coastline and within densely vegetated areas. These GNSS-RTK point capture data, obtained following the central line of the channel, served to refine the proposed method. This stretch presents particularly challenging conditions due to the dense riparian vegetation and the permanent presence of water.
2.3. The Fluvial Domain Method (Concept)
The method is based on the consideration that the direct use of the dense classified point cloud of elevations—that can be obtained from the photogrammetric survey—to obtain a DEM via interpolation (see Section 2.3) leads to an unsatisfactory result in two ways: (a) On the one hand, the surface of the floodplain is distorted (lowered) because of the anomalous low points detected in the channels; (b) on the other hand, the channel thalweg typically presents defects (bumps) that are clearly unrealistic (See Figure 4).
To address these limitations, our method integrates channel information into a floodplain DEM derived from the photogrammetric point cloud based on the fusion approach introduced by Legleiter (2012) [72] and the following concepts:
- (1)
- Avoid the problem (a) by a preprocessing step where the points that fall on top of the channels are identified and excluded (which implies filtering based on a delineation of the channel polygons) and, subsequently, a DEM of the floodplain alone without channels is generated from the remaining points.
- (2)
- Take advantage of the fact that, by design, the airborne image acquisition occurred during the dry season to use the complement of the dataset—that is, only those points falling on top of the channel polygons—to construct a DEM exclusive to such polygons. Owing to the scarcity of data and the fact that the channel, even in the dry season, is not necessarily completely without water, this surface also presents defects (bumps) along its main direction (the channel thalweg). Therefore, it does not yet solve the problem (b), but it is a first approximation of the channel bottom.
- (3)
- Correct the channel bottom with a priori criteria (that is, without using further data acquired on the ground). To do this, first, the elevation long profile (affected by defects during interpolation) is obtained; then, it is corrected using the semi-automatic smoothing procedure, applying the principle that the bottom cannot significantly ascend and should not display falls unless there is some geologic fault or rocky outcrop (detectable from the available thematic maps). This procedure yields a much more reasonable shape for the long profile. Eventually, field data (bottom elevation data from topographic measurements) can be included (see Section 2.2.3). This corrected elevation long profile is transformed into a new surface (the fluvial domain), constructed in a GIS a series of transects (with the width of the channel polygon), which are then interpolated into a smooth raster surface. This solves problem (b).
- (4)
- Finally, the floodplain DEM and the smoothed bottom surfaces of all channels, which are the primary outputs of the method, are integrated to obtain the final complete DEM.
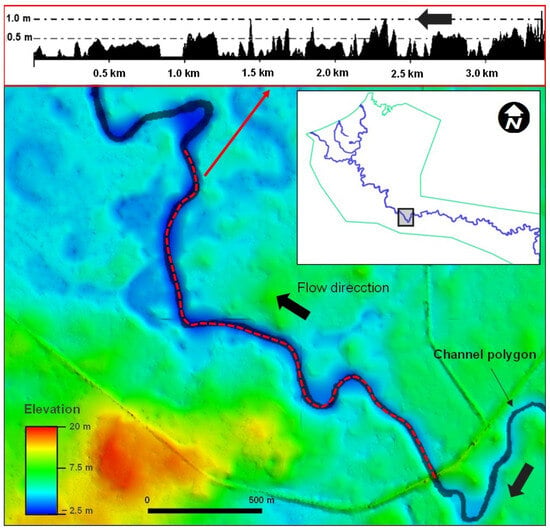
Figure 4.
Figure example shows a longitudinal channel profile (dashed red line) from the preliminary SfM-MVS DEM (without channel correction). Note the significant altimetric variability resulting from interpolation artifacts and the overestimation of the channel width due to the artificial lowering of the floodplain surface along the riverbanks. Flow direction is represented by the black arrow.
2.4. SfM-MVS Image Processing and Preliminary DEM Generation
This section details the photogrammetric image processing workflow and the generation of a preliminary DEM (before applying the proposed method), providing crucial altimetric input data.
- (1)
- Image alignment and obtaining a sparse point cloud (aero-triangulation): Photogrammetric aero-triangulation processing was performed using Agisoft Metashape®, version 2.1.2 on a 64-bit Windows system with an Intel Core i7-6700HQ processor at 2.60 GHz (4 physical and 8 logical cores) and 32 GB of RAM. For image alignment, a medium precision with a generic preselection of 120,000 key points was used. After removing outlier points using the gradual selection method, a reprojection error of 0.47 pixels was obtained in the preliminary sparse point cloud (<1 pixel being recommended). Subsequently, the synthetic control point method proposed by Escobar-Villanueva et al. (2019) [28] was implemented to optimize the geometry of the sparse point cloud. Using 33 control points derived from an orthomosaic (20 cm/pixel) and a Digital Terrain Model (DTM, 10 m), both deliverables from the contractor (Section 2.2.1), the Mean Error was reduced to 9.48 cm in X, 8.51 cm in Y, and 62.41 cm in Z, for a total of 63.70 cm.
- (2)
- Point cloud densification and ground classification: To densify the sparse point cloud, the SfM-MVS workflow with Metashape was continued: a medium-quality and moderate depth filtering were used [73]. Subsequently, a rectangular area covering the polygon of interest was delimited, and densification was carried out. Finally, the dense point cloud was exported in *.las format and cropped to the area of interest (green polygon, Figure 1). Ground point classification was performed semi-automatically, given the dense vegetation covering both the floodplain and the channel margins (see Figure 2). To ensure high reliability in the identification of exclusive ground points, very strict filtering parameters were established, with the aim of identifying and eliminating vegetation. The “Auto-classify Ground Points” tool of Global Mapper® version 18 software was used, combined with manual edits. This algorithm, based on the analysis of the terrain curvature and the elimination of outliers, applies a particularly severe filter to the dense point cloud, resulting in the classification of a significantly reduced number of ground points compared to the original total (8% of the points classified as terrain). The parameters used include a base cell size of 6 m to calculate curvature deviations; a minimum height of 0.15 m to exclude points not belonging to the terrain; and maximum values of 5 m for the height delta, 7.5 degrees for the slope, and 150 m for the width of structures such as buildings. Additionally, manual classifications were performed on linear features, such as embankments and roads, assigning them as part of the terrain. Furthermore, anomalous points were removed through visual inspection of wide transects (between 100 and 200 m wide).
- (3)
- Preliminary DEM generation: This step generates the initial DEM—a crucial input for the proposed method but not the final product. First, the point cloud classified as terrain, with an average distance of 2 m between points and irregular distribution, was interpolated to create a preliminary raster DEM (*.tif format) that included raw elevation data, including preliminary channel information. This early DEM serves as the main altimetric data input for the proposed bathymetric adjustment. Subsequently, to prevent artificial subsidence along the river channel surroundings (see Figure 4), the above-mentioned *.tif DEM is exported to *.las (a point cloud format), excluding the channel points from the interpolation process (defined by the delineated river–channel polygon with an additional buffer) and, therefore, filling the space between the river margins. This step mitigates the local influence of lower elevation point tendencies, which are often misclassified by the Global Mapper “Auto-classify Ground Points” algorithm. The obtained channel-free *.las DEM, corrected for subsidence anomalies, facilitates subsequent floodplain altimetric adjustment and integration with the proposed method’s channel output (also in *.las). ArcGIS Pro’s (version 3.0) “LAS Dataset to Raster” tool performed the interpolation, while Global Mapper’s version 18 “LIDAR-QC” tool handled the final altimetric adjustment, using the 31-ground survey GNSS-RTK points distributed in the study area (gray points Figure 3, Section 2.2.3).
2.5. River Channel Bottom Generation and Final DEM Integration (Detailed Explanation)
After obtaining the photogrammetric information (Section 2.3), the operational detail of the proposed method is described, composed of four stages, illustrated in Figure 5 as conceptually defined in Section 2.2.
Stage 1. Input data (raster/vector) and preprocessing: Both raster and vector data were required for the bathymetric correction. Vector data consisted of a manually digitized polygon defining the bankfull channel, generated in a GIS by a trained operator interpreting the 20 cm/pixel orthomosaic (derived from the contractor-supplied photogrammetry dataset). A central line representing the main channel direction was automatically extracted from this polygon using QGIS’s South Rivers Toolbox Valley Center Line module [19]. Raster data consisted of a preliminary DEM (.tif) derived from the classified point cloud, providing the initial elevation values.
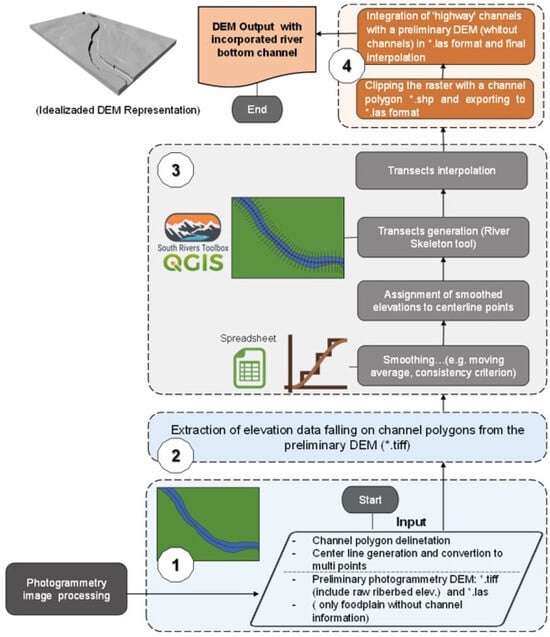
Figure 5.
General outline of the proposed method. The workflow starts with the input data at the bottom and culminates in the final product at the top, highlighting it as the process’s outcome: (1) Input data and preprocessing, (2) Elevation extraction from the preliminary DEM, (3) Bathymetric channel correction, and (4) Channel Integration with the preliminary DEM.
Stage 2. Extraction of elevations from the preliminary DEM: The central line is converted into a series of equidistant points (Generate Points Along Lines tool in ArcGIS PRO version 3.0). Subsequently, the corresponding elevation values for each point are extracted from the preliminary DEM (Extract Values to Multipoint tool in ArcGIS PRO).
Stage 3. Bathymetric correction procedure: The process consists of four (4) sequential stages. Firstly, to smooth abrupt variations in elevation and ensure the hydrological coherence of the longitudinal profile of the channel, a weighted moving average (with 500 step) was applied in a Microsoft-Excel® spreadsheet to the extracted elevation values. An additional condition was imposed: the smoothed elevation value could not be greater than the value of the previous point. This procedure guarantees the principle of hydraulic gradient (although local pools may well exist that are ignored here). A 500-point moving window was selected as a reasonable compromise; it captures typical channel slope variations while avoiding excessive smoothing that might obscure significant elevation changes. Secondly, once the smoothed elevation values were obtained in the spreadsheet, they were assigned to the points of the central line in their respective attribute table of the *.shp file. Additionally, an iterative process involving linear and polynomial regression models was applied to refine river channel bed elevations in complex areas. This improved the correspondence of the smoothed profile with ground truth data (see Section 2.2.3). Thirdly, from these points with corrected and smoothed Z elevation, a series of transects perpendicular to the channel of defined length were generated using the River Skeleton tool of South Rivers Toolbox [19]. Finally (fourth), these transects were interpolated to obtain a smooth and continuous surface of a raster representing the corrected channel bottom. This interpolation procedure was guided by the concepts presented in Merwade (2008) [74] for creating river terrain models, specifically utilizing the “Topo to Raster” tool within ArcGIS Pro.
Stage 4. Integration and generation of the final DEM: Finally, the smoothed raster surface generated was clipped to the channel polygon and exported in *.las format. Then, it was integrated with the channel-free preliminary DEM (both in *.las) and, finally, interpolated with “LAS Dataset to Raster” (ArcGIS Pro version 3.0) to obtain the final DEM. This output incorporates the bathymetric corrections and, finally, represents the result of the proposed method.
2.6. Validation of the Final DEM
To determine the altimetric (Z) accuracy and quality of the DEM generated using the proposed methodology (as well as assess the DSM), evaluations were conducted in two areas: the floodplain and the river channel.
- (1)
- Validation in the floodplain: The altimetric (Z) accuracy of the DSM and DEM generated (predicted) for the floodplain was validated by comparison with the reference topographic data (observed) obtained from GNSS RTK surveys (Figure 3, red triangles, Section 2.2.2). The Mean Error (ME—Equation (1)), the Mean Absolute Error (MAE—Equation (2)), and the Root Mean Square Error (RMSE—Equation (3)) were calculated to evaluate the accuracy of the DEM. The n term is the number of samples in altimetric surveys:
- (2)
- Validation in the river channel: To facilitate validation of the final DEM, its topographic sections were compared with standardized depth (h) profiles at eight cross-sections (see location Figure 1, Section 2.2.2). For this purpose, the Mean Absolute Percentage Error (MAPE—Equation (4) [75]) was considered as a metric to evaluate the accuracy of the final DEM of the proposed method. The validation of the final DEM for the channel output was performed by comparing its predicted channel depth profiles with the observed field data from eight (n = 8) cross-sections. The n term is the number of sample depth observations. The MAPE equation was used as follows:
The Mean Absolute Percentage Error (MAPE) (Equation (4)) was chosen as the evaluation metric due to its sensitivity to both positive and negative errors, which can be interpreted in terms of the geometric mean. The Mean Error (ME), Mean Absolute Error (MAE), and Root Mean Square Error (RMSE) were also calculated for the channel using the same Equations (1)–(3) but applied to the maximum depth (h) values. Lastly, depth profiles were plotted to visually assess the quality of the fit between the final DEM and the observed geometry channel conditions.
3. Results
This section presents the (i) results of the accuracy assessment of SfM-MVS photogrammetrically derived models (DSM and final DEM), (ii) application of the proposed method and refining the river channel bottom, and (iii) evaluation of the depth estimates.
3.1. Accuracy Assessment of Photogrammetrically Derived Models: Floodplain
Figure 6 illustrates the error distribution and accuracy of the DSM and DEM obtained from photogrammetric processing, providing both summary statistics and a visual comparison of their performance.
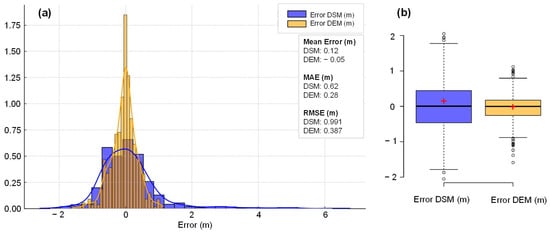
Figure 6.
Visualization of the error distribution and accuracy assessment of the digital models using histograms (a) and box plots (b). DSM as blue and DTM appears in yellow. Superimposed on the histogram are the expected normal distribution curves and white circles represents the outliers.
The quantitative descriptive statistics (Table 2), such ME, MAE, and RMSE, corroborate that the DEM errors are systematically smaller in magnitude and have lower variability compared to the DSM errors.

Table 2.
Accuracy metrics results for the photogrammetrically derived models.
Building on these findings, Figure 6a presents histograms with density curves for the error distribution in both models. The statistical metrics highlight significant differences in accuracy: the DSM exhibits a Mean Error of 0.12 m, while the DEM shows a smaller, near-zero bias with −0.05 m. Moreover, the MAE and RMSE further demonstrate the improved accuracy of the derived DEM output, with values of 0.28 m and 0.387 m, respectively, compared to the DSM’s higher errors of 0.62 m (MAE) and 0.991 m (RMSE). In addition, Figure 6b provides box plots summarizing the error spread and central tendency. The DSM displays a wider error distribution, with a higher variability and a greater number of outliers. Conversely, the DEM exhibits a more compact distribution, with fewer extreme values. The red crosses represent the Mean Error values, reinforcing the lower systematic error and overall improved performance of the SfM-MVS-derived DEM for the floodplain.
In general, the DSM errors exhibit greater dispersion, with a clear tendency to overestimate elevations, as evidenced by a more pronounced right tail in the histogram (Figure 6a) and a positive median in the box plots (Figure 6b). In contrast, the DEM errors are more centered around zero, showing less variability and greater accuracy compared to the DSM. This trend is particularly evident in the box plots (Figure 6b), where the box width is significantly larger in the DSM.
Finally, the DEM generated from the classified point cloud shows a 60.94% improvement in vertical accuracy compared to the DSM in terms of the RMSE. The lower accuracy of the DSM is attributed to the inclusion of vegetation points and artificial structures, which introduce significant noise (almost five times the GSD). The DEM, benefiting from the point classification that separates the terrain from objects above it, offers a more accurate representation of the topography, with an average relative error of approximately two times the GSD (20 cm/pixel). According to the ASPRS Positional Accuracy Standards for Digital Geospatial Data, this value corresponds to a vertical accuracy within the 1 m class (100 cm) at a 95% confidence level (meets a maximum error limit of 1 m for 95% of the evaluated points) [55]. These results confirm that the DEM meets the standards for moderate resolution applications, highlighting the importance of classification for accurately representing bare earth.
3.2. Proposed Method Application and Channel Bottom Refinements
Figure 7a shows the results of smoothing the longitudinal profile of the channel using the proposed method, evidencing a notable reduction in the discontinuities present in the original profile obtained from photogrammetry. The overestimation of the elevation in the distal zone of the profile, attributed to vegetation cover and partial coverage of the water surface, was corrected by imposing a flattening at a level of −1.5 m.a.s.l. from point ID 3100 (final red line in Figure 7a). This ad hoc adjustment, while seemingly arbitrary, is justified by a distinct break in slope at the 33 km mark (blue line in Figure 7). While this transition might not be perfectly represented by a sharp elevation change at that point, this methodological decision aims to create a realistic overall representation of the longitudinal elevation trend of the river bottom while acknowledging the limitations imposed by the data acquisition process in that specific area.
To refine the profile in complex areas, such as margins partially covered by vegetation (mangroves), GNSS-RTK measurements were incorporated following the centerline of the river in its final stretch near the coast. From the 37 km mark (Figure 7b), the smoothed bottom profile was adjusted using linear and second-order polynomial models. This adjustment improved the correspondence of the smoothed profile with the GNSS-RTK data, optimizing the bathymetric representation of the channel. Although not an integral part of the method, this adjustment demonstrates its flexibility to adapt to local conditions and take advantage of complementary information for a more accurate representation of the river bottom.
Figure 8 presents the comparison between the depths estimated using the proposed method (black curves) and the reference depths (purple curves) in eight cross-sections of the studied river. In general, the model estimates show a high coherence with the reference data, replicating the general geometry of the channel in most sections. In the central sections (for example, cross-sections 3, 5, and 7), the method remarkably reproduces the channel bottom. However, in certain cross-sections, such as 2 and 8, slight local deviations can be seen, possibly attributed to variations not captured in the interpolation or terrain classification process of the DEM. These deviations are likely attributable to limitations in the proposed method when addressing features such as steep slopes, dense vegetation, or occluded terrain. These results support the effectiveness of the proposed method for modeling the transverse geometry of the river, effectively approximating riverbed geometry in environments with limited data availability, even in areas with complex variations.
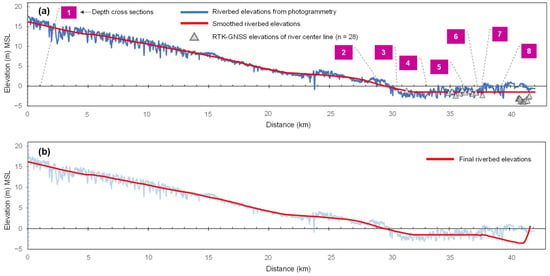
Figure 7.
Comparison between raw (blue) and smoothed elevation profiles of the channel obtained by SfM-MVS photogrammetry and the proposed method (red): (a) smoothed channel bottom, location of reference cross-sections and GNSS RTK observations (triangles); (b) refinement of the channel longitudinal profile using GNSS RTK adjustment in the last river reach (7 and 8). Purple boxes represent the cross-section location along the elevation profile.
3.3. Accuracy Assessment of Photogrammetrically Derived Models: River Channels
Figure 9 presents a comparison between the observed and estimated maximum depths using the proposed method in eight cross-sections of the river.
Figure 9a presents the maximum depth values for both observed (purple bars) and estimated (blue bars) datasets, and it shows that the method generally captures the trend of the observed maximum depths (MAPE = 11.7%), although significant discrepancies are observed in some cross-sections, particularly in 7 and 8 (relative errors 29% and 18%, respectively). The scatter plot (Figure 9b) illustrates the relationship between the observed and estimated depths through a scatter plot. The dashed red line represents perfect agreement (1:1 line), confirming a high correlation between the observed and estimated values (R2 = 0.86), with a MAE of 0.459 m and a RMSE of 0.526 m, and indicating an overall satisfactory performance of the proposed method. However, the greatest discrepancies are observed in cross-sections with greater geomorphological complexity (final stretch of the river near the highly vegetated mangrove coastline), suggesting that the method might have limitations in these conditions.
Finally, the evident correspondence between the estimated and reference depths indicates that the method of channel corrections in the photogrammetric DEM is potentially suitable for hydrological applications, such as flood hazard assessment, where a topographically coherent geometric representation of the channel is required, although not necessarily a high-detail geomorphological bathymetry.
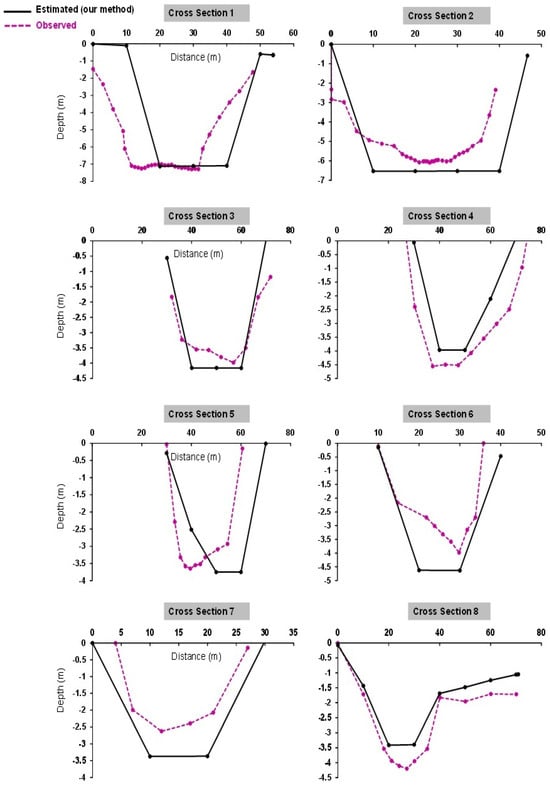
Figure 8.
Comparison of the cross-sectional depth (h) geometry along the studied river (n = 8). Black lines represent depths estimated by the proposed method; purple lines represent reference (observed) depths.
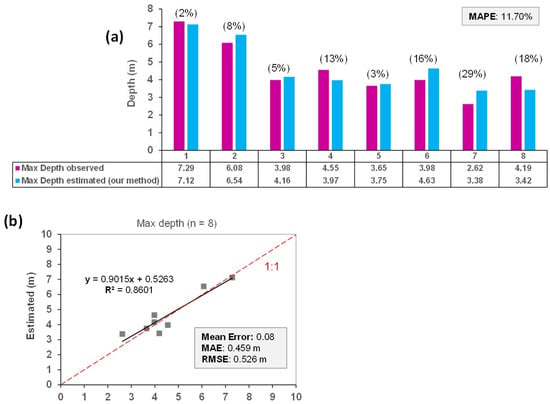
Figure 9.
Comparison of maximum depths obtained from field measurements and estimated using the proposed method at eight reference cross-sections of the Ranchería River: (a) relative error and Mean Absolute Percentage Error (MAPE) analysis; (b) scatter plot showing the relationship between the observed and estimated depths. The solid black line represents the linear regression fit to the depths data (grey boxes), with the corresponding equation and R-squared value shown (dashed red line indicates perfect agreement).
4. Discussion
This section presents the accuracy assessment discussion of the photogrammetrically derived models for both floodplain and river channels using the proposed method. The following sections delve into the evaluation of the proposed method, beginning with its advantages in data-scarce environments (Section 4.1), followed by a critical analysis of the method’s scope and limitations (Section 4.2), and concluding with a discussion on its implications for practical applications and directions for future research (Section 4.3).
In the case of the floodplain, the SfM-MVS strategy, as parametrized for our project, shows a notable improvement (60.94%) in DEM accuracy compared to the DSM. This is reflected in reduced error statistics and a more concentrated error distribution within the DEM. The improved accuracy is largely due to the effective removal of noise from vegetation and man-made structures during point cloud classification. The resulting accuracy falls within a medium-quality category.
For the river channels, the method effectively smooths the longitudinal channel profile, reducing discontinuities in the raw data input. It also demonstrates flexibility by incorporating GNSS-RTK data to refine the model, particularly in more complex areas. The overall accuracy is reasonable (approximately half a meter), with a strong correlation between the measured and estimated channel depths (11.7% error). However, some cross-sections exhibit higher errors, highlighting the method’s limitations in capturing riverbed details in more complex regions, such as densely vegetated areas and permanently flooded zones near the coast. Despite these challenges, the accuracy remains adequate for hydrological applications, especially for flood hazard assessments.
4.1. Advantages of the Fluvial Domain Method in Contexts with Limited Information
The results of the error metrics in the floodplain and channel demonstrate, at least for the case at hand, that the method generates a DEM with a coherent and robust geometric representation even in a complex environment such as that of the study area. These results validate the study thesis, demonstrating that it is possible to obtain a reasonable approximation of the riverbed from relatively scarce information, such as the SfM-MVS point clouds used.
This capability is particularly relevant considering DEMs that incorporate river channels are fundamental for hydrological spatial modeling [10,12,14,46,47], yet remain challenging to produce due to factors such as dense vegetation, shadows, and water turbidity [25,50,51,53]. The SfM-MVS workflow underlying the proposed method offers a practical approach to acquiring high-resolution topographic data, expanding the accessibility for river science. Unlike conventional approaches that require advanced equipment, such as LiDAR or multispectral imagery, and greater economic resources [10,22,58,61], our method based on the SfM-MVS technique achieves a simplified but coherent channel bottom representation, providing a potential DEM generation alternative for flood modeling in limited data availability contexts. Additionally, its flexibility to incorporate GNSS-RTK data and adapt to complex environments, such as narrow and vegetated channels, expands its applications [76]. The increasing availability of aerial images and their relative ease of implementation [77] make this method viable for terrain modeling studies in linear fluvial environments at an intermediate level of detail.
Finally, evaluating the accuracy in the DSM and DEM of the floodplain corroborates previous studies, underlining the importance of point cloud classification to improve the quality of models obtained from photogrammetry [36]. In this study, it was confirmed that the efficient classification of the dense point cloud derived from SfM-MVS of the DSM allows eliminating the noise associated with non-terrestrial elements, thus improving the accuracy and reliability of the final DEM.
4.2. Critical Analysis of the Method’s Scope
The proposed method generates a representation of the channel bed in DEMs; however, it presents inherent limitations due to photogrammetry challenges and environmental conditions.
Specifically, in environments with dense vegetation, steep slopes, or deep channels, photogrammetry may not accurately represent the bottom topography [37,51,53,54,78]. This limitation becomes particularly evident in ecosystems such as mangroves or forested riverine floodplains [79,80], which are prevalent in the study area (see Figure 2). Alternative methods like LiDAR also face challenges in these conditions due to limited foliage penetration [81]. While the classification filters applied in this study can partially mitigate these effects, they might not completely resolve inaccuracies in areas with dense vegetation.
However, it offers a viable alternative in situations where conventional methods are not applicable, so achieving a trade-off between precision and accessibility may be acceptable in several situations. In addition, if few topographic cross-sections are available, the method allows one to overcome this difficulty.
The post-processing SfM-MVS workflow, especially the manual classification of linear features and visual terrain inspection, is time-intensive. The time commitment varies significantly, depending on the data volume; point density; noise levels; channel geometry complexity; and the presence of vegetation, occlusions, or shadows. A skilled operator might require several hours, potentially extending to multiple days for large or complex datasets. Another limitation is related to the quality of aerial images: low-resolution or noisy images can compromise the accuracy of the model and generate an inaccurate representation of the channel topography. This problem is exacerbated in areas with dense vegetation, where occlusion and shadows hinder the capture of the actual ground elevation [37,79].
Additionally, the proposed method may oversimplify the channel morphology, potentially omitting geomorphological details like in-channel bars. This simplification limits its applicability to studies requiring high morphological precision, such as multi-temporal sediment analyses, where a lack of detail can hinder accurate fluvial dynamic modeling (e.g., sediment balance calculations [82,83]). However, given that most flood-exposed elements (people and goods) are typically located outside the river channel [59], the proposed method offers an alternative for flood hazard spatial modeling and risk assessment, prioritizing geometric and topographic consistency over high-resolution geomorphological detail of the river bottom.
The method’s accuracy may be compromised under extreme hydrological conditions (e.g., significant water depths, tidal influences, or variable flows). Aerial surveys conducted during high-water (but not flood) conditions may not accurately represent the riverbed topography [58]; as in deep bodies of water, phenomena such as light refraction and the difficulty in detecting the bottom negatively affect the accuracy of the model [25,50]. Likewise, in estuaries and deltas with dense vegetation, such as mangroves, and tidal dynamics, these challenges intensify [52]. Supplementary cross-sectional data (e.g., from ADCP and echo sounder surveys or subsequent dry season measurements) can mitigate the method’s limitations, unlike LiDAR, which is severely hampered, particularly in turbid waters. Finally, while the integration of supplementary field data, such as GNSS-RTK, improves accuracy, increased costs and resource demands may limit applicability in logistically challenging environments [84].
4.3. Implications for the Application of the Proposed Method and Future Work
Advances in geomatics and SfM-MVS processing support the method’s application in water resources management within data-scarce contexts [78], enabling cost-effective DEM generation using readily available imagery [85,86]. Beyond hydrological modeling, the resulting DEMs can also be used to calibrate and validate distributed hydrodynamic models for predicting extreme events like floods [57,87].
The method can be used in conjunction with terrain editing tools found in software such as the latest version of HEC-RAS Mapper [47,88]. The key difference is that HEC-RAS Mapper edits existing DEMs, while the present method generates a new DEM from photogrammetry. This combination would allow a synergistic approach: Our method generates an initial DEM, while HEC-RAS Mapper’s user-friendly interface allows for precise refinement by adding detailed field or supplemental data to compensate for the method’s morphological simplification. Thus, our approach provides an efficient basis for a generalized DEM, subsequently refined in HEC-RAS Mapper for improvement and actualizing them.
Future research should focus on improving the accuracy of the proposed method through advanced point cloud classification and filtering techniques such as machine learning, as well as integrating multi-sensor and multi-platform data, including satellite images, UAV, and in situ measurements. It would also be relevant to evaluate its compatibility with 2D hydrodynamic models and compare its performance against methods such as airborne LiDAR and satellite InSAR interferometry in various geomorphological scenarios (high, medium, and low slopes). Future development will focus on streamlining and automating the current workflow. This involves pursuing a unified software solution or an automated pipeline (a single GIS-based script or toolset) to minimize the dependence on multiple software tools, enhancing both the accessibility and reproducibility of the proposed method.
5. Conclusions
This study presents the Fluvial Domain Method, a novel approach for generating Digital Elevation Models (DEMs) that incorporate river channels. This method is particularly useful in data-scarce environments where information is limited to SfM-MVS photogrammetry (acquired under low-flow conditions).
In the floodplain, the final DEM achieved in our case study was accurate, with a RMSE of 0.38 m, approximately double the size of the input pixel. This performance is comparable to conventional methods, primarily attributed to point cloud classification, improving the altimetric quality. In the channel, the DEM presented a Mean Absolute Percentage Error of 11.7% in the estimated depths, adequately capturing the trend of the longitudinal profile. The results confirm the study’s hypothesis, demonstrating that it is possible to eliminate artificial peaks and valleys generated by vegetation, shadows, and artifacts in the photogrammetric SfM-MVS point cloud, achieving a more realistic representation of the riverbed channel. This could contribute to water resources management and flood risk management.
The proposed method positions itself as an alternative to improve DEMs in areas with limited access to advanced technologies (e.g., airborne LiDAR), prioritizing geometric generalization over geomorphological detail of the riverbed channel. This fluvial domain generalization, integrated with SfM-MVS-derived floodplain DEMs, emerges as a potentially useful approach for flood hazard and risk studies. Although it faces limitations in areas with dense vegetation or complex geomorphology, its flexibility allows for integrating complementary data, such as GNSS-RTK, to refine the accuracy in specific areas.
However, it is essential to understand the limitations, including sensitivity to data quality, such as low-resolution imagery or noise, and challenges in environments with dense vegetation or deep channels. The simplification of the channel morphology could omit critical geomorphological details. Moreover, its performance may degrade under extreme hydrological conditions, particularly in deeper channels, though this can be mitigated with occasional field surveys. The method also demands time-intensive manual processes, particularly in data preparation, point cloud classification, and GIS parametrization, requiring a trained operator.
Future research could explore the integration of multi-sensor and multi-platform data to increase accuracy, automate the proposed method workflow, and evaluate its performance in terms of hydrodynamic modeling (How relevant is the simplification of the bottom profile that disregards, for instance, bars and dunes?) within different geomorphological and hydrological contexts.
Author Contributions
A.G.C.N.: methodology conceptualization; A.G.C.N. and J.R.E.V.: writing; J.R.E.V.: GIS elaborations and photogrammetry processing and review and editing; A.G.C.N. and J.I.P.-M.: supervision; J.I.P.-M.: funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministerio de Ciencia, Tecnología e Innovación de Colombia, calling 890-2020, project number 82207, financial resources managed by the Instituto Colombiano de Crédito Educativo y Estudios Técnicos en el Exterior—ICETEX. Also, this paper was made possible thanks to financial support of the fieldwork by the Universidad de La Guajira (internal project grant number: PIUG-2018-082).
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Acknowledgments
We thank the University de La Guajira for the contributions of the J.I.P.-M and J.R.E.V to allocate time to the project; the authors also thank the CREACUA Foundation (Riohacha, Colombia) for the incentive given to this initiative. Special thanks to Fondo Adaptación de Colombia for providing the aerial photography information necessary for the generation of the DEM. Also, thanks to José Fragozo Arévalo for his help with the topographic surveys.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of the data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| DEM | Digital Elevation Model |
| DSM | Digital Surface Model |
| GIS | Geographic Information System |
| GNSS-RTK | Global Navigation Satellite System-Real-Time Kinematic |
| GSD | Ground Sample Distance |
| LiDAR | Light Detection and Ranging |
| m.a.s.l. | Meters above sea level |
| MSL | Mean sea level |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| RGBI | Red, Green, Blue, Infrared (referring to spectral bands in imagery) |
| RMSE | Root Mean Square Error |
| SfM-MVS | Structure from Motion-Multi-View Stereo |
| UAV | Unmanned Aerial Vehicle (drones) |
References
- Toschi, I.; Remondino, F. Geomatics Mapping of Natural Hazards: Overview and Experiences. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2018, XLII, 505–512. [Google Scholar] [CrossRef]
- Forlani, G.; Roncella, R.; Diotri, F. Production of High-Resolution Digital Terrain Models in Mountain Regions to Support Risk Assessment. Geomat. Nat. Hazards Risk 2015, 6, 379–397. [Google Scholar] [CrossRef][Green Version]
- Granshaw, S.I. Photogrammetric Terminology: Fourth Edition. Photogramm. Rec. 2020, 35, 143–288. [Google Scholar] [CrossRef]
- Guth, P.L.; Van Niekerk, A.; Grohmann, C.H.; Muller, J.P.; Hawker, L.; Florinsky, I.V.; Gesch, D.; Reuter, H.I.; Herrera-Cruz, V.; Riazanoff, S.; et al. Digital Elevation Models: Terminology and Definitions. Remote Sens. 2021, 13, 3581. [Google Scholar] [CrossRef]
- Alho, P.; Hyyppä, H.; Hyyppä, J. Consequence of DTM Precision for Flood Hazard Mapping: A Case Study in SW Finland. Nord. J. Surv. Real Estate Res. 2009, 6, 21–39. [Google Scholar]
- Tauro, F.; Pagano, C.; Phamduy, P.; Grimaldi, S.; Porfiri, M. Large-Scale Particle Image Velocimetry From an Unmanned Aerial Vehicle. IEEE/ASME Trans. Mechatronics 2015, 20, 3269–3275. [Google Scholar] [CrossRef]
- Flener, C.; Vaaja, M.; Jaakkola, A.; Krooks, A.; Kaartinen, H.; Kukko, A.; Kasvi, E.; Hyyppä, H.; Hyyppä, J.; Alho, P. Seamless Mapping of River Channels at High Resolution Using Mobile LiDAR and UAV-Photography. Remote Sens. 2013, 5, 6382–6407. [Google Scholar] [CrossRef]
- Wechsler, S.P. Uncertainties Associated with Digital Elevation Models for Hydrologic Applications: A Review. Hydrol. Earth Syst. Sci. 2007, 11, 1481–1500. [Google Scholar] [CrossRef]
- Li, J.; Wong, D.W.S. Effects of DEM Sources on Hydrologic Applications. Comput. Environ. Urban Syst. 2010, 34, 251–261. [Google Scholar] [CrossRef]
- Muhadi, N.A.; Abdullah, A.F.; Bejo, S.K.; Mahadi, M.R.; Mijic, A. The Use of LiDAR-Derived DEM in Flood Applications: A Review. Remote Sens. 2020, 12, 2308. [Google Scholar] [CrossRef]
- Hashemi-Beni, L.; Jones, J.; Thompson, G.; Johnson, C.; Gebrehiwot, A. Challenges and Opportunities for UAV-Based Digital Elevation Model Generation for Flood-Risk Management: A Case of Princeville, North Carolina. Sensors 2018, 18, 3843. [Google Scholar] [CrossRef] [PubMed]
- Annis, A.; Nardi, F.; Petroselli, A.; Apollonio, C.; Arcangeletti, E.; Tauro, F.; Belli, C.; Bianconi, R.; Grimaldi, S. UAV-DEMs for Small-Scale Flood Hazard Mapping. Water 2020, 12, 1717. [Google Scholar] [CrossRef]
- Nardini, A.; Yepez, S.; Zuniga, L.; Gualtieri, C.; Bejarano, M.D. A Computer Aided Approach for River Styles-Inspired Characterization of Large Basins: The Magdalena River (Colombia). Water 2020, 12, 1147. [Google Scholar] [CrossRef]
- Cea, L.; Costabile, P. Flood Risk in Urban Areas: Modelling, Management and Adaptation to Climate Change: A Review. Hydrology 2022, 9, 50. [Google Scholar] [CrossRef]
- Schumann, G.J.P.; Bates, P.D. The Need for a High-Accuracy, Open-Access Global Digital Elevation Model. Front. Earth Sci. 2020, 8, 225. [Google Scholar] [CrossRef]
- Liu, X. Airborne LiDAR for DEM Generation: Some Critical Issues. Prog. Phys. Geogr. 2008, 32, 31–49. [Google Scholar]
- Cian, F.; Marconcini, M.; Ceccato, P.; Giupponi, C. Flood Depth Estimation by Means of High-Resolution SAR Images and Lidar Data. Hazards Earth Syst. Sci. 2018, 18, 3063–3084. [Google Scholar] [CrossRef]
- Andualem, T.G.; Peters, S.; Hewa, G.A.; Myers, B.R.; Boland, J.; Pezzaniti, D. Channel Morphological Change Monitoring Using High-Resolution LiDAR-Derived DEM and Multi-Temporal Imageries. Sci. Total Environ. 2024, 921, 171104. [Google Scholar] [CrossRef]
- Yepez, S.; Salas, F.; Nardini, A.; Valenzuela, N.; Osores, V.; Vargas, J.; Rodriguez, R.; Piegay, H. Semi-Automated Morphological Characterization Using South Rivers Toolbox. Proc. Int. Assoc. Hydrol. Sci. 2024, 385, 189–196. [Google Scholar] [CrossRef]
- Smith, M.W.; Carrivick, J.L.; Quincey, D.J. Structure from Motion Photogrammetry in Physical Geography. Prog. Phys. Geogr. 2016, 40, 247–275. [Google Scholar] [CrossRef]
- Fonstad, M.A.; Dietrich, J.T.; Courville, B.C.; Jensen, J.L.; Carbonneau, P.E. Topographic Structure from Motion: A New Development in Photogrammetric Measurement. Earth Surf. Process. Landf. 2013, 38, 421–430. [Google Scholar] [CrossRef]
- Musa, Z.N.; Popescu, I.; Mynett, A. A Review of Applications of Satellite SAR, Optical, Altimetry and DEM Data for Surface Water Modelling, Mapping and Parameter Estimation. Hydrol. Earth Syst. Sci. 2015, 19, 3755–3769. [Google Scholar] [CrossRef]
- Braun, A. Retrieval of Digital Elevation Models from Sentinel-1 Radar Data—Open Applications, Techniques, and Limitations. Open Geosci. 2021, 13, 532–569. [Google Scholar] [CrossRef]
- Arrighi, C.; Campo, L. Effects of Digital Terrain Model Uncertainties on High-Resolution Urban Flood Damage Assessment. J. Flood Risk Manag. 2019, 12, e12530. [Google Scholar] [CrossRef]
- Dietrich, J.T. Bathymetric Structure-from-Motion: Extracting Shallow Stream Bathymetry from Multi-View Stereo Photogrammetry. Earth Surf. Process. Landf. 2017, 42, 355–364. [Google Scholar] [CrossRef]
- Watanabe, Y.; Kawahara, Y. UAV Photogrammetry for Monitoring Changes in River Topography and Vegetation. Procedia Eng. 2016, 154, 317–325. [Google Scholar] [CrossRef]
- Casado, M.R.; Gonzalez, R.B.; Kriechbaumer, T.; Veal, A. Automated Identification of River Hydromorphological Features Using UAV High Resolution Aerial Imagery. Sensors 2015, 15, 27969–27989. [Google Scholar] [CrossRef]
- Villanueva, J.R.E.; Martínez, L.I.; Montiel, J.I.P. DEM Generation from Fixed-Wing UAV Imaging and LiDAR-Derived Ground Control Points for Flood Estimations. Sensors 2019, 19, 3205. [Google Scholar] [CrossRef]
- Rusnák, M.; Sládek, J.; Kidová, A.; Lehotský, M. Template for High-Resolution River Landscape Mapping Using UAV Technology. Meas. J. Int. Meas. Confed. 2018, 115, 139–151. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned Aerial Systems for Photogrammetry and Remote Sensing: A Review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 79–97. [Google Scholar] [CrossRef]
- Wedajo, G.K. LiDAR DEM Data for Flood Mapping and Assessment; Opportunities and Challenges: A Review. J. Remote Sens. GIS 2017, 6, 4. [Google Scholar] [CrossRef]
- Eltner, A.; Kaiser, A.; Castillo, C.; Rock, G.; Neugirg, F.; Abellán, A. Image-Based Surface Reconstruction in Geomorphometry-Merits, Limits and Developments. Earth Surf. Dyn. 2016, 4, 359–389. [Google Scholar] [CrossRef]
- Brunier, G.; Fleury, J.; Anthony, E.J.; Gardel, A.; Dussouillez, P. Close-Range Airborne Structure-from-Motion Photogrammetry for High-Resolution Beach Morphometric Surveys: Examples from an Embayed Rotating Beach. Geomorphology 2016, 261, 76–88. [Google Scholar] [CrossRef]
- Eberhard, L.A.; Sirguey, P.; Miller, A.; Marty, M.; Schindler, K.; Stoffel, A.; Bühler, Y. Intercomparison of Photogrammetric Platforms for Spatially Continuous Snow Depth Mapping. Cryosph. Discuss. 2020, 15, 69–94. [Google Scholar] [CrossRef]
- Saglam, İ.E.; Karasaka, L. Evaluation of Multi-Camera Images in Different SfM-MVS Based Photogrammetric Software and Comparison of Digital Products in Generating 3D City Models. Ain Shams Eng. J. 2024, 15, 102700. [Google Scholar] [CrossRef]
- Yilmaz, V.; Konakoglu, B.; Serifoglu, C.; Gungor, O.; Gökalp, E. Image Classification-Based Ground Filtering of Point Clouds Extracted from UAV-Based Aerial Photos. Geocarto Int. 2018, 33, 310–320. [Google Scholar] [CrossRef]
- Tamminga, A.; Hugenholtz, C.; Eaton, B.; Lapointe, M. Hyperspatial Remote Sensing of Channel Reach Morphology and Hydraulic Fish Habitat Using an Unmanned Aerial Vehicle (UAV): A First Assessment in the Context of River Research and Management. River Res. Appl. 2015, 31, 379–391. [Google Scholar] [CrossRef]
- Zeybek, M.; Şanlıoğlu, İ. Point Cloud Filtering on UAV Based Point Cloud. Meas. J. Int. Meas. Confed. 2019, 133, 99–111. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, A.S.; Fu, G.; Djordjević, S.; Zhang, C.; Savić, D.A. An Integrated Framework for High-Resolution Urban Flood Modelling Considering Multiple Information Sources and Urban Features. Environ. Model. Softw. 2018, 107, 85–95. [Google Scholar] [CrossRef]
- Laks, I.; Sojka, M.; Walczak, Z.; Wrózyński, R. Possibilities of Using Low Quality Digital Elevation Models of Floodplains in Hydraulic Numerical Models. Water 2017, 9, 283. [Google Scholar] [CrossRef]
- Becker, C.; Häni, N.; Rosinskaya, E.; D’Angelo, E.; Strecha, C. Classification of Aerial Photogrammetric 3D Point Clouds. Photogramm. Eng. Remote Sens. 2018, 84, 287–295. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved Progressive TIN Densification Filtering Algorithm for Airborne LiDAR Data in Forested Areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef]
- Monteiro, E.S.V.; Fonte, C.C.; de Lima, J.L.M.P. Analysing the Potential of OpenStreetMap Data to Improve the Accuracy of SRTM 30 DEM on Derived Basin Delineation, Slope, and Drainage Networks. Hydrology 2018, 5, 34. [Google Scholar] [CrossRef]
- Li, W.; Li, D.; Fang, Z.N. Intercomparison of Automated Near-Real-Time Flood Mapping Algorithms Using Satellite Data and DEM-Based Methods: A Case Study of 2022 Madagascar Flood. Hydrology 2023, 10, 17. [Google Scholar] [CrossRef]
- Sahid, S. Enhancing Digital Elevation Model Accuracy for Flood Modelling—A Case Study of the Ciberes River in Cirebon Indonesia. Forum Geogr. 2024, 38, 40–56. [Google Scholar] [CrossRef]
- Coveney, S.; Roberts, K. Lightweight UAV Digital Elevation Models and Orthoimagery for Environmental Applications: Data Accuracy Evaluation and Potential for River Flood Risk Modelling. Int. J. Remote Sens. 2017, 38, 3159–3180. [Google Scholar] [CrossRef]
- Peramuna, P.D.P.O.; Neluwala, N.G.P.B.; Wijesundara, K.K.; DeSilva, S.; Venkatesan, S.; Dissanayake, P.B.R. Enhancing 2D Hydrodynamic Flood Model Predictions in Data-Scarce Regions through Integration of Multiple Terrain Datasets. J. Hydrol. 2024, 648, 132343. [Google Scholar] [CrossRef]
- Saksena, S.; Merwade, V. Incorporating the Effect of DEM Resolution and Accuracy for Improved Flood Inundation Mapping. J. Hydrol. 2015, 530, 180–194. [Google Scholar] [CrossRef]
- Dey, S.; Saksena, S.; Winter, D.; Merwade, V.; McMillan, S. Incorporating Network Scale River Bathymetry to Improve Characterization of Fluvial Processes in Flood Modeling. Water Resour. Res. 2022, 58, e2020WR029521. [Google Scholar] [CrossRef]
- Woodget, A.S.; Carbonneau, P.E.; Visser, F.; Maddock, I.P. Quantifying Submerged Fluvial Topography Using Hyperspatial Resolution UAS Imagery and Structure from Motion Photogrammetry. Earth Surf. Process. Landf. 2015, 40, 47–64. [Google Scholar] [CrossRef]
- Javernick, L.; Brasington, J.; Caruso, B. Modeling the Topography of Shallow Braided Rivers Using Structure-from-Motion Photogrammetry. Geomorphology 2014, 213, 166–182. [Google Scholar] [CrossRef]
- Parrot, J.F.; Ramírez Núñez, C. LiDAR DTM: Artifacts, and Correction for River Altitudes. Investig. Geogr. 2016, 2016, 28–39. [Google Scholar] [CrossRef]
- Brasington, J.; Vericat, D.; Rychkov, I. Modeling River Bed Morphology, Roughness, and Surface Sedimentology Using High Resolution Terrestrial Laser Scanning. Water Resour. Res. 2012, 48, 1–18. [Google Scholar] [CrossRef]
- Petrasova, A.; Mitasova, H.; Petras, V.; Jeziorska, J. Fusion of High-Resolution DEMs for Water Flow Modeling. Open Geospatial Data Softw. Stand. 2017, 2, 6. [Google Scholar] [CrossRef]
- Heidemann, H.K. Lidar Base Specification (Ver. 1.3, February 2018): U.S. Geological Survey Techniques and Methods, Book 11, Chapter B4; Office of Communications and Publishing: Reston, VA, USA, 2018. [Google Scholar]
- Griffiths, D.; Burningham, H. Comparison of Pre- and Self-Calibrated Camera Calibration Models for UAS-Derived Nadir Imagery for a SfM Application. Prog. Phys. Geogr. 2019, 43, 215–235. [Google Scholar] [CrossRef]
- Chen, Q.; Mudd, S.M.; Attal, M.; Hancock, S. Extracting an Accurate River Network: Stream Burning Re-Revisited. Remote Sens. Environ. 2024, 312, 114333. [Google Scholar] [CrossRef]
- Neal, J.; Hawker, L.; Savage, J.; Durand, M.; Bates, P.; Sampson, C. Estimating River Channel Bathymetry in Large Scale Flood Inundation Models. Water Resour. Res. 2021, 57, 2020WR028301. [Google Scholar] [CrossRef]
- Garrote, J.; González-Jiménez, M.; Guardiola-Albert, C.; Díez-Herrero, A. The Manning’s Roughness Coefficient Calibration Method to Improve Flood Hazard Analysis in the Absence of River Bathymetric Data: Application to the Urban Historical Zamora City Centre in Spain. Appl. Sci. 2021, 11, 9267. [Google Scholar] [CrossRef]
- Legleiter, C.J. The Optical River Bathymetry Toolkit. River Res. Appl. 2021, 37, 555–568. [Google Scholar] [CrossRef]
- Godfroy, J.; Lejot, J.; Demarchi, L.; Bizzi, S.; Piégay, H. Assessing the Feasibility of Mapping Channel Bathymetry of Long River Corridors from Hyperspectral Data across a Range of Flow Conditions. Int. J. Remote Sens. 2024, 45, 8123–8156. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. “Structure-from-Motion” Photogrammetry: A Low-Cost, Effective Tool for Geoscience Applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Manfreda, S.; Fortunato, S.; Sasso, D.; Pizarro, A.; Tauro, F. New Insights Offered by UAS for River Monitoring. In Applications of Small Unmanned Aircraft Systems; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Ngula Niipele, J.; Chen, J. The Usefulness of Alos-Palsar Dem Data for Drainage Extraction in Semi-Arid Environments in The Iishana Sub-Basin. J. Hydrol. Reg. Stud. 2019, 21, 57–67. [Google Scholar] [CrossRef]
- Vengoechea, A.; Rojano, R.; Arregoces, H. Dispersión y Concentración de Aerosoles Marinos PM 10 En Una Ciudad Costera Del Caribe Dispersion and Concentration of PM 10 Particles in a Caribbean Coastal City. Inf. Tecnológica 2018, 26, 123–130. [Google Scholar] [CrossRef]
- Castellanos Martínez, M.L.; Carabalí Angola, A. El delta del rio Ranchería: Una Mirada Biofísica y Social antes de la Represa; Universidad de La Guajira: Riohacha, Colombia, 2014; ISBN 978-958-8530-24-6. [Google Scholar]
- Fondo de Adaptación Contrato No. 127 de 2018 Consultoría para la Elaboración de un Ortofotomosaico Con la Georreferenciación de Todos los Elementos Existentes: (I) El Suministro de Fotografías Aéreas Digitales (II) la Digitalización de Elementos Cartográficos; y (III) la Ela. Available online: https://www.fondoadaptacion.gov.co/index.php/component/sppagebuilder/?view=page&id=934 (accessed on 8 April 2020).
- Fondo de Adaptación Contrato No. 217 de 2016 Elaborar Un Ortofotomosaico Con La Georeferenciación de Todos Los Elementos Existentes, Incluyendo: (I) La Toma de Fotografías Aéreas Digitales; (II) La Digitalización de Elementos Cartográficos; y (III) La Elaboración de Un Mode. Available online: https://www.fondoadaptacion.gov.co/index.php/component/sppagebuilder/?view=page&id=1559 (accessed on 8 April 2020).
- Pérez, J.I.; Escobar, J.R.; Fragozo, J.M. Modelación Hidráulica 2D de Inundaciones En Regiones Con Escasez de Datos: El Caso Del Delta Del Río Ranchería, Riohacha Colombia. Inf. Tecnológica 2018, 29, 143–156. [Google Scholar] [CrossRef]
- Yu, J.J.; Kim, D.W.; Lee, E.J.; Son, S.W. Determining the Optimal Number of Ground Control Points for Varying Study Sites through Accuracy Evaluation of Unmanned Aerial System-Based 3d Point Clouds and Digital Surface Models. Drones 2020, 4, 49. [Google Scholar] [CrossRef]
- Oniga, V.-E.; Breaban, A.-I.; Statescu, F. Determining the Optimum Number of Ground Control Points for Obtaining High Precision Results Based on UAS Images. Proceedings 2018, 2, 352. [Google Scholar] [CrossRef]
- Legleiter, C.J. Remote Measurement of River Morphology via Fusion of LiDAR Topography and Spectrally Based Bathymetry. Earth Surf. Process. Landf. 2012, 37, 499–518. [Google Scholar] [CrossRef]
- Agisoft LLC. Orthophoto and DEM Generation with Agisoft PhotoScan Pro 1.0.0; Agisoft LLC: St. Petersburg, Russia, 2013. [Google Scholar]
- Merwade, V.; Cook, A.; Coonrod, J. GIS Techniques for Creating River Terrain Models for Hydrodynamic Modeling and Flood Inundation Mapping. Environ. Model. Softw. 2008, 23, 1300–1311. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Gokceoglu, C. Spatial Modeling in GIS and R for Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 9780128152263. [Google Scholar]
- Strick, R.J.P.; Ashworth, P.J.; Sambrook Smith, G.H.; Nicholas, A.P.; Best, J.L.; Lane, S.N.; Parsons, D.R.; Simpson, C.J.; Unsworth, C.A.; Dale, J. Quantification of Bedform Dynamics and Bedload Sediment Flux in Sandy Braided Rivers from Airborne and Satellite Imagery. Earth Surf. Process. Landf. 2019, 44, 953–972. [Google Scholar] [CrossRef]
- Berra, E.F.; Peppa, M.V. Advances and Challenges of UAV SFM MVS Photogrammetry and Remote Sensing: Short Review. In Proceedings of the 2020 IEEE Latin American GRSS & ISPRS Remote Sensing Conference (LAGIRS), Santiago, Chile, 22–26 March 2020; pp. 533–538. [Google Scholar] [CrossRef]
- Kasvi, E.; Salmela, J.; Lotsari, E.; Kumpula, T.; Lane, S.N. Comparison of Remote Sensing Based Approaches for Mapping Bathymetry of Shallow, Clear Water Rivers. Geomorphology 2019, 333, 180–197. [Google Scholar] [CrossRef]
- Rusnák, M.; Goga, T.; Michaleje, L.; Michalková, M.Š.; Máčka, Z.; Bertalan, L.; Kidová, A. Remote Sensing of Riparian Ecosystems. Remote Sens. 2022, 14, 2645. [Google Scholar] [CrossRef]
- Zhang, K.; Gann, D.; Ross, M.; Biswas, H.; Li, Y.; Rhome, J. Comparison of TanDEM-X DEM with LiDAR Data for Accuracy Assessment in a Coastal Urban Area. Remote Sens. 2019, 11, 876. [Google Scholar] [CrossRef]
- Bigdeli, B.; Amini Amirkolaee, H.; Pahlavani, P. DTM Extraction under Forest Canopy Using LiDAR Data and a Modified Invasive Weed Optimization Algorithm. Remote Sens. Environ. 2018, 216, 289–300. [Google Scholar] [CrossRef]
- Tamminga, A.D.; Eaton, B.C.; Hugenholtz, C.H. UAS-Based Remote Sensing of Fluvial Change Following an Extreme Flood Event. Earth Surf. Process. Landf. 2015, 40, 1464–1476. [Google Scholar] [CrossRef]
- Woodget, A.S.; Dietrich, J.T.; Wilson, R.T. Quantifying Below-Water Fluvial Geomorphic Change: The Implications of Refraction Correction, Water Surface Elevations, and Spatially Variable Error. Remote Sens. 2019, 11, 2415. [Google Scholar] [CrossRef]
- Tonina, D.; McKean, J.A.; Benjankar, R.M.; Wright, C.W.; Goode, J.R.; Chen, Q.; Reeder, W.J.; Carmichael, R.A.; Edmondson, M.R. Mapping River Bathymetries: Evaluating Topobathymetric LiDAR Survey. Earth Surf. Process. Landf. 2019, 44, 507–520. [Google Scholar] [CrossRef]
- Manfreda, S.; Herban, S.; Arranz Justel, J.; Perks, M.; Mullerova, J.; Dvorak, P.; Vuono, P. Assessing the Accuracy of Digital Surface Models Derived from Optical Imagery Acquired with Unmanned Aerial Systems. Drones 2019, 3, 15. [Google Scholar] [CrossRef]
- James, M.R.; Chandler, J.H.; Eltner, A.; Fraser, C.; Miller, P.E.; Mills, J.P.; Noble, T.; Robson, S.; Lane, S.N. Guidelines on the Use of Structure-from-Motion Photogrammetry in Geomorphic Research. Earth Surf. Process. Landf. 2019, 44, 2081–2084. [Google Scholar] [CrossRef]
- Gichamo, T.Z.; Sazib, N.S.; Tarboton, D.G.; Dash, P. HydroDS: Data Services in Support of Physically Based, Distributed Hydrological Models. Environ. Model. Softw. 2020, 125, 104623. [Google Scholar] [CrossRef]
- US Army Corps of Enginners HEC River Analysis System: Terrain Modification Tools. Available online: https://www.hec.usace.army.mil/confluence/rasdocs/rmum/latest/terrain-modification (accessed on 15 January 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).