Projected Runoff Changes and Their Effects on Water Levels in the Lake Qinghai Basin Under Climate Change Scenarios
Abstract
1. Introduction
2. Materials and Methods
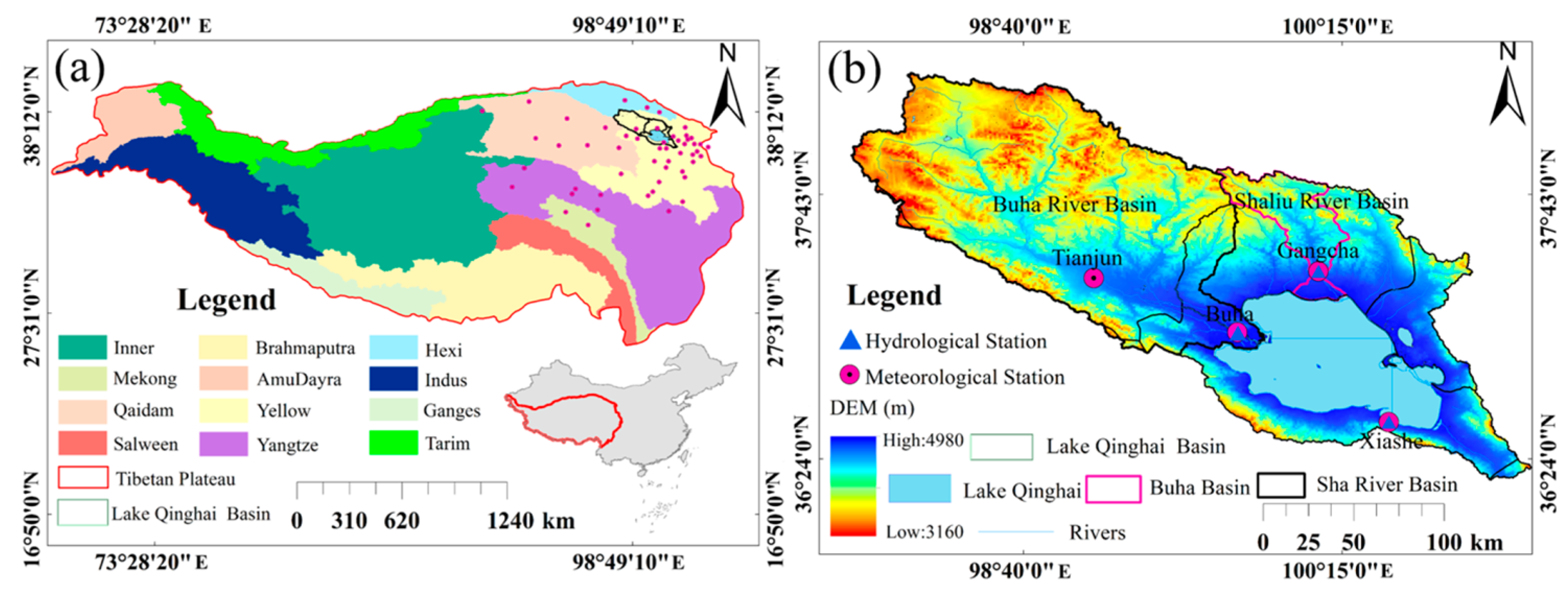
2.1. Study Region
2.2. Methodology
2.2.1. SWAT Water Balance Equation
2.2.2. Calculation of Surface Runoff
2.2.3. Calculation of Evaporation
2.2.4. Lake Water Balance
2.2.5. Simulation Accuracy and Applicability Evaluation
2.2.6. Selection of Climate Scenarios
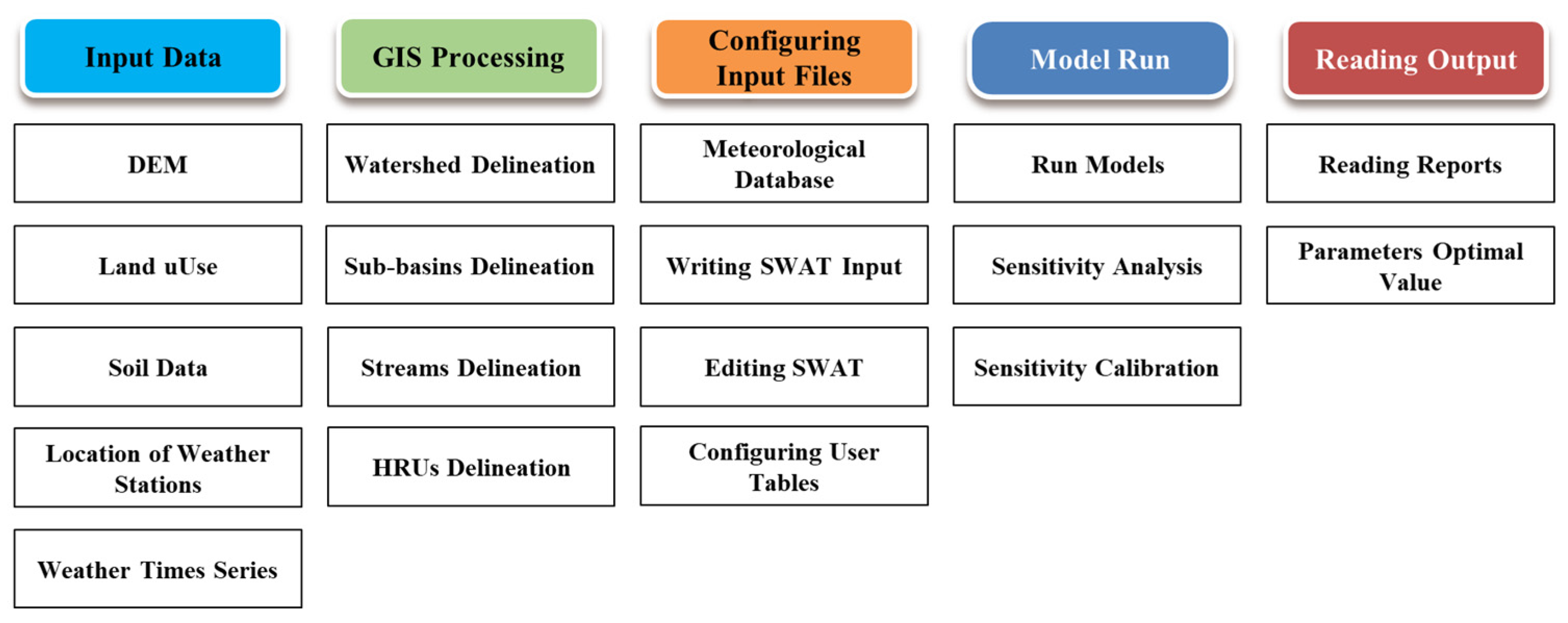
2.3. SWAT Model Construction Process
2.3.1. Database Construction
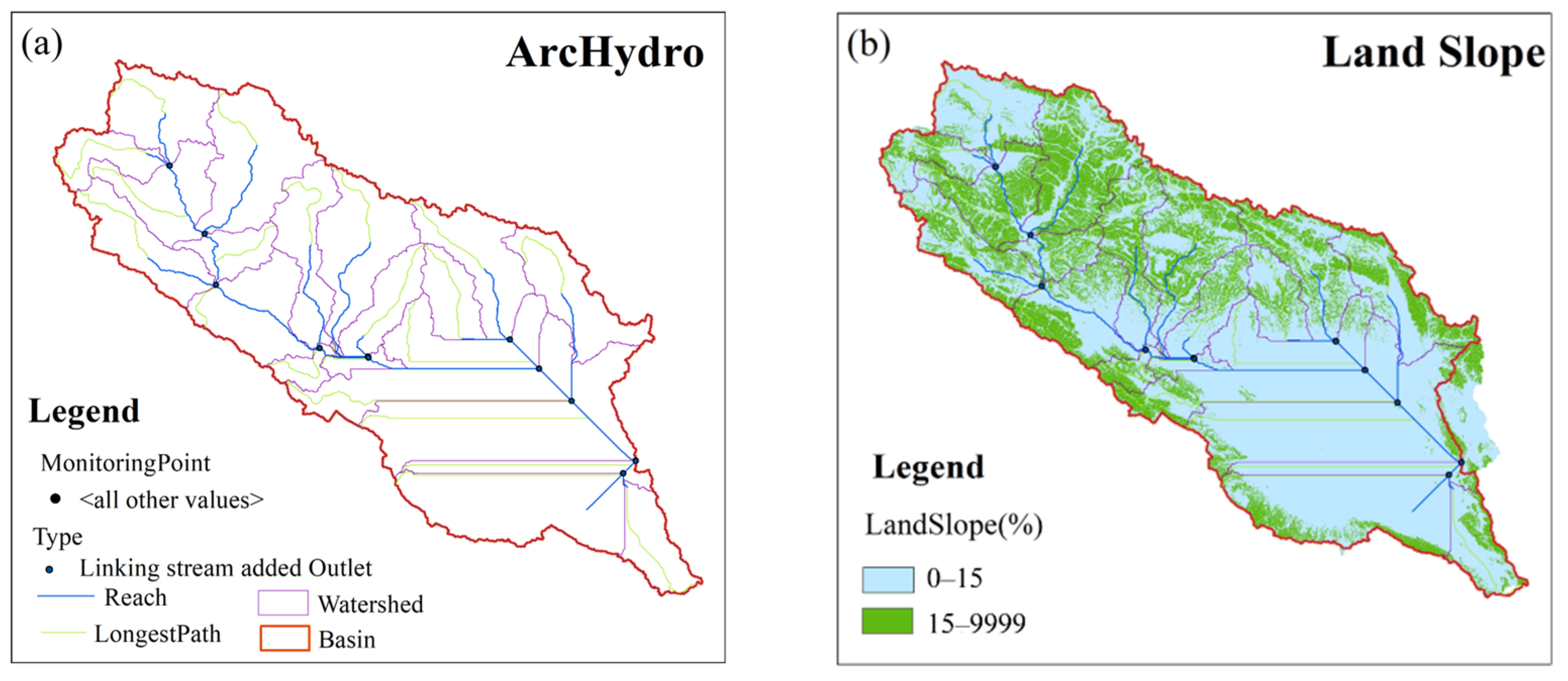
2.3.2. Subbasin Delineation and Hydrological Response Units (HRUs)
2.4. Data Sources and Collection
3. Results
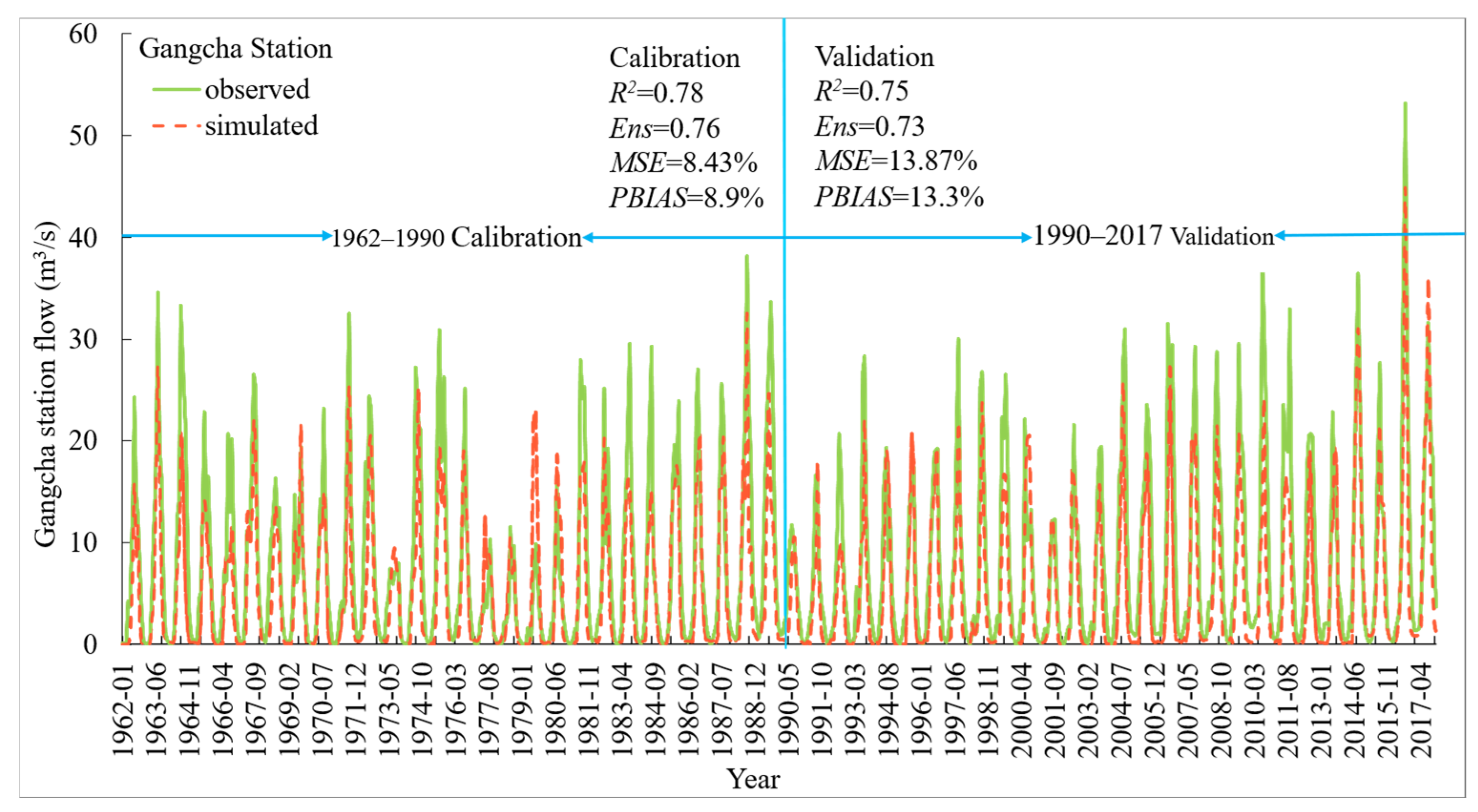
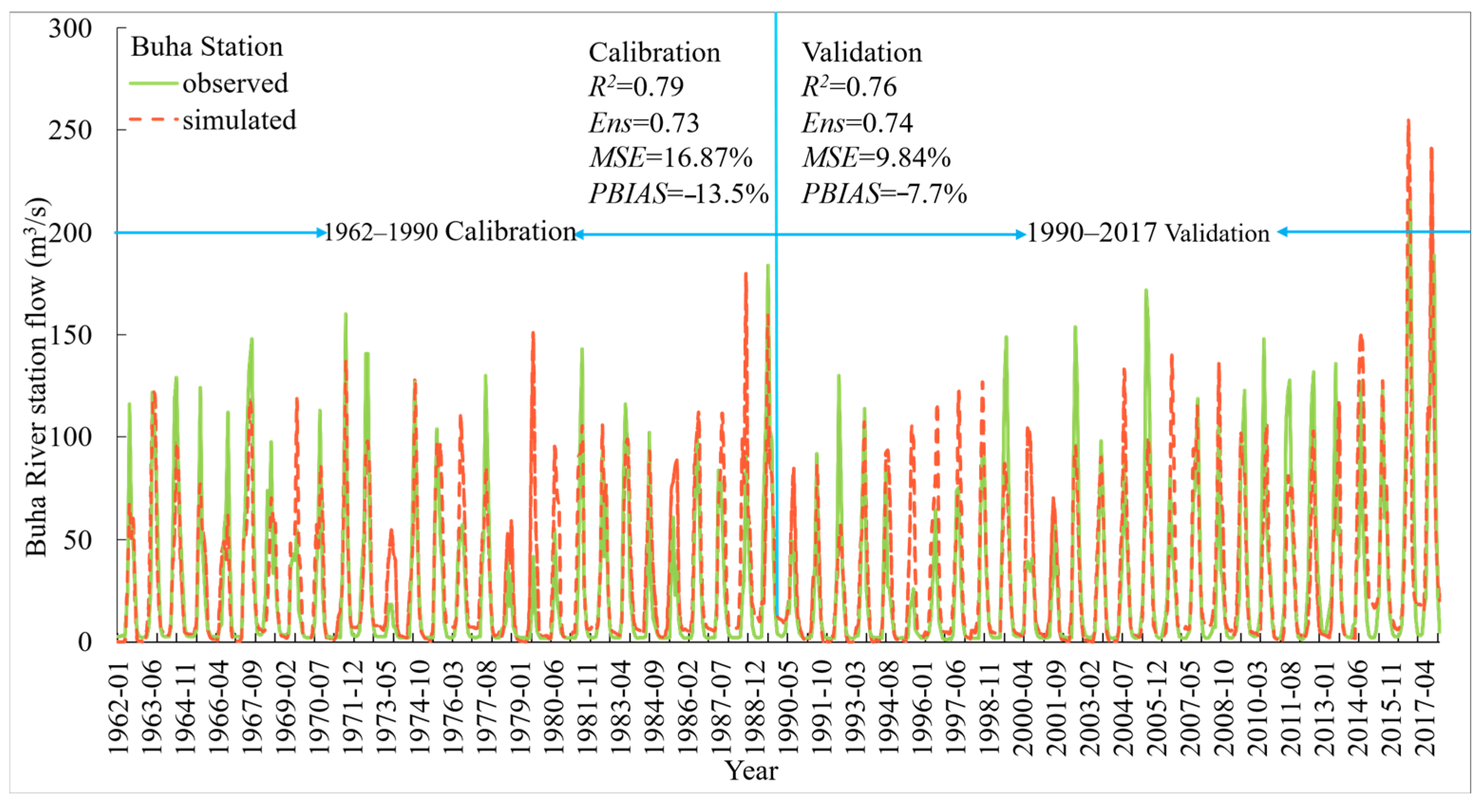
3.1. Calibration and Verification of the Simulations
3.1.1. Simulation Calibration and Verification
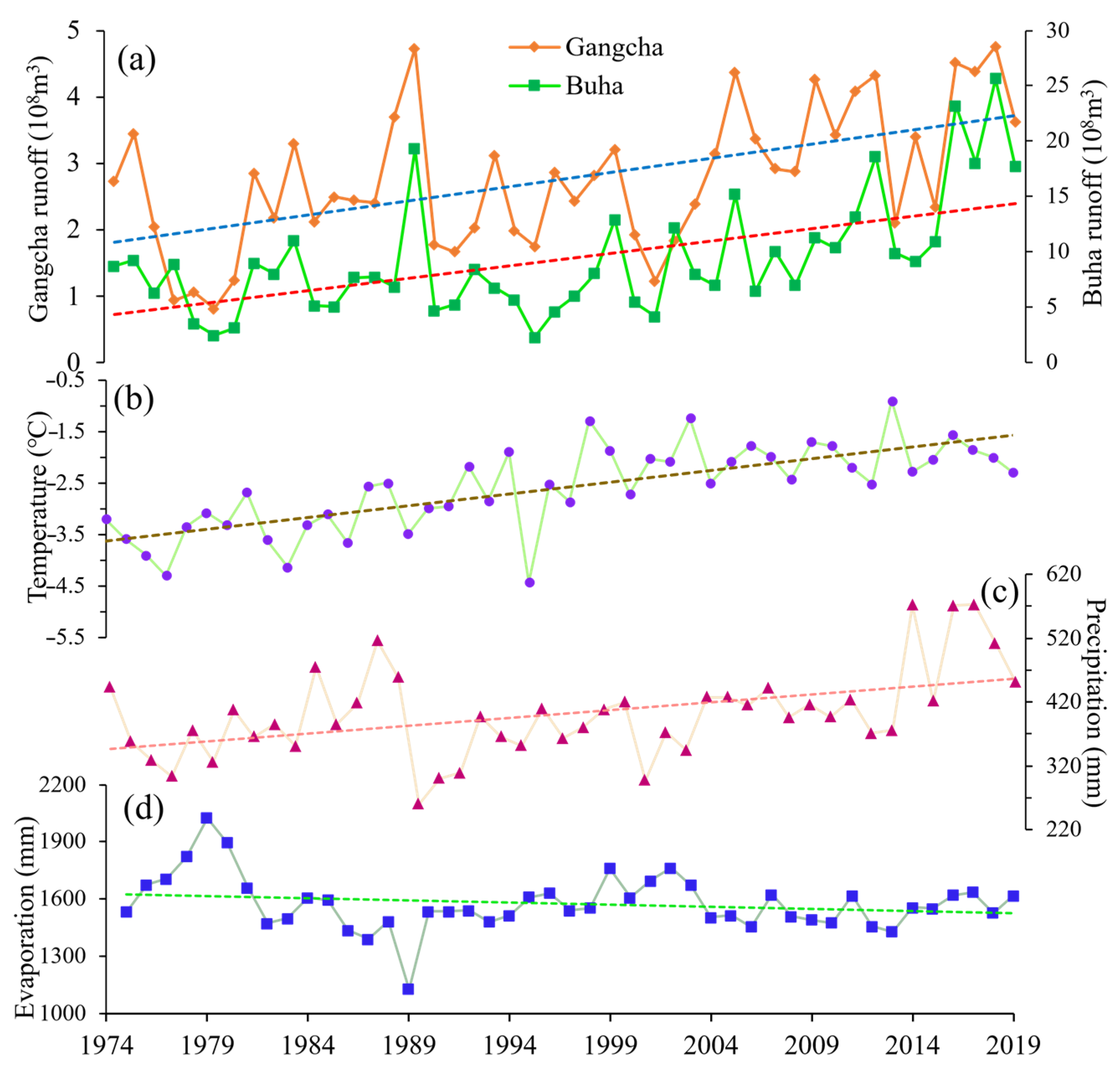
3.1.2. Runoff Calibration and Validation
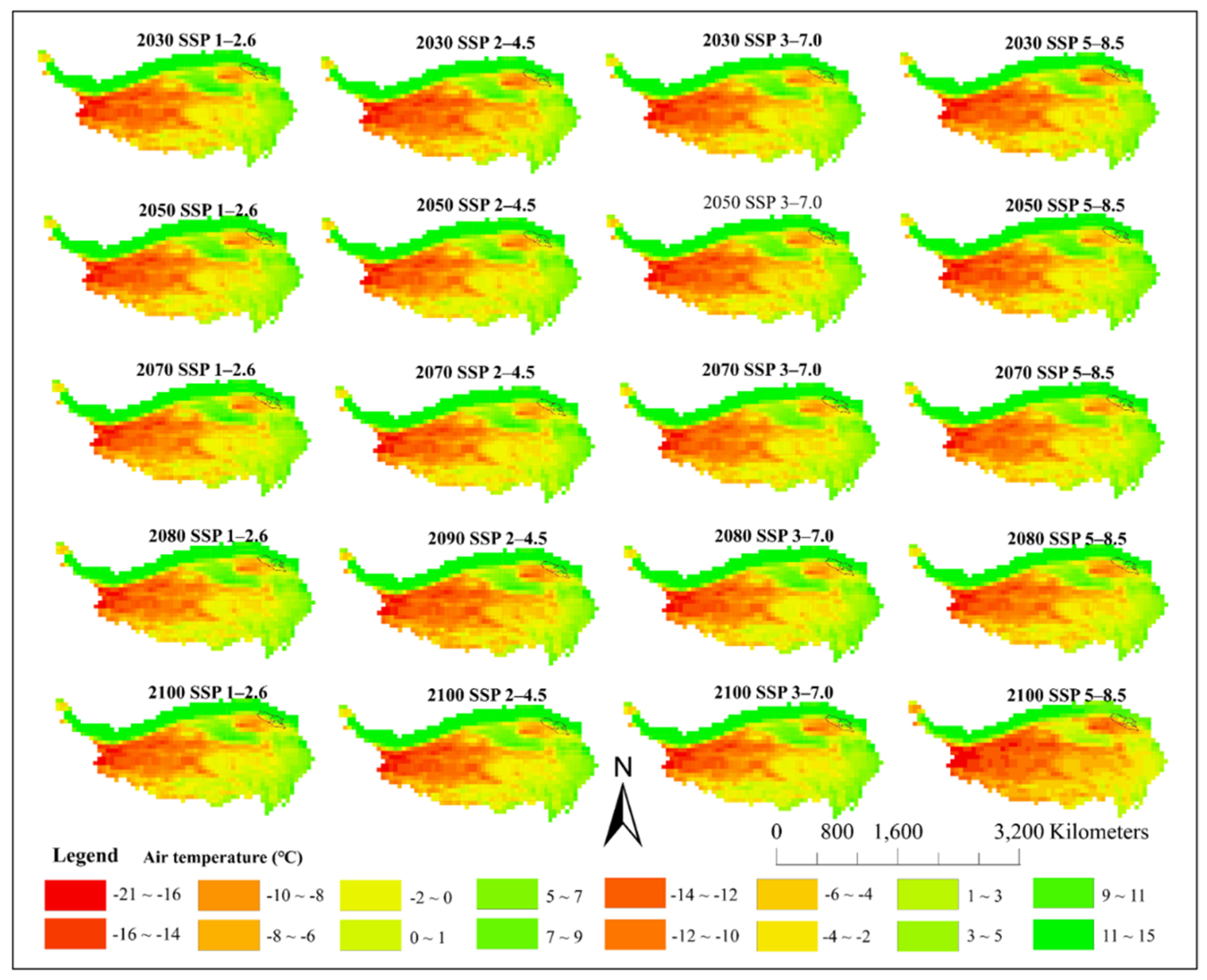
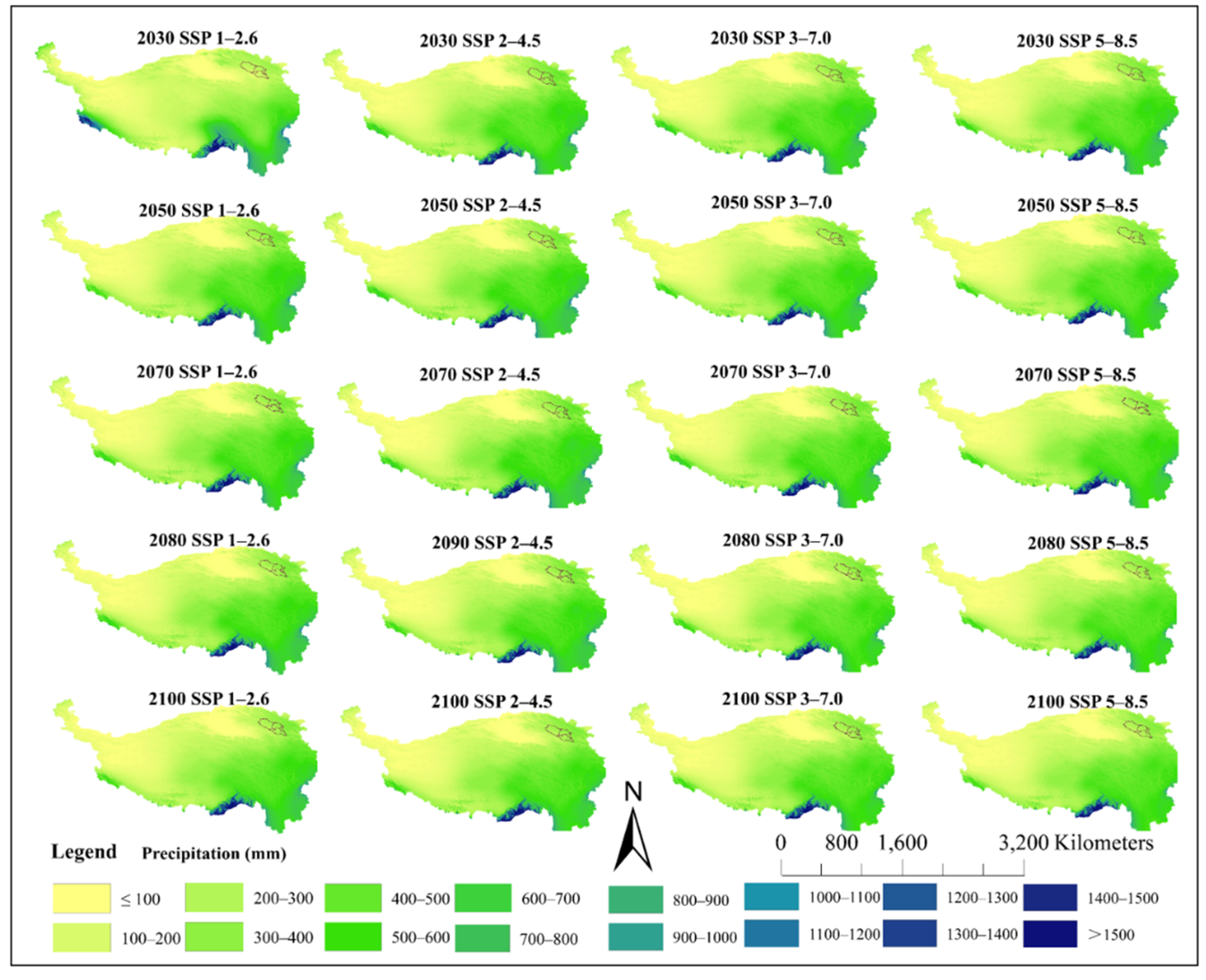
3.2. Changes in Future Climate Scenarios
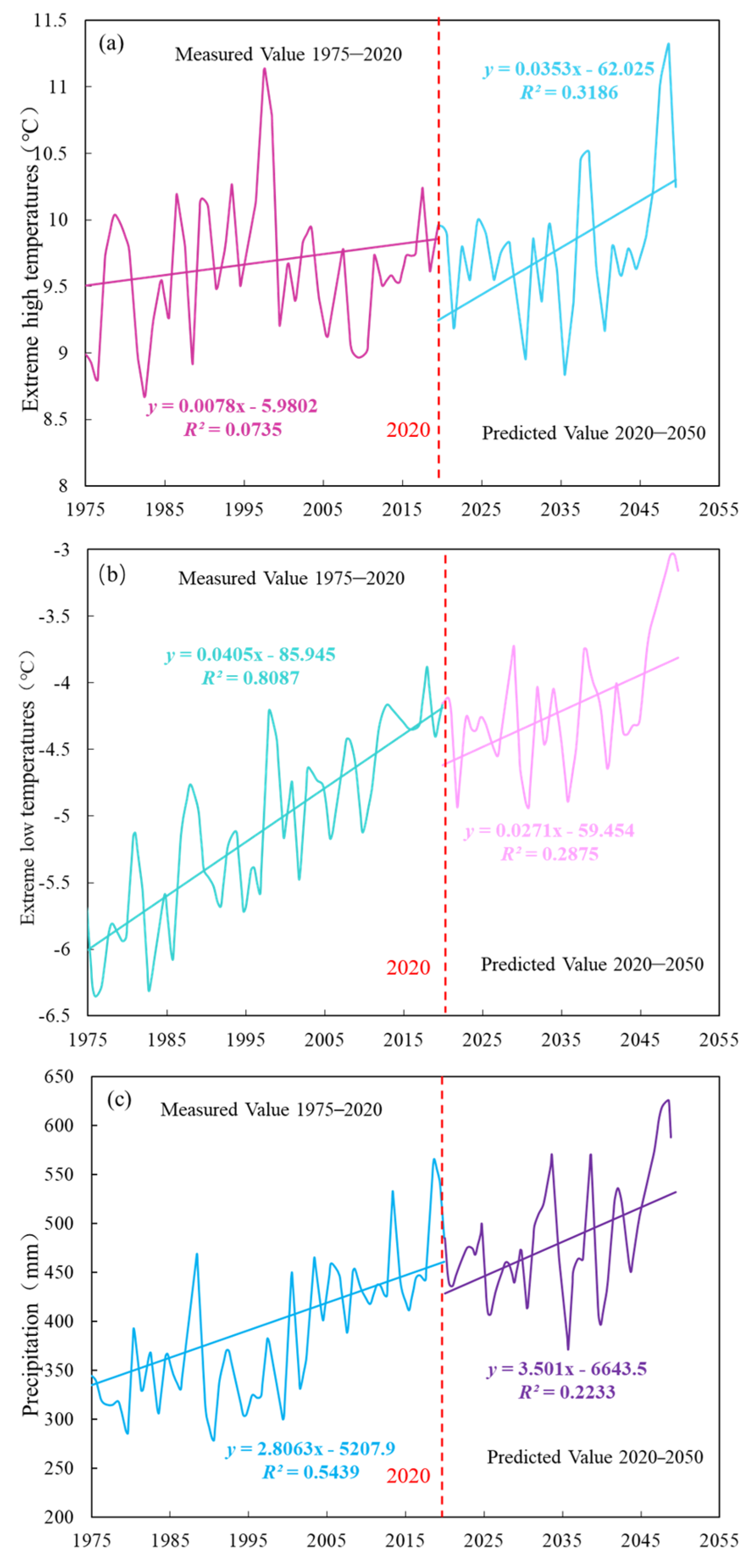
3.2.1. Changes in Surface Air Temperature and Precipitation
3.2.2. Changes in Extreme Temperatures and Precipitation
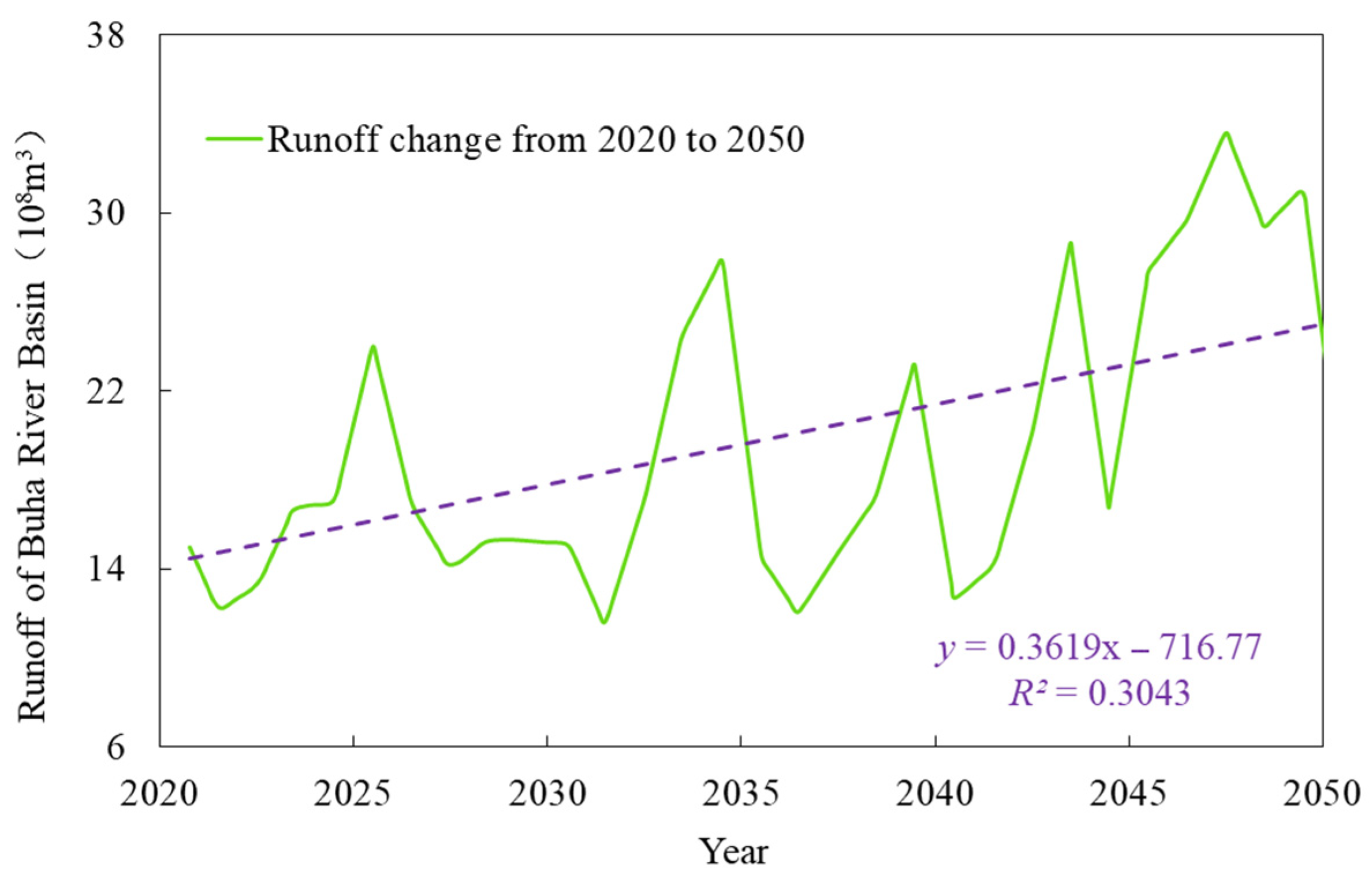
3.2.3. Changes in Runoff in the Buha River Basin over the Next 30 Years
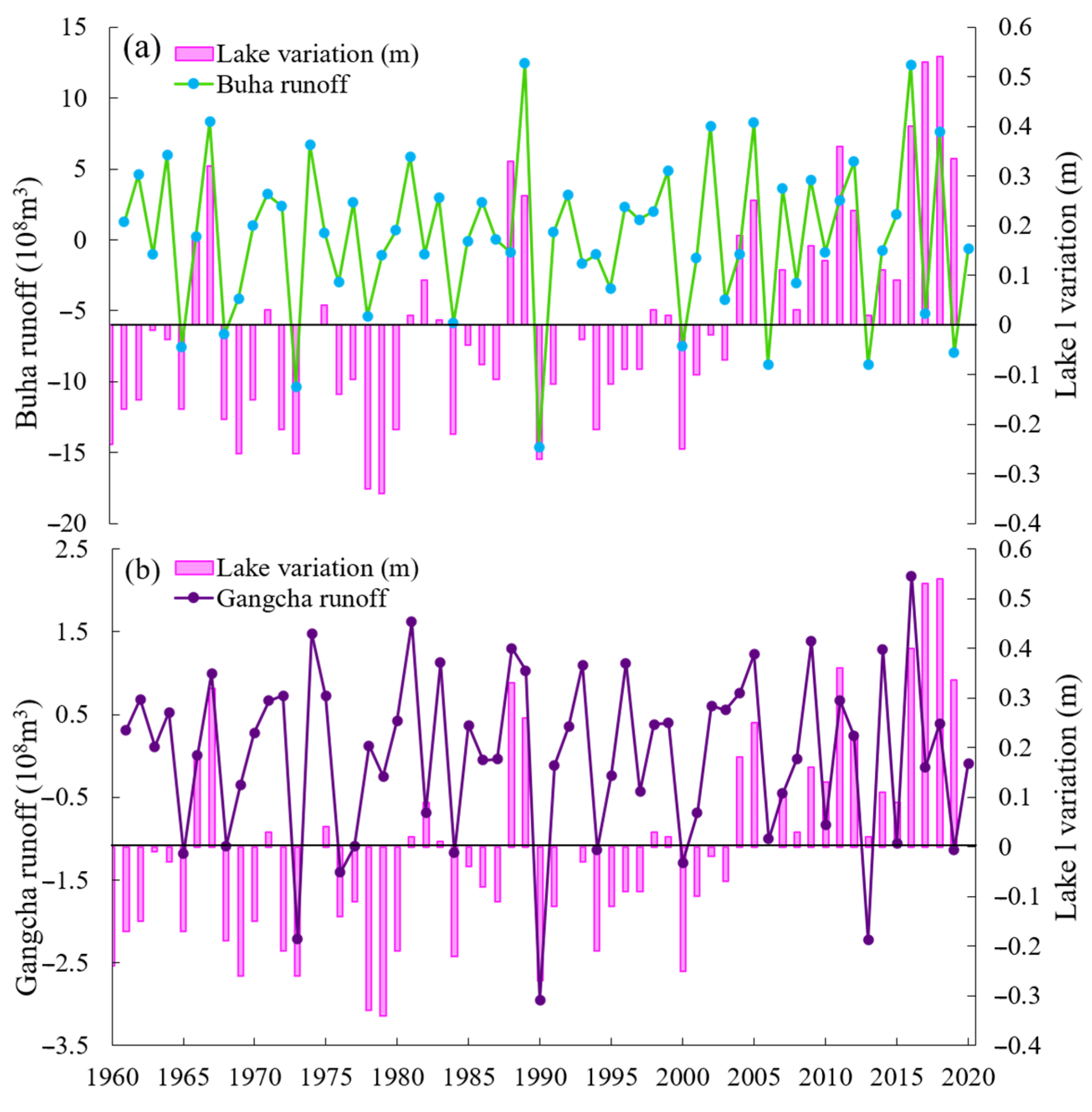
3.3. Changes in Water Level, Water Storage, and Lake Area over the Next 30 Years
4. Discussion
4.1. Runoff and Water Level
4.2. Impacts of Climate Change on Runoff
4.3. Limitations and Future Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Woolway, R.I.; Kraemer, B.M.; Lenters, J.D.; Merchant, C.J.; O’Reilly, C.M.; Sharma, S. Global lake responses to climate change. Nat. Rev. Earth Environ. 2020, 1, 388–403. [Google Scholar] [CrossRef]
- Zhang, G.; Ran, Y.; Wan, W.; Luo, W.; Chen, W.; Xu, F.; Li, X. 100 years of lake evolution over the Qinghai–Tibet Plateau. Earth Syst. Sci. Data 2021, 13, 3951–3966. [Google Scholar] [CrossRef]
- Yao, T.; Bolch, T.; Chen, D.; Gao, J.; Immerzeel, W.; Piao, S.; Su, F.; Thompson, L.; Wada, Y.; Wang, L.; et al. The imbalance of the Asian water tower. Nat. Rev. Earth Environ. 2022, 3, 618–632. [Google Scholar] [CrossRef]
- Moser, K.A.; Baron, J.S.; Brahney, J.; Oleksy, I.A.; Saros, J.E.; Hundey, E.J.; Smol, J.P. Mountain lakes: Eyes on global environmental change. Glob. Planet. Change 2019, 178, 77–95. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Chen, W.; Zheng, G.; Shum, C.K.; Yang, K.; Jia, Y. Regional differences of lake evolution across China during 1960s–2015 and its natural and anthropogenic causes. Remote Sens. Environ. 2019, 221, 386–404. [Google Scholar] [CrossRef]
- Grant, L.; Vanderkelen, I.; Gudmundsson, L.; Tan, Z.; Perroud, M.; Stepanenko, V.M.; Thiery, W. Attribution of global lake systems change to anthropogenic forcing. Nat. Geosci. 2021, 14, 849–854. [Google Scholar] [CrossRef]
- Huang, L.; Liu, J.; Shao, Q.; Liu, R. Changing inland lakes responding to climate warming in Northeastern Tibetan Plateau. Clim. Change 2011, 109, 479–502. [Google Scholar] [CrossRef]
- Zhang, Z.; Chang, J.; Xu, C.Y.; Zhou, Y.; Wu, Y.; Chen, X.; Duan, Z. The response of lake area and vegetation cover variations to climate change over the Qinghai-Tibetan Plateau during the past 30 years. Sci. Total Environ. 2018, 635, 443–451. [Google Scholar] [CrossRef]
- Hou, P.; Weidman, R.P.; Liu, Q.; Li, H.; Duan, L.; Zhang, X.; Liu, F.; Gao, Y.; Xu, J.; Li, H.; et al. Recent water-level fluctuations, future trends and their eco-environmental impacts on Lake Qinghai. J. Environ. Manag. 2023, 333, 117461. [Google Scholar] [CrossRef]
- Huang, C.; Lai, Z.; Liu, X.; Madsen, D. Lake-level history of Lake Qinghai on the NE Tibetan Plateau and its implications for Asian monsoon pattern-A review. Quat. Sci. Rev. 2021, 273, 107258. [Google Scholar] [CrossRef]
- Fan, C.; Song, C.; Li, W.; Liu, K.; Cheng, J.; Fu, C.; Chen, T.; Ke, L.; Wang, J. What drives the rapid water-level recovery of the largest lake (Lake Qinghai) of China over the past half century? J. Hydrol. 2021, 593, 125921. [Google Scholar] [CrossRef]
- Cui, B.L.; Li, X.Y. Stable isotopes reveal sources of precipitation in the Lake Qinghai Basin of the northeastern Tibetan Plateau. Sci. Total Environ. 2015, 527, 26–37. [Google Scholar] [CrossRef]
- Wan, W.; Xiao, P.; Feng, X.; Li, H.; Ma, R.; Duan, H.; Zhao, L. Monitoring lake changes of Qinghai-Tibetan Plateau over the past 30 years using satellite remote sensing data. Chin. Sci. Bull. 2014, 59, 1021–1035. [Google Scholar] [CrossRef]
- Wang, H.; Qi, Y.; Lian, X.; Zhang, J.; Yang, R.; Zhang, M. Effects of climate change and land use/cover change on the volume of the Lake Qinghai in China. J. Arid Land 2022, 14, 245–261. [Google Scholar] [CrossRef]
- Gong, J.; Li, J.; Yang, J.; Li, S.; Tang, W. Land use and land cover change in the Qinghai Lake region of the Tibetan Plateau and its impact on ecosystem services. Int. J. Environ. Res. Public Health 2017, 14, 818. [Google Scholar] [CrossRef]
- Chang, B.; He, K.N.; Li, R.J.; Sheng, Z.P.; Wang, H. Linkage of climatic factors and human activities with water level fluctuations in Qinghai Lake in the northeastern Tibetan Plateau, China. Water 2017, 9, 552. [Google Scholar] [CrossRef]
- Liang, J.; Lupien, R.L.; Xie, H.; Vachula, R.S.; Stevenson, M.A.; Han, B.P.; Lin, Q.; He, Y.; Wang, M.; Liang, P.; et al. Lake ecosystem on the Qinghai–Tibetan Plateau severely altered by climatic warming and human activity. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2021, 576, 110509. [Google Scholar] [CrossRef]
- Stuart-Smith, R.F.; Roe, G.H.; Li, S.; Allen, M.R. Increased outburst flood hazard from Lake Palcacocha due to human-induced glacier retreat. Nat. Geosci. 2021, 14, 85–90. [Google Scholar] [CrossRef]
- Trinh, T.; Ishida, K.; Kavvas, M.L.; Ercan, A.; Carr, K. Assessment of 21st century drought conditions at Shasta Dam based on dynamically projected water supply conditions by a regional climate model coupled with a physically based hydrology model. Sci. Total Environ. 2017, 586, 197–205. [Google Scholar] [CrossRef]
- Kaya, Y.; Sanli, F.B.; Abdikan, S. Refinement of ICESat-2 derived inland water surface levels with the TG20 local geoid model: In the case of Türkiye lakes. Phys. Chem. Earth Parts A B C 2025, 139, 103900. [Google Scholar] [CrossRef]
- Zhu, Z.; Fu, C.; Wu, H.; Wu, H.; Cao, Y.; Xia, Y. Decoding the hundred-year water level changes of the largest Saline Lake in China: A joint lake-basin modeling study based on a revised SWAT+. J. Hydrol. Reg. Stud. 2023, 49, 101521. [Google Scholar] [CrossRef]
- Li, X.; Yang, X.; Ma, Y.; Hu, G.; Hu, X.; Wu, X.; Wang, P.; Huang, Y.; Cui, B.; Wei, J. Qinghai Lake Basin critical zone observatory on the Qinghai-Tibet plateau. Vadose Zone J. 2018, 17, 1–11. [Google Scholar] [CrossRef]
- Wang, X.; Gao, B. Future hydrological changes of the upstream basin and their effects on the water level of the Qinghai Lake. J. Hydrol. Reg. Stud. 2025, 59, 102425. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, M.; Xie, Z.; Li, J.; Ma, M.; Lai, P.; Wang, J. Quantifying the contributions of climate change and human activities to water volume in Lake Qinghai, China. Remote Sens. 2021, 14, 99. [Google Scholar] [CrossRef]
- Lian, X.H.; Qi, Y.; Wang, H.W.; Zhang, J.L.; Yang, R. Assessing changes of water yield in Qinghai Lake watershed of China. Water 2019, 12, 11. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Z.; Xiong, S.; Zhang, W.; Li, R. Lake surface temperature predictions under different climate scenarios with machine learning methods: A case study of Lake Qinghai and Hulun lake, China. Remote Sens. 2024, 16, 3220. [Google Scholar] [CrossRef]
- Luo, Z.; Liu, J.; Zhang, S.; Shao, W.; Zhang, L. Research on climate change in Lake Qinghai Basin based on WRF and CMIP6. Remote Sens. 2023, 15, 4379. [Google Scholar] [CrossRef]
- Chen, C.; Gan, R.; Feng, D.; Yang, F.; Zuo, Q. Quantifying the contribution of SWAT modeling and CMIP6 inputting to streamflow prediction uncertainty under climate change. J. Clean. Prod. 2022, 364, 132675. [Google Scholar] [CrossRef]
- Yin, G.A.; Niu, F.J.; Lin, Z.J.; Luo, J.; Liu, M.H. Data-driven spatiotemporal projections of shallow permafrost based on CMIP6 across the Qinghai–Tibet Plateau at 1 km2 scale. Adv. Clim. Change Res. 2021, 12, 814–827. [Google Scholar] [CrossRef]
- Chen, F.; Wu, D.; Chen, J.; Zhou, A.; Yu, J.; Shen, J.; Huang, X. Holocene moisture and East Asian summer monsoon evolution in the northeastern Tibetan Plateau recorded by Lake Qinghai and its environs: A review of conflicting proxies. Quat. Sci. Rev. 2016, 154, 111–129. [Google Scholar] [CrossRef]
- Mo, L.; Yu, X.; Feng, Y.; Jiang, T. Runoff Variations and Quantitative Analysis in the Qinghai Lake Basin Under Changing Environments. Hydrology 2025, 12, 94. [Google Scholar] [CrossRef]
- Xiong, X.; Zhang, K.; Chen, X.; Shi, H.; Luo, Z.; Wu, C. Sources and distribution of microplastics in China’s largest inland lake–Lake Qinghai. Environ. Pollut. 2018, 235, 899–906. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Mishra, S.K.; Singh, V. Soil Conservation Service Curve Number (SCS-CN) Methodology; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Beven, K. A sensitivity analysis of the Penman-Monteith actual evapotranspiration estimates. J. Hydrol. 1979, 44, 169–190. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Busico, G.; Colombani, N.; Fronzi, D.; Pellegrini, M.; Tazioli, A.; Mastrocicco, M. Evaluating SWAT model performance, considering different soils data input, to quantify actual and future runoff susceptibility in a highly urbanized basin. J. Environ. Manag. 2020, 266, 110625. [Google Scholar] [CrossRef]
- Tokarska, K.B.; Stolpe, M.B.; Sippel, S.; Fischer, E.M.; Smith, C.J.; Lehner, F.; Knutti, R. Past warming trend constrains future warming in CMIP6 models. Sci. Adv. 2020, 6, eaaz9549. [Google Scholar] [CrossRef]
- Duan, A.; Xiao, Z. Does the climate warming hiatus exist over the Tibetan Plateau? Sci. Rep. 2015, 5, 13711. [Google Scholar] [CrossRef]
- You, Q.; Min, J.; Kang, S. Rapid warming in the Tibetan Plateau from observations and CMIP5 models in recent decades. Int. J. Climatol. 2016, 36, 2660–2670. [Google Scholar] [CrossRef]
- Ji, J.; Shen, J.; Balsam, W.; Chen, J.; Liu, L.; Liu, X. Asian monsoon oscillations in the northeastern Qinghai–Tibet Plateau since the late glacial as interpreted from visible reflectance of Lake Qinghai sediments. Earth Planet. Sci. Lett. 2005, 233, 61–70. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, T.; Liu, Y. Permafrost temperatures and thickness on the Qinghai–Tibet Plateau. Glob. Planet. Change 2010, 72, 32–38. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Xie, H.; Yang, K.; Zhu, L.; Shum, C.K.; Ke, C. Response of Tibetan Plateau lakes to climate change: Trends, patterns, and mechanisms. Earth-Sci. Rev. 2020, 208, 103269. [Google Scholar] [CrossRef]
- Song, C.; Huang, B.; Richards, K.; Ke, L.; Hien Phan, V. Accelerated lake expansion on the Tibetan Plateau in the 2000s: Induced by glacial melting or other processes? Water Resour. Res. 2014, 50, 3170–3186. [Google Scholar] [CrossRef]
- Chen, R.; Li, H.; Wang, X.; Gou, X.; Yang, M.; Wan, G. Surface air temperature changes over the Tibetan Plateau: Historical evaluation and future projection based on CMIP6 models. Geosci. Front. 2022, 13, 101452. [Google Scholar] [CrossRef]
- Wang, H.; Liu, J.; Luo, Z.; Nazli, S.; Shi, L. Hydrologic response and prediction of future water level changes in Qinghai Lake of Tibet Plateau, China. J. Hydrol. Reg. Stud. 2025, 57, 102168. [Google Scholar] [CrossRef]
- Su, F.; Zhang, L.; Ou, T.; Chen, D.; Yao, T.; Tong, K.; Qi, Y. Hydrological response to future climate changes for the major upstream river basins in the Tibetan Plateau. Glob. Planet. Change 2016, 136, 82–95. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Shum, C.K.; Yi, S.; Yang, K.; Xie, H.; Feng, W.; Bolch, T.; Wang, L.; Behrangi, A.; et al. Lake volume and groundwater storage variations in Tibetan Plateau’s endorheic basin. Geophys. Res. Lett. 2017, 44, 5550–5560. [Google Scholar] [CrossRef]
- Lei, Y.; Yao, T.; Yang, K.; Sheng, Y.; Kleinherenbrink, M.; Yi, S. Contrasting hydrological budgets of the adjacent lake systems on the Tibetan Plateau. J. Hydrol. 2023, 620, 129487. [Google Scholar]

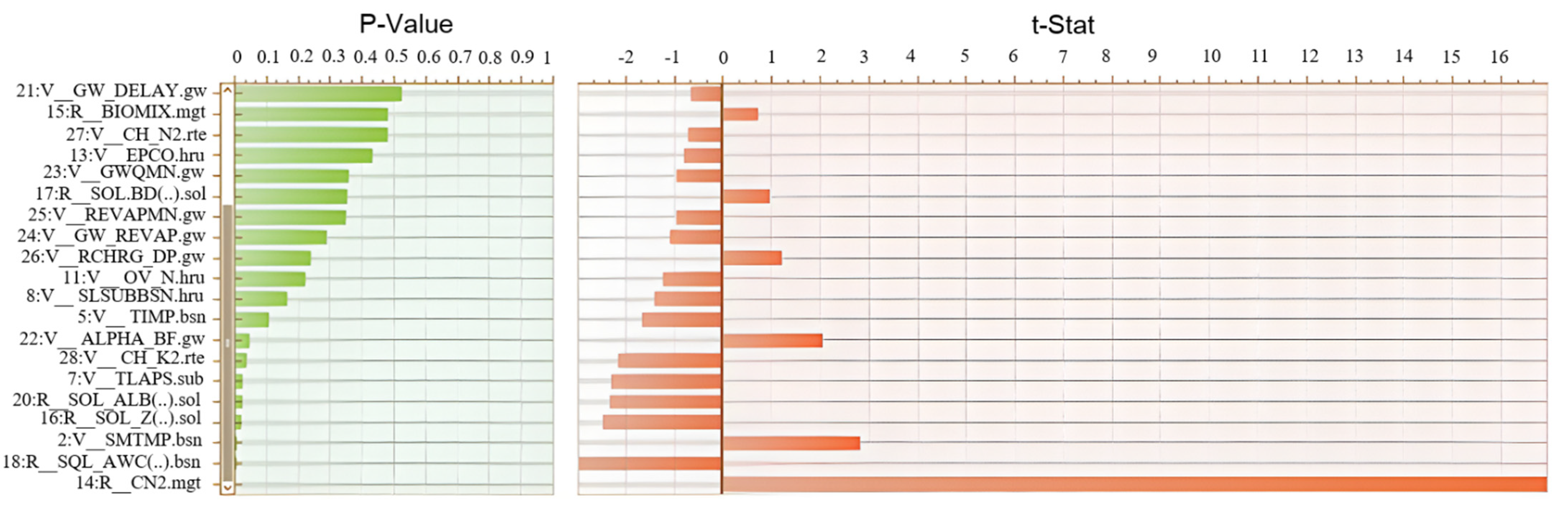

| Variable Name | Definition | Initial Range | Calibration Parameter Range | Calibration Result | Sensitivity Priority | ||
|---|---|---|---|---|---|---|---|
| Gangcha | Buha | Gangcha | Buha | ||||
| r__CN2 | Initial SCS runoff curve number for moisture condition II | −0.2–0.2 | 0.1546–0.5 | 0.03 | 0.26 | 0.1 | 0.1 |
| v__ESCO | Soil evaporation compensation factor | 0–1 | 0.18–0.87 | 0.51 | 0.06 | 0.2 | 0.5 |
| v__EPCO | Plant uptake compensation factor | 0–1 | 0.4519–0.8176 | 0.65 | 0.9 | ||
| v__OV_N | Manning’s “n” value for overland flow | 0.5–2 | −20–8.22 | 0.01 | 0.09 | 0.19 | 0.4 |
| r__SOL_Z | Depth from soil surface to bottom of layer (mm) | −0.5–0.5 | 0.071–0.41 | −0.25 | −0.25 | ||
| v__ALPHA_BF | Baseflow alpha factor (1/days) | 0–1 | 0.37–0.79 | 0.048 | 0.58 | 1 | 0.01 |
| v__GW_DELAY | Groundwater delay time (days) | 0–500 | 81.35–360.61 | 162.79 | 31 | 351 | 202 |
| v__GWQMN | Threshold depth of water in the shallow aquifer needed for return flow to occur (mm H2O) | 0–5000 | 984.9–3293.6 | 40.2 | 40.2 | 319 | 137.5 |
| v__GW_REVAP | Ground water “revap” coefficient | 0.02–0.2 | 0.102–0.1711 | 0.07 | 0.1 | ||
| v__RCHRG_DP | Deep aquifer percolation fraction | 0–1 | 0.25–0.75 | 1 | 0.05 | 1.4 | 0.9 |
| v__TLAPS | Temperature lapse rate (°C/km) | −10–10 | 1.89–7.3 | ||||
| v__CH_N2 | Manning’s “n” value for the main channel | −0.0–160.3 | 0.0146–0.1882 | 0.25 | 0.24 | 9 | 6 |
| v__CH_K2 | Effective hydraulic conductivity in main channel alluvium (mm/h) | −0.01–500 | 277.25–428.89 | 0 | 122.21 | 115.2 | 8 |
| v__SURLAG | Surface runoff lag coefficient | 0.05–24 | 4.0058–17.3426 | 20.31 | 2.18 | 6 | 2 |
| v__SLSUBBSN | Average slope length (m) | 10–150 | 107.5921–150 | 23.12 | 96.07 | 3 | 10 |
| v__SFTMP | Snowfall temperature (°C) | −20–20 | 7.4457–20 | 5 | 1 | 6.9 | 2.9 |
| v__SMTMP | Snow melt base temperature (°C) | −20–20 | −20–8.2285 | 5 | 0.5 | 0.7 | −3.4 |
| v__SMFMX | Melt factor for snow on June 21 (mm H2O/°C-day) | 0–20 | 8.6342–16.2167 | 10 | 3.5 | 8.5 | 5.6 |
| r__SOL_AWC | Available water capacity of the soil layer (mm H2O/mm soil) | −0.5–1.0 | 0.0196–0.3401 | −0.5 | 0 | 0.5 | 0.1 |
| v__SMFMN | Melt factor for snow on December 21 (mm H2O/°C-day) | 1–8 | 1.8524–13.9574 | 3 | 8 | 1.7 | 6.5 |
| v__TIMP | Snowpack temperature lag factor | 0.01–1.0 | 0.5929–1 | 0.04 | 0.68 | 1 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, P.; Du, J.; Qiu, S.; Wang, J.; Wang, C.; Wang, Z.; Jia, X.; Zhang, H. Projected Runoff Changes and Their Effects on Water Levels in the Lake Qinghai Basin Under Climate Change Scenarios. Hydrology 2025, 12, 259. https://doi.org/10.3390/hydrology12100259
Hou P, Du J, Qiu S, Wang J, Wang C, Wang Z, Jia X, Zhang H. Projected Runoff Changes and Their Effects on Water Levels in the Lake Qinghai Basin Under Climate Change Scenarios. Hydrology. 2025; 12(10):259. https://doi.org/10.3390/hydrology12100259
Chicago/Turabian StyleHou, Pengfei, Jun Du, Shike Qiu, Jingxu Wang, Chao Wang, Zheng Wang, Xiang Jia, and Hucai Zhang. 2025. "Projected Runoff Changes and Their Effects on Water Levels in the Lake Qinghai Basin Under Climate Change Scenarios" Hydrology 12, no. 10: 259. https://doi.org/10.3390/hydrology12100259
APA StyleHou, P., Du, J., Qiu, S., Wang, J., Wang, C., Wang, Z., Jia, X., & Zhang, H. (2025). Projected Runoff Changes and Their Effects on Water Levels in the Lake Qinghai Basin Under Climate Change Scenarios. Hydrology, 12(10), 259. https://doi.org/10.3390/hydrology12100259









