Estimation of Evapotranspiration in South Eastern Afghanistan Using the GCOM-C Algorithm on the Basis of Landsat Satellite Imagery
Abstract
1. Introduction
2. Materials and Methods
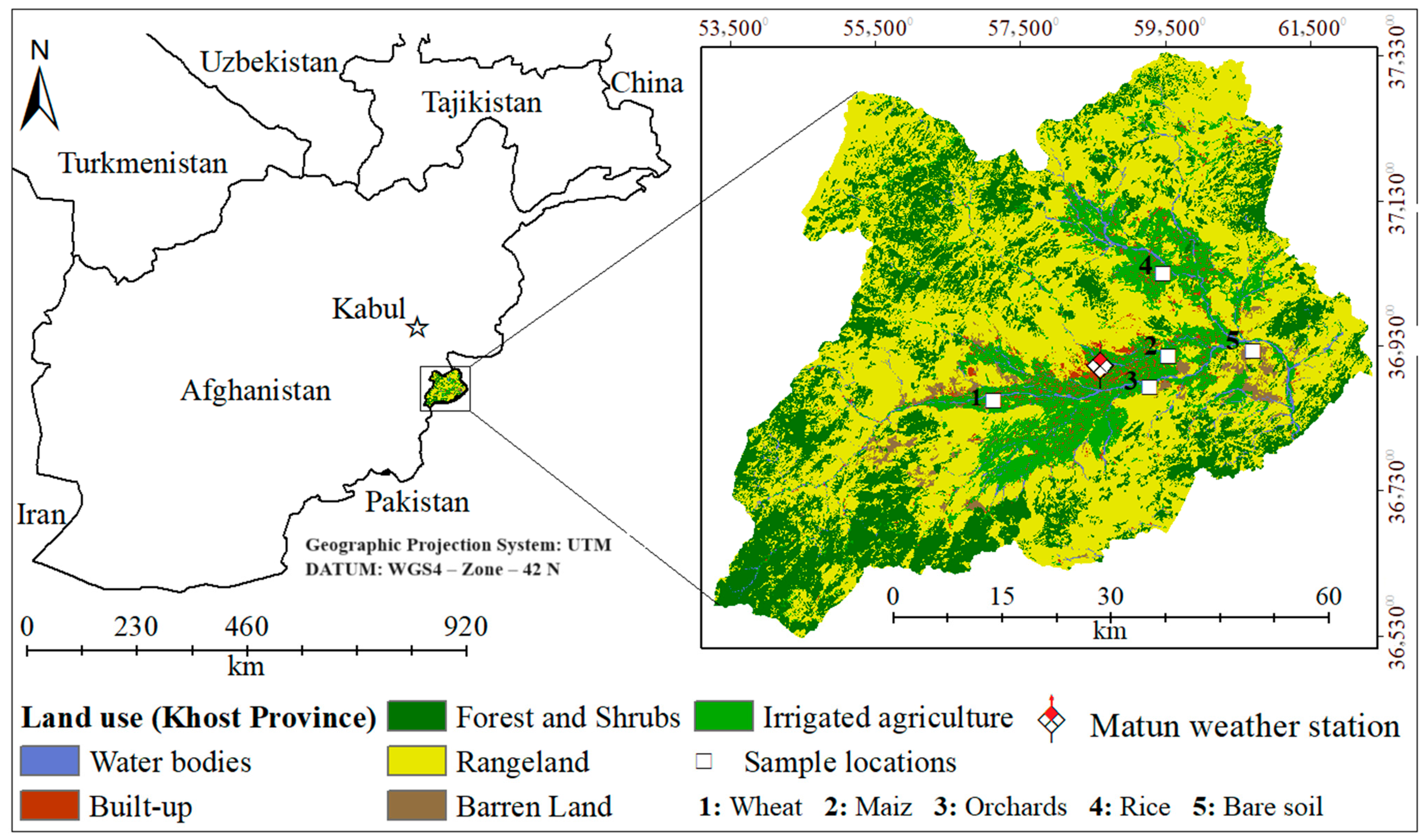
2.1. Study Area
2.2. Data Preparation
- ETa by METRIC: A series of ETr fraction (ETrF) images in the study period, derived by Landsat 8 Band 10, were obtained by METRIC-EEFlux (version 0.20.17). Thus, the image dates are identical to the dates listed in Table 1. The ETrF values of cloud-covered pixels were filled by interpolation between adjoining image dates that had valid ETrF values for the pixel of interest. ETrF is the fraction of alfalfa reference ET (ETr), which is the same as the crop coefficient (Kc) [31].
- ETa by MOD16: A series of 46 eight-day ETa maps of MOD16 for the study period was obtained from the United States Geological Survey (USGS) Earth Explorer website.
- ETa by the SEBS algorithm: ETa maps published by Akhtar et al. (2018) were obtained [25]. The ETa was estimated by the SEBS [11] model, as applied to the Kabul River Basin, including the entire Khost Province. The estimation used Moderate Resolution Imaging Spectroradiometer (MODIS) satellite images and the Global Land Data Assimilation System (GLDAS; [32]) weather dataset for 2003–2013. Their ETa agreed well with independent estimation by an advection–aridity approach [33,34].
- ETc by FAO-56: This was calculated for the study area using the abovementioned weather data with some crop information (such as the cultivation schedule) obtained by the local government, i.e., the directorate of agriculture, irrigation, and livestock, as well as through interviews with farmers. The computational procedure has been described by Allen et al. (1998) [5].
2.3. ETa Estimation by the GCOM-C Algorithm
2.4. Accuracy Assessment
- ETa by MOD16: Monthly ETa maps were computed from eight-day MOD16 ETa products. For the images where the eight-day period was spread over two months, the eight-day ETa was split in proportion to the number of days belonging to each of the two months.
- ETa by the SEBS algorithm: ETa maps as published by Akhtar et al. (2018) were directly used [25]. Note that the obtained SEBS ETa maps were for the cultivation seasons of 2012–2013. Some extra uncertainties may arise from comparing data originating from different years.
- ETc by FAO-56: ETc data for the period of November 2016 to October 2017 were estimated following the FAO’s manual [5] for wheat, maize, rice, and orchards. ETc is not identical to ETa but represents the evapotranspiration for standard cultivation conditions. The term “standard” stands for the absence of both water stress and any disease. Thus, the ETc is expected to provide an upper limit of the ETa, and the ETa reaches the ETc in well-managed fields. In addition to the ETc, evaporation from a typical silt–loam bare soil surface was computed by the soil water balance model as suggested in the FAO-56. Evaluation of satellite-based ETa by comparison with the ETc has been suggested by Stancalie et al. (2010) and Tasumi (2019) [17,37].
3. Results and Discussion
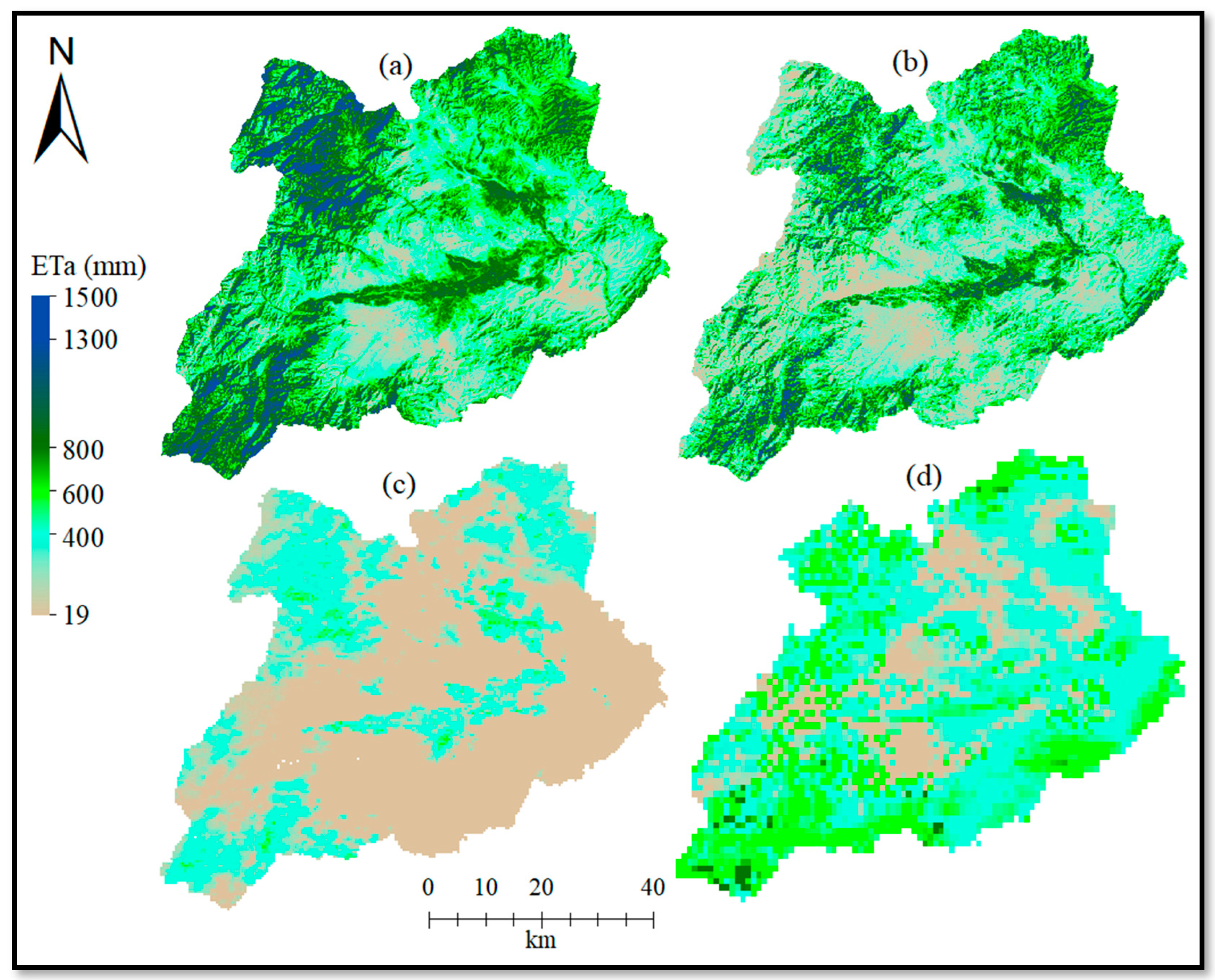
3.1. Results of ETa Estimation
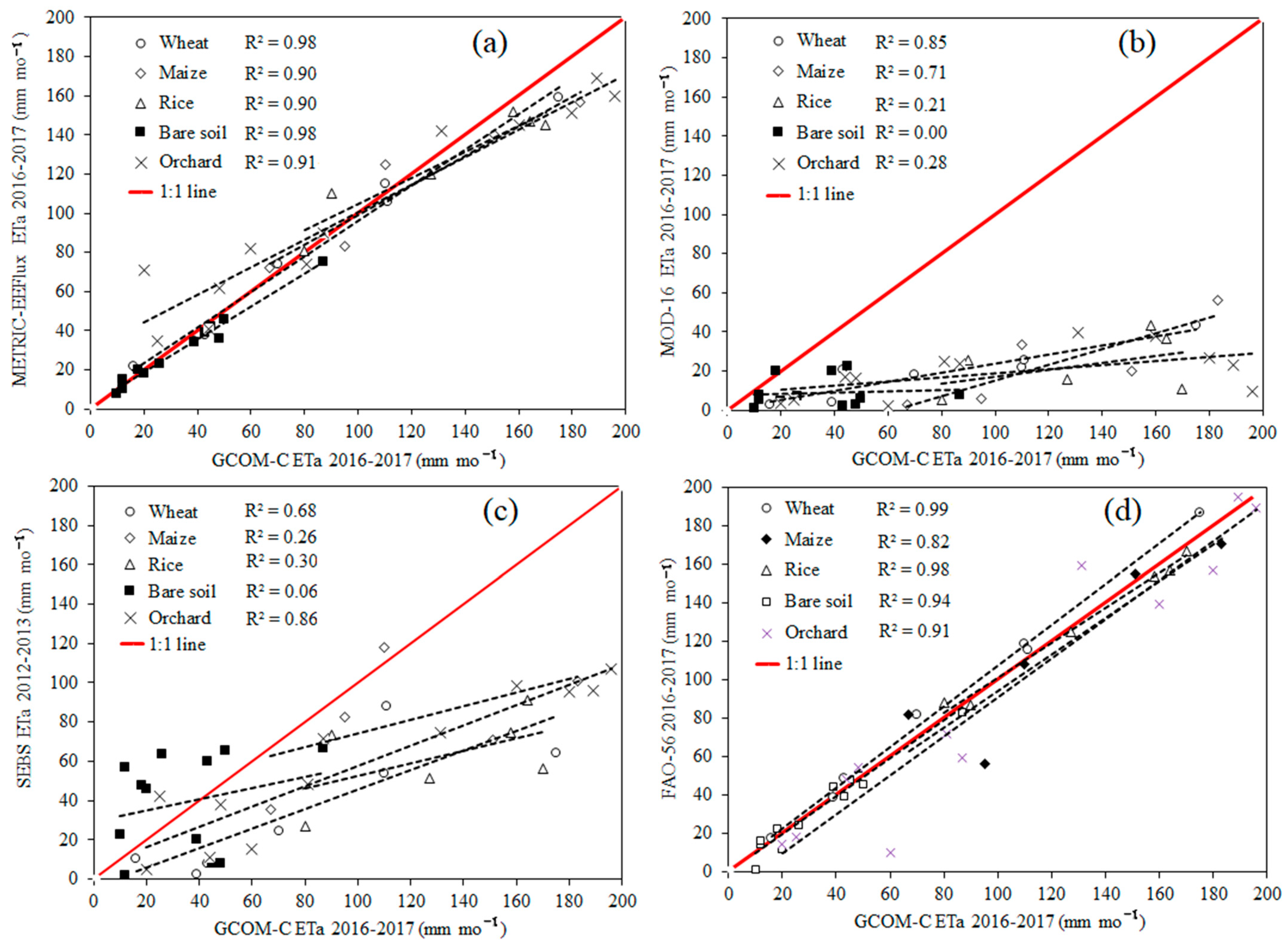
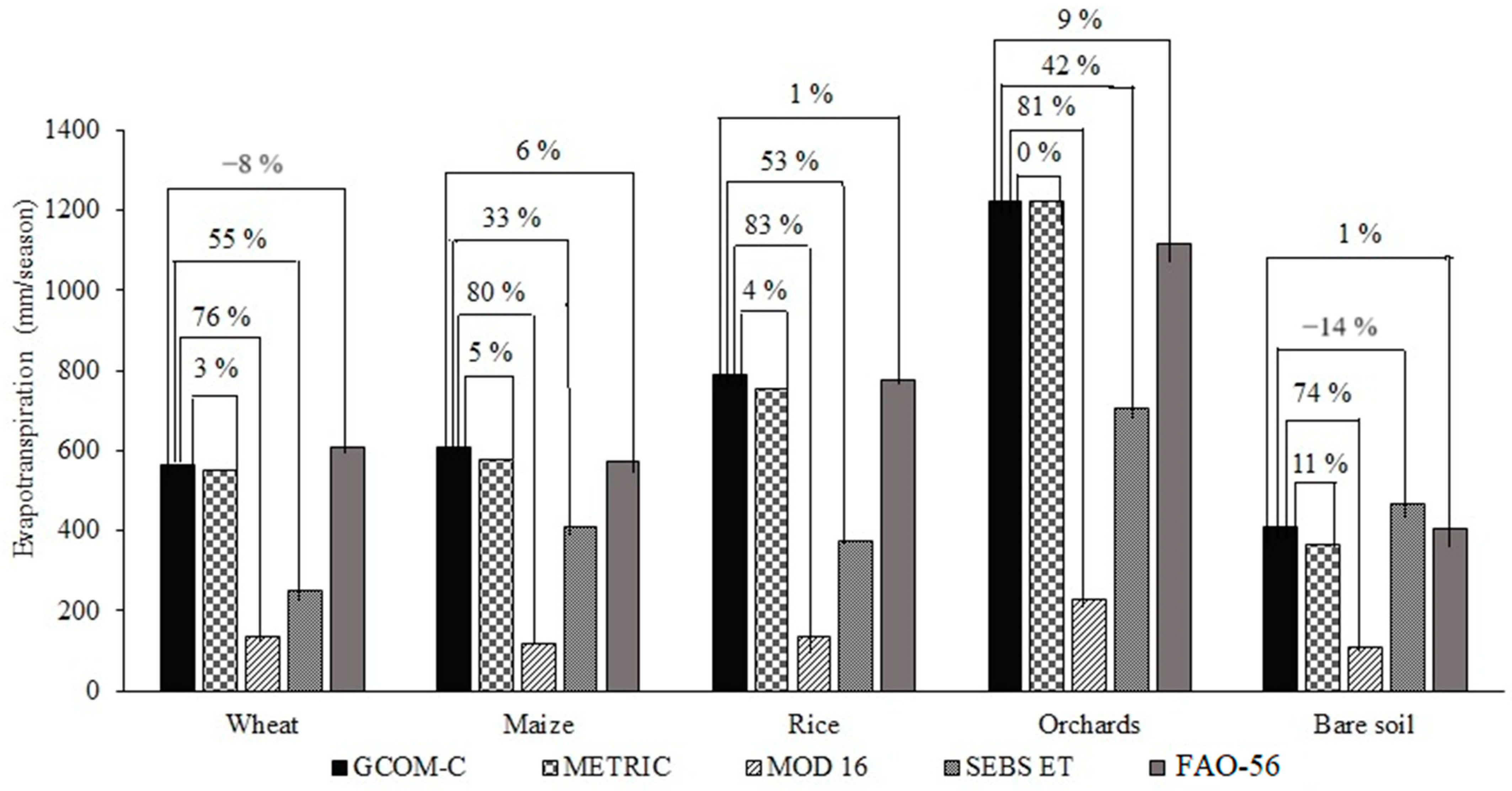
3.2. Comparison of Estimated ETa with METRIC, MOD16, SEBS ETa, and FAO-56 ETc
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Black, M. The Atlas of Water; University of California Press: Oakland, CA, USA, 2016. [Google Scholar] [CrossRef]
- Abdelfattah, M.A.; Shahid, S.A. A Comparative Characterization and Classification of Soils in Abu Dhabi Coastal Area in Relation to Arid and Semi-Arid Conditions Using USDA and FAO Soil Classification Systems. Arid. Land. Res. Manag. 2007, 21, 245–271. [Google Scholar] [CrossRef]
- Da Silva, J.L.B.; Bezerra, A.C.; de Moura, G.B.A.; Jardim, A.M.d.R.F.; Batista, P.H.D.; de Jesus, F.L.F.; Sanches, A.C.; da Silva, M.V. Spatiotemporal Dynamics of Agricultural Areas with Central Pivot Using Orbital Remote Sensing in the Brazilian Semiarid. Smart Agric. Technol. 2022, 2, 100052. [Google Scholar] [CrossRef]
- Abbaszadeh Afshar, F.; Ayoubi, S.; Jafari, A. The Extrapolation of Soil Great Groups Using Multinomial Logistic Regression at Regional Scale in Arid Regions of Iran. Geoderma 2018, 315, 36–48. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Salazar, L.; Tolisano, J.; Crane, K.; Wheeler, L.; Kuile, M.T.; Radtke, D. Irrigation Reference Manual; Information Collection & Exchange; Peace Corps: Washington, DC, USA, 1994; pp. 85–94. [Google Scholar]
- Jensen, M.E.; Allen, R.G. Evaporation, Evapotranspiration, and Irrigation Water Requirements; ASCE Press: Reston, VA, USA, 2016; pp. 1–744. [Google Scholar] [CrossRef]
- Biggs, T.; Petropoulos, G.P.; Velpuri, N.M.; Marshall, M.; Glenn, E.P.; Nagler, P.; Messina, A. Remote Sensing of Actual Evapotranspiration from Croplands. In Remote Sensing of Water Resources, Disasters, and Urban Studies; Thenkabail, P.S., Ed.; CRC Press: Boca Raton, FL, USA, 2015; pp. 59–100. [Google Scholar]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.F.; Roerink, G.J.; Van Der Wal, T. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL).: Part 2: Validation. J. Hydrol. 1998, 212–213, 213–229. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for Estimation of Turbulent Heat Fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Running, S.W.; Mu, Q.; Zhao, M.; Moreno, A. MODIS Global Terrestrial Evapotranspiration (ET) Product (MOD16A2/A3 and Year-End Gap-Filled MOD16A2GF/A3GF) NASA Earth Observing System MODIS Land Algorithm (for Collection 6); data set; National Aeronautics and Space Administration: Washington, DC, USA, 2019; Volume 6. [CrossRef]
- Drexler, J.Z.; Snyder, R.L.; Spano, D.; Paw, U.K.T. A Review of Models and Micrometeorological Methods Used to Estimate Wetland Evapotranspiration. Hydrol. Process 2004, 18, 2071–2101. [Google Scholar] [CrossRef]
- Allen, R.G.; Trezza, R.; Kilic, A.; Tasumi, M.; Li, H. Sensitivity of Landsat-Scale Energy Balance to Aerodynamic Variability in Mountains and Complex Terrain. J. Am. Water Resour. Assoc. 2013, 49, 592–604. [Google Scholar] [CrossRef]
- Tasumi, M.; Moriyama, M.; Shinohara, Y. Application of GCOM-C SGLI for Agricultural Water Management via Field Evapotranspiration. Paddy Water Environ. 2019, 17, 75–82. [Google Scholar] [CrossRef]
- Tasumi, M.; Moriyama, M. Evapotranspiration Estimation of Urmia Lake Basin Using GCOM-C Thermal Imagery. IOP Conf. Ser. Earth Environ. Sci. 2021, 958, 012010. [Google Scholar] [CrossRef]
- Umeno, H.; Shinohara, Y.; Tasumi, M. Application of the GCOM-C Global ETindex Estimation Algorithm in 40 Forests Located throughout Japan, North America, Australia, and the Tropical Region. J. Agric. Meteorol. 2019, 75, 193–202. [Google Scholar] [CrossRef]
- Tasumi, M.; Moriyama, M.; Hirakawa, K.; Fujii, A. Evaluation of the GCOM-C Global ETindex Estimation Algorithm. J. Agric. Meteorol. 2016, 72, 151–158. [Google Scholar] [CrossRef]
- Da Silva, J.L.B.; da Silva, M.V.; Jardim, A.M.d.R.F.; Lopes, P.M.O.; de Oliveira, H.F.E.; Silva, J.A.O.S.; Mesquita, M.; de Carvalho, A.A.; Cézar Bezerra, A.; de Oliveira-Júnior, J.F.; et al. Geospatial Insights into Aridity Conditions: MODIS Products and GIS Modeling in Northeast Brazil. Hydrology 2024, 11, 32. [Google Scholar] [CrossRef]
- da Silva, J.L.B.; de Albuquerque Moura, G.B.; da Silva, M.V.; de Oliveira-Júnior, J.F.; Jardim, A.M.d.R.F.; Refati, D.C.; Lima, R.d.C.C.; de Carvalho, A.A.; Ferreira, M.B.; de Brito, J.I.B.; et al. Environmental Degradation of Vegetation Cover and Water Bodies in the Semiarid Region of the Brazilian Northeast via Cloud Geoprocessing Techniques Applied to Orbital Data. J. South. Am. Earth Sci. 2023, 121, 104164. [Google Scholar] [CrossRef]
- Tasumi, M.; Kimura, R.; Allen, R.G.; Moriyama, M.; Trezza, R. Development of the GCOM-C Global ETindex Estimation Algorithm. J. Agric. Meteorol. 2016, 72, 85–94. [Google Scholar] [CrossRef]
- Wali, E.; Tasumi, M.; Shinohara, Y.; Takeshita, S. Mapping Crop Types and Crop Water Requirements over Small-Sized Irrigated Fields in the Khost Province of Afghanistan. J. Rainwater Catchment Syst. 2019, 24, 9–15. [Google Scholar] [CrossRef]
- Akhtar, F.; Awan, U.K.; Tischbein, B.; Liaqat, U.W. Assessment of Irrigation Performance in Large River Basins under Data Scarce Environment—A Case of Kabul River Basin, Afghanistan. Remote Sens. 2018, 10, 972. [Google Scholar] [CrossRef]
- De Oliveira Costa, J.; José, J.V.; Wolff, W.; de Oliveira, N.P.R.; Oliveira, R.C.; Ribeiro, N.L.; Coelho, R.D.; da Silva, T.J.A.; Bonfim-Silva, E.M.; Schlichting, A.F. Spatial Variability Quantification of Maize Water Consumption Based on Google EEflux Tool. Agric. Water Manag. 2020, 232, 106037. [Google Scholar] [CrossRef]
- Venancio, L.P.; Eugenio, F.C.; Filgueiras, R.; Da Cunha, F.F.; Dos Santos, R.A.; Ribeiro, W.R.; Mantovan, E.C. Mapping Within-field Variability of Soybean Evapotranspiration and Crop Coefficient Using the Earth Engine Evaporation Flux (EEFlux) Application. PLoS ONE 2020, 15, e0235620. [Google Scholar] [CrossRef] [PubMed]
- Salama, M.A.; Yousef, K.M.; Mostafa, A.Z. Simple Equation for Estimating Actual Evapotranspiration Using Heat Units for Wheat in Arid Regions. J. Radiat. Res. Appl. Sci. 2015, 8, 418–427. [Google Scholar] [CrossRef]
- Wali, E.; Datta, A.; Shrestha, R.P.; Shrestha, S. Development of a Land Suitability Model for Saffron (Crocus sativus L.) Cultivation in Khost Province of Afghanistan Using GIS and AHP Techniques. Arch. Agron. Soil. Sci. 2016, 62, 921–934. [Google Scholar] [CrossRef]
- NASA; METI. AIST, Japan Spacesystems, US/Japan ASTER Science Team. ASTER Global Digital Elevation Model 3; NASA: Washington, DC, USA, 2009; Volume 3.
- Irmak, A.; Allen, R.G.; Kjaersgaard, J.; Huntington, J.; Kamble, B.; Trezza, R.; Ratcliffe, I.; Irmak, A.; Allen, R.G.; Kjaersgaard, J.; et al. Operational Remote Sensing of ET and Challenges. In Evapotranspiration-Remote Sensing and Modeling; InTech Open: London, UK, 2012. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Brutsaert, W.; Stricker, H. An Advection-Aridity Approach to Estimate Actual Regional Evapotranspiration. Water Resour. Res. 1979, 15, 443–450. [Google Scholar] [CrossRef]
- Liaqat, U.W.; Choi, M.; Awan, U.K. Spatio-Temporal Distribution of Actual Evapotranspiration in the Indus Basin Irrigation System. Hydrol. Process 2015, 29, 2613–2627. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A Review of Current Methodologies for Regional Evapotranspiration Estimation from Remotely Sensed Data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef]
- Stancalie, G.; Marica, A.; Toulios, L. Using Earth Observation Data and CROPWAT Model to Estimate the Actual Crop Evapotranspiration. Phys. Chem. Earth 2010, 35, 25–30. [Google Scholar] [CrossRef]
- Tasumi, M. Estimating Evapotranspiration Using METRIC Model and Landsat Data for Better Understandings of Regional Hydrology in the Western Urmia Lake Basin. Agric. Water Manag. 2019, 226, 105805. [Google Scholar] [CrossRef]
- Djaman, K.; Irmak, S. Actual Crop Evapotranspiration and Alfalfa- and Grass-Reference Crop Coefficients of Maize under Full and Limited Irrigation and Rainfed Conditions. J. Irrig. Drain. Eng. 2012, 139, 433–446. [Google Scholar] [CrossRef]
- Djaman, K.; Mel, V.C.; Balde, A.B.; Bado, B.V.; Manneh, B.; Diop, L.; Mutiibwa, D.; Rudnick, D.R.; Irmak, S.; Futakuchi, K. Evapotranspiration, Irrigation Water Requirement, and Water Productivity of Rice (Oryza sativa L.) in the Sahelian Environment. Paddy Water Environ. 2017, 15, 469–482. [Google Scholar] [CrossRef]
- Kim, H.W.; Hwang, K.; Mu, Q.; Lee, S.O.; Choi, M. Validation of MODIS 16 Global Terrestrial Evapotranspiration Products in Various Climates and Land Cover Types in Asia. KSCE J. Civ. Eng. 2012, 16, 229–238. [Google Scholar] [CrossRef]
- Jahangir, M.H.; Arast, M. Remote Sensing Products for Predicting Actual Evapotranspiration and Water Stress Footprints under Different Land Cover. J. Clean Prod. 2020, 266, 121818. [Google Scholar] [CrossRef]
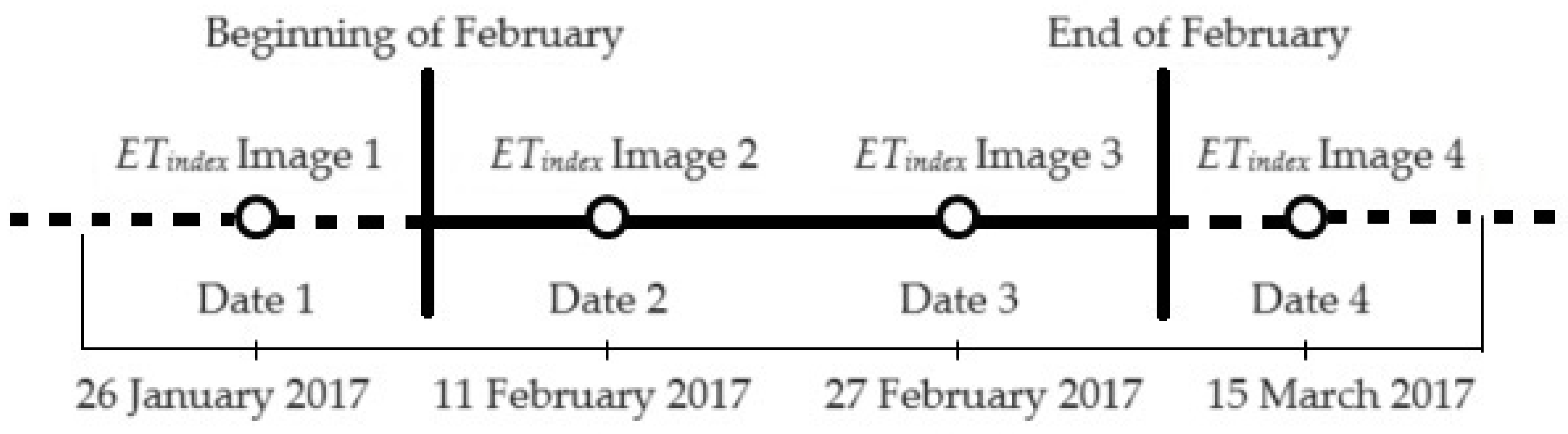

| Image # | Date | Usage | Image # | Date | Usage |
|---|---|---|---|---|---|
| 1 | 7 November 16 | Used | 13 | 18 May 17 | Not used |
| 2 | 23 November 16 | Used | 14 | 3 June 17 | Used |
| 3 | 9 December 16 | Used | 15 | 19 June 17 | Used |
| 4 | 25 December 16 | Used | 16 | 5 July 17 | Used |
| 5 | 10 January17 | Used | 17 | 21 July 17 | Not used |
| 6 | 26 January 17 | Used | 18 | 6 August 17 | Limited use |
| 7 | 11 February 17 | Limited use | 19 | 22 August 17 | Not used |
| 8 | 27 February 17 | Used | 20 | 7 September 17 | Limited use |
| 9 | 15 March 17 | Used | 21 | 23 September 17 | Used |
| 10 | 31 March 17 | Not used | 22 | 9 October 17 | Used |
| 11 | 16 April 17 | Used | 23 | 25 October 17 | Used |
| 12 | 2 May 17 | Used |
| Months | Wheat | Maize | Rice | Orchards | Bare Soil |
|---|---|---|---|---|---|
| November 2016 | 16 | 18 | 22 | 60 | 48 |
| December 2016 | 39 | 40 | 54 | 20 | 12 |
| January 2017 | 43 | 45 | 48 | 44 | 45 |
| February 2017 | 70 | 75 | 77 | 48 | 39 |
| March 2017 | 110 | 115 | 118 | 81 | 18 |
| April 2017 | 175 | 160 | 165 | 131 | 12 |
| May 2017 | 111 | 108 | 90 | 189 | 26 |
| June 2017 | 98 | 95 | 170 | 196 | 43 |
| July 2017 | 112 | 110 | 158 | 180 | 87 |
| August 2017 | 175 | 183 | 164 | 160 | 50 |
| September 2017 | 148 | 151 | 127 | 87 | 20 |
| October 2017 | 71 | 67 | 80 | 25 | 10 |
| Total ETa/Season | 564 | 606 | 789 | 1221 | 410 |
| Paired Differences | t | df | Sig. (2-Tailed) | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std. Error Mean | 95% Confidence Interval of the Difference | ||||||
| Lower | Upper | |||||||
| Pair 1 | GCOM-C—METRIC | 2.88 | 2.33 | −1.82 | 7.58 | 1.23 | 41 | 0.22 |
| Pair 2 | GCOM-C—MOD16 | 68.13 | 7.82 | 52.32 | 83.94 | 8.70 | 41 | 0.00 |
| Pair 3 | GCOM-C—SEBS | 32.98 | 6.29 | 20.26 | 45.70 | 5.23 | 41 | 0.00 |
| Pair 4 | GCOM-C—FAO-56 | 2.75 | 2.13 | −1.55 | 7.07 | 1.29 | 41 | 0.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wali, E.; Tasumi, M.; Klemm, O. Estimation of Evapotranspiration in South Eastern Afghanistan Using the GCOM-C Algorithm on the Basis of Landsat Satellite Imagery. Hydrology 2024, 11, 95. https://doi.org/10.3390/hydrology11070095
Wali E, Tasumi M, Klemm O. Estimation of Evapotranspiration in South Eastern Afghanistan Using the GCOM-C Algorithm on the Basis of Landsat Satellite Imagery. Hydrology. 2024; 11(7):95. https://doi.org/10.3390/hydrology11070095
Chicago/Turabian StyleWali, Emal, Masahiro Tasumi, and Otto Klemm. 2024. "Estimation of Evapotranspiration in South Eastern Afghanistan Using the GCOM-C Algorithm on the Basis of Landsat Satellite Imagery" Hydrology 11, no. 7: 95. https://doi.org/10.3390/hydrology11070095
APA StyleWali, E., Tasumi, M., & Klemm, O. (2024). Estimation of Evapotranspiration in South Eastern Afghanistan Using the GCOM-C Algorithm on the Basis of Landsat Satellite Imagery. Hydrology, 11(7), 95. https://doi.org/10.3390/hydrology11070095






