CMIP5 Decadal Precipitation over an Australian Catchment
Abstract
1. Introduction
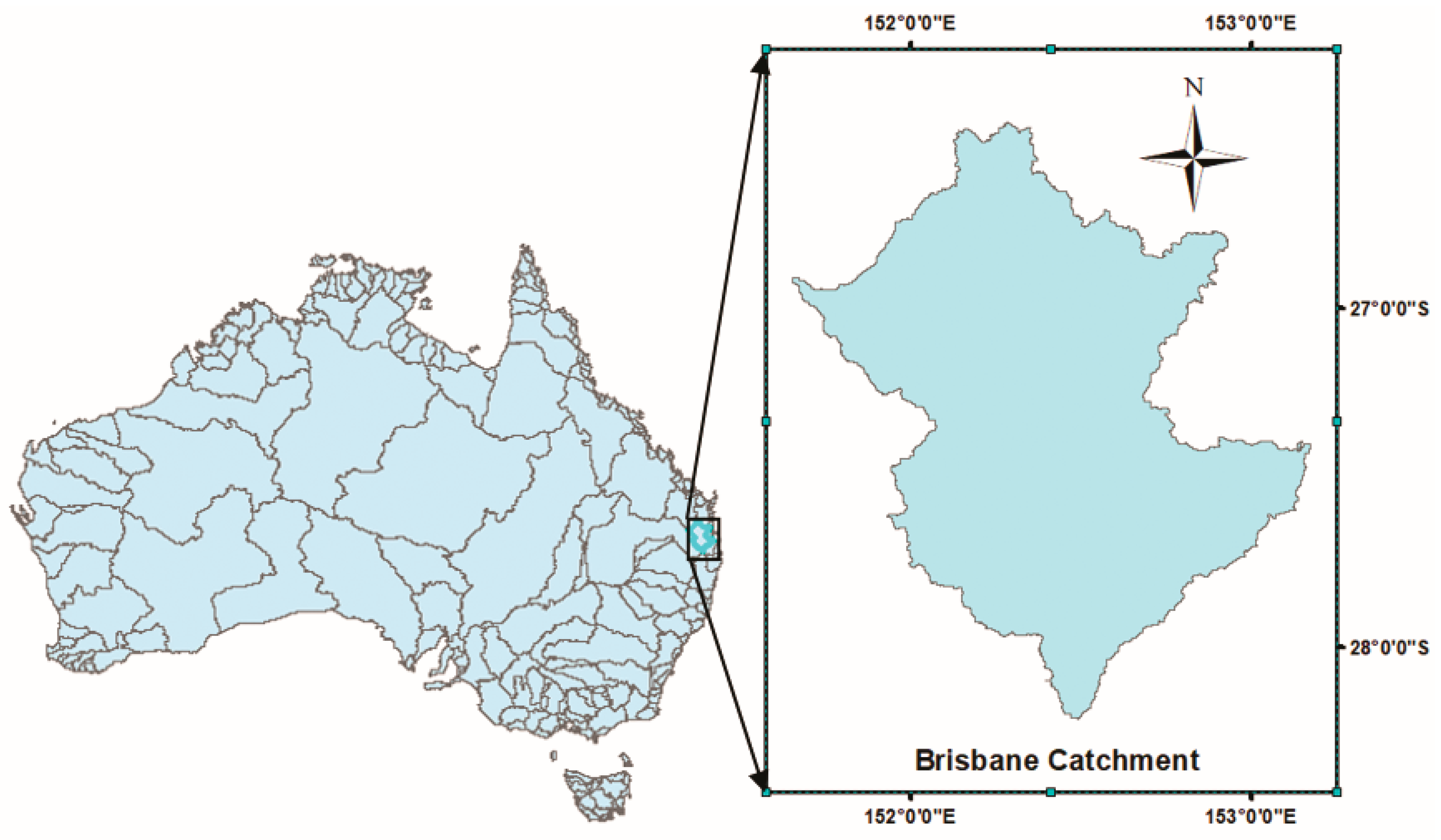
2. Study Area
3. Data Collection and Processing
3.1. Data Collection
3.2. Data Processing
4. Methodology
4.1. Correlation Coefficient (CC)
4.2. Anomaly Correlation Coefficient (ACC)
4.3. Index of Agreement (IA)
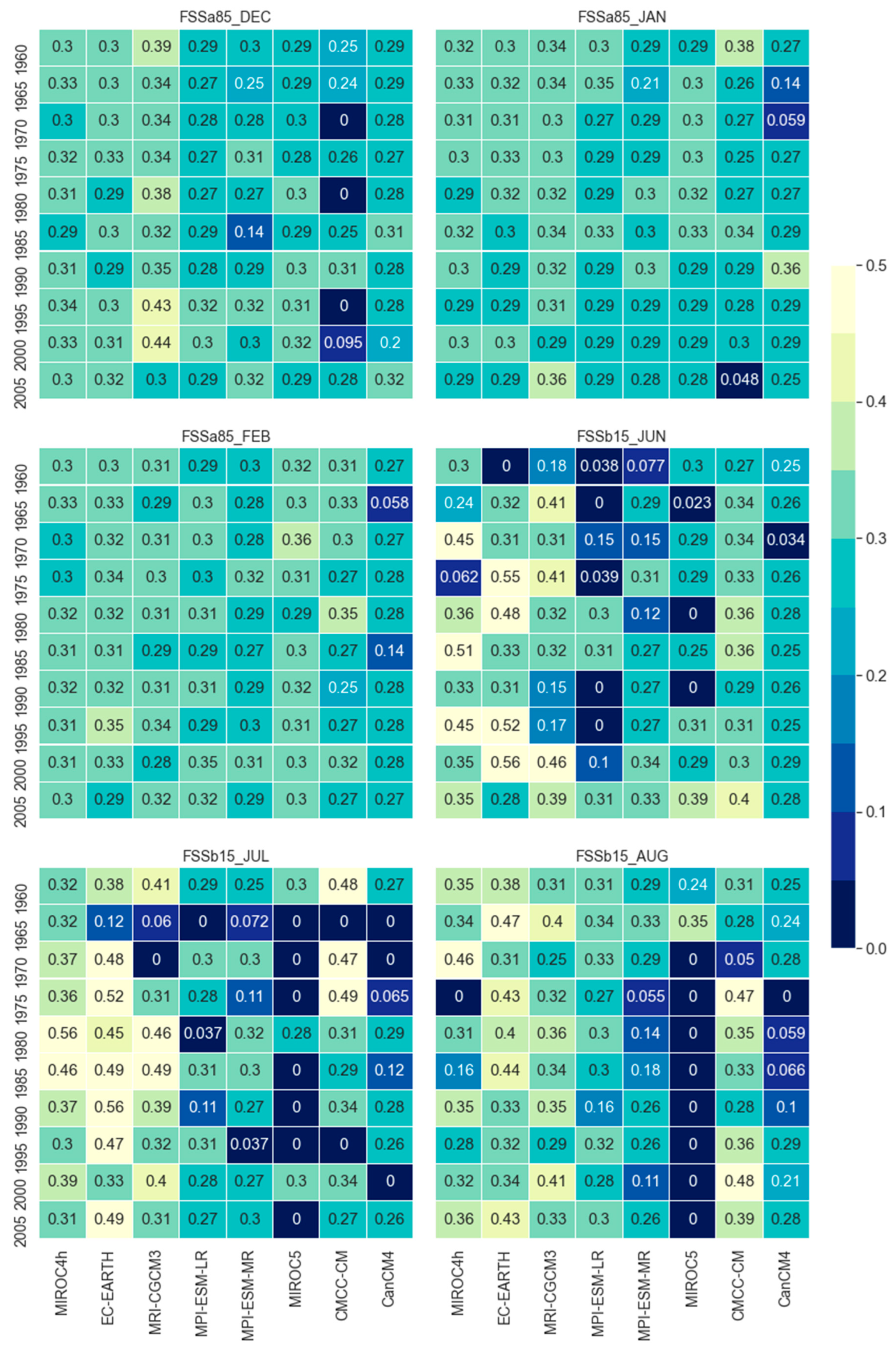
4.4. Fractional Skill Score (FSS)
4.5. Field-Sum and Total-Sum
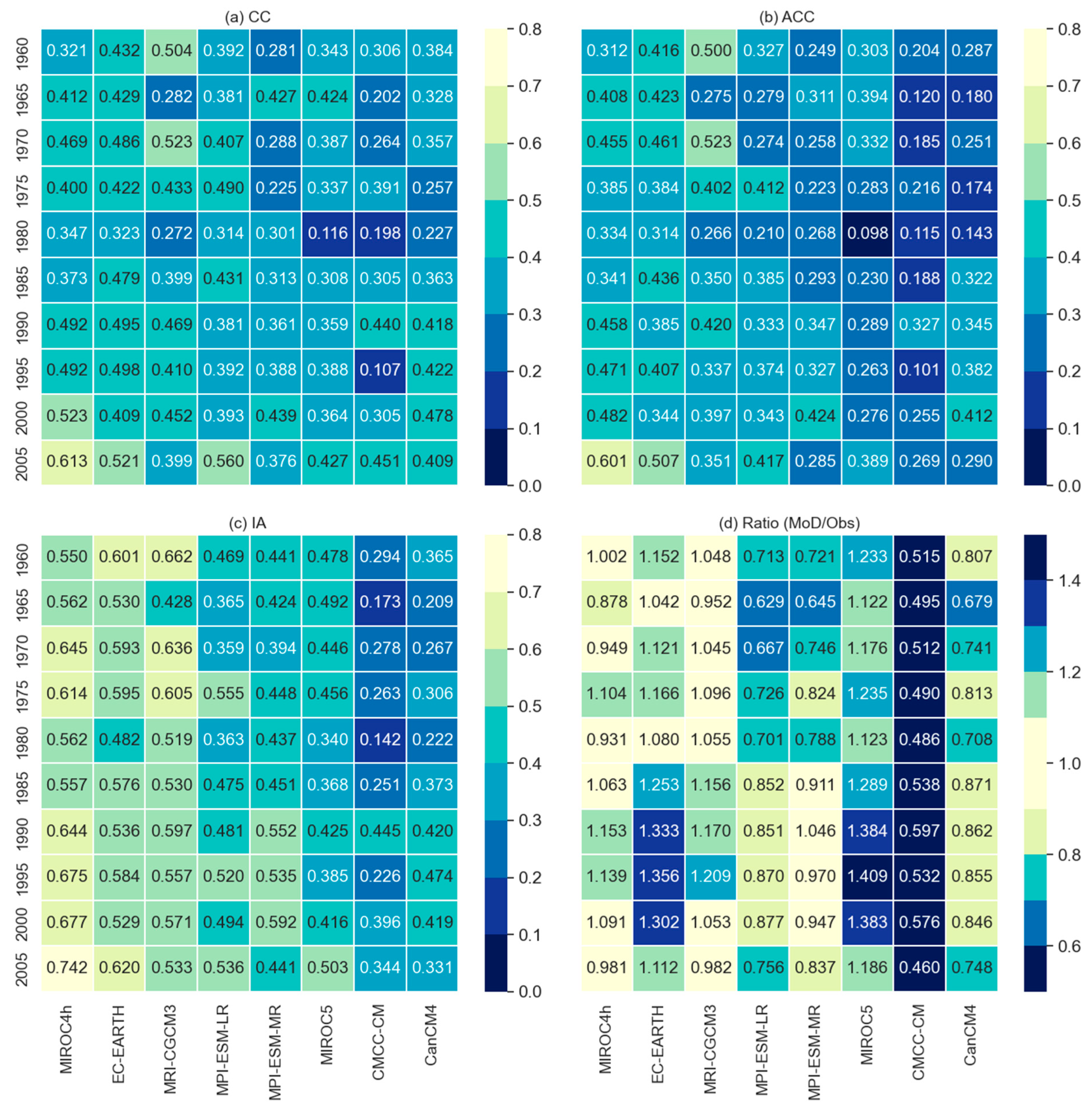
5. Results and Analysis
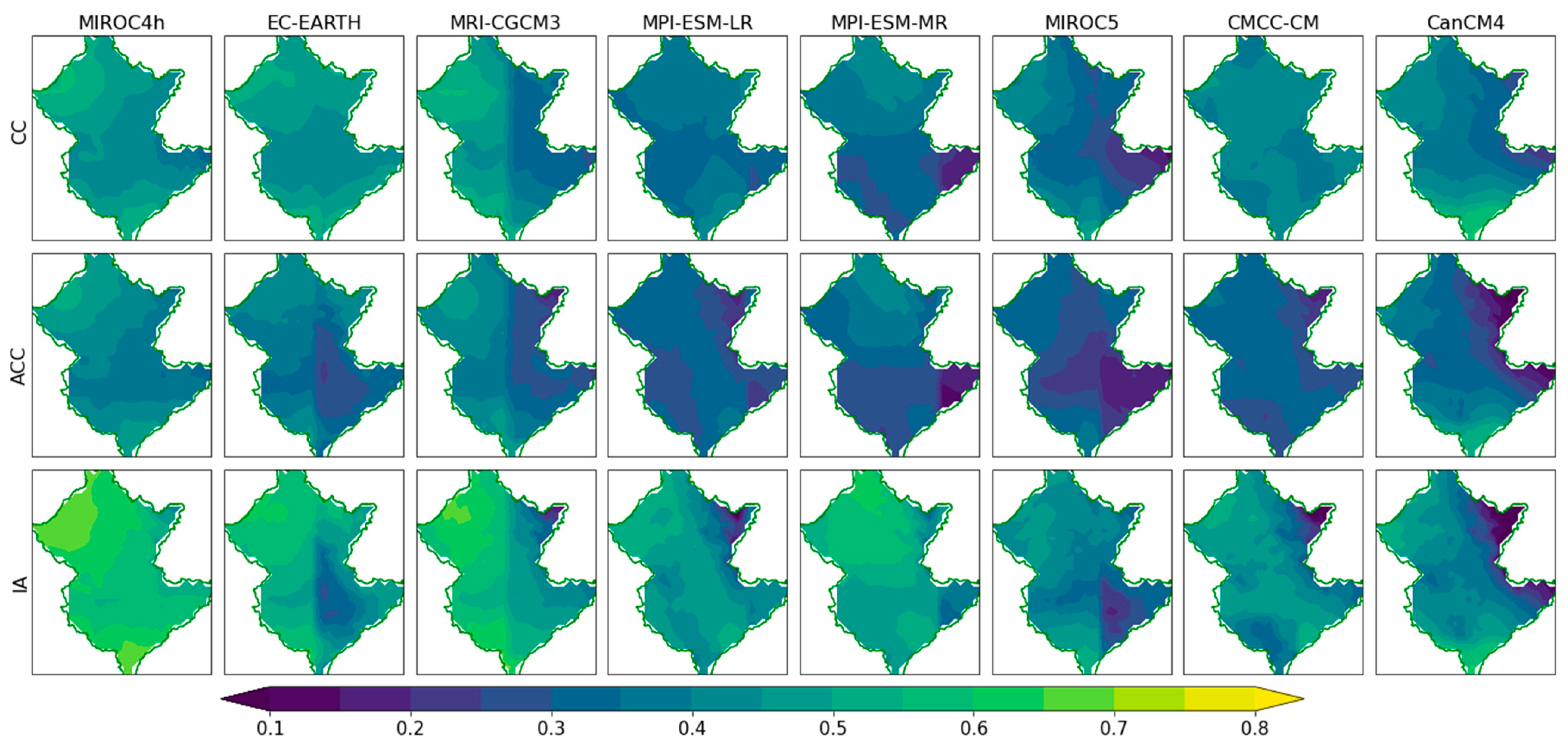
5.1. Temporal Skills
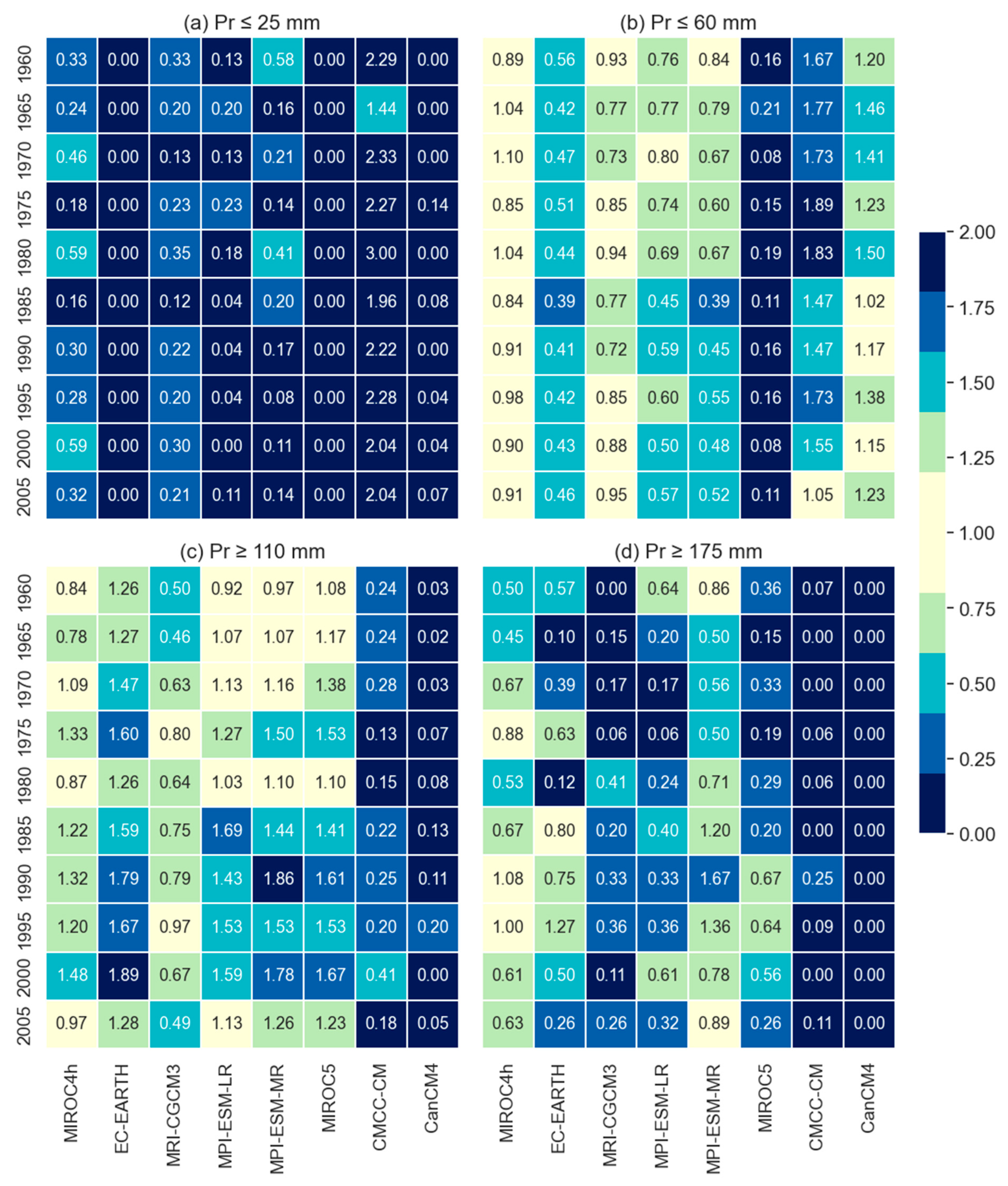
5.2. Evaluation for Dry and Wet Periods
5.2.1. At the Selected Grid
5.2.2. Over the Entire Catchment
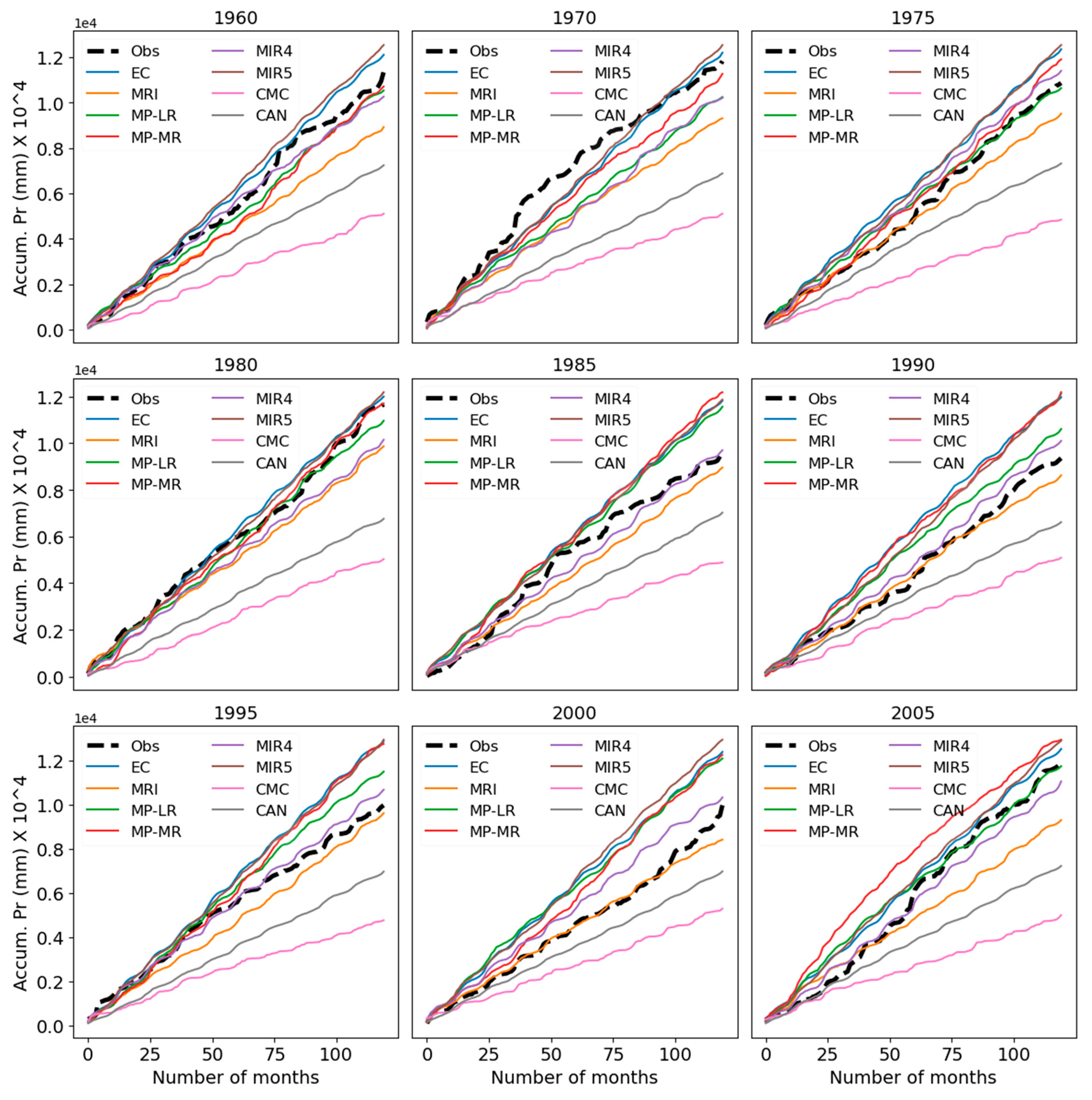
5.3. Evaluation for Total Precipitation
5.3.1. At the Selected Grid
5.3.2. Over the Entire Catchment
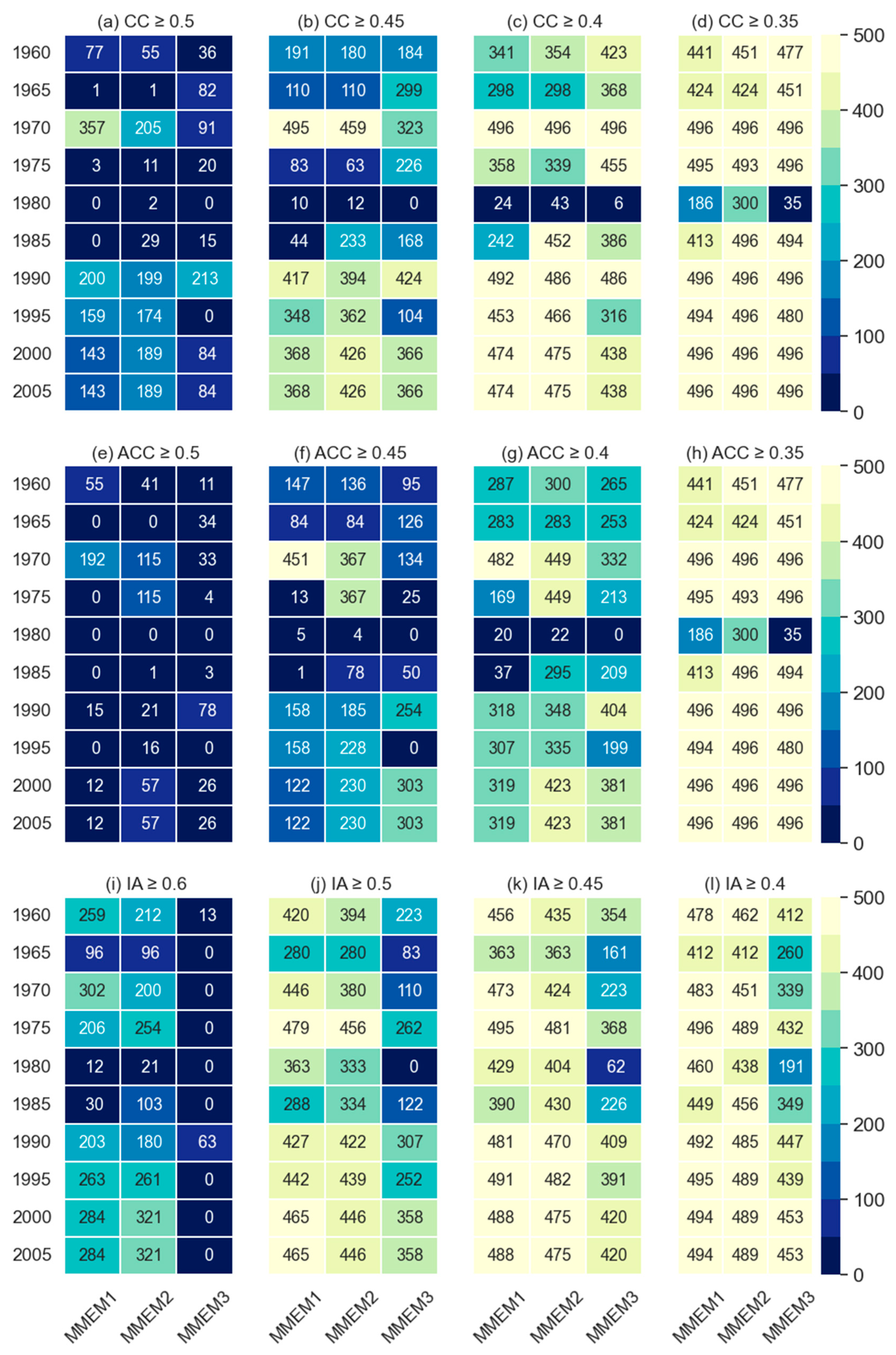
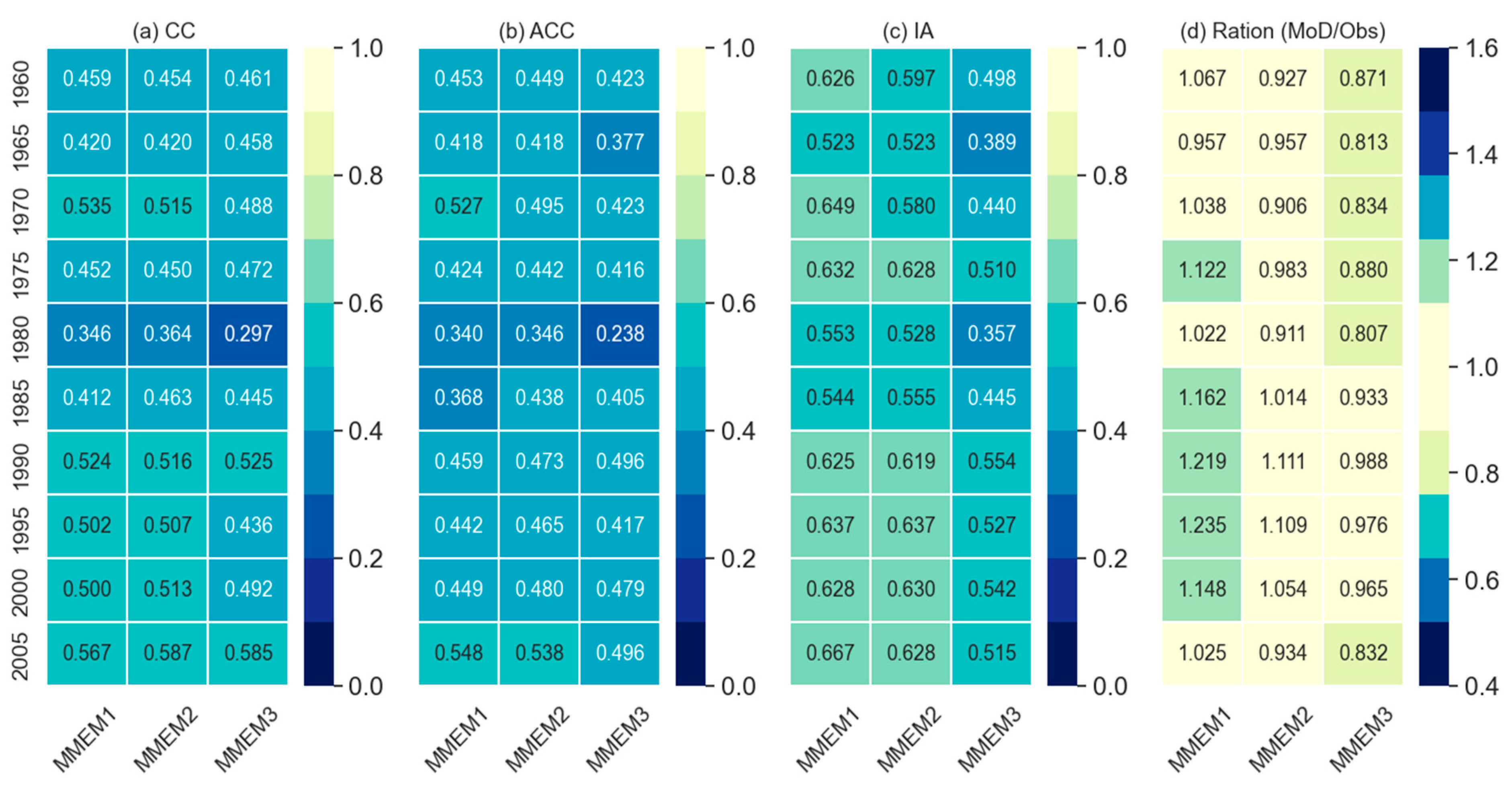
5.4. Model Categorisation and Formulation of MMEM
5.5. Performance of MMEMs
6. Discussion
7. Conclusions
- Models with higher atmospheric resolutions showed comparatively better performances as opposed to the models of coarse spatial resolutions.
- Model performances varied over the initialization years and across the catchment. From 1990 onward, the skills of all models improved across the catchment, where MIROC4h showed the highest skills followed by EC-EARTH and MRI-CGCM3, respectively. The internal structure of high atmospheric resolutions may be the main reason for MIROC4h reproducing the local climate variables comparatively better than the other.
- To reproduce the dry events and total precipitation over the entire catchment, EC-EARTH and MRI-CGCM3, respectively, outperformed all models, while CMCC-CM showed the lowest scores in all forms of skills. For capturing the wet periods, all models showed almost similar skills with little exceptions for CMCC-CM and CanCM4 but for the dry periods, models showed a range of skill scores.
- Based on the performance skills, the GCM models were ranked into three categories in ascending order: Category-I (MIROC4h, EC-EARTH, and MRI-CGCM3), Category-II (MPI-ESM-LR and MPI-ESM-MR), and Category-III (MIROC5, CanCM4, and CMCC-CM). MMEMs were formulated as MMEM1 of Category-I models, MMEM2 combining Category-I and Category-II models, and MMEM3 as the combination of all three categories. Out of these three different MMEMs, MMEM2 was found to perform better than other MMEMs based on the overall skills, but MMEM1 performed relatively better for the case of extreme wet events. This shows the necessity of forming suitable MMEM for practical purposes of GCM data use, especially for the decadal precipitation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Flato, G.; Marotzke, J.; Abiodun, B.; Braconnot, P.; Chou, S.C.; Collins, W.; Cox, P.; Driouech, F.; Emori, S.; Eyring, V.; et al. Evaluation of Climate Models. In Climate Change 2013—The Physical Science Basis; Intergovernmental Panel on Climate Change, Ed.; Cambridge University Press: Cambridge, UK, 2013; Volume 9781107057, pp. 741–866. [Google Scholar]
- Kumar, S.; Merwade, V.; Kinter, J.L.; Niyogi, D. Evaluation of temperature and precipitation trends and long-term persistence in CMIP5 twentieth-century climate simulations. J. Clim. 2013, 26, 4168–4185. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Choi, J.; Son, S.W.; Ham, Y.G.; Lee, J.Y.; Kim, H.M. Seasonal-to-interannual prediction skills of near-surface air temperature in the CMIP5 decadal hindcast experiments. J. Clim. 2016, 29, 1511–1527. [Google Scholar] [CrossRef]
- Lovino, M.A.; Müller, O.V.; Berbery, E.H.; Müller, G.V. Evaluation of CMIP5 retrospective simulations of temperature and precipitation in northeastern Argentina. Int. J. Climatol. 2018, 38, e1158–e1175. [Google Scholar] [CrossRef]
- McKellar, C.; Cordero, E.C.; Bridger, A.F.C.; Thrasher, B. Evaluation of the CMIP5 Decadal Hindcasts in the State of California. Master’s Thesis, San José State University, San Jose, CA, USA, 2013. [Google Scholar]
- Gaetani, M.; Mohino, E. Decadal prediction of the sahelian precipitation in CMIP5 simulations. J. Clim. 2013, 26, 7708–7719. [Google Scholar] [CrossRef]
- Mehrotra, R.; Sharma, A.; Bari, M.; Tuteja, N.; Amirthanathan, G. An assessment of CMIP5 multi-model decadal hindcasts over Australia from a hydrological viewpoint. J. Hydrol. 2014, 519, 2932–2951. [Google Scholar] [CrossRef]
- Choudhury, D.; Mehrotra, R.; Sharma, A.; Gupta, A.S.; Sivakumar, B. Effectiveness of CMIP5 Decadal Experiments for Interannual Rainfall Prediction Over Australia. Water Resour. Res. 2019, 55, 7400–7418. [Google Scholar] [CrossRef]
- Bhend, J.; Whetton, P. Evaluation of simulated recent climate change in Australia. Aust. Meteorol. Oceanogr. J. 2015, 65, 4–18. [Google Scholar] [CrossRef]
- Moise, A.; Wilson, L.; Grose, M.; Whetton, P.; Watterson, I.; Bhend, J.; Bathols, J.; Hanson, L.; Erwin, T.; Bedin, T.; et al. Evaluation of CMIP3 and CMIP5 Models over the Australian Region to Inform Confidence in Projections. Aust. Meteorol. Oceanogr. J. 2015, 65, 19–53. [Google Scholar] [CrossRef]
- Hossain, M.M.; Garg, N.; Anwar, A.H.M.F.; Prakash, M.; Bari, M. Intercomparison of drift correction alternatives for CMIP5 decadal precipitation. Int. J. Clim. 2021, 42, 1015–1037. [Google Scholar] [CrossRef]
- Hossain, M.M.; Garg, N.; Anwar, A.H.M.F.; Prakash, M.; Bari, M. Drift in CMIP5 decadal precipitation at catchment level. Stoch. Environ. Res. Risk Assess. 2021, 8, 5. [Google Scholar] [CrossRef]
- Choudhury, D.; Sharma, A.; Gupta, A.S.; Mehrotra, R.; Sivakumar, B. Sampling biases in CMIP5 decadal forecasts. J. Geophys. Res. Atmos. 2016, 121, 3435–3445. [Google Scholar] [CrossRef]
- Knutti, R.; Furrer, R.; Tebaldi, C.; Cermak, J.; Meehl, G.A. Challenges in Combining Projections from Multiple Climate Models. J. Clim. 2010, 23, 2739–2758. [Google Scholar] [CrossRef]
- McSweeney, C.F.; Jones, R.G.; Lee, R.W.; Rowell, D.P. Selecting CMIP5 GCMs for downscaling over multiple regions. Clim. Dyn. 2015, 44, 3237–3260. [Google Scholar] [CrossRef]
- Islam, S.A.; Bari, M.A.; Anwar, A.H.M.F. Hydrologic impact of climate change on Murray-Hotham catchment of Western Australia: A projection of rainfall-runoff for future water resources planning. Hydrol. Earth Syst. Sci. 2014, 18, 3591–3614. [Google Scholar] [CrossRef]
- Sheffield, J.; Camargo, S.J.; Fu, R.; Hu, Q.; Jiang, X.; Johnson, N.; Karnauskas, K.B.; Kim, S.T.; Kinter, J.; Kumar, S.; et al. North American Climate in CMIP5 Experiments. Part II: Evaluation of Historical Simulations of Intraseasonal to Decadal Variability. J. Clim. 2013, 26, 9247–9290. [Google Scholar] [CrossRef]
- Meehl, G.A.; Teng, H. CMIP5 multi-model hindcasts for the mid-1970s shift and early 2000s hiatus and predictions for 2016–2035. Geophys. Res. Lett. 2014, 41, 1711–1716. [Google Scholar] [CrossRef]
- Hossain, M.M.; Garg, N.; Anwar, A.H.M.F.; Prakash, M.; Bari, M. A comparative study on 10 and 30-year simulation of CMIP5 decadal hindcast precipitation at catchment level. In Proceedings of the MODSIM2021, 24th International Congress on Modelling and Simulation, Sydney, NSW, Australia, 5–10 December 2021; pp. 609–615. [Google Scholar] [CrossRef]
- Frost, A.J.; Ramchurn, A.; Smith, A. The Bureau’s Operational AWRA Landscape (AWRA-L) Model; Bureau of Meteorology Technical Report; Australian Government, Bureau of Meteorology: Melbourne, Australia, 2016.
- Salathé, E.P. Comparison of various precipitation downscaling methods for the simulation of streamflow in a rainshadow river basin. Int. J. Climatol. 2003, 23, 887–901. [Google Scholar] [CrossRef]
- Grotch, S.L.; MacCracken, M.C. The Use of General Circulation Models to Predict Regional Climatic Change. J. Clim. 1991, 4, 286–303. [Google Scholar] [CrossRef]
- Fowler, H.J.; Blenkinsop, S.; Tebaldi, C. Linking climate change modelling to impacts studies: Recent advances in downscaling techniques for hydrological modelling. Int. J. Climatol. 2007, 27, 1547–1578. [Google Scholar] [CrossRef]
- Hossain, M.M.; Garg, N.; Anwar, A.H.M.F.; Prakash, M. Comparing Spatial Interpolation Methods for CMIP5 Monthly Precipitation at Catchment Scale. Indian Water Resour. Soc. 2021, 41, 28–34. [Google Scholar]
- Skelly, W.C.; Henderson-Sellers, A. Grid box or grid point: What type of data do GCMs deliver to climate impacts researchers? Int. J. Climatol. 1996, 16, 1079–1086. [Google Scholar] [CrossRef]
- Jones, P.W. First- and Second-Order Conservative Remapping Schemes for Grids in Spherical Coordinates. Mon. Weather Rev. 1999, 127, 2204–2210. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2011; Volume 100, 676p. [Google Scholar]
- Wilmot, C.J. Some Comments on the Evaluation of Model Performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Roberts, N.M.; Lean, H.W. Scale-selective verification of rainfall accumulations from high-resolution forecasts of convective events. Mon. Weather Rev. 2008, 136, 78–97. [Google Scholar] [CrossRef]
- Jain, S.; Salunke, P.; Mishra, S.K.; Sahany, S. Performance of CMIP5 models in the simulation of Indian summer monsoon. Theor. Appl. Climatol. 2019, 137, 1429–1447. [Google Scholar] [CrossRef]
- Sakamoto, T.T.; Komuro, Y.; Nishimura, T.; Ishii, M.; Tatebe, H.; Shiogama, H.; Hasegawa, A.; Toyoda, T.; Mori, M.; Suzuki, T.; et al. MIROC4h-A new high-resolution atmosphere-ocean coupled general circulation model. J. Meteorol. Soc. Jpn. 2012, 90, 325–359. [Google Scholar] [CrossRef]
- Purwaningsih, A.; Hidayat, R. Performance of Decadal Prediction in Coupled Model Intercomparisson Project Phase 5 (CMIP5) on Projecting Climate in Tropical Area. Procedia Environ. Sci. 2016, 33, 128–139. [Google Scholar] [CrossRef]
- Homsi, R.; Shiru, M.S.; Shahid, S.; Ismail, T.; Bin Harun, S.; Al-Ansari, N.; Chau, K.-W.; Yaseen, Z.M. Precipitation projection using a CMIP5 GCM ensemble model: A regional investigation of Syria. Eng. Appl. Comput. Fluid Mech. 2020, 14, 90–106. [Google Scholar] [CrossRef]
- Kamworapan, S.; Surussavadee, C. Evaluation of CMIP5 global climate models for simulating climatological temperature and precipitation for southeast Asia. Adv. Meteorol. 2019, 2019, 1067365. [Google Scholar] [CrossRef]
- Kumar, D.; Kodra, E.; Ganguly, A.R. Regional and seasonal intercomparison of CMIP3 and CMIP5 climate model ensembles for temperature and precipitation. Clim. Dyn. 2014, 43, 2491–2518. [Google Scholar] [CrossRef]
- Ta, Z.; Yu, Y.; Sun, L.; Chen, X.; Mu, G.; Yu, R. Assessment of Precipitation Simulations in Central Asia by CMIP5 Climate Models. Water 2018, 10, 1516. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Lucas-Picher, P.; Caya, D. Impacts of weighting climate models for hydro-meteorological climate change studies. J. Hydrol. 2017, 549, 534–546. [Google Scholar] [CrossRef]
- Meehl, G.A.; Teng, H.; Maher, N.; England, M.H. Effects of the Mount Pinatubo eruption on decadal climate prediction skill of Pacific sea surface temperatures. Geophys. Res. Lett. 2015, 42, 10840–10846. [Google Scholar] [CrossRef]


| Model Name (Modelling Center or Group) Resolutions: ° lon × ° lat | Initialization Year (1960–2005) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 00 | 05 | |
| Number of Ensembles | ||||||||||
| EC-EARTH (EC-EARTH Consortium) 1.125 × 1.1215 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 10 | 18 |
| MRI-CGCM3 (Meteorological Research Institute) 1.125 × 1.1215 | 06 | 08 | 09 | 09 | 06 | 09 | 09 | 09 | 09 | 06 |
| MPI-ESM-LR (Max Planck Institute for Meteorology) 1.875 × 1.865 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| MPI-ESM-MR (Max Planck Institute for Meteorology) 1.875 × 1.865 | 03 | 03 | 03 | 03 | 03 | 03 | 03 | 03 | 03 | 03 |
| MIROC4h (AORI-Tokyo University, NIES and JAMEST) 0.5625 × 0.5616 | 03 | 03 | 03 | 06 | 06 | 06 | 06 | 06 | 06 | 06 |
| MIROC5 (AORI-Tokyo University, NIES and JAMEST) 1.4062 × 1.4007 | 06 | 06 | 06 | 06 | 04 | 06 | 06 | 06 | 06 | 06 |
| CanCM4 (Canadian Centre for Climate Modelling and Analysis) 2.8125 × 2.7905 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 |
| CMCC-CM (Centro Euro-Mediterraneo per I Cambiamenti Climatici) 0.75 × 0.748 | 03 | 03 | 03 | 03 | 03 | 03 | 03 | 03 | 03 | 03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, M.M.; Anwar, A.H.M.F.; Garg, N.; Prakash, M.; Bari, M.A. CMIP5 Decadal Precipitation over an Australian Catchment. Hydrology 2024, 11, 24. https://doi.org/10.3390/hydrology11020024
Hossain MM, Anwar AHMF, Garg N, Prakash M, Bari MA. CMIP5 Decadal Precipitation over an Australian Catchment. Hydrology. 2024; 11(2):24. https://doi.org/10.3390/hydrology11020024
Chicago/Turabian StyleHossain, Md Monowar, A. H. M. Faisal Anwar, Nikhil Garg, Mahesh Prakash, and Mohammed Abdul Bari. 2024. "CMIP5 Decadal Precipitation over an Australian Catchment" Hydrology 11, no. 2: 24. https://doi.org/10.3390/hydrology11020024
APA StyleHossain, M. M., Anwar, A. H. M. F., Garg, N., Prakash, M., & Bari, M. A. (2024). CMIP5 Decadal Precipitation over an Australian Catchment. Hydrology, 11(2), 24. https://doi.org/10.3390/hydrology11020024







