Next Article in Journal
The Development of a Hydrological Method for Computing Extreme Hydrographs in Engineering Dam Projects
Previous Article in Journal
A Simple Neural Network for Estimating Fine Sediment Sources Using XRF and XRD
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Hydrology
Volume 11
Issue 11
10.3390/hydrology11110193
hydrology-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Importance of Solving Subglaciar Hydrology in Modeling Glacier Retreat: A Case Study of Hansbreen, Svalbard

by
Eva De Andrés
1,*,†,
José M. Muñoz-Hermosilla
2,†,
Kaian Shahateet
3 and
Jaime Otero
1,4
1
Department of Applied Mathematics, ETSI de Telecomunicación, Universidad Politécnica de Madrid, 28040 Madrid, Spain
2
Institute of Science and Technology Austria (ISTA), 3400 Klosterneuburg, Austria
3
CNRS, IRD, Grenoble INP, IGE, Université Grenoble Alpes, 38031 Grenoble, France
4
School of GeoSciences, University of Edinburgh, Edinburgh EH8 9XP, UK
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Hydrology 2024, 11(11), 193; https://doi.org/10.3390/hydrology11110193
Submission received: 1 October 2024 / Revised: 6 November 2024 / Accepted: 9 November 2024 / Published: 12 November 2024
(This article belongs to the Section Hydrological and Hydrodynamic Processes and Modelling)
Browse Figures
Review Reports Versions Notes

Abstract

Arctic tidewater glaciers are retreating, serving as key indicators of global warming. This study aims to assess how subglacial hydrology affects glacier front retreat by comparing two glacier–fjord models of the Hansbreen glacier: one incorporating a detailed subglacial hydrology model and another simplifying the subglacial discharge to a single channel centered in the flow line. We first validate the subglacial hydrology model by comparing its discharge channels with observations of plume activity. Simulations conducted from April to December 2010 revealed that the glacier front position aligns more closely with the observations in the coupled model than in the simplified version. Furthermore, the mass loss due to calving and submarine melting is greater in the coupled model, with the calving mass loss reaching 6 Mt by the end of the simulation compared to 4 Mt in the simplified model. These findings highlight the critical role of subglacial hydrology in predicting glacier dynamics and emphasize the importance of detailed modeling in understanding the responses of Arctic tidewater glaciers to climate change.

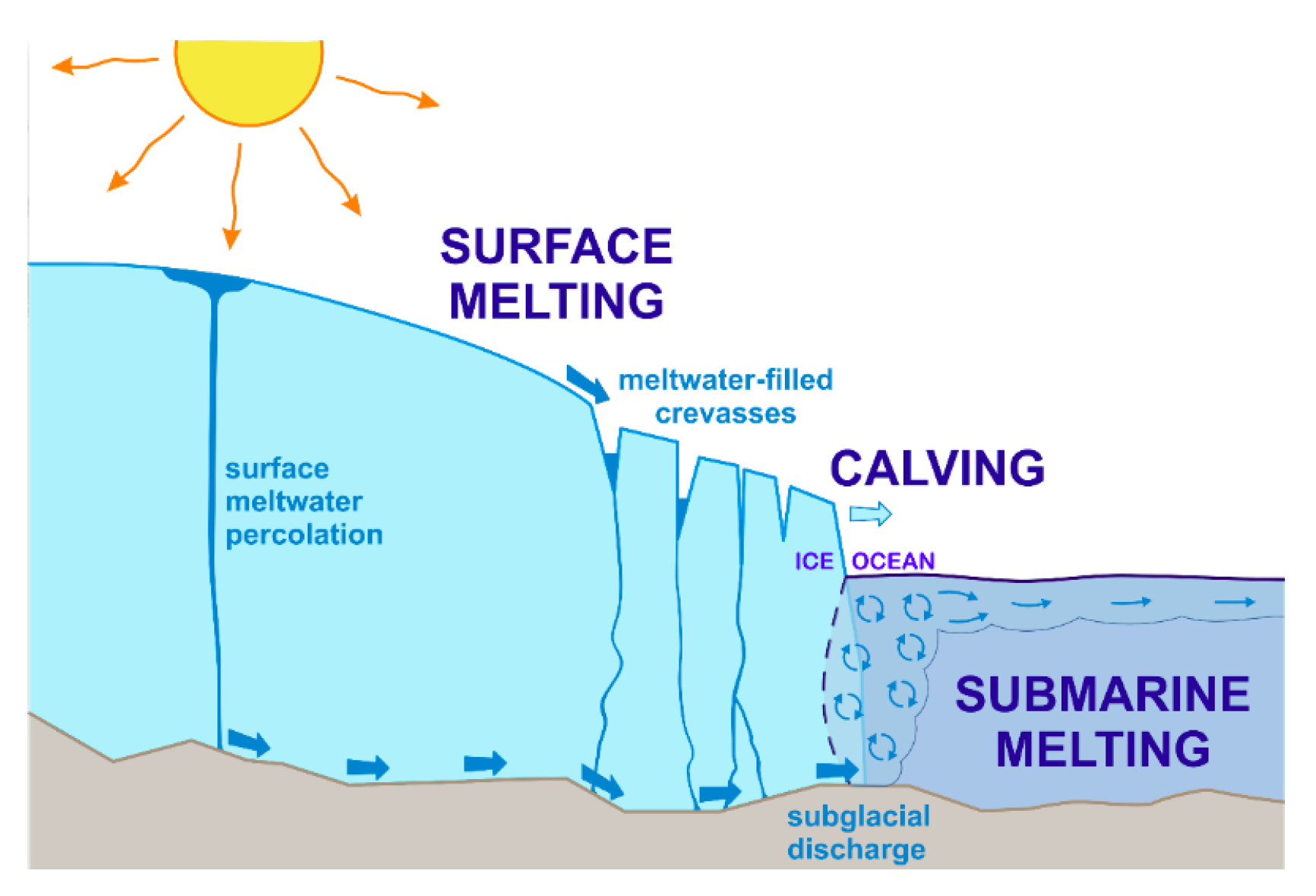
1. Introduction

Global warming and Arctic atlantification are driving significant changes in the polar regions [1,2], with implications for the stability of Arctic tidewater glaciers [3,4]. The retreat of these glaciers serves as a critical climate indicator, reflecting the impacts of rising atmospheric and oceanic temperatures [5,6,7,8,9].
The primary mechanisms of glacier mass loss include surface melting, iceberg calving, and submarine melting [10,11,12], all of which interact through different processes to influence glacier dynamics (Figure 1). During the melt season, positive degree days, characterized by atmospheric temperatures above freezing, lead to surface melting in Arctic tidewater glaciers [9]. As the glacier surface melts, the resulting meltwater percolates through the ice and reaches the subglacial bedrock, flowing toward the glacier terminus. This meltwater is subglacially discharged into the denser fjord waters and then forms a buoyant plume, which entrains the surrounding ambient fjord waters and carries sediments up to the fjord surface [13,14,15]. The rising plume generates overturning circulation within the fjord, effectively drawing warmer out-fjord waters toward the glacier terminus [16,17,18]. The influx of these warmer waters along with the flux of subglacial discharges enhance submarine melting at the glacier terminus [19,20,21,22,23], which in turn amplifies calving events [7,17,24,25,26,27] (see schematics in Figure 1).
The complex interplay between surface melting, subglacial flow, and fjord dynamics, along with their dependence on ambient factors such as atmospheric conditions, ocean temperatures, and bedrock topography, highlight the challenges in identifying the mechanisms driving glacier retreat in response to changing conditions. In this context, we pay special attention to the subglacial hydrology system, which is crucial for determining the number, width, and flow rate of discharging channels [28,29,30], thereby playing a key role in frontal ablation [31]. Moreover, the flow of meltwater beneath glaciers plays a critical role in influencing ice dynamics, including ice flow velocity and stability [32]. As the atmosphere warms during the melt season, the increased surface melting generates more meltwater, which can accumulate at the glacier base [33]. This meltwater can lubricate the bedrock, accelerating the ice flow toward the terminus [34,35,36], thus favoring calving by shear stress.
The formation of subglacial channels is a dynamic process that evolves throughout the melt season [37,38]. As meltwater accumulates on the glacier’s surface, it flows to the bedrock through crevasses and moulins, creating a drainage system [36,39,40,41]. Initially, water is distributed in thin films or small passageways, but, as more meltwater enters, it concentrates along specific flow paths influenced by the bedrock topography and pressure gradients [42]. This flow causes thermal erosion of the ice, creating a positive feedback loop: faster water flow generates heat, melts more ice, and enlarges the channel, leading to the development of larger, more efficient drainage channels over time [36,43,44].
However, despite its potential contribution to glacier retreat, subglacial hydrology represents one of the most significant yet poorly understood components of glacier dynamics. This complexity arises from the challenging access to subglacial environments, which are typically located beneath thick ice masses, making direct observations and measurements exceedingly difficult. The harsh conditions, including extreme cold, high pressure, and the dynamic nature of the ice above, pose substantial logistical challenges to studying these hidden systems. The scarcity of observations in subglacial environments has led to a reliance on models to infer the behavior of these systems [41,42].
Modeling glacier dynamics is essential for enhancing our understanding of Arctic glacier–fjord interactions by simulating the complex physical processes that govern these systems [27,42]. Recent studies have incorporated information of the subglacial system into glacier–ocean coupled models [45,46,47,48], recognizing its importance in glacier dynamics. However, when it comes to tidewater mass loss, it is crucial to quantify the trade-off between the increased computational cost of solving a subglacial hydrology model and the results obtained from models that simplify or parameterize the subglacial component.
In this study, we aim to assess the impact of subglacial hydrology on glacier front retreat simulations. We focus on the Hansbreen glacier, which offers a rich dataset for model testing, making it an ideal natural laboratory for our research. We use a 3D glacier dynamics–fjord model that accounts for surface mass balance, calving, and submarine melting. We then compare the outputs from two versions of the model: one that resolves the subglacial hydrology model and another that operates under the assumption of a single discharge channel at the flow line. By quantifying the differences in annual front retreat, submarine melting, and calving between these two models, we evaluate the role of subglacial hydrology in understanding glacier dynamics, which can enhance our ability to make more accurate predictions of future changes in response to ongoing atmospheric and oceanic warming.

2. Materials and Methods

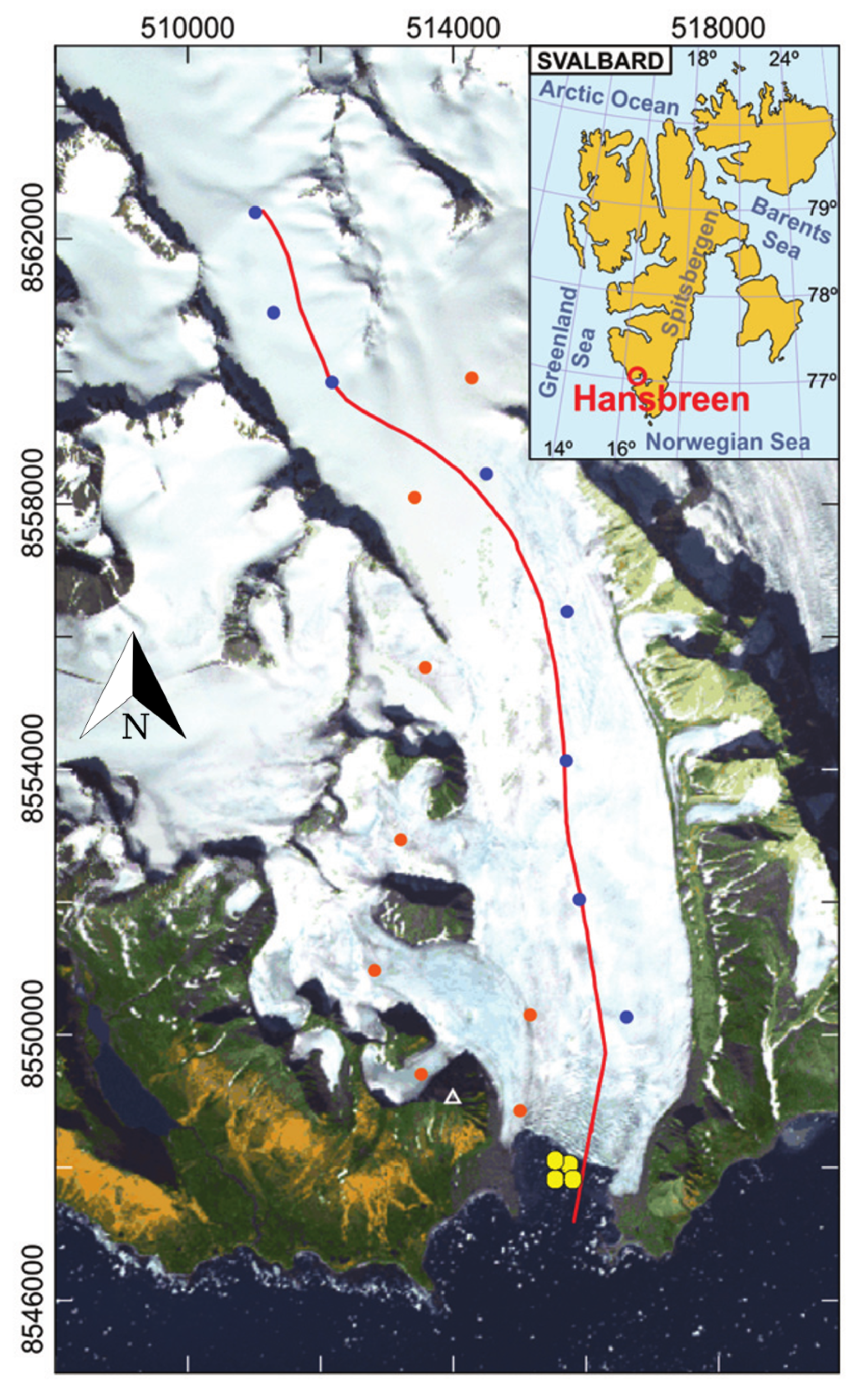
2.1. The Glacier–Fjord System of Study: Hansbreen-Hansbukta

The glacier–fjord system Hansbreen-Hansbukta is located in one of the branches of Hornsund fjord in southwest Spitsbergen, Svalbard, at ∼77° N, ∼15.6° E (Figure 2). Hansbreen is a polythermal tidewater glacier flowing southward that covers an area of ∼57 km2. It is about 16 km long with a low mean surface slope of around 1.8° on average along the central flowline [49]. Its calving front is 1.5 km wide with a vertical face ∼100 m thick at the central flowline, of which 50 to 60 m are below the sea level. The seasonal retreat of Hansbreen usually starts in June/July and lasts until late autumn/early winter, and the average summer and winter fluctuations amount to − 125 and 79 m, respectively [50]. As for Hansbukta, it is about a 2 km long bay, with a minimum depth of approximately 22 m recorded within the sill located at the fjord mouth. The maximum depth reaches around 77 m in a 200 m wide channel on the central west side of the Hansbreen front [51]. Temperature and salinity in Hansbukta experience strong seasonal variability, ranging from − 1.8 to 3 °C and from 34.6 to 31.8 psu between April and August, respectively.

2.2. Observations

There are a set of observations needed to constrain the glacier–fjord model: glacier velocities, surface meltwater, bedrock topography, glacier front position, and fjord properties.
We used the gridded surface velocity data of [45], which were obtained by applying Bayesian Kriging techniques [53] on daily horizontal velocities measured at a set of stakes located along the glacier in 2010 (see blue dots in Figure 2).
Surface mass balance (SMB) and surface meltwater (SMW) (Figure 3) were obtained from downscaled European Arctic Reanalysis data at 2 km horizontal and hourly temporal resolutions, constrained by automatic weather stations and stake observations [54]. The surface elevation came from the SPIRIT digital elevation model for gentle slopes, with a 30 m RMS absolute horizontal precision and 40 m resolution. Bedrock topography was inferred from ground-penetrating radar data [49,55].
We took the Hansbreen weekly front positions obtained in 2010 from time-lapse camera images processed and described in [56]. We also analyzed all the imagery searching for plume activity locations. In some of the winter images, plume activity was observed as a free-of-ice patch of the fjord surface attached to the glacier terminus. In summer periods, the imprint of the plume was recognized by a sediment patch at the fjord surface close to the glacier front (Figure 4).
Hydrography of Hansbukta has been monitored from 2010 to date by the IOPAS (Institute of Oceanology Polish Academy of Science), and the data used in this study were already published in [17,52], as well as used in [45]. We provide here some information of the fjord data used in this study. CTD (conductivity, temperature, and depth profiler) data were collected at different casts in Hansbukta (yellow points in Figure 2). Temperature and salinity measurements were vertically averaged every 1 dbar (1 kPa), providing a vertical resolution of 1 m.

2.3. The Models

We use the coupled glacier–fjord model of [45], which was built on the open-source full-Stokes finite element ice flow model Elmer/Ice [57]. The different processes of the system are coupled in [45]: glacier dynamics, calving, and subglacial hydrology models for the glacier component, as well as line plume and submarine melt models for the fjord component. The different models coupled are briefly explained in the following subsections, although we refer to [45] for exhaustive information.

2.3.1. Glacier Dynamics + Calving

The model solves the full-Stokes equations for ice flow, with rheology defined by Glen’s flow law (e.g., [58]), and uses the calving implementation described by [46,47,59,60]. This implementation was initially postulated by [61,62] and later improved by [63,64] for use in a 3D framework. This calving criterion has been chosen because Benn et al. [65] demonstrated that the crevasse depth (CD) calving law reflects the glaciological controls on calving and exhibits considerable skill in simulating seasonal fluctuations. CD is calculated by
σ n = 2 τ e s g n ( τ x x ) − ρ i g d + P w
where σ n is the net stress (positive for extension and negative for compression). The terms on the right-hand side represent the balance of forces: the first corresponds to the opening force of longitudinal stretching, where τ e represents the effective stress, τ e 2 = τ x x 2 + τ z x 2 and the sign function ( s g n ) ensures that crevasse opening is only produced under longitudinal extension; the second term corresponds to the ice overburden pressure, which leads to creep closure, where ρ i is the ice density, g is the gravity acceleration, and d the crevasse depth. P w stands for the water pressure inside crevasses, which is here considered to be zero for surface crevasses and controlled by the subglacial hydrological system for basal crevasses, and at the calving front can be expressed as
P w = ( Z s l − Z ) ρ w g ,
ρ w being the density of water at the calving front and Z the elevation with respect to sea level. The sea-level elevation, Z s l , is set to 0 m. When calving occurs, the model calculates a calving vector that is normal to the calving front, maps pre-calving to post-calving node positions, and remeshes the main mesh.

2.3.2. Buoyant Plume + Submarine Melting

Due to the density differences between meltwater and fjord water, subglacially discharged water rises in contact with the calving front, mixing turbulently with the surrounding water and producing melting at the ice–water interface.
We rely on the line plume model of [21,66] to simulate the buoyant plume generated by sublacial discharge of meltwater entering the fjord. This line plume model has shown to accurately reproduce this phenomenon in tidewater glacier terminus [28,67] and is implemented in Elmer/Ice [46,47] as a continuous sheet-style ’line’ plume, split into coterminous segments across the calving front. To compute the submarine melt rates at the glacier terminus, the thermodynamical equilibrium at the ice–ocean interface [68] is solved (see [17] for further details).
The plume model is initialized by the subglacial discharge at each node of the grounding line, where, depending on the experiment (Section 2.4), the subglacial discharge values are obtained either as a solution of the subglacial hydrology model (Section 2.3.3) or within a single imposed channel centered with the flow line. The calculated melt rates are then applied to modify the geometry of the submerged part of the calving front.

2.3.3. Subglacial Hydrology

The subglacial hydrology of Hansbreen is simulated by using the Glacier Drainage System module (GlaDS) of Elmer/Ice [69]. GlaDS simulates both inefficient distributed drainage, represented by a sheet of water that covers the whole area of the glacier, and efficient channelized drainage, represented by a series of channels generated on the edges of the mesh elements of the domain (see more details in [70]). The main parameters of the model are set out in Table 1.
We used GladS to obtain subglacial discharge estimates at the grounding line. Water is not permitted to flow through the lateral boundaries, and we set the hydraulic potential, ϕ , to zero at the grounding line. From the combination of Equation (2) and the hydraulic potential, we obtained
ϕ = ρ w g Z + P w
Water entering the hydrological system is mainly derived from surface meltwater (Figure 3). We account also for a small portion of basal meltwater, which is assumed to be spread and is calculated using a geothermal heat flux of 63 mW m−2 [69].

2.4. Experiments

We simulated the glacier–fjord system of Hansbreen-Hansbukta from April to December 2010. Two distinct models were employed, both incorporating the same components: glacier dynamics, calving, buoyant plume, and submarine melting. The primary difference between the models lies in the treatment of subglacial hydrology.
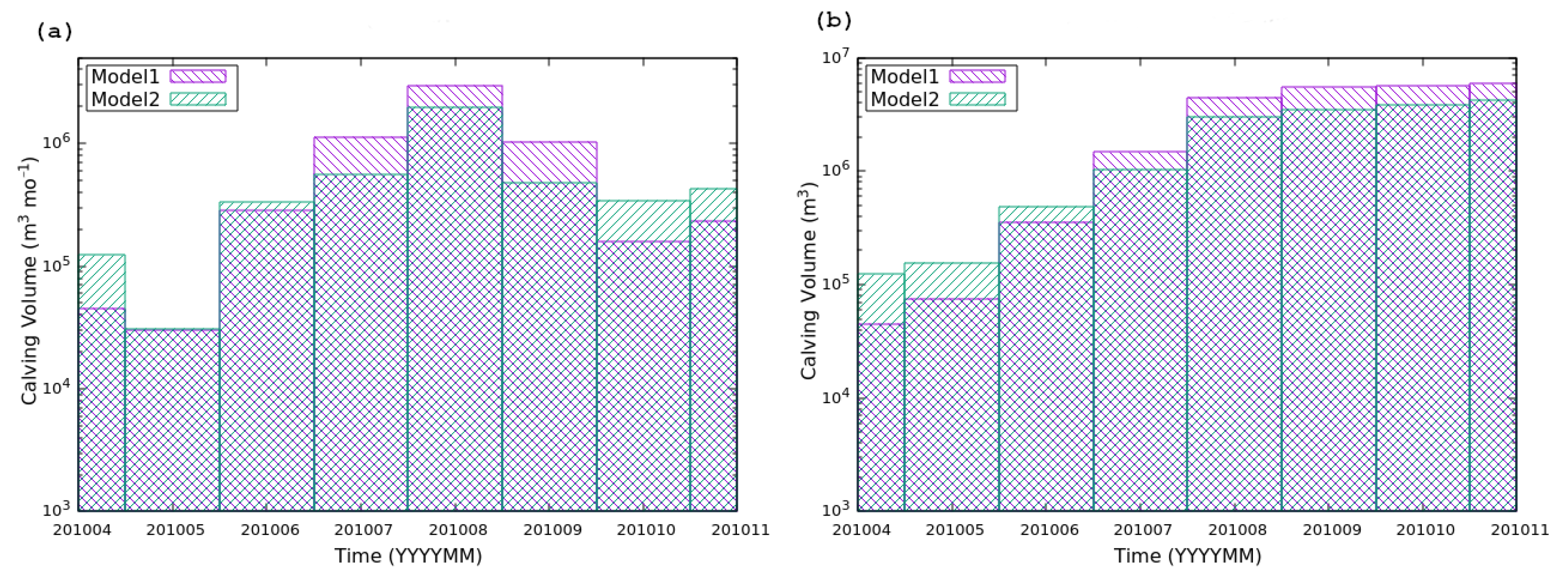
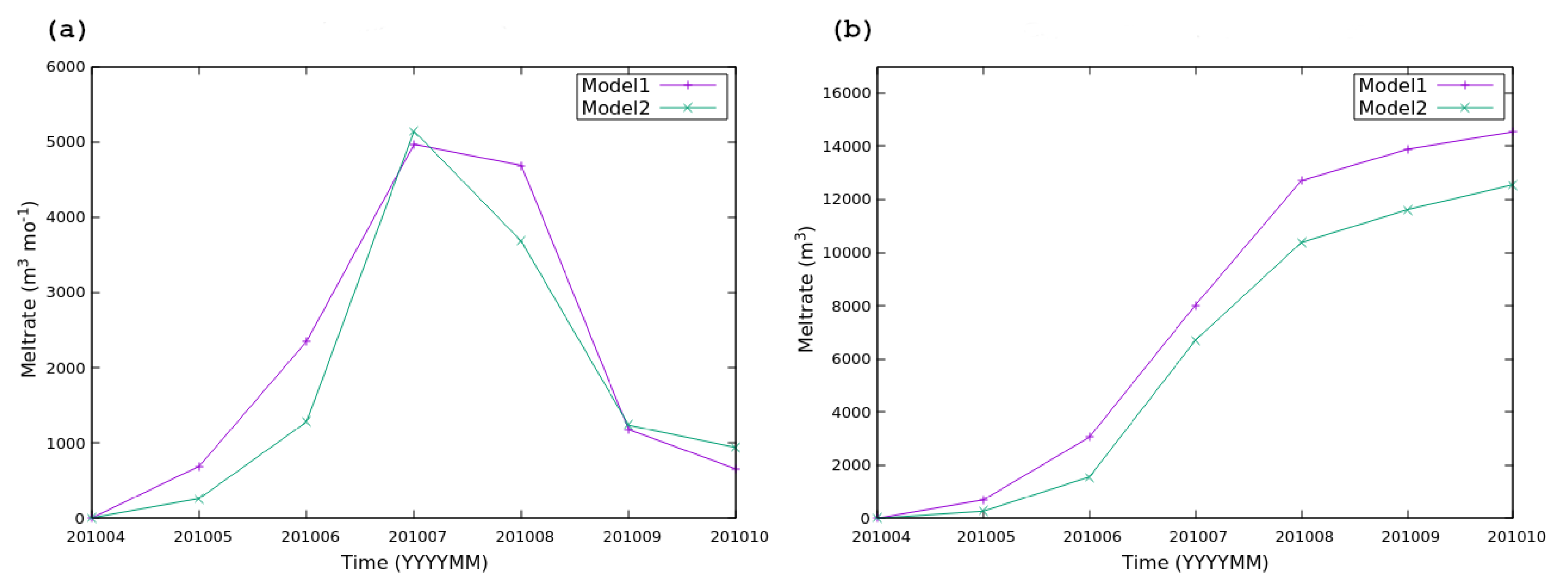
  • Model 1 is coupled with the subglacial hydrology model, allowing meltwater to flow freely through the discharge channels derived from the simulation. This approach enables a more realistic representation of the interactions between the glacier dynamics and the underlying hydrological system.
  • Model 2 does not resolve the subglacial hydrology component. Instead, it imposes a single discharge channel, centered along the glacier’s flow line, with an approximate width of 200 m, as described by [17,52]. With this ‘conventional’ configuration, we tested the impact of simplifying subglacial hydrology on the overall dynamics of the glacier–fjord system.
By comparing the results from both models, we aimed to gain insights into the role of subglacial hydrology in glacier front retreat and the dynamics of Hansbreen-Hansbukta system.

3. Results

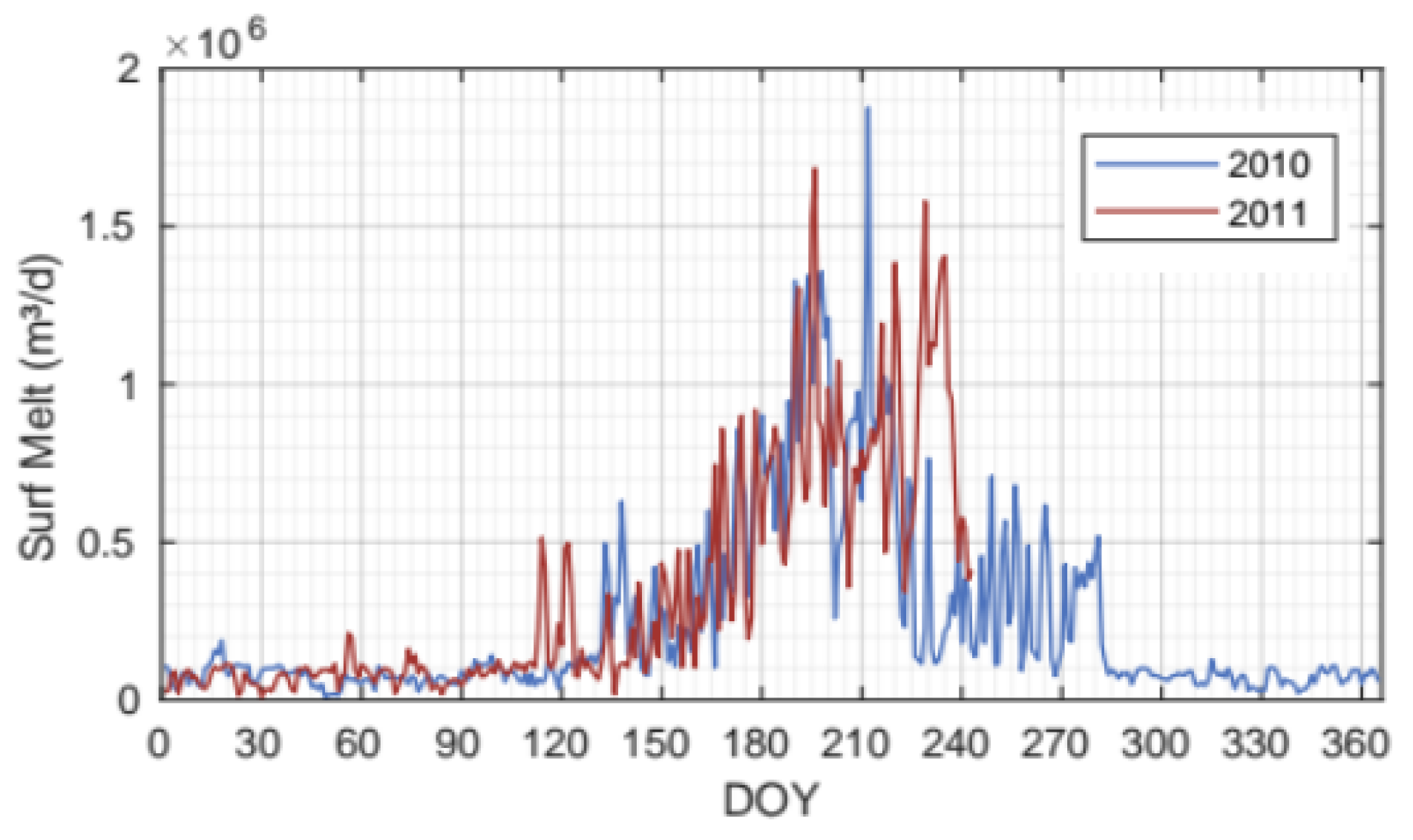
3.1. Discharging Channels from the Subglacial Hydrology Model

The subglacial hydrology model is coupled with the glacier dynamics and mass balance of Hansbreen. The subglacial water drainage system evolves dynamically over time, influenced by factors such as surface meltwater input, bedrock topography, and water-induced erosion within the ice. Figure 5 presents the modeled configuration of the subglacial drainage system in September, at the end of the melt season, when the drainage system is considered to be well established and more efficient.
The subglacial hydrology model identifies three distinct channels, each exhibiting unique characteristics. The largest channel, approximately 100 m in width, is situated in the deepest region (∼70 m depth) on the central western side of the Hansbreen terminus (highlighted in orange and labeled as channel 2 in Figure 5). The other two channels, each approximately 50 m wide and shallower (∼30 m depth), are located closer to the glacier margins (identified as channels 1 and 3 in Figure 5). This three-channel configuration predicted by the model corresponds closely with the observational data. The time-lapse imagery (Figure 4) shows distinct plume patches at the glacier terminus, which are consistent with the positions of the modeled channels, indicating the presence of subglacial water discharge.

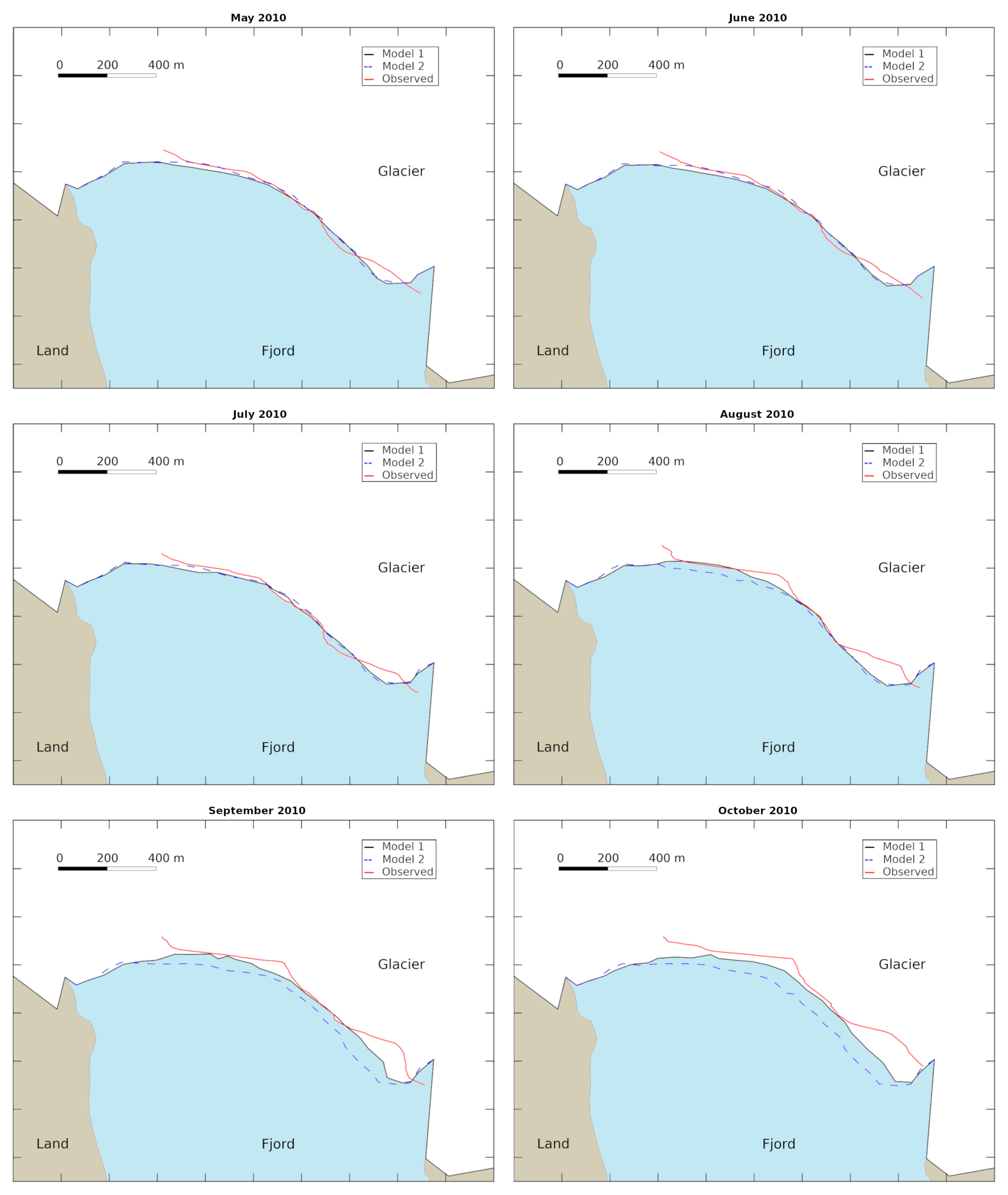
3.2. Performance of the Two Models Against Observed Glacier Terminus

After running Model 1 and Model 2 from April to December 2010, we obtain the various positions of the Hansbreen front over time. Figure 6 graphically represents the observed and modeled monthly positions for a qualitative analysis between Models 1 and 2. On the other hand, Table 2 quantifies the longitudinal differences of each model against the observations. This quantification is calculated as the area difference between the modeled and observed fronts divided by the observed width of the glacier front. In this context, negative values indicate that the observed front is more advanced than the modeled one.
The results in Figure 6 show a very good approximation of both models to the observations during the initial months of the simulation (May and June), during which there are minimal changes in the position and morphology of the glacier front. The longitudinal difference in April is so small (<1 m) that it is not graphically represented (see the values in Table 2). For the months of May and June, both models exhibit a longitudinal difference of <5 m compared to the observed front. However, it is noteworthy that Model 1 presents a glacier front that is a bit more retreated than observed.
Starting in July, this situation changes, and the front begins to retreat more significantly until October, thereby increasing the differences between both models and the observations. These differences become remarkable in the eastern margin from July, and at the center of the glacier terminus from August, and maintained in both cases until October. The longitudinal differences in Model 1 (Model 2) against the observations increase from ∼13 m (∼32 m) in July, to ∼ 76 m (∼122 m) in October (Table 2). Although neither model exactly matches the observed front position, Model 1, which is coupled with the sophisticated subglacial hydrology model, provides results that are much closer to the observations, reducing the longitudinal difference presented by Model 2 by up to 50%.

3.3. Comparison of Frontal Ablation Between the Two Models

Frontal ablation refers to the mass loss of a glacier at its terminus. As previously described in the Introduction (Section 1) and illustrated in Figure 1, the front of a tidewater glacier can experience mass loss primarily through two mechanisms: calving, which is associated with the detachment of icebergs, and submarine melting. The latter is influenced not only by the temperature of the fjord but is also enhanced by buoyant plumes generated by subglacial meltwater discharges. In this section, we quantify the frontal ablation associated with these two main mechanisms, calving and submarine melting, for the two models employed in the simulations. While changes in the Hansbreen front position could provide indirect estimates, we lack direct observations of the calving and submarine melt volumes and instead obtain this information as model outputs. Nevertheless, the glacier front position changes over time, as shown in Figure 6 and previous studies [17,45,52], serving as a useful indirect validation. Given that Model 1 aligns more closely with the observed front positions, as demonstrated in the previous section, we infer that Model 1 is likely to more accurately represent mass loss from calving as well.

3.3.1. Calving

In general terms, the simulation results indicate that the volume of mass loss due to calving increases throughout the melt season, peaking in August (Figure 7a). Following September, the mass loss from calving begins to decline. This trend is consistent with the pattern observed for surface meltwater (Figure 3), highlighting the interrelationship between these two mass loss mechanisms.
Focusing on the calving volume presented in Figure 7a, the minimum monthly mass loss rates, approximately 3 × 10 4 m 3 month − 1 , occur in May for both models. In April and June, Model 2, which assumes a single discharge channel, exhibits a greater calving volume than Model 1. However, this situation reverses in the subsequent months (July, August, and September), when the mass loss from calving is more pronounced. In July and September, the calving volume for Model 2 is around 4 × 10 5 m 3 month − 1 , while Model 1 reaches calving volumes of up to 10 6 m 3 month − 1 . This suggests that the resolution and coupling of the subglacial hydrology model with the glacier dynamics model (Model 1) facilitate more than double the frontal ablation due to calving during July and September, which are months characterized by significant surface melting (see Figure 3). In August, both models exhibit their highest monthly calving volumes, with Model 1 reaching 3 × 10 6 m 3 month − 1 and Model 2 reaching 2 × 10 6 m 3 month − 1 .
Except for the first three months (April to June), the total mass loss accumulated due to calving is greater in Model 1 along the melt season, which reaches a total of 6 × 10 6 m 3 (∼6 Mt) by November (Figure 7b). In Model 2, the mass loss from calving amounts to a total of 4 × 10 6 m 3 (∼4 Mt), which is one-third less than that of Model 1. This highlights the significant importance of incorporating the subglacial hydrology model into the glacier dynamics model when calculating frontal ablation due to calving.

3.3.2. Submarine Melting

Submarine melting refers to the submerged portion of a glacier terminus that melts due to direct contact with seawater or fjord waters. In our simulations of the Hansbreen glacier, we computed the monthly submarine ice melt (Figure 8a) and noticed that both models exhibit a similar general pattern to that of calving (Figure 7a) and surface meltwater (Figure 3) throughout the simulation period.
In April, submarine melting is minimal, coinciding with cold temperatures in the fjord and low subglacial discharge. This melting progressively increases, reaching its peak in July, which occurs one month prior to the maximum calving volume (see Figure 7a). Following this peak, the submarine melting decreases again until the end of the simulation.
The results indicate that the monthly submarine melting rates are consistently higher in Model 1 compared to Model 2 throughout the simulation, with the exception of July, when melting reaches its maximum of 5000 m3 month−1 in both models. Figure 8b illustrates the accumulation of frontal ablation resulting from submarine melting. It is evident that Model 1 generates greater mass loss due to submarine melting than Model 2 for the entire duration of the simulation. By the end of the simulation, the total ice volume loss attributed to submarine melting is 15,000 m3 in Model 1 and 12,500 m3 in Model 2.
Submarine melting contributes to mass loss that is approximately three orders of magnitude smaller than calving, making it negligible by comparison. However, despite its small volume, submarine melting alters the shape of the submerged glacier front, amplifying calving [7,17,24,26,71] by modifying the stress field near the terminus [52,72], likely increasing the total frontal ablation of tidewater glaciers.

4. Discussion

4.1. Subglacial Hydrology as an Important Component of the Glacier–Fjord System

Subglacial hydrology plays a crucial role in the dynamics of tidewater glaciers. It is interconnected with various processes, relying on surface meltwater while also influencing ice velocities, subglacial discharge, submarine melting, and iceberg calving [15,23,73,74,75]. Understanding these interactions is essential for accurately modeling glacier behavior [42] and predicting the future changes in response to climate variability.
Fjord temperature is also a key factor in glacier retreat, and, in both Model 1 and Model 2, the fjord temperature conditions are updated weekly based on observations [17,52]. These temperatures evolve seasonally but remain the same for both models. Therefore, the differences observed between Model 1 and Model 2 in our study are not due to variations in fjord temperature but rather to the differing representations of subglacial hydrology. Specifically, the incorporation of subglacial hydrology in Model 1 improves the accuracy of predicting the glacier front position (Figure 6 and Table 2). By resolving the subglacial water flow, we can account for the complex network of drainage channels that develop beneath the glacier (Figure 5). This complexity enables a more realistic simulation of how water moves and exerts pressure at the glacier base, altering the basal sliding coefficient and ultimately affecting glacier velocity and frontal stability [32,34,35].
These additional channels facilitate greater subglacial water flow, which aligns with the sediment plume observations in our study (Figure 4) and has also been reported by [15,74]. This increased flow contributes to higher submarine melting rates (Figure 8), consistent with the findings of [28,75]. Moreover, the presence of multiple drainage channels amplifies the mass loss through calving (Figure 7) as a consequence of enhanced net stress differences at the glacier terminus [52].
In contrast, simplifying subglacial hydrology by assuming a single discharge channel at the tidewater glacier terminus—an approach commonly found in the scientific literature e.g., [17,21,22,52,76]—leads to less accurate predictions of the glacier front position, as shown in Figure 6. In our study, the results from the oversimplified model indicate that the glacier front is further advanced than both the comprehensive model and actual observations. This suggests that subglacial hydrology is a crucial component in modeling the entire glacier–fjord system.
This discrepancy arises because the simplified model is limited to a single discharge channel, which fails to account for the multiple drainage pathways present at the glacier front. Consequently, it does not accurately capture the pressure distribution along the entire base of the glacier. This results in smaller differences in glacier velocities at the front, which hinders the destabilization of the glacier front and promotes less calving (Figure 7). Ultimately, this leads to a glacier terminus that is more advanced than what is actually observed (Figure 6).
In summary, the interaction between subglacial water dynamics and frontal ablation is essential for understanding the overall mass balance of Arctic tidewater glaciers.

4.2. Implications of Simplifying the Subglacial Hydrology Component in the Modeling Context

The complex interplay between surface meltwater, subglacial discharge, and iceberg calving highlights the essential requirement for the precise modeling of subglacial hydrology [42,46,47]. Our research demonstrates that, in the months characterized by reduced surface meltwater production (Figure 3), the variance in the glacier front position between the hydrology-resolving model and the simplified model is negligible (Figure 6 and Table 2). Conversely, as the surface meltwater production increases, the discrepancies between the two modeling approaches become increasingly significant (Figure 6 and Table 2). Importantly, the model that incorporates subglacial hydrology exhibits a closer alignment with the observations, indicating its superior accuracy in representing the underlying physical processes.
In our simulation, which encompasses a single year from April to December 2010, we observed a notable difference in mass loss attributed to calving between the two modeling approaches (Figure 7). The coupled model indicated a mass loss of 6 Mt, whereas the simplified model recorded a significantly lower mass loss of 4 Mt. This discrepancy underscores the importance of subglacial hydrology, particularly as surface meltwater increases. Consequently, in the context of rising atmospheric and oceanic temperatures, and the high sensitivity of tidewater glaciers to these changes [6,7,8,50], the reliance on predictive models that oversimplify the subglacial hydrological processes may result in a considerable underestimation of the glacier retreat rates in future climate change scenarios.
High-resolution models of this type often use short time frames due to computational demands [17,52]. Although our study focuses on a single time frame (April to December), it captures key seasonal dynamics across atmospheric, subglacial, and fjord systems that drive glacier behavior. While extending the time frame could enhance generalization, the chosen period effectively highlights the differences between the modeling approaches, particularly as the surface melt intensifies.
While simplified models present advantages in terms of reduced computational costs when studying glacier dynamics [52,62,77,78], it is crucial to consider these benefits in light of their inherent limitations. To properly adjust the parameterization of the subglacial hydrology, further comparative simulations of both modeling approaches (simplified and resolved) are necessary, using empirical observations from a diverse range of glacier–fjord systems with varying characteristics and under different atmospheric and oceanic conditions. This approach will provide a more comprehensive understanding of how each model responds to specific environmental factors. Furthermore, such studies would facilitate the incorporation of an appropriate error range for the simplified models, thereby addressing their limitations and enabling a more accurate assessment of mass loss and front retreat in Arctic glaciers.
Furthermore, the incorporation of artificial intelligence methodologies into glaciological research is increasingly being recognized as a valuable advancement for mapping glacier basal sliding [79], detecting glacier–snow lines [80], and modeling glacier melt dynamics [81] or surface mass balance (e.g., [82,83,84]). These techniques require training on observational datasets or data generated from existing models. Consequently, to ensure the reliability of the predictions derived from these advanced methodologies, it is imperative to produce model results that are both accurate and representative of the real glacier–fjord system. This foundational aspect will significantly enhance the credibility of future forecasts concerning glacier dynamics and their responses to climate change.

5. Conclusions

This study highlights the critical role of subglacial hydrology in the dynamics of tidewater glaciers, emphasizing its influence on glacier front position, submarine melting, and iceberg calving. Our findings demonstrate that coupling the glacier dynamics model with a resolved subglacial hydrology model significantly improves the accuracy of predicting glacier front positions compared to the simplified model that assumes a single discharge channel. The complexity of subglacial drainage networks seems to be essential for capturing the pressure distribution at the glacier base and within the crevasses, which directly affects glacier stability and mass loss through calving.
As the surface meltwater production increases, the discrepancies between the comprehensive and simplified models become more pronounced. Within a single melt season, the simplified model underestimates up to 1/3 of the mass loss due to calving, underscoring the necessity of incorporating subglacial hydrology in predictive models. The observed differences in mass loss due to submarine melting and calving further illustrate the importance of accurate modeling in understanding glacier responses to climate change.
In light of the rising temperatures and the sensitivity of tidewater glaciers, the reliance on oversimplified models may lead to significant underestimations of the glacier retreat rates. Future research should focus on comparative simulations across diverse glacier–fjord systems to refine the parameterizations of subglacial hydrology and enhance the reliability of predictions. Additionally, properly integrating artificial intelligence methodologies into glaciological research holds promise for reducing the computational effort for glacier dynamics modeling.
Our findings highlight that a comprehensive approach is essential for improving the predictions of glacier behavior and understanding the broader implications for sea-level rise and climate change.

Author Contributions

Conceptualization, E.D.A.; model implementation, J.M.M.-H.; formal analysis, E.D.A.; investigation, E.D.A.; data curation, K.S.; writing—original draft preparation, E.D.A. and J.M.M.-H.; writing—review and editing, K.S. and J.O.; funding acquisition, J.O. All authors have read and agreed to the published version of the manuscript.

Funding

E. De Andrés is supported by Margarita-Salas Grant No. UP2021-035 under the Next Generation-EU program. This research was also funded by grant PID2020-113051RB-C31 from MCIN/AEI/10.13039/501100011033/FEDER, UE.

Data Availability Statement

The data that support the results of this study and form the basis for all the figures presented in this paper are openly available from Zenodo at https://doi.org/10.5281/zenodo.8005258 (accessed on 6 November 2024).

Acknowledgments

We gratefully acknowledge Michal Cieply and Dariusz Ignatiuk from the Faculty of Natural Sciences, University of Silesia in Katowice, Poland, for their essential contributions to the Hansbreen data collection. We also extend our sincere thanks to Waldemar Walczowski from the Institute of Oceanology, Polish Academy of Sciences, Sopot, Poland, for providing Hansbuka data. Additionally, we would like to thank two anonymous reviewers for their constructive feedback, which helped to enhance the quality and clarity of this work.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Tesi, T.; Muschitiello, F.; Mollenhauer, G.; Miserocchi, S.; Langone, L.; Ceccarelli, C.; Panieri, G.; Chiggiato, J.; Nogarotto, A.; Hefter, J.; et al. Rapid Atlantification along the Fram Strait at the beginning of the 20th century. Sci. Adv. 2021, 7, eabj2946. [Google Scholar] [CrossRef] [PubMed]
  2. Strzelewicz, A.; Przyborska, A.; Walczowski, W. Increased presence of Atlantic Water on the shelf south-west of Spitsbergen with implications for the Arctic fjord Hornsund. Prog. Oceanogr. 2022, 200, 102714. [Google Scholar] [CrossRef]
  3. Tepes, P.; Gourmelen, N.; Nienow, P.; Tsamados, M.; Shepherd, A.; Weissgerber, F. Changes in elevation and mass of Arctic glaciers and ice caps, 2010–2017. Remote Sens. Environ. 2021, 261, 112481. [Google Scholar] [CrossRef]
  4. Tepes, P.; Nienow, P.; Gourmelen, N. Accelerating Ice Mass Loss Across Arctic Russia in Response to Atmospheric Warming, Sea Ice Decline, and Atlantification of the Eurasian Arctic Shelf Seas. J. Geophys. Res. Earth Surf. 2021, 126, 1–21. [Google Scholar] [CrossRef]
  5. Hock, R.; Huss, M. Glaciers and climate change. In Climate Change; Elsevier: Amsterdam, The Netherlands, 2021; pp. 157–176. [Google Scholar] [CrossRef]
  6. Nuth, C.; Gilbert, A.; Köhler, A.; McNabb, R.; Schellenberger, T.; Sevestre, H.; Weidle, C.; Girod, L.; Luckman, A.; Kääb, A. Dynamic vulnerability revealed in the collapse of an Arctic tidewater glacier. Sci. Rep. 2019, 9, 5541. [Google Scholar] [CrossRef]
  7. Luckman, A.; Benn, D.I.; Cottier, F.; Bevan, S.; Nilsen, F.; Inall, M. Calving rates at tidewater glaciers vary strongly with ocean temperature. Nat. Commun. 2015, 6, 8566. [Google Scholar] [CrossRef]
  8. Holmes, F.A.; Kirchner, N.; Kuttenkeuler, J.; Krützfeldt, J.; Noormets, R. Relating ocean temperatures to frontal ablation rates at Svalbard tidewater glaciers: Insights from glacier proximal datasets. Sci. Rep. 2019, 9, 9442. [Google Scholar] [CrossRef]
  9. Błaszczyk, M.; Ignatiuk, D.; Uszczyk, A.; Cielecka-Nowak, K.; Grabiec, M.; Jania, J.A.; Moskalik, M.; Walczowski, W. Freshwater input to the Arctic fjord Hornsund (Svalbard). Polar Res. 2019, 38. [Google Scholar] [CrossRef]
  10. Cogley, J.G.; Hock, R.; Rasmussen, L.A.; Arendt, A.A.; Bauder, A.; Braithwaite, R.J.; Jansson, P.; Kaser, G.; Möller, M.; Nicholson, L.; et al. Glossary of Glacier Mass Balance and Related Terms; Technical Report, UNESCO-IHP; IACS: Paris, France, 2011. [Google Scholar]
  11. Huss, M.; Hock, R. A new model for global glacier change and sea-level rise. Front. Earth Sci. 2015, 3, 54. [Google Scholar] [CrossRef]
  12. Hanna, E.; Pattyn, F.; Navarro, F.; Favier, V.; Goelzer, H.; van den Broeke, M.R.; Vizcaino, M.; Whitehouse, P.L.; Ritz, C.; Bulthuis, K.; et al. Mass balance of the ice sheets and glaciers—Progress since AR5 and challenges. Earth-Sci. Rev. 2020, 201, 102976. [Google Scholar] [CrossRef]
  13. Mankoff, K.D.; Straneo, F.; Cenedese, C.; Das, S.B.; Richards, C.G.; Singh, H. Structure and dynamics of a subglacial discharge plume in a Greenlandic fjord. J. Geophys. Res. Oceans 2016, 121, 8670–8688. [Google Scholar] [CrossRef]
  14. De Andrés, E.; Slater, D.; Straneo, F.; Otero, J.; Das, S.; Navarro, F. Surface emergence of glacial plumes determined by fjord stratification. Cryosphere 2020, 14, 1951–1969. [Google Scholar] [CrossRef]
  15. How, P.; Benn, D.I.; Hulton, N.R.J.; Hubbard, B.; Luckman, A.; Sevestre, H.; van Pelt, W.J.J.; Lindbäck, K.; Kohler, J.; Boot, W. Rapidly changing subglacial hydrological pathways at a tidewater glacier revealed through simultaneous observations of water pressure, supraglacial lakes, meltwater plumes and surface velocities. Cryosphere 2017, 11, 2691–2710. [Google Scholar] [CrossRef]
  16. Motyka, R.J.; Dryer, W.P.; Amundson, J.; Truffer, M.; Fahnestock, M. Rapid submarine melting driven by subglacial discharge, LeConte Glacier, Alaska. Geophys. Res. Lett. 2013, 40, 5153–5158. [Google Scholar] [CrossRef]
  17. De Andrés, E.; Otero, J.; Navarro, F.; Promińska, A.; Lapazaran, J.; Walczowski, W. A two-dimensional glacier–fjord coupled model applied to estimate submarine melt rates and front position changes of Hansbreen, Svalbard. J. Glaciol. 2018, 64, 745–758. [Google Scholar] [CrossRef]
  18. Straneo, F.; Cenedese, C. The Dynamics of Greenland’s Glacial Fjords and Their Role in Climate. Annu. Rev. Mar. Sci. 2015, 7, 89–112. [Google Scholar] [CrossRef]
  19. Sciascia, R.; Straneo, F.; Cenedese, C.; Heimbach, P. Seasonal variability of submarine melt rate and circulation in an East Greenland fjord. J. Geophys. Res. Oceans 2013, 118, 2492–2506. [Google Scholar] [CrossRef]
  20. Xu, Y.; Rignot, E.; Fenty, I.; Menemenlis, D.; Flexas, M.M. Subaqueous melting of Store Glacier, west Greenland from three-dimensional, high-resolution numerical modeling and ocean observations. Geophys. Res. Lett. 2013, 40, 4648–4653. [Google Scholar] [CrossRef]
  21. Slater, D.A.; Nienow, P.W.; Cowton, T.R.; Goldberg, D.N.; Sole, A.J. Effect of near-terminus subglacial hydrology on tidewater glacier submarine melt rates. Geophys. Res. Lett. 2015, 42, 2861–2868. [Google Scholar] [CrossRef]
  22. Slater, D.A.; Straneo, F.; Das, S.B.; Richards, C.G.; Wagner, T.J.W.; Nienow, P.W. Localized Plumes Drive Front-Wide Ocean Melting of A Greenlandic Tidewater Glacier. Geophys. Res. Lett. 2018, 45, 12350–12358. [Google Scholar] [CrossRef]
  23. Jackson, R.H.; Motyka, R.J.; Amundson, J.M.; Abib, N.; Sutherland, D.A.; Nash, J.D.; Kienholz, C. The Relationship Between Submarine Melt and Subglacial Discharge From Observations at a Tidewater Glacier. J. Geophys. Res. Oceans 2022, 127, e2021JC018204. [Google Scholar] [CrossRef]
  24. O’Leary, M.; Christoffersen, P. Calving on tidewater glaciers amplified by submarine frontal melting. Cryosphere 2013, 7, 119–128. [Google Scholar] [CrossRef]
  25. Vallot, D.; Adinugroho, S.; Strand, R.; How, P.; Pettersson, R.; Benn, D.I.; Hulton, N.R.J. Automatic detection of calving events from time-lapse imagery at Tunabreen, Svalbard. Geosci. Instrum. Methods Data Syst. 2019, 8, 113–127. [Google Scholar] [CrossRef]
  26. Schild, K.M.; Renshaw, C.E.; Benn, D.I.; Luckman, A.; Hawley, R.L.; How, P.; Trusel, L.; Cottier, F.R.; Pramanik, A.; Hulton, N.R.J. Glacier Calving Rates Due to Subglacial Discharge, Fjord Circulation, and Free Convection. J. Geophys. Res. Earth Surf. 2018, 123, 2189–2204. [Google Scholar] [CrossRef]
  27. Holmes, F.A.; van Dongen, E.; Kirchner, N. Modelled frontal ablation and velocities at Kronebreen, Svalbard, are sensitive to the choice of submarine melt rate scenario. J. Glaciol. 2023, 1–12. [Google Scholar] [CrossRef]
  28. Fried, M.J.; Catania, G.A.; Bartholomaus, T.C.; Duncan, D.; Davis, M.; Stearns, L.A.; Nash, J.; Shroyer, E.; Sutherland, D. Distributed subglacial discharge drives significant submarine melt at a Greenland tidewater glacier. Geophys. Res. Lett. 2015, 42, 9328–9336. [Google Scholar] [CrossRef]
  29. Fried, M.J.; Carroll, D.; Catania, G.A.; Sutherland, D.A.; Stearns, L.A.; Shroyer, E.L.; Nash, J.D. Distinct Frontal Ablation Processes Drive Heterogeneous Submarine Terminus Morphology. Geophys. Res. Lett. 2019, 46, 12083–12091. [Google Scholar] [CrossRef]
  30. Sutherland, D.A.; Jackson, R.H.; Kienholz, C.; Amundson, J.M.; Dryer, W.P.; Duncan, D.; Eidam, E.F.; Motyka, R.J.; Nash, J.D. Direct observations of submarine melt and subsurface geometry at a tidewater glacier. Science 2019, 365, 369–374. [Google Scholar] [CrossRef]
  31. Bunce, C.; Nienow, P.; Sole, A.; Cowton, T.; Davison, B. Influence of glacier runoff and near-terminus subglacial hydrology on frontal ablation at a large Greenlandic tidewater glacier. J. Glaciol. 2021, 67, 343–352. [Google Scholar] [CrossRef]
  32. Bartholomew, I.; Nienow, P.; Sole, A.; Mair, D.; Cowton, T.; King, M.A. Short-term variability in Greenland Ice Sheet motion forced by time-varying meltwater drainage: Implications for the relationship between subglacial drainage system behavior and ice velocity. J. Geophys. Res. Earth Surf. 2012, 117, 1–17. [Google Scholar] [CrossRef]
  33. Bell, R.E. The role of subglacial water in ice-sheet mass balance. Nat. Geosci. 2008, 1, 297–304. [Google Scholar] [CrossRef]
  34. Zwally, H.J.; Abdalati, W.; Herring, T.; Larson, K.; Saba, J.; Steffen, K. Surface Melt-Induced Acceleration of Greenland Ice-Sheet Flow. Science 2002, 297, 218–222. [Google Scholar] [CrossRef] [PubMed]
  35. van de Wal, R.S.W.; Boot, W.; van den Broeke, M.R.; Smeets, C.J.P.P.; Reijmer, C.H.; Donker, J.J.A.; Oerlemans, J. Large and Rapid Melt-Induced Velocity Changes in the Ablation Zone of the Greenland Ice Sheet. Science 2008, 321, 111–113. [Google Scholar] [CrossRef] [PubMed]
  36. Cowton, T.; Nienow, P.; Sole, A.; Wadham, J.; Lis, G.; Bartholomew, I.; Mair, D.; Chandler, D. Evolution of drainage system morphology at a land-terminating Greenlandic outlet glacier. J. Geophys. Res. Earth Surf. 2013, 118, 29–41. [Google Scholar] [CrossRef]
  37. Fountain, A.G.; Walder, J.S. Water flow through temperate glaciers. Rev. Geophys. 1998, 36, 299–328. [Google Scholar] [CrossRef]
  38. Nienow, P.; Sharp, M.; Willis, I. Seasonal changes in the morphology of the subglacial drainage system, Haut Glacier d’Arolla, Switzerland. Earth Surf. Process. Landf. 1998, 23, 825–843. [Google Scholar] [CrossRef]
  39. Weertman, J. General theory of water flow at the base of a glacier or ice sheet. Rev. Geophys. 1972, 10, 287–333. [Google Scholar] [CrossRef]
  40. Hodgkins, R. Glacier hydrology in Svalbard, Norwegian high arctic. Quat. Sci. Rev. 1997, 16, 957–973. [Google Scholar] [CrossRef]
  41. Decaux, L.; Grabiec, M.; Ignatiuk, D.; Jania, J. Role of discrete water recharge from supraglacial drainage systems in modeling patterns of subglacial conduits in Svalbard glaciers. Cryosphere 2019, 13, 735–752. [Google Scholar] [CrossRef]
  42. Flowers, G.E. Modelling water flow under glaciers and ice sheets. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20140907. [Google Scholar] [CrossRef]
  43. Kamb, B.; Raymond, C.F.; Harrison, W.D.; Engelhardt, H.; Echelmeyer, K.A.; Humphrey, N.; Brugman, M.M.; Pfeffer, T. Glacier Surge Mechanism: 1982-1983 Surge of Variegated Glacier, Alaska. Science 1985, 227, 469–479. [Google Scholar] [CrossRef] [PubMed]
  44. Kamb, B. Glacier surge mechanism based on linked cavity configuration of the basal water conduit system. J. Geophys. Res. Solid Earth 1987, 92, 9083–9100. [Google Scholar] [CrossRef]
  45. Muñoz-Hermosilla, J.M.; Otero, J.; De Andrés, E.; Shahateet, K.; Navarro, F.; Pérez-Doña, I. A 3D glacier dynamics–line plume model to estimate the frontal ablation of Hansbreen, Svalbard. Cryosphere 2024, 18, 1911–1924. [Google Scholar] [CrossRef]
  46. Cook, S.J.; Christoffersen, P.; Todd, J.; Slater, D.; Chauché, N. Coupled modelling of subglacial hydrology and calving-front melting at Store Glacier, West Greenland. Cryosphere 2020, 14, 905–924. [Google Scholar] [CrossRef]
  47. Cook, S.J.; Christoffersen, P.; Todd, J. A fully-coupled 3D model of a large Greenlandic outlet glacier with evolving subglacial hydrology, frontal plume melting and calving. J. Glaciol. 2022, 68, 486–502. [Google Scholar] [CrossRef]
  48. Möller, M.; Navarro, F.; Huss, M.; Marzeion, B. Projected sea-level contributions from tidewater glaciers are highly sensitive to chosen bedrock topography: A case study at Hansbreen, Svalbard. J. Glaciol. 2023, 69, 966–980. [Google Scholar] [CrossRef]
  49. Grabiec, M.; Jania, J.A.; Puczko, D.; Kolondra, L.; Budzik, T. Surface and bed morphology of Hansbreen, a tidewater glacier in Spitsbergen. Pol. Polar Res. 2012, 33, 111–138. [Google Scholar] [CrossRef]
  50. Błaszczyk, M.; Jania, J.A.; Ciepły, M.; Grabiec, M.; Ignatiuk, D.; Kolondra, L.; Kruss, A.; Luks, B.; Moskalik, M.; Pastusiak, T.; et al. Factors Controlling Terminus Position of Hansbreen, a Tidewater Glacier in Svalbard. J. Geophys. Res. Earth Surf. 2021, 126, 1–20. [Google Scholar] [CrossRef]
  51. Ćwia̧kała, J.; Moskalik, M.; Forwick, M.; Wojtysiak, K.; Giżejewski, J.; Szczuciński, W. Submarine geomorphology at the front of the retreating Hansbreen tidewater glacier, Hornsund fjord, southwest Spitsbergen. J. Maps 2018, 14, 123–134. [Google Scholar] [CrossRef]
  52. De Andrés, E.; Otero, J.; Navarro, F.J.; Walczowski, W. Glacier–plume or glacier–fjord circulation models? A 2-D comparison for Hansbreen–Hansbukta system, Svalbard. J. Glaciol. 2021, 67, 797–810. [Google Scholar] [CrossRef]
  53. Perez-Doña, I.; Otero, J. Sobre el uso de Kriging Bayesiano para estimar la evolución de las velocidades en superficie del Glaciar Hansbreen (Svalbard). In Proceedings of the 10a Asamblea Hispano-Portuguesa de Geodesia y Geofísica, Toledo, Spain, 28 November–1 September 2023. [Google Scholar]
  54. Finkelnburg, R. Climate Variability of Svalbard in the First Decade of the 21st Century and Its Impact on Vestfonna Ice Cap, Nordaustlandet. Ph.D. Thesis, Technischen Universität Berlin, Berlin, Germany, 2013. [Google Scholar] [CrossRef]
  55. Navarro, F.J.; Martín-Español, A.; Lapazaran, J.J.; Grabiec, M.; Otero, J.; Vasilenko, E.V.; Puczko, D. Ice Volume Estimates from Ground-Penetrating Radar Surveys, Wedel Jarlsberg Land Glaciers, Svalbard. Arct. Antarct. Alp. Res. 2014, 46, 394–406. [Google Scholar] [CrossRef]
  56. Otero, J.; Navarro, F.J.; Lapazaran, J.J.; Welty, E.; Puczko, D.; Finkelnburg, R. Modeling the Controls on the Front Position of a Tidewater Glacier in Svalbard. Front. Earth Sci. 2017, 5, 1–11. [Google Scholar] [CrossRef]
  57. Gagliardini, O.; Zwinger, T.; Gillet-Chaulet, F.; Durand, G.; Favier, L.; de Fleurian, B.; Greve, R.; Malinen, M.; Martín, C.; Råback, P.; et al. Capabilities and performance of Elmer/Ice, a new-generation ice sheet model. Geosci. Model Dev. 2013, 6, 1299–1318. [Google Scholar] [CrossRef]
  58. Cuffey, K.; Paterson, W. The Physics of Glaciers, 4th ed.; Elsevier: Oxford, UK, 2010. [Google Scholar]
  59. Todd, J.; Christoffersen, P.; Zwinger, T.; Råback, P.; Chauché, N.; Benn, D.; Luckman, A.; Ryan, J.; Toberg, N.; Slater, D.; et al. A Full-Stokes 3-D Calving Model Applied to a Large Greenlandic Glacier. J. Geophys. Res. Earth Surf. 2018, 123, 410–432. [Google Scholar] [CrossRef]
  60. Todd, J.; Christoffersen, P.; Zwinger, T.; Råback, P.; Benn, D.I. Sensitivity of a calving glacier to ice–ocean interactions under climate change: New insights from a 3-D full-Stokes model. Cryosphere 2019, 13, 1681–1694. [Google Scholar] [CrossRef]
  61. Benn, D.I.; Hulton, N.R.; Mottram, R.H. ‘Calving laws’, ‘sliding laws’ and the stability of tidewater glaciers. Ann. Glaciol. 2007, 46, 123–130. [Google Scholar] [CrossRef]
  62. Nick, F.; Van der Veen, C.; Vieli, A.; Benn, D. A physically based calving model applied to marine outlet glaciers and implications for the glacier dynamics. J. Glaciol. 2010, 56, 781–794. [Google Scholar] [CrossRef]
  63. Otero, J.; Navarro, F.J.; Martin, C.; Cuadrado, M.L.; Corcuera, M.I. A three-dimensional calving model: Numerical experiments on Johnsons Glacier, Livingston Island, Antarctica. J. Glaciol. 2010, 56, 200–214. [Google Scholar] [CrossRef]
  64. Todd, J.; Christoffersen, P. Are seasonal calving dynamics forced by buttressing from ice mélange or undercutting by melting? Outcomes from full-Stokes simulations of Store Glacier, West Greenland. Cryosphere 2014, 8, 2353–2365. [Google Scholar] [CrossRef]
  65. Benn, D.I.; Todd, J.; Luckman, A.; Bevan, S.; Chudley, T.R.; Åström, J.; Zwinger, T.; Cook, S.; Christoffersen, P. Controls on calving at a large Greenland tidewater glacier: Stress regime, self-organised criticality and the crevasse-depth calving law. J. Glaciol. 2023, 1–16. [Google Scholar] [CrossRef]
  66. Jenkins, A. Convection-driven melting near the grounding lines of ice shelves and tidewater glaciers. J. Phys. Oceanogr. 2011, 41, 2279–2294. [Google Scholar] [CrossRef]
  67. Jackson, R.H.; Shroyer, E.L.; Nash, J.D.; Sutherland, D.A.; Carroll, D.; Fried, M.J.; Catania, G.A.; Bartholomaus, T.C.; Stearns, L.A. Near-glacier surveying of a subglacial discharge plume: Implications for plume parameterizations. Geophys. Res. Lett. 2017, 44, 6886–6894. [Google Scholar] [CrossRef]
  68. Holland, D.M.; Jenkins, A. Modeling Thermodynamic Ice–Ocean Interactions at the Base of an Ice Shelf. J. Phys. Oceanogr. 1999, 29, 1787–1800. [Google Scholar] [CrossRef]
  69. Gagliardini, O.; Werder, M.A. Influence of increasing surface melt over decadal timescales on land-terminating Greenland-type outlet glaciers. J. Glaciol. 2018, 64, 700–710. [Google Scholar] [CrossRef]
  70. Werder, M.A.; Hewitt, I.J.; Schoof, C.G.; Flowers, G.E. Modeling channelized and distributed subglacial drainage in two dimensions. J. Geophys. Res. Earth Surf. 2013, 118, 2140–2158. [Google Scholar] [CrossRef]
  71. How, P.; Schild, K.M.; Benn, D.I.; Noormets, R.; Kirckner, N.; Luckman, A.; Vallot, D.; Hulton, N.R.J.; Borstad, C. Calving controlled by melt-under-cutting: Detailed calving styles revealed through time-lapse observations. Ann. Glaciol. 2019, 60, 20–31. [Google Scholar] [CrossRef]
  72. Ma, Y.; Bassis, J.N. The Effect of Submarine Melting on Calving From Marine Terminating Glaciers. J. Geophys. Res. Earth Surf. 2019, 124, 334–346. [Google Scholar] [CrossRef]
  73. Stevens, L.A.; Straneo, F.; Das, S.B.; Plueddemann, A.J.; Kukulya, A.L.; Morlighem, M. Linking glacially modified waters to catchment-scale subglacial discharge using autonomous underwater vehicle observations. Cryosphere 2016, 10, 417–432. [Google Scholar] [CrossRef]
  74. Jouvet, G.; Weidmann, Y.; Kneib, M.; Detert, M.; Seguinot, J.; Sakakibara, D.; Sugiyama, S. Short-lived ice speed-up and plume water flow captured by a VTOL UAV give insights into subglacial hydrological system of Bowdoin Glacier. Remote Sens. Environ. 2018, 217, 389–399. [Google Scholar] [CrossRef]
  75. Cowton, T.R.; Todd, J.A.; Benn, D.I. Sensitivity of Tidewater Glaciers to Submarine Melting Governed by Plume Locations. Geophys. Res. Lett. 2019, 46, 11219–11227. [Google Scholar] [CrossRef]
  76. Carroll, D.; Sutherland, D.A.; Hudson, B.; Moon, T.; Catania, G.A.; Shroyer, E.L.; Nash, J.D.; Bartholomaus, T.C.; Felikson, D.; Stearns, L.A.; et al. The impact of glacier geometry on meltwater plume structure and submarine melt in Greenland fjords. Geophys. Res. Lett. 2016, 43, 9739–9748. [Google Scholar] [CrossRef]
  77. Nick, F.; Oerlemans, J. Dynamics of tidewater glaciers: Comparison of three models. J. Glaciol. 2006, 52, 183–190. [Google Scholar] [CrossRef]
  78. Amundson, J.M.; Truffer, M.; Zwinger, T. Tidewater glacier response to individual calving events. J. Glaciol. 2022, 68, 1117–1126. [Google Scholar] [CrossRef]
  79. Umlauft, J.; Johnson, C.W.; Roux, P.; Trugman, D.T.; Lecointre, A.; Walpersdorf, A.; Nanni, U.; Gimbert, F.; Rouet-Leduc, B.; Hulbert, C.; et al. Mapping Glacier Basal Sliding Applying Machine Learning. J. Geophys. Res. Earth Surf. 2023, 128, e2023JF007280. [Google Scholar] [CrossRef]
  80. Prieur, C.; Rabatel, A.; Thomas, J.B.; Farup, I.; Chanussot, J. Machine Learning Approaches to Automatically Detect Glacier Snow Lines on Multi-Spectral Satellite Images. Remote Sens. 2022, 14, 3868. [Google Scholar] [CrossRef]
  81. Gogineni, A.; Chintalacheruvu, M.R.; Kale, R.V. Modelling of snow and glacier melt dynamics in a mountainous river basin using integrated SWAT and machine learning approaches. Earth Sci. Inform. 2024, 17, 4315–4337. [Google Scholar] [CrossRef]
  82. Bolibar, J.; Rabatel, A.; Gouttevin, I.; Galiez, C.; Condom, T.; Sauquet, E. Deep learning applied to glacier evolution modelling. Cryosphere 2020, 14, 565–584. [Google Scholar] [CrossRef]
  83. Bolibar, J.; Rabatel, A.; Gouttevin, I.; Zekollari, H.; Galiez, C. Nonlinear sensitivity of glacier mass balance to future climate change unveiled by deep learning. Nat. Commun. 2022, 13, 409. [Google Scholar] [CrossRef]
  84. Ren, W.; Zhu, Z.; Wang, Y.; Su, J.; Zeng, R.; Zheng, D.; Li, X. Comparison of Machine Learning Models in Simulating Glacier Mass Balance: Insights from Maritime and Continental Glaciers in High Mountain Asia. Remote Sens. 2024, 16, 956. [Google Scholar] [CrossRef]
Hydrology 11 00193 g001
Figure 1. Schematics of the main processes involved in mass loss of tidewater glaciers.
Figure 1. Schematics of the main processes involved in mass loss of tidewater glaciers.
Hydrology 11 00193 g001
Hydrology 11 00193 g002
Figure 2. Location of Hansbreen–Hansbukta, Svalbard (inset). ASTER image of Hansbreen–Hansbukta showing the location of the stakes for velocity measurements (blue circles for the flowline and red circles for the rest of the stakes) and the conductivity–temperature–depth (CTD) profiles in Hansbukta (yellow circles) [52]. The white triangle indicates the position of the time-lapse camera. The axes include the UTM coordinates (m) for zone 33X.
Figure 2. Location of Hansbreen–Hansbukta, Svalbard (inset). ASTER image of Hansbreen–Hansbukta showing the location of the stakes for velocity measurements (blue circles for the flowline and red circles for the rest of the stakes) and the conductivity–temperature–depth (CTD) profiles in Hansbukta (yellow circles) [52]. The white triangle indicates the position of the time-lapse camera. The axes include the UTM coordinates (m) for zone 33X.
Hydrology 11 00193 g002
Hydrology 11 00193 g003
Figure 3. Time evolution of daily surface meltwater production at Hansbreen glacier in 2010 (blue) and 2011 (red). Note that the Day of Year (DOY) on the x-axis has been grouped into 30-day intervals to facilitate the monthly sequence.
Figure 3. Time evolution of daily surface meltwater production at Hansbreen glacier in 2010 (blue) and 2011 (red). Note that the Day of Year (DOY) on the x-axis has been grouped into 30-day intervals to facilitate the monthly sequence.
Hydrology 11 00193 g003
Hydrology 11 00193 g004
Figure 4. Surface expression of sediment-laden plume patches attached to Hansbreen front in July 2010 and August 2011. The images were recorded by the time-lapse camera. The yellow arrows point to the plume patches.
Figure 4. Surface expression of sediment-laden plume patches attached to Hansbreen front in July 2010 and August 2011. The images were recorded by the time-lapse camera. The yellow arrows point to the plume patches.
Hydrology 11 00193 g004
Hydrology 11 00193 g005
Figure 5. Meshgrid of the subglacial hydrology of Hansbreen in September, obtained with Model 1. The white areas indicate water activity beneath the glacier. The three discharging channels identified at the glacier front have been circled and numbered in orange.
Figure 5. Meshgrid of the subglacial hydrology of Hansbreen in September, obtained with Model 1. The white areas indicate water activity beneath the glacier. The three discharging channels identified at the glacier front have been circled and numbered in orange.
Hydrology 11 00193 g005
Hydrology 11 00193 g006
Figure 6. Modeled and observed front positions of Hansbreen from May to October 2010. The red lines represent the observed glacier terminus positions. The dark solid line corresponds to the outputs from Model 1, which incorporates subglacial hydrology, while the dashed line illustrates the results from Model 2, which assumes a single discharging channel centered at the flow line.
Figure 6. Modeled and observed front positions of Hansbreen from May to October 2010. The red lines represent the observed glacier terminus positions. The dark solid line corresponds to the outputs from Model 1, which incorporates subglacial hydrology, while the dashed line illustrates the results from Model 2, which assumes a single discharging channel centered at the flow line.
Hydrology 11 00193 g006
Hydrology 11 00193 g007
Figure 7. Results from the models showing the temporal evolution of frontal ablation at Hansbreen due to calving, spanning from April to November 2010. (a) Monthly mass loss; (b) cumulative mass loss as the simulation progresses. Model 1 is coupled with a resolved subglacial hydrology model, whereas Model 2 operates under the assumption of a single discharge channel aligned with the flow line.
Figure 7. Results from the models showing the temporal evolution of frontal ablation at Hansbreen due to calving, spanning from April to November 2010. (a) Monthly mass loss; (b) cumulative mass loss as the simulation progresses. Model 1 is coupled with a resolved subglacial hydrology model, whereas Model 2 operates under the assumption of a single discharge channel aligned with the flow line.
Hydrology 11 00193 g007
Hydrology 11 00193 g008
Figure 8. Results from the models showing the temporal evolution of frontal ablation at Hansbreen due to submarine melting, spanning from April to October 2010. (a) Monthly mass loss and (b) cumulative mass loss as the simulation progresses. Model 1 is integrated with a resolved subglacial hydrology model, whereas Model 2 operates under the assumption of a single discharge channel aligned with the flow line.
Figure 8. Results from the models showing the temporal evolution of frontal ablation at Hansbreen due to submarine melting, spanning from April to October 2010. (a) Monthly mass loss and (b) cumulative mass loss as the simulation progresses. Model 1 is integrated with a resolved subglacial hydrology model, whereas Model 2 operates under the assumption of a single discharge channel aligned with the flow line.
Hydrology 11 00193 g008
Table 1. Parameters used for GlaDS model in this study.
Table 1. Parameters used for GlaDS model in this study.
DescriptionNameValueUnits
Pressure melt coefficient c t 7.5 × 10−8KPa−1
Heat capacity of water c w 4220J kg−1K−1
Sheet flow exponent α s 3
Sheet flow exponent β s 2
Channel flow exponent α c 5/4
Channel flow exponent β c 3/2
Sheet conductivity k s 0.005m s−1kg−1
Channel conductivity k c 0.1m3/2kg−1/2
Sheet width below channel l c 0.2m
Cavity spacing l r 0.5m
Bedrock bump ratio h r 0.02m
Englacial void ratio e v 10−4
Table 2. Longitudinal differences in modeled front position compared to observations. Model 1 is coupled with the subglacial hydrology model, while Model 2 assumes a single subglacial discharge channel.
Table 2. Longitudinal differences in modeled front position compared to observations. Model 1 is coupled with the subglacial hydrology model, while Model 2 assumes a single subglacial discharge channel.
DateModel 1Model 2
(mmmYYYY)Longitudinal Difference (m)Longitudinal Difference (m)
April 20100.77−0.03
May 2010−3.721.53
June 2010−4.83.91
July 201013.4231.97
August 201030.4764.7
September 201053.78100.22
October 201075.99121.9
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

De Andrés, E.; Muñoz-Hermosilla, J.M.; Shahateet, K.; Otero, J. The Importance of Solving Subglaciar Hydrology in Modeling Glacier Retreat: A Case Study of Hansbreen, Svalbard. Hydrology 2024, 11, 193. https://doi.org/10.3390/hydrology11110193

AMA Style

De Andrés E, Muñoz-Hermosilla JM, Shahateet K, Otero J. The Importance of Solving Subglaciar Hydrology in Modeling Glacier Retreat: A Case Study of Hansbreen, Svalbard. Hydrology. 2024; 11(11):193. https://doi.org/10.3390/hydrology11110193

Chicago/Turabian Style

De Andrés, Eva, José M. Muñoz-Hermosilla, Kaian Shahateet, and Jaime Otero. 2024. "The Importance of Solving Subglaciar Hydrology in Modeling Glacier Retreat: A Case Study of Hansbreen, Svalbard" Hydrology 11, no. 11: 193. https://doi.org/10.3390/hydrology11110193

APA Style

De Andrés, E., Muñoz-Hermosilla, J. M., Shahateet, K., & Otero, J. (2024). The Importance of Solving Subglaciar Hydrology in Modeling Glacier Retreat: A Case Study of Hansbreen, Svalbard. Hydrology, 11(11), 193. https://doi.org/10.3390/hydrology11110193

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop