Assessing Terrestrial Water Storage Variations in Southern Spain Using Rainfall Estimates and GRACE Data
Abstract
:1. Introduction
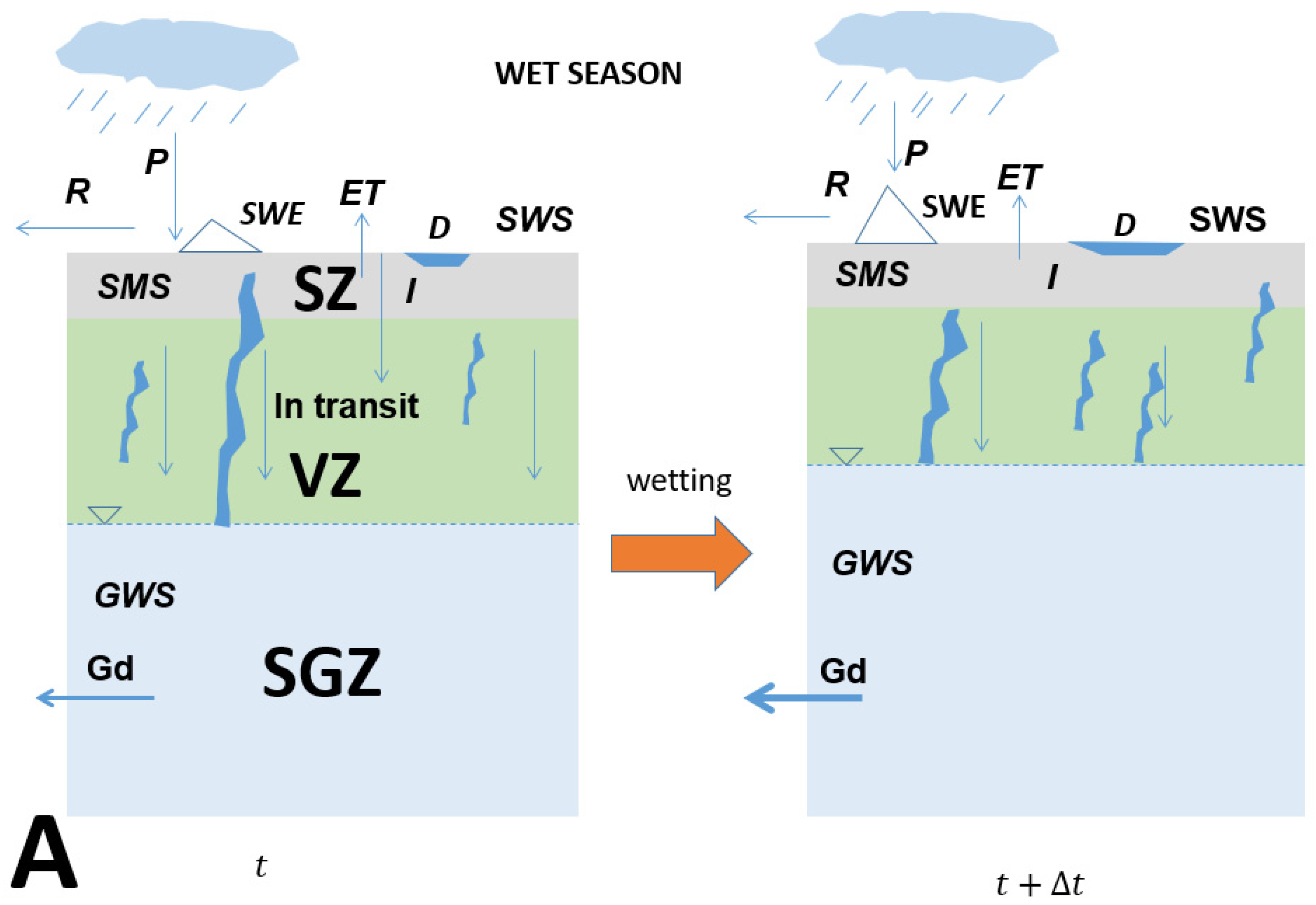
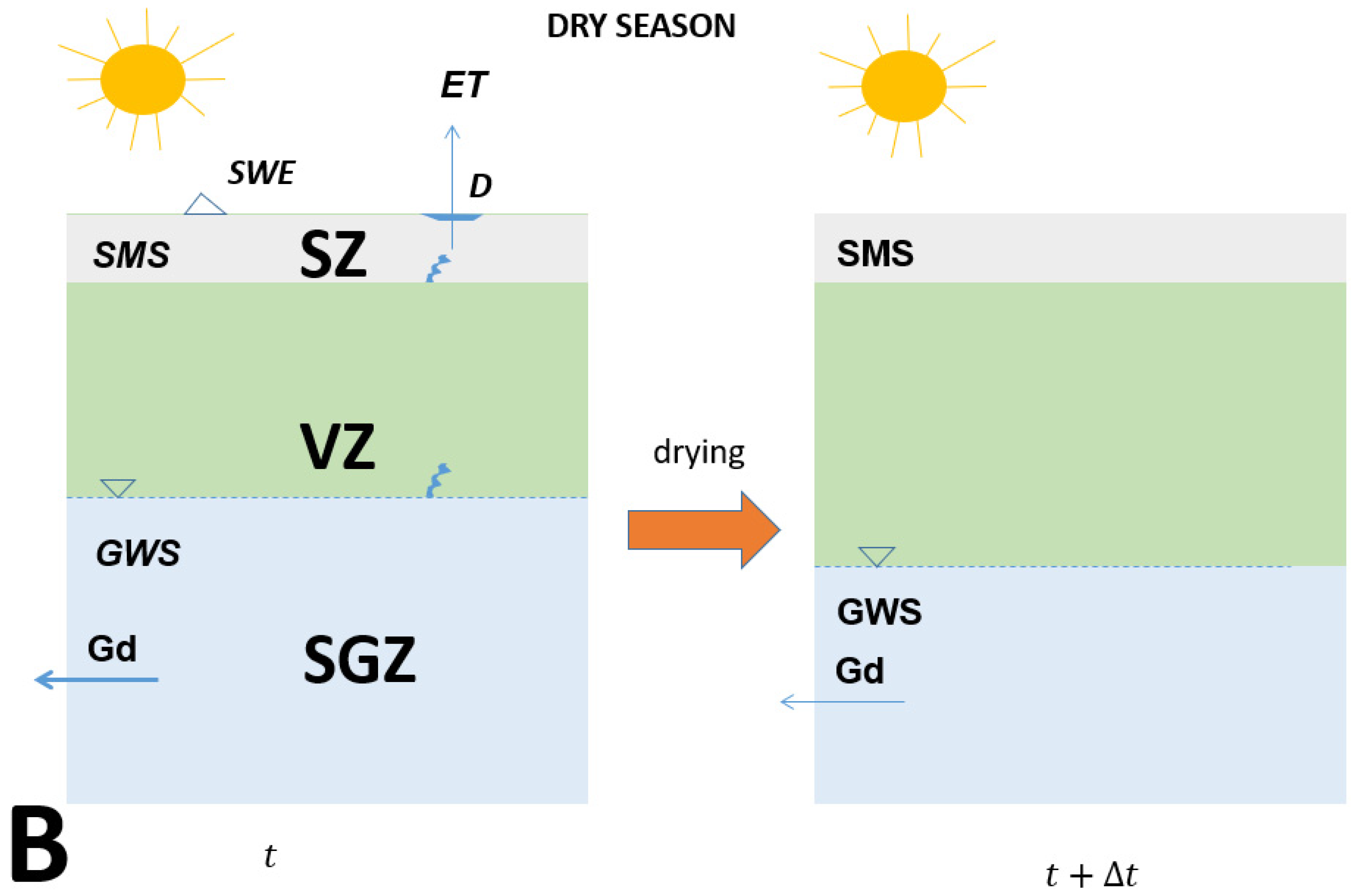
2. Methodology and Assumptions for the Hydrological Cycle, Rainfall Data and GRACE Observations
3. Case Study: The Andalucía Region of Southern Spain
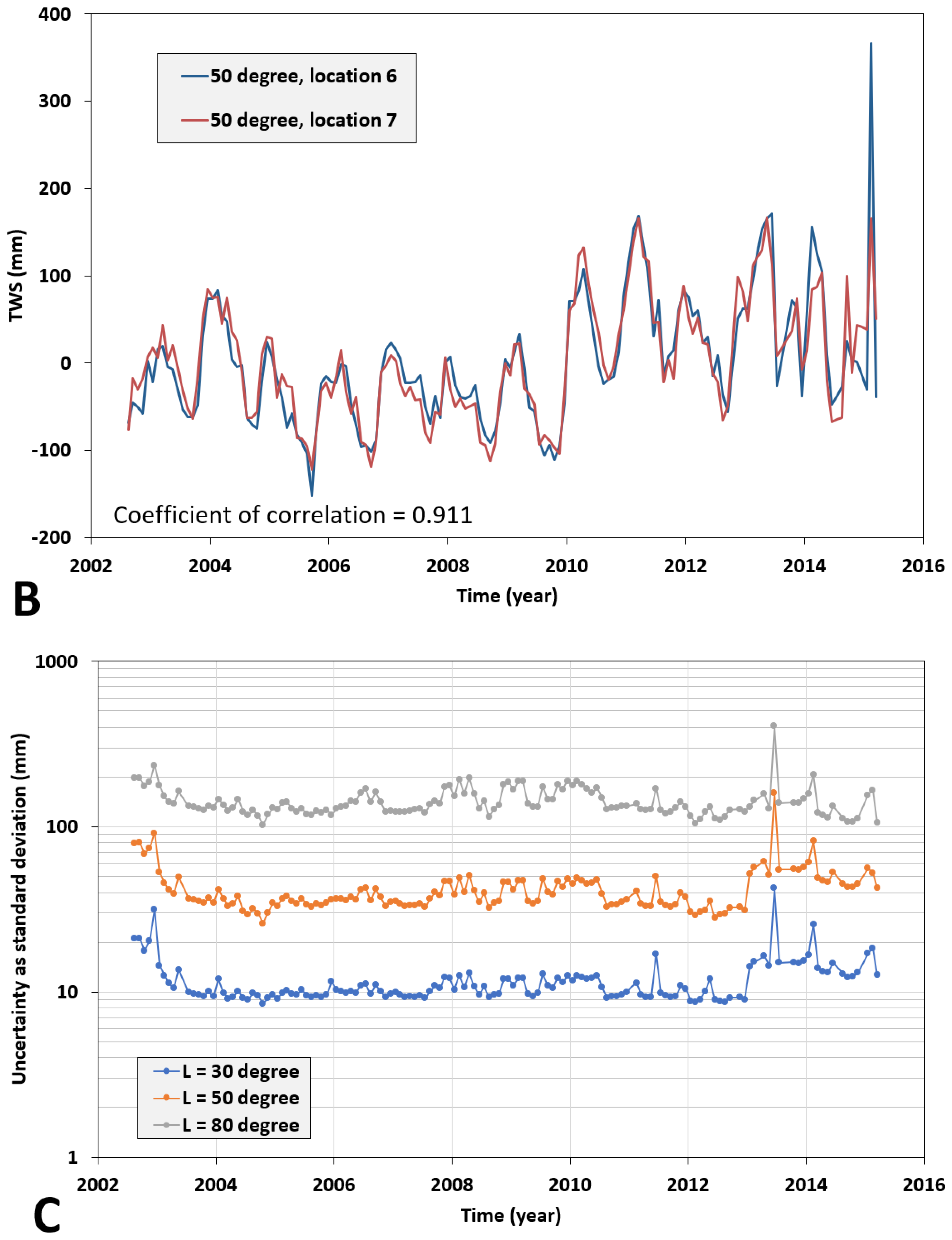
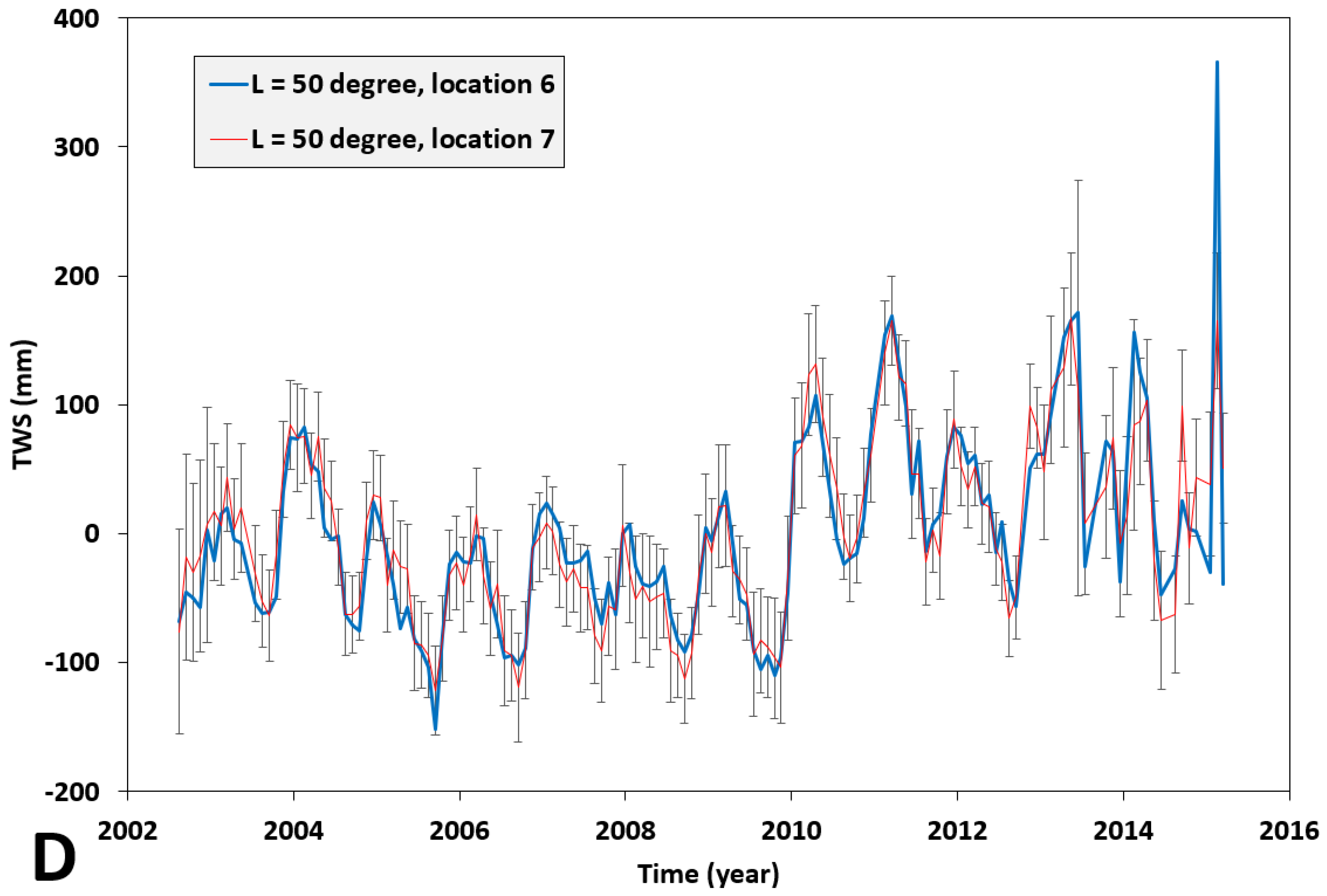
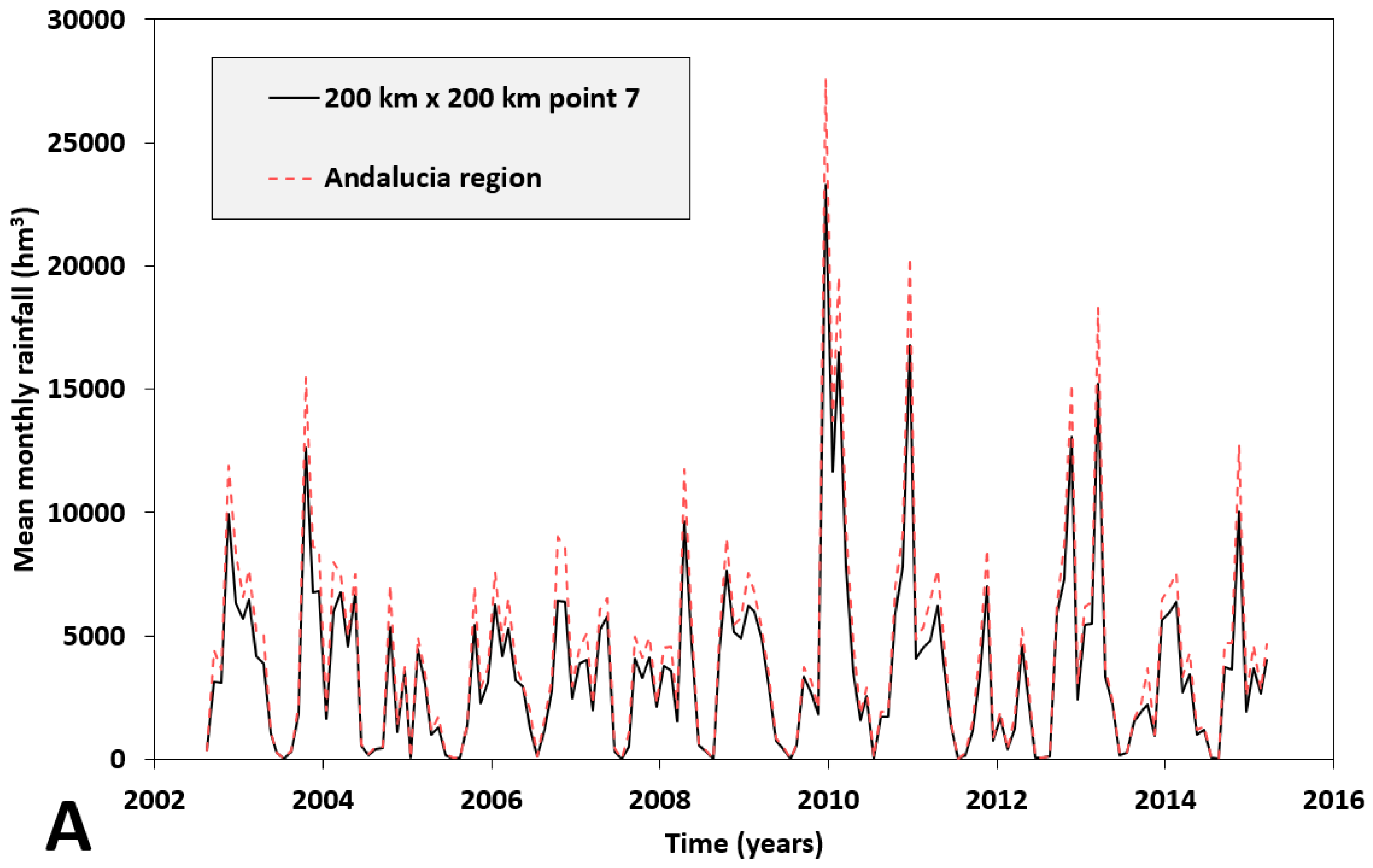
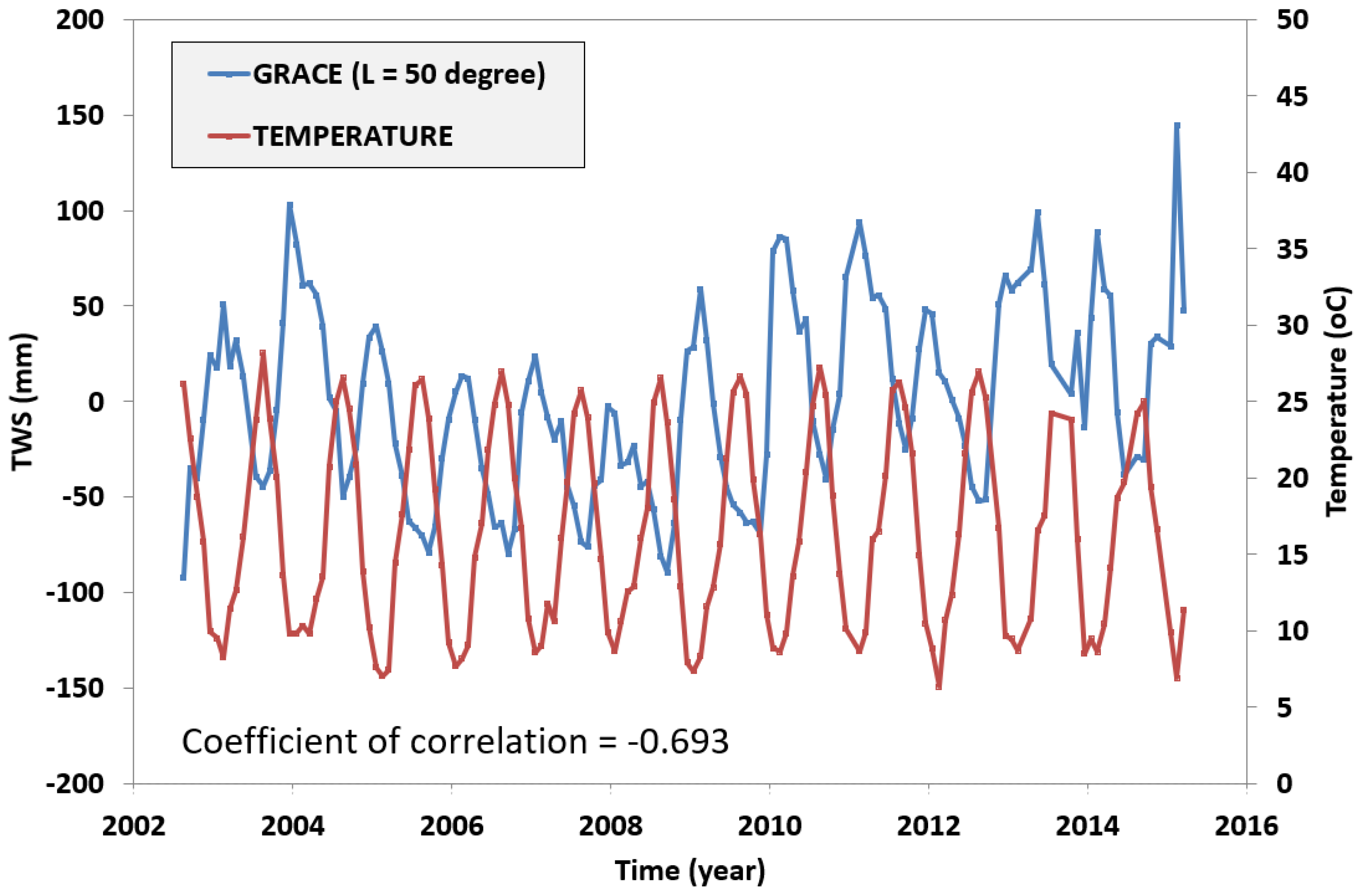
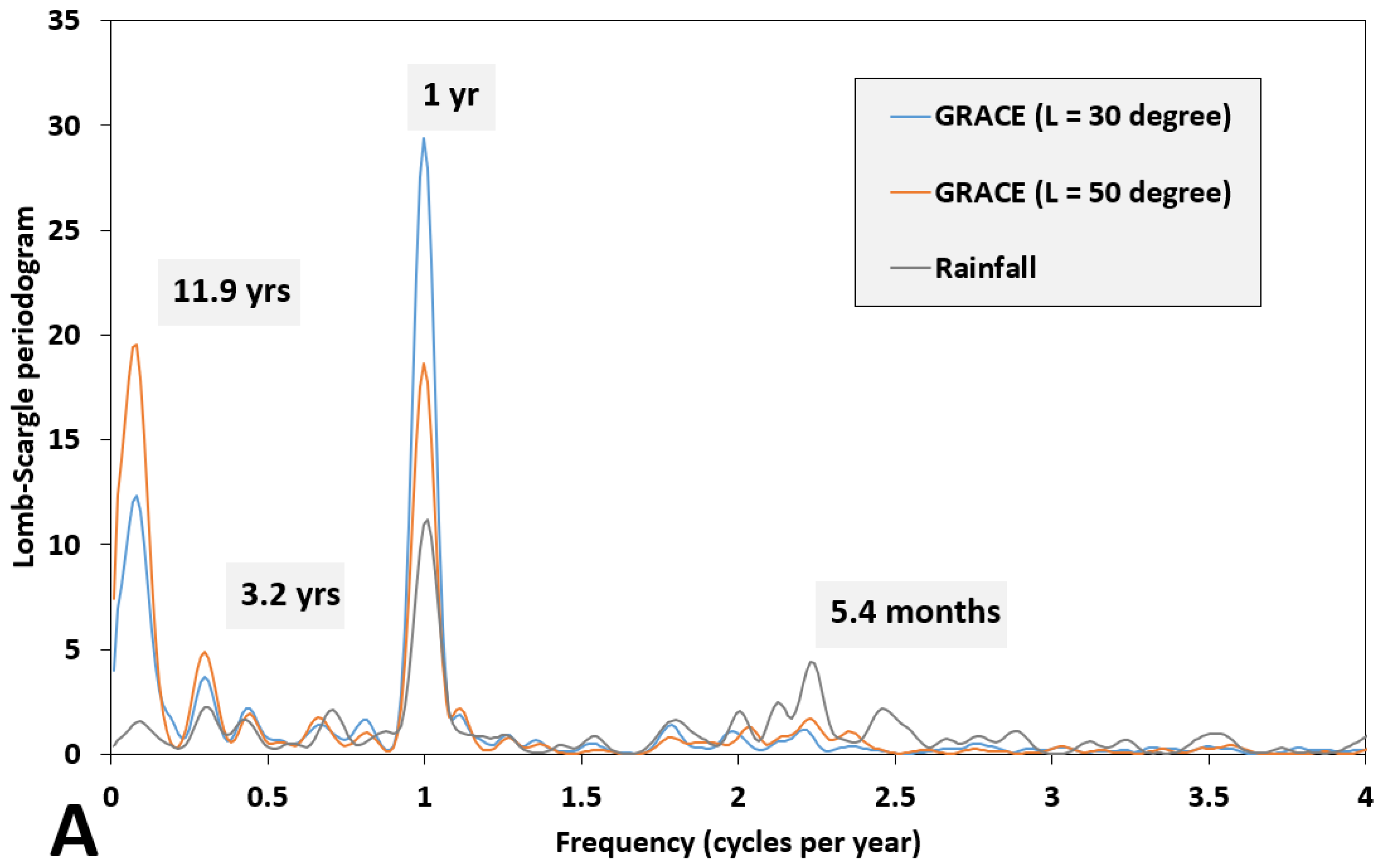
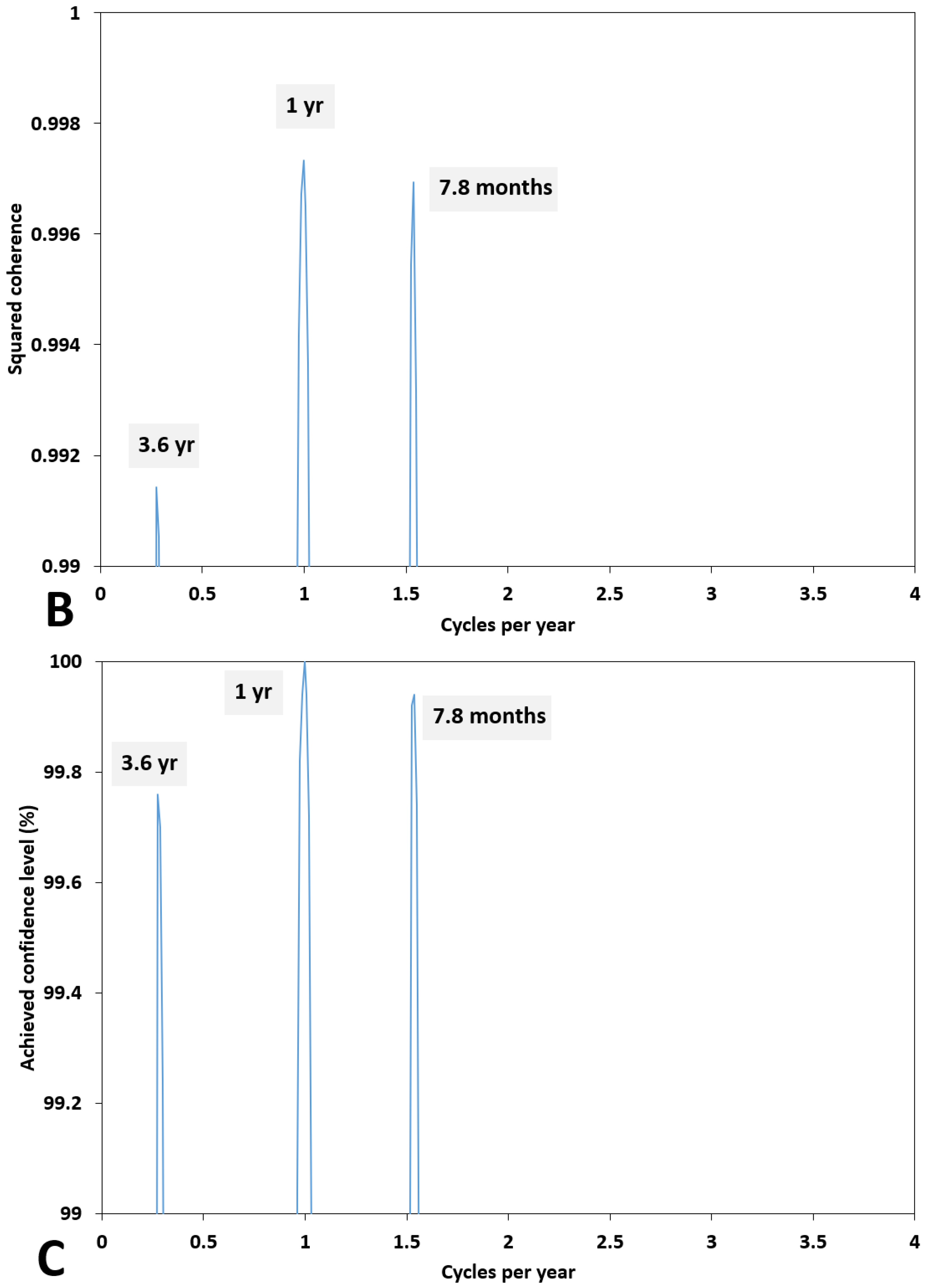
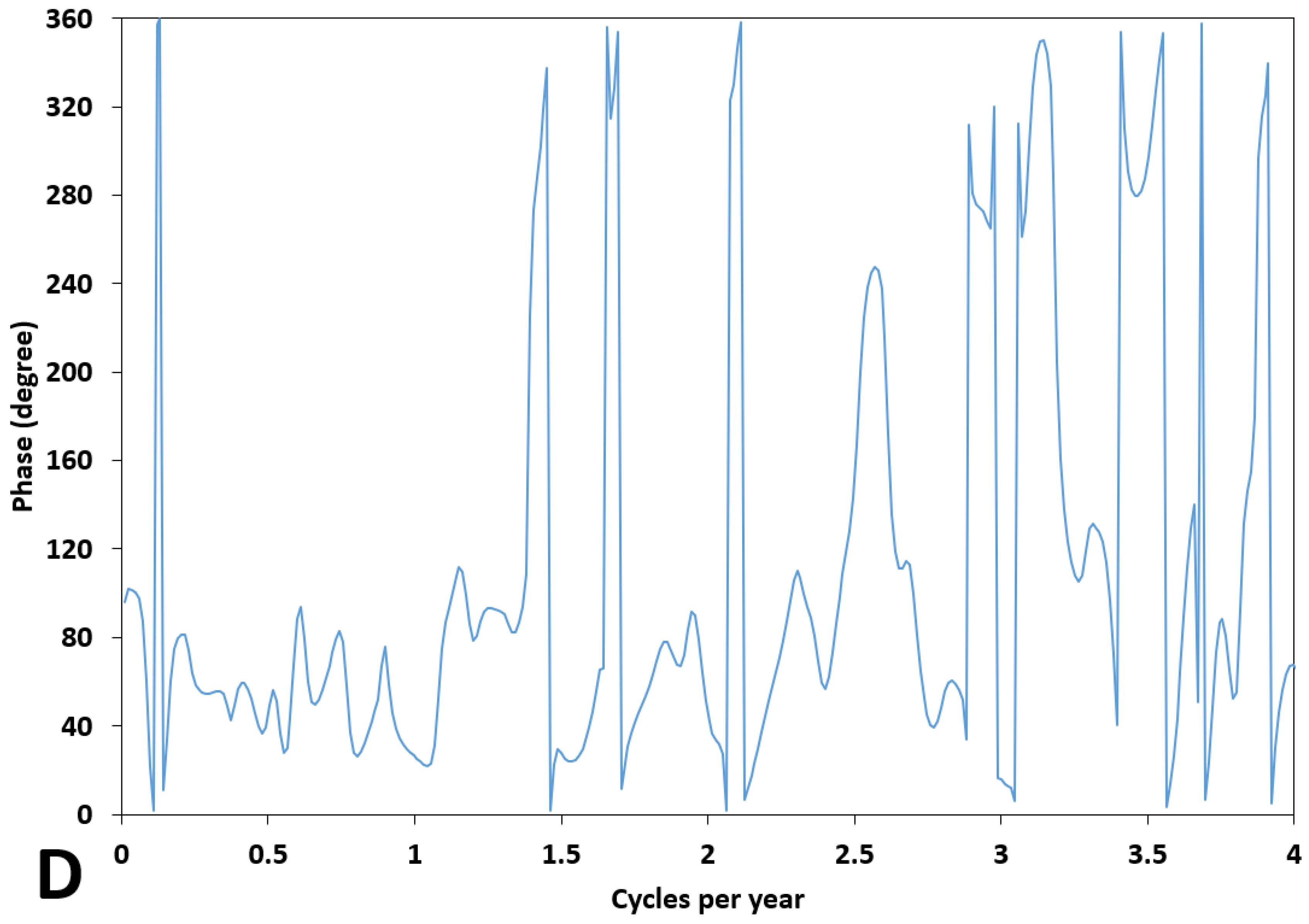
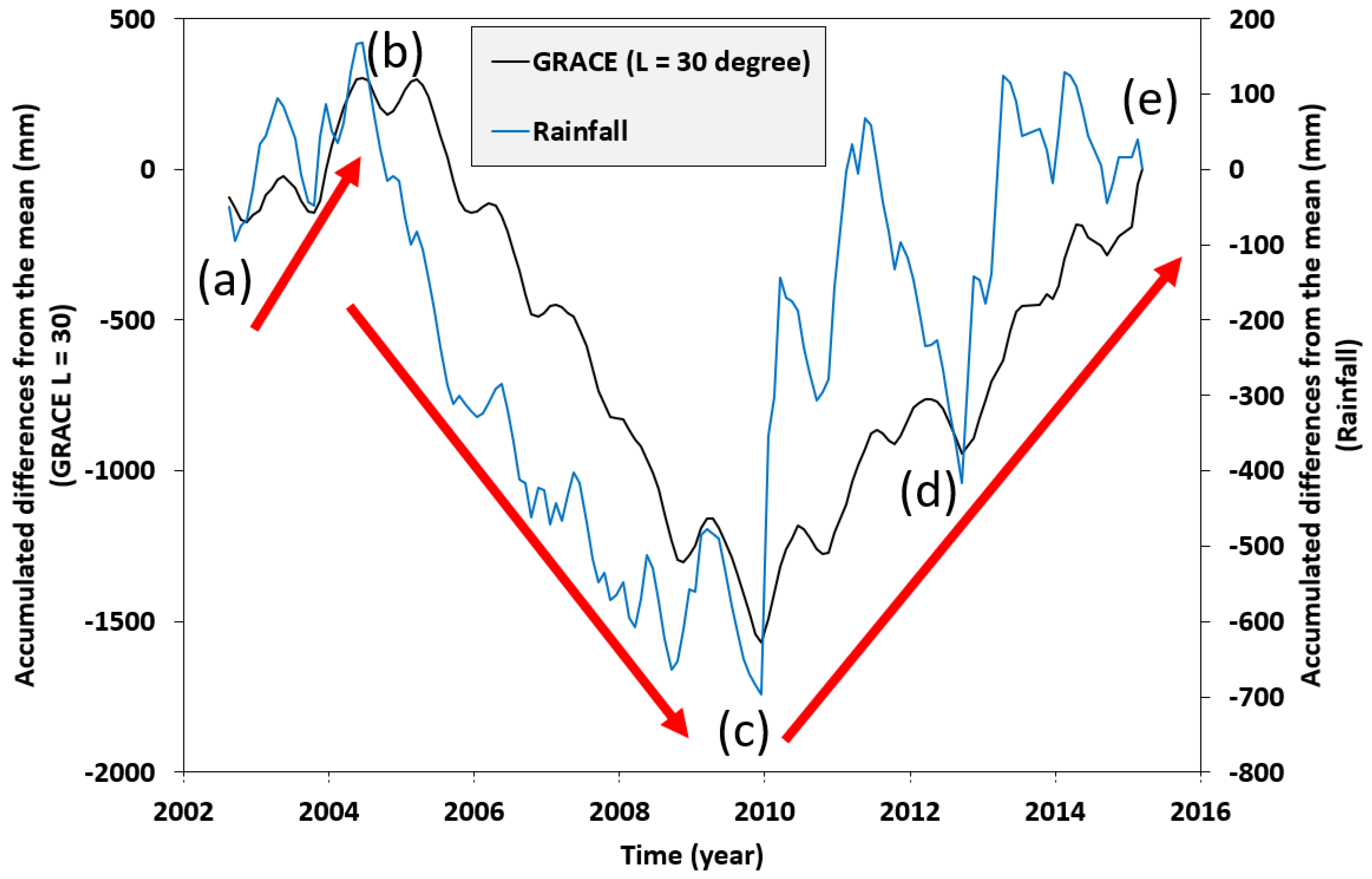
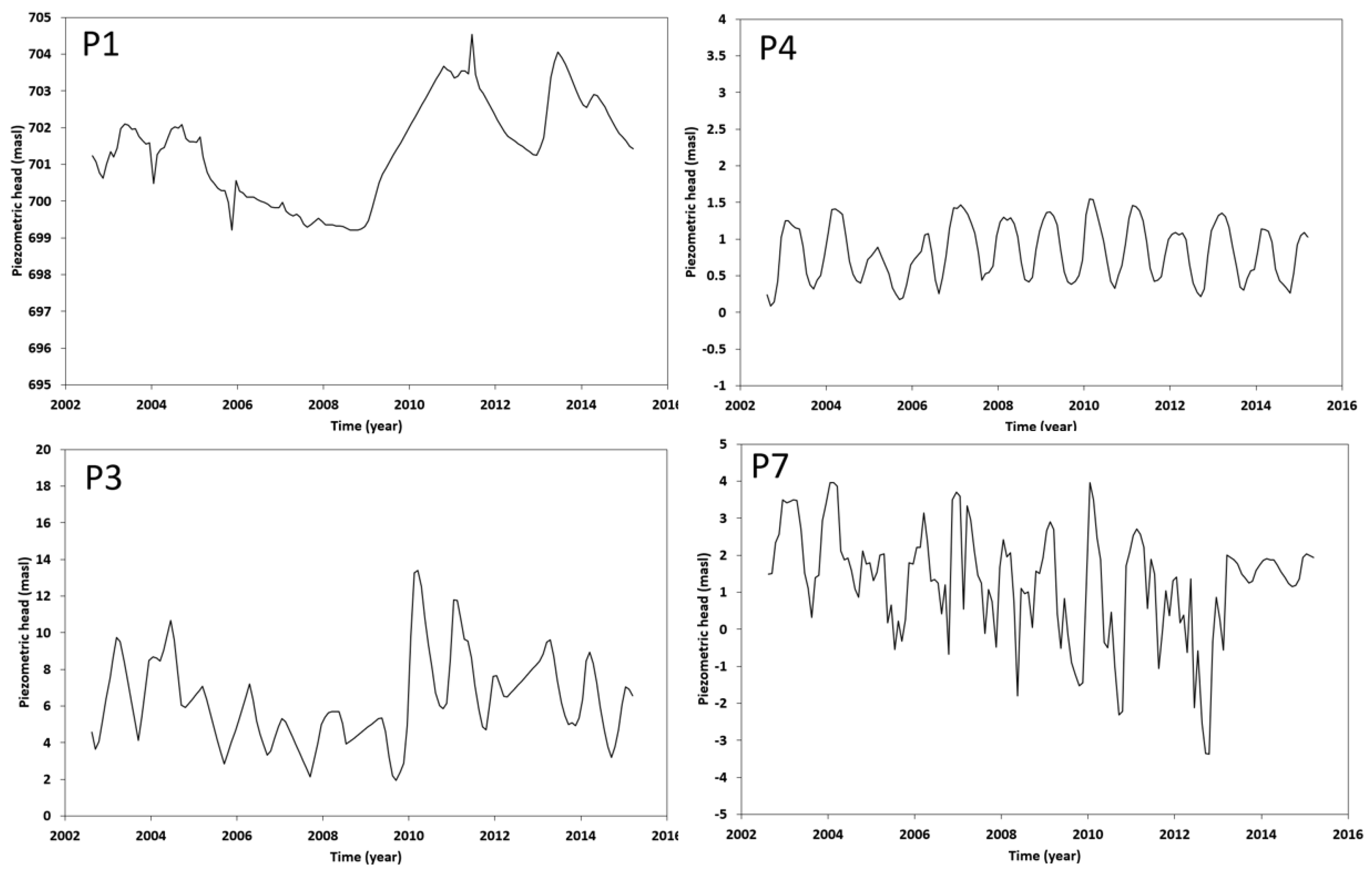
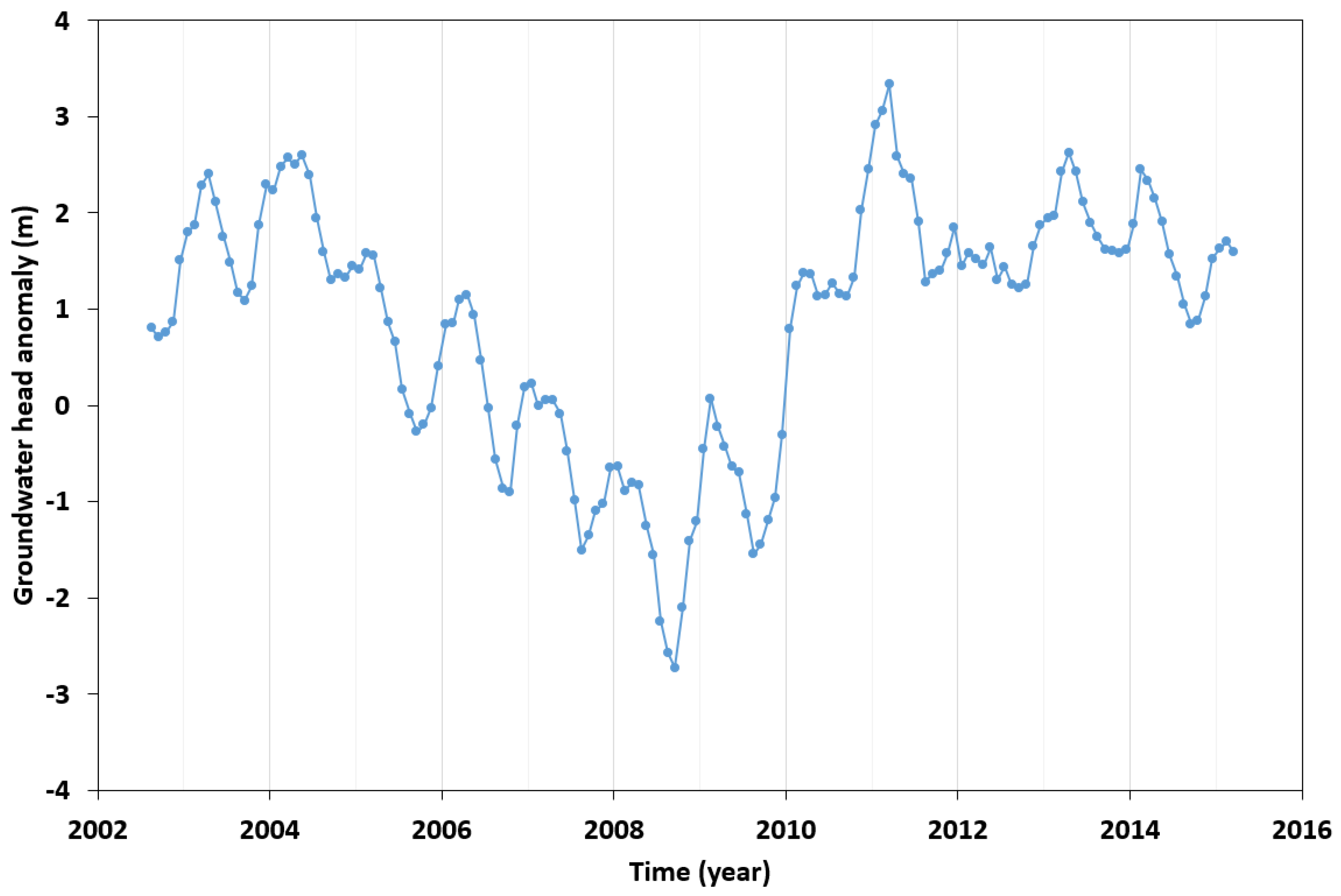
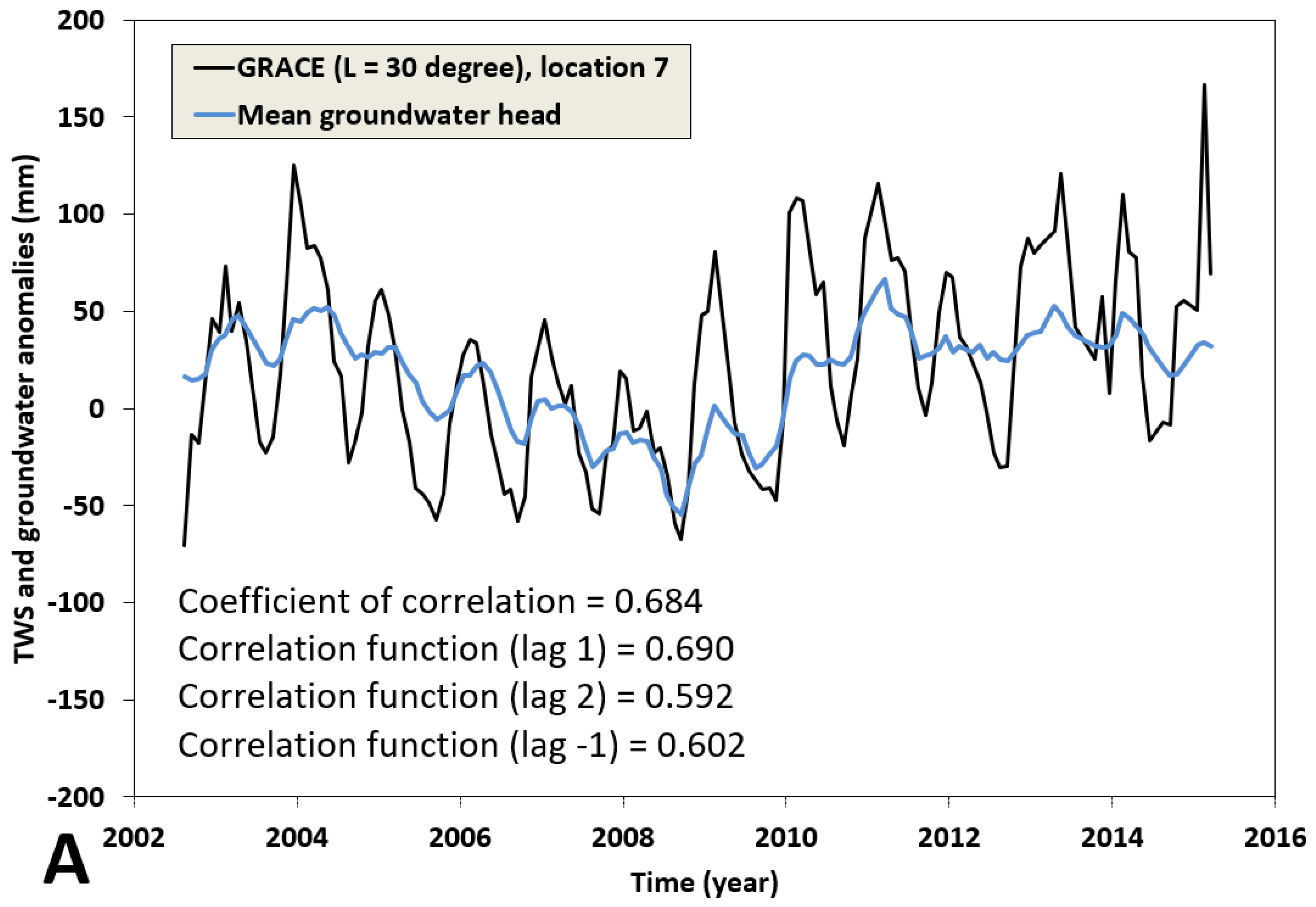
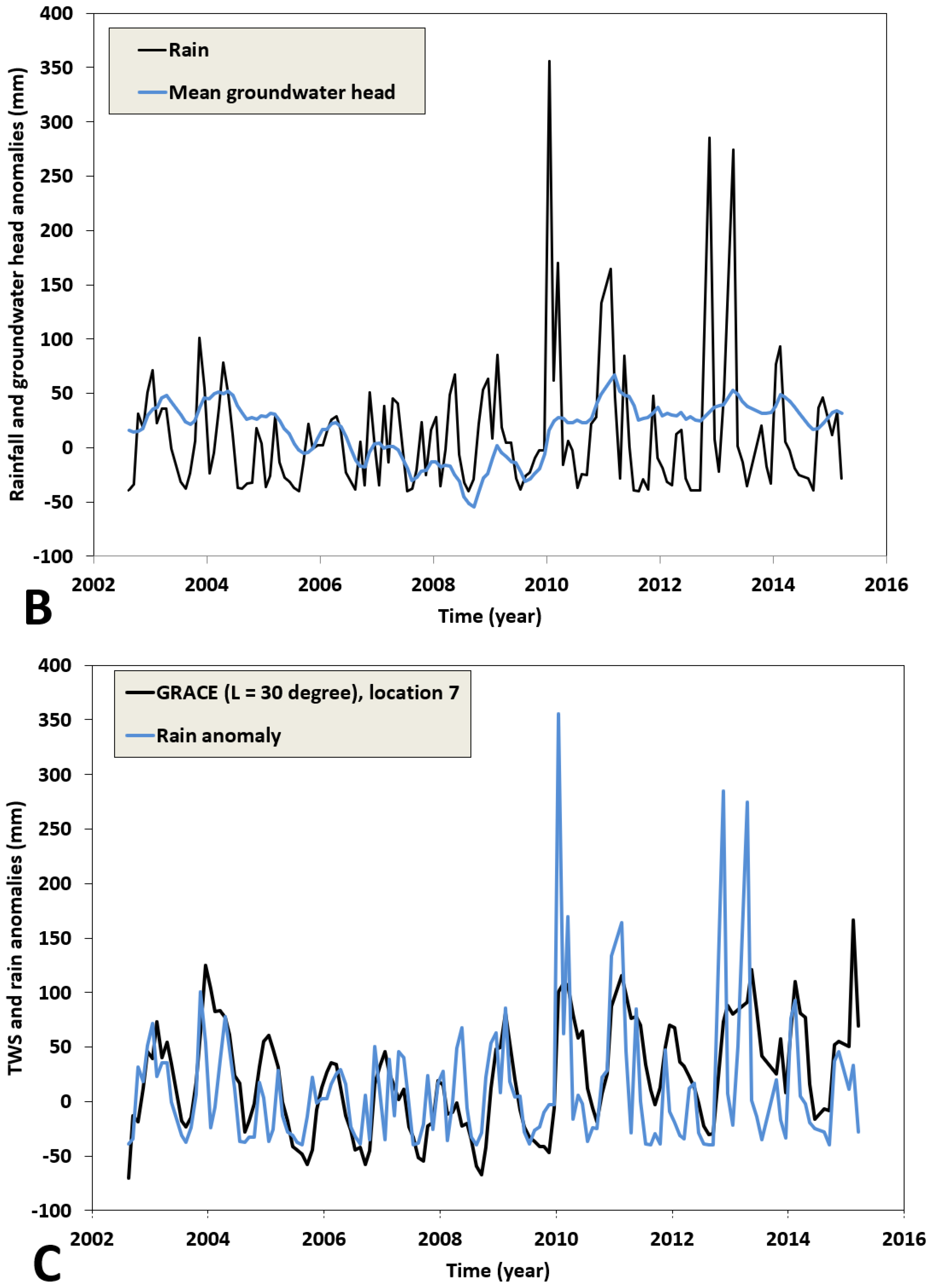
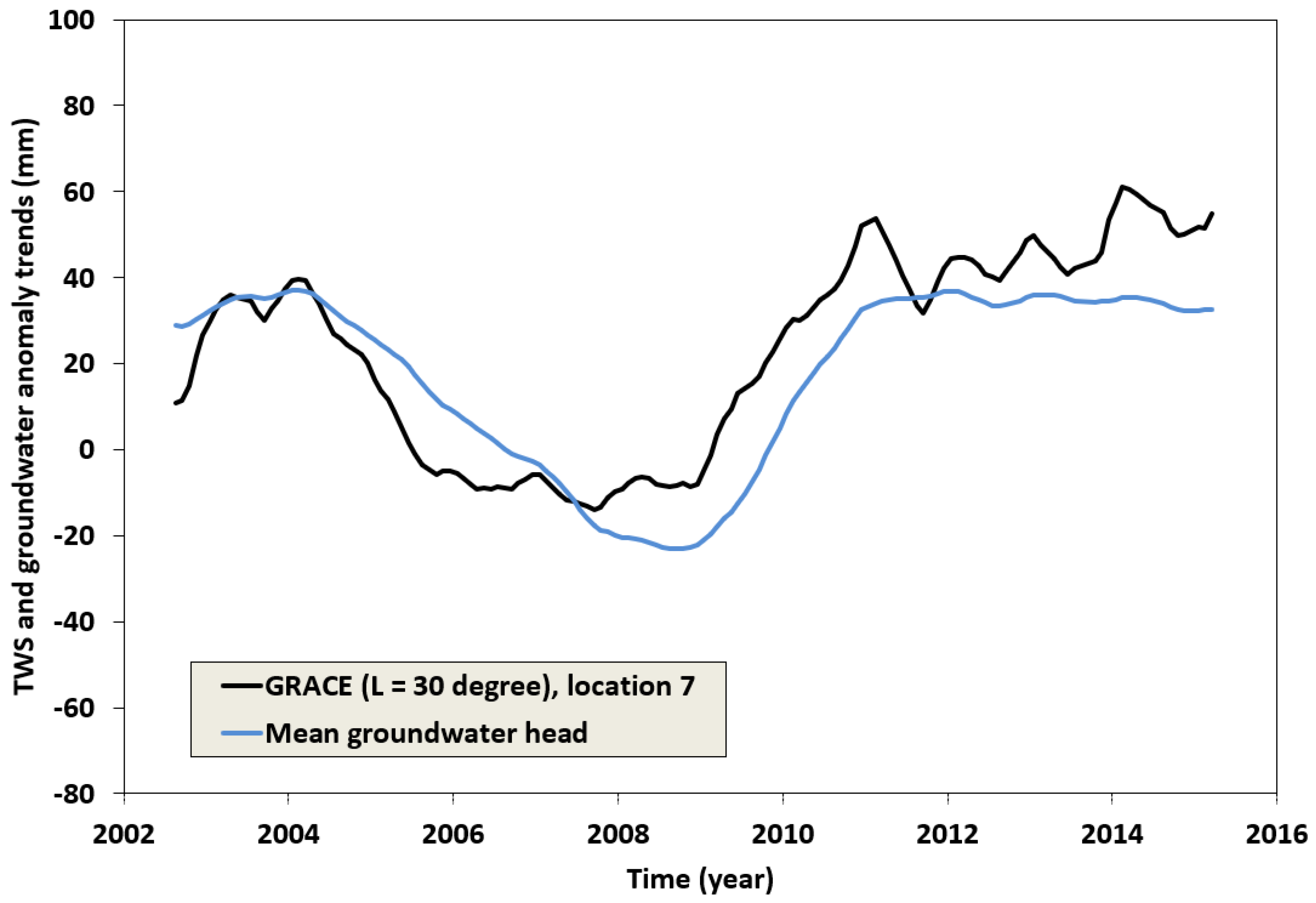
4. Analysis and Discussion of the Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CDMS | Cumulative departures from the mean statistic |
| CRD | Cumulative rainfall departure |
| CSR | Centre for Space Research |
| D | Water stored in dams |
| EGSIEM | European Gravity Service for Improved Emergency Management |
| ET | Evapotranspiration |
| Gd | Groundwater discharge |
| GF | Gravity field |
| GRACE | Gravity Recovery and Climate Experiment |
| GRACE-FO | Gravity Recovery and Climate Experiment Follow-on |
| GRGS | Groupe de Recherche en Geodesie Spatiale |
| GWS | Groundwater storage |
| I | Infiltration water |
| L | Maximum harmonic degree of the spherical harmonic expansion of the geoid |
| NAO | North Atlantic Oscillation |
| P | Precipitation water |
| R | Runoff water |
| SE | Standard error or standard deviation (square root of the error variance) |
| SGZ | Groundwater zone or saturated zone |
| SR | Spatial resolution |
| SZ | Soil zone |
| SWE | Snow water equivalent |
| SWS | Soil water storage |
| TWS | Terrestrial water storage |
| VZ | Vadose zone |
References
- Darbeheshti, N.; Wöske, F.; Weigelt, M.; Wu, H.; Mccullough, C. Comparison of Spacewise and Timewise Methods for GRACE Gravity Field Recovery. In Geodetic Time Series Analysis in Earth Sciences; Montillet, J.P., Bos, M., Eds.; Springer Geophysics; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef]
- Darbeheshti, N.; Zhou, L.; Tregoning, P.; McClusky, S.; Purcell, A. The ANU GRACE visualization web portal. Comput. Geosci. 2013, 52, 227–233. [Google Scholar] [CrossRef]
- EGSIEM. European Gravity Service for Improved Emergency Management Report No. 11. 2018. Available online: http://www.egsiem.eu/images/Newsletters/EGSIEM_newsletter_no_11.pdf (accessed on 30 March 2022).
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detec-tion using GRACE. J. Geophys. Res. 1998, 30, 205–229. [Google Scholar] [CrossRef]
- Seo, K.W.; Wilson, C.R.; Famiglietti, J.S.; Chen, J.L.; Rodell, M. Terrestrial water mass load changes from Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2006, 42, W05417. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48, W04531. [Google Scholar] [CrossRef]
- Frappart, F.; Ramillien, G. Monitoring Groundwater Storage Changes Using the Gravity Recovery and Climate Experiment (GRACE) Satellite Mission: A Review. Remote Sens. 2018, 10, 829. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S. An analysis of terrestrial water storage variations in Illinois with implications for the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2001, 37, 1327–1339. [Google Scholar] [CrossRef]
- García-García, D.; Ummenhofer, C.C.; Zlotnicki, V. Australian water mass variations from GRACE data linked to Indo-Pacific climate variability. Remote Sens. Environ. 2011, 115, 2175–2183. [Google Scholar] [CrossRef]
- Longuevergne, L.; Scanlon, B.R.; Wilson, C.R. GRACE Hydrological estimates for small basins: Evaluating processing approaches on the High Plains Aquifer, USA. Water Resour. Res. 2011, 46, W11517. [Google Scholar] [CrossRef]
- Shamsudduha, M.; Taylor, R.G.; Longuevergne, L. Monitoring groundwater storage changes in the highly seasonal humid tropics: Validation of GRACE measurements in the Bengal Basin. Water Resour. Res. 2012, 48, W02508. [Google Scholar] [CrossRef]
- Alshehri, F.; Mohamed, A. Analysis of Groundwater Storage Fluctuations Using GRACE and Remote Sensing Data in Wadi As-Sirhan, Northern Saudi Arabia. Water 2023, 15, 282. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S. The potential for satellite-based monitoring of groundwater storage changes using GRACE: The High Plains aquifer, Central US. J. Hydrol. 2002, 263, 245–256. [Google Scholar] [CrossRef]
- Strassberg, G.; Scanlon, B.R.; Rodell, M. Comparison of seasonal terrestrial water storage variations from GRACE with groundwater-level measurements from the High Plains Aquifer (USA). Geophys. Res. Lett. 2007, 34, L14402. [Google Scholar] [CrossRef]
- Döll, P.; Hoffmann-Dobrev, H.; Portmann, F.T.; Siebert, S.; Eicker, A.; Rodell, M.; Strassberg, G.; Scanlon, B.R. Impact of water withdrawals from groundwater and surface water on continental water storage variations. J. Geodyn. 2012, 59, 143–156. [Google Scholar] [CrossRef]
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; Van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M.; et al. Ground water and climate change. Nat. Clim. Chang. 2013, 3, 322–329. [Google Scholar] [CrossRef]
- Russo, T.A.; Lall, U. Depletion and response of deep groundwater to climate-induced pumping variability. Nat. Geosci. 2017, 10, 105–108. [Google Scholar] [CrossRef]
- Farr, T.G.; Jones, C.; Liu, Z. Progress Report: Subsidence in the Central Valley, California. 2015. Available online: https://cawaterlibrary.net/wp-content/uploads/2017/05/JPL-subsidence-report-final-for-public-dec-2016.pdf (accessed on 14 September 2015).
- Miller, M.M.; Shirzaei, M.; Argus, D. Aquifer mechanical properties and decelerated compaction in Tucson, Arizona. J. Geophys. Res. Solid Earth 2017, 122, 8402–8416. [Google Scholar] [CrossRef]
- Galloway, D.L.; Burbey, T.J. Review: Regional land subsidence accompanying groundwater extraction. Hydrogeol. J. 2011, 19, 1459–1486. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Lo, M.; Ho, S.L.; Bethune, J.; Anderson, K.J.; Syed, T.H.; Swenson, S.C.; de Linage, C.R.; Rodell, M. Satellites measure recent rates of groundwater depletion in California’s Central Valley. Geophys. Res. Lett. 2011, 38, L03403. [Google Scholar] [CrossRef]
- Gorelick, S.M.; Zheng, C. Global Change and the Groundwater Management Challenge. Water Resour. Res. 2015, 51, 3031–3051. [Google Scholar] [CrossRef]
- Richey, A.S.; Thomas, B.F.; Lo, M.H.; Reager, J.T.; Famiglietti, J.S.; Voss, K.; Swenson, S.; Rodell, M. Quantifying renewable groundwater stress with GRACE. Water Resour. Res. 2005, 51, 5217–5238. [Google Scholar] [CrossRef] [PubMed]
- Van Loon, A.F.; Kumar, R.; Mishra, V. Testing the use of standardized indices and GRACE satellite data to estimate the European 2015 groundwater drought in near-real time. Hydrol. Earth Syst. Sci. 2017, 21, 1947–1971. [Google Scholar] [CrossRef]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to Understanding Climate Change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef] [PubMed]
- Lemoine, J.-M.; Bourgogne, S.; Bruinsma, S.; Gégout, P.; Reinquin, F.; Biancale, R. GRACE RL03-v2 Monthly Time Series of Solutions from CNES/GRGS; European Geosciences Union: Vienna, Austria, 2015; id. 1 4461.
- Seo, K.-W.; Oh, S.; Eom, J.; Chen, J.; Wilson, C.R. Constrained Linear Deconvolution of GRACE Anomalies to Correct Spatial Leakage. Remote Sens. 2020, 12, 1798. [Google Scholar] [CrossRef]
- Vishwakarma, B.D.; Devaraju, B.; Sneeuw, N. What is the spatial resolution of GRACE satellite products in Hydrology? Remote Sens. 2018, 10, 852. [Google Scholar] [CrossRef]
- Chilès, J.-P.; Delfiner, P. Geostatistics: Modeling Spatial Uncertainty, 2nd ed.; Wiley: Hoboken, NJ, USA, 2012; 699p. [Google Scholar]
- Bevington, P.R.; Robinson, D.K. Data Reduction and Error Analysis for The Physical Sciences, 2nd ed.; WCB-McGraw-Hill: New York, NY, USA, 1996; 328p. [Google Scholar]
- Boergens, E.; Kvas, A.; Eicker, A.; Dobslaw, H.; Schawohl, L.; Dahle, C.; Murböck, M.; Flechtner, F. Uncertainties of GRACE-based terrestrial water storage anomalies for arbitrary averaging regions. J. Geophys. Res. Solid Earth 2022, 127, e2021JB022081. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33, L08402. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Famiglietti, J.S.; Rodell, M. Attenuation effect on seasonal basin-scale water storage changes from GRACE time-variable gravity. J. Geod. 2007, 81, 237–245. [Google Scholar] [CrossRef]
- Bruinsma, S.; Lemoine, J.-M.; Biancale, R.; Valès, N. CNES/GRGS 10-day gravity field models release 2 and their evaluation. Adv. Space Res. 2010, 45, 587–601. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Narasimhan, T. Hydrological Cycle Water Budgets in the Encyclopedia of Inland Waters; Likens, G.E., Ed.; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Weber, K.; Stewart, M. A critical analysis of the cumulative rainfall departure concept. Ground Water 2004, 42, 935–938. [Google Scholar]
- Micale, F.; Cammalleri, C. Drought News August 2014, Report from the European Drought Observatory. 2014. Available online: https://edo.jrc.ec.europa.eu/documents/news/EDODroughtNews201408.pdf (accessed on 30 March 2022).
- Jin, S.; Zou, F. Re-Estimation of Glacier Mass Loss in Greenland from GRACE with Correction of Land-Ocean Leakage Effects. Glob. Planet. Chang. 2015, 135, 170–178. [Google Scholar] [CrossRef]
- Reager, J.T.; Famiglietti, J.S. Characteristic mega-basin water storage behavior using GRACE. Water Resour. Res. 2013, 49, 3314–3329. [Google Scholar] [CrossRef]
- Herrera, S.; Gutiérrez, J.M.; Ancell, R.; Pons, M.R.; Frías, M.D.; Fernández, J. Development and Analysis of a 50-year high-resolution daily gridded precipitation dataset over Spain (Spain02). Int. J. Climatol. 2012, 32, 74–85. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Li, J.; Zhang, Z. Reducing Leakage Error in GRACE-Observed Long-Term Ice Mass Change. J. Geod. 2015, 89, 925–940. [Google Scholar] [CrossRef]
- Ospina, D.L.; Vargas, C.A. Monitoring runoff coefficients and groundwater levels using data from GRACE, GLDAS, and hydrometeorological stations: Analysis of a Colombian foreland basin. Hydrogeol. J. 2018, 26, 2769–2779. [Google Scholar] [CrossRef]
- Pardo-Igúzquiza, E.; Rodríguez-Tovar, F.J. Spectral and cross-spectral analysis of uneven time series with the smoothed Lomb-Scargle periodogram and Monte Carlo evaluation of statistical significance. Comput. Geosci. 2012, 49, 207–216. [Google Scholar] [CrossRef]
- Sumner, G.; Homar, V.; Ramis, C. Precipitation seasonality in eastern and southern coastal Spain. Int. J. Climatol. 2001, 21, 219–247. [Google Scholar] [CrossRef]
- Pozo-Vázquez, D.; Esteban-Parra, M.J.; Rodrigo, F.S.; Castro-Díez, Y. An analysis of the variability of the North Atlantic Oscillation in the time and the frequency domains. Int. J. Climatol. 2000, 20, 1675–1692. [Google Scholar] [CrossRef]
- Hurrell, J.M.; van Loon, H. Decadal variations in climate associated with the North Atlantic Oscillation. Clim. Chang. 1997, 36, 301–326. [Google Scholar] [CrossRef]
- García-Herrera, R.; Paredes, D.; Trigo, R.M.; Trigo, I.F.; Hernandez, E.; Barriopedro, D.; Mendes, M.A. The Outstanding 2004/05 Drought in the Iberian Peninsula: Associated Atmospheric Circulation. J. Hydrometeorol. 2007, 8, 483–498. [Google Scholar] [CrossRef]
- Borrego-Marín, M.M.; Gutiérrez-Martín, C.; Berbel, J. Water Productivity under Drought Conditions Estimated Using SEEA-Water. Water 2016, 8, 138. [Google Scholar] [CrossRef]
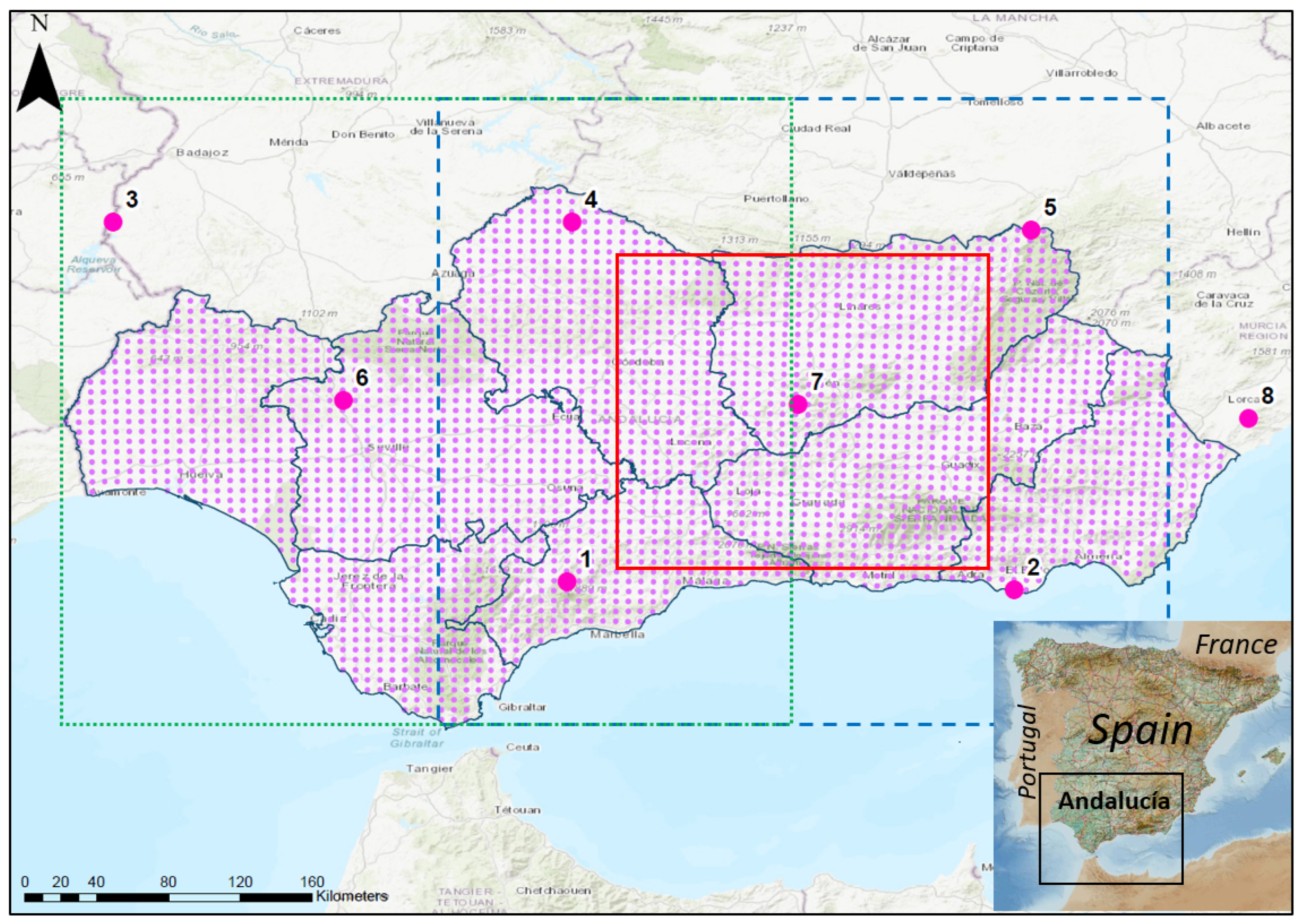


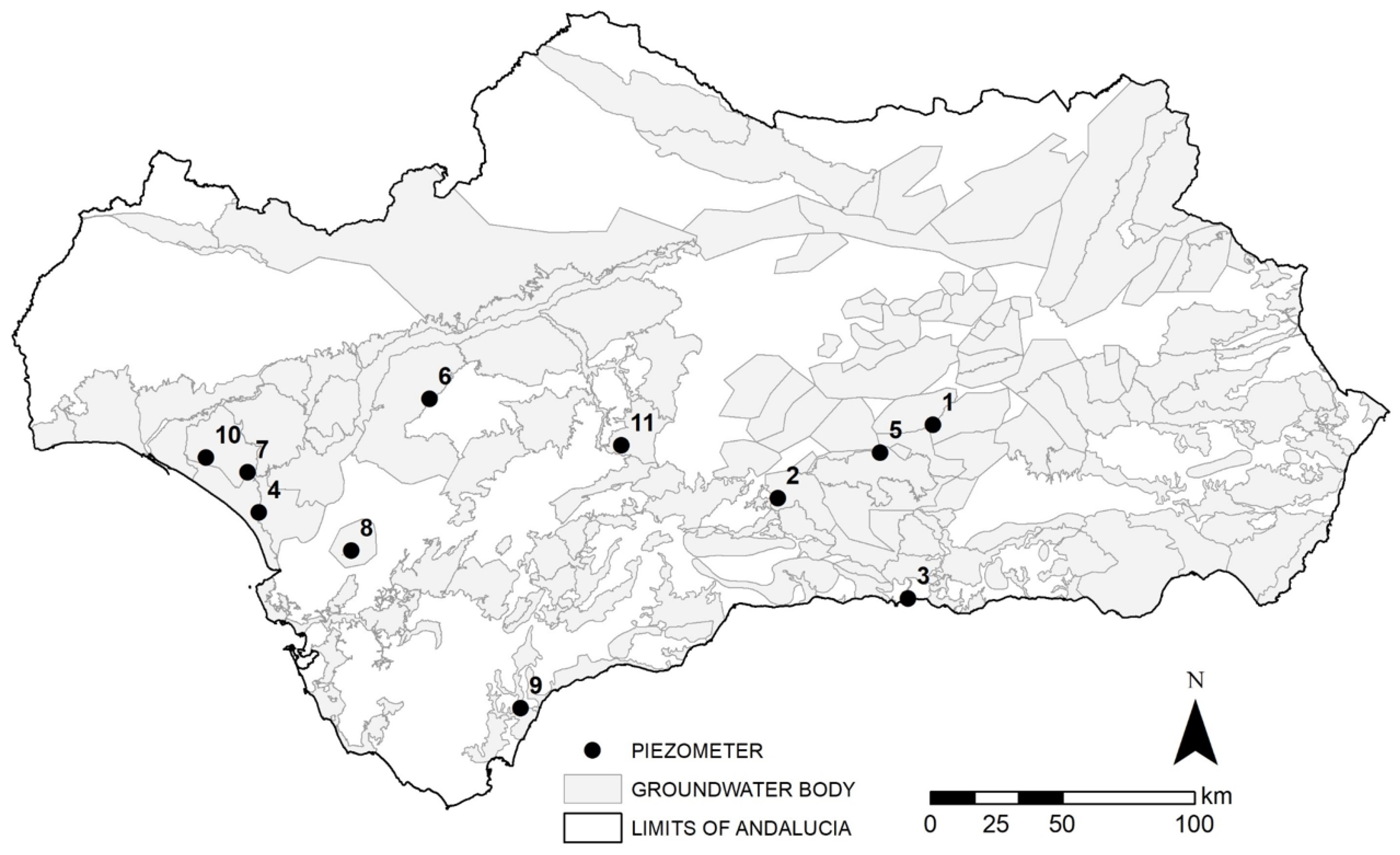

| Point | Longitude (Degree) | Latitude (Degree) |
|---|---|---|
| 1 | −5.004 | 36.745 |
| 2 | −2.763 | 36.701 |
| 3 | −7.278 | 38.543 |
| 4 | −4.978 | 38.545 |
| 5 | −2.678 | 38.501 |
| 6 | −6.123 | 37.651 |
| 7 | −3.845 | 37.628 |
| 8 | −1.588 | 37.562 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pardo-Igúzquiza, E.; Montillet, J.-P.; Sánchez-Morales, J.; Dowd, P.A.; Luque-Espinar, J.A.; Darbeheshti, N.; Rodríguez-Tovar, F.J. Assessing Terrestrial Water Storage Variations in Southern Spain Using Rainfall Estimates and GRACE Data. Hydrology 2023, 10, 187. https://doi.org/10.3390/hydrology10090187
Pardo-Igúzquiza E, Montillet J-P, Sánchez-Morales J, Dowd PA, Luque-Espinar JA, Darbeheshti N, Rodríguez-Tovar FJ. Assessing Terrestrial Water Storage Variations in Southern Spain Using Rainfall Estimates and GRACE Data. Hydrology. 2023; 10(9):187. https://doi.org/10.3390/hydrology10090187
Chicago/Turabian StylePardo-Igúzquiza, Eulogio, Jean-Philippe Montillet, José Sánchez-Morales, Peter A. Dowd, Juan Antonio Luque-Espinar, Neda Darbeheshti, and Francisco Javier Rodríguez-Tovar. 2023. "Assessing Terrestrial Water Storage Variations in Southern Spain Using Rainfall Estimates and GRACE Data" Hydrology 10, no. 9: 187. https://doi.org/10.3390/hydrology10090187
APA StylePardo-Igúzquiza, E., Montillet, J.-P., Sánchez-Morales, J., Dowd, P. A., Luque-Espinar, J. A., Darbeheshti, N., & Rodríguez-Tovar, F. J. (2023). Assessing Terrestrial Water Storage Variations in Southern Spain Using Rainfall Estimates and GRACE Data. Hydrology, 10(9), 187. https://doi.org/10.3390/hydrology10090187






